Abstract
Background
Image-based computational models are widely used to determine atherosclerotic plaque stress/strain conditions and investigate their association with plaque progression and rupture. However, patient-specific vessel material properties are in general lacking in those models, limiting the accuracy of their stress/strain measurements. A noninvasive approach of combining in vivo 3D multi-contrast and Cine magnetic resonance imaging (MRI) and computational modeling was introduced to quantify patient-specific carotid plaque material properties for potential plaque model improvements. Vessel material property variation in patients, along vessel segment, and between baseline and follow up were investigated.
Methods
In vivo 3D multi-contrast and Cine MRI carotid plaque data were acquired from 8 patients with follow-up (18 months) with written informed consent obtained. 3D thin-layer models and an established iterative procedure were used to determine parameter values of the Mooney-Rivlin models for the 81slices from 16 plaque samples. Effective Young’s Modulus (YM) values were calculated for comparison and analysis.
Results
Average Effective Young’s Modulus (YM) and circumferential shrinkage rate (C-Shrink) value of the 81 slices was 411kPa and 5.62%, respectively. Slice YM value varied from 70 kPa (softest) to 1284 kPa (stiffest), a 1734% difference. Average slice YM values by vessel varied from 109 kPa (softest) to 922 kPa (stiffest), a 746% difference. Location-wise, the maximum slice YM variation rate within a vessel was 311% (149 kPa vs. 613 kPa). The average slice YM variation rate for the 16 vessels was 134%. The average variation of YM values for all patients from baseline to follow up was 61.0%. The range of the variation of YM values was [-28.4%, 215%]. For plaque progression study, YM at follow-up showed negative correlation with plaque progression measured by wall thickness increase (WTI) (r = -0.7764, p = 0.0235). Wall thickness at baseline correlated with WTI negatively, with r = -0.5253 (p = 0.1813). Plaque burden at baseline correlated with YM change between baseline and follow-up, with r = 0.5939 (p = 0.1205).
Conclusion
In vivo carotid vessel material properties have large variations from patient to patient, along the diseased segment within a patient, and with time. The use of patient-specific, location specific and time-specific material properties in plaque models could potentially improve the accuracy of model stress/strain calculations.
1. Introduction
Cardiovascular disease is a major cause of death in the world [1]. A large number of fatal clinical events, such as strokes and heart attacks are caused by vulnerable atherosclerotic plaque rupture [2–5]. It is believed that mechanical forces play a very important role in plaque progression and rupture processes [6]. With the advances of medical imaging technologies [7–8], image-based computational models have been introduced to calculate plaque stress/strain conditions and investigate their association with plaque progression and rupture [9–20]. However, the accuracy of the computational results is heavily dependent on the data and assumptions used by those models. Data needed for image-based plaque computational models include: a) plaque morphology and components; b) vessel and plaque component material properties; and c) blood flow and pressure conditions [6]. While most researchers used patient-specific plaque morphology data, their computational models lack patient-specific vessel material properties [6, 9–23]. Non-invasive techniques to obtain in vivo patient-specific vessel material properties are needed to further improve in vivo image-based plaque models [24–26].
Considerable efforts have been made by several research groups to quantify mechanical material properties of atherosclerotic vessels. Holzapfel et al. used cyclic quasistatic uniaxial tension tests in axial and circumferential directions for different components of atherosclerotic lesions from human atherosclerotic iliac arteries [27]. Anisotropic and highly nonlinear tissue components properties as well as considerable interspecimen differences were identified by the experimental data of individual samples. The circumferential direction of the fibrous cap demonstrated the lowest fracture stress (254.8 +/- 79.8 kPa at stretch 1.182 +/- 0.1) of all intimal tissues. The adventitia exhibited the highest and the nondiseased media the lowest mechanical strength on average [27]. Different layers displayed different direction-dependent mechanical behaviors, which are of vital importance to the realistic computational models and accurate stress/strain prediction [16, 27–28]. Williamson et al. reported that artery wall stresses have low sensitivities for material properties variability [29]. In a histology-based model, a +/- 50% variation in elastic modulus was found to lead to less than a 10% change in artery wall stress at the site of rupture [29]. Tang et al. investigated the effects of plaque structure and material properties on stress behaviors in human atherosclerotic plaques by using 3D FSI models, and reported that the softer materials result in higher stress values [30]. Teng et al. performed uniaxial tests using different plaque components, axial and circumferential oriented adventitia, media and intact specimens prepared from human carotid arteries [31–32]. Most of the material properties investigations in the literature used ex vivo specimens and in vitro experimental techniques. Nieuwstadt et al. performed a numerical feasibility study for carotid plaque elasticity estimation using ultrasound elastography, MRI, and inverse FEA [24]. They were able to estimate material coefficients for carotid intima and lipid-rich necrotic core (lipid) with histology validations. Smoljkić et al. proposed a non-invasive, energy-based assessment of patient-specific material properties of arterial tissue [25]. Their results showed that imposing conditions on strain energy can provide a good estimation of carotid material properties from the non-invasively measured pressure and diameter data. Czernuszewicz et al. performed some preliminary study of non-invasive in vivo characterization of human carotid plaques with acoustic radiation force impulse ultrasound. Their method was able to differentiate soft tissues from stiffer tissues with histological validations [26]. In vivo vessels material properties and patient-specific material properties are still scarce in the current literature.
For plaque models based on in vivo image data, shrinkage rate (axial shrinkage and circumferential shrinkage) should be determined so that the in vivo vessel geometry could be shrunk to its “no-load” shape from which loaded stress/strain conditions could be obtained. Tang et al. and Yang et al. introduced a shrink-stretch process in their 3D fluid-structure interaction (FSI) models with in vivo plaque data [16, 33–35]. Their shrink-stretch process include: a) axial and circumferential shrink the vessel to get the numerical starting geometry; and b) axial stretch and circumferential pressurization were applied to recover the vessel in vivo shape. The axial shrinkage was 9% so that the in vivo vessel length could be recovered when a 10% axial stretch were applied. The Circumferential shrinkages of vessel lumen and outer wall were determined so that: a) the vessel volume was conserved; b) vessel shape after pressurization and 10% axial stretch recovered the original in vivo shape. Speelman et al. and Gee et al. also showed the importance and necessity of the pre-shrink process with their computed tomography (CT)-based simulations for abdominal aortic aneurysm [36–37]. Huang et al. reported a non-uniform shrink-stretch process which had better match with the in vivo vessel geometries [38]. Liu et al. introduced a non-invasive approach to quantify patient-specific vessel material properties and plaque circumferential shrinkage rate between vessel in vivo and “no-load” geometries [39]. Their material properties and circumferential shrinkage rate were calculated by 2D plaque models. Their results showed that effective Young’s Modulus (YM) from the 12 human carotid arteries varied from 137 kPa to 1435 kPa and vessel circumferential shrinkage to “no-load” condition varied from 6% to 32%. Overall, quantified patient-specific shrinkage rate using in vivo data are rare in the current literature.
In this paper, a non-invasive approach [39] of combining 3D multi-contrast MRI, in vivo Cine MRI and computational 3D thin-layer model [40] was used to quantify patient-specific carotid plaque material properties and circumferential shrinkage rates. The variation of the material properties among different subjects, within each diseased artery, and with time was investigated.
2. Methods
2.1 In vivo serial MRI data acquisition and segmentation
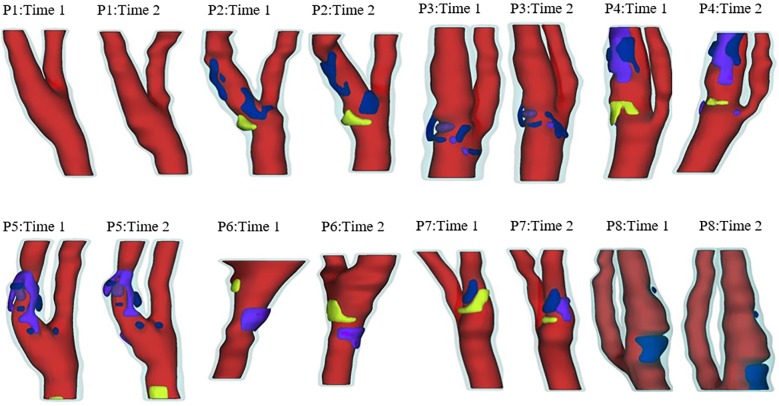
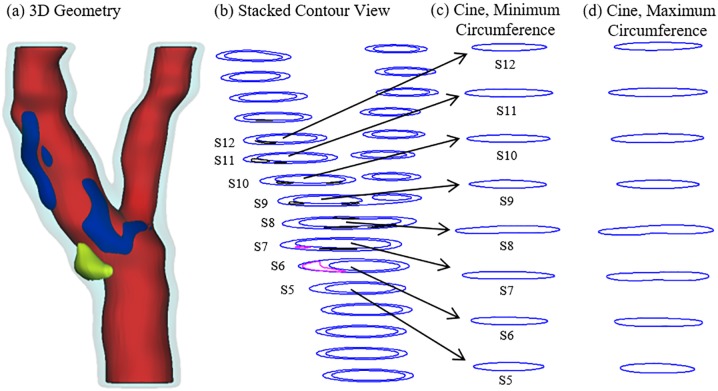
Serial MRI data of carotid atherosclerotic plaques from 8 patients (5 male, 3 female; age: 62–83, mean = 71; see Table 1 for details) were acquired at the University of Washington (UW), Seattle by the Vascular Imaging Laboratory (VIL) using protocols approved by the UW Institutional Review Board and with written informed consent obtained. For each patient, MRI slices at baseline (Time 1, T1) and follow-up (Time 2, T2, Scan time intervals were about 18 months) were matched up using vessel bifurcation, stenosis features and with careful review by the MRI group. For simplicity, the vessel segment assembled using the selected slices is called the plaque. Cuff systolic and diastolic arm pressure was recorded for modeling use. In vivo Cine and three-dimensional (3D) multi-contrast MR images of the carotid arteries were acquired using a 3.0T whole-body scanner (Philips Achieva, R2.6.1, Best, The Netherlands) and a dedicated 8-channel, phased array carotid coil. The carotid bifurcation was located on two-dimensional (2D) TOF (Time of Flight) and oblique black blood MR images. A 3.5cm region centered on the carotid bifurcation was imaged by high-resolution axial bright and black blood imaging. Detailed data acquisition and segmentation procedures were published before and are omitted here [10, 39]. For each patient, locations with Cine sequence and nearly-circular slices from 3D MRI were selected for calculating the material parameter values in the modified Mooney-Rivlin model used in our previous publications. Fig 1 gives plots of 16 re-constructed carotid plaques based on in vivo MRI data from 8 patients, each with 2 time points. Fig 2 gives a sample plaque with 3D MRI slices and matching Cine lumen contours at multiple locations corresponding to minimum and maximum pressure conditions. The Cine and 3D MRI sequences were designed with equal slice distance and matched using longitudinal position from the bifurcation.
Table 1. Patient information and pressure data at baseline and follow-up when available (Scan time intervals were about 18 months; L: left carotid artery; R: right carotid artery).
| Patients | Gender | Age | Weight (lbs) | Height | Pressure(mmHg) | Index Side |
|---|---|---|---|---|---|---|
| 1 | Female | 66 | 106 | 4'11" | T1 and T2 (120,80) | L |
| 2 | Male | 76 | 170 | 5'10" | T1(120,70); T2(141,72) | L |
| 3 | Male | 62 | 185 | 6'0" | T1(130,70); T2(143,80) | L |
| 4 | Female | 63 | 161 | 5'6'' | T1 and T2 (146,81) | L |
| 5 | Male | 63 | 140 | 6'2" | T1 and T2 (100,60) | L |
| 6 | Male | 83 | 180 | 5'8" | T1 and T2 (143,73) | R |
| 7 | Female | 70 | 140 | 5'7'' | T1 and T2 (143,90) | L |
| 8 | Male | 81 | 180 | 5'6" | T1 and T2 (143,65) | R |
Fig 1. 3D plots of re-constructions 3D geometries of the 16 plaques (8 time pairs).
Red: Lumen; Light blue: Vessel; Yellow: Lipid-rich core; Blue: Calcification; Dark Blue: Loose Matrix.
Fig 2. A human carotid plaque sample with matching Cine slices.
(a) 3D plaque geometry reconstructed from MRI; (b) Stacked contours; (c) Matching Cine contours with minimum circumference; (d) Matching Cine contours with maximum circumference.
2.2 The 3D thin-layer model to determine material parameter values
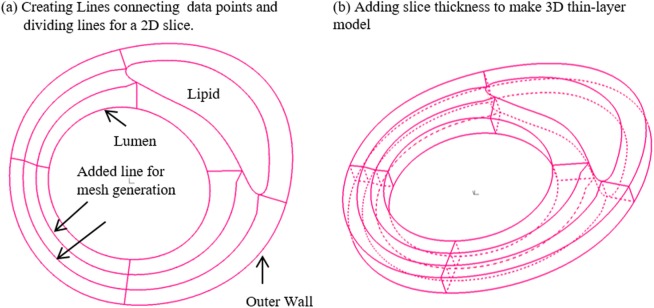
A 3D thin-layer modeling approach introduced by Huang et al. [40] was used to determine material parameter values in our selected material model. For every slice that Cine data was available, a thin slice thickness was added to make a 3D thin-layer model (see Fig 3). Then our established 3D model construction and mesh generation procedures with axial and circumferential shrink were applied in the material value determination process [40]. The carotid artery was assumed to be hyperelastic, isotropic, incompressible and homogeneous. The nonlinear modified Mooney-Rivlin (M-R) model was selected to describe the material properties of the vessel wall [41–42]. The strain energy function was given by:
| (1) |
| (2) |
where C = [Cij] = XTX is the right Cauchy-Green deformation tensor; I1 and I2 are the invariants of C; is the deformation gradient; c1, c2, D1 and D2 form the material parameter set. The modified Mooney-Rivlin model was selected because it was able to fit carotid artery vessel properties measured by uniaxial and biaxial mechanical testing data and good agreement was obtained [9, 43]. With our limited pressure data (only two pressure data points: maximum and minimum pressures), material parameter values could not be uniquely determined. According to our previous experiences [10, 16], we set c2 = 0 and D2 = 2. The c1/D1 value was adjusted. For lipid cores, we used parameter values in our previous publications: c1 = 0.5 kPa, D1 = 0.5 kPa, D2 = 0.5 [10].
Fig 3. 3D thin-layer model construction.
(a) Creating Lines connecting data points and dividing lines for a 2D slice; (b) Adding slice thickness to make 3D thin-layer model.
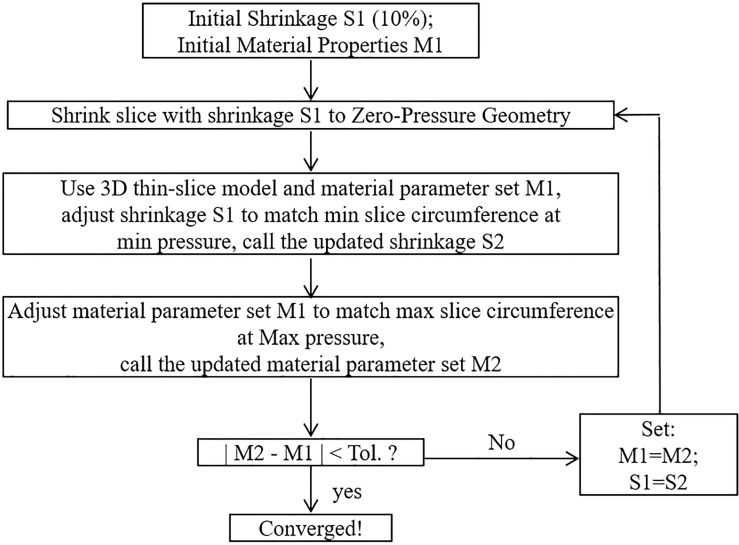
For each 3D thin-layer model, a 10% axial shrinkage rate was applied. Then an iterative procedure [39] was followed to adjust the parameter values in the modified M-R model and the circumferential shrinkage rate to match both maximum and minimum Cine lumen circumferences corresponding to systolic and diastolic pressures, respectively (see Fig 4 for details). Material parameters values c1 (36.6 kPa) and D1 (14.4kPa) from our previous paper [10] were used as initial estimates for each slice. The initial lumen circumferential shrinkage rate S1 was set to be 10%. The details of the iteration procedure are given in Fig 4. The 3D thin-layer model for each iteration was solved by ADINA (ADINA R & D, Watertown, MA).
Fig 4. The flow chart for the iterative procedure to determine material parameters and vessel circumferential shrinkage rate.
2.3 The 2D models for comparison purpose
To compare our 3D thin-layer model approach with 2D model approach, parameter values for Modified Mooney-Rivlin (MR) models and circumferential shrinkage values for the 81 slices were also calculated using 2D modeling method [29] with the iterative procedure given in Fig 4. The main difference between 2D model and 3D thin-layer model is that 2D model does not have axial stretch while 3D thin-layer model does which makes the 3D thin-layer model closer to full 3D models. Their differences are reported in Section 3.5.
2.4 Using an effective Young’s modulus as a stiffness indicator for material properties
The stress-stretch relationship for the Mooney-Rivlin model is given by:
| (3) |
where σ is Cauchy stress, and λ is stretch ratio. In order to facilitate comparison, it is easier to use a single parameter to compare vessel stiffness from different patients or slices. The effective Young’s modulus (YM) E for the stretch ratio interval [1.0, 1.3] is defined as:
| (4) |
The least-squares technique was used to calculate the YM values that best fit the M-R model.
2.5 Statistical method
For all correlation study related variables in Section 3.4, Shapiro-Wilk normality test showed no evidence of non-normal distribution. Standard student t-test was performed for possible correlations between plaque progression and material stiffness, plaque burden and wall thickness using our patient follow-up data. We also applied the Kolmogorov-Smirnov test to check the normality. A p-value 0.81 was obtained, still indicating no evidence of non-normality. In case the normality assumption was a concern, we calculated the correlation p-values under the non-parametric Spearman rank test (see 3.4), which does not require the normality assumption. The results were consistent with those by the parametric t-test.
3. Results
3.1 Overview of material parameter values, effective YM and circumferential shrinkage rates
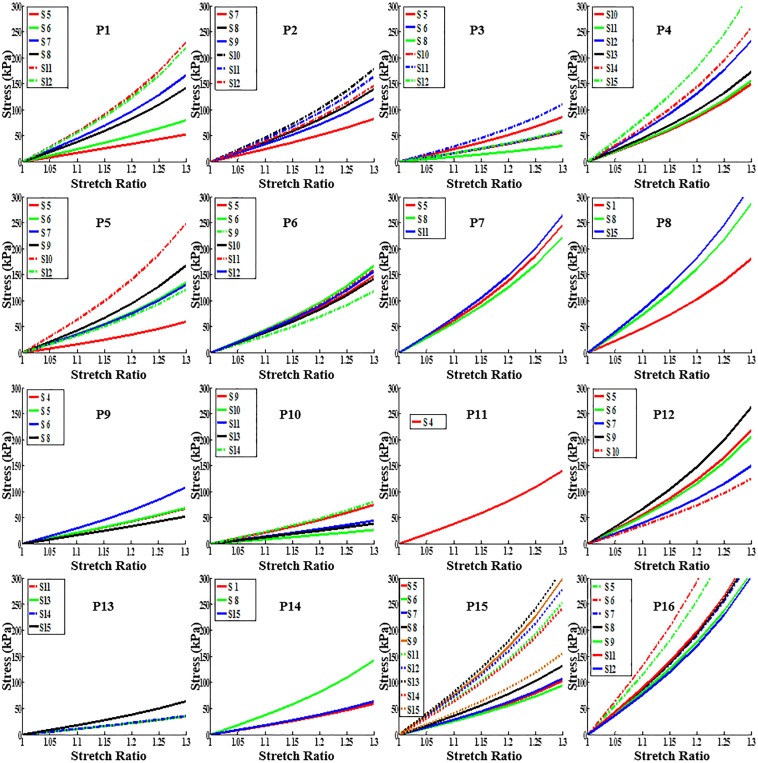
Fig 5 presents stress-stretch ratio plots of the 81 slices from the 16 plaque samples. For each plaque, choosing the stiffest (with maximum YM) and softest (with minimum YM) slices as representatives, the M-R model parameter values (C1 and D1), maximum and minimum Cine lumen circumferences (Cir-Max and Cir-Min), relative lumen circumferences variation rates (δ-Cir), maximum and minimum lumen pressure (P), effective Young’s modulus (YM) and circumferential shrinkage rate (C-Shrink) were provided by Table 2. The relative lumen circumferences variation rate (δ-Cir) is defined as:
| (5) |
Fig 5. Stress-stretch curves from Mooney-Rivlin Models using parameter values determined from Cine MRI for the 16 plaque samples studied.
Table 2. Maximum and minimum circumferences, pressure, material parameter and circumferential shrinkage values of the softest and stiffest slices from 16 plaque samples.
| Plaque | Slice | Cir-Max | Cir-Min | δ-Cir | P | C1 | D1 | YM | C-Shrink |
|---|---|---|---|---|---|---|---|---|---|
| (cm) | (cm) | (%) | (mmHg) | (kPa) | (kPa) | (kPa) | (%) | ||
| P1 | Softest | 2.374 | 2.003 | 15.6 | (120,80) | 27.1 | 0.47 | 139 | 15.3 |
| Stiffest | 2.025 | 1.944 | 4.01 | 37.0 | 27.9 | 564 | 1.59 | ||
| P2 | Softest | 3.086 | 2.744 | 11.1 | (120,80) | 31.0 | 4.39 | 212 | 13.8 |
| Stiffest | 1.970 | 1.877 | 4.76 | 36.5 | 19.2 | 443 | 2.87 | ||
| P3 | Softest | 2.936 | 2.498 | 14.9 | (120,70) | 13.0 | 1.10 | 78.8 | 19.7 |
| Stiffest | 2.420 | 2.197 | 9.23 | 25.0 | 11.1 | 275 | 6.67 | ||
| P4 | Softest | 2.352 | 2.141 | 8.97 | (141,72) | 30.0 | 16.3 | 370 | 3.19 |
| Stiffest | 2.095 | 1.988 | 5.15 | 50.0 | 40.2 | 797 | -1.11 | ||
| P5 | Softest | 2.460 | 2.160 | 12.2 | (130,70) | 15.0 | 5.52 | 149 | 12.6 |
| Stiffest | 2.017 | 1.906 | 5.50 | 45.0 | 28.6 | 613 | 0.09 | ||
| P6 | Softest | 2.275 | 2.038 | 10.4 | (143,80) | 30.0 | 10.9 | 296 | 7.29 |
| Stiffest | 2.167 | 2.030 | 6.34 | 36.0 | 17.4 | 416 | 1.70 | ||
| P7 | Softest | 2.509 | 2.355 | 6.16 | (146,81) | 40.0 | 25.6 | 548 | 1.31 |
| Stiffest | 3.172 | 2.931 | 7.59 | 45.0 | 31.4 | 651 | 3.75 | ||
| P8 | Softest | 2.553 | 2.321 | 9.12 | (146,81) | 35.0 | 20.1 | 448 | 4.87 |
| Stiffest | 1.485 | 1.430 | 3.68 | 60.0 | 36.6 | 797 | -1.55 | ||
| P9 | Softest | 1.659 | 1.441 | 13.2 | (100,60) | 25.0 | 1.10 | 138 | 9.87 |
| Stiffest | 2.850 | 2.638 | 7.46 | 30.0 | 9.11 | 272 | 3.83 | ||
| P10 | Softest | 1.080 | 0.922 | 14.6 | (100,60) | 13.0 | 0.45 | 69.9 | 13.8 |
| Stiffest | 1.445 | 1.320 | 8.65 | 25.0 | 6.03 | 205 | 5.78 | ||
| P11 | only one | 2.136 | 1.906 | 10.8 | (143,73) | 35.0 | 13.1 | 352 | 4.56 |
| P12 | Softest | 3.863 | 3.327 | 13.9 | (143,73) | 35.0 | 10.5 | 316 | 8.44 |
| Stiffest | 2.955 | 2.746 | 7.09 | 46.0 | 30.7 | 647 | 0.84 | ||
| P13 | Softest | 1.524 | 1.285 | 15.7 | (143,90) | 15.0 | 1.22 | 90.3 | 21.5 |
| Stiffest | 1.468 | 1.287 | 12.3 | 20.0 | 4.66 | 162 | 15.7 | ||
| P14 | Softest | 2.396 | 2.091 | 12.8 | (143,90) | 20.0 | 3.86 | 151 | 21.1 |
| Stiffest | 1.994 | 1.856 | 6.90 | 30.0 | 15.0 | 353 | 5.77 | ||
| P15 | Softest | 2.370 | 2.085 | 12.0 | (143,65) | 25.0 | 8.32 | 237 | 3.83 |
| Stiffest | 1.618 | 1.545 | 4.54 | 60.0 | 35.5 | 782 | -2.34 | ||
| P16 | Softest | 1.775 | 1.662 | 6.34 | (143,65) | 50.0 | 36.3 | 744 | -0.93 |
| Stiffest | 2.546 | 2.443 | 4.05 | 85.0 | 63.2 | 1284 | -2.74 | ||
| All | Ave | 2.192 | 1.997 | 8.91 | (133,74) | 35.5 | 17.3 | 411 | 5.62 |
Note: c2 = 0 and D2 = 2 were set for all cases. Ave: average from all 81 slices. Due to axial shrink applied to the 3D thin-layer model, some C-Shrink values in 3D thin-layer model were negative.
The averaged YM value of the 81 slices was 411kPa, which was consistent with the current literature [10–11, 28, 32]. The averaged C-Shrink and δ-Cir value of the 81 slices was 5.62%, 8.91%, respectively. Strong correlations were observed: a) negative correlation between δ-Cir values and YM values (r = -0.8083, p<0.0001); b) positive correlation between δ-Cir values and C-Shrink values (r = 0.8537, p<0.0001; c) negative correlation between YM and C-Shrink values (r = -0.8005, p<0.0001).
3.2. Plaque material properties have large patient-to-patient variations
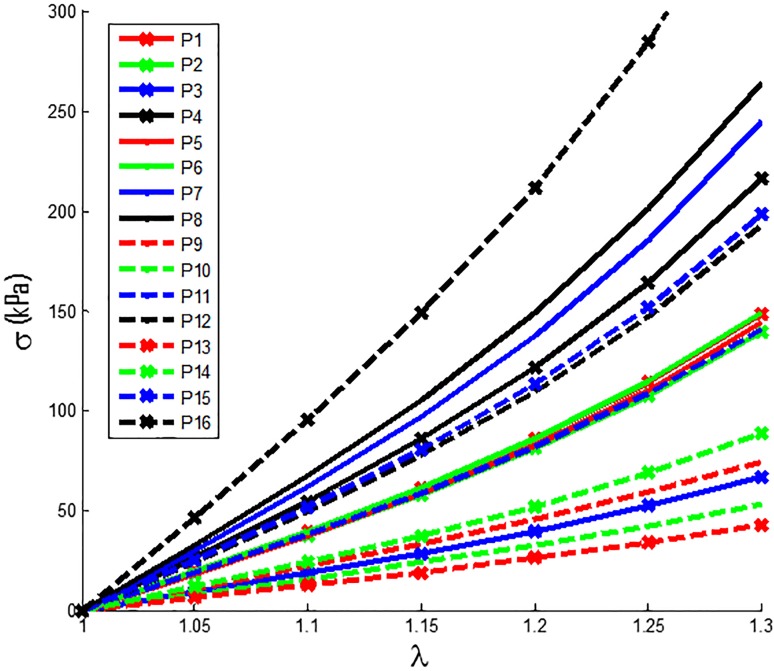
Stress-Stretch Ratio curves from Mooney-Rivlin models for the 16 plaque samples using average parameter values of their slices are presented in Fig 6. The average YM values and circumferential shrinkage (C-Shrink) values from 16 plaque samples were given in Table 3. The average YM values for the stiffest plaque sample (P16) was 922 kPa, 746% higher than that for the softest plaque (P13, YM = 109 kPa). This showed that plaque material properties have large variations from patient to patient and patient-specific material properties should be used in plaque models. It should be noted that pressure difference had a big effect on the material properties of vessels. Average C-shrink value from the 16 samples was 6.29%. The softest sample had 21.7% C-shrink, while the stiffest sample had a negative C-Shrink value (-1.78%). Negative C-Shrink means to obtain the zero-load geometry of the 3D thin-layer model, the in vivo slice lumen needed to expand slightly so that it could regain the in vivo circumference when 10% axial stretch and pressure were applied. Axial stretch makes the vessel to shrink in radial direction.
Fig 6. Stress-Stretch curves of Mooney-Rivlin Models for the 16 plaque samples.
Each curve used average parameter values for all available slices for the given plaque sample.
Table 3. Average material parameter values and circumferential shrinkage for 16 human carotid plaque samples based on Cine MRI data.
Due to axial shrink applied to the 3D thin-layer model, some C-Shrink values in 3D thin-layer model were negative.
| Plaque | Cir-Max | Cir-Min | δ-Cir | P | C1 | D1 | YM | C-Shrink |
|---|---|---|---|---|---|---|---|---|
| (cm) | (cm) | (%) | (mmHg) | (kPa) | (kPa) | (kPa) | (%) | |
| P1 | 2.564 | 2.350 | 8.35 | (120,80) | 34.6 | 14.6 | 370 | 7.40 |
| P2 | 2.328 | 2.163 | 7.11 | (120,80) | 34.8 | 12.9 | 348 | 6.26 |
| P3 | 2.415 | 2.119 | 12.3 | (120,70) | 19.5 | 5.31 | 169 | 12.3 |
| P4 | 2.208 | 2.050 | 7.15 | (141,72) | 37.5 | 25.3 | 531 | 1.05 |
| P5 | 2.089 | 1.903 | 8.90 | (130,70) | 30.0 | 15.3 | 357 | 4.51 |
| P6 | 2.130 | 1.950 | 8.44 | (143,80) | 34.3 | 14.7 | 371 | 4.11 |
| P7 | 2.952 | 2.747 | 6.93 | (146,81) | 41.7 | 28.9 | 601 | 2.45 |
| P8 | 2.073 | 1.942 | 6.33 | (146,81) | 48.3 | 30.1 | 650 | 1.07 |
| P9 | 2.341 | 2.094 | 10.6 | (100,60) | 28.8 | 3.66 | 191 | 7.48 |
| P10 | 1.301 | 1.150 | 11.6 | (100,60) | 20.6 | 2.61 | 137 | 9.88 |
| P11 | 2.136 | 1.906 | 10.8 | (143,73) | 35.0 | 13.1 | 352 | 4.56 |
| P12 | 2.658 | 2.389 | 10.1 | (143,73) | 38.2 | 21.1 | 476 | 3.96 |
| P13 | 1.537 | 1.306 | 15.0 | (143,90) | 16.3 | 2.16 | 109 | 21.7 |
| P14 | 2.018 | 1.801 | 10.8 | (143,91) | 23.3 | 7.84 | 222 | 14.7 |
| P15 | 2.127 | 1.933 | 9.11 | (143,65) | 41.5 | 21.0 | 492 | 0.92 |
| P16 | 2.191 | 2.075 | 5.28 | (143,65) | 66.4 | 43.4 | 922 | -1.78 |
| Ave by Patient | 2.192 | 1.992 | 9.3 | (133,74) | 34.4 | 16.4 | 394 | 6.29 |
| Ave by Slice | 2.192 | 1.997 | 8.91 | (133,74) | 35.5 | 17.3 | 411 | 5.62 |
3.3. Plaque material properties change with location: slice-specific material properties
Stress-Stretch plots for all the slices from 16 plaque samples were already presented by Fig 5. It is clear that slices at different locations had different material properties. Table 4 lists the effective Young’s modulus (YM) values for all slices from the 16 plaque samples. Our results showed that the arterial segment downstream of the bifurcation (average YM value is 536 kPa) is stiffer than the common carotid artery segment (the average YM value is 321 kPa). For comparison purpose, the variation of YM (δ-YM) for all slices in a plaque is defined as:
| (6) |
Table 4. The YM values for all slices from 16 plaque samples based on Cine MRI data.
| Plaque | YM (kPa) | δ-YM | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S-5 | S-4 | S-3 | S-2 | S-1 | Bi- | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | (%) | |
| P1 | 139 | 207 | 416 | 355 | - | - | 564 | 538 | - | - | - | - | - | - | - | - | 306 |
| P2 | - | - | - | 212 | 349 | 307 | 443 | 408 | 367 | - | - | - | - | - | - | - | 109 |
| P3 | - | - | 218 | 146 | 79 | 144 | 275 | 150 | - | - | - | - | - | - | - | 248 | |
| P4 | - | - | - | - | - | - | 370 | 385 | 572 | 429 | 632 | 797 | - | - | - | - | 115 |
| P5 | - | - | - | - | 149 | 336 | 325 | 413 | 613 | 304 | - | - | - | - | - | - | 311 |
| P6 | - | - | 369 | 416 | - | - | 296 | 356 | 397 | 389 | - | - | - | - | - | - | 41.0 |
| P7 | - | - | - | 604 | - | - | 548 | - | - | 651 | - | - | - | - | - | - | 19.0 |
| P8 | 448 | - | - | - | - | - | 706 | - | - | - | - | 797 | - | - | - | - | 78.0 |
| P9 | - | - | 176 | 178 | 272 | - | 138 | - | - | - | - | - | - | - | - | - | 97.0 |
| P10 | - | - | - | - | - | - | 191 | 70 | 116 | 102 | 205 | - | - | - | - | - | 193 |
| P11 | 352 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 0.0 |
| P12 | 537 | 508 | 374 | 647 | 316 | - | - | - | - | - | - | - | - | - | - | 105 | |
| P13 | - | - | - | - | - | - | 90 .0 | 91.0 | 94 .0 | 162 | - | - | - | - | - | - | 80.0 |
| P14 | 151 | - | - | - | - | 353 | - | - | - | - | 162 | - | - | - | - | - | 134 |
| P15 | - | - | - | - | - | 257 | 237 | 269 | 332 | 735 | - | 625 | 692 | 782 | 602 | 386 | 230 |
| P16 | - | - | - | - | - | - | - | - | 1126 | 1284 | 828 | 841 | 769 | - | 861 | 744 | 73.0 |
| Ave. | 273 | 372 | 337 | 326 | 299 | 314 | 338 | 312 | 419 | 507 | 457 | 765 | 731 | 782 | 732 | 565 | 134 |
Note: Bi- is the bifurcation. c2 = 0 and D2 = 2 for all cases.
δ-YM is the YM variation rate of the stiffest slice over the softest slice. The biggest δ-YM values for the slices from one vessel (P5) was 311%. The smallest δ-YM value for the slices from one vessel (P7) was 19.0%. The YM values variation of 13 plaque samples from 16 plaque samples were more than 50.0%. It showed that material properties change considerably along the artery segments and tend to become stiffer at downstream side. Location-specific material properties should be used when available in image-based plaque models for improved accuracy of the plaque models.
3.4 Plaque material properties change over time
We investigated whether vessel stiffness changed over time, and how material stiffness changes were associated with plaque progression and other risk factors. The effective Young’s modulus (YM), wall thickness (WT) [44], plaque burden (PB) and circumferential shrinkage (C-shrink) values at baseline (T1) and follow-up (T2) for the 8 patients are given in Table 5. The variation of YM over time (δYM-Time), the difference of PB (δPB) and the WT increase (WTI) are given by:
| (7) |
| (8) |
| (9) |
where YMT1, PBT1 and WTT1 are the YM, PB and WT values at T1, and YMT2, PBT2 and WTT2 are the YM, PB and WT values at T2, respectively. The average δYM-Time, δPB and WTI values in Table 5 were calculated using absolute values since otherwise positive and negative changes could cancel against each other give misleading lower averaged changes. The average variation of YM values for all patients was 61.0%. The range of variation of YM values was [-28.4%, 215%]. 3 patients had increased PB while 5 showed PB decrease. The average PB change for the 8 patients was 6.11%. 3 patients had positive WTI, while 5 had negative WTI. The range of WTI was [-0.225, 0.216] (mm). YM at T1 could have positive correlation with YM at T2 but the statistical significance is not strong (Pearson's product-moment correlation coefficient r = 0.7030, p = 0.0518 under t-test, and p = 0.1323 under Spearman’s rank test). YM at T2 showed strong negative correlation with WTI, with r = - 0.7764 (p = 0.0235 under t-test and p = 0.0154 under Spearman’s rank test). WT at T1 seems to be negatively correlated with WTI, but cannot statistically confirmed yet (r = -0.5253, p = 0.1813 under t-test and p = 0.1511 under Spearman’s rank test). Also, the seemly positive correlation between PB at T1 and δYM-Time cannot be statistically confirmed yet (r = 0.5939, p = 0.1205 under t-test and p = 0.0962 under Spearman’s rank test). No evidences show that the data distributions of these variables departure from Gaussian because the Shapiro-Wilk normality test p-values are all significantly larger than 0.05. Larger patient size will potentially lead to better confirmation of the variable correlations.
Table 5. The time-specific material YM values for carotid atherosclerotic plaques for 8 patients based on Cine MRI data by using thin-layer model.
| Time 1 | Time 2 | Variation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pts | δ-Cir | PB | WT | YM | δ-Cir | PB | WT | YM | δ-PB | WTI | δYM-Time |
| (%) | (%) | (mm) | (kPa) | (%) | (%) | (mm) | (kPa) | (%) | (mm) | (%) | |
| 1 | 8.35 | 32.0 | 0.911 | 370 | 7.11 | 34.2 | 0.883 | 348 | 2.11 | -0.028 | -5.95 |
| 2 | 12.3 | 49.4 | 1.337 | 169 | 7.15 | 46.5 | 1.145 | 531 | -2.90 | -0.192 | 215 |
| 3 | 8.90 | 47.3 | 1.126 | 357 | 8.44 | 42.1 | 1.059 | 371 | -5.2 | -0.067 | 3.87 |
| 4 | 6.93 | 43.9 | 1.364 | 601 | 6.33 | 49.8 | 1.327 | 650 | 5.90 | -0.037 | 8.17 |
| 5 | 10.6 | 39.4 | 1.077 | 191 | 11.6 | 64.1 | 1.293 | 137 | 24.7 | 0.216 | -28.4 |
| 6 | 10.8 | 39.0 | 0.872 | 352 | 10.1 | 38.0 | 1.016 | 476 | -0.98 | 0.144 | 35.5 |
| 7 | 15.0 | 49.7 | 0.980 | 109 | 10.8 | 44.3 | 1.159 | 222 | -5.34 | 0.179 | 103 |
| 8 | 9.11 | 40.2 | 1.098 | 492 | 5.28 | 38.4 | 0.873 | 922 | -1.76 | -0.225 | 87.5 |
| *Ave. | 10.2 | 42.6 | 1.096 | 330 | 8.35 | 44.7 | 1.094 | 457 | 6.11 | 0.136 | 61.0 |
Pts is patients. PB is plaque burden. WT is wall thickness. WTI is wall thickness increase.
*: The average δYM-Time, δPB and WTI values were calculated using absolute values. c2 = 0 and D2 = 2 for all cases. Due to axial shrink applied to the 3D thin-layer model, some C-Shrink values in 3D thin-layer model were negative.
Data normality was checked by the Shapiro-Wilk test. For the YM data over time in Table 5, it has a Shapiro-Wilk p-value 0.17, indicating no evidence of non-normality. We also applied the Kolmogorov-Smirnov test to check the normality. We got p-value 0.81, still indicating no evidence of non-normality. When the Kolmogorov test is applied, data have to be re-scaled based on its mean and standard deviation. If the YM data were not re-scaled, the Kolmogorov test would give a small p-value. Since our data size is small and the normality assumption could be a concern, we also reported the correlation p-values under the non-parametric Spearman rank test, which does not require the normality assumption. The results are consistent with those by the parametric t-test.
3.5 The differences between 2D model and 3D thin-layer model
To compare our 3D thin-layer model approach with 2D model approach, parameter values for Modified Mooney-Rivlin (MR) models and circumferential shrinkage values for the 16 plaque samples from 8 patients were also calculated using 2D modeling method [29] with the iterative procedure given in Fig 4. The average effective YM and C-Shrink values for the 16 plaque samples calculated by the 2D model and 3D thin-layer model are given in Table 6. The variation of YM (δ-YM-Model) and the difference of C-Shrink (δC-Shrink) between the 2 models are given by:
| (10) |
| (11) |
where YM2D and C-Shrink2D are the YM and circumferential shrinkage values, respectively, calculated by the 2D model, and YM3D and C-Shrink3D are the YM and circumferential shrinkage values, respectively, calculated by the 3D thin-layer model.
Table 6. The average effective Young’s modulus (YM) values and circumferential shrinkage values for 16 carotid plaque samples based on Cine MRI data by using 2D and 3D thin-layer model.
| Plaque | 2D model | 3D thin-layer model | Variation | |||
|---|---|---|---|---|---|---|
| YM | C-Shrink | YM | C-Shrink | δ˗YM˗Model | δ˗C˗Shrink | |
| (kPa) | (%) | (kPa) | (%) | (%) | (%) | |
| P1 | 342 | 12.3 | 370 | 7.40 | 8.38 | -4.86 |
| P2 | 320 | 11.2 | 348 | 6.26 | 8.44 | -4.91 |
| P3 | 156 | 16.8 | 169 | 12.3 | 7.98 | -4.56 |
| P4 | 493 | 6.29 | 531 | 1.05 | 7.99 | -5.24 |
| P5 | 328 | 9.53 | 357 | 4.51 | 9.04 | -5.02 |
| P6 | 341 | 9.15 | 371 | 4.11 | 8.74 | -5.04 |
| P7 | 561 | 7.54 | 601 | 2.45 | 7.11 | -5.09 |
| P8 | 604 | 6.31 | 650 | 1.07 | 7.91 | -5.24 |
| P9 | 177 | 12.1 | 191 | 7.48 | 7.85 | -4.62 |
| P10 | 126 | 14.4 | 137 | 9.88 | 8.90 | -4.48 |
| P11 | 323 | 9.62 | 352 | 4.56 | 8.85 | -5.05 |
| P12 | 441 | 9.12 | 476 | 3.96 | 8.00 | -5.16 |
| P13 | 104 | 25.0 | 109 | 21.7 | 5.19 | -3.29 |
| P14 | 208 | 19.0 | 222 | 14.7 | 6.85 | -4.24 |
| P15 | 453 | 6.20 | 492 | 0.92 | 8.67 | -5.29 |
| P16 | 856 | 3.67 | 922 | -1.78 | 7.78 | -5.44 |
| Ave by Patient | 365 | 11.1 | 394 | 6.29 | 7.98 | -4.85 |
| Ave (81 Slices) | 380 | 10.5 | 411 | 5.62 | 8.16 | -4.88 |
| Min | 104 | 3.67 | 109 | -1.78 | 5.19 | -5.44 |
| Max | 856 | 25.0 | 922 | 21.7 | 9.04 | -3.29 |
Note: c2 = 0 and D2 = 2 for all cases. Due to axial shrink applied to the 3D thin-layer model, some C-Shrink values in 3D thin-layer model were negative. Both averages by patients and by slices are given.
YM values from the 3D thin-layer models were 7.98% higher than that from the 2D models. The range of δ-YM-Model values was [5.19%, 9.04%]. C-Shrink values from the 3D thin-layer models were 4.85% lower than that from the 2D models. The range of δ-C-Shrink values was [-5.44%, -3.29%]. These differences showed that using 3D thin-layer model to replace 2D model would lead to improved accuracy of material parameter value estimations.
4. Discussions
4.1. Significance of in vivo patient-specific and location-specific vessel material properties
Most of the research on determining arterial wall material properties has been performed using ex vivo specimens and in vitro experimental techniques. In vivo estimation of patient-specific material properties is scarce, which is a serious limitation for patient-specific plaque models. A noninvasive approach of combining in vivo Cine and 3D MRI and simple 3D thin-layer modeling was introduced to quantify patient-specific and location-specific vessel material properties and improve model prediction accuracies. Our results from 16 plaques and 81 slices showed that slice YM values could vary from 70 kPa to 1284 kPa, 16 times of the lowest YM value. YM values from slices of the same vessel could vary by 311% (Table 4). Future studies should render 3D plaque models using patient-specific and location-specific material properties to quantify their impact on stress/strain calculations.
4.2. Significance of the 3D thin-layer model
Full 3D computational models are essential for plaque stress and strain calculations. They should also be used in the iteration process to determine the material parameter values that fit the variation in luminal circumference with the cardiac cycle, as provided by imaging techniques such as MR Cine data. However, full 3D model construction is time consuming. The material parameter adjusting process takes 20–50 iterations. The labor cost is unbearable if full 3D models were used. Previously, 2D models were used as an approximation [39]. We proposed a 3D thin-layer modeling method as an approximation with much less computational cost than full 3D models. 3D axial stretch was applied to the 3D thin-layer models, mimicking full 3D model procedures. The 3D thin-layer model was closer to the real in vivo conditions than used 2D models. This 3D thin-layer approach needs less computational cost than a full 3D model to achieve convergence for both circumferential shrinkage rate and material parameter value. Compared to 2D model results, the YM values from the 3D thin-layer models were 7.98% higher. The difference showed that using 3D thin-layer model to replace 2D model would lead to improved accuracy of material parameter value estimations.
4.3. Vessel material properties change over time and plaque component material properties
Plaque material properties changed over time with a 61.0% average variation of YM among all patients. It is clearly of great importance to be able to quantify patient-specific, location-specific and time-specific vessel material parameter values under in vivo conditions. However, there are some limitations as the available Cine MR data did not provide plaque component size change information needed to calculate plaque component material parameter data. In this study, lipid core parameter values were extracted from previous publications [10]. New imaging protocols or in vitro experimental techniques could be used to obtain patient-specific plaque component properties.
4.4. Impact of hypertension
It is well-accepted that hypertension is a common thread in most cardiovascular diseases. Table 2 shows that the six patients who had higher than 140 mmHg systolic pressure had higher YM values. The average YM value for the six patients was 612 kPa, whereas the average YM value for the remaining patients was 263 kPa. Since we do not have direct pressure measurements at present time, we plan to investigate the impact of hypertension when better pressure data becomes available. And the number of patient is the important limitation for the correlation prediction between hypertension and vessel material.
4.5 Model limitations
Cine MRI was used to determine vessel material parameter values, matching in vivo plaque geometries under both systolic and diastolic pressure conditions. Cine MRI is widely accepted to acquire time-dependent vessel motion and deformation. Multi-layer structure and anisotropic material properties of arteries were not considered since MRI does not provide layer information. Cine data provided only circumference variations under cardiac pressure. Another limitation was that location-specific pressure measurement was not available. Currently, arm cuff pressure values are used in most image-based studies. Noninvasive acquisition of intraplaque pressure data remains a challenge.
Data Availability
The study involved data from human subjects. The study was approved by New England IRB with IRB number 05-163. Written informed consent was obtained from all participants in this study. Data cannot be made publicly available for ethical or legal reasons (public availability would compromise patient privacy). Interested researchers and individuals should contact the Data Access Committee made of DT (dtang@wpi.edu), Michael Malone (mmalone@wpi.edu), Rhonda Podell (rpodell@wpi.edu).
Funding Statement
This work was supported by National Institute of Biomedical Imaging and Bioengineering R01 EB004759, DT, https://www.nibib.nih.gov/; National Natural Science Foundation of China, 11672001, DT, https://isisn.nsfc.gov.cn/egrantweb/; and Jiangsu Province Science and Technology Agency grant BE2016785, DT, http://www.jstd.gov.cn/. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.World Health Organization. Global Atlas on cardiovascular disease prevention and control. Geneva: World Health Organization; 2011. [Google Scholar]
- 2.Fuster V. The vulnerable atherosclerotic plaque: understanding, identification, and modification. Cardiovascular drugs & therapy. 1999; 13(4):363–363. [Google Scholar]
- 3.Fuster V, Stein B, Ambrose JA, Badimon L, Badimon JJ, Chesebro JH. Atherosclerotic plaque rupture and thrombosis, evolving concept. Circulation. 1990; 82(3 Suppl):47–59. [PubMed] [Google Scholar]
- 4.Naghavi M, Libby P, Falk E, Casscells SW, Litovsky S, Rumberger J, Badimon JJ, Stefanadis C, Moreno P, Pasterkamp G, Fayad Z, Stone PH, Waxman S, Raggi P, Madjid M, Zarrabi A, Burke A, Yuan C, Fitzgerald PJ, Siscovick DS, de Korte CL, Aikawa M, Juhani Airaksinen KE, Assmann G, Becker CR, Chesebro JH, Farb A, Galis ZS, Jackson C, Jang IK, Koenig W, Lodder RA, March K, Demirovic J, Navab M, Priori SG, Rekhter MD, Bahr R, Grundy SM, Mehran R, Colombo A, Boerwinkle E, Ballantyne C, Insull W Jr, Schwartz RS, Vogel R, Serruys PW, Hansson GK, Faxon DP, Kaul S, Drexler H, Greenland P, Muller JE, Virmani R, Ridker PM, Zipes DP, Shah PK, Willerson JT. From vulnerable plaque to vulnerable patient: a call for new definitions and risk assessment strategies: Part I. Circulation. 2003; 108(14):1664–72. doi: 10.1161/01.CIR.0000087480.94275.97 [DOI] [PubMed] [Google Scholar]
- 5.Naghavi M (co-authors are the same as above). From vulnerable plaque to vulnerable patient: a call for new definitions and risk assessment strategies: Part II. Circulation. 2003; 108(15):1772–8. doi: 10.1161/01.CIR.0000087481.55887.C9 [DOI] [PubMed] [Google Scholar]
- 6.Tang D, Kamm RD, Yang C, Zheng J, Canton G, Bach RG, Huang XY, Hatsukami TS, Zhu J, Ma G, Maehara A, Mintz GS, Yuan C. Image-based modeling for better understanding and assessment of atherosclerotic plaque progression and vulnerability: Data, modeling, validation, uncertainty and predictions. Journal of Biomechanics. 2014; 47(4):834–846. doi: 10.1016/j.jbiomech.2014.01.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Underhill HR, Hatsukami TS, Fayad ZA, Fuster V, Yuan C. MRI of carotid atherosclerosis: Clinical implications and future directions. Nat Rev Cardiol.2010; 7(3):165–73. doi: 10.1038/nrcardio.2009.246 [DOI] [PubMed] [Google Scholar]
- 8.Yuan C, Zhang SX, Polissar NL, Echelard D, Ortiz G, Davis JW, Ellington E, Ferguson MS, Hatsukami TS. Identification of fibrous cap rupture with MRI is highly associated with recent transient ischemic attack or stroke. Circulation.2002; 105:181–5. [DOI] [PubMed] [Google Scholar]
- 9.Friedman MH, Krams R, Chandran KB. Flow interactions with cells and tissues: Cardiovascular flows and fluid-structure interactions. Ann Biomed Eng. 2010; 38(3):1178–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tang D, Teng Z, Canton G, Yang C, Ferguson M, Huang X, Zheng J, Woodard PK, Yuan C. Sites of rupture in human atherosclerotic carotid plaques are associated with high structural stresses: an in vivo MRI-based 3D fluid-structure interaction study. Stroke.2009; 40:3258–3263. Featured article on MDlinx.com. doi: 10.1161/STROKEAHA.109.558676 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Holzapfel GA, Stadler M, Schulze-Bause CA. A layer-specific three dimensional model for the simulation of balloon angioplasty using magnetic resonance imaging and mechanical testing. Ann Biomed Eng. 2002; 30(6):753–767. [DOI] [PubMed] [Google Scholar]
- 12.Bluestein D, Alemu Y, Avrahami I, Gharib M, Dumont K, Ricotta JJ, Einav S. Influence of microcalcifications on vulnerable plaque mechanics using FSI modeling. J Biomech.2008; 41(5):1111–1118. doi: 10.1016/j.jbiomech.2007.11.029 [DOI] [PubMed] [Google Scholar]
- 13.Teng Z, Canton G, Yuan C, Ferguson M, Yang C, Huang X, Zheng J, Woodard PK, Tang D. 3D critical plaque wall stress is a better predictor of carotid plaque rupture sites than flow shear stress: an in vivo MRI-based 3D FSI study. J Biomech Eng.2010; 132(3):031007 doi: 10.1115/1.4001028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kaazempur-Mofrad MR, Isasi AG, Younis HF, Chan RC, Hinton DP, Sukhova G, Lamuraglia GM, Lee RT, Kamm RD. Characterization of the atherosclerotic carotid bifurcation using MRI, finite element modeling, and histology. Ann Biomed Eng. 2004; 32(7):932–946. [DOI] [PubMed] [Google Scholar]
- 15.Suo J, Oshinski JN, Giddens DP. Blood flow patterns in the proximal human coronary arteries: relationship to atherosclerotic plaque occurrence. Mol Cell Biomech. 2008; 5(1):9–18. [PubMed] [Google Scholar]
- 16.Tang D, Yang C, Zheng J, Woodard PK, Sicard GA, Saffitz JE, and Yuan C. 3D MRI-based multi-component FSI models for atherosclerotic plaques: a 3-D FSI model. Ann. Biomed. Eng.2004; 32(7): 947–960. [DOI] [PubMed] [Google Scholar]
- 17.Li ZY, Howarth S, Trivedi RA, U-King-Im JM, Graves MJ, Brown A, Wang LQ, Gillard JH. Stress analysis of carotid plaque rupture based on in vivo high resolution MRI. J Biomech.2006; 39(14):2611–2622. doi: 10.1016/j.jbiomech.2005.08.022 [DOI] [PubMed] [Google Scholar]
- 18.Gao H, Long Q, Das SK, Sadat U, Graves M, Gillard JH, Li ZY. Stress analysis of carotid atheroma in transient ischemic attack patients: evidence for extreme stress-induced plaque rupture. Ann Biomed Eng. 2011. August;39(8):2203–12. doi: 10.1007/s10439-011-0314-5 [DOI] [PubMed] [Google Scholar]
- 19.Gao H, Long Q, Kumar Das S, Halls J, Graves M, Gillard JH, Li ZY. Study of carotid arterial plaque stress for symptomatic and asymptomatic patients. J Biomech. 2011. September 23;44(14):2551–7. doi: 10.1016/j.jbiomech.2011.07.012. Epub 2011 Aug 6. [DOI] [PubMed] [Google Scholar]
- 20.Gallo D, Steinman DA, Morbiducci U. An insight into the mechanistic role of the common carotid artery on the hemodynamics at the carotid bifurcation. Ann Biomed Eng. 2015. January;43(1):68–81. doi: 10.1007/s10439-014-1119-0. Epub 2014 Sep 19. [DOI] [PubMed] [Google Scholar]
- 21.Yang C, Tang D, Atluri S. Three-dimensional carotid plaque progression simulation using meshless generalized finite difference method based on multi-year MRI patient-tracking data. Computer Modeling in Engineering and Sciences.2010; 57(1):51–76. [PMC free article] [PubMed] [Google Scholar]
- 22.Yang C, Tang D, Yuan C, Kerwin W, Liu F, Canton G, Hatsukami TS, Atluri S. Meshless generalized finite difference method and human carotid atherosclerotic plaque progression simulation using multi-year MRI patient-tracking data. Computer Modeling in Engineering and Sciences.2008; 28(2):95–107. [PMC free article] [PubMed] [Google Scholar]
- 23.Yang C, Canton G, Yuan C, Ferguson M, Hatsukami TS, Tang D. Advanced human carotid plaque progression correlates positively with flow shear stress using follow-up scan data: an in vivo MRI multi-patient 3D FSI study. J Biomech. 2010; 43(13):2530–8. doi: 10.1016/j.jbiomech.2010.05.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Nieuwstadt HA, Fekkes S, Hansen HH, de Korte CL, van der Lugt A, Wentzel JJ, van der Steen AF, Gijsen FJ. Carotid plaque elasticity estimation using ultrasound elastography, MRI, and inverse FEA—A numerical feasibility study. Med Eng Phys. 2015. August;37(8):801–7. doi: 10.1016/j.medengphy.2015.06.003 [DOI] [PubMed] [Google Scholar]
- 25.Smoljkić M, Vander Sloten J, Segers P, Famaey N. Non-invasive, energy-based assessment of patient-specific material properties of arterial tissue. Biomech Model Mechanobiol. 2015. October;14(5):1045–56. doi: 10.1007/s10237-015-0653-5 [DOI] [PubMed] [Google Scholar]
- 26.Czernuszewicz TJ, Homeister JW, Caughey MC, Farber MA, Fulton JJ, Ford PF, Marston WA, Vallabhaneni R, Nichols TC, Gallippi CM. Non-invasive in vivo characterization of human carotid plaques with acoustic radiation force impulse ultrasound: comparison with histology after endarterectomy. Ultrasound Med Biol. 2015. March;41(3):685–97. doi: 10.1016/j.ultrasmedbio.2014.09.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Holzapfel GA, Sommer G, Regitnig P. Anisotropic mechanical properties of tissue components in human atherosclerotic plaques. J Biomech Eng. 2004; 126(5):657–665. [DOI] [PubMed] [Google Scholar]
- 28.Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J Elasticity. 2000; 61(1): 1–48. [Google Scholar]
- 29.Williamson SD, Lam Y, Younis HF, Huang H, Patel S, Kaazempur-Mofrad MR, Kamm RD. On the sensitivity of wall stresses in diseased arteries to variable material properties. J Biomech Eng. 2003; 125(1):147–155. [DOI] [PubMed] [Google Scholar]
- 30.Tang D, Yang C, Zheng J, Woodard PK, Saffitz JE, Sicard GA, Pilgram TK, Yuan C. Quantifying effects of plaque structure and material properties on stress behaviors in human atherosclerotic plaques using 3D FSI models. J Biomech Eng. 2005; 127(7):1185–1194. doi: 10.1115/1.2073668 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Teng Z, Tang D, Zheng J, Woodard PK, Hoffman AH. An experimental study on the ultimate strength of the adventitia and media of human atherosclerotic carotid arteries in circumferential and axial directions. J Biomech. 2009; 42(15):2535–9. doi: 10.1016/j.jbiomech.2009.07.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Teng Z, Zhang Y, Huang Y, Feng J, Yuan J, Lu Q, Sutcliffe MP, Brown AJ, Jing Z, Gillard JH. Material properties of components in human carotid atherosclerotic plaques: a uniaxial extension study. Acta Biomaterialia. 2014; 10(12):5055–5063. doi: 10.1016/j.actbio.2014.09.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tang D. Modeling flow in healthy and stenosed arteries Wiley Encyclopedia of Biomedical Engineering, editor: Akay Metin, Hoboekn, John Wiley & Sons, Inc., New Jersey.2006; Article 1525:1–16. [Google Scholar]
- 34.Tang D, Yang C, Mondal S, Liu F, Canton G, Hatsukami TS, Yuan C. A negative correlation between human carotid atherosclerotic plaque progression and plaque wall stress: in vivo MRI-based 2D/3D FSI models. J Biomech. 2008; 41(4):727–736. doi: 10.1016/j.jbiomech.2007.11.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Yang C, Tang D, Yuan C, Hatsukami TS, Zheng J, Woodard PK. In vivo/ex vivo MRI-based 3D models with fluid-structure interactions for human atherosclerotic plaques compared with fluid/wall-only models. Computer Modeling in Engineering and Sciences. 2007; 19(3):233–245. [PMC free article] [PubMed] [Google Scholar]
- 36.Speelman L, Bosboom EM, Schurink GWH, Buth J, Breeuwer M, Jacobs MJ, van de Vosse FN. Initial stress and nonlinear material behavior in patient-specific AAA wall stress analysis. J Biomech.2009; 42(11):1713–1719. doi: 10.1016/j.jbiomech.2009.04.020 [DOI] [PubMed] [Google Scholar]
- 37.Gee MW, Reeps C, Eckstein HH, Wall WA. Prestressing in finite deformation abdominal aortic aneurysm simulation. J Biomech. 2009; 42(11):1732–9. doi: 10.1016/j.jbiomech.2009.04.016 [DOI] [PubMed] [Google Scholar]
- 38.Huang Y, Teng Z, Sadat U, Hilborne S, Young VE, Graves MJ, Gillard JH. Non-uniform Shrinkage for Obtaining Computational Start Shape for in-vivo MRI based Plaque Vulnerability Assessment. J Biomech. 2011; 44(12):2316–9. doi: 10.1016/j.jbiomech.2011.06.014 [DOI] [PubMed] [Google Scholar]
- 39.Liu H, Canton G, Yuan C, Yang C, Billiar K, Teng Z, Hoffman AH, Tang D. Using in vivo cine and 3D multi-contrast MRI to determine human atherosclerotic carotid artery material properties and circumferential shrinkage rate and their impact on stress/strain predictions. J Biomech Eng. 2012; 134(1):223–233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Huang X, Yang C, Zheng J, Bach R, Muccigrosso D, Woodard PK, Tang D. 3D MRI-based multicomponent thin layer structure only plaque models for atherosclerotic plaques. J Biomechanics.2016; accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bathe KJ, 1996. Finite Element Procedures, Prentice Hall, Inc. New Jersey. [Google Scholar]
- 42.Bathe KJ, Editor. 2002. Theory and Modeling Guide, Vol I & II: ADINA and ADINA-F, ADINA R & D, Inc., Watertown, MA. [Google Scholar]
- 43.Kural MH, Cai M, Tang D, Gwyther T, Zheng J, Billiar KL. Planar biaxial characterization of diseased human coronary and carotid arteries for computational modeling. J Biomech. 2012; 45(5):790–798. doi: 10.1016/j.jbiomech.2011.11.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wang L, Wu ZY, Yang C, Zheng J, Bach R, Muccigrosso D, Billiar K, Maehara A, Mintz GS, Tang D. IVUS-based FSI models for human coronary plaque progression study: component, correlation and predictive analysis. Annals of biomedical engineering. 2015; 43(1): 107–21. doi: 10.1007/s10439-014-1118-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The study involved data from human subjects. The study was approved by New England IRB with IRB number 05-163. Written informed consent was obtained from all participants in this study. Data cannot be made publicly available for ethical or legal reasons (public availability would compromise patient privacy). Interested researchers and individuals should contact the Data Access Committee made of DT (dtang@wpi.edu), Michael Malone (mmalone@wpi.edu), Rhonda Podell (rpodell@wpi.edu).