Abstract
Objective
We evaluated the performance of our previously developed seizure prediction approach on thirty eight seizures from ten patients with focal hippocampal epilepsy.
Methods
The seizure prediction system was developed based on the extraction of correlation dimension, correlation entropy, noise level, Lempel-Ziv complexity, largest Lyapunov exponent, and nonlinear interdependence from segments of intracranial EEG.
Results
Our results showed an average sensitivity of 86.7% and 92.9%, an average false prediction rate of 0.126 and 0.096/h, and an average minimum prediction time of 14.3 and 33.3 min, respectively, using seizure occurrence periods of 30 and 50 min and a seizure prediction horizon of 10 s. Two-third of the analyzed seizures showed significantly increased complexity in periods prior to the seizures in comparison with baseline.
In four patients, strong bidirectional connectivities between epileptic contacts and the surrounding areas were observed. However, in five patients, unidirectional functional connectivities in preictal periods were observed from remote areas to epileptogenic zones.
Conclusions
Overall, preictal periods in patients with focal hippocampal epilepsy were characterized with patient-specific changes in univariate and bivariate nonlinear measures.
Keywords: intracranial EEG, complexity, connectivity, focal hippocampal epilepsy, preictal identification, seizure prediction
1. Introduction
Epilepsy is a neurological disorder affecting 1% of the world’s population. It causes seizures characterized by recurrent synchronous abnormal electrical discharges in the brain (Chaovalitwongse et al. 2006; Browne and Holmes 2008). Epileptic patients are often at high risk of serious injury or death (Cockerell et al. 1994). Moreover, accompanying psychological stress and helplessness can cause impaired everyday functioning (Buck et al. 1997, Baker et al. 1997). Thereby, reliable prediction of seizures can considerably improve the quality of life of epileptic patients by warning them of impeding seizures to avoid potentially dangerous situations like driving or swimming and enable administration of treatments (Cook et al., 2013; Ramgopal et al., 2014).
To date, linear and nonlinear analysis techniques have been applied in order to identify preictal periods by investigating various properties of the electroencephalography (EEG) signal, with varying degrees of success (see Litt and Echauz 2002, Iasemidis 2003, Mormann et al. 2006, 2007, and Gadhoumi et al. 2016 for a review). A number of studies have employed univariate measures taken from the nonlinear dynamics chaos theory, including the correlation dimension (Lehnertz and Elger 1995, Lehnertz et al. 2001), correlation density (Martinerie et al. 1998), largest Lyapunov exponent (Iasemidis et al. 1990), dynamic similarity index (Le Van Quyen et al. 2001), entropy (Van Drongelen et al. 2003) and predictability (Drury et al. 2003). Nonlinear EEG analysis using univariate measures has provided evidence that transitions between interictal and ictal states may begin from minutes to hours prior to seizures, with characteristic changes evolving from a high complexity (possibly chaotic) to a low complexity (rhythmic behavior during a seizure) (Basar 1998).
Based on the hypothesis that interactions between different neuronal networks involved in the epileptogenic process may also change prior to the seizure onset, many researchers have employed bivariate measures, such as nonlinear interdependence (Arnhold et al. 1999), phase synchronization, and cross correlation (Mormann et al. 2000, 2003) to predict seizures.
In our previous study, we developed a patient-specific method with significantly improved performance to predict partial seizures in patients with focal neocortical epilepsy using intracranial EEG (iEEG) data by combining the univariate and bivariate nonlinear measures (Aarabi and He, 2012). In the present study, we employed the same seizure prediction system to iEEG data of patients with medically intractable focal hippocampal epilepsy. The dynamic characteristics of the iEEG were extracted and spatiotemporally integrated using patient-specific rules established based on a template seizure from each patient. We evaluated the performance of the individual univariate and bivariate measures as well as the combination method for seizure prediction. Finally, the dynamic of the preictal states associated with focal hippocampal seizures was compared with that we previously reported in patients with focal neocortical epilepsy (Aarabi and He, 2012).
2. Methods
2.1. EEG data
The iEEG data analyzed in this study were obtained from the Freiburg Seizure Prediction EEG (FSPEEG) database collected from 21 patients with medically intractable focal neocortical and hippocampal epilepsy (Maiwald et al. 2004). We already used the iEEG data of 11 patients with neocortical focal epilepsy to evaluate the performance of our seizure prediction method (Aarabi and He, 2012). In the present paper, we evaluated the same system with the remaining iEEG recordings of 10 patients with seizures initiated in the hippocampus, which is known as a region more susceptible to make abrupt transitions to seizures (Sackellares et al. 2000). To record the iEEG data, patients had been implanted with intracranial electrodes, from which three within the epileptogenic zone and three in remote locations had been selected by an experienced epileptologist and included in the FSPEEG database. In total, 280 h of iEEG data containing 38 seizures with at least 50 min preictal data and 24-hour seizure-free interictal data for each patient were analyzed in this study (Table 1).
Table 1.
Patients and intracranial EEG data characteristics.
| Patient | Sex | Age | Seizure type | Origin | Electrodes | # seizures | Interictal EEG duration (hours) | ||
|---|---|---|---|---|---|---|---|---|---|
| Training set | Testing set | Training set | Testing set | ||||||
| 1 | M | 38 | SP,CP,GTC | Temporal | d | 1 | 2 | 4 | 20 |
| 2 | F | 26 | SP,CP,GTC | Temporal | d,g,s | 1 | 4 | 4 | 20 |
| 3 | F | 31 | CP,GTC | Temporo/Occipital | d,g,s | 1 | 2 | 4 | 20 |
| 4 | F | 42 | SP,CP,GTC | Temporal | d | 1 | 2 | 4 | 20.6 |
| 5 | M | 47 | SP,CP,GTC | Temporal | d | 1 | 4 | 4 | 20.5 |
| 6 | F | 42 | SP,CP,GTC | Temporal | d,g,s | 1 | 3 | 4 | 21 |
| 7 | F | 22 | SP,CP,GTC | Temporo/Occipital | d,s | 1 | 1 | 4 | 20 |
| 8 | F | 41 | CP,GTC | Fronto/Temporal | d,s | 1 | 3 | 4 | 20 |
| 9 | M | 31 | SP,CP,GTC | Temporal | d,s | 1 | 3 | 4 | 20 |
| 10 | F | 50 | SP,CP,GTC | Temporal | d,s | 1 | 4 | 4 | 20 |
| Total | 7F/3M | 10 | 28 | 40 | 202 | ||||
| Mean | 3 | 20 | |||||||
SP = simple partial, CP = complex partial, GTC = generalized tonic-clonic, g: grid, s:strip, d:depth
2.2. Overall system
Figure 1 depicts the diagram of our seizure prediction tool (Aarabi and He, 2012). In brief, in the preprocessing stage, the iEEG data were band-pass filtered between 0.5 and 100 Hz using a 4th order digital Butterworth filter and notched to remove possible 50 Hz power line noise. Then, the iEEG data were divided into 10-second nonoverlapping segments. A set of six univariate and bivariate features including correlation dimension (CD), correlation entropy (CEN), noise level (NL), Lempel-Ziv complexity (LZC), largest Lyapunov exponent (LLE), and nonlinear interdependence (NI) were extracted from iEEG segments.
Figure 1.
Schematic diagram of the rule-based seizure prediction system.
The time profiles of the features were first smoothed using a backward-moving-average filter of 5 min. For each patient, a simple thresholding procedure was then applied to the time profiles to determine significant changes in the values of the selected features in comparison with a baseline, defined as a reference period remote in time from any seizure. In this procedure for each channel, the mean (µ) and standard deviation (σ) of each feature were calculated over the feature values obtained from the baseline. For each patient, the feature values of the entire iEEG dataset were then scanned segment by segment, and the location and the feature values of the segments exhibiting values greater than (µ+σ) or less than (µ-σ) were saved and passed to the next stage.
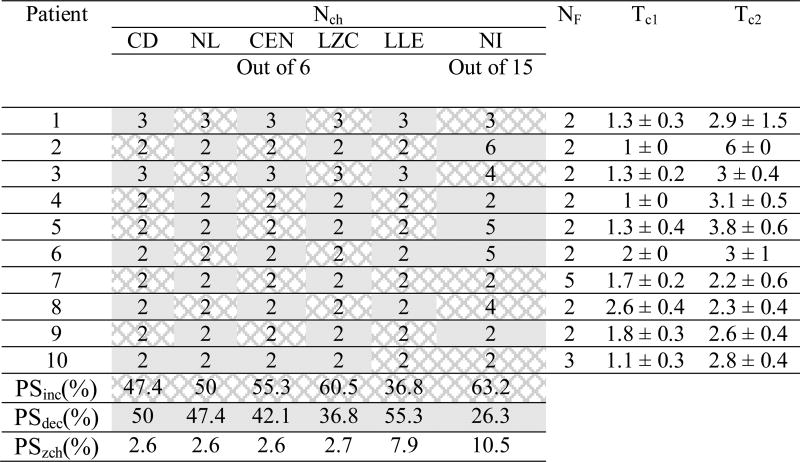
To locate seizure precursors, a rule-based decision-making stage was used to reach a single decision for any epoch (multichannel iEEG segments) in two steps. First, a spatial combiner integrated the information from different channels on a feature-by-feature. In total, there were six spatial combiners acting on the univariate and bivariate features. At this stage, an epoch indicated a preliminary seizure precursor if Nch channels (out of 6 for the univariate measures and out of 15 for the bivariate measure) exhibited significant changes in comparison with the reference period. In this case, a primary seizure prediction flag was raised for the epoch.
In the second step, a feature integrator integrated the information from different features for each EEG epoch. The feature integration was performed in two stages. Stage 1 included the feature integrator I operating on the primary flags at the output of the spatial combiners. At this stage, for each segment, if NF primary flags showed significant changes above a predefined threshold (Tc1), a secondary flag was raised for the epoch indicating a higher probability for the epoch to be considered as a seizure precursor.
The feature integrator II operated on the secondary flags of the univariate measures as well as on the primary flag raised by the spatial combiner of the bivariate measure. At this step, for any epoch, if a primary flag for the bivariate measure and a secondary flag together exhibited significant changes above the thresholds Tc1 and Tc2, respectively, then a final flag indicating a definitive seizure precursor was raised for the segment. At the final step, consecutive final flags lasting less than 40 sec were rejected as false short predictions.
To determine the thresholds Nch, Tc1, Tc2 and NF for each patient, we divided the iEEG data into optimization and test sets. In order to avoid biases in performance evaluation, we used the repeated random sub-sampling cross-validation method1. For each patient, the seizures and 24 one-hour seizure-free interictal iEEG data files were split into optimization and test sets. This procedure was then repeated 10 times. At each run, four one-hour interictal iEEG files and a sample seizure were randomly assigned to the optimization set and the remaining seizures and interictal iEEG data files were used for testing. Then, the system was tuned using the optimization sets and evaluated on the test sets. The optimization sets were used to determine the optimal thresholds. Finally, for each patient, the overall performance of the system was averaged over the ten runs (see Aarabi and He, 2012 for more details).
2.3. Performance evaluation
Using the optimal values of the thresholds, the performance of the seizure prediction system was assessed on test sets in terms of sensitivity, specificity, false prediction rate, minimum prediction time, and portion of time under false predictions (Mormann et al. 2006) over the seizure occurrence period (SOP) of 30 and 50 min and a prediction horizon (SPH) of 10 sec.
We further compared the performance of the system based on single features. This step was performed in order to test the predictive power of individual features. In this step, we deactivated both feature integrators I and II to tune our system on each feature separately. Then, the performance of single feature-based systems was evaluated on test sets and saved for further comparison. To compare the seizure predictive power of each of the six features, we tested the performance of the single-feature prediction systems using the baselines selected at the beginning of the seizure-free interictal iEEG recordings for each patient. In addition, the system performance was compared with those obtained using the random and periodical prediction methods described by Maiwald et al. (2004). We also investigated the significance of preictal changes of the features for each patient using the method described in Aarabi and He (2012).
2.4. Connectivity map
To achieve a better insight into interactions between epileptic zones and remote areas, a connectivity map was provided for each patient by statistically comparing bidirectional synchronization levels SX→Y and SY→X within preictal periods with those found in reference windows using the Mann-Whitney U-test (Mann and Whitney 1947) with p<0.05. Since for each patient, more than one seizure was included in this study, inter-channel connectivity patterns with maximum occurrence rate were computed to obtain connectivity maps between different cerebral regions.
3. Results
3.1. Feature significance evaluation
Table 2 lists the performance of the system using single features. For each patient, the performance evaluation was performed with the optimal thresholds listed in Table 3. The mean and the absolute deviation of the optimal values of Tc1, and Tc2 (displayed in the two leftmost columns) were computed over ten randomly selected reference windows. For each patient, the median values of nonlinear measures computed within the 50-minute preictal periods were statistically compared with the values obtained in the reference periods. For each feature, the last three rows in Table 3 indicate the percentages of seizures whose preictal periods showed a significant decrease, increase, or no change in comparison with baseline.
Table 2.
Average performance of the single-feature based systems compared to the entire system performance for a seizure prediction horizon of 10 sec.
| SOPmax (min) |
system | SEN (%) |
SPE (%) |
FPR (/h) |
PT (%) |
MPT (min) |
|---|---|---|---|---|---|---|
| CD-based | 86.7 ± 18.7 | 91.8 ± 8.1 | 0.26 ± 0.21 | 8.4 ± 7.9 | 12.5 ± 10.9 | |
| 30 | NL-based | 65.8 ± 27.7 | 91.1 ± 7.1 | 0.33 ± 0.24 | 9.4 ± 6.9 | 11.7 ± 9.9 |
| CEN-based | 47.5 ± 26.3 | 95.6 ± 3.1 | 0.23 ± 0.15 | 4.9 ± 3.8 | 14.7 ± 11.9 | |
| LZC-based | 79.2 ± 25 | 89.4 ± 5.8 | 0.36 ± 0.16 | 11.7 ± 7.3 | 17.6 ± 11 | |
| LLE-based | 75.8 ± 24.2 | 92.8 ± 5.6 | 0.26 ± 0.17 | 7.9 ± 6.1 | 18 ± 9.9 | |
| NI-based | 85.8 ± 17 | 93.2 ± 6.9 | 0.26 ± 0.23 | 6.8 ± 6.9 | 14.8 ± 7.4 | |
|
|
||||||
| Entire system | 91.7 ± 13.3 | 95.9 ± 3.5 | 0.135 ± 0.13 | 4.9 ± 4.3 | 13.9 ± 8.2 | |
|
| ||||||
| CD-based | 91.7 ± 13.3 | 91.8 ± 8.1 | 0.17 ± 0.13 | 8.4 ± 7.9 | 21.9 ± 18.2 | |
| 50 | NL-based | 85.8 ± 17 | 91.1 ± 7.1 | 0.23 ± 0.16 | 9.4 ± 6.9 | 33.1 ± 16.9 |
| CEN-based | 78.3 ± 21.7 | 95.6 ± 3.1 | 0.17 ± 0.098 | 4.9 ± 3.8 | 30 ± 15 | |
| LZC-based | 91.7 ± 13.3 | 89.4 ± 5.8 | 0.25 ± 0.12 | 11.7 ± 7.3 | 31.7 ± 15.7 | |
| LLE-based | 94.1 ± 9.5 | 92.8 ± 5.6 | 0.18 ± 0.12 | 7.9 ± 6.1 | 31.6 ± 15.1 | |
| NI-based | 90.8 ± 12.8 | 93.2 ± 6.9 | 0.2 ± 0.15 | 6.8 ± 6.9 | 25.2 ± 14.9 | |
|
|
||||||
| Entire system | 94.2 ± 9.3 | 95.9 ± 3.5 | 0.1 ± 0.1 | 4.9 ± 4.3 | 36.7 ± 17.1 | |
The results have been averaged across patients. CD: correlation dimension; NL: noise level; CEN: correlation entropy; LZC: Lempel-Ziv complexity; LLE: largest Lyapunov exponent; NI: nonlinear interdependence; SOPmax: maximum seizure occurrence period; SEN: sensitivity; SPE: specificity; FPR: false prediction rate; PT: portion of time under false predictions; MPT: Mean prediction time.
Table 3.
Optimal thresholds used for seizure prediction in iEEG data from patients with focal hippocampal epilepsy.
Nch : number of channels; NF: number of features; Tc1 and Tc2: significance thresholds for raising flags II and III (see Section 2.2 for details); CD: correlation dimension; NL: noise level; CEN: correlation entropy; LZC: Lempel-Ziv complexity; LLE: largest Lyapunov exponent ; NI: nonlinear interdependence. PSinc, PSdec and PSzch are the percentages of seizures showing significant preictal increase (dark gray), decrease (light gray) and no change, respectively, in comparison with reference periods. Results are expressed as mean ± absolute deviation. Similarly, the dominant preictal changes in the median of feature values have been shown for each patient separately.
As shown, the entire system based on the combined features achieved the highest mean sensitivity and specificity and the lowest mean false prediction rate with SOPs of 30 and 50 min and SPH=10 sec. Overall, CD, LZC, LLE and NI-based systems achieved highest performance. However, the contribution of these features in performance improvement was slightly different with a slight improvement for the CD and LLE-based systems. The correlation entropy-based system obtained the lowest sensitivity with a relatively higher specificity and lower false prediction rate in comparison with the other single feature-based systems.
3.2. Cross validation
The average performance of the system with SOPs of 30 and 50 min and SPH=10 sec is listed in Table 4 for each patient. Grand statistics were calculated on the test sets using the crossvalidation technique (see Section 2.2). As shown, with a SOP of 30 min slight changes were observed in the system performance using different reference windows. No significant changes in the system performance were observed in 8 out of the 10 patients. Relatively lower sensitivities were observed in patients 3, 8 and 10 with a SOP of 30 min. Patients 1, 3, and 10 showed higher false prediction rates with both SOPs of 30 and 50 min.
Table 4.
Overall system performance with a seizure prediction horizon of 10 sec.
| Patient | SOPmax (min) |
SEN (%) |
FPR (/h) |
MIT (min) |
SPE (%) |
PT (%) |
|---|---|---|---|---|---|---|
| 1 | 30 | 100 ± 0 | 0.28 ± 0.03 | 5.7 ± 2.6 | 90.2 ± 1.7 | 8.1 ± 1.3 |
| 50 | 100 ± 0 | 0.18 ± 0.02 | 48.2 ± 2.5 | |||
|
| ||||||
| 2 | 30 | 100 ± 0 | 0 ± 0 | 11.4 ± 0 | 100 ± 0 | 0 ± 0 |
| 50 | 100 ± 0 | 0 ± 0 | 40.9 ± 2 | |||
|
| ||||||
| 3 | 30 | 55 ± 19 | 0.32 ± 0.06 | 26.8 ± 4.6 | 93.2 ± 2.5 | 5.6 ± 2 |
| 50 | 100 ± 0 | 0.23 ± 0.05 | 40.1 ± 6.4 | |||
|
| ||||||
| 4 | 30 | 100 ± 0 | 0 ± 0 | 15.1 ± 5.7 | 100 ± 0 | 0 ± 0 |
| 50 | 100 ± 0 | 0 ± 0 | 42.9 ± 11 | |||
|
| ||||||
| 5 | 30 | 100 ± 0 | 0 ± 0 | 16.8 ± 6.7 | 100 ± 0 | 0 ± 0 |
| 50 | 100 ± 0 | 0 ± 0 | 48.8 ± 1.5 | |||
|
| ||||||
| 6 | 30 | 100 ± 0 | 0.11 ± 0.01 | 28.5 ± 2.4 | 95 ± 0.2 | 8.3 ± 0.2 |
| 50 | 100 ± 0 | 0.06 ± 0.01 | 49.8 ± 0 | |||
|
| ||||||
| 7 | 30 | 100 ± 0 | 0.04 ± 0.04 | 1.9 ± 1.4 | 99.3 ± 1.2 | 0.6 ± 1 |
| 50 | 100 ± 0 | 0.02 ± 0.02 | 1.9 ± 1.4 | |||
|
| ||||||
| 8 | 30 | 67 ± 0 | 0.11 ± 0.03 | 1 ± 0.5 | 98.1 ± 0.7 | 1.6 ± 0.6 |
| 50 | 67 ± 0 | 0.11 ± 0.03 | 1 ± 0.5 | |||
|
| ||||||
| 9 | 30 | 100 ± 0 | 0.13 ± 0.07 | 18.4 ± 2.8 | 98.5 ± 1.3 | 1.3 ± 1.1 |
| 50 | 100 ± 0 | 0.11 ± 0.04 | 18.9 ± 2.5 | |||
|
| ||||||
| 10 | 30 | 45 ± 8 | 0.27 ± 0.1 | 17.7 ± 7 | 93.3 ± 3.7 | 5.6 ± 3 |
| 50 | 63 ± 13 | 0.24 ± 0.09 | 40.6 ± 10.8 | |||
|
| ||||||
| Grand Average | 30 | 86.7 ± 18.9 | 0.126 ± 0.11 | 14.3 ± 9 | 96.7 ± 3.2 | 3.8 ± 3.8 |
| 50 | 92.9 ± 11.3 | 0.096 ± 0.085 | 33.3 ± 17.1 | |||
Mean and absolute deviation (AD) over the performance parameters obtained using the ten reference windows randomly selected for each patient. Results are rounded and expressed as mean ± AD. SOPmax: maximum seizure occurrence period; SEN: sensitivity; SPE: specificity; FPR: false prediction rate; PT: portion of time under false predictions; MPT: Mean prediction time.
3.3. Overall performance of the system
The overall performance of the system was computed by averaging the performance values obtained for all patients. The system achieved an average sensitivity of 86.7% and 92.9% with an average false prediction rate of 0.126/h and 0.096/h, and an average specificity of 96.7% with SOPs of 30 and 50 min (SPH=10 sec), respectively. On average, the portion of time under false predictions was about 3.8% of the test data. The mean minimum prediction time was about 14 and 33 min for SOPs of 30 and 50 min (SPH=10 sec), respectively.
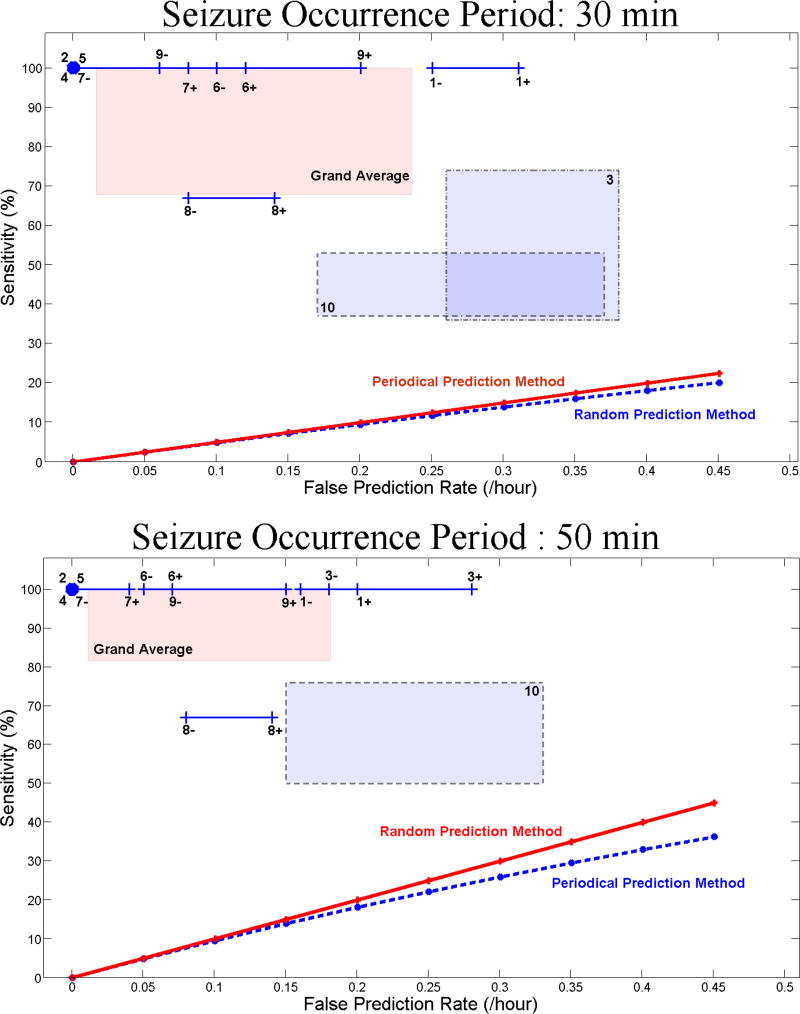
For each patient, Figure 2 (A and B) shows the range of variation of the sensitivity versus the false prediction rate with SOPs of 30 and 50 min and SPH=10 sec. As shown, for each patient the system outperformed the random and periodical prediction methods.
Figure 2.
Sensitivity versus false prediction rate for each patient (as indicated by patient number in Table 1) and for the grand average across patients (labeled in pink as Grand Average) using the seizure occurrence period of (A) 30 and (B) 50 min. For each patient, the box or line shows the range of variation of sensitivity versus false prediction rate obtained using different randomly selected reference windows. Plus and minus signs used with the patients’ number denote the upper and lower bounds of the corresponding ranges of variation. The sensitivities of the random and periodical prediction methods are also shown in panels A and B.
3.4. Connectivity map
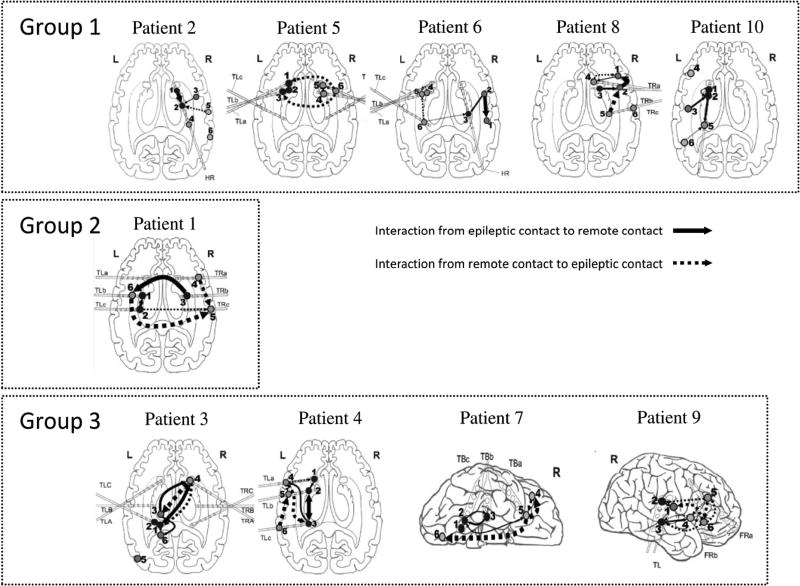
Figure 3 shows connectivity maps depicting interactions between intracranial electrodes implanted in epileptogenic zones and remote areas. In this figure, significant connectivities are shown with arrows whose widths indicate interaction strength. The direction of the arrows indicates the driving-response interactions between electrodes, with no reference to any specific sequence of events over time.
Figure 3.
Connectivity maps characterizing the preictal strength of synchronization and the direction of interaction for each patient. The thickness of the arrows reflects the strength of interactions. For the sake of simplicity, we projected all the contacts on the same cross-sectional view. In these maps, numbers 1–3 and 4–6 refer to the electrodes implanted in the epileptogenic zone and remote areas, respectively. Group I shows interdependencies between the remote contacts (as driving systems) and the epileptic contacts (as response systems). In Group II the nonlinear interdependencies were observed between epileptic contacts (as driving system) and the remote contacts (as response system). Group III shows bilateral interactions between epileptic and remote contacts.
We classified the patients into three groups based on their connectivity maps. The first group containing patients 2, 5, 6, 8 and 10 shows strong interactions between remote contacts (as driving systems) and epileptic contacts (as response systems). For patients 2 and 10, the remote contacts were located in cortical regions, whereas for patients 5, 6 and 8 they were implanted in deep brain areas. In contrast, in the second group including only patient 1, strong connectivities were observed between epileptic contacts (as driving systems) and remote contacts (as response systems).
The third group includes patients 3, 4, 7 and 9 whose preictal states showed strong bidirectional connectivities between epileptic and remote contacts. For patients 3 and 4, the interaction loops were between cortical and deep sources in the hippocampus, whereas for the other patients in this group the interactions constituted cortico-cortical loop.
With respect to distance, the interactions were classified into short- and long-range. The short range distance was observed in patients 2, 4, 6, 8 and 10, between epileptic contacts, remote contacts or between epileptic and remote contacts. Patients 1, 3, 5 and 7 were characterized with long-range interactions.
4. Discussion
In the present study, we evaluated the performance of our rule-based patient-specific seizure prediction system which has been already tested on long-term iEEG recordings from patients with focal neocortical epilepsy (Aarabi and He, 2012). The prediction process included the spatio-temporal integration of univariate and bivariate nonlinear features extracted from iEEG data using the patient-specific rules established based on the characteristics of preictal periods for individual patients. We evaluated the system performance on iEEG data collected from patients with hippocampal epilepsy. Over 38 seizures with hippocampal origin, our rule-based seizure prediction system achieved an average sensitivity of 86.7% and 92.9%, an average specificity of 96.7%, and an average false prediction rate of 0.126/h and 0.096/h with SOPs of 30 and 50 min (SPH=10 sec), respectively. Our system showed relatively better prediction performances for patients with focal hippocampal epilepsy compared to those with focal neocortical epilepsy (Aarabi and He, 2012). The performance improvement might be partly explained by higher inhomogeneity in clinical manifestations and electrographic characteristics between patients with focal neocortical epilepsy (Lee et al., 2000). The performance of our system has been compared with those of others (see Aarabi and He, 2012, for more discussion).
4.1. Seizure predictability power of univariate and bivariate measures
In our previous work, we investigated the significance of changes in univariate and bivariate nonlinear measures prior to seizures with neocortical origin. The results of the significance analysis were compared with those previously reported in the literature (see Aarabi and He, 2012 and the references therein). In this study, we applied the same nonlinear measures for the identification of preictal periods before seizures with hippocampal origin. Table 5 lists the sensitivities and false prediction rates reported in our previous and current studies. Overall, we achieved higher sensitivities and lower false prediction rates for patients with hippocampal epilepsy compared to those with neocortical epilepsy with SOPs of 30 and 50 min and SPH= 10 s using each of the features used in our study. In the current study, the percentage of seizures exhibiting significant preictal decreases or increases in univariate measures (compared with baselines) were not significantly different from those reported in our previous study. As indicated in Table 5, the only exception was the Lempel-Zip complexity for which a higher percentage of seizures with significant preictal increases were observed in the current study.
Table 5.
Overall single-feature system performance in patients with hippocampal epilepsy (currect study) and neocortical epilepsy (previous study, Aarabi and He, 2012) with a seizure prediction horizon of 10 sec.
| Feature | Study | SEN % |
FPR /h |
Preictal change compared to baseline | ||
|---|---|---|---|---|---|---|
| Decrease | increase | No-change | ||||
| Correlation dimension | Previous | 78.8 | 0.26 | 44.9 | 44.9 | 10.2 |
|
|
||||||
| Current | 91.7 | 0.17 | 50 | 47.4 | 2.6 | |
|
| ||||||
| Lyapunov exponent | Previous | 73.5 | 0.21 | 51 | 36.7 | 12.3 |
|
|
||||||
| Current | 94.1 | 0.18 | 55.3 | 36.8 | 7.9 | |
|
| ||||||
| Lempel-Ziv complexity | Previous | 68.9 | 0.24 | 36.7 | 44.9 | 18.4 |
|
|
||||||
| Current | 91.7 | 0.25 | 36.8 | 60.5 | 2.7 | |
|
| ||||||
| nonlinear interdependence | Previous | 84.9 | 0.26 | 81.6 | 6.2 | 12.2 |
|
|
||||||
| Current | 90.8 | 0.2 | 26.3 | 63.2 | 10.5 | |
SEN: sensitivity; FPR: false prediction rate;
We also observed that the percentage of seizures with hippocampal origin, whose preictal state showed no significant changes in univartate measures in comparison with baseline, were less than those reported for the seizures with neocortical origin (Table 5, last column).
Surprisingly, the majority of the seizures with hippocampal origin showed significant increases in nonlinear interdependence values within preictal periods compared with baseline. This observation is opposed to that we previously reported for the seizures with neocortical origin.
4.2. Spatial synchronization patterns
We used the nonlinear interdependence to study functional connectivity of neuronal networks in preictal periods. Based on significant differences between synchronization values found within preictal and reference periods, three connectivity patterns could be distinguished. In 50% of the patients, functional interactions showed preictally that neuronal networks became either synchronized or desynchronized in a drive (remote contacts) – response (epileptic contacts) relationship. In some cases, interconnections extended over large regions of the brain. This may reflect the effect of nonepileptic brain regions in initiating seizures. This observation is supported by other studies (D’Alessandro et al. 2003, 2005, Mormann et al. 2003, 2005, Esteller et al. 2005, Le Van Quyen et al. 2005). However, in some cases remote areas may already be involved in the “epileptic network” for generating seizures (Wendling et al. 2002).
Only in 10% of the patients, an inverse relationship was observed, i.e. the epileptogenic foci behaved as driving systems and remote areas as response systems. This may reflect the role of epileptic neuronal networks as synchronizers in initiating seizures. The same preictal changes in intracranial contacts within or close to the epileptogenic zone have also been reported in other studies (Elger and Lehnertz 1998, Martinerie et al. 1998, Le Van Quyen et al. 1999).
In the remaining 40% of the patients, strong bidirectional connectivities were observed between epileptic contacts and the surrounding areas, between remote contacts as well as between epileptic and remote contacts. We also found both short- and long-range interactions in all patients. These findings show that best information for seizure prediction and preictal identification does not necessarily come from electrodes near the seizure-onset focus. In addition, each patient showed a similar connectivity pattern between different brain regions across seizures. Our findings are in line with the results of other studies (Gadhoumi et al. 2013; D’Alessandro et al., 2005; Litt et al., 2001).
We could classify the seizures with hippocampal origin based on the characteristic preictal changes in univariate measures in comparison with baselines.
As indicated in Table 5, almost half of the seizures with neocortical or hippocampal origin showed a preictal decrease of the correlation dimension or the largest Lyapunov exponent. These observations are partly concordant with those reported by Aschenbrenner-Scheibe et al. (2003) who observed a dimension drop in 38% of hippocampal seizures and 33% of neocortical seizures at least 50 min prior to seizures. However, in our studies, about 40% of the neocortical or hippocampal seizures exhibited increased correlation dimension or largest Lyapunov exponent.
As a dominant pattern across seizures with both hippocampal and neocortical origins, increased preictal complexity (quantified by Lempel-Ziv complexity) was observed accompanied with high-frequency oscillations, which might cause the initiation of seizures in temporal lobe and neocortical epilepsies (Bragin et al., 1999; Worrell et al., 2004). We also observed increased complexity always accompanied with a significant increase in the level of dynamic noise with high-frequencies in both temporal lobe and neocortical epilepsies.
We found increased complexity and noise level accompanied with decreased correlation dimension and largest Lyapunov exponent in seizures with hippocampal origin. This may reflect low dimensional neuronal networks in the hippocampus with abnormal structural changes, more likely due to neuronal loss, altered neurotransmitter receptor density, dendritic simplification, and axonal sprouting of dentate granule cell axons (Babb and Brown, 1987; De Lanerrole et al., 1989; McDonald et al., 1991; Sackellares et al., 1999). Loss of neuronal inhibition as well as an elevated number of excitatory-excitatory feedback connections can be led to epileptic neuronal networks without self-controlling inhibitors, or, in other words, an increased level of complexity with stochastic components. Sackellares et al. (1999) hypothesized that structural changes in the epileptic hippocampus disrupt excitatory and inhibitory feedback circuits normally present in the hippocampus, an occurrence which leads to disturbances in the dynamic behavior of the epileptic hippocampus. In a recent study, we used a neural mass model for seizure prediction to investigate changes in biophysical parameters such as connectivity strengths between excitatory and inhibitory neuronal populations in periods prior to neocortical and hippocampal seizures. In that study, we also observed disruption in coupling strengths between excitatory and inhibitory interneurons in patients with neocortical and/or hippocampal seizures (Aarabi and He, 2014). In the current study, we quantified these disturbances by estimating the noise level in the dynamics of epileptic networks and showed that an increase in the dynamic noise level may decrease the synchronization level or increase the complexity of the epileptic neural networks.
As the characteristic synchronization pattern, the majority of the hippocampal seizures exhibited a decreased level of preictal synchronization in comparison with baseline, while the synchronization level increased preictally in most of the neocortical seizures studied in our previous study (Aarabi and He, 2012). On the other hand, based on the spatial connectivity maps in 6 (out of 10) patients with focal hippocampal epilepsy, an involvement of the ipsilateral hippocampus was observed, whereas in the remaining four patients a strong involvement of the contralateral hippocampus were observed in the epileptogenic process. These findings are in agreement with the observations reported by Ende et al. (1997).
5. Conclusions
In this study, we evaluated the performance of our seizure prediction tool on seizures with hippocampal origin. We obtained higher sensitivities and lower false prediction rates for hippocampal seizures in comparison with neocortical seizures. Using univariate and bivariate measures, we also observed persistent spatio-temporal preictal patterns exhibiting patient-specific dynamic signatures for most of the patients included in this study. These patterns provided us robust seizure precursors, which could be used for seizure prediction and consequently preictal identification. Preictal changes in the dynamics of epileptic networks were observed in electrodes located in the epileptogenic zone as well as in remote areas.
Highlights.
Our rule-based seizure prediction system provided an average sensitivity of >90%.
Nonlinear analysis revealed patient-specific changes prior to hippocampal seizures.
Preictal changes in iEEG data occurred in epileptogenic zones and remote areas.
Significance.
The spatio-temporal characterization of preictal periods may help to better understand the mechanism underlying seizure generation in patients with focal hippocampal epilepsy.
Acknowledgments
We wish to thank Kaitlin Cassady for proofreading of the manuscript. This work was supported in part by NIH EB021027 and NS096761.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Disclosures
No conflicts of interest, financial or otherwise, are declared by the authors.
References
- Aarabi A, He B. A rule-based seizure prediction method for focal neocortical epilepsy. Clin Neurophysiol. 2012;123:1111–22. doi: 10.1016/j.clinph.2012.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aarabi A, He B. Seizure prediction in hippocampal and neocortical epilepsy using a model-based approach. Clin Neurophysiol. 2014;125:930–40. doi: 10.1016/j.clinph.2013.10.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aboy M, Hornero R, Abasolo D, Alvarez D. Interpretation of the Lempel-Ziv complexity measure in the context of biomedical signal analysis. IEEE T Biomed Eng. 2006;53:2282–8. doi: 10.1109/TBME.2006.883696. [DOI] [PubMed] [Google Scholar]
- Alvarez-Silva S, Alvarez-Silva I, Alvarez-Rodriguez J, Perez-Echeverria MJ, Campayo-Martinez A, Rodriguez-Fernandez FL. Epileptic consciousness: concept and meaning of aura. Epilepsy Behav. 2006;8:527–33. doi: 10.1016/j.yebeh.2005.12.013. [DOI] [PubMed] [Google Scholar]
- Arnhold J, Grassberger P, Lehnertz K, Elger CE. A robust method for detecting interdependencies: application to intracranially recorded EEG. Physica D. 1999;134:419–30. [Google Scholar]
- Aschenbrenner-Scheibe R, Maiwald T, Winterhalder M, Voss HU, Timmer J, Schulze-Bonhage A. How well can epileptic seizures be predicted? An evaluation of a nonlinear method. Brain. 2003;126:2616–26. doi: 10.1093/brain/awg265. [DOI] [PubMed] [Google Scholar]
- Baker GA, Jacoby A, Buck D, Stalgis C, Monnet D. Quality of life of people with epilepsy: a European study. Epilepsia. 1997;38:353–62. doi: 10.1111/j.1528-1157.1997.tb01128.x. [DOI] [PubMed] [Google Scholar]
- Basar E. Brain Function and Oscillations. Berlin: Springer-Verlag; 1998. [Google Scholar]
- Baumgartner C, Serles W, Leutmezer F, Pataraia E, Aull S, Czech T, et al. Preictal SPECT in temporal lobe epilepsy: regional cerebral blood flow is increased prior to electroencephalography-seizure onset. J Nucl Med. 1998;39:978–82. [PubMed] [Google Scholar]
- Buck D, Baker GA, Jacoby A, Smith DF, Chadwick DW. Patients’ experiences of injury as a result of epilepsy. Epilepsia. 1997;38:439–44. doi: 10.1111/j.1528-1157.1997.tb01733.x. [DOI] [PubMed] [Google Scholar]
- Cao L. Practical method for determining the minimum embedding dimension of a scalar time series. Physica D. 1997;110:43–50. [Google Scholar]
- Casdagli MC, Iasemidis LD, Savit RS, Gilmore RL, Roper SN, Sackellares JC. Non-linearity in invasive EEG recordings from patients with temporal lobe epilepsy. Electroencephalogr Clin Neurophysiol. 1997;102:98–105. doi: 10.1016/s0921-884x(96)95195-4. [DOI] [PubMed] [Google Scholar]
- Chaovalitwongse WA, Prokopyev QA, Pardalos PM. Electroencephalogram (EEG) time series classification: Applications in epilepsy. Ann Oper Res. 2006;148:227–50. [Google Scholar]
- Cockerell OC, Johnson AL, Sander JW, Hart YM, Goodridge DM, Shorvon SD. Mortality from epilepsy: results from a prospective population-based study. Lancet. 1994;344:918–21. doi: 10.1016/s0140-6736(94)92270-5. [DOI] [PubMed] [Google Scholar]
- Cook MJ, O’Brien TJ, Berkovic SF, Murphy M, Morokoff A, Fabinyi G, et al. Prediction of seizure likelihood with a long-term, implanted seizure advisory system in patients with drug-resistant epilepsy: a first-in-man study. Lancet Neurol. 2013;12:563–71. doi: 10.1016/S1474-4422(13)70075-9. [DOI] [PubMed] [Google Scholar]
- D’Alessandro M, Esteller R, Vachtsevanos G, Hinson A, Echauz J, Litt B. Epileptic seizure prediction using hybrid feature selection over multiple intracranial EEG electrode contacts: a report of four patients. IEEE T Biomed Eng. 2003;50:603–15. doi: 10.1109/tbme.2003.810706. [DOI] [PubMed] [Google Scholar]
- D’Alessandro M, Vachtsevanos G, Esteller R, Echauz J, Cranstoun S, Worrell G, et al. A multi-feature and multi-channel univariate selection process for seizure prediction. Clin Neurophysiol. 2005;116:506–16. doi: 10.1016/j.clinph.2004.11.014. [DOI] [PubMed] [Google Scholar]
- DeCoster GP, Mitchell DW. Nonlinear Monetary Dynamics. J Bus Econ Stat. 1991;9:455–62. [Google Scholar]
- Drury I, Smith B, Li D, Savit R. Seizure prediction using scalp electroencephalogram. Exp Neurol. 2003;184:9–18. doi: 10.1016/s0014-4886(03)00354-6. [DOI] [PubMed] [Google Scholar]
- Elger C, Lehnertz K. Ictogenesis and chaos. In: Wolf P, editor. Epileptic seizures and syndromes Sydney. John Libbey & Company Ltd; 1994. pp. 541–46. [Google Scholar]
- Elger CE, Lehnertz K. Seizure prediction by non-linear time series analysis of brain electrical activity. Eur J Neurosci. 1998;10:786–9. doi: 10.1046/j.1460-9568.1998.00090.x. [DOI] [PubMed] [Google Scholar]
- Elger CE. Future trends in epileptology. Curr Opin Neurol. 2001;14:185–6. doi: 10.1097/00019052-200104000-00008. [DOI] [PubMed] [Google Scholar]
- Esteller R, Echauz J, D’Alessandro M, Worrell G, Cranstoun S, Vachtsevanos G, et al. Continuous energy variation during the seizure cycle: towards an on-line accumulated energy. Clin Neurophysiol. 2005;116:517–26. doi: 10.1016/j.clinph.2004.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldwisch-Drentrup H, Schelter B, Jachan M, Nawrath J, Timmer J, Schulze-Bonhage A. Joining the benefits: combining epileptic seizure prediction methods. Epilepsia. 2010;51:1598–606. doi: 10.1111/j.1528-1167.2009.02497.x. [DOI] [PubMed] [Google Scholar]
- Gadhoumi K, Lina JM, Gotman J. Seizure prediction in patients with mesial temporal lobe epilepsy using EEG measures of state similarity. Clin Neurophysiol. 2013;124:1745–54. doi: 10.1016/j.clinph.2013.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gadhoumi K, Lina JM, Mormann F, Gotman J. Seizure prediction for therapeutic devices: A review. J Neurosci Methods. 2016;260:270–82. doi: 10.1016/j.jneumeth.2015.06.010. [DOI] [PubMed] [Google Scholar]
- Iasemidis LD, Sackellares JC, Zaveri HP, Williams WJ. Phase space topography and the Lyapunov exponent of electrocorticograms in partial seizures. Brain Topogr. 1990;2:187–201. doi: 10.1007/BF01140588. [DOI] [PubMed] [Google Scholar]
- Iasemidis LD, Sackellares JC. Chaos theory and epilepsy. Neuroscientist. 1996;2:118–26. [Google Scholar]
- Iasemidis LD. Epileptic seizure prediction and control. IEEE T Biomed Eng. 2003;50:549–58. doi: 10.1109/tbme.2003.810705. [DOI] [PubMed] [Google Scholar]
- Larter R, Speelman B, Worth RM. A coupled ordinary differential equation lattice model for the simulation of epileptic seizures. Chaos. 1999;9:795–804. doi: 10.1063/1.166453. [DOI] [PubMed] [Google Scholar]
- Le Van Quyen M, Martinerie J, Baulac M, Varela F. Anticipating epileptic seizures in real time by a non-linear analysis of similarity between EEG recordings. Neuroreport. 1999;10:2149–55. doi: 10.1097/00001756-199907130-00028. [DOI] [PubMed] [Google Scholar]
- Le Van Quyen M, Martinerie J, Navarro V, Baulac AM, Varela FJ. Characterizing neurodynamic changes before seizures. J Clin Neurophysiol. 2001;18:191–208. doi: 10.1097/00004691-200105000-00001. [DOI] [PubMed] [Google Scholar]
- Le Van Quyen M, Soss J, Navarro V, Robertson R, Chavez M, Baulac M, et al. Preictal state identification by synchronization changes in long-term intracranial EEG recordings. Clin Neurophysiol. 2005;116:559–68. doi: 10.1016/j.clinph.2004.10.014. [DOI] [PubMed] [Google Scholar]
- Lehnertz K, Andrzejak RG, Arnhold J, Kreuz T, Mormann F, Rieke C, et al. Nonlinear EEG analysis in epilepsy: its possible use for interictal focus localization, seizure anticipation, and prevention. J Clin Neurophysiol. 2001;18:209–22. doi: 10.1097/00004691-200105000-00002. [DOI] [PubMed] [Google Scholar]
- Lehnertz K, Elger CE. Spatio-temporal dynamics of the primary epileptogenic area in temporal lobe epilepsy characterized by neuronal complexity loss. Electroencephalogr Clin Neurophysiol. 1995;95:108–17. doi: 10.1016/0013-4694(95)00071-6. [DOI] [PubMed] [Google Scholar]
- Litt B, Echauz J. Prediction of epileptic seizures. Lancet Neurol. 2002;1:22–30. doi: 10.1016/s1474-4422(02)00003-0. [DOI] [PubMed] [Google Scholar]
- Litt B, Esteller R, Echauz J, D’Alessandro M, Shor R, Henry T, Pennell P, Epstein C, Bakay R, Dichter M, Vachtsevanos G. Epileptic seizures may begin hours in advance of clinical onset: a report of five patients. Neuron. 2001;30(1):51–64. doi: 10.1016/s0896-6273(01)00262-8. [DOI] [PubMed] [Google Scholar]
- Maiwald T, Winterhalder M, Aschenbrenner-Scheibe R, Voss HU, Schulze-Bonhage A, Timmer J. Comparison of three nonlinear seizure prediction methods by means of the seizure prediction characteristic. Physica D. 2004;194:357–68. [Google Scholar]
- Mann HB, Whitney DR. On a test of whether one of two random variables is stochastically larger than the other. Ann Math Stat. 1947;18:50–60. [Google Scholar]
- Martinerie J, Adam C, Le Van Quyen M, Baulac M, Clemenceau S, Renault B, Varela FJ. Epileptic seizures can be anticipated by non-linear analysis. Nat Med. 1998;4:1173–76. doi: 10.1038/2667. [DOI] [PubMed] [Google Scholar]
- Matsumoto H, Marsan CA. Cortical Cellular Phenomena in Experimental Epilepsy: Interictal Manifestations. Exp Neurol. 1964;9:286–304. doi: 10.1016/0014-4886(64)90025-1. [DOI] [PubMed] [Google Scholar]
- Mirowski P, Madhavan D, Lecun Y, Kuzniecky R. Classification of patterns of EEG synchronization for seizure prediction. Clin Neurophysiol. 2009;120:1927–40. doi: 10.1016/j.clinph.2009.09.002. [DOI] [PubMed] [Google Scholar]
- Moon YI, Rajagopalan B, Lall U. Estimation of mutual information using kernel density estimators. Phys Rev E. 1995;52:2318–21. doi: 10.1103/physreve.52.2318. [DOI] [PubMed] [Google Scholar]
- Mormann F, Andrzejak RG, Elger CE, Lehnertz K. Seizure prediction: the long and winding road. Brain. 2007;130:314–33. doi: 10.1093/brain/awl241. [DOI] [PubMed] [Google Scholar]
- Mormann F, Elger CE, Lehnertz K. Seizure anticipation: from algorithms to clinical practice. Curr Opin Neurol. 2006;19:187–93. doi: 10.1097/01.wco.0000218237.52593.bc. [DOI] [PubMed] [Google Scholar]
- Mormann F, Kreuz T, Andrzejak RG, David P, Lehnertz K, Elger CE. Epileptic seizures are preceded by a decrease in synchronization. Epilepsy Res. 2003;53:173–85. doi: 10.1016/s0920-1211(03)00002-0. [DOI] [PubMed] [Google Scholar]
- Mormann F, Kreuz T, Rieke C, Andrzejak RG, Kraskov A, David P, et al. On the predictability of epileptic seizures. Clin Neurophysiol. 2005;116:569–87. doi: 10.1016/j.clinph.2004.08.025. [DOI] [PubMed] [Google Scholar]
- Mormann F, Lehnertz K, David P, Elger CE. Mean phase coherence as a measure for phase synchronization and its application to the EEG of epilepsy patients. Physica D. 2000;144:358–69. [Google Scholar]
- Rajna P, Clemens B, Csibri E, Dobos E, Geregely A, Gottschal M, et al. Hungarian multicentre epidemiologic study of the warning and initial symptoms (prodrome, aura) of epileptic seizures. Seizure. 1997;6:361–8. doi: 10.1016/s1059-1311(97)80035-0. [DOI] [PubMed] [Google Scholar]
- Ramgopal S, Thome-Souza S, Jackson M, Kadish NE, Sanchez Fernandez I, Klehm J, et al. Seizure detection, seizure prediction, and closed-loop warning systems in epilepsy. Epilepsy Behav. 2014;37:291–307. doi: 10.1016/j.yebeh.2014.06.023. [DOI] [PubMed] [Google Scholar]
- Rosenstein MT, Collins JC, De Luca CJ. A practical method for calculating the largest Lyapunov exponents from small datasets. Physica D. 1993;65:117–34. [Google Scholar]
- Sackellares JC, Iasemidis LD, Gilmore RL, Roper SN. Epilepsy: when chaos fails. In: Lehnertz K, Arnhold J, Grassberger P, Elger CE, editors. Chaos in the Brain. World Scientific Singapore; 2000. [Google Scholar]
- Schelter B, Winterhalder M, Maiwald T, Brandt A, Schad A, Timmer J, Schulze-Bonhage A. Do false predictions of seizures depend on the state of vigilance? A report from two seizure-prediction methods and proposed remedies. Epilepsia. 2006;47:2058–70. doi: 10.1111/j.1528-1167.2006.00848.x. [DOI] [PubMed] [Google Scholar]
- Schindler K, Wiest R, Kollar M, Donati F. EEG analysis with simulated neuronal cell models helps to detect pre-seizure changes. Clin Neurophysiol. 2002;113:604–14. doi: 10.1016/s1388-2457(02)00032-9. [DOI] [PubMed] [Google Scholar]
- Stein AG, Eder HG, Blum DE, Drachev A, Fisher RS. An automated drug delivery system for focal epilepsy. Epilepsy Res. 2000;39:103–14. doi: 10.1016/s0920-1211(99)00107-2. [DOI] [PubMed] [Google Scholar]
- Takens F. Detecting strange attractors in turbulence. In: Rand DA, Young LS, editors. Dynamic systems and turbulence lecture notes on mathematics. Vol. 898. New York: Springer; 1988. pp. 366–81. [Google Scholar]
- van Drongelen W, Nayak S, Frim DM, Kohrman MH, Towle VL, Lee HC, et al. Seizure anticipation in pediatric epilepsy: use of Kolmogorov entropy. Pediatr Neurol. 2003;29:207–13. doi: 10.1016/s0887-8994(03)00145-0. [DOI] [PubMed] [Google Scholar]
- Wendling F, Bartolomei F, Bellanger JJ, Chauvel P. Epileptic fast activity can be explained by a model of impaired GABAergic dendritic inhibition. Eur J Neurosci. 2002;15:1499–508. doi: 10.1046/j.1460-9568.2002.01985.x. [DOI] [PubMed] [Google Scholar]
- Winterhalder M, Schelter B, Maiwald T, Brandt A, Schad A, Schulze-Bonhage A, et al. Spatio-temporal patient-individual assessment of synchronization changes for epileptic seizure prediction. Clin Neurophysiol. 2006;117:2399–413. doi: 10.1016/j.clinph.2006.07.312. [DOI] [PubMed] [Google Scholar]
- Wolf A, Swift JB, Swinney L, Vastano A. Determining Lyapunov exponents from a time series Physica D. 1985;16:285–317. [Google Scholar]
- Yaari Y, Beck H. “Epileptic neurons” in temporal lobe epilepsy. Brain Pathol. 2002;12:234–9. doi: 10.1111/j.1750-3639.2002.tb00438.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu D, Small M, Harrison RG, Diks C. Efficient implementation of the gaussian kernel algorithm in estimating invariants and noise level from noisy time series data. Physical Rev E. 2000;61:3750–6. doi: 10.1103/physreve.61.3750. [DOI] [PubMed] [Google Scholar]
- Zhang DD, Zhou XH, Freeman DH, Jr, Freeman JL. A non-parametric method for the comparison of partial areas under ROC curves and its application to large health care data sets. Stat Med. 2002;21:701–15. doi: 10.1002/sim.1011. [DOI] [PubMed] [Google Scholar]