Abstract
Purpose
Establish the essential requirements for characterization of a transversely isotropic material by magnetic resonance elastography (MRE).
Theory and Methods
Three methods for characterizing nearly incompressible, transversely isotropic (ITI) materials were used to analyze data from: closed-form expressions for traveling waves; finite element (FE) simulations of waves in homogeneous ITI material; and FE simulations of waves in heterogeneous material. Key properties are the complex shear modulus μ2, shear anisotropy ϕ = μ1/μ2 − 1, and tensile anisotropy ζ = E1/E2 − 1.
Results
Each method provided good estimates of ITI parameters when both slow and fast shear waves with multiple propagation directions were present. No method gave accurate estimates when the displacement field contained only slow shear waves, only fast shear waves, or waves with only a single propagation direction. Methods based on directional filtering are robust to noise and include explicit checks of propagation and polarization. Curl-based methods led to more accurate estimates in low noise conditions. Parameter estimation in heterogeneous materials is challenging for all methods.
Conclusion
Multiple shear waves, both slow and fast, with different propagation directions, must be present in the displacement field for accurate parameter estimates in ITI materials. Experimental design and data analysis can ensure these requirements are met.
Keywords: MR Elastography, anisotropy, transversely isotropic material, shear waves, inversion algorithms, heterogeneity
INTRODUCTION
Magnetic Resonance Elastography (MRE) (1) is a noninvasive, imaging technique which has been used widely to estimate the material properties of living tissue. In MRE, the displacements of small-amplitude shear waves are measured as the waves travel through the tissue. For isotropic, homogeneous materials such as the liver, an elastic modulus is readily estimated from the wave speed (2). However, biological tissue is often fibrous, resulting in material properties that depend on direction. Such a tissue is anisotropic and requires several material parameters to describe it. A number of MRE studies have been conducted for anisotropic tissues such as skeletal muscle (3,4), breast tissue (5), and the white matter in the brain (6). Additional complexities encountered in living tissue include heterogeneity and boundary effects, such as those observed in the brain (7–9).
The speed of a shear wave travelling in an anisotropic tissue depends on both the direction of propagation and the direction of material motion (polarization) (10). Instead of a single elastic modulus, a more sophisticated material model is required to interpret the MRE image of anisotropic tissues. Material models such as the transversely isotropic (TI) model (11) or the orthotropic model (6,12) require five or more material parameters. The number of material parameters can be reduced by approximating the tissue as incompressible. The incompressible, transversely isotropic (ITI) material model requires three elastic material parameters, which is the fewest material parameters required to fully describe a fiber-reinforced tissue (13). In earlier work by Romano et al. (6) the components of the full TI elasticity tensor were sought by MRE. In contrast, in the ITI model the elasticity tensor is not estimated, as its components diverge as the bulk modulus becomes infinite. In practice, while the bulk modulus of soft tissue is finite, it is usually several orders of magnitude greater than the shear modulus. As a consequence, the elements of the elasticity tensor vary over a similar range, making the accurate recovery of the full TI elasticity tensor very difficult. This is also true for the isotropic case; in isotropic MRE it is typical to estimate only the shear modulus, rather than the full elasticity tensor as in (6). In the isotropic case the shear modulus uniquely specifies the incompressible compliance tensor. Similarly in anisotropic MRE, the ITI model requires only the 3 key parameters that uniquely determine the compliance tensor.
Spatial heterogeneity is an additional complication that must be considered when estimating material parameters in tissue such as the brain. The brain has regions of white and grey matter and cerebrospinal fluid which can affect the accuracy of estimates. Many investigators (Clayton et al. (14), e.g.) have reported spatial differences when estimating an isotropic, viscoelastic shear modulus across the brain. In studies incorporating an orthotropic model, Romano et al. (6) incorporated the heterogeneity of white and gray matter to estimate viscoelastic material parameters. McGrath et al. (15) evaluated the effects of heterogeneity and boundary conditions on isotropic, viscoelastic material parameters estimates from finite element models (FEM). They showed that errors tended to occur at material boundaries due to the violation of the local homogeneity assumption of the direct inversion algorithm (15).
We seek to clarify what minimum set of experimental measurements from MRE are needed to estimate anisotropic material parameters, particularly in a realistic case with heterogeneous properties. It is intuitive that more data should be required to estimate the material properties of an anisotropic tissue than for an isotropic material. In particular, since properties depend on direction, it is clear that experimental conditions should create wave motions that depend upon all of the anisotropic material parameters. To date, minimum requirements for parameter estimation have been reported only for specific methods, such as impulse excitation in ITI materials (Papazoglou et al. (3) and Rouze et al. (16)).
Recently, Guo et al. (17) and Tweten et al. (18) proposed methods to estimate ITI material parameters from MRE images during harmonic excitation. The paper of Guo et al. (17) does not explicitly specify the minimum conditions required for material parameter estimates from their curl-based inversion method (henceforth denoted as the “Curl” algorithm). The directionally filtered inversion (DFI) method proposed by Tweten et al. (18) specifies two requirements in experimental measurements: 1) both slow and fast shear wave polarizations and 2) shear waves propagating in multiple directions. In addition, both methods assume local homogeneity, which may lead to errors, as shown by McGrath et al. (15). To our knowledge, neither the DFI nor the Curl methods have been systematically evaluated in heterogeneous materials using simulations with known material parameter values. Establishing the minimum experimental conditions required for estimating TI material parameters, independent of estimation approach, would be of great value to the MRE experimentalist.
The primary objective of this paper is to show that the minimum experimental conditions for estimating anisotropic material parameters proposed by Tweten et al. (18) for the DFI method apply to other methods which incorporate an ITI material model. Using analytically created data sets and FE simulations, we evaluate the performance of the Curl (17) and DFI (18) methods using displacement fields which either meet or do not satisfy the proposed minimum requirements. We also introduce a modification to the DFI method which enables estimates of the viscoelastic shear modulus. The performance of both methods is evaluated for a heterogeneous FE simulation with known material parameter values. Finally, we discuss how to assess whether MRE measurements meet the minimum conditions and how to accommodate experiments when no single MRE measurement meets the minimum conditions.
THEORY
We start with an incompressible, transversely isotropic material as our model for fiber-reinforced tissues. An ITI material is fully described using three parameters (13,17,18), which can be a combination of two tensile moduli (E1 and E2 ) and two shear moduli (μ1 and μ2 ). Here the tensile modulus is defined as E1 and the shear modulus is defined as μ1. The three ITI material parameters are defined in this paper as the substrate shear modulus μ = μ2, shear anisotropy ϕ = μ1/μ2 − 1, and tensile anisotropy ζ = E1/E2 − 1. For this set of parameters, the subscript 1 indicates the fiber orientation, which is assumed to be in the x = x1 direction (18,19). However, the following equations are applicable for any arbitrary fiber direction.
During MRE studies of anisotropic tissue, multiple shear waves travel through the material and the resulting displacement field is measured. For small, elastic displacements such as those excited in MRE, individual waves can be modeled using the solution for traveling plane waves:
| [1] |
where u is the displacement, m is the polarization unit vector of the wave, u0 is the amplitude, k is the wavenumber, x is the spatial location, n is the propagation direction unit vector, and ω is the frequency. Note that the polarization indicates the direction of shear displacements. Equation [1] is the solution to the equation of motion
| [2] |
where σ is a second order Cauchy stress tensor, ∇ · σ is the divergence of σ, ρ is the density, and t is the time.
For an ITI material, the acoustic tensor from Christoffel’s equation (20) can be found by combining Eqs. [1] and [2] with the material mode (compliance and stiffness tensors) from Tweten et al. (18). This eigenvalue problem provides the speeds (eigenvalues) and polarizations (eigenvectors) of the slow (pure transverse, or PT) and fast (quasi-transverse, or QT) shear waves. The slow and fast shear wave speeds are given by
| [3] |
| [4] |
respectively, where cos(θ) = n · a and a is the fiber direction unit vector. The polarizations of the slow and fast shear waves are given by
| [5] |
| [6] |
respectively. A third eigenvalue and associated eigenvector represent longitudinal waves which will have much longer wavelength; longitudinal waves may be removed by filtering approaches (18). The loss factor of the material can be estimated by
| [7] |
which requires estimating complex material properties (μ = μ′ + iμ;″ ). Note that to use Eqs. [3] and [4] with LFE, the loss factor is assumed to be small, so μ′ ≈ |μ|. For the DFI-LDI method, the complex shear modulus μ is estimated explicitly.
Using the Curl method, Guo et al. (17) estimated the shear moduli μ12 and μ13 and the tensile modulus in the fiber direction E3, but individual slow and fast shear waves were not resolved. Table 1 provides a comparison of the material properties used by both Tweten et al. (18) and Guo et al. (17), see Appendix A for more details.
Table 1.
A standard set of elastic moduli of a transversely isotropic material E//, E⊥, E//, and E⊥ and the bulk modulus κ are defined in terms of the parameter sets proposed by Feng et al. (13), Guo et al. (17), Rouze et al. (16) (consistent with Papazoglou et al. (3)), and Royer et al. (11). The first three parameter sets include the approximation of incompressibility which leads to κ → ∞ and require a total of only three parameters. All five parameters are required to describe the TI material of model without the incompressibility approximation, as expressed by Royer et al. (11).
METHODS
Directional Filter Methods
In this section, we summarize the DFI method presented by Tweten et al. (18) which relies on LFE (21) to estimate wave speed, and introduce a modified DFI method which instead uses local direct inversion (LDI) (22) to estimate complex wave speed. LDI adds the capability of estimating the loss factor to the DFI method. Steps in the DFI approach are: (i) isolate shear waves, (ii) estimate wave speeds, (iii) apply inclusion criteria, and (iv) estimate material parameters.
First, the fiber direction α must be known, and a set of arbitrary propagation directions (or filter directions) n are selected. For each filter direction, a dot product is taken between the displacement field and ms and mf, resulting in two polarized displacement fields (us and uf ). Each polarized field is directionally filtered along n in Fourier space (23), resulting in directionally filtered (DF) data sets.
Next, the wave speeds of the DF displacement fields are estimated using the LFE method (21), which we refer to as DFI-LFE. DFI-LFE cannot estimate η. In a second method, we use the LDI method proposed by Okamoto et al. (22) to estimate wave speeds, which we refer to as DFI-LDI. LDI provides estimates of complex wave numbers and can be used to estimate η.
In this paper, we use amplitude and “certainty” thresholds as inclusion criteria. For the amplitude threshold, the amplitude of the DF displacement field must be larger than a specified fraction of the median amplitude of the unfiltered field.
Finally, material properties are either estimated for an entire homogeneous volume (global) or for each voxel (local) using a least squares (LS) approach (18). Local estimates use a kernel or “sphere” of voxels with the estimated parameters assigned to the voxel at the center of the kernel. In DFI-LFE the LS approach is weighted by the relative amplitude of the filtered wave field at each voxel (18).
For each data set, we selected a set of filter directions based on the observed wave propagation patterns, which are defined in the following sections. For the DFI-LDI method, we chose a total least squares parameter of λ=1 for all data sets (22). For DFI-LFE, we chose a “certainty” threshold of 0.25 for all data sets. For both methods we chose an amplitude threshold of 0.2 for all data sets. Finally, we removed the outer four layers of voxels from all homogeneous volumes to reduce errors due to boundary effects.
Curl Method
In this section we extend the Curl method (17) to accommodate arbitrary fiber directions using a Bond transformation (20) and to incorporate multiple data sets. Guo et al. (17) begins with Navier’s equation applied to the curl of the displacement field:
| [8] |
where q = ∇ × u is the curl of the displacement field and Δq is the Laplacian of the curl.
The original derivation of the Curl method assumes the fiber direction is the z = x3 direction. The Bond transform (20) can be applied to accommodate arbitrary fiber directions. First, we completely expand the vectors in Eq. [8] in terms of their derivatives:
| [9] |
| [10] |
| [11] |
| [12] |
The components of the displacement u are defined by u = u1, v = u2, and w = u2, and the components of the direction x are defined by x = x1, y = x2, and z = x3.
Next, we create a rotation matrix R̂ that transforms the arbitrary fiber direction a = [a1, a2, a3] into a new coordinate system in which , where the superscript R indicates the new coordinate system. In most cases, the rotation matrix can be defined by
| [13] |
The final step is to transform the derivatives of the displacements in Eq. [9] through [12] using R̂. The transformation for a single derivative is given by
| [14] |
where i refers to the components of uR and m refers to the components of u. The index j indicates the components of xR and n indicates the components of x. Eq. [14] is in Einstein notation, in which the summation occurs over the indices m and n. The transformation for a third derivative is given by
| [15] |
where i refers to the components of uR and m refers to the components of u. The indices j, k, and l indicate the components of xR, and the indices n, r, and s indicate the components of x. A concrete example is given by .
In order to apply a kernel approach or incorporate multiple data sets, we implement a LS approach for estimating material parameters. Least squares methods require an equation in the form of
| [16] |
where H is the observation matrix, x is a set of parameters to be estimated, and y is a set of measurements. The parameters x can be estimated using
| [17] |
where x̃ are the estimated parameters. After modifying Navier’s equation to fit the form of Eq. [16] we have
| [18] |
where the subscript on each variable is the component of the corresponding vector. The subscripts on the parentheses indicate an additional voxel which may come from a kernel approach or a different data set or both. For example, (Bm)n indicates the mth component of the vector B and the nth voxel of the kernel.
In this paper, we apply the Curl method by (i) applying a spatial filter, (ii) calculating the first and third derivatives, (iii) applying the Bond transformation, and (iv) estimating the material parameters.
Following the example of Guo et al. (17), a Butterworth low-pass spatial filter is applied to the displacement field u in all three directions.
We calculate the 1st derivatives using Matlab’s® gradient command and calculate the 3rd derivatives using a combination of the central difference method (2nd derivative) and the gradient command. All derivatives are taken of the filtered displacement field from step (i).
Next we apply a Bond transformation (20) to the 1st and 3rd derivatives.
The vectors q, δq, A, and B in Eq. [8] are constructed from the transformed 1st and 3rd derivatives from step (iii). Material parameters are found using the LS approach, and we use the same kernel approach for the local inversions as we use for the DFI methods.
For all data sets, we chose a cut-off frequency of 1000 rad/m for the low-pass filter. Finally, we removed the outer four layers of voxels from all homogeneous volumes to reduce errors due to boundary effects.
Analytical Data from Closed-Form Solutions of the Wave Equation
We generated analytical displacement fields based on harmonic plane wave motion in anisotropic viscoelastic media to represent MRE data. For a harmonic excitation, Eq. [1] can be reduced to
| [19] |
where up is the slow or fast displacement fields of the pth propagation direction np. The polarization mp and the wave number kp correspond to the pth propagation direction for the slow or fast shear wave. The complex wavenumbers are calculated from kp = f/cp and from Eq. [3] and [4] using a complex shear modulus. The magnitude of the shear wave displacements are u0 = 70 μm, and the frequency is f = 150 Hz for all shear waves. The displacement field is a 70×70×70 grid of 1 mm3 voxels.
We created six independent data sets with either slow or fast shear waves in one of three directions, see Figure 1. The data sets analyzed in this study are obtained by combining these independent data sets using superposition. For all of the data sets, we selected the parameters μ′ =1000 Pa, ϕ=1, ζ=2, η=0.2, and . We chose the following three propagation directions n1 = [−sin15°, 0, −cos15°], n2 = [sin1°, 0, −cos1°], and n3 = [sin15°, 0, −cos15°], with θ = 30°, θ ≈ 45°, θ = 60°, respectively. We chose the filter directions for the DFI methods to be the known propagation directions of the waves.
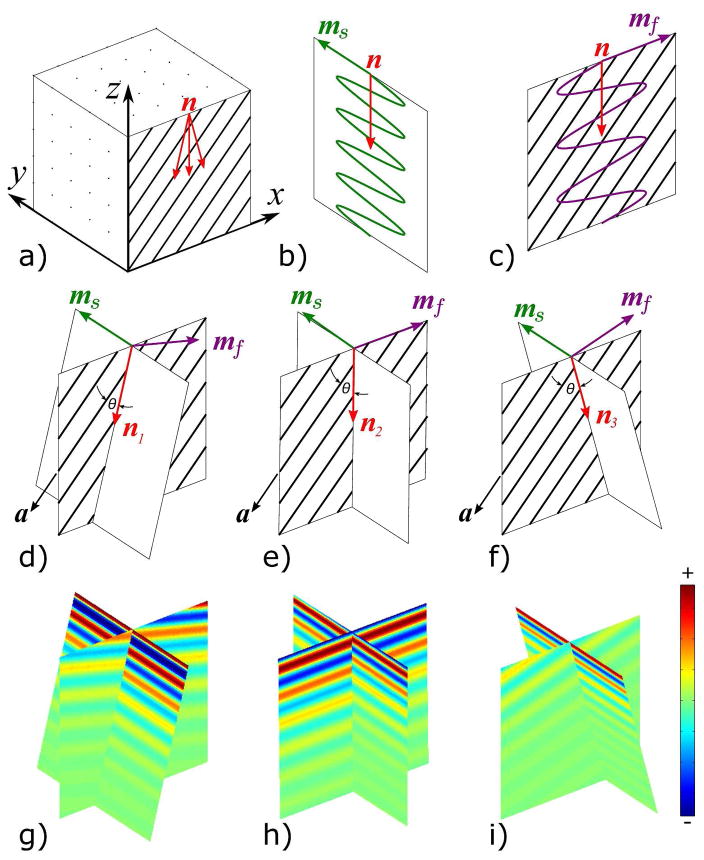
Figure 1.
Approach for creating analytical slow and fast shear wave data sets in three propagation directions. (a) The analytical data sets were created in a 70×70×70 mm3 cube of ITI material with a voxel size of 1 mm3; a fiber direction of ; and material properties of μ = 1000 Pa, ϕ = 1, ζ = 2, and η = 0.2. The displacements of the slow and fast shear waves relative to their polarizations are shown in (b) and (c), respectively. The polarizations of the slow ms and fast mf shear waves are shown with respect to the propagation directions in (d) n1 = [− sin 15°,0, − cos 15°], (e) n2 = [sin 1°,0, − cos 1°], and (f) n3 = [sin 15°,0, − cos 15°]. Relative displacements of the slow and fast shear waves are compared for the propagation directions (g) n1, (h) n2, and (i) n3. Slow shear wave displacements are displayed in the white planes in (d), (e), and (f), and the fast shear wave displacements are shown in the planes which include the fiber directions (black stripes).
Simulation Approach
FE simulations of wave propagation in homogeneous and heterogeneous anisotropic materials were performed using the commercial FE software Comsol™ (Comsol v.5.1, Comsol, Inc., Burlington, MA). In all simulations, we set the parameters μ′ =1000 Pa, ϕ=1, ζ=2, and η=0.2 for the ITI material, which are similar to recent experimental values in fibrin gels (10). In the simulations of the heterogeneous material, we chose μ′ =1000 Pa and η=0.2 for the isotropic material. The Young’s moduli and Poisson’s ratios in the FE simulations were calculated from E1 = μ(4ζ + 3), , ν12 = 0.49, , and ν23 = 1 − ν21 − 0.01. Based on prior work (18), we expect shear wave speeds and ITI parameters to be insensitive to bulk modulus for nearly incompressible materials (K > 100 μ). In the current simulations, bulk modulus , corresponding to slight compressibility. This is intended to complement the analytical cases above, which correspond to the ideal case of perfect incompressibility. Since estimates of soft tissue bulk modulus range up to ~3 GPa (from longitudinal wave data at MHz frequencies) (11), representative computations were performed with a factor of 10 increase in bulk modulus, with quantitatively consistent results.
Schematic depictions of the four simulations with homogeneous material are shown in Figure 2. All simulations have a uniform fiber direction of . We chose n = y and n = −z corresponding to expected primary propagation directions (See Figure 2). The geometry consists of a 50×50×50 mm3 cube with a swept mesh with 13 elements in each direction. The results are sampled with 1 mm3 voxels. The excitation of a 5 N/m2 distributed force at 100 Hz is applied on one face of the cube for each of the four simulations.
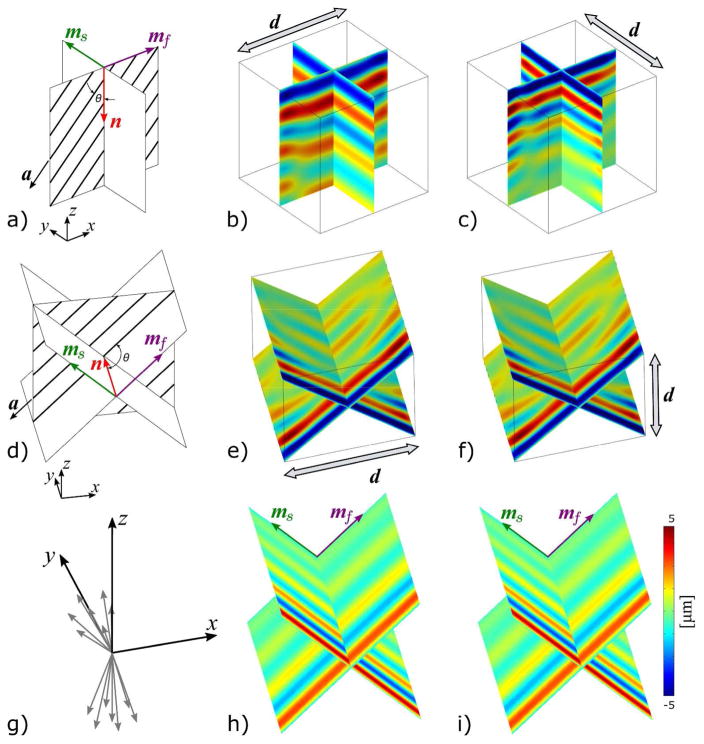
Figure 2.
Approach for simulation of wave propagation in an ITI, homogeneous material with the material parameters shear modulus μ = 1000 Pa, shear anisotropy ϕ = 1, tensile anisotropy ζ = 2, and loss modulus η = 0.2. The cube volume is 50×50×50 mm3 with a voxel size of 1 mm3, and the fiber direction is given by . The top xy-plane is excited with 5 N/m2 at 100 Hz in the (b) x-direction and (c) y-direction. This excitation is expected to result in a primary propagation direction of n = −z. The expected primary polarizations for both simulations in (b) and (c) are shown in (a). For the simulations in which The xz-plane is excited with 5 N/m2 at 100 Hz in the (e) x-direction and (f) z-direction, the expected primary propagation direction is n = y. The expected primary polarizations for both simulations in (e) and (f) are shown in (d). The displacement in the x-direction is plotted in (b) and (e), the displacement in the y-direction is plotted in (c), and the displacement in the z-direction is plotted in (f). Directionally-filtered (DF) displacements from (e) are shown in (h), and DF displacements from (f) are shown in (i). In both cases, the assumed primary polarizations from (d) are used for the filter. Displacements for the slow and fast shear waves are plotted in the planes containing the ms and mf polarizations, respectively. Note that the fast shear waves have longer wavelengths than the slow shear waves. The set of filter directions in (g) were used as the filter directions in Table 3.
The effects of noise were studied by adding normally-distributed white noise to the real and imaginary components of the displacement field in all three directions. The level of noise is defined by
| [20] |
where SNR is the signal-to-noise ratio, A is the median amplitude of the displacement field, and σ is the standard deviation of the noise.
The three simulations of the heterogeneous material are shown in Figure 3. The geometry of each simulation is a 70×70×55 mm3 box with a free tetrahedral mesh (maximum element size of 0.00385 mm and a minimum size of 2.8×10−4 mm). The material is composed of two lobes of ITI material with a fiber direction of and two lobes of ITI material with a fiber direction of . For the Curl method, we assume a constant rotation matrix R̂ for each lobe. We chose n = −x and n = −z corresponding to expected primary propagation directions (See Figure 3). The remainder of the volume contains isotropic material. The lobes have a width of 28 mm and are oriented in the same direction as the fiber. An excitation of 5 N/m2 distributed force at 150 Hz is applied on one face of the box for each simulation.
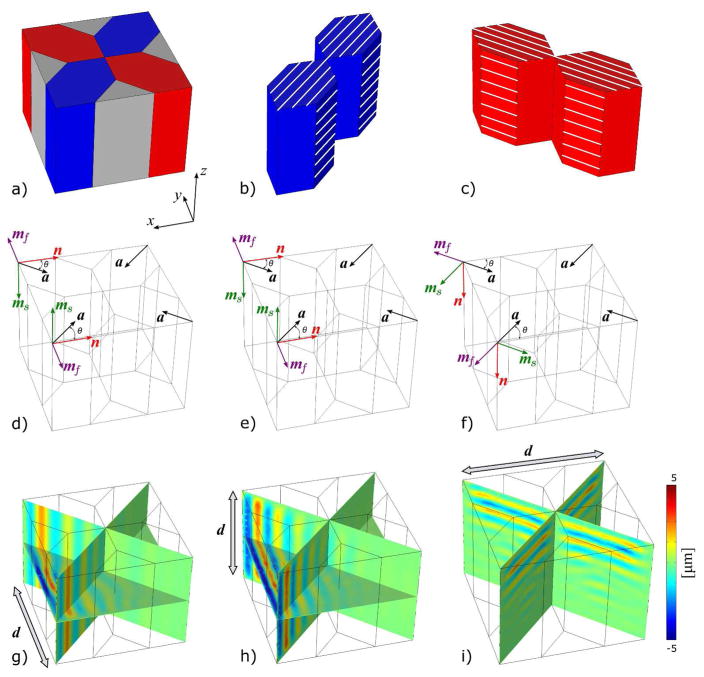
Figure 3.
Approach for simulation of wave propagation in heterogeneous anisotropic material. The overall volume is 70×70×55 mm3 with a voxel size of 1 mm3. Each of the four lobes in (b) and (c) contain ITI, homogeneous material with the parameters μ = 1000 Pa, ϕ = 1, ζ = 2, and η = 0.2. The fiber direction in the lobes are (b) and (c) . The material outside the lobes is isotropic with the material parameters μ = 1000 Pa and η = 0.2. For the simulation shown in (g), the yz-surface farthest from the origin is excited in the y-direction by 5 N/m2 at 150 Hz with an expected primary propagation direction of n = − x as shown in (d). The same yz-surface is excited in the z-direction in the simulation (h) by 5 N/m2 at 150 Hz with an expected primary propagation direction of n = −x as shown in (e). Finally, the top yz-surface is excited in the x-direction in the simulation (i) by 5 N/m2 at 150 Hz with an expected primary propagation direction of n = −z as shown in (f). The primary polarizations for the simulations are shown in (d), (e), and (f). The displacement in the x-direction is plotted in (i), the displacement in the y-direction is plotted in (g), and the displacement in the z-direction is plotted in (h).
RESULTS
Estimates of Anisotropic Parameters from Analytical Data
Global parameter estimates for the analytical data sets, from all three inversion methods, are compared in Table 2. For the data set with only fast shear waves, none of the methods were able to estimate μ, ϕ, or ζ accurately. For the data set with only slow shear waves, the DFI-LFE and Curl methods led to estimates of μ and ϕ within 25% of the known values. For the data sets in which only a single propagation direction was present, none of the methods were capable of accurately estimating the material parameters. When both slow and fast shear waves were present in the data set in all three propagation directions, all three inversion methods were able to estimate all the material parameters within 25% of the known values except DFI-LFE which estimated ζ within 30% of the known value.
Table 2.
Global parameter estimates for the combined analytical data sets (see Figure 1). The “Slow” data set includes the slow shear wave displacement fields from all three propagation directions. The “Fast” data set includes the fast shear wave displacement fields from all three propagation directions. The “Slow + Fast” data set includes all six analytical data sets. The θ = 30°, θ = 45°, and θ = 60° data sets include both slow and fast shear wave displacement fields in a single propagation direction. Since the DFI-LFE method is not able to estimate the loss factor η, no estimate is given in the Table. The known material parameters used for all six analytical data sets are μ = 1000 Pa, ϕ = 1, ζ = 2, and η = 0.2.
| Method | Data set | μ | ϕ | ζ | η |
|---|---|---|---|---|---|
| DFI-LFE | Slow | 966 | 1.17 | 0.44 | - |
| Fast | 2160 | 0.30 | 0.21 | - | |
| Slow + Fast | 962 | 1.27 | 1.95 | - | |
| DFI-LDI | Slow | 1220 | 0.53 | 0.0 | 0.24 |
| Fast | 1820 | 0.66 | 0.46 | 0.18 | |
| Slow + Fast | 1100 | 0.88 | 1.77 | 0.18 | |
| Curl | Slow | 1070 | 0.90 | −2 × 1016 | 0.21 |
| Fast | 3550 | −0.46 | −0.15 | 0.20 | |
| Slow + Fast | 1040 | 0.89 | 1.86 | 0.23 | |
| θ = 30° | 1430 | 0.35 | 1.13 | 0.34 | |
| θ = 45° | 2×108 | −2.00 | −1.00 | 0.11 | |
| θ = 60° | 1420 | −0.38 | 1.35 | −0.04 |
Estimates of Anisotropic Parameters from Simulations of Homogeneous Material
Global parameters estimated for each of the four simulations of the homogeneous material are given in Table 3. In the first simulation, predominantly fast shear waves are excited, and estimates from all three methods are poor. In the second simulation, slow shear waves are mainly excited, and all three inversion methods are able to estimate the μ within 25% of the known values. The Curl method was also able to estimate ϕ within 25% of the known value. Both the third and fourth simulations include displacement fields in which both slow and fast shear waves are excited equally. In these simulations, the DFI-LFE method estimates μ and ζ within 25% of the know values, and the Curl method estimates all material parameters (with the exception of ζ ) within 25% of the known values.
Table 3.
Global parameter estimates for each of the four simulations of wave propagation in homogeneous ITI material. Mainly fast shear waves are excited in simulation 1 (see Figure 2b). A mix of slow and fast shear waves are excited in simulation 2 (see Figure 2c). Slow and fast shear waves are excited equally in simulations 3 and 4 which are shown in Figure 2e and Figure 2f, respectively. The material parameters used for all four simulations are μ = 1000 Pa, ϕ = 1, ζ = 2, and η = 0.2. The filter directions in Figure 2g are implemented in both DFI methods. Since the DFI-LFE method is not able to estimate the loss factor η, no estimate is given in the table.
| Method | Simulation | μ | ϕ | ζ | η |
|---|---|---|---|---|---|
| DFI-LFE | 1 | 2520 | 0.05 | −0.07 | - |
| 2 | 1290 | 0.12 | −0.06 | - | |
| 3 | 981 | 0.62 | 1.79 | - | |
| 4 | 981 | 0.62 | 1.79 | - | |
| DFI-LDI | 1 | 2760 | −0.03 | −0.04 | 0.15 |
| 2 | 1390 | 0.07 | −0.07 | 0.21 | |
| 3 | 1050 | 0.67 | 1.20 | 0.17 | |
| 4 | 1050 | 0.67 | 1.20 | 0.17 | |
| Curl | 1 | 188 | −0.18 | 14.6 | 0.28 |
| 2 | 1000 | 0.87 | 1.29 | 0.26 | |
| 3 | 1010 | 0.93 | 0.86 | 0.17 | |
| 4 | 1010 | 0.93 | 0.86 | 0.17 |
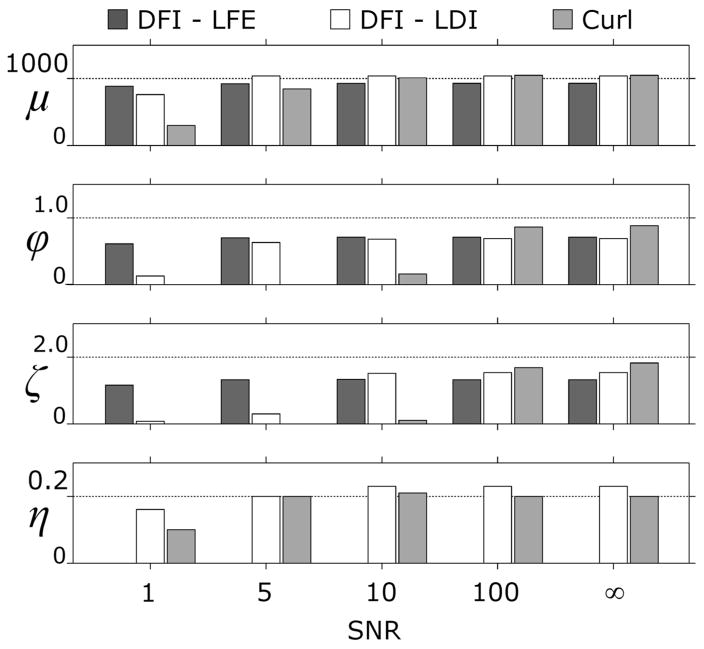
Global material parameter estimates using all four simulations with added noise are compared in Figure 4. Typical experimental MRE displacement fields are expected to have SNR values between 1 and 10. The DFI-LFE method estimated μ within 25% and ϕ and ζ within about 40% of the known values for SNRs between 1 and 10. The DFI-LDI method estimated all four material parameters within 25% of the known values for a SNR of 10 and μ and η within 25% of the known values for SNRs below 10. The Curl method gave estimates of μ and η within 25% of the known values for SNRs of 5 and 10 but was not able to accurately estimate any of the parameters within 25% for a SNR of 1.
Figure 4.
Global estimates of parameters obtained by combining four simulations of waves in homogeneous material are shown for a signal-to-noise ratio (SNR) of 1, 5, 10, 100, and ∞ (no noise added). Noise was added to all displacement directions of each of the four simulations. The bars represent the estimated value for each material parameter; the dotted lines are the known parameter values (μ = 1000 Pa, ϕ = 1, ζ = 2, and η = 0.2.). Note that the DFI-LFE method cannot provide an estimate the loss factor η; only estimates of η from the DFI-LDI and Curl methods are shown.
Local parameter estimates using all four simulations of the homogeneous material are compared in Figure 5. All three inversion methods provide reasonably consistent and accurate estimates for μ and ϕ. In general, estimation errors tend to be larger near the boundaries. For estimates of ζ, the DFI-LFE method provides consistent estimates, while the DFI-LDI and Curl methods have larger areas of greater errors. For the Curl method, we compared the direct inversion approach (17) and the kernel approach using least squares. Supplementary Figure S1 shows that using a kernel approach results in better local estimates in this case.
Figure 5.
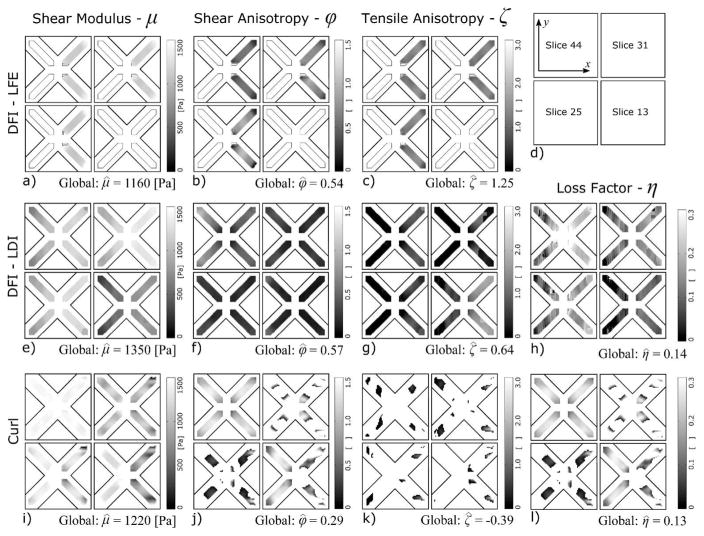
Local parameter estimates obtained from combining the four simulations of waves in homogeneous material are shown for the xy-planes of 13, 25, 31, and 44. An estimation kernel with a radius of 5 voxels is used for all three estimation methods. The outlining box indicates the full extents of the material (50 nm × 50 nm). The outer 4 voxels have been removed from the estimates leaving a smaller shaded region (42 nm × 42 nm) of local parameter estimates. Color bars show a range for each material parameter from a minimum value of zero to a maximum value of 150% of the known values of μ = 1000 Pa, ϕ = 1, ζ = 2, and η = 0.2. Estimates from the DFI-LFE method for (a) μ, (b) ϕ, and (c) ζ are shown in the top row. Estimates from the DFI-LDI method for (e) μ, (f) ϕ, (g) ζ, and (h) η are shown in the second row. Estimates from the Curl method (with kernel approach) for (i) μ, (j) ϕ, (k) ζ, and (l) η are shown in the third row.
Estimates of Anisotropic Parameters from Simulations of Heterogeneous Material
Global and local parameters estimated by combining the three simulations of the heterogeneous material are compared in Figure 6. Under these conditions and for all methods, the global estimates of μ and η are within 35% of the known values. Errors in global estimates of both ϕ and ζ are typically at least 50% of the correct values. A notable exception is the global estimate of ζ by the DFI-LFE method, which is within 30% of the known value. Local estimates of μ are noticeably better than estimates of the other parameters.
Figure 6.
Local and estimates of parameters from combining the three simulations of waves in heterogeneous material are shown for the xy-planes of 13, 25, 31, and 44. The outlining box indicates the full extents of the material (70 nm × 70 nm), and the outlined “X” within each box indicates the outline of the 4 lobes. The outer 4 voxels have been removed from the estimates leaving a smaller shaded “X” region of local parameter estimates. Color bars show a range for each material parameter from a minimum value of zero to a maximum value of 150% of the known values of μ = 1000 Pa, ϕ = 1, ζ = 2, and η = 0.2. Global estimates are given under the local results for each parameters and method. Estimates obtained by the DFI-LFE method for (a) μ, (b) ϕ, and (c) ζ are shown in the top row. The smaller outlines in (a), (b), and (c) indicate areas for which the DFI-LFE indicated that insufficient information was available for estimates. Estimates obtained by the DFI-LDI method for (e) μ, (f) ϕ, (g) ζ, and (h) η are shown in the second row. Estimates obtained by the Curl method for (i) μ, (j) ϕ, (k) ζ, and (l) η are shown in the last row. Note that in the case of the DFI-LDI and Curl methods, estimates were found for all voxels and the white areas are outside the chosen range of the material parameters.
DISCUSSION
Requirements for Accurate Parameter Estimation in Transversely Isotropic Materials
In order to estimate properties of an ITI material, (I) both slow and fast shear waves and (II) multiple shear waves propagating in different directions must be present in the displacement field. These conditions are explicitly required by the directional filter methods (DFI, e.g.). In the initial exposition of the Curl method (17), requirements for both slow and fast shear waves in multiple propagation directions are not explicitly specified. Current results using analytical data sets and simulations of waves in homogeneous material confirm that the Curl method requires the same minimum set of experimental measurements as the DFI approaches.
First, if only slow or fast shear waves were present, neither the Curl nor the DFI methods were capable of accurately estimating all of the material parameters, as shown in Table 2. For the analytical data set with only fast shear waves, none of the three methods estimated the material parameters accurately. For the analytical data set with only slow shear waves, it is possible to estimate the parameters μ, ϕ, and η, since the slow and fast shear waves are independent from each other. However, the estimates for the slow data set are deceptive, since accurate estimates of parameters μ, ϕ, and η, are not sufficient to describe the material anisotropy.
During a MRE experiment it is also possible to excite either predominantly slow or fast shear waves. Fast shear waves dominate in the first simulation in Figure 2b, and the results in Table 3 show poor parameter estimates for all three methods. We designed the second simulation in Figure 2c to excite mainly slow shear waves, but the amplitudes of both slow and fast shear waves are nearly equivalent. The results in Table 3 show that the Curl method is able to accurately estimate μ and ϕ, which is consistent with the analytical results. Due to the presence of the fast shear waves, the Curl method estimates ζ within 40% of the known value as well. The poor estimates by the DFI methods may be due to a suboptimal choice of filter directions. For example, shear waves induced by reflections at the boundaries would not be accounted for in the chosen filter set.
Second, we consider the condition that multiple shear waves propagating in different directions must be present in the displacement field. This requirement is most clearly observed in the results from the analytical data in Table 2. Neither DFI method is capable of estimating parameters from a single propagation direction, by definition. While the Curl method can estimate the parameters from data sets with a single propagation direction, the estimated parameters from these data sets are poor. The results illustrate that the Curl method also requires the condition of shear waves traveling multiple propagation directions.
Recommended Procedures for MRE Measurements in ITI Materials
Directional filters can be used to evaluate whether a MRE measurement meets the two basic conditions (I & II) required for estimating ITI material parameters in the following way.
Steps (i) and (ii) of the DFI method are applied to each MRE measurement. The filter set is chosen to include at least three expected propagation directions differing by at least 10–15 degrees, or an evenly spaced set of directions if the propagation directions are not known.
Next, the amplitudes of the filtered fields, for each filter direction and for each polarization, are compared. Amplitudes for both slow and fast shear waves in at least two different directions must meet a minimum threshold. Selecting directions for which the amplitude of the filtered field is at least 20% of the maximum unfiltered amplitude is a reasonable guideline.
The number of slow and fast shear waves should be balanced (we suggest no more than 75% of the included wave components be of one type).
If waves from a single propagation direction are dominant, no method we investigated will provide reliable material parameter estimates. Additional experiments may be necessary to provide waves in other directions. Fortunately, directional filtering can readily identify a single strong filter direction, for example by identifying cases in which a single filtered field contains more than a given fraction (say 50%) of the variance in the data.
Once a set of MRE measurements is obtained that meet the two minimum conditions (I & II) for estimation, according to the practical guidelines above, the measurements may be combined and the ITI parameters estimated. For example, in the analytical data sets, the six data sets each include either a slow or fast shear wave in one direction. When the six data sets are combined, all three methods are able to estimate the material parameters accurately. Likewise, combining all four simulations of the homogeneous material results in most of the estimates within 25% of the known values as shown in Figure 4 (SNR = ∞). The improvement in the estimates by the Curl method when using all four simulations is especially noteworthy, since diversity of shear wave type and propagation direction were not explicitly stated as requirements for that method.
Effects of Noise
The Curl method is more sensitive to noise than either DFI method, as shown in Figure 4. Since the Curl method requires additional numerical derivatives compared to either DFI method, this sensitivity to noise is not surprising. The DFI-LFE method is the most robust to noise with a maximum percent difference in parameters (based on the known value) of about 10% between the maximum and minimum SNR values. LFE relies on filters in the Fourier domain rather than taking derivatives of the data to estimate wave speed, so this result is also reasonable. The DFI-LDI method falls between the other two methods since it requires fewer derivatives than the Curl method but more than the DFI-LFE method.
Effects of Heterogeneity
The three methods compared in this paper assume local homogeneity, which can lead to errors when characterizing heterogeneous materials. Since estimation errors tend to arise at the interfaces of dissimilar materials (15), we chose to erode four voxels from around the region of interest to limit the impact of interface errors. Errors can also arise from reducing the number of wavelengths in the eroded volume. The simulations of the heterogeneous material were designed to include a minimum of 2 wavelengths per domain in the expected propagation directions after erosion to reduce potential errors from a smaller volume.
Both global and local estimates of the heterogeneous material are poor for all three methods with the exception of the global estimates of μ. The local estimates in Figure 6 provide additional insight to these global estimates. Local estimates from the DFI-LFE approach are fairly uniform throughout the estimated region suggesting that the global estimates are also reliable. We believe that the DFI-LFE method is more effective in removing poor estimates than the other approaches due to its multiple selection criteria. The additional complexity of directional filters and selection criteria is an advantage in this case. For the DFI-LDI and Curl methods, local estimates vary, sometimes significantly, from one region to another, creating the appearance of heterogeneity. This variance in the local estimates suggests that the global estimates may not be entirely reliable.
Even using analytical or numerical solutions of waves in uniform samples, the effects of discretization, finite domain size, and finite filter bandwidth limit the accuracy of each anisotropic inversion method. Just as in isotropic MRE, the best estimates can be obtained when the spatial extent of the sample contains many wavelengths, and each wavelength contains many voxels. In addition, it should be noted that separating wave polarizations with finite bandwidth filters, and estimating three elastic parameters (anisotropic case) is significantly more difficult than estimating one parameter (isotropic case), especially in a realistic domain size with realistic discretization. These effects may explain why the results were typically only within 20–30% of the correct values, even though the data is noiseless. For example with data that is closer to ideal (more than 6 wavelengths in the domain, at least 10 points per wavelength, and at least 6 propagation directions), all three methods were capable of estimating the three elastic parameters within 10% of the known parameters.
CONCLUSION
In this paper, we demonstrate that there are two essential requirements for the accurate estimation of material parameters in (nearly incompressible) transversely isotropic materials. The displacement field must include:
both slow and fast shear waves and
multiple shear waves propagating in different directions.
While these conditions are explicit for the DFI methods, we show that these requirements also apply to the Curl method (and, by extension, any other method). This finding is notable since the Curl method is independently derived and has no explicit reference to requirements for slow or fast shear waves or propagation direction (17). The two minimum conditions identified in this paper can be used to both design experiments and evaluate MRE measurements. We also show how to combine multiple measurements to meet the minimum conditions for estimation when individual measurements do not meet the conditions.
All three methods considered in this paper assume local homogeneity of the material. Using this assumption, the simplicity of the underlying equations provides an intuitive relationship between shear wave behavior and material parameters. However, as we show in the case of the heterogeneous material in Figure 6, this assumption can break down, especially when wavelengths are longer than locally homogeneous regions.
Supplementary Material
Local parameter estimates obtained from combining the four simulations of waves in homogeneous material are shown for the xy-planes of 13, 25, 31, and 44. An estimation kernel with a radius of 5 voxels is used the kernel approach. The outlining box indicates the full extents of the material (50 nm × 50 nm). The outer 4 voxels have been removed from the estimates leaving a smaller shaded region (42 nm × 42 nm) of local parameter estimates. Color bars show a range for each material parameter from a minimum value of zero to a maximum value of 150% of the known values of μ = 1000 Pa, ϕ = 1, ζ = 2, and η = 0.2. Estimates from the Curl method (with kernel approach) for (b) μ, (c) ϕ, (d) ζ, and (e) η are shown in the first row. Estimates using the Curl method with the original direct inversion for (f) μ, (g) ϕ, (h) ζ, and (i) η are shown in the second row.
Acknowledgments
This study was supported by NIH Grant NS055951 (Bayly) and NSF Grant CMMI-1332433 (Bayly).
Appendix A: Comparison of Nearly Incompressible, Transversely Isotropic Material Parameters
In this appendix, we compare four sets of parameters from Feng et al. (13), Guo et al. (17), Rouze et al. (16), and Royer et al (11) used to describe nearly-incompressible, transversely isotropic (TI) material models in the literature. TI materials are specified with five independent parameters, and incompressible TI materials require only three parameters. These parameters can be defined using elastic moduli, the stiffness matrix, or a combination of these approaches.
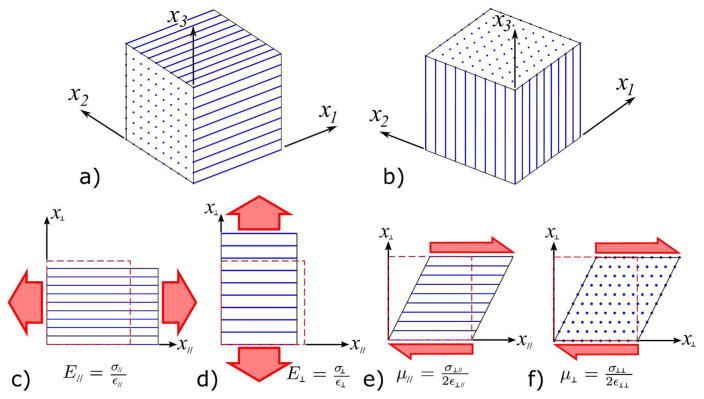
First, we specify a standard set of elastic moduli for TI material. The Young’s modulus in the fiber direction (normal to the plane of isotropy) is defined as E//, and the modulus perpendicular to the fiber direction is defined as E⊥. The shear modulus in planes parallel to the fiber direction is defined as μ//, and the modulus in the plane perpendicular to the fiber direction is defined as μ⊥, as shown in Figure 7. The fiber direction a is arbitrary for this definition of the elastic moduli. Fiber directions are defined as a = x1 (13) or a = x3 (11,16,17).
Figure 7.
Transversely isotropic material with a fiber orientation defined by (a) a = x = x1 and (b) a = z = x3. Tensile moduli in directions (c) parallel and (d) perpendicular to the fibers are given by E// and E⊥, respectively. Shear moduli in planes (e) parallel and (f) perpendicular to the fibers are given by μ// and μ⊥, respectively. The dashed boxes indicate the undeformed case.
A TI constitutive model using the stiffness matrix ℂ can be defined by
| [A.1] |
where σ = ℂε, σαβ are the Cauchy stresses, and εαβ are the strains. In the case of a = x1, the following equalities are defined for a TI material: c22 = c33, c12 = c13, c22 = c66, and c23 = c22 – 2c44 (13). For the case of a = x3, a different set of inequalities are defined: c11 = c22, c23 = c13, c44 = c55, and c12 = c11 – 2c66 (25).
In Table 1, the universal set of elastic moduli and the bulk modulus are defined in terms of each parameter set. Feng et al. (13) chose the parameters μ, ϕ, and ζ; Guo et al. (17) chose the parameters μ12, μ13, and E3; and Rouze et al. (16) chose the parameters μT, μL, and the ratio ET/EL. Royer et al. (11) used the components of the stiffness matrix as parameters.
Footnotes
Conflict of Interest Statement
None of the authors have a conflict of interest that could influence the work described in this manuscript.
References
- 1.Muthupillai R, Lomas DJ, Rossman PJ, Greenleaf JF, Manduca A, Ehman RL. Magnetic resonance elastography by direct visualization of propagating acoustic strain waves. Science (New York, N Y ) 1995;269(5232):1854–1857. doi: 10.1126/science.7569924. [DOI] [PubMed] [Google Scholar]
- 2.Klatt D, Friedrich C, Korth Y, Vogt R, Braun J, Sack I. Viscoelastic properties of liver measured by oscillatory rheometry and multifrequency magnetic resonance elastography. Biorheology. 2010;47(2):133–41. doi: 10.3233/BIR-2010-0565. [DOI] [PubMed] [Google Scholar]
- 3.Papazoglou S, Rump J, Braun J, Sack I. Shear wave group velocity inversion in MR elastography of human skeletal muscle. Magnetic Resonance in Medicine. 2006;56(3):489–497. doi: 10.1002/mrm.20993. [DOI] [PubMed] [Google Scholar]
- 4.Klatt D, Papazoglou S, Braun J, Sack I. Viscoelasticity-based MR elastography of skeletal muscle. Physics in medicine and biology. 2010;55(21):6445–6459. doi: 10.1088/0031-9155/55/21/007. [DOI] [PubMed] [Google Scholar]
- 5.Sinkus R, Tanter M, Catheline S, Lorenzen J, Kuhl C, Sondermann E, Fink M. Imaging anisotropic and viscous properties of breast tissue by magnetic resonance-elastography. Magnetic Resonance in Medicine. 2005;53(2):372–387. doi: 10.1002/mrm.20355. [DOI] [PubMed] [Google Scholar]
- 6.Romano A, Scheel M, Hirsch S, Braun J, Sack I. In vivo waveguide elastography of white matter tracts in the human brain. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine/Society of Magnetic Resonance in Medicine. 2012;68(5):1410–1422. doi: 10.1002/mrm.24141. [DOI] [PubMed] [Google Scholar]
- 7.Sack I, Beierbach B, Wuerfel J, Klatt D, Hamhaber U, Papazoglou S, Martus P, Braun J. The impact of aging and gender on brain viscoelasticity. NeuroImage. 2009;46(3):652–657. doi: 10.1016/j.neuroimage.2009.02.040. [DOI] [PubMed] [Google Scholar]
- 8.Green MA, Bilston LE, Sinkus R. In vivo brain viscoelastic properties measured by magnetic resonance elastography. NMR in Biomedicine. 2008;21(7):755–764. doi: 10.1002/nbm.1254. [DOI] [PubMed] [Google Scholar]
- 9.Clayton EH, Garbow JR, Bayly PV. Frequency-dependent viscoelastic parameters of mouse brain tissue estimated by MR elastography. Phys Med Biol. 2011;56(8):2391–2406. doi: 10.1088/0031-9155/56/8/005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Schmidt JL, Tweten DJ, Benegal A, Walker CH, Portnoi T, Okamoto RJ, Garbow JR, Bayly PV. Magnetic resonance elastography of slow and fast shear waves illuminates differences in shear and tensile moduli in anisotropic tissue. Journal of Biomechanics. 2006;2016:1–8. doi: 10.1016/j.jbiomech.2016.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Royer D, Gennisson J, Deffieux T, Tanter M. On the elasticity of transverse isotropic soft tissues ( L ) 2011 May;129:2757–2760. doi: 10.1121/1.3559681. [DOI] [PubMed] [Google Scholar]
- 12.Romano AJ, Abraham PB, Rossman PJ, Bucaro JA, Ehman RL. Determination and analysis of guided wave propagation using magnetic resonance elastography. Magnetic Resonance in Medicine. 2005;54(4):893–900. doi: 10.1002/mrm.20607. [DOI] [PubMed] [Google Scholar]
- 13.Feng Y, Okamoto RJ, Namani R, Genin GM, Bayly PV. Measurements of mechanical anisotropy in brain tissue and implications for transversely isotropic material models of white matter. Journal of the Mechanical Behavior of Biomedical Materials. 2013;23:117–132. doi: 10.1016/j.jmbbm.2013.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Clayton EH, Genin GM, Bayly PV. Transmission, attenuation and reflection of shear waves in the human brain. Journal of the Royal Society, Interface/the Royal Society. 2012;9(76):2899–2910. doi: 10.1098/rsif.2012.0325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mcgrath DM, Ravikumar N, Wilkinson ID, Frangi AF, Taylor ZA. Magnetic resonance elastography of the brain: An in silico study to determine the influence of cranial anatomy. Magnetic Resonance in Medicine. 2015 Jul; doi: 10.1002/mrm.25881. [DOI] [PubMed] [Google Scholar]
- 16.Rouze NC, Wang MH, Palmeri ML, Nightingale KR. Finite element modeling of impulsive excitation and shear wave propagation in an incompressible, transversely isotropic medium. Journal of Biomechanics. 2013;46(16):2761–2768. doi: 10.1016/j.jbiomech.2013.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Guo J, Hirsch S, Scheel M, Braun J, Sack I. Three-Parameter Shear Wave Inversion in MR Elastography of Incompressible Transverse Isotropic Media : Application to In Vivo Lower Leg Muscles. Magnetic Resonance in Medicine. 2016;75(4):1537–1545. doi: 10.1002/mrm.25740. [DOI] [PubMed] [Google Scholar]
- 18.Tweten DJ, Okamoto RJ, Schmidt JL, Garbow JR, Bayly PV. Estimation of material parameters from slow and fast shear waves in an incompressible, transversely isotropic material. Journal of Biomechanics. 2015;48(15):4002–4009. doi: 10.1016/j.jbiomech.2015.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Feng Y, Namani R, Okamoto RJ, Genin GM, Bayly PV. Anisotropic mechanical properties of brain tissue characterized by shear and indentation tests. SEM Annual Conference and Exposition on Experimental and Applied Mechanics; 2012. [Google Scholar]
- 20.Auld BA. Acoustic fields and waves in solids. 2. Malabar, Fla: R.E. Krieger; 1990. [Google Scholar]
- 21.Knutsson H, Westin C-F, Granlund G. Local multiscale frequency and bandwidth estimation. Image Processing. 1994:36–40. [Google Scholar]
- 22.Okamoto RJ, Clayton EH, Bayly PV. Viscoelastic properties of soft gels: comparison of magnetic resonance elastography and dynamic shear testing in the shear wave regime. Phys Med Biol. 2011;56(19):6379–6400. doi: 10.1088/0031-9155/56/19/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Manduca A, Lake DS, Kruse SA, Ehman RL. Spatio-temporal directional filtering for improved inversion of MR elastography images. Medical Image Analysis. 2003;7(4):465–473. doi: 10.1016/s1361-8415(03)00038-0. [DOI] [PubMed] [Google Scholar]
- 24.Sinkus R, Tanter M, Catheline S, Lorenzen J, Kuhl C, Sondermann E, Fink M. Imaging anisotropic and viscous properties of breast tissue by magnetic resonance-elastography. Magnetic Resonance in Medicine. 2005;53(2):372–387. doi: 10.1002/mrm.20355. [DOI] [PubMed] [Google Scholar]
- 25.Royer D, Gennisson JL, Deffieux T, Tanter M. On the elasticity of transverse isotropic soft tissues. Journal of the Acoustical Society of America. 2011;129(5):2757–2760. doi: 10.1121/1.3559681. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Local parameter estimates obtained from combining the four simulations of waves in homogeneous material are shown for the xy-planes of 13, 25, 31, and 44. An estimation kernel with a radius of 5 voxels is used the kernel approach. The outlining box indicates the full extents of the material (50 nm × 50 nm). The outer 4 voxels have been removed from the estimates leaving a smaller shaded region (42 nm × 42 nm) of local parameter estimates. Color bars show a range for each material parameter from a minimum value of zero to a maximum value of 150% of the known values of μ = 1000 Pa, ϕ = 1, ζ = 2, and η = 0.2. Estimates from the Curl method (with kernel approach) for (b) μ, (c) ϕ, (d) ζ, and (e) η are shown in the first row. Estimates using the Curl method with the original direct inversion for (f) μ, (g) ϕ, (h) ζ, and (i) η are shown in the second row.