Automated Template-based Brain Localization and Extraction for Fetal Brain MRI Reconstruction

Abstract

Most fetal brain MRI reconstruction algorithms rely only on brain tissue-relevant voxels of low-resolution (LR) images to enhance the quality of inter-slice motion correction and image reconstruction. Consequently the fetal brain needs to be localized and extracted as a first step, which is usually a laborious and time consuming manual or semi-automatic task. We have proposed in this work to use age-matched template images as prior knowledge to automatize brain localization and extraction. This has been achieved through a novel automatic brain localization and extraction method based on robust template-to-slice block matching and deformable slice-to-template registration. Our template-based approach has also enabled the reconstruction of fetal brain images in standard radiological anatomical planes in a common coordinate space. We have integrated this approach into our new reconstruction pipeline that involves intensity normalization, inter-slice motion correction, and super-resolution (SR) reconstruction. To this end we have adopted a novel approach based on projection of every slice of the LR brain masks into the template space using a fusion strategy. This has enabled the refinement of brain masks in the LR images at each motion correction iteration. The overall brain localization and extraction algorithm has shown to produce brain masks that are very close to manually drawn brain masks, showing an average Dice overlap measure of 94.5%. We have also demonstrated that adopting a slice-to-template registration and propagation of the brain mask slice-by-slice leads to a significant improvement in brain extraction performance compared to global rigid brain extraction and consequently in the quality of the final reconstructed images. Ratings performed by two expert observers show that the proposed pipeline can achieve similar reconstruction quality to reference reconstruction based on manual slice-by-slice brain extraction. The proposed brain mask refinement and reconstruction method has shown to provide promising results in automatic fetal brain MRI segmentation and volumetry in 26 fetuses with gestational age range of 23 to 38 weeks.

1. Introduction

Fetal MRI has attracted a lot of attention and is being incrementally used as a complementary diagnostic tool to prenatal ultrasound imaging as it provides a better soft tissue contrast. Fast single shot multi-slice MRI sequences are used to freeze maternal and fetal motion; but the acquisition of thick slices (about 2 to 4mm) is necessary to obtain acceptable Signal-to-Noise Ratio (SNR) given the short acquisition time used to avoid motion at each slice acquisition. Thick slices and interslice motion artifacts limit the accuracy of volumetric analysis for clinical diagnosis and neuroscience studies [1].

In the last years, interest in finding a high-resolution (HR) volumetric image given a set of low-resolution stacks composed of thick slices with inter-slice motion artifacts has grown considerably. In [2, 3], the first reconstruction techniques based on slice-to-volume registration and scattered data interpolation were introduced. Later, super-resolution (SR) techniques [4– 10] have boosted the quality of the reconstructed image by modeling an inverse problem for fetal image reconstruction. By providing finer details of the fetal brain, such techniques have enabled the neuroscience community to perform new research on early human brain development [11–18].

The fetal MRI reconstruction pipeline consists of various image processing steps (intensity standardization, motion estimation, and SR reconstruction). In general, algorithms [2–10, 19] rely only on brain tissue-relevant voxels of low-resolution (LR) images to warrant the assumption of motion rigidity used in rigid motion correction. This is a crucial step of the reconstruction algorithms. Consequently, the fetal brain (or brain region) needs to be first localized and then extracted prior to motion estimation and SR reconstruction. These two successive processes are known as (1) brain localization and (2) brain extraction. Brain localization typically aims to detect a bounding box containing the brain in the acquired images. Fetal brain extraction, on the other hand, aims to delineate (mask) the brain in the acquired images.

Fetal brain localization and extraction is typically done manually or semi-automatically, thus corresponds to the most time-consuming, non-automatic step of the entire image reconstruction pipeline. It is therefore not a realistic solution for large-scale studies. In the literature, even though accurate brain extraction tools have been developed for adult and infant brain MRI [20, 21], those tools are not readily applicable to fetal MRI. Fetal brain MRI differs in many ways from neonatal or adult brain MRI in terms of image content (with maternal tissues surrounding the fetal brain), image contrast, brain size, and especially the arbitrary (non-standard) fetal position and orientation which also changes due to motion. Recent studies have addressed the problem of brain localization and/or extraction in fetal MRI by adopting either template-based segmentation [18, 22–25] or machine learning [26–29] techniques.

In this work, we present a template-based brain localization, extraction and segmentation in a standard orientation and common coordinate space for in-utero fetal brain MRI. Specifically, our contributions are:

• An automated slice-by-slice brain extraction method in every stack of thick slices (LR image). It couples robust template-to-slice block matching based on L₁ norm optimization for automatic brain localization with a novel deformable slice-to-template brain extraction method.

• The combination of the masking process with intensity standardization, motion correction, and super-resolution reconstruction: brain masks are refined in the spatial space of the template using a consensus fusion voting process and are re-applied to the LR images as the reconstruction proceeds.

• An extensive validation of our brain extraction and localization methods on clinical data including healthy and pathological cases where:

  • –we show the influence of the rotation sampling step parameter of our brain localization algorithm on brain detection success rate.
  • –we compare the success rate and average run time of our brain localization technique against one of the state-of-the-art machine-learning techniques.
  • –we evaluate the brain extraction performance in terms of overlap measures with manual delineations,
  • –we study the impact of automatic brain extraction performance on the final reconstruction quality,
  • –we conduct a perceptual evaluation by expert observers to compare the quality of the final reconstruction using brain masks obtained manually and automatically with the proposed technique, and

• We perform brain volumetry based on the reconstructed images: intra-cranial fetal brain volume is computed directly from our brain extraction and we exploit our common reference space to perform brain segmentation.

The paper is organized as follows. Section 2 gives an overview of existing brain localization and extraction techniques for fetal MRI. Section 3 presents the details of the proposed template-based brain extraction and reconstruction approach. Section 4 presents the clinical fetal dataset used for evaluation. Section 5 includes the results of extensive validation of the proposed brain localization and extraction methods in terms of brain localization success rate, brain extraction performance as well as their impact on reconstruction quality and brain volumetry. Finally, Section 6 involves the discussion and Section 7 draws a conclusion.

2. Overview of fetal brain localization and extraction

Several, relatively recent, studies have addressed the automatic localization and/or extraction of fetal brain in MRI through either template-based segmentation [18, 22–25] or machine learning [26–29] techniques. The first attempt [22] of fetal brain extraction proposed to estimate the location of the eyes (based on rigid template registration) in order to segment the fetal brain using contrast, morphological and biometrical prior information. This method gave precise brain delineations in 22 out of 24 MRI stacks of fetuses aged between 30 and 35 gestational weeks; however, they relied on the assumption of minor motion between slices, which limits the robustness of the method to clinical databases. A supervised approach, based on a two-phase random forest classifier, was adopted in [26] in order to obtain a method applicable to all fetal ages and more robust with respect to (w.r.t) motion between slices. This method has shown comparable results to the method in [22] but the whole brain was contained inside the final bounding box in only 28% (coronal) to 58% (transversal, sagittal) of the cases. Later, localization accuracy of the brain was drastically improved by combining prior knowledge of the fetal head size with maximally stable extremal regions detection, bundled Scale-Invariant Feature Transform (SIFT) features and a bag-of-words model: the whole brain was contained inside the final bounding box in 85% of the cases [27]. The method, limited to the localization of the fetal brain (bounding box), was further improved with the use of spherical Gabor descriptors and 2D level-sets to provide an accurate final segmentation of the fetal brain with a Dice overlap metric above 90% [28].

More recently, those techniques have been integrated in the reconstruction pipeline. Brain localization, done manually by reorienting and cropping the LR images as a first step, and automatic multi-atlas based brain extraction have been combined with motion correction and SR reconstruction in [24]. However, such manual localization prevents a completely automated image reconstruction pipeline. The authors in [29] have proposed to localize the fetal brain using a Bag-of-Words model using SIFT features plus the RANdom SAmple Consensus (RANSAC) method for robust fitting and to provide a segmentation of the brain using a combination of a random forest classifier and a 3D conditional random field. Brain extraction is then refined as the reconstruction progresses, generating a final segmentation of the reconstructed fetal brain with a mean Dice value of 93%. Finally, a patch-based alternative to brain localization and extraction with GPU implementation has been proposed in [30]. Its principles rely on separating the whole stack in patches, where assumption on robust motion can be made, in order to adopt a patch-to-volume registration and final super-resolution, allowing the reconstruction of the full field-of-view of fetal MRI and not only the fetal brain. However, this approach is very computationally expensive and would be unrealistic to run it only on CPUs.

While prior knowledge is learnt and used as feature and scale based on gestational age in previous works [28, 29], we propose in this work to use age matched templates [31, 32] as priors to automatize brain localization and extraction in the fetal brain MRI reconstruction pipeline. Our approach only requires approximate gestational age of the query subject and is training-free in contrast to machine-learning approaches. It localizes the brain in each slice and extracts it using a template-to-slice block matching approach and using label propagation through deformable registration, therefore effectively estimates a brain mask through the reconstruction process. We combine brain localization and extraction with intensity standardization, motion estimation, and SR reconstruction. The integration of this approach into the reconstruction pipeline provides automatic image reconstruction of conventionally oriented fetal brain images in a common space, in contrast to existing methods that (1) reconstruct images in the space of the clinical stack used as reference for motion correction, and (2) reorient afterwards the reconstructed image to radiological conventions.

3. Novel template-based brain localization and extraction for fetal MRI

The whole reconstruction pipeline is illustrated by Figure 1. Firstly, brain localization is performed in each of the original acquired stacks (Box I in Figure 1) using the technique described in Section 3.1. It generates an initial alignment of the stack and position of the brain that crops and reorients the image to the template space. Secondly, all stacks are automatically masked using the proposed brain extraction method (Box II in Figure 1 and Section 3.2) and stack intensities are made consistent through intensity standardization as described in Section 3.3. Thirdly, 6-degrees-of-freedom (DOF) rigid slice-to-volume registration is performed for motion estimation where the NCC (normalized cross correlation) is used as the optimization metric. This step includes firstly global stack registration to initialize the transformations followed by 6-DOF rigid slice-to-volume registration. To reduce the chance of the registration process to fall into local minima, LR images are first denoised. Once motion parameters of all slices are estimated, we refine the brain mask in the thick slices. Intensity standardization (Box III in Figure 1) and brain mask refinement (Box V in Figure 1) are repeated at each iteration of slice-to-volume registration for motion estimation (Box IV in Figure 1). Finally, an HR image is reconstructed by solving the super-resolution inverse problem (Box VI in Figure 1) that follows the Total-Variation (TV) regularized SR algorithm developed in [8, 10]. All the code was implemented in C++ with Insight Toolkit [33] and Python.

Figure 1.

Pipeline for fetal MRI reconstruction. The brain masks are progressively refined using the updated motion parameters.

3.1. Template-to-slice block matching brain localization

We aim to localize the brain in every stack of slices based on an extension of the preliminary technique presented in [25], where robustness to outlier slices has been improved. In contrast to the approach presented in [29], we use an age-matched template [31, 32] as prior and match it directly to each slice through an accelerated block matching approach. The main benefit of this approach is not only it can retrieve the location of the brain in each image but it can also retrieve their global alignment in a common 3D template space. The localization problem is formulated as a block matching algorithm in which the similarity between each block, i.e. a whole 2D slice, extracted from the template and a query image (a fetal MRI slice) is maximized (Figure 2). However, the search space is large and the problem is computationally expensive as we do not know a priori the position of the fetal head. We reduce the search space by breaking the transformation model to rotation (θ) and translation (T^θ) parts for which parameters are estimated separately. Then we estimate the translation parameters for each rotation angle through the proposed block matching technique. The algorithm involves three steps: 1) block extraction and dimension reduction, 2) block matching using expectation maximization (EM), and 3) calculation of final transformation by maximizing similarity.

Figure 2.

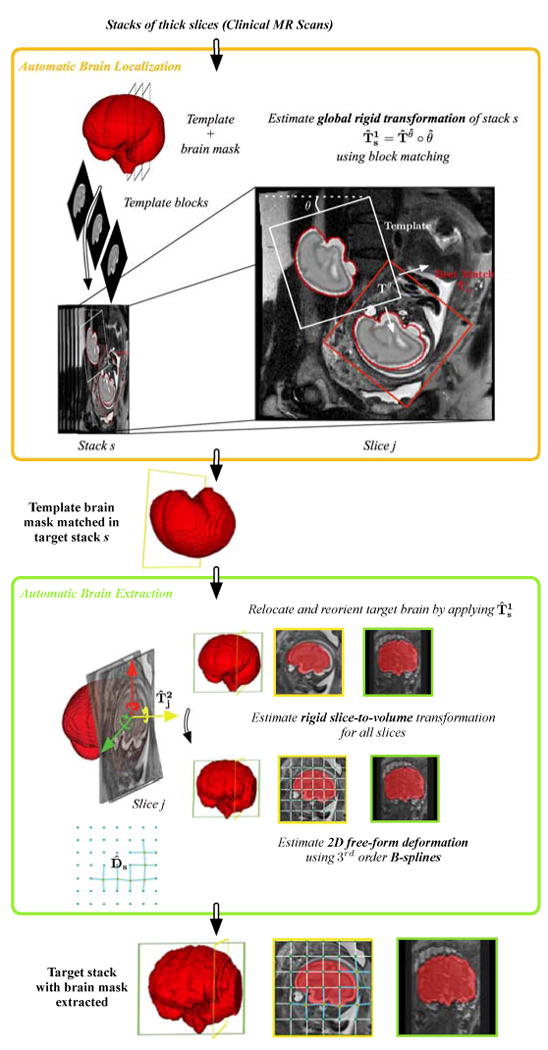
Template-based brain localization and extraction from clinical MR images. In each stack s, the initial global alignment and position of the fetal brain (global rigid transformation ${\widehat{\mathbf{T}}}_s^1$) is estimated using a block matching approach: Slices of the age-matched template image are matched to slices in the fetal brain MRI stack. It corresponds to the brain localization step. The contour of the best match is indicated in red. Then, brain masks are obtained through the brain extraction step. It consists of (i) cropping and reorienting the stack to the template space using ${\widehat{\mathbf{T}}}_s^1$, (ii) performing rigid slice-to-template registration to refine the brain localization within the slice and to correct for inter-slice motion (rigid slice-to-template transformation ${\mathbf{T}}_j^2$), (iii) performing a 2D B-Spline deformable registration to take into account anatomical variability between the processed brain and the template brain (deformation field D̂_sj), and (iv) propagating the template brain mask to each slice, using the estimated transformations and deformation field.

Block extraction and dimension reduction

A similarity matrix SM is generated by computing the Sum of Square Distances (SSD) between a slice i in a template image and a slice j in the query image. SM_ij is defined as:

$${\mathbf{\text{SM}}}_{ij}=\frac{e^{-{\text{SSD}}_{ij}}}{{\sum }_k{e}^{-{\text{SSD}}_{ik}}}$$ (1)

Since SSD is not rotation invariant, the template image needs to be initially rotated using a 3D rotation matrix (θ). The 3D rotational space is sampled using a Δθ sampling step. Slices are then extracted from the template and the similarity matrix SM^θ is computed for each rotation matrix. In addition, computation of SM^θ is accelerated by projection of each slice to a lower dimensional space though a random matrix based on Johnson-Lindenstrauss Lemma [34].

Expectation maximization for match detection

Let R be the template image, S be the query image, and M be a binary matrix representing the match between slices in the two images [35], thus E_M[M_ij] = P(M_ij = 1). Matches between slices and the translation are then iteratively updated within an EM framework. The expectation step corresponds to calculating

$${\mathbf{E}}_{\mathbf{M}}[{\mathbf{M}}_{ij}|\mathbf{R},\mathbf{S},{\mathbf{T}}^{\theta }]=\mathrm{P}({\mathbf{M}}_{ij}=1|\mathbf{R},\mathbf{S},{\mathbf{T}}^{\theta }),$$ (2)

where T^θ is the translation transferring the template to the fetal brain in the image after initial rotation θ. Then, the translation T is initially set to zero, and iteratively updated to maximize the probability of the slice r_i in R being matched to the slice s_j in S

$$\begin{array}{r}\hfill \begin{array}{cc}{\widehat{\mathbf{T}}}^{\theta }=& arg\underset{{\mathbf{T}}^{\theta }}{max}{\mathbf{E}}_{\mathbf{M}}[\mathit{\text{log}}(\mathrm{P}(\mathbf{R},\mathbf{M}|\mathbf{S},{\mathbf{T}}^{\theta }))]\end{array}\end{array}$$ (3)

$$\begin{array}{r}\hfill \begin{array}{cc}=& arg\underset{{\mathbf{T}}^{\theta }}{min}\text{∑}_{ij}\mathrm{P}({\mathbf{M}}_{ij}=1|\mathbf{R},\mathbf{S},{\mathbf{T}}^{\theta }){\Vert {\mathbf{T}}^{\theta }\circ r_i-s_j\Vert }_p.\end{array}\end{array}$$ (4)

where ‖.‖_p is the L_p norm. If P(s_j|r_i,T^θ)) follows a normal Gaussian distribution, the optimal solution of Eq. (4) is obtained by p = 2 as proposed in [25], i.e. by least squares optimization. Nonetheless, because of outliers P(s_j|r_i, T^θ)) does not follow a Gaussian distribution. Robust estimation of the conditional probabilities in Eq. (4) is thus desired. In contrast to the algorithm presented in [25], in this work we propose robust estimation through L₁ norm optimization, i.e. p = 1.

Matches are iteratively updated through Eq. (2) and Eq. (4). Through iterations of the EM steps, weights are assigned to a set of blocks with highest similarity and are updated to find the best match.

Final transformation

Once the translations T̂^θ are estimated, we apply T̂^θ and the initial rotation θ to the template, and calculate the similarity between the transformed template and the fetal image. Finally, since image intensities may not be the same between the query and template images, we select the transformation maximizing the Normalized Cross Correlation as the most probable transformation, that is,

$${\widehat{\mathbf{T}}}_s^1=arg\underset{\theta }{max}\mathit{\text{NCC}}((\underset{{\mathbf{T}}_s^1}{\underbrace{{\widehat{\mathbf{T}}}^{\theta }\circ \theta }})\mathbf{R},\mathbf{S})$$ (5)

where ${\widehat{\mathbf{T}}}_s^1={\widehat{\mathbf{T}}}^{\widehat{\theta }}\circ \widehat{\theta }$ is the optimal global rigid transformation estimated between the s-th query stack S and the template (see Figure 2). This corresponds to the initial 3D global alignment of the stack in the template space.

Parallel implementation

A high level of data independence is present in the proposed block matching algorithm. It is therefore well-suited to parallelization. In this work, parallelization has been made at the rotation level. Each parallel processing block estimates the optimal 3D translation for a given angle, which corresponds to the most computationally expensive part of the process. The parallelized version is thus expected to be very scalable up to the number of sampled angles and according to the number of available processing cores.

3.2. Deformable slice-to-template brain extraction

Propagating the template brain mask by applying the global 3D rigid transformation estimated by the localization method may not be sufficient to obtain an accurate brain mask as 1) localization may not be perfect, 2) the shape of the template may be different from the query image, and 3) inter-slice motion can occur inside a stack of slices. In this section we develop a new deformable slice-to-template brain extraction method to obtain a more accurate brain mask to address these issues. The proposed template-based technique differs in several aspects from our previous multi-atlas method [24]. First, we propose a very different registration scheme. As opposed to the global 3D deformable registration performed in [24], where a set of existing interpolation-based reconstructed images were used as reference volumes, in this work we perform slice-to-volume deformable registration, where an unbiased, deformable spatiotemporal template is used as reference volume. For this, we take advantage of the global alignment in the 3D template space obtained from our template-based localization algorithm. This was previously performed by aligning the image centers after manual image reorientation and cropping tasks.

Deformable transformations

Let a local coordinate system be defined for every slice of every query stack s. The rigid slice-to-volume transformation between the j-th slice in the s-th query image S_sj and the template (high resolution volume) is defined as

$${\mathbf{S}}_{sj}\left(x,y,z\right)=\underset{{\mathbf{T}}_{sj}}{\underbrace{{\mathbf{T}}_j^2{\widehat{\mathbf{T}}}_s^1}}\mathbf{R}\left(x,y,z\right),$$ (6)

where S_sj(x, y, z) is slice voxel coordinate, R(x, y, z) is the voxel coordinate in the template, ${\mathbf{T}}_j^2$ corresponds to a slice-to-template (2D-to-3D) transformation and ${\widehat{\mathbf{T}}}_s^1$ is the global 3D rigid transformation previously estimated by the brain localization method. ${\mathbf{T}}_j^2$ is used to refine the brain mask within the slice and to correct for inter-slice motion. The deformation between the slice in the s-th query stack and the template (high resolution volume) is defined as

$${\stackrel{\sim }{\mathbf{S}}}_{sj}\left(x,y,z\right)={\widehat{\mathbf{T}}}_{sj}^{-1}\mathbf{R}\left(x,y,z\right)+{\mathbf{D}}_{\mathbf{\text{sj}}}\left(\mathbf{R}\left(x,y,z\right)\right),$$ (7)

where S˜_sj(x, y, z) is the voxel coordinate of the template deformed in the j-th slice of the s-th query image, and D_sj is a 2D free-form deformation field. D_sj is modeled using B-Splines [36]. We determined a B-Spline order of 3 with grid size of 6 × 7 (as fetal brain is more elongated in the sagittal direction) yields the best compromise between an adequate amount of deformation and accuracy. It addresses the local anatomical variabilities/deformation that may exist between the template slice and the query slice. Therefore, the proposed method corrects for possible brain localization inaccuracy as well as for the inter-slice motion and takes into account anatomical variability between the processed brain and the template brain.

Metric and optimization

Similarly to the block matching algorithm, we select NCC as the optimization metric for both registration steps. Each registration phase is performed through maximizing NCC. The rigid slice-to-volume transformation ${\widehat{\mathbf{T}}}_j^2$ is found through the following optimization

$${\widehat{\mathbf{T}}}_j^2=arg\underset{{\mathbf{T}}_j^2}{max}\mathit{\text{NCC}}({\widehat{\mathbf{T}}}_j^2{\widehat{\mathbf{T}}}_s^1{\mathbf{R}}_{sj},{\mathbf{S}}_{sj}).$$ (8)

The 2D B-spline deformation field D̂_sj is calculated through

$${\widehat{\mathbf{D}}}_{sj}=arg\underset{{\mathbf{D}}_{sj}}{max}\mathit{\text{NCC}}({\stackrel{\sim }{\mathbf{S}}}_{sj},{\mathbf{S}}_{sj}).$$ (9)

Using NCC is very attractive as we can use common optimization algorithms. By considering this strategy in both steps, we first apply a regular-step gradient descent algorithm for the optimization of the slice-to-volume registration algorithm. The free-form deformation, however, has a much larger number of parameters as it is composed by the set of all the deformations associated with the nodes of the b-spline grid. For efficient optimization of the free-form deformation model, we choose to employ the Limited memory Broyden Fletcher Goldfarb Shannon optimization algorithm with simple Bounds (LBFGSB). This optimization technique also gives us the opportunity to fix an upper bound, set to 4mm, on B-Spline control point displacements to prevent non-topology preserving deformations.

Brain label propagation

The brain mask in each slice is obtained by propagating the template brain mask to the slice using the estimated deformation field. Figure 2 illustrates the steps of our brain localization and extraction technique.

3.3. Intensity standardization

In fetal MRI, image intensities in the stacks may not be coherent with each other. This is due to inherent bias field inhomogeneity as well as possible maternal and fetal motions. To tackle this problem, we propose to successively correct slice-by-slice for the bias field using N4 [37] and standardize the intensities using 1) slice-by-slice mean intensity equalization and 2) global brain histogram equalization [38] (Box III in Figure 1). The rationale behind this approach is that the statistics and shape of the image histogram should be similar in the stacks as they represent the same brain anatomy.

3.4. Joint brain mask refinement and reconstruction

We propose to integrate our brain extraction method with the SR reconstruction process in an iterative fashion. The brain masks generated with our brain extraction method are more reliable for the central slices than those for the extremal slices; however, stacks are acquired in the three (approximately) orthogonal directions, and the masks of the extremal slices in one direction correspond to the masks of the central slices in the other two directions. Moreover, motion estimation and reconstruction is able to recover the alignment of slices in 3D HR space which allows refinement of the brain masks. We use these properties to design our brain mask refinement process, which is illustrated by the pipeline in Figure 3. It consists of:

Figure 3.

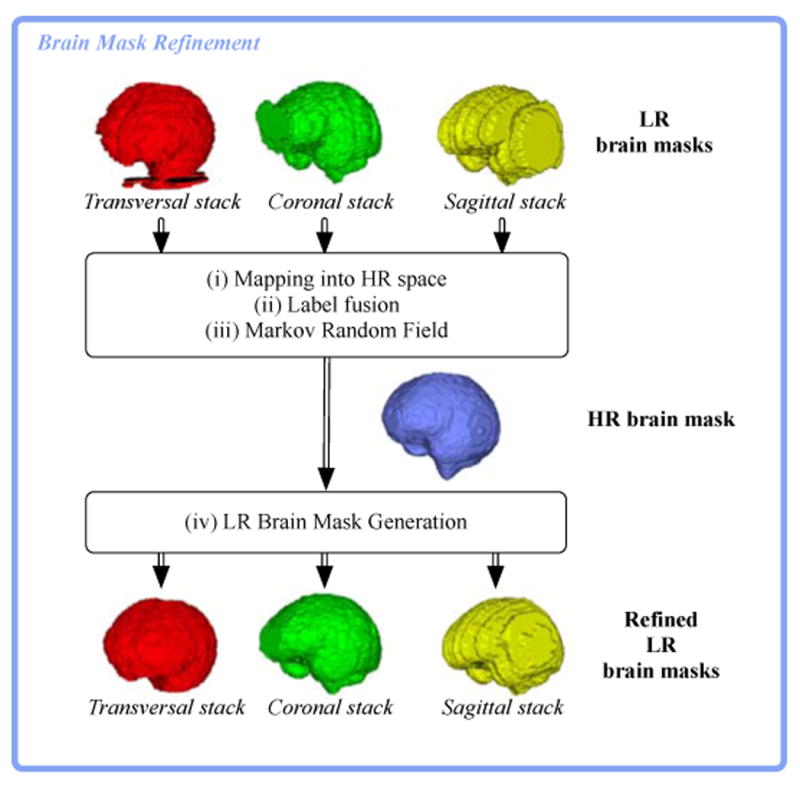
Pipeline for refining LR brain masks. (i) maps slice-by-slice the brain mask of every stack into the HR space using the motion parameters estimated during motion estimation. (ii) applies a voting strategy to obtain a unique HR brain mask. (iii) applies a Markov Random Field filter to obtain a coherent HR brain mask. (iv) maps the refined HR brain mask back to each slice of the stacks. Note that this has been simplified for illustration; there are usually more than one stack of slices with their corresponding masks in each direction.

1. mapping slice-by-slice every brain mask in the HR space using the estimated motion parameters,

2. adopting a fusion strategy to obtain a unique HR brain mask,

3. filtering using a Markov Random Field to obtain a coherent and smooth HR brain mask, and finally

4. mapping back the HR brain mask to each slice of every stack.

Brain masks mapped in the HR space are combined ((ii) in Figure 3) using Simultaneous Truth And Performance Level Estimate (STAPLE) [39]. Let H be the hidden binary refined HR brain mask and P be the propagated brain masks. The STAPLE fusion consists of computing the most likely binary refined HR brain mask. STAPLE simultaneously estimates a probabilistic consensus brain mask and the quality of each brain mask using an Expectation-Maximization (EM) framework. It aims to estimate the sensitivity and specificity parameters (p, q) characterizing the quality of the brain mask that maximizes the log likelihood function

$$\widehat{\mathbf{p}},\widehat{\mathbf{q}}=arg\underset{\mathbf{p},\mathbf{q}}{max}\mathit{\text{ln}}f\left(\mathbf{P},\mathbf{H}|\mathbf{p},\mathbf{q}\right)$$ (10)

where f (P, H | p, q) represents the probability mass function of the complete data. The process to identify quality parameters of the propagated brain mask and the HR brain mask is performed through iterations between 1) estimating the hidden HR mask given a previous estimate of the quality parameters of the propagated brain masks, and 2) estimating the quality parameters based on how accurate they are given the new estimate of the HR mask.

A binary estimate of the HR brain mask is made by thresholding the probabilistic HR brain mask at 0.5. However, it may result in a mask with holes due to motion-induced scattered nature of the acquisitions (the fetal brain might not be entirely covered by the acquired slices, thus the computed HR brain mask may contain gaps and holes.). To tackle this problem, we adopt an approach based on Markov Random Fields (MRF) ((iii) in Figure 3). Let C₁ and C₂ be a set of two classes. Let's consider H_i (i-th voxel of the HR brain mask) belongs to C₂ with centroid of 1 if it is a brain voxel, otherwise to C₁ with centroid of 0. The generation of the binary estimate of the HR brain mask is performed as follows. A distance classifier is first employed to determine the Euclidean distance between each voxel to C₁ and C₂. Then the distances of each voxel are updated by evaluating the influence of its neighbors based on a MRF model in a 7 × 7 × 3 neighborhood. Influence of the neighbor voxels (in the same slice or in neighboring slices) are assumed to be equal with a weight value of 1. We used the iterated conditional modes (ICM) algorithm [40] to minimize the MRF labeling function. Each voxel is then classified to the class for which it has the minimum distance, and we obtain a closed binary estimate of the HR brain mask.

Finally, the HR brain mask is mapped back to each slice of every stack using the estimated motion parameters. As the reconstruction progresses, the segmentation of the original slices is refined thanks to their recovered alignment in 3D space.

3.5. Total variation super-resolution

Fetal MRI reconstruction aims at finding a high-resolution image from a small set of low-resolution images. We model it as an inverse problem where the regularization term plays a central role in the reconstruction quality. Literature has considered several regularization terms such as Dirichlet/Laplacian energy [4], Total Variation (TV)-based energies [6, 9, 30] and non-local means (NLM) [5]. Although TV energies are quite attractive because of their ability in edge preservation, standard explicit steepest gradient techniques have been applied to optimize them. Here, we use our previous work based on TV regularization [10]. Specifically, it relies on the introduction of a well-posed and efficient TV super-resolution algorithm based on recent advances in fast convex optimization. This algorithm has proven to be optimal with respect to the asymptotic and iterative rates of convergence, i.e. O(1/n²) and $1/\sqrt{\epsilon }$, whereas the previous techniques were in O(1/n) and 1/ε orders. TV regularization has shown to be the most robust to motion error residuals compared to Tikhonov and NLM regularizes when no outlier rejection was integrated in the algorithm. Adaptive regularization as presented in [10] is also performed to estimate a quasi optimal weight regarding the quality of the reconstructed image with respect to the acquired stacks. All parameters of the optimization algorithm are identical to the ones adopted in [10]. Note that the TV SR algorithm does not include robust statistics to remove artifacts from inaccurate slice motion estimation and severe intensity artifacts, therefore in this work we do not aim at robust reconstruction in the presence of motion-corrupted slice data which appears as severe intensity artifacts.

The average computational time for the different steps of the pipeline (boxes I to VI in Figure 1) is shown in Table 1.

Table 1.

Computational time of the separate steps of the proposed pipeline on an Intel i7-3770 @ 3.40GHz (8-core) system with 32 GB RAM. Computing time for Localization is given for two different rotation sampling steps (see Section 5.2).

Step	Time
Localization (Δθ = 45°)	20min-1h30 per stack
Localization (Δθ = 10°)	1h30-6h per stack
Extraction	3min per stack
Intensity standardization	3min overall
Motion estimation	10-30min
Super-resolution	1-2min

4. Material

Our clinical dataset is formed by 154 stacks of thick slices coming from clinical T2-weighted MRI acquisitions of 15 fetuses with normal brain and 5 fetuses with abnormal brain, aged between 25 and 35 weeks GA (see Table 2), where the two first steps of the pipeline (Localization and extraction) have been performed.

Table 2.

The clinical datasets used in this study consisted of a total of 154 stacks used for testing brain localization and extraction. Motion level has been qualitatively graded “Minor” (little,1, or none,0), “Moderate” (2,3) or “Severe” (4,5,excluded when necessary). A subset of 87 stacks that led to successful baseline reconstruction were further used to evaluate and compare the complete reconstruction pipeline. Selection criteria for a stack to be used in the reconstruction included: homogeneous in-plane and slice resolution in all stacks; stacks with thinner slices in cases where different slice thicknesses where available; fetuses with at least one stack per slice-select acquisition direction; and having no spin history or significant motion-induced intensity distortion artifact that could corrupt the reconstruction. The goal in this paper was not to challenge motion estimation or super-resolution reconstruction but to evaluate the performance of the proposed brain localization and extraction methods and their impact on final reconstruction.

Case	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13	F14	F15	P1	P2	P3	P4	P5
GA (weeks)	27	28	28	29	29	30	30	31	31	32	33	33	34	35	35	25	26	26	30	34
Stacks (Localization-only)	6	7	6	5	6	14	9	7	3	8	11	8	6	9	4	10	4	15	6	10
Motion (0=none,5=severe)	2	5	4	3	3	1	1	2	3	3	3	4	4	3	2	4	1	1	2	2
Stacks (Reconstruction)	5	5	3	4	4	5	6	4	3	6	3	5	5	3	4	4	3	6	4	5

Brain pathologies in this study were: abnormal cerebellum (P1), limited but normal gyration (P2), unilateral ventriculomegaly (P3), occipital meningocele (P4), and cerebellar hypoplasia (P5). Each fetal MRI study consists of a set of 3 to 6 stacks, where at least one stack is available in each anatomical direction. Cases F1-F15, P1, P3 and P4 were scanned at Boston Children's Hospital, Boston, USA, using three different MRI scanners, including (1) a 1.5T Philips Achieva (SSH-TSE sequence) with two available resolutions of 1.3 × 1.3 × 2mm³ (TE/TR = 120/12500ms) and 1.3 × 1.3 × 4mm³ (TE/TR = ALI/ALIms), (2) a 3T Siemens Trio (HASTE sequence) with a resolution of 1.2×1.2×3mm³ (TE/TR = 121/1600ms), and (3) a 3T Siemens Skyra (HASTE sequence) with a resolution of 1.0× 1.0 × 2mm³ (TE/TR = 116-119/1600ms). Case P2 was scanned at Centre Hospital Universitaire de Vaud (CHUV), Lausanne, CH, using a 1.5T Siemens Aera (HASTE sequence) with a resolution of 1.1×1.1×4.8mm³ (TE/TR = 89/1000ms). CaseP5 was scanned at Hôpital Femme Mère Enfant, Lyon, France, using a 1.5T Philips Achieva and a (SSH-TSE sequence) with a resolution of 1.1 × 1.1 × 5.4mm³ (TE/TR = 180/7000ms). Repeated acquisitions with these settings provided sufficient number of stacks that were only affected by minor to moderate motion (see details in Table 2). Examples of stacks corrupted by different levels of motion as well as examples of the success and failure of our method are shown in Figure 4. We excluded stacks and cases with severe motion and significant motion-induced intensity artifacts, as clinically acquired images of comparable quality are typically unused or skipped by the reading radiologist in favor of higher quality images. An example of a stack with severe motion excluded from our study can be seen in the online Supplementary Material.

Figure 4.

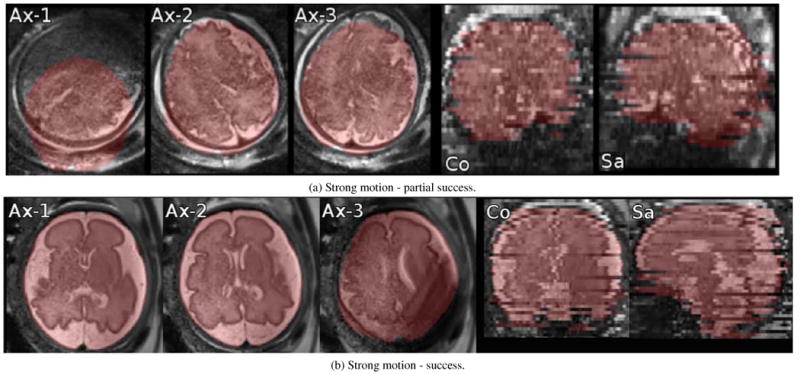
Examples of localization and segmentation algorithm failure (a) and success (b) for stacks with motion. (a) Ax-1: Intra-slice motion artifact corrupted the image and localization failed; (a) Ax-1,2,3: Inter-slice motion can be observed between adjacent slices. Localization partially succeeded but it failed to capture the anterior edge of the brain; (a) Co, Sa: coronal and sagittal out-of-plane views. (b) Ax-1,2,3: Inter-slice motion and intra-slice motion artifact (in Ax-3) are present yet localization succeeded; (b) Co, Sa: coronal and sagittal out-of-plane views.

The patient information from all data used in this study was anonymized and de-identified prior to analysis. Retrospective analysis of this data was approved by the corresponding committee / institutional review board committee: USA (institutional review board committee at Boston Children's Hospital), Switzerland (Cantonal Research Ethics Committee of Vaud) and France (Comité de Protection des Personnes).

5. Evaluation

In this section we present the results of qualitative and quantitative evaluations of the proposed brain localization and extraction techniques and study the influence of brain masking on the final reconstructed image quality.

Firstly, we compare its brain localization success rate and run times against a state-of-the-art machine learning approach. Secondly, we evaluate the performance of the proposed brain extraction technique compared to manual brain extraction. We also study the impact of rigid slice-to-template registration and 2D B-Spline deformation on the quality of the reconstructed image and we conduct a perceptual evaluation of the reconstructed images by expert observers (a clinical expert in pediatric neuro-radiology and an imaging scientist, both with more than 8 years of experience in evaluating fetal MRI). Finally, we investigate the potential of the brain mask refinement method to estimate the intra-cranial fetal brain and main brain tissues volume in the reconstructed images. We assessed statistical significance of the results using the two-tailed Wilcoxon signed-rank test. The studies were performed on an Intel i7-3770 @ 3.40GHz (8-cores) system with 32 GB RAM. In all experiments, a time step Δt = 0 has been considered in the TV-based optimization algorithm.

5.1. Influence of rotation sampling step on brain localization success rate

To evaluate the sensibility of our proposed brain localization method to the rotation sampling step, Δθ, we conduct a visual inspection where the brain localization success rate is compared for two different sampling steps, Δθ = {10°, 45°}. One expert observer was asked to evaluate if brain localization was a success or a failure for each of the 109 acquired stacks of healthy cases. Success was indicated if the final bounding box fully contained the brain, in which the brain orientation was close to conventions. Results are reported in Table 3.

Table 3.

Influence of rotation step parameter of the proposed block matching algorithm. The best values (higher success rate and lower computational time) are highligted in bold.

Our template-based approach	# of failures (failure rate)	# of success (success rate)	Average computational time
Δθ = 45°	35 (32.1%)	74 (67.9%)	1h15min
Δθ = 10°	6 (5.5%)	103 (94.5%)	5h35min

We observe that our brain localization method with Δθ = 10° provided the best localization performance, having a success rate value of 94.5%. It was expected that adopting a fine rotation sampling step (Δθ = 10°) would lead to significantly higher success rate in localization than a coarse rotation sampling step. Brain localization with a coarse rotation sampling step provided accurate localization in 67.9% of the stacks. This suggests that this approach could be made more efficient using a hierarchical supervised strategy in which coarse rotation sampling steps are tried first and are refined as needed.

5.2. Success rate of brain localization

We evaluated the success of brain localization based on visual inspection where we compared template-based brain localization against one of the most recent and publicly available state-of-the-art machine-learning techniques [29]. One expert observer was asked to indicate for each of the 154 stacks if the final bounding box fully contained the brain. Results are reported in Table 4.

Table 4.

Brain localization: comparison between the state-of-the-art machine learning technique [29] and our template matching technique. Best scores are highlighted in bold.

Brain localization method	# of failures (failure rate)	# of success (success rate)
Machine-learning [29]	10 (6.5%)	144 (93.5%)
Proposed approach	11 (7.1%)	143 (92.9%)

The results show that the detection performance of our localization algorithm, having a success rate of 92.9%, was comparable to the performance of the machine-learning-based algorithm, having a success rate of 93.5%. Nonetheless, on top of brain detection, our algorithm matches the brain, i.e. finds its orientation and determines a mask. The current machine learning algorithm was not designed to do this. The two algorithms, therefore, cannot be directly compared as they address different problems.

In the next sections, we compare the performance of brain extraction using three variations of our method. A fair comparison with the most recent machine learning approach could not be conducted as this technique did not aim to extract the exact intracranial region. Instead it only provided an approximate large area around the skull.

5.3. Performance of brain extraction

We assess the evolution of the performance of our slice-to-template brain extraction in terms of brain segmentation quality, as motion-estimation and brain mask refinement progress, using manual delineation as ground truth. Only a subset of stacks were used for reconstruction as our goal here was not to challenge the super-resolution with motion corrupted stacks but to evaluate the performance of the proposed brain localization and extraction methods and their impact on final reconstruction. Therefore, a subset of 87 stacks, which led to successful baseline reconstructions without outlier rejection, were selected and used for the evaluation of the whole reconstruction pipeline. Selection criteria involved 1) having homogeneous in-plane and slice resolution in all stacks, 2) stacks with thinner slices in cases where different slice thicknesses are available, 3) having at least one stack per slice-select acquisition direction, and 4) having no spin history or significant motion-induced intensity distortion artifact that could corrupt the reconstruction. Manual delineations were performed for every stack used for reconstruction after they were reoriented and cropped around the fetal brain thanks to the brain localization method. Similar to [29], the performance is quantified by three overlap metrics: Dice, recall and precision. While Dice summarizes recall and precision, recall quantifies the proportion of true positive brain voxels included in the mask and precision quantifies the proportion of non-brain voxels excluded. We compare the full brain extraction method that combines global rigid block matching with rigid slice-to-template registration and 2D B-Spline deformation with a method that uses only the rigid slice-to-template registration without deformation. The experiment was performed by repeating the brain mask refinement loop three times.

The results of the rigid-only and the full brain extraction methods as well as results obtained right after brain localization are reported in Table 5. Figure 5 illustrates the evolution of the brain mask of one coronal stack through the developed pipeline.

Table 5.

Evolution of brain extraction performance as reconstruction progresses using (i) rigid-only slice-to-template registration and (II) rigid and B-Spline based deformable slice-to-template registration (full method). Loop #L corresponds to the L^th brain mask refinement loop. Loop #0 corresponds to the performance of brain extraction without any refinement. Best results (highlighted in bold), specifically in terms of the overall agreement with manual delineation (Dice) and in terms of the proportion of true positive brain voxels included in the mask (recall), can be observed using the full method after repeating two times the refinement loop.

	Dice	Recall	Precision
Localization	92.0 ± 3.5	89.8 ± 5.3	94.6 ± 4.0
Extraction
Loop #0
Rigid-only	93.4 ± 2.6	92.7 ± 2.6	94.3 ± 4.3
Full	93.5 ± 2.7	92.9 ± 2.9	94.3 ± 4.3
Loop #1
Rigid-only	94.2 ± 1.9	94.3 ± 2.8	94.1 ± 2.6
Full	94.5 ± 1.6	94.6 ± 2.6	94.4 ± 2.7
Loop #2
Rigid-only	94.3 ± 1.6	94.8 ± 2.4	94.0 ± 2.5
Full	94.5 ± 1.5	94.9 ± 2.4	94.2 ± 2.5
Loop #3
Rigid-only	94.4 ± 1.6	94.7 ± 2.4	94.1 ± 2.6
Full	94.5 ± 1.6	94.9 ± 2.5	94.1 ± 2.6

Figure 5.

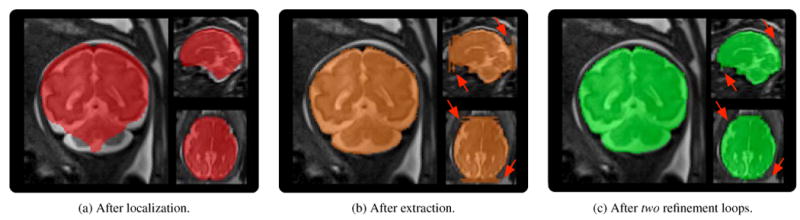
Brain mask evolution of one coronal stack (case F10). Arrows indicate extremal slices where the proposed slice-to-template brain extraction method failed. The brain masks are progressively refined thanks to motion estimation and reconstruction that helped recovering the slice alignment in 3D HR space.

It is clear that the proposed brain extraction method improves the quality of the brain masks obtained from brain localization, i.e., only global alignment. The results also show that the full pipeline helps to enhance the quality of the brain masks compared to the rigid-only approach. This shows it is important to take into account anatomical variability between the age-matched template brain and the target brain to obtain accurate brain masks. Finally, it is observed that the proposed iterative strategy to refine the brain masks as the motion estimation and reconstruction proceed, improves the quality of the brain masks particularly with an increase in the proportion of true positive brain voxels (recall). This shows that brain masks in orthogonal stacks are complimentary to each other. Alignment in 3D HR space recovered by motion estimation can indeed serve as a useful feedback to refine the extremal slices of stacks where the slice-to-template brain extraction method may fail (See arrows in Fig. 5 (b) and (c)).

5.4. Influence of brain extraction on reconstruction quality

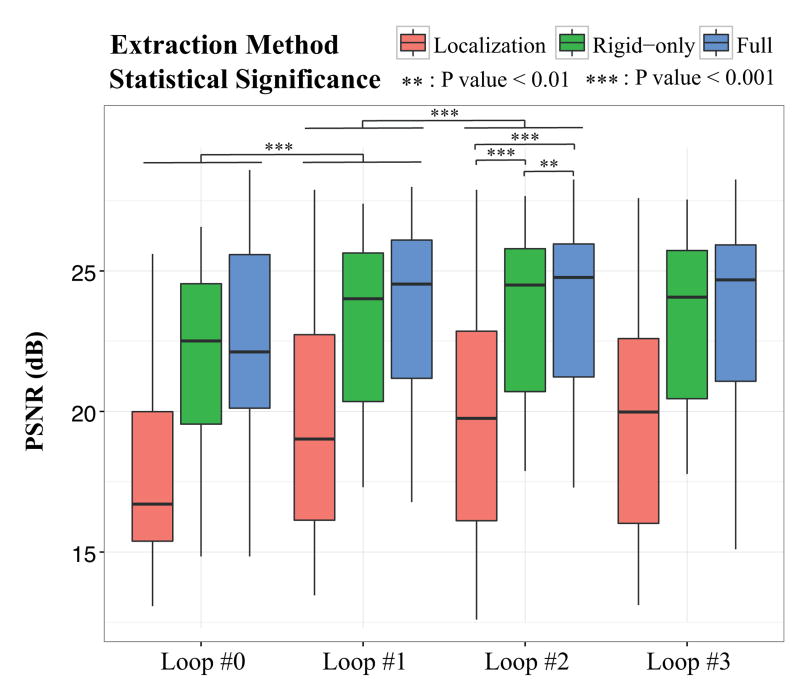
Our ultimate goal is to reconstruct high-resolution, high-quality images of the fetal brain while we achieve brain segmentation simultaneously. Statistically significant improvement of the quality of brain extraction is however not an indicator of quality improvement of the reconstructed image. We propose to investigate the influence of automatic brain extraction on the reconstruction quality, as performed in [24] for the first time. We compare the reconstruction quality in terms of Peak Signal-to Noise Ratio (PSNR) of the final HR image reconstructed using brain masks obtained by performing (i) only brain localization (no slice-to-template registration), denoted as Localization, (ii) both brain localization and extraction while using rigid-only slice-to-template registration, denoted as Rigid-only, and (iii) both brain localization and extraction while using the full slice-to-template brain extraction method (rigid and B-Spline deformation), denoted as Full. The HR image reconstructed using manual brain masks is considered the reference for PSNR calculation. We also study the evolution of the image reconstruction quality as we iterate over motion-estimation and brain mask refinement. Figure 6 shows the boxplot analysis of the evolution of the PSNR values of 20 cases for 3 methods. Figure 7 gives a comparison of the reconstructed images with the different approaches for one case, representative of all cases.

Figure 6.

Influence of brain extraction on image reconstruction quality in terms of Peak-Signal-to-Noise Ratios (PSNR) as reconstruction progresses using (i) only brain localization (Localization-only), (ii) rigid-only slice-to-template registration (Rigid-only) and (iii) the full method (Full). We use as reference the image reconstructed with the help of brain masks manually drawn after brain localization. Loop #L corresponds to the L^th brain mask refinement loop. Loop #0 corresponds to the first image reconstructed using brain masks without any refinement. A two-tailed Wilcoxon test was used for statistical significance evaluation. A significant improvement of the PSNR values can be observed after the first refinement (Loop #1) that becomes not significant after the second refinement (Loop #2). Adopting a rigid-only slice-to-template registration significantly improves the quality of the reconstructed HR image obtained at Loop #2 with an average increase of 3.8dB in the PSNR value. Using the full method allows us to further significantly enhance the quality with an average increase of 4.1dB w.r.t using only brain localization and an average increase of 0.3dB w.r.t using the rigid-only method.

Figure 7.

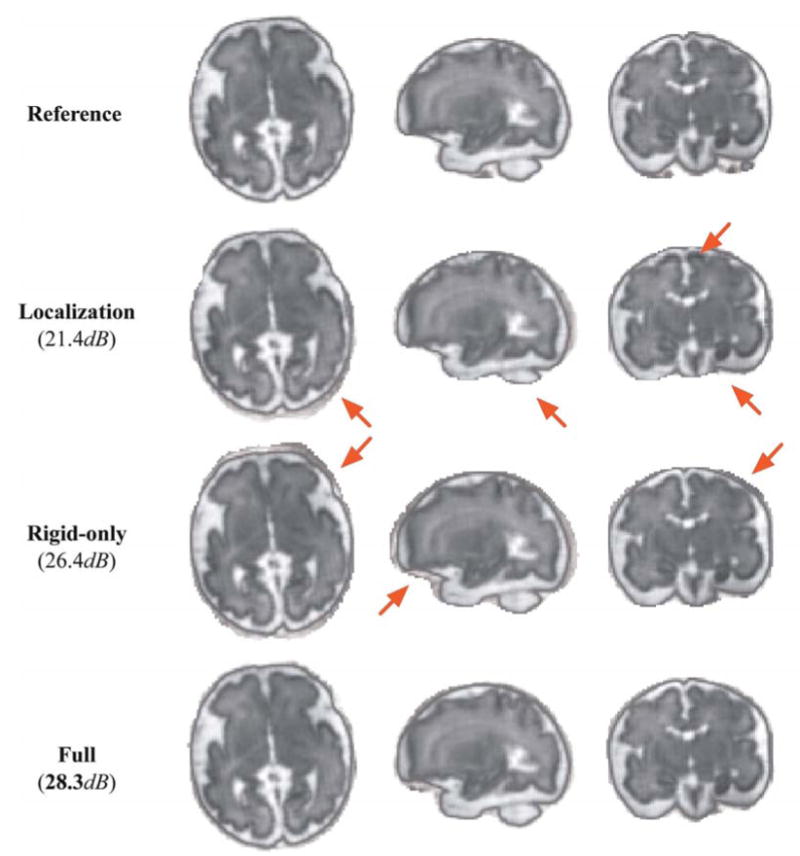
Comparison of reconstruction results of case F10 using (i) only brain localization (Localization-only), (ii) rigid-only slice-to-template registration (Rigid-only) and (ii) the full method (Full). Arrows indicate artifacts and non-brain regions included in the reconstructed image. In general, we can observe a reconstructed image of poor quality when we use brain masks obtained right after localization (method (i)). Using the brain masks obtained by methods (ii) and (iii) allows us to have a reconstructed image with a quality very similar to the quality of the image obtained using manually drawn brain masks (Reference). Only small differences can be observed at the periphery of the brain.

Quantitative results and visual inspection confirm that a better brain extraction performance (as shown in Section 5.3) results in a better final reconstruction quality. We can observe a significant increase of the PSNR value after the first refinement loop (Loop #1 in Figure 6) that, in conjunction to the brain extraction performance, stabilizes after the second refinement (Loop #2 in Figure 6), independently of the method adopted. In addition, we can also clearly see that adopting a rigid-only slice-to-template registration significantly improves the quality of the reconstructed HR image obtained at Loop #2 with an average increase of 3.8dB (p-value=5.9e − 4) in the PSNR value. Using the full method allows us to further enhance the quality with an average increase of 4.1dB (p-value=3.9e − 4) w.r.t. using only brain localization and an average increase of 0.3dB (p-value=0.047) w.r.t. using the rigid-only method. This indicates that best brain extraction performace and best reconstruction quality are obtained with the proposed pipeline after repeating only two refinement loops. Based on these observations, for the next analyses we used images reconstructed by the proposed pipeline after two refinement loops.

5.5. Perceptual evaluation of final reconstruction by expert observers

Quantitative evaluation of the quality of the reconstruction and perceived visual quality may differ in clinical settings. We propose in this section to conduct a perceptual evaluation by expert observers to compare the reconstructed images using the fully automated reconstruction pipeline with two brain mask refinement loops (as supported by results presented in Sections 5.3 and 5.4) against images reconstructed using manually drawn brain masks. We adopted a multi-alternative force-choice approach where we asked two expert observers to indicate the best HR image in terms of perceived image quality, brain localization and extraction accuracy. The two reconstructed images were presented in random order. The experts had the choice between either choosing one of the images as the best or judging both having similar quality.

Ratings of the two expert observers are reported in Table 6, and representative reconstructed images of a pathological brain (Figure 8a), diagnosed with unilateral ventriculomegaly, and a healthy brain (Figure 8b) are shown in Figure 8. All reconstructed images were evaluated in the standard orientation.

Table 6.

Qualitative rating of final reconstruction by two expert observers. Experts were asked to indicate the best HR image in terms of perceived image quality between images reconstructed using the full reconstruction pipeline and images reconstructed using manually drawn brain masks. For each expert, we report the number of cases when he preferred the image reconstructed using manually drawn brain masks (Manual), the image reconstructed with the full reconstruction pipeline (Full), or when both images were judged having similar quality (Similar).

	Manual	Full	Similar
Expert #1	7	7	6
Expert #2	8	4	8

Figure 8.

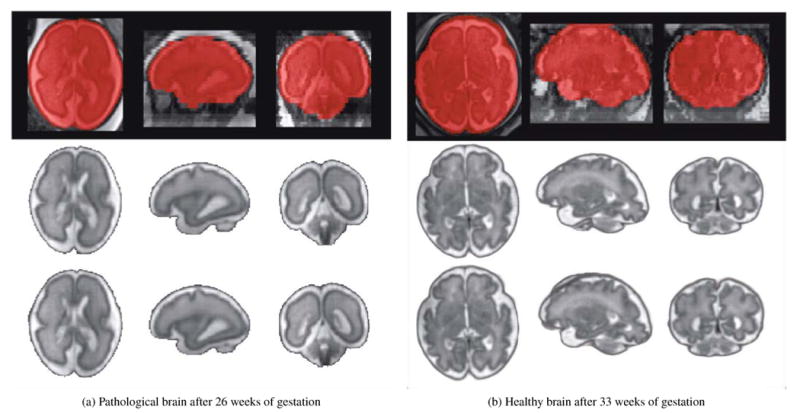
Brain extraction and reconstruction results of one pathological brain diagnosed with unilateral ventriculomegaly (Case P3) and one healthy brain (Case F12). An overlay of the original low-resolution image with the final brain mask automatically extracted is shown in the first row. The reconstruction results obtained using the brain masks manually drawn and the brain masks automatically extracted are shown in the second and third row respectively. Case P3 illustrates one case where the expert observers judged both reconstructed images having the same quality. Case F12 illustrates one case where the expert observers preferred the image reconstructed using manual brain masks as a small region outside the brain was included in the fully automated reconstruction. These results showed that using the proposed brain localization and extraction methods allowed us to obtain fully automatic high-quality reconstructions, where the brain is conventionally oriented, without any further effort.

These results showed that using the proposed template-based methods allowed us to obtain fully automatic high-quality reconstructions, where the brain is conventionally oriented, with-out the need for manual brain localization or extraction.

In summary, images reconstructed by the proposed automatic pipeline were respectively judged in 65% of the cases as having similar or better quality to images reconstructed where manual brain masks were used. In the cases where the automatically estimated brain masks did not achieve comparable or better reconstruction quality than the manual masks, there is still an advantage as the expert would only need to make quick corrections on brain masks thus significantly saves time. We found three reasons why images reconstructed using manual brain masks were preferred: 1) the reconstruction quality of both images was similar but small regions of the brain were missing in the reconstructed image; 2) the reconstruction quality of both images was similar but small regions outside the brain were included in the images reconstructed by the proposed pipeline (Figure 8b); 3) the region reconstructed containing the brain was similar in both images but a few more artifacts were present in the images reconstructed by the proposed pipeline. It has been shown that small regions outside the brain do not hamper further tissue; In [41], we combined reconstructed images using the proposed pipeline in combination with the state-of-the-art multi-atlas multi-shape segmentation and cortical folding quantification tools developed for adult brains. We observed that small extra regions around the brain were regularized and automatically filtered by multi-atlas segmentation and did not affect tissue segmentation results. Finally, successful reconstruction of brain images with mild pathologies such as the unilateral ventriculomegaly (in Figure 8a) shows that the proposed pipeline may be used for fully automatic fetal brain MRI reconstruction for both healthy and mild pathological cases.

5.6. Application to fetal brain volumetry

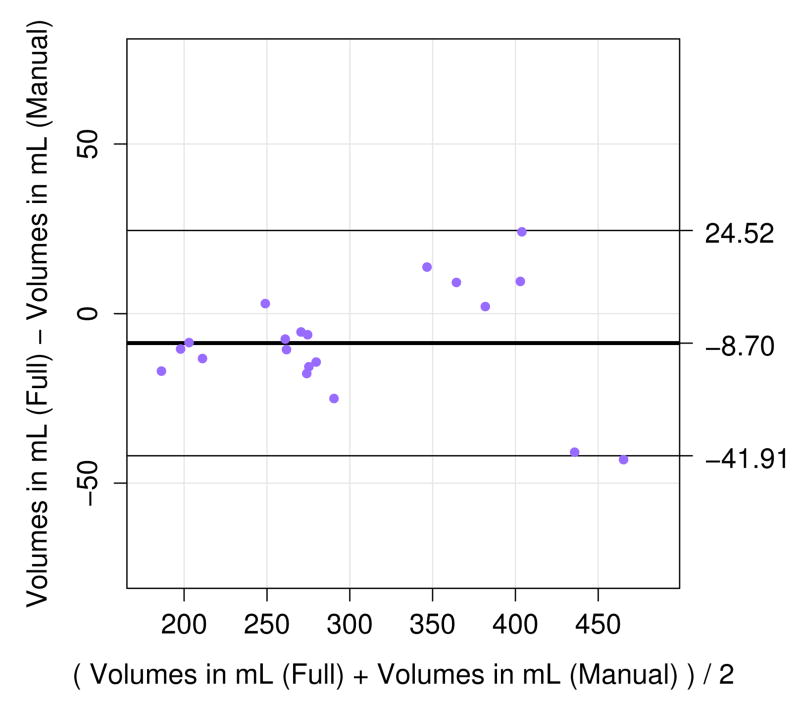
In previous sections we evaluated the performance of brain localization and extraction in the LR space of the clinical stacks. In this section we evaluate the potential of the proposed full brain extraction method combined with the proposed brain mask refinement method to estimate in milliliters (mL) the intra-cranial fetal brain volume from the brain mask in the HR space of the template. The intra-cranial brain volume is considered a pertinent measure for evaluating normal brain development, which as a 3D extension of linear measurements like bi-parietal diameter, occipitofrontal diameter, and head circumference, highly correlates with the fetal gestational age. We compare the volumes estimated after one iteration of the proposed pipeline where we used the manually drawn brain masks after brain localization (hence no need for mask refinement) against volumes estimated using our fully automatic method. The total intra-cranial volume was estimated from the refined HR brain mask. Figure 9 shows the results of Bland-Altman analysis.

Figure 9.

Bland-Altman plot of intra-cranial fetal brain volumetry results. It shows a good correlation between volumes estimated using manually drawn brain masks and volumes estimated using brain masks obtained by the full method. However, we can observe a tendency to slightly underestimate the volumes (−8.7mL on average) while using the automatic brain masks.

This analysis indicates that HR volumes obtained automatically are highly correlated with HR volumes obtained using manual masks. This indicates that the combination of the proposed brain extraction and brain mask refinement methods (originally designed to update brain masks in the stacks of slices) can be used to estimate the intra-cranial fetal brain volume with an average approximate accuracy of 3.1%. But the analysis also shows the tendency to slightly underestimating the HR volumes with a mean difference of -8.7mL while using the automatically extracted brain masks. This provides an additional insight into the amount of HR volume underestimation.

With the developed algorithm, high-resolution volumetric images of the fetal brain are readily reconstructed in the atlas space. This enables automatic atlas-based tissue segmentation using fetal brain MRI atlases [32] and probabilistic label fusion [42] algorithms. Preliminary results of fetal brain structural segmentation using this approach can be found in the online Supplementary material, where MRI scans of 6 additional fetuses (Table 7) were processed to achieve fetal brain volumetry in the GA range of 23 to 38 weeks.

Table 7.

Six additional clinical datasets included for atlas-based tissue segmentation and volumetry. Motion level has been qualitatively graded “Minor” (little,1, or none,0), “Moderate” (2,3) or “Severe” (4,5).

Case	F16	F17	F18	F19	F20	F21
GA (weeks)	23	25	34	36	36	38
Acquired stacks	11	19	12	9	11	12
Motion (0=none,5=severe)	3	4	2	2	3	3
Stacks (Reconstruction)	4	4	5	5	3	4

6. Discussion

The proposed template-based methodology enable automatic fetal brain localization and segmentation, showing a final average Dice overlap measure of 94.5% with respect to manually-drawn brain masks. In addition, the success of motion correction is highly dependent on the initial alignment of all stacks. After brain localization, the orientation of the brain in each stack is known as the localization method aims to estimate the global rigid transformation between each stack and the template brain which is correctly oriented. Thus, after brain localization and application of the rigid transform, each stack is oriented to match the template orientation making the alignment of all stacks consistent. Such global alignment could not be retrieved with existing machine learning approaches. While the two approaches should not be compared side-by-side as they address different problems (localization vs. extraction), we note that our block matching algorithm is much slower than the existing machine learning algorithms. In fact, machine learning approaches are often very fast at the test stage for object detection once the system has been well trained. The search space of our template matching algorithm in the target image is relatively large, being proportional to the whole in-plane field-of-view and inversely proportional to the slice thickness. It would be possible to speed up brain localization by using a machine learning approach as a first step to identify an approximate region-of-interest (ROI) containing the brain. This would significantly reduce the search space for template matching while still providing the global alignment of the stacks in the common 3D template space. Another approach to reduce the search space would be to rely on the fact that most images are acquired almost orthogonal with respect to the fetal brain by the MR technologist, so a 3D ROI can be first defined as the intersection of the set of images. In this work, we did not focus on algorithm speed-up through adding such peripheral implementation components. In fact, while we parallelized parts of our algorithm on multiple CPUs, the whole algorithm would benefit significantly from an optimized massively parallel implementation on Graphical Processing Units (GPUs), leading to much faster and more efficient computations.

The study of the evolution of brain extraction performance (Section 5.3) and its impact on reconstruction quality (Section 5.4) shows that it is crucial to refine the global 3D alignment slice-by-slice as slice acquisition is interleaved and fetal and maternal motion may result in the inclusion of non-brain tissue and amniotic fluid that can decrease the quality of motion estimation and consequently image reconstruction. In addition, the inclusion of 2D B-Spline deformable registration in the slice-to-template extraction method has shown to generate 1) superior brain extraction performance, and 2) superior-quality reconstructions compared to rigid alignment methods. This confirms the importance of taking into account anatomical variability between the age-matched template brain and the target brain in the brain extraction framework. In this work, selection of the best age-specific template has been done manually. This could be automatized by selecting the template that gave the maximal NCC with the target image. Although a multi-atlas strategy has shown to improve extraction performance in [24] as regards best single-atlas-based extraction, this was highly motivated by the fact that a set of multiple existing interpolation-based reconstructed images was employed as templates. Here we preferred to adopt a best single-atlas strategy as our brain localization algorithm was computationally expensive. We have selected an unbiased deformable spatiotemporal MRI atlas of the fetal brain which was built at all gestational ages between 22 and 38 weeks based on reconstructed fetal brain MRI scans of 81 normal fetuses. Due to the lack of age-matched templates below 22 weeks, our algorithm would fail to localize and extract brain in younger fetuses. Moreover, the larger range and amount of motion, or the small size of the brain and its features would hinder matching for localization and registration at these ages.

Results show the success of the integration of the proposed template-based localization and extraction method into our new reconstruction pipeline that iterates over intensity standardization, inter-slice motion estimation and brain mask refinement, statistically improving both brain extraction performance and image reconstruction quality. The use of age-specific templates, provided by an unbiased deformable spatiotemporal atlas, has enabled the reconstruction of images of fetal brains conventionally oriented within a common space. It has also shown to be a very promising way to automatically estimate at the same time the intra-cranial fetal brain volume in the final reconstructed image, which, as a direct outcome of the algorithm, provides an automatic 3D measurement beyond 2D fetal brain biometric measurements such as head circumference, biparietal diameter, and occipitofrontal diameter that are used to evaluate normal brain development or possible abnormalities such as microcephaly or growth restriction.

Successful brain localization, extraction, and reconstruction is highly dependent on good image acquisition practice and on the robustness of the automatic image processing algorithms [1]. Good image acquisition practice addresses the need for 1) appropriate MRI sequence parameters that allow motion-robust slice acquisitions at about few hundred milliseconds instant of k-space sampling for each slice and 2) multiple repeated stacks to provide the required redundancy for brain extraction refinement, motion estimation, and reconstruction. Even if good acquisition practice is fulfilled, minor to severe motions can still occur resulting in minor to severe artifacts in the acquired slices. This justifies the need for automatic robust image processing algorithms that can detect and reject motion-corrupted data and use only data with minor to moderate motion and a few or no corrupted slices for reconstruction. With the integration of smart motion detection algorithms and robust reconstruction it will be possible to handle the reconstruction of fetal MRI cases with severe motion artifacts with the proposed pipeline to significantly improve the efficacy of fetal MRI reconstruction in terms of accuracy and reliability.

7. Conclusion

We developed and evaluated a template-based approach automatizing localization, extraction and refinement of the fetal brain in the fetal MRI reconstruction pipeline. It combines a robust template-to-slice block matching algorithm to localize the brain, a novel slice-to-template brain extraction approach to find automatically, slice-by-slice, the brain masks, and a novel brain mask refinement method that updates the mask as reconstruction proceeds. The methods have been integrated in a reconstruction pipeline to evaluate the impact of their quality on the quality of the final reconstructed images. We had to exclude stacks with severe motion artifacts from the reconstruction as the proposed pipeline was not designed to handle such cases. This will be possible if smart motion detection and robust reconstruction algorithms are integrated in the proposed pipeline. The results confirm the success of the method on healthy and mild pathological cases: a template-based approach adopted for automatic brain localization, is followed by brain extraction and brain mask refinement, to generate conventionally-oriented 3D reconstructed images of the fetal brain from stacks of slices. The proposed automatic brain extraction and reconstruction method mitigates the need for manual brain localization and the subjectivity of manual delineation. In addition, the use of templates in the brain localization and extraction processes has enabled for the first time the reconstruction of brain images conventionally oriented in a common template space. This is considered an advantage for large-scale population studies.