Probability and magnitude evaluation in schizophrenia

Abstract

Alterations in reinforcement learning and decision making in schizophrenia have been linked with orbitofrontal cortex (OFC) dysfunction, a region critical for weighing reward magnitude in the calculation of expected value (EV). However, much of this work has used complex tasks that require combined learning and EV calculation. Here we used a simple “Roulette” task that examined the calculation of EV directly through a combination of text and/or pictorial representation of reward probability and magnitude. Forty-four people with schizophrenia and 30 controls were recruited. Patients were less sensitive to adjustments in a parameter combining probability and magnitude into one EV construct. Breaking down the construct into independent contributions of probability and magnitude, we found that negative symptoms were associated with magnitude sensitivity. This is consistent with the hypothesized role of OFC in actively representing magnitude and the notion that negative symptoms may involve a failure to appropriately estimate and use future reward magnitude to guide decision making.

1. Introduction

Patients with schizophrenia exhibit deficits on a range of decision making and reinforcement learning tasks which often correlate with negative symptom severity (Gold et al., 2008, Gold et al., 2012, Strauss et al., 2011a). However many of the studied tasks involve multiple learning and decision processes so that the specific processes implicated in negative symptoms remain uncertain. For example, the widely used Iowa gambling task (IGT), requires the calculation of expected value (EV: reward magnitude multiplied by reward probability) to guide decision making based on learning from feedback. In general, patients perform worse than controls on the IGT (Sevy et al., 2007) in a manner that suggests less influence of EV on deck selection compared to controls (Brown et al., 2015). However, performance on the IGT is heavily dependent on risk attitudes, learning reward probabilities and magnitudes through experience, and reward/punishment sensitivity (Schonberg et al., 2011). Thus, it is not clear if the patient deficit is due to difficulties in learning from feedback or actual alterations in the way information is weighed in guiding choices.

Several studies (Brown et al., 2013, Gold et al., 2013, Heerey and Gold, 2007, Trémeau et al., 2008) have shown alterations in how patients represent the value of alternative stimuli or potential responses using tasks that do not involve feedback learning. For example, Strauss et al. (2011b) showed reduced transitivity in patients' preference judgements of picture stimuli. That is, if one prefers A > B and B > C the preference for A over C should be expected. However, patients were less likely than controls to show such order preferences, suggesting less precise value representations. The same pattern is seen in patients with damage to ventromedial prefrontal cortex (vmPFC; Fellows and Farah, 2007), an area consistently related to EV (see Chase et al., 2015). This leads to the possibility that patients show less optimal learning from outcomes because they fail to adequately represent the EV of different alternatives, consistent with vmPFC/OFC deficits seen in schizophrenia (Barch and Dowd, 2010, Davatzikos et al., 2005). We have shown similar difficulties in the representation of EV in high negative symptom patients during a reinforcement learning task (Gold et al., 2012).

Using a simpler task in which participants were presented directly with the information necessary to calculate EV, we showed that patients were resistant to the ‘Framing effect’ (Tversky and Kahneman, 1981). That is, patients were resistant to the normatively increased likelihood of accepting a gamble despite certain loss (Brown et al., 2013), suggesting that patients had reduced loss-aversion due to poorer tracking of EV (Brown et al., 2013). Interestingly, a number of high negative symptom patients were excluded because they failed the ‘catch trials’ (where there was an obvious preferable choice if participants could compute EV properly), suggesting that these participants were extremely poor EV calculators.

Recently, Sharp et al. (2012) reported on results from a task that assesses EV calculation where participants were able to calculate directly the EV of an option without needing to maintain a representation of stimulus value from a stored history of reinforcements. In controls, performance was biased towards the prospect with a comparatively higher probability of reward, despite equivalent EV for high reward magnitude options, consistent with Prospect theory (Kahneman and Tversky, 1979). This was formalized through the addition of two parameters to the initial model that adjust for known subjective evaluations of probability and magnitude: a ‘Prospect function’, that modifies rewards magnitude, and a Prelec function that modifies reward probability. The inclusion of these two modifications resulted in a reduction of the distance between subjects' choices and that of a theoretical rational decision-maker. This task offers a simplified approach to explore weighting of information for decision making in schizophrenia, without the need for learning from feedback.

Using this design, we anticipated a shallower relationship between EV and behavior in the patient group due to poorer integration of magnitude information when calculating EV, consistent with a role for OFC/vmPFC in representing relative reward magnitudes and OFC/vmPFC deficits observed in schizophrenia. We further anticipate that this pattern of poor magnitude integration will correlate with negative symptom severity.

2. Methods

2.1. Participants

Forty-eight participants with a diagnosis of schizophrenia or schizoaffective disorder and 34 controls were recruited. Sample sizes and demographic characteristics are presented in the Results and Table 1. Patients were clinically and pharmacologically stable (>4 weeks) outpatients from the Maryland Psychiatric Research Center or nearby clinics. Diagnosis was determined by the Structured Clinical Interview for DSM–IV Axis I Disorders (SCID) (First et al., 1997, Pfohl et al., 1997), past medical records, and clinician reports. Controls were screened with the SCID and free from a history of psychosis, current Axis I disorder, and family history of psychosis in first-degree relatives. Participants were excluded based on a history of drug dependence, neurological disorder, or cognitively impairing medical disorder. Participants were compensated $15 per hour. Written and informed consent was obtained from every participant. Approval was obtained from the University of Maryland IRB.

Table 1.

Demographic, neuropsychological and symptom variables.

	HC (N = 30)		SZ (N = 44)
	Mean	SD	Mean	SD	t/χ2	p
Age (y)	40.8	10.4	39.1	10.6	0.7	0.47
Gender (M | F)	22 | 12		34 | 14		0.1	0.73
Haloperidol equivalent dose			9.9	8.0
Number of APs (1 | 2+)			39 | 5
Education (yrs)	15.2	1.9	12.7	2.1	4.9	<0.0001
Maternal education (y)	13.8	2.6	14.0	2.9	−0.3	0.74
Paternal education (y)	14.3	3.5	15.0	3.2	−1.0	0.38
Cognitive ability
WMS forward	9.0	1.8	7.6	2.1	3.4	0.001
WMS back	8.3	1.8	6.8	2.1	3.5	0.001
WASI verbal sum IQ	113.6	10.6	96.5	14.8	5.5	<0.0001
WASI performance sum IQ	112.4	12.6	99.7	14.1	3.8	0.0003
WASI combined IQ	118.2	10.6	100.3	14.3	6.5	<0.0001
WTAR	112.0	9.7	97.6	17.4	4.8	<0.0001
Symptom ratings
SANS asociality anhedonia			8.0	4.2
SANS role functioning			7.5	4.1
SANS affective blunting			9.2	6.4
SANS alogia			1.3	1.8
SANS total			25.9	13.6
BPRS affect			5.5	2.7
BPRS negative symptoms			6.2	2.6
BPRS reality distortion			7.2	3.0
BPRS disorganization			3.4	1.0
BPRS total			32.3	6.3
BNSS motivation and pleasure			11.7	6.9
BNSS emotional expressivity			10.5	8.9
BNSS total			21.6	14.2

2.2. Neuropsychological and symptom measurements

Participants completed a battery of neuropsychological and symptom assessments including the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999), Wechsler Test of Adult Reading (WTAR; Wechsler, 2001), Brief Psychiatric Rating Scale (BPRS; Overall and Gorham, 1962), Brief Negative Symptom Scale (BNSS; Kirkpatrick et al., 2011), the Scale for the Assessment of Negative Symptoms (SANS; Andreasen, 1984), and the Clinical Assessment Interview for Negative Symptoms (CAINS; Forbes et al., 2010).

2.3. Task

The task was programmed in E-Prime and administered via computer. The task narrative is presented in Supplementary material along with an example test stimulus (Supplementary Fig. 1). Participants were presented with two prospects that differed in EV and responded by clicking on their chosen prospect. Prospects were parametrically manipulated by adjusting the probability of winning and the magnitude of reward to cover a range of EVs. Participants were instructed to select the prospect that they thought would maximize return. Participants were told at the beginning of the experiment that the probabilities and magnitudes were veridical and that outcomes on one trial did not influence outcomes on later trials.

Magnitude information was presented pictorially (casino chips) and in text ($0.02 per unit), while probability information was presented pictorially (chance wheel with 10 segments, probability of winning indicated via filled in sections). There were 10 blocks, with 17 trials per block (14 test stimuli; 3 control stimuli). Side of presentation was counterbalanced within prospect pairs and trial order was randomized within blocks. Participants were told that they would receive the money that they won, translated as $0.02 per magnitude unit.

Pairs of stimuli comprising fourteen EV-ratios were presented to the participant 10 times each. Reward probabilities ranged from 0.6 to 0.8 (Prospect 1) and 0.2 to 0.4 (Prospect 2). Reward magnitudes ranged from 1 to 4 (Prospect 1) and 2 to 5 (Prospect 2). This gave EV-ratios that ranged from −0.91 to 0.91 (see Table 1 in (Sharp et al., 2012) for the full set of combinations used). Three catch trials were included, in each of the three pairs: 1) one Prospect had greater magnitude and probability, 2) one had the same magnitude but different probability, and 3) one had the same probability but different magnitude. In these catch trials, the most optimal Prospect was obvious. These trials were used to assess if subjects were approaching the task rationally.

2.4. Curve fitting

The EV of each condition was calculated according to an idealized rational decision maker (though see below allowing for non-linear utilities), where EV is calculated by:

$$\mathit{EV}=\mathit{RewardMagnitude}\ast \mathit{RewardProbability}$$ (1)

A comparison between two competing EVs was made by calculating the ratio between the EV of choice 1 versus the EV of choice 2:

$$E{V}_{\mathit{ratio}}=\frac{E{V}^1-E{V}^2}{\left(E{V}^1+E{V}^2\right)/2}$$ (2)

The EV ratio informs the most appropriate action to take between two choices. Prospects with the highest reward probability were arbitrarily designated as Prospect 1.

A two parameter sigmoidal function was fit using hierarchical Bayesian non-linear regression, whereby overarching parameters inform subject level parameters through shrinkage towards a common estimate. The priors could be described as mildly informative and did not bias towards an effect of group (See supplementary material for model priors and further modeling information). Parameter k describes the shift in intercept, where a positive value indicates bias towards prospect 1. Parameter λ describes the steepness of the slope at the mid-point, where a positive value indicates enhanced EV discrimination. Model 1 (M1) was defined as:

$$P\left(\mathit{Prospect}1\right)=\frac{1}{1+exp\left(-\lambda \left(\mathit{EVratio}\left(x,p\right)+k\right)\right)}$$ (3)

A second model (M2) included Prospect and Prelec function modifiers to reward magnitude and probability respectively (Sharp et al., 2012) that make non-linear adjustments to reward magnitude and probability to make them more consistent with the subjective appraisal of magnitude and probability (Kahneman and Tversky, 1979). The Prospect and Prelec functions adjusted reward magnitudes and probabilities such that:

$$\mathit{SubjectiveMagnitude}=\mathit{Magnitud}{e}^{0.57}$$ (4)

$$\mathit{SubjectiveProbability}=e^{\left(-{\left(-log\left(\mathit{Probability}\right)\right)}^{0.77}\right)}$$ (5)

EV ratios were then calculated as in formulas 1 and 2.

2.5. Alternate models

The alternative models included independent contributions of frequency and magnitude and were incorporated as the difference in probability or magnitude between the two prospects:

$$\mathit{\Delta Prob}=\mathit{Probabilit}{y}_{\mathit{Prospect}1}-\mathit{Probabilit}{y}_{\mathit{Prospect}2}$$ (6)

$$\mathit{\Delta Mag}=\mathit{Magnitud}{e}_{\mathit{Prospect}1}-\mathit{Magnitud}{e}_{\mathit{Prospect}2}$$ (7)

Positive estimates for the intercept indicate a bias towards selecting Prospect 1. For the first of the alternate models, model 3 (M3), the probability of selecting Prospect 1 was:

$$P\left(\mathit{Prospect}1\right)=\frac{1}{1+e^{-\left({\beta }_0+{\beta }_{\mathit{Prob}}\left(\mathit{\Delta Prob}\right)+{\beta }_{\mathit{Mag}}\left(\mathit{\Delta Mag}\right)\right)}}$$ (8)

providing a base model for the remaining model additions. Models 4 and 5 (M4 and M5) incorporated estimation of the Prospect and Prelec theory functions. Finally, model 6 (M6) incorporated the magnitude for both prospects, accounting for the visual impact of the magnitude of reward:

$$P\left(\mathit{Prospect}1\right)=\frac{1}{1+e^{-\left({\beta }_0+{\beta }_{\mathit{Prob}}\left(\mathit{\Delta Pro}{b}_{\mathit{PRELEC}}\right)+{\beta }_{\mathit{Mag}}\left(\mathit{\Delta Ma}{g}_{\mathit{PROSPECT}}\right)+{\beta }_{\mathit{VisMag}}\left(\left(\mathit{Ma}{g}_{\mathit{Prsopect}1}+\mathit{Ma}{g}_{\mathit{Prospect}2}\right)\ast 0.5\right)\right)}}$$ (9)

Models were fit using the Monte Carlo sampler Stan 2.8.2 (Stan Development Team, 2013) and R version 3.2 (R Development Core Team, 2013). Model comparisons used the widely applicable information criteria (WAIC) (Watanabe, 2013), leave-one-out-cross-validation information criteria (LOO-IC) (Vehtari et al., 2015), and expected log posterior difference (ELPD_diff) of the WAIC and LOO-IC. Credible differences between groups were determined through estimation of the 95% credible intervals of the contrast estimates.

3. Results

3.1. Participants

Nineteen out of 34 (56%) control participants showed error free performance on catch trials compared to 16 out of 49 (33%) in the patient group (χ²_(df=1) = 3.5, p = 0.06). We excluded one patient who performed poorer than 60% correct on catch trials (exclusion criteria from Sharp et al., 2012). Four patients and four controls did not show any deviation from responding by selecting the prospect with a higher probability of gain in every trial (Prospect 1). There was little difference in the results when these participants were excluded, so these participants were kept in the analysis giving 44 patients and 30 controls. Demographic characteristics are presented in Table 1.

3.2. Sharp et al. model

Fig. 1 presents the averaged performance by EV-ratio across groups, and logistic regression curves derived from the full posterior (the density of the fine curves can be treated as a continuous credible interval of the curve fit and significant overlap indicates no credible differences between curve fits). Fig. 1 shows that both groups performed with a strong bias towards Prospect 1 as would be expected based on the results in (Sharp et al., 2012). There was a credible reduction in the slope parameter λ in patients, indicating lower sensitivity to EV. There was not a credible difference in the shift/bias (k) parameter.

Fig. 1.

Curve fits and group parameter estimates (+95% HDI) for the Sharp et al. model M2 (Left) and model M6 from the alternative logistic regression models (Right). Solid lines represent the median of the posterior estimates, while the faint lines represent a single curve fit to one posterior sample from the Bayesian model. Crosses represent the group median probability of selecting prospect 1 across each EV-ratio. The adjusted EV-ratio for the Sharp model reflects the EV-ratio after accounting for the constant Prospect and Prelec functions. N = 30 controls, 44 people with schizophrenia.

3.3. Alternate models

Due to consistent data departures from the fitted model shown here (jagged fit in Fig. 1) and in Sharp et al. (2012), we hypothesized that these deviations could be captured by taking into account variations in sensitivity to probability and magnitude. Alternate models separating out these effects of probability and magnitude were fitted (see Methods). The model fits in Supplementary Table 1 are presented in increasing order of complexity. The logistic regression models gave improvements in fit reflected by reductions in LOO-IC and WAIC (Supplementary Table 1, see M3 vs M2 contrast). Both LOO-IC and WAIC indicated the best fitting model was M6 against all other models except for M5, where the ELPD_diff ratio [ELPD_diff/SE(ELPD_diff)] was <2. Given the complexity of M6, we also provide a comparison model M4 that was simpler, yet still well performing, in the Supplementary material.

Fig. 1 illustrates the curve fits to the data. There were no credible differences between patients and controls evident in M6. There was, however, a credible reduction in probability sensitivity (but not magnitude sensitivity) in patients seen in M4 and M5 (see M4 in Supplementary Fig. 2), which was consistent with the direction of the effect in M6. Deviations from the Sharp et al. model may be because reward magnitude and probability are combined into a single predictor in M1 and M2, while the logistic regression models separate these effects into independent contributions that may both contribute to the effect, potentially making it more difficult to find an effect of diagnosis in this instance.

3.4. Correlations

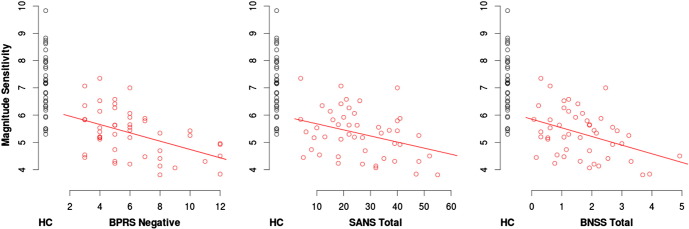
To reduce the number of correlations performed model parameters for the intercept, probability sensitivity and magnitude sensitivity from all alternative models (M3–M6) were averaged together to form model averaged parameter estimates. This was considered a suitable compromise as the magnitude of the correlations across models M3–6 were consistent, increasing confidence that notable correlations were unlikely to be idiosyncratic for a particular model. Table 2 presents Spearman's correlation coefficients for the task. There were strong correlations between modeled parameters and estimated full-scale IQ, indicating that the ability to use Probability, Magnitude and the synthesis of Probability and Magnitude into EV is related with cognitive ability. We also observed negative associations between magnitude sensitivity and Negative symptom scores from the BPRS Negative factor; the Alogia, Affective Bluntening, and Avolition subscales from the SANS; and the Emotional Expressivity subscale from the BNSS (Fig. 2 illustrates the correlations between magnitude sensitivity and the total negative symptom scores). In addition, estimated full-scale IQ was correlated with BPRS Negative symptoms (ρ = −0.31, p = 0.03) but not with SANS total (ρ = −0.19, p = 0.20), CAINS total (ρ = −0.13, p = 0.40), or BNSS total (ρ = −0.19, p = 0.20).

Table 2.

Spearman correlation coefficients between model parameters and neuropsychological and symptom variables.

	Sharp et al. model		Logistic regression model		Averaged
	Int	Slope	Int	Prob	Mag
Patients + Controls
WASI IQ	−0.43	0.61	−0.10	0.44	0.70
Controls
WASI IQ	−0.18	0.42	−0.09	0.12	0.42
Patients
WASI IQ	−0.51	0.48	−0.35	0.27	0.56
BPRS
AGD	0.16	−0.19	0.03	0.05	−0.20
Negative	0.21	−0.16	0.12	−0.22	−0.37
Reality distortion	0.03	0.01	−0.14	−0.05	0.02
Disorganization	0.05	0.09	0.15	−0.04	−0.05
Total	0.28	−0.16	0.11	−0.18	−0.30
SANS
Anhedonia asociality	0.02	0.11	−0.12	−0.07	0.01
Avolition	0.16	−0.24	0.01	−0.25	−0.31
Affective bluntening	0.09	−0.14	−0.05	−0.22	−0.31
Alogia	0.18	−0.13	0.08	−0.21	−0.33
Total	0.10	−0.08	−0.04	−0.20	−0.25
BNSS
Motivation and pleasure	0.07	−0.11	−0.05	−0.14	−0.19
Emotional expressivity	0.16	−0.12	0.05	−0.20	−0.30
Total	0.11	−0.13	−0.02	−0.22	−0.27
Medication
Haloperidol equivalents	0.37	−0.25	0.08	−0.45	−0.36

Fig. 2.

Model averaged magnitude sensitivity (averaged over M3-M6) as a function of total negative symptom scores: BPRS negative, SANS total and BNSS total. BPRS Negative symptoms was significantly associated with magnitude sensitivity, and while SANS total and BNSS total were not significant, the effect size was similar to BPRS Negative and they contained several subscales that were significant (see Table 2).

Red = p < 0.05, Bold Red = p < 0.01; Int = intercept, Prob = Probability Sensitivity, Mag = Magnitude Sensitivity, MagE = Magnitude Effect, Prosp = Prospect Function, Prelec = Prelec Function.

4. Discussion

We observed a reduction in EV sensitivity in patients using a model that combines probability and magnitude information into a single EV-ratio estimate. After isolating the independent contributions of probability and magnitude on prospect selection with the alternative models, probability integration may have been a driver of the reduced EV sensitivity in patients (e.g., results from M4 Supplementary Fig. 2). However, it was magnitude sensitivity that was significantly associated with negative symptoms, consistent with our hypothesis that deficits in magnitude integration would be amplified in patients with high negative symptoms.

The Sharp et al. (2012) models showed reduced sensitivity to EV in patients, suggesting that they are less able to integrate probability and magnitude information even on simplified tasks. EV sensitivity was strongly correlated with IQ, but not with positive or negative symptoms (although the correlation between SANS Avolition and EV-sensitivity = −0.24), suggesting patient impairments were more related to cognitive ability rather than symptoms. This is to be expected, as higher cognitive capacity would better equip participants to perform the calculations needed for integrating EV from probability and magnitude. Nevertheless, it is still an important finding that cognitive ability in patients with schizophrenia can impede optimal decision making through an inability to effectively weigh evidence.

The Sharp et al. (2012) model, failed to capture some systematic deviations in the data. To account for these deviations, we fit a series of logistic regression models with independent contributions from probability and magnitude. These models were increasingly able to catch departures from the smoothed EV-ratio curves, reflected by improvements in fit statistics.

Using the best fitting logistic regression model, there was no credible group difference between patients and controls on any of the six parameters obtained. However, there was reduced sensitivity for probability information in some of the simpler models (e.g., M4 & M5), potentially explaining one aspect of the findings discussed above using the combined EV-sensitivity models (M1 and M2). However, it was only magnitude sensitivity that was associated with both cognitive ability and negative symptoms. Importantly, the relationships between magnitude sensitivity and negative symptoms were generally consistent across different negative symptom scales, increasing confidence in the association. We initially hypothesized a relationship between negative symptoms and magnitude integration based on the reduced ability to track gain and loss magnitudes, noting that patients with greater negative symptoms were disproportionately excluded for poor catch trial performance (Brown et al., 2013). The cluster of symptom sub-scales that were significantly associated with magnitude sensitivity were SANS Avolition, SANS Affective Bluntening, SANS Alogia and the BNSS Emotional Expressivity Scale, spanning experiential and expressive dimensions of negative symptoms. These associations are tempered by the lack of a credible contrast between patients and controls on magnitude sensitivity, suggesting that the associations with negative symptoms may reflect a more general association not specific to the pathophysiology of schizophrenia. Nevertheless, given that the OFC is a critical component of the representation of reward magnitude (Frank and Claus, 2006), these findings suggest that some aspects of negative symptom formation may be related to poor OFC evaluation and a resultant devaluation of the possible expected future utility of reinforcement.

We (Gold et al., 2013) and others (Barch et al., 2014, Fervaha et al., 2013) have shown that patients with high negative symptoms were less willing to expend effort for greater reward, suggesting that effort is either more aversive or that reward valuation is reduced, thereby decreasing the cost-reward ratio. The associations presented here between reward magnitude and negative symptoms support the reward devaluation explanation, i.e., reduced reward magnitude sensitivity would impair efficient effort allocation. Interestingly, the ability to accurately appraise prospects was related to general cognitive ability and may also be tied to OFC function, potentially offering a parallel account of decision making performance in patients. Notably, this was despite our attempts to minimize the influence of cognitive complexity on decision making, implicating more directly general cognitive ability and reward magnitude appraisal. Overall, these results are consistent with the idea that negative symptoms represent a failure to appropriately estimate and maintain future reward magnitude/utility, whether through concomitant general cognitive ability impairments or more specifically through OFC dysfunction.

Funding

This work was supported by National Institute of Mental Health (2R01MH080066-06 A1); National Health and Medical Research Council (APP1090716 to MA); and the Department of Health Western Australia. The Authors have declared that there are no conflicts of interest in relation to the subject of this study.

Conflict of interest statement

We report no conflicts of interest.

Appendix A. Supplementary data

Supplementary material.