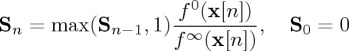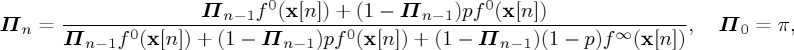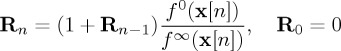Detecting changes in real-time data: a user’s guide to optimal detection

Abstract

The real-time detection of changes in a noisily observed signal is an important problem in applied science and engineering. The study of parametric optimal detection theory began in the 1930s, motivated by applications in production and defence. Today this theory, which aims to minimize a given measure of detection delay under accuracy constraints, finds applications in domains including radar, sonar, seismic activity, global positioning, psychological testing, quality control, communications and power systems engineering. This paper reviews developments in optimal detection theory and sequential analysis, including sequential hypothesis testing and change-point detection, in both Bayesian and classical (non-Bayesian) settings. For clarity of exposition, we work in discrete time and provide a brief discussion of the continuous time setting, including recent developments using stochastic calculus. Different measures of detection delay are presented, together with the corresponding optimal solutions. We emphasize the important role of the signal-to-noise ratio and discuss both the underlying assumptions and some typical applications for each formulation.

This article is part of the themed issue ‘Energy management: flexibility, risk and optimization’.

1. Introduction

Methods for detecting changes as quickly as possible in a noisily observed signal have a wide array of applications including finance [1], cyber security [2], epidemiology [3], metrology [4], statistical diagnosis [5] and, recently, the detection of instability in power systems [6]. These problems have been studied since the 1930s. Motivated by applications in production and defence, they were cast as parametric constrained optimization problems. To date a wide variety of formulations have been posed and solved, including both Bayesian and classical (non-Bayesian) settings, and in both continuous and discrete time. This theory now finds applications in domains including radar, sonar, seismic activity, global positioning, psychological testing, quality control, communications and power systems engineering.

The most basic detection problem is that of hypothesis testing. In the simplest problem, a fixed dataset is given and the goal is to detect which of two distinct hypotheses has better statistical support. An optimal solution was provided in 1933 by Neyman & Pearson [7]. In the 1940s the field of sequential analysis emerged in which the dataset is not fixed but is assumed to be observed sequentially. The goal is to decide between the two hypotheses as quickly as possible, while respecting constraints on detection accuracy. Wald and co-authors proposed the sequential probability ratio test (SPRT) in 1940s [8]. In this approach, a test statistic is calculated at each step in the sequence. Depending on the value of this statistic, it is decided to either accept one hypothesis or the other, or to seek more data by continuing to the next observation in the sequence. The optimality of this approach was proved in 1948 [9].

A natural extension is the sequential change-point detection problem, in which the process generating the data is assumed to change its probabilistic characteristics at an unknown change-point in the sequence. In this problem, the challenge is to detect the change-point with minimal average delay under constraints on premature detections (known as false alarms). Such problems were considered in a classical setting by Shewhart in 1931 [10] then later by Girshick & Rubin in 1952 [11] and Page in 1954 [12]. In the classical approach, the change is assumed to occur at a deterministic unknown time. This contrasts with the Bayesian approach, in which a prior probabilistic distribution is assigned to the change-point and then used to inform the constrained optimization procedure. In 1963, Shiryaev studied this Bayesian formulation of the change-point detection problem [13]. The optimality of Page’s approach was later established by Moustakides [14] (see also [15]) in the context of a formulation due to Lorden [16] in 1971.

In this paper, we review techniques which can be shown to be optimal in the above problems, in the sense that they solve the constrained optimization problem exactly. We also wish to emphasize the important role that the signal-to-noise ratio (SNR) plays throughout these problems. For a clearer exposition, we formulate the problems in discrete time and provide a separate discussion of the continuous time setting. While technically more demanding, the latter setting has the advantage that solutions may be obtained using stochastic calculus.

In line with the canonical work of Neyman and Pearson and the first algorithms for change-point detection in 1931 by Shewhart [10], our running example is that of normally distributed data whose mean takes one of two possible values. We use this example to connect the problems and their solutions. Since both classical and Bayesian settings are presented, random variables will be denoted using bold font throughout this review. We do not assume prior knowledge of the material.

The paper is organized as follows. Section 2 considers the hypothesis testing problem and the SPRT. Section 3 presents the change-point detection problem in various formulations, including possible formulations of average delay and constraints on false alarms. Discussion of the continuous time setting is provided in §4.

2. Hypothesis testing

A main distinction in detection theory is between online and offline testing. In offline testing, the dataset is fixed and detection accuracy is the only concern. In online testing, the data arrive in sequence to form a running (i.e. increasing) dataset and the average detection delay is also of primary importance.

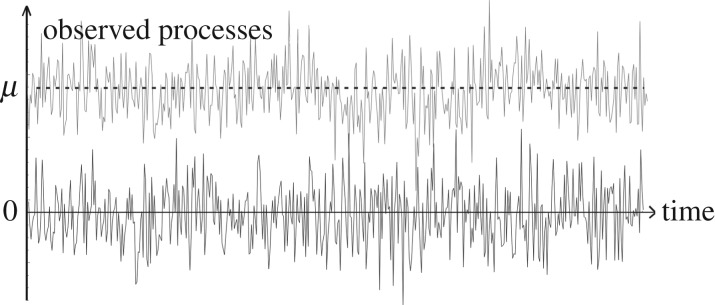
The observed data are assumed to be generated by a particular stochastic process. The probabilistic properties of this process are known, conditional on the value of an unknown parameter. In both the offline and online formulations, we must decide which of two or more hypotheses about this parameter are best supported by the data. Figure 1 shows examples of observed stochastic processes generated with two different parameter values. They are simulations from a Gaussian white noise process with differing mean values, and this model will be used in a running example below.

Figure 1.

Observed processes from two possible hypotheses, one with a mean of zero (H₀) and the other with a mean μ different from zero (H₁). In this scenario, the underlying hypotheses are easily recognized in the datasets; however as μ decreases towards zero (or the variance increases) the underlying hypothesis becomes more difficult to determine and so sequential analysis is required.

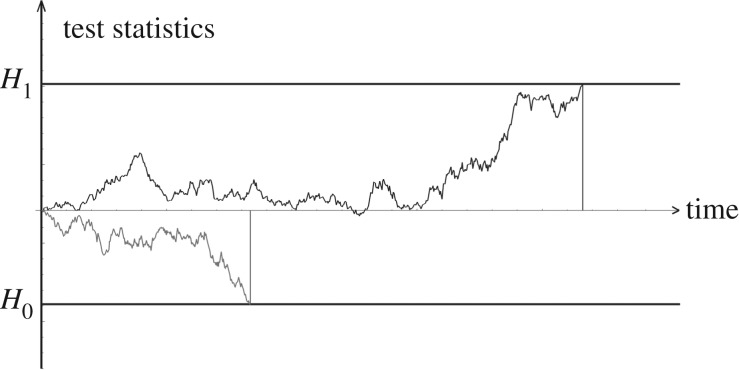
The general methodological approach is to create a sufficient statistic (a test statistic) from the data which contains all information necessary to make a decision optimally. In online testing, we therefore seek a process of sufficient statistics, updated with each new observation. This process of sufficient statistics is a stochastic process itself (see figure 2).

Figure 2.

An example of possible test statistics which can be compared to define boundaries in order to detect which hypothesis the data are deemed to be derived from. In this case, hitting the upper boundary would provide the decision that the data are derived from the alternative hypothesis H₁, while on hitting the lower boundary we accept H₀.

In the canonical setting, we consider two hypotheses, the null hypothesis H₀ and the alternative hypothesis H₁. It is apparent that there are two errors to be avoided in this setting. A type 1 error is to accept H₁ when H₀ is true. This is also known as a false alarm and in the following we shall denote the probability of false alarm by P_FA. Conversely, a type 2 error occurs upon accepting H₀ when H₁ is true. This is a missed detection or a false serenity, the probability of which will be denoted P_FS. Hence the probability of detection is given by P_D=1−P_FS.

The offline case was solved by Neyman and Pearson in 1933, resulting in the classical Neyman–Pearson (NP) test [7]. For a fixed dataset that has a known distribution under each hypothesis, the NP test was proven to be optimal in terms of maximizing the probability of detection for a given probability of false alarm. When the distribution of the fixed or sequential data is known under each hypothesis, this is known as a simple hypothesis test.

The NP test has been adapted to the online setting in the form of a sliding NP test. However, the former is fundamentally designed to maximize the detection probability rather than to address detection delay. Indeed the sliding NP test has not been shown to be optimal in terms of minimizing any useful notion of detection delay, such as those discussed in §3, under fixed false alarm constraints. We therefore begin consideration of online detection with the pioneering work of Wald on sequential analysis and the SPRT in the 1940s.

(a). Sequential probability ratio testing

The SPRT originated in Abraham Wald’s canonical work on sequential analysis in the 1940s. Building on the NP test, he derived a sequential hypothesis test which is designed to gather data until a desired level of confidence has been reached in one of the hypotheses.

The following example will be used throughout this paper. Consider a probability space 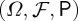on which a stochastic process

2.1

is defined where it is assumed that σ>0 and μ≠0. The discrete-time Gaussian white noise w[i] (for i=1,2,…) is defined to be independent and identically distributed (i.i.d.) N(0,1) random variables. We set the task of choosing between the hypotheses

2.2

2.3

so that the generating processes under the two hypotheses are

2.4

2.5

for i≥1. These are the two processes depicted in figure 1. In this example, we are therefore aiming to detect the presence of a constant signal μ with additional random noise w, where under H₀ only the white Gaussian noise is observed while under H₁ the signal is also present. At each time i, Wald’s SPRT statistic makes one of three decisions: to stop and decide that θ=0, stop and decide that θ=1, or to continue the observations.

It is clear from (2.4) and (2.5) that the hypothesis determines the probability distribution of the observations x[i], and hence their associated probability measure. In the following, we will write P₀(⋅)=P(⋅|H₀) and P₁(⋅)=P(⋅|H₁). Hence P₀(A) indicates the probability of an event A under the null hypothesis H₀, and P₁(A) indicates its probability under the alternative hypothesis H₁. Similarly, we define the associated expectation operators E₀(⋅)=E(⋅|H₀) and E₁(⋅)=E(⋅|H₁). Letting X_n denote the random vector of the first n observations so that X_n=(x[1],x[2],…,x[n]), its (joint) probability density function under the two hypotheses will be denoted by 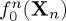and 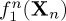under H₀ and H₁, respectively. For simplicity throughout the paper, the notation will be simplified by writing f_i(X_n) instead of 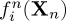under H_i, for i=0,1. By the assumption of independence we have

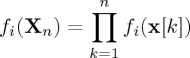2.6

for i=0,1.

Before stating the main result of this section, we introduce the relative entropy or Kullback–Leibler distance between the densities f₀ and f₁ by setting

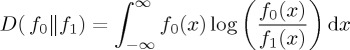2.7

and similarly

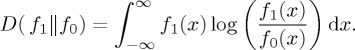2.8

Theorem 2.1 (sequential probability ratio test, cf. [17, ch. 2]). —

Let X_n=(x[1],x[2],…,x[n]) where x[i] are i.i.d. random variables with density either f₁ or f₀. The likelihood ratio is then defined as

2.9

Then the first entry time τ to the stopping set given by

2.10

with

2.11

minimizes the expected test length E_i[τ] for both i=0 and i=1, with false alarm probability P_FA and detection probability P_D. The expected test lengths are approximately given by

2.12

2.13

(i). Signal-to-noise ratio

In the case where the observed data are normally distributed as in (2.4) and (2.5) we have that D(f₀∥f₁)=D(f₁∥f₀)=μ²/2σ².

The ratio μ²/σ² is often referred to as the SNR and it follows from (2.12) and (2.13) that in the Gaussian case, increasing the SNR decreases the average test length under both hypotheses. A practical consequence of this fact is that if the SNR can be increased (e.g. using signal processing techniques—see, for example, [18]) while preserving the Gaussian data output, then this will increase the average speed of detection. This ratio is also important in continuous-time sequential analysis due to the Gaussian nature of the Brownian motion (see §4).

More generally, it can be seen that the relative entropies, or Kullback–Leibler distances, between the densities f₁ and f₀ are inversely proportional to the expected detection delays. This corresponds to the intuitive idea that two distributions may be distinguished more quickly when they are more distinct.

(ii). Example

In our running example of detecting a constant amplitude signal among Gaussian white noise, the likelihood ratio derived from the first n observations X_n=(x[1],x[2],…,x[n]) is

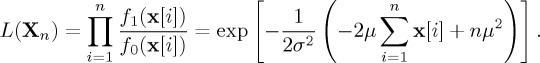2.14

By theorem 2.1, for each n≥1 it is optimal to compare the value of L(X_n) with the boundaries given by (2.11). Equivalently, we may define

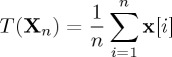2.15

and

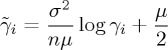2.16

for i=0,1 and compare the running mean test statistic T(X_n)_n≥1 with the thresholds 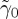and 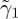as follows. At each time step (n=1,2,…), one of the following decisions is made:

• (i) if 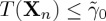, stop observing and accept the hypothesis H₀;

• (ii) if 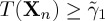, stop observing and accept the hypothesis H₁;

• (iii) if 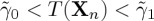, continue to time step n+1.

(b). Bayesian formulation

In the Bayesian formulation of the hypothesis testing problem, the unknown value θ is assumed to be a random variable taking the value 0 or 1 with a known distribution (and independent of the noise process (w[i])_i≥1). In this setting, we work with the prior probability measure P_π, which is derived from the probability measures P_i above for i=0,1. Writing π for the probability that θ takes the value 1, and setting

2.17

and

2.18

we define the prior probability measure P_π(⋅) as

2.19

Under this new measure we have

2.20

and similarly P_π(θ=0)=1−π.

Then we define the posterior process to be the probability of H₁ (equivalently θ=1) given the data we have observed

2.21

This posterior process can be related to the likelihood ratio at time n. For simplicity, we indicate the derivation in the case that the observations are drawn from a discrete distribution; the derivation for continuous random variables is analogous. Using Bayes’ formula P(A|B)=P(A)P(B|A)/P(B), and the law of total probability P(B)=P(A)P(B|A)+P(A^c)P(B|A^c), we have that

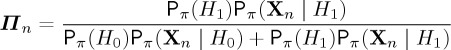2.22

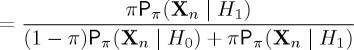2.23

2.24

where the likelihood ratio at time n is defined as

2.25

Theorem 2.2 (Bayesian sequential testing, cf. [19, ch. 4]). —

Let X_n=(x[1],x[2],…,x[n]) where x[i] are i.i.d. random variables having density f₁ with probability π and density f₀ with probability 1−π. Let

2.26

with

2.27

Then the first entry time τ of Π_n to the stopping set D=(0,A]∪[B,1) given by

2.28

minimizes the expected test length E_i[τ] for both i=0 and i=1, where the constants 0<A<B<1 are chosen such that the required false alarm probability P_FA and detection probability P_D satisfy

2.29

2.30

For further details, see [19, pp. 172–180].

This Bayesian formulation generalizes the classical formulation (2.14) by taking account of the prior probability measure P_π. In particular, if prior information about the value of θ is available then the Bayesian formulation offers the advantage of including it in the analysis. It also allows the observer to monitor a running probability Π_n that the data are derived from the alternate hypothesis H₁. It may be checked that the classical formulation is recovered as a special case upon taking the uninformed prior 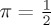, which favours both hypotheses equally.

Recent work has also used neural network techniques to estimate this posterior process and hence test hypotheses for observed data with complicated dynamics [6].

3. Change-point detection

In this paper, we have real-time engineering applications in mind. Therefore, although detection problems may be formulated either online or offline (as for hypothesis testing), we consider only the online setting. In this setting, we wish to find a stopping time τ at which point we declare that there is sufficient evidence that a change-point has occurred. An optimal stopping time is then one which minimizes a given measure of delay under certain false alarm constraints. This means that, given this performance criterion and the modelling assumptions, the method cannot be outperformed by any other method. In this section, we will consider which procedures provide optimal stopping times for different measures of the delay and false alarm constraints.

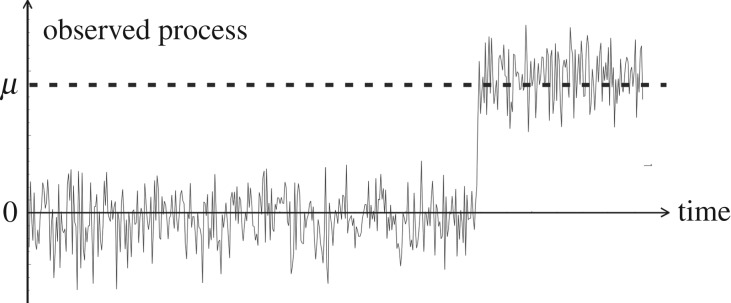
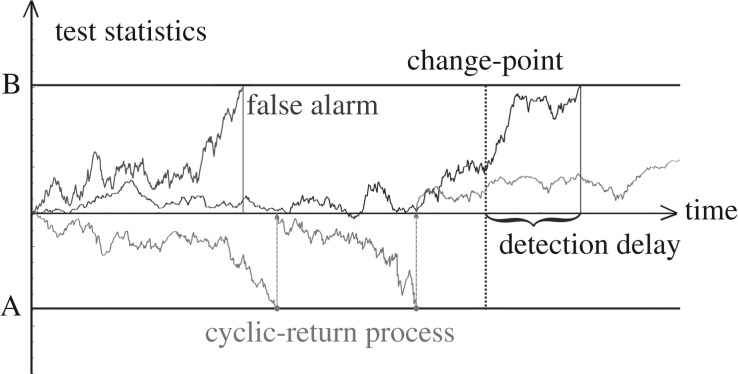
In the change-point detection problem, the observed data (x[1],x[2],…,x[i],…) are generated by the following variation on the process (2.1). There is now an unobservable change-point at time ν such that for times i=1,2,.…,ν we have θ=0 while for times i=ν+1,ν+2,… we have θ=1. This construction is illustrated in figure 3. It is interesting to note that in the sequential hypothesis testing problem of the previous section there are just two hypotheses in total (H₀ and H₁). However in change-point detection, while only two hypotheses are considered at each time step i, there are effectively as many hypotheses as there are possible change-points: an interesting explanation of this is provided in [17, §2.6]. Detection algorithms then convert all the required information from the observed process into a test statistic. When this test statistic hits a corresponding boundary B, then it is declared that a change has occurred. If this hitting time τ occurs before a change has occurred, then this is called a false alarm while if this happens after the change-point then the distance between these times is called the detection delay (see figure 4). In the classical approach, ν is assumed deterministic and unknown, while the Bayesian approach assumes ν to be a random variable which is assigned a prior distribution.

Figure 3.

An observed process with a change in mean, from zero to μ, at an easily observable change-point. However as μ decreases towards zero (or the variance increases), the change-point becomes more difficult to determine and so sequential analysis is required.

Figure 4.

Three possible trajectories for test statistics in change-point detection problems. For the change-point shown, the black test statistic results in a detection with the indicated detection delay; the dark grey test statistic results in a false alarm; and the light grey test statistic (a cyclic-return process, see §3b) results in no detection over this time period.

We define the following probability measures. Let P^ν(A) denote the probability of the event A given that the change-point takes the value ν, with E^ν the associated expectation and f^ν,n the (joint) probability density function of X_n=(x[1],x[2],…,x[n]) under P^ν. Hence P⁰ is the measure under which the change occurs at time zero (effectively before the first observation) and under 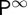the change never occurs. Similar to the previous sequential testing problems, we will simplify the notation of the joint densities f^0,n, 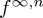and f^ν,n which in the following will be denoted f⁰, 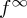and f^ν, respectively. It can be noted that the sequential testing problem may be interpreted as a special case of this set-up, with just two possible change-points: namely, ν=0 and 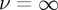. As such it is possible to see that 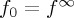and f₁=f⁰ and the likelihood ratio process from the sequential testing problem may be written

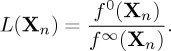3.1

In change-point detection, the problem is to minimize the average delay in detecting the change given defined constraints on the false alarms. We now make these terms precise.

(i). Constraints on false alarms

In the Bayesian setting, we may simply restrict the probability of false alarm (P_FA) to lie below a prescribed level α. Then, we consider only those stopping times τ that satisfy

3.2

In the classical setting, this false alarm probability depends on the deterministic unknown value of ν, and so an alternative formulation must be used. Lorden [16] suggested bounding the frequency of false alarms by considering only those stopping times τ which are on average greater than a parameter T if the change never occurs, i.e. requiring

3.3

There has also been some work which limits a certain conditional probability of false alarm during time intervals of a given length l [20,21], specifying for any k>0 that

3.4

However, this is a much more complicated problem.

(ii). Measures of delay

Having specified the set of admissible stopping times τ in the previous section, it remains to specify the concept of optimality. In general, if a false alarm does not occur then we define the detection delay as τ−ν and the goal is to minimize the average detection delay, which we will abbreviate ADD. That is, we seek to find a stopping time τ* such that 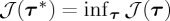given the relevant constraint from §3(i), where 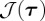is one of the ADD formulations defined below.

(1) In the Bayesian formulation the ADD may be defined simply as the average of τ−ν given that the change-point has occurred

3.5

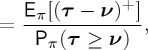3.6

where the second equality follows from Bayes’ formula. A version of this constrained minimization problem was solved in [13] when the prior distribution of the change-point ν is geometric with the possible addition of a weight at zero (see §3b). The key points about the Bayesian formulation are

• (i) Provides a means to include useful information known about the change-point.

• (ii) Provides a running probability of a change-point having occurred.

• (iii) Can constrain the probability of false alarm as described in (3.2).

There are also a number of proposed classical (non-Bayesian) measures of delay where the change-point is seen as a deterministic unknown. In this classical setting, it is not possible to minimize the probability of false alarm constraint (3.2) so often the frequency of false alarms are bounded as in (3.3).

(2) One classical ADD proposed is the relative integral average detection delay (RIADD)

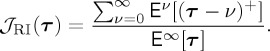3.7

The RIADD formulation may also be obtained theoretically as a certain limit of the formulation (3.6), as the prior distribution of the change-point tends to the (improper) uniform distribution between zero and infinity. This means that in most cases a false alarm will be expected before the change-point occurs and so it may be preferable to allow a string of false alarms before the successful detection [22]. This makes the RIADD very suitable to situations where the cost of false alarms is low but long delays are costly. When the data are i.i.d. the RIADD is also equivalent to the stationary average detection delay (STADD) defined in [22, thm 2]. The key points about the RIADD formulation are

• (i) Good delay measure if the first change-point is as likely in the very distant future as it is now.

• (ii) Assumes any change-point is equally likely.

• (iii) Practically this assumption means that the change-point is likely to occur after one or more false alarms.

(3) In the classical formulation, Pollak and Siegmund [23,24] proposed to minimize the ADD for the worst possible change-point by setting

3.8

Since this approach minimizes the delay for the change-point at which the delay is the greatest on average (maximum), this is termed a minimax formulation. The key points about the Pollack–Siegmund formulation are

• (i) Assumes that the pre-change data/noise has no effect on the change-point (i.e. these are independent).

• (ii) Takes into account the worst possible change-point.

• (iii) Currently no known optimal procedure for any given constraint on the frequency of false alarms.

(4) At a similar time, Lorden proposed another minimax formulation [16] which additionally considered the most unfavourable pre-change data X_ν so that the ADD is formulated as

3.9

This means it is a good measure of delay to use if the pre-change data can affect the time the change-point appears. The key points about Lorden’s formulation are

• (i) Good delay measure to consider if the pre-change data/noise affects the change-point (i.e. these are not independent).

• (ii) Takes into account the worst possible change-point and pre-change data.

• (iii) If pre-change data and change-point are independent, this may be too pessimistic.

The formulations (3.5), (3.8) and (3.9) are related by the inequalities 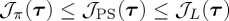[25]; however, this does not mean that one delay measure outperforms the others. Rather the Bayesian measure assumes that (a) the probability distribution of the change-point is known and (b) the change-point is independent from the pre-change data; in contrast the Pollak–Siegmund measure drops (a) while still retaining (b); finally Lorden’s measure drops both (a) and (b). For further discussion, see [25].

While (3.8) is more natural if the change-point is not affected by the pre-change data, currently there is no known optimal solution in the latter formulation under the constraint that 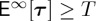. In contrast, it is known that Page’s CUSUM procedure minimizes 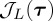given the additional constraint 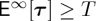[14].

(a). CUSUM algorithm

The CUSUM (CUmulative SUM) procedure was formulated by Page [12] shortly after Wald’s work with the SPRT. In contrast with the SPRT, there is a single boundary for the test statistic.

Theorem 3.1 (CUSUM procedure, cf. [14]). —

Let (x[1],…,x[ν],x[ν+1],…) be a sequence of observed data where the x[i] are independent random variables with probability density for i≤ν and f⁰ for i>ν but the change-point ν is a deterministic unknown.

Define the sufficient statistic at time n by the recursive relation

3.10

and the stopping time

3.11

where B is chosen as small as possible subject to the constraint

3.12

Then the first entry time τ of S_n above the boundary B is the optimal stopping time which minimizes Lorden’s delay measure (3.9) subject to the bounded frequency of false alarm constraint (3.12).

It should be noted here that the optimal stopping time is not an estimate of the change-point but the point at which there is enough evidence that a change-point has already occurred. Offline change-point identification can then be used to estimate the exact change-point in the data. However, the CUSUM procedure can also provide an estimate of the change-point, which is

3.13

The CUSUM procedure can be thought of in a few different ways. First, it can be thought of as a SPRT which restarts if the sufficient statistic L(X_n) given in (2.9) falls below the level 1. This is a type of cyclic return process, a process that is returned to a given level upon hitting/crossing a boundary, which in this case is the level A=1 (see figure 4).

Second, it is also sometimes viewed as

3.14

whereby S_n is the divergence of the SPRT sufficient statistic (3.1) from its current minimum. Finally, it can also be seen as a sliding SPRT or a reverse time SPRT starting from the latest data point. For further discussion on the CUSUM procedure, see [17, §2.6].

(i). Example

In our Gaussian example, we see that by letting 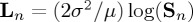for n>0 we have

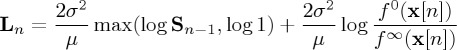3.15

3.16

3.17

The first hitting time can then be seen to be equivalent for the formulation which is often used, where

3.18

(b). Bayesian quickest detection

In §3(ii) we referred to the work [13] on the Bayesian quickest detection problem, in which the prior distribution on ν is the geometric distribution with a weight π at zero. This choice is typical when one has knowledge of the average value of the change-point, but no further information. This follows since in the set of all distributions on the positive integers with a given mean, the geometric distribution has the greatest entropy and hence is the most uncertain. The probability measure associated to the quickest detection problem is then

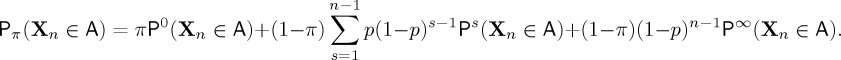3.19

This expansion can be seen as the summation of probabilities of three scenarios: (i) the change occurs at time zero, (ii) the change occurs at a geometrically distributed time 1≤s≤n−1 and (iii) the geometrically distributed change-point has not yet happened in the observed data X_n.

Theorem 3.2 (Bayesian quickest detection, cf. [19]). —

Let (x[1],…,x[ν],x[ν+1],…) be a sequence of observed data where the x[i] are independent random variables with probability density for i≤ν and f⁰ for i>ν. The change-point ν is a weighted geometrically distributed random variable with parameter p and a weighting of π at time zero. Define the sufficient statistic at time n by the recursive relation

3.20

and the stopping time

3.21

where

3.22

Then the first entry time τ of Π_n above the boundary B is the optimal stopping time which minimizes the Bayesian (weighted-geometric) delay measure (3.5) subject to the probability of false alarm constraint

3.23

In theorem 3.2, the process (Π_n)_n≥1 is the running probability that the change-point has occurred given the information observed until time n, i.e.

3.24

which is also known as the posterior probability process. This is linked to the likelihood ratio L(X_n) from (3.1), which has been present throughout these problems, via

3.25

where

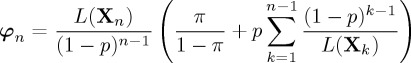3.26

and φ₀=π/(1−π) and the summation is defined to be equal to zero at n=1. It can be seen that

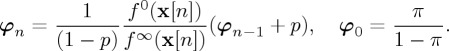3.27

The recursive formula (3.20) is then given by combining (3.25) and (3.27).

(c). Shiryaev–Roberts procedure

When and , the weighted-geometric distribution used in the previous section may be interpreted as approaching an improper (i.e. non-normalized) uniform distribution on the positive integers. In the limit, we obtain a generalized Bayesian approach in which the change is equally likely to occur at any time between 1 and 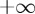. The solution in this case is provided by the Shiryaev–Roberts (SR) procedure.

Theorem 3.3 (SR procedure, cf. [22]). —

Let (x[1],…,x[ν],x[ν+1],…) be a sequence of observed data where the x[i] are independent random variables with density for i≤ν and density f⁰ for i>ν where the change-point ν is a deterministic unknown value.

Define the sufficient statistic at time n by the recursive relation

3.28

and the stopping time

3.29

where B is chosen as small as possible subject to the constraint

3.30

Then the first entry time τ of R_n above the boundary B is the optimal stopping time which minimizes the RIADD delay measure (3.7) subject to the frequency of false alarm constraint (3.30).

In our Gaussian running example, it is known that the optimal boundary is equal to the lower bound on the frequency of false alarm constraint [26], i.e.

3.31

It can also be noted that the sufficient statistic for the SR procedure can be defined in terms of the likelihood ratio function L(X_n) as follows:

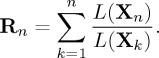3.32

(i). Relationship with Bayesian setting

It can be seen that starting with the Bayesian delay measure and sufficient statistic from (3.26), one has

3.33

as and . It is also known that

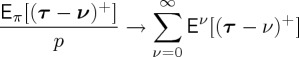3.34

and

3.35

and hence the delay measure

3.36

as and .

(ii). The SR-r procedure

The SR procedure with a starting point R₀=r such that

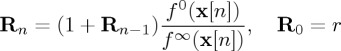3.37

is also referred to as the SR-r procedure. In [24], it is shown that by letting r be a defined random variable the SR-r procedure is asymptotically optimal in minimizing the Pollak–Siegmund delay metric as the frequency of false alarm constraint 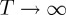. However, a counter example in [27] showed that this procedure is not strictly optimal for any given lower bound on the frequency of false alarms.

4. Continuous time processes

The above problems have natural analogues in the continuous time setting, when time is indexed by the non-negative real numbers. In our white noise example, the process (2.1) corresponds naturally to Brownian motion (B_t)_t≥0, the fundamental continuous time stochastic process, and in the hypothesis testing problem we then have

4.1

4.2

The hypotheses therefore differ through the presence or absence of the drift term μt. In the analogous change-point problem, we have

4.3

The optimal procedures for the Bayesian hypothesis testing problem and the constrained quickest detection problems have also been solved in the setting of a Brownian motion with a possible (constant) drift. The Bayesian hypothesis testing problem was solved in [28], the Bayesian quickest detection problem in [29], Lorden’s constrained problem in [30,31] and the relative integral average delay formulation in [32].

The continuous time setting can serve as an approximation to the discrete time setting (or vice versa), but has the advantage that methods of continuous-time stochastic calculus may be applied. This has led to further progress on problems with more general observed processes in continuous time, which we now mention briefly.

(a). General diffusion processes

Consider the continuous-time observed process

4.4

for the hypothesis testing problem, or

4.5

in the case of change-point detection.

These observation processes have been considered in the Bayesian framework [33,34]. In this setting, the SNR is also important and is similarly defined as (μ₁(x)−μ₀(x))²/σ(x)² (e.g. [33, eqn (2.16)]). When the SNR is constant the one-dimensional theory of optimal stopping may be applied. Non-constant SNR processes give rise to two-dimensional sufficient statistics, which depend on both the posterior process and the current position of the observed process, making their analysis more challenging. However, recent breakthroughs have been made for certain processes with non-constant SNR [35,36]. For a general discussion of this problem and the causes of increased dimensionality, see [35, §2] and [36, §3].

(b). Further results

The above problems have also been considered with a finite time horizon [37,38], exponential time-costs [34,39,40] and in the context of multiple hypothesis testing [41,42]. Discontinuous processes in continuous time have been studied [43–45]. The first two papers deal with a continuous time counting process (a Poisson process), which is a natural model in the problem of detecting nuclear material against noise from background radiation. Further extensions include problems where the change-point depends on the observed trajectory (termed self-exciting processes, see [46]) and problems in which the change occurs when the observed process hits an unobservable random level in space rather than in time [47,48]. Further details may also be found in [26,49,50] and, specifically for quickest detection problems, in [51].

Authors' contributions

This review is a collection of the experience of all three authors, who together drafted and revised the manuscript and approved the final text.

Competing interests

The authors declare that there are no competing interests.

Funding

This work was supported by the UK Engineering and Physical Sciences Research Council (EPSRC) grants EP/K00557X/2 and EP/M507969/1.