Exploring the Dynamics of Propeller Loops in Human Telomeric DNA Quadruplexes Using Atomistic Simulations

Abstract

We have carried out a series of extended unbiased molecular dynamics (MD) simulations (up to 10 μs long, ∼162 μs in total) complemented by replica-exchange with the collective variable tempering (RECT) approach for several human telomeric DNA G-quadruplex (GQ) topologies with TTA propeller loops. We used different AMBER DNA force-field variants and also processed simulations by Markov State Model (MSM) analysis. The slow conformational transitions in the propeller loops took place on a scale of a few μs, emphasizing the need for long simulations in studies of GQ dynamics. The propeller loops sampled similar ensembles for all GQ topologies and for all force-field dihedral-potential variants. The outcomes of standard and RECT simulations were consistent and captured similar spectrum of loop conformations. However, the most common crystallographic loop conformation was very unstable with all force-field versions. Although the loss of canonical γ-trans state of the first propeller loop nucleotide could be related to the indispensable bsc0 α/γ dihedral potential, even supporting this particular dihedral by a bias was insufficient to populate the experimentally dominant loop conformation. In conclusion, while our simulations were capable of providing a reasonable albeit not converged sampling of the TTA propeller loop conformational space, the force-field description still remained far from satisfactory.

Introduction

Telomeres are specialized structures present at the linear ends of chromosomes. They protect the cells from homologous recombination, nonhomologous end-to-end fusion, and exonuclease degradation.¹⁻⁴ Human telomeric DNA comprises tandem repeats of d(TTAGGG) sequences of 2–10 kb with single-stranded 3′ overhang of 100–300 nucleotides.⁵⁻⁷ In normal cells, telomeres are shortened at every cycle due to the end-replication problems until they reach a critical size, inducing cellular senescence.^8,9 However, in human stem cells, cancer cells, and specialized cells (such as germ-line cells), the telomerase reverse transcriptase enzyme complex maintains telomere length and uses its intrinsic RNA as the template on which telomeric DNA synthesis occurs.^10,11 Increased telomerase expression in comparison to normal cells has been found in almost all human cancers.^8,10,12−16 Therefore, inhibition of telomerase is a potential attractive selective approach for cancer therapy.¹⁷⁻²⁰

Guanine-rich DNA (as telomeric DNA) sequences can arrange in square planar alignment and utilize both Watson–Crick (WC) and Hoogsteen faces of guanine bases to form four-stranded secondary structure termed G-quadruplexes (GQs).²¹⁻²⁴ GQ formation in telomeres has been shown to inhibit telomerase invitro and is therefore recognized as important structure for therapeutic intervention in cancer.²⁵⁻³⁰ Based on this paradigm, many GQ-stabilizing ligands have been explored for potential anticancer activity.^29,31−39

The core structural unit of a GQ is a G-quartet, which is formed by alignment of four guanines linked by Hoogsteen hydrogen bonds.^21,23,40 G-quartets can stack together to form a G-stem (GS), and the interlinking nucleotides form the loops of the GQ.^21,23 Cations coordinate with the center-facing carbonyl oxygen of guanine bases in a G-quartet and counterbalance the electrostatic repulsion between them. The guanine bases can adopt syn (s) or anti (a) glycosidic orientation in the GSs. The syn/anti-orientation of guanines, strand directionality, length, and arrangement of loops all add structural versatility to GQs and determine their topology.^21,41−46

The human telomeric (Htel) GQ is extremely polymorphic, at least in dilute solution, with variations in 5′ and 3′ terminal sequence playing a role in determining the relative stability of particular polymorphs, as well as GQ concentration and the nature of the associated cation. So far, six distinct GQ topologies of the Htel d(TTAGGG) sequence have been observed in dilute solution experimental conditions and can be said to populate the experimental conditions as the thermodynamic minima (see Table S1 and Figure S1 in the Supporting Information). The X-ray crystal structures of 22-mer 5′-AGGG(TTAGGG)₃-3′ and 12-mer 5′-TAGGG(TTAGGG)T-3′ revealed that these oligonucleotides form parallel-stranded GQs in the presence of K⁺ ions,⁴⁶ at least in the crystalline state, in concentrated solution, and possibly under cellular conditions. The 12-mer sequence forms a bimolecular GQ, while the 22-mer sequence forms an intramolecular GQ. The NMR structure of the same 22-mer sequence in the presence of Na⁺ ions forms a GQ with antiparallel basket topology,⁴⁵ whereas it forms the parallel topology in the presence of K⁺ ions in solution crowded conditions,⁴⁷ as observed in the crystalline state.⁴⁶ The antiparallel topology was also observed in K⁺ ions as the 5′-GGG(TTAGGG)₃T-3′ sequence forms an antiparallel basket GQ but with only two quartets as shown by NMR analysis.⁴¹ This two-quartet structure represents an example of strand-slippage GQ architecture which has been suggested to commonly occur during the process of GQ folding.⁴⁸ The two G-quartets of this structure are stabilized by extensive loop alignments above and below the G-quartets. Interestingly, in the presence of K⁺ ions, two distinct hybrid topologies characterized by a mixed parallel/antiparallel (3+1) G-quartet-core have been observed by NMR spectroscopy.^43,44,49,50 They differ in the glycosidic orientation of guanines within the GSs and the progression of loops around the G-quartet core. The sequences 5′-AAAGGG(TTAGGG)₃AA-3′, 5′-TAGGG(TTAGGG)₃-3′, and 5′-TTGGG(TTAGGG)₃A-3′ adopt a hybrid-1 topology in the presence of K⁺ ions.^43,49,50 This is characterized by a 5′-saa--saa--ssa--saa-3′ strand arrangement with propeller-lateral-lateral loops in the 5′ to 3′ direction (s and a stand for syn and anti guanosines, respectively, see Figure S1 in the Supporting Information). The sequences 5′-TTAGGG(TTAGGG)₃TT-3′ and 5′-TAGGG(TTAGGG)₃TT-3′ form a hybrid-2 topology with a 5′-saa--ssa--saa--saa-3′ strand arrangement and lateral-lateral-propeller loops in the 5′ to 3′ direction.^44,50 Additional diversity was revealed with the 27-mer Htel sequence 5′-TTAGGG(TTAGGG)₃TTA-3′, which forms an antiparallel GQ with (2+2) topology in Na⁺ ions.⁴² The strand arrangement of this GQ is 5′-ssa-saa-saa-ssa-3′, and the loop arrangement in the 5′ to 3′ direction is lateral-propeller-lateral.⁴² It is not uncommon for several distinct folds of the Htel GQ to coexist in equilibrium under specific sequence/environment conditions, which often precludes determination of the structures in solution experiments using NMR. Competition between the hybrid-1 and hybrid-2 arrangements has been explicitly shown to determine the folding kinetics of the final stage of folding of 5′-TTGGG(TTAGGG)₃A-3′ in the presence of K⁺ using time-resolved NMR.⁵¹ While the hybrid-1 arrangement has been determined to be the thermodynamic minimum, the kinetically more accessible hybrid-2 structure acted as the main competing fold, temporarily dominating the population. This experimental finding is consistent with theoretical models of GQ folding suggesting that Htel GQ folding is a multipathway process that can be best understood using the kinetic partitioning mechanism with diverse GQ folds acting as the dominant free energy basins on the free energy landscape.⁵² This has also been supported by additional recent experimental data.⁵³⁻⁵⁵ Multiple factors determine the folding of a GQ-forming sequence into a specific GQ topology.^47,56−58 Evidently, one of the main factors affecting the GQ folding is structural versatility of the single-stranded loop sequences linking the G-strands. Further, specific interactions between ligands and loops may play a key role in the design of ligands that would selectively bind only to specific GQs. Thus, understanding the behavior of GQ loops is one of the key problems in studies of GQs structure and dynamics and definitely not restricted to the Htel GQs.

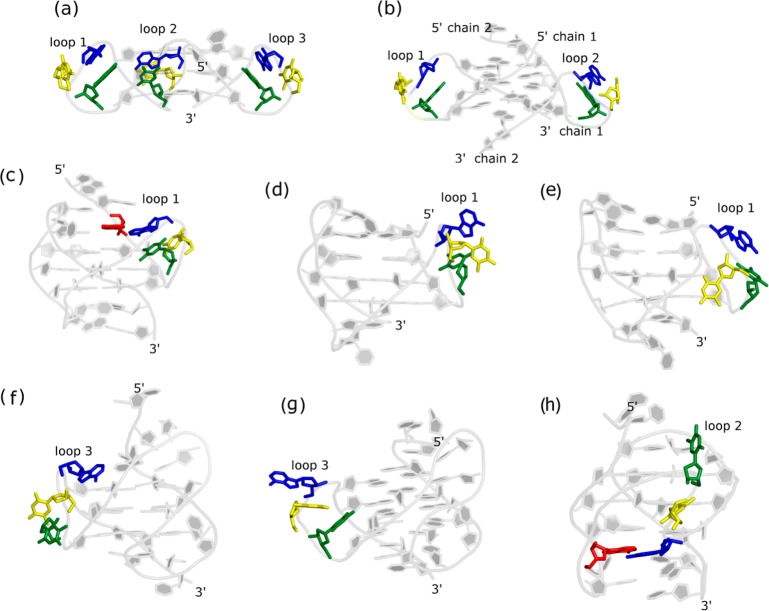
To date, all crystal structures and GQ-ligand complexes of Htel sequence have been observed to adopt parallel-stranded all-anti topology with all propeller TTA loops (Figure 1a and b).^{33,36,38,46,59} In the TTA propeller loops of GQ-crystal structures, adenine is intercalated in between the two thymines to form a T/A/T stack.⁴⁶ The numerous GQ-ligand crystal structures have sampled various conformations of the loops though the most abundant conformation in these complexes resembles the structure of the uncomplexed Htel GQ.⁶⁰ Single TTA propeller loops were found in three of the five remaining folds, namely the hybrid-1, hybrid-2, and antiparallel (2+2) structures.⁴²⁻⁴⁴ The propeller loops in the solution structures also exhibit conformational variability in the different Htel GQs (Figure 1), although their predicted structures are probably not unambiguously determined due to lack of appropriate primary NMR data and the relative flexibility of the GQ loop regions.

Figure 1.

Propeller loop conformations in the experimental structures of Htel topologies (model 1 is shown for the NMR structures). The GQs are shown in cartoon, while the propeller loop nucleosides are shown in sticks. In the TTA propeller loop, PT1, PT2, and PA3 (see abbreviations in Methods) are colored in green, yellow, and blue, respectively. In GQs where the PA3 formed alignment with the flanking base, the flanking base is shown in red sticks. The PDBs of the structures are (a) 1KF1, (b) IK8P, (c) 2HY9, (d) 2JSM, (e) 2GKU, (f) 2JPZ, (g) 2JSL, and (h) 2MBJ. The a-b, c-e, f-g, and h show various parallel-stranded, hybrid-1, hybrid-2, and antiparallel (2+2) GQs, respectively. The propeller loops and 5′ and 3′ ends of GQs are labeled in the figure. Chains 1 and 2 are also labeled in bimolecular parallel-stranded GQ.

Besides experimental studies, molecular dynamics (MD) simulations have been widely used to investigate various aspects of structural dynamics of Htel GQs.^48,61−72 The loops of GQs are highly flexible, and as MD can provide a dynamic view of GQs, it can be useful in the identification of characteristic loop conformations in Htel topologies. On the other hand, a MD description of the GQ loops is very challenging in view of the two key limitations of the MD technique: the force-field approximation and the sampling. Previous simulations have indicated that the parmbsc0 version⁷³ of the Cornell et al.⁷⁴ force field is not fully satisfactory in its description of the propeller loops of the Htel GQ.^61,63 Namely, the force field vigorously eliminates the conformations with γ-dihedral of the first thymine (PT1) of the TTA propeller loops in a trans region (γ-trans) as seen in the X-ray structures, with subsequent overall rearrangement of the loop.^61,63 Even with some more recent force-field refinements, the crystal-structure-like conformation of propeller loops could not be sampled in simulations carried out on a 100 ns-time scale,⁷⁵ since the force fields still needed to include the bsc0 α/γ correction that is crucial for the basic stability of DNA simulations. Further, our MD simulations on the c-kit promoter GQ showed that although the MD description of GSs was more or less converged on a sub-μs-time scale, the loop regions required multiple μs-timescales to achieve satisfactory sampling of the loop dynamics.⁶⁴

We report in the present paper on a series of 10-μs-long standard simulations of all the known Htel GQ topologies with propeller loops, using several recent versions of the AMBER force field. We have also used the recently introduced replica-exchange with collective-variable tempering (RECT) enhanced-sampling method, which appeared to be especially well-suited for loops.⁷⁶ To the best of our knowledge, this is the most comprehensive study so far in terms of the length of simulations carried out for the GQ loops. Further, we constructed the Markov state model (MSM)^77,78 using one of our unbiased simulations to reveal metastable states of TTA propeller loops and their dynamics. In this work, for space reasons, we analyze only the TTA propeller loops: behavior of the remaining loop types will be reported elsewhere.

We find that there is a surprisingly good correspondence between the standard and RECT simulations. Thus, the multiple 10-μs scale unbiased simulations provide a representative sampling of the conformational space of the TTA propeller loops, though we are far from claiming that the results have converged in terms of populations of different substates. In other words, the 10-μs scale conventional simulations achieve the minimal sampling requirement to characterize this type of loop and to identify all its relevant substates. Thus, the sampling problem has been resolved to a large extent. On the other hand, the current force fields are not capable of stabilizing the most common propeller conformation of the TTA loop with the first thymidine having a γ-trans dihedral angle in the T/A/T stack. Although it cannot be fully ruled out that this loop conformation may be to a certain extent stabilized by crystal packing interactions involving the propeller loop nucleotides, it is more likely that the force-field description of the propeller loops is not flawless. Since the γ-trans states need to be penalized to maintain B-DNA structure in MD simulations, it is not clear if any straightforward general-purpose force-field modification improving the description of the propeller loops is presently achievable. Because the latest OL15 variant of the AMBER DNA force field^79,80 already includes reparametrization of all dihedral angles of the original Cornell et al. force field,⁷⁴ it is evident that reparametrization of dihedral angle potentials is not sufficient to obtain a fully satisfactory description of GQ loops. The force field thus emerges as the most significant limitation in MD studies of GQ loops and their interactions with ligands.

Materials and Methods

Starting Structures

We took representatives of all propeller loop-forming Htel GQ topologies for the present study (Figure 1 and Table 1). The coordinates for the parallel-stranded topology were taken from both unimolecular and bimolecular DNA GQs, PDB ids 1KF1 and 1K8P, respectively.⁴⁶ The coordinates for hybrid-1 and hybrid-2 topologies were taken from NMR structures, PDB ids 2HY9 and 2JPZ, respectively.^44,49 We also carried out simulations for the hybrid-1 GQ topology using the NMR structure coordinates from PDB id 2GKU.⁴³ The coordinates for the antiparallel (2+2) GQ topology were taken from PDB id 2MBJ.⁴² In all the NMR structures, coordinates were taken from model 1 of the deposited ensembles of structures. The brominated bases were replaced by corresponding unmodified bases in the starting structures, where applicable.

Table 1. List of the Simulations Carried out in the Present Study.

quadruplex topology	loop sequence	PDB id	ion conditions	force field	length of the simulation	simulation reference number used in the text
intramolecular parallel-stranded DNA GQ	propeller-propeller-propeller	1KF1	excess 0.15 M NaCl	bsc0χOL4	10 μs	1
			excess 0.15 M NaCl	bsc0χOL4εζOL1	10 μs	2
			excess 0.15 M KCl	bsc0χOL4	10 μs	3
bimolecular parallel-stranded DNA GQ	propeller	1K8P	excess 0.15 M NaCl	bsc0χOL4	10 μs	4
	propeller		excess 0.15 M NaCl	bsc0χOL4εζOL1	4 μs	5
(3+1) hybrid-1 DNA GQ	propeller-lateral-lateral	2HY9	excess 0.15 M NaCl	bsc0χOL4	10 μs	6
			excess 0.15 M NaCl	bsc0χOL4εζOL1	10 μs	7
		2GKU	excess 0.15 M NaCl	bsc0χOL4εζOL1	10 μs	8
(3+1) hybrid-2 DNA GQ	lateral–lateral-propeller	2JPZ	excess 0.15 M NaCl	bsc0χOL4	10 μs	9
			excess 0.15 M NaCl	bsc0χOL4εζOL1	10 μs	10
antiparallel (2+2) DNA GQ	lateral-propeller-lateral	2MBJ	excess 0.15 M NaCl	bsc0χOL4	10 μs	11
			excess 0.15 M NaCl	bsc0χOL4εζOL1	10 μs	12
intramolecular parallel-stranded DNA GQ	propeller-propeller-propeller	1KF1	excess 0.15 M NaCl	bsc0χOL4εζOL1 and restraints on γ-dihedral (γ ∼ 180°) of the first thymine of all three propeller loops	3.4 μs	13
			excess 0.15 M NaCl	bsc1	2 * 1 μs	14, 15
			excess 0.15 M NaCl	OL15	10 μs	16
			excess 0.15 M NaCl and OPC waters	OL15	10 μs	17
			excess 0.15 M KCl and OPC waters	OL15	10 μs	18

Water and Ionic Conditions in Standard Simulations

The simulations were carried out in 0.15 M excess salt, using either NaCl or KCl. The structural water molecules and ions in the X-ray PDB (except of the two channel cations) were removed in the starting structure. The channel K⁺ ions in coordinates taken from crystal structures were replaced by Na⁺ in the starting structures of NaCl simulations. In the NMR structures, the cations were manually placed between the quartets in the GSs.

Note that the differences between NaCl and KCl environments in μs-scale simulations of GQs are minor, and so far no systematic differences have been documented when comparing NaCl and KCl GQ simulations. The cation-type effects in simulations of specific GQ folds should not be compared with the effect of ions on relative stability of different GQ folds in equilibrium thermodynamic experiments, which allow transitions between the different folds via the unfolded ensemble. In other words, to sense the difference between cation types, the length of the simulations would have to be comparable to the 1/k_unfold kinetic constant; for more discussion on why NaCl and KCl simulations of folded GQs should be considered as essentially equivalent see ref (64), p 8688 and ref (55).

The solvent molecules and additional ions for simulations were added using the xleap module of AMBER12. The system was first neutralized by Na⁺ or K⁺, and then excess NaCl or KCl of 0.15 M concentration was further added to the system. AMBER-adapted Joung and Cheatham parameters were used for Na⁺ (radius 1.212 Å and well depth of 0.3526418 kcal mol^–1), K⁺ (radius 1.593 Å and well depth 0.4297054 kcal mol^–1), and Cl^– ions (radius 2.711 Å and well depth 0.0127850 kcal mol^–1).⁸¹ Unless otherwise mentioned, all the systems were solvated with the SPC/E water model and placed in a truncated octahedral box with a minimal distance of 10 Å of solute from the box border. For comparison and completeness, we have carried out additional simulations of intramolecular GQ PDB 1KF1 with the recently suggested OPC water model.⁸² The simulations were carried out in both 0.15 M NaCl and KCl independently, and the systems were simulated in the same way as for SPC/E water model.

DNA Force Fields

The simulations were carried out with different variants of the AMBER DNA force field, starting from the parmbsc0 (bsc0)⁷³ modification of the Cornell et al. force field⁷⁴ supplemented by χ_OL4,⁸³ marked as bsc0χ_OL4 throughout the paper. Bsc0χ_OL4 improves the behavior of simulated DNA GQs compared to simulations carried out with the bsc0 refinement alone,⁸³ specifically for syn nucleotides. The χ_OL4 refinement facilitates transition through the 120° χ region by decreasing the energy barrier through this region and increasing for transitions through the 350° χ region. It also subtly modulates the χ anti-region. A further refinement is εζ_OL1⁸⁴ which was added to the bsc0χ_OL4 force field, abbreviated as bsc0χ_OL4εζ_OL1. The εζ_OL1 change corrects the ε = g⁺ region and improves the barrier between BI and BII B-DNA conformations. The εζ_OL1 parameters markedly improve the description of B-DNA (its helical twist as well as BI/BII populations) and antiparallel GSs.⁸⁴ Additionally, we have carried out test simulations (Simulations 14, 15, and 16) using two force-field versions that emerged in the course of this project.^79,85 Namely, we carried out 1 μs long two test simulations with the intramolecular parallel-stranded GQ (PDB id: 1KF1) using the parmbsc1 (bsc1) DNA force-field dihedral angle reparametrization⁸⁵ which is roughly comparable to bsc0χ_OL4εζ_OL1, see ref (80) for extended comparison of the DNA force fields. Test simulations using the intramolecular parallel-stranded GQ were also carried out using the latest OL15 force field, which is obtained by adding β_OL1 refinement for the β dihedral angle of DNA in the bsc0χ_OL4εζ_OL1 force field. OL15 is essentially completing the reparametrization of all dihedral angle potentials compared to the original Cornell et al. force field.⁷⁹ However, none of the two latest dihedral angle potential refinements affects the behavior of the presently studied systems, suggesting that any possibility of further improvement of the AMBER nucleic acids force fields using refinements of the one-dimensional dihedral angle potentials has been essentially exhausted, as anticipated earlier.⁶⁵ As explained below, within the limits of conformational sampling, all force-field variants used in this study can be considered as of comparable quality for the description of the TTA propeller loops and suffer from similar force-field limitations. The list of all the simulations is given in Table 1.

MD Simulations

The starting structures were equilibrated using standard protocols (see the Supporting Information). The final MD simulations were performed with the PMEMD CUDA version of AMBER12.⁸⁶⁻⁸⁸ The periodic boundary conditions were defined by the PME algorithm and the nonbonded cutoff was set to 9 Å.⁸⁹ Covalent bonds involving hydrogen atoms were constrained using the SHAKE algorithm with a tolerance of 0.0001 Å, which allowed us to use an integration time step of 2 fs.⁹⁰ Simulations 8 and 13–18 were carried out with version AMBER14 using the hydrogen mass repartitioning of solute atoms and an integration time step of 4 fs.⁹¹ All the simulations were carried out at constant pressure and temperature of 1 atm and 300 K, respectively. The temperature and pressure were maintained using the Berendsen weak coupling thermostat.⁹² The final production run without restraints (unless specified) was carried out for a continuous 10 μs period (unless specified), and the frames were written at every 10 ps, so the analyses are based on 10⁶ data points. Analyses of trajectories were performed using the cpptraj module of AMBER, and VMD and the PYMOL programs were used for visualization.⁹³⁻⁹⁵

Energy Comparison of GQ Topologies

Later in this project we decided to evaluate enthalpy differences between the six studied GQ topologies. For this reason, we ran six other 2 μs-long MD simulations containing the same sequence and identical number of waters and ions, one for each HTEL GQ topology. The enthalpies were estimated by total energies averaged over canonical NPT ensemble obtained from the simulations. Note that such calculations do not account for differences in entropy, which would be needed to obtain free energy differences determining relative stabilities of GQ topologies. We refrained from entropy calculation because of its unreliability, but in general, entropy should be similar for all the GQ folds, and thus their enthalpy should reflect the order in free energy. The obtained estimates of relative enthalpies were subsequently decomposed into contributions corresponding to different force-field terms, and based on these results, they were further decomposed on the contributions of particular residues. Details on the methodology and the differences between these simulations and the simulations described above are given in the Supporting Information.

RECT Simulations

In order to enhance sampling and calculate free-energy differences between various propeller loop conformations, we employed the recently developed replica exchange with the collective-variable tempering (RECT) method.⁷⁶ Here, many local collective variables (CVs) are biased at the same time using independently accumulated history-dependent potentials built by means of concurrent well-tempered metadynamics simulations.^96,97 This scheme is integrated in a replica-exchange framework, in which the strength of the biases is increased across the replica ladder. The bias strength is regulated by the bias factor γ. The bias factor value is different for each replica, ranging from 1 in the lowest replica (no bias potential is applied) to a value high enough so as to compensate the free-energy barriers along the chosen CVs. Replicas can mutually exchange coordinates at attempts held periodically during the simulation. A major advantage of this kind of simulation for nucleic acids is that it is possible to accelerate conformational transitions in nucleic acids with very little a priori knowledge. For example, all backbone, puckering, and χ dihedral angles of several residues could be biased at the same time. In this way, coupled transitions of these torsions into the most relevant conformational substates are promoted, without the need of defining complicated ad hoc CVs.^76,98

Three structures have been studied by RECT: 1KF1, biasing the second loop; 2GKU, biasing its first loop; and 2MBJ, biasing the second loop. The systems were built in the same way as those for the standard simulations. The solute molecules were solvated by a SPC/E water box with distances of at least 10 Å between solute and the box border.⁹⁹ The systems were then neutralized by Na⁺ cations, and excess 0.15 M NaCl was added.⁸¹ The topology and coordinate files were then converted to the Gromacs format by the script Acpype.py.¹⁰⁰ The simulations were performed in Gromacs 4.6.7¹⁰¹ with Plumed 2.2.0 (developer’s version)¹⁰² under the bsc0χ_OL4εζ_OL1 force field. The temperature was set to 300 K, and the pressure was set to 1 atm. Bonds involving hydrogen atom were constrained using the LINCS algorithm.¹⁰³ The integration step was set to 2 fs.

We performed seven RECT simulations. Details of the biases used in the simulations are given in Table 2. We employed eight replicas per RECT simulation. The values of the bias factor γ for each replica were selected using a geometric progression, from γ = 1 in the lowest replica to γ = 4 in the highest one (Table S2).⁷⁶ Details of the RECT simulations are summarized in Table S2 in the Supporting Information. Replica exchange attempts were performed every 200 steps, and acceptance was resolved by the Metropolis criterion. The setup led to average acceptance probability between 0.53 and 0.56 in all the RECT simulations (Table S3). The length of each replica was 500 ns, giving cumulative time of 8 × 500 ns = 4 μs per RECT simulation. The total simulation time of all the RECT simulations combined was 7 × 4 μs = 28 μs.

Table 2. Collective Variables (CVs) Biased in the RECT Simulations.

simulation	residues with biases	CVs biased in each of the residuesa	additional biased CVsb	penaltyc
1KF1 A	T11, T12, A13	α, β, γ, ε, ζ, χ, pucker, base-coor.
1KF1 B	T11, T12, A13	α, β, γ, ε, ζ, χ, pucker, base-coor.		zg
1KF1 C	T11, T12, A13	α, β, γ, ε, ζ, χ, pucker, base-coor.	dist G9(H22)-T11(O4)
1KF1 D	T11, T12, A13	α, β, γ, ε, ζ, χ, pucker, base-coor.	dist G9(H22)-T11(O4)	zg
2GKU A	T6, T7, A8	α, β, γ, ε, ζ, χ, pucker, base-coor.
2MBJ A	T13, T14, A15	α, β, γ, ε, ζ, χ, pucker, base-coor.
2MBJ B	T13, T14, A15	α, β, γ, ε, ζ, χ, pucker, base-coor.	dist. G11-T14

^aα, β, γ, ε, ζ, and χ = dihedral angles; pucker = x-axis component of pucker; “base-coor.’’ = nucleobase coordination number i.e. number of nucleobases in proximity of the corresponding nucleobase (each nucleobase is approximated by its center of mass), computed using 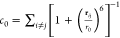, where r₀ = 4Å.

^bdist = distance; measured either between selected atoms (in parentheses) or nucleobases’ centers of mass.

^czg = flat-well potential function applied on ζ(G10) and γ(T11) (Figures S2 and S3).

Potential Energy Penalty to γ-trans

To keep the γ(T11) angle of 1KF1 in a trans region and thus counteract the effect of the bsc0 correction for only a selected nucleotide, we applied flat-well restraints on ζ(G10) and γ(T11) in two RECT simulations and one standard simulation (Tables 1 and 2), with a constant penalty potential energy of 2 kcal/mol in regions far away from the crystal structure value. Energy profiles of the restraints are shown in Figures S2 and S3 in the Supporting Information. Note that the restraint does not impose any force acting on the system if the dihedral value is in the native region or in the far-away region, because there is zero energy gradient there. The idea stems from an analogous solution which worked very well for tuning the stability of H-bonds in RNA tetraloops.¹⁰⁴

Clustering

The MMTSB tool kit (http://feig.bch.msu.edu/mmtsb/) was used to cluster the propeller loop conformations in the 10 μs long trajectories.¹⁰⁵ Our aim of clustering was to sieve major distinct conformations sampled by the propeller loops in each GQ trajectory. For classification, the root mean squared deviation (RMSD) of all the atoms in the propeller loops was used as the distance metric. Pairwise distances measured as coordinates between the structures were defined by a cutoff reflecting the range of conformations and their relative populations. Trajectory files containing only the atoms of a propeller loop were used for the clustering. For a GQ having multiple propeller loops, clustering was carried out for each loop separately. The frames were extracted at a time interval of 200 ps yielding 50,000 frames from every 10 μs long trajectory. The k-means clustering (kclust) algorithm was used, employing a fixed cutoff radius of 3.5 Å for all the propeller loops. The algorithm generated centroids describing each cluster and gave an average RMSD between each cluster member and the cluster centroid. The TTA geometry closest to each cluster centroid found in the standard simulations was set as the representative of that particular cluster. The cluster representatives from all the trajectories were then compared both by visual inspection and RMSD analysis. The cluster representatives that showed nearly similar position of TTA loop bases and an all heavy-atom RMSD difference of <1 Å were considered equivalent. Our MMTSB clustering was thus performed in a trajectory after trajectory fashion, with a posteriori elimination of the cluster redundancy. The work-flow for clustering is presented in Figure S4 in the Supporting Information.

We also performed clustering on the unbiased ensembles of loop conformations generated by the RECT simulations. Frames were extracted every 200 ps from the unbiased replica of each RECT simulation. Each given frame was then assigned to one of the clusters selected before using the standard MD trajectories based on the lowest RMSD. In case the lowest RMSD value was greater than 3.5 Å, the structure was left unassigned. The population of unassigned structures was very low, and the reference-RMSD-based method provided a satisfactory comparison of standard and RECT simulations. We even tried independent clustering of the RECT simulations by the MMTSB toolkit, but the resulting clusters were sometimes difficult to compare with the clusters from the standard simulations (see the Supporting Information for more details) due to common uncertainties of clustering methods.

Additional methods that were used for clustering are described in the Supporting Information. We emphasize (see the Results section) that we have used several types of clustering methods and codes, extensively varying the parameters. This was because of the known ambiguities inherent to clustering procedures. Thus, we selected results obtained with one of the methods for the presentation in the main text, which appears to us to be best suited for the purpose of the study. Nevertheless, the conclusions that we derived from the clustering are robust and do not depend on some specific setup of the clustering procedure.

Markov State Modeling

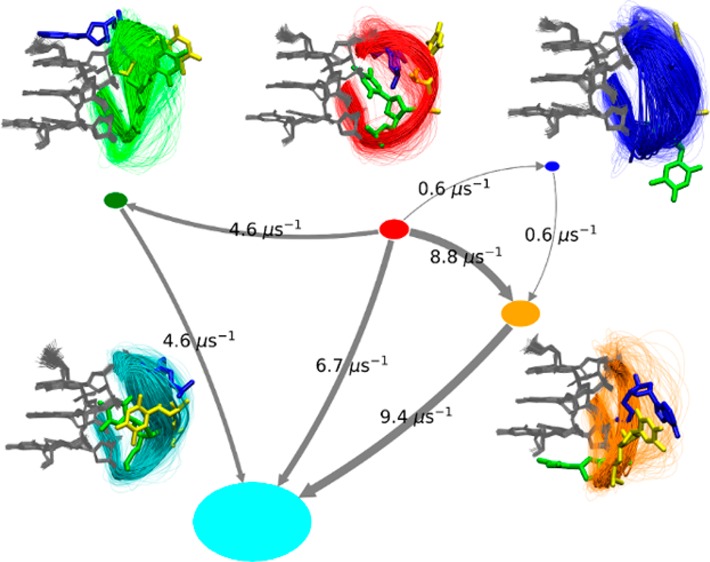
The MD simulation data was used to construct MSM using the pyEMMA software, version 2.3.2 (http://www.emma-project.org).^106,107 The simulation data of the three propeller loops from Simulation 2 were used to build the MSM as the largest number of conformations was sampled in this simulation. Each propeller loop of structure 1KF1 was extracted as separate trajectory and was treated individually. Thus, a total of 3*100,000 frames of simulation data were used to construct the MSM.

The α, β, γ, δ, ε, ζ, and χ-dihedrals of the propeller loop nucleotides were used as input features as (sin,cos)-pairs, yielding a total of 42 dimensions (seven (sin,cos)-pairs per three nucleotides of the loop). This high-dimensional input space was then reduced by using the time-lagged independent component analysis (TICA) method^108,109 at a TICA lag time of 750 ns. TICA combines information from a time-lagged covariance matrix of the data to identify slowest degrees of freedom and has been suggested for finding an optimal approximation to the Markov operator’s eigenvalues and eigenfunction.^108,109 95% of the total kinetic variance was retained for analysis ultimately leading to a slow subspace of only ten TICA components. The data was then clustered in the 10D-TICA space into 500 microstates by k-means, and MSMs were subsequently calculated at different lag times.^108,110 The simulations travel extensively through the conformational space, so we assume that the MSM is executed in a data-rich regime and thus should be reliable.¹¹¹ The implied time scale plot was used to identify a suitable MSM lag time (τ = 250 ns) for building the Markov model (Figure S5a). The 500-microstate MSM at 250 ns lag time was coarse-grained in five macrostates using the Perron-Cluster cluster-Analysis (PCCA+)^{106,107,112,113} method and further validated by the Chapman–Kolmogorow (CK) test¹¹⁴ (Figure S5b). Finally, Transition Path Theory (TPT)^{106,107,115−117} was used on this coarse-grained MSM to identify pathways and mean first passage times (MFPTs) by which the initial structure (start structure of simulation) progresses to a more populated dominant state. Further details of computing transition pathways using TPT can be found in refs (106 and 117).

Selected Abbreviations

The guanine strand closest to the 5′-end of GQ is termed strand 1, followed by strands 2, 3, and 4. Similarly, the first G-quartet refers to the G-quartet closest to the 5′-end of the GQ, the second G-quartet refers to the middle G-quartet, and the third G-quartet is closest to the 3′-end. The groove between the strands 1 and 2 is called as groove 1, between strands 2 and 3 as groove 2, strands 3 and 4 as groove 3, and strands 4 and 1 as groove 4. When referring to the nucleotides of the TTA propeller loops, the first and the second thymine nucleotides of the loop are termed PT1 and PT2, respectively. The adenine nucleotide of the propeller loop is termed PA3.

Results and Discussion

Overall Stability of the GQs in 10 μs Long Simulations

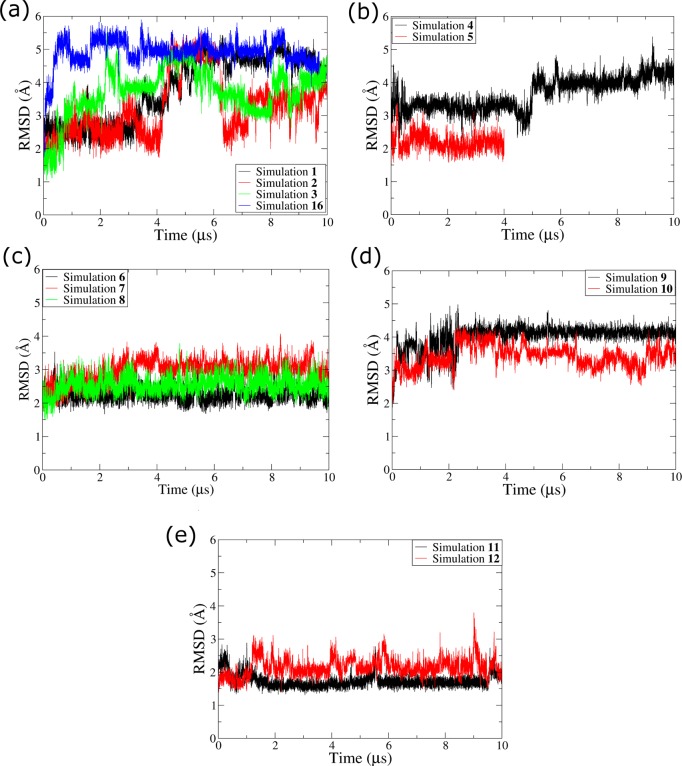
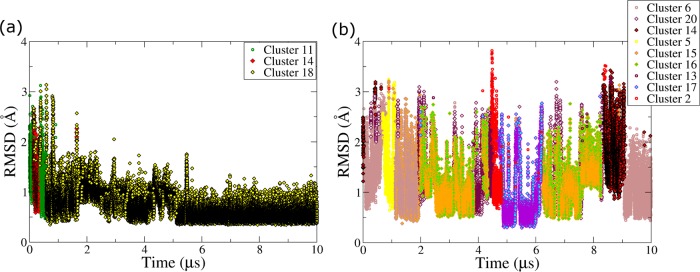
All the GQ topologies were stable in the bsc0χ_OL4 and bsc0χ_OL4εζ_OL1 force fields, the primary force-field variants used in our work (Figure 2). The TTA propeller loops were the most flexible segments of the simulated molecules. The flexibility of the propeller loops and alignments formed in the same GQ topologies were broadly similar in the two force-field versions. The RMSD plots of backbone atoms of the GQs are compatible with the expected conformational fluctuations around the native structure (Figure 2).

Figure 2.

RMSD plots of GQ backbone atoms in the standard Simulations 1–12 and 16: (a) intramolecular parallel-stranded GQ, (b) bimolecular parallel-stranded GQ, (c) hybrid-1 GQs, (d) hydrid-2 GQ, and (e) antiparallel (2+2) GQ.

The largest RMSD variations were observed in the backbone atoms of parallel-stranded GQs (Figure 2a and b). The intramolecular parallel-stranded GQ showed increased deviation from the starting structure after 4.5–5 μs of the simulations in the bsc0χ_OL4 and bsc0χ_OL4εζ_OL1 force fields. The bimolecular parallel-stranded DNA GQ showed broadly similar dynamics (Simulations 4 and 5) to the intramolecular parallel-stranded GQ. However, the RMSD variations in bimolecular GQ simulations were smaller (Figure 2b). The hybrid-1, hybrid-2, and antiparallel (2+2) GQs also showed lower RMSD values (Figure 2c-e). The antiparallel (2+2) GQ was very stiff in Simulation 11 (Figure 2e), while the same GQ in Simulation 12 showed greater variations.

Few events involving cation exchange between the GS and bulk were observed in the intramolecular parallel-stranded GQ simulations (Figure S6 in the Supporting Information). It could be because the intramolecular parallel-stranded GQ does not have any stacking bases at the top and below the GS, while additional stacking bases are present in the other topologies from lateral loops and flanking nucleotides. Further details of cation dynamics in intramolecular parallel-stranded GQs are presented in the Supporting Information.

The RMSD analysis reflects stable simulations having very stiff GQ GSs supplemented by local dynamics of the loops.⁵⁵ In the following text, we analyze exclusively conformational dynamics of the propeller loops.

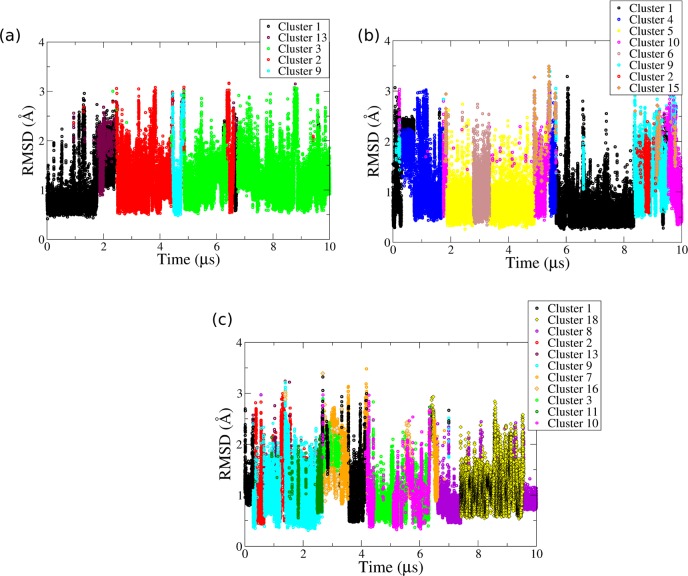
Clustering of the Propeller Loop Conformations via MMTSB

We used the MMTSB program for RMSD-based clustering to compare the major conformations sampled by the propeller loops in the simulations (see Methods). These conformations and their populations in the parallel-stranded, hybrid-1, hybrid-2, and antiparallel (2+2) GQ simulations are presented in Figure 3 and Table 3 and further in Table S4 in the Supporting Information. We have identified altogether 23 different clusters (discrete conformations) of propeller loops in these structures. Note that not all of them were populated in each simulation. Obviously, the clustering procedures are always subject to some ambiguities, and there is not any perfect recipe to perform clustering.¹¹⁸ The clustering results that we present are based on multiple clustering attempts and numerous cross-verifications (see the Supporting Information). Thus, we suggest that our set of clusters is representative of the simulation behavior of the TTA propeller loops. Due to the limited accuracy of the force field (see below) we suggest that further attempts to refine the clustering procedure would not result in any real improvement of the information content of the clustering. Instead, additional alternative analysis of one simulation with three propeller loops was undertaken using Markov state modeling (see below).

Figure 3.

All the major conformations of the TTA propeller loop sampled in the present simulations as obtained by MMTSB clustering analysis. PT1, PT2, and PA3 are shown as green, yellow, and blue sticks, respectively. The backbone of the loops and guanine strands connected by the loops are shown in gray cartoon.

Table 3. Clustering Analysis of Trajectories from Parallel-Stranded GQ Simulations.

simulation no.	starting structure and conditionsa	loop no.b	no. of clusters obsd	cluster	population (%)	loop no.b	no. of clusters obsd	cluster	population (%)	loop no.b	no. of clusters obsd	cluster	population (%)
1	1KF1 with Na+ in bsc0χOL4	loop 1	5	1	27.8	loop 2	9	1	30.0	loop 3	4	10	18.6
				3	60.6			9	3.4			16	28.9
				16	7.8			4	53.8			1	33.1
				8	3.5			8	1.2			3	19.3
				additional one cluster with sampling <1%				7	5.2
								5	5.4
								additional three clusters with each sampling <1%
2	1KF1 with Na+ in bsc0χOL4εζOL1	loop 1	6	1	23.9	loop 2	11	1	32.8	loop 3	16	1	9.8
				13	2.8			4	14.2			18	21.2
				3	47.4			5	25.8			8	12.6
				2	21.8			10	7.5			2	7.2
				9	3.5			6	5.6			13	1.2
				additional one cluster with <1% sampling				9	9.7			9	13.6
								2	1.4			7	5.8
								15	1.1			16	4.3
								additional three clusters with each sampling <1%				3	15.6
												11	1.8
												10	5.0
												additional five clusters with each sampling < l%
3	1KF1 with K+ in bsc0χOL4	loop 1	10	3	25.6	loop 2	7	1	4.7	loop3	16	15	3.2
				9	2.5			10	6.7			1	9.8
				1	39.1			12	69.3			18	2.1
				10	5.1			16	1			10	12.8
				2	19.3			3	7.4			12	33.7
				18	4.2			19	10.4			6	15.4
				17	2.6			additional one cluster with sampling <1%				4	9.7
				additional three clusters with each sampling <1%								3	4.4
												19	1.9
												20	2.6
												5	1.7
												additional five clusters with each sampling <1%
4	lK8P with Na+ in bsc0χOL4	loop 1	5	1	88.1	loop 2	7	1	45.2
				3	1.8			7	17.0
				4	7.9			4	17.2
				7	2.1			11	9.8
				additional one cluster with <1% sampling				18	5.4
								12	2 2
								19	3.3
5	lK8P with Na+ in bsc0χOL4εζOL1	loop 1	2	1	98.4	loop 2	3	1	14.8
				19	1.6			4	29.3
								8	55.8

^aOnly the stabilizing cations and the force field used for simulations are listed here. See Methods for a detailed description of simulation conditions.

^bThe number of the loop counted from the 5′-end of the GQ.

Alternative Clustering Attempts

For comparison, various other methods and approaches for clustering were examined, but none of them provided any significant changes in the results. The first issue was our large data set; when we have created a cumulative propeller loop trajectory using Simulations 1–3, 6–12, and 16 even at a time step of 0.5 ns, it had ∼380,000 frames. We attempted an alternative Amber cpptraj clustering using RMSD, with this cumulative trajectory (applying in practice a time step of 2 ns), and not all of the clusters extracted by MMTSB program were obtained (see Table S5 and Figures S7 and S8 in the Supporting Information). The second issue was the appropriate number of clusters. Our aim in clustering was to represent the conformational dynamics of the system; too few clusters could be misleading, while too many clusters could complicate the analyses and make them difficult to understand. We have also examined the use of recent eRMSD¹⁰⁴ based clustering. In eRMSD, the relative base arrangement is taken into account by collecting the scaled vectors calculated using the six-membered ring of nucleic acids.¹¹⁹ This metric can discriminate the structures with different base–base interactions and has been shown to be suitable for analyzing and biasing simulations of RNA systems.^104,119 We obtained 13 clusters at a cutoff of 0.7 eRMSD (see Figure S9 in the Supporting Information). The methods and results of clustering by cpptraj and eRMSD-based clustering are presented in the Supporting Information (Table S5 and Figures S7–S11). We reiterate that clustering in this work was used for qualitative analyses of the trajectories, and we have taken care not to derive any quantitative conclusions from the clustering data.

Dynamics of Propeller Loops in the Parallel-Stranded GQ Simulations (Simulations 1–5)

The propeller loops of both the intramolecular and bimolecular parallel-stranded GQs are in similar conformations in the X-ray structures (Figure 1a and b). PA3 is sandwiched between PT1 and PT2 to form a T/A/T arrangement (Figure 1a). This arrangement of propeller loop bases has also been observed in GQ-ligand crystal structures.^{21,33,36,38,120} In this conformation, the γ-dihedral angle of PT1 is in the trans region.⁶⁰ However, as bsc0 refinement in the present simulations (bsc0 remains a key component of all the subsequent force-field versions) penalizes γ-trans, the γ-dihedral angle of PT1 is quickly forced in the canonical g⁺ region. Hence, in all the parallel-stranded GQ simulations, the starting structure of propeller loops was lost in a few hundred ps to a few ns and could not be sampled throughout the simulations.

The propeller loops were highly flexible in the simulations (Simulations 1–3). The loop dynamics also affected the backbone dihedrals of guanosines linked to the loops. Consequently, the α and ζ dihedral angles of those guanosines succeeding and preceding the propeller loops, respectively, deviated from the experimentally observed values (see Figures S12–S14 in the Supporting Information). The dihedral angles of the central G-quartet showed fewer fluctuations and remained close to the experimentally observed values as the backbones of these guanines are not directly connected to the loops (see Figure S13 in the Supporting Information).

The clustering analyses of propeller loops in Simulations 1, 2, and 3 are presented in Figure 4 and Figure S15 in the Supporting Information. In all three simulations, the first propeller loop sampled two main conformations, Clusters 1 and 3 (Figure 4 and Table 3 and Figure S15 in the Supporting Information). The behavior of loops 2 and 3 varied in the three simulations. Cluster 1 was attained by loop 1 just after moving away from the starting structure (Figure 4 and Figure S15 in the Supporting Information). In this conformation, PT1 inserts into the groove and forms hydrogen bonds with one guanosine of the central G-quartet. PT2 and PA3 stack together and are aligned at an angle of ∼90° relative to PT1 of the same propeller loop (Figure 3a). Cluster 1 was also sampled by loops 2 and 3 in Simulations 1–3 and was also observed in our previous μs-scale MD simulations of this GQ carried out with the bsc0 force field.⁶³

Figure 4.

Clustering of propeller loops of intramolecular parallel-stranded GQ (PDB 1KF1) in bsc0χ_OL4εζ_OL1simulation (Simulation 2). The clustering was carried out individually on the three propeller loops and is shown for (a) loop 1, (b) loop 2 and (c) loop 3 in the Figure. The RMSD in this figure represents the RMSD of the structure from the centroid of the respective cluster.

Cluster 3 is the second major conformation of loop 1 sampled in Simulations 1, 2, and 3 (Figure 4, Table 3, and Figure S15 in the Supporting Information). In this cluster, PT1 moves to stack below the third G-quartet of the GQ (Figure 3c). PT2 and PA3 of the loops stack together and are exposed to the solvent. As PT1s of all three loops align below the third G-quartet, they come in close contact and intermittently form thymine–thymine base pairs. However, such interloop interactions are highly unstable as they stretch and consequently strain the loops.

Besides these major conformations, variable other arrangements of the propeller loop bases were observed. In Cluster 2 sampled by all the loops in Simulation 2 and only by loop 1 in Simulation 3, the position of PT1 was the same as in Cluster 1, i.e., it interacts in the groove with the guanosine of the central G-quartet. The conformations differ in the orientation of PT2 and PA3 relative to PT1 (Figure 3b and a). Also, PT2 and PA3 do not show any stacking interactions in Cluster 2, while they stack together in Cluster 1 (Figure 3b and a). The propeller loops also sample a triple stack-like arrangement of TTA bases when all three bases orient toward GS, PT2, and PA3 stack together and align above PT1 (Cluster 4, Figure 3d). In Cluster 5, PT1 and PT2 stack together and are exposed to the solvent. PA3 in this conformation does not show any significant interaction and is oriented perpendicularly to the plane of the G-quartet (Figure 3e). Both Clusters 4 and 5 are sampled by loop 2 in Simulations 1 and 2 and loop 3 in Simulation 3 (Figure 4b and Figures S15b and f in the Supporting Information). In Cluster 6, PA3 resides on top of the first G-quartet, while PT1 and PT2 stack together and are exposed to the solvent. PA3 forms a cis Watson–Crick base pair with the 5′-adenine of the GQ. It was sampled between 2.8 and 3.2 μs by loop 2 in Simulation 2 and by loop 3 in Simulation 3 from 8 to 10 μs. Such an A/A base pair between the 5′-adenine and the adenine of the propeller loop has also been observed in our previous simulations of intramolecular parallel-stranded Htel GQ and the c-kit promoter GQ.^63,64 We also observed that a propeller loop can readily interconvert between Clusters 4, 5, and 6 in Simulations 2 and 3.

Clusters 7–13 and 15–20 were also sampled in Simulations 1–3. Cluster 12 was sampled only in the simulation carried out in K⁺ ions. It was sampled by loop 2 for 69.3% and loop 3 for 33.7% of the simulation time. We emphasize that appearance of this cluster in Simulation 3 could be a sampling effect and may not be related to the Na⁺/K⁺ change. Also, this cluster differed from Cluster 3 only in the orientation of the PT2 and PA3 stack relative to PT1 (Figure 3).

The propeller loops of the bimolecular parallel-stranded GQ showed similar dynamics (Simulations 4 and 5). In Simulation 4, in both the propeller loops, PT1 interacted with the guanines of the second G-quartet, while PT2 and PA3 stack together to sample Cluster 1 for most of the simulation time as in Simulation 1 (Table 3 and Figure S16 in the Supporting Information). Cluster 1 was stable up to ∼8.5 μs in the loop 1, while it lasted up to 4.3 μs in loop 2. At ∼4.3 μs, PT1 of loop 2 moved into the plane of the third G-quartet, while PT2 and PA3 were flexible and sampled multiple conformations, similar to Simulations 1–3. The behavior of the propeller loops of the bimolecular DNA GQ was similar in the bsc0χ_OL4εζ_OL1 force field (Simulation 5), and therefore this simulation was not continued beyond 4 μs (Figure S16 in the Supporting Information).

In summary, the TTA propeller loops sampled multiple different conformations in simulations (essentially all the clusters except for 14 and 21–23) of the parallel-stranded Htel GQ. However, the geometry that is predominantly observed in the X-ray structures was entirely suppressed by the force field. Note that due to the multiple loops present in the parallel GQs we have more sampling for these loops compared to the other system.

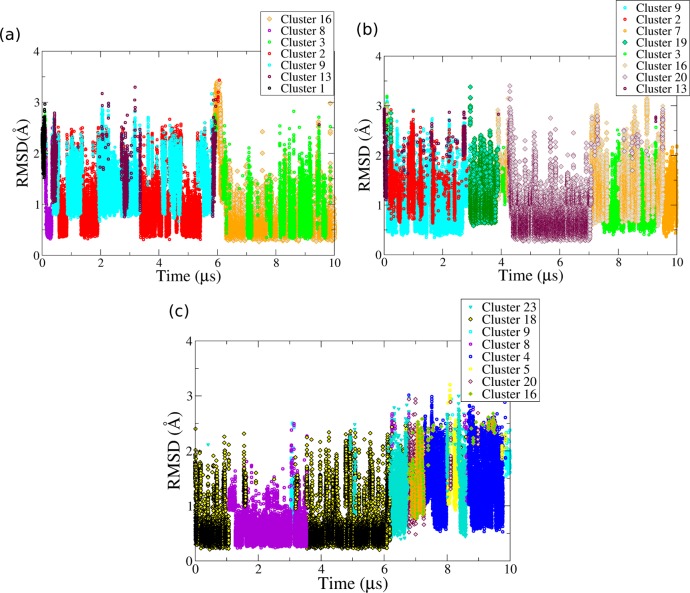
Dynamics of Propeller Loop in Hybrid-1 GQ Simulations (Simulations 6–8)

The first loop in the hybrid-1 GQ structure is the propeller loop. Three solution structures of Htel hybrid-1 GQ have been observed. These are represented by the NMR structures 2HY9, 2JSM, and 2GKU (Figure 1c-e).^43,49,50 We have carried out independent simulations using coordinates from 2HY9 and 2GKU (Figure 1c and e) as the starting structures, to improve sampling. The core sequence of both the structures and the syn/anti orientation of the GS guanines (PDB ids: 2HY9 and 2GKU) are identical, but the GQs differ in the number and sequence of the flanking nucleotides, which may be important for loop-flanking bases interactions.^43,49

The 2HY9 PDB structure is characterized by an adenine triplet as the capping structure above the first G-quartet.⁴⁹ This triplet is formed by the 5′-flanking base A3, A9 (i.e., PA3), and A21 from the lateral loop 3 of this GQ. The O4 atom of T7 (i.e., PT1) interacts with G10(H22) of the first G-quartet, while T8 (i.e., PT2) is aligned in the groove between strands 1 and 2 in all the ensemble models deposited in the PDB (Figure 1c). However, we suggest that A3, PA3, and A21 alignment on the top of this GQ cannot be regarded as a triad as A3 and PA3 are not co-planar in all of the models deposited in the PDB database (PDB id: 2HY9). The interactions between A3 and PA3 were unstable in both simulations with 2HY9 as the starting structures, i.e., Simulations 6 and 7. It appears to us that the starting configuration may be also not compatible with the primary NOE data and may be thus affected by the NMR refinement protocol.

In the bsc0χ_OL4 simulation (Simulation 6), the interaction between flanking base A3 and PA3 (i.e., A9) was lost in the equilibration step as soon as the restraints were removed from the GQ. The loss of this interaction was initiated by the movement of PA3 from the top of the first quartet toward groove 2 of the GQ. PA3 then stacked with PT2. PT1 formed hydrogen bonds with the bases of the second quartet, thus sampling Cluster 1 very briefly at the start of the simulation. The propeller loop then sampled Clusters 8, 13, 9, and 2 within 1 μs of the start of the simulation (Figure 5a). The loop interconverted between Clusters 2, 9, and 13 between 500 ns–6 μs. The interconversion between these three clusters was also sampled by the loop 3 in Simulation 2. The position of PT1 is similar in these three clusters. PA3 stacked with the deoxyribose of PT2 in Cluster 9, while there were no stacking interactions between these residues in Clusters 2 and 13. Clusters 2 and 13 mainly differ in the orientation of PA3 (Figure 3b and m). At ∼6.2 μs, the ζ-dihedral angle of G6 changed from ∼60° to 120°, and PT1 moved to interact with G6 of the third quartet. The position of PT1 was stabilized by a H-bond between its O4 and G6(H22) which lasted until the end of the simulation. PT2 and PA3 stack was also stable, but orientation of the two bases fluctuated. These stacked bases were oriented either toward the solvent as in Cluster 3 or aligned in the groove as in Cluster 16. Thus, between 6.2 to 10 μs the loop conformation fluctuated between Clusters 16 and 3; similar dynamics was also sampled by loop 3 in Simulation 1 (Figure S15c).

Figure 5.

Clustering of propeller loops in hybrid-1 GQ simulations: (a) 2HY9 in bsc0χ_OL4 (Simulation 6), (b) 2HY9 in bsc0χ_OL4εζ_OL1 (Simulation 7), and (c) 2GKU in bsc0χ_OL4εζ_OL1 force field (Simulation 8).

In the bsc0χ_OL4εζ_OL1 simulation (Simulation 7) of 2HY9, the flanking base A3:PA3 interaction was again lost early (∼5 ns) in the simulation. PT1 interacted with guanosine (G5) of the second quartet, and PT2 of the propeller loop was exposed to the solvent. PA3 was flexible and did not sample any stable interaction. From the start until 3 μs, the loop interconverted between Clusters 9 and 2 with short appearances of Cluster 13 (Figure 5b). This part of the dynamics was similar to first 6.2 μs of Simulation 6. PA3 then stacked on PT1 and sampled Cluster 19 between 3 and 4 μs. Following this, PT1 moved in plane with the third G-quartet as in the bsc0χ_OL4 simulation and sampled Clusters 16 and 3. In between these two clusters, Cluster 20 was sampled from ∼4.2 to 7 μs as PT1 oriented toward the solvent (Figure 5b). The position of the PT2/PA3 stack is similar in Clusters 16 and 20 (Figure 3p and t). The loop again sampled Clusters 16 and 3 from 7 to 9.5 μs, and behavior in this part of Simulation 7 was essentially equivalent to the dynamics during the latter part of Simulation 6. At ∼9.5 μs, all three bases of the propeller loop changed their orientation as the loop populated Cluster 7. Cluster 7 was sampled from ∼9.5 until the end of the simulation. We conclude that besides sampling more clusters, which we suggest is a pure sampling issue, the behavior and dynamics of the propeller loop in Simulation 7 were similar to its behavior during Simulation 6.

In the hybrid-1 GQ represented by PDB 2GKU, PT1 is aligned across the groove 1, while PT2 is in the same plane as the second G-quartet and interacts with the GS (Figure 1e). Note that in the PDB 2HY9 structure, the orientation of the thymine residues in the propeller loops is opposite to that in PDB 2GKU, with PT1 in that structure interacting with the GS while PT2 aligned across the groove 1 (Figure 1c and e). PA3 is also aligned in the groove 1 of the GQ just above PT1. However, the orientation of PT1 and PA3, with respect to each other, is not consistent in all the models of 2GKU in the PDB database. In some models, PA3 and PT1 are stacked together, while in the other they are nearly perpendicular to each other. In the starting structure (first model), PT1 and PA3 are aligned in the groove and are staggered relative to each other (Figure 1e).

The propeller loop of the GQ in PDB 2GKU (Simulation 8) sampled different conformations compared to those in the 2HY9 hybrid-1 GQ Simulations 6 and 7. From the start until ∼6.2 μs of Simulation 8, PT1 and PT2 interacted with GS bases and stacked together, while PA3 (A8) was sampled in two major orientations (Figure 5c). Cluster 18 was sampled from the start until ∼1 μs and from 3.5 to 6.2 μs. In this conformation, PA3 was aligned along the groove, while PT1(O4) and PT2(O2) interacted with G4(H22) and G9(H3′), respectively. In Cluster 8 sampled from 1 to 3.2 μs, a triple stack of propeller loop bases was formed as PA3 stacked over PT1 and PT2. The interconversion between Clusters 18 and 8 was also sampled by loop 3 in Simulation 2 (Figure 4c).

PT1 and PT2 changed their orientation and moved toward the solvent at ∼6.2 μs, and PA3 aligned in the groove across the first G-quartet thus sampling Cluster 23 from 6.2 to 6.8 μs. The loop then also sampled Clusters 5 and 4 later in the simulation (Figure 5c). Such transitions between Clusters 4 and 5 were also observed in Simulations 1–3. In many of these transitions Cluster 6 or 23 were also sampled. Both Clusters 23 and 6 differ mainly in the position of PA3. In Cluster 6, PA3 is stacked above the first G-quartet, while in Cluster 23 it could not stack above it and instead is in the groove. It may be assumed that such a change in position of PA3 is in large part due to its interaction with the flanking or other loop bases. Cluster 6 was attained when PA3 formed stable hydrogen bond interactions with other bases, while in Cluster 23 PA3 interacted with the backbone atoms of GS. In general, the fact that many of these clusters have been sampled by the parallel GQs (where we have more sampling) indicates that the loop behavior may be primarily explained by random sampling. Thus, the simulations of the propeller loops in the hybrid-1 structures, on one hand, illustrate the uncertainty (resolution limits) of the NMR structures; on the other hand, they reveal (within the genuine limits of sampling) a reasonable consistency with the simulations of the propeller loops in the parallel-stranded GQs.

Dynamics of Propeller Loop in Hybrid-2 GQ (Simulations 9 and 10)

The third loop is the propeller loop in the Htel hybrid-2 GQs. Two independent solution structures of hybrid-2 GQs have been determined (PDB ids 2JSL and 2JPZ).^44,50 As in the case of hybrid-1 GQs, they differ in the sequence of flanking bases, while the orientation and sequence of core nucleotides are identical. We have used the 2JPZ structure⁴⁴ in the simulation start. In this structure, A21 (i.e., PA3) is partially positioned above the first G-quartet and is aligned along the third groove in most of the models including the starting structure (Model 1). Its orientation is stabilized by the interaction of PA3 hydrogens atoms (H62 and H61) with G16(O4′) and G17(OP1) of the third strand. PT1 is aligned below the PA3, closer to the third G-quartet. T20 (i.e., PT2) is in plane with the second G-quartet and interacts with the backbone atoms of G23 in the fourth strand (Figure 1f) or is exposed to the solvent. The orientation of PT2 is ∼180° with respect to PT1 and PA3. In the 2JSL, all three nucleotides of the propeller loop are sequentially staggered one on another, and the loop bases do not show any significant interaction with the GS.

In the bsc0χ_OL4 Simulation 9, PA3 was stacked onto the 5′-terminal thymine (T1) of GQ. A cation binding site was formed near PA3 which mediates its interaction with the backbone atoms of G16 from the first G-quartet. The PA3 and T1 stack was stable throughout the simulation. PT2(O2) formed a hydrogen bond with G17(H22) of the second G-quartet, which was sampled throughout except between 100 and 300 ns. At ∼650 ns, PT1 oriented toward the groove and stacked with PT2, attaining Cluster 18 (Figure 6a). The PT1 and PT2 stacking was further stabilized by a hydrogen bond between PT1(H4′) and PT2(O4′). This arrangement was sampled from ∼650 ns until the end of the simulation and was an example of interactions between the loop and the GS or flanking bases, which can lock the loop in a stable conformation. As this propeller loop showed limited flexibility, the ε/ζ dihedral angles of the preceding guanosine and the α/γ dihedral angles of the guanosine succeeding the propeller loop were sampled close to the values suggested by the NMR model (we again reiterate that the NMR loop structures may not be unambiguously determined by the primary NMR data).

Figure 6.

Clustering of propeller loops in hybrid-2 GQ (PDB 2JPZ) simulations in (a) bsc0χ_OL4 (Simulation 9) and (b) bsc0χ_OL4εζ_OL1 (Simulation 10) force fields.

The propeller loop of hybrid-2 GQ sampled more conformations in the bsc0χ_OL4εζ_OL1 Simulation 10. At the start of the simulation, PA3 was aligned over the first G-quartet and formed a hydrogen bond with adenosine of the second lateral loop (A15). PT1 and PT2 were stacked together, and the resulting loop conformation resembled Cluster 6 (Figure 3f). The loop sampled Clusters 5 and 15 between 750 ns and 2 μs of the simulation (Figure 6b). The transition from Cluster 6 to 5 was similar to that observed in Simulations 1–3 and 6–8. PT1 then moved to interact with the third G-quartet and sampled Clusters 16 and 20 between 2 and 4.5 μs and again between 6.2 and 8.3 μs. The dynamics between Clusters 16 and 20 was also observed in Simulations 7 and 8. During 4.5 to 6.2 μs, the loop sampled Clusters 2 and 17. At ∼8.3 μs, PT1 was oriented toward the solvent and the loop sampled Cluster 14 until 9 μs. PA3 then moved again and stacked over the first G-quartet to interact with the adenosine of the second lateral loop (A15). PT1 and PT2 were stacked and exposed to the solvent, and the loop sampled the (initial) Cluster 6 at the end of the simulation. The trends in transitions of loop clusters in this simulation resembled simulations of intramolecular parallel-stranded and hybrid-1 GQs.

We would like to clarify here that in Clusters 16 and 3 sampled in the hybrid-1 and hybrid-2 GQ simulations, PT1 bases of the loops remained in plane with the third quartet and could not stack below it as in the intramolecular parallel-stranded GQ (Figure S17). This could be because the intramolecular parallel-stranded GQ does not have any flanking base at the 3′-end, while there are bases already stacked below the hybrid-1 and hybrid-2 GQs. Nevertheless, this rather minor difference in the position of PT1 is not large enough to separate them in our cluster analysis (Figure S17).

Dynamics of the Propeller Loop in the (2+2) Antiparallel GQ (Simulations 11 and 12)

In the (2+2) antiparallel GQ, the second loop is the propeller loop.⁴² In the starting conformation (PDB id: 2MBJ), T13 (i.e., PT1) is exposed to the solvent, T14 (i.e., PT2) interacts with the guanosine of the second G-quartet (G11) via the second groove, and A15 (i.e., PA3) is stacked below the third G-quartet, being involved in hydrogen bond interactions with A9 of the first loop (Figure 1h).

In the bsc0χ_OL4 Simulation 11, the interactions of PT2 and PA3 were stable throughout the 10 μs simulation. PT1 also showed minor flexibility and therefore only one cluster; Cluster 21 was sampled in Simulation 11 (Figure 7a). Cluster 21 was equivalent to the starting conformation.

Figure 7.

Clustering of propeller loop in antiparallel (2+2) GQ simulations. The propeller loop in (a) the bsc0χ_OL4 force field (Simulation 11) sampled only one conformation but was more flexible in (b) the bsc0χ_OL4εζ_OL1 force field (Simulation 12).

The bsc0χ_OL4εζ_OL1 Simulation 12 sampled more conformations than Simulation 11, analogously to the simulations of other GQ topologies (Figure 7b and Table S4 in the Supporting Information). The interactions of PT2 and PA3 with the middle quartet and flanking bases respectively were stable throughout in Simulation 11, but in Simulation 12 these bases showed flexibility in their orientation mainly after 1 μs of the simulation. Thus, while the loop in the first 1 μs of Simulation 12 was nearly similar to the starting structure and that in Simulation 11, it was more dynamic in the later 9 μs of the simulation. Along with Cluster 21, three more clusters were sampled in Simulation 12 (Figure 7b). In Cluster 22 sampled after Cluster 21, PT1 and PT2 stacked together and interacted with the third and second quartet, respectively, while PA3 did not show any stable interaction with the GS. Cluster 22 was sampled mainly from 1 to 4.2 μs. The loop then sampled Cluster 23 until the end of the simulation. In Cluster 23, the PT1 and PT2 stack was exposed to the solvent, while PA3 was in the plane with the third quartet and interacted with the backbone atoms of GS. The loop also marginally sampled Cluster 14 (Figure 7b and Table S4 in the Supporting Information).

Simulation Structures Do Not Correspond to X-ray Structures

We compared conformations of the propeller loops based on the orientations of their bases and backbone dihedral angles sampled in the simulations, with the TTA propeller loop types observed in the various crystal structures. A total of 23 clusters were observed in the simulations, while 12 TTA propeller loop types (i.e., type-1 to type-12) have been observed in the X-ray structures.⁶⁰ Only Clusters 1, 2, 6, and 15 showed significant resemblance to the propeller loop types observed in the X-ray structures (Figure 8). It is further evidence that the force field is not sufficiently accurate to provide a quantitatively correct description of the total TTA propeller loop conformational space.

Figure 8.

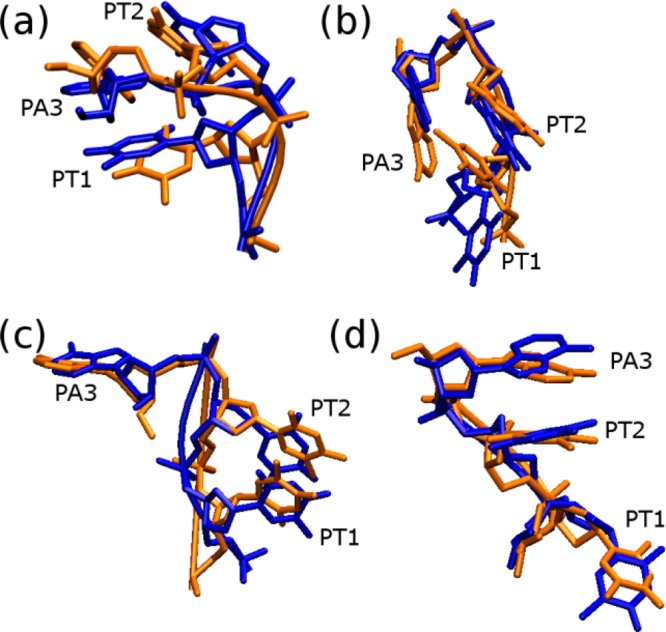
Comparison of the experimentally observed (X-ray, blue) TTA propeller loop types and selected cluster representations sampled in the simulations (orange). All the structures were compared, but only the cluster representatives with alignments similar to the crystal structures are shown in the figure. Overlays of (a) Cluster 1 and type-1, (b) Cluster 2 and type-7, (c) Cluster 6 and type-2, and (d) Cluster 15 and type-12 are shown. The loops of PDBs 1KF1 (loop 1), 3CE5 (loop 2), 2HRI (loop 1), and 4DAQ (loop 3) were taken as the representatives of type-1, type-7, type-2, and type-12 propeller loop types.

In Cluster 1, PT1 aligned within the groove between two strands and formed hydrogen bond interactions with guanosine of the middle G-quartet (Figure 8a). PT2 and PA3 stacked together. This conformation was sampled in all the simulations of parallel-stranded DNA GQs (Figure 4 and Table 3). An overlay of Cluster 1 with the experimentally observed propeller loop T/A/T conformation (type-1) shows good correspondence between the base orientations (Figure 8a). Note that type-1 is the most common TTA loop propeller geometry.⁶⁰ However, as pointed out above, the α/γ dihedral angles of PT1 in the loop are different (Figure S18a in the Supporting Information). The γ-dihedral angle of PT1 in the type-1 propeller loop is in the the trans region, but as the bsc0 correction wipes out γ-trans, the propeller loops deviate from the experimental conformation in Cluster 1. We consider this to be a significant difference, despite the fact that the dihedral angles of PT2 and PA3 are similar in Cluster 1 and type-1 propeller loop (Figure S18a in the Supporting Information). Perhaps Cluster 1 can be regarded to be a modification of one of the T/A/T loop arrangements observed in the crystal structure, but the imperfections in the backbone description are clear. However, as the nucleic acids backbone is known to adopt distinct families and backbone torsion angles are coupled,¹²¹ identical geometries should have all the dihedral angles being simultaneously compatible. Interestingly, the first loop of the Htel GQ bound to a tetrasubstituted naphthalene diimide ligand (PDB id: 3CDM) (propeller loop type-5)¹²² has similar dihedral values of PT1 to those in Cluster 1 (Figure S18a in the Supporting Information). Therefore, the Cluster 1 position of PT1 is an experimentally realistic conformation for propeller loops. However, for the remaining two residues the type-5 loop differs substantially from Cluster 1.

Cluster 2 resembles the type-7 propeller loop observed in loop 2 of the X-ray structure of bimolecular parallel stranded GQ in complex with an acridine ligand (PDB id 3CE5).³⁶ The orientations of PT2 and PA3 in Cluster 2 and the experimental type-7 loop are similar but that of PT1 is different (Figure 8b). In Cluster 2, PT1 of the propeller loop is in the same plane as the second G-quartet of the GQ. In the experimentally observed type-7 propeller loop, PT1 is exposed to the solvent and is perpendicular to the plane of the GS guanines (Figure 8b). There is a significant difference in the dihedral angles of PT1 between Cluster 2 and the type-7 loop (Figure S18b in the Supporting Information).

Cluster 6 is almost equivalent to the type-2 propeller loop. Propeller loop 1 in the X-ray structure (PDB id 2HRI) is a representative of the type-2 propeller loop.⁵⁹ The alignment of Cluster 6 with this loop shows minor differences in the backbone conformation and orientation of the PT1/PT2 stack (Figure 8c). Regarding dihedrals, the only significant difference is observed in the ζ-dihedral angle of PA3 (Figure S18c in the Supporting Information).

Cluster 15 resembles the type-12 propeller loop represented by loop 3 of the GQ crystal structure in PDB id 4DAQ.³⁸ In the type-12 propeller loop, the three bases of the loop are exposed to the solvent and PT2/PA3 are stacked together. We observe a similar alignment of the bases in Cluster 15 and an overlay of Cluster 15 with type-12 loop shows similarity in the orientation of loop nucleotides in these two structures (Figure 8d). However, while the α/γ dihedral angles of PT2 are in the g^–/t region in the experimental structure, they sample in the t/g⁺ region in the simulations (Figure S18d in the Supporting Information).

Due to the uncertainty of the propeller loop conformations in the NMR structures, we did not attempt their comparison with the simulation clusters, beyond the analyses given above.

Additional Simulations of the Parallel-Stranded GQ - the Effect of γ-trans Restraints, β-Dihedral Reparametrization, and Water Model

As discussed above, the γ-trans dihedral angle of PT1 was not sampled in any of the simulations. We therefore tried to stabilize the experimental (type-1) loop conformation by an appropriate energy penalty (bias) on the γ potential of PT1. We applied a flat-well restraint (see Methods) on the γ-dihedral angle leaving its trans region unchanged and penalizing the non-native regions by 2 kcal/mol (Simulation 13). The γ-dihedral angle of PT1 of the second loop (T11) switched to the g⁺ region at ∼225 ns and then fluctuated between g⁺ and the trans region until the end of the simulation. PT1 of the first and third loops also left the γ-trans region at ∼230 and 275 ns. The loops sampled the starting conformation only intermittently (for short durations) during the simulation, thus the restraint was not sufficient to stabilize the target conformation. The loops sampled various other conformations, similar to those without the restraint.

We also carried out two 1 μs long simulations with the bsc1 force field (Simulations 14 and 15). In both these simulations the γ-dihedral angle of PT1 in all three propeller loops switched from trans to the g⁺ region within 30 ns. The conformations sampled by the propeller loops in these simulations were also similar to those sampled in the bsc0χ_OL4εζ_OL1 force field, as expected, and thus the simulations were terminated. In recent extensive B-DNA tests, bsc1 and bsc0χ_OL4εζ_OL1 showed similar performance.^79,80,84

The propeller loops showed similar dynamics even in the 10 μs long simulation with the OL15 force field (Simulation 16). The γ-dihedral angle of PT1 of all three loops switched from trans to g⁺ again. This is not surprising as both bsc1 and OL15 continue to use the α/γ bsc0 dihedral potential. The OL15 modification of the β-dihedral angle did not lead to any significant improvement in the propeller loop behavior of GQs; see the Supporting Information for full details including the clustering (Figure S19).

It has been reported that water models affect the backbone behavior of DNA and RNA.^83,123 We thus carried out simulations of structure 1KF1 in the OPC water model with both KCl and NaCl (Simulations 17 and 18) with the OL15 force-field version. The OPC water model (Simulations 17 and 18) did not improve the simulations compared to the SPC/E one (Simulations 1, 2, 3, 14, 15, and 16). In Simulation 17, all three loops were eventually trapped in one conformation. Loops 1 and 3 were frozen in Cluster 8 after 3.1 μs and 500 ns, respectively (see Figure S20a and c in the Supporting Information). Loop 2 was trapped in Cluster 21 after 5.5 μs (see Figure S20b in the Supporting Information), and thus no significant dynamics was observed in the whole GQ after 5.5 μs. In Simulation 18, PT1 of loops 1 and 3 was stacked below the third G-quartet to form thymine–thymine base pair. This locked the conformation of loops 1 and 3 in Cluster 3 after 5 and 3 μs, respectively (see Figure S21a and c in the Supporting Information). Loop 2 was dynamic for the entire 10 μs (see Figure S21b in the Supporting Information), resembling the SPC/E simulations. In other words, the conformations sampled by the propeller loop in the OPC water model were similar to those sampled in the SPC/E water model. The OPC water model perhaps might slow down the transitions, but it does not affect the sampled clusters in a way that could be considered to be an improvement.

Propeller Loops Are Associated with a Strain of the Force-Field Backbone Dihedral Energy

Comparison of energy terms for the GQ simulation boxes reveals that the parallel GQ 1KF1 system is among all studied GQ topologies highest in enthalpy, followed by the basket topology represented by structure 143D (see Table S6 in the Supporting Information). These results are in qualitative agreement with recent theoretical calculations by Luo and Mu,¹²⁴ who found out that in their temperature replica exchange MD simulations 1KF1 and 143D systems were the least thermally stable of the five studied (the study did not include 2MBJ). Thus, these two topologies appear to be less enthalpically stable in the force-field description.

Potential energy decomposition to different force-field terms shows that too high enthalpy of 1KF1 GQ topology is due to the least favorable sum of dihedral potentials, while other energetic contributions look similar to the other topologies. On the other hand, 143D and 2KF8, which do not contain any propeller loops, have the most favorable (lowest) sum of dihedral terms (see Table S7 in the Supporting Information). Decomposition of the dihedral part of the enthalpy into contributions per residue shows that the dihedral enthalpic penalty of the parallel GQ topology originates consistently from first guanosines following the propeller loops (see Table S8 in the Supporting Information). The dihedral part of the total enthalpy of the loop residues at first sight is not responsible for high total enthalpy of parallel GQ topology and varies with no clear trend. However, we suggest that the dihedral structural strain still originates in the propeller loops and is subsequently transferred to the deformation of the 5′-quartet. Thus, the results support the view that propeller loops are, in the force-field description, associated with some topological strain of the whole GQ.^52,55,64 Whether the dihedral strain is the primary problem or a symptom of more complex imbalances involving nonbonded interactions and solvation remains an open question for further research. We consider the later scenario as more likely, due to insensitivity of the loop behavior to the modifications of the dihedral potentials observed throughout this study.

RECT Simulations

The performance of the RECT simulations was analyzed by calculating the round-trip times (RTT). RTT measures time required for a replica to move from the less-ergodic state (γ = 1) to the more ergodic state (highest γ) and back. Smaller RTT means shorter overall converge time of the simulation.¹²⁵ Subsequently, the reference replica ensembles were clustered by assigning each frame to one of the 23 clusters that were defined using the unbiased MD simulations (Figure 3).

In all our RECT simulations, the longest RRTs were in the order of tens of ns (see Table S3 in the Supporting Information), just one order of magnitude smaller than the simulated time per replica, and considerably higher than the minimum theoretical RTT (∼12 ps). This indicates, on one hand, that a different replica distribution or a higher replica density should be used to minimize the RTT, and on the other hand, that other CVs could be included in the simulation to avoid kinetic traps and increase the ergodicity of the replicas. Note that, as shown above, the standard simulations were also very far from being converged.

The results of the cluster assignments (only clusters with population >1%) are given in Table 4 and Tables S9 and S10 in the Supporting Information. In the four 1KF1 RECT simulations, seven, nine, ten, and ten clusters were found, respectively (Table 4). The overall most populated cluster was Cluster 1. The 2GKU RECT simulation sampled 12 significant clusters, with Cluster 18 being the most populated (Table S9 in the Supporting Information). The two 2MBJ RECT simulations displayed five and eight clusters, respectively (Table S10 in the Supporting Information). Cluster 21 was the most dominant. Qualitative analysis of all RECT simulations (Table 5) reveals that out of all the clusters, Cluster 6 appeared in six of the seven RECT simulations. Clusters 4, 6, 14, 15, and 22 were observed in RECT simulations of all three different GQ systems (1KF1, 2GKU, and 2MBJ). Nine other clusters were shared by two GQ systems. Six clusters were exclusive for only one GQ system, and out of them three were found in only one RECT simulation. Two clusters, 7 and 13, were not populated above the 1% threshold in any RECT simulation. Importantly, the fraction of structures that was not assigned to any cluster was less than 1% in all RECT simulations except for 1KF1 D, where the value was 1.32%.

Table 4. Propeller Loop Clusters Observed in the RECT Simulations of the Middle Propeller Loop (the Biased One) of the Parallel Stranded GQ.

simulation name	loop no.	no. of clusters obsda	cluster	population (%)
1KF1 A	Loop 2	7	1	75.32
			16	7.16
			10	5.16
			19	4.92
			20	3.20
			3	1.52
			17	1.24
1KF1 B	Loop 2	9	1	50.52
			18	19.48
			12	9.04
			19	6.20
			16	3.76
			17	3.60
			8	3.04
			6	1.72
			22	1.36
1KF1 C	Loop 2	10	6	35.12
			1	29.28
			18	9.28
			23	6.24
			8	4.08
			9	2.40
			14	2.08
			20	1.64
			5	1.60
			17	1.40
1KF1 D	Loop 2	10	18	42.28
			1	21.96
			6	10.00
			2	5.20
			15	4.64
			11	4.20
			23	3.12
			17	1.40
			unassignedb	1.32
			4	1.24
			9	1.00

^aClusters of population <1% are omitted.

^bDoes not belong to any cluster observed in standard MD simulations.

Table 5. Summary of Cluster Appearance in RECT Simulations of Different GQs^a.

	cluster
simulation name	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23
1KF1 A	×		×							×						×	×		×	×
1KF1 B	×					×		×				×				×	×	×	×			×
1KF1 C	×				×	×		×	×					×			×	×		×			×
1KF1 D	×	×		×		×			×		×				×		×	×					×
2GKU A	×			×		×		×	×					×	×	×		×			×	×	×
2MBJ A						×				×											×	×	×
2MBJ B				×	×	×					×			×	×						×	×

^aClusters that appeared in the simulations are indicated by a ‘×’ sign.

The results thus show that the propeller loop samples very similar conformational space regardless of the GQ system. The exact populations of the clusters are likely different among the three studied GQs, because of their nonidentical topologies and interactions with other loops and flanking bases. Quantification of the populations is, however, beyond the available simulation time scales.

Most importantly, qualitative comparison of the clusters populated in the RECT simulations (Table 5) and those found in the standard MD simulations (Table 6) shows no significant difference. Both methods utilizing a very diverse approach to sample the conformational space gave a very consistent picture of TTA propeller loop flexibility.

Table 6. Summary of Cluster Appearance in MD Simulations of Different GQs^a.

		cluster
PDB and (simulation no.)	loop no.	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23
1KF1 (1)	1	×		×					×								×
	2	×			×	×		×	×	×
	3	×		×							×						×
1KF1 (2)	1	×	×	×						×				×
	2	×	×		×	×	×			×	×					×
	3	×	×	×				×	×	×	×	×		×			×		×
1KF1 (3)	1	×	×	×						×	×							×	×
	2	×		×							×		×				×			×
	3	×		×	×	×	×				×		×			×			×	×	×
1K8P (4)	1	×		×	×			×
	2	×			×			×				×	×						×	×
2HY9 (6)	1	×	×	×					×	×				×			×
2HY9 (7)	1		×	×				×		×				×			×			×	×
2GKU (8)	1				×	×			×	×							×		×		×			×
2JPZ (9)	3											×			×				×
2JPZ (10)	3		×			×	×							×	×	×	×	×			×
2MBJ (11)	2																					×
2MBJ (12)	2														×							×	×	×

^aClusters that appeared in the simulations are indicated by a ‘×’ sign.

Markov State Model

The main aim of constructing MSM is to identify the network of states and transition probabilities among them. These states are called macrostates when the MSM has been coarse-grained from a microstate representation (as in this case), and they are also referred to as metastable states, because they represent long-lived states in the dynamics of the system. In MD simulations, metastable states typically encompass whole ensembles of molecular conformations that interconvert quickly within the ensemble and slowly between ensembles. These ensembles approximately map to the different basins of the free energy surface (FES), and their stationary probability, π, corresponds to their Boltzmann weights. We used α, β, γ, δ, ε, ζ, and χ-dihedrals of the propeller loop nucleotides in Simulation 2 as input data to construct the MSM as described above in the Methods section. The data was clustered into 500 microstates, and their distribution on the FES is presented in Figure S22 in the Supporting Information.

Figure 9a depicts the five-state MSM on the FES. The macrostates are located in the FES-minima. The FES graph has a three-basin shape where the crystal-structure-encompassing macrostate (red) and two other strongly connected metastable states (orange and blue) lie in one basin and the other two macrostates, cyan and green, lie farther in their own basin (Figure 9a). The stationary population of the cyan state is highest and is therefore labeled as the dominant state with 80% of the stationary population. The network between these five macrostates is shown in Figure 9b.

Figure 9.

Markov state modeling. (a) Free energy surface (FES) projected onto the first two independent components of TICA (TICs) at a TICA lag time of 750 ns. The centers of five metastable states obtained by PCCA+ decomposition are superimposed on the contour plot. The area of each circle represents its equilibrium population. (b) Network representation of the MSM (lag time of 250 ns) coarse-grained onto the five metastable states. The population of each state (π) is indicated in the figure. The state number 1 (red) is the state to which all the starting frames of the trajectories have been assigned, thus we consider this macrostate to be the crystal structure-encompassing state. The state number 4 (cyan) is the state with the highest population, thus we label it as dominant state. c) Transition Path Theory (TPT) analysis of the loop dynamics, i.e., the ensemble of reactive pathways connecting the crystal structure-encompassing and the dominant state. Reactive transitions probabilities (fluxes) are shown as rates (probability per time unit) in μs⁻¹. The guanine strands connected by the loops are shown in gray lines. The ensemble of loop backbone geometries contained in each state is shown by displaying overlays of the most probable structures of the state (opaque lines) on top of samples of the entire state (transparent lines) to show both the intrastate conformational variability and the interstate conformational differences. The most probable position of loop nucleotides in each state is shown in licorice; PT1, PT2, and PA3 are shown in green, yellow, and blue, respectively.

We also generated the transition pathway from the crystal-structure-encompassing red macrostate to the dominant cyan state. The mean first passage time from red to cyan macrostate was estimated to be 19.5 μs. The transition pathway and structures of all the macrostates are shown in Figure 9c. In the blue macrostate, PT1 was flexible, but most of the conformations were similar to Cluster 20. PT1 was exposed to the solvent, while PT2 and PA3 stacked together and aligned in the groove. In the crystal-structure-encompassing red macrostate, PT1 interacted with guanine of the second quartet, while PT2 and PA3 showed different orientations. It was populated by Clusters 1, 2, 9, 13, and 17 thus showing that these clusters have small kinetic barriers. Let us reiterate that although the native experimental loop conformation is part of the red macrostate within the TICA dimensions and thus the trajectories appear to revisit it several times, in terms of exact atom positions (i.e., not in the TICA coarse-grained coordinates) the X-ray geometry has never been regained after its initial loss, as it is discussed in the section Simulation structures do not correspond to X-ray structures. In the orange macrostate, PT1 aligned below or close to third quartet. It was populated by Clusters 3, 10, and 16. The green macrostate contained ensembles of Clusters 4, 5, and 6. The dynamics between these three clusters (Clusters 4, 5, and 6) has been observed in most of our simulations. The dominant cyan state was more heterogeneous. The most common structure in this macrostate belonged to Cluster 18 although it was also populated by Clusters 7, 8, 11, 15, and 19. The transition states and rates of MSM are in broad agreement with our clustering analysis. We suggest that the MSM provides a fair estimate of the time scale of the conformational dynamics of the TTA propeller loops within the description of the used force field. Because we assume that the force-field description of the propeller loops is imperfect, no further refinement of MSM was attempted.

Conclusions

The Htel GQs are polymorphic (at least in dilute solution) since the d(TTAGGG) repeats can adopt variable topologies depending on the flanking sequence and solvent conditions. This is inherent to many GQ-forming sequences with G₃ tracts.^126,127 The Htel parallel-stranded, hybrid-1, hybrid-2, and antiparallel (2+2) GQ topologies all include propeller loops, which themselves exhibit conformational polymorphism.

We have performed a series of standard 10 μs-long simulations supplemented by state-of-the-art RECT enhanced sampling simulations on all of these Htel GQ topologies to systematically investigate the behavior of propeller loops. The GSs of all the topologies were stable, while the loops moved flexibly in the simulations. The internal cations in the GSs were stably retained in all the topologies except for a few instances of ion exchange in the intramolecular parallel-stranded GQ simulations. This could be due to two reasons: first, all the topologies other than the intramolecular parallel-stranded GQ have flanking bases at both the 5′ and 3′ ends which can form alignments above and below the GQs, obstructing ion exchanges. Second, all the loops of parallel-stranded GQ are propeller loops that show significant fluctuations during simulations, which could contribute to a reduction of the kinetic barrier for ion exchange between the stem and the bulk. However, the cation losses were always accompanied by a simultaneous entry of another cation into the GS, minimizing the structural deformation of the GQ due to a transient cation deficiency. Thus, we can consider the GSs to be stable parts of the simulated structures.

We have carried out RMSD-based clustering of propeller loop trajectories to analyze the dynamics of the loops in the simulations. Different clustering algorithms with diverse criteria were tried, but none of the combinations of methods/parameters could be considered to produce fully unambiguous results. A major limitation was that our large data set could not be clustered as a single concatenated propeller loop trajectory. Therefore, we carried out clustering of individual propeller loop trajectories and then compared the cluster representatives of all the trajectories to derive 23 major Clusters after numerous cross-verifications. Our results demonstrate the general ambiguity of the clustering methods for single-stranded nucleic acids regions; nevertheless, we suggest that our set of clusters provides a meaningful characterization of the propeller loop conformational space.

One of the main issues that we tried to clarify is whether the contemporary simulation methods are capable of identifying the principle substates on the free energy landscape of TTA propeller loops, as described by the force field. We observed a surprisingly good agreement between the propeller loop behavior in the unbiased MD and enhanced-sampling RECT simulations. Although results of both methods are very far from being quantitatively converged, we suggest that our computations capture all the major conformational substates of the TTA propeller loops, within the limits of the force-field description. We suggest that this represents a significant success of the simulation methodology used here.

Comparison of the simulation data with the available structural experimental data is less optimistic. The simulations agree with experiments in the sense that the TTA propeller loops can adopt multiple conformations depending on the flanking sequences, ligand binding, and even crystal packing. The clustering analyses show that propeller loop behavior in simulations is similar irrespective of the topology of the GQ. However, the most common X-ray substate is very decisively destabilized by the force field due to the vigorous penalty of the γ-trans preference introduced by the bsc0 correction, which is transferred also to all subsequent AMBER force-field refinements. Other than this, the propeller loop dynamics seems to be primarily determined by the stacking, H-bonding, and solvent exposure of the bases. Importantly, the sampled structures of the TTA propeller loops are insensitive to details of the DNA backbone dihedral angle parametrizations, as demonstrated using a series of recent refinements of the AMBER DNA force field. We interpret the results as indicating a force-field imbalance in the description of TTA propeller loops which cannot be eliminated by tuning of the dihedral part of the force field. A comparison of Clusters with the experimental structures shows that even when there is some correspondence between some of the simulation clusters and the experimentally observed conformations, we typically do not achieve a full agreement between the backbone dihedral angles sampled in simulations with those seen in the experiment.

Even with the evident force-field limitations, the fact that we see multiple loop conformations coexisting indicates limitations of any ensemble averaging in structural experiments. It should be taken into consideration in interpretation of solution experiments. Our result is very consistent with the broadness of the quasi-static TTA propeller loop conformations in the GQ-ligand X-ray structures. The data indicate that the loop conformations typically interconvert on time scale from one to dozens of μs.

Markov state modeling was used to understand the trends of structural transitions in the propeller loops. The transition rates estimated by transition path theory also show that loop interconversions take place on a microsecond to dozens of microseconds time-scales. Thus, a series of multiple 10-μs-scale simulations are a minimum requirement for achieving the most basic sampling of TTA propeller loops in Htel GQs. MSM could be a very efficient tool in quantification of the GQ loop conformational space, provided that the force-field description is improved.

In summary, we show that contemporary MD simulations can, in principle, provide a quite reliable analysis of the conformational space of GQ loops in terms of sampling. Although the simulations in the present paper (150 μs of standard and 28 μs of RECT simulations) remain far from converged, they likely visualize all the main conformational substates on the landscape of the TTA propeller loops. Further increase in computational power will most likely allow a semiquantitative or even quantitative description of the loop conformational space. However, it is also apparent that the contemporary simulation force fields are not sufficiently accurate to utilize the capability to sample the conformational space of the GQ propeller loops. Thus, the quality of the force-field description remains the major challenge in simulations of GQs.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.7b00226.

• Methods of equilibration, energy comparison of GQ topologies, clustering of RECT simulations, DBSCAN-based cpptraj clustering, and eRMSD-based clustering, results of cation dynamics and analyses of additional intramolecular parallel-stranded GQ simulations, and supporting results in Figures S1–S22 and Tables S1–S10 (PDF)

Author Present Address

^# Department of Molecular Physiology and Biophysics, University of Iowa, Iowa City, IA 52242, USA.

This work was supported by the Czech Science Foundation grant 16-13721S. Institutional funding was in addition obtained from the Ministry of Education, Youth and Sports of the Czech Republic (LO1305). J.S. acknowledges support by Praemium Academiae. B.I. and P.S. greatly appreciate access to storage facilities owned by parties and projects contributing to the National Grid Infrastructure MetaCentrum, provided under the programme “Projects of Large Research, Development, and Innovations Infrastructures” (CESNET LM2015042). A.G. and G.B. received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement n. 306662, S-RNA-S. S.H. is funded by UCL excellence fellowship.

The authors declare no competing financial interest.