Reference Correlation for the Viscosity of Carbon Dioxide

Abstract

A comprehensive database of experimental and computed data for the viscosity of carbon dioxide (CO₂) was compiled and a new reference correlation was developed. Literature results based on an ab initio potential energy surface were the foundation of the correlation of the viscosity in the limit of zero density in the temperature range from 100 K to 2000 K. Guided symbolic regression was employed to obtain a new functional form that extrapolates correctly to T → 0 K and to 10 000 K. Coordinated measurements at low density made it possible to implement the temperature dependence of the Rainwater-Friend theory in the linear-in-density viscosity term. The residual viscosity could be formulated with a scaling term ρ^γ/T the significance of which was confirmed by symbolic regression. The final viscosity correlation covers temperatures from 100 K to 2000 K for gaseous CO₂, and from 220 K to 700 K with pressures along the melting line up to 8000 MPa for compressed and supercritical liquid states. The data representation is more accurate than with the previous correlations, and the covered pressure and temperature range is significantly extended. The critical enhancement of the viscosity of CO₂ is included in the new correlation.

1. Introduction

Carbon dioxide (CO₂) is a key compound in nature. Together with water it is the feedstock for photosynthesis of carbohydrates, the process by which plants convert sunlight to chemical energy.¹ Recent interest in the flow properties of CO₂ has developed in conjunction with its use as a working fluid in advanced power and refrigeration cycles and with its separation from combustion flue gases and sequestration in underground formations.^{2, 3}

Viscosity quantifies a material’s ability to transmit momentum. The dynamic viscosity η as defined by Newton’s law⁴ is the momentum conductivity and the kinematic viscosity, ν = η/ρ, that was introduced by Maxwell,⁵ is the momentum diffusivity with the mass density ρ. Accurate knowledge of momentum transfer properties is needed in the sciences and in engineering to understand flow phenomena of the fluid phases. Numerous viscosity measurements of CO₂ have been carried out since Graham’s first experiments in 1846,⁶ but they were not assembled in one comprehensive database. In this work, references for viscosity data of CO₂ from previous analyses^7–15 as well as those included in the current versions of the AIChE DIPPR database,¹⁶ the NIST ThermoData Engine,¹⁷ and the Landolt-Börnstein compilations^18–20 were retrieved to combine all known literature data for the viscosity of CO₂ in one repository.

A re-correlation of the viscosity of CO₂ is timely for a number of reasons. The equation of state (EoS) of Span and Wagner of 1996,²¹ which is the most accurate EoS currently available for CO₂, was not part of the most recent viscosity correlation of Fenghour et al.¹⁴ in 1998. There have also been several experimental viscosity data sets published since the correlation of Fenghour et al.¹⁴ that increase the range or accuracy of the available data. Results from ab initio calculations were published for the viscosity in the limit of zero density by Hellmann,²² and Vogel²³ used recent reference viscosities with reduced uncertainties to re-analyze the measurements that had been performed in his group in 1986 and 1993. Shortly after the publication of Fenghour et al.,¹⁴ correlation methodology advanced with a theory-based representation of the temperature dependence of the second viscosity virial coefficient²⁴ while scaling terms were increasingly applied to represent viscosities at high densities.²⁵ Finally, the measurement results of Berg and Moldover²⁶ for the critical enhancement of the viscosity of CO₂ have yet to be included in a reference correlation.

The development of the viscosity correlation for CO₂ is described in the remainder of this paper as follows. After an initial orientation about the molecular uniqueness of CO₂, its pressure-volume-temperature relation is discussed as given by three equations of state. Because the viscosity correlation is formulated in terms of temperature T and density ρ. η(T, ρ), it is necessary to use an EoS to convert viscosities measured as a function of temperature and pressure η(T, p) to η(T, ρ). Then, the available viscosity data for CO₂ and their uncertainties are reviewed and the assembly of the fit data set is explained. The viscosity formulation consists of four contributions, (i) for the limit of zero density, (ii) for the initial density dependence, (iii) for the residual viscosity, and (iv) for the singularity of the viscosity at the critical point. The discussion of each of these contributions gives details of the new approaches that were introduced in this study. The performance of the new viscosity correlation for CO₂ is documented in the final section by comparison with literature data from measurements and molecuar simulations and by an estimation of its uncertainties in various subregions of the fluid domain. The paper concludes with identifying needs for additional experimental and computational studies of the viscosity of CO₂.

2. Molecular Basis

John H. Dymond²⁷ wrote in 1996 in his introduction to the chapter on Dense Fluids in the book Transport Properties of Fluids—Their Correlation, Prediction and Estimation that “Data representation can be considered truly satisfactory only when it has a molecular basis.” The development of the viscosity correlation in this work tried to adhere to this guideline whenever possible. Current state of the art is to calculate macroscopic properties from potential energy surfaces (PES) that are based on approximate quantum-mechanical solutions of the Schrödinger equation for the nuclei and electrons of a molecule. A landmark advance in that regard is the work of Cencek et al. who calculated the properties of helium in the limit of zero density with substantially smaller uncertainties than have been achieved in measurements.²⁸ Their viscosity value for gaseous helium at 298.15 K has an expanded uncertainty of 0.001 %. CO₂ is a much more complex molecule than helium so that such calculations cannot yet be performed with the same rigor with current computational resources. However, in the latest study, Hellmann²² probed the PES of CO₂ with sufficient accuracy to produce results for the viscosity in the limit of zero density that agree with accurate experimental data within 0.55 %. Because of the simplicity of the intermolecular interactions at states in the limit of zero density, the sophisticated PES can be used to calculate properties for dilute gases but not for higher densities, much less for liquids at increasing compressions.

Here, CO₂ is compared with its two precursor molecules, methane, CH₄, and formaldehyde, CH₂O, and with ethane, C₂H₆, as ethane and CO₂ have been often investigated together because of their similar critical temperatures. Figure 1 shows the sizes, shapes, and charge distributions of these molecules as calculated at the MP2 Møller-Plesset theory level with the 6-311G** basis set. The scale of the electrostatic potential that is color-mapped on the isoelectron density surfaces which include 99 % of each molecule is that of formaldehyde. It is the most polar of the four compounds due to the electronegativity of the double-bonded oxygen atom that replaces two of the four hydrogens in methane. Formaldehyde has a gas-phase dipole moment of 2.33 debyes¹⁶ with 1 debye = 3.335 640 95×10⁻³⁰ C m.²⁹ CO₂ is obtained when the remaining pair of hydrogen atoms in formaldehyde is replaced by a double-bonded oxygen. As a result, the charge in CO₂ is more uniformly distributed (from −19.7 kJ mol⁻¹ to 29.4 kJ mol⁻¹) than in the other three compounds and the shape of the molecule is simplified to a linear cylinder with spherical ends. Ethane in comparison has the most complex shape of the four compounds with a similar charge distribution to methane, from −15.4 kJ mol⁻¹ to 41.5 kJ mol⁻¹ vs. −14.2 kJ mol⁻¹ to 47.1 kJ mol⁻¹, respectively. While not being dipolar, CO₂ has a relatively large quadrupole moment.³⁰

Fig. 1.

Frontal and top views of the molecular sizes, shapes and charge distributions of CO₂ and its precursors methane and formaldehyde. Ethane is also included because it has often been investigated together with CO₂.

A qualitative understanding of the balance between repulsive and attractive contributions to the molecular interactions can be deduced from the length of the vapor pressure curve of a compound, because a liquid phase cannot be formed if only repulsive forces are present.^31–35 The vapor pressure curves of the four compounds are shown in Fig. 2 from their triple points to their critical points. The fluid region of methane is in the lowest temperature range (T_c = 190.56 K)³⁶ because it is the smallest of the four molecules. Its length is T_c – T_t = 99.87 K. The high polarity of formaldehyde gives rise to electrostatic attractions between these molecules that not only shift the vapor pressure curve to higher temperatures (T_c = 420.0 K)¹⁶ but also widen the fluid region to a range of T_c – T_t = 264.85 K. The magnitude of these attractive forces is also indicated in comparison with CO₂ and its more isotropic charge distribution by the downward shift of the vapor pressure curve to the lower critical temperature of T_c = 304.1282 K.²¹ Even more noteworthy is the associated contraction of the fluid region of CO₂ to a temperature range of only T_c – T_t = 87.54 K. This means that the intermolecular potential of CO₂ is dominated by repulsion which results from the stiffness of the electron clouds of the oxygen atoms that bind their electrons tightly due to their high electronegativity. This dominance of the intermolecular repulsion was weighed in the formulation of the residual viscosity contribution to the new correlation for CO₂ described in section 5.3 below.

Fig. 2.

Vapor-pressure curves of the molecules shown in Fig. 1. T_t denotes triple-point temperature, T_c critical temperature.

In a final note on the molecular basis, the fluid region of CO₂ is compared with that of ethane as these compounds have often been measured jointly. While the critical temperature of ethane is only 1.2 K higher (T_c = 305.32 K)³⁷ than that of CO₂, Fig. 2 shows that its fluid region spans a significantly wider temperature range of T_c – T_t = 214.95 K and also a particularly wide pressure range. Thus, the intermolecular potential between ethane molecules has a substantially stronger attractive part than that of CO₂. This example of two compounds with similar critical temperatures shows that critical properties, despite their remarkable viability as corresponding-states parameters, do not capture all features of molecular interactions. More complete descriptors would include the extent of the fluid region as given by the temperature difference T_c - T_t. At present, triple-point properties have been determined for far fewer compounds than critical point properties. Closing this gap is a constructive direction of future research.

3. Conversion of Pressures to Densities

For theoretical and phenomenological reasons, viscosity formulations for the entire fluid region are developed in terms of temperature and density. As a consequence, experimental viscosity data that are reported for temperatures and pressures must be converted to a common basis of temperatures and densities by means of an equation of state. The temperatures of all viscosity data prior to 1991 were converted to the International Temperature Scale of 1990 (ITS-90) with VisualBasic routines provided by our NIST colleague Eric Lemmon. The reference-quality fundamental equation of state for the Helmholtz energy of fluid CO₂ was developed by Span in 1993 ³⁸ and published internationally by Span and Wagner in 1996.²¹ This was too late to be included in the viscosity correlation of Fenghour et al. in 1998,¹⁴ which was published nevertheless because it was more urgent to remove the viscosity uncertainties that existed in the compressed liquid region of CO₂.

Where appropriate, densities for the viscosity data for CO₂ were computed from the fundamental equation of state of Span and Wagner.²¹ However, because the pressure conditions of Abramson’s viscosity measurements³⁹ exceeded the range of validity of the Span-Wagner equation of state, Abramson referred to the study of Giordano et al.⁴⁰ as a source of more recent equation of state information for fluid CO₂. Giordano et al. found “… that above 500 K the fluid is less compressible than predicted from various phenomenological models.” The comparison in Fig. 3 shows that densities from the Span-Wagner equation of state are up to 3.24 % higher than those of Giordano et al. at the highest temperature (673.8 K) and highest pressure (7960 MPa) of Abramson’s measurements. Therefore, in this work densities from the analytical equation of state of Giordano et al. were associated with Abramson’s viscosity data above 500 K.

Fig. 3.

Deviations of densities calculated with the Span-Wagner equation of state²¹ from those calculated with the equation of state of Giordano et al.⁴⁰ at the state points of the viscosity measurements of Abramson.³⁹

The performance of the equation of state in the critical region is important with respect to the viscosity of CO₂ because it is one of the few fluids for which the enhancement of this transport property toward the critical point has been explored because of the exceptional experimental efforts involved. To prepare for the discussion of the enhancement in section 5.6 it is noted here that the Span-Wagner equation of state marked a significant achievement in representing surfaces of thermodynamic properties near the gas-liquid critical point with analytical terms. However, a complete, consistent representation of the nonanalytic behavior of the thermodynamic properties in this region requires power-law-terms with universal critical exponents and universal scaling functions. Because the critical region of CO₂ has been of scientific interest even before Andrews’ first quantitative determination of the p-ρ-T surface in 1869,⁴¹ the scaled crossover equation of state for the Helmholtz energy of CO₂ in the vicinity of the critical point by Chen et al. of 1990⁴² should be mentioned in this context for completeness. Span and Wagner presented extensive comparisons of the representation of the critical region of CO₂ by their Helmholtz energy formulations with that of Chen et al. and specified temperature and density ranges where the equation by Chen et al. yields more consistent representations of various thermodynamic properties.

4. Review of Viscosity Data

The known literature references with experimental and computational studies of the viscosity of CO₂ were compiled and are tabulated in the supplementary material⁴³ in chronological order up to the present with annotations about methods used, uncertainties, temperature and pressure ranges, and other pertinent information lest no future student be tasked with the duplication of this time-consuming collection effort. Given the prominence of some of the earliest investigators, a few historical notes are in order. Thomas Graham (1805–1869)⁶ was in 1846 professor of chemistry at University College London and became in 1854 Master of the Mint, an office that was held earlier by Isaac Newton.⁴⁴ While Graham was more interested in diffusion,⁴⁵ his extensive measurements of efflux times of various gases and their mixtures including CO₂ through capillaries of various materials, lengths, and internal diameters were important for the development of capillary viscometers for gases. August Kundt (1839–1896) and Emil Warburg (1846–1931) developed in their paper of 1875⁴⁶ the Kundt-Warburg correction for slip flow that was quoted 115 years later in the paper by van den Berg et al.⁴⁷ that will be discussed below. Kundt later became the doctoral advisor of Wilhelm Conrad Röntgen, and in 1905 Emil Warburg became the third president of the Physikalisch-Technische Reichsanstalt, now Physikalisch-Technische Bundesanstalt (PTB).

The two most recent data analyses and correlations of the viscosity of CO₂ were performed by Vesovic et al.¹² in 1990 and by Fenghour et al. in 1998.¹⁴ Vesovic et al. identified systematic deviations between some data sets in the compressed liquid region, which prompted a request for new viscosity measurements by the then IUPAC Subcommittee on Transport Properties (since 2001 International Association for Transport Properties IATP). These were carried out by van der Gulik⁴⁸ with a vibrating-wire viscometer at the Van der Waals-Laboratory in Amsterdam, The Netherlands. These measurement results formed the basis for the revised viscosity correlation of Fenghour et al.¹⁴ Since then, a number of experimental and computational data sets have been published for the viscosity of CO₂, yet only two expanded the temperature and pressure range. The measurements of Estrada-Alexanders and Hurly⁴⁹ with a Greenspan viscometer expanded the coverage of the vapor and gas region to low temperatures between 220 K and 370 K and pressures up to the vapor pressure or 3.15 MPa, whichever is lower. Abramson³⁹ measured extremely compressed liquid states in a diamond anvil cell at temperatures from 308 K to 670 K with pressures from 480 MPa to 7960 MPa. Several contributions provided results with lower uncertainty in regions where measurements had been carried out before. Mal’tsev et al.⁵⁰ published three data points from a coiled capillary viscometer for the dilute gas at 500 K, 800 K, and 1100 K. Sih et al.⁵¹ measured with a falling-body viscometer at three near-critical temperatures but supercritical pressures from 10 MPa to 19 MPa. Pensado et al.⁵² reported density and viscosity data measured simultaneously with a vibrating-wire viscometer at six temperatures between 303.15 K and 353.15 K with pressures from 10 MPa to 60 MPa. Heidaryan et al.¹⁵ claimed to have measured the viscosity of CO₂ with a falling-sphere viscometer from 313.15 K to 523.15 K with pressures between 7.7 MPa and 81.1 MPa. This region had previously been sparsely explored. However, the data were neither reported in the publication nor were they provided upon request of the present authors. Davani et al.⁵³ reported measurements with a rolling-sphere viscometer at nine temperatures from 309.82 K to 388.71 K and at five pressures from 27.6 MPa to 55.2 MPa. Vogel²³ recalculated the results of Vogel and Barkow of 1986⁵⁴ and those of Hendl et al. of 1993⁵⁵ by referencing them to the highly accurate viscosity value of helium at room temperature by Cencek et al.²⁸ Locke et al.⁵⁶ contributed five data points for gaseous CO₂ at 303.2 K and pressures from 0.5 MPa to 4.5 MPa that were measured with a newly developed vibrating-wire viscometer. Most recently, Schäfer et al.⁵⁷ reported highly accurate measurements in the dilute gas region from 253.15 K to 473.15 K with an advanced magnetically levitated rotating-cylinder viscometer. Their work was carried out in consultation with the present authors and it was honorably mentioned by Moldover in his Touloukian Award Lecture at the 19^th Symposium on Thermophysical Properties in 2015.⁵⁸

Besides these experimental measurements, an increasing number of computational studies contributed to a more detailed understanding of the viscosity of CO₂. Major advances were achieved in the ab initio calculation of the potential energy surface (PES) that governs pairwise interactions of CO₂ molecules. The most recent of these studies by Hellmann²² concisely reviews preceding work in this area which contribute to quantify the properties of the gas phase in the limit of zero density. It is important to recognize the transition in methodology that is underway. While the properties of gases in the limit of zero density could formerly be derived only from experimental measurements, increasing processing capacities have made ab initio computations possible that have now superseded experimental capabilities in accuracy. A landmark in this development is the aforementioned study of Cencek et al. of 2012²⁸ for the special case of helium. Due to its more complex atomic and molecular structure than that of helium, ab initio calculations of the PES and the properties of dilute CO₂ gas have not yet advanced below the uncertainty of experimental measurements, but they have characterized the viscosity of CO₂ in the limit of zero density over a wider temperature range than that explored in measurements and thus have contributed an important building block of the new viscosity correlation as a whole. Details will be given in Section 5.1.

The above mentioned data sets of Estrada-Alexanders and Hurly,⁴⁹ Abramson,³⁹ and Schäfer et al.⁵⁷ were included in the critically analyzed data on which the new viscosity correlation was based. The measurement results of Schäfer et al. confirmed an increased uncertainty of the data of Estrada-Alexanders and Hurly with decreasing density, which had been already noted by these authors themselves.⁴⁹ Therefore, data from the contribution of Estrada-Alexanders and Hurly below a density of 16 kg m⁻³ were not included in the development of the new viscosity correlation. Fully included were the data of Kestin and Whitelaw,⁵⁹ of Docter et al.,⁶⁰ of Vogel and Barkow,⁵⁴ and those of Hendl et al. of 1993⁵⁵ as revised by Vogel in 2016,²³ as well as the data by van der Gulik⁴⁸ and Golubev and Shepeleva⁶¹ in the liquid region. The comprehensive measurements of Golubev and Petrov⁶² and the careful study of Michels et al.⁶³ were carried out with capillary viscometers across the critical region where the compressibility increases strongly towards its singularity at the critical point. However, the working theory of this type of instrument was at that time only applicable to incompressible fluids. Challenged by Kestin at the meeting of the IUPAC Subcommittee on Transport Properties in Boston in 1987, van den Berg and colleagues^{47, 64, 65} extended the working theory of the instrument to compressible fluids. In their paper of 1990⁴⁷ they discussed the viscometer that was used by Michels et al. for CO₂ and demonstrated the effect of the extended working theory in correcting their own viscosity data for ethylene that had been obtained in the same instrument and were yet to be published. Unfortunately, van den Berg et al. did not re-analyze the CO₂ measurements of Michels et al. with the extended working theory which would have been a great service to the community by preventing any further misunderstandings of the results of Michels et al. Neither is there a publication record of the viscosity data for ethylene that were discussed in the paper of 1990.⁴⁷ For lack of instrument details, the extended working theory by van den Berg et al. could not be applied to correct the data set of Golubev and Petrov.⁶² Therefore, some points in regions of high compressibility were excluded from these data sets for the development of the new viscosity correlation. For reasons of internal consistency, only a subset of the data by Haepp⁶⁶ was used from 370 K to 450 K with pressures from 3 MPa to 150 MPa. Systematic deviations occur in these data on the three isobars that are closest to the critical pressure of CO₂ and at temperatures of 333 K and below. This suggests that the performance of the instrument was affected by critical-point-related property changes that were not accounted for in the data analysis. The data by Kurin and Golubev⁶⁷ that were included in previous correlations were no longer considered in the present work because they appeared inconsistent with the data by Golubev and Petrov⁶² at lower pressures and with those by Abramson³⁹ at higher pressures.

Updated uncertainty assessments of publications that reported viscosity data of CO₂ and of ethane have been presented recently by Vogel et al.⁶⁸ in their development of a reference correlation for the viscosity of ethane. An error of the temperature measurement system in the high-temperature oscillating-disk viscometer of Kestin’s group⁶⁹ had been discussed in detail by Vogel et al. in 1998.²⁴ Obviously, this error was not considered in the two preceding correlations of the viscosity of CO₂ in 1990¹² and 1998.¹⁴

One aspect of note in conjunction with experimental studies of CO₂ is its ability to act as a supercritical solvent slightly above room temperature. We know that van der Gulik et al.⁷⁰ were not the only ones who dealt with contamination of their CO₂ by dissolving lubricant, but they documented their experience. Unusual damping phenomena were noticed by Pádua et al.⁷¹ that prevented them from continuing their vibrating-wire measurements below 260 K. A similar observation was noticed by van der Gulik,⁴⁸ although he was able to measure with his vibrating-wire viscometer down to 220 K.

Table 1 lists the viscosity data sources that were selected for the new correlation. Figure 4 shows how the selected experimental viscosity data cover the fluid region of CO₂ relative to the melting curve, the vapor-pressure curve, and the sublimation curve. A wide gap extends at pressures from 0.5 MPa to about 700 MPa and above 550 K, where only 24 data points were measured by Golubev et al.⁷² New measurements in this region would provide a significant improvement in the knowledge of the viscosity of CO₂.

Table 1.

List of Data Sources Selected for the Correlation.

Authors	Method	Reported Uncertainty	Temperature Range (K)	Pressure Range (MPa)	Comments
Golubev and Petrov62	Capillary flow	1 %	293.15 – 523.15	0.1 – 80
Michels et al.63	Transpiration, capillary flow	_	273.15 – 348.15	0.9 – 209.7	see text
Kestin, Whitelaw59	Oscillating disk	0.5 %	297 – 525	0.126 – 6.85
Golubev et al.72	Capillary flow	1.5 %	473.1 – 773.1	0 – 49
Golubev, Shepeleva61	Capillary flow	1 %	252.8 – 293.8	3.9 – 49
Haepp66	Oscillating disk	0.9 % – 1.6 %	298 – 473	0.1 – 15	see text
Vogel, Barkow54	All-quartz oscillating disk	±0.1 % to 0.2 % or 0.3 % at high T	295.09 – 646.91	4 isochors	Revised in 201623
Hendl, Vogel55	All-quartz oscillating disk	±0.15 % at low T to 0.3 % at high T	297 – 685	6 isochors	Revised in 201623
Docter et al.60	Rotating cylinder viscometer Single sinker densimeter	0.6 % – 1.2 %	298.15, 523.15	0.10 – 14.74
van der Gulik48	Vibrating wire	1 %	220.01 – 308.15	0.56 – 453.20
Estrada-Alexanders, Hurly49	Greenspan acoustic viscometer	0.6 %	220 – 370	0.195 – 3.146	see text
Abramson39	Rolling sphere	5 %	308 – 673	480 – 7960
Hellmann22	ab initio calculations	0.2 % (150 – 700 K), 1 % at min and max T	150 – 2000	ρ → 0 zero density limit	see text
Schäfer et al.57	Rotating cylinder viscometer	(0.20 % to 0.41) %	253 – 473	< 1.2

Fig. 4.

Distribution of selected viscosity data for CO₂ to develop the new correlation.

5. Formulation Concept

The viscosity correlation for CO₂ was formulated in the following general structure

$$\eta (T,\rho )={\eta }_0(T)+\rho {\eta }_1(T)+\mathrm{\Delta }{\eta }_{\mathrm{r}}(T,\rho )+\mathrm{\Delta }{\eta }_{\mathrm{c}}(T,\rho ).$$ (1)

Here, η is the dynamic viscosity in units of mPa s throughout this work, T the absolute temperature in kelvin and ρ the density in kg m⁻³. On the right-hand side of Eq. (1), η₀(T) denotes the viscosity in the limit of zero density, η₁(T) the linear-in-density viscosity coefficient, Δη_r(T,ρ) the temperature- and density-dependent residual viscosity, and Δη_c(T, ρ) is the term for the enhancement of the viscosity toward the gas-liquid critical point where the viscosity becomes infinite.⁷³ The establishment of the four contributions to the formulation will be detailed in the next sections.

5.1 Viscosity in the limit of zero density

Significant additional information about the temperature dependence of η₀(T), the viscosity in the limit of zero density of CO₂, has been contributed since 1998 through measurements and computations. In 1999, Bukowski et al.⁷⁴ published a PES that was followed in 2002 by that of Bock et al.⁷⁵ Bock et al. calculated η₀ values from both PE surfaces, analyzed the most reliable experimental data, readjusted the parameters in the correlation of Vesovic et al.,¹² and compared the deviations of the experimental and calculated η₀ values relative to this revised correlation.

In the initial phase of the present analysis, this comparison was continued by including data that had become available since 2002. The ratios η_CO2/η_N2 measured by Maitland and Smith in 1970⁷⁶ with a capillary viscometer to almost 1500 K were converted to viscosities for CO₂ by multiplying them with reference viscosities for nitrogen that Hellmann published in 2013.⁷⁷ As an example for the importance of accurate reference standards, this improved the agreement of the results of Maitland and Smith with other data significantly. In 2014, Hellmann²² published calculated η₀ values for CO₂ between 150 K and 2000 K based on a new PES and graciously contributed unpublished values down to 100 K during discussions with the present authors about ensuring the correct extrapolation behavior of η₀ correlations in the limit of T → 0 K. To obtain η₀ values from the data of Schäfer et al.⁵⁷ they were regressed in the present analysis isothermally by linear density functions and extrapolated to ρ = 0. The straight lines represented the data within ±0.05 %, well within their estimated experimental uncertainty of 0.2 % to 0.41 %. From the measurements of Vogel and Barkow⁵⁴ and Hendl et al.,⁵⁵ η₀ values were included as re-analyzed by Vogel.²³

A graphical representation of the deviations is shown in Fig. 5 with the correlation of Bock et al. as baseline. It is remarkable that the data measured by von Obermayer⁷⁸ with a capillary viscometer in 1876 deviate from the correlation only between −0.05 % and 1.66 %. Agreement within their estimated uncertainties exists between the re-analyzed data of Vogel and collaborators²³ and the data extrapolated from the results of Schäfer et al.⁵⁷ The data by Timrot and Traktueva,⁷⁹ Harris et al.⁸⁰ (except one point at 276.897 K), and the data by Hunter et al.⁸¹ (except for two points at 213.15 K and 253.15 K) are consistent with the data from the other two laboratories. This applies even for the low-temperature measurements of Johnston and McCloskey of 1940.⁸² The re-analysis of the data of Maitland and Smith reduced their deviation range from −1.4 % to 1.3 % to −0.52 % to 0.94 %. The other experimental data in Fig. 5 deviate more systematically from this group of results. To bring the PES-based calculated values in agreement with this group of results, Hellmann²² suggested to multiply them by a factor of 1.0055. This shift is indicated in Fig. 5 by the dotted and the full green lines of deviations. Below 150 K, the deviations between the data by Hellmann²² and the correlation by Bock et al.⁷⁵ turn negative and increase rapidly while they oscillate systematically from 150 K to 2000 K in a pattern that is paralleled by the deviations of the values that were calculated by Bock et al. based on the PES of Bukowski et al.⁷⁴

Fig. 5.

Deviations of data for the viscosity of CO₂ in the limit of zero density from the correlation of Bock et al.⁷⁵

Both phenomena indicate shortcomings of the correlating function that was used by Bock et al. and many others before and thereafter. Rooted in the kinetic theory of gases, the form

$${\eta }_0(T)=\frac{21.357\times {10}^{-6}{(MT)}^{\frac{1}{2}}}{{\sigma }^2{\mathfrak{S}}_{\eta }^{\ast }(T^{\ast })},$$ (2)

with η₀ in units of mPa s, the molar mass M in g mol⁻¹, the length scaling parameter σ in nm and the reduced generalized cross section

$${\mathfrak{S}}_{\eta }^{\ast }(T^{\ast })=exp\left[\sum _{i=0}^4{a}_i{(\text{ln}{T}^{\ast })}^i\right]$$ (3)

in terms of the temperature T reduced by an energy scaling parameter T^* = T/(ε/k_B) has been employed for many years by adjusting the parameters a_i, σ, and (ε/k_B). Expressing ${\mathfrak{S}}_{\eta }^{\ast }$ as a function of the logarithm of T^* was proposed by Kestin et al. out of correlational convenience.⁸³ The increasing availability of ab-initio-calculated results prompts one to rethink this correlation method of viscosities in the limit of zero density. Since such results are based on more and more accurate potential energy surfaces for intermolecular interactions, they contain all information about the size, shape, charge distribution, and polarizability of a molecule so that the length and energy scaling parameters σ and (ε/k_B) are no longer meaningful. Besides, the temperature function of ${\mathfrak{S}}_{\eta }^{\ast }$ is too inflexible for accurate representations over wide temperature ranges. Several such correlations in the literature were found to exhibit unphysical singularities at low temperatures and incorrect extrapolation behavior for T → 0 K as well as to high temperatures.

Given the availability of tools to optimize the functional form of correlations, we decided to develop for CO₂ an improved expression for the temperature dependence of η₀(T) based on the calculated values by Hellmann.²² Symbolic regression was performed with the Eureqa^* software^{84, 85} to minimize deviations of the objective function $\mathfrak{S}(T)=\sqrt{T}/{\eta }_0(T)$. This strategy was found more effective than minimizing the deviations in η₀(T). Symbolic regression was guided further by allowing powers of the temperature terms in 𝔖(T) in multiples of T^1/6 because such terms have been successfully used in correlations of collision integrals. Eureqa returned five functional forms that all represented the data by Hellmann equally well, but only one of them satisfied the additional criteria of physically meaningful extrapolation behavior without any singularities. This function has the following form

$${\eta }_0(T)=\frac{1.0055\sqrt{T}}{\left(a_0+a_1{T}^{1/6}+a_{2}exp\left(a_3{T}^{1/3}\right)+\frac{a_4+a_5{T}^{1/3}}{exp\left(T^{1/3}\right)}+a_6\sqrt{T}\right)}.$$ (4)

It includes seven adjustable parameters, the values of which are listed in Table 2. The scaling factor 1.0055 was proposed by Hellmann²² to match the calculated ab-initio results with η₀ values derived from the most accurate experimental data. Equation (4) represents the extended data of Hellmann with maximum deviations from −0.059 % to 0.026 %, which are significantly below their estimated uncertainties of 0.2 % between 300 K and 700 K while increasing to 1 % at 150 K and 2 000 K, respectively. Equation (4) has no singularity below 100 K, yields the value η₀ = 0 for T → 0 K, and extrapolates physically meaningfully to 10 000 K. With the absolute temperature T in the unit of kelvin the viscosity η₀(T) is obtained from Eq. (4) in mPa s.

Table 2.

Values of the parameters a_i in Eq. (4).

i	ai
0	1749.354893188350
1	−369.069300007128
2	5423856.34887691
3	−2.21283852168356
4	−269503.247933569
5	73145.021531826
6	5.34368649509278

The performance of Eq. (4) is illustrated in Figs. 6 to 8. Figure 6 shows the relative deviations of values calculated with Eq. (4) from the unscaled data of Hellmann.²² Figure 7 shows the representation of the unscaled η₀ data calculated by Hellmann and the extrapolation behavior of Eq. (4) in the temperature range from 0 K to 1000 K. Fig. 8 shows a comparison of η₀ data derived from measurements considered to be most accurate relative to Eq. (4) in the temperature range from 100 K to 1900 K. The data of Johnston and McCloskey⁸² deviate from Eq. (4) between 0.12 % at 198 K and −0.33 % at 273.13 K and still show a systematically different temperature dependence than the new correlation. In a similar trend, the data by Wobser and Müller⁸⁶ deviate between −0.37 % and −0.59 %. Nevertheless, these deviations are remarkably small considering that the measurements were performed with a rolling-sphere Höppler viscometer.

Fig. 6.

Fractional deviations of viscosity data for CO₂ in the limit of zero density calculated with the new correlation Eq. (4) from the PES-based data calculated by Hellmann.²²

Fig. 8.

Comparison of η₀ data derived from measurements considered to be most accurate and those calculated by Bock et al.⁷⁵ based on the PES of Bukowski et al.⁷⁴ relative to the new correlation Eq. (4) in the temperature range 100 K to 1900 K.

Fig. 7.

Representation of the viscosity of CO₂ in the limit of zero density by Eq. (4) compared to the unscaled data of Hellmann²² calculated to 100 K and extrapolation behavior of Eq. (4) in the limit T → 0 K. Note that for this comparison the factor 1.0055 in the numerator of Eq. (4) was set to unity.

The re-analysis of the data of Maitland and Smith⁷⁶ has a significant effect on their deviations from Eq. (4). Except for four points at 292.695 K, 497.260 K, 1051.265 K, and 1496.987 K, the deviations range between -0.04 % and 0.22 % up to 1350 K and thus support the calculations of Hellmann closely. The highest internal consistency is indicated by the deviations of the data of Vogel and Barkow⁵⁴ and Hendl et al.⁵⁵ as re-analyzed by Vogel.²³ They range between ±0.1 %. The η₀ values derived from the measurements of Schäfer et al.⁵⁷ agree with the new correlation with deviations of −0.06 % to −0.26 %, which are smaller than their estimated experimental uncertainty.

A group of data with slightly higher deviations includes the measurements of Timrot and Traktueva⁷⁹ with an oscillating-disk viscometer and an estimated experimental uncertainty of 0.7 %, the results of Harris et al.⁸⁰ from a coiled-capillary viscometer with an estimated experimental uncertainty of 1 %, and the values reported by Hunter et al.⁸¹ that were determined with the same instrument and uncertainty. Except for two points in the data of Harris et al. at 213.15 K and at 253.15 K and one point in the series of Hunter et al. at 276.897 K, the deviations of these three data sets range from −0.17 % to 0.31 %. The deviations of all points of these three data sets are between −0.54 % and 0.44 %, which is smaller than their estimated experimental uncertainties.

Figure 8 also shows deviations of data of two measurement series of Kestin and collaborators^{87, 88} and of one data point that was determined in this analysis by extrapolation from the measurements of Docter et al. at 523.15 K.⁶⁰ The instrument of Docter et al. was an earlier version of that of Schäfer et al.⁵⁷ The viscosity value at 523.15 K is 0.52 % higher than the new correlation, which is within the reported estimated total uncertainty of ±0.6 % to ±1 %. The deviations of the data of Kestin et al. are smallest near room temperature with −0.2 %⁸⁷ and 0.03 %,⁸⁸ but increase with temperature to maxima of 0.66 % at 463.11 K⁸⁷ and 1.10 % at 473.11 K⁸⁸ from which they decrease to higher temperatures. Due to the error in the temperature measurement in their viscometer, the originally reported uncertainties of 0.3 % and less at elevated temperatures have to be revised.

As a non-experimental data set, Fig. 8 includes also deviations of values that Bock et al.⁷⁵ calculated on the basis of the PES of Bukowski et al.⁷⁴ from 185 K to 2000 K. They deviate from Eq. (4) with a constant offset of −0.22 % from 640 K to higher temperatures but increase towards lower temperatures to −0.59 % at 185 K. The rather small deviation at high temperatures lends support to the temperature dependence of the calculation results of Hellmann²² in addition to the small deviations of the re-analyzed experimental data of Maitland and Smith.⁷⁶ The uncertainty estimates of Hellmann of 1 % below 300 K, 0.2 % to 700 K, and 1 % to 2000 K are adopted for the performance of Eq. (4) but appear conservative.

Overall, thanks to the calculations of Hellmann and due to its new functional form, the new correlation for the viscosity of CO₂ in the limit of zero density η₀(T), Eq. (4), has a lower uncertainty and a significantly wider range of applicability than previous correlations for this property. It is also the component in the new viscosity correlation with the strongest molecular basis.

5.2 Initial density dependence of viscosity

The linear-in-density viscosity coefficient η₁(T) represents the initial density dependence of the viscosity. It is given by

$${\eta }_1(T)={\eta }_0(T)B_{\eta }^{\ast }(T^{\ast }){\sigma }^3{N}_{\mathrm{A}}/M,$$ (5)

with η₀(T) according to Eq. (4), the temperature-dependent reduced second viscosity virial coefficient $B_{\eta }^{\ast }(T^{\ast })$ as detailed below, the length scaling parameter σ in meters, the Avogadro constant⁸⁹ N_A = 6.022 140 857(74)×10²³ mol⁻¹, and the molar mass of CO₂ M = 44.0095×10⁻³ kg mol⁻¹. The temperature dependence of the reduced second viscosity virial coefficient $B_{\eta }^{\ast }(T^{\ast })$ was theoretically calculated for the Lennard-Jones 12-6 potential by Rainwater and Friend^{90, 91} and later adjusted to experimental results by Vogel and Hendl.⁹² An accurate and wide-ranging correlation of their results was published by Vogel et al.²⁴ and adopted in this work. The correlation is formulated in terms of the reduced temperature T^* as

$$B_{\eta }^{\ast }(T^{\ast })=b_0+\sum _{i=1}^8\frac{b_i}{{(T^{\ast })}^{t_i}}.$$ (6)

For convenience of implementation, the values of the coefficients b_i and of the exponents t_i are reproduced in Table 3 from Vogel et al.²⁴

Table 3.

Values of the parameters b_i and exponents t_i in Eq. (6).

i	bi	ti
0	−19.572 881	—
1	219.739 99	0.25
2	−1015.322 6	0.5
3	2471.012 5	0.75
4	−3375.171 7	1
5	2491.659 7	1.25
6	−787.260 86	1.5
7	14.085 455	2.5
8	−0.346 641 58	5.5

Equation (6) is based on data²⁴ in the range 0.5 ≤ T^* ≤ 100, but extrapolates safely to T^* = 0.3 and above T^* = 100. Applying this dimensionless function to real compounds requires values for the energy scaling parameter ε/k_B to convert between absolute and reduced temperature T^* = k_BT/ε and for the length-scaling parameter σ. They were determined here from the data of Schäfer et al.,⁵⁷ in an approach that is illustrated in Figs. 9 and 10. Instead of fitting them by least-squares regression to all data of Schäfer et al., they were determined from two characteristic points of Eq. (6) that are indicated in Fig. 9, namely the temperature of the sign change of $B_{\eta }^{\ast }$ at T^* = 1.24527 and from its maximum at T^* = 2.1652.

Fig. 9.

Temperature dependence of the reduced second viscosity virial coefficient $B_{\eta }^{\ast }(T^{\ast })$ with characteristic points.

Fig. 10.

Temperature dependence of the reduced second viscosity virial coefficient B_η and of the linear-in-density viscosity coefficient η₁ of CO₂.

Figure 10 shows data and the resulting correlation of the second viscosity virial coefficient B_η and of the linear-in-density viscosity coefficient η₁ of CO₂ in the temperature range from 200 K to 1000 K. The most noteworthy feature of these properties is their steep decrease below 300 K. The measurements of Vogel and colleagues at the University of Rostock did not record this decrease because their viscometer operated from room temperature upward. Figure 10 also shows that the revised values for B_η and for η₁ by Vogel and collaborators²³ exhibit considerable scatter and give no clear indication of the temperature dependence of these properties. The importance of measurements below 300 K was communicated during this project to Schäfer et al. at the Ruhr-University Bochum. They responded to this need and carried out the measurements⁵⁷ that made it possible to apply Eq. (6) to CO₂. Values of B_η were obtained as the slopes of the linear regressions of the isotherms that were explained in Section 5.1. As noted in Section 4, the only other data set in the low-density gas region at low temperatures by Estrada-Alexanders and Hurly⁴⁹ could not be used in the present analysis because of their increased uncertainty at low density.

The value of the energy scaling parameter ε/k_B = 200.760 K was determined from the sign change temperature of $B_{\eta }^{\ast }$ at T^* = 1.24527 and the value of 250 K deduced from the experimental data of Schäfer et al.⁵⁷ as indicated by the blue dashed line in Fig. 10. With this value of ε/k_B and the temperature of the maximum of $B_{\eta }^{\ast }$ at T^* = 2.1652, the temperature of the maximum of B_η was obtained as 434.685 K as indicated by the red dashed line in Fig. 10. The value of B_η at this temperature was interpolated from the experimental data of Schäfer et al.⁵⁷ Finally, having determined the maxima of B_η and $B_{\eta }^{\ast }$, the value of the length scaling parameter σ = 0.378421 nm was obtained from Eq. (5).

Figure 10 shows that the η₁ data of Schäfer et al.⁵⁷ agree closely with the temperature dependence of Eq. (5). It also indicates the improvement of the new viscosity correlation from its predecessors by Vesovic et al.¹² and by Fenghour et al.¹⁴ These correlations included temperature-independent constants as linear-in-density viscosity coefficients η₁ which are correct only near room temperature but do not represent the steep decrease at lower temperatures, nor the maximum at higher temperatures. The theory-based range of validity of Eq. (6) of 0.3 ≤ T^* ≤ 100 translates with the value of ε/k = 200.760 K for CO₂ to a fluid-specific range of applicability of Eq. (6) from 60 K to approximately 20 000 K, well above the range of any practical need.

5.3 Residual viscosity contribution

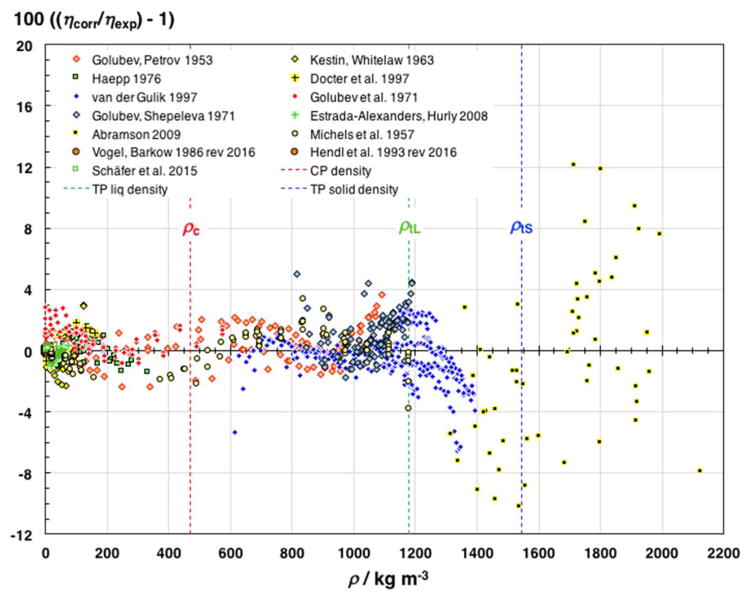
Having established the terms η₀(T) and η₁(T) in Eq. (1), the next step in the correlation is the formulation of the temperature- and density-dependence of the residual viscosity term Δη_r(T, ρ). Figure 11 shows this contribution as a function of density when calculated from the selected data via

Fig. 11.

Residual viscosity of CO₂ versus density. The densities at the critical point, ρ_c, and of the liquid and solid at the triple point, ρ_tL and ρ_tS, are indicated for orientation.

$$\mathrm{\Delta }{\eta }_{\mathrm{r}}(T,\rho )=\eta (T,\rho )-{\eta }_0(T)-{\eta }_1(T)\rho .$$ (7)

Three ranges can be discerned in the diagram. First, the residual viscosity increases with density at a decreasing rate up to about 800 kg m⁻³. Above this density, the logarithm of viscosity seems to be a linear function of density with narrow temperature dependence although the data cover a wide range from 200 K to 773 K. The closest congruence of the data occurs at about 900 kg m⁻³. A growing temperature dependence in the Δη_r-ρ relationship emerges at higher densities, as indicated by the combined data of van der Gulik⁴⁸ and of Abramson.³⁹

The two preceding correlations expressed the residual viscosity of CO₂ in part¹² or in its entirety¹⁴ as polynomials in density. While such terms have a limited theoretical basis in solutions of the Boltzmann equation for moderately complex molecular interactions,⁶⁸ their application to represent the viscosity of liquids is purely empirical and limited to the range of the data to which such terms were adjusted. Extrapolations to higher densities or pressures usually fail, as was found for the CO₂ correlation of Fenghour et al.¹⁴ with the high pressure measurements of Abramson.³⁹ A more accurate representation of viscosities of liquids and more meaningful extrapolations are offered by the two variants of free-volume terms. The first term V/(V-V₀) is often associated with Batschinski⁹³ and Hildebrand,⁹⁴ although Bingham⁹⁵ considered the relation between fluidity and free volume already in 1914 for the entire fluid region and was never cited by Hildebrand. The second variant exp[V/(V-V₀)] was introduced by Doolittle⁹⁶ as a conclusion of his high-pressure measurements of hydrocarbons. The difference V-V₀ is called free volume and V₀ is a limiting or close-packed volume. Vesovic et al.¹² represented the viscosity of CO₂ in the liquid region with a Batschinski-Hildebrand term and combined it with the polynomial terms with a sigmoid transition function. Independently and at the same time, a free-volume term was combined with a cubic density polynomial in the reference correlation for the viscosity of oxygen.⁹⁷ The capability of this type of formulation was applied in several other reference correlations^{24, 98–102} but it was shown that the singularity of the viscosity for V → V₀ leads to significant overpredictions even at modest extrapolations.¹⁰³ Therefore, free-volume terms were no longer considered in the present study.

A singularity-free representation of viscosities and other properties to high compressions was proposed by Ashurst and Hoover^{104, 105} based on the congruence of the dynamic evolution of systems with different soft-sphere potentials.¹⁰⁶ This congruence is obtained when the initial conditions of the dynamic evolutions are scaled in terms of time and length and when dimensionless variables are used for temperature, density, viscosity and other properties. It turned out that the reduced residual viscosity is a function of the single variable ρ^γ/T and not of density and temperature separately. This consolidation of two independent variables into one has become known as thermodynamic scaling. Fernandez and Lopez²⁵ have reviewed this development including its relation to isomorphy.^{107, 108} In the initial approach, the exponent γ is related to the strength of the repulsive soft-sphere potential. Given the dominance of the repulsive part of the intermolecular interaction between CO₂ molecules and the close congruence of Δη_r(T, ρ) near 900 kg m⁻³, it appeared appropriate to include scaling terms into the development of the residual viscosity term Δη_r(T, ρ) via symbolic regression.

The symbolic regression software returned several functional forms that represented the critically evaluated viscosity data equally well. However, only the following form was free from unphysical artifacts in the data range and extrapolates in a physically meaningful manner

$$\mathrm{\Delta }{\eta }_{\mathrm{r}}(T,\rho )={\eta }_{\text{tL}}\left(c_1{T}_{\mathrm{r}}{\rho }_{\mathrm{r}}^3+\left({\rho }_{\mathrm{r}}^2+{\rho }_{\mathrm{r}}^{\mathrm{\gamma }}\right)/(T_{\mathrm{r}}-c_2)\right).$$ (8)

The dimensioning factor

$${\eta }_{\text{tL}}=\frac{{\rho }_{\text{tL}}^{2/3}\sqrt{R{T}_{\mathrm{t}}}}{M^{1/6}{N}_{\mathrm{A}}^{1/3}}=\frac{{\rho }_{\text{tL}}^{2/3}\sqrt{k_{\mathrm{B}}{T}_{\mathrm{t}}}}{m^{1/6}}$$ (9)

arises from Enskog’s theory for transport properties of hard spheres¹⁰⁹ but is often used with critical point coordinates T_c and ρ_c. Now that the singularity of the viscosity at the critical point is firmly established, it appears preferable to form the dimensioning factor with the coordinates of the triple point instead of the critical point to avoid ambiguities. Therefore, the reduced temperature T_r = T/T_t is formed here with the triple-point temperature of CO₂, T_t = 216.592 K, and the reduced density ρ_r = ρ/ρ_tL with the density of the liquid phase at the triple point,²¹ ρ_tL = 1178.53 kg m⁻³. The molar gas constant is R = 8.314 4598(48) J mol⁻¹ K⁻¹ and the Boltzmann constant k_B = 1.380 648 52(79) × 10⁻²³ J K^−1.89 The molar mass M of CO₂ and the Avogadro constant N_A have been given in Section 5.2; m denotes the mass of a molecule m = M/N_A. With these quantities, the value of the dimensioning factor η_tL is approximately 0.094 36 mPa s (the complete non-rounded result from Eq. (9) is used in the correlation). The values of the coefficients γ, c₁, and c₂ are given in Table 4.

Table 4.

Values of the parameters in Eq. (8).

γ	8.06282737481277
c1	0.360603235428487
c2	0.121550806591497

The symbolic regression^{84, 85} that resulted in the compact function in Eq. (8) was a complex and time-consuming process. It required the specification of a custom optimization function that allowed for finding the simplest functional form that fit the data over its entire, very wide range (three orders of magnitude) while also preventing the fit from being over-weighted by outliers. The final optimization function used the absolute value of the percent deviations and only considered the operators addition, subtraction, multiplication, division, exponentiation and log. Unsurprisingly, we also found that the more accurate the starting condition for the residual viscosity, the better the performance of symbolic regression. In other words, the best possible determination of η₀(T) and ρ η₁(T) was critical to the fitting process.

The final function for Δη_r(T, ρ) includes only three adjustable parameters associated with a quadratic, a cubic and a density term with the non-integer power γ. The previous correlations of Vesovic et al.¹² and of Fenghour et al.¹⁴ contained density terms with powers of 2, 6, and 8. The new correlation represents a data set that covers a wider temperature and pressure range than for most other fluids. Figures 12 and 13 illustrate the quality of representation of the data that were included in the regression in terms of density and temperature, respectively. Up to a density of 1000 kg m⁻³, the deviations are within ±3 %, increasing to ±4 % in the range up to 1400 kg m⁻³ except for the 260 K isotherm of van der Gulik⁴⁸ where deviations down to −6.6 % occur. Deviations from −10.3 % to 12 % occur for the high-pressure data of Abramson³⁹ in the density range up to 2127 kg m⁻³, and Fig. 13 indicates that the spread of the deviations increases systematically with temperature and hence with decreasing roll times of the sphere in the diamond-anvil cell. While Abramson³⁹ estimated an uncertainty of his data of 5 %, deviations of the free-volume correlation that was also reported with the data exceed that estimate and range from −11 % to 7.4 %. Our discussions with Dr. Abramson give us confidence that the representation of this data set by the new correlation is consistent with the uncertainty of the data.

Fig. 12.

Percent deviations of viscosities calculated with the new correlation for CO₂ from experimental data selected for the regression as a function of density. The densities at the critical point, ρ_c, and of the liquid and solid at the triple point, ρ_tL and ρ_tS, are indicated for orientation.

Fig. 13.

Percent deviations of viscosities calculated with the new correlation for CO₂ from experimental data selected for the regression as a function of temperature.

5.4 Comparisons with experimental data

Experimental data that were published since 1998 are compared in this section with the new correlation. In 2001, Mal’tsev et al.⁵⁰ reported three data points for CO₂ gas at 500 K, 800 K, and 1100 K which were determined with a coiled-capillary viscometer at a reported uncertainty of 3 %. While the viscosities deviate from the new correlation within that margin from −1.5 % at 500 K to 2.8 % at 1100 K, the analysis of the flow measurements does not include a correction for radial acceleration of the sample gas in the coiled capillary.¹¹⁰ Given the diameter of the capillary of 0.9 mm, its length of 700 mm, and in particular its tight coil diameter of 15 mm, the radial acceleration of the flowing gas appears likely to have contributed to the measured viscosities, but the paper does not report sufficient experimental details to apply this correction retroactively. It can only be concluded that the actual experimental uncertainty is probably higher than reported by the authors.

In 2007, Sih et al.⁵¹ reported results of measurements with a falling-body viscometer at four isotherms from 298.15 K to 313.15 K with pressures from 10.9 MPa to 19.1 MPa. The viscometer was calibrated with methanol at 0.1 MPa and with CO₂ against the correlation of Fenghour et al.¹⁴ as reference. As shown in Fig. 14, the deviations of the experimental data from that correlation ranged from −0.93 % to 0.97 % with an average of the absolute relative deviations from their mean (AAD) of 0.49 %. Compared with the new correlation, which was not adjusted to the data of Sih et al.,⁵¹ the deviations are shifted by about −1.2 % to the range from −2.1 % to −0.21 % with an AAD of 0.52 %. In that temperature and density range the new correlation is based on the data by Golubev and Petrov from 1953,⁶² of Michels et al. of 1957,⁶³ and of van der Gulik of 1997,⁴⁸ which are mutually consistent within ±2 %. Despite the apparently systematic offset of −1.2 %, the measurements of Sih et al.⁵¹ are also consistent with these data sets.

Fig. 14.

Representation of the data of Sih et al. (2007)⁵¹ by the correlation of Fenghour et al. (1998)¹⁴ and by the new correlation.

It is particularly interesting to compare the 2008 experimental data of Estrada-Alexanders and Hurly⁴⁹ with the previous and with the new correlation. As seen in the pressure-temperature diagram of Fig. 4, these measurements were conducted in a rarely explored part of the gas region from 370 K to 220 K, close to the triple-point temperature of 216.592 K. As already mentioned in Section 4, the results below a density of 16 kg m⁻³ were not included in the development of the new correlation because of systematic uncertainties stemming from the decreasing resolution of the acoustic Greenspan viscometer at lower densities. Other than that, Estrada-Alexanders and Hurly⁴⁹ reported an estimated uncertainty of 0.6 % of the measured viscosities. Figures 15 and 16 show percent deviations of these experimental data relative to the correlation of Fenghour et al.¹⁴ and to the new correlation, respectively. In Fig. 15, the deviations from the correlation of Fenghour et al.¹⁴ are within ±1 % above the density of 16 kg m⁻³ except for one point at 250 K and 35.65 kg m⁻³ which deviates by −1.23 %. The deviations show systematic offsets for each isotherm from 250 K up to 370 K. Compared with the new correlation in Fig. 16, these offsets are greatly reduced and the deviations scatter within a band of only ±0.3 % above a density of 16 kg m⁻³, again with the exception of one point at 250 K and 35.65 kg m⁻³. Above the density of 25 kg m⁻³, the data are represented well within their estimated experimental uncertainty. This improved representation results from the temperature dependence of the linear-in-density viscosity coefficient η₁(T) that was incorporated in the new correlation by Eq. (6) that is based on the Rainwater-Friend theory, whereas η₁ was treated as an adjustable parameter in the previous correlation of Fenghour et al.¹⁴ The deviations of the experimental data below 16 kg m⁻³ are only marginally different between the previous correlation of Fenghour et al.¹⁴ and the new correlation, which indicates their systematic nature that is independent of temperature.

Fig. 15.

Representation of the data of Estrada-Alexanders and Hurly⁴⁹ by the correlation of Fenghour et al. (1998).¹⁴ Data of two isotherms are connected by lines for easier comparison.

Fig. 16.

Representation of the data of Estrada-Alexanders and Hurly⁴⁹ by the new correlation. Data of two isotherms are connected by lines for easier comparison.

In 2008, Pensado et al.⁵² published results of viscosity measurements of compressed liquid CO₂ that were performed with a vibrating-wire viscometer in the temperature range from 303.15 K to 353.15 K with pressures from 10 MPa to 60 MPa. The experimental uncertainty was reported as 3 %. The deviation plot vs. pressure in Fig. 17 shows that, except for one point at 313.15 K and 10 MPa that deviates from the new correlation by 6.2 %, the data are represented with maximum deviations of −2.5 % and 2.9 % and an AAD of 1.4 %. The smallest deviations between −0.83 % and 0.25 % occur along the isotherm at 303.15 K, except for the point at 20 MPa which deviates by 1 % and appears to scatter high. Similar deviations between −0.7 % and 0.47 % with an out-of-trend deviating point by 1.1 % at 30 MPa are seen at 333.15 K. Each of the isotherms at 313.15 K to 343.15 K exhibits scattering points which occur at varying pressures. The deviations are systematic with temperature and are positive above 303.15 K and negative above 333.15 K. Note that these data were not included in the development of the new correlation. However, their deviations indicate a considerable consistency with the data on which the new correlation is based. In fact, the data by Pensado et al.⁵² are among the most accurate for the viscosity of CO₂.

Fig. 17.

Representation of the data of Pensado et al.⁵² by the new correlation. Lines are drawn to help the reader to discern the pressure and temperature dependence of the deviations.

Additional viscosity measurements of compressed liquid CO₂ were reported by Davani et al. in 2012.⁵³ A commercial rolling-sphere viscometer was used in this study at nine temperatures from 309.8 K to 388.7 K with pressures from 27.6 MPa to 55.2 MPa. The CO₂ sample had a purity of 99.9999 %. The reported experimental uncertainty of 3 % was not assessed through a rigorous analysis but by comparing the measurement results with the correlation of Fenghour et al.¹⁴ Percent deviations of the experimental data by Davani et al.⁵³ from the new correlation are shown vs. pressure in Fig. 18. They range overall between a lowest and a highest value of −5.0 % and 2.3 %, respectively, with an AAD of 2.0 %. Only the results at 319.8 K are consistent with the reported uncertainty of 3 % as they vary in a band of 1.7 %. Ranges of increasingly random scattering expand from 3.5 % at 377.6 K and 3.8 % at 366.5 K to 4.7 % at 329.8 K and eventually 6.5 % at 309.8 K. Because of this imprecision, the data of Davani et al.⁵³ were not used in the development of the new correlation.

Fig. 18.

Representation of the data of Davani et al.⁵³ by the new correlation. Lines are drawn to help the reader to discern the variations of the deviations with pressure and temperature.

The most recent experimental data set for the viscosity of CO₂, that was not used in the development of the new correlation, was measured by Locke et al.⁵⁶ at 303.2 K in their study of the mixture {x_CO2 + (1 − x)_CH4} with mole fraction x = 0.5174 to benchmark the newly developed vibrating-wire viscometer with a van-der-Gulik design of the sensor where the wire is clamped at both ends. These measurement results were kindly provided by Professor Eric May, who also reported estimated uncertainties between 0.9 % and 3.1 %. Figure 19 illustrates the differences in the representation of these data between the previous correlation of Fenghour et al.¹⁴ and the new correlation. While the deviations from the former correlation range between −0.46 % and 0.72 %, the new correlation represents these data between −0.005 % and 0.36 %. This indicates the consistency of the results of Locke et al.⁵⁶ with the data that were used in the new correlation to establish the viscosity contribution in the limit of zero density (Section 5.1) and the initial density dependence of the viscosity (Section 5.2).

Fig. 19.

Deviations of the data of Locke et al.⁵⁶ at 303.2 K from values calculated with the correlation of Fenghour et al.¹⁴ and with the new correlation. Lines are drawn to guide the reader.

5.5 Comparison with results from molecular simulations

Computational molecular science is making increasingly accurate contributions to the knowledge of thermophysical properties and CO₂ is often studied by such methods. It is therefore of interest to compare the viscosity results of molecular simulations with the new correlation developed in this work.

Selected sources of CO₂ viscosity data from molecular simulations are included in the table in the supplementary material.⁴³ The selection was narrowed to reports of numerical data at more than one state point. This includes the results of Nieto-Draghi et al.,¹¹¹ Liang and Tsai,¹¹² Merker et al.,¹¹³ Aimoli et al.,¹¹⁴ Zhong et al.,¹¹⁵ and Jiang et al.¹¹⁶ Simulation studies before 2007 are referenced by Nieto-Draghi et al.¹¹¹ except for that of Palmer¹¹⁷ in 1994.

The distribution of the state points where the viscosity of CO₂ was studied by simulation is indicated in the pressure-temperature diagram of Fig. 20. They cover a temperature range from 223 K to 573 K with pressures from 0.1 MPa to 792 MPa. Note that some of the results of Zhong et al.¹¹⁵ are for metastable liquid CO₂ beyond the melting pressure curve. The simulation studies considered here used equilibrium molecular dynamics (EMD) where the viscosity is derived without applying an external shear from the particle fluctuations in macroscopic equilibrium.¹¹⁸ Of key importance for the accuracy of any simulation is the accuracy of the intermolecular force field model for the particle interactions. Among the six studies selected here, Liang and Tsai¹¹² used the most refined force field model, namely the aforementioned potential energy surface by Bukowski et al.⁷⁴ Nieto-Draghi et al.¹¹¹ used the rigid EPM2-model that was proposed in 1995 by Harris and Yung¹¹⁹ but rescaled to reproduce critical properties. The three-center Lennard-Jones model with superimposed quadrupole moment of Merker et al.¹¹³ was optimized for vapor-liquid equilibria and subsequently applied to predict viscosity and other properties. Similarly, Jiang et al.¹¹⁶ developed a polarizable and a nonpolarizable force field model, optimized both for vapor-liquid equilibria, and applied them to viscosity and other properties. Aimoli et al.¹¹⁴ and Zhong et al.¹¹⁵ compared the performance of seven and three, respectively, previously proposed force-field models with regard to viscosity predictions. Deviations of the viscosities from EMD simulations from the new correlation developed in this work are shown in Figs. 21 to 23.

Fig. 20.

Distribution of selected molecular simulation results for the viscosity of CO₂ in the pressure-temperature plane.

Fig. 21.

Deviations of molecular simulation results for the viscosity of CO₂ from the new correlation developed in this work. Lines are drawn to help the reader to discern the deviations of some data series.

Fig. 23.

Deviations of molecular simulation results for the viscosity of CO₂ from the new correlation developed in this work. Shown are the deviations of the results that Zhong et al.¹¹⁵ obtained with the flexible EPM2 force field model.

Figure 21 illustrates the progress of molecular simulations for the viscosity of CO₂ with time and the influence of the force-field model on the accuracy of the results. The deviations of the results of Nieto-Draghi et al.¹¹¹ at 328.15 K from the new correlation decrease systematically with density from 30 % at 200 kg m⁻³ to −1.7 % at 1300 kg m⁻³, except for the point at 400 kg m⁻³ which deviates by only 0.013 %. The most recent results of Jiang et al.¹¹⁶ with the polarizable force field model deviate between −3.3 % and 12 % on four isotherms between 273 K and 423 K and at densities from 327 kg m⁻³ to 1285 kg m⁻³. While the polarizable force field should be more realistic, the results with the nonpolarizable force field have deviations of only 0.7 % to 9.7 %. Both data sets of Jiang et al.¹¹⁶ show high internal consistency. Considerable systematic and random deviations are seen in the earlier results of Merker et al.,¹¹³ particularly when the results on the joint isotherms of 273 K and 373 K are compared with those of Jiang et al.¹¹⁶ The deviations of all results of Merker et al.¹¹³ range from −22 % to 12 %. This is within the uncertainties from 14 % to 33 % that were reported by the authors. The results of Liang and Tsai¹¹² at low densities and 300 K deviate from the new correlation between −3.7 % and 1.8 % with a systematic trend in density that the authors ascribe to the inadequacy of the potential energy surface of Bukowski et al.⁷⁴ for the CO₂ dimer for three-body interactions that increase with pressure or density. Therefore, these simulations were limited to a maximum pressure of 5.06 MPa corresponding to a density of 131.243 kg m⁻³. The two points at the lowest densities deviate by −1 % and −0.6 %, which is within the range of deviations of experimental data from the new correlation for the viscosity in the limit of zero density η₀(T) that is shown in Fig. 8. While this is a remarkably close agreement between viscosity results from simulation and measurement for CO₂, it should be kept in mind that the estimated uncertainty of the most accurate experimental data in that region is still one fifth and one third of the deviations of the two points of Liang and Tsai,¹¹² respectively.

The most comprehensive study of the influence of the force-field model on the quality of the viscosity results of EMD simulations was carried out by Aimoli et al.¹¹⁴ Calculations were performed for seven force fields on five isotherms from 273.15 K to 523.15 K in the same density range as that of Nieto-Draghi et al.¹¹¹ from 200 kg m⁻³ to 1300 kg m⁻³ (however with increments of 100 kg m⁻³) corresponding to a maximum pressure of 792 MPa. Aimoli et al.¹¹⁴ found that the force field model of Zhang and Duan¹²⁰ gave the most accurate viscosity results of the seven models that were examined. Therefore, only these results are compared with the new correlation developed in this work. Their uncertainties are reported as ranging from 1.5 % to 11 %. Percent deviations are shown in Fig. 22 vs. density. One immediately notices three points at 273.15 K with deviations from 15.3 % to 7 % at densities from 400 kg m⁻³ to 600 kg m⁻³. These deviations are inconsistent with the systematic density trend of the others which is the second apparent feature. Ranging between −18 % and −11 % at 200 kg m⁻³, the deviations decrease with increasing density and continue largely parallel to the new correlation from 500 kg m⁻³ upwards with maxima of −7.5 % and 4.6 %. At the highest density of 1300 kg m⁻³, the deviations contract to a range from −7.5 % to −2.4 %. The magnitude of the deviations above 500 kg m⁻³ is remarkably low, but it exceeds the representation of the experimental data by the new correlation shown in Figs. 12 and 13 by roughly a factor of two.

Fig. 22.

Deviations of molecular simulation results for the viscosity of CO₂ from the new correlation developed in this work. Shown are the deviations of the results that Aimoli et al.¹¹⁴ obtained with the force field model of Zhang and Duan.¹²⁰

The final comparison in this section is made between EMD simulation results of Zhong et al.¹¹⁵ and the new correlation developed in this work. These authors examined the performance of three previously proposed force-field models with added terms for bond stretching and angle bending. They concluded that the flexible EPM2 model gave the most satisfactory results with regard to viscosity. Their percent deviations from the new correlation are shown versus density in Fig. 23. They were calculated with the densities that are tabulated by Zhong et al.¹¹⁵ The most noteworthy deviations occur on the two isotherms with the highest temperatures. They reach 42 % at 450 K and 48 % at 424 K. The results at the next lower temperatures from 373 K to 298 K deviate from the correlation between −4.9 % and 5.2 % over a density range from 290 kg m⁻³ to 1245 kg m⁻³. These are the smallest deviations at elevated densities among the simulation results in this comparison and they are close to the estimated uncertainty of the new correlation at these conditions. The deviations at 273 K are also partly in this band, but indicate systematically lower viscosities at the three highest densities. This trend continues at the two lowest temperatures, 243 K and 223 K, with deviations eventually reaching −21 % at 223 K and 1370 kg m⁻³ or 200 MPa. This is far beyond the estimated uncertainty of the new correlation which will be detailed in Section 6 below.

This is the first comparison between simulation and measurement results for the viscosity of CO₂ in such detail. The closest agreement has been achieved in the limit of zero density where the new viscosity correlation is largely based on results of computations. While the size, shape, and charge distribution of the CO₂ molecule (cf. Fig. 1) is often considered rather simple, the proposed force fields are not yet refined enough to achieve computational results at elevated densities with uncertainties that would be comparable to those of measurements. In particular, three-body interactions need to be taken into account. Given the continued growth of hardware capabilities, computational determinations of the viscosity of CO₂ may reach experimental uncertainties in one or two decades.

5.6 The critical enhancement

Because of its near-ambient temperature range, the critical region of CO₂ has been of interest ever since Andrews’ first quantitative determination of the gas-liquid critical point in 1869.⁴¹ CO₂ was also the first fluid for which the critical enhancement of the thermal conductivity was unambiguously proven in the measurements of Sengers.¹²¹ The critical enhancement of the viscosity of CO₂ has also been investigated more often than for other fluids. Interest in the viscosity in the critical region arose in 1935 with the measurements of Schröer and Becker.¹²² The English translation of the subtitle of their paper reads “Contribution to the knowledge of the viscosity in the critical state.” However, the reported data at 293 K are in the two-phase region significantly below the critical temperature T_c = 304.1282 K²¹ and the falling-sphere viscometer that was employed is not a suitable instrument for compressible fluids. Not surprisingly, the results by Schröer and Becker¹²² appear to be burdened by systematic deviations. In 1940, Naldrett and Mass¹²³ measured the variation of viscosity with temperature on 14 isochores and explored the critical region systematically. They used an oscillating-disk viscometer that is more suitable because no pressure difference occurs in the instrument. As seen in Fig. 24, their results provided evidence for a critical enhancement of the viscosity of CO₂. The results of Michels et al.,⁶³ which were already discussed in Section 4, prompted Kestin et al.¹²⁴ to re-determine the viscosity of CO₂ with an oscillating-disk viscometer in the single-phase region surrounding the critical dome. Figure 24 shows that their results indicated a milder viscosity enhancement than had been found by Naldrett and Mass.¹²³ The most extensive study of the viscosity in the critical region was carried out in 1981 by Iwasaki and Takahashi,¹²⁵ also with an oscillating-disk viscometer, for both CO₂ and ethane. Assessments of their CO₂ data have been given by Vesovic et al.¹² and by Luettmer-Strathmann et al.¹²⁶ Vogel et al.⁶⁸ provided a detailed assessment of the ethane data of Iwasaki and Takahashi,¹²⁵ which applies likewise to their results for CO₂. The closest approach to the critical point was accomplished by Berg and Moldover²⁶ with a torsion-oscillator viscometer at low shear rate and low frequency. Measuring along the critical isochore, they detected a viscosity enhancement of up to 9 % just 3 mK above the critical temperature. No other viscosity measurements in the critical region of CO₂ have been performed since then.

Fig. 24.

Experimental data for the critical enhancement of the viscosity of CO₂. The points shown for Berg and Moldover²⁶ were calculated by them and reported in Table IX of their publication. They range from 30.4 K above T_c (lowest viscosity) to 30.4 μK above T_c (highest viscosity).

The data of Berg and Moldover²⁶ were not included in the correlation of Vesovic et al.¹² because the two publications overlapped. Neither were they referenced in the correlation update of Fenghour et al.¹⁴ in 1998, although Luettmer-Strathmann et al.¹²⁶ had used them in addition to those by Iwasaki and Takahashi¹²⁵ in 1995 to provide representative equations for the critical enhancement Δη_c(T,ρ) of the viscosity of CO₂ and ethane based on an approximate solution of the mode-coupling theory for critical fluctuations. That crossover model Δη_c(T, ρ) with the system-dependent constants for CO₂ as given by Luettmer-Strathmann et al.¹²⁶ can be used with the new viscosity correlation developed in this project for the background contribution η_b(T,ρ) to calculate the critical enhancement of the viscosity of CO₂. η_b(T,ρ) consists of the first three terms of Eq. (1)

$${\eta }_{\mathrm{b}}(T,\rho )={\eta }_0(T)+\rho {\eta }_1(T)+\mathrm{\Delta }{\eta }_{\mathrm{r}}(T,\rho ),$$ (10)

which have been detailed in Sections 5.1, 5.2, and 5.3. The local background viscosity correlation that was developed by Luettmer-Strathmann et al.¹²⁶ agrees with the new correlation within ±0.66 % in the density range 300 kg m⁻³ to 700 kg m⁻³ and in the near-critical temperature range 304.29 K ≤ T ≤ 304.99 K. The critical enhancement term of the viscosity is written as

$$\mathrm{\Delta }{\eta }_{\mathrm{c}}(T,\rho )={\eta }_{\mathrm{b}}(T,\rho )exp[z_{\eta }H],$$ (11)

with the universal critical exponent z_η and the crossover function H. Luettmer-Strathmann et al.¹²⁶ used a modified crossover model H′ that represents the data of Iwasaki and Takahashi¹²⁵ and of Berg and Moldover²⁶ more closely than the formulation of Vesovic et al.¹² This model is recommended here for the most accurate treatment of the critical enhancement of the viscosity of CO₂. Alternatively, one may use for Δη_c(T,ρ) the simplified closed-form solution of the mode-coupling equations by Bhattacharjee et al.¹²⁷ as was done by Berg and Moldover²⁶ and by Vogel et al.⁶⁸ in their reference correlation for the viscosity of ethane. It requires the wave number q_c to account for the influence of the background thermal conductivity λ_b(T_c,ρ_c) and viscosity η_b(T_c,ρ_c) at the critical point on the decay of critical fluctuations. This is given by

$$q_{\mathrm{c}}=\frac{k_{\mathrm{B}}{T}_{\mathrm{c}}^2}{16{\eta }_{\mathrm{b},\mathrm{c}}{\lambda }_{\mathrm{b},\mathrm{c}}{p}_{\mathrm{c}}}\frac{{\mathrm{\Gamma }}_0}{{\xi }_0^2}{\left(\frac{\partial p}{\partial T}\right)}_{T_{\mathrm{c}},{\rho }_{\mathrm{c}}}^2.$$ (12)

The values of the quantities in Eq. (12) are compiled in Table 5. The complete formalism of the crossover function H of Bhattacharjee et al.¹²⁷ is given in the paper of Berg and Moldover.²⁶

Table 5.

Fluid-specific parameters for the calculation of the critical enhancement of the viscosity of CO₂

Parameter	Reference	Value	Unit
ξ0	126	0.15	nm
Γ0	126	0.0481	nm
ηb(Tc,ρc)	this work	32.3585	μPa s
λb(Tc,ρc)	128	45.0769	mW (m K)−1
(∂p/∂T)Tc, ρc	21	0.170536	MPa K−1
qc−1	Eq. (12)	0.217	nm
qD−1	126	0.2	nm

Vesovic et al.¹² concluded “…that the relative critical viscosity enhancement is smaller than 1 % at densities and temperatures outside a range bounded approximately by 300 K < T < 310 K and 300 kg m⁻³ < ρ < 600 kg m⁻³.” This corresponds to a lenticular region from the vapor pressure at 300 K (p_s = 6.713 MPa) to the pressures 7.855 MPa and 8.882 MPa at 310 K. This delineation remains in effect but it may vary slightly depending on the crossover model that is used in the calculation of Δη_c(T,ρ).

6. Uncertainty Estimates and Extrapolation of the New Correlation

The estimated uncertainties of the current correlation are indicated in the pressure-temperature diagram of Fig. 25 from 200 K to 1000 K with pressures from 0.01 MPa to the melting pressure or 10 000 MPa, whichever is smaller. The estimates are based on the expanded uncertainties quoted in the data sources, on the mutual consistency of the data which is indicated by their representation by the new formulation as documented in Sections 5.1 to 5.4, and on the long-term experience of the authors. The range of Fig. 25 is a considerable extension over the range of validity of previous viscosity correlations for CO₂. The extension beyond the previous limit of 300 MPa is mainly due to the measurements of Abramson.³⁹ The uncertainty estimate in this region is based on the representation of Abramson’s data by the new correlation. The estimated uncertainty of 4 % in the region between the vapor pressure curve and the melting pressure curve at temperatures from the triple point to the critical point is rather conservative. It results from the highest deviations between the new correlation and the data of van der Gulik,⁴⁸ cf. Figs. 12 and 13, except those on the 260 K isotherm which appear to deviate systematically. Figure 4 shows that the data sets of van der Gulik⁴⁸ and Abramson³⁹ have only one temperature in common. Further improvements of the correlation require measurements in the gap seen in Fig. 4 between the data of Golubev and Petrov⁶² and Golubev et al.⁷² and those of Abramson.³⁹ Absent such measurements, and shown in Fig. 25, an uncertainty of (5 – 10) % is assigned to the correlation in this region. In the other areas, the correlation represents the viscosity data within their estimated experimental uncertainties. The uncertainty of 2 % in the critical region is carried over from the study of Fenghour et al.,¹⁴ although it may be a conservative estimate because the work of Luettmer-Strathmann et al.¹²⁶ provided a more accurate representation of the critical enhancement. Significantly reduced uncertainty estimates became possible at moderate to low pressures in the entire temperature range of Fig. 25 and even up to 2000 K. These improvements are due to the careful measurements of Estrada-Alexanders and Hurly,⁴⁹ Schäfer et al.,⁵⁷ and Vogel,²³ as well as the calculations of Hellmann.²² Below the triple-point pressure of 0.51795 MPa, the uncertainty of the correlation is 0.2 % from 200 K to 700 K and 1 % up to 2000 K. Extrapolations below 200 K and above 2000 K at these conditions are physically realistic as shown in Fig. 7.

Fig. 25.

Estimated uncertainty of viscosities of CO₂ calculated with the new correlation.

The extrapolation behavior of a correlation should be examined, because it may be necessary in engineering or scientific applications to obtain values at conditions where no experimental data were available in the establishment of a property formulation and to ensure that the correlation performs at least in physically plausible ways. Figure 26 shows how the new correlation extrapolates to a rather high density of 3000 kg m⁻³ along the isotherms of 220 K and 700 K, which is the range where it is based on data, and at 1000 K and 2000 K. The corresponding pressures of these extreme conditions are in the metastable liquid region above the melting pressure curve. Figure 26 also includes the experimental data on which the new correlation was based and the densities at the critical point as well as those of the liquid and solid at the triple point. Because of the small number of density terms in the residual viscosity term Δη_r(T, ρ), Eq. (8), only minor oscillations of the isotherms occur in the subcritical vapor-liquid dome. At 220 K this unconstrained region extends from 14.3751 kg m⁻³ to 1135.48 kg m⁻³. More noticeable is a bulge on the 2000 K isotherm in the approximate range from 500 kg m⁻³ to 2000 kg m⁻³. Due to this incorrect feature, the new correlation may yield in this temperature and density range viscosities that may be 50 % higher than the unknown actual value, which can only be inferred because neither measurements nor simulations have been extended to such conditions. Figure 26 gives an indication of the leverage that the measurements of Abramson³⁹ exercised on the regression of the new correlation up to 700 K. From a density of 1110 kg m⁻³ the previous correlation of Fenghour et al.,¹⁴ which was established when the data of Abramson³⁹ were not yet available, yields systematically higher viscosities at 700 K, ending up 169 % higher at 3000 kg m⁻³. This discrepancy is even greater at 1000 K and 2000 K because the correlation of Fenghour et al.¹⁴ exhibits at high densities the opposite temperature dependence than the new correlation. Unlike many other thermophysical properties, viscosity increases with temperature at low and moderate densities (“gas-like behavior”) but decreases with temperature at elevated and high densities (“liquid-like behavior”). The correlation of Fenghour et al.¹⁴ exhibits gas-like temperature dependence at all densities. The measurements of Abramson³⁹ were of key importance to implement the liquid-like behavior in the new correlation. However, Fig. 26 shows that the crossover from gas-like to liquid-like behavior occurs over a wide density range from 1040 kg m⁻³ at 220 K to 2000 kg m⁻³ at 2000 K. Narrowing down the crossover requires additional measurements in the regions that are denoted in Fig. 25.

Fig. 26.

Extrapolation behavior of the new correlation for the viscosity of CO₂.

7. Check Values to Validate Implementations of the New Correlation

Check values are given in Table 6 to five significant digits. Comparisons in this laboratory between an implementation in FORTRAN for REFPROP,¹²⁹ and an implementation as a VisualBasic function in Excel showed no differences.

Table 6.

Check values to validate implementations of the correlation.

T (K)	ρ (kg m−3)	η (mPa s)
η0(T) correlation only, Eq. (4)
100	0	0.0053757
2 000	0	0.066079
10 000	0	0.17620
Full correlation, Eq. (1) without Δηc(T, ρ)
220	3	0.011104
225	1 150	0.22218
300	65	0.015563
300	1 400	0.50594
700	100	0.033112
700	1 200	0.22980

Tables 7 and 8 provide recommended values for the viscosity of CO₂ as quick lookup at temperatures and pressures that cover most application needs. They were calculated with the new correlation in conjunction with the equation of state of Span and Wagner²¹ as implemented in NIST Standard Reference Database 23, REFPROP.

Table 7.

Recommended values for the viscosity of coexisting liquid and vapor of CO₂ (mPa s).

T (K)	ηliquid (mPa s)	ηvapor (mPa s)
216.592	0.2534	0.01089
220	0.2393	0.01106
225	0.2202	0.01132
230	0.2028	0.01158
235	0.1870	0.01184
240	0.1725	0.01212
245	0.1592	0.01242
250	0.1469	0.01273
255	0.1356	0.01306
260	0.1251	0.01342
265	0.1152	0.01381
270	0.1060	0.01425
275	0.09720	0.01476
280	0.08876	0.01536
285	0.08050	0.01609
290	0.07219	0.01705
295	0.06345	0.01842
300	0.05319	0.02081
301	0.05066	0.02160
302	0.04775	0.02264

Table 8.

Recommended values for the viscosity of CO₂ (mPa s).

p MPa	Temperature (K)
	240	300	400	500	600	700	800	900	1000	1100
0	0.01209	0.01499	0.01962	0.02391	0.02786	0.03152	0.03493	0.03814	0.04118	0.04407
0.1	0.01209	0.01500	0.01964	0.02392	0.02788	0.03153	0.03494	0.03815	0.04118	0.04407
20	0.2068	0.09405	0.03136	0.02916	0.03139	0.03418	0.03704	0.03985	0.04259	0.04525
40	0.2392	0.1220	0.05657	0.04036	0.03781	0.03854	0.04027	0.04237	0.04462	0.04692
60	0.2693	0.1444	0.07501	0.05307	0.04605	0.04431	0.04459	0.04576	0.04737	0.04919
80	0.2981	0.1647	0.08984	0.06478	0.05474	0.05083	0.04968	0.04986	0.05074	0.05203
100	0.3260	0.1839	0.1030	0.07537	0.06326	0.05764	0.05520	0.05443	0.05461	0.05534
120	0.3533	0.2023	0.1151	0.08511	0.07144	0.06449	0.06095	0.05932	0.05882	0.05902
140	0.3802	0.2203	0.1267	0.09426	0.07926	0.07125	0.06680	0.06442	0.06329	0.06298
160	0.4068	0.2381	0.1379	0.1030	0.08678	0.07788	0.07267	0.06963	0.06794	0.06715
180	0.4332	0.2556	0.1489	0.1114	0.09404	0.08437	0.07852	0.07491	0.07272	0.07149
200	0.4595	0.2731	0.1597	0.1197	0.1011	0.09072	0.08432	0.08021	0.07758	0.07595

8. Concluding Remarks

A new correlation for the viscosity of CO₂ has been developed. This property and this fluid are among the most often measured since 1846. All available viscosity data have been compiled in this project for a complete historical documentation of these measurement efforts. The collected publications and data records have been added to the holdings of the NIST Thermodynamics Research Center from where they can be obtained.

The new correlation could be significantly advanced in accuracy and range compared to its predecessor¹⁴ because of highly accurate experimental and computational determinations of the viscosity of CO₂ that were carried out since 1998. All three terms of the new correlation benefitted from these efforts. The viscosity in the limit of zero density, η₀(T), which represents most of the entire viscosity-temperature dependence, could be extended to the range from 100 K to 2000 K based on viscosities calculated by Hellmann²² with a high-level ab initio potential energy surface. A new functional form was developed for accurate representation of the viscosity in this wide temperature range, which supersedes a formula that had been in use since 1972.⁸³ Comparisons with experimental data indicate an uncertainty of 0.2 % in the temperature range from 200 K to 700 K, 0.6 % to 100 K and 1500 K, and 1 % to 2000 K. The correlation extrapolates physically meaningfully to T → 0 K and far beyond 2000 K, the highest temperature of the viscosities calculated by Hellmann.²²

In collaboration with experimenters, temperature dependence was introduced to the linear-in-density term η₁(T). Thanks to the targeted measurements of Schäfer et al.,⁵⁷ a correlation of results of the Rainwater-Friend theory first introduced by Vogel et al.²⁴ could be applied to CO₂. While the previous correlations were correct in that term only near room temperature, the expanded correlation is valid from 60 K to the thermal decomposition temperature range of CO₂ and beyond.

The residual viscosity contribution to the correlation Δη_r(T, ρ) was formulated for the first time with terms ρ^γ/T where the exponent γ is related to the strength of the repulsion of the intermolecular potential. This was motivated because repulsion dominates the intermolecular potential of CO₂ and because the data for Δη_r(T, ρ) indicate a density region where this property is isomorphic.^{25, 107, 108} The functional form that was adopted from several variants obtained with symbolic regression has three density terms with three adjustable parameters and represents the viscosity of CO₂ at temperatures to 1000 K and up to the melting pressure curve or 10 GPa, whichever is smaller. This range extension was primarily made possible by the measurements of Abramson.³⁹ Their second benefit was that the new correlation features the inversion of the viscosity-temperature dependence from gas-like to liquid-like behavior.

The critical enhancement of the viscosity of CO₂ has been included in the new correlation by reference to the analysis of Luettmer-Strathmann et al.,¹²⁶ who developed a crossover model that represents the measurements of Berg and Moldover, who found an enhancement of 9 % at 3 mK above the critical temperature. These measurements had been missed in the preceding correlations.^{12, 14}

The greatest uncertainty reduction to 0.2 % was achieved in the dilute gas region from 200 K to 700 K at pressures below 0.5 MPa or the sublimation pressure, whichever is lower. The subcritical vapor region to 3 MPa and 450 K is represented with an estimated uncertainty of 1 %. Uncertainties of 4 % and 3 % are estimated for the subcritical liquid and for supercritical states below 100 MPa and below 550 K. A wide gap of measurements extends at pressures from 0.5 MPa to about 700 MPa and above 550 K where only 24 data points were measured by Golubev et al. ⁷² New measurements in this region would bring about a significant improvement of the knowledge of the viscosity of CO₂.

The properties of carbon dioxide have been increasingly studied by computer simulations. Viscosity results from such studies since 2007 have been compared with the new correlation in this work. Deviations between −3.7 % and 1.8 % were found for the results of Liang and Tsai¹¹² at low densities and 300 K. The smallest deviations in the sub- and supercritical liquid region were found for the results of Jiang et al.¹¹⁶ with the nonpolarizable force field. They deviate between 0.7 % and 9.7 %. With further improvements of the intermolecular force field models and inclusion of three-body interactions, computer simulations of the properties of CO₂ may reach the uncertainty of measurements within one or two decades.

This new correlation for the viscosity of CO₂ employed for the first time scaling terms in a wide-ranging viscosity formulation. These appear most suitable for highly compressed liquid states. Future improvements of viscosity formulations should aim to incorporate the transition from gas-like to liquid-like behavior more accurately. This approach was pursued in the correlation of Vesovic et al.¹² If the data gaps identified in this work will be filled by future measurements or simulations, it will be worthwhile to revisit the approach of Vesovic et al.¹² not only for carbon dioxide but for other fluids as well.