Triplet–triplet energy transfer in artificial and natural photosynthetic antennas

Significance

Rapid chlorophyll-to-carotenoid triplet–triplet energy transfer (T-TET) in photosynthetic organisms is crucial to photoprotection from singlet oxygen. Photosynthesis reengineered for increased efficiency will result in increased oxygen levels in the cells, and the need to ensure adequately rapid T-TET will arise. Using a combination of theoretical and experimental studies on artificial and natural carotenoid–chlorophyll complexes, we have identified spectroscopic markers indicative of specific pigment–pigment interactions promoting fast T-TET. These interactions comprise essential design principles necessary for photoprotection in reengineered photosynthesis. Antenna systems from anoxygenic organisms suitably reengineered for photoprotection could be used to gather solar energy in the near infrared, which would markedly increase photosynthetic efficiency by better matching the solar spectrum to water oxidation and CO₂ reduction.

Abstract

In photosynthetic organisms, protection against photooxidative stress due to singlet oxygen is provided by carotenoid molecules, which quench chlorophyll triplet species before they can sensitize singlet oxygen formation. In anoxygenic photosynthetic organisms, in which exposure to oxygen is low, chlorophyll-to-carotenoid triplet–triplet energy transfer (T-TET) is slow, in the tens of nanoseconds range, whereas it is ultrafast in the oxygen-rich chloroplasts of oxygen-evolving photosynthetic organisms. To better understand the structural features and resulting electronic coupling that leads to T-TET dynamics adapted to ambient oxygen activity, we have carried out experimental and theoretical studies of two isomeric carotenoporphyrin molecular dyads having different conformations and therefore different interchromophore electronic interactions. This pair of dyads reproduces the characteristics of fast and slow T-TET, including a resonance Raman-based spectroscopic marker of strong electronic coupling and fast T-TET that has been observed in photosynthesis. As identified by density functional theory (DFT) calculations, the spectroscopic marker associated with fast T-TET is due primarily to a geometrical perturbation of the carotenoid backbone in the triplet state induced by the interchromophore interaction. This is also the case for the natural systems, as demonstrated by the hybrid quantum mechanics/molecular mechanics (QM/MM) simulations of light-harvesting proteins from oxygenic (LHCII) and anoxygenic organisms (LH2). Both DFT and electron paramagnetic resonance (EPR) analyses further indicate that, upon T-TET, the triplet wave function is localized on the carotenoid in both dyads.

Photoprotection is central to the maintenance of photosynthesis. Under certain circumstances, chlorophyll excited triplet states may form from intersystem crossing and from electron–hole recombination reactions in reaction centers. Chlorophyll triplet species can sensitize the formation of singlet oxygen, a deleterious reactive oxygen species (1). In photosynthetic complexes, this sensitization reaction is precluded by sufficiently rapid transfer of the triplet excited state from chlorophyll (Chl) or bacteriochlorophyll (BChl) to carotenoid molecules. The triplet states of carotenoids involved in photoprotection are well below the energy of singlet oxygen and therefore do not sensitize singlet oxygen. This quenching reaction reduces the lifetime of the Chl or BChl triplet state by many orders of magnitude (1) and renders it kinetically incompetent to sensitize singlet oxygen. Moreover, carotenoids can quench singlet oxygen directly in the event that it is inadvertently formed.

In the light-harvesting (LH) proteins from most (anoxygenic) purple bacteria, triplet–triplet energy transfer (T-TET) from BChl to carotenoid molecules occurs on the nanosecond timescale (2, 3). By contrast, in light-harvesting complexes (LHCs) from oxygenic organisms, we recently showed that this transfer is ultrafast, on the subnanosecond timescale and therefore much faster than intersystem crossing so that the chlorophyll triplet species was not observed (4). The mechanisms underlying this ultrafast T-TET, which was proposed to represent an adaptation of oxygenic photosynthetic organisms to their oxygen-rich environment, are not yet fully understood. Some relevant observations are that, when ultrafast T-TET occurs between chlorophyll and carotenoid molecules, the presence of the triplet state on the carotenoid has an unusually strong influence on the chlorophyll Q_y electronic transition, and this spectral perturbation decays with the carotenoid lifetime (2, 5, 6). Moreover, the carotenoid triplet species exhibits a spectroscopic marker, an anomalous resonance Raman shift, defined by a smaller downshift of the carbon–carbon (CC) stretch (ν₁ band) than observed in the isolated carotenoid or in LH complexes, suggesting a unique perturbation of the typical carotenoid triplet state character (4). Because this perturbation correlates with ultrafast T-TET, it is of interest to determine the role of the underlying electronic and atomic-level structure of the carotenoid in the electronic coupling that results in ultrafast T-TET. It was tentatively proposed that the triplet state could be delocalized over the carotenoid/chlorophyll couple, and thereby shared between these molecules (4). The delocalization of the triplet state would decrease the electron population in the antibonding π* orbital of the carotenoid, thereby resulting in a smaller downshift of the ν₁ band associated with the CC stretch. However, recent electron paramagnetic resonance (EPR) experiments on LHCs suggest that, upon T-TET, the triplet resides essentially on the carotenoid (7). Although understanding the detailed mechanisms underlying the ultrafast T-TET in oxygenic photosynthesis will require further investigation, our combined theoretical and experimental results provide insight into the structural features characteristic of ultrafast T-TET, and reconciles resonance Raman and EPR data that were previously inconsistent. These structural features provide the required electronic coupling while avoiding spin delocalization, which could lead to reactivity that would be detrimental to the stability of the system. It is of interest to extend mechanisms of photoprotection based upon T-TET to reengineered photosynthetic systems where the production of oxygen and therefore the steady-state concentration of oxygen in the membranes would be much higher than current levels (8).

Over the last three decades, many carotenotetrapyrrole synthetic dyads have been designed and synthesized in which the absorption of a photon is followed by the formation of the tetrapyrrole triplet species by intersystem crossing; subsequent T-TET from the tetrapyrrole to the carotenoid produces the carotenoid triplet species (9–12). In these dyads, depending on their precise chemical properties and on the way the tetrapyrrole and the carotenoid molecules are linked, the T-TET kinetics ranges from tens of microseconds to the subnanosecond range. In the latter, the actual T-TET rate could not be determined because intersystem crossing in the tetrapyrrole is the rate-limiting step (9, 10, 13). In this work, we have studied two closely related dyads, one exhibiting slow and the other fast T-TET, using a combination of vibrational and transient absorption spectroscopic methods, EPR measurements, and density functional theory (DFT) calculations. These dyads, which mimic the dynamics and spectroscopic signatures characteristic of the LH and LHC natural systems, are ideal model systems for understanding the origin of the T-TET kinetics and for precisely characterizing the nature of their triplet states involved. Theoretical study of both dyads led to a comprehensive description of the triplet states and T-TET rates in both of these dyads, including the structural features in the carotenoid backbone resulting in the anomalous resonance Raman shift of its triplet state. Hybrid quantum mechanics/molecular mechanics (QM/MM) simulations of LHCII and LH2 identified similar structural features associated with the anomalous resonance Raman shift previously observed in those natural systems.

Results and Discussion

Steady State and Transient Electronic Absorption Spectra.

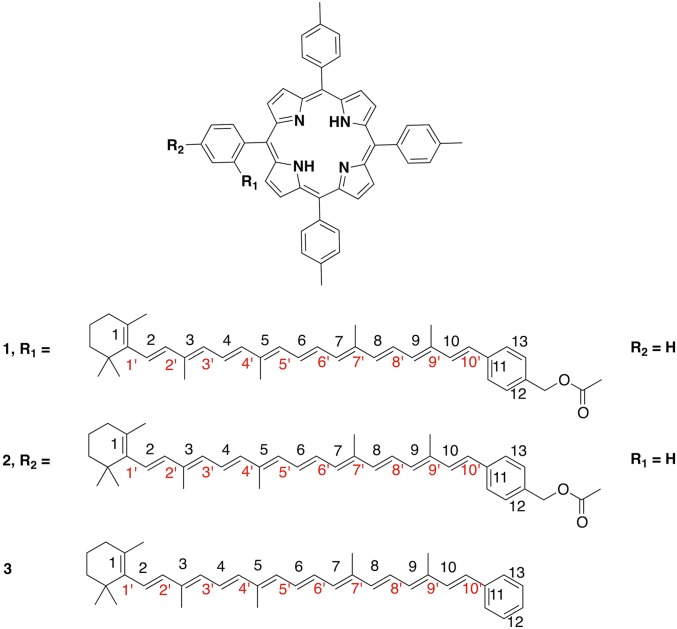
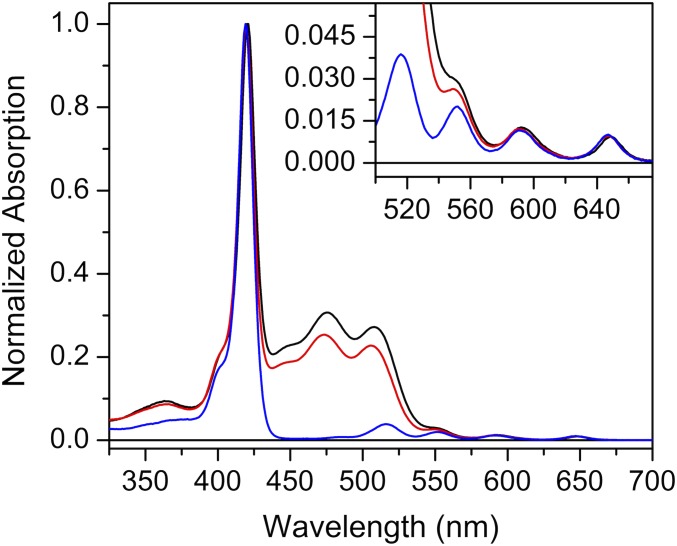
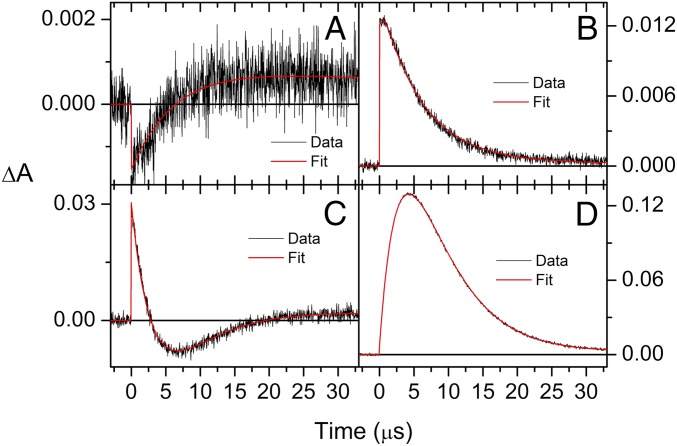
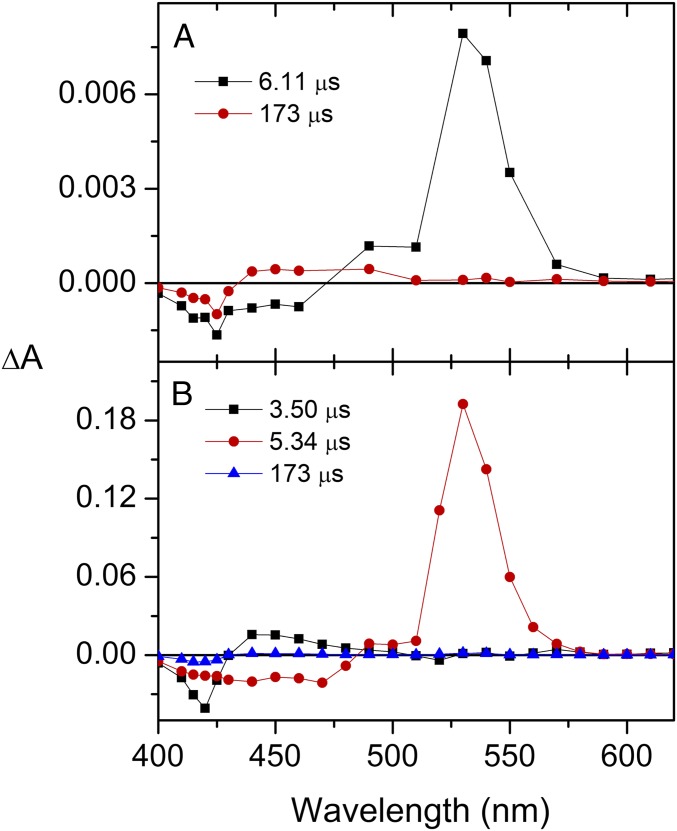
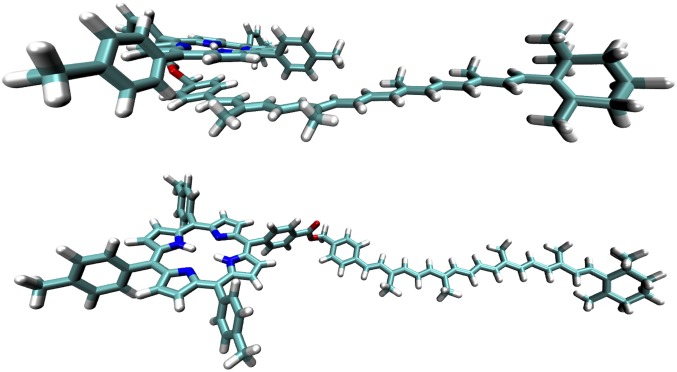
Both ortho-carotenoporphyrin (dyad-1) and para-carotenoporphyrin (dyad-2), which are constitutional isomers, comprise a carotenoid having 10 conjugated double bonds and a phenyl group, linked to a 5,10,15,20-tetra(4-methylphenyl)porphyrin (H₂TTP) by a methylene and an ester group (Fig. 1); the only difference between these two dyads is the linker point of attachment on the meso-phenyl group of the porphyrin. The electronic absorption spectra of these dyads are nearly identical, with slightly increased absorptivity in the region of the carotenoid in the case of dyad-1 (Fig. 2). In these spectra, porphyrins display intense contributions at 419 nm (Soret band) and relatively weak transitions in the visible range at 516, 552, 591, and 647 nm (Q bands). In both dyads, excitation of the porphyrin in the range of 413–417 nm or at 514 nm is followed by intersystem crossing over the porphyrin singlet lifetime to yield the porphyrin triplet state, which decays by T-TET to the linked carotenoid (9). Kinetic traces measured both in the porphyrin ground-state bleaching and carotenoid triplet induced absorption range evidence dramatic porphyrin triplet lifetime differences between the two dyads (Figs. 3 and 4), as reported by Bensasson et al. (9). Fig. 4A shows that after porphyrin excitation only one species with absorption characteristic of carotenoid triplet is observable (the long-lived state probably corresponds to slow-decaying porphyrin triplet arising from molecules detached from the carotenoid moiety). In Fig. 4B, by contrast, a species with absorption characteristic of the porphyrin triplet species is observed, with a 3.50-µs lifetime. Thus, in dyad-1, no intermediate species can be observed between the porphyrin excitation and the appearance of the carotenoid triplet state species (Fig. 4A). This indicates that the rise of porphyrin triplet state through intersystem crossing is slower than the T-TET to the carotenoid molecule, which means that T-TET to the carotenoid occurs in the subnanosecond time range. On the contrary, in dyad-2, a porphyrin triplet is clearly observed, the energy of which is transferred in 3.5 µs to the carotenoid molecule.

Fig. 1.

Molecular structure of the two dyads (1 and 2) and carotenoid (3).

Fig. 2.

Room temperature electronic absorption spectra of dyad-1 and dyad-2 in methyl-THF. Black line, dyad-1; red line, dyad-2; blue line, TTP (model porphyrin).

Fig. 3.

Transient absorption measurements of dyad 1 at 460 nm (A) and 540 nm (B) with excitation at 413 nm and 515 nm, respectively. Similar measurements for dyad 2 at 450 nm (C) and 540 nm (D) with excitation at 417 nm. Both dyads were dissolved in argon-saturated methyl-THF.

Fig. 4.

Evolution-associated difference spectra (EADS) after porphyrin excitation in dyad-1 (A) and dyad-2 (B) in methyl-THF.

Resonance Raman Analysis.

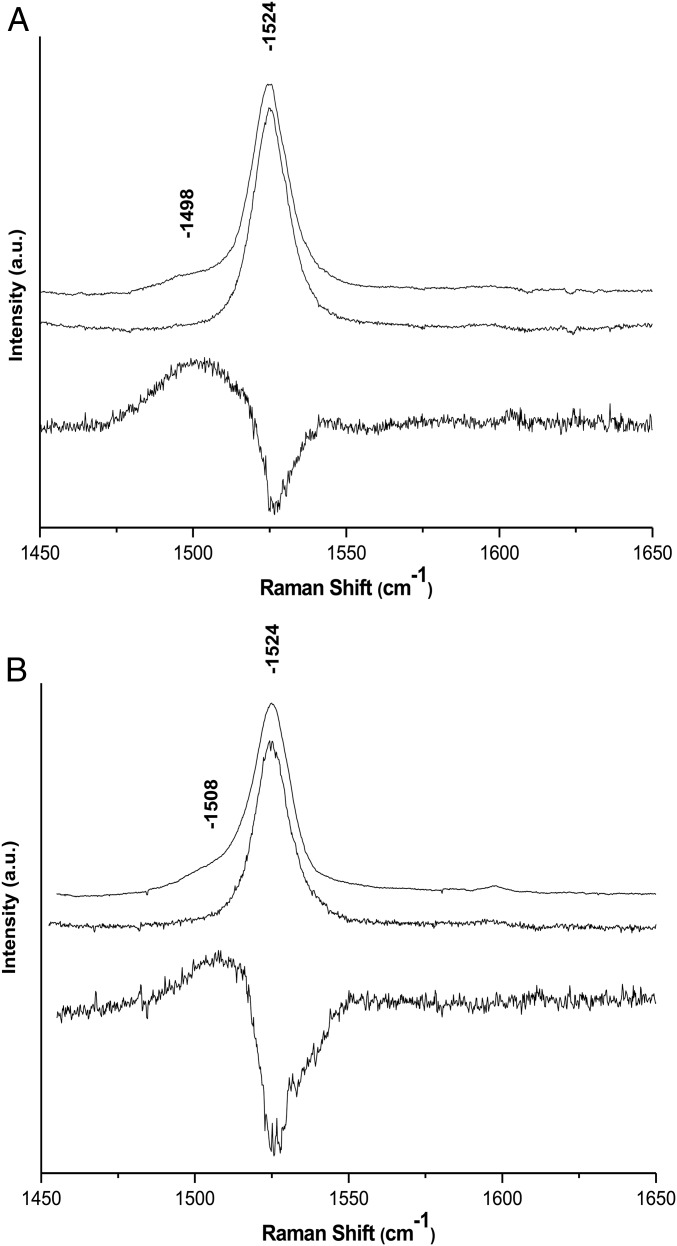
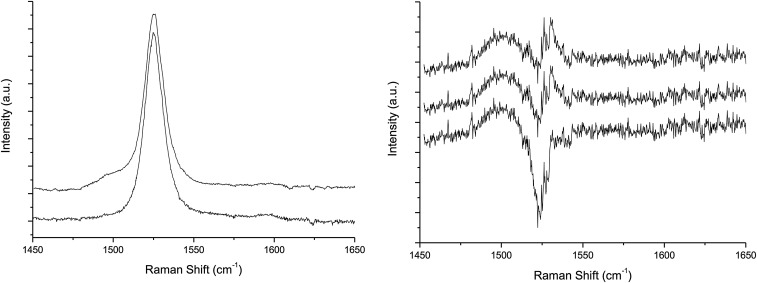
Resonance Raman spectra of both dyads were recorded in tetrahydrofuran (THF) using 514-nm excitation. As this excitation wavelength lies within the position of the S₀/S₂ electronic transition of the carotenoid in the dyads, it is expected to enhance the contribution of the carotenoid moiety only. Raman spectra of carotenoid molecules generally contain four groups of bands: (i) the ν₁, observed around 1,530 cm⁻¹, arises from the C=C stretching modes; (ii) the ν₂, at 1,160 cm⁻¹, arises from a combination of C–C stretching modes and in-plane C-bending modes; (iii) the ν₃ at about 1,000 cm⁻¹ from in-plane rocking vibrations of the methyl groups attached to the conjugated chain; and (iv) the weak ν₄ band, at about 950 cm⁻¹, from C–H out-of-plane wagging motions coupled with C=C torsional modes. The frequency of ν₁ and the structure of ν₂ are exquisitely sensitive to the carotenoid structure (14). Both of these bands indicate that the carotenoid in both dyads is all-trans, and, altogether, the resonance Raman of both dyads are nearly identical. These spectra do not change after dyad illumination at 77 K or at room temperature, indicating that no light-induced cis–trans isomerization occurs, even though the carotenoid triplet state is populated at the end of the excitation energy decay cascade. With increasing laser power, using an excitation at 514 nm, located close to the T₁/T_n transition of the carotene, a number of small bands appear in the spectrum. As discussed elsewhere (4), the observed power dependence of the appearance of these features is consistent with the progressive, dynamic accumulation of a transient state. The bands observed at higher laser intensity are characteristic of the resonance Raman spectra of carotenoid molecules in their triplet states (15–19). Fig. 5 displays the ν₁ region of the resonance Raman spectra of both dyads obtained with a 514.5-nm excitation at low and high power (5- and 25-µW laser power reaching the sample, respectively). For both dyads, increasing the intensity of the excitation results in the appearance of a signal in the ν₁ region that is downshifted relative to the position of the carotenoid ground-state ν₁ and typical of the ν₁ of carotenoid triplet state species. In dyad-2, this band occurs at 1,498 cm⁻¹, that is, downshifted by 26 cm⁻¹ compared with the frequency of the carotenoid ground state ν₁, whereas it occurs at 1,508 cm⁻¹ in dyad-1, downshifted by only 16 cm⁻¹ relative to the ground state ν₁. As discussed previously (4), the buildup of a “normal” triplet state of a carotenoid results in a 24 cm⁻¹ downshift of this band due to the change in electronic structure and concomitant change in bond order accompanying transition of one electron from the bonding highest occupied molecular orbital (HOMO) to an antibonding orbital. The carotenoid triplet state in dyad-2 is thus similar to that observed for isolated carotenoid molecules, whereas in dyad-1 a smaller downshift of this mode reflects a more specific perturbation due to interaction with the porphyrin. It is therefore essential to elucidate the nature of the underlying electronic and conformation changes responsible for changes in the resonance Raman shifts and T-TET rates.

Fig. 5.

Resonance Raman spectra (excitation wavelength, 514.5 nm; T, 77 K) of dyad-2 (A) and dyad-1 (B) in THF. Middle spectrum: low excitation intensity. Top spectrum: high excitation intensity. Bottom spectrum: computed difference between spectra obtained at high and low excitation intensity.

EPR analysis.

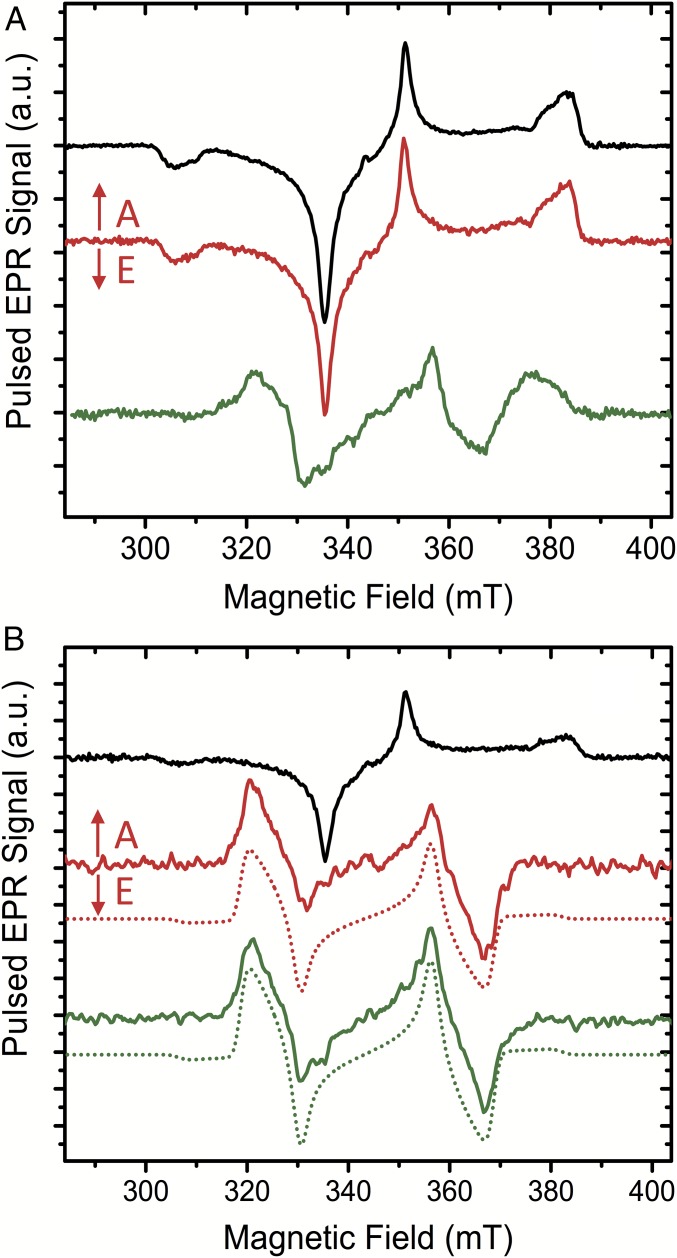
EPR measurements provide a more comprehensive insight into the triplet excited state of the carotenoid. As predicted by DFT (see below), the EPR spectroscopy confirms the absence of significant spin population in the porphyrin groups of the ortho and para dyads (Fig. 6). Therefore, it is clear that there is no detectable spin delocalization of the carotenoid triplet into the porphyrin. Specifically, Fig. 6A compares the time-resolved pulsed EPR spectra of H₂TPP, dyad-1, and dyad-2 in 2-MeTHF as recorded at 1 µs after light excitation [delay after flash (DAF)]. The spin-polarized EPR spectrum of ³H₂TPP is fully consistent with previously reported time-resolved spectra of ³H₂TPP in organic solvents, typical of the excited triplet states of porphyrins exhibiting the polarization pattern EAEAEA (A, absorption; E, emission) and zero-field splitting (ZFS) parameters |D| = 378 × 10⁻⁴ cm⁻¹, |E| = 79 × 10⁻⁴ cm⁻¹ (20, 21). Consistently, the spin-polarized triplet spectrum of the carotenoid/porphyrin mixture is also very similar to that of the ³H₂TPP, whereas the neat carotenoid solution shows no light-induced EPR signals.

Fig. 6.

Time-resolved pulsed EPR spectra of H₂TPP (black), the ortho- and para-carotenoporphyrin dyads [dyad-1 (green) and dyad-2 (red), respectively] in 2-MeTHF solution excited with 650-nm laser light at 77 K. (A) Delay after laser flash time (DAF) = 1 μs. (B) At longer DAF: H₂TPP at DAF = 102 µs, dyad-1 at DAF = 10 µs, and dyad-2 at DAF = 20 µs. DAF times for the dyads were chosen such that the carotenoid triplet signal at 366.2 mT is close to maximum (Fig. S1). Parameters were extracted from the simulation: zero-field splitting (ZFS) parameters of ³H₂TPP are |D| = 378 × 10⁻⁴ cm⁻¹, |E| = 79 × 10⁻⁴ cm⁻¹, and g ∼ g_e. The simulations (dotted lines) of the carotenoid triplets in the dyads used the following ZFS parameters: |D| = 355 × 10⁻⁴ cm⁻¹, |E| = 37 × 10⁻⁴ cm⁻¹, and g ∼ g_e. The signs of D and E cannot be determined from the spectra; thus, only the modulus is given. A, absorption; E, emission.

The early spectrum of the dyad-2 is essentially identical to the porphyrin triplet, whereas the spectrum of dyad-1 exhibits different resonances characteristic of the carotenoid triplet. The absence of any significant carotenoid triplet signals for dyad-2 at these early times (≤1 µs after laser flash) indicates that the T-TET energy transfer rate at cryogenic temperatures is substantially slower in dyad-2 than in dyad-1. At longer delay times after the laser flash, the spectra exhibit significant changes (Fig. 6B). For H₂TPP, there is only a loss of triplet signal intensity. For dyad-1, the carotenoid signal is essentially the same as for the DAF of 1 μs, but with increased intensity. The rise of the carotenoid triplet signal can be explained by differences in the decay rates of the triplet sublevels. Similar effects have been previously observed and discussed (22). For dyad-2, however, the spectrum is drastically changed, showing a new strong triplet signal with EAEAEA polarization pattern, similar to dyad-1. Parts of the changes are only obvious upon closer inspection, because the polarization pattern and the ZFS parameter |D| are not very different. The most pronounced differences, which are due to the different ZFS parameter |E|, are observed in the 320- to 335-mT region and the 355- to 370-mT region.

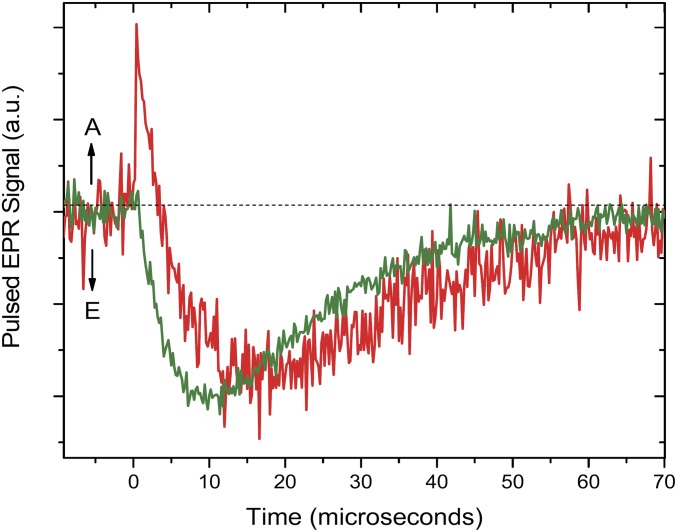
The reported EPR results (Fig. 6) are consistent with our optical kinetics analysis, finding faster triplet–triplet energy transfer for dyad-1 than for dyad-2. Fig. S1 shows the kinetics of the two dyads at a magnetic field (366.2 mT) where the emissive triplet signals of the carotenoid moiety dominate. The maximum carotenoid triplet signal is present around 10 and 20 µs for dyad-1 and dyad-2, respectively. The simulations of the carotenoid triplet in the two dyads used identical ZFS parameters |D| = 355 × 10⁻⁴ cm⁻¹ and |E| = 37 × 10⁻⁴ cm⁻¹. These ZFS parameters are in very good agreement with previous triplet EPR studies on similar carotenoids in organic solvents (23–25). In light of the good agreement between dyads as well as with the literature data, it seems unlikely that there is any significant (>5%) spin delocalization from the carotenoid triplet into the porphyrin of either of the two dyads.

Fig. S1.

Kinetics of the dyad-1 (green) and dyad-2 (red) in 2-MeTHF solution at a magnetic field of 366.2 mT where the emissive triplet signals of the carotenoid moiety are dominating. Temperature was 77 K. A, absorption; E, emission.

DFT Analysis.

DFT calculations were carried out to simulate the Raman spectra for both dyads in THF to better understand the origin of the resonance Raman signal of the carotenoid triplet state observed for dyad-1. Normal mode, bond order, and spin population analyses were also carried out to explain the spectral features in both dyads.

Geometries.

Systematic conformer searches were carried out to locate the global minimum energy structure for each dyad in THF solution. Fig. 7 shows the optimized geometries of the dyads obtained at the ωB97XD/6-31G(d) level of theory (Dataset S1). In dyad-1, the porphyrin moiety is stacked ∼3 Å above the aromatic ring of the carotenoid. By comparison, dyad-2 adopts an extended conformation where the porphyrin is considerably distant from the carotenoid. The stacked conformation of dyad-1 is supported by experimental ¹H NMR data where very large upfield shifts of about 3 ppm were observed for the carotenoid aryl ring, which is indicative of strong shielding by the porphyrin π system (26). For dyad-2, the carotenoid resonances have frequencies that are all within 0.2 ppm of the corresponding values in the carotenoid benzoate (26), indicating a negligible interaction between the porphyrin and carotenoid moieties. It is worth mentioning that the optimized geometries are sensitive to the choice of DFT method. Notably, only the ωB97XD and M06-2X methods led to a stacked conformation for the dyad-1, signifying the importance of dispersion corrections in modeling the structures of compounds of these types. As discussed in more detail below, the calculated Raman spectra also depend intimately on geometry, and this dictates our choice of DFT methods for simulating the Raman spectra.

Fig. 7.

Minimum energy geometries of dyad-1 (Top) and dyad-2 (Bottom) in the singlet ground electronic state S₀.

Raman spectra and normal modes.

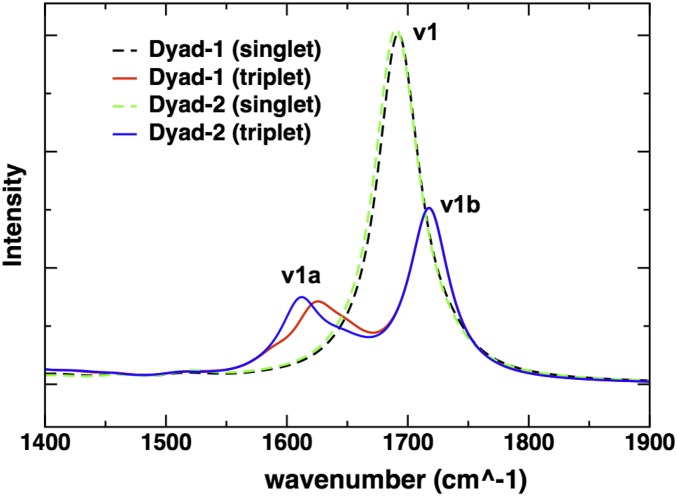
Fig. 8 shows the computed Raman spectra of the dyads in the ground singlet and excited triplet states. The spectra were calculated for fully optimized geometries of the dyads in the corresponding singlet or triplet states and reported with scaled frequencies, as described in Table 1. Different scaling factors were applied to the ν₁ and ν₁a bands because the systematic errors incurred by the DFT functional are different in the singlet ground and triplet excited-state vibrational frequencies (27, 28). Different scaling factors, however, do not affect the conclusion that a smaller Raman shift is observed in dyad-1 (Fig. 8). The ν₁ band of the C=C carotenoid stretch is split into two bands, ν₁a and ν₁b, when the dyad is in an excited state made up of a porphyrin ground state and carotenoid lowest triplet state [Por(S0)–Car(T1)]. Notably, the ν₁a band of dyad-2 is downshifted relative to the ν₁ band by 26 cm⁻¹ (Δν), whereas the corresponding Δν is only 16 cm⁻¹ for dyad-1. Calculations based on a model carotenoid-3 depicted in Fig. 1 shows a Δν that is very similar to that of dyad-2. The calculated downshift ΔΔν compares favorably with the experimental values (∼10 cm⁻¹ in Fig. 5). It is worth pointing out that when the calculations were carried out on geometries optimized using DFT methods without dispersion corrections (e.g., B3LYP), there were no discernible differences in the Raman spectra for dyad-1 and dyad-2. As noted before, dispersion-corrected DFT methods predict a folded conformation for dyad-1 where the porphyrin ring is stacked ∼3 Å above the aromatic ring of the carotenoid, thus providing further evidence for the link between the anomalous resonance Raman shift and the interchromophore interactions in dyad-1.

Fig. 8.

Calculated ωB97XD/6-31G(d) Raman spectra of the ground and triplet states of dyad-1 and dyad-2. The frequencies are unscaled, and the normal modes have been fitted to a Lorentzian (FWHM, 20 cm⁻¹).

Table 1.

Calculated C=C stretching frequencies (per centimeter), obtained at the DFT ωB97XD/6-31G(d) or ONIOM[ωB97XD/6-31G(d):AMBER] level of theory

Carotenoid	ν1*	ν1a†	Δν‡
Dyad-1 in THF	1,524 (1,524)§	1,510 (1,508)§	14 (16)§
Dyad-2 in THF	1,524 (1,524)§	1,498 (1,498)§	26 (26)§
Carotenoid in THF¶	1,529	1,503	25
Lutein in LHCII monomer	1,525 (1,526)§	1,502 (1,508)§	22 (18)§
Rhodopin glucoside in LH2	1,531 (1,517)§	1,502 (1,493)§	29 (24)§
Lutein in gas	1,527	1,496	31
Rhodopin glucoside in gas	1,528	1,498	30

^*Scaled by 0.9018.

^†Scaled by 0.9292.

^‡Δν = ν₁ − ν₁a.

^§Experimental frequencies in parentheses.

^¶Model carotenoid depicted in Fig. 1.

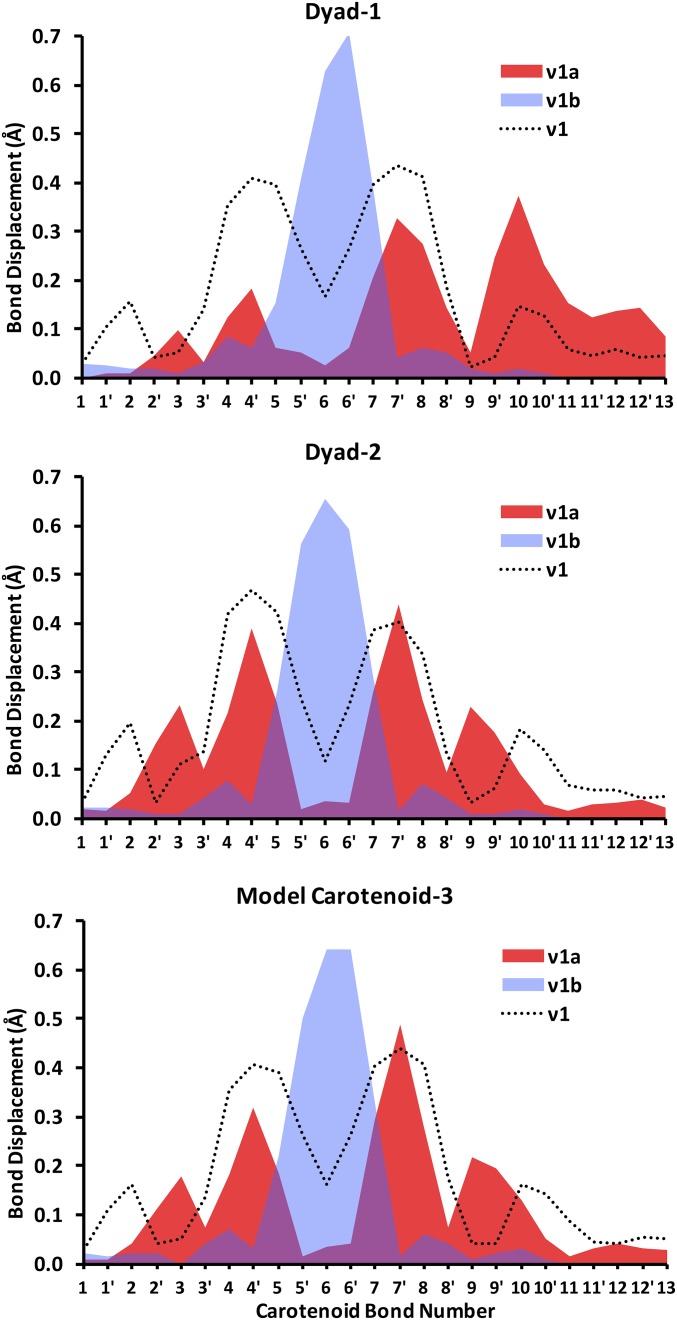
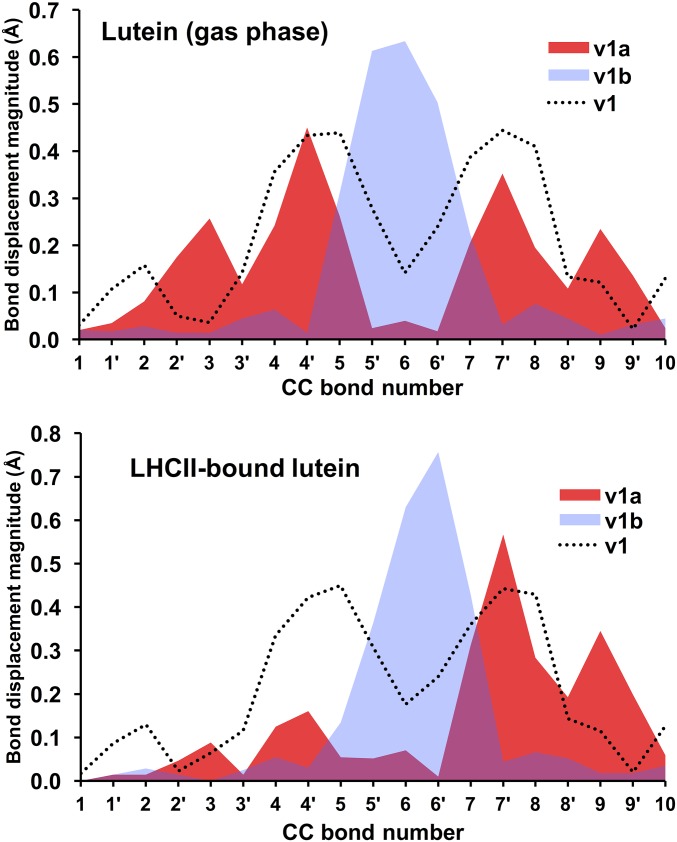
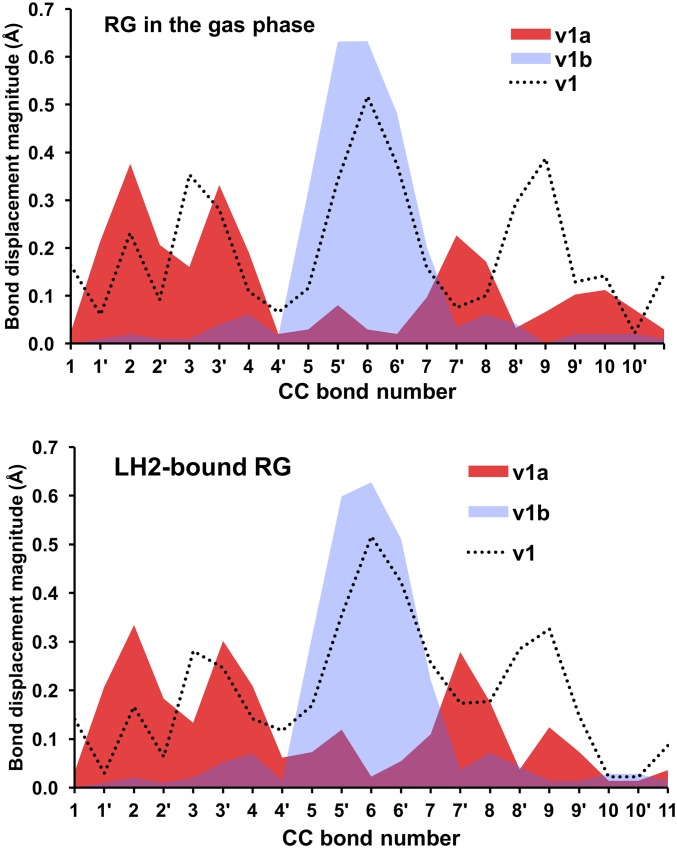
The DFT-predicted upshifted ν₁b band is interesting because it has not been previously reported in the experimental resonance Raman spectra of triplet carotenoids. As explained in more detail in Fig. S2, we find preliminary experimental evidence of that upshifted band, although quantification by spectral difference is difficult. Measurements with external standards would be necessary to unambiguously quantify the intensity of this band; however, because of the very high intensity of the carotenoid resonance Raman signal, these experiments are particularly difficult to perform. Our analysis of normal modes indicates that the ν₁b band corresponds to a relatively localized C=C stretch of the innermost double bonds 5′ and 6′, as depicted in Fig. 1. The ν₁a band at ∼1,505 cm⁻¹ is associated with the C=C stretch of the double bonds 2′ to 4′ and 7′ to 9′. Consistent with previous studies (15, 29, 30), our bond order analysis indicates that the innermost CC single bonds become double bonds, and the double bonds become single upon transition of the carotenoid to the triplet state. For example, following the bond numbering scheme of Fig. 1, the C=C bond 6 in the singlet state becomes a C–C bond in the triplet state, and the C–C bond 6′ becomes a double C=C bond in the triplet state. Normal mode simulations indicate that both ν₁a and ν₁b bands are composed of CC stretches of different groups of double bonds in the carotenoid. Fig. 9 illustrates the nature of these normal modes, represented in terms of the displacement of individual CC bonds associated with each normal mode. As shown, the dominant normal mode in the ν₁ band (in the singlet ground state) and corresponding ν₁a band (in the triplet state) are relatively delocalized across the carotenoid (with a node around CC bond 6), whereas the corresponding normal mode for the ν₁b band is localized around the inner 6, 6′ CC bonds. Furthermore, it is also clear that dyad-2 features a normal mode displacement profile that is almost identical to that of the model carotenoid-3. In contrast, the normal mode corresponding to ν₁a band in dyad-1 is significantly skewed toward the aromatic ring of the carotenoid (CC bonds 10–13) that is in close proximity to the porphyrin. The normal mode corresponding to ν₁b band is relatively similar for dyad-1, dyad-2, and carotenoid-3.

Fig. S2.

(Left) Spectra obtained at low- and high-laser power for dyad-1. (Right) Difference spectra obtained to take into account (i) that ν₁ from the ground state should be negative (Bottom), (ii) that ν₁ from the ground state should be cancelled to measure precisely the frequency of the ν_1a of the triplet (Middle), and (iii) letting some intensity for the presence of the ν_1b of the triplet state (Top).

Fig. 9.

Displacements of individual CC bonds (Å) for the individual normal modes associated with the Raman bands of dyad-1 and dyad-2 and carotenoid-3 shown in Fig. 1.

Analysis of bond order and spin population.

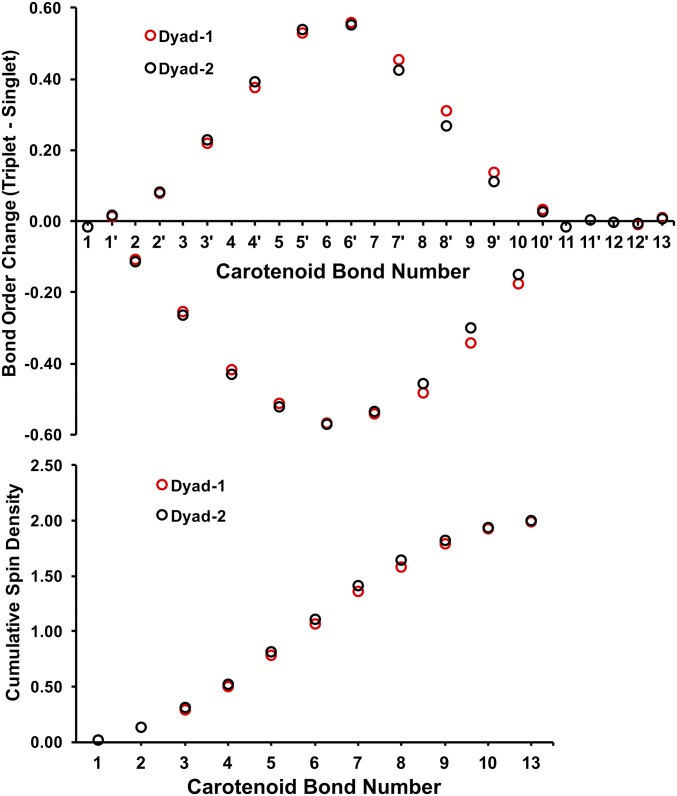
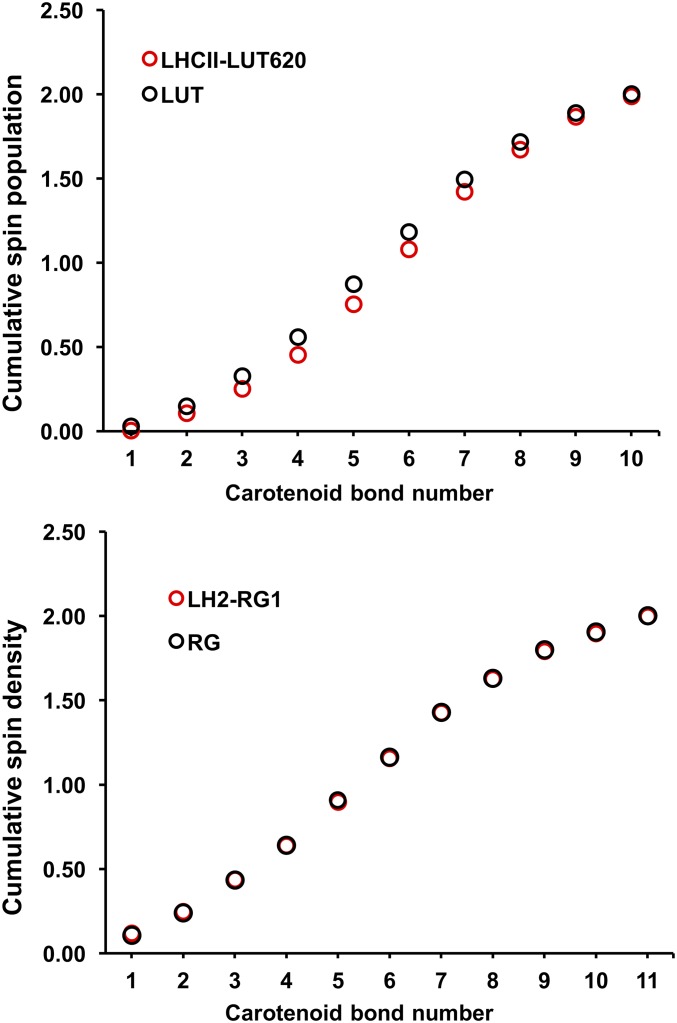
Our analysis of bond order changes along the carotenoid chain upon singlet to triplet transition indicates a significant gain in double-bond character of the CC bonds (7′ to 10′) in the triplet state for dyad-1 (Fig. S3). By comparison, the bond order changes in dyad-2 are almost identical to those of the unperturbed carotenoid-3.

Fig. S3.

Bond order changes of individual CC bonds (Top) and cumulative spin density in the carotenoid for dyad-1 and dyad-2 (Bottom). Bond numbers correspond to labels in Fig. 1 where the CC bond 13 is closest to the ester linkage.

As shown in Fig. 9, the ν₁a band has significant contributions from the CC stretches proximal to the porphyrin end of the carotenoid (relative to dyad-2 and model carotenoid-3), and the gain in double-bond character of these C–C bonds are therefore consistent with a ν₁a band that is less downshifted for dyad-1. By comparison, the ν₁b band remains unchanged in both dyads mainly because it involves only CC bonds 5, 5′, 6, 6′, and 7 (Fig. 9), whose bond orders are unaffected by the interchromophore interaction. These results also indicate that there must be a higher spin population close to the porphyrin end of the carotenoid in dyad-1 relative to that of dyad-2 (Fig. S3). Admittedly, the differences in bond order and spin population profiles are relatively small, which is consistent with the magnitude of the resonance Raman shift (10 cm⁻¹) that corresponds to ∼0.03 kcal⋅mol⁻¹ shift in vibrational energy.

It has been postulated in earlier work (4) that the origin of the anomalous resonance Raman signal is due to delocalization of the carotenoid triplet to the proximal porphyrin. Indeed, as extensively documented in the literature (see, for example, refs. 31–33), the C=C stretching frequency has consistently been reported to be sensitive to the conjugation length and configuration (cis/trans) of the carotenoid molecule, as well as to the polarizability of their environment, none of which is expected to change upon formation of the triplet (4, 34). This “triplet-sharing” mechanism would lead to a decreased electron population in the antibonding π* orbital of the carotenoid, thereby resulting in a smaller downshift of the ν₁a band. However, our DFT calculations indicate that the spin population in the porphyrin of dyad-1 when the molecule is in its carotenoid triplet state is very small (∼0.35%), although it is higher than in dyad-2 (0.06%). Consistent with these theoretical results, our EPR experiments find no measurable spin delocalization in these dyads (Discussion and Supporting Information). Interestingly, when the model carotenoid-3 is constrained to be in the same geometry as that in the triplet state of dyad-1, the calculations predict a very similar Δν, ∼15 cm⁻¹ (Table 1), to that of dyad-1. Because the spin population in the model carotenoid must be localized in the carotenoid, these control calculations strongly suggest that the observed Δν for dyad-1 is in fact due to perturbation of the carotenoid geometry as a result of stacking interactions with the porphyrin and not due to delocalization of the triplet state by triplet sharing with the porphyrin.

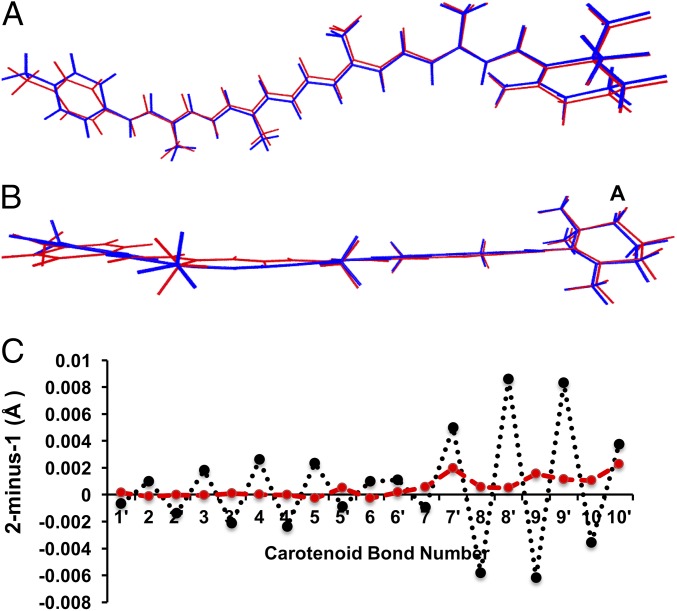
Our findings have raised the question of why the spectra of the triplet excited state are apparently sensitive to the geometric distortion caused by the stacking in the dyad-1, whereas the spectra of the ground state are relatively unaffected. To address that question, we compared the structures of the two dyads in their triplet and ground states. Stacking interactions between the porphyrin and the carotenoid moieties in dyad-1 (blue) results in noticeable changes in the CC bond lengths in the triplet state (Fig. 10). The 2-minus-1 CC bond length difference (black line in Fig. 10C) shows that the bonds 2, 3, 4, and 5 are shorter in dyad-1, whereas bonds 8, 9, and 10 are longer. These changes are entirely consistent with our analysis of changes in bond order parameters and spin populations induced by the ground-state singlet-to-excited triplet-state transition. By comparison, there is little geometrical distortion in the singlet ground state. The 2-minus-1 CC bond length difference in the ground-state geometries are significantly smaller (red line in Fig. 10C). Energy decomposition analysis (Table S1) indicates that the interchromophore interaction is enhanced in the Por(S0)–Car(T1) state [by ∼1.5 kcal⋅mol⁻¹ relative to the Por(S0)–Car(S0) state], primarily due to favorable electrostatic effects. As such, the anomalous resonance Raman shift results from geometrical perturbation of the carotenoid induced by enhanced interchromophore interactions in the triplet state.

Fig. 10.

Aligned structures of the carotenoid moiety of dyad-1 (blue) and dyad-2 (red) in their triplet state geometry. (A) Top view. (B) Side view. (C) Difference in C–C bond distance (2-minus-1) in the singlet (red) and triplet (black) states. The bond numbers correspond to labels in Fig. 1.

Table S1.

Energy decomposition analysis of the interchromophore interaction in dyad-1

Energy term	ΔE, kJ/mol
Dyad-1 in Por(S0)–Car(S0) state
Frozen density (FRZ)*	−70.8
Polarization (POL)†	−3.2
SCF delocalization (V-DEL)	−32.6
SCF basis set superposition error (V-BSSE)	28.1
SCF charge transfer (V-CT = V-DEL + V-BSSE)‡	−4.5
Dyad-1 in Por(S0)–Car(T1) state
Frozen density (FRZ)*	−75.1
Polarization (POL)†	−3.6
SCF delocalization (V-DEL)	−32.8
SCF basis set superposition error (V-BSSE)	27.2
SCF charge transfer (V-CT = V-DEL + V-BSSE)‡	−5.6

^*The frozen density term is a sum of the Coulomb (electrostatic) term and an exchange-correlation term in the Kohn–Sham theory.

^†The polarization energy is defined as the energy lowering due to intramolecular relaxation of each fragment’s absolutely localized molecular orbitals in the field of all other fragments in the system.

^‡The charge transfer term corresponds to the remaining portion of the total interaction energy and includes counterpoise correction.

QM/MM analysis of natural systems.

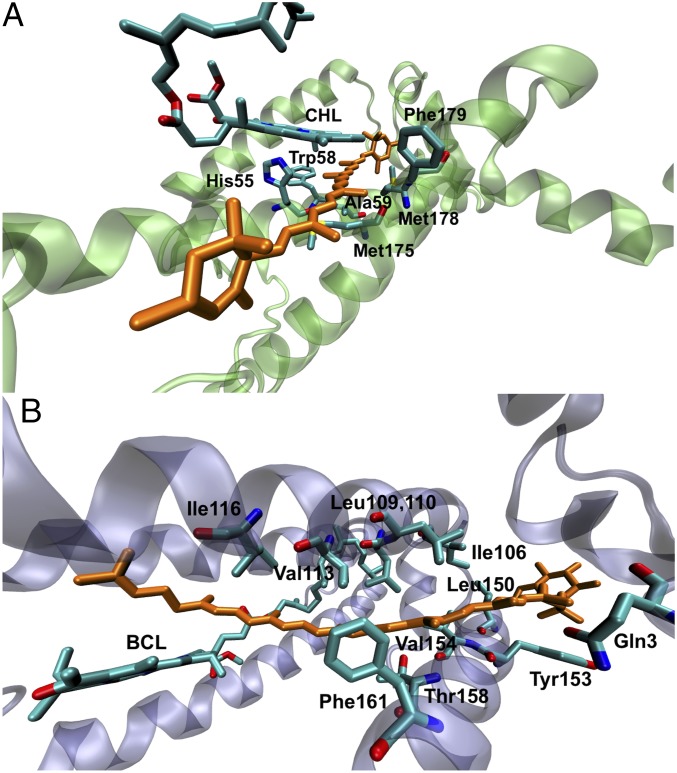
Table 1 compares the experimental ν₁ and ν₁a vibrational band positions in the resonance Raman spectra of ground and triplet states from protein-bound carotenoids. The observed Δν in dyad-1 and dyad-2 parallels lutein in LHCII and rhodopin glucoside in LH2, and we extend our theoretical investigation to these natural systems using hybrid QM/MM simulations. Here, we have used the two-layer ONIOM[ωB97XD/6-31G(d):AMBER] method where the “high layer” is modeled at the ωB97XD/6-31G(d) level of theory and the MM layer is simulated using the AMBER force field. Fig. 11 illustrates different natural environments surrounding known carotenoids/chlorophyll dyads. There are multiple (bacterio)chlorophyll molecules in the vicinity of the carotenoid molecules. In the QM/MM model, we consider in the QM layer only the (bacterio)chlorophyll that is closest to the carotenoid backbone, including all amino acid residues that are within a distance of 3.5 Å.

Fig. 11.

(A) Structural model of lutein 2 (orange) in LHCII monomer. (B) Structural model of rhodopin glucoside (orange) in LH2. The proximal (bacterio)chlorophyll, and amino acid residues that are within 3.5 Å of lutein are shown. These residues make up the “QM” layer in the QM/MM simulations.

Our theoretical simulations correctly predict the qualitative features of the Raman spectra of protein-bound lutein and rhodopsin glucoside in the ground and triplet states. Notably, lutein in LHCII is predicted to have a ν₁a band that is ∼9 cm⁻¹ upshifted relative to lutein in the gas phase, whereas rhodopsin glucoside in LH2 and in the gas phase display a Δν shift that are essentially identical (Table 1). Repeating the normal mode and spin population analyses on LHCII and LH2 reveal a direct parallel with dyad-1 and -2 (Figs. S4–S6). In particular, the normal-mode displacement profiles indicate changes to the ν₁a normal mode between LHCII-bound lutein compared with the gas phase, whereas there are no noticeable changes for rhodopsin glucoside in the LH2 protein or gas phase. This result is not so surprising because the closest B(Chl) lies at the tail of rhodopsin glucoside, whereas in LHCII lutein is in direct van der Waals contact (3.5 Å) with a chlorophyll (Fig. 11).

Fig. S4.

Displacements of individual CC bonds (in angstroms) for the individual normal modes associated with the Raman bands of lutein in LHCII and in the gas phase.

Fig. S6.

Cumulative spin density (Top) lutein in LHCII and in the gas phase. (Bottom) Rhodopsin glucoside in LH2 and in the gas phase.

Fig. S5.

Displacements of individual CC bonds (in angstroms) for the individual normal modes associated with the Raman bands of rhodopsin glucoside in LH2 and in the gas phase.

We were further able to reproduce the ν₁a frequency when lutein is constrained to the same geometry as that in the triplet state of LHCII. This lends additional support to our finding that interchromophore interactions in tightly coupled systems are accompanied by a geometrical perturbation of the triplet state geometry that is the origin of the resonance Raman spectroscopic marker. These results are also consistent with recent EPR measurements (7, 35), which indicate no detectable spin population in the porphyrin for a related natural system having very fast T-TET.

Correlation with T-TET rates.

The electronic coupling between the two triplet states is the major factor that determines the rate of triplet energy transfer. We have calculated the T-TET coupling for dyad-1 and dyad-2 using the fragment excitation difference (FED) scheme (36). Consistent with the experimentally observed T-TET rates, the coupling is approximately three orders of magnitude higher in dyad-1 (∼32 cm⁻¹) compared with dyad-2 (0.024 cm⁻¹) due to more significant overlap of donor and acceptor states in the stacked conformation. The coupling calculations were carried out on Por(S1)–Car(S0) geometries [which we approximate using the Por(S0)–Car(S0) geometry] assuming that there is not sufficient time for geometrical relaxation into the Por(T1)–Car(S0) conformation before T-TET (intersystem crossing is the rate-limiting step for dyad-1). In any case, repeating the calculations on the Por(T1)–Car(S0) and Por(S0)–Car(T1) conformations results in a diminished T–T coupling to ∼3 cm⁻¹ for dyad-1, whereas the coupling for dyad-2 remains largely unchanged. The reduced coupling at these conformations for dyad-1 is due to the tilting of the carotenoid relative to the porphyrin, which results in poorer wavefunction overlap between the chromophores. Presumably, the reduced T–T coupling at the Por(S0)–Car(T1) conformation also partly accounts for the localization of the triplet on the carotenoid.

Conclusions

A spectroscopic marker, the anomalous resonance Raman shift or Δν, for interchromophore interactions conducive to fast triplet–triplet energy transfer has been described. Our combined experimental and theoretical studies of two isomeric carotenoid–porphyrin molecular dyads indicate that its origin is a perturbation of the carotenoid geometry when the chromophores are in van der Waals contact, which is essential for the orbital overlap and strong coupling necessary for very fast T-TET. Hybrid QM/MM simulations confirm that this is also the case for carotenoid–chlorophyll interactions in natural photosynthetic pigment–protein complexes (LHCII and LH2). In detail, the DFT calculations indicate that, once dyad-1 is in the Por(S0)–Car(T1) [or LHCII is in the Chl(S0)Car(T1)] electronic state, that is, after T-TET, the carotenoid geometry changes slightly from that of the ground state giving rise to the observed resonance Raman signal; a slight change in tilt of the triplet carotenoid relative to the tetrapyrrole reduces the electronic coupling, which ensures that the triplet state is essentially localized on the carotenoid with no spin transfer component in either dyad. In natural systems, suppressing spin transfer in Chl(S0)–Car(T1) electronic states lowers the probability of deleterious chemical reactions that could arise from charge transfer states. Therefore, the observed anomalous Raman shift reports that the system conformational dynamics and electronic coupling necessary for fast T-TET kinetics to prevent singlet oxygen sensitization and spin delocalization are in place. In reengineered photosynthesis, this signal can be used as a marker for an adequate photoprotective package in antenna protein designs in which LH-type antenna will be repurposed for use in oxygen-evolving photosynthesis (8).

Methods

Experimental Procedures.

The para- and ortho-carotenoporphyrin dyads (see structures in Fig. 1) were synthesized as described in refs. 26 and 37. Steady-state absorption spectra were measured on a Shimadzu UV-3101PC spectrometer. The nanosecond–millisecond transient absorption measurements were performed using a ∼5-ns pulse from an optical parametric oscillator driven by the third harmonic of a Nd:YAG laser (Ekspla NT342B) with a repetition rate of 10 Hz, and a spectrometer (Proteus) from Ultrafast Systems. The instrument response function was 4.8 ns. Global analysis of the transient absorption data were carried out using locally written software (ASUFIT) developed in a MATLAB environment (MathWorks). Evolution-associated difference spectra (EADS) were obtained by global analysis of the transient absorption data using a kinetic model consisting of sequentially interconverting species, for example, 1→2→3→…. The arrows indicate successive monoexponential decays with increasing time constants, which can be regarded as the lifetimes of each species. Associated with each species are a lifetime and a difference spectrum. Each EADS corresponds in general to a mixture of states and does not portray the spectrum of a pure state or species. This procedure enables us to visualize clearly the evolution of the transient states of the system. The global analysis procedures described here have been extensively reviewed (38). Random errors associated with the reported lifetimes obtained from transient absorption measurements were typically ≤5%.

Resonance Raman spectra were obtained using a 24-W Sabre laser (Coherent) and were recorded at 77 K with 90° signal collection using a two-stage monochromator (U1000; Jobin Yvon), equipped with a front-illuminated, deep-depleted CCD detector (Jobin Yvon). A low sample temperature was ensured using a helium flow cryostat (Air Liquide). Resonance Raman spectra of both dyads were measured at different excitation wavelengths (488, 496.5, 501, 514, and 528 nm) with the whole spectral range recorded for each excitation energy. As reported in ref. 4, the most intense signal from the triplet was obtained at full resonance with the T₁/T_n absorption transition at 514 nm.

For EPR experiments, the ortho- and para-carotenoporphyrin dyads were dissolved in 2-MeTHF (Sigma-Aldrich) under anaerobic conditions in a N₂ dry box. Control samples containing the corresponding porphyrin, the carotenoid, and a mixture of porphyrin and carotenoid were also prepared. The concentrations of the solutions were in the 2–3 mM range. The solutions were filled into EPR quartz tubes, sealed under N₂ atmosphere, and then frozen quickly in liquid nitrogen. The work was performed under dimmed light.

Continuous wave (cw) and pulsed X-band (9–10 GHz) EPR experiments were carried out with a Bruker ELEXSYS E580 EPR spectrometer (Bruker Biospin), equipped with a Flexline dielectric ring resonator (Bruker ER 4118X-MD5-W1) and a helium gas-flow cryostat (CF935; Oxford Instruments). The temperature controller was an ITC (Oxford Instruments). Light excitation was done in situ with 7-ns laser pulses (Nd:YAG Laser INDI, Newport, operating at 20 Hz, pumping an OPO, basiScan, GWU) through an optical fiber. Excitation wavelengths were 650 and 515 nm. Typical incident light intensities at the sample were 80 mW (4 mJ per pulse per cm²). Measurements were performed at 77 K, matching the temperature used for the Raman experiments. Selected experiments at 20 K gave similar results as the 77 K experiments. Data processing was done using Xepr (Bruker BioSpin) and Matlab 7.11.2 (MathWorks) software. The magnetic parameters were obtained from theoretical simulation of the EPR spectra. These simulations were performed using the EasySpin software package (version 5.0.20) (39).

Theoretical Methods.

All electronic structure calculations were performed using the Gaussian 09 (revision D01) (40) and Q-CHEM (version 4.0.1) (41) programs. The ground-state singlet and excited-state triplet geometries of both dyads were optimized using ωB97XD (42) and M06-2X (43) DFT methods in conjunction with the 6-31G(d) basis set (Dataset S1). Solvent effects (THF) were simulated using the SMD solvation model (44). The Raman spectra and relative intensities of Raman peaks were simulated at the same levels of theory on corresponding optimized geometries. This approach was successfully applied in previous studies to model substituent effects on the Raman spectra of carotenoid molecules (45, 46). The ultrafine grid keyword was specified for all DFT calculations and the Raman and Wiberg bond order calculations (47) were carried out in Gaussian 09. The bond displacement profiles (Fig. 9) were obtained by comparing the carotenoid C–C bond distances in the equilibrium geometry and displaced geometry along a specific normal mode. The FED scheme (36, 48) was used to quantify the triplet–triplet electronic couplings, and these were evaluated at the CIS/6-31G(d) level of theory using the Q-CHEM program. In the FED calculation, the boundary between donor and acceptor domains of each dyad was defined to be at the ester oxygen–methylene carbon bond. Analysis of the contributions to the interchromphore interaction was carried out using the energy decomposition scheme (49) as implemented in Q-CHEM. The crystal structures of the light-harvesting LHCII complex from Spinacia oleracea (PDB ID code 1RWT) (50) and the LH2 complex from Rbl. Acidophilus (PDB ID code 1KZU) (51) were used as starting structures for the two-layer ONIOM[ωB97XD/6-31G(d):AMBER] simulations (52). The “high” layer is composed of a lutein (or rhodopsin glucoside) and the nearest (bacterio)chlorophyll, as well as all amino acid residues that are within 3.5 Å of lutein (or rhodopsin glucoside). The rest of the system constitutes the “low” layer. The AmberTools14 package (53) was used to add missing hydrogen atoms and the TAO package (54) was used to set up the ONIOM input files. The AMBER parameters for the cofactors (Chl and BChl) were obtained from Vasil’ev and Bruce (55), and the General Amber Force Field (GAFF) (56) was used to simulate the lutein and rhodopsin glucoside molecules.

Supporting Information.

Cartesian coordinates of optimized geometries of dyads, bond orders, normal modes, spin population analyses of the natural systems, and kinetic analysis of the EPR experiments on dyad-1 and dyad-2 are presented in Supporting Information.

SI EPR Analysis

At the magnetic field of 366.2 mT, the emissive triplet signals of the carotenoid moiety are dominating, resulting in negative signals. A positive absorption at this field corresponds to presence of the porphyrin triplet. Thus, the fast initial positive rise in dyad-2 (within our time resolution) can be attributed to porphyrin triplet absorption, followed by appearance of the carotenoid triplet signal. For dyad-1, the initial signal after the laser flash is negative with very small intensity that increases with time. These results are in agreement with the optical kinetics, which found faster triplet–triplet energy transfer for dyad-1 than dyad-2. The (slower than optical room temperature data) initial rises of the negative carotenoid triplet signals (negative amplitude) can be explained by difference in the decay rates of the different triplet sublevel. Similar effects have been observed and previously discussed (22). If, as a consequence of T-TET, all carotenoid triplet sublevels are populated equally or almost equally, the intensity of the triplet EPR signal will be zero or very small. The signal will be built up in time due to the difference in the sublevel decay rates.

The simulations of the carotenoid triplet in the two dyads used identical ZFS parameters, |D| = 355 × 10⁻⁴ cm⁻¹ and |E| = 37 × 10⁻⁴ cm⁻¹. These ZFS parameters are in very good agreement with previous triplet EPR studies on similar carotenoids in organic solvents (23–25). Considering the good agreement between dyad-1 and -2 as well as the literature data, we can safely reject delocalization of the triplet excited state over both the carotenoid and the porphyrin moieties.

SI Preliminary Experimental Evidence for an Upshifted ν_1b Band in the Carotenoid Triplet State

DFT calculations predict an upshifted ν_1b band in the Raman spectra of the carotenoid triplet state, which has not yet been experimentally reported. However, obtaining a pure resonance Raman of a carotenoid in its triplet state is not possible, as the intense signal of carotenoid ground state contributes at the excitations used for probing carotenoid triplet state. As a result, populating carotenoid triplet state induces both the appearance of the signal of this species, together with the bleaching of the carotenoid ground-state signal, including that of the intense ν₁, which is located close to the ν_1b band. The appearance of the ν_1b band will thus depend on how the difference spectra are computed. Proper normalization of resonance Raman difference would ideally require the presence of external standards. However, the very high-resonance cross-section of the resonance Raman of carotenoid (10⁷, actually close to the highest observed) makes it very difficult to introduce in the sample high concentrations of standards that would allow (i) to observe the Raman signal of these standards and (ii) not to perturb the samples under measurement.

We are thus left with artificial normalization of the spectra before calculating differences. Of course, it is easy to cancel the ν₁ from the ground state, so to observe only the shifted ν_1a from the triplet state, and measure its frequency. However, upon buildup of the triplet state, part of the ground-state signal should be depleted, which would result in the S-shaped signal with a positive ν_1a from the triplet and a negative ν₁ from the ground state. Performing such a difference leads to inaccurate frequency measurement of the ν_1a of the triplet state.

It is possible to perform a difference leading to evidence the ν_1a and ν_1b from the triplet state (see below). However, it is emphasized that this depends on the way we normalize the spectra, and more elaborate measurements are needed to unambiguously confirm the presence of the ν_1b of the triplet state.

SI DFT Analysis

Fig. S3 shows the analysis of bond order changes along the carotenoid chain induced by singlet- to triplet-state transition. Defining the change in bond order as the triplet-minus-singlet bond orders, a positive change indicates an increase in double-bond character upon excitation to the triplet state. Following the numbering of double bonds as in Fig. 1, there is a gradual increase in bond order of the C–C bonds toward the center of the carotenoid. Additionally, the C=C bonds (8–10) in dyad-1 exhibit a more significant reduction of double-bond character compared with those of dyad-2. This effect is also mirrored in terms of a more significant gain in double-bond character of the CC bonds in the triplet state (7′ to 10′). In contrast, bond order changes in dyad-2 are almost identical to those of the unperturbed carotenoid-3.