Mechanochemical feedback underlies coexistence of qualitatively distinct cell polarity patterns within diverse cell populations

Significance

Directional cell migration accompanied by cell polarization is key to progression of aggressive cancers, such as melanoma. Cells can display diverse dynamical patterns, with no single mechanism proposed to account for all of them. We show that a simple model predicts the simultaneous presence of random, oscillatory, and persistent dynamic polarization and migration patterns. This mechanism postulates spatially distributed, mechanochemical feedback, coupling the dynamically changing extracellular matrix–cell contacts to the activation of signaling downstream of the Rho-family small GTPases. We validate this mechanism experimentally and use it to explain the transition from a more benign to a more aggressive cell behavior in melanoma progression. This mechanistic analysis framework is general and can be used for diverse stochastic cell migration behaviors in cancer.

Abstract

Cell polarization and directional cell migration can display random, persistent, and oscillatory dynamic patterns. However, it is not clear whether these polarity patterns can be explained by the same underlying regulatory mechanism. Here, we show that random, persistent, and oscillatory migration accompanied by polarization can simultaneously occur in populations of melanoma cells derived from tumors with different degrees of aggressiveness. We demonstrate that all of these patterns and the probabilities of their occurrence are quantitatively accounted for by a simple mechanism involving a spatially distributed, mechanochemical feedback coupling the dynamically changing extracellular matrix (ECM)–cell contacts to the activation of signaling downstream of the Rho-family small GTPases. This mechanism is supported by a predictive mathematical model and extensive experimental validation, and can explain previously reported results for diverse cell types. In melanoma, this mechanism also accounts for the effects of genetic and environmental perturbations, including mutations linked to invasive cell spread. The resulting mechanistic understanding of cell polarity quantitatively captures the relationship between population variability and phenotypic plasticity, with the potential to account for a wide variety of cell migration states in diverse pathological and physiological conditions.

Cell migration involves complex interactions with the extracellular matrix (ECM) (1–4). Beyond providing cells with the substratum for adhesion and traction during the migration process, the ECM can activate signaling networks through biochemical engagement of the integrin complexes within focal adhesions (FAs) (5–7). The signaling pathways activated by integrins can impinge on the Rho-family small GTPases that are thought to be central regulators of cell polarity and migration (8–10). Varying ECM density can differentially control activation of two proteins belonging to this family, Rac1 and RhoA, which frequently display antagonistic interactions (11, 12). Activation of Rac1 and RhoA can in turn regulate the mechanical properties of the cell, thus influencing how the cell interfaces with complex local organization of ECM fibers (13–15). The intricate nature of this ECM–Rac1–RhoA feedback interaction and the wide diversity of topographic ECM structures have made comprehensive analysis of the resulting cell migration behavior very challenging.

In vivo cell migration can display diverse dynamic patterns. It can vary from random exploratory migration characterized by poor FA formation, frequent pseudopod extension, and a lack of stress fibers in dense 3D ECM (so-called 3D cell migration) to highly persistent migration along single ECM fibers in sparse 3D ECM (essentially 1D cell migration) (16–18). Recently, oscillatory migration patterns have also been observed following perturbation of cytoskeletal components, with cells retracing their positions over multiple cycles (19–21). Local alignment of ECM fibers can further enhance the persistence and speed of directional cell migration (22). Despite the clear indications that ECM organization is instrumental in eliciting these cell locomotion patterns, we still lack a complete understanding of the underlying molecular mechanisms. In particular, it is not clear whether diverse modes of cell migration are all parts of the same spectrum, and whether this spectrum can be affected by intrinsic/extrinsic changes accompanying a transition to more aggressive and invasive cell locomotion in vivo.

Genetic alterations can lead to profound changes in both cell–matrix interaction and the propensity for extensive cell migration. One of the most striking examples of such a dramatic alteration in cell behavior is the onset of invasive cell migration within the context of many aggressive cancers (23–25). For instance, the transition to invasive, vertical growth in melanoma is accompanied by a range of mutations, some of which can directly drive invasion (e.g., mutations in integrins) or alter ECM (e.g., mutations affecting matrix metalloproteinases) (26–29). The role of other mutations is less clear; for example, although the loss of phosphatase and tensin homolog (PTEN) is frequently correlated with enhanced melanoma invasiveness (30, 31), the exact nature of how the corresponding change in the signaling network activity might affect invasive cell migration is not known.

In this study, we analyzed how the genetic cell makeup and the organization of ECM could jointly control the patterns of cell migration. We used an experimental model of highly controlled graded changes in the ECM topography in the context of metastatic or noninvasive melanoma cell lines to show that these cells can display a range of well-defined migration patterns, related to the spatial organization of intracellular PI3K signaling. In particular, an increase in the anisotropic nature of the ECM organization converted essentially random cell polarity and migration to oscillatory and then to persistent patterns, as cell migration persistence correspondingly increased. Strikingly, a simple mechanism relying on mechanochemical feedback coupling the dynamically changing ECM–cell contacts to the activation of signaling downstream of Rac1 and RhoA could explain this response and outcomes of additional perturbations of the underlying signaling network. In particular, the model predicted and experiments confirmed that the loss of PTEN, which frequently accompanies transition to more aggressive, invasive cell migration in vivo, results in a dramatic increase in the spatial stabilization of intracellular signaling and persistence of cell migration. We argue that the mechanisms identified in this analysis elucidate the long-observed complex dependencies of cell migration on ECM organization, and can further inform our understanding of invasive cell migration.

Results

Diverse Dynamical Cell Polarity Patterns Can Coexist, with Their Relative Occurrence Modulated by Topographic Cues.

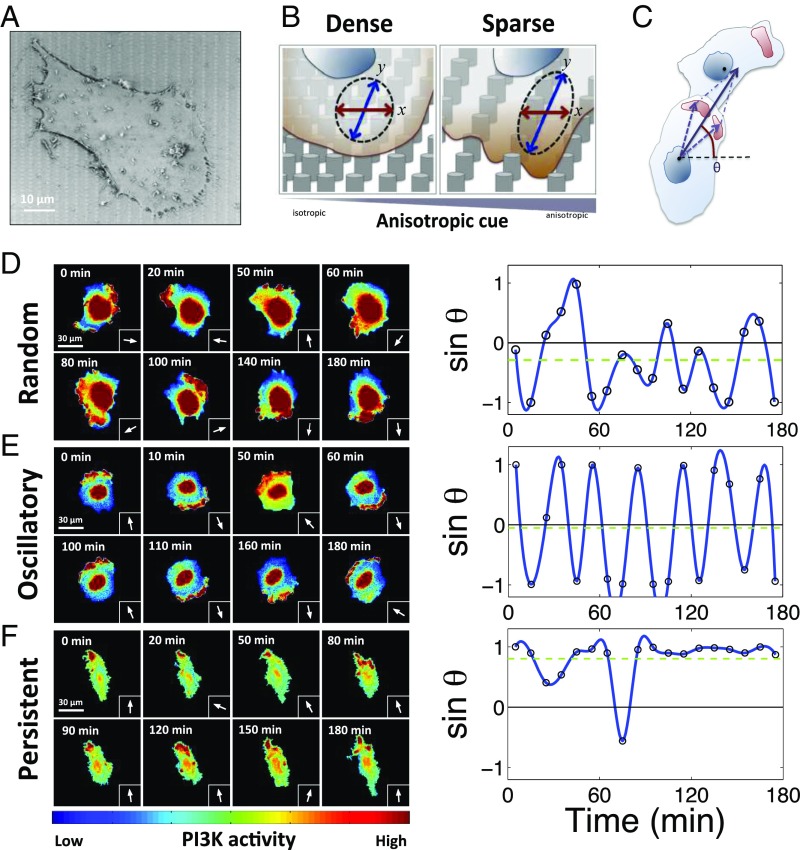
Cell migration can display diverse patterns, varying in degree of directional persistence (32). The modes of cell locomotion strongly depend on organization and density of the ECM (2, 33, 34), but it is not clear whether a gradual change in these ECM features precipitates a commensurately graded and predictable change in the cell migration persistence. To explore this in quantifiable detail, we investigated polarization of cell signaling and patterns of cell migration on surfaces with graded texture. In particular, we varied the density of the nanoscale posts protruding from the cell adhesion surfaces (“cell adhesion substrata”), thus creating a complex extracellular environment presenting cells with nanotopographically complex interface analogous to ECM structure. On such surfaces, if cells are capable of enveloping individual posts, the extent of the overall cell–substratum contact can be much higher than would occur on flat surfaces, modulating the chemical and mechanical input that cells can receive from the ECM-coated surfaces (35). The post distribution varied from essentially isotropic to highly anisotropic, gradually increasing along one of the orthogonal axes (x axis). The density along a second orthogonal axis (y axis) was constant (Fig. 1 A and B) (for specific dimensions of the surface, see Materials and Methods) (35). We used this system of x–y coordinates in further analysis.

Fig. 1.

A melanoma cell population displays three coexistent polarity patterns whose relative abundance is modulated by the topography of the cell adhesion substratum. (A) A scanning electron microscopy image of a 1205Lu (aggressive melanoma cell line) cell cultured on fibronectin (FN)-precoated post arrays. (B) Schematic of a single 1205Lu cell sensing anisotropic topographic cues from the nanofabricated graded density post array substrata. In the dense post region (Left), the nanopost density is equal in x and y directions, whereas, in the sparse post region, where penetration between posts of cells results in greater contact with the substratum adhesion, the substratum anisotropy is the greatest due to a much larger spacing in the x but not y direction. (C) The angle of a signaling vector (θ) of an individual cell is defined as the direction from its centroid to the sum of centroids of its hot spots of PI3K activity with respect to the x direction. Details are described in Materials and Methods. (D–F) Three dynamic patterns of cell polarity seen in sequential images of PI3K activation and indicated by the signaling vector defined in C in three representative cells. Representative pseudocolor images of elevated spatial PI3K activation (color scale at the Bottom) (left panels) and sinθ(t) at each time point (arrows) (right panels), with the indicated time resolution; (D) the random polarity pattern, (E) the oscillatory polarity pattern, and (F) the persistent polarity pattern.

We used these cell adhesion substrata to culture an aggressive melanoma cell line, 1205Lu, constitutively expressing GFP- or RFP-tagged pleckstrin homology domain of Akt (Akt-PH), a commonly used readout of the activity of PI3K. This kinase has been extensively implicated in regulating cell migration and is usually localized to the front of a motile cell. We found that the spatial distribution of PI3K signaling, quantified using the “signaling vector” described in Fig. 1C, displayed three distinct dynamic spatial intracellular localization patterns (Fig. 1 D–F). The first was characterized by apparently random (RD) localization of PI3K activity “hot spots” over the course of 3 h around the whole cell periphery (Fig. 1D and Movie S1). The second PI3K activity pattern was oscillatory (OS) (Fig. 1E and Movie S2), with the PI3K signaling persistently alternating between the two sides of the cell along the y axis of the pattern, with a ∼30-min period. Finally, the remaining subset of cells displayed a signaling pattern that was characterized by persistent localization (PS) of the PI3K signaling activity to one side of the cell only, along the direction of the y axis (Fig. 1F and Movie S3). These results suggested that cell interaction within topographically complex cell–ECM interfaces can lead to diverse PI3K signaling profiles within the same cell population.

Given the graded density of the topography features and concomitant substratum anisotropy, we explored whether and how the three signaling patterns depend on the local substratum topography. To facilitate this analysis, we subdivided the substratum into three zones of distinct post densities, from isotropic (the densest post array, zone 1) to most anisotropic (the sparsest post array, zone 3), and a zone of intermediate anisotropy (and post density, zone 2) (Fig. 1B and SI Appendix, Fig. S1A). We found that, although in all three zones, cells displayed all three signaling patterns, the frequency of the cells displaying the RD pattern decreased and the frequency of the cells with PS pattern increased with decreasing post density (SI Appendix, Fig. S1A). The fraction of cells exhibiting the OS signaling dynamics remained approximately constant in all zones. Furthermore, when we used FA localization as a measure of cell polarity (SI Appendix, Fig. S2), we found that the fraction of cells polarized along the y axis (in one or both directions) was approximately equal to the sum of the fractions of cells with PS and OS signaling patterns in each of the three substratum topography zones (SI Appendix, Fig. S1A). Cells with PS and OS signaling patterns also had a lower degree of spatial randomness of PI3K signaling and had more elongated shapes vs. the cells with the RD pattern (SI Appendix, Fig. S1 B–D). Furthermore, we found a decrease in the average spatial randomness and increase in the average cell elongation as the post density decreased, consistent with a concurrently higher occurrence of cells with the PS patterns (SI Appendix, Fig. S1 A–D). Interestingly, despite being polarized, the cells with the OS patterns displayed very low migratory persistence, similar to that of the cells with the RD signaling patterns (SI Appendix, Figs. S1 E and F and S3). On the other hand, the migratory persistence of cells with the PS signaling patterns was substantially greater than cells having the other two PI3K signaling patterns (SI Appendix, Figs. S1 E and F and S3). These results were consistent with the hypothesis that the spatially localized PI3K activity is indeed enriched at the fronts of migrating cells. In particular, the limited migration of the cells with the OS signaling patterns is a reflection of continuous alteration in the direction of the front–rear polarity, with cells thus remaining polarized along the y axis, but not persistently moving along it.

A Single Mechanism Can Quantitatively Account for Different Cell Polarity and Migration Patterns.

What might account for distinct spatial PI3K signaling patterns and different migratory and polarization characteristics of 1205Lu cells on nanopatterned surfaces? ECM components, including fibronectin (FN), can stimulate PI3K signaling (36, 37). An increasing engagement of ECM can also lead to stimulation of the members of the Rho family of small GTPases, particularly RhoA (38, 39). We indeed found that increasing FN surface density stimulated, in a dose-dependent fashion, both PI3K activity (as evaluated by phosphorylation of its substrate, Akt) and RhoA activity [as evaluated by the activity of a RhoA-dependent kinase, ROCK, and the downstream phosphorylation of myosin light chain (MLC)] (SI Appendix, Fig. S4). Furthermore, pharmacological inhibition of PI3K led to a decrease in Akt phosphorylation, but also to a proportional down-regulation of a Rac1-dependent kinase PAK, further suggesting coordinated activation of Rac1 and PI3K signaling (SI Appendix, Fig. S5). Rac1 and PI3K activation can lead to actin polymerization and formation of protrusive lamellipodia (40, 41). We indeed found that localized PI3K was accompanied by local protrusive activity causing directional migration (SI Appendix, Fig. S6). Formation of lamellipodia can increase local ECM engagement, and thus further increase local ECM-dependent Rac1–PI3K activity leading to a putative positive feedback. However, lamellipodia extension can also increase cell–ECM contact and thus the local ECM-dependent activation of RhoA–ROCK and myosin-mediated contractile forces, which may trigger the lamellipodial retraction, constituting a negative feedback. The interplay between these spatially distributed mechanochemical feedback interactions, as well as the more direct antagonistic interaction between Rac1 and RhoA (42, 43), can potentially lead to complex local signaling activity patterns. We thus mathematically explored whether this postulated signaling network can account for the RD, OS, and PS patterns of PI3K activity and the corresponding regulation of cell polarity and migration persistence.

Multiple feedback interactions outlined above as possibly controlling cell polarity can be described as several alternative hypotheses, which can be quantitatively expressed in a series of alternative mathematical models [full details in the modeling paper by Holmes et al. (44)]. Their behavior qualitatively corresponds to the well-known dynamical systems theory wherein a bistable system can be driven to oscillate by slow negative feedback (45). However, as explained in detail in the study (44), different models can generate distinct experimentally verifiable predictions that we have tested experimentally, arriving at a single mechanism (Fig. 2A) that proved to be consistent with all experimental observations. In this mechanism, mutual antagonism of Rac1 and RhoA (correlated respectively with PI3K and ROCK signaling) gives rise to robust polarity, provided the total amount of each GTPase in the cell is sufficiently limited (a conservation constraint). This antagonistic interaction can occur in an ECM-modulated fashion both at the front and the rear of a polarized cell within a pair of lamellipodia that are mechanically coupled [e.g., due to a buildup of membrane tension (46, 47)], with the mechanical interaction limiting the extension of each of the lamellipodia.

Fig. 2.

The proposed molecular mechanism and associated mathematical model can quantitatively account the observed dynamic polarity patterns. (A) Mechanism schematic (Top) and classification of cell behavior (Bottom). RhoA–ROCK signaling and Rac1–PI3K signaling are mutually inhibitory in coupled signaling networks activated at the front or rear of a cell. Signals from the ECM activate RhoA (and possibly Rac1–PI3K; see text). Rac1–PI3K-induced cell spreading increases contact with (and signaling from) ECM. RhoA–ROCK-induced cell contraction decreases the contact with (and signaling from) ECM. The model accounts for the three main classes of behaviors: random (no Rac1–PI3K-dominated hot spots established), oscillatory (cycling between hot spots in the front and rear), and persistent (polarization of hot spot to one lamellipodium). (B) The mathematical model emerging from the mechanism described in A leads to the bifurcation diagram specifying parameter domains leading to each of three different polarity patterns (the bifurcation parameters are the intrinsic activation rates of GTPases, RhoA, and Rac1; see the model description in SI Appendix). Outboxes at the Top show the dynamics of a lammelipodium–ECM contact at the front (Cell–ECM contact_front) and at back (Cell–ECM contact_back) lamellipodia of a model cell for random, oscillatory, and persistent polarity patterns. Deterministic and stochastic simulations are shown to illustrate the effect of noise, particularly on the random polarity dynamics. The details of models are in SI Appendix. (C) Cell populations cultured in different nanopost density zones are mapped onto the bifurcation diagrams as described in the text. Intensity of gray shading corresponds to three zones of distinct density of posts in nanofabricated substrata (lightest gray represents densest post region). The mappings are inferred based on experimentally determined fractions of cells with different polarity patterns, as explained in detail in SI Appendix. Variation of ECM (FN) density is predicted to shift the oscillatory/persistent bifurcation boundary, thus changing fractions of cells adopting these patterns in a population. (D) Comparison of modeling predictions (in silico) and experimental results (in vitro) for the dependence of fractions of different cell polarity patterns on surfaces with varying post and FN densities. Dashed lines indicate the fraction of cells having polarized focal adhesion (FA) localization (see details in SI Appendix, Fig. S2, and Materials and Methods). (E) Variation of migration persistence metric, D_y/T_y, that correlates with the polarity patterns (D_y is the distance traveled by the cell along the y direction, and T_y is the total distance traveled by the cell along the y direction) over 3 h for different post and FN densities. *Statistical significance of D_y/T_y among each group, *P < 0.05 and all paired Student’s t test.

When described mathematically as a series of coupled ordinary differential equations describing biomolecular dynamics at the front and the back lamellipodia (see SI Appendix, SI Discussion, for detail), this model [denoted the “Hybrid Model” by Holmes et al. (44)] successfully accounted for diverse patterns of localized Rac1–PI3K activity and lamellipodia extension dynamics (Fig. 2B). In particular, in distinct parameter regimes, this mechanism generated either highly persistent Rac1–PI3K activation on one side of the cell and inhibition on the other side (consistent with the PS signaling pattern and persistent migration observed experimentally), or out-of-phase oscillations of activity on both sides of the cell (consistent with the OS signaling pattern). Alternatively, the model predicted that the activities on both sides of the cell could be low on average, and thus potentially sensitive to stochastic fluctuations in signaling activity and/or ECM engagement. This behavior was interpreted as leading to random local activity patterns (consistent with the RD signaling pattern observed experimentally). We validated this interpretation by explicitly introducing dynamic random fluctuations to the equations, and demonstrating their limited effect on OS and PS patterns, but a profound random fluctuation in the RD simulation case (Fig. 2B; see SI Appendix for details). These three patterns of model behavior can be conveniently represented in a bifurcation diagram, illustrating the dependence of cell dynamics on the basal (i.e., intrinsic) Rac1 and ECM-dependent RhoA activation rates (Fig. 2B and SI Appendix, Fig. S7). These two parameters were chosen to respectively account for the intrinsic variability in the population and to link the analysis to the ECM input, the main experimental stimulus for the cell migration (see SI Appendix, SI Discussion, for details). Similar results have been obtained using other pairs of parameters, as shown in the paper by Holmes et al. (44).

To generate experimentally testable predictions for melanoma cells analyzed here, this mathematical model had to be first constrained (“trained”) using experimental data to (i) define the ranges of model parameter values that would model particular cell populations under specific conditions and (ii) understand how the inherently “noisy” cell populations with cell properties corresponding to distinct model parameter values could be “mapped” onto the bifurcation diagram described above. Furthermore, it was also important to reflect in the model the local differences in the nanotopographic structure of the cell adhesion substratum. Its effect can limit, in a post spacing-dependent way, the ability of a cell to form extensive contact with the posts and thus the ECM-mediated input into the FA-triggered signaling pathways, consistent with the prior analysis of the differential depths of FAs formed by cells on these surfaces (35). Therefore, we assumed that the average ECM contact and thus “intrinsic” Rac1 and ECM-dependent RhoA activation rates would depend on the local cell–ECM contact, and thus change from lowest in zone 1 (highest post density) to highest in zone 3 (lowest post density). Because we also observed considerable variability of cell penetration into the interpost spaces, we further hypothesized that this variability would translate in each zone into the variability in the extent of cell–ECM contact and thus into corresponding variability in intrinsic Rac1 and RhoA–ECM activation rates. We thus assumed that cell populations in each topographic zone could span a considerable range of parameter values and cross the boundaries separating different signaling regimes in the bifurcation diagram. To further constrain the extent of cell heterogeneity and the values of the model parameters, we have fit the model to the experimental results, as shown in Fig. 2D and explained in detail in SI Appendix, SI Discussion. This completed the “model training” for melanoma cells cultured on topographically complex substrata, and allowed us to explore the predictive power of the parameterized model, and thus the plausibility of the assumed underlying mechanism of signaling and migration patterns in this system.

The Proposed Mechanism Is Validated by a Range of Perturbations of the Postulated Molecular Network.

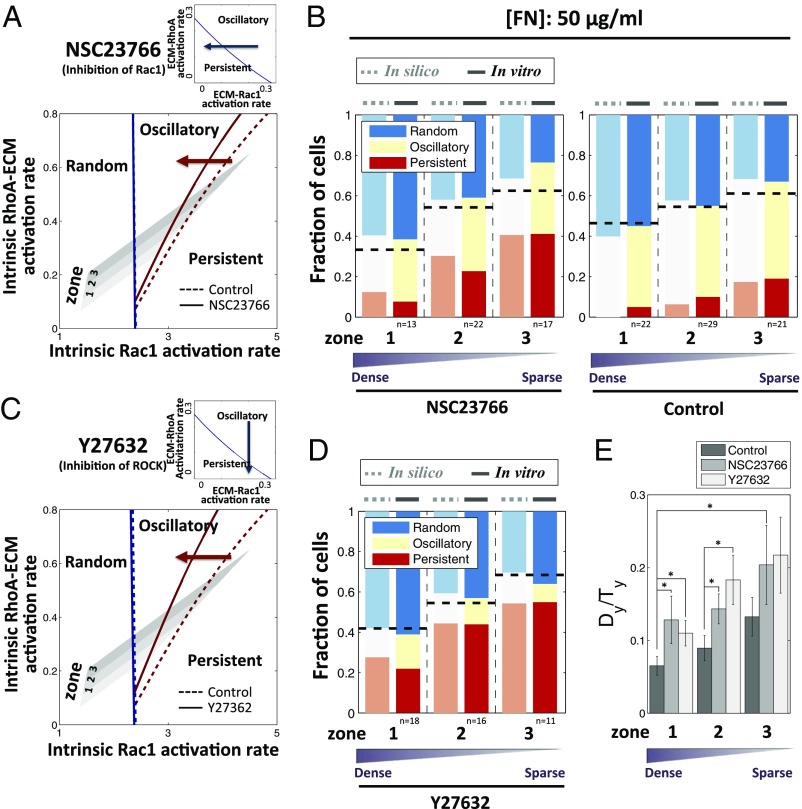
We next tested the postulated mechanism by performing a series of theoretical and experimental perturbations affecting assumed molecular interactions, as shown schematically in Fig. 2A. The model and experimental analysis focused on how the fractions of cells exhibiting distinct signaling and polarity patterns would change following these perturbations. First, we perturbed the ECM input levels, which was experimentally achieved by varying the coating density of fibronectin, [FN]. We explored whether this would alter the relative frequencies of PI3K signaling patterns and the corresponding polarity and migration phenotypes. The critical model prediction was that this perturbation would shift a single boundary of the bifurcation diagram, separating the PS and OS signaling regimes. Thus, the model predicted that the fraction of cells displaying the RD signaling pattern would not change as ECM density was varied, whereas the frequency of the cells displaying the PS would decrease with increasing ECM (Fig. 2 C and D). Keeping model parameters the same as determined during model training for 10 μg/mL [FN] condition, we extended the model to quantitatively predict cell behavior in the new 2 and 50 μg/mL [FN] condition (see SI Appendix, SI Discussion, for detail), determining the corresponding deviations in two model parameters characterizing changes in the ECM-induced RhoA and Rac1 activities (the effect of ECM on RhoA and Rac1 signaling was experimentally investigated in SI Appendix, Figs. S4 and S5). Using this simple adjustment reflecting different ECM densities, the model was further used to predict frequencies for all PI3K patterns for all topographic zones, with model predictions closely matching the experimental findings (Fig. 2 C and D and SI Appendix, Fig. S8). Consistent with model predictions (assuming direct correspondence between the PS pattern of PI3K activity and the extent of cell migration), we found that cells moved less persistently with increasing [FN], and that the persistence increased at all [FN] values with decreasing post density (see Fig. 2E, and note that the ratio of net cell displacement, D_y, to total trajectory length, T_y, increases, consistent with increased persistence of migration).

We next perturbed another node of the signaling system (Fig. 2A): modulating the influence of Rac1 activity on lamellipodium extension (48, 49), with 10 μM Rac1 inhibitor, NSC23766. The mathematical model indicated that, following this perturbation, the fraction of cells with the RD pattern would not change. However, this perturbation was predicted to increase the fraction of PS cells, while decreasing the fraction of OS cells (Fig. 3A). We indeed found that this prediction was confirmed by experiments with individual cells frequently changing their signaling patterns from OS to PS soon after addition of the Rac1 inhibitor (SI Appendix, Fig. S9 A and B, and Movie S4). We quantitatively modeled the effect of Rac1 inhibition by adjusting a single model parameter, the ECM-mediated Rac1 activation rate, to match a single experimental data point (see SI Appendix, SI Discussion, for details). As before, this allowed us to predict the rest of the experimental results, with a very good match between the model and experiments (Fig. 3B). Again, as predicted by the model, the persistence of cell migration was enhanced by Rac1 inhibition in all post density zones (Fig. 3E).

Fig. 3.

Effect of pharmaceutical perturbations of Rho GTPase-dependent signaling on relative abundance of distinct polarity patterns. (Top) Blue arrow depicts Rac1 inhibition by Rac1 inhibitor, NSC23766 (A), and ROCK inhibition by ROCK inhibitor, Y27632 (C), which biases cells toward persistent dynamics (shown in the ECM-induced Rac1 and RhoA activation rates parameter plane). (Bottom) Rac1 inhibition (A) and ROCK inhibition (C) shift the boundary between oscillatory and persistent regime to the left, increasing the persistent regime and hence the fraction of cells exhibiting persistent dynamics. Comparison of model (in silico) and experiment (in vitro) results for the dependence of PI3K dynamics on nanofabricated substrata coated with 50 μg/mL FN after Rac1 inhibition (B) and ROCK inhibition (D). Dashed lines indicate the fraction of cells having polarized FA localization on corresponding experimental conditions. (E) Dependence of the persistence metric, D_y/T_y, evaluated over 3 h on the post density with Rac1 and ROCK inhibition. Both inhibitions enhance the persistence of cell migration. *P < 0.05 for D_y/T_y values in each group, using all paired Student’s t test.

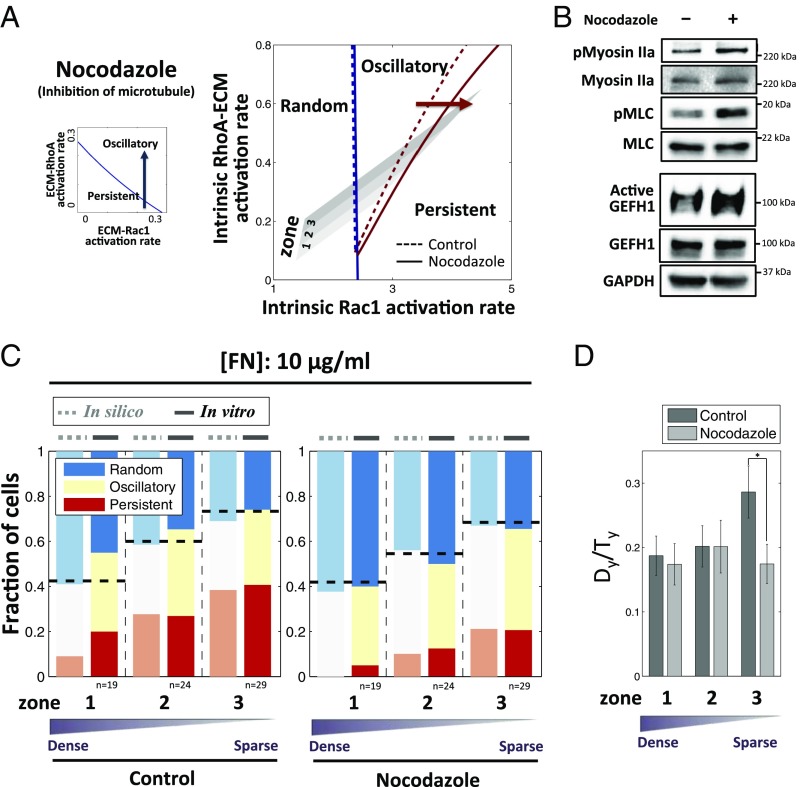
We then performed similar experimental and theoretical perturbation of another parameter: the dependence of ROCK activity on ECM. Surprisingly, even though ROCK displays activity antagonistic to Rac1, inhibition of ROCK activity with 10 μM ROCK inhibitor, Y27632 (Fig. 3C), was predicted to have similar effects to that of inhibition of Rac1, that is, increasing the frequency of PS cells. We indeed experimentally observed an increase in persistent signaling and cell migration following this perturbation (Fig. 3E, SI Appendix, Fig. S9 C and D, and Movie S5), with the model predictions again yielding excellent quantitative agreement with experimental results. The role of ROCK was then tested through an independent perturbation. Recently, the inhibition of microtubules was reported to promote oscillation of cell protrusion (20). Treatment with 100 nM nocodazole interferes with the polymerization of microtubules, preventing sequestration of GEF-H1, a RhoA GTP exchange factor, in the cytosol by microtubules, and thus causing GEF-H1 to be released into cytosol where it eventually activates ROCK (50). Thus, nocadozole treatment can results in up-regulation of ROCK, which indeed led to model predictions opposite to the effect of inhibition of ROCK, that is, an increase in the fraction of OS cells at the expense of PS cells (Fig. 4A). We confirmed that the inhibition of microtubule polymerization indeed activated GEF-H1 and subsequently ROCK, without changing PI3K activity (Fig. 4B and SI Appendix, Fig. S10A). In a close agreement with the model prediction, we found an increase in the fraction of OS cells (accompanying the corresponding decrease of the PS fraction) and a less persistent cell migration, which indeed was the result that was opposite to ROCK inhibition (Fig. 4 C and D, SI Appendix, Fig. S10 B and C, and Movie S6). Overall, our results strongly supported the proposed mechanism and its quantitative predictive power in accounting for a diverse range of pharmacological perturbations of the underlying biochemical network.

Fig. 4.

Effect of pharmacological perturbation of microtubule dynamics on dynamic cell polarity patterns. (A, Left) Blue arrow depicts increasing RhoA–ROCK activity by microtubule inhibition, which biases cells toward oscillatory dynamics. (Right) Microtubule inhibition shifts the boundary between oscillatory and persistent regime to the right, decreasing the persistent regime and hence the fraction of cells exhibiting persistent dynamics. (B) Microtubule inhibition increases RhoA–ROCK activity as measured by immunoblotting of phosphorylated Myosin IIa/Myosin IIa and phosphorylated MLC/MLC, which potentially results from higher activation of GEF-H1, a RhoGEF whose activity is affected by nocodazole (Materials and Methods, Active Rho GTPase Exchange Factor Assay). (C) Comparison of model (in silico) and experiment (in vitro) results for the dependence of PI3K dynamics on post density with 10 μg/mL FN after microtubule inhibition. (D) Dependence of the ratio D_y/T_y for 1 h on post density substrata and nocodazole: Inhibition of microtubule reduces the persistence of cell migration. *P < 0.05 for D_y/T_y values in each group using all paired Student’s t test.

The Proposed Mechanism Links a Common Mutation to Cancer Cell Invasiveness.

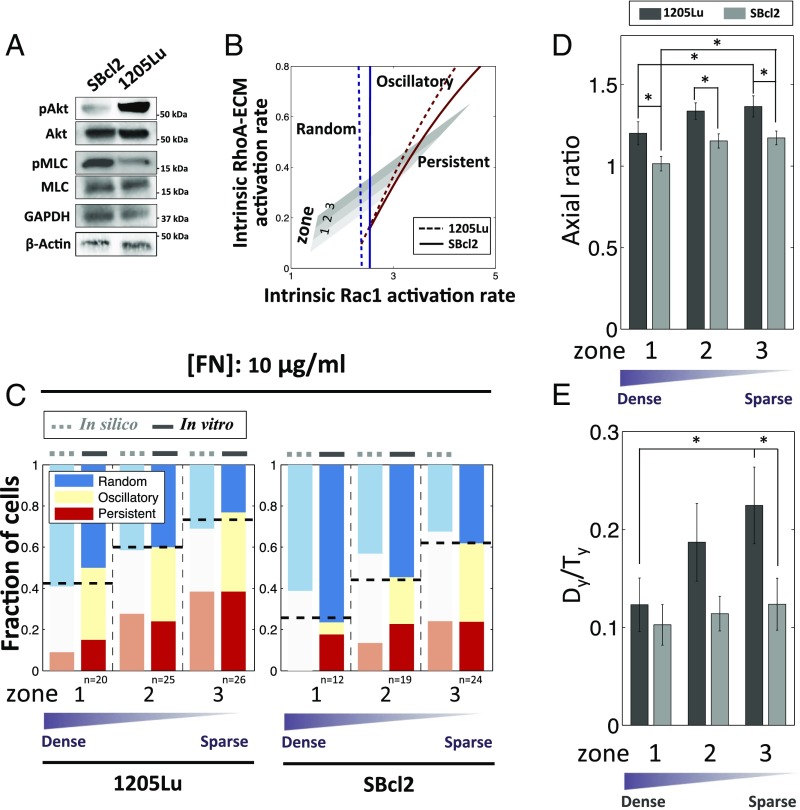
Finally, we investigated whether the model was capable of predicting the behavior of a less invasive melanoma cell line, SBcl2 (Fig. 5). The invasive cell line, 1205Lu, used in our study thus far, carries a well-established genetic alteration, loss of expression of PTEN, a phosphatase antagonizing PI3K signaling (24), whereas in SBcl2 expression of PTEN is unperturbed. Consistent with this change, we found that, compared with 1205Lu cells, SBcl2 cells displayed lower PI3K activity and higher ROCK activity (Fig. 5A). When incorporated into the model, these perturbations of the signaling network found in noninvasive melanoma cell line resulted in the prediction that both of the bifurcation diagram boundaries (separating PS from OS, and OS from RD signaling patterns) would be shifted, thus predicting an increased fraction of cells with the RD pattern, primarily at the expense of cells with the PS signaling pattern (Fig. 5B). These predictions were indeed supported by experimental observations (Fig. 5C). Furthermore, again consistent with the analysis, we found that both cell polarity and the persistence of cell migration decreased in SBcl2 cells relative to 1205Lu cells (Fig. 5 C–E), suggesting that more invasive cells can undergo a more directional migration while guided by chemical and mechanical cues provided by ECM.

Fig. 5.

The alteration of dynamic polarity patterns in metastatic cells vs. noninvasive melanoma cells is explained by the proposed feedback mechanism. (A) SBcl2 cells display lower Rac1–PI3K activity and higher RhoA–ROCK activity than 1205Lu cells, as measured by immunoblotting of phosphorylated Akt and Akt (Rac1–PI3K) and phosphorylated MLC and MLC (RhoA–ROCK). (B) Assuming a decrease in ECM–Rac1 activation rate and increase in ECM–RhoA–ROCK activation rate in SBcl2 cells shifts the boundary between oscillatory and persistent regime and boundaries between random and oscillatory regimes toward the right, predicting smaller fraction of cells in the persistent Rac1–PI3K regime and a larger fraction in the random regime. (C) Comparison of model (in silico) and experiment (in vitro) results for the dependence of PI3K dynamics of SBcl2 cells on nanofabricated substrata coated with 10 μg/mL FN. (D) Axial ratio (the degree of aligned elongation) in the two cell lines. (E) D_y/T_y for 3 h of the two cell lines. The noninvasive SBcl2 cells have inhibited elongation and directional cell migration. *P < 0.05 for D_y/T_y values in each group using all paired Student’s t test.

Discussion

The results presented here argue that diverse patterns of signaling and migratory cell responses guided by ECM organization, as well as genetic alterations or pharmacological perturbations of signaling components within a cell, can be explained by a simple mechanism supported by a quantitative mathematical model. The integrative, mathematical–experimental analysis leading to these results can provide a powerful tool for understanding normal and pathological phenomena associated with cell migration. This mechanistic understanding, supported by extensive experimental validation, strongly suggests the importance of mechanochemical regulatory network, regulating lamellipodial extension through both positive (via Rac1) ECM input and negative (via RhoA) feedback stemming from modulation of the lamellipodia–ECM interactions. Conservation of the total amount of small GTPases in a cell effectively leads to a double negative feedback between the front and the back of the cell, preventing simultaneous high activation in both front and back cellular compartments. This simple mechanism and the associated model provide a powerful way to translate biochemical and genetic intracellular interactions and the structural and biochemical complexity of the surrounding ECM into a single analytical framework. The bifurcation diagram resulting from this model provides an intuitive and quantitative explanation of cell locomotion, wherein a domain of instability corresponding to the oscillatory migration separates the domains of random and persistent migration patterns. Our results show that genetic and pharmacological perturbations can shift the borders separating these domains, making specific migration patterns more likely to occur. Specific cell populations can be “mapped” onto this diagram providing precise quantitative predictions of fractions of cells undergoing distinct migration responses. Therefore, heterogeneity of cell properties, or cellular “noise,” commonly observed in cell populations can allow the same population to explore diverse phenotypic responses. Although we assumed simple uniform parameter distributions within each of the cell population “clouds” during the mapping, the predictive power of this modeling technique was quite strong, yielding good agreement with experimentally observed changes in fractions of cells displaying distinct signaling and polarity patterns. The “mapping” can be unique to specific cell types, thus producing diverse results, with the underlying “phenotypic bifurcation diagram,” however, being universal and accounting for the chemical nature of the conserved signaling network.

It is important to assess the predictive power of any model, including the one developed here, beyond the experimental system under investigation, that is, to assess the potential universality of the proposed mechanism. Previous analysis indicated that depletion of zyxin, a protein mediating coupling between ECM and intracellular signaling components, induced oscillatory migration patterns in fibrosarcoma cells (21). This result is completely consistent with our analysis, which underscores interaction between ECM and small Rho-family GTPases as critical for determining the relative fraction of oscillating cells. Furthermore, our model explains why inhibition of ROCK in neutrophil-like cells increases the propensity for persistent cell migration, whereas microtubule disruption decreases it (51), and why microtubule disruption promotes oscillatory migration in retinal pigment epithelial cells (20). The model also provides an explanation for the prior findings that inhibition of Rac1 can increase persistence of cell migration (52). Combined with our study in melanoma cells, the predictive power of the model argues that the underlying mechanism may indeed represent a universal account of the emergence of diverse migration modes triggered by cell interaction with ECM.

Our results also shed light on an ostensibly paradoxical localization of both Rac1 and RhoA activities to the front of many migrating cells (53). Although, Rac1–PI3K activity is frequently associated with the cell “frontness” and RhoA activity with the cell “backness,” our data indicate that RhoA can be activated if the ECM–plasma membrane contact at the cell front becomes sufficiently extensive, which might arrest the extension of a lamellipodium and lead to its retraction. This dynamic view of cell migration, with the possibility of repolarization, suggests that, locally, Rac1 and RhoA activities are in a continuous “balancing act,” with some degree of ECM-triggered activation of both of these small GTPases occurring at any time. This dynamic balance can endow a migrating cell with higher directional flexibility as observed in our analysis.

The mechanism of cell migration directionality supported by our analysis also suggests that the topography of the cell adhesion substratum defines the cell migration patterns in large part by controlling the extent of cell–substratum contact. Increasing cell–matrix contact in sparser topographies can enhance activation of ECM-regulated signaling pathways, which increases the migration persistence. The anisotropic nature of the substratum in these sparser migration zones provides an additional cue, specifying migration directionality. Previously, we provided experimental evidence for differential cell–matrix contact on these substrata, supporting this hypothesis (35). This mechanism is also consistent with previous evidence emphasizing the importance of differential cell compliance with the nanoscale texture of adhesive surfaces (54, 55), suggesting that this mechanism of sensing of the nanoscale features can be very general.

The findings presented here also argue that mutations leading to a switch to more aggressive and invasive expansion in melanoma and other invasive cancers might increase the fraction of cells undergoing persistent migration, and thus following more faithfully the cues provided by the organization of the surrounding ECM. Synergic with ECM organization that can be highly anisotropic and well-defined in many normal tissues, such as the dermis underlying normal or cancerous melanocytes, or can become highly anisotropic during progression to invasive growth, as in invasive cancer progression (56, 57), a more persistent cell migration can enhance the spread of the invading cells guided by these nonrandom ECM cues. Furthermore, our prior analysis suggested that mutational changes observed in aggressive, invasive melanoma cells can direct them toward sparser matrix areas, which might further enhance cell–matrix contact and increase persistence of cell migration (35). These considerations can provide important insights into the still poorly understood biology of invasive cancer growth and emphasize the importance of accounting for the structure of the surrounding matrix in guiding this dangerous phase of cancer progression.

Overall, our results argue that, despite the complexity of biochemical and mechanical processes leading to cell locomotion in complex microenvironments, quantitative mechanisms can be proposed that can account for this complexity and accurately predict the effects of a diverse set of genetic, pharmacological, and biochemical perturbations of cells and their milieu. These mechanisms are general, and thus applicable to many cell types, and yet quantitative and predictive enough to allow for precise description of diverse cell populations adopting a multitude of cell migration patterns. We anticipate that this and other examples of such quantitative modeling of signaling and phenotypic behavior will be essential for both fundamental description of cell biology, and for the development of more precise and targeted therapeutic interventions.

Materials and Methods

Fabrication of Topographical Patterned Arrays.

We used polyurethane acrylate (PUA) as a mold material from a silicon master as previously described elsewhere (58), to construct graded post density array. Briefly, we drop-dispensed the UV-curable PUA onto a silicon master and then brought a flexible and transparent polyethylene terephthalate film into contact with the dropped PUA liquid. Then, the film was exposed to the UV light (λ = 200–400 nm) for 30 s through a transparent backplane (dose, 100 mJ⋅cm⁻²). After UV curing, we peeled off the mold from the master and further cured overnight. The resulting PUA mold used in the experiment was a thin sheet (∼50 μm thick).

The topographic patterns with variable local density and anisotropy were fabricated on glass coverslips, using UV-assisted capillary molding techniques (35). Before applying the PUA mold onto the glass substratum, we cleaned the glass substratum with isopropyl alcohol, thoroughly rinsed in distilled ionized water, and then dried in a stream of nitrogen. Next, we spin-coated an adhesive agent (phosphoric acrylate:propylene glycol monomethyl ether acetate = 1:10, volume ratio) to make a thin layer (∼100 nm) for 30 s at 1,000 × g. A small amount of the same PUA precursor was drop-dispensed on the substrate and a PUA mold was directly placed onto the surface. Capillary action allows the PUA precursor spontaneously to fill the cavity, and then, this was cured by exposure to UV light (λ = 250–400 nm) for ∼30 s through the transparent backplane (dose, 100 mJ⋅cm⁻²). After curing, we peeled off the mold from the substrate using sharp tweezers. The nanofabricated patterns used in this study has the post spacing gradient along the x direction. The diameter of nanoposts was 600 nm with the varying post-to-post spacing from 300 nm [spacing ratio (spacing/diameter) of 0.5] to 4.2 μm (spacing ratio of 7) in the x direction, but constant post-to-post spacing of 600 nm (spacing ratio of 1) in the y direction.

Cell Culture.

Melanoma cell lines, 1205Lu and SBcl2, from the Wistar Institute collection were gifts from Dr. Rhoda Alani (Boston University, Boston, MA). We also transfected the plasmids coding for 3-phosphoinotitide–specific Akt-PH domain fused with GFP in 1205Lu and SBcl2 using Lipofectamine 2000 transfection reagents (Thermo Fisher; 11608027) as described in the product’s manual. GFP–Akt PH plasmids were gifts from the laboratory of Dr. Jin Zhang (University of California, San Diego, La Jolla, CA) (59). We cultured the cells in DMEM (Gibco) supplemented with 10% FBS (Gibco), 50 U/mL penicillin/streptomycin (Invitrogen), and 90% humidity, and split 1:4 after trypsinization every 2–3 d. We attached a glass coverslip with the topographical patterned substratum onto the bottom surface of the custom-made MatTek dish (P35G-20-C) after removing the original glass. Then, cells were reseeded on the pattern precoated by FN (Sigma-Aldrich) for 3 h and incubated overnight. To change the activities of small GTPases, 5 μM Y27632 (Sigma-Aldrich), 10 μM NSC23766 (Tocris), and 100 nM nocodazole (Acros Organics) were used.

Immunoblotting Analysis.

We lysed cells in RIPA buffer (Thermo Scientific) with protease/phosphatase inhibitor mixture (Thermo Scientific), and then centrifuged at 12,000 × g at 4 °C for 15 min. Next, we collected the supernatant and measured its protein concentration using BCA assay kit (Pierce). Protein samples were subsequently diluted with sample buffer, heated at 70 °C for 10 min, and 10–20 μg of proteins were used for Western blotting. We incubated protein-transferred membrane in 1:2,000 diluted solution of MLC (Abcam; ab11082), 1:1,000 diluted solution of phosphorylated MLC (Cell Signaling; 3671), 1:2,000 diluted solution of Akt (Cell Signaling; 9272), 1:1,000 diluted solution of phosphorylated Akt (Cell Signaling; 9271), 1:1,000 diluted solution of PAK (Cell Signaling; 2602), 1:1,000 diluted solution of phosphorylated PAK (Cell Signaling; 2601), 1:1,000 diluted solution of myosin IIa (Cell Signaling; 3403) and 1:1,000 diluted solution of phosphorylated myosin IIa (Cell Signaling; 5026), β-actin (Santa Cruz; sc-1616), and 1:1,000 diluted solution of GAPDH (Abcam; ab9484) in blocking solution at 4 °C overnight.

Time-Lapse Microscopy.

For long-term observation, we mounted samples onto the stage of a motorized inverted microscope (Zeiss Axiovert 200M) equipped with a Cascade 512B II CCD camera that has an environmental chamber for maintaining 37 °C and 5% CO₂. We used the Slidebook 4.1 (Intelligent Imaging Innovations) for 3 h at 10-min intervals or for 2 h at 2-min intervals for automatic phase-contrast and epifluorescent live-cell imaging.

Tracking Cells and Quantification of Cell Shape/Migration.

With the help of the fluorescence-tagged Akt-PH in melanoma cells, we tracked cells automatically by thresholding epifluorescent images taken in a time-lapse fashion. Infrequently, we also manually segmented images that were poorly segmented in the automatic procedure, by outlining the boundary of each cell. Then, using MATLAB Image Processing Toolbox (The MathWorks), the positions of cell centroids were calculated as a function of time, and the persistence of cell migration, D_y/T_y [the ratio of the shortest distance in y axis direction between the initial location of an individual cell and its final location (D_y) to the length of whole trajectory of the cell during live cell imaging (L_y)], was measured. Axial ratio representing the degree of elongation of cells was defined as the ratio of length of longest axis of cells in y axis to that in x axis. Statistical analysis was performed using two-paired Student’s t tests.

Quantification of Spatial PI3K Translocation.

Image segmentation from epifluorescent images was performed as follows. We read the pixel values representing the intensity in manually segmented single cells with MATLAB Image Processing Toolbox. Then, hot spots, the regions on the cell membrane having higher intensity value than the averaged intensity values of total pixels in a single cell, were further segmented. We acquired the area (A), average intensity (F), and centroid coordinates of each hot-spot region to calculate a signaling vector. The position of the hot spot x_i = (x_i, y_i), relative to the cell centroid, was defined by subtracting the coordinates of the cell’s centroid from those of the hot spot, i. The vector, s_i, had the magnitude proportional to the fluorescence intensity integrated over the overall area of the hot spots (A_iF_i) to account for the corresponding signaling intensity; and the overall signaling vector, S, describing the spatial PI3K activity polarization for a given cell was calculated as the sum of all s_i, as described in Fig. 1C (60) and equations below:

$$s_i=A_i{F}_i\frac{x_i}{\sqrt{x_i^2+y_i^2}};\hspace{1em}S={\displaystyle \sum _N^{i=1}}{s}_i.$$

For calculating the spatial randomness of a polarization signal, a virtual circle around the centroid of an individual cell was drawn and divided into four sectors evenly (upper and lower along the y axis of the pattern; right and left along the x axis). Then, the probabilities of the signaling vector localization to each sector over 3 h of measurements (p_i) were determined and used for entropy (E) calculation. This entropy value (E) was used to evaluate spatial randomness according to the following equations (SI Appendix, Fig. S11):

$$E=-{\displaystyle \sum _{i=1}^4}{p}_i{\log }_2{p}_i\hspace{1em}\mathrm{Spatial}\hspace{0.17em}\mathrm{randomness}=2^E.$$

On a more intuitive level, if the probabilities of the signaling vectors located in either upper or lower sectors along the y axis of patterns were below 0.6, we considered this polarity pattern to be random. Otherwise, if the difference between the probabilities of the signaling vector localizing within either upper or lower sections vs. the opposite section were below 0.2, we categorized the cells as oscillatory. The rest of cases, that is, when the differences of probabilities were over 0.2, were considered to display persistent polarization dynamics.

Immunofluorescence Staining.

We replated cells on the nanofabricated coverslip after FN coating as described above. Samples were fixed with ice-cold 4% paraformaldehyde for 20 min and permeabilized with 0.1% Triton X-100 in PBS for 5 min. After washing with ice-cold PBS, we blocked samples with 10% goat serum for 1 h, and then incubated them with primary antibody against vinculin (1:200; Sigma-Aldrich; V9131) for 3 h at room temperature. After subsequent washing, the samples were incubated with a secondary antibody for vinculin (1:500), with Alexa Fluor 594-conjugated phalloidin (1:40; Molecular Probes) and/or Hoechst (Invitrogen) for 1 h at room temperature. The slides were mounted with antifade reagent (SlowFade gold; Invitrogen) and imaged by confocal microscope (Zeiss 510 Meta confocal) with a 63× oil immersion objective (Zeiss; 1.6 N.A.).

Quantification of Polarized FA Localization.

For quantifying spatial PI3K dynamics, a virtual circle around the centroid of an individual cell was drawn and divided into four sectors evenly (upper and lower along the y axis of the pattern; right and left along the x axis). Then, the probabilities of the FA localization to each sector were determined and used for categorization. If the probabilities of the FA localization located in either upper or lower sectors along the y axis were over 0.8, we considered this FA localization to be polarized. Otherwise, we categorized the cells as having random FA spatial distribution.

Active Rho GTPase Exchange Factor Assay.

Active Rho GTPase exchange factor (RhoGEF) pull-down assay has been described in detail elsewhere (61, 62). Briefly, cells were lysed in RhoGEF buffer, which is combined with 20 mM Hepes, 150 mM NaCl, 5 mM MgCl₂, 1% (vol/vol) Triton X-100, 1 mM DTT, and protease inhibitor mixture. Fifteen grams of GST–RhoA^G17A beads were then added to each equalized lysates, and samples were rotated slowly at 0.03 × g for 45 min at 4 °C. After washing the beads three times in the RhoGEF buffer, SDS/PAGE analysis was processed and immunoblotting was performed with GEF-H1 antibody (Cell Signaling; 4076S). RhoA^G17A mutant plasmid was a generous gift from Dr. Rafael Garcia-Mata (University of Toledo, Toledo, OH).

Mathematical Analysis and Simulations.

The details of the mathematical analysis and simulations are given in the SI Appendix, SI Discussion. Briefly, we used MatLab (MathWorks) with built-in ODE library (ODE45). Simulations were performed at the resolution of 500 time points. In a subset of simulations, noise was introduced as described in SI Appendix, SI Discussion, for all time points.