Tetragonal CH₃NH₃PbI₃ is ferroelectric

Significance

Halide perovskite (HaP) semiconductors are revolutionizing the field of photovoltaic (PV) solar energy conversion by showing remarkable performance of solar cells made with HaPs. “Ferroelectrics” is one frequently suggested reason because it may allow the spatial separation of the flow of electrons from where they were generated (holes). Unlike common, electrically insulating, ferroelectric materials, HaPs [especially tetragonal methylammonium lead triiodide (MAPbI₃)] are semiconducting, and to find out whether they are ferroelectric requires an approach that is different from what is done customarily. Using such an approach, we prove that tetragonal MAPbI₃ is definitely ferroelectric. What still remains to be seen is whether this ferroelectric nature is important for how MAPbI₃-based solar cells operate around room temperature.

Abstract

Halide perovskite (HaP) semiconductors are revolutionizing photovoltaic (PV) solar energy conversion by showing remarkable performance of solar cells made with HaPs, especially tetragonal methylammonium lead triiodide (MAPbI₃). In particular, the low voltage loss of these cells implies a remarkably low recombination rate of photogenerated carriers. It was suggested that low recombination can be due to the spatial separation of electrons and holes, a possibility if MAPbI₃ is a semiconducting ferroelectric, which, however, requires clear experimental evidence. As a first step, we show that, in operando, MAPbI₃ (unlike MAPbBr₃) is pyroelectric, which implies it can be ferroelectric. The next step, proving it is (not) ferroelectric, is challenging, because of the material’s relatively high electrical conductance (a consequence of an optical band gap suitable for PV conversion) and low stability under high applied bias voltage. This excludes normal measurements of a ferroelectric hysteresis loop, to prove ferroelectricity’s hallmark switchable polarization. By adopting an approach suitable for electrically leaky materials as MAPbI₃, we show here ferroelectric hysteresis from well-characterized single crystals at low temperature (still within the tetragonal phase, which is stable at room temperature). By chemical etching, we also can image the structural fingerprint for ferroelectricity, polar domains, periodically stacked along the polar axis of the crystal, which, as predicted by theory, scale with the overall crystal size. We also succeeded in detecting clear second harmonic generation, direct evidence for the material’s noncentrosymmetry. We note that the material’s ferroelectric nature, can, but need not be important in a PV cell at room temperature.

New optoelectronic materials are of interest for producing solar cells with higher power and voltage efficiencies, lower costs, and improved long-term reliability. A very recent entry is the family of halide perovskites (HaPs), in particular those based on methylammonium (MA) lead iodide (MAPbI₃), MAPbBr₃, and its inorganic analog CsPbBr₃. Devices based on these perform remarkably well as solar cells (1, 2), as well as in other optoelectronic applications, such as LEDs and electromagnetic radiation detectors (3–5). Understanding possible unique characteristics of HaPs may show the way to other materials with similar key features.

The ABX₃ (X = I, Br, Cl) HaP semiconductors (SCs), that is, with perovskite or perovskite-like structures, reach, via a steep absorption edge, a high optical absorption coefficient (∼10⁵ cm⁻¹) (6, 7), long charge carrier lifetimes (∼0.1–1 μs) (8), and reasonable carrier mobilities (less than or equal to ∼100 cm²·V⁻¹·s⁻¹) (9), and have a low exciton binding energy (10). With these characteristics, the thickness of the optical absorber layer can be ≤0.5 μm, which allows the charge carriers (separated electrons and holes) to diffuse/drift throughout the entire width of the absorber without strong recombination. HaP-based solar-cell devices can, usually, function with a continuous HaP layer, that is, also without filling a high surface area, non-HaP, scaffold, such as mp-TiO₂ (11). Photogenerated electrons and holes will then spend a significant time in the bulk of the HaP film. Consequently, because the dielectric nature of a SC strongly affects the charge dynamics in it, the performance of HaP-based devices should be strongly affected by the dielectric behavior of the HaP itself. Here, we present experimental results that bear on possible ferroelectricity, the type of dielectric behavior that has been suggested to aid photovoltaic activity of HaPs, in particular MAPbI₃, which is one of the materials that has yielded high efficiency solar cells.

“Ferroelectricity” is the ability to change the spontaneous polarization in a material by an external electric field. It is a well-known dielectric phenomenon, existing in many oxide perovskites (12–14), and has been suggested to be present in HaPs, in particular MAPbI₃ (15, 16). A short overview of the “origins of polarity in perovskite and its detection” is given in SI Appendix, section 1. If the material is indeed ferroelectric, then this suggests the possible existence of bulk photovoltaics, which can arise due to existing spontaneous polarization in the bulk of the material (17). Ferroelectric MAPbI₃ could, however, have as main benefit (as broadly discussed elsewhere) (15–18) charge transport via domain walls between adjacent polar domains. The existence of polar domains induces charge separation, lowers charge recombination, and allows high conductivity due to local degeneracy of the SC along the domain walls (19, 20). If this is so, then it can explain the remarkably high voltage efficiency, that is, low voltage loss in HaP-based solar cells [estimated as the difference between, or ratio, of open-circuit voltage and band gap: (E_G − V_OC) and (V_OC/E_G), respectively (21, 22)], especially for those with iodide as the halide. A further indication for a low recombination rate of photogenerated carriers is the respectable voltage and current at maximum power that these HaP-based devices possess, which makes the question whether HaPs can be ferroelectric of more than fundamental scientific interest.

Whereas existence of ferroelectricity in MAPbI₃ was suggested theoretically (15, 16), evidence on whether HaPs actually possess the domain structure that typifies a ferroelectric material are found to be quite contradictory (22–35). To analyze the question whether HaPs are actually ferroelectric, we need to test for the presence/absence of several fundamental phenomena that are tightly related to it.

Necessary conditions for bulk ferroelectricity to exist are as follows: (i) absence of an inversion symmetry (i.e., a noncentrosymmetric material), which may lead to (ii) a unit cell with a permanent polarity, where (iii) an assembly of polar unit cells facing the same direction, which will form a so-called “polar domain.” An assembly of periodically ordered polar domains, facing different directions (usually 180° or 90° to each other), will form the bulk of a ferroelectric material. (iv) The polarity of these polar domains must switch when sufficiently high electric fields are applied.

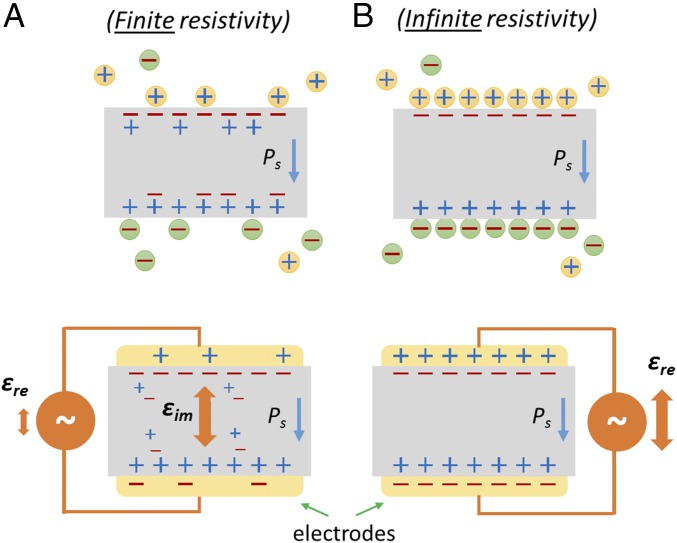
The most straightforward way to prove a material is ferroelectric is by showing switchable polarization (P) under an applied electric field (E), which results in a commonly presented P–E hysteresis loop (36, 37). In materials for which the energetic cost to reverse their polarity is too high (due to lattice rigidity, as is the case for ZnO) or the required electric potential is higher than the dissociation potential of the material, observing a switchable polarization may be very challenging. In MAPbI₃, which has a low bandgap (1.55–1.60 eV) (38) with relatively high electronic, and possibly some ionic conductivity (39), with low formation energy (40, 41), detection of possible ferroelectric switching is challenging. Indeed, previous attempts to find such evidence (23, 24) showed results that were contradictory to what was predicted from theory (15, 16). Here, we use the lossy part of the dielectric response (in contrast to using the energy storage part of the dielectric response as can be done with insulating ferroelectrics; Fig. 1), which yields clear ferroelectric P–E behavior from tetragonal MAPbI₃ crystals.

Fig. 1.

Illustration of the conceptual difference between (A) a lossy SC and (B) an insulator; both are shown without (Top) and with (Bottom) electrodes. Under an applied AC bias, for the lossy SC the dielectric response related to energy dissipation (ε_im) will dominate, whereas for the insulator the dielectric response related to energy storage (ε_re) will dominate. P_s represents a spontaneous polarization.

Still, as this is a highly debated issue, further evidence for ferroelectricity of the material must exist and is, therefore, shown. Under steady-state conditions (i.e., under zero applied field), there will be an energetic cost to having a dipole in the bulk of a solid. One (or more) of the following screening mechanisms will, therefore, be active (19):

• i)Accumulation of oppositely charged species at the outer surface of the polar bulk (e.g., adsorption of charged molecules or free charges from the environment or adjacent electrodes, respectively). By depositing electrodes on opposite crystal faces, one can measure the reorganization charge flow of these charges, when the temperature, which changes the spontaneous polarization, is changed. This phenomenon is called “pyroelectricity” and is direct evidence for existing polarity. Earlier, we showed clear experimental evidence that at room temperature (RT), cubic MAPbBr₃ is not pyroelectric (22). Here, we prove experimentally that tetragonal MAPbI₃, the stable RT phase of this material, is pyroelectric and thus polar.
• ii)Accumulation of mobile electrons and holes from the polar bulk material itself can occur if the bulk materials is sufficiently conductive, greater than ∼10⁻⁶ S·cm⁻¹, a reasonable value for a low bandgap SC, such as MAPbI₃. In this sense, leakage currents should dominate the dielectric response and, as we will see, are affected by the bulk overall polarization.
• iii)Stacking of domains of opposite polarity to decrease Coulomb repulsion, but at the cost of forming a “domain-wall.” For many known ferroelectric (as well as ferromagnetic) materials, the periodicity between the domains, ω, scales with the crystal thickness along its polar axis, D, as $\omega \hspace{0.17em}\sim \hspace{0.17em}{D}^{\gamma }$. γ is the power dependence that theoretically should be equal to 0.5 (according to the Landau–Lifshitz–Kittel model) (42, 43). We show that the tetragonal MAPbI₃ follows this rule.

To complete the picture, as polar materials are also noncentrosymmetric, we show positive results of second harmonic generation (SHG), which must exist in a polar medium (44). Based on our results related to domain size and orientation, we explain why previous attempts to detect SHG in MAPbI₃ were not successful (25).

Results and Discussion

Pyroelectricity.

As in our earlier work on MAPbBr₃ (22), we used periodic pulse pyroelectric measurements (45–47) to determine whether tetragonal MAPbI₃ is polar along its c axis. Pyroelectric currents can be distinguished from other possible thermally stimulated electric response (TSER) (thermoelectricity or flexoelectricity) (22, 48) by heating once one, and once the other side of the crystal periodically. Pyroelectric currents will reverse their sign once a crystal, together with its electrical leads, is flipped (by 180° on its other face). Thermoelectricity, however, is generated due to a temperature gradient between the two sides of a (semi)conducting bulk and will not depend on an internal direction of a dipole. Therefore, two complementary measurements were done, heating once one, and once the other side of a crystal.

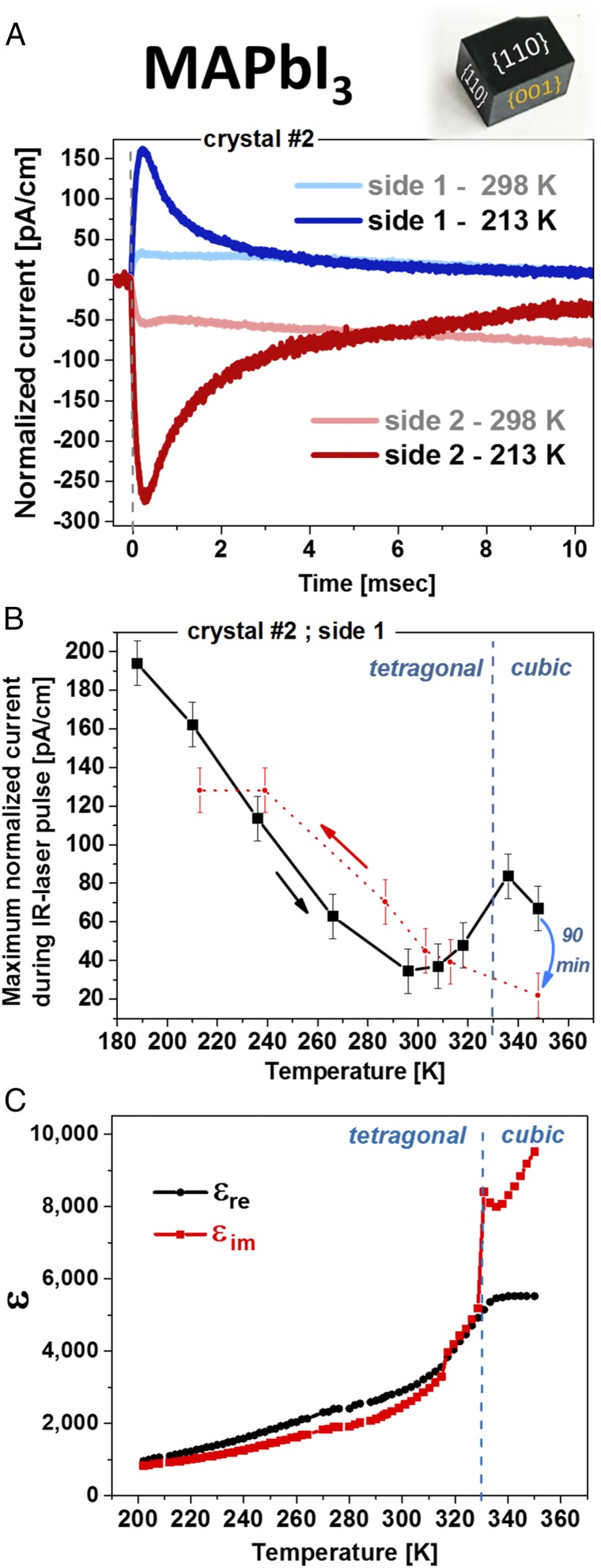
Fig. 2A shows that, along the <001> direction (if the electrodes are deposited on the {001} planes), a clear pyroelectric response, J_pyro, is observed. The experiment is done at low temperatures (LTs), ∼210 K, to reduce any thermoelectric contribution to the TSER. Direct proportionality between a SC’s thermoelectricity and conductivity implies that thermoelectric currents will become more dominant at higher temperatures, because the conductivity of a SC increases with temperature (SI Appendix, Fig. S2C). Although at RT the pyroelectric response is still present, it is much weaker than at LT (SI Appendix, Fig. S2 A and B), where it become the dominating part of the TSER. Apart from reduced thermoelectricity, lower electrical conductivity also should decrease leakage currents and, usually increase the effective spontaneous polarization. Both of these two factors should increase the pyroelectric response.

Fig. 2.

Pyroelectric response and relative permittivity measurements. (A) Pyroelectric response at RT (pale-colored plots) and 213 K, LT (deep-colored plots), with contacts on the {001} planes of a MAPbI₃ crystal. At RT, the response is convoluted with some thermoelectric currents. Evidence from different crystals can be found in SI Appendix, Fig. S2. (B) Peak-current value dependence on temperature, which shows a TSER that is characteristic for a pyroelectric material (for details, see main text). Evidence for all of the points in the plot can be found in SI Appendix, Fig. S3. (C) The real and imaginary parts of the dependence of the relative permittivity on temperature at 1 kHz (on different crystals than those used for A). The dielectric anomaly at the cubic-tetragonal phase transition is typical for ferroelectric materials.

Fig. 2B shows, based on the peak-current value dependence on temperature, further evidence for the pyroelectric nature of MAPbI₃. The local maximum around the phase transition temperature (T_c) at 330 K reflects a rise in the pyroelectric response as expected from Ginsburg–Landau theory (49) at a ferroelectric-to-paraelectric phase transition. Thus, a local extremum around T_c is a strong indication that tetragonal MAPbI₃ is ferroelectric (50). Measuring real (ε_re) and the imaginary (ε_im) relative permittivity as a function of temperature shows a dielectric anomaly around T_c (Fig. 2C), as also previously observed in polycrystalline MAPbI₃ films (30), which supports the conclusion that tetragonal MAPbI₃ is ferroelectric (14, 51). The disappearance and reappearance of the pyroelectric response after exceeding the T_c to the cubic phase and cooling back to the tetragonal phase, lends further support to the polar nature of tetragonal MAPbI₃ and the nonpolar nature of the cubic phase, a result that agrees with our results for MAPbBr₃ (22). This also indicates that the response to the heat pulse is not related to trapped charges, as commonly found for MAPbBr₃.

The effect of the growth environment, which may induce a permanent dipole due to defects (e.g., as result of the presence of anti-solvent or stabilizer molecules in the lattice) (52), is checked by measuring pyroelectricity from crystals grown in different environments, all below T_c (SI Appendix, Fig. S2 A and B). Although there are some differences in the TSER profile, the basic pyroelectric behavior persists in all cases, a strong indication that pure tetragonal MAPbI₃ is polar, with a I4cm space group [and not I4/mcm as occasionally reported (25)]. Furthermore, the fast rise, followed by a decay, as seen in the TSER profile for all three types of crystals, indicates a polar-domain–like structure, as expected from a ferroelectric material. Further proof for ferroelectricity is presented in the following sections.

We note that the current measurements were carried out only after the surrounding temperature around the crystal was stabilized to ±1 K. This is done to avoid currents that are generated by a flexoelectric polarization (48, 53, 54), as can occur upon fast heating or cooling (SI Appendix, Fig. S4). Measuring along the nonpolar {110} direction under stable temperature conditions did not show any evidence of pyroelectricity. This is expected for measurement along a nonpolar direction where the polarization (which equals zero) does not change upon pulsed heating.

To check whether other tetragonal MAPbX₃ compounds are also pyroelectric, we measured tetragonal MAPbBr₃ (well below its T_c, which equals 235 K) (55) and found no pyroelectric response (SI Appendix, Fig. S5). Because the crystals were grown in their cubic phase, the absence of a pyroelectric response in tetragonal MAPbBr₃ may be due to the absence of polar domains or due to formation of randomly oriented polar domains that create an overall absence of polarization. Distinguishing between these options will require further investigation.

Ferroelectricity.

Classic, insulating, ferroelectric materials, where leakage currents are negligible, commonly show a distinctive dependence of their relative permittivity, ε, on a bias electric field, E (SI Appendix, Fig. S6A) (37, 56). For such insulating materials, the real part of the relative permittivity, ε_re, which is the dielectric response related to energy storage, dominates the complex relative permittivity. The imaginary part of the relative permittivity, ε_im (the dielectric response related to energy dissipation), is therefore usually neglected (SI Appendix, Fig. S6B and Fig. 1B).

In semiconducting ferroelectric materials, however, leakage currents, which are represented by ε_im (Fig. 1A), can become a significant part of the response (24, 57), as shown in Fig. 3A. To reconstruct a P–E hysteresis loop, we can simply integrate ε_im over the bias electric field, $E_{DC}$, based on the following equation:

$$\mathrm{\Delta }P={\epsilon }_0{\displaystyle \int }\epsilon \cdot \partial E\approx {\epsilon }_0{\displaystyle \int }{\epsilon }_{im}\cdot \partial E.$$ [1]

Here, ΔP is the change in polarization from the initial one, and ${\epsilon }_0$ is the vacuum permittivity. The first part of the equation is the relation between P and E, where the dielectric constant, which is directly related to the susceptibility, is a proportionality factor. The last part results directly for the case where ε_re can be neglected.

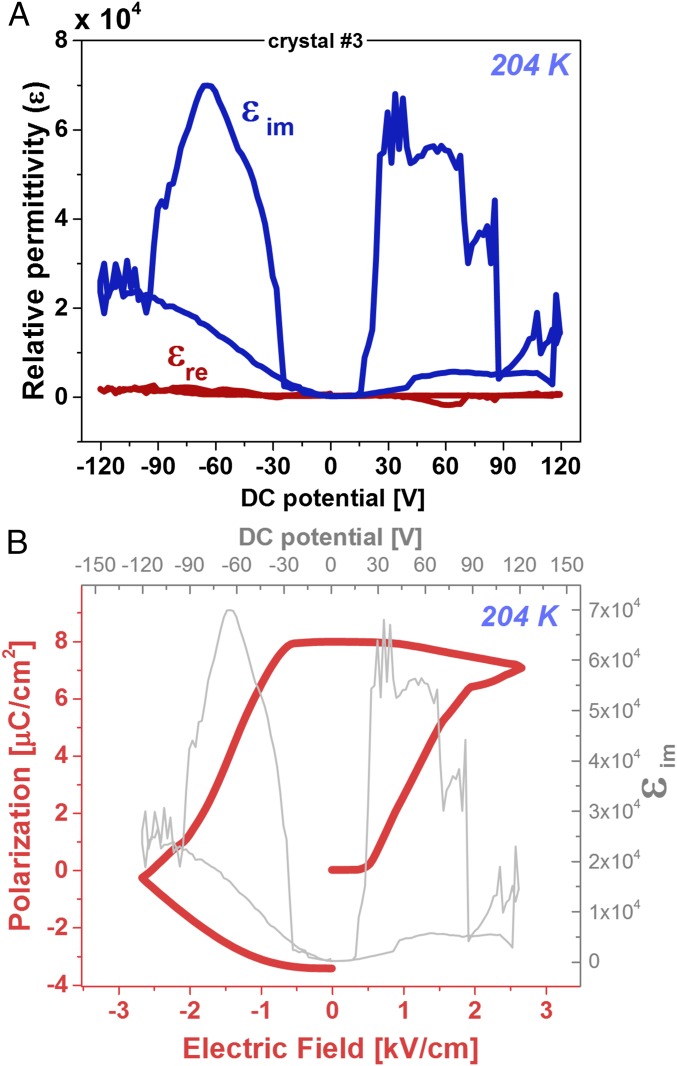
Fig. 3.

Ferroelectric response measurement. (A) Dielectric response at 204 K of a MAPbI₃ crystal along its <001> direction, measured at 2,222 Hz and V_AC = 0.1 V, as a function of applied bias, E_DC (x axis), showing that the imaginary (dissipative) part dominates the dielectric response. (B) P–E hysteresis loop obtained from integration of ε_im over E_DC (Eq. 1). The hysteresis loop is convoluted from a lossy bulk (i.e., resistor) response and ferroelectric polarization response, as illustrated in SI Appendix, Fig. S7A.

Note that the values of the polarization (P₀ + ΔP) in Fig. 3B are not centered around 0 (kilovolts per centimeter). This is a result of integration starting from ΔP = 0 and a nonzero net polarization (P₀ ≠ 0) to begin with, without which no pyroelectric response could exist.

Fig. 3B shows the result of the integration of ${\epsilon }_{im}$ over $E_{DC}$ measured on a tetragonal MAPbI₃ crystal. The shape of the hysteresis loop resembles clearly a ferroelectric polarization as a function of applied bias. Therefore, our result presents clear evidence for ferroelectric P–E switching in single crystals of tetragonal MAPbI₃. This result is a direct outcome from using the dissipative part of the permittivity to observe polarization switching of a ferroelectric bulk. In the previous cases, where only the real part of the permittivity was similarly analyzed (23, 24, 58) and it was concluded that did not exist.

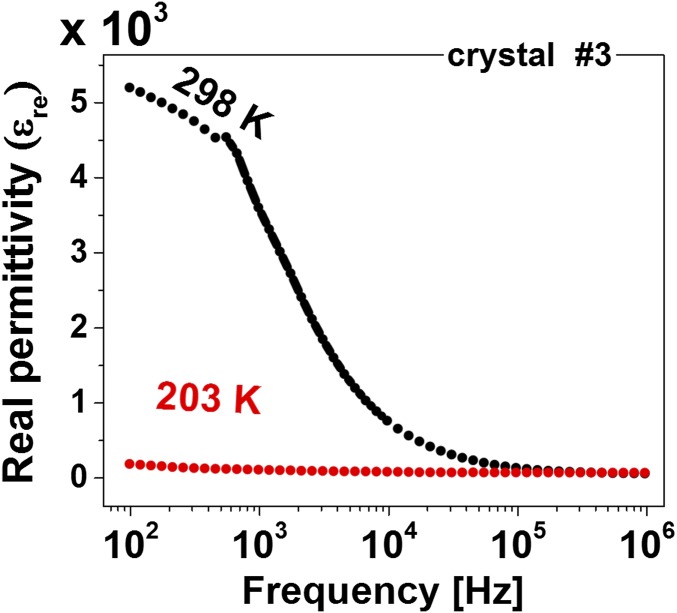
In the case of MAPbI₃, the ε_im–E dependence should be measured at as low a temperature as possible (in our case, at 204 K, to be well above the next tetragonal ↔ orthorhombic phase transition) for the following reasons: (i) the spontaneous polarization should increase with decreasing temperature, following the pyroelectric measurements (Fig. 2B); (ii) the rate of electrochemical and other decomposition reactions decreases with reduced temperature and conductivity; (iii) ionic conduction and/or dielectric relaxation, which can screen the ferroelectric behavior, decrease with decreasing temperature. The last possible reason (iii) is consistent with the frequency dependence of ε_re (Fig. 4), with a much larger increase in ε_re with decreasing frequency at RT than at 203 K. The reconstructed P–E hysteresis loop has the characteristics of a semiconducting ferroelectric material (59), the above-noted convolution of a ferroelectric part with a resistor part (SI Appendix, Fig. S7A).

Fig. 4.

Relative permittivity dependence on the sweeping frequency at RT and LT. The RT response shows a sharp increase with decreasing frequency, starting above 0.1 MHz, which can be related to ionic migration or dielectric relaxation response to an applied field (0.1 V_AC in this case).

The measured coercive field, E_c, is ∼0.6 kV·cm⁻¹, and the saturation field, E_sat, is around ∼2 kV·cm⁻¹ (SI Appendix, Fig. S7B). The saturation change in polarization, ΔP_sat, is ∼7 μC·cm⁻², which is very close to the 8 μC·cm⁻² predicted by Fan et al. (24) for MAPbI₃ at RT, although somewhat smaller than the 38 μC·cm⁻² predicted by Frost et al. (60).

At RT, the sample decomposed around −1.2 kV·cm⁻¹ (SI Appendix, Fig. S8). Before decomposition occurs, the P–E loop resembles a ferroelectric loop, although such loop can originate also from electrochemical or ionic migration effects (61), which are not negligible at 2,222 Hz as can be seen in Fig. 4.

Ferroelectric Domain Size.

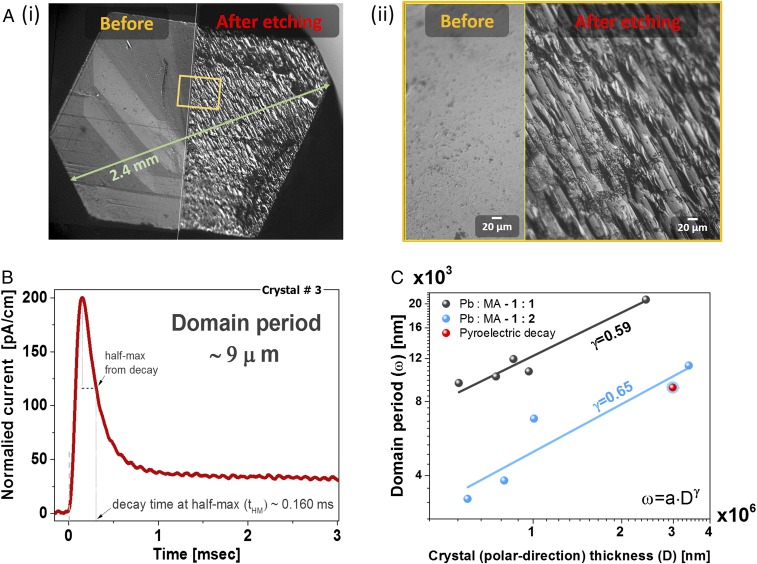
After showing MAPbI₃ responds to an electric bias as a ferroelectric material, and to periodic thermal change, it is now left to prove the existence of polar domains to complete the picture. Due to a different charge density between adjacent domains and/or between a domain and a domain wall, the chemical activity should vary between the different parts. Following this logic, chemical etching should uncover a periodic structuring as was demonstrated for different ferroelectric materials (62–64).

After testing several solvents, acetone was found to reveal beautifully ordered periodic domains stacked along the polar axis of the crystal (Fig. 5A and SI Appendix, Fig. S10). This exposed pattern can explain both the smooth cleaving along the c (polar) planes of the crystal and the jagged cleaving perpendicular to it that we find. This simple etching procedure can also reveal twin grain boundaries at which the polar domains are perpendicular to each other (SI Appendix, Fig. S9B).

Fig. 5.

Evidence for polar domains and their scalability with crystal size. (A) Bright-field image from a light microscope of a crystal before and after etching in acetone for 120 s. The crystal (2.4 mm) was grown from a 1:1 PbI₂:MAI solution, using ethyl acetate as antisolvent (for comparison, an example for 0.56-mm crystal is shown in SI Appendix, Fig. S9). (ii) Magnification of the yellow rectangle marked in i. (B) The pyroelectric decay from crystal #3 (SI Appendix, Fig. S2B) when measured with amplification of 10⁷ (discharge time, ∼0.02 ms). Crystal #3 was grown from a 1:2 PbI₂-to-MAI solution. Based on the analysis related to Eq. 2, the domain period should be ∼9 μm. (C) Domain periodicity with respect to the crystal thickness in the polar direction. The data are an average derived from microscope images after etching in acetone for ∼120 s. The red dot represents the value obtained from the pyroelectric TSER (crystal #3) from B. The values of γ are obtained by fitting to ω = a·D^γ.

Another indication for the existence of polar domains is the decaying TSER profile. When polar domains are stacked opposite to each other (head-to-head, 180°), the TSER should vanish when the externally induced temperature change is equilibrated between two adjacent domains. The rate of this equilibration is related to the polar domain thickness, or domain period, ω, and the thermal diffusivity, δ, of the polar bulk. Taking the 200 K value of δ = 6 × 10⁻³ cm²·s⁻¹ for MAPbI₃ (65), and the decay time from the maximum current until it reaches its half-maximum value (subtracting the system delay, 0.02 ms), t_HM, one can estimate ω by using the following equation (for further information, see SI Appendix, section 2) (66):

$$\omega =0.48\sqrt{4\cdot \delta \cdot t_{HM}}.$$ [2]

With t_HM = 0.16 ms, we find that ω ∼ 9 μm, which is comparable, in terms of order of magnitude, to what we find from chemical etching (Fig. 5A and SI Appendix, Fig. S10).

ω should scale with the total crystal thickness along its polar axis, D, as $\omega \hspace{0.17em}=\hspace{0.17em}a\cdot D^{\gamma }$, where a is a prefactor that depends on the domain-wall thickness and γ is theoretically 0.5 (42, 43) and empirically between ∼0.4 and 0.6 (67–69). By relating ω to D from several single crystals (without grain boundaries; SI Appendix, Fig. S9B), in Fig. 5C we find $\omega \sim D^{0.6}$. Despite an uncertainty in γ due to having only a few points over a small range of crystal sizes, it is interesting to note that, for BiFeO₃, which is a known ferroelectric SC, γ was found to be 0.59. Comparison with scaling relations of other ferroic materials is shown in SI Appendix, Fig. S10. It is also found that crystals grown in 1:1 or 1:2 PbI₂ to MAI solutions give a slightly different result, mostly in the a prefactor. Because an excess of MAI was found to reduce carrier concentration in MAPbI₃ films (70), this small difference may be related to a doping effect.

Although the scaling relation is clear, quantitative extrapolation to dimensions of thin films will require further tuning. For instance, by extrapolating to D = 100 nm, ω of the 1:1 and 1:2 (of PbI₂:MAI) cases result in domains of 56 or 13 nm, respectively. For the former case, it would mean less than two domains in the sample in the polar direction. In the latter, it implies that each domain contains less than ∼10 unit cells (71), a value that should be treated with caution. On the other hand, on the scale where D = 2 μm, the typical size of a crystal shown in Hermes et al. (27), ω reaches values of few hundreds of nanometers, which is of the scale of the ferroelastic domains they observed.

Second Harmonic Generation.

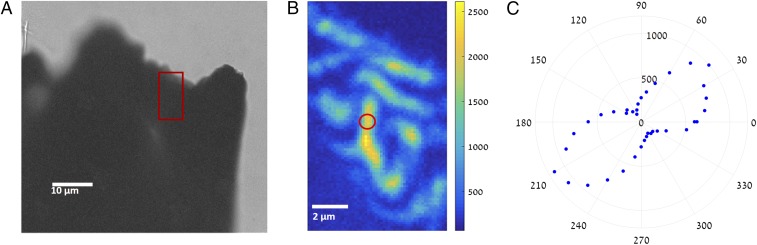
Under the measurement conditions where the Rayleigh range (i.e., axial extent of the focal spot) of the excitation beam is much smaller than the crystal thickness, second harmonic generation (SHG) can be observed only from the vicinity of the microcrystal surface due to phase-matching conditions leading to destructive interference even from a SHG-active bulk sample (44). Still, the observed stripe pattern of the SHG signal that appears in Fig. 6B may be attributed to the ferroelectric domains of MAPbI₃ as seen after etching the crystals. Unfortunately, this stripe pattern was observed only in some of the measured samples (SI Appendix, Fig. S11). This may be due to the sample preparation procedure (whereby the fragments are not always faceted along the axes exhibiting domains) but could also indicate that the source of the SHG is in the uneven surface of the crystal. The signal dependence on polarization, which revealed a dipolar-like pattern similar in orientation (Fig. 6C) across the measured area regardless of the exact position, is in agreement with the presence of ferroelectric domains. The reason is that, in each one of the domains, the crystal orientation, which determines the SHG polarization response, is similar throughout the scanned area.

Fig. 6.

Second harmonic generation (SHG) response. (A) Bright-field transmission image of a crystal fragment. (B) A scan of the SHG signal from an area of a crystal fragment, marked approximately by the red box; the patchy nature of the SHG signal may indicate the ferroelectric domains. The color bar is in photon counts per second (CPS). (C) A polar plot of the SHG signal from the marked point in B, which reveals a dipolar-like pattern from CPS vs. polarization angle of the excitation laser.

Our results do not agree with a recent report on SHG in MAPbI₃ where no evidence of SHG activity was found in polycrystalline samples (25). We will now explain why our results do not necessarily contradict their experimental findings. In the presence of multiple ferroelectric domains, destructive interference between SHG, scattered from domains with inverted polarity, is likely to lead to extremely low SHG signals, observed in such an ensemble measurement. To be able to observe SHG in such a case, we need to optically excite a single domain that is larger than the scanned pixel—a case that easily can be found by scratching a millimeter-sized single crystal.

Summary and Conclusions

We have shown multiple experimental evidence that proves that the tetragonal phase of MAPbI₃ is ferroelectric. It behaves as a ferroelectric bulk material (i.e., polarization inversion under an external electric field; Fig. 3), and it expresses all of the necessary ferroelectricity-related features: lack of an inversion symmetry (proven by existence of SHG; Fig. 6), spontaneous polarization (proven by showing existing pyroelectricity; Fig. 2), and presence of polar domains (as seen after chemical etching; Fig. 5).

By analyzing the imaginary part of the permittivity, ε_im, we find the coercive and saturation fields to be ∼0.6 and ∼2 kV·cm⁻¹, respectively. The saturation change in polarization was found to be ∼7 μC·cm⁻², a value that is very close to one of the theoretical estimates (∼8 μC·cm⁻²) (24). We note that, to obtain the changes in the polarization, we used the response of ε_im instead of that of ε_re, which is uncommon, and, in fact, we are not aware of the use of such analysis before. The reason to do so, is, however, very clear: in a leaky dielectric (a SC) as MAPbI₃, where the imaginary (energy-dissipative) part dominates over the real (energy-conservative) part, the dielectric response will be mostly pronounced by the loss-related permittivity, that is, ε_im. Such analysis should, indeed, be considered when analyzing any dielectric response of leaky SCs—for thin films/ceramics as well as single crystals.

Besides the electric response, ferroelectricity is being expressed also structurally by creating periodically ordered polar domains.

We see these polar domains after etching with acetone or from analyzing the pyroelectric decay. Both give a similar result. As common in other ferroelectric (as well as ferromagnetic) materials, in MAPbI₃ the relation between domain periodicity, ω, and the crystal thickness, D, also follows the Landau–Lifshitz–Kittle model scaling relation as $\omega \sim D^{0.6}$. We find that crystal preparation may influence the ω–D relation—possibly as a result of difference in doping, that is, electrical conductivity. Based on the etching and periodic structure, the domains seem to form a head-to-head orientation.

The existing pyroelectricity and SHG are two expressions of the crystallographic nature of the material with no applied external fields. The results confirm that the material has a noncentrosymmetric structure and is polar, which will hopefully put an end to the confusion in the literature regarding the space-group of this tetragonal HaP: it is I4cm and not I4/mcm. It is still interesting to know whether such symmetry is common to all organic–inorganic tetragonal symmetries, or something specific to MAPbI₃. Although this question about the symmetry is proven by the existence of pyroelectricity, the recent report on the absence of SHG in MAPbI₃ (25) gave reason to doubt, and, thus, we show clear evidence for SHG and explain why no SHG was found in ref. 25.

How will ferroelectricity affect the operation of photovoltaic cells, based on MAPbI₃? To answer this question, we need to take into account the leaky nature of MAPbI₃, which will prevent the buildup of an internal electric field to help separate electrons and holes due to spontaneous polarization. However, within a single domain, this effect might possibly play a role by reducing intradomain charge-recombination. Still, there is a quite a road ahead to find evidence in favor of such a mechanism (of interest as we want to explain the low electron-hole recombination rate). Our finding that etching reveals a domain-like structure, implies a high density of charge carriers at the domain walls, which might fit the idea of “ferroelectric highways” (60).

We stress that semiconducting ferroelectric materials are much less abundantly studied than normal insulating ferroelectric materials, on which our knowledge of ferroelectricity is built on. The leaky nature of SC–ferroelectric materials, as exemplified here, together with the highly dynamic nature of the MAPbI₃ lattice (especially at RT; Fig. 4) made the task of proving its ferroelectric nature very challenging. Analysis of the most dominant dielectric response, probing millimeter-sized single crystals with a defined orientation, and probing a small fraction of this crystal when looking for a SHG response has been proven here to be a good general strategy.

Experimental Procedures

Precursor Solution.

In total, 714 mg of methylammonium iodide (MAI) (Dyesol) and 2,070 mg of PbI₂ (99.999%; Sigma-Aldrich) were mixed with 15 mL of acetonitrile (HPLC grade; ≥99.7%; BioLab). For a 1:2 molar ratio of PbI₂:MAI, the amount of Pb was 1,035 mg. The solution was sonicated for 5 min and then mixed with 1.5 mL of hydroiodic acid (57% in H₂O, distilled, stabilized with hypophosphorous acid ≤1.5%, 99.95%; Sigma-Aldrich).

Crystal Growth.

MAPbI₃ single crystals were grown at room temperature (below the tetragonal → cubic phase transition temperature, 330 K; SI Appendix, Fig. S12) using the slow vapor saturation of an antisolvent method (8, 72). A glass vial with the precursor solution was placed in a second, larger glass vial containing an antisolvent—ethyl acetate (AR, ≥99.7%; BioLab) or diethylether (AR; BioLab). We used equal volumes of the solution and the antisolvent. The lid of the inner vial was loosened to control the antisolvent evaporation into the precursor solution. The lid of the outer vial was thoroughly sealed to prevent water penetration into the system and leakage of the solvent and/or antisolvent vapor. Millimeter-sized crystals were taken out of the system, dried (with a Kimwipe; Kimtech Science Brand), and stored in a silica-filled dry box.

We present results, based on 10 different crystals of MAPbI₃. Three out of the 10 were used for pyroelectricity experiments, 2 for ferroelectric domain-switching experiments, 9 for exposure of periodically ordered domains, and 1 for SHG measurements. Other supporting results, mainly from attempted ferroelectric domain switching that led to complete destruction of the sample, are not presented. In a few cases, we used crystals that were grown from modified precursor solutions [changing the amount of the stabilizer (hypophosphorous acid), normally present in HI (73), or varying the precursor ratio] to check whether the polar nature of MAPbI₃ depends on these parameters. Apart from some quantitative differences (Fig. 5C and SI Appendix, Fig. S3), no qualitative differences were observed.

Crystallographic Identification and Preparation.

For investigation of a polar dielectric crystal, identification of the polar crystallographic orientation is required. Following powder X-ray diffraction of pulverized crystals, which confirmed the grown crystals to be MAPbI₃ (71), we determined the polar direction of a crystal, using specular diffraction from the surface of a single crystal (SI Appendix, section 3 and Fig. S1). After selecting crystals of a rectangular-prism shape, of a few millimeters size, their crystallographic orientation was identified to be the {110} and {001} planes (SI Appendix, Fig. S1). The planes, orthogonal to the polar direction in a I4cm space group (to which polar MAPbI₃ should belong) (25), are the {001} ones. The {110} planes, which are orthogonal to {001}, are perpendicular to nonpolar directions of the crystal. To maximize the polar nature of an analyzed single crystal, all of the crystals were grown at RT, which is below the cubic-to-tetragonal phase transition temperature of MAPbI₃ at 330 K (SI Appendix, Fig. S12). The reason is that cooling down through the phase transition might create orthogonally oriented polar domains, which would complicate data analysis.

After planar identification, the crystals were cleaved to ∼0.5- to 1-mm-thick plates with an area of ∼6–9 mm².

Crystal Preparation for Electrical Characterizations.

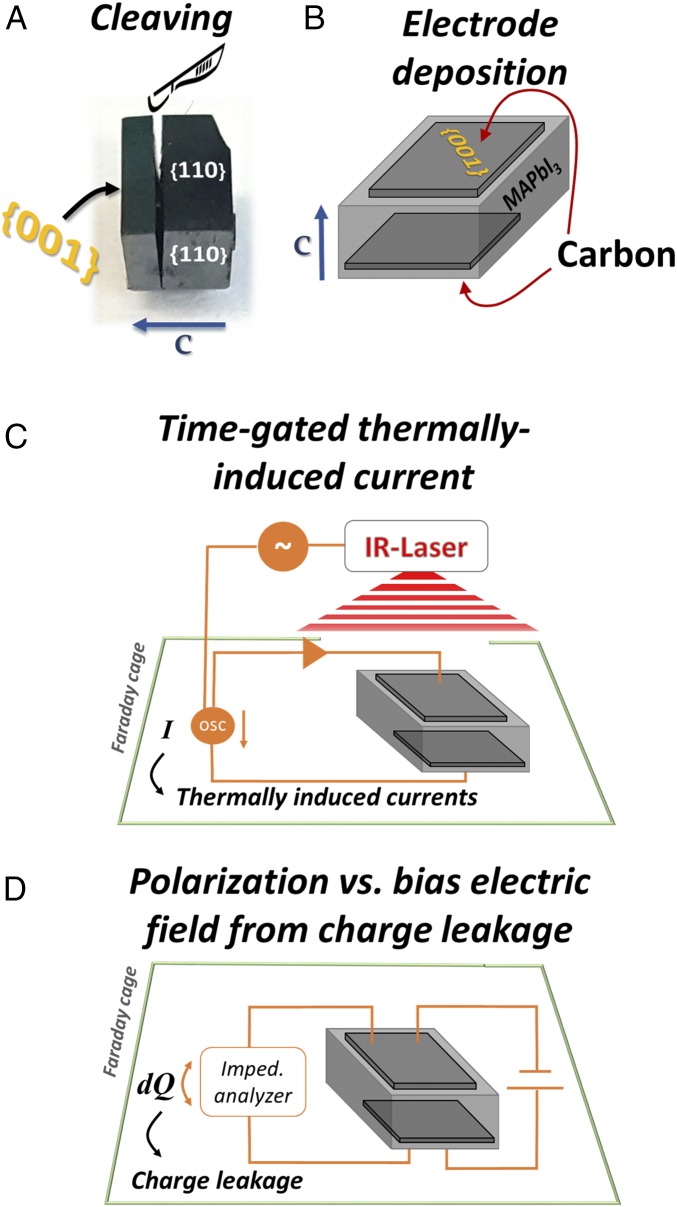
The expression of both pyroelectricity and polarization change in ferroelectric hysteresis loops is a function of the net dipole change in the material. Therefore, probing the change across the potentially polar direction (i.e., <001>) should, conceptually, give the most significant expression of polarization change, induced by changing the temperature, that is, pyroelectricity, and for ferroelectric domain switching, by applying bias. For this reason, after identifying the crystal faces by X-ray diffraction (SI Appendix, Fig. S1), the crystal was cleaved along the {001} planes. For the cleaving, a fine home-made alignment station and a sharp blade were used (for visualization, see Fig. 7A). Cleaving along the {001} planes was very clean, resulting in a highly reflective fresh surface. Cleaving along the {110} planes, on the other hand, always resulted in a jagged surface. This is an additional way of identifying the crystal’s orientation. Further discussion is in Results and Discussion.

Fig. 7.

Illustrations for sample preparation and dielectric-nature measurements. (A) Photograph of a MAPbI₃ crystal (#3), cleaved along its {001} planes after identifying its polar direction. (B) Illustration of the locations where the carbon electrodes were deposited. (C) General scheme of pyroelectricity generation and measurement setup. The circle with the “∼” symbol indicates a function generator. A circle with “OSC” indicates an oscilloscope. A triangle symbol indicates a current-to-voltage amplifier. (D) General scheme of the polarization measurements under external bias.

After cleaving, carbon electrodes were deposited (using a conductive carbon paint; SPI) on two parallel {001} planes (Fig. 7B). To make electrical contacts to the measuring circuit, one face of a crystal was placed on top of a copper plate (set as the Low terminal), while the opposite face was connected to a copper wire (set as the High terminal).

Pyroelectricity.

A periodic temperature change (Chynoweth) method, was used to measure pyroelectricity (45–47). A general scheme of the setup (heat generation and pyroelectric current measurement) is visualized in Fig. 7C. A sample was placed in a thermally isolated Faraday cage through which N₂ gas flowed. The temperature of the sample’s surrounding was controlled via a constant flow of cooled N₂ gas and electrical resistance heaters. The temperature was measured by a K-type thermocouple coupled to the copper plate, on which the crystals were mounted.

Periodic heating was achieved by pulsing a 1,470-nm IR-laser, triggered by a function generator. A sharp rectangular pulse (rise time, <<0.01 ms) was set to 15.2 ms with an overall duty cycle of 12.5%. The area on which the laser hit the crystal (∼3–8 mm⁻²) received ∼1.1 W·cm⁻². Under these conditions, the overall heating that can be expected is up to 3 K. The TSER was amplified through a current to voltage amplifier and was read by an oscilloscope synchronized to the function generator, which triggered the laser. The currents are normalized to the thickness of the crystal and the area of the electrodes, to get a result that allows comparison between the scanned crystals (SI Appendix, section 2) (46).

Ferroelectricity.

To determine the dielectric nature of MAPbI₃, we measured the permittivity, ε, as function of external DC bias, E_DC, using a high-resolution impedance analyzer (Alfa; Novocontrol) at 2,222 Hz with V_AC = 0.1 V (Fig. 7D). The electrical leads (carbon electrodes), connector architecture (Cu plate/crystal/Cu wire), and temperature control were identical to those used for the pyroelectricity setup. The choice of frequency (2,222 Hz) was made to avoid the response from the carbon contacts, which could appear at higher frequencies (approximately megahertz), a result of a nonnegligible AC current due to the low impedance of the sample (>10 kHz), or contributions from ion migration or external discharge at lower frequencies (approximately a few hertz), which makes the construction of the polarization hysteresis from the permittivity challenging (24, 56). Dielectric measurements as a function of temperature were done with the same impedance analyzer setup. To achieve the desired temperature control, a Lakeshore temperature controller and a custom-made vacuum chamber were used.

The polarization change, ΔP, is calculated (following Eq. 1) by integrating ε_im over an increment of E_DC (the reasoning for this is discussed in Results and Discussion). Therefore, to extract the correct change in polarization, the integration is done over the absolute incremental change in the applied bias, multiplied by the sign of the polarity of the applied bias. Due to degradation of the crystal under high bias, the reported results are from a single (first) P–E_DC scan, at each temperature.

Ferroelectric Domain-Size Evaluation.

Two approaches were used to estimate the domain size (or “domain periodicity,” ω). The first is etching a crystal in acetone for 120 s under continuous stirring of the solvent around the crystal at RT. The crystal was photographed using a light microscope (Zeiss AXIO with a DO3THINK/DS CB Y300E-H digital camera). The second approach was via the pyroelectric decay. At the amplifications of 10⁷ to 10⁹ that were used, the discharge time of the amplifier is ∼0.02–1 ms. Estimates of polar domain thickness were made, using the signals collected at the lower amplification (10⁷) to avoid distortion of the signal’s profile (which was found to be of the order of 0.5–5 ms). Further clarification of domain-size estimates from the pyroelectric decay signal can be found in SI Appendix, section 2.

SHG Measurements.

The 100-fs pulses at 800 nm at an 80-MHz repetition rate from a Ti:sapphire laser (Coherent; Chameleon Ultra II) were downconverted, using a synchronously pumped OPO (Coherent; Chameleon Compact OPO), to get the 1,100-nm laser wavelength, desired for excitation. The laser was directed into a microscope (Zeiss Axiovert 200 inverted microscope) and focused using an oil-immersion objective (Zeiss Plan Apochromat; 63×, N.A. 1.4). A clean-up polarizer and a rotation stage with a half-wave plate were placed before the microscope to control the excitation polarization. The spectrally filtered (Semrock; 561/40; Thorlabs KG3 heat glass) signal was epidetected (i.e., excitation and collection were from the same side of the crystal), coupled to a multimode fiber, and detected by a single-photon avalanche photodiode (Perkin-Elmer; SPCM), which was connected to a time-correlated single-photon counting system (Picoquant HydraHarp 400). Samples were placed onto a no. 1 coverslip, yielding some crystal fragments, prepared by scraping a crystal’s {110} face, with dimensions of ∼10–100 µm. SHG images were formed by scanning the excitation spot along the side lying on the coverslip. The exact crystallographic orientation of each scanned face was not analyzed.