Theory of long binding events in single-molecule–controlled rotation experiments on F₁-ATPase

Significance

The treatment of nucleotide (ATP and ADP) binding and release in our previous papers is now extended to include a much wider range of rotor angles. It now treats composite events associated with ATP hydrolysis and ADP release and, in the reverse direction, ATP synthesis and release. A method of treating composite events is formulated and used to extract reaction rate constants in the system and to predict the lifetime distribution of long binding events that can be compared with and used to analyze future experimental data.

Abstract

The theory of elastic group transfer for the binding and release rate constants for nucleotides in F₁-ATPase as a function of the rotor angle is further extended in several respects. (i) A method is described for predicting the experimentally observed lifetime distribution of long binding events in the controlled rotation experiments by taking into account the hydrolysis and synthesis reactions occurring during these events. (ii) A method is also given for treating the long binding events in the experiments and obtaining the rate constants for the hydrolysis and synthesis reactions occurring during these events. (iii) The theory in the previous paper is given in a symmetric form, an extension that simplifies the application of the theory to experiments. It also includes a theory-based correction of the reported “on” and “off” rates by calculating the missed events. A near symmetry of the data about the angle of −40° and a “turnover” in the binding rate data vs. rotor angle for angles greater than $\sim$40° is also discussed.

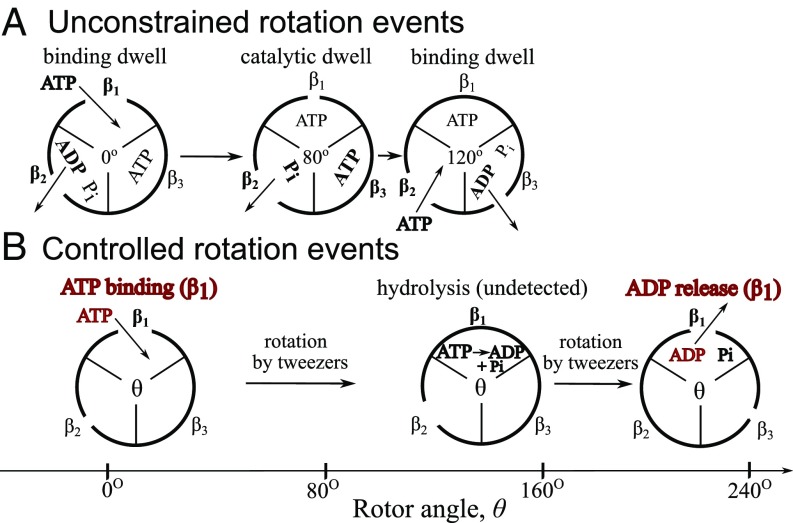
Controlled rotation experiments directly monitor events of nucleotide binding and release in single F₁-ATPase molecules, (1, 2) processes that trigger, together with P_i release, the “energetic” steps in the F₁-ATPase. In the F₁-ATPase, the spontaneous rotation of the rotor shaft proceeds in substeps of 80° associated with the concerted ATP binding and ADP release (from a different subunit), and 40° associated with ATP hydrolysis and P_i release from different subunits (Fig. 1A.). In the complete F_oF₁ ATP synthase, a cross-membrane ion transfer generates a torque (3, 4) that is used to synthesize ATP (1, 5).

Fig. 1.

Unconstrained rotor chemo-mechanical coupling scheme for stepping rotation of the F₁-ATPase (A) and a controlled rotation example of a composite event of ATP binding, ATP hydrolysis, and ADP release (B). The $\beta$ subunits (and species) that change during a step are in bold. The nucleotides that are monitored by fluorescence are shown in dark red.

Previously, we used theory and independent data on stalling and other experiments to predict and compare with controlled rotation experimental data for the ATP binding and release rate constants. The rate constants of ATP binding and release were calculated as a function of the rotor angle $\theta$ and agreed with the experimentally observed values in these experiments, using no adjustable parameters. In both theory and experiment, there was an exponential-like dependence of the rate constants on $\theta$, observed over a range of angles (6, 7).

In the present work, part of a series (6, 7), we treat the nucleotide binding and release in the F₁-ATPase for various species over a more extended angular domain than before. As a result, in the controlled rotation experiments, the processes now also include what Adachi et al. (2) termed long binding events, in which, as seen in Fig. 1B, the hydrolysis of an ATP is sandwiched between an ATP binding at an angle ${\theta }_0$ and an ADP release at $\theta$, the latter being followed by P_i release. Our analysis draws heavily on the “lifetime distribution” $\psi (\theta |{\theta }_0)$ of an event, defined in terms of the survival probability $p(\theta |{\theta }_0)$ for an event that begins at an angle of rotation ${\theta }_0$ and has survived at an angle $\theta$. Defined with respect to rotor angle rather than time, the lifetime distribution is $\psi (\theta |{\theta }_0)=-dp/d\theta =-dp/(\omega dt)$, where $\omega$ is the constant angular velocity in the controlled rotation experiment. Each event is labeled by a subscript, such as “hyd” for hydrolysis. The $\psi$’s are useful for describing a composite event in terms of the integrated product of the $\psi$’s of its individual events. Theory has been used to treat fast, undetected events of conformational change in proteins that occur during composite events in single-molecule FRET experiments (8).

A method is first developed (Calculating Lifetime Distributions) for obtaining lifetime distributions from long binding events associated with the binding, hydrolysis, and release of a nucleotide. The method is extended, for a system rotated in the opposite direction, to treating the longtime composite events associated with ADP and P_i binding and subsequent ATP synthesis. These lifetime distributions are then used (Extraction of $\theta$-Dependent Rate Constants of Synthesis and Hydrolysis from Long Binding Events) to obtain expressions for extracting angle-dependent rate constants from the experimental trajectory data when the latter become available. Procedures for implementing these methods are given in Procedures in the Calculation of Lifetime Distributions and the Rate Constants, and an application is given in An Application for the Predictive Calculation of Lifetime Distributions.

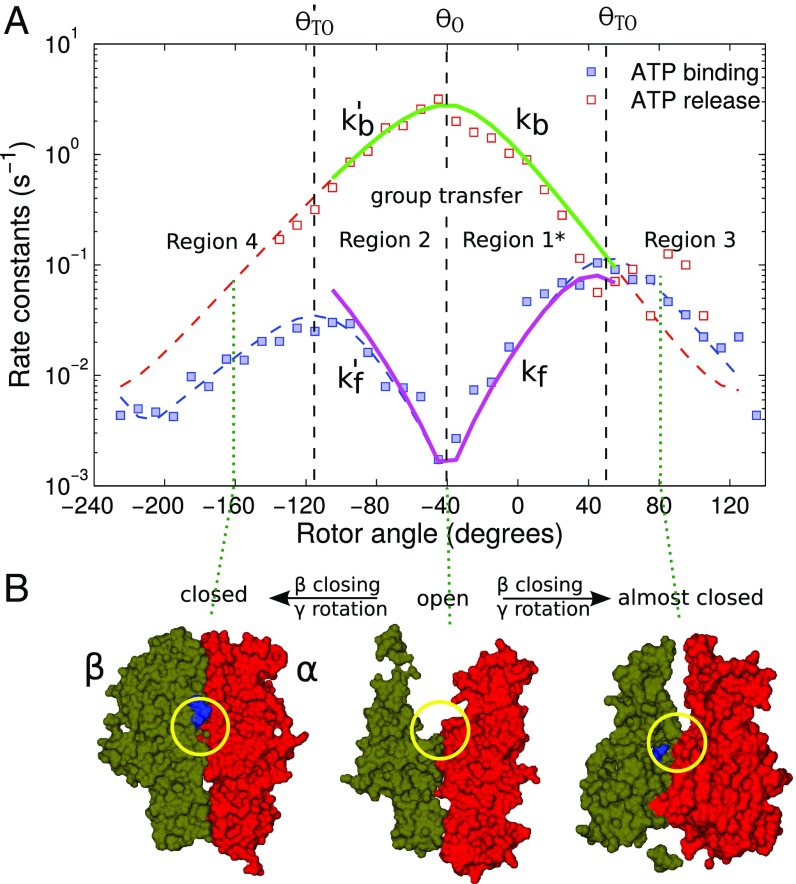
Our previous work is extended in two other respects: (i) a mathematically equivalent, but more symmetric, equation is given in Theory for the earlier (7) ATP binding rate vs. rotor angle expression; and (ii) the implementation for binding and release processes that was formerly from $-{45}^{\circ }$ to ${45}^{\circ }$ (region 1 in Fig. 2) is extended in Application of Theory in an Extended Angular Region to predict the rate constants in the broader $\theta$-range from $-{110}^{\circ }$ to ${50}^{\circ }$ (approximately regions 1 and 2 in Fig. 2). The range now includes in the hydrolysis direction ATP binding and, after hydrolysis, ADP and P_i release. In the synthesis mode, it now includes ADP binding and, after synthesis, ATP release. We treat the latter as the inverse of the hydrolysis scheme. A mirror-like symmetry of the ATP binding and release rate constants, $k_f$ and $k_b$, vs. $\theta$ function centered around $\theta \cong -{40}^{\circ }$ as seen in Fig. 2 is also discussed in Application of Theory in an Extended Angular Region.

Fig. 2.

Angular dependence of rate constants reported in controlled rotation experiments (A) and corresponding structural changes of the nucleotide binding host $\beta$ subunit at the cited rotor angle (dotted lines; B). Red open and blue filled symbols in A are data points for binding and release processes for ATP at 25-nM concentration monitored in experiments to which dashed lines of matching colors were fitted as guides. Solid lines are the theoretically predicted rate constants, taking into account effects such as missed events and using the total time T instead of the time in the empty state T₀.

Calculation of the Lifetime Distribution and Extraction of the $𝜽$-Dependent Rate Constants of Synthesis and Hydrolysis from Long Binding Events

Calculating Lifetime Distributions.

In the controlled rotation experiments, Adachi et al. (2) used small intervals of angles (bins) to detect changes in the F₁-ATPase the nucleotide occupancy $\sigma$ in the single-molecule fluorescence trajectories, so as to estimate the binding and release rates. They focused on the statistics of switching events in $\theta$ intervals of 10°.

To extract rate constants of the individual steps in the composite events systems, we first obtain the lifetime distributions involved in the steps. To treat the lifetime distribution data available from these experiments (e.g., from the long binding events), we describe a method that incorporates the strong $\theta$-dependence of the associated binding, hydrolysis, and ADP release processes.

In the experiments by Adachi et al. (2), the $\gamma$ shaft is rotated either in a positive (hydrolysis) or negative (synthesis) direction at a fixed angular velocity of $\omega =\pm 360/5=\pm 72{}^{\circ }/s$, which yields a time-dependent angle $\theta (t)=\omega (t-t_0)+{\theta }_0$. During rotation in the positive direction, if a binding of ATP from solution occurs in the vicinity of $\theta =0°$ and is followed by a long binding event of time $\tau$ corresponding to a rotation of >$120°$, the subsequent release event is classified as ADP release, meaning that hydrolysis occurred during the time $\tau$. Accordingly, a long binding event of ATP involves a series of three events: ATP binding at ${\theta }_0$, hydrolysis at ${\theta }_1$, and ADP release at ${\theta }_2$. Similarly, during rotation in the negative direction, if an ADP in the presence of P_i binds somewhere in the vicinity of $-40°$, a long binding event lasts for >$120°$ during a rotation in a negative direction. The latter events include an ATP release, because ATP synthesis presumably occurred. Such composite events can also occur for long delay events beginning at ${\theta }_0>140°$ or so, even for short binding times, due to the high rate of hydrolysis at those angles. The present treatment includes these long delay events as well.

To treat the long binding or long delay events, we use the $\psi (\theta |{\theta }_0)$ defined earlier. For the successive events, binding at ${\theta }_0$, hydrolysis of ATP at ${\theta }_1$, with a lifetime density ${\psi }_{\mathit{\text{hyd}}}$, and ADP release at $\theta$, with a lifetime density ${\psi }_{\mathit{\text{off,ADP}}}$, the lifetime density of these combined events, ${\psi }_{\mathit{\text{hyd-off}}}$, equals (e.g., ref. 9):

$${\psi }_{\mathit{\text{hyd-off}}}(\theta |{\theta }_0)={\int }_{{\theta }_0}^{\theta }{\psi }_{\mathit{\text{off,ADP}}}(\theta |{\theta }_1){\psi }_{\text{ℎ𝑦𝑑}}({\theta }_1|{\theta }_0)d{\theta }_1.$$ [1]

Recalling that $p(\theta |{\theta }_0)$ is the probability that a state at rotor angle ${\theta }_0$ has survived at $\theta$, when the $\theta$-dependent rate constant $k(\theta )$ is known for a process that changes that state, such as hydrolysis or ADP release (and we determine it below), then $dp(\theta |{\theta }_0)/dt$ can be calculated from the rate equation $\omega dp(\theta |{\theta }_0)/d\theta =-k(\theta )p(\theta |{\theta }_0)$, yielding

$$p(\theta |{\theta }_0)=\exp [-(1/\omega ){\int }_{{\theta }_0}^{\theta }k(\theta \prime )d\theta \prime ].$$ [2]

Consider a pair of events during rotation in the hydrolysis (positive) direction, ATP binding at ${\theta }_0$, and hydrolysis at $\theta$ with a hydrolysis rate of $k_{\text{ℎ𝑦𝑑}}(\theta )$. Then, using Eq. 2, the lifetime density for hydrolysis is given by

$${\psi }_{\text{ℎ𝑦𝑑}}(\theta |{\theta }_0)=-d{p}_{\text{ℎ𝑦𝑑}}(\theta |{\theta }_0)/d\theta =[k_{\text{ℎ𝑦𝑑}}(\theta )/\omega ]\exp [-(1/\omega ){\int }_{{\theta }_0}^{\theta }{k}_{\text{ℎ𝑦𝑑}}(\theta \prime )d\theta \prime ].$$ [3]

An expression similar to Eqs. 1–3 applies to the composite events during rotation in the synthesis (negative) direction: ADP binding at ${\theta }_0$, followed by synthesis at ${\theta }_1$, and then by ATP release at a more negative angle $\theta$, yielding the lifetime distribution function ${\psi }_{\mathit{\text{syn-off}}}(\theta |{\theta }_0)$,

$${\psi }_{\mathit{\text{syn-off}}}(\theta |{\theta }_0)={\int }_{{\theta }_0}^{\theta }{\psi }_{\mathit{\text{off,ADP}}}(\theta |{\theta }_1){\psi }_{\text{𝑠𝑦𝑛}}({\theta }_1|{\theta }_0)d{\theta }_1.$$ [4]

Here, the expressions for ${\psi }_{\mathit{\text{off,ADP}}}$ and ${\psi }_{\text{𝑠𝑦𝑛}}$ are similar to Eq. 3, with $k_{\text{ℎ𝑦𝑑}}(\theta )$ replaced by $k_{\text{𝑜𝑓𝑓𝐴𝐷𝑃}}(\theta )$ and $k_{\text{𝑠𝑦𝑛}}(\theta )$, respectively. Thereby, these lifetime distributions can be calculated from the $\theta$-dependent rate constants $k_{\mathit{\text{off,ADP}}}$ and $k_{\text{𝑠𝑦𝑛}}$ estimated from independent experiments in $\theta$ ranges where data are available, or calculated from theory. The integrals in Eqs. 1 and 4 can be evaluated numerically, thereby yielding ${\psi }_{\mathit{\text{hyd-off}}}(\theta |{\theta }_0)$ and ${\psi }_{\mathit{\text{syn-off}}}(\theta |{\theta }_0)$ that can be compared with experimental data or used to predict the experimental lifetime distributions when they become available, as described later.

The single-molecule fluorescence of ATP and ADP analogs is indistinguishable in the experiments. In addition to binding events during which the bound ATP hydrolyzed events without a hydrolysis step (ATP binds at ${\theta }_0$ and ATP releases at $\theta$) with a lifetime distribution ${\psi }_{\mathit{\text{off,ATP}}}(\theta |{\theta }_0)$ can also contribute to the observed distribution, although typically may be small (e.g., later in Fig. 4). Accordingly, we have

$${\psi }_{\mathit{\text{obs,hyd}}}(\theta |{\theta }_0)={\psi }_{\mathit{\text{hyd-off}}}(\theta |{\theta }_0)+{\psi }_{\mathit{\text{off,ATP}}}(\theta |{\theta }_0).$$ [5]

Eq. 5 will be used in a later section to calculate the observed lifetime distribution, or by inverting it, to extract hydrolysis rate constants from the experimental $\psi$.

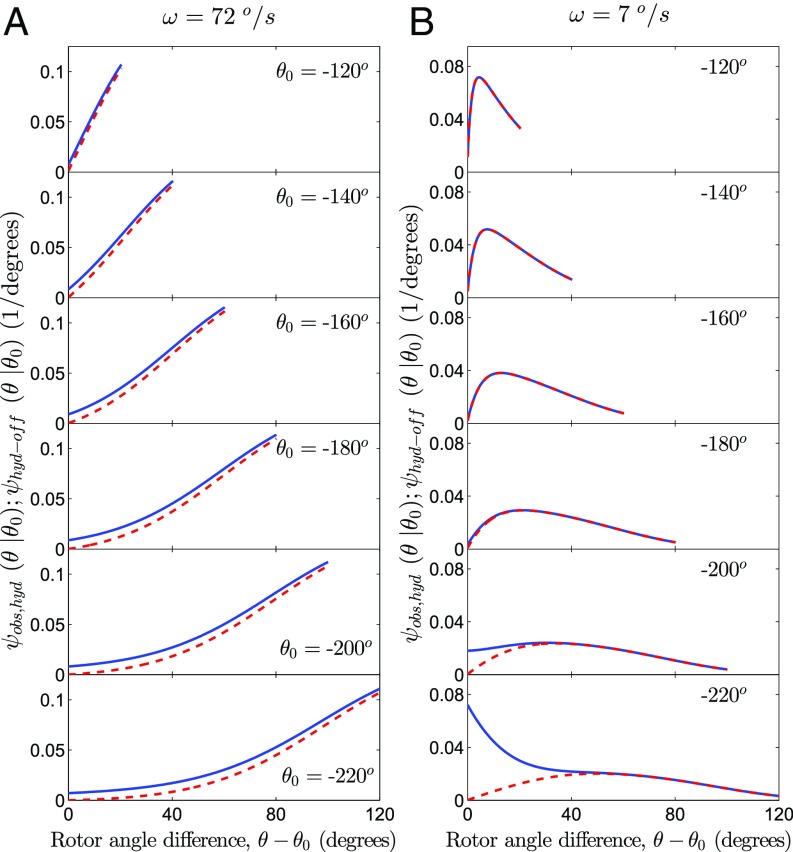
Fig. 4.

Lifetime distributions for binding events lasting from ${\theta }_0$ to $\theta$ during rotation in the hydrolysis direction for a series of long delay events with ${\theta }_0$’s ranging from 140° to 240°. The rotation rate in A was $\omega =0.2$ Hz [used by Adachi et al. in experiment (2)], and in B it was $\omega =0.02$ Hz. The ${\psi }_{\mathit{\text{obs,hyd}}}(\theta |{\theta }_0)$’s are shown as solid lines, and the contribution from the ${\psi }_{\mathit{\text{hyd-off}}}$’s are shown as dashed lines. In the calculations $k_{\text{off}}$ data were taken from Fig. 3 ($\theta$-range in yellow shading).

Extraction of $𝜽$-Dependent Rate Constants of Synthesis and Hydrolysis from Long Binding Events.

If $K_{\mathit{\text{off,ADP}}}(t)$ is defined by the indefinite integral

$$K_{\mathit{\text{off,ADP}}}(\theta )=(1/\omega )\int k_{\mathit{\text{off,ADP}}}(\theta )d\theta ,$$ [6]

then using an equation for ${\psi }_{\mathit{\text{off,ADP}}}(\theta |{\theta }_1)$ analogous to Eq. 3, we obtain

$${\psi }_{\mathit{\text{off,ADP}}}(\theta |{\theta }_1)=[k_{\mathit{\text{off,ADP}}}(\theta )/\omega ]e^{-K_{\mathit{\text{off,ADP}}}(\theta )}{e}^{K_{\mathit{\text{off,ADP}}}({\theta }_1)}.$$ [7]

Eq. 1 can be then expressed as

$${\psi }_{\mathit{\text{hyd-off}}}(\theta |{\theta }_0)=[k_{\mathit{\text{off,ADP}}}(\theta )/\omega ]e^{-K_{\mathit{\text{off,ADP}}}(\theta )}\times {\int }_{{\theta }_0}^{\theta }{\psi }_{\text{ℎ𝑦𝑑}}({\theta }_1|{\theta }_0)e^{K_{\mathit{\text{off,ADP}}}({\theta }_1)}d{\theta }_1.$$ [8]

Changing this equation so as to place only the integral on the left-hand side (LHS), then taking a derivative, and using Eq. 5 yields

$${\psi }_{\text{ℎ𝑦𝑑}}(\theta |{\theta }_0)=\omega e^{-K_{\mathit{\text{off,ADP}}}(\theta )}\frac{d}{d\theta }\left[\frac{{\psi }_{\mathit{\text{obs,hyd}}}(\theta |{\theta }_0)-{\psi }_{\mathit{\text{off,ADP}}}(\theta |{\theta }_0)}{k_{\mathit{\text{off,ADP}}}(\theta )e^{-K_{\mathit{\text{off,ADP}}}(\theta )}}\right].$$ [9]

In Eq. 9, quantities on the right-hand side (RHS) can be estimated from controlled rotation experiments. The derivative can be evaluated either numerically from the discretized data, if the scatter of the data are not significant, or by using a smooth fitting function. Just as ${\psi }_{\text{ℎ𝑦𝑑}}$ can be obtained from $k_{\text{ℎ𝑦𝑑}}(\theta )$ using Eq. 3, the latter can be inverted as in SI Appendix to obtain $k_{\text{ℎ𝑦𝑑}}(\theta )$:

$$k_{\text{ℎ𝑦𝑑}}(\theta )=\omega {\psi }_{\text{ℎ𝑦𝑑}}(\theta |{\theta }_0)/[1-{\int }_{{\theta }_0}^{\theta }{\psi }_{\text{ℎ𝑦𝑑}}(\theta \prime |{\theta }_0)d\theta \prime ].$$ [10]

We note that two quantities on the RHS of Eq. 10 depend on ${\theta }_0$, but one sees from the LHS that the ratio is independent of ${\theta }_0$ and depends only on $\theta$. So, in applications, $k_{\text{ℎ𝑦𝑑}}(\theta )$’s can be estimated at multiple ${\theta }_0$’s and then averaged. (A formal proof that the RHS is independent of ${\theta }_0$ is given in SI Appendix.) In a special case of $k_{\mathit{\text{off,ADP}}}(\theta )\gg k_{\text{ℎ𝑦𝑑}}(\theta )$ in the $\theta$ window of interest, Eq. 9 reduces to

$${\psi }_{\mathit{\text{obs,hyd}}}(\theta |{\theta }_0)\cong {\psi }_{\text{ℎ𝑦𝑑}}(\theta |{\theta }_0)+{\psi }_{\mathit{\text{off,ADP}}}(\theta |{\theta }_0).$$ [11]

To prove Eq. 11, we note that ${\psi }_{\mathit{\text{off,ADP}}}(\theta |{\theta }_0)$ satisfies the normalization condition,

$${\int }_{{\theta }_0}^{\mathrm{\infty }}{\psi }_{\mathit{\text{off,ADP}}}(\theta |{\theta }_0)d\theta =-{\int }_{{\theta }_0}^{\mathrm{\infty }}(dp/d\theta )d\theta =1.$$ [12]

If the $p_{\mathit{\text{off,ADP}}}(\theta |{\theta }_0)$ decreases very rapidly with $\theta$ in the vicinity of its initial value of unity at $\theta ={\theta }_0$, then its (negative) derivative $-{\psi }_{\mathit{\text{off,ADP}}}(\theta |{\theta }_0)$ can serve as a delta function. In that case, we can write

$${\psi }_{\mathit{\text{off,ADP}}}(\theta |{\theta }_0)\cong \delta (\theta -{\theta }_0).$$ [13]

When $k_{\text{𝑜𝑓𝑓𝐴𝐷𝑃}}(\theta )$ is very large, in the region where ${\psi }_{\text{ℎ𝑦𝑑}}(\theta |{\theta }_0)$ is slowly varying, then, using Eq. 13, Eq. 1 can be approximated by

$${\psi }_{\mathit{\text{hyd-off}}}(\theta |{\theta }_0)\cong {\psi }_{\text{ℎ𝑦𝑑}}(\theta |{\theta }_0).$$ [14]

Eqs. 5 and 14 then yield Eq. 11. When analyzing the experimental data, the lifetime distribution ${\psi }_{\mathit{\text{obs,hyd}}}$ can be estimated from occupancy trajectories. As in Adachi et al. (2), the 360° cycle is divided into small intervals (e.g., of $\mathrm{\Delta }\theta =10°$), centered at ($\theta$, ${\theta }_0$). Then, the number $\mathcal{N}(\theta ,{\theta }_0)$ of occupancy-change event pairs at ${\theta }_i$ and ${\theta }_{i+1}$ for which the ${\theta }_i$’s are within $\mathrm{\Delta }\theta /2$ of ${\theta }_0$ and the ${\theta }_{i+1}$’s are within $\mathrm{\Delta }\theta /2$ of $\theta$, is counted. A normalized $\psi$ is found by dividing $\mathcal{N}(\theta ,{\theta }_0)$ by the number of event pairs for which ${\theta }_i$ is within $\mathrm{\Delta }\theta /2$ of ${\theta }_0$.*

We note that if the number $\mathcal{N}(\theta ,{\theta }_0)$ is small for some $(\theta$,${\theta }_0)$, the experimental ${\psi }_{\mathit{\text{obs,hyd}}}(\theta |{\theta }_0)$ can be calculated by introducing variable $\mathrm{\Delta }\theta$ intervals. The choice of the $\mathrm{\Delta }\theta$’s at different $\theta$’s would be guided by distribution functions from available data or theoretical calculations independent of the trajectories to be analyzed. For example, the rate constants of synthesis/hydrolysis and binding/release universally show exponential dependence on $\theta$, so the $\mathrm{\Delta }\theta$’s at different $\theta$’s should be also exponential, albeit inversely proportional to the lifetime distribution, as described elsewhere (10).

Procedures in the Calculation of Lifetime Distributions and the Rate Constants.

Procedure to obtain lifetime distributions ${𝝍}_{\mathit{\text{obs,hyd}}}$ from hydrolysis and ADP release experimental data.

• i)A window of $\theta$’s of interest is identified in which $k_{\mathit{\text{off,ADP}}}(\theta )$ is available from controlled rotation experiments and $k_{\text{ℎ𝑦𝑑}}(\theta )$ is available from stalling experiments.
• ii)A grid of (${\theta }_0$,$\theta$) points is defined separated by $\mathrm{\Delta }\theta$ [e.g., $\mathrm{\Delta }\theta ={\mathrm{\hspace{0.17em}10}}^{\circ }$ in Adachi et al. (2)], on which the ${\psi }_{\mathit{\text{off,ADP}}}(\theta |{\theta }_0)$ and ${\psi }_{\text{ℎ𝑦𝑑}}(\theta |{\theta }_0)$ are numerically calculated by using the analogs of Eq. 3.
• iii)On the same grid, the ${\psi }_{\mathit{\text{hyd-off}}}(\theta |{\theta }_0)$ appearing in Eq. 1 is evaluated. Eq. 5 then yields the observed lifetime distribution ${\psi }_{\mathit{\text{obs,hyd}}}(\theta |{\theta }_0)$.

Procedure for extracting $𝜽$-dependent hydrolysis rate constants from long binding events.

• i)For each (${\theta }_0$,$\theta$) grid point (compare Procedure to Obtain Lifetime Distributions ${\psi }_{\mathit{\text{obs,hyd}}}$ from Hydrolysis and ADP Release Experimental Data), the number of (${\theta }_i,{\theta }_{i+1}$) is counted (${\theta }_i$ is a binding and ${\theta }_{i+1}$ is a release event). Only events for which ${\theta }_i$ lies within $\mathrm{\Delta }\theta /2$ of ${\theta }_0$ while ${\theta }_{i+1}$ lies within $\mathrm{\Delta }\theta /2$ of $\theta$ are counted.
• ii)For each grid point, the number of events from step i is divided by the sum over all binding events within $\mathrm{\Delta }\theta /2$ of ${\theta }_0$, yielding ${\psi }_{\mathit{\text{obs,hyd}}}$.
• iii)The $\theta$-dependent $k_{\mathit{\text{off,ADP}}}(\theta )$ obtained from controlled rotation experiments is used to calculate $K_{\mathit{\text{off,ADP}}}$ (e.g., by fitting a combination of two exponential functions to the experimental data, as seen later in Eq. 15).
• iv)By using the experimental ${\psi }_{\mathit{\text{obs,hyd}}}$, $k_{\mathit{\text{off,ADP}}}$ and $K_{\mathit{\text{off,ADP}}}$ on the grid, the derivative in Eq. 9 is solved numerically, with a smoothing function for rough data.
• v)Using Eq. 10 $k_{\text{ℎ𝑦𝑑}}(\theta )$’s are estimated at multiple ${\theta }_0$’s and then averaged to yield an improved estimate.

An Application for the Predictive Calculation of Lifetime Distributions.

We consider next as an example a calculation of the ${\psi }_{\mathit{\text{hyd-off}}}(\theta |{\theta }_0)$ in an angular window of ${140}^{\circ }$ to ${260}^{\circ }$, in which stalling experiments provide a value of the $\theta$-dependent rate constant $k_{\text{ℎ𝑦𝑑}}$, $\ln k_{\text{ℎ𝑦𝑑}}(\theta )=\ln 0.17+\mathrm{\hspace{0.17em}0.02}(\theta -{\mathrm{\hspace{0.17em}200}}^{\circ })$ for a mutant species (11). In the calculations based on Eq. 5, we also use the fluorescent ATP- and ADP release rate constants in this window (yellow shaded area in region 4) reported in the controlled rotation experiments and shown in Fig. 3.

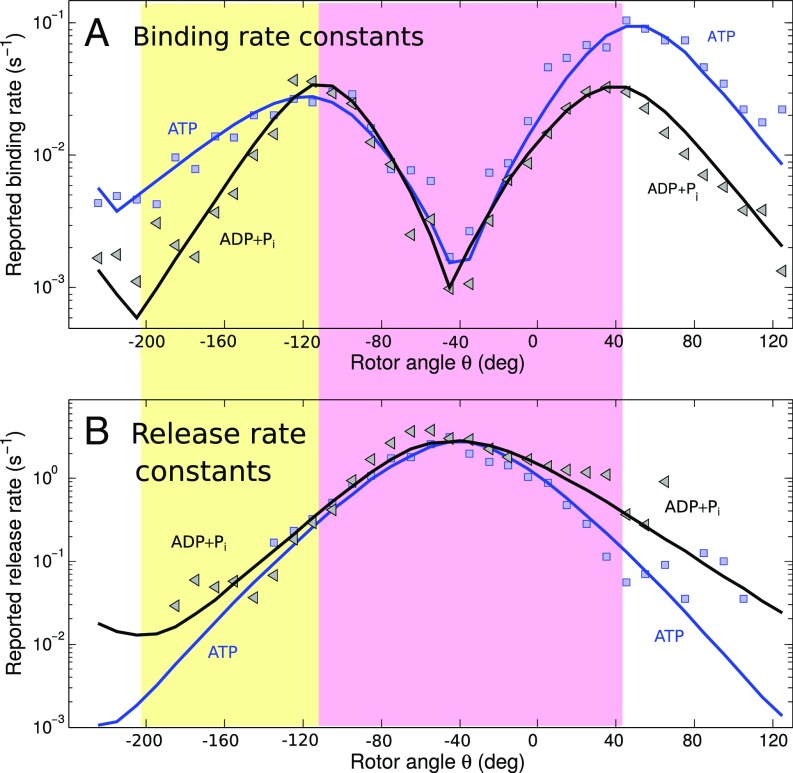
Fig. 3.

Binding (A) and release (B) rate constants as a function of the $\theta$ from controlled rotation experiments used in the calculations for the lifetime probability density functions ($\psi$’s) from Fig. 4. (The ATP data are also plotted on Fig. 2A.) Symbols are reported experimental data. Solid lines are from theoretical prediction (ATP in regions 1 and 2) or fitting assuming a 25-nM nucleotide concentration. The functional form of the group transfer theory was used in the magenta-shaded $\theta$-range (compare the text for specific quantities), and exponential functions were used elsewhere (compare SI Appendix).

To extract the $k_{\text{ℎ𝑦𝑑}}$ vs. $\theta$ data, a functional form is used for $k_{\mathit{\text{off,ADP}}}(\theta )$ that fits the controlled rotation experiments. For the long binding events that cover a $\theta$-range spanning regions 1–4 (defined in Fig. 2) $k_{\mathit{\text{off,ADP}}}(\theta )$ has a minimum at ${\theta }_m$, where the recovery from the decaying exponential trend in the turnover region 3 occurs and, as seen in Fig. 3 a growing exponential trend in region 4 in Fig. 2A starts,

$$k_{\mathit{\text{off,ADP}}}(t)=A{e}^{-a(\theta -{\theta }_m)}+B{e}^{b(\theta -{\theta }_m)}$$ [15]

is a good fit for the experimental rate constants (compare Fig. 3B, black line), if $A=\mathrm{\hspace{0.17em}0.25}\times {\mathrm{\hspace{0.17em}10}}^{-3}$ s⁻¹, $a=0.063$ 1/°, $B=0.83\times {\mathrm{\hspace{0.17em}10}}^{-3}$ s⁻¹, $b=0.048$ 1/° and ${\theta }_m=-{205}^{\circ }$. Then,

$$K_{\mathit{\text{off,ADP}}}(\theta )=-(A/a)\left[e^{-a(\theta -{\theta }_m)}-e^{-a({\theta }_0-{\theta }_m)}\right]+(B/b)\left[e^{b(\theta -{\theta }_m)}-e^{b({\theta }_0-{\theta }_m)}\right],$$ [16]

The algorithms for the numerical integrations in Eqs. 1–3 are given in SI Appendix, and the results for ${\psi }_{obs,hyd}(\theta |{\theta }_0)$ obtained from Eq. 5 are shown in Fig. 4. We note that Adachi et al. used the number of binding and release events during the small $\mathrm{\Delta }\theta ={\mathrm{\hspace{0.17em}10}}^{\circ }$ windows to extract the $k_{on}$ and $k_{off}$ of both ATP and ADP.^† Because the $\psi$’s were not used in their procedure, these data are independent of the rate constants.

A Symmetric Expression for the $\theta$-Dependent Rate Constants

Theory.

In the Procedure to Obtain Lifetime Distributions ${\psi }_{o\mathit{}b\mathit{}s\mathrm{,}h\mathit{}y\mathit{}d}$ from Hydrolysis and ADP Release Experimental Data, step (i) and in the Procedure for Extracting $\theta$-Dependent Hydrolysis Rate Constants from Long Binding Events, step (iv), theoretical rate constant vs. $\theta$ data can be used, as an alternative to forthcoming experimental data, to evaluate the convolutions and calculate long binding events. In the theory proposed in our previous treatment (scheme 1 of ref. 7), a thermodynamic cycle relates the free energy of binding in unconstrained rotation, $\mathrm{\Delta }{G}_0^0$, from one dwell angle ${\theta }_i$ to the next one ${\theta }_f$, to the binding standard free energy $\mathrm{\Delta }{G}^0(\theta )$ at angle $\theta$ (6). It is assumed that in the torque-generating steps, the rotation of the $\gamma$ subunit is coupled to conformational changes in the catalytic $\beta$ subunits (4). The harmonic response to structural twisting torques is described by a spring constant $\kappa$ (12–14). As in refs. 6 and 7, the free energy to distort the system from angle ${\theta }_i$ to the angle $\theta$ by the tweezers before a nucleotide transfers into the pocket is given by a work term $w^r=(\kappa /2){\left(\theta -{\theta }_i\right)}^2$. If the tweezers hold the $\gamma$ at an angle $\theta$, and the nucleotide is in the $\beta$ subunit pocket, then a relaxation to the final dwell angle ${\theta }_f$ is achieved by turning off an external magnetic field, and the work done by the system is $w^p=(\kappa /2){\left(\theta -{\theta }_f\right)}^2$. The quadratic terms cancel in a plot of $\mathrm{\Delta }{G}^0$ vs. $\theta$, and so the latter is linear in $\theta$ (6),

$$\mathrm{\Delta }{G}^0(\theta )=\mathrm{\Delta }{G}_0^0-\kappa ({\theta }_f-{\theta }_1)[\theta -({\theta }_i+{\theta }_f)/2].$$ [17]

In the theory the $\theta$-dependence of $\mathrm{\Delta }{G}^0(\theta )$ yields a $\theta$-dependent $\mathrm{\Delta }{G}^{†}(\theta )$ via a well-known quadratic free energy relation, $\mathrm{\Delta }{G}^{†}(\theta )=W^r+{\left[\lambda +\mathrm{\Delta }{G}^0(\theta )\right]}^2/4\lambda$ (15). It contains a reorganization energy $\lambda$ and a work term $W^r$ needed to bring the nucleotide to the weak binding site (16) (SI Appendix, Fig. S4). We include any orientational restrictions in this initial binding. The idea of a weakly bound state at the entrance of the binding channel was previously suggested in a model for ATP binding (17–19).

To apply the treatment to the full range of $\theta$, we allow for nonzero ${\theta }_i$. From the free energy of activation, by reshaping the equations deduced previously (6, 7) relative to $\overline{\theta }=({\theta }_i+{\theta }_f)/2$ symmetric expressions result for the binding and release rate constants $k_f$ and $k_b$, by using equation 12 of ref. 6 and equations 3 and 4 of ref. 7

$$kT\ln \frac{k_{f/b}(\theta )}{k_{f/b}(\overline{\theta })}=\left(\pm \frac{1}{2}+\frac{\mathrm{\Delta }{G}_0^0}{2\lambda }\right)\mathrm{\Delta }{\theta }_r-\frac{{(\mathrm{\Delta }{\theta }_r)}^2}{4\lambda },$$ [18]

$$\text{where}\hspace{0.17em}\mathrm{\Delta }{\theta }_r=\kappa ({\theta }_f-{\theta }_i)(\theta -\overline{\theta }),\text{and}\hspace{0.17em}\overline{\theta }=({\theta }_i+{\theta }_f)/2.$$ [19]

Here, $\mathrm{\Delta }{\theta }_r$ has units of energy. In the term linear in $\mathrm{\Delta }{\theta }_r$ in Eq. 18 the “+” sign applies to $k_f$ and the “–” sign to $k_b$. For the equilibrium constant $K(\theta )$, we have (6)

$$kT\ln K(\theta )=kT\ln K(\overline{\theta })+\kappa ({\theta }_f-{\theta }_i)(\theta -\overline{\theta }),$$ [20]

and so $\ln K(\theta )$ is predicted to be linear in $\theta$, a result confirmed in the experiments (2, 11). The forward and back rate constants in the unconstrained system are denoted by $k_{f0}$ and $k_{b0}$ in ref. 6. Eqs. 18–20 constitute a more symmetrical interpretation for the rate constants, compared with equations 3 and 4 in ref. 7.

In Table 1, for binding of all nucleotides in region 1, we have ${\theta }_i={\mathrm{\hspace{0.17em}0}}^{\circ }$ and ${\theta }_f={\mathrm{\hspace{0.17em}80}}^{\circ }$ for the dwell angles from free rotation experiments. When applying the theory in region 2, the relevant dwell angles are those before and after the release of ADP in the rotation scheme (13) (SI Appendix, Fig. S6A), during an 80° step from ${240}^{\circ }$ to ${320}^{\circ }$, so counting $\theta$ in the reverse direction, ${\theta }_i=-{40}^{\circ }$ and ${\theta }_f=-{120}^{\circ }$. For the effective $\kappa$ on Fig. 2, we use the same value for both the left and right branches, previously found to be $\kappa =16$ pN$\cdot$nm/rad² for ATP and $\kappa =$12 pN$\cdot$nm/rad² for ADP (6). In region 1 (Figs. 2A and 3), rate constant predicted in our previous work (7) for Cy3-ATP were used.^‡

Table 1.

Summary of constants in the theory and their experimental sources for the calculation of rate vs. $𝜽$ data

Constants	Source
$k_f\left(\overline{\theta }\right)$, $k_b\left(\overline{\theta }\right)$	Stalling (11), free rotation,* and controlled rotation (2)
$\mathrm{\Delta }{G}_0^0$, $W^r$	Ensemble data (16)
$\kappa$, ${\theta }_i$, ${\theta }_f$	Free rotation (1, 14)
$Z$	Known
$\lambda$	From the above quantities (6)

^*Since $k_{f/b}\hspace{0.17em}(({\theta }_i+{\theta }_f)/2)\hspace{0.17em}=k_{f/b,0}$ and $k_{f,0}$ for species such as fluorescent and nonfluorescent ATP and GTP is readily available from free rotation experiments (1), from which, by using the other quantities in the table, and according to the present theory $k_{b,0}=(kT/hZ)k_{f,0}\hspace{0.17em}\text{exp}\left[-(\mathrm{\Delta }{G}_0^0+W^r)/kT\right]$ can be also calculated.

Because of the missed events in the fluorescence microscopy and the replacement of the time $T_0$ in occupancy 0 with the total time $T$, the reported rate constants $k_{\text{on}}^{\text{rep}}$ and $k_{\text{off}}^{\text{rep}}$ should be corrected to yield the actual $k_{\text{on}}$ and $k_{\text{off}}$ in Figs. 2 and 3. The reported rates are obtained by subtracting the average number of missed events from the average total number of events. Here, we generalize the previous results (7) by taking into account the effect of the finite rate of rotation, by calculating, in a separate step, the probability terms $p_0$ or $p_1$ of being in state 0 or 1 when the system enters a bin $\mathrm{\Delta }\theta$ (compare SI Appendix).

Application of Theory in an Extended Angular Region.

In Fig. 2A, region 1, the rise of $\ln k_{\text{𝑜𝑛}}$ of the RHS coincides with the range of $\theta$ where the theory predicted the $k_f$ and $k_b$ for Cy3-ATP binding in good agreement with the experimental data. Concomitantly, the ATP binding/release vs. $\theta$ data can be also predicted in region 2, by matching the $k_{\text{𝑜𝑛}}$ and $k_{\text{𝑜𝑓𝑓}}$ of regions 1 and 2 at the “dip” in the $k_{\text{𝑜𝑛}}$, at ${\theta }_{\text{O}}\cong -{40}^{\circ }$. Thereby, the $\log k(\theta )$ plots in regions 1 and 2 are linear in $\theta$, with slopes equal in magnitude but opposite in sign (6, 7).

The $k_{\text{𝑜𝑛}}$ and $k_{\text{𝑜𝑓𝑓}}$ show opposite $\theta$-dependence consistent with the group transfer theory. A rotation of the $\gamma$ either to the left or right of the most open conformation at $\sim$−40 ° induces the closing of a $\beta$ subunit, accelerates the binding, and retards the release. The $k_{\text{𝑜𝑛}}$ shows turnovers at ${\theta }_{\text{TO}}^{\prime }$ and ${\theta }_{\text{TO}}$, presumably due to the closing of the channel in the $\beta$ subunit, through which the nucleotide has to diffuse to the weak binding site. A narrowing of the channel would slow both forward and back diffusion. For further details on the diffusion, we refer to SI Appendix. In a future treatment of the diffusion and transfer processes (20, 21), when more single-molecule data become available (compare the scatter in SI Appendix, Fig. S5), it will become feasible to use the ratio of the forward and back reaction rates at any $\theta$, which is equal to $K(\theta )$ (22), even though the reaction rate constant is a composite of diffusion- and reaction-controlled rates.

Discussion and Conclusions

In the present work, we provide methods that can be applied to experimental data in two ways. (i) By using the experimental lifetime distributions of the long binding events, the hydrolysis or synthesis rate constants vs. $\theta$ data can be extracted and compared with either a theory of the type used in refs. 6 and 7 or compared with the rate constants estimated from stalling experiments. (ii) Lifetime distribution predictions using hydrolysis or synthesis rate constant data from stalling or other independent experiments, or from theory, are made obtained for binding at large $\theta$, in this work from 140° to 260°. They can be tested against distributions estimated from the controlled rotation experiments. This work shows similarities to a treatment (23) of single-molecule force ramp experiments in which the distribution of rupture forces is determined. Therein a procedure is given to invert this distribution to extract the force-dependent rates or lifetimes in a constant force experiment. A notable difference is that in the present work, composite events are considered as opposed to a single process.

For the long binding events, $\theta -{\theta }_0>{\mathrm{\hspace{0.17em}120}}^{\circ }$, in Fig. 4 hydrolysis will have typically occurred with a high probability, so using only the first term in Eq. 5, ${\psi }_{\mathit{\text{hyd-off}}}(\theta |{\theta }_0)$, will be a good estimate for the ${\psi }_{\mathit{\text{obs,hyd}}}(\theta |{\theta }_0)$. This finding is apparent in Fig. 4, even though the calculations are limited to the range of available $k_{\text{hyd}}(\theta )$ data: The contribution of events without hydrolysis peak at some smaller angle ($\theta -{\theta }_0\approx {\mathrm{\hspace{0.17em}60}}^{\circ }$ for $\omega ={\mathrm{\hspace{0.17em}72}}^{\circ }$/s in Fig. 4B; $\theta -{\theta }_0\approx {\mathrm{\hspace{0.17em}0}}^{\circ }$ for $\omega ={\mathrm{\hspace{0.17em}7}}^{\circ }$/s on Fig. 4D), beyond which it becomes small.

The results in Fig. 4 illustrate that ${\psi }_{\text{𝑜𝑏𝑠}}(\theta |{\theta }_0)$ is not stationary: It depends both on the difference $\theta -{\theta }_0$ and on ${\theta }_0$. Hence, an average $\psi$ of long binding times is not suitable for an analysis, so instead we used a 2D $\theta -{\theta }_0$ and ${\theta }_0$ dependent lifetime distribution ${\psi }_{\text{𝑜𝑏𝑠}}(\theta |{\theta }_0)$. The present method of extracting $k_{\text{hyd}}$ or $k_{\text{syn}}$ is most sensitive to these processes when their values are not too high relative to the rate of ADP release, conditions that apply for the calculations in Fig. 4. We note that the rates of these processes can be reduced by engineering mutations in the $\beta$ subunits or by using modified nucleotides (1, 13). The calculations can be developed further to account for multiple hydrolysis/synthesis cycles during one binding event by using multidimensional integrals (7, 24).

In the present work, it has been shown how to extract lifetime distributions of experimental events and from them how to calculate the rate constants involved in the composite events.