Using Petri Net Tools to Study Properties and Dynamics of Biological Systems

Abstract

Petri Nets (PNs) and their extensions are promising methods for modeling and simulating biological systems. We surveyed PN formalisms and tools and compared them based on their mathematical capabilities as well as by their appropriateness to represent typical biological processes. We measured the ability of these tools to model specific features of biological systems and answer a set of biological questions that we defined. We found that different tools are required to provide all capabilities that we assessed. We created software to translate a generic PN model into most of the formalisms and tools discussed. We have also made available three models and suggest that a library of such models would catalyze progress in qualitative modeling via PNs. Development and wide adoption of common formats would enable researchers to share models and use different tools to analyze them without the need to convert to proprietary formats.

Introduction

With the exponential growth in the volume of biological data, it is becoming extremely important to integrate and organize the data into coherent descriptive models that portray system behavior. Such models can shed insight into complex biological processes and suggest new directions for research. Scientists can study and analyze such models to make predictions about the behavior of the system under different conditions and to discuss novel relationships among the different components of a biological system. The ability to predict system behavior with a model helps evaluate model completeness as well as improve our understanding of the mechanisms of biological processes. Differences between the behavior of the model and the behavior of the real system, as determined from experimental data, can suggest new components that may account for the differences. Descriptive models may also serve as educational aids.

A modeling methodology that is especially tailored for representing and simulating concurrent dynamic systems is Petri Nets (PNs).¹ An advantage of PNs is that they can represent system behavior even when the biological mechanism is not fully understood, by combining different levels of abstraction in a single model. Petri Nets enable qualitative simulation and allow a representation of a process that is broken down into subprocesses that may be described at variable granularities. Most PNs have a visual representation that facilitates user comprehension. Petri Net tools enable users to verify system properties, verify system soundness, and simulate dynamic behavior.

There is a plethora of different PN tools available that differ in their capabilities. We undertook this study to understand these differences and explore their suitability in the context of creating simulation models of different biological systems.

Background

The most basic PN is a directed, bipartite graph in which nodes are either places or transitions, where places represent Boolean conditions (e.g., parasite in the bloodstream) and transitions represent activities (e.g., invasion of a host cell). ▶ explains and demonstrates an example of a PN. Tokens in places represent local (atomic) states signifying that the condition associated with that place holds. The placement of tokens in the net, called marking, defines the PN's global state. A PN can be “executed” or simulated by moving tokens according to a firing rule; when all the places with arcs leading to a transition have a token, the transition is enabled and may fire by removing a token from each input place and adding a token to each output place. The results of the simulation can be visualized as graphs or analyzed quantitatively or qualitatively.

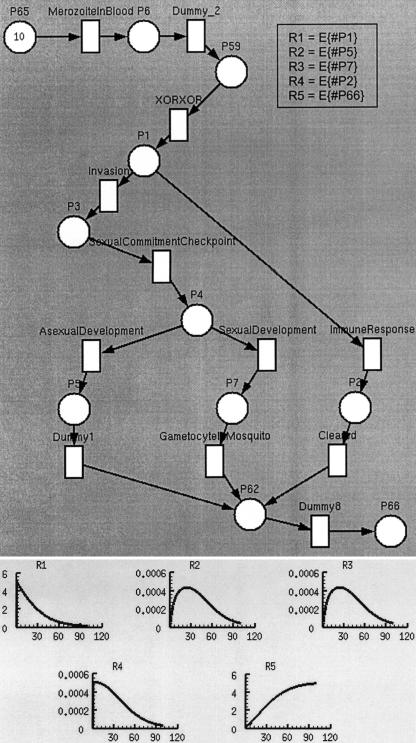
Figure 1.

TimeNet's representation of the malaria example and the results of kinetic experiments, corresponding to this Petri Net (PN). Places are represented as circles and transitions as squares. The number 10 written inside the place P65 represents a marking of ten tokens that correspond to ten malaria parasites (merozoites). In this marking of the PN, only the transition MerozoiteInBlood is enabled because there are tokens in all its input places (in the case of this transition, there is only one input place: P65). When this transition fires, a token is passed from the input place P65 to all the output places. In this case, there is only one output place: P6. Tokens that reach place P1 may flow either through the transition Invasion or the transition ImmuneResponse. In the graph shown below the PN, the y-axis shows the values of the performance measures (average number of tokens at certain places) from time zero to a given time on the x-axis. These kinetic curves use a smoothing function, which does not measure the number of tokens at a given time but rather the average number of tokens over a time interval. R5 is a hyperbolic curve showing sink places that accumulate all the tokens in the system. The curve corresponds to place P66. R2 and R3 are parabolic curves showing transient stages. Tokens gradually enter these stages, stay there for a while, and then transition to the next stage. The curves correspond to places P5 and P7, respectively. R1 and R4 are curves showing stages that start with many tokens and lose them over time. The curves correspond to places P1 and P2, respectively.

Petri Nets have been applied mostly in manufacturing and safety-critical systems. They are most suitable for modeling and analyzing the dynamics of concurrent systems whose behavior could be described by finite sets of atomic processes and atomic states. Several groups have used PNs to create qualitative models of metabolic pathways and analyze them structurally.^2,3,4 These groups represented several characteristics of biological systems and modeled them in a way that enables the following distinctions: separation of external and internal metabolites, existence of enzyme-substrate complexes, and reversible reactions occurring at cellular conditions, which were modeled as two reactions occurring in opposite directions.

Structural analysis can identify properties that are conserved during execution of the modeled system. Such properties include the following:

1. Liveness: Checking that all processes that are modeled can be executed.

2. Boundedness: Checking that there is no infinite accumulation of tokens in a place. This may correspond to an accumulation of a metabolite at toxic concentration.

3. Place invariants: Identifying a set of places in which the total amount of tokens is constant. When modeling a large number of reactions that occur in an organism, identification of place invariants may identify reactions that constitute a pathway.

4. Circuits: Flux conservation is achieved when the rate at which tokens are being produced equals the rate at which tokens are being consumed. When the flux for a given firing sequence starts and ends at the same point, it is called a circuit. An algorithm for identifying cycles in metabolic pathways has been described.⁵

5. T-Invariants: Identifying a set of transitions that have to fire from some initial marking to return the PN to that marking. T-invariants indicate the presence of cycles that are in a state of continuous operation.

6. Reachability: Deciding whether a certain marking (state) is reachable from another marking. This type of analysis can be used to determine whether certain outcomes are possible, given a modeled net and an initial marking (initial state), or to determine whether certain states are reachable when specific reactions are inhibited.

Structural analysis may provide insights to biologists. For example, pathways may be automatically constructed from data residing in metabolic and sequence databases. By comparing pathways in different organisms, gaps in specific pathways were identified.⁴ In Zevedei-Oaneca and Schuster,³ structural analysis explained a surprising finding that indicated that an enzyme (triose-phosphate isomerase) is necessary for the glycolysis pathway, although it seemed possible for this pathway to proceed without it.

Petri Nets have also been used to model ecological and evolutionary processes and to analyze different modes of evolution.⁶ In this work, ecological niches were defined as a structural property of PNs: a set of interconnected autonomous places. A niche does not produce any indispensable resource for another niche. Recently, an approach to automatically generate PNs was used to construct PN models of penetrance of a disease given a particular combination of genotypes that was inherited.⁷ The approach is based on taking a language that is specified as a grammar and subsequently producing code from it, in any language. The approach is called “genetic evolution” because, using the grammar, a binary string written in the language to be translated (the “genome”) is translated into code, which is analogous to a phenotype.

The expressive power of basic PNs is limited. Not surprisingly, a number of PN extensions have been defined.⁸ These extensions add expressive power, allowing more elaborate models to be developed. On the other hand, the added features make the representation more complex. The PN formalisms that we evaluated in this study are reviewed below. Although previous studies have evaluated the use of PN tools for modeling biological processes,^3,9,10,11 they have concentrated on either structural analysis or quantitative simulation, usually of a single tool. The goal of our assessment was to explore the range of capabilities of PN tools and the types of biological questions that PN tools allow us to explore, whether they are structural or behavioral, and not to recommend particular tools.

High-Level Petri Nets

High-level PNs include extensions for representing hierarchy, time, and data.¹² Hierarchical PNs have been used to model biological processes at different levels of granularity, starting from high-level processes, such as a malaria parasite invading a host's red blood cell and hierarchically decomposing processes into processes of lower granularity, ending at molecular-level processes, such as protein phosphorylation.⁸ Colored hierarchical PNs were used to study effects of mutations in tRNA on the process of protein translation.¹³ Color was used to distinguish among molecules that share some aspects (e.g., they are all tRNA molecules) but are different in other aspects, such as the type of amino acid that they carry or a mutation that they exhibit. Colored PNs (CPNs) were also used to perform steady-state analysis of metabolic pathways.⁹ In this work, color was used to separate out places that may be involved in conflicting paths, enabling rigorous symbolic analysis.

Hybrid Petri Nets

Hybrid PNs contain places and transitions that may be discrete or continuous, allowing representation of continuous processes.¹⁴ Hybrid PNs have been used to model gene-regulatory networks,^11,14 biochemical pathways,¹⁰ and signal transduction.¹¹ Hybrid PNs can be used to create quantitative models using continuous transitions whose rate is a differential equation that may depend on place markings. In this way, transitions may have rates that correspond to concentrations of reactants and may be used to model kinetics of enzymatic reactions, binding reactions, and diffusion transportation.¹⁰ Hybrid PNs also support inhibitory and test arcs.¹¹ An inhibitory arc connects an input place to a transition. When tokens are present in that input place, the transition is inhibited. This feature is very useful for modeling repressors in gene regulation. Test arcs do not consume the tokens in an input place but only test the presence of tokens there. Test arcs have been used to model the transcription process when mRNA is not consumed.¹¹ Chen and Hofestaedt¹⁰ outlined a process for taking a biological system and modeling it using a hybrid PN. The process includes a stage of tuning the model so that it behaves like the real system. A similar process was described by Doi and colleagues.¹⁵

Stochastic Extensions to Petri Nets

Stochastic PNs may contain timed transitions that have expolynomially distributed firing delays (i.e., firing delays that can be piecewise defined by exponential polynomials) in addition to instantaneous transitions.¹⁶ Colored-stochastic PNs have been used to model mechanisms of infectious disease.¹⁷ The simulation results were consistent with other stochastic epidemiologic models.

Stochastic activity networks (SANs) may contain timed transitions (activities) with time distribution functions. Stochastic activity networks introduce another kind of uncertainty, in the form of activity cases. Transitions that have identical input places are represented as a single activity with several cases. Each case has a probability distribution.¹⁸ SANs use input and output gates to flexibly define enabling and completion rules for activities. Input gates link input places to an activity. They have enabling predicates and function. Enabling predicates are Boolean functions on the marking of the places connected to the input gate that have to be evaluated to true for the activity to be enabled. The function of an input gate describes the resulting marking of the input places connected to the input gate, which will be achieved on the completion of the activity to which the input gate is connected. Output gates link an activity to a set of output places. They have functions that describe the resulting marking of the output places of the gate, which will be executed on the completion of the activity leading to the output gate.

SANs have been used to create qualitative and quantitative models of molecular pathways.^18,19,20 The simulation results of the quantitative model were very similar to experimental results of the biological systems that had been modeled, which confirmed the completeness of the model.¹⁸

The Work Flow Model of the Workflow Management Coalition

The Workflow Management Coalition defined a work flow model for modeling business processes,²¹ consisting of a process model and an organizational model. As has been shown by van der Aalst,²² this work flow model can be mapped to PN, which can be analyzed for correctness. We found that the work flow model can be mapped to biological systems.^8,13 In the following definitions, the biological analogous entities are given in parentheses. The Process Model provides a dynamic and functional model that consists of a network of activities (i.e., logical steps in the process), and their relationships (i.e., whether they are done concurrently or are mutually exclusive), criteria to indicate the start and termination of the process, and information about the participants of individual activities (e.g., enzyme). Activities are connected to each other using transitions, which may contain conditions (conditional transition). Four types of activities can be expressed: (1) activities that are used for routing and do not contain process definitions (route activity), (2) activities that are hierarchical and can be nested into subflows (high-level processes, such as protein translation), (3) loop activities, and (4) generic activities that do not contain subflows and loops (low-level processes, such as amino acid acylation). The Organizational Model (Participants/Role Model) represents the relationships among participants (e.g., protein complexes have component proteins) and the roles that participants play in processes (e.g., a protein has enzymic function: phosphorylation). We used the Workflow model as a biological process model by mapping workflow activities to biological processes, organizational units to biomolecular complexes, humans (individuals) to biopolymers, and roles to biological processes and functions. We defined the biological components of the model by using codes from controlled biological and medical ontologies. Mapping from workflows to PNs translates every workflow process into a PN, where every workflow activity is translated into a PN transition, and single or multiple places are inserted between a transition and its consecutive transition(s) depending on whether the consecutive transitions are concurrent or mutually exclusive.²²

Limits on Petri Nets for Modeling Biological Systems

Petri Nets are not suitable for studying systems exhibiting continuous dynamic behavior that: (1) cannot be described by a set of discrete states, (2) cannot be broken down to atomic processes, or (3) are dependent on spatial properties. Examples include fluid dynamics and protein folding.

Other Methods Exist for Modeling and Simulating Dynamic Biological Systems

The most widespread formalism is differential equations (ordinary and partial), which describe the rate of production of a system component as a function of concentrations of other system components. Differential equations have been used to model a variety of biological systems, ranging from deterministic, coarse-grained models to fully detailed quantitative models, such as E-CELL,²³ which aim to model an entire cell, inspired by the exponential increase in functional genomics data. Many other modeling and simulation methods have been used to model gene regulatory systems²⁴ and/or metabolic pathways, including directed graphs, Boolean networks, Bayesian networks, qualitative differential equations, stochastic equations, and rule-based formalisms.

The advantage of PNs over other modeling and simulation methods is that they employ a very simple model that has an intuitive graphical representation, can represent systems at coarse- or fine-grained levels, and enables both qualitative and quantitative analysis. In addition, the PN token game (interactive animation) aids in system validation.

Design Objectives

We surveyed five PN formalisms and tools and compared them based on their mathematical capabilities as well as on their appropriateness to represent typical biological processes and answer biological questions. The criteria for evaluation are described in this section, and the evaluation results are presented in the Status Report section.

Mathematical Capabilities for Modeling and Analysis and Desired Technical Features

▶ summarizes the main features of each tool. They include modeling features, analysis types that the tools support, and technical features such as the exchange format, operating systems, quality of the user interface and technical support, and whether the license is free to the public or for academic use.

Table 1.

The Five Petri Net (PN) Tools and Their Mathematical and Usability Capabilities

	Mobius	TimeNET	Design/CPN	Genomic Object Net	Woflan
Formalism	SAN	EDSPN	HLPN	Hybrid PN	PN
Modeling features
Hierarchy (transition decomposed into a net of [sub]processes)			+
Composition (several copies of a net interact)	+
Process duration is stochastic (e.g., exponential rate)	+	+
Process duration is constant,>1	+	+	+	+
Continuous transitions (transition expressed as a differential equation)				+
Probabilities of conflicting processes (e.g., 80% of the time a malaria parasite pursues a non-sexual life cycle; 20% sexual)	+	Not working	Not directly	Not working
Inhibition arcs linking a place to a transition represent transitions that are disabled when there are tokens in the linked input places		+		+
Test arcs are like inhibition arcs, but firing the transition does not consume the tokens in the input places				+
Arc weight requires more than one item to flow from/to a place when a transition fires (e.g., 2P1 + P2→P3)	Can be modeled by gates	+	+	+
Gates can be used to express complex marking changes when transitions fire	+
Colored tokens have data values; transitions in the net depend on these values			+
Analysis types
Boundedness (no infinite token accumulation); liveness (all transitions may fire)					+
Place invariants (set of places in which the total amount of tokens is constant); Conflicting transitions (enabled under same conditions)		+			+
State space (number of different states)		+
Traps (once a token enters a trap place, it does not leave it)		+
Siphons (once a token leaves a siphon, it does not return to it)
Token game (interactive simulation of tokens moving in net)		+	+	+
Performance measures + simulation/numerical analysis	+	+	Not directly	+
Plots of simulation results		+	Not directly	+
Reachability (is a marking reachable from initial marking)		Not working
Technical features
Exchange format	+	+	+		+
Operating system	Windows, Solaris, Linux	Linux, Solaris	Solaris, Linux, HP-UX SGI-Irix	Mac, Windows, Solaris	Windows
User interface	++++	+++	++	++++	+++
Technical support	++++		+++	+++	+++
License	Free acd	Free acd	Free	Free	Free

EDSPN = extended deterministic and stochastic Petri Nets (immediate or expolynomially timed transitions in which at most one expolynomially timed transition may be enabled in each marking); SAN = stochastic activity networks; CPN = colored Petri Net; HLPN = high-level Petri Nets (color, hierarchy, time); acd = academic; Not directly = functions that can be defined in code but are not supported directly. The number of + signs indicates the level of support.

Biological Processes That Petri Nets Can Model

Examining biological systems that we have modeled in the past while working with domain experts, other biological systems that are discussed in biological textbooks of biochemistry and cellular biology, and an extensive literature study of PN models of biological systems,^{2,3,4,5,6,7,8,9,10,11,12,13,14,15,17,18,19,20} we defined features that characterize biological processes. They include the following:

1. Facts about biological processes are known at different levels of granularity, ranging from organisms to organ systems, cells, and molecular level details.

2. Biological processes may affect individuals or populations. For example, we may be interested in modeling a single parasite infecting a single cell as well as a population of parasites infecting a population of host cells.

3. Populations exhibit variation. For example, we need to be able to represent different alleles and their effect on processes as well as genetic drift, in which an allele gets established in a population.

4. Metabolism is carried out by biochemical reactions, which are characterized by participating substrates and products with stoichiometric coefficients, catalysts, and inhibitors or allosteric effectors.

5. Process inhibition may occur in (a) gene regulatory networks, where transcription of a gene may be inhibited by a repressor or in (b) metabolic networks, where a reaction rate may be slowed down by an allosteric effector.

6. Biological reactions usually have typical kinetic curves. These include hyperbolic curves (typical of enzyme saturation) and sigmoid curves (typical of allosteric effects).

7. Alternative pathways can be executed given some initial condition of the system. These pathways contain competitive reactions with different probabilities for their occurrence. For example, malaria parasites in a host's blood system can invade a host cell or can be cleared by the immune system.

8. Processes in a biological system can occur concurrently.

9. Regulation of gene expression and the levels of resulting protein in an organism involves a complex network (gene regulatory network) controlled by complex interactions between transcriptional regulation, translational control, and mRNA and protein stability. DNA-binding proteins are an important component of a gene regulatory network. They respond to changes in the cellular environment by binding to DNA sequences and altering the gene expression of relevant genes in the vicinity of their binding sites.

10. The cell responds to outside signals that are converted into a functional change within the cell (signal transduction). The signal, often a hormone (e.g., luteal hormone) interacts with a receptor on the cell surface; this interaction causes a change in a second messenger (such as calcium) and eventually a change is triggered in the cell's function (e.g., luteal cell production of progesterone).

We defined a library of diverse test cases consisting of typical biological processes, based on our experience in modeling biological systems. The test cases are drawn from three domains: malaria invasion of human host cells, effects of mutations in tRNA on protein translation, and the pathway of the drug gemcitabine in a human cell. The collection of the three test cases possesses most of the features of the biological systems that we defined above. Thus, they are comprehensive enough for the purpose of this study. The test cases do not cover the last two features of biological systems described above: gene regulation and signal transduction. These features are discussed in the Status Report section.

The invasion of human host erythrocytes by the malaria parasite Plasmodium falciparum²⁵ is a cellular level process that involves populations of parasites and host cells. As shown in ▶, at the start of the invasion process, the malaria parasite is at the developmental stage called merozoite and appears in the host's bloodstream. The merozoites can be cleared by the host immune system or can invade host red blood cells. After invasion, the merozoites can follow two alternative life cycles: undergo sexual development or undergo asexual development and be released as merozoites into the bloodstream. The invasion process (details not shown in the figure) includes cellular level as well as molecular level metabolic activities that can be inhibited with inhibitors. Some activities are done in parallel, whereas others are alternatives. The system's behavior over time can be followed by kinetic curves. ▶▶▶ present PN models and analysis results of the malaria example.

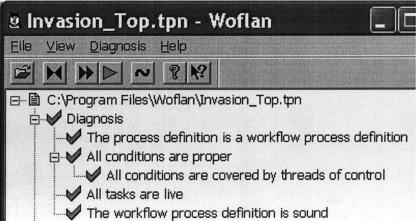
Figure 2.

Woflan's verification of the malaria Petri Net (PN). Woflan can be used to convert work flows in different work flow tool formats into PNs. The diagnosis option of Woflan verifies properties of the resulting PNs. Petri Nets can also be directly entered into Woflan, without the need to start from workflows. The properties that Woflan verifies are transition liveness and place boundedness (no infinite accumulation of tokens at places of the PN). Together, these two properties are termed soundness.

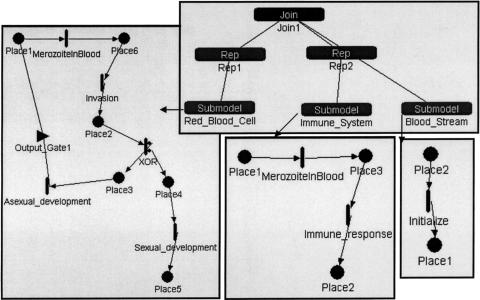
Figure 3.

A Mobius model of malaria parasites invading a human host. Mobius uses composition to compose several atomic Petri Nets (PNs) into a composed model. Top: Shows a model composed of Rep1 copies of a Red_Blood_Cell PN (bottom left), Rep2 copies of the host's immune system cells PN (middle bottom), and one copy of the host's bloodstream PN (bottom right). The three atomic nets have a shared place (Place1). In the atomic PNs, places are depicted by circles and timed transitions as vertical bars. Small circles attached to a vertical bar depict transition cases (i.e., mutually exclusive processes that are all enabled by the same set of input places). Triangle depicts output gate. The output gate shown in the figure produces an integer number of tokens (burst size) in the output place to which it is linked, which allows the representation of several malaria parasites that are released from the host cell at the end of asexual development.

The second test case involves the effect of mutations and genetic variation in tRNA genes on molecular level functions involved in protein translation, including metabolic reactions.¹³ ▶ shows part of this test case. tRNA genes are transcribed into tRNA molecules that are folded. Most tRNA variants are acylated with amino acids, and some variants are not. Depending on the type of tRNA molecule, tRNA molecules form complexes with different translation factors (initiation factors, elongation factors, or termination factors) and with guanosine triphosphate (GTP). During the translation process, different mutations of tRNA cause the translation process to proceed abnormally, resulting in misreading, frame shifting, or halting.

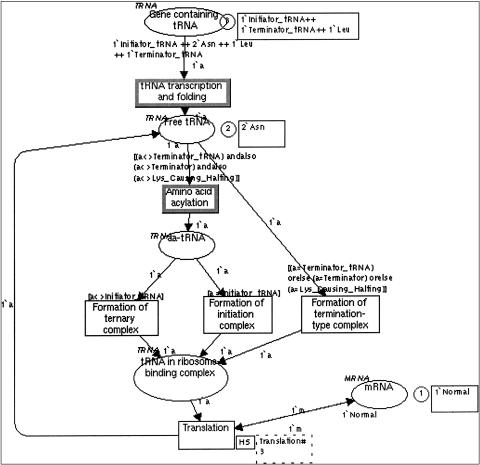
Figure 4.

A Design/CPN model describing tRNA transcription and incorporation into proteins. The transition labeled as “Translation” is hierarchical and is expanded into a lower level Petri Net (not shown). Places are depicted as ovals and transitions as squares. Enabled transitions have a bold contour. Circles with a number in them indicate place marking. To the right of the circles, squares with text strings indicate the kind of tokens that mark a place. Each place has a color set (tRNA, mRNA, at the top left of each place), defined by a set of allowed token types (e.g., Initiator_tRNA, Asn). The places “Gene containing tRNA” and “mRNA” (bottom right) are initially marked, as specified in the expression below the place. The arcs are marked with 1'a and 1'm representing tokens belonging to the color sets tRNA and mRNA, respectively. The expressions in square brackets above transitions represent guarding conditions that must be true for a transition to be enabled. Hierarchical transitions (e.g., Translation) are labeled by two squares to their right. Transitions with bold contours indicate transitions that are enabled in the current marking. During the execution of the token game, one of the enabled transitions is randomly selected, and the tokens flow to create a new marking.

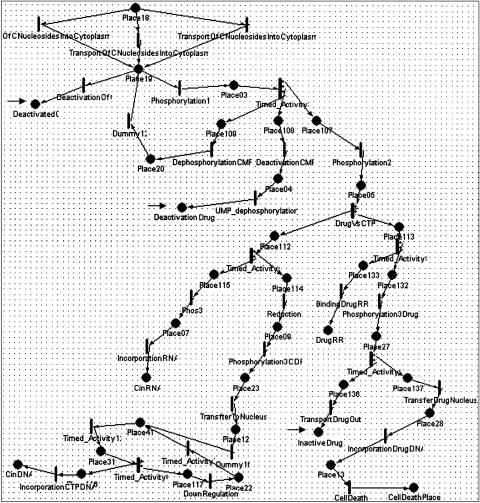
The third example (▶▶▶) concerns the molecular level biochemical and regulatory pathway of the drug gemcitabine and of the endogenous nucleotide cytidine, for which gemcitabine is an analog. Cytidine participates in transcription and in DNA replication, whereas its analog, which participates in DNA replication, causes cell death. The pathway starts with the drug's intake by the cell and ends in its effect on cancerous and rapidly dividing cells resulting in cell death. The pathway shows cellular reactions that inactivate the drug and inhibition of the drug's processing in the cell by deoxycytidine triphosphate nucleotide (dCTP).

Figure 5.

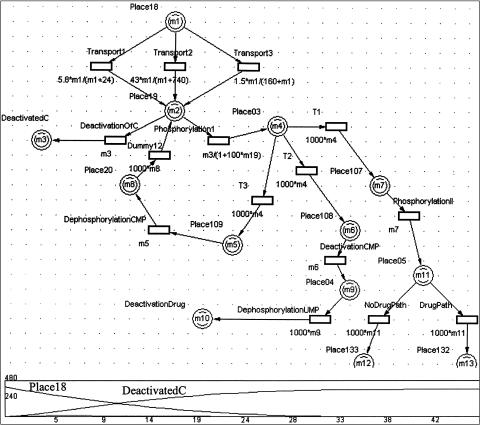
A Mobius model of the gemcitabine model. Gemcitabine is a chemotherapeutic drug that is an analog of the normal cytidine that participates in transcription and in DNA replication. The pathway starts from the drug's intake by the cell and ends in its effect on cancerous cells resulting in cell death. The pathway shows cellular reactions that inactivate the drug and negative feedback of the drug's processing by the cell, which is inhibited by normal deoxycytidine triphosphate nucleotide (dCTP). The part of the PN that is shown in the figure represents transport of the cytidine or the drug analog into the cytoplasm, followed by two phosphorylation steps or inactivation of these molecules. At the bottom, the Petri Net branches into two paths: one for cytidine and one for the drug analog. dCTP downregulates the drug effect by inhibiting the first phosphorylation step of the drug (and cytidine). This is represented in the model by the rate of the phosphorylation1 reaction, which is proportional to the concentration of the phosphorylation substrate (Place19) and inversely proportional to the concentration of dCTP. The reactions are modeled as activities with exponential time distribution function.

Figure 6.

Part of the Genomic Object Net's Petri Net of the gemcitabine example shown in ▶ and some of the graphs produced that follow the number of tokens at some places as a function of time. These graphs were produced by the Cell Illustrator tool, version 1.02, which is a new version of Genomic Object Net, which has better capabilities but is not freely available.

Figure 7.

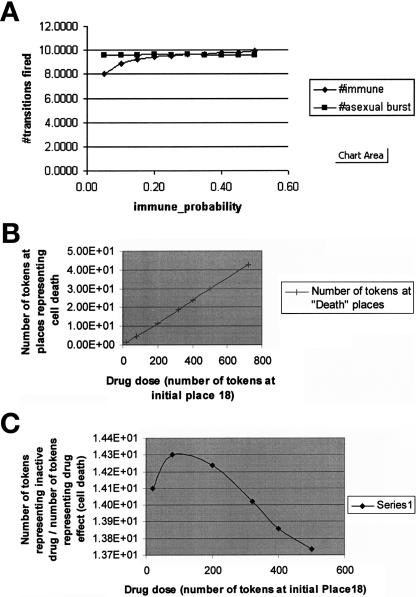
The results of experiments performed by the Mobius tool (plotted using Microsoft Excel). Whereas in TimeNET and Genomic Object Net, a single experiment can examine individual places (or sets of places in TimeNET) as a function of time, a Mobius experiment measures the number of tokens in a place or the number of times that a transition was fired at a single point in time or the total or average number over an interval of time. To generate a kinetic profile in Mobius, several experiments need to be executed. On the other hand, in a single experiment in Mobius, the user can vary many structural parameters. However, plots are not generated automatically by Mobius. A: The number of transitions fired as a function of immune_probability with burst size 50. This curve plots the number of two transitions that were fired: Immune_Response and Asexual_Development as a function of the probability of going in the path of an immune response from Place1 of the composed model shown in ▶, rather than executing the other transition that uses Place1 as an input place (MerozoiteInBlood, left-hand SAN in ▶). The parameter burst size indicates the number of tokens that are output by the output gate shown on the left-hand side of ▶. B: Drug effect (cell death as a function of drug dose). C: Inactive drug/drug effect as a function of drug dose. B, C: Results that were generated from simulation of the Gemcitabine model shown in ▶. The plots show token markings as a function of time: the number of tokens at a place that indicates drug effect (CellDeathPlace + Place13) (B) and the ratio of the sum of tokens in the places that indicate inactivated drug (DeactivatedC, DeactivationDrug, InactiveDrug, marked by arrows in ▶) divided by the number of tokens at the place that represents drug effect (CellDeath + Place13) (C). Because the places that indicate inactivated drug include two places that store both drug tokens and cytidine tokens (DeactivatedC, DeactivationDrug), we multiplied the number of tokens stored in those places by the ratio of drug concentration to the concentration of cytidine + drug.

Biological Questions That Petri Nets Can Answer

In comparing PN formalisms and tools, we were driven not by the mathematical capabilities of the tools but by the types of biological questions that could be analyzed by the PN tools. We divided the typical biological questions into two categories: those that depend on the static structure of the PNs and those that depend on dynamic simulation using the PNs.

1. Qualitative questions that depend on the structure of the net

   A PN's topology can be used to answer qualitative questions, such as determining the conditions under which modeled processes are active or inhibited, identifying biochemical pathways, and identifying states of the system that may be reached in the course of system execution.

   • 1.1. Active processes: Studying the conditions under which processes are active or inhibited and the resulting system states under normal conditions or in the presence of inhibition of processes. Specifically, there are three types of questions that can be analyzed topologically:

     • 1.1.1. Does an inhibitor inhibit an entire high-level process? This question can be answered by reachability analysis (▶). Reachability examines whether, given a certain state (marking) M of a PN, another state, M', is reachable from state M. For example, if we block the immune system, can we still reach a state where the parasite is cleared from the blood system?
     • 1.1.2. Does inhibition of an activity cause a state in which not all other activities can be activated? This question can be answered by verifying the liveness property of PNs (see ▶ for a definition of liveness). Liveness guarantees that all transitions (biological processes and reactions) can be enabled.
     • 1.1.3. Is there accumulation of metabolites at toxic levels? This question can be answered by verifying the boundedness property of PNs (see ▶ for a definition of boundedness). Boundedness guarantees that in every place, the number of tokens is always less than n. Tokens may be used to represent amount of metabolites, where each metabolite molecule is represented by one token.
   • 1.2. Biochemical or regulatory network structure: Analysis of the PN's structure can identify metabolites that are likely to belong to a confined pathway as well as processes that compete for the same set of metabolites. Four types of such structural questions can be answered:

     • 1.2.1. Can we identify parts of pathways? This can be done through place invariants—sets of places in which the total amount of tokens is constant. Invariants may represent metabolites that exist in invariant amounts, suggesting the existence of a pathway.²
     • 1.2.2. Can we identify sets of metabolites that are likely to be affected by inhibition of a reaction? Locating place invariants containing input/output places of the inhibited reaction can identify such sets.² This directs biologists in confining experiments to those places.
     • 1.2.3. Can we identify conflicting transitions (i.e., processes that are enabled under the same conditions) and concurrent processes? This can be done through analysis of the structure of the PN (structural analysis).
     • 1.2.4. Can we identify continuous operation and cycles? This can be done through identification of T-invariants—sets of transitions that have to fire, from the initial marking M₀, to return the PN to M₀.
   • 1.3. Reachable states of the system: It is often interesting to analyze possible states of the system that can be achieved under different environmental conditions. Such questions can be answered by reachability analysis.¹ For example, three specific questions can be analyzed:

     • 1.3.1. Is a certain state of the system reachable from the initial state? It may be interesting to determine the initial states from which a desired or undesired system states can be reached.
     • 1.3.2. If an activity is inhibited, can we still get to a specified state? This type of analysis helps us in finding key activities whose inhibition may result in reaching a desired state.
     • 1.3.3. What are the key compounds necessary for a biotransformation? Some compounds or participants are generated by reactions in pathways, whereas other participants must be made available to the system from external sources to allow reactions in the system to occur.

2. Qualitative results that depend on simulation

   Although the questions discussed above are related to the topology of the modeled system, many interesting questions concern the dynamic behavior of the system. These questions concern the examination of the flow of tokens throughout the net, as well as in silico experiments that we can perform by simulating the system over a range of varying conditions. Other measures that we can determine include the degree of process utilization and whether the system reaches a state of equilibrium.

   • 2.1. Tracing possible execution paths in a network of reactions: Exploration of the processes that are carried out when the PN is activated and the movement of tokens helps modelers in understanding a PN's behavior over time. Two questions can be asked.

     • 2.1.1. Can we follow individual molecules through a pathway/network? This can be done through an interactive simulation (“token game”), which highlights enabled transitions (▶) and markings, and lets the user step through the transitions that are fired and the markings that result.
     • 2.1.2. Can we validate the network's behavior? Carrying out several interactive simulations under different initial conditions allows modelers to experiment with the network's behavior, gaining confidence in the model's validity.
   • 2.2. System behavior as a function of time: Performing kinetics experiments and measuring the number of tokens in a place over time to obtain results that answer the following questions.

     • 2.2.1. What is the kinetic profile of a local or global system state? Can we identify bottlenecks where tokens accumulate at a place before they are able to flow through the following transitions?
     • 2.2.2. Measurement of the time it takes for 50% of the molecules to reach a specified state. This can be done by simulation or numerical analysis.
   • 2.3. Testing system behavior as a function of initial conditions: Initial conditions include metabolite concentration, absence of reactions, probabilities of conflicted processes, and process rates.
   • 2.4. Measuring process utilization, i.e., the percentage of time in which a process is operational.
   • 2.5. Steady state: We are often interested in determining the state of the system at the steady state.

Systems Descriptions

We selected PN formalisms and tools based on their availability, exchange format, and support for analysis and simulation. The tools include Mobius²⁶ (http://www.crhc.uiuc.edu/PERFORM/) for SANs, TimeNET²⁷ (http://pdv.cs.tu-berlin.de/∼timenet/) for stochastic PNs, Design/CPN (http://www.daimi.au.dk/designCPN/)²⁸ for high-level PNs, Genomic Object Net¹⁵ (http://www.genomicobject.net/member3/index.html) for hybrid PNs, and Woflan²⁹ (http://tmitwww.tm.tue.nl/research/woflan/index.htm) for regular PNs. The tools are reviewed below, and their main features are summarized in ▶.

Mobius²⁶ is a software tool for modeling and studying the reliability, availability, and performance of complex systems that has been developed at the University of Illinois and is available at http://www.crhc.uiuc.edu/PERFORM. It is a successor of the UltraSAN tool. Mobius supports multiple high-level modeling formalisms, including stochastic extensions to PNs, Markov chains and extensions, and stochastic process algebras. Mobius models may support two types of uncertainty: activity duration and the probabilities of occurrence of mutually exclusive activities. First, activities may be associated with delays that have a distribution function. The types of functions supported include exponential, normal, gamma, binomial, geometric, and triangular distributions. The distribution function may depend on the net's marking. If an activity has a distribution function that depends on the state of the net, then the activity's delay may be either evaluated when the activity is initially enabled or computed continuously (reactivation). Activities that are mutually exclusive can be represented as a single activity with several mutually exclusive cases that result in different outcomes. The probability of each of the cases can be specified and may depend on marking. In Mobius, activities (transitions) may be connected to places directly or via gates. Gates specify the marking required for the activity to be enabled and the marking changes that will occur when the activity terminates. These changes may be functions of marking. A unique feature of Mobius is the ability to combine multiple copies of different PNs to examine alternative system designs. Mobius supports extended places, places that are typed, and whose values can take on types, which can be data structures. This feature allows many of the capabilities of CPNs. Mobius (version 1.5) enables time- and space-efficient, discrete-event simulation and numerical solution based on compact MDD-based Markov processes and multiple solution techniques. Measurements can be conducted at specific time points, over periods of time, or when the system reaches steady state. Performance measures that can be evaluated may relate to the number of tokens in places or to the number of activity completions. Experiments can be performed by varying the range of input parameters, including activity delays, initial marking, and probabilities of transition cases and running the simulation once to obtain results under different parameter values. Mobius uses several optimization methods to reduce the complexity of its simulation algorithm. For example, Mobius uses the fact that, in practice, model events (activity completions) often have only a local impact on a model's state variables to achieve efficient simulation. To do so, Mobius stores information about the relationships between a state variable and activities that are related to them. Mobius can be run on Windows, Solaris, and Linux operating systems. Mobius has superb technical support from its development team.

TimeNET (Timed Net Evaluation Tool, version 3.0) is a software package for the modeling and evaluation of stochastic PNs with nonexponentially distributed firing times.²⁷ TimeNET has been developed at the Technische Universitat Berlin in several research projects and is available at http://pdv.cs.tu-berlin.de/∼timenet/. TimeNET supports the specification of arc weights that allow passing multiple tokens simultaneously through transitions and inhibition arcs that represent transitions that are disabled when there are tokens in the linked input places. TimeNET runs on Sun and Linux environments and supports different types of analyses, including the detection of place invariants, conflicting transitions (i.e., transitions that are enabled under the same marking), estimation of the number of different states that the system can reach (state space), traps (i.e., places that once a token enters them it does not leave them), siphons (i.e., places that once a token leaves them it does not return to them), token game animation (i.e., interactive animation of tokens moving in a net), simulation of the net, and evaluation of performance measures. The types of performance measures that can be defined are expressions relating to the expected number of tokens in a place or to the probability that some logical condition holds (e.g., the number of tokens in Place 1 is greater than 5). The evaluation may be performed in discrete or continuous time until a specified time (transient) or in steady state. Different types of evaluation are possible: numerical analysis with a full exploration of the reachability graph or a standard Monte Carlo style simulation approach. When tested on our examples, the only evaluation that functioned was transient simulation with continuous time. Experiments can be run in which the same algorithm is executed with different parameter values and the model is evaluated automatically for all specified values of one marking or delay parameter. The parameter can be changed linearly or logarithmically. The results of the evaluation are plotted automatically. The complexity of reachability analysis and other types of analyses performed by the TimeNET tool are discussed in German et al.²⁷ Reachability analysis is conducted by generating a reduced reachability graph of a timed PN model after a decomposition of the net into subnets by removing the timed transitions. The memory requirements of a reachability graph generation algorithm should not exceed the main memory available on a given workstation. If the estimated memory requirements exceed the main memory on a given workstation, the space efficient variation is used.

Design/CPN (version 4.0) is a tool package supporting the use of CPNs that is available at http://www.daimi.au.dk/designCPN/.²⁸ It is being developed at the University of Aarhus, Aarhus, Denmark. Design/CPN supports CPN models with complex data types (color sets) and complex data manipulations (arc expressions and activity guard conditions that must be met for transitions to fire), both specified in the functional programming language standard machine language (ML).³⁰ The package also supports hierarchical CPNs, net models that consist of a set of separate subnets with well-defined interfaces. In Design/CPN, tokens may be associated with numbers representing time stamps. A timed token is not available for any purpose whatever unless the clock time is greater than or equal to the token's time stamp. A typical industrial model often consists of 50 to 200 modules, each with ten to 50 different places and transitions. Design/CPN supports analysis by means of simulation and construction and analysis of state spaces. ML can be used to define performance measures, which are assessed during activity operation, and to plot graphs of these performance measures.

Design/CPN runs on Solaris, Linux, HP-UX, and SGI-Irix. Design/CPN is being replaced by CPN Tools, which runs on Windows operating systems. Design/CPN has excellent technical support from its development team. The technical support in the future will be given only to CPN tools users.

Genomic Object Net is a tool that supports hybrid functional PNs and was developed at the University of Tokyo (http://www.genomicobject.net/member3/index.html).¹⁵ In hybrid functional PNs, transitions and places can be either discrete or continuous. Any function, including marking-dependent functions, can be assigned to arcs and transitions for controlling the speed/condition of firing. Inhibition arcs can be used to represent process inhibition in the presence of metabolites that are represented by tokens in the input places linked by inhibition links. A commercial version of Genomic Object Net, named Cell Illustrator, is now available. Both tools include a powerful graphical user interface realizing more biological intuitions when designing PNs. The tools support both animation and simulation. The kinetics behavior of the system is measured by following the marking of individual places. The resulting behavior is automatically plotted as graphs. Genomic Object Net is the only tool reviewed in this paper that does not have an exchange format. It can export a PN representation but does not import PN representations. This fact impedes the exchange of models between various PN tools. Genomic Object Net has excellent technical support from its development team. It runs on Windows®, Mac Intosh®, and Solaris® operating systems.

Woflan (version 2.3) is a verification tool for workflow analysis, developed at the University of Eindhoven, the Netherlands.²⁹ Workflow models are converted into PNs and verified for soundness (a combination of boundedness and liveness). When soundness does not hold, the tool walks the user through the verification steps, suggesting reasons why the soundness property does not hold. These reasons include:

1. Synchronization problems—synchronization problems may occur when activities (transitions) that are executed in parallel are synchronized by waiting for only one of them to terminate or when activities that are mutually exclusive are synchronized at an activity that waits for all the mutually exclusive activities to terminate.

2. Mixing synchronization and choice—such mixing may occur by specifying several tasks that share some but not all preconditions. In this case, confusion can occur if at least one of the tasks synchronizes and there is a choice between the tasks.

3. Improper termination—when biological processes have one start condition and one termination condition, then improper termination can be checked by identifying transitions that are active while the system has reached its termination condition. When improper termination is detected, Woflan lists the sequence of activities that can lead to improper states.

4. No termination state—when biological processes have one start condition and one termination condition, Woflan can check whether the process can reach the termination condition and, if not, identify reachable states from which termination cannot be achieved.

5. Tasks that are not live.

The exact complexity of deciding whether a PN is sound (liveness and boundedness) is not known.³¹ From a practical point of view, this is not an unconquerable problem. Woflan can verify the soundness property for complex workflows encountered in practice.³² Woflan has a simple exchange format for PN. Woflan runs on Windows operating systems. The verification results are displayed through a graphical user interface. However, the PN itself is not shown graphically. Woflan has excellent technical support from its development team.

A Tool for Converting Biological Work Flow Models into Petri Nets in Various Formats

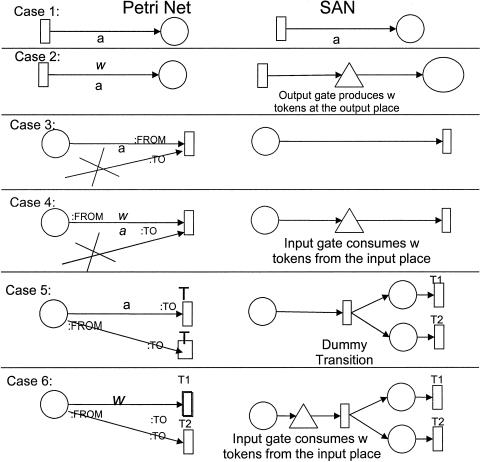
In most cases, we did not use the PN tools directly to compose PNs. Instead, we created work flow models of biological systems using a biological process ontology⁸ that we developed using the Protégé-2000 knowledge modeling environment.³³ We wrote software that automatically translates work flow models into PNs of three of the tools discussed in this article: Woflan, Genomic Object Net, and Mobius.³⁴ The design of the scripts that map the work flow model into a plain PN and maps the plain PN format into TimeNET and Woflan, and the mapping algorithm used by those scripts are discussed elsewhere.³⁴ The script for translating the plain PN model into the Mobius formalism and tool was prepared especially for this work. Its algorithm is shown in Appendix 1. Genomic Object Net does not allow import of XML or text files that store PN models. Therefore, we could not create scripts to translate a PN model into a storage format for that tool and had to manually create the model. We also created manually the models in the Design/CPN tool.

Status Report

We found that PN formalisms and tools can model a variety of biological systems characterized by the features enumerated in the Design Objectives section as well as answer different biological questions based on their analysis and simulation capabilities. When describing the modeling of a feature, sometimes the formalism is mentioned and other times the tool is mentioned. These tools are complete implementations and representations of their formalisms. Therefore, we use the name of a PN formalism and its supporting tool interchangeably. Throughout the paper, when we note that certain tools are not able to address certain features and questions, it is a limitation of the formalisms that they support rather than of the implementation.

Mathematical Capabilities for Modeling and Analysis and Desired Technical Features

The extensions to PNs have special features that make them more suitable to represent and analyze certain biological features than regular PNs. These features are summarized in ▶. There are cases in which the tool does not adequately support its formalism. These cases are noted as “not working” or “not directly” in ▶.

The Way in Which Petri Nets Can Represent Typical Features of Biological Systems

To show the diversity of the abilities of the tools, we implemented the case study examples using subsets of the tools, choosing to implement an example so that the different capabilities of the tools could be demonstrated. ▶▶▶ show PN models and their analysis corresponding to the malaria example. The PNs in the TimeNET format (▶) and Woflan format were automatically derived from a work flow model that we created and is available at http://mis.hevra.haifa.ac.il/∼morpeleg/NewProcessModel/Malaria_PN_Example_Files.html.⁸ The full work flow model includes ten work flow diagrams. For brevity, we only show PNs corresponding to the top-level work flow diagram. The bottom of ▶ shows the results of the kinetic profile of the system, obtained by simulation performed using TimeNET, whereas ▶ shows the analysis results obtained by Woflan for the same PN structure as that of ▶. We created the Mobius model, shown in ▶, manually, using our judgment to split the PN into three component PNs that are composed together, operating concurrently. This allowed us to represent populations of red blood cells and to model how each malaria parasite that occupies the bloodstream can either be removed by the immune system or invade populations of red blood cells and to study the system's behavior for the population of parasites. We initialized the PN with 20 copies of an “immune system” PN and 80 copies of the red blood cell PN so that the 100 malaria parasites in the bloodstream would compete for interaction with these copies of immune system and red blood cells. The Design/CPN and Genomic Object Net models of the malaria example are not shown in this report because they do not show any characteristics not shown by the other PN models presented.

The CPN in the Design/CPN format shown in ▶ shows the second test case that models the effect of genetic variation in tRNA genes on protein translation. This example was generated from a work flow model that we had previously created.¹³ We used our software to automatically create PNs in Woflan format from the work flow model and manually created the Design/CPN model corresponding to the PN, adding colored tokens. This tool is most appropriate for modeling systems whose behavior differs for variants of participating molecules. We did not create models of this system using TimeNET, Genomic Object Net, or Mobius because their unique capabilities were mainly demonstrated in the first (for TimeNET and Mobius) and third test cases (for Genomic Object Net and Mobius).

▶▶▶ correspond to the third example representing the molecular pathway of the drug gemcitabine. We modeled the gemcitabine example as a workflow and automatically converted it to PNs in the Mobius, TimeNET, and Woflan formats. We manually created the corresponding Genomic Object Net applying a direct mapping from the Mobius model. We do not show the Woflan results because they are similar to the results obtained by Woflan for the malaria example. We did not create the Design/CPN model for the gemcitabine example because it would not show capabilities of this formalism and tool that were not demonstrated in the tRNA example. We show some of the simulation results obtained by Mobius and Genomic Object Net. The results obtained by TimeNET are not shown, as explained in the Limitations section of the Discussion.

We now evaluate the tools according to the biological features that the examples possess (summarized in the top of ▶).

1. Abstractions that allow decomposing a biological system to a set of PNs. Many biological systems are described hierarchically as components of subsystems. In Design/CPN, complex processes are hierarchically decomposed into atomic processes. This helps in managing complexity by partitioning the system specification into different levels of granularity. For example, ▶ shows a PN describing the processes of tRNA transcription and incorporation into proteins. The translation process, represented by the bottom transition, is expanded into another PN (not shown). In Mobius, several copies of atomic PNs can be composed together to form a complex system. This is very useful for modeling populations that share mutual resources. For example, we have used this feature to represent copies of red blood cells that may be infected by a pool of malaria parasites that enter the bloodstream. As shown in ▶, the system is composed of copies of PNs representing the parasite life cycle in the human red blood cells, human immune system clearing parasites, and human bloodstream. These three PNs interact by sharing a common place, Place1, which corresponds to the parasites in the bloodstream. Therefore, the parasite may enter any red blood cell or may be removed by the host's immune system.

2. Processes that affect individuals as well as populations. Biological systems often deal with populations that are studied both as aggregates and individually. Mobius can use composition to create copies of SANs. Each copy represents an individual. The number of individuals in a population can be controlled by the number of copies of a SAN in a composed model. For example, the model of parasites infecting host cells, shown in ▶, allows the user to follow a single parasite infecting a single cell as well as a population of parasites infecting a population of host cells. The other PN tools, except for Woflan, can treat populations by multiple tokens. Arc weights can be used to transfer multiple tokens, corresponding to multiple individuals of a population, from and to transitions.

3. Genetic variation. Individual molecules or organisms may have small differences that must be modeled while retaining fundamental biological similarities. The most suitable for modeling genetic variation is Design/CPN, which uses different colored tokens that belong to one color set to represent variants. ▶ shows a Design/CPN model of protein translation that is affected by different tRNA molecules that are the products of normal and mutated alleles. The tRNA molecules differ by the type of amino acid that they carry and, in addition, by their normal versus mutated structure. In this model, transitions have guarding conditions that ensure that reactions take place only for certain tRNA alleles. The transition “tRNA transcription and folding” occurs for all variants of tRNA genes. The transition “amino acid acylation” occurs only for tRNA molecules that are not terminator tRNA molecules and are not mutated alleles of the lysine tRNA molecule that causes halting of the translation process.

   The Mobius tool has extended places that are typed and whose values can take on types, which can be data structures. This feature allows many of the capabilities of CPNs. However, extended places cannot be directly connected to transitions (only via gates), and the gate functions need to specify explicitly which type of tokens should be passed to a transition. Therefore, unlike CPNs, Mobius does not easily support a model that can have reactions that depend on token type and at the same time include other reactions that occur with any type of token, where typed tokens are passed to and from both types of reactions.

4. Biochemical reactions. Biological transformations are characterized by participating substrates and products with stoichiometric coefficients, catalysts, and inhibitors or allosteric effectors. All the PN tools that we have assessed can represent biochemical reactions. Reactions that consume or produce more than one individual item, for example, metabolites in biochemical reactions whose stoichiometric coefficient is greater than one, or cell division, which produces two cells, require the use of arc weights or gates in Mobius.

   In Mobius, TimeNET, and Genomic Object Net, the reactions may have rates that depend on the concentrations of participating molecules (marking). ▶ and ▶ show pathways related to metabolism of the drug gemcitabine. We have followed the main metabolites of the pathways, representing them as tokens in places. We have assumed that currency metabolites, such as adenosine triphosphate and reduced nicotinamide adenine dinucleotide, are abundant and therefore are not representing them in the model. We chose to represent enzymes as the reactions that change a substrate into a product. Quantitative models can be created by relating kinetic constants to transition rates.^35,36 SANs and hybrid PNs allow the representation of reaction rates (enzymatic reactions or transport reactions) that depend on substrate concentrations. The rates of continuous transitions of hybrid PNs can be expressed by any function, which may be marking dependent. In contrast, Mobius does not allow any function to specify the rates of transitions. Rather, the transition rates can be specified as a time distribution function that specifies the time between firings of two transitions. Many distribution functions are supported, such as the exponential function, which may serve as an approximation for the Michaelis-Menten equation. For example, the exponentially distributed transitions “transport of nucleosides into the cytoplasm,” shown at the top of ▶ and ▶, have a rate equal to V*_max (marking of input place)/(K_m + marking of input place). In modeling the gemcitabine case study, we had reaction rates for only a few of the reactions modeled.

   To use a quantitative model, we used these reaction rates but had to estimate the rates of other reactions. The strategy that we devised for specifying reaction rates was to give all the other reaction rates that depend linearly on the concentration of reaction substrates multiplied by a constant that made these reaction rates of the same order as the known reaction rates that biologists had provided us. Some transitions in the PN do not convey biological information and serve for branching and synchronization purposes. We gave these transition rates that were proportional to the concentration of metabolites that served as inputs to the transitions multiplied by a factor that caused these reactions to occur at a much higher rate (1,000-fold) than the biologically relevant reactions. In cases in which substrates needed to accumulate to produce an effect (e.g., in the negative regulation of gemcitabine phosphorylation by dCTP), we used a reaction rate that was of the same order as the rates of reactions of which we had biological information. We used the same rates as the rates of the continuous transitions in the Genomic Object Net model that we created. Qualitative models can be created if rough estimates are used for rates. Mounts and Liebman²⁰ discuss an approach for modeling transition rates that are marking dependent. However, the authors note that this approach does not scale well to large systems.

5. Process inhibition. Process inhibition can be modeled in TimeNET and Cell Illustrator (the next generation of Genomic Object Net) using inhibitory arcs. In Mobius, in which inhibitory arcs are not part of the model, reaction rates may be expressed as a function that is correlated with the concentration (marking) of substrates and negatively correlated with the concentration of the inhibitor. For example, the rate of the exponentially timed transition “phosphorylation 1,” shown in ▶, is equal to the marking of its input place (Place19, which represents a drug that had entered the cytoplasm) divided by (1 + 100 times the marking of Place22), where Place22 represents dCTP molecules that serve as negative regulators of the phosphorylation process.

6. Kinetic curves. Reactions with typical kinetic curves can be represented in PNs. These include hyperbolic curves, which are typical of enzyme saturation (see R5 in ▶) and sigmoid curves, typical of allosteric effects. All the PN tools reviewed, except for Woflan, support simulation whose results could be plotted.

7. Competitive reactions. Different reactions may occur under the same conditions or compete for the same substrates. Sometimes we have information on the probabilities of such competitive reactions. Competitive reactions are modeled in PNs as transitions that have the same set of input places and occur under the same guarding conditions. For example, in ▶, the transitions “formation of ternary complex” and “formation of initiation complex” have the same set of input places but are not competitive because they have mutually exclusive guarding conditions regarding the type of participating tRNA molecule. All the PN tools can represent competing transitions, but only in SANs can the probabilities of the competing transitions be expressed. In SANs, competitive reactions are modeled as single transitions that have multiple cases, as shown in ▶. In that example, the transition labeled as “XOR” controls whether a token will follow asexual or sexual development. Controlling probability of conflicting transitions is useful because this is more realistic and we may have that kind of data available. For example, in the gemcitabine model, shown in ▶, the transition DrugVsCTP splits the pathway into a branch that follows reactions of the normal cytidine only and a branch that follows only the drug gemcitabine. This transition has two cases (nondrug and drug), each with its own probability. By experimenting with different rates of drug probabilities, we can obtain graphs that depict the system's behavior as a function of drug dose (▶b,c). Similarly, as shown in the left part of ▶, there are two competing reactions shown in the Mobius model of the malaria example: asexual and sexual development. In Mobius, we could specify different probabilities for these competing reactions, reflecting current biological knowledge on the occurrence of these life cycle processes.

8. Concurrent processes are represented in all the PN tools by transitions that produce tokens in several output places. This enables more than one thread of control to be active.

9. Regulation of gene expression and

10. Signal transduction are not covered by our case study examples but have been previously modeled using hybrid PNs and the Genomic Object Net tool^11,14 as well as by SANs.¹⁸ We briefly explain how these features can be (or have been) modeled using the different PN formalisms that we discuss without providing our models for these features. Modeling of signal transduction and genetic regulation involves response to levels of molecules (hormones, second messengers). This cannot be easily done using regular PNs or CPNs but can be modeled using test arcs in Genomic Object Net or the dependence of the rate of molecular level functions on the time during a hormonal cycle in Mobius and in TimeNET. The third example in our study, described in item 5 above, includes downregulation of the phosphorylation reaction (phosphorylation1) carried out by the enzyme dCK.

Table 2.

Petri Net Tools Characterized by the Typical Biological Systems That They Can Represent and by the Biological Questions That They Can Answer

	Mobius	TimeNET	Design/CPN	Genomic Object Net	Woflan
Typical process characteristics
Abstractions of complex processes	+ Composition		+ hierarchy
Populations	++ Composition gates	+ Arc weight	+ Arc weight	+ Arc weight
Genetic variation			+*
Substrates, products, catalysts	+ I/O place	+ I/O place	+ I/O place	+ I/O place	+ I/O place
Stoichiometric coefficients	+	+	+	+
Reaction rates	+++	++	+	+++
Inhibitors and allosteric effectors	Competing cases	+ Inhibitory arcs	Competing transitions	Competing transitions	Competing transitions
Typical kinetic behavior	+	+	+	+
Competing reactions with different probabilities	+	Probabilities not working	Not directly supported	Not working
Concurrent processes	+	+	+	+	+
Typical questions
Active processes					+*
Network structure		+*
Network behavior/interactive simulation		+	+	+
Reachable states		Not working
Kinetic profile	++	+++	Not directly supported	+++
Process utilization	+		Not directly supported	+
Equilibrium state	+++	+++	Not directly supported	+++

The number of + signs indicates the level of support.

CPN = Colored Petri Net; I/O = input or output.

^*Features that are supported by at most a single tool.

The Way in Which Petri Nets Can Answer Biological Questions

In the Design Objectives section, we defined types of biological questions that are of interest to researchers. In this section, we discuss the way in which the different tools can answer these questions and summarize the results in the lower half of ▶.

Qualitative questions that depend on the structure of the net can be answered by the Woflan and TimeNET tools. These questions fall into three categories, numbered by the same numbers used in the Design Objectives section:

• 1.1 Active processes: Studying the conditions under which processes are active or inhibited and the resulting system states under normal conditions or in the presence of inhibition of processes can be analyzed by the Woflan tool. We performed liveness analysis using Woflan for the malaria example to show that an inhibitor (neuraminidase) can inhibit the entire invasion process, by which the parasite invades host red blood cells. We verified liveness and boundedness by Woflan for all three case study examples. ▶ shows an example of liveness and boundedness verification. In the malaria example, we showed that an inhibition of the tight junction formation activity results in the PN not being live.

• 1.2. Biochemical or regulatory network structure: Analysis of the PN's structure to identify metabolites that are likely to belong to a confined pathway as well as processes that compete for the same set of metabolites can be done by the TimeNET tool. We performed place-invariant analysis for the malaria example to find the sets of places in which the total amount of tokens is constant and obtained a trivial result consisting of all the places in the PN, limiting us from identifying key metabolites that are likely to be affected by inhibition of a reaction. We showed for the malaria example (▶) that conflicting transitions include invasion and immune response as well as asexual development and sexual development.

• 1.3. Reachable states of the system: Analyzing possible states of the system that can be achieved under different environmental conditions can be answered by reachability analysis, which is described as being supported by the TimeNET tool (it was not functional when we tried to implement it in our test cases, but this is a limitation of the tool and not of the formalism that it supports). We manually performed reachability analysis for the malaria example to find reachable states with and without inhibition of activities, as discussed elsewhere.⁸ For the gemcitabine example, we manually showed that the drug must be introduced externally for the system to reach the cell death state.

Qualitative results that depend on simulation can be obtained by Mobius, TimeNET, Design/CPN, and Genomic Object Net. They include the following:

• 2.1. Tracing possible execution paths in a network of reactions: We performed interactive simulation (“token game”) and checked the validity of models by Genomic Object Net for the malaria and gemcitabine examples, by TimeNET for the malaria example, and by Design/CPN for the tRNA example (▶).

• 2.2. System behavior as a function of time: We performed kinetics experiments to determine the kinetic profile and the time that it takes for 50% of the molecules to reach a specified state using Genomic Object Net, Mobius, and TimeNET. Design/CPN does not support directly the generation of quantitative simulation results. However, code can be written inside PN transitions to calculate the number of tokens that pass through a transition to produce quantitative results. Kinetic profiles are shown in ▶, ▶, and ▶. Curves R2 and R3 in ▶ show places that act as bottlenecks. Curve R5 in ▶ shows that it takes roughly 40 time units for the level of tokens (molecules) to reach a value of 2.5, which is 50% of their maximum value.

• 2.3. Testing system behavior as a function of initial conditions: We performed this analysis using Genomic Object Net, Mobius, and TimeNET. Design/CPN can produce such results by writing code inside transitions. ▶ shows behavior measured as a function of initial marking representing drug dose.

• 2.4. Measuring process utilization (i.e., the percentage of time in which a process is operational): The Mobius tool can define this type of performance measure. For example, in ▶, the percentage of time in which the processes (transitions) immune response and asexual burst (i.e., following asexual life cycle development) are active is measured as a function of the probability of following the immune response path rather than the asexual path. Kinetic results can be obtained by Genomic Object Net and Mobius. Design/CPN can produce such results by writing code inside transitions.

• 2.5. Steady state: Steady-state analysis can be performed using Genomic Object Net, Mobius, and TimeNET. Design/CPN can produce such results by writing code inside transitions.

Discussion

Significance

Previous studies have evaluated the use of PN tools for modeling biological processes.^3,9,10,11 However, these studies have concentrated on either structural analysis or quantitative simulation. Their focus was on demonstrating the utility of a simulation technique rather than comparing techniques and tools. The goal of our assessment was to explore the range of capabilities of PN tools and the types of biological questions that PNs can explore, whether they are structural or behavioral.

We took a pragmatic approach, motivated by modeling three different biological processes and exploring a range of biological questions that can be answered. We found that there is not a single tool that can be used to answer all the biological questions that we identified as of potential interest. Instead, tools must be chosen based on the types of questions that are most interesting to researchers and on the characteristics of the process to be modeled. There are constraints of modeling a given biological system into different formalisms; the plain PN model, without extensions, cannot model all possible biological features. For example, to create a model that represents both normal and mutant alleles, Design/CPN is most suitable because it is the only model that uses colored tokens. Design/CPN is also the only model that allows decomposing a high-level process into a network of lower level processes, allowing complexity management. On the other hand, SAN, used by Mobius, is the only model/tool that can compose models of systems (e.g., blood system) from several copies of component subsystems (e.g., blood cells), modeled as PNs acting in parallel. In addition, SAN/Mobius is the only model/tool that can model uncertainty on the probability of competing processes allowing modeling of the percentage of time that different completing reactions take place when the exact mechanism that controls the execution of these reactions in unknown.

The different tools also vary in terms of questions that they can answer. For example, to detect place invariants that may indicate biochemical pathways in large PNs and to find sets of processes that occur under the same conditions, TimeNET is the tool that provides this functionality. To verify that all the modeled processes can be executed, Woflan is the tool of choice. Reachability is very useful for answering questions about states (markings) that are reachable from a given initial state of the system. It is especially interesting to find conditions under which a state is not reachable (e.g., when a certain reaction is blocked). Of the tools that we evaluated, TimeNET is the only one that has a function for checking reachability. However, we were unable to make this function operate in our PN examples.

To answer the most diverse set of questions, a combination of tools is needed. We have developed code to translate a biological work flow or plain PN model in Protégé-2000 format into various PN formats. Admittedly, translation to multiple PN formalisms is a somewhat difficult and redundant approach and does not automatically make use of the special features available in PN extensions, but it allows one to exploit the useful analysis capabilities of each tool and provide a certain degree of experimental quality control through redundant trials. The automatically generated PN models can be extended using special features of the different PN formalisms, as we have done for the tRNA example.

Limitations

Some analysis capabilities are provided by more than one tool. A troubling result that we have observed is that when we modeled one biological system, under the same assumptions in different tools, we obtained apparently different simulation results. TimeNET evaluates the average number of tokens that have accumulated until a time stamp has been reached. It does not evaluate the number of tokens present at a specified time stamp. This accounts for the difference in simulation results between TimeNET and Mobius/Genomic Object Net. However, for kinetic experiments, we are interested in the value of metabolites at a time stamp and less often at the average number of tokens until a specified time stamp. Mobius and Genomic Object Net have produced results that differ quantitatively but follow the same qualitative trends when the same model was simulated. After discussion with the development teams of these tools, we concluded that the different simulation behavior is due to differences between the PN models, not their supporting tools. While hybrid PNs allow fractions of tokens to flow continuously through transitions whose rate is proportional to marking, Mobius moves whole tokens after delays that have a time distribution function that is proportional to marking. Unlike Genomic Objet Net, Mobius runs the simulation many times and reports an average of the performance measures (e.g., number of tokens in a place). When used in a straightforward way, the two tools are appropriate for modeling different types of biological systems; the SAN model is more appropriate for following single molecules (or single cells or organisms) than the hybrid PN model, which uses continuous transitions, whereas the hybrid PN model is more appropriate for following populations (concentrations) of molecules. For following small populations of molecules belonging to interacting systems, Mobius can compose several copies of SANs and follow the behavior of the composed model. We note that it has been demonstrated that even in a system with as few as 100 molecules, simulation results of a deterministic method coincide closely with stochastic methods, suggesting that a deterministic approach may be a valid one to use.³⁷ The deterministic approach discussed above uses the law of mass action, an empirical law that relates reaction rates and molecular component concentrations. Given initial molecular concentrations, the law of mass action allows the calculation of the component concentrations at all future time points. Although such results have not been demonstrated in Cell Illustrator (the new generation of Genomic Object Net), it may use discrete entities and processes with random activities to simulate stochastic behavior as well as the mass action approach. Similarly, it may be possible to simulate continuous processes in Mobius using gate functions and places that hold floating point numbers of tokens.

Many of the PN formalisms supported by the different PN tools share common constructs. It would be most valuable to have a standard PN format. This would enable users to use different PN tools to simulate and analyze their models, without the need to use many proprietary PN formats. There is a proposal for high-level PN Standard ISO/IEC 15909. Its adoption by the different groups who develop PN tools would be very valuable to the biomedical informatics community.

Petri Nets are most suitable for modeling systems that can be described by finite sets of atomic processes and atomic states. They are not appropriate for modeling systems that have thousands of states, which depend on molecular sequences or spatial configurations. Although PNs have been used to model processes that work on genetic sequences,¹³ they do not have built-in capabilities to represent sequences as sets of places with initial marking. Longer biological sequences can result in PNs of bigger size and complexity, which do not scale up well. In addition, PNs have not been used to model dynamics that depend on three-dimensional configurations. Because PNs do not have built-in features for expressing spatial properties, each configuration has to be expressed as a different system state, and transitions need to be defined that move the system from each state to one of the next possible states. The size of the model does not scale up well when the number of possible configurations is large.

Although PNs can be used to create quantitative models, they require a large amount of information to gain accuracy. This problem is common to many biological modeling methods. For example, to specify a rate for a timed process (transition), data need to be collected about concentrations of the process' participants. It is difficult to specify a rate when partial information is known (e.g., the average duration of a process). In modeling the gemcitabine case study, we had reaction rates for only a few of the reactions modeled. To use a quantitative model, we used these reaction rates but had to estimate other reaction rates. Partial information can lead to overly simplistic models that fail to predict system behavior. Therefore, the models produced must be compared with experimental results for corroboration.

Future Work

We developed three case studies representing typical biological systems. We suggest that a library of such models would catalyze progress in qualitative modeling via PNs. Another direction of development is to generate scripts that would map the generic PN model into the formalism and format of Design/CPN. A third direction of research is to develop learning algorithms to help in fine tuning the transition rates in Mobius and Genomic Object Net models so that the simulation results of the modeled system would match experimental results of the real system.

Conclusion

Despite their limitations, PNs provide a promising method of modeling and simulating biological systems, given the acceptability of the associated assumptions. The extensions to PNs provide much more modeling and analysis support than basic PN. The value gained is generally greater than losses due to simplicity of the representation and the increase in computational complexity.

We have illustrated the kinds of biological questions and insights that these models can address, discussing formalization issues of: (1) active processes, (2) network structure, (3) reachable system states, (4) validation of system behavior, (5) system's behavior as function of time, (6) system's behavior under different initial conditions, (7) process utilization, and (8) steady state. Studying five PN tools, we found that there is no single tool that can answer all these questions. Most of the tools available (with the exception of TimeNET) concentrate on either topological analysis or simulation, and both of these capabilities are needed to study biological systems. Hence, the best tool (or combination of tools) to model a system must be selected based on the questions posed or multiple tools must be used. We have summarized formalism and tool capabilities to assist researchers who need to choose among the available tools in creating future models. Researchers can use biological data found in the literature (as we have done in the malaria and tRNA examples) as well as a combination of published data with new experimental results obtained by a biological laboratory (as we have done in the gemcitabine example) to create models of biological systems. The application areas for using PNs to model biological systems are wide and include areas such as biochemical pathways, signal transduction, and gene regulatory networks.

Development and wide adoption of common formats would enhance the field because it would enable researchers to share models of systems and use different tools to analyze and simulate the models without the need to convert to proprietary formats. We have developed a library of common biological test cases and a preliminary set of scripts to translate from biological work flow and PN models in Protégé-2000 format to various PN formalisms and tool formats.

Appendix 1. An Algorithm for Converting Petri Nets (PNs) to Stochastic Activity Networks (SANs)

The algorithm is described below. Steps 3–8 are illustrated by the drawing.

1. Convert every PN Place to a SAN Place. Copy the name and number of tokens.

2. Convert every PN transition to a timed activity with exponential distribution. The rate of the transition = 1/(min_transition_time + (max_transition_time–min_transition_time)/2) if these parameters have values. Otherwise, the rate is 1.

3. Convert a PN arc a that connects a transition to a place and has no weight or a weight of 1 into the corresponding straight line connector from transition to place (see Case 1 below).

4. Convert a PN arc that connects a transition to a place p and has weight w into the corresponding straight line connector from transition to output gate. The gate function will add w to the number of tokens at place p. Link the gate to p (see Case 2 below).

5. Convert a PN arc a that connects a place to a transition and has no weight or a weight of 1, and there is no other arc whose :TO slot equals the :TO slot of a into the corresponding straight line connector from place to transition (see Case 3 below).

6. Convert a PN arc a that connects a place to a transition and has weight w, and there is no other arc whose :TO slot equals the :TO slot of a into the corresponding straight line connector from place to input gate and set the function of the gate to consume w tokens from :TO. Then link the gate to the transition (see Case 4 below).

7. Convert a PN arc a that connects a place to a transition and has no weight or a weight of 1, and there is another arc whose :FROM slot equals the :FROM slot of a into the corresponding straight line connector from place to transition. This transition should have n cases, where n equals the number of arcs on that PN whose :TO slot equals the :TO of a. Link each case to a place. Give the new transition and the new places dummy names. Each case probability will be determined from the probability of each arc. Link the new place that corresponds to the case whose probability was determined from the arc's probability to the transition that is specified in that arc's :FROM slot. Do the same to all the other arcs that share the same input place, remembering not to process them again during the PN → SAN conversion (see Case 5 below).

8. Modification of the previous step for arcs that have weight w: instead of simply linking a new place to the corresponding transition, place an input gate between the two and update its function according to w (see Case 6 below).

▶

Figure 8.