Text Categorization Models for High-Quality Article Retrieval in Internal Medicine

Abstract

Objective Finding the best scientific evidence that applies to a patient problem is becoming exceedingly difficult due to the exponential growth of medical publications. The objective of this study was to apply machine learning techniques to automatically identify high-quality, content-specific articles for one time period in internal medicine and compare their performance with previous Boolean-based PubMed clinical query filters of Haynes et al.

Design The selection criteria of the ACP Journal Club for articles in internal medicine were the basis for identifying high-quality articles in the areas of etiology, prognosis, diagnosis, and treatment. Naïve Bayes, a specialized AdaBoost algorithm, and linear and polynomial support vector machines were applied to identify these articles.

Measurements The machine learning models were compared in each category with each other and with the clinical query filters using area under the receiver operating characteristic curves, 11-point average recall precision, and a sensitivity/specificity match method.

Results In most categories, the data-induced models have better or comparable sensitivity, specificity, and precision than the clinical query filters. The polynomial support vector machine models perform the best among all learning methods in ranking the articles as evaluated by area under the receiver operating curve and 11-point average recall precision.

Conclusion This research shows that, using machine learning methods, it is possible to automatically build models for retrieving high-quality, content-specific articles using inclusion or citation by the ACP Journal Club as a gold standard in a given time period in internal medicine that perform better than the 1994 PubMed clinical query filters.

Introduction

Evidence-based-medicine (EBM) is an important development in clinical practice and scholarly research. The aim of EBM is to provide better care with better outcomes by basing clinical decisions on solid scientific evidence. EBM involves three distinct steps: (a) identification of evidence from the scientific literature that pertains to a clinical question, (b) evaluation of this evidence, and (c) application of the evidence to the clinical problem.¹

In practice, the application and adoption of EBM to real-life clinical questions is challenging. Insufficient time for searching, inadequate skills to appraise the literature, and limited access to relevant evidence are among the most cited obstacles. Coupled with the scientific literature's exponential growth, applying EBM in daily practice proves a challenging and daunting task.² This article addresses the barriers to EBM by improving physician access to the best scientific evidence (i.e., the first step of EBM).

We hypothesize that by using powerful text categorization techniques and a suitably constructed, high-quality, and content-labeled article collection for training, we can automatically construct quality filters to identify articles in the content areas of treatment, prognosis, diagnosis, and etiology in internal medicine that perform with better sensitivity, specificity, and precision than current Boolean methods. We note that throughout this article, references are made to both full-text articles and MEDLINE records. We clarify that (a) our filters make judgments about articles and (b) these judgments are made using the MEDLINE records (i.e., titles, abstracts, journal, MeSH terms, and publication types) as the latter are provided by PubMed. Hence, when the context is about processing the records, we use “MEDLINE records,” whereas when we discuss making judgments about the articles we use the term “articles.”

The Background section describes previous approaches for identifying the best scientific evidence. The Methods section describes corpus construction, the representation of an article (i.e., as a MEDLINE record), articles that meet rigorous EBM standards (high quality) and those that do not, and the learning methods applied to differentiate high-quality articles from articles that do not meet EBM criteria. In the Results and Discussion sections, we compare the machine learning methods with each other using receiver operating characteristic (ROC) curve analysis and 11-point precision recall and with current methods with standard sensitivity, specificity, and precision metrics and a sensitivity/specificity match method. We further discuss advantages, limitations, and extensions of this work. We conclude with a broad overview of the findings of this study.

Background

Specialized sources for high-quality scientific evidence include the Cochrane Collaboration's Library, Evidence-Based Medicine, and the ACP Journal Club.^3,4,5 Each group and journal bring together expert reviewers who routinely review the literature and select articles that warrant attention by clinicians. These articles are either cited by the Cochrane Collaboration or republished with additional commentary as in Evidence-Based Medicine and the ACP Journal Club.

These manual methods are labor intensive, and the reporting of high-quality articles is slow due to the expert review process. In light of these limitations, more recent approaches address finding high-quality, content-specific articles as a classification problem. The problem is to classify documents as both high quality and content specific or not.

In 1994, Haynes and colleagues⁶ used the classification approach to find high-quality articles (as represented by their MEDLINE record) in internal medicine. Evaluating articles in ten journals from 1986 and 1991, three research assistants defined high-quality articles by constructing a gold standard according to content and methodological criteria. The content areas included etiology, prognosis, diagnosis, and treatment, and the methodological criteria were similar to the criteria currently used by the ACP Journal Club.⁷ The authors selected terms that would most likely return high-quality articles in these content categories based on interviews with expert librarians and clinicians. Valid MeSH terms, publication types, and wild-carded word roots (i.e., random* matching randomize and randomly) in the title and abstract were collected. Using the above gold standard and the selected terms, they ran an exhaustive search of all disjunctive Boolean set term models of four to five terms and evaluated each disjunctive set on an independent document set according to sensitivity, specificity, and precision of returning high-quality articles. The optimal Boolean sets (▶) were shown to have high sensitivity, specificity, and precision and are currently featured in the clinical queries link in PubMed.⁸ This method required interviewing to select terms, a gold standard constructed by an ad hoc review panel of expert clinicians, and reliance on National Library of Medicine (NLM) assigned terms. The learning method also relied on a search of term disjunctions that grow exponentially with the number of search terms.

Table 1.

Clinical Query Filters Described in the “Filter Table” Used in the Clinical Queries Link in PubMed³

Category	Optimized for	PubMed equivalent
Therapy	Sensitivity	“Randomized controlled trial” [PTYP] OR “drug therapy” [SH] OR “therapeutic use” [SH:NOEXP] OR “random*” [WORD]
	Specificity	(Double [WORD] AND blind* [WORD]) OR placebo [WORD]
Diagnosis	Sensitivity	“Sensitivity and specificity” [MESH] OR “sensitivity” [WORD] OR “diagnosis” [SH] OR “diagnostic use” [SH] OR “specificity” [WORD]
	Specificity	“Sensitivity and specificity” [MESH] OR (“predictive” [WORD] AND “value*” [WORD])
Etiology	Sensitivity	“Cohort studies” [MESH] OR “risk” [MESH] OR (“odds” [WORD] AND “ratio*” [WORD]) OR (“relative” [WORD] AND “risk” [WORD]) OR “case” control*” [WORD] OR case-control studies [MESH]
	Specificity	“Case-control studies” [MH:NOEXP] OR “cohort studies” [MH:NOEXP]
Prognosis	Sensitivity	“Incidence” [MESH] OR “mortality” [MESH] OR “follow-up studies” [MESH] OR “mortality” [SH] OR prognos* [WORD] OR predict* [WORD] OR course [WORD]
	Specificity	Prognosis [MH:NOEXP] OR “survival analysis” [MH:NOEXP]

These Boolean filters were run on the gold standard corpus, and sensitivity, specificity, and precision were measured.

PTYP = publication type; MESH = MeSH main heading; SH = MeSH subheading; NOEXP = MeSH subtree for the term is not exploded.

Other researchers have applied a similar methodology to developing sets of search terms for controlled trials, systematic reviews, and diagnostic articles.^{9,10,11,12,13,14}

The common methodological features of these studies are as follows: (a) that the search term sets are selected through interviews or article inspection by health professionals and/or librarians and (b) the search is conducted via Boolean queries involving combinations of MeSH qualifiers, MeSH terms, publication types, and text words. The selection of a gold standard varies with more recent research utilizing reproducible, expert-derived gold standards. In the present research, we follow an expert-derived, publisher-based methodology for gold standard construction while automating term selection from the corpus. Additionally, we use more sophisticated classifiers to build models for high-quality, content-specific article retrieval.

Methods

Definitions

In this paper, we chose not to build new criteria to define quality but instead we build on existing criteria⁸ that the ACP Journal Club uses to evaluate full-text articles.¹⁵

The ACP Journal Club is a highly rated meta-publication. Every month expert clinicians review a broad set of journals⁷ in internal medicine and select articles in these journals according to specific criteria⁷ in the content areas of: treatment, diagnosis, etiology, prognosis, quality improvement, clinical prediction guide, and economics. Selected articles are further subdivided into articles that are summarized and abstracted by the ACP Journal Club because of their “clinical importance”¹⁵ and those that are only cited because they meet all the quality selection criteria but may not pertain to vitally “important clinical areas.”¹⁵ For the purposes of the present study, abstracted and cited articles published in the ACP Journal Club for a given year are considered high quality and are denoted as ACP+; all other MEDLINE articles not abstracted or cited in the ACP Journal Club but present in the journals reviewed by the ACP Journal Club, are denoted as ACP−. By using articles abstracted and cited by the ACP Journal Club as our gold standard, we capitalize on an existing, focused quality review that is highly regarded and uses stable explicit quality criteria.

Corpus Construction

We constructed two corpora that reflect the progression of our experiments. Corpus 1 has 15,786 MEDLINE records used for high-quality treatment and etiology article prediction. Corpus 2 has 34,938 MEDLINE records used for high-quality prognosis and diagnosis article prediction. To learn high-quality models, sufficient ACP+ articles must exist in each category. For our initial experiments including treatment and etiology, we selected a publication time period from July 1998 to August 1999. This chosen period did not yield sufficient ACP+ articles for the prognosis and diagnosis categories, so we obtained additional prognostic and diagnostic articles by lengthening the selected publication time period from July 1998 to August 2000. The resulting distribution of positive/negative articles in each category is 379/15,407 in treatment, 205/15,581 in etiology, 74/34,864 in prognosis, and 102/34,836 in diagnosis.

We downloaded all the MEDLINE records in the respective time periods and marked the articles as ACP+. We used a custom script to match word for word the ACP+ title, authors, and journal to the downloaded citations. Next, we downloaded all MEDLINE records from PubMed with abstracts from the journals reviewed by the ACP Journal Club in the publication period of July 1998 through August 1999 for corpus 1 and July 1998 to August 2000 for corpus 2. Two conditions motivated this period of time. As discussed above, each selected time period provided sufficient ACP+ articles in each category. Selecting a period of several years before the start of the present study gave ample time for the ACP Journal Club to review the published full-text articles for republication in the ACP Journal Club. Thus, to ensure that no ACP+ articles were missed, the ACP Journal Club was reviewed from the journal time periods of July 1998 to December 2000 and July 1998 to December 2001 for each respective corpus. From these two selected ACP journal time periods, we marked in the publication time periods any cited or abstracted articles.

Furthermore, as stated before, we identified 49 journals⁷ appearing in the review lists of the table of contents of the first ACP Journal Club in July 1998 to the last ACP Journal Club in December 2001. By collating all articles from these select journal sources that the ACP Journal Club stated it used in preparing the metajournal, a complete set of references (for the purposes of the current study) was obtained.

At the time of this study, the Esearch and Efetch services of PubMed did not exist.¹⁶ We instead created custom Python scripts that simulated a user search session to download the MEDLINE records. Each search was limited to the title of one of the 49 journals and set to only retrieve records with abstracts and during the publication period. These MEDLINE records were downloaded in XML format, stored in a MySQL database,¹⁷ and parsed for PubMedID, title, abstract, publication type, originating journal, and MeSH terms with all qualifiers.

Corpus Preparation

We partitioned each corpus into n-fold cross-validation sets to estimate the classification and error of the constructed models. Each cross-validation set had a train, validation, and test split with the proportions of ACP+ and ACP− articles maintained in each split.

We chose the number n of n-fold cross-validation sets based on the frequency of ACP+ high-quality articles. For all categories, we chose an n of 5. This choice for n provided sufficient high-quality positive samples for training in each category and provided sufficient article samples for the classifiers to learn the models in our preliminary experiments.

Specifically, the cross-validation sets were constructed as follows. First, each corpus was partitioned into five disjointed “test” subsets whose union is the complete corpus. For each test split, the remaining 80% of the articles were further partitioned into a 70% “train” split and a 30% “validation” split. In all cases, the train, validation, and test splits are chosen so that the proportions of ACP+ articles and ACP− articles are as close as possible to the proportions in the corpus. The validation split was used to optimize any specific learning model parameters. We optimized the models using maximization of area under the ROC curves (AUC).¹⁸

Article Preparation

The abstracts, titles, and originating journal were parsed into tokens using the algorithm described below and weighted for classifier input. Additionally, we extracted MeSH terms including headings and subheadings and publication types for each MEDLINE record and encoded these as phrases. For example, the publication type case reports is encoded as a single variable and, following the algorithm below, would be encoded as “pt_Case Reports.” Next, individual words in the title and abstract were further processed by removal of stop words identified by PubMed¹⁹ such as “the,” “a,” and “other” that are not likely to add semantic value to the classification. The words were further stemmed by the Porter stemming algorithm, which reduced words to their roots.²⁰ Stemming increases the effective sample by removing word forms that often do not add additional semantic value to the classification.

We then encoded each term into a numerical value using log frequency with redundancy (see online supplement at www.jamia.org for mathematical details⁷). The log frequency with redundancy scheme weights words based on their usefulness in making a classification because words that appear frequently in many articles are assumed to be less helpful in classification than (more selective) words that appear in fewer articles. This weighting scheme was chosen due to its superior classification performance in the text categorization literature.²¹ In summary, the algorithm for processing each article is described below:

• For each article/MEDLINE record in the set

• Extract original journal

• Extract MeSH terms

  • replace all punctuation and spaces with ‘_’
  • associate main headings with each subheading ||i.e., Migraine:etiology and Migraine: therapy||
  • precede all terms with ‘mh_’ ^*thus all MeSH terms are encoded as single variables^*
• Extract publication types

  • precede all terms with ‘pt_’
  • replace all punctuation with ‘_’
• For abstract and title words separately

  • if title word: precede term with ‘title_’
  • convert all words to lower case
  • remove all punctuation and replace with ‘_’
  • remove MEDLINE stop words
  • Porter-stem all words
  • calculate weights using log frequency with redundancy²¹
  • calculate raw frequency occurrence of terms
• For each encoded word

  • If the word appears in fewer than three documents, remove it from the calculations.

Finally, we calculated the raw occurrence of terms in each article. Naïve Bayes and the first version of the Boostexter algorithm are designed to work with discrete data using frequency of term occurrence as input. The second version of Boostexter and support vector machines used the log frequency with redundancy weighted terms as input.²² In all cases, no term selection was employed, and each algorithm used all available terms for learning.

Statistical and Machine Learning Methods

Naïve Bayes

Naïve Bayes is a common machine learning method used in text categorization. The Naïve Bayes classifier²³ estimates the probabilities of a class c given the raw terms w by using the training data to estimate P(w|c). The class predicted by the Naïve Bayes classifier is the max a posteriori class.

We coded the algorithm in C as described in Mitchell 1997.²⁴ No parameter optimization is necessary for Naïve Bayes. (See the online supplement at www.jamia.org for equations.⁷)

Text-specific Boosting

Boostexter is a collection of algorithms that apply boosting to text categorization.²² The idea behind boosting is that many simple and moderately inaccurate classification rules (called the “weak learners”) can be combined into a single, highly accurate rule. The simple rules are created sequentially, and, for each iteration, rules are created for examples that were more difficult to classify with preceding rules. The prototypical algorithm for boosting is AdaBoost.²⁵ (See the online supplement at www.jamia.org for mathematical details.⁷)

The AdaBoost.MR algorithm in the Boostexter suite uses boosted trees to rank outputs with real values. AdaBoost. MR attempts to put correctly labeled articles at the top of the rankings. The algorithm minimizes the number of misordered pairs, i.e., pairs where an incorrectly labeled article is higher in the ranking than a correctly labeled article. The AdaBoost.MR algorithm runs with real valued weights and discrete counts of word frequencies as inputs depending on the version.

Support Vector Machines

Support vector machines (SVMs) can function as both linear and nonlinear classifiers for discrete and continuous outputs. The type used in this study was the soft-margin hyperplane classifier that calculates a separating plane by assigning a cost to misclassified data points. The solution is found by solving a constrained quadratic optimization problem. In addition, for the nonlinear case, the problem is solved by using a “kernel” function to map the input space to a “feature” space where the classes are linearly separated. Linear separation in feature space results in a nonlinear boundary in the original input space.^26,27,28

For the text categorization task, the words were weighted using log frequency with redundancy and utilized as features for the linear and polynomial SVMs. We use the soft-margin implementation of SVMs in SVM-Light.²⁹ For the linear SVM, we used misclassification costs of {0.1, 0.2, 0.4, 0.7, 0.9, 1, 5, 10, 20, 100, 1000} for optimization on the validation set. For the polynomial SVM, we used misclassification costs of {0.1, 0.2, 0.4, 0.7, 0.9, 1, 5, 10, 20} and polynomial degrees of {2, 3, 5, 8}. These costs and degrees were chosen based on previous empirical research³⁰ because the theoretical literature on domain characteristics as it relates to optimal parameter selection is not yet well developed in this domain. Combinations of both cost and degree were run exhaustively on the validation set, and the optimal cost and degree were applied to the test set in each fold cross-validation set. (See the online supplement at www.jamia.org for the mathematical details.⁷)

Clinical Query Filters

We ran the category-specific Boolean queries shown in ▶ on the corresponding test sets. As described above, two sets of Boolean queries exist (i.e., optimized separately for sensitivity and specificity⁶). We measured the optimized sensitivity and specificity values independently for each cross-validation set. For the best learning method, we fixed these values in each fold and calculated the corresponding sensitivity, specificity, and precision. We report the average optimized and matched values across all folds in ▶.

Table 2.

Best Learning Method Compared with Clinical Query Filters Fixed at Optimal Sensitivity and Specificity

Category	Optimized for	Method	Sensitivity	Specificity	Precision
Treatment	Sensitivity	Query filters	0.96 (0.91–0.99)	0.75 (0.74–0.76)	0.09 (0.08–0.09)
		Poly SVM		0.86 (0.68–0.93)	0.18 (0.07–0.25)
	Specificity	Query filters	0.4 (0.37–0.42)	0.96 (0.95–0.96)	0.19 (0.17–0.21)
		Poly SVM	0.80 (0.74–0.83)		0.33 (0.31–0.34)
Etiology	Sensitivity	Query filters	0.70 (0.61–0.78)	0.85 (0.85–0.86)	0.06 (0.06–0.06)
		Poly SVM		0.95 (0.92–0.97)	0.15 (0.11–0.21)
	Specificity	Query filters	0.28 (0.24–0.37)	0.93 (0.92–0.94)	0.05 (0.04–0.06)
		Poly SVM	0.76 (0.68–0.78)		0.12 (0.12–0.12)
Prognosis	Sensitivity	Query filters	0.88 (0.80–0.93)	0.70 (0.70–0.71)	0.006 (0.006–0.007)
		Poly SVM		0.71 (0.32–0.86)	0.009 (0.003–0.013)
	Specificity	Query filters	0.51 (0.33–0.80)	0.94 (0.94–0.94)	0.02 (0.011–0.026)
		Poly SVM	0.62 (0.60–0.67)		0.20 (0.02–0.02)
Diagnosis	Sensitivity	Query filters	0.95 (0.86–1.0)	0.7 (0.69–71)	0.009 (0.009–0.010)
		Poly SVM		0.53 (0.04–0.95)	0.015 (0.003–0.048)
	Specificity	Query filters	0.67 (0.48–0.80)	0.96 (0.96–0.96)	0.048 (0.034–0.056)
		Poly SVM	0.77 (0.70–0.86)		0.055 (0.049–0.059)

The first number is the average across five folds. The numbers in parentheses report the minimum and maximum values across the five folds. Cells in bold denote the performance for the filter optimized for sensitivity and specificity, respectively.

Poly SVM = polynomial support vector machine.

Evaluation Criteria

We used four evaluation criteria: (a) area under the ROC curve (AUC) of each method with statistical comparison between methods using the Delong paired ROC comparison test,³¹ (b) 11-point precision-recall curves, (c) comparison with the specificity of the clinical query filters at the point of equal sensitivity, and (d) comparison with the sensitivity of the clinical query filters at the point of equal specificity. For (c) and (d), we used McNemar's test to statistically compare each method with the best learning method.

We calculated the AUC and ROC for each method in each fold and calculated the averaged statistical significance of the difference of the best performing method over all folds to each of the other methods using the Delong method.³¹ For a single learning method, we estimated the statistical significance across all cross-validation sets. We averaged the p-values for all the sets to obtain an empirical mean. We statistically evaluated this empirical mean by examining the distribution of means obtained by randomly permuting a complete experiment (i.e., in this case, randomly permuting five cross-validation sets for one method and obtaining a permuted mean) 500 times. With the empirical mean and the distribution of means created by the permutations, we report a significance value for the empirical mean and thus conclude a statistical p-value difference between the best learning method and the compared method.

Note that although several parametric tests for comparing mean p-values exist, they assume independence between measurements.³² These independence assumptions do not apply in an n-fold cross-validation setting; thus, we resorted to a random permutation test here.

We compared the sensitivity and specificity of the machine learning methods with the sensitivity and specificity of the respective optimized Boolean clinical query filter. The query filters return articles with the query terms present, whereas the learning algorithms return a score. To make the comparison, in each fold, we fixed the sensitivity value returned by the sensitivity-optimized filter and varied the threshold for the scored articles until the sensitivity was matched. We report the averaged fixed sensitivity and matched threshold in ▶. The same procedure was run for the specificity returned by the optimized specificity filter.

We assessed the statistical significance of differences of sensitivities (or specificities) between the best learning method and the clinical query filter Boolean models using McNemar's test (calculated for each cross-validation set).³³ To report the significance across all cross-validation sets, we followed the same procedure as described above in comparing ROC curves. Instead of using the Delong method, we compared the best learning method with the Boolean models with McNemar's test for all the sets to obtain an empirical mean. We statistically evaluated this empirical mean by examining the distribution of means obtained by randomly permuting a complete experiment (i.e., in this case, randomly permuting five cross-validation sets and obtaining a permuted mean) 500 times.

Results

Area under the Receiver Operating Curve Analysis

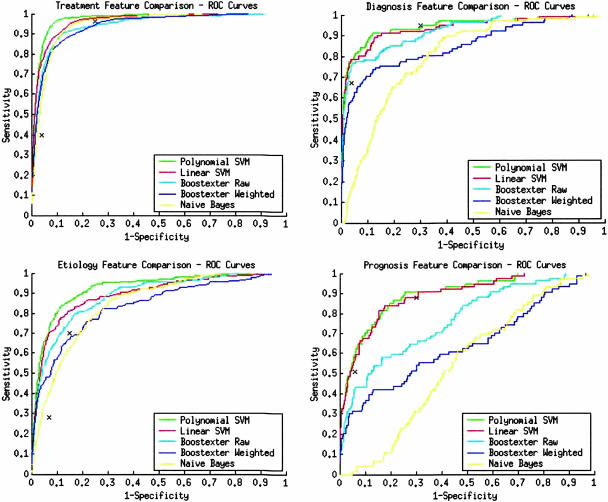
The AUC for each category averaged over five folds are presented in ▶. Values upward of 0.91 with ranges for the best learning methods suggest that the corresponding learning methods can distinguish very well between positive and negative class articles. The polynomial SVM turned out best, and it was compared as a baseline with all other learning methods and the clinical query filters. In the treatment and etiology categories, in nearly all cases except Boostexter raw in etiology, the difference of the polynomial SVM output to the other methods was not due to chance. In contrast, in the sample limited diagnosis category, the difference between the polynomial SVM output and the Boostexter algorithms and the linear SVM may be due to chance. Similarly, in the sample limited prognosis category, the linear and polynomial SVM difference may be due to chance as well.

Table 3.

Area under the Receiver Operating Curve (AUC) Performance of Each Machine Learning Method in Each Category

Diagnosis					Prognosis
Learning Method	Average AUC*	Min AUC*	Max AUC*	Significance† (Delong)	Learning Method	Average AUC*	Min AUC*	Max AUC*	Significance (Delong)
Naïve Bayes	0.82	0.80	0.84	0.001 (0)	Naïve Bayes	0.58	0.47	0.66	0 (0)
Boostexter, weighted	0.87	0.85	0.90	0.10 (0)	Boostexter, weighted	0.71	0.56	0.86	0.01 (0)
Boostexter, raw frequency	0.94	0.91	0.97	0.43 (0.03)	Boostexter, raw frequency	0.79	0.73	0.85	0.04 (0)
Linear SVM	0.95	0.93	0.97	0.11 (0)	Linear SVM	0.91	0.86	0.94	0.39 (0.01)
Polynomial SVM	0.96	0.95	0.98	N/A	Polynomial SVM	0.91	0.87	0.95	N/A
Treatment					Etiology
MLmethod	Average AUC	Min AUC	Max AUC	Significance (Delong)	MLmethod	Average AUC	Min AUC	Max AUC	Significance (Delong)
Naïve Bayes	0.95	0.94	0.95	0.01 (0)	Naïve Bayes	0.86	0.84	0.88	0.02 (0)
Boostexter, weighted	0.94	0.92	0.95	0.03 (0)	Boostexter, weighted	0.85	0.83	0.87	0.01 (0)
Boostexter, raw frequency	0.94	0.93	0.96	0.01 (0)	Boostexter, raw frequency	0.90	0.88	0.93	0.25 (0)
Linear SVM	0.96	0.95	0.97	0.03 (0)	Linear SVM	0.91	0.86	0.93	0.03 (0)
Polynomial SVM	0.97	0.96	0.98	N/A	Polynomial SVM	0.94	0.89	0.95	N/A

^*Average, minimum (min), and maximum (max), AUC across the respective number of folds for each category.

^†Mean significance using the Delong method across all folds comparing the best learning method in each category (polynomial support vector machine [SVM]) with each other learning method. The number in parentheses is the significance produced by random permutation test as described in the Methods section under Evaluation Criteria.

The ROC curves for each category and learning method are depicted in ▶. In all cases, the learning methods perform well with the exception of Naïve Bayes in the prognosis and diagnosis categories. Finally, in each ROC graph, the corresponding clinical query filter performances are shown by small Xs. The leftmost symbol corresponds to fixed specificity and the rightmost symbol corresponds to fixed sensitivity.

Figure 1.

Receiver operating characteristic (ROC) curves for each category. X is clinical query filter performance at optimized sensitivity (right-most x) and specificity (left-most x). SVM = support vector machine.

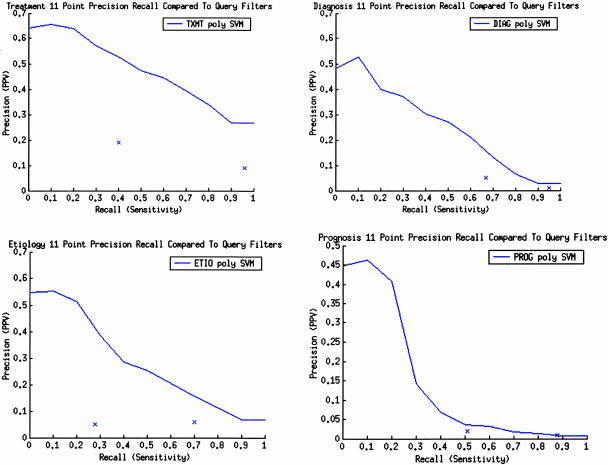
11-Point Precision Recall

We further compared qualitatively the clinical query filters to the best learning method (polynomial SVM) in each category in ▶. For each category, we marked on the 11-point precision recall graph the corresponding precision-recall performance for the optimized sensitivity and specificity clinical query filters. The leftmost point is the filter optimized for specificity and the rightmost point is the filter optimized for sensitivity. For treatment, etiology, and diagnosis, the polynomial SVM performed better than either optimized clinical query filter using this metric. For prognosis, the polynomial SVM performed as well as the clinical query filters using this metric.

Figure 2.

Eleven-point precision-recall curves compared with optimized sensitivity and specificity clinical query filters. X is clinical query filter (right-most x) optimized for sensitivity and specificity (left-most x). DIAG = diagnosis; ETIO = etiology; PPV = positive predictive value; PROG = prognosis; SVM = support vector machine.

Comparison to Clinical Query Filters

For the most part, the learning methods outperformed the query filters for each sensitivity, specificity, and precision measure. ▶ compares the best learning method by AUC and the results of the clinical query filters fixed for sensitivity and specificity respectively for each category. The average with the ranges across five folds across all cross-validation sets appear inside parentheses.

In comparison with the clinical query filters, the polynomial SVM has better performance in the treatment and etiology categories. In the prognosis category, the polynomial SVM model and the clinical query filters perform similarly. In the diagnosis category, the polynomial SVM performs better than the specificity optimized filter but worse than the sensitivity optimized filter (see Discussion). The polynomial SVM model for treatment and etiology at a threshold that matches the sensitivity of the sensitivity-optimized clinical query filter has at least double precision compared with the clinical query filters, although remaining below 20% in both categories. Specificity of the polynomial SVM model is also better (by approximately 10% in both categories). Likewise, in the same categories, the polynomial SVM model at a threshold that matches the specificity of the specificity-optimized clinical query filter has almost double precision compared with the clinical query filters. Sensitivity of the polynomial SVM model is also better (by 40% and 48%, respectively). For the prognosis category, the polynomial SVM model performs comparably with the sensitivity- and specificity-optimized clinical query filters. For diagnosis, the polynomial SVM model has a 10% improvement in sensitivity for the specificity-optimized filter, but a 17% decline in specificity for the sensitivity-optimized filter (see Discussion for details).

▶ compares statistically the polynomial SVM and the clinical query filters using McNemar's test. As described in the Methods section, we report the average p-values across all cross-validation sets and the significance using a random permutation test.

Table 4.

McNemar's Test p-Values Averaged over Five Folds with Significance Tests

Category	Filter Compared	Mean p-Values	Permutation Significance
Treatment	Sensitivity	<0.0001	<0.0001
	Specificity	0.019	<0.0001
Etiology	Sensitivity	<0.0001	<0.0001
	Specificity	0.34	0.14
Prognosis	Sensitivity	<0.0001	<0.0001
	Specificity	0.95	1.0
Diagnosis	Sensitivity	0.07	<0.0001
	Specificity	0.90	1.0

The permutation significance is produced by random permutation tests as described in the Methods section under Evaluation Criteria.

When comparing the optimized sensitivity filters with the polynomial SVM, the mean p-values are significant at the 0.05 level except for the sensitivity-optimized diagnosis filter at the 0.07 level. Thus, the improvements compared with the clinical query filters in both precision and specificity are not due to chance.

When comparing the optimized specificity filter with the polynomial SVM in etiology, prognosis, and diagnosis categories, the mean p-values are not significant, whereas in the treatment category, the polynomial SVM models are significant at the 0.05 level. Hence, we conclude that the differences between the polynomial SVM fixed at optimized specificity and the query filters are not due to chance in the treatment category but may be due to chance in the other three categories. We speculate that in these three categories, nonsignificant differences are due to the low ratios of ACP+ to ACP− articles (i.e., low priors).

Discussion

We have shown that machine learning methods applied to categorizing high-quality articles in internal medicine for a given year perform better than the widely-used 1994 Boolean methods in most categories. This work is a step toward efficient high-quality article retrieval in medicine.

Performance in the Diagnosis Category

In light of the comparable or superior performance of the SVM model over the clinical query filters in treatment, etiology, and prognosis, the lower performance of the diagnosis polynomial SVM versus the sensitivity-optimized query filter warranted further attention.

Recall that we match the sensitivity returned from the optimized diagnosis Boolean query to the sensitivity produced by varying the threshold for the SVM output. Because the number of positive articles in the diagnosis category is very small (and even smaller within the splits of cross-validation), and because the clinical query filters exhibit very high sensitivity in the content category, even a small number of outliers (i.e., MEDLINE documents receiving a low score), in terms of SVM model scores, will result in a significant reduction of the specificity once we set the SVM threshold to match the near-perfect sensitivity of the clinical filters.

Indeed, we identified such outliers and verified that they were the source of the reduced performance in the diagnosis category once we fixed the thresholds to match the clinical query filter sensitivity. On close examination, we found that the ACP+ articles scored low because the terms used to identify these articles were not used in training of the SVM model. More specifically, MeSH subheadings were not encoded individually. For example, one of the ACP+ articles scoring low was identified by the diagnosis clinical query filters with the MeSH subheading “diagnosis” (▶). Recall from the article preparation procedure in the Methods section that MeSH subheadings are not encoded explicitly but only as part of the matching major heading. Thus, “diagnosis” would not be encoded individually, but only as part of the major heading as in “Migraine:diagnosis.” If the ACP+ article was encoded as “Pneumonia:diagnosis,” it would not score high. The SVM classifiers did not have sufficient information to give some ACP+ articles a high score because none of these words were found in the text.

It is evident that this problem can be fixed simply by encoding the subheadings individually in future versions of the models discussed here. However, we do note that in such circumstances, using the human assigned MeSH indexing terms provides a slight edge over not using them.

Implicit Selection Bias

A potential drawback of the constructed models is that they may reflect implicit selection biases by the editors of the ACP Journal Club, and the high-quality articles selected by the models are not based on sound methodology. For example, it is conceivable that editors for a particular year could have a favorable bias toward a particular subject, and the subject rather than the methodology causes a high-quality classification.

We answer this concern through cross-validation and a method previously described³⁴ to convert the models to Boolean queries. Specifically, we built Boolean models using an approximate Markov blanket feature selection technique³⁴ modified from Aliferis et al.³⁵ to obtain the set of minimal terms and a decision tree to build the corresponding Boolean query. The feature selection/decision tree method⁷ shows that the models emphasize methodological words in nature rather than topic specific ones.

Labor Reduction

The machine learning–based methods may significantly reduce labor through automated term selection; reliance on an existing, publisher-based, expert-derived gold standard; and a reduced feature set, without manually assigned MeSH terms and publication types, that has equivalent performance to the full set with terms and types.

Recall from the Background section the strategy for development of the clinical query filters.⁷ In the Haynes approach, significant time is spent interviewing people for the selected terms, building the gold standard, and running an exhaustive search through the space of term disjunctions. In addition, the filters rely on MeSH terms and publication types that must be assigned before the filters can be used.

In contrast, the methods here are less labor intensive. First, there is no selection of terms because these are implicit in the training articles. Second, we have a framework for automatic generation of a gold standard through the ACP Journal Club that is reliable and reproducible. Manual review is not needed as long as the ACP Journal Club is electronically available. Finally, we use sophisticated classifiers that can build models in four to eight hours (depending on model and experiment design) on a Pentium IV, 2-GHz computer with full term sets versus several days depending on the number of selected terms with the exhaustive search of term disjunctions.⁷

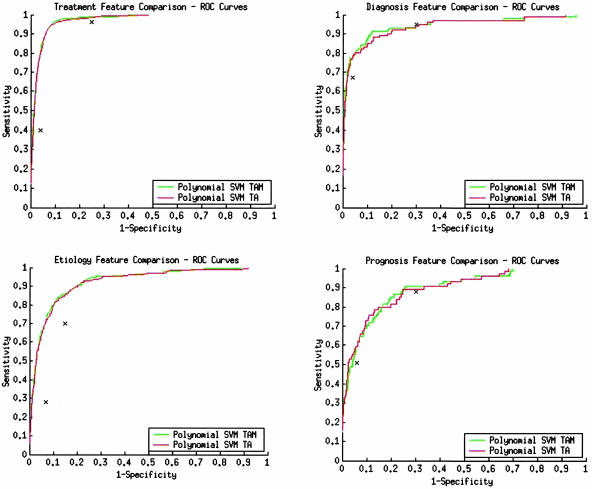
In an additional experiment, we compared the inclusion/exclusion of manually assigned, labor-intensive MeSH terms and publication types (NLM-assigned terms) as model input features. We compared the ROC performance of a feature set with inclusive NLM-assigned terms with a feature set without both. The ROC curves in ▶ show that the reduced feature set without NLM-assigned terms has ROC curves comparable with those of the feature set inclusive of these terms. Although we do not show the results here (see online supplement at www.jamia.org for further details⁸), each average AUC was not significantly different for each feature set using the Delong et al. method.³¹ The results suggested, with our methods, we can make quality and content determinations without the labor-intensive NLM term indexing process. Note that we do not advocate abandoning human indexing in general, but for this task, no additional benefit is gained from manual term assignments.

Figure 3.

Title + abstract (TA) vs. Title + abstract + MeSH + publication types (TAM) performance comparisons. X is clinical query filter performance at optimized sensitivity (right-most x) and specificity (left-most x). ROC = receiver operating characteristic. SVM = support vector machine.

Extensions

Another avenue to explore is the use of additional predictor information. For example, we hypothesize that additional information such as general word location, impact factors, citation information, author locations, or user feedback information may improve model performance.

We also plan to extend these models to areas outside internal medicine. One approach is to build a gold standard that considers articles in other specialties. Evidence-Based Medicine is the sister journal of the ACP Journal Club that could be used for a more general gold standard because its scope of review covers all aspects of medicine.

Limitations

In general, the prognosis and diagnosis samples sizes are limited. We chose not to alter the ratio of positive to negative articles to maintain the priors across all learning tasks and produce realistic estimates of future performance. The small priors for both these categories make learning difficult. Nevertheless, with these sample sizes, our system performs at least comparably with the clinical query filters in prognosis and, in some cases, in diagnosis.

Another admitted limitation of our comparisons with the clinical query filters is that the new models and filters were built for the exact same goals but with different gold standards. Our comparisons simply show that the new models implement the present gold standard better than the clinical query filters. In the future, using an independent gold standard and evaluating both methods trained on independent sets would strengthen this comparison.

A potential limitation of any information retrieval study is the choice of gold standard. A gold standard is only as good as the experts brought together to create it. The use of the ACP Journal Club articles meets our criteria, and we propose that currently it is the best general method to create such gold standards. The ACP Journal Club articles are easily obtained from their Web site, the cited articles are readily available for use by other researchers, and the gold standard is created by recognized experts and editors in the field of internal medicine.

This work is a step toward more efficiently returning high-quality articles. The work does not address explicitly the utility of these models in a clinical setting or outside internal medicine. Finally, the learning method's built models are constrained to one specific time period in internal medicine.

In summary

Text categorization methods can learn models that identify high-quality articles in specific content areas (etiology, treatment, diagnosis, and prognosis) by analyzing MEDLINE records in internal medicine using the operational gold standard of articles that match the ACP Journal Club inclusion criterion for methodological rigor. These learning methods exhibit high discriminatory performance as measured by the AUC. The performances are also comparable with or better than the 1994 Boolean-based clinical query filters for each category by direct comparisons of sensitivity, specificity, and precision at fixed levels and by 11-point precision-recall comparisons. Polynomial SVMs had the best performance, whereas linear SVMs came close in terms of AUC. We have presented an efficient and improved means for identifying high-quality articles in internal medicine.