Tensor Factorization for Precision Medicine in Heart Failure with Preserved Ejection Fraction

Abstract

Heart failure with preserved ejection fraction (HFpEF) is a heterogeneous clinical syndrome that may benefit from improved subtyping in order to better characterize its pathophysiology and to develop novel targeted therapies. The United States Precision Medicine Initiative comes amid the rapid growth in quantity and modality of clinical data for HFpEF patients ranging from deep phenotypic to trans-omic data. Tensor factorization, a form of machine learning, allows for the integration of multiple data modalities to derive clinically relevant HFpEF subtypes that may have significant differences in underlying pathophysiology and differential response to therapies. Tensor factorization also allows for better interpretability by supporting dimensionality reduction and identifying latent groups of data for meaningful summarization of both features and disease outcomes. In this narrative review, we analyze the modest literature on the application of tensor factorization to related biomedical fields including genotyping and phenotyping. Based on the cited work including work of our own, we suggest multiple tensor factorization formulations capable of integrating the deep phenotypic and trans-omic modalities of data for HFpEF, or accounting for interactions between genetic variants at different -omic hierarchies. We encourage extensive experimental studies to tackle challenges in applying tensor factorization for precision medicine in HFpEF, including effectively incorporating existing medical knowledge, properly accounting for uncertainty, and efficiently enforcing sparsity for better interpretability.

Introduction

Heart failure is a common and morbid condition affecting over 5.7 million Americans¹ and defined by fatigue, shortness of breath, and exercise intolerance. Heart failure is typically divided into two subtypes: heart failure with preserved ejection fraction (HFpEF) and heart failure with reduced ejection fraction (HFrEF). Patients in these groups tend to have different demographics, co-morbidities, and responses to therapy. Several large, randomized controlled trials in patients with HFrEF have shown therapeutic benefit for a range of neurohormonal medications and intracardiac devices; however, large clinical trials have not demonstrated similar clinical benefit in patients with HFpEF^2,3. The heterogeneity in the pathogenesis and in the clinical phenotypes of HFpEF may have contributed to lack of large, positive clinical trials⁴.

Recent studies have identified the centrality of chronic systemic inflammation in the pathogenesis of HFpEF⁵. Patients with HFpEF tend to be older females with several co-morbidities, including obesity, hypertension, diabetes, coronary artery disease, chronic obstructive pulmonary disease, and chronic kidney disease. The combination of older age and these comorbidities may contribute to the systemic inflammation that in turn affects multiple signaling cascades and organ systems, including the heart, lungs, skeletal muscles, and kidneys⁴. The culmination of these pathways leads to different manifestations of the clinical syndrome of HFpEF, including unique combinations of co-morbidities, changes in cardiac remodeling and mechanics, biomarker profiles, and clinical symptoms^3,4,6. Understanding these combinations may be informative to the design of future trials testing targeted therapeutic approaches.

Unsupervised machine learning has been previously used to identify clusters, or “phenogroups”, of patients with HFpEF using demographic, physical characteristics, and laboratory, electrocardiographic, and echocardiographic data⁷. Layering in genetic data may elucidate the mechanistic underpinnings of different HFpEF phenotype groups or even lead to additional refinement in the classification of patients with HFpEF. Prior studies have demonstrated genetic differences in cardiac geometry and mechanics^8–10, risk for new onset heart failure^11,12, and mortality after heart failure diagnosis¹³. Additionally, linking epigenetic signatures to specific HFpEF phenotypic subgroups may provide additional mechanistic understanding of pathogenesis and identify future targets for therapy¹⁴. Identifying methodologies for a trans-omic approach, including with de-tailed phenotypic data, is therefore essential to better subtyping patients with HFpEF and identifying the mechanistic underpinnings of the syndrome.

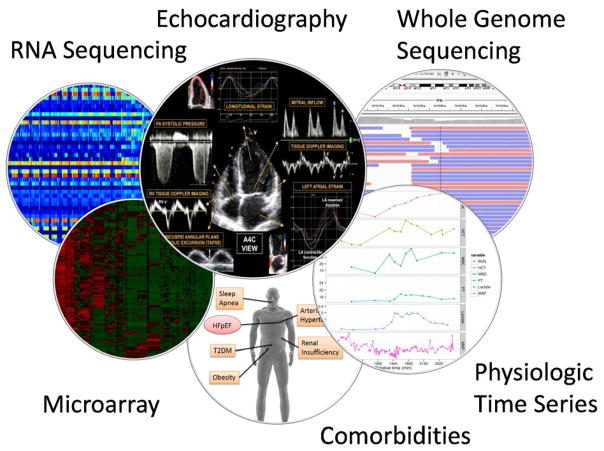
Precision medicine aims to utilize information from multiple modalities—including phenotypic, genomic, and environmental measurements—to develop an individualized and comprehensive view of a patient’s pathophysiologic progression, to identify unique subtypes of the patient, and to administer personalized therapies¹⁵. Existing efforts are often based on only a selected set of biomarkers. The rapid growth of phenotypic, genetic, medication prescription, and environmental data for HFpEF patients poses technical challenges for subtyping them, due to the large volume of data, diversity of data types, and uncertainty from noise and missing data. However, the rapid growth of multiple data modalities, when linked to the right patients, may provide a prismatic view of the patients’ pathophysiologic evolution and offers a basis for meaningful subtyping of these patients. Figure 1 shows multiple data modalities for HFpEF patients, including deep phenotyping and trans-omic data. One of the example datasets with linked evaluation on multiple modality measurements is the Multi-Ethnic Study of Atherosclerosis (MESA) dataset¹⁶, which is curated by a medical research study involving more than 6,000 men and women from six communities in the United States. In particular, over 6000 patients in MESA were genotyped using Affymetrix 6.0, in addition to routinely collected laboratory tests and exams measurements. In addition, the advent of RNAseq and epigenetic data will likely offer trans-omic evidence to HFpEF patient subtyping and identify individualized therapy targets. We will use the scenario of MESA dataset containing both a high density of phenotypic variables and genome-wide genetic variants as an illustrative example in this review.

Figure 1.

Illustration of electronic health record data sources from multiple modalities including deep phenotyping and trans-omics data. T2DM – Type 2 diabetes mellitus.

The Problem of Complex, Multi-Modal Data in Precision Medicine

The lack of positive, large-scale HFpEF clinical trials may be due to distinct systemic and myocardial signaling in HFpEF (compared to HFrEF) and the underlying heterogeneity of HFpEF. A precision medicine approach, leveraging multiple modalities and sources of information, including deep phenotyping and trans-omic data, may better define subtypes of HFpEF that are more homogeneous in their responses to specific targeted therapies. With the rapid development of Next Generation Sequencing and sophisticated phenotyping tools such as comprehensive cardiovascular imaging, the linked data for HFpEF patients from various modalities are becoming increasingly complex, defined as.

• Data Complexity: The data objects themselves are becoming more complex. They are becoming larger in scale, higher in dimension (e.g., millions of genetic loci identified by whole genome sequencing). The features (especially phenotypic features) are usually heterogeneous, sparse and time-evolving.

• Relation Complexity: The relationships between multiple modalities of electronic health record (EHR) data are becoming more complex. Such relationships can link RNA expression to phenotypic abnormalities, or link epigenetic signature changes (e.g., DNA methylation, histone modifications) to upregulation or downregulation of genes (e.g. α-MHC gene and SPR-Ca²⁺ ATPase gene). Relations also hold between features in the same measurement modality. For example, some phenotypic variables can be grouped into echocardiographic measurements (e.g., global longitudinal strain, left ventricular end-diastolic volume) or electrocardiogram (ECG) parameters (e.g., PR interval, QRS-T angle).

Recent advances in machine learning have opened avenues towards more effective mining and modeling from EHRs to facilitate translational research¹⁷. However, clinicians often regard existing machine learning models as hard-to-interpret black boxes. Traditional machine learning algorithms usually treat phenotypic variables as independent features instead of exploring clinically meaningful groups of phenotypic variables that together can characterize HFpEF subtypes (e.g., younger patients with moderate diastolic dysfunction and relatively normal BNP as a distinct HFpEF archetype⁷). It is also difficult for conventional machine learning algorithms to model patient physiologic temporal progressions for disease/syndrome subtyping. Patients are often monitored in physiological time series in which vital measurements and laboratory test values fluctuate as time progresses (e.g., there is significant intra-person variation in blood pressure measurements due to setting, method of measurement, time of day, and health status). The fact that these physiologic time series are sampled at irregular time intervals and may contain missing data further complicates complexity of feature modeling. Intuitively, the temporal trends, and in general relations as features, are more expressive and informative, but their extraction is often difficult and often involves manual work such as pre-specifying rules or patterns¹⁸ and matching against clinical time series¹⁹. In contrast, independent measurements (e.g., individual blood pressure measurements) have been widely used because they are simple to extract and have robust statistical properties. However, these independent measurements are less informative and inter-pretable than relational features. In fact, modeling relational features are usually ignored by machine learning algorithms that mostly adopt a flat patient-by-feature matrix view (patients as rows and features as columns). Because of complexity the data required to capture HFpEF characteristics, the traditional vector- or matrix-based representations (e.g., non-negative matrix fac-torization²⁰, topic modeling²¹) are not flexible enough to capture all the degrees of freedom contained in the data. Although theoretically one can add interactions as additional features or embed graphical models to account for feature interactions, the problem quickly becomes intractable for large feature dimensionality (e.g. at the genome scale). Our previous research in cancer subtyping and intensive care unit (ICU) mortality prediction shows that using the relational features and independent raw features jointly can take advantage of both in order to improve the interpretability and accuracy of the machine learning model^22–24.

Tensor Factorization: A Potential Solution for Multi-Modal Data in HFpEF

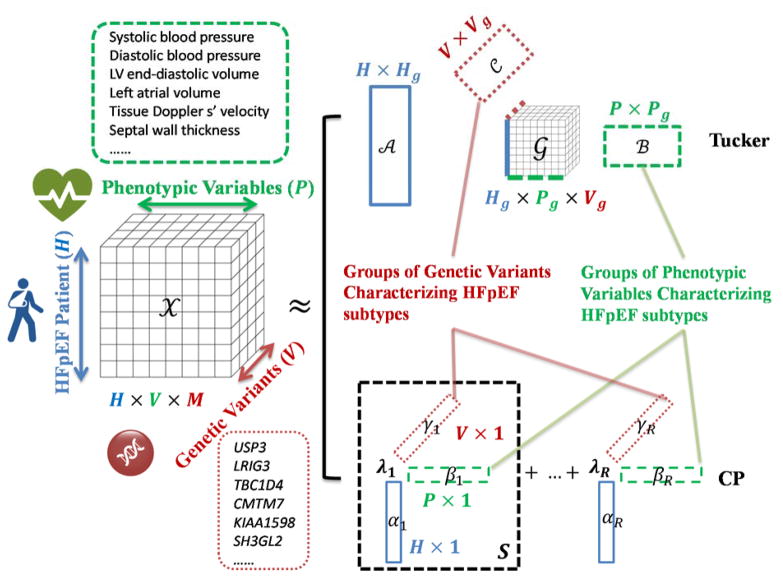
Tensor modeling has emerged as a promising solution for the computational challenges of precision medicine. A tensor is a multidimensional array where each modality spans one axis (denoted as mode in tensor terminology). In matrix representation, one may have to concatenate multiple data modalities into a single second dimension of the matrix, thus disallowing explicit representation of interactions among these modalities. Tensors, as natural generalizations of vectors and matrices, are becoming increasingly popular for representing multi-modality data. Figure 2 shows the tensor for modeling interactions among patients, phenotypic measurements, and genetic variants. Various tensor factorization models with such parsimonious structures and accompanying computational tools have been integral in the analysis and process of big tensor data (see Kolda et al.²⁵ and Cichocki et al.²⁶ for further reading). These factorization models not only reduce dimensionality but also help discover latent groups in each data modality and identify group-wise interactions. In addition, specifically designed tensor factorizations can also integrate additional domain-specific prior knowledge to constrain the tensor structure^27,28. Following our illustrative MESA dataset, Figure 2 shows a visualization of two types of factorization—Tucker²⁹ and CANDECOMP/PARAFAC (CP)³⁰—in order to integrate the phenotypic and genetic measurements and model their relations for the subtyping of HFpEF. The Tucker factorization²⁹ (top panel in Figure 2) decomposes the data tensor 𝒳 into three factor matrices specifying groups in each mode and a core tensor 𝒢 specifying levels of interaction between the groups from different modes. In general, number of groups in each mode is less than the dimensionality of that mode and the core tensor 𝒢 can be regarded as a compression of 𝒳. The CANDECOMP/PARAFAC (CP) factorization³⁰ (bottom panel in Figure 2) decomposes 𝒳 as a weighted sum of rank-1 sub-tensors, each of which is the outer-product (S, S_ijk = α_iβ_jγ_k) of a patient factor vector (α), an intervention factor vector (β) and a biomarker factor vector (γ). The weights λ_r, r = 1 … R indicate relative importance of sub-tensors. When interpreting the Tucker factorization regarding HFpEF subtyping, the factor matrix 𝒜 corresponds to HFpEF subtypes, the factor matrix ℬ corresponds to groups of phenotypic variables that characterize HFpEF subtypes, and the factor matrix 𝒞 corresponds to groups of genetic variants that characterize HFpEF subtypes. With CP factorization, the factor vectors α_i’s correspond to HFpEF subtypes, the factor vectors β_i’s correspond to groups of phenotypic variables that characterize HFpEF subtypes, and the factor vectors γ_i’s correspond to groups of genetic variants that characterize HFpEF subtypes. Compared to Tucker, the structural hypothesis of CP requires the same number of groups for each mode. The simplified structures in CP allows easier linkage from phenotypic variable groups and genetic variant groups to HFpEF subtypes (simply linking those are in the same sub-tensor). On the other hand, the structural flexibility by Tucker factorization may offer more accurate data fitting but typically requires more intensive computation²³. In practice, care needs to be taken when trading off model flexibility with simplified interpretation and computation³¹.

Figure 2.

Tensor modeling and factorization schemes for identifying HFpEF subtypes using phenotypic variables and genetic variants as modes. The data tensor 𝒳 models the interactions among modes including patient, phenotypic variables, and genetic variants. The factor matrix ℬ in Tucker factorization or the length-P factor vectors β_i’s in CP factorization correspond to groups of phenotypic variables that characterize HFpEF subtypes. The factor matrix 𝒞 in Tucker factorization or the length-V factor vectors γ_i’s in CP factorization correspond to groups of genetic variants that characterize HFpEF subtypes. LV = left ventricle.

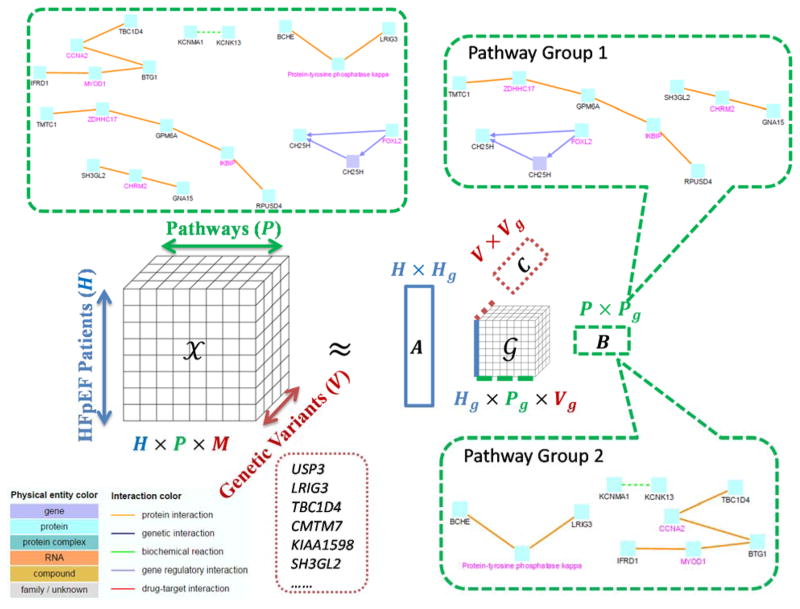
When modeling HFpEF patients subtyping using tensor factorization, certain types of features can in fact display a hierarchical structure. Although genetic variants, such as single nucleotide polymorphisms (SNPs) and copy number variations (CNVs) are the most primitive components in trans-omic features, other trans-omic data such as epigenetics and pathways can arguably provide invaluable information. It is widely acknowledged that viewing SNPs and CNVs as independent features and fitting them to linear models loses critical information such as the interaction between proteins encoded by the affected genes^32,33. Decades of trans-omic research have resulted in evidence of protein interaction, transcription factor regulation and signaling. Much of the data are curated and archived as public databases such as STRING³⁴, KEGG³⁵, InterPro³⁶, Aceview³⁷ and Pfam³⁸. These databases provide information sources for regulatory or interaction pathways involving genes affected by SNPs or CNVs. Thus, we can build a tensor that account for higher-order relations between SNPs and CNVs as follow. For a particular patient, we scan through genetic variants, such as SNPs or CNVs, and use interval tree search³⁹ to identify relevant genes whose chromosomal regions contain those of the genetic variants. Next, we query the pathway databases to identify pathways or gene sets that involve the identified genes. Then the tensor entry, indexed by the patient, the pathway, and the genetic variant, is increased by the genotype of the variant (0, 1, or 2 corresponding to none, single-allelic or bi-allelic variant). The SNPs and CNVs may be of high dimensionality, thus one may need to aggregate the SNP and CNV counts according to the affected genes to avoid impractically large tensor. The tensor constructed this way falls into the category of subgraph augmented tensor, and in particular, pathways or gene sets can be precisely represented as graphs or subgraphs. Pathways as a mode of the tensor help to put the genetic variants in the context of functional relations between genes. Genetic variants help to link correlated pathways in order to render a comprehensive view of the HFpEF pathophysiology (Figure 3). Our previous research showed that subgraph augmented tensor can be efficiently factorized and the groups of pathways, which functionally link the related genetic variants, can be linked to patient groupings²³.

Figure 3. Tensor model for hierarchical genetic pathway analysis to subtyping HFpEF patients.

In the figure, we show the pathway features and genetic variant features as separate modes. The left hand side is the tensor modeling. The right hand side is the Tucker factorization results, which include a core tensor and three factor matrices. The factor matrix A is the 〈patient, patient group〉 matrix, B the 〈pathway, pathway group〉 matrix, C the 〈variant, variant group〉 matrix. The core tensor 𝒢 captures the interactions between the patient groups, pathway groups and variant groups.

The tensor formulations in Figure 2 and Figure 3 are alternative schemes that focus on exploring the interactions between different feature types and exploring hierarchical structures of features of the same type, respectively. Both Tucker and CP factorization seem to have broader adoptions in non-genomic biomedical fields, perhaps due to the relative ease of imposing probabilistic and other regularizations. Although CP produces summation of rank-1 sub-tensors (Figure 2) and leads to simplified interpretation, Tucker provides a more flexible and sometimes more realistic factorization by allowing varying number of groups in different modalities. The choice between these two alternatives depend on data availability, outcome to track, and focus of hypothesis, and are open questions in the clinical domain of HFpEF that deserves extensive experimental studies and characterizations. Although to our knowledge no prior research studies have applied tensor factorization to subtype HFpEF patients, a substantial body of research on applying tensor factorization to handle multiple modalities of biomedical data has emerged over the past decade. We refer the reader to general reviews^40,41 for tensor modeling application in biomedical domains. Below, we provide a more detailed discussion on the applications of tensor modeling in cardiovascular medicine.

In cardiovascular disease, prior studies have investigated the interactions between heart failure related diagnoses and administered medications to heart failure patient groupings. Ho et al. ⁴² studied the problem of heart failure onset prediction with clinically meaningful subtensors. They build a patient-diagnosis-procedure tensor and derive patient clusters on specific diagnoses and medications by applying CP while enforcing sparsity constraints. In a follow-up study, Ho et al.⁴³ investigated Centers for Medicare and Medicaid Services (CMS) claims data to predict high cost (above 75th percentile) beneficiaries by using phenotypes within chronic diseases including hypertension, arthritis, heart failure and diabetes as features (generated by tensor factorization). They build a patient-diagnosis-procedure tensor and apply CP-APR factorization to decompose it as summations of rank-1 bias tensors and rank-R interaction tensors with sparsity constraints on the factor matrices of interaction tensors, in order to explicitly account for interactions among groups of the same modality. Wang et al.⁴⁴ studied the problem of predicting the onset risk of patients with heart failure. They applied tensor modeling to generalize sparse logistic regression to multiple modalities on EHR data, such as comorbidity diagnosis codes and medications, and called their model High Order Sparse Logistic Regression (HOSLR). They reported that HOSLR not only achieved good prediction accuracy on newly diagnosed heart failure, but also discovered interesting predictive patterns capturing the interaction between diagnosis and medications. Wang et al.²⁸ studied the problems of detecting sub-phenotypes of hypertension, type 1 and 2 diabetes, and heart failure based on EHR data. Their tensor formulation incorporated medical knowledge via customized regularization terms. Medical knowledge guidance is as a subset of columns in the target factor matrix and the resultant factor matrix is required to be close to the target on the pre-specified subset of columns. They also constrained that the columns of the factor matrix should be close to pairwise orthogonal to ensure distinct phenotypes.

Applying Tensor Factorization to HFpEF: Potential Challenges

The advent of precision medicine initiatives in HFpEF, coupled with the welcome growth of new modes of data in cardiovascular medicine, produces not only opportunities but also challenges when moving towards tensor modeling. Although tensor factorization naturally integrates multiple modalities or hierarchies of features, common factorization schemes such as Tucker and CP usually lack the machinery to incorporate existing medical knowledge as probabilistic priors, or to evaluate extracted and grouped relations as clinical evidence from a Bayesian perspective (e.g., posterior probability and confidence interval). Confidence intervals and prior and posterior probabilities are the most basic primitives for statistical decision making, but few tensor-based approaches have adopted them in clinical decision support. Our preliminary data show that mining and grouping relation subgraphs leads to improved accuracy and better interpretability in diagnostic reasoning but calls for a Bayesian formulation to incorporate existing medical knowledge, provide confidence estimation, and further improve prediction accuracy to practical level^22,23.

To account for uncertainty, multiple authors proposed probabilistic Tucker and/or CP factorizations to incorporate priors on tensor structural parameters. Those priors can specify dependence between environmental exposures and SNP level differences ⁴⁵, or probability of gene sequence conditioned on the composing nucleotides and chromosomal positions^46,47. In addition, probabilistic CP was shown to improve EEG classification accuracy when missing data is present⁴⁸. The above Bayesian formulations allow incorporating existing medical knowledge as probability priors and reliably estimating the posterior probabilities and confidence intervals of any findings from the model. In Tucker factorization in Figure 2, the vectors {β₁ … β_M} in the factor matrix ℬ that correspond to phenotypic subtyping criteria and outcome risk predictors can be used to integrate existing medical knowledge. We can select a subset {β₁ … β_M′} where M′ < M. Upon initialization, the existing knowledge that comes from diagnosis guidelines or other clinical guidelines is encoded in a guidance vector β_m ∈ {β₁ … β_M′} where positive entries indicate relevant feature dimensions. For example, we can have a guidance vector corresponding to a HFpEF subtype of “obese, diabetic patients with a high prevalence of obstructive sleep apnea who have the worst LV relaxation”, where the disease-related entries are set to positive values (e.g., close to one), and the remaining entries are zero.

The efficient enforcement of sparsity constraints represents another challenge in applying tensor factorization to HFpEF patients. In tensor factorization, it is desirable to have sparse factor representations for improved interpretability. In the case of using CP tensor factorization to integrate phenotypic variables and genetic variants, we need sparse phenotypic factor vectors and sparse genetic variant factor vectors so that each time we specify a group interaction (i.e., only a small subset of phenotypic variables and a small subset of genetic variants are linked). To achieve this goal, Morup et al. proposed a sparse non-negative Tucker decomposition approach by using a specially designed penalty to regulate number of non-zero entries in the factor vectors⁴⁹. However, it is computational expensive due to sparse optimization after factorization. More recently, the approach called Tensor Truncated Power (TTP)⁵⁰ shows promise compared to sparse Tucker tensor factorization by incorporating an efficient truncation step in the iteration step of computation of factors. More work still needs to be done in order to generalize this approach to accommodate Bayesian tensor factorization under Tucker or SP schemes.

Conclusion

Heart failure with preserved ejection fraction (HFpEF) is a heterogeneous clinical syndrome that may benefit from improved subtyping in order to inform the design of future clinical trials and to identify responders to therapies. Modern medicine has accumulated multiple modalities of clinical data for HFpEF patients ranging from deep phenotypic to trans-omic data. Precision medicine with phenotypic and trans-omic data from multiple domains appears to be feasible and may result in meaningful, clinically relevant HFpEF subtypes with significant differences in the underlying etiology, pathophysiology, and risk of adverse outcomes. By integrating the multiple modalities of data for HFpEF, by properly accounting for interactions between genetic variants at different -omic hierarchies, by integrating existing medical knowledge as priors, and by utilizing Bayesian inference to provide uncertainty estimates, tensor factorization is a promising machine learning technique that could be helpful for HFpEF subtyping and contribute to the development of novel targeted therapies. However, applying tensor factorization for precision medicine in HFpEF faces a number of challenges, including effectively incorporating existing medical knowledge, properly accounting for uncertainty, and efficiently enforcing sparsity for better interpretability. The successful application of tensor factorization for the development of precision medicine approaches in the diagnosis and treatment of HFpEF is contingent on answering all these challenges.