3D-Accelerated, Stack-of-spirals Acquisitions and Reconstruction of Arterial Spin Labeling MRI

Abstract

Purpose

We aimed to develop a 3D acceleration and reconstruction method to improve image quality and resolution of background-suppressed arterial spin labeled (ASL) perfusion MRI.

Methods

Accelerated acquisition was implemented in all three k-space dimensions in a stack-of-spirals readout using variable density spirals and partition undersampling. A single 3D self-consistent parallel imaging (SPIRiT) kernel was calibrated and iteratively applied to reconstruct each imaging volume. Whole-brain (including cerebellum) perfusion imaging was obtained at 3mm isotropic resolution (nominal) using 1- and 2-shot acquisitions and at 2mm isotropic resolution (nominal) using 4-shot acquisitions, achieving effective acceleration factors between 5.5 and 6.6. The signal-to-noise (SNR) performance of 3D SPIRiT was evaluated. The temporal SNR (tSNR) of the cerebral blood flow (CBF) maps and the gray-matter-to-white-matter CBF ratios were quantified.

Results

The readout of the ASL sequence was significantly shortened with acceleration. The CBF values were consistent between accelerated and fully sampled ASL. With shorter spiral interleaves and shorter echo trains, the accelerated images demonstrated reduced blurring and signal dropout in regions with high susceptibility gradients, resulting in improved image quality and increased gray-matter-to-white-matter CBF ratios. The shortened readout was accompanied by a corresponding decrease in tSNR.

Conclusions

The 3D acceleration and reconstruction allow a rapid whole-brain readout that improved the quality of ASL perfusion imaging.

Introduction

Arterial spin labeling (ASL) is a noninvasive method for quantification of regional cerebral blood flow (CBF) (1–3). Because CBF is an important biomarker of brain physiology, ASL has been widely used in understanding both regional brain function (4–6) and brain disease (7,8). High-resolution (9), whole-brain ASL (including cerebellum (10)) is particularly desirable in these applications. However, because blood accounts for only a few percent of the tissue mass in the brain (11), ASL has mostly been combined with relatively low spatial resolution imaging to boost sensitivity. Increasing the spatial resolution has often required reduced field-of-view (FOV) (9) or many-segment acquisitions (12), with corresponding sacrifices in spatial coverage and temporal resolution. Whole-brain ASL with both excellent spatial and temporal resolutions has been challenging to implement in practice.

Gradient- and Spin-Echo (GRASE) (13) and Stack-of-SPirals (SoSP) (14) are frequently used trajectories for 3D imaging of the brain and both GRASE and spin-echo-based SoSP (RARE-SoSP) have been implemented for ASL perfusion MRI (15–17). As 3D acquisition trajectories, both are SNR-efficient and can be optimally combined with background suppression (BS) of static brain signals to effectively reduce physiological noise (11,18,19). Compared to GRASE, SoSP is more efficient in traversing k-space (20) and less sensitive to motion artifacts (21,22). However, to further improve spatial resolution with a given temporal resolution, RARE-SoSP requires longer readouts and/or longer echo trains to collect more data. A long spiral readout in general leads to image distortion or signal dropout in regions of high static susceptibility gradients or short T₂^* (e.g., in orbitofrontal cortex) (23); long echo trains tend to result in highly uneven k-space weighting across partitions due to T₂ decay, causing through-slice (z) blurring (24). Therefore, increasing spatial resolution occurs with tradeoffs in data quality.

One way to reduce the acquisition length is to undersample k-space and reconstruct the images using parallel imaging (25,26). Parallel imaging takes advantage of the spatial variation of each receive-coil’s sensitivity in a receive-array to compute the missing data in k-space (25,27) or to perform unaliasing in the image domain (26). In the first approach, explicit measurement of coil sensitivity can be avoided by fully sampling a region of k-space to compute the parallel imaging reconstruction kernel, a quantity relating each missing data point to the nearby acquired data. This process is called calibration, and techniques involving kernel calibration using additionally acquired k-space data are generally referred to as self-calibrated parallel imaging. Self-consistent parallel imaging (SPIRiT) (28) is a self-calibrated parallel imaging technique that uses all nearby data surrounding each missing datum, regardless of the sampling pattern. This feature makes SPIRiT particularly suitable for non-Cartesian parallel imaging as it avoids the requirement of collecting data on a specific Cartesian grid.

Parallel imaging was shown to benefit ASL data acquisition (23). Recently, a simultaneous multi-slice (SMS) approach was used for 2D-accelerated Cartesian acquisition with high in-plane resolution and gaps between slices (29). Undersampling has also been used in the non-Cartesian SoSP trajectories to reduce k-space data. Variable-density acquisition in all three dimensions in k-space was first implemented by Lee et al. (30). Non-Cartesian SENSE (31) was used by Duhamel and Alsop for ASL with acceleration, also in all three dimensions (15). More recently, Zhao et al. implemented a 2D variable-density SoSP for dynamic perfusion imaging by incorporating a model of flow dynamics into the SPIRiT solver (32), which led to rapid quantification of the arterial transit time. However, due to the lack of acceleration in the partition direction, the overall acceleration factor was relatively low, resulting in partial brain coverage (no cerebellum) and moderate spatial resolution.

3D SPIRiT, in which a 3D kernel instead of a 2D kernel (28) is used for SPIRiT reconstruction, was first implemented in Cartesian acquisitions together with l₁-denoising (33), and later in retrospectively undersampled SoSP data with a third dimension in the velocity space (34). It was also used to reconstruct accelerated, variable-density SoSP in cardiac imaging (35). In that study, like in the one of Zhao et al. (32), no partition acceleration was used (the apparent 3D acceleration was realized by rotating the undersampled 2D spirals) and the overall acceleration factor was fairly low (less than 2). Other published studies related to accelerated SoSP acquisitions include compressed-sensing (36) reconstruction of SoSP with density variation across partitions (37,38) and 3D non-Cartesian GRAPPA reconstruction of rotated constant-density SoSP (39).

In this work we developed a 3D-accelerated RARE-SoSP data acquisition and reconstruction routine to achieve whole-brain perfusion MRI at high spatial and temporal resolution. In this method, acceleration is implemented in all three dimensions of k-space with variable-density spirals and partition undersampling, taking advantage of the 3D arrangement of modern receive-arrays to minimize noise penalty due to parallel imaging reconstruction (26,40). Particularly, the partition acceleration enables significantly higher total acceleration factors than in the previous SoSP acquisitions that were accelerated by 2D variable-density spirals alone (32,35). Images were reconstructed using 3D SPIRiT with a single 3D kernel. In this study, the performance of 3D SPIRiT reconstruction of such 3D-accelerated acquisitions is evaluated. Another important feature of our method is that it is completely self-contained as no additional calibration (e.g., coil sensitivity) or models are required for reconstruction. This purely data-driven approach potentially simplifies its implementation and has wider applications in practice. Note that because of the intrinsically low contrast in ASL and the inevitable SNR loss due to undersampling, the proposed method may not reduce the total scan time, which mainly depends on both labeling parameters and requirements for signal averaging (41). However, given a limited number of acquisition segments, we anticipated that the accelerated volumes and the derived perfusion maps would show improved quality such as reduced signal dropout in regions of high static susceptibility and reduced through-slice blurring as compared to fully sampled images, with acceptable compromises in SNR. Although we focused on ASL in this work, the technique is applicable for brain imaging in general. Whole-brain perfusion maps at 2mm isotropic resolution (nominal) were obtained to demonstrate its potential utility in high-resolution perfusion imaging.

Theory

A brief review of SPIRiT

If a 2D Cartesian data set is N₁ by N₂, and if there are Q channels in the receive-coil, the data point x at the k-space location (n₁,n₂) of the qth channel, denoted by x_n1n2q, can be computed by

$$x_{n_1{n}_{2}q}=S_{m_1{m}_{2}q}^p{\mathrm{X}}_{n_1{n}_{2}p}^{m_1{m}_2}$$ [1]

Here S is the SPIRiT kernel of size M₁ by M₂; m₁ and m₂ are indices of S (0<m₁≤M₁; 0<m₂≤M₁); X is the k-space region surrounding x_n1n2q that has the same size as S; p is also the channel index (0<p≤Q). Summations are performed over m₁, m₂ and p (Einstein summation rule). Note that since S is 2D (without the channel dimension), it is invariant across the 2D k-space (23,42). Because by moving the indices n₁ and n₂ over a fully sampled k-space one should obtain the same k-space data, Eq. [1] is equivalent to

$$x=Sx$$ [2]

where S is the SPIRiT operator and x now represents the entire k-space data. This is the kernel consistency (or self-consistency) of the fully sampled k-space data, which leads to the notion of null operator (28), expressed as (S-I):

$$(S-I)x=0$$ [3]

where I is the identity operator. Note that by Fourier transforming the kernel S into the image space the kernel consistency can be equivalently formulated in the image space (28). In practice, images are reconstructed by imposing the data consistency in addition to kernel consistency

$$\mathit{arg}\underset{x}{\text{min}}{\Vert Dx-y\Vert }^2+\lambda {\Vert (S-I)x\Vert }^2$$ [4]

The first portion ||Dx − y||² represents data consistency, where y is the acquired data and D is the operator that transforms the reconstructed data (in k-space or image space) to the raw (acquired) data; λ is the trade-off between data consistency and kernel consistency. Note that Eq. [4] is not limited to Cartesian k-space – if y is non-Cartesian, then gridding or inverse gridding (43) can be used to transform data between Cartesian and non-Cartesian k-space.

3D extension

To reconstruct 3D accelerated data using SPIRiT, we only need to expand Eq.[1] into 3D by using a 3D SPIRiT kernel (33):

$$x_{n_1{n}_2{n}_{3}q}=S_{m_1{m}_2{m}_{3}q}^p{\mathrm{X}}_{n_1{n}_2{n}_{3}p}^{m_1{m}_2{m}_3}$$ [5]

Other than the third index that runs from 1 to M₃, the theory is the same as for 2D. Since the kernel is 3D, it is invariant across the entire 3D k-space. That is, only a single SPIRiT operator is required for reconstructing an entire volume. Specific for RARE-SoSP acquisitions, the operator D in Eq. [4] consists of a 2D inverse gridding operator and a 1D Fourier transform operator.

Methods

Comparison to GRAPPA

As the data and acceleration dimensions increase, the choice of reconstruction becomes wider (44,45). For 3D-accelerated SoSP acquisitions, reconstruction of the missing data in all three dimensions could be performed by using single-step 3D SPIRiT (i.e., simultaneous reconstruction of in-plane and partition data) or by combining 2D SPIRiT for in-plane reconstruction of each partition and GRAPPA for reconstruction of the missing partitions. The latter approach is feasible because the partition data fall on a Cartesian grid and is also a natural choice because both 2D SPIRiT and GRAPPA are well established and readily available. In addition, the latter could be run much faster (33). However, GRAPPA is known to have reduced performance at high acceleration (46). To find the optimal approach for our study, we compared the reconstruction performance of 3D SPIRiT and 3D GRAPPA (i.e., using a 3D GRAPPA kernel (47)) on a simulated, 1D-accelerated pair of control and label volumes. A fully sampled pair of volumes (3mm isotropic resolution; more details see below) was Fourier transformed into 3D Cartesian k-space and then undersampled along partition (k_z) by a factor of 3. Out of the 48 partitions, the middle 13 partitions (19 to 31) were kept intact as the calibration volume. The pair was reconstructed using 3D GRAPPA with a 5X5X2 kernel (the last one is partition, indicating the two acquired k_z lines closest to the target k_z line) and 3D SPIRiT with a 5X5X3 kernel and 30 iterations. Note that in this comparison we assumed a perfect first-stage (in-plane) reconstruction in the 2D-SPIRiT + GRAPPA approach and only focused on the GRAPPA portion of the reconstruction chain.

Imaging Experiments

5 healthy subjects (2M + 3F, age 25–37) were imaged in a 3T Trio whole-body scanner (Siemens Medical Solutions) using a 32-channel head coil. The study was approved by our internal review board; informed consents were obtained from all subjects.

For each subject, a T₁-weighted structural image (MPRAGE) (48) was first acquired, followed by a time-of-flight angiogram at the base of the brain used to position the ASL labeling plane at a location perpendicular to the carotid and vertebral arteries. Then, perfusion maps at 3mm isotropic resolution (nominal) were obtained with 1- and 2-shot accelerated ASL acquisitions, and 4-shot fully sampled acquisitions for comparison. Additionally, as an application of the 3D acceleration technique, high-resolution perfusion maps at 2mm isotropic resolution (nominal) were also obtained with accelerated 4-shot acquisitions, accompanied by fully sampled 4-shot acquisitions for comparison. Note that 3mm and 2mm resolutions are labeled as nominal because they are determined by the parameters of the imaging sequences. The real image resolution may be lower, especially in the z-direction, due to T₂ relaxation. Such z-blurring is quantified using phantom data shown in the Appendix for this study, and the estimated real z-resolutions are reported in the Results. Unless specially noted, all resolutions mentioned later in this work refer to the nominal resolution.

The ASL sequence consists of noise calibration at the very beginning, followed by calibration of gradient delay (49) and a series of label-control images acquired with 2.0-s pseudo-continuous labeling (50) and 1.5-s post-labeling delay (PLD). Background suppression (BS) (11,17) was used to suppress about 90% of the signal contribution from static tissues to reduce physiological noise. Partition encoding was centrically ordered to optimize SNR; no slice partial Fourier was used. For each ASL scan a pair of M₀ images was acquired and averaged for CBF quantification with longer TR, no magnetization preparation, but otherwise the same readout scheme (accelerated or fully sampled). Additional imaging parameters can be found in previous work (12,17).

Fully sampled and accelerated acquisitions

Images were collected using RARE-SoSP with 216X216X144 mm³ FOV to cover the entire brain. Following the excitation RF pulse, each partition was acquired with the same 2D spiral interleave. The number of spiral interleaves in each partition is equal to the number of “shots” used in the imaging volume. For fully sampled volumes, each partition consists of 4 interleaves of Archimedean spirals in 4 shots. The gradient waveforms were designed subject to the 22 mT/m amplitude and 120 mT/m/ms ramp constraints. The acquisition dwell time was 2.5 μs, and the radial spacing between the spiral revolutions was 1/FOV (in-plane) to ensure full sampling. The fully sampled 3mm and 2mm isotropic-resolution trajectories are illustrated in Supporting Figure S1.

For accelerated acquisitions, as illustrated by the k-space trajectories in Figure 1, data were fully sampled at the center of each partition up to about 25% of radius; then 3X undersampled between 30% to about 60%, and finally 5X undersampled in the outer k-space beyond 65%. Linear density-variation was used between 25% and 30% and between 60% and 65% of radius for smooth transitions (30). The total in-plane acceleration factor was 2.75 (Table 1). In k_z, data were fully sampled near the center and undersampled in the outer k-space. Specifically, for the 3mm isotropic-resolution volumes the central 13 partitions were fully sampled, and the outer k_z-space was 3X undersampled. Overall, 24 out of the 48 partitions were acquired, resulting in an effective acceleration factor along z (R_z) of 2. For the 2mm isotropic-resolution volumes the central 17 partitions were fully sampled, and the outer k-space was 4X undersampled, resulting in R_z of 2.4. The total effective acceleration factors (including both in-plane and k_z, relative to the fully sampled trajectories described above) for the 3mm and 2mm volumes were 5.5 and 6.6, respectively (Table 1).

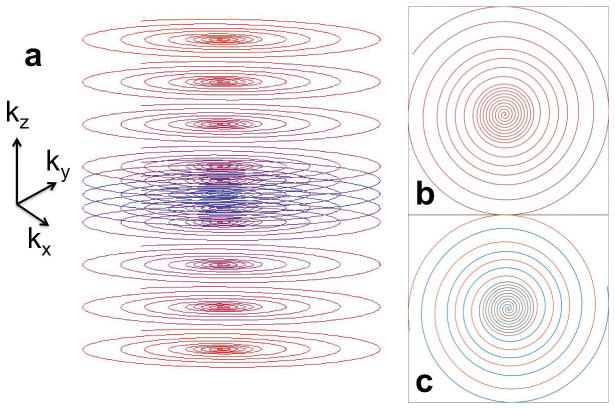
Figure 1.

(a) Illustration of the accelerated RARE stack-of-spirals (RARE-SoSP) trajectories in k-space. In the partition direction (k_z), the center is fully sampled and the outer k-space is undersampled. The acquisition was centrically ordered. In each 2D partition, variable density spirals were used to accelerate acquisitions as well as to provide a fully sampled region for kernel calibration. (b) and (c) are plots of 2D k-space trajectories for single-shot and 2-shot acquisitions, respectively. Outside the fully sampled center, each partition consists of a 3X undersampled region from about 30% to 60% of radius, and a 5X undersampled beyond 65%. Linear transitions were used in the transition regions.

Table 1.

Acquisition details of the 3mm and 2mm isotropic-resolution (nominal) volumes (A-1S = accelerated single-shot, F-4S = fully sampled 4-shot, etc.). TE is the delay from the center of the excitation RF pulse to the beginning of the first spiral; echo spacing (ESP) is the distance between the centers of two adjacent refocusing pulses; partition acceleration factor R_z is the ratio of the echo-train lengths of the fully sampled and the accelerated acquisitions; total acceleration factor (R_eff) is the product of the in-plane acceleration factor (R_inp) and R_z; data acquisition time (T_a) is the duration of the data-acquisition echo-train from the 90° excitation RF pulse to end of the last spiral readout multiplied by the number of shots, i.e., the total echo-train duration for the acquisition of an entire volume. Note that T_a may not scale in exact proportion to 1/R_eff for accelerated acquisitions because the refocusing RF pulses in the echo-train are the same for both accelerated and fully sampled sequences.

	3 mm isotropic			2 mm isotropic
	A-1S	A-2S	F-4S	A-4S	F-4S
# Shots	1	2	4	4	4
Spiral Length (ms)	10.13	5.09	6.87	4.59	12.59
Echo-train length	24	24	48	30	72
TE (ms)	9.85	7.39	8.33	7.39	11.39
TR (s)	4.50	4.50	4.80	4.50	5.50
Echo spacing (ESP) (ms)	14.96	10.04	11.92	9.84	17.84
Temporal Resolution (s)	9.0	18.0	38.4	36.0	44.0
# Pairs	24	24	8	12	8
Total Scan Time (min)	3.60	7.20	5.12	7.20	5.33
In-plane Acc. Factor (Rinp)	2.75	2.75	1	2.75	1
Partition Acc. Factor (Rz)	2	2	1	2.4	1
Total Acc. Factor (Reff)	5.5	5.5	1	6.6	1
Data Acq. Time (Ta) (s)	0.36	0.49	2.30	1.19	5.16

24 control/label pairs were acquired for the 3mm isotropic-resolution volumes with TR of 4.5 s, which took 3.60 min for single-shot and 7.20 min for 2-shot acquisitions. 8 pairs were acquired for the corresponding 4-shot fully sampled images with TR of 4.8 s (minimum), which took 5.12 min. The numbers of pairs were roughly chosen to ensure sufficient perfusion signal with averaging and a reasonable overall scan time for each subject. More details of the acquisition parameters, including temporal resolution, echo time (TE), echo-train length, etc., and those of the 2mm isotropic resolution images are listed in Table 1. The data acquisition time (T_a) in Table 1 reveal that the acquisitions of the accelerated sequences were much shorter than in their fully sampled counterparts, demonstrating more rapid coverage of the brain.

Image reconstruction

The 3D SPIRiT kernel was calibrated using the fully sampled Cartesian volume at the center of k-space obtained with gridding (43). Image volumes were reconstructed using MATLAB (Natick, MA) in the image domain (28) by imposing both kernel consistency (null condition) and data consistency, as described in Eq. [4]. As demonstrated in the original SPIRiT paper, optimization of SPIRiT may not be straightforward (28), which becomes more challenging in 3D. To optimize image quality, a few degrees of SPIRiT reconstruction freedom were explored, such as the kernel size and the number of iterations. The selection of these parameters was empirical and was based on the quality of the magnitude images and the CBF maps. Specifically, kernels of 5X5X3 (M₁=5, M₂=5, M₃=3) were used for the 3mm isotropic-resolution volumes and kernels of 5X5X5 were used for the 2mm isotropic-resolution volumes; 50 iterations were run for images at both resolutions. The parameter λ in Eq. [4] was empirically chosen to be 2. More details about the reconstruction procedure can be found in our code available at https://github.com/yulinchang/SP3.

SNR evaluation

To evaluate the SNR of the image volumes in this study, a pseudo-multiple-replica method (51) was performed to quantitatively compare the SNRs of a fully sampled volume and the derived undersampled volume. Specifically, a fully sampled volume at 3mm isotropic resolution was Fourier transformed, undersampled in k_z, and then each remaining partition was inversely gridded to the undersampled k-space trajectory using non-uniform fast Fourier transform (FFT) (43). The resulting trajectory of the undersampled k-space is identical to the trajectory of the accelerated acquisitions (Fig. 1) except that there were 4 spiral interleaves (to match the original acquisition). The total acceleration factor was 5.5. Complex Gaussian noise was generated based on the acquired noise data from each channel and the data bandwidths (the dwell times for noise calibration and image acquisition were 106.6 μs and 2.5 μs, respectively) and added to the fully sampled and undersampled data. Image volumes were obtained by direct gridding and 1D-FFT for fully sampled data and by 3D SPIRiT at 10, 25, 50, and 100 iterations for undersampled data using the 5X5X3 kernel. The procedure was repeated 100 times to obtain 100 image volumes for fully sampled and undersampled acquisitions at each iteration number. SNR maps were computed by dividing the mean by its standard deviation for each voxel.

CBF quantification and Image Analysis

All ASL image pairs were re-aligned and co-registered to the concurrently acquired structural T₁ scans using SPM12 (Wellcome Trust Centre of Neuroimaging, University College of London, UK). Gray matter (GM) and white matter (WM) probability maps were generated using the SPM12 Segment Tool (52). CBF was calculated using the single-compartment model (23), where the labeling efficiency was assumed to be 0.72 (17) and blood T₁ was assumed to be 1.65 s. Mean CBF of the GM and WM of each scan were computed by applying GM and WM masks, generated by empirically thresholding the respective probability maps (0.72 for GM and 0.9 for WM). The GM/WM CBF ratio was computed as a metric for assessment of image blurring. A whole-brain mask was also obtained by combining the GM and WM probability maps, which included the internal voxels containing ventricles.

To assess the potential of the proposed imaging method for detecting dynamic changes in CBF as would occur with functional activation, the tSNR of the CBF maps were computed for each voxel. That is, for each voxel, the tSNR was calculated by dividing the temporal mean (average of the time series) by the temporal standard deviation of the CBF values. To summarize the results, the tSNR values were averaged over the GM, WM, and the whole brain.

Results

Figure 2 compares the magnitude and the control-label difference images of a pair of simulated 1D-accelerated volumes reconstructed by 3D GRAPPA and 3D SPIRiT. For the magnitude images, artifacts are reduced in both GRAPPA and SPIRiT images. However, residual aliasing is still visible in the GRAPPA image, as indicated by the yellow arrow. For the control-label difference images, both GRAPPA and SPIRiT volumes have higher background noise than in the original fully sampled volume, but the noise in the GRAPPA image is significantly higher, such as in the orbitofrontal cortex (red arrow). This comparison demonstrates that even if the 2D SPIRiT had worked perfectly for the in-plane reconstruction of each partition, the reconstruction of missing partitions by GRAPPA would still have led to both residual artifact and enhanced noise. In comparison, 3D SPIRiT resulted in less residual artifact and less noise, and smoothly incorporates the in-plane and partition reconstructions into a single step. A 3D-reconstruction approach has the additional SNR advantage of averaging over the entire volume (33). Therefore, 3D SPIRiT was determined to be a superior approach for our purpose of CBF quantification.

Figure 2.

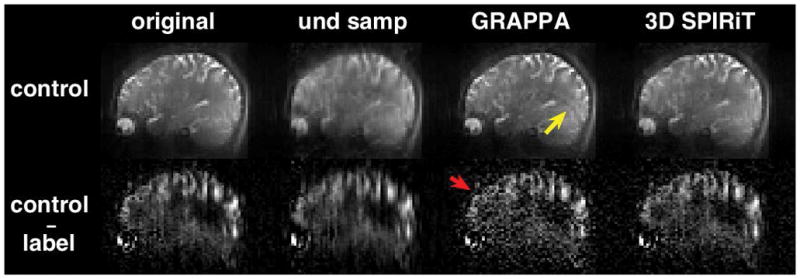
Comparison of the performance of 3D GRAPPA and 3D SPIRiT for the reconstruction of a pair of 1D-accelerated 3D volumes. One representative sagittal slice of the control volume (top) and the corresponding control-label difference volume (bottom) are shown. Acceleration was simulated in the superior-inferior direction (k_z). The original fully sampled image volume was used as the reference. For the control images, artifacts are reduced in both GRAPPA and SPIRiT volumes compared to the undersampled volume without parallel-imaging reconstruction (“und samp”, 2^nd from left). However, residual aliasing is still visible in the GRAPPA image, as indicated by the yellow arrow. For the control-label difference volumes, both GRAPPA and SPIRiT images have higher background noise than the original reference volume, but the noise in the GRAPPA image is significantly higher. For example, in the frontal cortex (red arrow), perfusion signal is nearly obscured by noise.

Supporting Figure S2 demonstrates the effect of kernel size on the quality of the SPIRiT-reconstructed magnitude and the control-label difference images for an accelerated single-shot scan at 3mm isotropic resolution. Images using the 3X3X3 and 5X5X3 kernels were both reconstructed with the same number of iterations (50 times). Compared to the raw images, artifacts in the control and label magnitude images using both kernels are significantly reduced. However, visible residual artifacts exist in the difference image of the 3X3X3 kernel, such as the ringing indicated by the yellow arrow and the blurring indicated by the red arrow. Both types of artifacts are ameliorated in the difference image using the 5X5X3 kernel.

Supporting Figure S3 demonstrates the effect of the number of iterations for an accelerated single-shot volume of 3mm isotropic resolution. For the control images, image quality improves as the number of iterations increases from 25 to 100 (kernel size 5X5X3); artifacts and blurring are still visible at 25 iterations but are nearly gone at 100 iterations. However, the single-pair control-label difference image at 100 iterations displays a significant noise enhancement, as can be seen in the background of the image. The iteration number of 50 was therefore empirically chosen to optimize both the overall magnitude image quality and the noise level in the difference images.

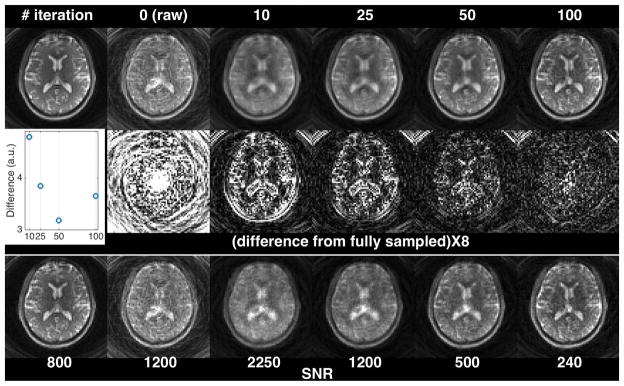
Figure 3 evaluates the residual artifact and the SNR of the 3D-SPIRiT-reconstructed volumes at different numbers of iterations in comparison to the fully sampled volume in a representative axial slice. As the number of iterations increases, the residual artifact decreases, so does the empirical SNR. The inset plots show the total absolute difference (summed over the entire volume) of each SPIRiT volume from the reference volume (upper left) as a function of the number of iterations. Initially the total difference decreases as the iteration number increases from 10 to 50, but increases again at 100 iterations. The initial decrease was evidently due to the reduced artifacts, while the increase was due to the elevated image noise. The results presented in this figure agree with the findings shown in Supporting Fig. S3.

Figure 3.

Evaluation of the residual artifact and SNR of the 3D-SPIRiT-reconstructed volumes at different numbers of iterations. Only a representative axial slice is shown. The image on the upper left is from the fully sampled volume (reference). The undersampled k-space data were derived from the fully sampled volume by undersampling in k_z and inverse gridding to the variable-density spiral trajectories using non-uniform FFT. From top to bottom are magnitude images, the absolute difference maps from the reference (multiplied by 8), and the computed empirical SNR maps. The inset in the 2^nd row plots the total absolute difference of each SPIRiT volume from the reference volume (i.e., sum of all voxels in each difference volume) as a function of the number of iterations. The numbers in the SNR panel indicate the scales used to plot the corresponding SNR maps at similar brightness. These numbers can be used to approximate the empirical SNR of these images relative to the reference image. For example, at 100 iterations, the image SNR is approximately 30% (240/800) of the SNR of the fully sampled volume.

Figure 4 compares the accelerated single-shot (A-1S) control volumes of a representative subject without and with 3D SPIRiT reconstruction and the fully sampled 4-shot (F-4S) magnitude volume, both at 3mm resolution, in triaxial views. Compared to the raw images (left), the aliasing artifacts of the SPIRiT-reconstructed images (middle) are significantly reduced. Compared to the 4-shot fully sampled counterparts (right) the SPIRiT-reconstructed accelerated images show slightly more blurring because the single-shot spirals are longer (Table 1).

Figure 4.

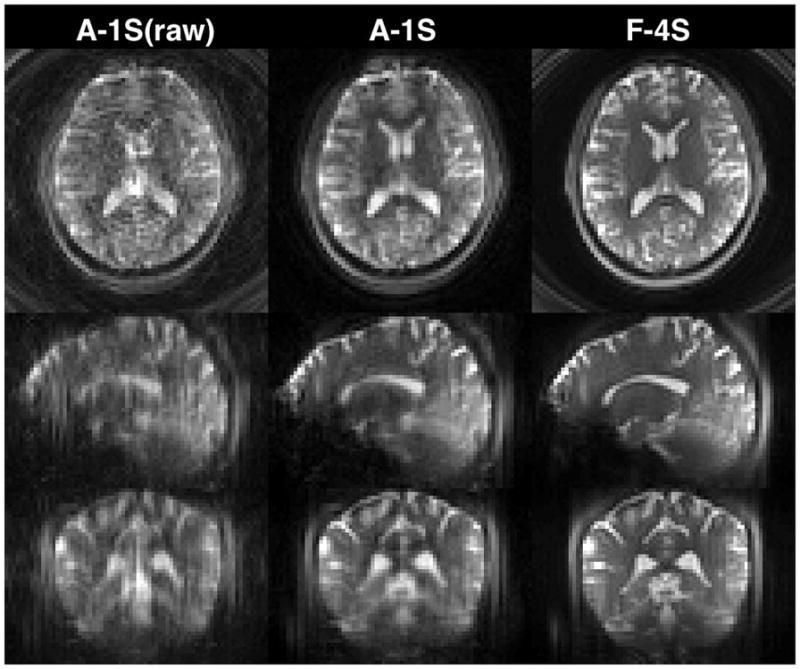
Accelerated single-shot (A-1S) magnitude images without and with SPIRiT reconstruction and fully sampled 4-shot (F-4S) images, both at 3mm isotropic resolution (nominal). Compared to the raw images (left), the aliasing artifacts of the SPIRiT-reconstructed images (A-1S) are significantly reduced. Compared to the 4-shot fully sampled counterparts (F-4S), the A-1S images show slightly more blurring because the single-shot spirals are longer (Table 1).

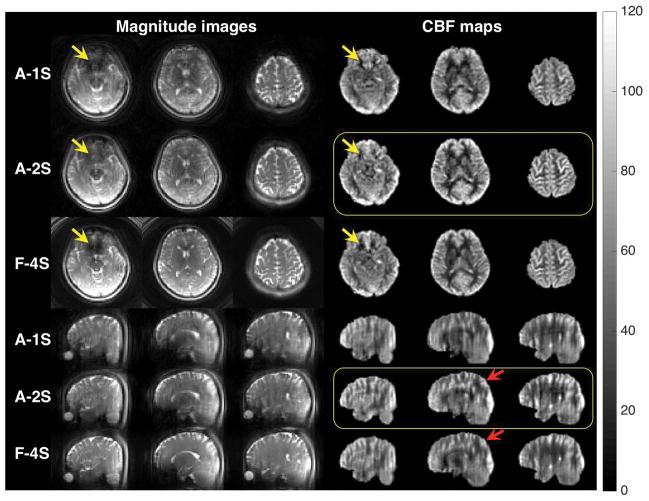
Figure 5 compares the control images and the CBF maps of selected slices in the axial and sagittal views from accelerated 1- and 2-shot (A-1S and A-2S) and fully sampled 4-shot (F-4S) volumes at 3mm resolution. For the magnitude images, both A-1S and F-4S images show dropout in the orbitofrontal cortex (yellow arrow), which is reduced in the A-2S images. This can be explained by the spiral-length parameter in Table 1 as a longer readout tends to result in higher dropout. Note that even though the fully sampled images were acquired in 4 shots, the images still displayed more signal dropout than the accelerated 2-shot images because each of the 4 spiral interleaves is longer (6.87 ms vs. 5.09 ms). Slight ringing artifacts exist in the axial view of the multi-shot images (e.g., A-2S, F-4S, 2^nd column). These may be a result of slight data and trajectory inconsistencies between different shots caused by motion and/or blood-induced field fluctuations (20).

Figure 5.

Comparison of the control images and the CBF maps of selected slices in axial and sagittal views from accelerated 1- (A-1S) and 2-shot (A-2S) and fully sampled 4-shot (F-4S) volumes at 3mm resolution. The colorbar is in units of ml/min/(100 g). The control images are from a single repetition, while the CBF maps are averaged over all pairs (A-1S: 24 pairs in 3.6 min; A-2S: 24 pairs in 7.2 min; F-4S: 8 pairs in 5.12 min). Yellow arrows indicate signal dropout in orbitofrontal cortex. Red arrows indicate where the A-2S image shows less blurring than the F-4S image in the sagittal view. Note that even though the fully sampled images (F-4S) were acquired in 4 shots, the images still display more signal dropout (yellow arrows) than the accelerated 2-shot images (A-2S) because each spiral is longer (6.87 ms vs. 5.09 ms). The A-2S CBF maps in yellow boxes have the least signal dropout and z-blurring. The single-shot images (A-1S) have the best temporal resolution of 9 s.

In the sagittal view, all images demonstrate z-blurring due to the inevitable k-space weighting of the constant-flip-angle RARE. Note that the k-space weighting results from the apparent-T₂ decay, which depends on both echo-spacing (53) and echo-train length. For the fully sampled volume, blurring is mainly caused by the long echo train (48 echoes); however, because the acquisition was split into 4 excitations, each spiral is shorter. For the A-1S volume, the situation is the opposite: although the echo train is shorter (24 echoes), each spiral is significantly longer, pushing the echo-spacing to be longer. The long echo-spacing leads to increased T₂ decay between echoes, which broadens the point-spread function (PSF) and leads to significant z-blurring (see Appendix). The A-2S image has both short spirals and short echo train, and the corresponding CBF maps (in yellow box) demonstrate the least blurring, as evidenced in the areas indicated by red arrows.

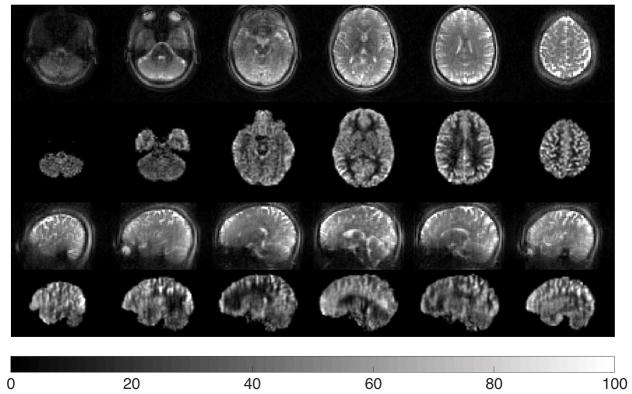
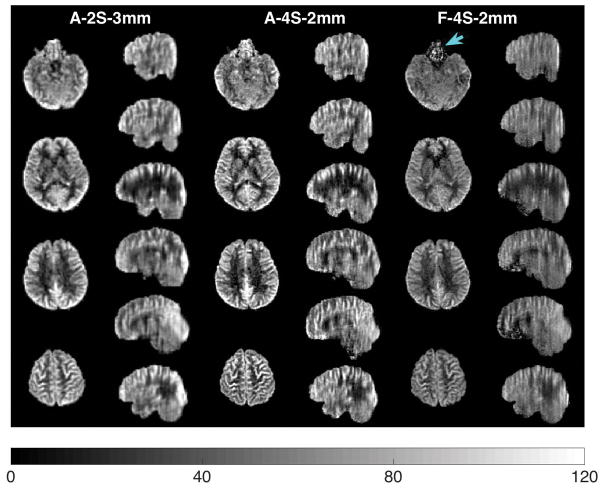
Figure 6 shows selected control images and the corresponding CBF maps in axial and sagittal views from a representative subject acquired at 3mm resolution using the accelerated 2-shot acquisition. Selected CBF maps from the accelerated 4-shot acquisitions at 2mm isotropic resolution in the axial and sagittal views are shown in Figure 7. Note that changing the voxel size from 3mm to 2mm corresponds to a 3-fold decrease in voxel volume. Figure 8 provides a side-by-side comparison of the accelerated 2-shot 3mm resolution CBF maps (A-2S-3mm), accelerated 4-shot 2mm resolution CBF maps (A-4S-2mm), and the fully sampled 4-shot 2mm resolution CBF maps (F-4S-2mm), from the same subject. As shown, by combining acceleration and 4-shot acquisitions, the accelerated 2mm resolution CBF maps reveal more details of regional perfusion than their counterparts at 3mm resolution, at the cost of temporal resolution (18 s vs. 36 s). The fully sampled 2mm isotropic resolution show severe signal dropout in orbitofrontal cortex (blue arrow) as well as z-blurring, as expected based on the results of the 3mm resolution with and without acceleration (Figure 5).

Figure 6.

Selected control images and the corresponding CBF maps of one subject at 3mm resolution in axial and sagittal views using the accelerated 2-shot acquisitions (A-2S-3mm). The CBF maps were averaged over 24 pairs in 7.2 min. The colorbar is in units of ml/min/(100 g).

Figure 7.

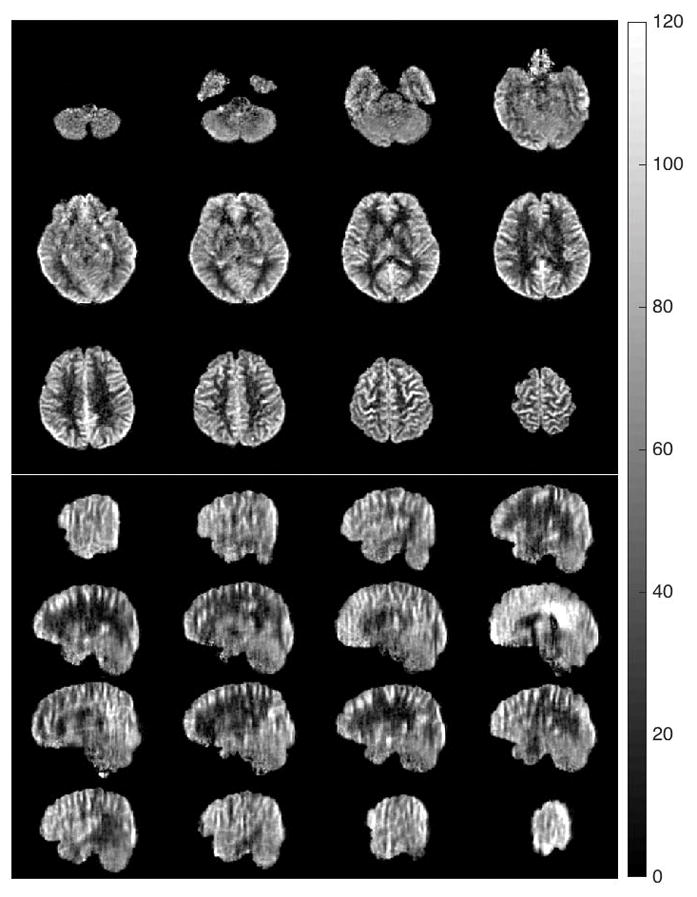
Selected axial and sagittal views of the CBF maps using accelerated 4-shot acquisitions at 2mm isotropic resolution (A-4S-2mm). These maps were averaged over 12 pairs in 7.2 min. The colorbar is in units of ml/min/(100 g).

Figure 8.

Side-by-side comparison of the 3mm isotropic-resolution CBF maps with accelerated 2-shot acquisitions (A-2S-3mm, 24 pairs in 7.2 min), the 2mm isotropic-resolution CBF maps with accelerated 4-shot acquisitions (A-4S-2mm, 12 pairs in 7.2 min), and the 2mm isotropic-resolution CBF maps with fully sampled 4-shot acquisitions (F-4S-2mm, 8 pairs in 5.33 min), from a representative subject. With acceleration and 4-shot acquisitions, the A-4S-2mm CBF maps reveal more details of regional CBF than do the CBF maps of A-2S-3mm, at the cost of temporal resolution (18 s vs. 36 s). The F-4S-2mm CBF maps show severe signal loss in the orbitofrontal cortex (blue arrow) as well as z-blurring, as can be seen in the sagittal view. The colorbar is in units of ml/min/(100 g).

To evaluate the real z-resolutions in this study, we conducted theoretical and experimental investigations of the z-blurring using a resolution phantom, presented in the Appendix. From the results shown in the Appendix, the real resolutions in the z-direction of the five acquisition schemes are estimated to be: 8 mm (A-1S-3mm), 8 mm (A-2S-3mm), 10 mm (F-4S-3mm), 5 mm (A-4S-2mm), and 11 mm (F-4S-2mm). To the best of our knowledge, despite z-blurring, 2mm nominal isotropic is the highest resolution CBF maps with whole-brain coverage within a reasonable scan time; 1.9 mm isotropic-resolution CBF maps without cerebellum were previously obtained by Ye et al. with zero filling in 39 min (18).

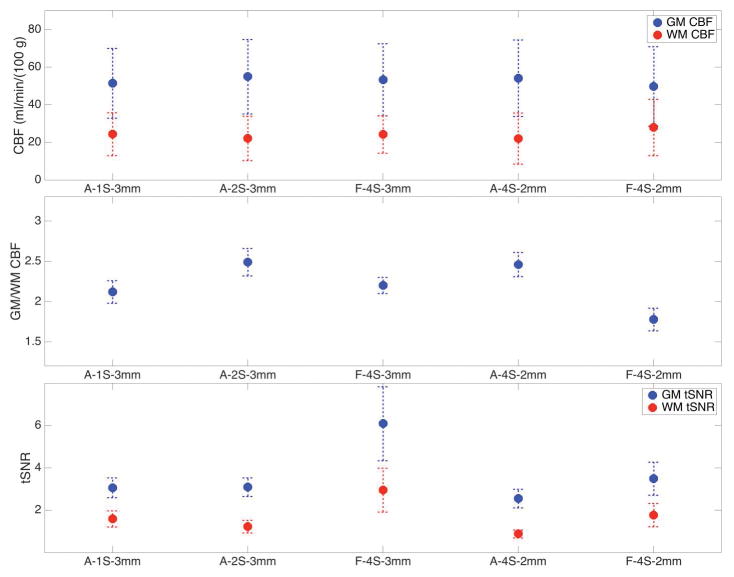
The GM and WM CBF, the GM/WM CBF ratios, and the GM and WM CBF tSNRs (all averaged over subjects) are plotted in Fig. 9 for the five acquisition schemes used in this study. These values, together with the mean CBF, mean CBF tSNR, and the mean CBF tSNR per unit time (obtained by dividing the mean CBF tSNR by the temporal resolution) (54), are listed in the Supporting Tables S1 and S2 for each individual subject. As shown in Fig. 9, the CBF values were consistent across all acquisition schemes, regardless of acceleration or resolution. The A-2S-3mm and A-4S-2mm volumes had the highest GM/WM CBF ratio, while the F-4S-2mm volumes had the lowest ratio. For the A-1S- and A-2S-3mm volumes the tSNRs are very similar, while the F-4S-3mm tSNRs are about twice as high. This reduction in tSNR for accelerated volumes is expected from the reduced SNR of the SPIRiT-reconstructed volumes as shown in Fig. 3, which is mainly due to the reduced sampling time (Table 1). The 2mm-resolution volumes were not used for tSNR comparison as the fully sampled volumes have significantly longer TE and in particular longer spirals that cause severe signal dropout.

Figure 9.

The GM and WM CBF (top), the GM/WM CBF ratios (middle), and the GM and WM CBF tSNRs (bottom) (all averaged over subjects) for the five acquisition schemes used in this study. The values from each individual subject, as well as the averages, are listed in the Supporting Tables S1 and S2. The label “A-1S-3mm” stands for accelerated single-shot acquisition at 3mm isotropic resolution (nominal). Other labels are similarly interpreted.

Discussion

In this work, a self-calibrated, 3D-accelerated data acquisition and image reconstruction routine was implemented based on the RARE-SoSP trajectories to obtain whole-brain ASL perfusion imaging with background suppression and pseudo-continuous labeling. By accelerating in 3D, the method takes advantage of the 3D arrangement of the receive-array, allowing for higher total acceleration with relatively low SNR penalty (40).

The superior performance of 3D SPIRiT over 3D GRAPPA for reconstructing 1D-accelerated data agrees with the comparison in the original SPIRiT paper (28). The main reason for the reduced performance of GRAPPA at high acceleration is likely due to the lack of nearest neighbors in the k-space GRAPPA kernel when the apparent acceleration factor is higher than 2. Such neighboring components were previously shown to be important in reconstructing the missing data (55). For the same reason, CAIPIRINHA (56) reconstruction of 2D-accelerated 3D data performs better than conventional GRAPPA because the components in a CAIPIRINHA kernel were rearranged by acquisition to be closer to the targets. Comparing to a GRAPPA kernel, a SPIRiT kernel forms a complete square or cube (except at the center) that includes all the nearest neighbors. Because a 3D kernel smoothly integrates both in-plane and partition reconstruction, 3D SPIRiT was chosen to reconstruct our 3D-accelerated volumes.

In the SNR quantification of Fig. 3, the empirical SNR appeared to be high relative to the reference image when strong residual artifact still existed (at 10 and 25 iterations), which would result in exceedingly low g-factor values from the relation (26)

$${\text{SNR}}^{\mathrm{A}}=\frac{{\text{SNR}}^{\text{FS}}}{g\sqrt{R}}$$

where the superscripts A and FS stand for accelerated and fully sampled, and R (=5.5) is the acceleration (reduction) factor. A similar effect was observed in the 2D case in the original SPIRiT work (28). The magnitude images and the difference maps reveal that such high SNR is due to smoothing at the early stage of the iterative process. As the iteration number increases, the empirical SNR becomes a more plausible estimate of the SNR achievable by the reconstruction. In fact, at 100 iterations, where the residual artifact is largely gone, the empirical SNR is likely close to the true SNR, implying a moderate elevation of the g-factor values from 1. Based on this, we argue that the SNR and hence the g-factor calculations are only valid in the absence of residual artifact. At 50 iterations, although slight artifact still existed, there was little effect on the derived perfusion maps.

Despite the reduced SNR due to undersampling, several aspects of accelerated images were improved relative to the fully sampled images. First, as shown in Fig. 5 (A-2S) and Fig. 8, signal dropout was reduced in brain regions with high susceptibility gradients or short T₂^*, such as in the orbitofrontal cortex. Second, blurring was reduced for accelerated volumes compared to the fully sampled volumes. This image quality improvement is mainly the result of the shorter spirals and shorter echo-train, which reduces intra-voxel de-phasing and uneven k-space weighting along k_z. Note that similar improvement could also be obtained for GRASE-based perfusion imaging. Specifically, acceleration can be implemented in the phase- and partition-encoding directions to reduce both readout lengths and the spin-echo trains. However, because of the Cartesian nature of GRASE, such an acquisition is only 2D accelerated as opposed to the 3D acceleration used in this study (i.e., the readout direction of GRASE is not accelerated). The under-utilized acceleration in readout may lead to lower total acceleration factors. One possible way of addressing the issue of readout acceleration is to use a “cork screw” trajectory in the readout direction (40).

As with SNR, the tSNR is also penalized for undersampling. A quantitative evaluation of the relation between SNR and tSNR for ASL, analogous to blood-oxygen level dependent (BOLD) fMRI (57), is beyond the scope of this work. However, their relation can still be qualitatively determined from our results. For the 3mm-resolution volumes, the tSNRs of both A-1S-3mm and A-2S-3mm volumes for both GM and WM decreased roughly by a factor of 2 from those of the F-4S-3mm volumes (Fig. 9 bottom panel and Table S2); on the other hand, with 50 iterations, the SNR of accelerated volumes also decreased nearly by a factor of 2 (scaled from 800 to 500 in Fig. 3). Therefore, the relation between tSNR and SNR is within or near the “linear regime” (58). This comparison is qualitative because the three 3mm-resolution volumes had different TEs, spiral lengths, and echo-train lengths. A more quantitative approach would require better control of these imaging parameters. As a consequence of the lower tSNR, the total scan time with acceleration may not be shorter than that of the fully sampled scans (41). However, with less signal dropout and less inter-acquisition noise, we expect higher-quality CBF quantification with a given temporal-resolution constraint (e.g., A-4S-2mm vs. F-4S-2mm in Fig. 8). We also note that for A-2S-3mm and A-4S-2mm, the WM tSNR was lower, despite their shorter TE’s. This is likely due, at least in part, to the reduced GM contamination as evidenced by the increased GM/WM CBF ratios for these acquisitions.

There are two related factors that lead to inaccurate determination of the GM/WM CBF ratio. One is the partial volume (PV) effect (59), which is intrinsic to all imaging methods. To minimize the PV effect only the interior voxels of GM and WM were used for the CBF ratio calculation (17). The other factor is blurring caused by relaxation, which leads to decreased effective spatial resolution. As the results of the Appendix show, out of the five imaging schemes used in this work, A-2S-3mm and A-4S-2mm have the highest effective z-resolution (5 mm and 3 mm, respectively), while F-4S-2mm has the lowest (9 mm). On the other hand, Fig. 9 (middle panel) reveals that A-2S-3mm and A-4S-2mm have the highest GM/WM CBF ratios, while F-4S-2mm has the lowest. This qualitative agreement indicates that 1) the GM/WM CBF ratio measurement is strongly affected by the real resolution of the image volumes and that 2) even the GM/WM CBF ratios of A-2S-3mm and A-4S-2mm are likely still lower than the true GM/WM CBF ratio (12,59) due to the remaining z-blurring. Therefore, increasing the accuracy of the measured GM/WM CBF ratio will depend on further reduction of blurring instead of increasing the nominal resolution.

Several aspects of this method may be improved in future work. 1) 3D SPIRiT is generally computationally intensive – on average, it took our MacBook Pro (2015 model, 15″) 9 minutes to calculate one volume at 3mm isotropic resolution). There are two main factors that contribute to the long processing time: One is the iteratively applied conjugate-gradient algorithm for matrix inversion (Eq. [4]); the other is the repetition of image calculation for all receive-channels. The first factor may be addressed by the rapidly developing computer hardware, especially the graphical processing unit (GPU) (60). For the second factor, it may be helpful to use a SENSE-like (26) reconstruction which, instead of computing the images repetitively for each individual channel, only reconstructs a single final complex image (61). 2) z-blurring may be significantly reduced by using variable-flip-angle (24,62) or low-flip-angle (63,64) refocusing RF pulses. In particular, the variable-flip-angle approach may help reduce the acquisition segments with even longer echo trains (65), also further improving temporal resolution. 3) It was shown in the original SPIRiT paper (28) and soon after (33) that L₁-denoising could be combined with SPIRiT to significantly reduce noise. Denoising was not implemented in this work for a faithful evaluation of the performance of 3D SPIRiT and to keep the reconstruction time manageable. As more powerful reconstruction hardware and algorithms become available, 3D denoising may be implemented as an intermediate step in the iterative conjugate-gradient algorithm of Eq. [4] to further improve image quality, which would in turn improve the tSNR.

Conclusions

We presented a 3D-accelerated data acquisition and reconstruction method with stack-of-spirals trajectories for the quantification of cerebral blood flow using arterial spin labeling. As compared to the images of fully sampled acquisitions, the accelerated acquisitions improved image quality with reduced signal dropout and less through-slice blurring, resulting in increased GM:WM CBF ratios. The image SNR was primarily penalized for undersampling, as revealed by the pseudo multiple replica method, and the tSNR was proportionally penalized. High quality whole brain CBF maps at 2mm isotropic resolution (nominal) were obtained with segmented acquisitions within a reasonable acquisition time. Although image reconstruction times were long, several strategies exist for reducing them. Highly accelerated ASL offers new opportunities to measure regional CBF with increased accuracy.

Supplementary Material

Supp Fig&Tab

Supporting Figure S1. 2D spiral trajectories of the 4-shot, fully sampled acquisitions at 3mm (a) and 2mm (b) isotropic resolutions used in this study, plotted in the same k-space scale.

Supporting Figure S2. The effect of kernel size on the quality of the magnitude image and the control-label difference image for an accelerated single-shot volume at 3mm isotropic resolution. Compared to the raw images, the artifacts of the control and label images of the 3X3X3 and 5X5X3 kernels are both significantly reduced (both at 50 iterations). However, visible artifacts exist in the difference image of the 3X3X3 kernel, such as the ringing artifacts indicated by the yellow arrow and the blurring indicated by the red arrow, which are both ameliorated in the difference image reconstructed using the 5X5X3 kernel.

Supporting Figure S3. The effect of the number of iterations for an accelerated single-shot image set at 3mm isotropic resolution. The top and bottom rows show control images and the corresponding single-pair control-label difference images at different numbers of iterations (kernel size 5X5X3). For the control images, the image quality improves as the number of iterations increases from 25 to 100. Artifacts and blurring are still visible at 25 iterations (as indicated by the red arrow) but are nearly gone at 100 iterations. However, the control-label difference image at 100 iterations shows a significant increase of noise visible in the background.

Supporting Figure S4. Partition weights of the accelerated (A-4S-2mm) and fully sampled (F-4S-2mm) 4-shot 2mm-resolution volumes of the phantom plotted as functions of the delay time in the upper panel and as functions of partition index in the lower panel. These weights were calculated by summing over the first 20 points of all spiral interleaves at the center of each partition k-space. Data were acquired using RARE-SoSP with the partition-encoding gradients removed so that the signal variations across partitions were exclusively caused by T₂ relaxation. Both plots were normalized by the weights of the central partition (i.e., C=1 in Eq. [A2]). In the delay plot (top), data corresponding to negative partitions are placed on the left side of the central partition. The exponential decay function S(t) = Aexp(-t/T₂) was used to fit the data to compute the apparent T₂. These apparent T₂ values varied slightly due to difference in echo time, but all were between 72 and 80 ms. The k_z-index plots (bottom) show relatively less uneven k-space weighting in the accelerated acquisition than in its fully sample counterpart thanks to the shorter echo spacing (Table 1) and fewer acquired partitions.

Supporting Figure S5. Experimental determination of z-blurring using a resolution phantom. (a) shows an example sagittal brain slice from each of the five data acquisition schemes tested in this study, along with the MPRAGE anatomical image. The corresponding images of a slice of the phantom are shown in (b), where the resolution of the reference phantom image is 1.2 mm. (c) shows the expansion of the region enclosed by the blue rectangle in (b) for each acquisition scheme. The horizontal bar at the center of this region with a z-width of 6 mm was used as the object to quantify z-blurring. The direction of z and the z=0 location are indicated in (c). To quantify z-blurring, a projection was first obtained perpendicular to z (horizontal in the image) over the bar region for each image. The projections were then plotted against z (along with the reference), all normalized to 2 at z=0, as demonstrated in the bottom figure. The PSF width, or the FWHM, was computed as twice of the distance between the edge of the bar and the location where the signal falls below 50% (i.e., below 1), indicated by the vertical dashed lines (the two lines of A-1S-3mm and A-2S-3mm overlapped in the figure). For example, for the F-4S-3mm volume, the edge of the bar (from the reference) is at 3mm and the signal falls below 50% at 12 mm. Thus the FWHM was calculated to be (12-3)X2 = 18 mm. Accordingly, the FWHM’s of the five listed acquisition schemes were determined to be, respectively, 12 mm, 12 mm, 18 mm, 8 mm, and 16 mm. The last measurement for the F-4S-2mm volume was likely not accurate and was not shown due to the strong interference from other parts of the image. Its FWHM is estimated to be 21 mm from Eq. [A5]. These results are consistent with image quality shown in (b). For example, the ‘CS’ symbol was most legible in the A-4S-2mm image, as indicated by the double-arrow, whereas the F-4S-2mm image was the blurriest.

Supporting Table S1. The (average ± standard deviation (SD)) of the GM and WM CBF of each subject measured using the five acquisition schemes. A-1S/A-2S/A-4S = Accelerated single-, 2- and 4-shot acquisition, F-4S = Fully sampled 4-shot acquisition.

Supporting Table S2. The mean CBF, GM/WM CBF ratio, mean CBF tSNR (tSNR_CBF), GM CBF tSNR (tSNR_GM), WM CBF tSNR (tSNR_WM), and the mean CBF tSNR per unit time of the 5 healthy volunteers using accelerated and fully sampled acquisitions at 3mm and 2mm isotropic resolutions. The mean CBF tSNR per unit time was calculated by dividing the mean CBF tSNR by the temporal resolution.

Appendix

A Brief Theory of z-blurring in RARE Imaging

In 3D imaging with RARE, each partition in k_z corresponds to a spin echo, which is subject to T₂ decay that leads to an uneven weighting of the partitions. By Fourier transform the uneven weighting is translated into a finite-width point-spread function (PSF) along z in the image volume, resulting in image smoothing/blurring. Here we briefly review the theory of such blurring (66,67) and provide a simple estimate of z-blurring in this study.

In general, the image signal f(z) can be computed as a weighted inverse Fourier transform of the k-space data P(k_z):

$$f(z)=\int P(k_z)W(k_z)e^{i2\pi k_{z}z}d{k}_z=\int \rho (z^{\prime })w(z-z^{\prime })d{z}^{\prime }$$ [A1]

where P(k_z) is the Fourier transform of the water density, ρ(z), and W(k_z) is the weighting function in k_z due to T₂ decay, often referred to as the modulation transfer function (MTF). The PSF, or the smoothing kernel, w(z), is the inverse Fourier transform of W(k_z). The second equation is from the Convolution theorem, revealing that each single voxel in z, which ideally should be a delta or a box function, is “spread out” by the PSF, to an extension typically quantified by the full width at half maximum (FWHM) of the PSF.

For fully sampled, CPMG-based RARE imaging with centric ordering, the MTF can be approximated by

$$W(k_z)=C{e}^{-2\left((\mid k_z\mid /R_z)/\delta k_z\right)·\text{ESP}/T_2}=C{e}^{-\mid k_z\mid /k_0}$$ [A2]

In the above equation, C is a constant, representing the signal amplitude of the first echo, i.e., k_z = 0 for centric ordering; R_z is the effective acceleration factor in k_z; δk_z = 1/FOV_z is the partition encoding increment; ESP is echo spacing (Table 1); the factor of 2 results from centric ordering; the equation was simplified with the substitution

$$k_0=\frac{R_z\delta k_z{T}_2}{2\text{ESP}}$$ [A3]

The corresponding PSF, w(z), is a Lorentzian

$$w(z)=\frac{C/(\pi k_0)}{z^2+1/{(2\pi k_0)}^2}$$ [A4]

with a FWHM of

$$\text{FWHM}=\frac{1}{\pi k_0}=\frac{1}{R_z\delta k_z}\frac{2\text{ESP}}{\pi T_2}=\frac{{\text{FOV}}_z}{R_z}\frac{2\text{ESP}}{\pi T_2}$$ [A5]

Experimental Quantification of z-blurring

To validate the above theory and to quantify the real z-resolutions in this study, a resolution phantom was imaged using the same five sequences of in vivo ASL (with no labeling or background suppression). To quantify the apparent T₂, each sequence was repeated with the partition-encoding gradients removed, which is equivalent to repeated 2D imaging of the entire volume using the CPMG echoes. The signal intensity of each volume represents the relative weight of the corresponding partition. The sum of the first 20 points of the spiral interleaves at the center of each k-space was used to estimate the weight, denoted by S(t), where t is the time delay from the first echo. S(t) was then fitted to the exponential decay function S(t) = Aexp(-t/T₂) to calculate T₂, where A is a constant.

Supporting Figure S4 demonstrates the partition weighting due to T₂ decay. For clarity only results from the accelerated and fully sampled 2mm acquisitions are plotted, both normalized to the weights of k_z=0. In the top panel the weights are plotted against delay time, from which the apparent T₂’s were calculated. For the five acquisition schemes (Table 1), the apparent T₂’s were between 72 and 80 ms. Note that in this experiment the T₂ values depend slightly on the echo spacing, gradient, etc. (53). For simplicity the average value of 76 ms was used in the following calculations. The bottom panel of Fig. S4 plots the same weights against z-partition index, from which a relatively less acute and uneven k_z weighting is clearly shown for the accelerated acquisition due to shorter echo spacing as well as k_z undersampling.

Supporting Figure S5 shows the experimental determination of z-blurring of the phantom. We focused on the horizontal bar at the center of the blue box in panel (b), and its range in z was used for the quantification of blurring. Specifically, for each of the five acquisition schemes, the corresponding image was first projected horizontally (parallel to the bar), and then the FWHM was taken as twice the distance between the edge of the bar in the reference image and the position of 50% signal intensity. This process is illustrated by the plot at the bottom of Fig. S5. To validate the theory of blurring (Eq. [A5]) against the measurement, the PSF widths were calculated using the following parameters: FOV_z = 144 mm, T₂ = 76 ms, ESP values are from Table 1, R_z = 2 for A-1S-3mm and A-2S-3mm, R_z = 2.4 for A-4S-2mm, and R_z = 1 for F-4S-3mm and F-4S-2mm (Table 1). The calculated/measured FWHMs of the A-1S-3mm, A-2S-3mm, F-4S-3mm, A-4S-2mm, F-4S-2mm images are, respectively: 9 mm/12 mm, 6 mm/12 mm, 14 mm/18 mm, 5 mm/8 mm, and 21 mm/16 mm. Except for the last one (F-4S-2mm, too blurry for accurate measurement), all measured widths are slightly higher than calculated ones within one or two voxel widths. Sources of discrepancy may include: 1) imperfect parallel imaging reconstruction as demonstrated earlier (Fig. 3); 2) Eq. [A5] being only an approximation in the presence of auto-calibration partitions as k_z is non-uniformly undersampled; 3) effect of low SNR: in practice the partitions too far from the k-space center may have very low SNR when a long echo-train is used (e.g., F-4S-2mm of Fig. S4) and they contribute little to the image quality. Overall, however, the above results are consistent with the quality of the brain and phantom images. For example, the A-4S-2mm image shows least z-blurring, with the letters “CS” most legible out of all images (double-arrow in Fig. S5(b)), while the F-4S-2mm image is the most blurry. Also, although the z-resolutions of both A-1S-3mm and A-2S-3mm are measured to be 12 mm, the A-1S-3mm is apparently blurrier, possibly due to the longer spiral readout (Table 1) that induces in-plane blurring. Using the measured FWHMs in the phantom images, the blood T₂ of 186 ms (68), and the reciprocal relation between FWHM and T₂, we estimated that the FWHM’s of our perfusion imaging of the brain for the A-1S-3mm, A-2S-3mm, F-4S-3mm, A-4S-2mm, and F-4S-2mm (from theory alone) volumes were, respectively: 5 mm, 5 mm, 7 mm, 3 mm, and 9 mm. Adding the respective nominal resolutions, the real z-resolutions of these acquisition schemes should be no coarser than, in the same order: 8 mm, 8 mm, 10 mm, 5 mm, and 11 mm. The results indicate that the proposed accelerated acquisition scheme significantly reduced z-blurring in RARE-SoSP imaging.