Identifying Stages of Kidney Renal Cell Carcinoma by Combining Gene Expression and DNA Methylation Data

Abstract

In this study, in order to make use of complementary information from different types of data for better disease status diagnosis, we combined gene expression with DNA methylation data and generated a fused network, based on which the stages of KIRC (Kidney Renal Cell Carcinoma) can be better identified. It is well recognized that a network is important for investigating the connectivity of disease groups. We exploited the potential of the network’s features to identify the KIRC stage. We first constructed a patient network from each type of data. We then built a fused network based on network fusion method. Based on the link weights of patients, we used a generalized linear model to predict the group of KIRC subjects. Finally, the group prediction method was applied to test the power of network-based features. The performance (e.g., the accuracy of identifying cancer stages) when using the fused network from two types of data is shown to be superior to using two patient networks from only one data type. The work provides a good example for using network based features from multiple data types for a more comprehensive diagnosis.

1 Introduction

The American Cancer Society’s most recent estimate for kidney cancer in the United States for 2015 indicates that about 61,560 new cases of kidney cancer (38,270 in men and 23,290 in women) will occur and about 14,080 people (9,070 men and 5,010 women) will die from the disease. Kidney cancer is among the 10 most common cancers in both men and women. Overall, the lifetime risk for developing kidney cancer is about 1 in 63 (1.6%). Renal cell carcinoma (KIRC) is by far the most common type of kidney cancer. About 9 out of 10 kidney cancers are renal cell carcinomas [1].

The stage of a cancer describes how far it has spread. The treatment and prognosis depend, to a large extent, on the cancer’s stage. The stage is based on the results of the physical exam, biopsies, and imaging tests (CT scan, chest x-ray, PET scan, etc.). Knowing the stage of cancer can be a factor in deciding treatment and can also help your doctor determine if your cancer might be due to an inherited genetic syndrome.

Recent multiomics data and clinical information emerging from cancer patients have provided unprecedented opportunities for investigating the multilayered genetic basis of disease in order to improve the ability to diagnose treat and prevent cancer. The Cancer Genome Atlas (TCGA) [2] is a large-scale collaborative initiative to improve our understanding of the multilayered molecular basis of cancer. While TCGA has opened numerous opportunities for revealing new insights on the molecular basis of cancer [2–5], it is imperative to address the issue of integration with the available multiomics data to better understand cancer phenotypes, and thereby provide an enhanced global view of the interplay between different levels of data and knowledge.

Recently there has been much research exploring the potential of connectivity networks of patients for classification in biomedical field [6–8]. However, there is little research on network construction and analysis from multiple types of biological data. In a topological sense, a network is a set of nodes and a set of directed or undirected edges between the nodes. Networks focus on the organization of the system rather than on the system’s components. So we can exploit the features of networks to classify disease subtypes and predict clinical outcomes.

In the past few decades, many researchers have investigated the classification of cancer using one type of biology data [9–12]. In our current study, we integrated two types of data: gene expression and DNA methylation data to construct a fused network for classifying the KIRC patients. At first, for each type of data, we constructed a network and then used a network fusion method to combine the two single networks. Therefore, we got three networks, including two networks from each type of data and their fused one. Based on the three networks, we predicted the stage of KIRC for a new subject.

The remainder of the paper is structured as follows. Section 2 describes the collection of datasets and provides the details of important steps such as feature selection, network fusion, and graph-based label prediction used in our study. In Section 3, we present the experimental results, including performance comparisons with other network-based label prediction method. In the last section, we conclude the study and give prospects on our future work.

2 Materials and Methods

In this section, we will first introduce the datasets used in our study and its preprocessing. Then we will describe three critical steps used in our approaches. An important method is similarity network fusion (SNF), which is used to fuse two or more networks into one network. Another approach is sparse partial least squares regression (SPLS) for feature selection. And the last approach is our network-based LASSO Label Prediction (NLLP) method, which is used to predict the stage of KIRC in our study.

2.1 The Cancer Genome Atlas KIRC Data Retrieval

Clinical and pathological features, genomic alterations, DNA methylation profiles, and RNA and proteomic signatures have been evaluated in KIRC studies and are available from TCGA. We used more than 500 primary nephrectomy specimens from patients with histologically confirmed KIRC that conformed to the requirements for genomic study defined by the Cancer Genome Atlas (TCGA). We used the TCGA data portal to download gene expression profiles, DNA methylation expression and clinical data. For all of three types of data, we used the level 3 data set. After preprocessing, we got 66 samples with these two types of data. 72 samples were obtained for the gene expression data; 130 samples were obtained for the DNA methylation data re are. There are only 66 samples for both types of data.

2.2 Methods

2.2.1 Similarity Network Fusion

Here, we employed the similarity network fusion (SNF) method proposed by Wang et al. [13], for which an R package SNFtool [13] is also available. The SNF is inspired by the multi-view learning framework, which was developed for computer vision and image processing applications [14]. The SNF constructs fused networks of samples by comparing samples’ molecular (or phenotypic) profiles. The fused networks are then used for classification and label prediction.

Suppose we have n samples (e.g., patients) and m measurements (e.g., DNA methylation). A patient similarity network is represented as a graph G = (V, E). The vertices V correspond to the patients {x₁, x₂, ···, x_n} and the edges E are the weighted value of the similarity between patients. The edge weights are represented by an n × n similarity matrix W, with each W(i, j) indicating the similarity between patients x_i and x_j. ρ(x_i, x_j) is represented as the Euclidean distance between patients x_i and x_j. A scaled exponential kernel is used to determine the weight of the edge:

$$\mathbf{W}(i,j)=exp(-\frac{{\rho }^2(x_i,x_j)}{\mu {\epsilon }_{i,j}})$$ (1)

where μ is a hyperparameter that can be empirically set and ε_i,j is used to overcome the scaling problem. Here we define

$${\epsilon }_{i,j}=\frac{\mathit{mean}(\rho (x_i,N_i))+\mathit{mean}(\rho (x_j,N_j))+\rho (x_i,x_j)}{3}$$ (2)

where mean(ρ(x_i, N_i)) is the average value of the distances between x_i and its neighbors. μ is recommended to have the value in the range of [0.3, 0.8].

To calculate the fused matrix from multiple types of measurements, we applied a full and sparse kernel on the vertex set V. The full kernel is a normalized weight matrix P=D⁻¹W, where D is the diagonal matrix with entries D (i, i) = Σ_j W(i, j), so that Σ_j P(i, j) = 1.

Let N_i represent the set of x_i’s neighbors including x_i in G. Given a graph G, K nearest neighbors (KNN) is used to measure the local affinity as follows:

$$\mathrm{S}(\mathrm{i},\mathrm{j})=\{\begin{array}{ll}\hfill \frac{\mathrm{W}(\mathrm{i},\mathrm{j})}{{\sum }_{\mathrm{k}\in {\mathrm{N}}_{\mathrm{i}}}\mathrm{W}(\mathrm{i},\mathrm{k})},& \mathrm{j}\in {\mathrm{N}}_{\mathrm{i}}\hfill \\ \hfill 0.& \text{otherwise}\hfill \end{array}$$ (3)

Note that P carries the full information about the similarity of each patient to all others whereas S only encodes the similarity to the K most similar patients for each patient. The algorithm always starts from P as the initial state and uses S as the kernel matrix in the fusion process for both capturing local structure of the graph and computational efficiency.

We first calculated the status matrices P⁽¹⁾ and P⁽²⁾ from two input similarity matrices; then the kernel matrices S⁽¹⁾ and S⁽²⁾ were obtained as in Equation (3).

Let ${\mathrm{P}}_{\mathrm{t}=0}^{(1)}={\mathrm{P}}^{(1)}$ and ${\mathrm{P}}_{\mathrm{t}=0}^{(2)}={\mathrm{P}}^{(2)}$ represent the initial two status matrices at t=0. The key step of SNF is to iteratively update the similarity matrix corresponding to each data type as follows:

$${\mathrm{P}}_{\mathrm{t}+1}^{(1)}={\mathrm{S}}^{(1)}\times {\mathrm{P}}_{\mathrm{t}}^{(2)}\times {({\mathrm{S}}^{(1)})}^{\mathrm{T}}$$ (4)

$${\mathrm{P}}_{\mathrm{t}+1}^{(2)}={\mathrm{S}}^{(2)}\times {\mathrm{P}}_{\mathrm{t}}^{(1)}\times {({\mathrm{S}}^{(2)})}^{\mathrm{T}}$$ (5)

where ${\mathrm{P}}_{\mathrm{t}+1}^{(1)}$ is the status matrix of the first data type after t iterations, while ${\mathrm{P}}_{\mathrm{t}+1}^{(2)}$ is the similarity matrix for the second data type. This procedure updates the status matrices each time, generating two parallel interchanging diffusion processes. After t steps, the overall status matrix is calculated as follows

$${\mathrm{P}}^{(\mathrm{c})}=\frac{{\mathrm{P}}_{\mathrm{t}}^{(1)}+{\mathrm{P}}_{\mathrm{t}}^{(2)}}{2}$$ (6)

The input to SNF algorithm can be feature vectors, pairwise distances, or pairwise similarities. The learned status matrix P^(c) can then be used for clustering and classification. In this work, we mainly focus on clustering and label prediction.

2.2.2 Sparse Partial Least Squares Regression

We used sparse partial least squares regression (SPLS)[15] to do feature selection. The main principle of this methodology is to impose sparsity within the context of partial least squares and thereby carry out dimension reduction or variable selection. SPLS performs well even when the sample size is much smaller than the total number of variables. An additional advantage of SPLS is its ability to handle both univariate and multivariate responses.

Chun H[15] and Efron et al.[16] formulated the estimation of the SPLS direction vector by imposing an additional constraint L₁ on the objective function in the following problem;

$$\underset{w}{max}{w}^{T}Mws.t.w^{T}w=1,{\Vert w\Vert }_1\le \lambda$$ (7)

where M = X^T YY^T X and λ determines the level of sparsity.

To get a sparse enough solution, authors in [15] reformulated the SPLS by generalizing the regression formulation of SPCA[17]. This formulation promotes exact zero property by imposing L₁ penalty on a surrogate of direction vector (c) instead of the original direction vector (α), while keeping α and c close to each other:

$$\begin{array}{c}\underset{\alpha ,c}{min}-k{\alpha }^{T}M\alpha +(1-k){(c-\alpha )}^{T}M(c-\alpha )+{\lambda }_1{\Vert c\Vert }_1+{\lambda }_2{\Vert c\Vert }_2\\ s.t.{\alpha }^T\alpha =1\end{array}$$ (8)

The first L₁ penalty encourages sparsity on c. And the second L₂ penalty takes care of potential singularity in M when solving for c.

An R package “spls” is available and is used to implement the feature selection method in our study.

2.2.3 Network-based LASSO Label Prediction

We employed a network-based semi-supervised learning (NSSL) method to predict the label of a new sample; this scheme falls halfway in between unsupervised and supervised learning for improving the prediction power by using unlabeled data [18–21]. When applied to a biological system, NSSL is more computationally efficient. The accuracy is comparable to other methods such as the kernel-based methods with a longer learning time, although the learning time of NSSL increases nearly linearly with the number of graph edges [6, 22]. In addition, the graph structure could be used to improve the interpretation of biological phenomena [23–25] when using NSSL.

After combining the labeled and unlabeled samples, we used Equation (1) to construct an affinity matrix. We implemented a network-based LASSO Label Prediction (NLLP) method to predict the labels of the unlabeled samples. Let us assume a weighted graph G with n nodes indexed as 1, 2,…, n. A symmetric weight matrix is nonnegative, and if w_ij=0, there is no edge between nodes i and j. We assume that the first p training nodes have labels, y₁, y₂, y₃, ···, y_p, where y_i ∈ {1, 2, 3}, and the remaining q=n−p test nodes are unlabelled. The goal is to predict the labels y_p+1, y_n by exploiting the linkage in the graph.

$$\underset{({\beta }_0,\beta )\in R^{p+1}}{min}{R}_{\lambda }({\beta }_0,\beta )=\underset{({\beta }_0,\beta )\in R^{p+1}}{min}\left[\frac{1}{2N}\sum _{i=1}^N{(y_i-{\beta }_0-w_i^T\beta )}^2+\lambda {\Vert \beta \Vert }_1\right]$$ (9)

The dimension of W_train is p×n, and then W_test is a (n − p) × n matrix.

When the categorical response variable G has K > 2 levels, the linear logistic regression model can be generalized to a multi-logit model. The traditional approach is to extend $log\frac{Pr(\mathrm{G}=1\mid \mathrm{x})}{Pr(\mathrm{G}=2\mid \mathrm{x})}={\mathrm{\beta }}_0+{\mathrm{x}}^{\mathrm{T}}\mathrm{\beta }$ to K − 1 logits

$$log\frac{Pr(G=l\mid x)}{Pr(G=K\mid x)}={\beta }_{0l}+x^T{\beta }_l,l=1,\dots ,K-1$$ (10)

Here β_l is a p-vector of coefficients. Here we choose a more symmetric approach. We model

$$Pr(G=l\mid x)=\frac{e^{{\beta }_{0l}+x^T{\beta }_l}}{{\sum }_{k=1}^K{e}^{{\beta }_{0k}+x^T{\beta }_k}}$$ (11)

The authors in [24] fit the model (10) using the regularized maximum likelihood estimation. Using a similar notation as before, let p_l (x_i) = Pr(G = l|x_i), and let g_i ∈ {1, 2, …, K} be the i th response. We maximize the penalized log-likelihood.

$$\underset{{\{{\beta }_{0l},{\beta }_l\}}_1^K\in R^{K(p+1)}}{max}\left[\frac{1}{N}\sum _{i=1}^{N}log{p}_{g_i}(x_i)-\lambda \sum _{l=1}^K{P}_a({\beta }_l)\right]$$ (12)

In our study, P_a(β_l) refers to ||β_l||₂ We used the R package “glmnet” [26] to implement the generalized linear model and our NLLP method.

3 Results and Discussions

3.1 Method overview

Given two or more types of data for the same sample (e.g., KIRC subjects), we first create a network for each type of data (Fig. 1, 2) and then fuse these networks into one similarity network (Fig. 3). The initial step is to use a similarity measure for each pair of samples to construct a sample-by-sample similarity matrix for each data type. The matrix represents a similarity network, where the nodes are samples and the weighted edges measure the similarity between a pair of samples. The network-fusion step uses a nonlinear method based on message-passing theory [27], which iteratively updates every network, making it more similar to the others per iteration. After a few iterations, SNF converges to a single network, a common subset whose vertices have strong local affinity.

Fig. 1.

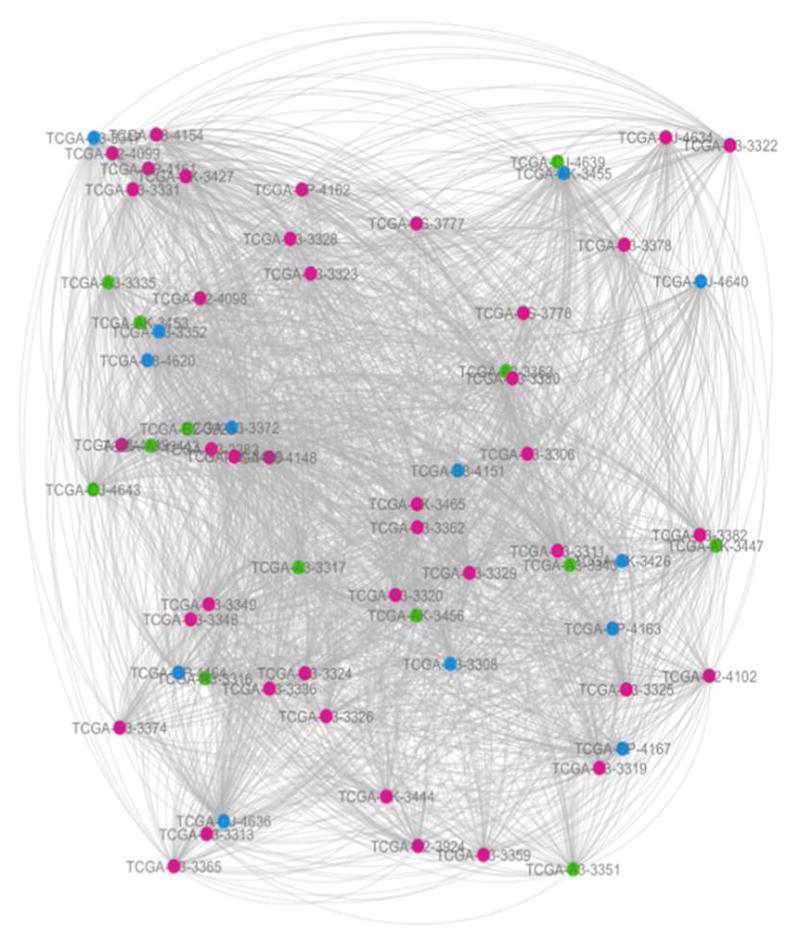
The network constructed from gene expression data.

Fig. 2.

The network constructed from DNA methylation data.

Fig. 3.

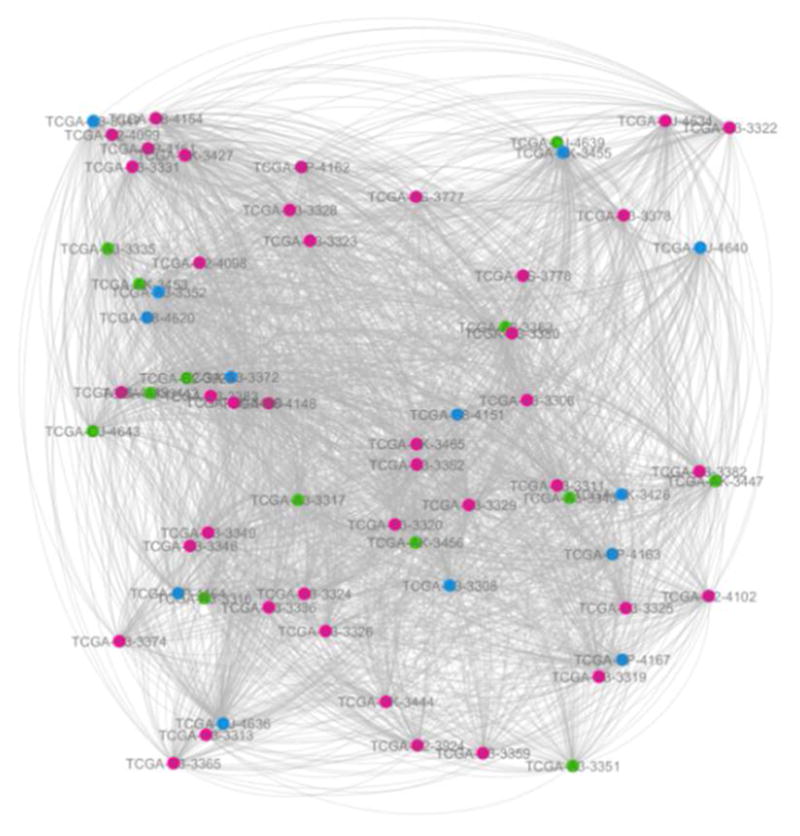
The fused network from two data types: gene expression and DNA methylation.

The red, green and blue circles represent the patients at KIRC stage I, stage II and stage III respectively. The link transparency shrinks as the link weight increases. These are all the same for the following two figures (Fig. 2 and Fig. 3).

The following experimental results are all based on three networks (Fig. 1–3).

3.2 Cancer Stage Prediction

In order to investigate the potential of using networks as a diagnostic tool, we predicted the cancer stage of new patients based on network fusion. We used resample validation to evaluate the performance of our prediction method. We denoted acu_GM by the prediction accuracy using the fused network from two types of data, i.e., gene expression and methylation. Similar notations are used for other networks, i.e., acu_genexpr for the network from gene expression data, and acu_Methy for the network from DNA methylation data. “avg_acu_GM” represents the average value of prediction accuracy “acu_GM” of 1000 times of sampling. It is similar for other two networks. Table 1 showed the average prediction accuracy of 1000 times of sampling. From the experimental results (Table 1), the fused network performs the best (avg_acu_GM≈0.76). We generally expect that results using the fused network, which uses two types of data, is superior to approaches using only one type of data (avg_acu_GM > avg_acu_genexpr or avg_acu_GM > avg_ acu_Methy).

TABLE 1.

The average prediction accuracy based on networks from different types of data

	NLLP	KNN71	MLW2	WDC3
avg_acu_GM	0.757	0.526	0.640	0.679(λ=0.9)
avg_genexpr	0.732	0.667	0.527	0.601 (λ=0.5)
avg_Methy	0.696	0.308	0.443	0.593(λ=0.9)

¹K nearest neighbors, k=7;

²Maximum link weight;

³Large link weight and small difference of degree centrality

In the current NLLP approach, we achieved a good accuracy of predicting the KIRC cancer stage using the fused network. In our future work, we will incorporate prior knowledge (e.g. Pathway information) to further improve our NLLP method.

In addition, we also calculated the variance of prediction accuracy of 1000 times of sampling (Table 2). We used “var_acu_GM” to indicate the variance value of prediction accuracy “acu_GM” of 1000 times of sampling. Similar methods were used for the other two networks. From the results shown in Table 2, we can see that the prediction methods are all very stable whether they were applied to two single networks or the fused network.

TABLE 2.

The variance of prediction accuracy based on networks from different types of data

	NLLP	KNN71	MLW2	WDC3
var_acu_GM	4.23E-03	5.04E-02	1.50E-02	1.60E-02 (λ=0.9)
var_genexpr	3.79E-03	1.28E-02	0.00E+00	1.53E-02 (λ=0.5)
var_Methy	2.46E-03	5.20E-02	1.99E-02	1.16E-02 (λ=0.9)

¹K nearest neighbors, k=7;

²Maximum link weight;

³Large link weight and small difference of degree centrality

3.3 Comparisons with Other Network-based Methods

Sharan et al. [28] separated the network-based label prediction methods into two types of approaches: direct schemes, which infer the label of a node based on its connections in the network, and module-assisted schemes, which first identify module of related nodes and then label each module based on the known labels of its members. However, the premise of the latter type of prediction method is an accurate module identification method. They [28] also presented a simple comparison between two types of network-based label prediction methods and it showed that the direct methods have better performance than the module-assisted methods. Just because of this, in the study, we only compared our NLLP method with some direct prediction methods, including k nearest neighbors [29, 30] (k=7) (KNN7), Maximum link weight (MLW) and Large link weight and small difference of degree centrality [31] (WDC). In KNN7, an unlabelled patient is assigned to the label of the patient with the largest count among 7 nearest neighbors. For MLW, it is assumed that two patients (one labeled and the other unlabeled) with the maximum link weight have the same label.

In WDC, the assumption is that if there is a larger link weight and a smaller difference of degree centrality between an unlabeled patient and a labeled patient, the two patients have identical labels. For each test patient j, we first found the solution of the objective function as follows:

$${max}_{i\in S_{\mathit{train}}}\lambda W_{ij}+(1-\lambda )\text{exp}(-\lfloor D_i-D_j\rfloor )$$ (13)

where S_train is the training labelled samples. Based on this, the label of optimal i then was assigned to the test patient j. W_ij is the link weight between the unlabelled patient j and the labelled patient i. D_i denotes the degree centrality of patient i in the network. λ is a nonnegative tuning parameter. We used resample validation (1000 times) to find the optimal λ. Table 1 and Table 2 presented the comparison results about prediction accuracies and the variance of the prediction accuracies for four network-based prediction methods, respectively. It is shown that our NLLP method achieved the highest accuracy (Table 1). For the fused network, the NLLP method shows the least variance (Table 2), which indicates that our prediction method is the most stable compared with other three prediction methods. Therefore, compared with other three network-based prediction methods, our proposed method NLLP achieved the best performance.

3.4 Evaluation on Hybrid KIRC dataset

In order to make up the insufficiency of samples, we added simulated data to the experimental datasets as follows. For each stage of gene expression data, we randomly sampled one gene expression value of each gene with replacement and generated one simulated sample. We repeated doing the resampling 20 times and generated 20 simulated samples of each stage. Similar methods were used with the DNA methylation data. Then we combined the KIRC dataset downloaded from TCGA and the simulated KIRC dataset into a hybrid KIRC dataset. We applied our NLLP method to the hybrid KIRC dataset and evaluated the performance. Besides the average prediction accuracy, we also computed true positive rate (TPR), and false negative rate (FNR) for each stage of the KIRC subjects. TPRk denotes ture positive rate of samples at stage k. FNRij represents the false negative rate that the samples at stage i are identified to be at stage j. Table 3 and Table 4 show the average performance of NLLP based on the networks from different types of data using 5-fold cross validation. The variance value of the performance can be seen in Table 5.

TABLE 3.

The average TPR and Accuracy of NLLP based on the networks from different types of data

	GM	genexpr	Methy
ACC	0.852	0.783	0.663
TPR1	1.000	1.000	1.000
TPR2	0.756	0.685	0.568
TPR3	0.658	0.673	0.658

TABLE 4.

The average FNR of NLLP based on networks from different types of data

	GM	genexpr	Methy
FNR12	0	0	0
FNR13	0	0	0
FNR21	0.244	0.315	0.432
FNR23	0	0	0
FNR31	0.342	0.327	0.432
FNR32	0	0	0

TABLE 5.

The variance of the performance of NLLP based on networks from different types of data

	GM	Genexpr	Methy
ACC	6.81E-02	6.81E-02	7.51E-02
TPR1	0	0	0
TPR2	1.24E-02	1.24E-02	1.02E-02
TPR3	3.47E-04	3.47E-04	3.47E-04
FNR12	0	0	0
FNR13	0	0	0
FNR21	5.33E-02	5.33E-02	3.88E-02
FNR23	0	0	0
FNR31	3.77E-02	3.77E-02	2.62E-02
FNR32	0	0	0

From these three tables, it can be seen that the TPR of stage III is the least for each network comparing with other two stages. Stage II and III are both predicted as stage I with high probability (FNR21=0.244 and FNR31=0.342) and we will try our best to address the problem. What’s more, it is indicated that our prediction method is very robust as demonstrated in Table 5.

4 Conclusions

With the rapid development of high-throughput genomic technology, it has become easier and cheaper to collect diverse types of genomic data for biological discovery. In order to make use of the complementary information from different types of data, data integration has been a hot research field. However, multi-type data integration is a pressing challenge. In this study, we combined gene expression and DNA methylation data to construct a fused network containing integrated information from both data types. We tested the potential of network based approaches in disease status identification from three networks: two networks from each type of data (gene expression, DNA methylation), and their fused networks. We classified the KIRC subjects into three groups (three stages) based on these three networks respectively. Furthermore, we used resample (1000 times) validation to evaluate the performances. The experimental results show that the prediction accuracy is the highest for each prediction method when using the fused network. This further confirms that we should comprehensively employ multi-type data for better diagnosis. From the comparison with other three network-based prediction methods, it is shown that our NLLP method achieves the best performance. We believe that the performance could be further improved by incoporating prior biological knowledge (e.g., pathway information from KEGG). Although we used NLLP method to predict the KIRC stage as an example of using network based approaches, our prediction method can also be used for early diagnosis of other cancers and diseases.

Biographies

Su-Ping Deng received the B. Sc. degree from Henan University, China in 2003. She received the M.Sc. degree from Central South University in 2006. From July 2006 to March 2012, she worked as a teacher in West Anhui University. She received the Ph.D degree from Tongji University, China in 2012. Currently, Dr. Deng is a postdoc in the college of Electronics and Information Engineering, Tongji, University, China. She is mainly interested in computational biology and bioinformatics.

Shaolong Cao received B.Sc. degree in Applied Mathematics from Xi’an Jiaotong University, China, 2011. Now, he is a Ph.D student in Biomedical Engineering, Tulane University, USA. His research interests include High-dimensional genetic data inference, Generalized linear mixed model and Genetic network based approach.

De-Shuang Huang received the B.Sc., M.Sc. and Ph.D. degrees all in electronic engineering from Institute of Electronic Engineering, Hefei, China, National Defense University of Science and Technology, Changsha, China and Xidian University, Xian, China, in 1986, 1989 and 1993, respectively. During 1993–1997 period he was a postdoctoral research fellow respectively in Beijing Institute of Technology and in National Key Laboratory of Pattern Recognition, Chinese Academy of Sciences, Beijing, China. In Sept, 2000, he joined the Institute of Intelligent Machines, Chinese Academy of Sciences as the Recipient of “Hundred Talents Program of CAS”. In September 2011, he entered into Tongji University as Chaired Professor. From Sept 2000 to Mar 2001, he worked as Research Associate in Hong Kong Polytechnic University. From Aug. to Sept. 2003, he visited the George Washington University as visiting professor, Washington DC, USA. From July to Dec 2004, he worked as the University Fellow in Hong Kong Baptist University. From March, 2005 to March, 2006, he worked as Research Fellow in Chinese University of Hong Kong. From March to July, 2006, he worked as visiting professor in Queen’s University of Belfast, UK. In 2007, 2008, 2009, he worked as visiting professor in Inha University, Korea, respectively. At present, he is the director of Institute of Machines Learning and Systems Biology, Tongji University. Dr. Huang is currently Fellow of International Association of Pattern Recognition (IAPR Fellow), senior members of the IEEE and International Neural Networks Society. He has published over 180 journal papers. Also, in 1996, he published a book entitled “Systematic Theory of Neural Networks for Pattern Recognition” (in Chinese), which won the Second-Class Prize of the 8th Excellent High Technology Books of China, and in 2001 & 2009 another two books entitled “Intelligent Signal Processing Technique for High Resolution Radars” (in Chinese) and “The Study of Data Mining Methods for Gene Expression Profiles” (in Chinese), respectively. His current research interest includes bioinformatics, pattern recognition and machine learning.

Dr. Yu-Ping Wang received the BS degree in applied mathematics from Tianjin University, China, in 1990, and the MS degree in computational mathematics and the PhD degree in communications and electronic systems from Xi’an Jiaotong University, China, in 1993 and 1996, respectively. After his graduation, he had visiting positions at the Center for Wavelets, Approximation and Information Processing of the National University of Singapore and Washington University Medical School in St. Louis. From 2000 to 2003, he worked as a senior research engineer at Perceptive Scientific Instruments, Inc., and then Advanced Digital Imaging Research, LLC, Houston, Texas. In the fall of 2003, he returned to academia as an assistant professor of computer science and electrical engineering at the University of Missouri-Kansas City. He is currently a Professor of Biomedical Engineering and Biostatistics & Bioinformatics at Tulane University School of Science and Engineering & School of Public Health and Tropical Medicine. He is also a member of Tulane Center of Bioinformatics and Genomics, Tulane Cancer Center and Tulane Neuroscience Program. His research interests have been computer vision, signal processing and machine learning with applications to biomedical imaging and bioinformatics, where he has about 160 peer reviewed publications. He has served on numerous program committees and NSF/NIH review panels, and served as editors for several journals such as Neuroscience Methods.