Summary
Quantitative measurement of the material properties (e.g., stiffness) of biological tissues is poised to become a powerful diagnostic tool. There are currently several methods in the literature to estimating material stiffness and we extend this work by formulating a framework that leads to uniquely identified material properties. We design an approach to work with full field displacement data — i.e., we assume the displacement field due to the applied forces is known both on the boundaries and also within the interior of the body of interest — and seek stiffness parameters that lead to balanced internal and external forces in a model. For in vivo applications, the displacement data can be acquired clinically using magnetic resonance imaging while the forces may be computed from pressure measurements, e.g., through catheterization. We outline a set of conditions under which the least-square force error objective function is convex, yielding uniquely identified material properties. An important component of our framework is a new numerical strategy to formulate polyconvex material energy laws that are linear in the material properties and provide one optimal description of the available experimental data. An outcome of our approach is the analysis of the reliability of the identified material properties, even for material laws that do not admit unique property identification. Lastly, we evaluate our approach using passive myocardium experimental data at the material point and show its application to identifying myocardial stiffness with an in silico experiment modeling the passive filling of the left ventricle.
Keywords: Inverse problems, unique identification, passive myocardium, convexity, material modeling
1. Introduction
Significant changes in the stiffness of biological tissues are associated with disease progression. Among numerous examples, cancerous tumors [1, 2] and fibrotic myocardium [3, 4] have a different stiffness than their healthy tissue counterparts. Therefore, the tissue stiffness may be used as an indicator of the presence of disease and response to therapy, and its identification is part of a cogent and emerging diagnostic strategy. In addition, the identified material properties, which define the material stiffness, are a critical input to construct biomechanical models and study the functioning of healthy and diseased organs such as the heart.
Given the importance of characterizing the material response of biological tissue, many direct and iterative methods have been developed and presented in the literature. Here we focus on methods applied to full-field measures [5], where either strains or displacements due to known applied loads are measured on the surface or the boundaries of the domain of interest and also in its interior. For example, using magnetic resonance imaging (MRI), the heart's displacement field due to the filling pressure can be measured at many hundreds of homogeneously spaced locations (e.g., 2×2 mm in plane resolution) inside the myocardial wall (see, e.g., [6, 7, 8])
In a so-called “direct” approach to material parameter identification using full filed measures, the discretized equations of the forward problem are rewritten in terms of the material properties and the pressure, which are treated as the unknowns to be solved for. Raghavan and Yagle [9] have first proposed this approach in the context of the finite difference discretization. This original formulation is only applicable to a specific set of ideal problems and it is difficult to implement in biomechanics, where the tissue pressure term cannot be measured directly through imaging techniques [10]. In order to circumvent this problem, Skovoroda et al. [11] assumed material incompressibility and removed the undetermined pressure from the unknowns in the Navier's equations of elasticity. They were able to distinguish between regions of high and low stiffness (inclusions), but the modulus reconstruction was not accurate near parts of the boundaries. Similar to Skovoroda et al., Sumi et al. [12] analytically substitute the undetermined pressure term with a mean normal stress. They were able to successfully reconstruct the material shear modulus using 2D (but not 1D) strain measurements. Nevertheless, as indicated by Barbone et al. [13], this approach requires the elastic moduli to be constant along the domain's boundaries and leads to relative — not absolute — values for the elastic moduli. This assumption is further restricted to an idealized set of specific boundaries and does not easily apply to general problems in biomechanics.
A second approach for solving inverse problems is the iterative approach, see e.g., [14]. This approach requires the optimization of a non-linear objective function, usually computed as the L2 error norm between experimentally measured and numerically computed (e.g., solving the equilibrium equations with the finite element method) displacements. A commonly used iterative method is the Finite Element Model Updating (FEMU) method [15, 16, 17, 18]. FEMU minimizes the least squares difference between measured and numerically computed displacements (FEMU-U) or forces (FEMU-F). In the FEMU method, a weighting matrix is typically used to modify the objective function. Furthermore, Cottin et al. [16] show that if the material law is linear in the material properties, the FEMU-F method yields a linear system in terms of the material properties. While the FEMU-F method minimizes the difference between applied and computed forces, the Constitutive Equations Gap Method (CEGM) approach minimizes the difference between applied traction loads and internal stresses [19]. In a modified version of the CEGM method, [20, 21, 22] the L2 displacement error norm is added to the objective function to identify elastic moduli with noisy and perturbed measurements. Banerjee et al. [21] control the contribution from the additional term through a continuation scheme on a penalty term and have demonstrated that approximately ten iterations are sufficient to identify the material properties from noisy experimental measures.
Starting from direct and iterative approaches presented above, our first objective is to construct a method to identify uniquely mechanical material stiffness properties so that their identified values do not depend on initial guesses or fine-tuning of the solution algorithm. Additionally, our second objective is to formulate a method applicable to general 3D finite kinematics problems, whereas several previous studies have been confined to linearized kinematics or simplified biaxial loading/plane-strain scenarios. In order to achieve these objectives, we propose a framework consisting of: 1) Equilibrium based objective function; 2) Material energy function optimization; and 3) Stability and uniqueness analysis of the identified material properties. For reference in the remaining of the manuscript, we refer to our framework by the three initials of its basic components: EMS.
Our approach shares the strength of the direct methods and results in a linear system of equations in terms of the unknown material properties. This system of equations can be solved efficiently and, in our approach, leads to unique material properties. In contrast with other direct methods, our approach is applicable in the general settings of finite elasticity and does not require ad hoc physical assumptions.
Further, although non-iterative, our approach shares with several iterative schemes the objective of minimizing the difference between measured and computed forces or stresses. In particular, the objective function we formulate in our approach is recovered with the FEMU-F method if the FEMU-F weighting matrix is equal to the identity and the chosen material energy density is linear in the material properties. In this case, as also observed by Cottin et al. [16], the optimization problem will yield a linear system of equations.
Key to our approach is the definition of the objective function based on the difference between applied (external) and internal forces (Section 2). This is in contrast with other common approaches, which minimize the difference between computed and measured displacements and do not guarantee uniqueness of the identified material properties. The second component of our approach consists in a strategy to formulate material energy laws based on the available experimental data (Section 3). In this formulation we require the material energy law to be polyconvex so that material stability and the existence of minimizers of the boundary value problems are guaranteed [23, 24, 25, 26]. The chosen definition of the objective function and class of material energy laws allows us to analyze the stability and uniqueness of the identified material properties (Section 3). Finally, in order to test our approach and show its potential application as a diagnostic tool, we apply it to identify the passive material properties of the heart (Section 4). The passive myocardial material properties characterize the heart's response during filling, which is critical to understanding pathological conditions such as heart failure with preserved ejection fraction (HFpEF)†. Uniquely identified material properties may serve to detect the onset and monitor the progression of HFpEF, whose diagnosis and treatment have so far been difficult [29].
2. Formulation of an Equilibrium Based Objective Function
Throughout the manuscript, we consider the general setting of a body Ω with boundary Γ = ΓN ⋃ ΓD, ΓN ⋂ ΓD = {}, where ΓN is the Neumann boundary and ΓD is the Dirichlet boundary. We assume that the body is subjected to body forces B in Ω, traction boundary condition T on ΓN, and displacement boundary condition ū on ΓD. Moreover, here we formulate the problem in the framework of finite elasticity and, in order to preserve material frame indifference, the material behavior of the body Ω is described by an energy density W (α, C). C = FTF is the right Cauchy-Green deformation tensor, F = ∇X φ is the deformation gradient and φ = X + u is the deformation mapping, where X denotes the body reference configuration and u is the displacement field measured from the reference configuration. The material energy density W (α, C(u)) is therefore a function of the displacement field u through φ, i.e., C(φ) = C(X + u), and of the material properties α. In the following, we will explicitly indicate the dependency on α and u only when needed for clarity. We summarize the hyperelastic equilibrium problem in the continuum setting as
| (1a) |
| (1b) |
| (1c) |
| (1d) |
where P is the first Piola-Kirchhoff stress tensor and N̂ is the unit normal to ΓN. Correspondingly, the weak form of equilibrium problem (1) can be obtained in terms of the first variation of the potential energy as
| (2) |
taking into account the boundary conditions (1b) and (1c). Herein, δu and δF denote the first variations of the displacement and deformation gradient.
Before continuing, we select the finite element method (FEM) to discretize the weak form of the equilibrium problem (2). We focus on this numerical method in the remainder of this work, but an equivalent derivation is obtained if other numerical methods are chosen. In order to discretize eqn. (2), we approximate the continuum displacement field as
| (3) |
where Da is the displacement at the location xa of finite element node a — e.g., u(xa) = Da, Na is the finite element shape function associated with node a. As in the following, we used Einstein notation to indicate summation over repeated indices. We also indicate the component i of a nodal vector using a double subscript, e.g., the component i of displacement Da is indicated as Dai, where Dai = ui(xa). By inserting eqn. (3) into eqn. (2) and using indicial notation, we obtain the discretized form
| (4) |
where (,.) defines the derivative with respect to (·). In compact column matrix notation, eq (4) can be written as
| (5) |
where fint, fext, and δD are the discrete global vectors containing, respectively, the components (ai) of the internal forces ( ), external forces ( ), and variations of displacements (δDai). According to eqn. (4) and using Gaussian quadrature to compute the integrals numerically, the nodal force components ( ) are:
| (6a) |
| (6b) |
In eqns. (6a)-(6b), nQP is the number of quadrature points, F(Xq) is the deformation gradient evaluated at the location Xq of quadrature point q, wq is the weight associated with quadrature point q, and tai are point loads applied directly to node a in direction i. The components tai may also be due to distributed surface loads and can be computed by appropriate numerical integration over the surface.
Several standard approaches (e.g., [30, 31]) to identify unknown material properties in biomechanics aim at minimizing the difference between experimental (uexp) and computed (u) displacement fields for a given set of applied forces and boundary conditions. The computed displacement field depends on the material properties through the equilibrium equations and a chosen material energy density (eqns. (1)). Therefore, by changing the material properties, it is possible to modify the computed displacements and reduce the difference between uexp and u. The computed displacements are usually obtained by solving the balance of linear momentum using a numerical method, e.g., the finite element method. A schematic illustration of the standard approach based on minimizing the difference between uexp and u is given in Figure 1. Once the numerical model is constructed, the material properties are initialized based on an educated guess. Subsequently, a set of forces and boundary conditions are applied corresponding to the experimental conditions for which uexp is recorded. In this setting, the displacements u are computed and their difference with uexp is evaluated at discrete locations according to a chosen objective function, e.g., the discrete L2 norm , with DΔ := D – Dexp, where, in the finite element context, D is the global vector containing the nodal displacements. If a predetermined convergence criterion is reached, the material properties have been computed. Otherwise the material properties are updated and the discrete displacements D are recomputed until a satisfactory agreement with Dexp is reached. At each iteration, several algorithms, such as Genetic Algorithms, may be used to systematically change the material properties, and decrease the computed value of the objective function g* until an optimal set of properties is obtained.
Figure 1.
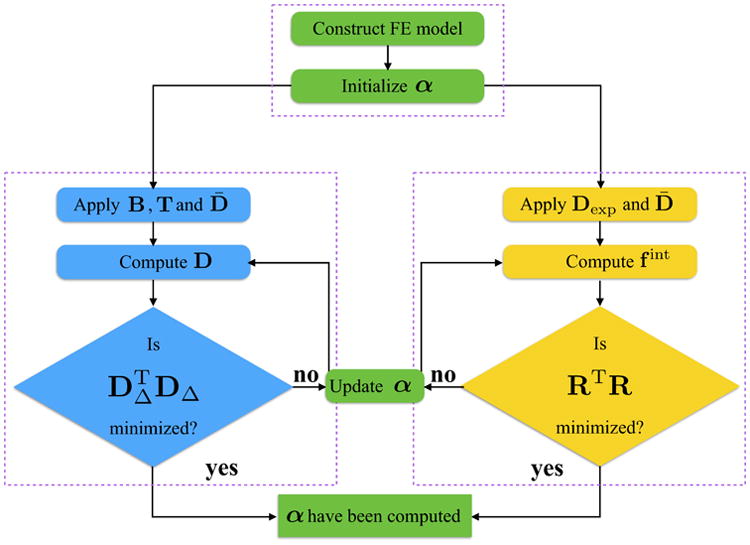
Comparison of the approaches based on minimizing the difference between measured and computed displacements — left — or forces — right — for material properties identification. D̄ denotes the vector of discretized displacement boundary conditions.
In the general setting of finite elasticity there is, however, no guarantee that the standard approaches based on minimizing g* lead to unique material properties. Indeed, for each evaluation of the objective function g*, the measured displacements are compared with the computed displacement field obtained by solving a nonlinear forward equilibrium problem. Through equilibrium the computed displacement field depends on the material properties to be identified, but this dependence is only implicit and via the solution of a nonlinear equilibrium problem. This implies that the objective function g* itself is a nonlinear implicit function of the material properties and for this reason we cannot guarantee a unique solution to minimizing g*.
Here, to avoid this implicit dependence on material properties, and with the goal of formulating a problem with a unique solution that is robust with respect to initial guesses, we turn the standard approach on its head. Whereas the standard approach applies the known forces and computes the displacements to be compared with the experimental displacement data, in our approach, similar to the FEMU-F method, we apply the experimental displacements as known inputs, and from them compute the corresponding internal forces. These are then used to identify the material properties by minimizing the difference between the computed and the experimental forces (Figure 1-right).
2.1. Objective function at the model level
In presenting our EMS framework and objective function, we start by defining prerequisites P1 and P2:
P1 For a given body Ω, we assume that the displacement field u in Ω due to a set of externally applied forces (B, T) is known. Our aim is to identify the material properties α of the body Ω once a suitable material energy function W (α, C(u)) has been chosen, i.e, once the functions of the deformation invariants in W have been selected. W can be selected from the literature or through the strategy outlined in Section 3.2. We solve the problem of identifying the material properties α in the discrete setting, i.e., after the equilibrium equations are discretized using a chosen numerical method.
P2 We assume that W (α, C(u)) is linear in α and polyconvex. In Section 3.1 we describe the motivations for formulating polyconvex material energy functions, although polyconvexity is not directly required to guarantee uniqueness of the identified material properties.
Once we have chosen an appropriate material energy function W (α, C(u)) to describe the material response of the body Ω, we can compute the internal forces in direction i at node a in the discretized domain Ω. If u is known from experiments, W (α, C(u)) and consequently become a function only of α, i.e., . Equivalently, given the measured body forces B and tractions T, the external forces can also be computed. The exact expression for and depends on the chosen numerical method (e.g., eqn. (6)).
In general, the equilibrium between external (experimental) and internal forces will be inexact due to errors in the measured displacements and pressure, as well as imperfections of the adopted material model. Indeed, the material model will always describe the response of the real material only approximately and therefore the internal forces computed using the real displacement field cannot match exactly the applied loads. As a consequence, when inserting suitable material properties into the balance of linear momentum, the equilibrium is only approximately satisfied. Thus, the deviation from perfect equilibrium, i.e., the residual, is considered here as the basis for the objective function to be minimized. Given B, T, and corresponding u, force equilibrium can be imposed as closely as possible by least-squares minimization with respect to α of the error between and . The identified material properties α correspond to the internal forces that most closely balance the applied external forces. To compute the material properties that lead to the closest equilibrium between fint and fext we define the functional
| (7) |
where R is the residual vector with components
| (8) |
Then the material properties corresponding to fint that is closest to fext in the L2 norm sense are identified as
| (9) |
In order to prove uniqueness of the material properties α as minimizers of g, we argue as follows:
For any given u, g(α, u) becomes a function only of α, i.e., g(α, u) = g(α)
Since W is linear in α (prerequisite P2), is also linear in α and therefore g(α) is a quadratic function in α.
By inspection of eqn. (7), g(α) ≥ 0.
Given 1, 2, and 3, the Hessian Hg of g(α) with respect to α is constant and semi-positive definite for any given displacement field u.
Hg is semi-positive definite and not strictly positive definite if the applied displacement field does not “excite” all the deformation modes included in W (α, C(u)). For example, if multiple terms are used in W to describe the anisotropic response of the material and only one uniaxial experiment at a fixed stretch ratio is available, we do not expect to identify all the material properties in W. A semi-positive Hessian does not show an inadequacy of the proposed method in certain cases, but rather indicates that insufficient data are used to characterize the material properties contained in the chosen energy function.
Depending on the complexity of the problem geometry, loading conditions and accuracy/amount of the recorded displacement field, it is possible to choose W so that the problem of identifying its material properties is well posed, i.e., enough data are available to characterize the stiffness associated with all the deformation modes contained in W. This implies that all the eigenvalues in Hg are non-zero. Consequently the uniqueness of α is guaranteed since g(α) is a quadratic function with a strictly positive definite Hessian (e.g., [32]).
In practice, using the proposed framework, it is always possible to check the rank of Hg and be certain of its positive definiteness throughout the identification process. Moreover, once Hg is known, we can compute its condition number, κ(Hg) as
| (10) |
The 2-norm condition number of the Hessian can be written using the maximum and minimum eigenvalues e as
| (11) |
and can be used to quantify the robustness of the calculated set of material properties. For example, if Hg is ill-conditioned, i.e., possesses a large condition number, the identified material properties will be, in principle, inaccurate because of sensitivity to small errors in the recorded data (a high condition number, i.e., a nearly singular Hessian, leads to linearly dependent material properties [33]). Equivalently, in presence of a high condition number for Hg, different sets of material properties correspond to nearly identical values of g(α, u), eventually leading to the inaccurate identification of α. In this regard, we proceed to show how to minimize g and how Hg is computed during the solution procedure.
By inserting eqns. (6) into eqn. (8), and subsequently eqn. (8) into eqn. (7), we obtain a version of the objective function that can be minimized numerically by solving ∇g = 0 with respect to α. Since we are interested in computing Hg to determine its rank, we choose to take advantage of the already computed Hg to efficiently identify the minimizers of g and thus, we employ the Newton-Raphson method. Theoretically one Newton-Raphson iteration suffices for well-conditioned Hg since the gradient of the objective function is linear in α. Therefore, the calculation of the Hessian represents a specific method to determine the coefficient matrix of the linear problem ∇g = 0. The individual components of the gradient ∇g are calculated as
| (12) |
where
| (13) |
Differentiating eqn. (12) with respect to α we compute the components of Hg as
| (14) |
where
| (15) |
Note that, since in Section 3.5 we are interested in the analysis of models from the literature where prerequisite P2 does not apply, we compute the general expression for the Hessian including the second term in (14).
One of the key advantages in formulating the objective function as presented in eqn. (7) is the fact that g depends directly on the material properties α, through the internal forces fint (6a). This explicit dependency permits analysis of the uniqueness of the identified material properties — a key feature that is, in general, not shared by other methods based on the minimization of the difference between experimental and computed displacements.
2.2. Restriction to a single material point
In many instances, experiments are carried out on tissue samples to characterize the material response in a controlled setting and under simple loading conditions, e.g., uniaxial and biaxial stretch experiments. The objective function and the algorithm presented in Section 2.1 simplify and carry over to the material point level. In this case, given the experimental stresses and deformation, the material properties α are computed by minimizing the objective function
| (16) |
wherein the least-square function g̃k at each experimental stress state Pk is
| (17) |
where is the experimental Piola-Kirchhoff stress tensor and is the internal Piola-Kirchhoff stress tensor (1d) computed based on the experimental deformation.
By selecting W (α, C(u)) to be linear in the material properties α, it follows that g̃ is quadratic with respect to α. Following the same argument presented in Section 2.1, the minimum of g̃ with respect to α exists and is unique as long as Hg̃ is positive definite. As before, the Newton-Raphson method is the method of choice given its simplicity, fast implementation, and convergence behavior, and the availability of Hg̃, which is already required for checking its rank and condition number. To apply the Newton-Raphson method, both ∇g̃ and Hg̃ at the material point level are needed and their components can be computed based on
| (18a) |
| (18b) |
3. Formulation of Material Laws
According with P2 presented in Section 2.1, the material energy density W (α, C(u)) should be both polyconvex and linear in α, i.e.,
| (19) |
where α = [α1, α2, … αN]T with αi > 0 ∀ i ∈ {1, 2, … N}; Φi(C(u)) are polyconvex functions of the deformation invariants, and N is the number of energy components included to describe the material response. Moreover, we want to construct W (α, C(u)) so that the experimentally observed material is well captured and each term Φi(C(u)) represents different isotropic and anisotropic contributions to the material response. The latter requirement will allow direct association of changes in the linear material properties αi to changes in the tissue structure. For example, a change in the isotropic material response may be associated with diffuse fibrosis while a change in the anisotropic material response may suggest fiber degeneration.
3.1. Candidate polyconvex material energy laws
In the context of hyperelastic materials, polyconvexity of the material energy density in the sense of Ball [23], together with coercivity, is the essential condition to guarantee a priori the existence of minimizers of variational problems associated with the equilibrium of internal and external forces, i.e., Rint = Rext. Polyconvexity requires convexity of the material energy density with respect to a 19-dimensional space spanned by the deformation gradient F, its cofactor cof(F) = (det(F))F−T and its determinant det(F). Moreover, polyconvexity directly guarantees material stability in the sense of Legendre-Hadamard ellipticity ensuring that only real wave speeds occur in the physical body (positive definite acoustic tensors), see Schröder et al. [25]. This aspect is strongly linked with the reliability of numerical calculations in the sense of mesh-independent solutions, see e.g. [34]. The first anisotropic polyconvex energy densities were derived in Schröder and Neff [26]. In addition, some earlier proposed anisotropic functions were also found to be polyconvex, such as the well-known material energy density for arterial tissues presented in Holzapfel et al. [35]. Since then, polyconvex energy densities have been applied to various problems, e.g., patient-specific simulations of atherosclerotic arteries in [36], and textile membranes in [37]. A principle for the construction of polyconvex energy functions that a priori fulfill the condition of a stress-free reference configuration and, based thereon, a variety of functions for soft biological tissues are given in [24]. Here we consider a subset of these functions as bases for our material energy densities (Table I). These bases are formulated in terms of the invariants of C and the structural tensor A ⊗ A:
Table I.
Examples of polyconvex functions to be used in constructing W. All the terms reported here ensure a stress-free reference configuration. The fourth function adapts the idea presented in Gasser et al. [39]; the symbol 〈·〉 represents the Macaulay brackets 〈·〉=0.5((·) + |(·)|).
| Response type | Φi(C(u)) | Notes | |
|---|---|---|---|
| Isotropic |
|
a ≥ 1, b ≥ 1 | |
|
|
a ≥ 1, b ≥ 1 | ||
| Anisotropic |
|
a ≥ 1, b ≥ 1 | |
|
|
a ≥ 1, b ∈ [0, 1] | ||
| 〈(I1I4 – I5)b – 2b〉a | a ≥ 1, b ≥ 1 |
| (20a) |
| (20b) |
A is a unit vector identifying the preferred direction of material anisotropy, e.g., the fiber direction. Our choice of candidate polyconvex functions Φi includes isotropic and anisotropic terms to model both responses in biological tissues, e.g., to model the matrix (isotropic) and fiber (anisotropic) response of passive myocardium. Moreover, we choose the terms Φi so that their expression is a power law and they remain polyconvex for different values of the exponent ‘a’ under the conditions reported in the third column of Table I. The importance of this aspect is highlighted in Sections 3.2 and 3.3 describing our strategy to identify viable candidate material energy laws.
We model the almost incompressible response typical of biological materials by including the term
| (21) |
in W, where b ≥ a ≥ 1 and β is the penalty parameter; see Hartmann and Neff [38] for a detailed analysis of the advantages of this function.
3.2. Strategy to identify viable material laws
The material energy law to be used with our approach can be selected from the literature provided it is linear in α. Alternatively, we propose in this section a new strategy to formulate W based on available experimental data. In either case, only after W is chosen, the linear material properties α can be identified uniquely.
In general, we want to construct a material energy law to describe a set of available experimental data relating strains and stresses, e.g., the strain-stress relation recorded during a biaxial stretch test on a tissue sample. We call this data set 𝒟 and each element describing a strain-stress state 𝒟k, i.e., 𝒟k = (Fk, Pk), k = 1, 2, … M. We denote with M the size of the set 𝒟.
In our strategy, we aim to select the terms Φi to be included in W, to compute their exponents (i.e., the material non-linearity), and finally to identify the linear material properties α. We proceed as described in the following steps and summarized in Algorithm 1:
S1. Choose a candidate W. Construct a candidate material energy density of the form (eqn. (19)) using a specific set of functions Φi of the form listed in Table I. This includes the initialization of internal parameters
S2. Compute internal parameters γi in Φi. Using the procedure shown in Section 2.2, identify a set of material properties αik for each strain-stress state 𝒟k independently by
| (22) |
where we arrange
We denote with αi the vector of the material properties αik computed for different k and fixed i, i.e.,
Furthermore, for each Fk ∈ 𝒟k, we evaluate the functions Φik and, similar to the vector αi, we construct the vector
Lastly, for every term i, we associate every component of the vector αi to the corresponding component of the vector Φi and compute the pairs
These pairs describe how the material properties αi associated with each function Φi vary for different deformation states Fk. If the considered energy density was able to perfectly capture the material behavior, αi would be constant over Φi, and there would be no need to adjust αi for a changing deformation state. In general this is not the case and the nonlinearity of the functions Φi needs to be adapted. This can be achieved by modifying the internal parameters γi until αi becomes as constant as possible over Φi. For this purpose, we compute γ by
| (23) |
where γ is defined as the collection of all sets γi, i.e,
The objective function h is defined as
| (24) |
For each evaluation of the function h, a series of internal optimization problems has to be solved according to (22) in order to obtain αk.
The objective function h is minimized once the material properties αi are as constant as possible, i.e., as close as possible to their average ᾱi, over the range {i, …, M} of deformation states considered. Indeed, the aim of solving (23) is to identify the nonlinearities γ so that the material law represents as well as possible all the experimental stress/strain states at once, without changing material properties αi per each state. By changing γ, the formulation of the material law is modified until αi is as close as possible to ᾱi for every term {i, …, N} in the material law. Therefore, γ appears implicitly in (23) through the formulation of the material law used to identify αi.
Since h is in general not a convex function, we solve it using the algorithm presented in [40], which is derivative-free and based on function evaluations only. We use the implementation provided in MATLAB [41] through the function fminsearch. We chose this algorithm because it performed well in all the cases studied (e.g., see the examples presented in Section 3.3 and Figure 5) and for its simplicity and easy accessibility. However, other derivative-free methods may be used as well and specific problems may require different algorithms.
We remark that the solution to problem (23) is generally not unique. However, once a final form of W has been chosen based on the identified γ, the uniqueness of α is still guaranteed as shown in Section 2.2.
S3. Identify material properties α. Using the values γi identified previously and all the experimental data Dk simultaneously for all k, we identify unique material properties α through the procedure presented in Section 2.2.
|
| |
| Algorithm 1 Identification of internal parameters and material properties | |
|
| |
| Choose candidate | ▷ Initialization |
| Initialize γi = [ai, bi]T | |
| while h (γ, α) is not minimized do | ▷ Identify internal parameters γ |
| ∀𝒟k compute αk = argminα g̃k (α) | |
| Evaluate | |
| with | |
| Minimize h (γ, α) using gradient free algorithm | |
| end while | |
| Compute α = argminα g̃ (α) | ▷ Identify material properties α |
|
| |
3.2.1. Example using synthetic data
In order to illustrate the formulation of the energy function W, which is a central part of our approach, we first use pseudo-experimental data generated from a known material law. Specifically, here we choose the energy basis functions of the candidate W to coincide with the ones used to generate the pseudo-experimental data. Subsequently, in Section 3.3 we consider real experimental data, where we do not have a priori knowledge of the terms Φi to be included in W. As an example, we consider the energy law
| (25) |
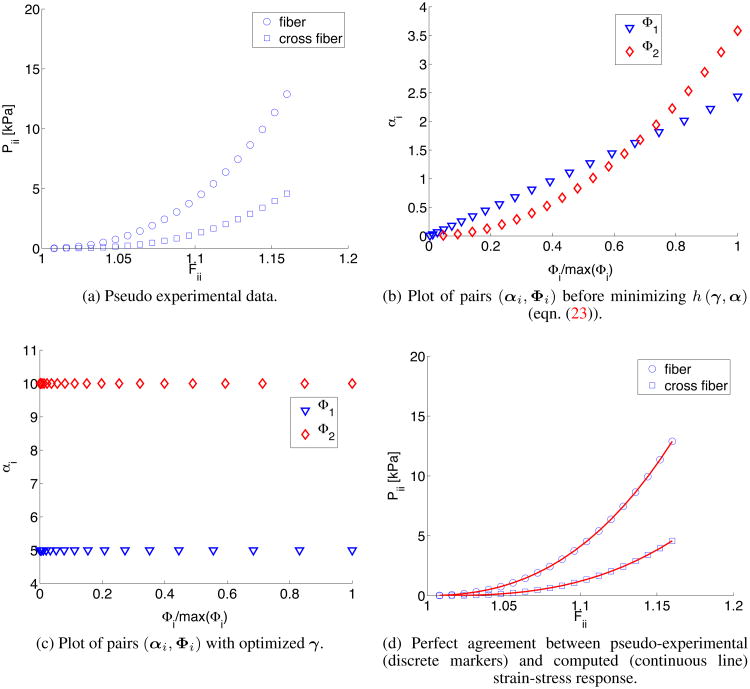
which is a particular form of eqn. (19) with N = 2 including one isotropic and one anisotropic term of the type listed in Table I, and b1 = b2 = 1. Furthermore, we chose α1 = 5.0 kPa, α2 = 10.0 kPa, a1 = 2.0, and a2 = 3.0. The generality of the example presented here does not depend on the chosen values and any other combination of α1, α2, a1, a2 is equally suitable. Using the material energy law (25), we proceed to generate a set of pseudo-experimental data 𝒟 of size M = 20 resulting from an equibiaxial stretch loading configuration (Figure 2a). Next, we apply the procedure described in steps S1 through S3 above.
Figure 2.
The procedure to compute the internal parameters γ that define the material non-linearity is exemplified with synthetic experimental data in steps a-d.
In Step S1, we select a candidate energy function of the same form presented in (25), but with different α and γ, i.e.,
| (26) |
where the initial guess specifies a1 = a2 = 1 and we initialize α1 = α2 = 1.
In Step S2, for every k = 1 to 20, we identify α1k and α2k and compute
The pairs (αi, Φi) for i = 1, 2 are not constant (Figure 2b) since Φi in (26) are not the same as the terms in (25). We solve problem (23) and recover the correct values for γ, i.e., a1 = 2, a2 = 3. Note that αi are now constant with respect to Φi (Figure 2c) and equal to the values used in (25).
In Step S3, using the values a1 = 2, a2 = 3 previously computed and the full set of experimental data 𝒟 simultaneously, we compute the material properties α1 = 5 and α2 = 10 (Figure 2d).
In this specific case, the correct material properties were already identified at the end of the previous step since (αi, Φi) were exactly constant and equal to α1, α2. However, this is only the case if the candidate energy function can represent exactly the experimental data as in the current example where (25) and (26) contain the same terms. If this is not the case, as with real experimental data, the pairs (αi, Φi) will not be constant at the end of step S2 and the final material properties α will be identified in step S3.
We conclude by emphasizing that the strategy presented is applicable to any material energy law of the general form shown in (19), even if here we restrict ourselves to polyconvex W with terms of the form listed in Table I.
3.3. Identification of a viable material law based on experimental data
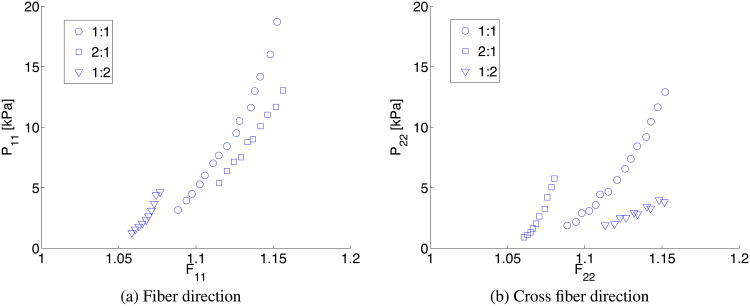
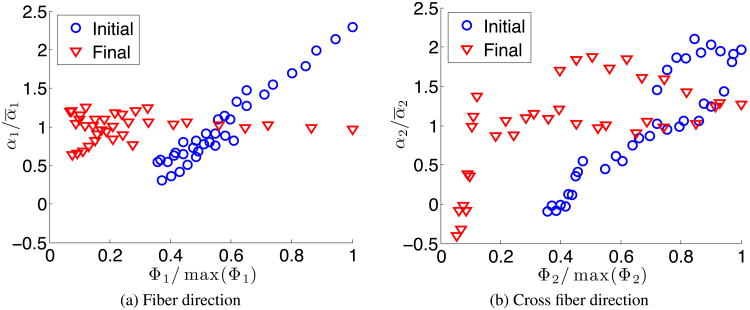
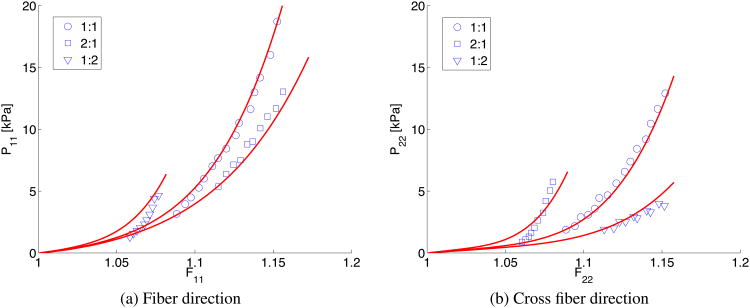
We demonstrate the applicability of the strategy described in Section 3.2 by constructing a material energy law that describes the passive constitutive response of myocardial tissue. For this purpose, we use the experimental data reported in [42], which was obtained in biaxial stretch experiments (Figure 3). These experiments are carried out for three different ratios of fiber stretch λ1 to cross fiber stretch λ2, i.e., 1:1 (equibiaxial, λ1 = λ2), 2:1 (λ1 = 2λ2), and 1:2 (λ2 = 2λ1). The form of the energy density W is unknown a priori in this example — i.e., we do not know which terms Φi will best represent the measured data. However, given the response shown in Figure 3, we expect that both isotropic and anisotropic components should be present. For simplicity, we limit our choice to material laws composed of one isotropic and one anisotropic term Φi taken from Table I. We consider the resulting six different forms of energy densities when applying the strategy described in Section 3.2 and collect the results in Table II. In particular, for each candidate form of the energy density we report the value of h (γ, α) (eqn. (24)), the optimized exponents {a1, a2}, the minimized objective function g̃(α) (eqn. (16)), and the identified material properties {α1, α2}. In this example, we only optimized the exponents ai and we fixed the values bi. Among all combinations of isotropic and anisotropic terms we choose the one that leads to the minimum value for h (γ, α), i.e., the pair that best describes the material behavior at different states of deformation (see Section 3.2 and the discussion before eqn. (23)). According to this criterion, we select and Φ2 = 〈I4 – 1〉a2 and identify a1 = 2.60 and a2 = 2.82. Similarly to Figures 2b and 2c, Figure 4 illustrates how the variability of α is reduced by minimizing h (γ, α), especially for intermediate to high Φi/max(Φi).
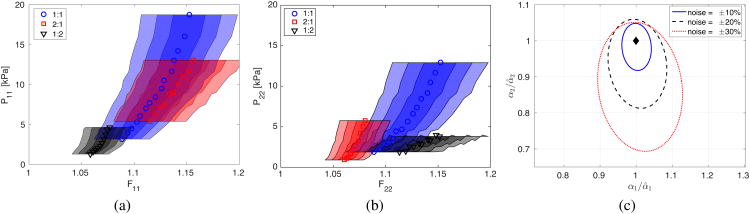
Figure 3.
Experimental data reported in [42] describing the anisotropic response of the passive myocardium. The strain-stress data are obtained in biaxial stretch tests for different stretch ratios in the fiber and cross fiber directions, i.e, 1:1, 2:1, and 1:2, respectively. The strain-stress data are shown in the fiber (left) and cross fiber (right) direction using the deformation gradient tensor F and the first Piola Kirchhoff tensor P.
Table II.
For each candidate energy density we report: 1) the minimized values of h (γ, α) and corresponding optimized exponents {a1, a2}; and 2) the minimized values of g̃(α) and corresponding identified material properties {α1, α2}.
| Φ1 | Φ2 | h (γ, α) | {a1, a2} | g̃(α) | {α1, α2} | |
|---|---|---|---|---|---|---|
|
|
〈I4 – 1〉a2 | 4.50 | {2.60, 2.82} | 31.69 | {30.48, 7.25} | |
|
|
4.77 | {2.59, 2.84} | 31.17 | {28.25, 0.66} | ||
| 〈(I1I4 – I5) – 2〉a2 | 9.68 | {1.58, 1.89} | 280.40 | {5.82, 2.66} | ||
|
|
〈I4 – 1〉a2 | 5.26 | {2.30, 2.26} | 58.14 | {1.35, 4.36} | |
|
|
5.53 | {2.28, 2.22} | 61.12 | {1.28, 0.63} | ||
| 〈(I1I4 – I5) – 2〉a2 | 9.76 | {1.39, 1.56} | 353.64 | {1.04, 1.74} |
Figure 4.
Normalized αi/ᾱ versus Φi/max(Φi) for the isotropic (a) and anisotropic (b) terms in the material energy law. We report the normalized pairs before optimizing the exponent ai (blue circles) and after solving eqn. (23) to calculate the optimal ai values (red triangles).
Using the strain energy function
| (27) |
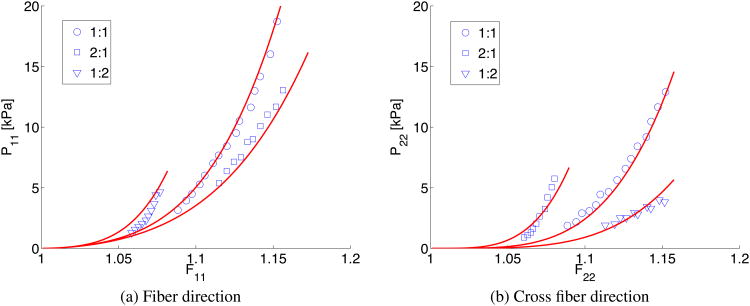
and all the experimental data simultaneously we compute the material properties α1 = 30.48 kPa and α2 = 7.25 kPa. The identified energy function accurately describes the strain-stress data obtained by Yin et al. during biaxial stretch experiments (Figure 5). It is emphasized that the procedure presented herein enables an optimized formulation of strain energy densities in terms of computing the internal parameters γ and a unique identification of the material properties α.
Figure 5.
Experimental data [42] (markers) versus modeled response (solid lines) obtained using the material law reported in eqn. (27) and the material properties and parameters reported in Table II. Three different ratios between fiber stretch λ1 and cross fiber stretch λ2 are considered, i.e., 1:1 (equibiaxial, λ1 = λ2 - circular markers ○), 2:1 (λ1 = 2λ2 - square markers □), and 1:2 (λ2 = 2λ1 - triangular markers ▽). Note the good agreement obtained for all three stretch ratios by using a single set of material properties.
3.4. Effect of experimental noise
In order to address the effect of experimental noise on the identified material properties, we perform two preliminary tests. First, we subsample the data from [42] without replacement to understand the impact of the number of measurement points on the identified material properties. Second, we add noise to the experimental data from [42] to better understand the impact of measurement uncertainty on the identified material properties. The experimental data reported in [42] is also used in the example presented in Section 3.3.
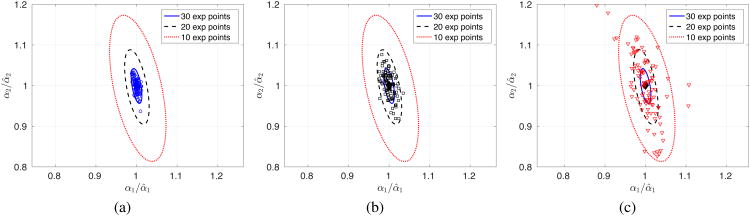
In the first test we identify the material properties using only a subset of the thirty-five available experimental data points. In subsequent analyses we randomly choose thirty, twenty, and ten experimental strain/stress states to identify the material properties α1 and α2. The exponents a1 and a2 in the material laws are kept constant and equal to the values computed in Section 3.3 using the full set of experimental data, i.e., we only identify the linear material properties, not the form of the material energy law and the nonlinear internal parameters [a1, a2]. For each subsampling level (thirty, twenty, and ten) we repeat the analyses one thousand times by randomly choosing a set of material points each time. Based on the identified material properties we plot the corresponding 95% confidence ellipses (Fig. 6) for the material properties normalized with respect to the values computed using the full set of experimental data. We observe that even considering ≈ 30% of the total experimental data, the 95% confidence ellipse is within ±7% and ±18% error‡ for the isotropic (α1) and fiber direction (α2) material properties, respectively. This result suggests that the identified material properties are relatively robust with respect to the number of available experimental data points. We also note the absence of bias (i.e., the ellipses are centered at [α1/α̂1 = 1, α2/α̂2 = 1]) and slight covariance of α1 and α2 (i.e., the axes of the ellipses are almost aligned with the normalized α1/α̂1 and α2/α̂2 axes).
Figure 6.
95% confidence ellipses obtained by subsampling (without replacement) the available experimental data. The three confidence ellipses in each subfigure correspond to subsets of experimental data obtained with 30 (red dotted line), 20 (black dashed line), and 10 (blue solid line) experimental points. Together with the confidence ellipses, we plot a subset of the identified material properties obtained considering 30 (panel a - blue circles), 20 (panel b, black squares), and 10 (panel c, red triangles) experimental points. All plots are normalized with respect to the material properties α̂1, α̂2 identified using all 35 experimental points.
In a second test we add noise to the components of the deformation gradient tensor F in the fiber and cross fiber directions. Specifically, we choose:
where i = 1 (fiber direction) and i = 2 (cross fiber direction), rand(0, σ) is a random number chosen from a Gaussian distribution with mean μ = 0 and standard deviation σ. We select σ so that the 97.5% percentile is at ±0.1, ±0.2, and ±0.3, i.e., the 97.5% percentile corresponds to ±10%, ±20%, and ±30% error in the fiber and cross-fiber stretches (Figs. 7a and 7b). For each standard deviation σ corresponding to a different level of experimental noise, we repeat the material properties identification one thousand times and plot the resulting confidence ellipses (Fig. 7c). For an experimental noise with a 97.5% percentile equal to 30% stretch error, the 95% confidence ellipses are within [+13%, −11%] and [+5%, −31%] error for material properties α1 and α2, respectively. As in the subsampling test, we observe a slight covariance and, more importantly, that the anisotropic material property α2 is more sensitive to experimental noise than the isotropic material property α1. In this case, there is also a clear bias toward lower values of α2.
Figure 7.
Gaussian distributed noise added to the recorded stretch experimental data (discrete markers) in the fiber (a) and cross fiber (b) directions. Three different ratios between fiber stretch λ1 and cross fiber stretch λ2 are considered, i.e., 1:1 (λ1 = λ2, circular markers ○), 2:1 (λ1 = 2λ2, square markers □), and 1:2 (λ2 = 2λ1, triangular markers ▽). On each side of the experimentally measured curves in panels (a) and (b), the 97.5% percentile limit corresponding to 10%, 20%, and 30% is reported (shaded regions on each side of the experimental markers). The confidence ellipses corresponding to the three levels of noise (±10%, ±20%, and ±30%) are reported in panel (c). The confidence ellipses are normalized with respect to the material properties α̂1 and α̂2 identified without noise.
Both the tests suggest that the method presented herein lead to identified material properties robust with respect to the amount of experimental data and noise in biaxial stretch experiments. Therefore, under this framework not only the objective function has a unique minimum, but also the location of its minimum appears to be stable with respect to the amount of experimental data and noise at the material point level. We remark that the tests presented here are only preliminary and much more in depth studies are warranted. Moreover, the noise considered here was added directly to the deformation gradient F. In full 3D applications the noise affects directly the displacement field and may be significantly amplified by the differentiation required to compute F.
3.5. Analysis of material energy densities
As discussed in Section 2, the Hessian Hg̃ of the objective function (16) allows us to determine if the available experimental data are sufficient to identify the material properties in the candidate energy density. In particular, the robustness of the identified material properties depends on the condition number κ(Hg̃), see eqns. (10) and (11).
3.5.1. Analysis of material energy densities linear in α
For all the material laws formulated as a linear combination of energy basis functions (19), Hg̃ is independent of the material properties and therefore its condition number (and its positive definiteness) will depend only on the deformation state. The fact that Hg̃ is independent of the material properties guarantees that the minimization of g̃(α) is independent of the initial guess for the material properties.
In practice, it is often possible to express Hg̃ analytically in terms of the appropriate invariants of C. This simplifies greatly the analysis of κ(Hg̃) for any type of deformation. For example, for the material energy density reported in (27) Hg̃ can be expressed as
| (28) |
We observe that Hg̃ depends exclusively on the three isotropic invariants (I1, I2, I3) and the anisotropic invariant I4. Such closed-form expressions for the Hessian are useful for assessing which data are best suited (or sufficient if the experiments have already been performed) to identify the material properties.
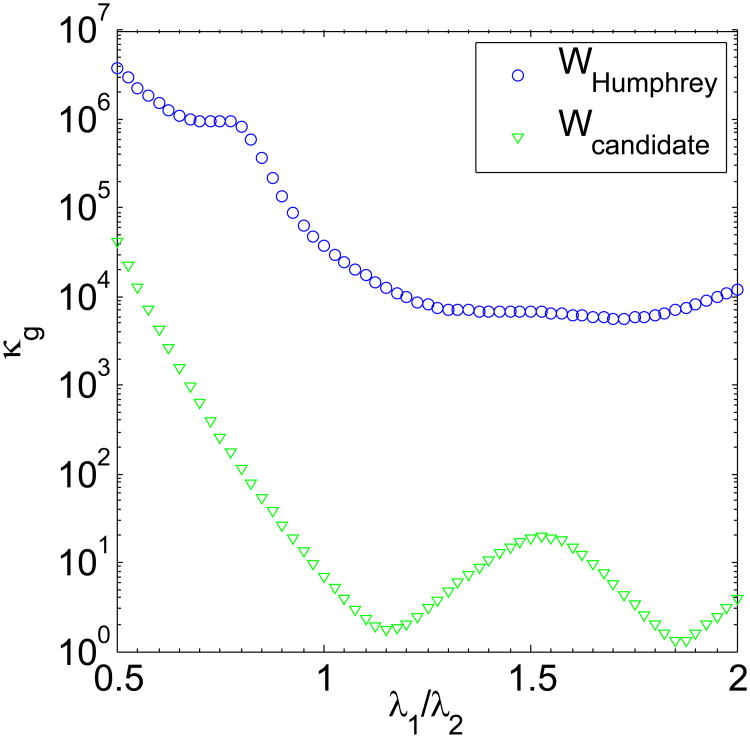
For instance we compute κ(Hg̃) according to eqn. (11) for different simulated biaxial stretch simulated experiments. In this example we vary the ratio of the stretch along the fiber direction (λ1) and cross fiber direction (λ2). Each data set is composed of ten stretch/stress points and the maximum stretch in the fiber direction is equal to 1.5. We observe that, in this example, experiments with λ1/λ2 ≳ 1 are associated with lower κ(Hg̃) and therefore lead to more robustly identified α (Figure 8).
Figure 8.
Condition number κ(Hg̃) as a function of stretch ratio λ1/λ2 during biaxial stretch experiments for the material energy density reported in eqn. (27) and for the Humphrey et al. [43] material energy density (see also Section 3.5.2).
Several other material energy laws have been proposed in the literature to describe the material behavior of passive myocardium. Among them, the material law proposed by Humphrey et al. [43], see (29), respects the constraint set forth in eqn. (19) and therefore it is an example of an existing material energy law for which the same analysis reported in the foregoing can be adopted.
| (29) |
As before, the Hessian Hg̃ associated with (29) is independent of the material properties and can be computed as a function only of the deformation invariants (see Appendix 6.1). Hg̃ can then be used to determine the condition number κ(Hg̃) along different deformation paths and evaluate the robustness of the identified material properties (see for instance Figure 8). Note that, in this example, the condition number obtained using the Humphrey material model is up to three orders of magnitude larger than for the energy density reported in eqn. (27).
3.5.2. Analysis of material energy densities including terms nonlinear in α
As discussed in Section 2, it is not possible to guarantee uniqueness of α if eqn. (19) is not satisfied. As an example, we consider the material laws for passive myocardium proposed by Guccione et al. [44] and Holzapfel et al. [45]
| (30a) |
| (30b) |
In (30a) and (30b), , f, s, and n represent the fiber, cross fiber, and sheet-normal directions, respectively. The associated direction vectors are given as f and s, and accordingly we have I4f = f · Cf, I4s = s · Cs, and I8fs = f · Cs.
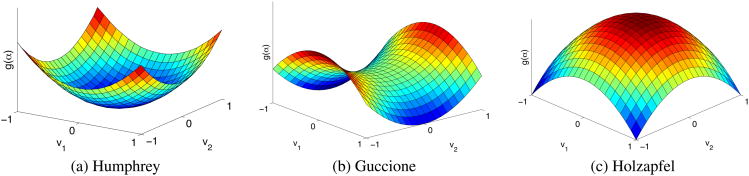
We expand the objective function g̃ (16) obtained using the energy densities (30a) and (30b) in a Taylor series in the proximity of a set of material properties αinit used to initialize the identification algorithm. Note that since (19) is not satisfied, Hg̃ depends on α. A detailed description of the calculation leading to these Taylor expansions is given in Appendix 6.2. We notice that the objective function g̃ is not convex for these material laws, exposing the existence of multiple minima and the lack of uniqueness in the identified material properties (Figure 9).
Figure 9.
Quadratic term of the Taylor expansion of g̃ at αinit for (a) Humphrey et al. [43], (b) Guccione et al. [44] and (c) Holzapfel et al. [45] material models. υ1 and υ2 are the eigenvectors associated with the smallest eigenvalues of Hg̃ (See Appendix 6.2 for more details). Note that only the Humphrey et al. energy density leads to a convex objective function since WHumphrey is linear in the material properties (however WHumphrey is not polyconvex.)
The material laws of Guccione et al. [44] and Holzapfel et al. [45] are based on knowledge of tissue physics and structure at the microscopic level, which provides a solid foundation for predictive modeling of the passive myocardium response. This will be the case provided that reliable estimates for the model parameters can be obtained by validation with experiments. If model predictions are insensitive to parameter variations — as it appears to be the case for these two models — then parameter uniqueness is not of much concern. However, when the focus is on use of a material model as a diagnostic tool — the chief concern of the present work — then it is crucial that a modeling scheme associates each set of experimental data to a unique set of material properties. For this reason it is not appropriate to apply our method using models nonlinear in α spaces (Figure 9).
Nevertheless, our method can still be of value with such nonlinear models. First, evaluation of the Hessian of our objective function and its eigenvalues can serve as a stability analysis to quantify how degenerate the material properties are. Furthermore, we can apply our approach in its entirety with the Guccione et al. [44] and Holzapfel et al. [45] material models if we fix the parameters appearing nonlinearly in eqns. (30a) and (30b). In doing so, these material energy laws take the form in eqn. (19), with linear coefficients as the only unknowns. By identifying only the linear material properties, uniqueness of the identified properties is recovered. For example by setting a priori α2, α3, and α4 in (30a) and identifying only α1, then the material law proposed by Guccione et al. leads to a unique solution. Equivalently, by fixing α2, α4, α6, and α8 in (30b), the remaining properties may be identified uniquely in the material law proposed by Holzapfel et al. The material properties that appear nonlinearly may be set a priori — if preliminary knowledge about their values is available — or possibly computed in a way similar to the internal parameters γ.
4. Application to Left Ventricular Model
We show the applicability of our EMS framework in a setting consistent with a real case scenario and apply it to measure the myocardium material properties during passive filling. This case is particularly relevant because the full field measures needed to apply our method can be acquired for patients with HFpEF. A similar application has recently been investigated by Hadjicharalambous et al. [46], who also studied the pressing problem of unique identifiability of material properties for passive myocardium. Cardiac geometry, fiber orientations, and full field displacement data can be acquired through MRI and DTMRI [47] while the intraventricular pressure is measured through catheterization. We remark that in a real case scenario there will be several additional challenges not considered here at this stage. Among them, the presence of experimental noise and error that may compromise the identification of material properties. The tests we present are intended to verify and validate the derivation of our method and to show its potential applicability with real clinical data.
In order to test our approach we: 1) Generate a finite element mesh based on MRI acquired geometry (Section 4.1); 2) Include microstructural fiber information in our finite element mesh (Section 4.2); 3) Generate synthetic experimental data consisting of intraventricular pressure and corresponding displacement field, obtained by prescribing reference tissue properties and solving the boundary value problem (Section 4.3); 4) Identify the myocardial material properties using the synthetic data as input to our objective function (Section 4.4). We repeat these tests using models with uniform or regionally-defined material properties and using data from one or multiple filling steps (Section 4.4). In all the examples presented, we asume that intraventricular pressure is the main force acting during passive filling. Although this is a realistic assumption, we note that the left ventricle is subjected to other forces due, for instance, to the contact with the pericardium, the connection with the atria, and the loading exerted by the right ventricle.
4.1. Left ventricular mesh generation
We generate the left ventricular (LV) geometry and finite element mesh based on the biventricular model of a white New Zealand rabbit. During the acquisition of MRI and DTMRI data, we have adhered to the guidelines set forth by the National Institutes of Health Guide for the Care and Use of Laboratory Animals and the Institutional Animal Care and Use Committee at the University of California, Los Angeles (Animal protocol #2008-161-12 was approved by the UCLA Chancellor's Animal Research Committee.) The details of the imaging protocol and finite element mesh generation are provided in [48]. For this study, we extracted the left ventricular geometry from the biventricular model (Figure 10) by excising the right ventricle using Hypermesh (Altair Hyperworks). We also removed the papillary muscles to create a smooth inner cavity and preserve element quality while reducing the element count (the original biventricular finite element mesh contains more than 800k hexahedral elements.) The coarsened mesh generated herein contains 19834 ten-noded (quadratic) tetrahedral elements and 30908 nodes. The corresponding average element edge length is approximately 1.25 mm. We note that a more advanced mixed element formulation would be required to enforce myocardium incompressibility without locking. However, in the following examples we do not reach this limit and the current element formulation is deemed appropriate. Although employing more advanced finite elements for incompressible materials may be required in real clinical applications, the method presented does not depend on enforcing exact or quasi incompressibility.
Figure 10. Left ventricular mesh generation.
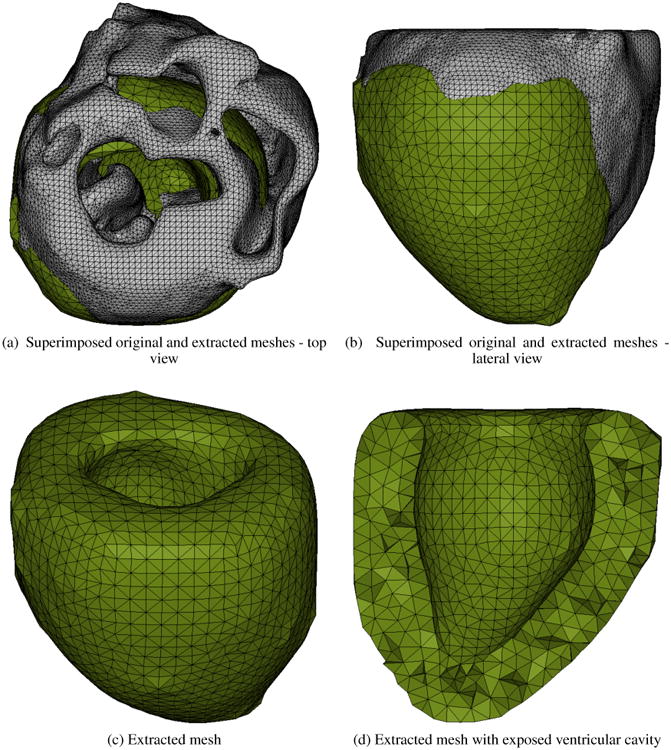
In order to assess that the mesh processing steps preserved the overall LV structure and geometry, we computed the ratio between the volumes of the LV cavity and LV myocardium and required for it to be approximately preserved. The cavity to myocardium ratio is equal to 0.36 in the fine original mesh while it is equal to 0.35 in the coarsened mesh used in the following. Finally, in order to test our method's ability to identify different material properties in different regions, we construct two additional models. In the first non-uniform model, we subdivide the LV domain using the seventeen-segment American Heart Association model [49] (Figure 11a). In the second nonuniform model, we simulate the presence of an infarcted area with stiffer isotropic and fiber directed material response (Figure 11b).
Figure 11.
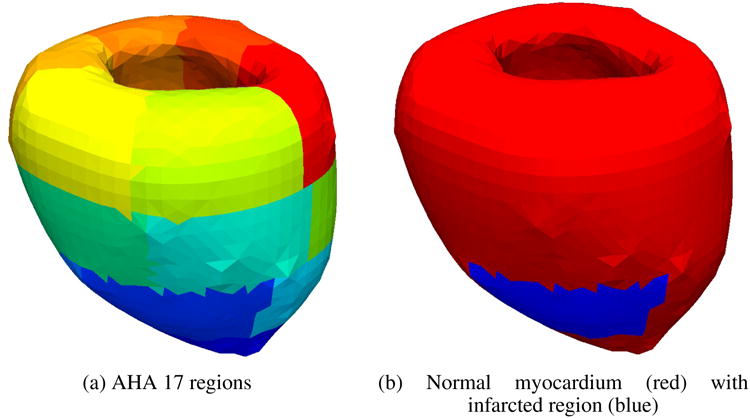
Domain segmentation into the seventeen AHA segments (a) and normal versus infracted myocardium (b).
4.2. Myocardial microstructure and fiber interpolation
Essential in constructing a realistic LV model is the inclusion of the myocardial microstructure, i.e., the fiber orientation throughout the LV. Fiber orientation is measured using diffusion tensor magnetic resonance imaging (DT-MRI). DT-MRI data are acquired on a structured grid and subsequently interpolated to the finite element mesh. In this study we consider one fiber orientation per element and therefore the fiber orientation data are interpolated from the DT-MRI grid to the barycenter of each tetrahedral elements using the nearest neighbor interpolation method [50]. Fiber orientations for sample slices through the LV are shown in Figure 12.
Figure 12.
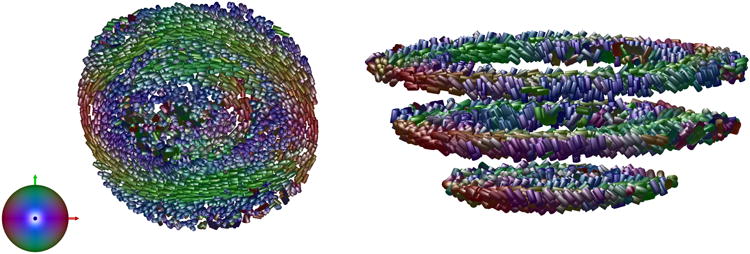
Fiber orientation throughout the LV finite element mesh on representative slices. In each element a bar is plotted in the direction of the fibers. The color of each bar is associated with its direction: blue in the longitudinal direction, and green and red in the two orthogonal transverse directions. Notice the clear midwall circumferential myocyte organization (left - top view) and the changes in myocyte orientation from circumferential to more longitudinal moving from the midwall to the epicardium and endocardium (right - lateral view).
4.3. Generation of displacement input data
We compute the full displacement field, which in clinical applications would be acquired through MRI, by solving the equilibrium problem. We first assign different reference material properties to each region of the myocardium. Subsequently, we apply a single or multiple intraventricular pressure increments Δp = 0.05 kPa and compute the corresponding displacement field. We reach a maximum filling pressure equal to 1.5 kPa, which is representative of a healthy human diastolic filling pressure. In solving the forward equilibrium problem, we assign zero displacement boundary conditions at the nodes at the base of the heart. Given the computed displacement field and the corresponding pressure load, we aim to identify and recover the input reference material properties in Section 4.4.
In all the following examples we choose to model the myocardium according to the material law described in eqn. (27), together with the function Wvol specified in (21), with parameters β = 100.0 kPa, b = 2.0, and a = 1.0. However, without any modification, (27) leads to a singular stiffness matrix at F = I, since then the coefficients of the elasticity tensor ∂FP become zero. In turn, the Newton-Raphson method could not be used to solve the FEM boundary value problem. If displacement data were available through MRI and solving a forward equilibrium problem was not necessary, such a material law would still be viable and may be used with our approach. However, in order to solve the forward problem using the Newton-Raphson method, we regularize the numerical calculations by adding a linear isotropic term to the energy density:
| (31) |
such that the complete energy reads
| (32) |
where θ = 0.025. The parameter θ is intentionally chosen small because it has only a regularization role. Employing the same procedure and experimental data described in Section 3.3, we recomputed the exponents {a1, a2} and the material properties {α1, α2} as reported in Table III. We observe that the material properties associated with the regularized material energy density differ only slightly from the properties obtained using the original material law (27). The new fit of the experimental data is reported in Figure 13 and again shows a good agreement of the model with the experiments.
Table III.
Material properties and exponents computed to fit the biaxial experimental data of Yin et al. [42] using eqn. (32) with θ = 0 (original material law) or θ = 0.025 (regularized material law.)
| Material law | h (γ, α) | {a1, a2} | g(α) | {α1, α2} |
|---|---|---|---|---|
| θ = 0 | 4.50 | {2.60, 2.82} | 31.69 | {30.48, 7.25} |
| θ = 0.025 | 4.62 | {2.87, 2.82} | 34.86 | {35.19, 7.06} |
Figure 13.
Experimental data [42] (markers) versus modeled response (continuous lines) using the regularized material law described by eqn. (32).
4.4. Identification of myocardial properties during passive filling
In the following examples we compute the displacement field as described in Section 4.3. Accordingly to the computed displacement field, we move the finite elements nodes and calculate the corresponding internal forces. Finally, we compute the external forces corresponding to the pressure load for which the input displacement field was obtained using the reference material properties. These are the necessary data to build and minimize the objective function g (Section 2.1). In all the following examples we assume that the form of the material law has been chosen, either based on tissue sample tests or based on literature data. Therefore, in this section, we identify only the linear material properties α and not the material law's terms Φi and their non-linearities γi as previously done in Sections 3.3 and 4.3. Fixing a material law is necessary to compare directly the linear material properties α between healthy subjects and patients and to use them as diagnostic markers.
In a first example, we assume that the myocardium is homogeneous and therefore only two material properties (α = [α1, α2]) are identified. We compute the input displacement field due to a single filling step, i.e., due to a pressure load Δp = 0.05 kPa, and corresponding to α1 = 35.19 kPa and α2 = 7.06 kPa. Then, by applying the computed displacement field as input data, we re-identify the reference material properties using our EMS approach. Given multiple uniformly distributed random initial guesses for the material properties, our method always identifies the correct material properties, i.e, it recovers the material properties used to generate the input displacement field with an error close to machine precision. In in vivo applications the error between identified and ‘true’ material properties cannot be computed, since ‘true’ material properties cannot be defined. However, achieving an accuracy close to machine precision in the presented tests based on in silico data is an important validation of our method. Accuracy equivalent to the one obtained with a single pressure increment was achieved also when multiple pressure states are considered at once in constructing the objective function g. This represents a more realistic scenario since pressure and displacement data will be clinically available at multiple time points during passive filling. In this case, the expression of the objective function g is simply modified as
| (33) |
where t represents the time points at which data are available. Also in this case, we identify the correct material properties used to generate the input displacement field (Figure 14) independently of the initial guess (see Table IV). In this and the following examples, we use ten time points, each corresponding to a pressure increment Δp = 0.15 kPa starting from p = 0.05 kPa, i.e., the first time point corresponds to an applied pressure equal to 0.05 kPa, the second time point to 0.20 kPa, the third time point to 0.35 kPa, and so on. We observe that the total solution time to identify the material properties is ≈ 17s on a standard single core Intel CPU. In contrast, a classic inverse method based on the iterative minimization of the difference between computed and experimental displacements (see Section 2) will require several solutions of the forward problem, each iteration requiring ≈ 10 hours for the same model and computational resources used herein. Depending on the number of iterations, which could easily reach one hundred, our method can provide a significant speedup. Although this is only an estimate and depends on the alternative method employed, the speedup offered by our approach could be of several orders of magnitude when compared to iterative methods.
Figure 14.
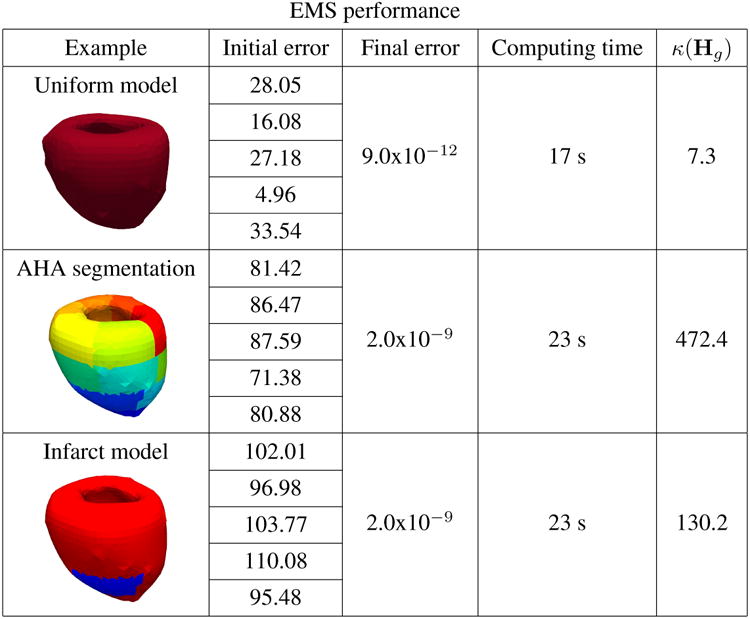
Material properties identification results reported for five representative cases per each model using the uniform model, the model segmented in seventeen AHA regions, and the model containing a stiffer region representing an infarct. In each case we report the L2 norm of the initial (i.e., based on the initial random guess) and final (i.e., after identifying the material properties) error computed by comparing the exact and current material properties in all regions.
Table IV.
Reference material properties and material properties initial values used in five representative test cases with the uniform LV model.
| Property | Reference | Initial guess per test number | ||||
|---|---|---|---|---|---|---|
| Test 1 | Test 2 | Test 3 | Test 4 | Test 5 | ||
| α1 | 35.19 | 7.49 | 19.60 | 8.36 | 31.52 | 2.15 |
| α2 | 7.06 | 2.69 | 3.11 | 2.67 | 3.73 | 1.32 |
Using pressure and displacement data at multiple time points, we proceeded to identify the material properties in an inhomogeneous LV model. We setup the problem using the AHA segmentation in seventeen regions and assign different isotropic and anisotropic material properties to each region (see Table V). Also in this case, our approach was able to identify the different material properties in one iteration and ≈ 23s (see Figure 14).
Table V.
Reference material properties and material properties initial values used in five representative test cases with the LV model segmented according to the seventeen AHA regions. The isotropic α1 and anisotropic α2 material properties are assigned separately in each region.
| Region | Property | Reference | Initial guess per test number | ||||
|---|---|---|---|---|---|---|---|
|
| |||||||
| Test 1 | Test 2 | Test 3 | Test 4 | Test 5 | |||
|
| |||||||
| 1 | α1 | 17.59 | 7.05 | 3.13 | 11.57 | 20.38 | 33.62 |
| α2 | 3.53 | 0.55 | 1.21 | 0.43 | 0.32 | 3.52 | |
|
| |||||||
| 2 | α1 | 19.79 | 9.44 | 12.82 | 12.82 | 13.79 | 2.56 |
| α2 | 3.56 | 2.29 | 3.08 | 2.39 | 0.26 | 2.48 | |
|
| |||||||
| 3 | α1 | 21.99 | 0.49 | 11.88 | 10.83 | 32.57 | 22.57 |
| α2 | 3.64 | 0.16 | 2.38 | 0.63 | 7.05 | 2.72 | |
|
| |||||||
| 4 | α1 | 24.19 | 23.71 | 14.64 | 40.13 | 4.89 | 3.57 |
| α2 | 3.78 | 0.54 | 1.25 | 4.78 | 2.85 | 0.42 | |
|
| |||||||
| 5 | α1 | 26.39 | 21.86 | 37.55 | 37.87 | 50.69 | 41.76 |
| α2 | 3.97 | 1.99 | 0.83 | 2.90 | 5.75 | 5.25 | |
|
| |||||||
| 6 | α1 | 28.59 | 23.49 | 12.83 | 41.12 | 14.77 | 23.29 |
| α2 | 4.22 | 3.59 | 5.06 | 2.24 | 7.44 | 5.69 | |
|
| |||||||
| 7 | α1 | 30.79 | 19.67 | 18.28 | 49.30 | 34.06 | 9.07 |
| α2 | 4.52 | 4.38 | 1.12 | 1.97 | 6.01 | 4.22 | |
|
| |||||||
| 8 | α1 | 32.99 | 10.33 | 1.66 | 47.14 | 46.59 | 19.65 |
| α2 | 4.88 | 2.52 | 0.73 | 5.52 | 0.25 | 7.63 | |
|
| |||||||
| 9 | α1 | 35.19 | 26.13 | 22.46 | 19.30 | 15.72 | 17.79 |
| α2 | 5.29 | 2.27 | 7.53 | 3.16 | 7.29 | 6.77 | |
|
| |||||||
| 10 | α1 | 37.39 | 19.16 | 56.33 | 37.12 | 42.93 | 53.24 |
| α2 | 5.76 | 2.38 | 1.19 | 8.65 | 3.94 | 6.53 | |
|
| |||||||
| 11 | α1 | 39.59 | 30.16 | 38.96 | 25.55 | 35.50 | 18.25 |
| α2 | 6.29 | 1.80 | 11.61 | 2.84 | 4.55 | 10.23 | |
|
| |||||||
| 12 | α1 | 41.79 | 7.43 | 5.77 | 36.26 | 56.70 | 23.44 |
| α2 | 6.87 | 3.12 | 6.65 | 9.88 | 2.27 | 6.44 | |
|
| |||||||
| 13 | α1 | 43.99 | 19.27 | 6.14 | 66.74 | 57.86 | 31.48 |
| α2 | 7.50 | 4.44 | 8.03 | 12.84 | 10.12 | 3.69 | |
|
| |||||||
| 14 | α1 | 46.19 | 19.55 | 73.01 | 89.66 | 76.38 | 22.72 |
| α2 | 8.19 | 1.64 | 10.18 | 15.06 | 4.74 | 15.54 | |
|
| |||||||
| 15 | α1 | 48.39 | 24.89 | 58.80 | 28.77 | 25.67 | 59.61 |
| α2 | 8.94 | 7.32 | 9.13 | 16.02 | 11.51 | 16.93 | |
|
| |||||||
| 16 | α1 | 50.59 | 11.32 | 19.94 | 26.68 | 76.62 | 3.83 |
| α2 | 9.74 | 8.91 | 13.56 | 12.19 | 16.44 | 11.13 | |
|
| |||||||
| 17 | α1 | 52.78 | 51.46 | 72.00 | 101.05 | 72.81 | 47.02 |
| α2 | 10.59 | 7.42 | 11.03 | 12.44 | 2.24 | 2.17 | |
In the last example we consider an LV model containing an infarct characterized by different material properties in an otherwise homogeneous myocardium. As expected, we identify the material properties associated with the pseudo-experimental displacement field generated for this example (Figure 14) independently of the initial guess (see Table VI). Similarly to the previous examples, the total computation time is ≈ 23s.
Table VI.
Reference material properties and material properties initial values used in five representative test cases with the LV model containing a significant stiffer region representing an infarct (region 16). Different random initial values for the material properties are assigned in each AHA region to initialize subsequent tests.
| Region | Property | Reference | Initial guess per test number | ||||
|---|---|---|---|---|---|---|---|
|
| |||||||
| Test 1 | Test 2 | Test 3 | Test 4 | Test 5 | |||
|
| |||||||
| 1 | α1 | 35.19 | 30.27 | 2.50 | 46.87 | 9.26 | 5.63 |
| α2 | 7.06 | 2.40 | 4.43 | 1.99 | 4.48 | 10.07 | |
|
| |||||||
| 2 | α1 | 35.19 | 9.41 | 6.73 | 61.02 | 28.58 | 49.93 |
| α2 | 7.06 | 4.57 | 0.46 | 9.53 | 4.16 | 13.17 | |
|
| |||||||
| 3 | α1 | 35.19 | 6.31 | 12.78 | 34.92 | 32.88 | 60.84 |
| α2 | 7.06 | 1.74 | 6.77 | 1.59 | 12.39 | 0.73 | |
|
| |||||||
| 4 | α1 | 35.19 | 28.11 | 11.47 | 48.93 | 49.37 | 10.80 |
| α2 | 7.06 | 4.45 | 5.78 | 11.47 | 11.11 | 1.89 | |
|
| |||||||
| 5 | α1 | 35.19 | 34.05 | 12.34 | 63.42 | 1.55 | 25.94 |
| α2 | 7.06 | 3.47 | 1.19 | 0.88 | 12.95 | 8.27 | |
|
| |||||||
| 6 | α1 | 35.19 | 23.38 | 23.87 | 17.46 | 48.06 | 69.56 |
| α2 | 7.06 | 0.44 | 5.66 | 14.10 | 9.64 | 8.52 | |
|
| |||||||
| 7 | α1 | 35.19 | 31.70 | 21.60 | 31.28 | 49.96 | 60.33 |
| α2 | 7.06 | 4.02 | 1.08 | 9.290 | 10.81 | 2.15 | |
|
| |||||||
| 8 | α1 | 35.19 | 0.40 | 9.38 | 15.11 | 34.40 | 62.22 |
| α2 | 7.06 | 0.40 | 5.97 | 12.01 | 8.10 | 12.17 | |
|
| |||||||
| 9 | α1 | 35.19 | 23.40 | 33.60 | 47.52 | 63.37 | 41.29 |
| α2 | 7.06 | 4.70 | 1.74 | 12.62 | 7.95 | 7.60 | |
|
| |||||||
| 10 | α1 | 35.19 | 31.10 | 6.37 | 2.05 | 10.24 | 3.97 |
| α2 | 7.06 | 0.80 | 5.93 | 0.32 | 9.86 | 1.59 | |
|
| |||||||
| 11 | α1 | 35.19 | 10.71 | 19.52 | 36.11 | 59.21 | 46.62 |
| α2 | 7.06 | 4.86 | 2.01 | 10.90 | 9.23 | 3.89 | |
|
| |||||||
| 12 | α1 | 35.19 | 12.78 | 9.11 | 52.24 | 57.84 | 39.80 |
| α2 | 7.06 | 3.83 | 3.88 | 4.38 | 5.41 | 3.77 | |
|
| |||||||
| 13 | α1 | 35.19 | 18.15 | 13.04 | 58.33 | 64.56 | 20.46 |
| α2 | 7.06 | 6.54 | 2.07 | 11.78 | 8.45 | 2.20 | |
|
| |||||||
| 14 | α1 | 35.19 | 20.79 | 8.94 | 5.80 | 40.51 | 9.93 |
| α2 | 7.06 | 3.16 | 6.41 | 12.90 | 0.25 | 12.48 | |
|
| |||||||
| 15 | α1 | 35.19 | 1.15 | 24.77 | 66.20 | 64.65 | 7.35 |
| α2 | 7.06 | 0.76 | 5.48 | 12.31 | 9.85 | 1.98 | |
|
| |||||||
| 16 Infarct | α1 | 70.38 | 8.20 | 35.16 | 18.17 | 132.76 | 89.09 |
| α2 | 14.12 | 12.61 | 10.94 | 17.13 | 1.41 | 5.21 | |
|
| |||||||
| 17 | α1 | 35.19 | 15.72 | 14.21 | 0.88 | 1.02 | 60.02 |
| α2 | 7.06 | 2.71 | 4.88 | 14.07 | 4.93 | 4.83 | |
In order to test if the linear systems solved in the identification process are well conditioned, we compute the 2-norm condition number of the Hessian κ(Hg). As reported in Figure 14, κ(Hg) ranges from ≈ 7 to ≈ 470 in the different examples indicating well conditioned linear systems.
The in-house C++ code used to identify the material properties, the LV finite element mesh, and the microstructure information are available at https://github.com/luigiemp/voom2.
5. Conclusions
We have developed a new framework termed EMS with the goal of identifying uniquely material properties and formulating optimal material laws based on full field displacement measurements. In addition, we compute explicitly the Hessian Hg of our objective function and, based on its condition number, assess if the available experimental data are sufficient to identify the sought material properties. Furthermore, our method could lead to a significant speedup with respect to standard approaches based on the minimization of the differences between measured and simulated displacements. Although a thorough comparative study is needed, our method's speed is a key benefit in applications where material properties need to be identified quickly.
As part of our approach, we present a new strategy to formulate material energy laws to be used together with our objective function. These material energy densities W are linear in α (eqn. 19). The resulting W is polyconvex and represents one optimal description of the available experimental data. The latter is achieved by choosing the functions of deformation invariants (i.e., Φi) and their non-linearities (i.e., internal parameters γi) according to the scheme proposed in Section 3.2. We remark that the strategy described in Section 3.2 and used at a single material point (Sections 3.2.1 and 3.3) to identify the exponents γi could be adapted and used at the 3D model level, e.g., with experimental data describing the left ventricle passive filling. In this case, the states of deformation at different instants in time and different locations would be used together to identify the exponents γi and characterize the nonlinear response of the material. This strategy may provide insights in formulating optimal material laws, but the proposed approach to identify α is also applicable with material laws selected from the literature as far as they are linear in the material properties to be identified.
In our current framework we separate the formulation of the material law (i.e., the identification of the functions Φi and non-linearities γi) from the identification of the linear material properties. Once a material law has been chosen, the linear material properties are identified uniquely. The material response depends not only on the linear material properties, but also on the deformation invariants and their non-linear dependence in the material law. By not identifying the material law and the material properties at the same time, we do not allow the material law to change, for example, between healthy subjects and patients. Fixing a material law however is necessary to compare directly material properties between healthy subjects and HF patients.
We recall that the identified material properties α must be greater than zero (see eqn. (19)). In the examples presented herein, we found that α were always positive. If not automatically satisfied, this constraint may be imposed by solving an inequality constrained minimization problem as described, for example, in [32].
Although our framework can be applied in any instance where full field measures and traction boundary conditions (e.g., LV intraventricular pressure measures) are available, we have developed our approach with particular attention to biomechanical applications. In this latter case, uniquely identified material properties may become diagnostic measures to distinguish between health and disease and to monitor therapeutic response. For example, in the study of HFpEF, an increase in passive myocardium material stiffness is associated with disease onset and progression. Patients suffering from moderate to advanced HFpEF may undergo both left ventricular catheterization to measure intraventricular pressure and MRI exams, from which geometry and displacement information can be extracted. Our framework is designed based on the availability of patient-specific data that are acquired as part of routine clinical exams. The identification of the material properties at the tissue level carries several advantages over previous approaches to measure passive myocardium stiffness. In a clinical setting, the most common estimates of diastolic ventricular stiffness are based on pressure-volume (PV) loops. These estimates only measure the “apparent” global stiffness of the left ventricle and are unable to characterize changes in the material stiffness. In fact, due to geometric effects (changes in myocardial wall thickness or ventricle geometry), PV-loop estimates of apparent global stiffness can decrease while local myocardial tissue stiffness increases [51]. However, it is important to note that, being a global estimate, PV-loop based measures may be less susceptible to experimental noise. Beside the standard PV loop approach, other methods to estimate diastolic ventricular stiffness are emerging as research protocols. These approaches use the same data required by EMS but, as described in Section 2, employ the external forces as known inputs and identify the passive myocardial properties by matching as well as possible computed and MRI displacement data. When (as it is true for the heart) the equilibrium problem is nonlinear, uniqueness of the identified material properties becomes challenging. Here we have shown how our approach can overcome this challenge and uniquely identify the passive myocardium material properties independently from their initial values.
Finally, we highlight that the proposed EMS framework measures the material properties of biological tissues in vivo, avoiding material changes occurring in ex vivo tissue and the environment changes occurring when a tissue sample is extracted from the organ (e.g., alteration of the pre-stress state). This advantage is shared by several other approaches based on in vivo measures. In our current approach we have chosen to absorb the pre-stress effect in the material properties themselves. In future work we will analyze the effect of tissue pre-stress in more detail and consider additional terms in W to explicitly account for this phenomenon.
One of our major objectives in further developing our EMS framework for clinical, and biomechanical applications in general, is to investigate its robustness in presence of standard experimental noise and error. For instance, in cardiac applications with the aim of identifying the passive myocardial material properties, MRI displacements and fiber data may be affected by imaging noise while the measure of intraventricular pressure is subject to mis-calibration. Moreover, sensitivity to noise may be higher when an exact solution does not exist — as it is the case in real applications since material models are only an idealization of the real material response. An important concluding test consists in solving the forward boundary value problem during passive filling using the identified material properties and measured pressure loading. The computed displacements can then be compared with the measured displacements and, based on their agreement, test how closely the chosen material model and identified material properties describe the passive myocardium behavior. Reduced sensitivity to noise and more accurate material modeling may be achieved by choosing among orthogonal invariants to form the material energy density to be used in EMS. Several studies (e.g., [52, 53]) have made significant advances in this direction and have shown the advantage of identifying material properties using orthogonal deformation invariants or strain attributes [54]. We plan to incorporate these advantages in our approach by investigating how to form polyconvex functions of orthogonal deformation invariants and by formulating material energy densities based on them.
In addition, to evaluate and mitigate the effect of experimental error and noise, the influence of model simplifications on the identified material properties needs to be carefully assessed. For example, given the additional uncertainties and complications involved, we have excluded from this first heart model both the right ventricle and the pericardium. Further analyses are required to evaluate these simplifications when combined with in vivo measures.
Finally, in the examples involving inhomogeneous LV models (AHA segmentation and infarct models) we have held the number and location of material properties constant. In principle, different material properties may be assigned to different regions of the finite element mesh. However, in practice, a very high number of unknown material properties may lead to a singular Hg. In future work, the optimal number of identifiable material properties needs to be determined to: 1) avoid large κ(Hg); and 2) achieve the highest spatial resolution in terms of varying material properties. The optimal number of identifiable material properties will likely depend on the spatial and temporal resolution of the experimental data, and on their quality.
Acknowledgments
We would like to dedicate this work to our friend and colleague William S. Klug, whose insight and knowledge inspired this work and many other contributions in computational biomechanics. The authors gratefully acknowledge the support from the American Heart Association postdoctoral fellowship 14POST19890027 to Luigi E. Perotti, the National Institutes of Health grant P01 HL78931, and the Institutional Strategy “The Synergetic University” as part of the Excellence Initiative by the German Research Foundation (DFG) to Daniel Balzani.
American Heart Association; contract/grant number: 14POST19890027
National Institutes of Health; contract/grant number: P01 HL78931
German Research Foundation, Excellence Initiative
appendix.
6. Appendix
6.1. Analytical form of Hg̃ for the material model by Humphrey et al [43]
| (34) |
6.2. Taylor expansion of g̃ for Guccione et al. [44] and Holzapfel et al. [45] material laws
As an example we consider an incompressible deformation that combines stretch along the fiber direction and shear according to
| (35) |
where α varies from 1 to 1.1 and γ varies from 0 to 0.2 in five increments. We compute using αG = {0.831, 14.3, 4.49, 0.762} for WG and αH = {0.059, 8.023, 18.472, 16.026, 2.481, 11.120, 0.216, 11.436} for WH (here ‘G’ and ‘H’ refer, respectively, to the Guccione et al. and Holzapfel et al. material energy densities). Both sets of material properties αG and αH have been previously identified in the literature and are representative of realistic passive myocardium behavior (αG is from Table 2 in [30] and αH is from Table 1 in [45].) We then expand g̃ (Figure 9) around another set of material properties αG,init and αH,init, which represent potential initial guesses for the material properties to be identified. We choose αG,init = {1.2, 26.7, 2.0, 14.7} and αH,init = {2.280, 9.726, 1.685, 15.779, 0.0, 0.0, 0.0, 0.0} from the same tables cited above. This represents a real situation when, in order to identify unknown material properties, we would base our initial guess on values already reported in the literature.
We notice that, if αG,init =αG and αH,init = αH, then the Taylor expansion of g̃ is locally convex, i.e., close to its minimum g̃ is locally convex. In other words, only if the initial guess is close enough to the absolute minimum we are able to find the exact material properties. Otherwise, since g̃ is not globally convex for eqns. (30a) and (30b), there is no guarantee that the material properties corresponding to the global minimum can be found.
6.3. Reference and initial guess material properties used in the test cases shown in Section 4.4
For completeness and to allow for reproducibility of all the results presented in Section 4.4, we report in Tables IV-VI the material properties used to generate the displacement field applied as input in the optimization procedure (reference material properties) and the initial guess for the material properties used to initialize subsequent tests.
Footnotes
HFpEF is a debilitating and growing health problem [27, 28] affecting more than 50% of heart failure patients in the US, and is associated with the signs and symptoms of heart failure (e.g., dyspnea, fatigue, exercise intolerance) even when ejection fraction is normal (> 50%).
The percentage error is computed with respect to the material properties identified in Section 3.3
References
- 1.Swaminathan V, Mythreye K, O'Brien ET, Berchuck A, Blobe GC, Superfine R. Mechanical stiffness grades metastatic potential in patient tumor cells and in cancer cell lines. Cancer research. 2011;71(15):5075–5080. doi: 10.1158/0008-5472.CAN-11-0247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Murphy MC, John Huston KJG, III, Manduca A, Meyer FB, Lanzino G, Morris JM, Felmlee JP, Ehman RL. Preoperative assessment of meningioma stiffness by magnetic resonance elastography. Journal of neurosurgery. 2013;118(3):643. doi: 10.3171/2012.9.JNS12519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Conrad CH, Brooks WW, Hayes JA, Sen S, Robinson KG, Bing OH. Myocardial fibrosis and stiffness with hypertrophy and heart failure in the spontaneously hypertensive rat. Circulation. 1995;91(1):161–170. doi: 10.1161/01.cir.91.1.161. [DOI] [PubMed] [Google Scholar]
- 4.Yamamoto K, Masuyama T, Sakata Y, Nishikawa N, Mano T, Yoshida J, Miwa T, Sugawara M, Yamaguchi Y, Ookawara T, et al. Myocardial stiffness is determined by ventricular fibrosis, but not by compensatory or excessive hypertrophy in hypertensive heart. Cardiovascular research. 2002;55(1):76–82. doi: 10.1016/s0008-6363(02)00341-3. [DOI] [PubMed] [Google Scholar]
- 5.Avril S, Bonnet M, Bretelle AS, Grediac M, Hild F, Ienny P, Latourte F, Lemosse D, Pagano S, Pagnacco E, et al. Overview of identification methods of mechanical parameters based on full-field measurements. Experimental Mechanics. 2008;48(4):381–402. [Google Scholar]
- 6.Wehner GJ, Suever JD, Haggerty CM, Jing L, Powell DK, Hamlet SM, Grabau JD, Mojsejenko WD, Zhong X, Epstein FH, et al. Validation of in vivo 2D displacements from spiral cine DENSE at 3T. Journal of Cardiovascular Magnetic Resonance. 2015;17(5):1–11. doi: 10.1186/s12968-015-0119-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhong X, Spottiswoode BS, Meyer CH, Kramer CM, Epstein FH. Imaging three-dimensional myocardial mechanics using navigator-gated volumetric spiral cine DENSE MRI. Magnetic resonance in medicine. 2010;64(4):1089–1097. doi: 10.1002/mrm.22503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Aletras AH, Balaban RS, Wen H. High-resolution strain analysis of the human heart with fast-DENSE. Journal of Magnetic Resonance. 1999;140(1):41–57. doi: 10.1006/jmre.1999.1821. [DOI] [PubMed] [Google Scholar]
- 9.Raghavan K, Yagle AE. Forward and inverse problems in elasticity imaging of soft tissues. Nuclear Science, IEEE Transactions on. 1994;41(4):1639–1648. [Google Scholar]
- 10.Doyley M, Meaney P, Bamber J. Evaluation of an iterative reconstruction method for quantitative elastography. Physics in Medicine and Biology. 2000;45(6):1521. doi: 10.1088/0031-9155/45/6/309. [DOI] [PubMed] [Google Scholar]
- 11.Skovoroda A, Emelianov S, O'Donnell M. Tissue elasticity reconstruction based on ultrasonic displacement and strain images. Ultrasonics, Ferroelectrics, and Frequency Control, IEEE Transactions on. 1995;42(4):747–765. [Google Scholar]
- 12.Sumi C, Suzuki A, Nakayama K. Estimation of shear modulus distribution in soft tissue from strain distribution. Biomedical Engineering, IEEE Transactions on. 1995;42(2):193–202. doi: 10.1109/10.341832. [DOI] [PubMed] [Google Scholar]
- 13.Barbone PE, Bamber JC. Quantitative elasticity imaging: what can and cannot be inferred from strain images. Physics in medicine and biology. 2002;47(12):2147. doi: 10.1088/0031-9155/47/12/310. [DOI] [PubMed] [Google Scholar]
- 14.Moulton MJ, Creswell LL, Actis RL, Myers KW, Vannier MW, Szabo BA, Pasque MK. An inverse approach to determining myocardial material properties. Journal of biomechanics. 1995;28(8):935–948. doi: 10.1016/0021-9290(94)00144-s. [DOI] [PubMed] [Google Scholar]
- 15.Lecompte D, Smits A, Sol H, Vantomme J, Van Hemelrijck D. Mixed numerical–experimental technique for orthotropic parameter identification using biaxial tensile tests on cruciform specimens. International Journal of Solids and Structures. 2007;44(5):1643–1656. [Google Scholar]
- 16.Cottin N, Felgenhauer HP, Natke H. On the parameter identification of elastomechanical systems using input and output residuals. Ingenieur-Archiv. 1984;54(5):378–387. [Google Scholar]
- 17.Genovese K, Lamberti L, Pappalettere C. Mechanical characterization of hyperelastic materials with fringe projection and optimization techniques. Optics and Lasers in Engineering. 2006;44(5):423–442. [Google Scholar]
- 18.Wittek A, Karatolios K, Bihari P, Schmitz-Rixen T, Moosdorf R, Vogt S. In vivo determination of elastic properties of the human aorta based on 4D ultrasound data. Journal of the Mechanical Behavior of Biomedical Materials. 2013;27:167–183. doi: 10.1016/j.jmbbm.2013.03.014. [DOI] [PubMed] [Google Scholar]
- 19.Florentin E, Lubineau G. Identification of the parameters of an elastic material model using the constitutive equation gap method. Computational Mechanics. 2010;46(4):521–531. [Google Scholar]
- 20.Allix O, Feissel P, Nguyen HM. Identification strategy in the presence of corrupted measurements. Engineering Computations. 2005;22(5/6):487–504. [Google Scholar]
- 21.Banerjee B, Walsh TF, Aquino W, Bonnet M. Large scale parameter estimation problems in frequency-domain elastodynamics using an error in constitutive equation functional. Computer methods in applied mechanics and engineering. 2013;253:60–72. doi: 10.1016/j.cma.2012.08.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Feissel P, Allix O. Modified constitutive relation error identification strategy for transient dynamics with corrupted data: the elastic case. Computer Methods in Applied Mechanics and Engineering. 2007;196(13):1968–1983. [Google Scholar]
- 23.Ball J. Convexity conditions and existence theorems in non-linear elasticity. Archive for Rational Mechanics and Analysis. 1977;63:337–403. [Google Scholar]
- 24.Balzani D, Neff P, Schröder J, Holzapfel G. A polyconvex framework for soft biological tissues. Adjustment to experimental data. International Journal of Solids and Structures. 2006;43(20):6052–6070. [Google Scholar]
- 25.Schröder J, Neff P, Balzani D. A variational approach for materially stable anisotropic hyperelasticity. International Journal of Solids and Structures. 2005;42(15):4352–4371. [Google Scholar]
- 26.Schröder J, Neff P. Invariant formulation of hyperelastic transverse isotropy based on polyconvex free energy functions. International Journal of Solids and Structures. 2003;40:401–445. [Google Scholar]
- 27.Zile MR, Baicu CF, Gaasch WH. Diastolic heart failure abnormalities in active relaxation and passive stiffness of the left ventricle. New England Journal of Medicine. 2004;350(19):1953–1959. doi: 10.1056/NEJMoa032566. [DOI] [PubMed] [Google Scholar]
- 28.Sakata Y, Ohtani T, Takeda Y, Yamamoto K, Mano T. Left ventricular stiffening as therapeutic target for heart failure with preserved ejection fraction. Circulation journal: official journal of the Japanese Circulation Society. 2012;77(4):886–892. doi: 10.1253/circj.cj-13-0214. [DOI] [PubMed] [Google Scholar]
- 29.Meyer T, Shih J, Aurigemma G. Heart failure with preserved ejection fraction (diastolic dysfunction) Annals of internal medicine. 2013;158(1):ITC1–1. doi: 10.7326/0003-4819-158-1-201301010-01001. [DOI] [PubMed] [Google Scholar]
- 30.Wang VY, Lam H, Ennis DB, Cowan BR, Young AA, Nash MP. Modelling passive diastolic mechanics with quantitative MRI of cardiac structure and function. Medical image analysis. 2009;13(5):773–784. doi: 10.1016/j.media.2009.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Krishnamurthy G, Ennis DB, Itoh A, Bothe W, Swanson JC, Karlsson M, Kuhl E, Miller DC, Ingels NB. Material properties of the ovine mitral valve anterior leaflet in vivo from inverse finite element analysis. American Journal of Physiology-Heart and Circulatory Physiology. 2008;295(3):H1141–H1149. doi: 10.1152/ajpheart.00284.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Boyd S, Vandenberghe L. Convex optimization. Cambridge university press; 2004. [Google Scholar]
- 33.Mahnken R, Stein E. Parameter identification for viscoplastic models based on analytical derivatives of a least-squares functional and stability investigations. International Journal of Plasticity. 1996;12(4):451–479. [Google Scholar]
- 34.Balzani D, Ortiz M. Relaxed Incremental Variational Formulation for Damage at Large Strains with Application to Fiber-Reinforced Materials and Materials with Truss-like Microstructures. International Journal for Numerical Methods in Engineering. 2012;92:551–570. [Google Scholar]
- 35.Holzapfel GA, Gasser T, Ogden R. A new constitutive framework for arterial wall mechanics and a comparative study of material models. Journal of Elasticity. 2000;61:1–48. [Google Scholar]
- 36.Balzani D, Böse D, Brands D, Erbel R, Klawonn A, Rheinbach O, Schröder J. Parallel Simulation of Patient-specific Atherosclerotic Arteries for the Enhancement of Intravascular Ultrasound Diagnostics. Engineering Computations. 2012;29(8) [Google Scholar]
- 37.Balzani D, Gruttmann F, Schröder J. Analysis of thin shells using anisotropic polyconvex energy densities. Computer Methods in Applied Mechanics and Engineering. 2008;197:1015–1032. [Google Scholar]
- 38.Hartmann S, Neff P. Existence Theory for a Modified Polyconvex Hyperelastic Relation of Generalized Polynomial-Type in the Case of Nearly-Incompressibility. International Journal of Solids and Structures. 2003;40:2767–2791. [Google Scholar]
- 39.Gasser T, Ogden R, Holzapfel G. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. Journal of the Royal Society Interface. 2006;3:15–35. doi: 10.1098/rsif.2005.0073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lagarias JC, Reeds JA, Wright MH, Wright PE. Convergence properties of the Nelder-Mead simplex method in low dimensions. SIAM Journal on optimization. 1998;9(1):112–147. [Google Scholar]
- 41.The Mathworks, Inc. Natick, Massachusetts. MATLAB version 8.6 (R2015b) 2015 [Google Scholar]
- 42.Yin FC, Strumpf RK, Chew PH, Zeger SL. Quantification of the mechanical properties of noncontracting canine myocardium under simultaneous biaxial loading. Journal of biomechanics. 1987;20(6):577–589. doi: 10.1016/0021-9290(87)90279-x. [DOI] [PubMed] [Google Scholar]
- 43.Humphrey J, Strumpf R, Yin F. Determination of a constitutive relation for passive myocardium: I. A new functional form. Journal of biomechanical engineering. 1990;112(3):333–339. doi: 10.1115/1.2891193. [DOI] [PubMed] [Google Scholar]
- 44.Guccione J, McCulloch A, Waldman L. Passive material properties of intact ventricular myocardium determined from a cylindrical model. Journal of biomechanical engineering. 1991;113(1):42–55. doi: 10.1115/1.2894084. [DOI] [PubMed] [Google Scholar]
- 45.Holzapfel GA, Ogden RW. Constitutive modelling of passive myocardium: a structurally based framework for material characterization. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2009;367(1902):3445–3475. doi: 10.1098/rsta.2009.0091. [DOI] [PubMed] [Google Scholar]
- 46.Hadjicharalambous M, Chabiniok R, Asner L, Sammut E, Wong J, Carr-White G, Lee J, Razavi R, Smith N, Nordsletten D. Analysis of passive cardiac constitutive laws for parameter estimation using 3D tagged MRI. Biomechanics and modeling in mechanobiology. 2015;14:807–828. doi: 10.1007/s10237-014-0638-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wang V, Lam H, Ennis D, Young A, Nash M. Passive ventricular mechanics modelling using MRI of structure and function. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2008. 2008:814–821. doi: 10.1007/978-3-540-85990-1_98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Krishnamoorthi S, Perotti LE, Borgstrom NP, Ajijola OA, Frid A, Ponnaluri AV, Weiss JN, Qu Z, Klug WS, Ennis DB, et al. Simulation methods and validation criteria for modeling cardiac ventricular electrophysiology. PloS ONE. 2014;9(12):e114494. doi: 10.1371/journal.pone.0114494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Cerqueira MD, Weissman NJ, Dilsizian V, Jacobs AK, Kaul S, Laskey WK, Pennell DJ, Rumberger JA, Ryan T, Verani MS, et al. Standardized myocardial segmentation and nomenclature for tomographic imaging of the heart a statement for healthcare professionals from the cardiac imaging committee of the Council on Clinical Cardiology of the American Heart Association. Circulation. 2002;105(4):539–542. doi: 10.1161/hc0402.102975. [DOI] [PubMed] [Google Scholar]
- 50.Cover TM, Hart PE. Nearest neighbor pattern classification. Information Theory, IEEE Transactions on. 1967;13(1):21–27. [Google Scholar]
- 51.Costandi PN, Frank LR, McCulloch AD, Omens JH. Role of diastolic properties in the transition to failure in a mouse model of the cardiac dilatation. American Journal of Physiology-Heart and Circulatory Physiology. 2006;291(6):H2971–H2979. doi: 10.1152/ajpheart.00571.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Criscione JC, Humphrey JD, Douglas AS, Hunter WC. An invariant basis for natural strain which yields orthogonal stress response terms in isotropic hyperelasticity. Journal of the Mechanics and Physics of Solids. 2000;48(12):2445–2465. [Google Scholar]
- 53.Srinivasa A. On the use of the upper triangular (or QR) decomposition for developing constitutive equations for Green-elastic materials. International Journal of Engineering Science. 2012;60:1–12. [Google Scholar]
- 54.Criscione JC, McCulloch AD, Hunter WC. Constitutive framework optimized for myocardium and other high-strain, laminar materials with one fiber family. Journal of the Mechanics and Physics of Solids. 2002;50(8):1681–1702. [Google Scholar]