Assessing the impact of selection bias on test decisions in trials with a time‐to‐event outcome

Abstract

If past treatment assignments are unmasked, selection bias may arise even in randomized controlled trials. The impact of such bias can be measured by considering the type I error probability. In case of a normally distributed outcome, there already exists a model accounting for selection bias that permits calculating the corresponding type I error probabilities. To model selection bias for trials with a time‐to‐event outcome, we introduce a new biasing policy for exponentially distributed data. Using this biasing policy, we derive an exact formula to compute type I error probabilities whenever an F‐test is performed and no observations are censored. Two exemplary settings, with and without random censoring, are considered in order to illustrate how our results can be applied to compare distinct randomization procedures with respect to their performance in the presence of selection bias. © 2017 The Authors. Statistics in Medicine Published by John Wiley & Sons Ltd.

1. Introduction

When two treatments are compared in a clinical trial, various sources of bias such as a dissimilarity in the composition of treatment groups can affect the study outcome. The error induced if patient cohorts differ systematically with respect to their baseline covariates is referred to as selection bias 1, and it is widely acknowledged that its presence is of great concern in any clinical trial. A necessary, yet not sufficient, technique to protect against selection bias is the randomized allocation of patients to treatments 2. This was evidenced by Berger who identified 30 randomized clinical trials that show signs of selection bias 1. Another equally necessary technique to prevent selection bias is the non‐disclosure of upcoming treatment allocations (allocation concealment). However, allocation concealment alone does not rule out the possibility of selection bias because already, the disclosure of past treatment assignments poses a risk with regard to the predictability of future allocations. Consequently, in order to truly rule out the possibility of selection bias, it is also vital to conceal past treatment assignments, and the ICH E9 guideline therefore recommends to choose a double‐blinded randomized study design 3. However, blinding may not always be feasible for all types of clinical trials; for example, for obvious reasons, surgical trials are often conducted in an unblinded or single‐blinded manner 2. Moreover, even with regard to double‐blinded trials, there are serious doubts as to whether perfect blinding can be attained 4. For example, there is a chance that previous allocations might be identified by characteristic side effects, which hence endangers allocation concealment. Following Berger's notation, we will refer to this circumstance as third‐order selection bias 5.

From a clinical perspective, this poses the challenge of measuring the strength of such bias if present. One method that is recommended in the ICH E9 guideline is to study the impact on the test decision, for example, p‐value 3. For normally distributed outcome data in a parallel group design, a corresponding model was introduced by Proschan 6. Particularly, he derived a formula to compute biased type I error probabilities in the case when patients are assigned to treatments using the random allocation rule (RAR) and the analysis is performed using a Z‐test. This work was then continued by Kennes et al. 7, who considered permuted block randomization and further extended the consideration to multi‐center trials. Relaxing the assumption of known variance in the Z‐test setting, Langer 8 then investigated the distribution of a t‐test in the presence of selection bias, leading to a doubly noncentral t‐distribution. Incorporating Langer's findings, Uschner et al. 9 recently introduced a software tool enabling researchers to assess the impact of selection and chronological bias for trials with a normally distributed outcome. However, despite the extensive research for studies with a normal outcome, similar models are currently underdeveloped for trials with a time‐to‐event outcome. The aim of the present investigation is to introduce a new biasing policy to model selection bias for settings with an exponentially distributed time‐to‐event outcome.

The paper is organized as follows: In the next section, we introduce our terminology and statistical model. Within Section 3, we propose a new biasing policy to describe selection bias that can be applied in the context of exponentially distributed time‐to‐event data. Based on this biasing policy, we establish a formula to compute rejection probabilities in the presence of third‐order selection bias if an F‐test without censoring is performed (Section 4). Within Section 5, we analyze which factors affect the inflation of type I error probability, emphasizing differences caused by the random allocation of patients as well as the influence of censoring. Finally, we briefly discuss our limitations and comment on possible generalizations (Section 6).

2. Preliminaries

We consider a parallel group trial with a time‐to‐event outcome where we investigate the equality of two treatments that will be referred to as control (0) and experimental (1) treatments. Let the total sample size of participating patients n be fixed. Defining the sample space by $\mathrm{\Omega }={\left\{0,1\right\}}^n$, a randomization sequence is an element $\mathit{t}=\left(t_1,\dots ,t_n\right)\in \mathrm{\Omega }$, where $t_i\in \left\{0,1\right\}$ denotes the allocation of the ith patient to either the control (t _i=0) or experimental group (t _i=1). Note that t is the realization of a random variable $\mathit{T}=(T_1,\dots ,T_n)$, which takes values in ${\left\{0,1\right\}}^n$ and contains full information on the allocation of patients. The distribution of T is determined by the randomization procedure at hand. We suppose that all survival times are independent and that the control and experimental groups are of sizes n ₀ and n ₁, respectively, where n=n ₀+n ₁ and $n_0,n_1⩾1$.

Without loss of generality, presume that the treatment is intended to prolong survival and that the survival times follow an exponential distribution. Denoting the random survival times by Y ₁,…,Y _n, where Y _i is the random variable corresponding to the ith enrolled patient, yields

$$Y_i\sim \mathrm{Exp}\left({\lambda }_0\left(1-T_i\right)+{\lambda }_1{T}_i\right),\text{for}i=1,\dots ,n,$$

where λ ₀,λ ₁>0 denote the respective hazard rates. In order to decide whether one of the treatments is superior with respect to prolonging survival, we consider the following two‐sided hypotheses for Δ=λ ₀/λ ₁:

$$H_0:\mathrm{\Delta }=1\text{vs.}{H}_1:\mathrm{\Delta }\ne 1.$$ (1)

2.1. F‐test without censoring

If no censoring takes place, the aforementioned hypotheses can be tested performing an F‐test 10, 11. The maximum likelihood estimators of λ ₀ and λ ₁ are then given by the inverse arithmetic means of the respective samples. Hence, the following statistic is an estimator for Δ:

$$S_F=\frac{{\widehat{\lambda }}_0}{{\widehat{\lambda }}_1}=\frac{1/n_1\sum _{i=1}^n{Y}_i{T}_i}{1/n_0\sum _{i=1}^n{Y}_i\left(1-T_i\right)}=\frac{Y_1/n_1}{Y_0/n_0},\text{where}{Y}_1=\sum _{i=1}^n{Y}_i{T}_i\text{and}{Y}_0=\sum _{i=1}^n{Y}_i\left(1-T_i\right),$$ (2)

and with $S_F=\left(2{\lambda }_1{Y}_1/n_1\right)/\left(2{\lambda }_0{Y}_0/n_0\right)$ if the null hypothesis holds. The random variables 2λ ₁ Y ₁ and 2λ ₀ Y ₀ are then chi‐square distributed with 2n ₁ and 2n ₀ degrees of freedom, which further implies that S _F follows an F‐distribution with 2n ₁ and 2n ₀ degrees of freedom. Thus, the two‐sided null hypothesis is tested by comparing whether $F_{2n_1,2n_0,\alpha /2}⩽S_F⩽F_{2n_1,2n_0,1-\alpha /2}$, where $F_{2n_1,2n_0,\gamma }$ denotes the γ‐quantile of an F‐distribution with 2n ₁ and 2n ₀ degrees of freedom.

2.2. F‐test with censoring

Because the maximum likelihood estimators change in the presence of censoring, the aforementioned statistic (2) has to be adjusted in the case of censored data. The statistic can easily be extended to the case of type II censored data where the trial ends after a predetermined number of events have been observed within both treatment groups. Provided that k ₀ and k ₁ events shall occur within the control and experimental groups, respectively, the adjusted test statistic follows an F‐distribution with 2k ₁ and 2k ₀ degrees of freedom 12. If all patients enter the trial at the same date and the trial ends at a predetermined time such that all patients having survived until then are censored, this is a special case of type I censoring with one common censoring time. In that situation, the resulting statistic is approximately F‐distributed with 2K ₁ and 2K ₀ degrees of freedom, where K ₁ and K ₀ are the random number of events observed within the groups. It has been pointed out that this approximation yields slightly increased type I error probabilities, especially if the expected number of observed events is too small 13. As we believe that neither of the two censoring mechanisms listed previously frequently applies to clinical trials, we focus on a random censoring mechanism.

We assume that the censoring mechanism can be modeled by a probability distribution that is independent of the survival distribution. By defining the random censoring times as C ₁,…,C _n, the possibly censored event time for the ith enrolled patient is given by $Z_i:=\min \left\{Y_i,C_i\right\}$. Under the null hypothesis of no treatment effect, the following statistic then approximately follows an F‐distribution with (2K ₁+1) and (2K ₀+1) degrees of freedom 12:

$${\tilde{S}}_F=\frac{(1+0.5/K_0)}{(1+0.5/K_1)}·\frac{{\widehat{\lambda }}_0}{{\widehat{\lambda }}_1}=\frac{(1+0.5/K_0)}{(1+0.5/K_1)}·\frac{Z_1/K_1}{Z_0/K_0},\text{where}{Z}_1=\sum _{i=1}^n{Z}_i{T}_i\text{and}{Z}_0=\sum _{i=1}^n{Z}_i\left(1-T_i\right).$$ (3)

3. Biasing policy

In case of missing or imperfect blinding, the possibility of third‐order selection bias should not be overlooked 1. This is due to the fact that knowledge of prior assignments will mostly contain information on future allocations, eventually enabling those in charge of recruiting participants to predict the next upcoming treatment. Let us consider a setting where the recruiting researcher favors the experimental treatment. Now, if he or she anticipates that the next patient will be allocated to the experimental group, this might unconsciously affect his or her decisiveness to enroll a terminally ill patient who meets all the required entry criteria.

Based on Proschan's biasing policy for normally distributed data 6, we define the following biasing strategy: We assume that the recruiting researcher is aware of all past treatment assignments but has no knowledge of future allocations and the randomization procedure at hand. We further assume that he or she guesses the next upcoming treatment according to the convergence strategy by Blackwell and Hodges 14 and that he or she is able to decline presenting participants until someone suiting his or her guess presents for enrollment. More specifically, keeping count of previous assignments, let N ₀(i−1) and N ₁(i−1) denote the number of patients that have been assigned to the control and to the experimental groups within the first i−1 allocations, i=1,…,n. It should be noted that N ₀(i−1) and N ₁(i−1) are random variables that depend on the randomization sequence. Then the ith patient enrolled will have a survival distribution of

$$Y_i\sim \mathrm{Exp}\left({\lambda }_0{\tau }_i\left(1-T_i\right)+{\lambda }_1{\tau }_i{T}_i\right),\text{for}i=1,\dots ,n,$$ (4)

where τ _i is given by the following:

$${\tau }_i=\left\{\begin{array}{cccc}1/\delta & ,& \text{if}& N_0(i-1)<N_1(i-1),\\ 1& ,& \text{if}& N_0(i-1)=N_1(i-1),\\ \delta & ,& \text{if}& N_0(i-1)>N_1(i-1),\end{array}\right.$$

with δ∈(0,1) being the biasing factor. In accordance with the survival prolonging objective of the treatments, we will furthermore refer to patients as either having a good (τ _i=1/δ), neutral (τ _i=1), or bad (τ _i=δ) expected response. Notice that if δ approaches 0, this resembles the case where patients with bad expected response are about to experience an event within a short time, whereas patients with good expected response will probably not. On the other hand, if δ is close to 1, this reflects the circumstance when all patients are approximately comparable regarding their medical condition.

An obvious consequence of biasing policy (4) is that the survival distributions of our random sample depend on the order in which patients are allocated, and hence on the randomization sequence at hand. This can be seen by considering the minimal case of n=2 patients, where the survival distribution of the secondly enrolled patient depends on the firstly enrolled patient's treatment affiliation. However, this obstacle can be overcome by conditioning on the underlying realized randomization sequence t, which contains full information on the distribution of our random sample Y ₁,…,Y _n. We will see that despite knowing the survival distribution of each patient, for our purpose, it is sufficient to only know the number of patients with good, neutral, and bad expected response within each treatment group as outlined in Table 1. Given the realized randomization sequence t, those can be computed directly.

Table 1.

Composition of expected responses within control and experimental groups.

	Good	Neutral	Bad	Total
Control	n 01	n 02	n 03	n 0
Experimental	n 11	n 12	n 13	n 1

4. Biased distribution of the F‐statistic

We will derive the distribution of the F‐statistic for a fixed randomization sequence t in a setting where patients are enrolled in accordance with biasing policy (4). The conditional density function $f_{S_F|\mathit{T}=\mathit{t}}$ can then be computed applying results for the sum of independent gamma‐distributed random variables. A concise description of the derivation is given in Appendix A.1. We obtain that $f_{S_F|\mathit{T}=\mathit{t}}\left(x\right)=0$ for $x⩽0$ and

$$f_{S_F|\mathit{T}=\mathit{t}}\left(x\right)=C\sum _{k=0}^{\infty }{d}_1\left(k\right)x^{n_1+k-1}\sum _{l=0}^{\infty }\frac{d_0\left(l\right){\left(\mathrm{\Delta }{n}_0/n_1\right)}^{n_0+l}\mathrm{B}{(n_1+k,n_0+l)}^{-1}}{{\left(x+\mathrm{\Delta }{n}_0/n_1\right)}^{n_1+k+n_0+l}},\text{for}x>0,$$ (5)

where B(a,b) denotes the beta function, $C={\delta }^{2n_{01}+2n_{11}+n_{02}+n_{12}}$, and

$$d_j\left(k\right)=\frac{1}{k}\sum _{i=1}^k\left(n_{j1}{\left(1-{\delta }^2\right)}^i+n_{j2}{\left(1-\delta \right)}^i\right)d_j(k-i),d_j\left(0\right)=1,$$ (6)

where j∈{0,1}. It can furthermore be shown that the corresponding distribution function is given by $F_{S_F|\mathit{T}=\mathit{t}}\left(x\right)=0$ for $x⩽0$ and

$$F_{S_F|\mathit{T}=\mathit{t}}\left(x\right)=C\sum _{k=0}^{\infty }{d}_1\left(k\right)\sum _{l=0}^{\infty }{d}_0\left(l\right){\mathrm{\Delta }}^{n_0+l}\mathrm{B}{(n_1+k,n_0+l)}^{-1}d(n_1+k,n_0+l,x),\text{for}x>0,$$ (7)

where

$$d(a+1,b,x)=\frac{1}{a+b}\left(-\frac{{\left(x{n}_1/n_0\right)}^a}{{(x{n}_1/n_0+\mathrm{\Delta })}^{a+b}}+ad(a,b,x)\right),d(1,b,x)=\frac{1}{b}\left({\mathrm{\Delta }}^{-b}-{\left(x{n}_1/n_0+\mathrm{\Delta }\right)}^{-b}\right).$$ (8)

Equations (5) and (7) imply that the F‐statistic is affected by the presence of selection bias because of the density's and distribution's dependence on the biasing factor δ. Thus, performing the regular F‐test in the presence of selection bias does not maintain the nominal significance level and power. Using (7), however, allows computing the true, biased power or type I error probability. In case of a two‐sided F‐test, this is accomplished by computing the probability to observe a value at least as extreme as the critical values from the unbiased test setting, that is,

$$P\left(\text{reject the null hypothesis}\right|\mathit{T}=\mathit{t})=F_{S_F|\mathit{T}=\mathit{t}}(F_{2n_1,2n_0,\alpha /2})+\left(1-F_{S_F|\mathit{T}=\mathit{t}}\left(F_{2n_1,2n_0,1-\alpha /2}\right)\right),$$

where, again, $F_{2n_1,2n_0,\gamma }$ denotes the γ‐quantile of an F‐distribution with 2n ₁ and 2n ₀ degrees of freedom. It can further be noted that the biased distribution of the F‐statistic is, like the unbiased distribution, independent of the baseline hazard rates and only depends on the biasing factor δ, as well as on the hazard ratio Δ=λ ₀/λ ₁.

5. Impact on the test decision

We illustrate the impact of selection bias on the test decision in the event of no treatment effect, that is, Δ=1. Following the ICH E9 guideline recommendations, the evaluation of this impact should involve consideration of the corresponding p‐value 3. With regard to clinical relevance, this can be accounted for by studying the probability to observe a p‐value less than the nominal significance level, which in case of no treatment effect corresponds to the type I error probability. In an unbiased scenario, the type I error probabilities of (2) and (3) correspond to the nominal significance level, either exactly if no censoring occurs or approximately if random censoring takes place. Consequently, comparing the true, biased type I error probabilities to the nominal significance level serves as a measure to assess the impact of selection bias. We have shown that in the presence of selection bias without censoring, corresponding type I error probabilities can be computed using (7); in a scenario with random censoring, type I error rates can be obtained via simulation.

We begin by studying the dependency between type I error probability and the magnitude of the biasing factor δ, as well as the particular allocation sequence t. In the second part, we investigate how distinct randomization procedures differ with respect to their susceptibility to selection bias in two exemplary settings with and without random censoring. As bias poses a particular challenge in small population trials 15, we also include an example of smaller sample size. The following computations were partly performed using the randomizeR package 9.

5.1. Comparison of distinct biasing factors and randomization sequences

It follows directly from expressions (5) and (7) that the type I error probability depends on the magnitude of the biasing factor δ, as well as on the randomization sequence at hand. To illustrate this relation for all possible allocation scenarios with final balance in group sizes, we consider the very small example of n=4 patients. The results are shown in Table 2 for varying biasing factors. As a decrease in biasing factor reflects an increase in difference between patients with good and bad expected response, it is plausible that the type I error probability increases if δ decreases. It can further be seen how the type I error probability increases more rapidly the smaller δ becomes. Considering the distinct randomization sequences, it becomes apparent that in the presence of selection bias, the allocation of patients has a large impact on the type I error probability. For instance, for δ=0.5, the error probability ranges from 5.98% to 9.32%.

Table 2.

Type I error probabilities for distinct randomization sequences with varying biasing factor.

	Biasing factor δ
Randomization sequence t	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
(1,1,0,0)	0.2910	0.1498	0.0992	0.0760	0.0638	0.0571	0.0533	0.0512	0.0503
(1,0,1,0)	0.5159	0.2726	0.1676	0.1150	0.0860	0.0691	0.0592	0.0536	0.0508
(0,1,1,0)	0.5127	0.3035	0.1910	0.1286	0.0932	0.0727	0.0608	0.0542	0.0509
(1,0,0,1)	0.5127	0.3035	0.1910	0.1286	0.0932	0.0727	0.0608	0.0542	0.0509
(0,1,0,1)	0.5153	0.2726	0.1676	0.1150	0.0860	0.0691	0.0592	0.0536	0.0508
(0,0,1,1)	0.1251	0.0938	0.0766	0.0663	0.0598	0.0555	0.0528	0.0511	0.0503

Setting: n=4 patients and nominal significance level α=5%.

The set of randomization sequences shown in Table 2 corresponds to the set obtained when assigning patients according to the well‐known RAR. Figuratively speaking, this procedure can be implemented by sampling without replacement from an urn, which contains two equally sized sets of marbles of distinct color. The order in which the marbles are drawn then specifies the allocation sequence. Given the biasing factor δ, we have recently seen how we can assign a randomization sequence to its corresponding type I error probability. A reasonable method of evaluating the performance of a randomization procedure therefore consists in computing the expected type I error probability across all randomization sequences. We illustrate this procedure based on our previous example for n=4 patients, assuming participants are allocated using the RAR (Table 2). Because in the case of the RAR, all sequences are generated equally likely, for example, with probability 1/6 in the previous example, the expected type I error probability simply corresponds to the arithmetic mean of the type I error probabilities of all sequences. For instance, if the biasing factor δ can be quantified by 0.5, the expected type I error probability amounts to 8.03%. This equality, however, does not generally apply to other randomization procedures where certain sequences are more likely to occur 2. In order to account for this, a general way to derive the expected type I error probability is to compute the weighted mean with respect to the sequence probabilities.

5.2. Comparison of distinct randomization procedures

In practice, researchers have to decide on a randomization procedure as part of the study design at the trial planning stage. Because of the disparate behavior of different allocation sequences (Table 2), this decision should involve studying distinct randomization procedures with respect to the impact of bias on the test decision, especially if the possibility of selection bias cannot be ruled out. In the following, we will demonstrate how distinct randomization procedures can be compared with regard to their behavior in the presence of selection bias. Particularly, we will investigate the previously described RAR, as well as the following three randomization procedures 2:

• Big stick design (BSD(b)): Patients are randomly assigned by tossing a fair coin. If a maximum tolerated imbalance b in group sizes is reached, the next patient is allocated deterministically to the less frequently assigned treatment 16.

• Maximal procedure (MP(b)): To account for imbalances during the allocation process, this procedure uniformly chooses from the subset of sequences generated by RAR, which never exceed a maximum tolerated imbalance b in group sizes throughout the entire allocation 4.

• Permuted block randomization (PBR(k)): Patients are assigned in blocks of length k, where within each block, patients are allocated like in RAR. As a consequence, besides achieving final balance in group sizes, the PBR design additionally forces balances after each block of k patients.

As an example, we investigate the behavior of those randomization procedures for n=20 and n=100 patients. For PBR, we consider blocks of length 4, and for BSD and MP, we choose a maximum tolerated imbalance of 2. In both cases, we assume a biasing factor of δ=0.7 and a nominal significance level of α=5%. As the inclusion of all possibly generated randomization sequences does not scale nicely for large sample sizes 2, we use Monte Carlo simulations with 10,000 sequences per design, instead of considering the full set of randomization sequences. The type I error probabilities corresponding to those two exemplary settings are depicted in Figures 1 and 2.

Figure 1.

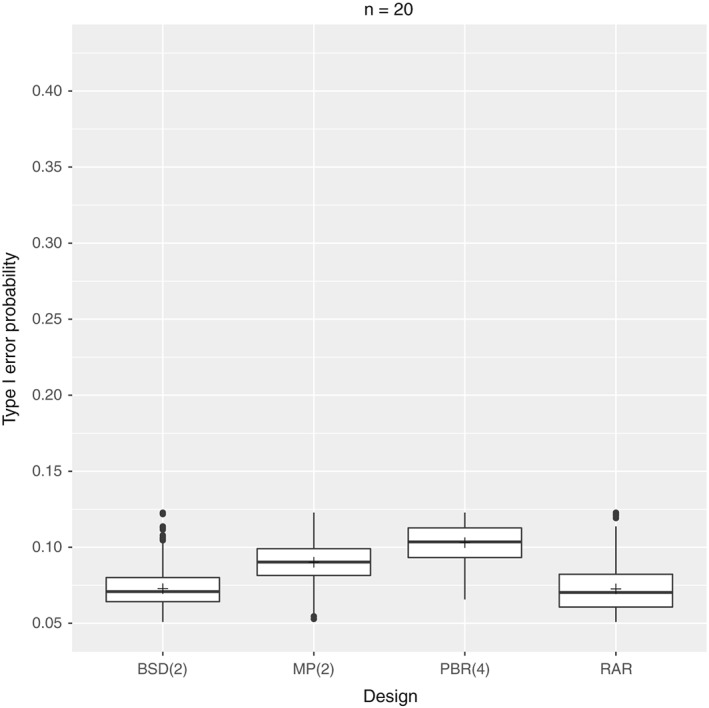
Setting: n=20 patients with biasing factor δ=0.7, nominal significance level α=5%, and 10,000 sequences per design. BSD, big stick design; MP, maximal procedure; PBR, permuted block randomization; RAR, random allocation rule.

Figure 2.

Setting: n=100 patients with biasing factor δ=0.7, nominal significance level α=5%, and 10,000 sequences per design. BSD, big stick design; MP, maximal procedure; PBR, permuted block randomization; RAR, random allocation rule.

One striking feature is that apparently, none of the randomization sequences generated by any design seems to maintain the nominal significance level of 5%. As expected, distinct randomization procedures can be associated with distinct sets of type I error probabilities, because of being associated with distinct randomization sequences. This is reflected by the shape of the box plots as well as by the mean type I error probabilities. For example, for n=20 patients, the mean type I error probability is 10.3% for PBR(4), compared with only 7.26% for RAR. In addition, the corresponding boxes do not overlap. The differences between the distinct randomization procedures become even more apparent for n=100 patients. Here, the mean type I error probabilities range from 8.24% for RAR to 31.65% for PBR(4). Also, the spread of possible type I error probabilities increases, resulting in more outliers. Another observation is that the type I error probabilities increase with increasing sample size, which has also been noted by Kennes et al. for PBR only 7.

Concerning our initial objective to compare distinct randomization procedures with regard to their behavior in the presence of selection bias when an F‐test is performed, we can conclude that some procedures are indeed less susceptible to selection bias than others. As an example, assume we are at the trial planning stage of a time‐to‐event trial with n=100 patients where it is reasonable to assume that no censoring will take place and where the equality of the treatments will be investigated performing an F‐test. If in addition, the possibility of selection bias cannot entirely be ruled out, for example, if blinding is at risk, this establishes the need to evaluate and compare possible randomization procedures in a way as described previously. With regard to the four randomization procedures considered, we can conclude that in the course of our exemplary study, the procedures BSD(2) and RAR are better suited to protect against selection bias than PBR(4) or MP(2) as the expected type I error probability will be less inflated.

5.3. Comparison of distinct randomization procedures with random censoring

We have seen that the type I error probability inflates in the presence of selection bias if an F‐test is performed and no censoring occurs. In order to understand the effect of censoring on the elevation of type I error probability, we will investigate the type I error rates of the previous randomization procedures in two simulation settings assuming random censoring probabilities of c=10% and c=30%, respectively. In particular, we assume an exponential censoring mechanism C ₁,…,C _n∼Exp(θ) with θ such that the probability for neutral patients to be censored is c. We consider a setting with n=100 patients, biasing factor 0.7, and nominal significance level of 5% where the equality of treatments is tested performing an F‐test with random censoring (3). The results are depicted in Figures 3 and 4. The mean type I error probabilities of the approximate F‐test without bias, that is, δ=1, are approximately 5%(5.12% and 5.13%).

Figure 3.

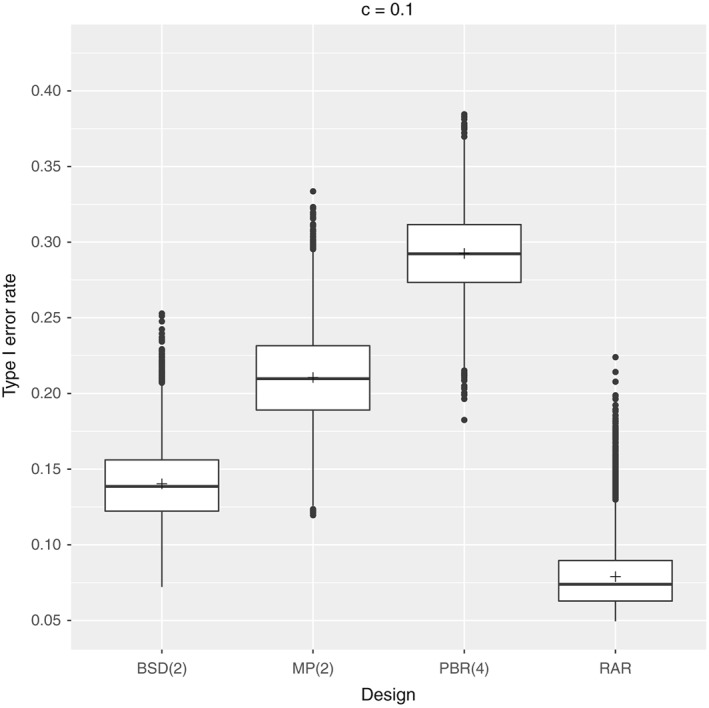
Setting: n=100 patients with biasing factor δ=0.7, censoring probability c=10%, nominal significance level α=5%, 10,000 sequences per design, and 100,000 repetitions per sequence. BSD, big stick design; MP, maximal procedure; PBR, permuted block randomization; RAR, random allocation rule.

Figure 4.

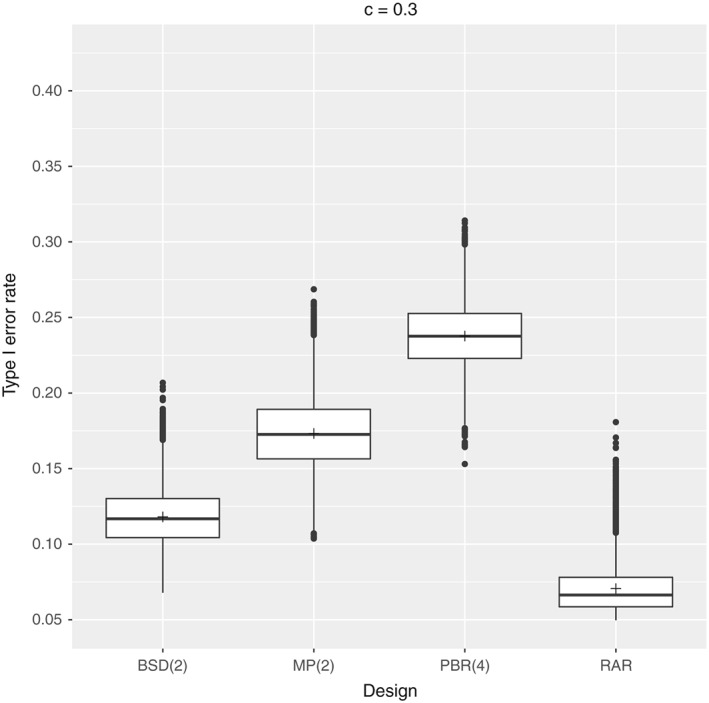
Setting: n=100 patients with biasing factor δ=0.7, censoring probability c=30%, nominal significance level α=5%, 10,000 sequences per design, and 100,000 repetitions per sequence. BSD, big stick design; MP, maximal procedure; PBR, permuted block randomization; RAR, random allocation rule.

Comparing Figures 2, 3, 4, it appears that the presence of censoring reduces the inflation of type I error probability. This trend can be compared with the power loss due to censoring, as the presence of selection bias impacts the survival distribution within the treatment groups. Thus, our exact analysis of type I error probabilities can be considered as a worst‐case scenario such that the impact of selection bias would only reduce in the presence of censoring.

6. Sensitivity analysis

We believe that our results can serve as a good starting point for further considerations of selection bias in trials with a time‐to‐event outcome, but we are also aware of the current limitations. In particular, assuming an exponentially distributed outcome may seldom prove valid in clinical practice, which is why future research should address extending our considerations to other important survival distributions such as Weibull and Gamma distribution. We comment on this in the following in order to illustrate that this is non‐trivial and requires further study. In addition, we briefly discuss our choice of biasing policy with respect to the biasing strategy considered.

6.1. Other distribution assumptions

Because both our biasing policy and test method are parametric, assuming another distribution implicates the consideration of a different test method as well as the formulation of a new biasing policy. Parametric methods to compare two Weibull distributions, respectively, Gamma distributions, are for example given in 12, 17, 18, 19. We outline a possible extension of our biasing policy in the case where the equality of the two scale parameters is tested under the assumption of equal shape parameters.

A natural extension of biasing policy (4) is to model the impact of bias in terms of a proportional hazards model such that the medical condition of a patient acts as a multiplicative effect on the hazard function. If we additionally require that, regardless of the medical condition, all survival times are based on the same distribution assumption, for example, Weibull or Gamma, this extension is straightforward for Weibull‐distributed outcome only. Specifically, in the case of a Weibull‐distributed outcome, the survival times can be modeled as Weibull distributed with common shape parameter and scale parameter depending on the medical condition and treatment affiliation. In the case of Gamma distribution, however, both requirements cannot be met simultaneously as the ratio of two hazard functions is not constant in time. A slightly modified approach could consist in exploiting the asymptotic convergence of the hazard functions 12 and in postulating proportional limiting hazard functions instead. The resulting survival times can then be modeled as Gamma distributed, sharing the same shape parameter and with scale parameter depending on the medical condition and treatment affiliation.

6.2. Other biasing strategies

As selection bias can occur in multiple ways, we believe that there are several approaches to model a reasonable biasing strategy. Within this paper, we chose to formulate biasing policy (4) following the assumptions by Blackwell and Hodges 14. More specifically, we assumed that all prior assignments are known to the recruiting investigator, that the recruiting investigator has no knowledge of the randomization procedure at hand, and that the investigator chooses patients pursuant to the convergence strategy; that is, in case of imbalance, he or she always expects that the next patient will be assigned to the hitherto less frequently assigned treatment. Changing the aforementioned assumptions results in a modified biasing policy and thus affects the survival distribution assumptions and distribution of the test statistic. The results of Section 5 therefore only prove valid for the aforementioned biasing policy and might change if another biasing strategy is considered. For example, it is frequently assumed that the investigator is aware of the randomization procedure used 4, 5, 20, 21, 22, 23. In this situation, the biasing strategy can be modeled with regard to the probability that the next patient will be assigned to the experimental treatment, varying from guessing all predictable allocations, that is, probability greater than 0.5, up to biasing only deterministic allocations, that is, probability of 1. Especially, the comparison of different procedures with regard to a biasing policy based on deterministic allocations instead of treatment imbalance can yield very different results 20. It has also been considered that in blinded trials or multi‐center trials, it could appear more realistic that blinding only fails partially, making only some previous allocations known to the investigator 4, 6. Others have incorporated the possibility of failed biasing attempts 21, 22 or of an adjusted biasing factor based on previous allocations 24.

7. Discussion

For some time, researchers have been demanding that the choice of randomization method should be made with respect to relevant criteria 4. However, in practice, this is seldom implemented because of the prominent use of block randomization 4. As Berger et al. point out, this predominant use of block randomization usually does not follow any scientifically sound advise but has evolved by virtue of its easy implementation and the lack of willingness to contemplate other randomization procedures. We therefore support their commitment to create awareness for the existence of other randomization procedures. Above all, we want to emphasize the direct influence of the randomization design on the outcome of the trial, in terms of test decision, so as to stress the importance of evaluating multiple options.

The biasing policy introduced for exponentially distributed data and our theoretical derivation of the biased distribution of the F‐statistic without censoring are a first step towards permitting such considerations for trials with a time‐to‐event outcome. Performing a simulation study with and without random censoring, we were able to illustrate that the possible impact of selection bias already depends on the randomization procedure used, because of its dependence on the randomization sequence at hand. This confirms our call for weighing different randomization procedures at the trial planning stage, as well as careful consideration of possible selection bias. We furthermore wish to emphasize that, based on our model assumptions, the impact of selection bias apparently reduces in the presence of random censoring as the inflation of type I error probability decreases. Consequently, our theoretical results for the case of no censoring can be used for worst‐case analysis.

Of course, the scope of the previously considered exemplary settings is limited. First of all, we restricted our comparison to only four exemplary randomization designs, whereas a comprehensive analysis should certainly include more randomization methods in terms of different procedures or parameters. Above all, however, the process of choosing an appropriate randomization method should always incorporate several criteria in line with the existing requirements of the particular study. For example, it is widely recognized that randomization procedures that are less susceptible to selection bias usually perform worse in terms of chronological bias 1, 20. Our findings can therefore only be applied to assess randomization procedures with regard to their behavior in the presence of selection bias and are not meant to serve as a general assessment criteria. In order to fully understand the nature and influence of selection bias on test decisions, further research in the field of trials with a time‐to‐event outcome must strive to also incorporate the consideration of other forms of bias such as chronological bias.

With regard to the biasing policy presented within this paper, a point of criticism might include determining the magnitude of the biasing factor δ. In practice, the exact magnitude of δ will be unknown at the trial planning stage, and setting an appropriate magnitude will certainly depend on the particular study. One reasonable method to overcome this might be to estimate δ based on clinical experience similar to the estimation of the effect size and conduct a sensitivity analysis for distinct values of δ. In case of no prior knowledge, a first approach might be to set the magnitude in dependence of the estimated effect size as performed by Tamm et al. 22. A further concern regarding δ might be that for some purposes, it will be more suitable to model the biasing factor as a random instead of a fixed effect. In that case, the biasing policy can be adapted such that the biasing factor is a random variable whose probability distribution depends on previous allocations 22. However, these investigations are out of the scope of the present paper and topic of future research. Regarding our limitation to the exponential model, we must admit that assuming exponentially distributed data may seldom be a valid distribution assumption. However, this simplification is often used to provide a general idea of the data or to allow a comparison with other more complex model assumptions 25, 26. Overall, we therefore feel that our model is a promising starting point for further elaboration and might serve as a suitable reference model to get a first impression of the impact of selection bias in time‐to‐event studies. In Section 6, we outlined possible generalizations to other distribution assumptions such as Weibull and Gamma distribution, explaining why those generalizations were not made within the scope of the present paper and will require a closer inspection in the future. Also, in order to handle more frequently encountered settings, future research must address extending our initial contemplations to other test statistics such as the log rank test.

Overall, we both aim at extending our theoretical results to more general models as well as making our findings available to the community. In particular, we are seeking to include our results in the recently developed software tool by Uschner et al. 9, which provides a comprehensive tool to investigate bias in parallel group trials with a normally distributed outcome but does not yet address the unmet need of studying the impact of bias in trials with a time‐to‐event outcome. In the long term, we also wish to provide a method to correct for selection bias 23, 27, 28, that is, which allows to draw valid conclusions despite the presence of bias. The presence of third‐order selection bias in completed studies can, for example, be detected using the Berger–Exner test 28 or graph 1.

Appendix 1.

1.1.

A.1. Derivation of the biased distribution

Given the realized randomization sequence t, we can compute the number of patients with good, neutral, and bad expected response within each treatment group (Table 1) as a result of the biasing policy (4). The F‐statistic consequently can be decomposed into three sums within numerator and denominator, where each sum comprises all patients sharing the same expected response within one study group, that is,

$$S_F=\frac{Y_1/n_1}{Y_0/n_0}=\mathrm{\Delta }{n}_0/n_1\frac{{\lambda }_1{Y}_1}{{\lambda }_0{Y}_0}\text{such that}{\lambda }_j{Y}_j=Y_{n_{j1}}+Y_{n_{j2}}+Y_{n_{j3}},\text{for}j\in \{0,1\},$$

where $Y_{n_{j1}}\sim \text{Erl}(\delta ,n_{j1}),Y_{n_{j2}}\sim \text{Erl}(1,n_{j2})$, and $Y_{n_{j3}}\sim \text{Erl}(1/\delta ,n_{j3})$. Recall that conditional upon t, the random variables Y ₁,…,Y _n are mutually independent, and hence, the same applies to $Y_{n_{01}},\dots ,Y_{n_{13}}$. The problem to derive the distribution of λ _j Y _j can generally be described as the problem to derive the distribution of a sum of k independent random variables Z ₁,…,Z _k, where Z _i∼Erl(β _i,α _i) follows an Erlang distribution such that

$$f_{Z_i}\left(t\right)=\left\{\begin{array}{cc}\frac{{\beta }_i^{{\alpha }_i}}{\mathrm{\Gamma }\left({\alpha }_i\right)}{t}^{{\alpha }_i-1}{\mathrm{e}}^{-t{\beta }_i}& \text{for all}t>0,\\ 0& \text{for all}t⩽0,\end{array}\right.$$ (A.1)

with ${\alpha }_i\in \mathbb{N}$ and β _i>0. The problem to derive the distribution of such a sum for the case that β _i≠β _j for i≠j has been addressed by several authors. We studied the approaches presented by Mathai 29, Kordecki and Jasiulewicz 30, Akkouchi 31, and Moschopoulos 32. Because we found that for our purposes, Moschopoulos's formula appears to perform best with regard to run time and numerical stability of the evaluation, we will only present the resulting biased distribution corresponding to his approach.

In particular, using Moschopoulos's formula yields the following conditional density distribution function for λ _j Y _j:

$$f_{{\lambda }_j{Y}_j|\mathit{T}=\mathit{t}}\left(x\right)={\delta }^{2n_{j1}+n_{j2}}\sum _{k=0}^{\infty }{\delta }^{-n_j-k}{d}_j\left(k\right)x^{n_j+k-1}{\mathrm{e}}^{-x/\delta },\text{for}x>0\text{and}0\text{elsewhere},$$ (A.2)

where d _j is defined in (6) and j∈{0,1}. Given those two densities, we can compute the conditional density of the ratio $Y:=\left({\lambda }_1{Y}_1\right)/\left({\lambda }_0{Y}_0\right)$ using the following identity 33:

$$f_{Y|\mathit{T}=\mathit{t}}\left(x\right)={\int }_{-\infty }^{\infty }y{f}_{{\lambda }_1{Y}_1|\mathit{T}=\mathit{t}}\left(xy\right)f_{{\lambda }_0{Y}_0|\mathit{T}=\mathit{t}}\left(y\right)dy,\text{for}x\in \mathbb{R}.$$

Inserting (A.2), we obtain that for $C={\delta }^{2n_{01}+2n_{11}+n_{02}+n_{12}}$ and x>0,

$$\begin{array}{ccc}\hfill f_{Y|\mathit{T}=\mathit{t}}\left(x\right)& ={\int }_0^{\infty }C\sum _{k=0}^{\infty }\frac{d_1\left(k\right)x^{n_1+k-1}}{\mathrm{\Gamma }(n_1+k)}\sum _{l=0}^{\infty }\frac{d_0\left(l\right){\delta }^{-n_1-k-n_0-l}}{\mathrm{\Gamma }(n_0+l)}{y}^{n_1+k+n_0+l-1}{\mathrm{e}}^{-y/\delta (x+1)}dy\hfill & \hfill \\ \hfill & =C\sum _{k=0}^{\infty }\frac{d_1\left(k\right)x^{n_1+k-1}}{\mathrm{\Gamma }(n_1+k)}\sum _{l=0}^{\infty }\frac{d_0\left(l\right){\delta }^{-n_1-k-n_0-l}}{\mathrm{\Gamma }(n_0+l)}{\int }_0^{\infty }{y}^{n_1+k+n_0+l-1}{\mathrm{e}}^{-y/\delta (x+1)}dy,\hfill \end{array}$$

where the last equality follows from the monotone convergence theorem. Straightforward calculations then yield that the conditional density can be expressed as f _Y|T=t(x)=0, for $x⩽0$, and

$$f_{Y|\mathit{T}=\mathit{t}}\left(x\right)=C\sum _{k=0}^{\infty }{d}_1\left(k\right)x^{n_1+k-1}\sum _{l=0}^{\infty }\frac{d_0\left(l\right)\mathrm{B}{(n_1+k,n_0+l)}^{-1}}{{(x+1)}^{n_1+k+n_0+l}},\text{for}x>0.$$ (A.3)

Again, using the monotone convergence theorem, we further find that the corresponding distribution function is given by F _Y|T=t(x)=0 for $x⩽0$, and

$$\begin{array}{ccc}\hfill F_{Y|\mathit{T}=\mathit{t}}\left(x\right)& ={\int }_0^{x}C\sum _{k=0}^{\infty }{d}_1\left(k\right)y^{n_1+k-1}\sum _{l=0}^{\infty }\frac{d_0\left(l\right)\mathrm{B}{(n_1+k,n_0+l)}^{-1}}{{(y+1)}^{n_1+k+n_0+l}}dy\hfill & \hfill \\ \hfill & =C\sum _{k=0}^{\infty }{d}_1\left(k\right)\sum _{l=0}^{\infty }{d}_0\left(l\right)\mathrm{B}{(n_1+k,n_0+l)}^{-1}{\int }_0^x\frac{y^{n_1+k-1}}{{(y+1)}^{n_1+k+n_0+l}}dy\hfill \\ \hfill & =C\sum _{k=0}^{\infty }{d}_1\left(k\right)\sum _{l=0}^{\infty }{d}_0\left(l\right)\mathrm{B}{(n_1+k,n_0+l)}^{-1}\tilde{d}(n_1+k,n_0+l,x),\text{for}x>0,\hfill \end{array}$$ (A.4)

where

$$\tilde{d}(a+1,b,x)=\frac{1}{a+b}\left(-\frac{x^a}{{(x+1)}^{a+b}}+a\tilde{d}(a,b,x)\right),\tilde{d}(1,b,x)=\frac{1}{b}\left(1-{(x+1)}^{-b}\right).$$

The conditional distribution of S _F can then easily be derived from (A.3) and (A.4), as for all $x\in \mathbb{R}$:

$$F_{S_F|\mathit{T}=\mathit{t}}\left(x\right)=P(S_F⩽x|\mathit{T}=\mathit{t})=F_{Y|\mathit{T}=\mathit{t}}\left(n_{1}x/\left(n_0\mathrm{\Delta }\right)\right)\text{and}{f}_{S_F|\mathit{T}=\mathit{t}}(x)=n_1/(n_0\mathrm{\Delta })f_{Y|\mathit{T}=\mathit{t}}\left(n_{1}x/\left(n_0\mathrm{\Delta }\right)\right).$$

Rückbeil, M. V. , Hilgers, R.‐D. , and Heussen, N. (2017) Assessing the impact of selection bias on test decisions in trials with a time‐to‐event outcome. Statist. Med., 36: 2656–2668. doi: 10.1002/sim.7299.