Evaluation of climate‐related carbon turnover processes in global vegetation models for boreal and temperate forests

Abstract

Turnover concepts in state‐of‐the‐art global vegetation models (GVMs) account for various processes, but are often highly simplified and may not include an adequate representation of the dominant processes that shape vegetation carbon turnover rates in real forest ecosystems at a large spatial scale. Here, we evaluate vegetation carbon turnover processes in GVMs participating in the Inter‐Sectoral Impact Model Intercomparison Project (ISI‐MIP, including HYBRID4, JeDi, JULES, LPJml, ORCHIDEE, SDGVM, and VISIT) using estimates of vegetation carbon turnover rate (k) derived from a combination of remote sensing based products of biomass and net primary production (NPP). We find that current model limitations lead to considerable biases in the simulated biomass and in k (severe underestimations by all models except JeDi and VISIT compared to observation‐based average k), likely contributing to underestimation of positive feedbacks of the northern forest carbon balance to climate change caused by changes in forest mortality. A need for improved turnover concepts related to frost damage, drought, and insect outbreaks to better reproduce observation‐based spatial patterns in k is identified. As direct frost damage effects on mortality are usually not accounted for in these GVMs, simulated relationships between k and winter length in boreal forests are not consistent between different regions and strongly biased compared to the observation‐based relationships. Some models show a response of k to drought in temperate forests as a result of impacts of water availability on NPP, growth efficiency or carbon balance dependent mortality as well as soil or litter moisture effects on leaf turnover or fire. However, further direct drought effects such as carbon starvation (only in HYBRID4) or hydraulic failure are usually not taken into account by the investigated GVMs. While they are considered dominant large‐scale mortality agents, mortality mechanisms related to insects and pathogens are not explicitly treated in these models.

1. Introduction

Model projections show considerable differences in the carbon uptake by terrestrial ecosystems until 2100, and a continued carbon sink remains questionable (Ahlström, Schurgers, Arneth & Smith, 2012; Friedlingstein et al., 2014). The feedback between the land carbon cycle and climate is determined by carbon turnover processes and productivity (Carvalhais et al., 2014). Dynamics of carbon turnover processes can be quantified by the concept of carbon turnover rate, which describes the fraction of carbon released from a carbon pool (vegetation, soil, or entire ecosystem) during a specific time. It equals the reciprocal of carbon turnover time and, under steady state conditions, approximates carbon residence time, which denotes the average residence time of carbon in a certain pool. With regard to the vegetation, the uncertainty in the response of carbon residence time to climate change was found to contribute more strongly to the variance in predicted carbon stock change than differences between global vegetation models (GVMs) in the response of net primary production (NPP) to future climate and CO₂ (Friend et al., 2014). Contrasting results were found in another model intercomparison study, which might, however, be caused by missing representations of turnover processes in the investigated models (Koven et al., 2015). Furthermore, the uncertainty in projected vegetation carbon residence time, but not in NPP, is dominated by the difference in GVM projections rather than the uncertainty in emission scenarios and climate projections in boreal and temperate forests (Nishina et al., 2015). The spatial variation with climate has been more extensively studied for NPP than for carbon turnover processes. Spatial gradients of increasing productivity with temperature and precipitation in boreal and temperate forests have both been observed in estimates of NPP (Luyssaert et al., 2007) and gross primary production (GPP; Beer et al., 2010), and their broad‐scale features can be reproduced by GVMs (Beer et al., 2010; Cramer et al., 1999). However, the upper bound of NPP is mostly limited by temperature in boreal regions, and by radiation and temperature in winter, temperature in spring and precipitation in summer in temperate ecosystems (Running et al., 2004), and in general also by nutrient availability (LeBauer & Treseder, 2008).

The relationship between vegetation carbon turnover processes and climate and their response to climate change is less well understood (Friend et al., 2014). Current GVMs contain a wide range of different assumptions regarding mortality due to a lack of understanding (McDowell et al., 2011). The complex nature and interactions of mortality agents, comprising long‐term background mortality as well as short‐term disturbance events and management‐related mortality, complicate the derivation of consistent estimates from field studies. Background mortality denotes any process other than catastrophic events contributing to forest mortality rates (van Mantgem et al., 2009). It involves age‐related mortality (Penuelas, 2005) as well as mortality due to competition for limited resources (Craine & Dybzinski, 2013), which are influenced by environmental conditions including climate. In addition to mortality of individuals, other processes such as herbivory and litterfall (senescence of tree components) contribute to background vegetation carbon turnover in forests. Concerning extreme events, research has focused mainly on direct and indirect effects of drought stress on forest mortality (Allen et al., 2010). In North America, insects are considered the most important mortality agent, contributing substantially to the carbon balance (Kurz et al., 2008; Logan, Régnière & Powell, 2003). Insect epidemics are triggered by elevated minimum winter temperatures, which determine survival rates (Safranyik & Carroll, 2006). In addition, fire and extreme climate events other than drought and heat, including storms, ice storms, and frost, can contribute significantly to large‐scale forest mortality (Frank et al., 2015; Reichstein et al., 2013). However, despite numerous local and regional studies, hypotheses for the dominant climate drivers of large‐scale vegetation carbon turnover remain speculative. Direct observations of the variety of forest turnover processes acting at such different spatial and temporal scales would require long‐term or continental‐scale inventory efforts which are unavailable and in practice nearly impossible.

Due to this knowledge gap and shortcomings such as neglect of forest management, models are unable to correctly simulate spatial patterns of vegetation carbon stock at a global scale (Carvalhais et al., 2014). In the tropics, the spatial variation in simulated woody aboveground biomass (AGB) by the ORCHIDEE GVM was found to differ significantly from observations, but could be improved after introducing a positive (empirical) relationship between productivity and mortality rates (Delbart et al., 2010). In contrast, a more recent study (Johnson et al., 2016) making use of a collection of in situ measurements in intact Amazonian forests identifies stem mortality as the most important predictor of the spatial variation in AGB, whereas strong relationships between woody NPP and AGB are simulated by GVMs, differing from the observations and highlighting the need for more sophisticated mortality representations within models. Galbraith et al. (2013) reported a sixfold variation in the carbon residence time of woody biomass across tropical forests, illustrating that these differences cannot be reproduced by GVMs relying on a constant residence time within plant functional types (PFTs). Outside the tropics, the evaluation of modelled carbon stocks was hampered by the unavailability of spatially extensive and consistent observations, until a carbon density map based on radar remote sensing, and covering the northern boreal and temperate forests recently became available (Santoro et al., 2015; Thurner et al., 2014). Coupled Model Intercomparison Project Phase 5 (CMIP5) models show a large spread in simulated vegetation carbon stocks, ranging from roughly 100 to 400 Pg C stored in the Northern Hemisphere (20–90°N; Anav et al., 2013). Although a version of the ORCHIDEE model with improved vegetation dynamics accounting for mortality by extreme cold, spring frost, fire, and competition was able to better reproduce observed carbon density in some northern boreal and temperate forest regions, there are still substantial differences in the biomass spatial variation between model and observations (Zhu et al., 2015).

Recently, remote sensing based NPP and biomass products have been used to identify climate variables and related processes explaining the spatial variation in vegetation carbon turnover rate (k) in boreal and temperate forests (Thurner et al., 2016). In boreal forests, it was found to be associated with winter temperature and winter length, suggesting that frost damage and the trade‐off between growth and frost adaptation are important turnover processes in this ecosystem. In contrast, for temperate forests drought stress and winter length with potential repercussion on insect and pathogen abundance have been found to be related to broad‐scale gradients in k (Thurner et al., 2016).

Here, we investigate the extent to which GVMs are able to reproduce these observation‐based broad‐scale relationships. ISI‐MIP comprises a wide range of state‐of‐the‐art GVMs with the same spatial grid size (.5° × .5°). Among the variety of processes determining k (photosynthesis, autotrophic respiration, carbon allocation, carbon turnover including background mortality, disturbances, and management), we are especially interested in climate effects on simulated turnover processes. Furthermore, we aim to separate deviations from observation‐based k caused by mismatches in productivity from those related to inadequate representation of turnover processes.

2. Materials and Methods

2.1. Carbon turnover concepts in GVMs

GVMs participating in ISI‐MIP (Warszawski et al., 2014), including HYBRID4 (Friend, Stevens, Knox & Cannell, 1997; Friend & White, 2000), JeDi (Pavlick, Drewry, Bohn, Reu & Kleidon, 2013), JULES (Clark et al., 2011), LPJml (Sitch et al., 2003), ORCHIDEE (Delbart et al., 2010; Krinner et al., 2005), SDGVM (Woodward & Lomas, 2004), and VISIT (Inatomi, Ito, Ishijima & Murayama, 2010; Ito & Oikawa, 2002), have been considered in this study. These GVMs contain different levels of complexity of implemented carbon turnover processes (Table 1). Vegetation is not necessarily in steady state given the simulation of productivity, mortality, establishment, succession, and recovery dynamics of vegetation in response to changes in climate and atmospheric CO₂.

Table 1.

Implemented carbon turnover processes in investigated GVMs (modified from Friend et al. 2014 and McDowell et al. 2011)

Model	Carbon turnover processes
	Background rated	Competition	Fire	Growth efficiency, NPP or carbon balance dependence	Heat stress	Phenology affected by climate
HYBRID4 c , e	+a	Forest gap model; competition for light, water and N; controls mortality of individuals due to the carbon balance of the tree (see on the right)	‐b	Mortality of individual trees if insufficient C available in foliage + storage C or fine root + storage C; effects of drought‐induced embolism and frost damage on carbon uptake	‐b	Phenology of dry‐ and cold‐deciduous trees is affected by drought and frost
JeDi c , f	Turnover times are affected by functional trait parameters	Abundances of different plant growth strategies determined from their biomass	‐b	Increased leaf and fine root turnover if current NPP < 0 and long‐term NPP < 0	‐b	Phenology affected by plant strategy and climate
JULES c , g	Division into disturbance and turnover rate	Density dependent competition for light	‐b	‐b	‐b	Leaf turnover increases in case of low temperatures
LPJml c , h	+a	Competition for light and water (canopy cover upper threshold)	f(Fuel load, litter moisture) (Thonicke et al., 2001)	Growth efficiency dependent mortality = f(Biomass increment/Leaf area)	f(Annual growing degree‐days (GDD) above a PFT‐specific threshold); linear; only in boreal forests	In dependence of GDD and frost for deciduous trees
ORCHIDEE i	PFT‐specific background rate (including rate lost due to herbivory; fraction of leaves and fine roots lost dependent on leaf age)	‐b	‐b	‐b	‐b	Leaf longevity is reduced in case of soil moisture stress, atmospheric dryness, and very high temperatures
SDGVM j	Maximum age and fixed rate	Thinning as a result of competition between cohorts within each individual PFT	f(Monthly averages of precipitation and temperature)	Mortality of cohort if storage C depleted; mortality = 1 for annual NPP < 10 g m−2 yr−1 which decreases up to 0 for NPP ≥600 g m−2 yr−1	‐b	‐b
VISIT k	+a	‐b	f(Fuel load, litter moisture) (Thonicke et al., 2001)	‐b	‐b	‐b

^aImplemented mortality algorithm.

^bMortality algorithm not implemented.

^cDGVM: Mortality of PFTs occurs, for example, if long‐term climate exceeds climatic tolerances (LPJml).

^dBackground mortality rate usually divided between foliage, wood, and fine root turnover rates.

^eFriend and White (2000); Friend et al. (1997).

^fPavlick et al. (2013).

^gClark et al. (2011).

^hSitch et al. (2003).

ⁱKrinner et al. (2005); Delbart et al. (2010).

^jWoodward and Lomas (2004).

^kIto and Oikawa (2002); Inatomi et al. (2010).

All models simulate background carbon turnover as a constant rate, usually varying between PFTs and separating between compartments. SDGVM in addition prescribes mortality at a maximum forest age. Such simple carbon turnover concepts do not respond to climate or other environmental factors. However, in JULES leaf turnover increases under low temperatures (Clark et al., 2011). Similarly, in the majority of the models phenology is affected by climate, for instance in HYBRID4 by drought and frost in deciduous trees. In the version of ORCHIDEE used for ISI‐MIP, soil moisture stress and low temperatures also modulate leaf longevity, which in turn changes leaf carbon turnover (Krinner et al., 2005). Although in most of the models many climate‐driven mortality processes are not explicitly treated, temperature and precipitation directly or indirectly influence several implemented mortality algorithms.

In HYBRID4, individual trees compete for light, water, and nitrogen, and mortality is finally dependent on the carbon balance as a result of insufficient labile carbon in foliage, fine root, and storage pools (Friend & White, 2000). While in JeDi competition between plants with different growth strategies is based on their respective biomass, in JULES it is a function of available space, with taller vegetation dominating shorter (competition for light) and competition (and thus turnover) increasing at higher vegetation densities. In LPJml, competition between PFTs for light leads to mortality (self‐thinning) when an upper threshold of canopy cover is exceeded (Sitch et al., 2003). Thinning as a result of competition is also considered by SDGVM, whereas forest cohorts compete within each individual PFT.

Fire schemes dependent on fuel availability and moisture are incorporated in LPJml (Thonicke, Venevsky, Sitch & Cramer, 2001), SDGVM (Woodward & Lomas, 2004), and VISIT (fire scheme of Thonicke et al., 2001). Litter or soil moisture is directly influenced by climatic conditions, including precipitation and temperature. LPJml is the only GVM within ISI‐MIP accounting for mortality due to low growth efficiency and to heat stress. The former is inversely related to growth efficiency, which is defined as the ratio of annual biomass increment to leaf area. In boreal forests, heat stress occurs when the annual degree‐day sum exceeds a PFT‐specific threshold and increases linearly with further increasing annual degree‐day sum (Sitch et al., 2003). Mortality is dependent on NPP or the carbon balance and thus indirectly on climatic factors in HYBRID4, JeDi, and SDGVM. In a mechanistic approach in HYBRID4, where drought‐induced embolism (reducing xylem conductivity and thus potential leaf area and stomatal conductance) and frost damage (reducing the photosynthetic capacity of leaves) can lead to a decreased carbon uptake, mortality occurs if the available labile carbon plus either foliage carbon or fine root carbon falls to zero (Friend & White, 2000). In contrast, in JeDi (Pavlick et al., 2013) a negative overall carbon balance is considered to lead to increased mortality, whereas in SDGVM death of forest cohorts occurs when the storage carbon pool is depleted, and in addition, low annual NPP causes increased mortality.

Instead of PFTs, JeDi uses a large set of functional trait combinations, with some traits affecting turnover rates of biomass pools as well as NPP effects on senescence. The response time to favourable growing conditions and the turnover time of structural, leaf, and fine root pools are formulated as traits which differ between plant growth strategies and are indirectly related to climate. Furthermore, in dynamic GVMs (DGVMs), including HYBRID4, JeDi, JULES, and LPJml, exceeding bioclimatic tolerances over long time periods (or, in the case of HYBRID4, competition between PFTs) leads to a redistribution of PFTs (or, for JeDi, the abundance of different plant growth strategies), and thus, turnover rates are influenced indirectly. Overall, direct frost and drought stress effects on the simulated carbon balance and thus on mortality are explicitly considered in HYBRID4 only, but indirectly or not at all in the other GVMs. Insects and pathogens are not explicitly accounted for in any of the GVMs participating in ISI‐MIP.

2.2. Derivation of vegetation carbon turnover rate from GVMs

The simulated vegetation carbon turnover rate k is derived from GVM results in a similar manner as in Thurner et al. (2016). Under the assumption of steady state, the influx (NPP) to the forest vegetation carbon reservoir (biomass) is balanced with its efflux (biomass × k). Thus, k can be derived from the flux and the reservoir size:

$$k=\frac{\mathrm{NPP}}{\mathrm{Biomass}}.$$ (1)

Here, k (yr⁻¹) indicates the rate at which carbon is lost from the forest biomass pools. It equals the reciprocal of vegetation carbon turnover time or, under steady state conditions, vegetation carbon residence time.

Simulated 5‐year average NPP (2000–2004; kg C m⁻² yr⁻¹) and biomass (or vegetation carbon density; kg C m⁻²; accounting for stem, branch, root, and foliage biomass) in 2004 from historical model runs are used, focusing on the northern hemisphere boreal and temperate forests (30–80°N). These settings provide the best possible comparability to former observation‐based investigations of k (Thurner et al., 2016; refer to Appendix S2 for an updated description of the observation‐based analysis). For JeDi, JULES, ORCHIDEE, and VISIT, monthly simulations are available, and biomass is obtained as the average of the biomass values in June–August to account for the maximum leaf biomass during that year, whereas for the other models (HYBRID4, LPJml, SDGVM), NPP and biomass are derived from yearly model outputs. Simulations used here are based on the bias‐corrected Met Office Hadley Centre Global Environment Model version 2 – Earth System (HadGEM2‐ES; Collins et al., 2011) climate data and CO₂ forcing applied within ISI‐MIP at .5° resolution. Boreal and temperate ecoregions are separated according to Olson et al. (2001). Only .5° grid cells containing at least 40% forest covered grid cells at .01° scale (according to the GLC2000 land‐use/land‐cover map (Bartholomé & Belward, 2005; available from JRC, 2003)) are considered to be dominated by forest and included in the analysis. Nevertheless, in some grid cells nonforest vegetation might contribute significantly to the carbon stocks and fluxes simulated by the GVMs. However, underlying PFT distributions are not available for all of the GVMs, as JeDi is based on individual plant strategies rather than a PFT concept. To further minimize the influence of nonforest vegetation on our results, grid cells with biomass <1 kg C m⁻² are masked out in all of the model outputs.

2.3. Evaluation of k, NPP, and biomass at biome level

In addition to the spatial patterns of k and their relationships to climate variables, modelled k, NPP, and biomass are evaluated at a biome level (boreal and temperate forests) against observation‐based products (in terms of biome averages and their spatial correlation). Comparing modelled and observation‐based k, NPP and biomass can reveal systematic biases in the simulated carbon fluxes and stocks. Here, we compare modelled k to spatially explicit estimates of k (Thurner et al., 2016) derived from a combination of remote sensing based estimates of biomass (Santoro et al., 2011, 2015; Thurner et al., 2014) and NPP, where the latter products include MODIS (Collection 5 version 55; Running et al., 2004; Zhao, Heinsch, Nemani & Running, 2005; Zhao & Running, 2010), BETHY/DLR (Tum, Zeidler, Günther & Esch, 2016; Wißkirchen et al., 2013), and an average of both. While the spatial variation in MODIS and BETHY/DLR NPP is mainly driven by remote sensing observations of biophysical variables like the fraction of photosynthetically active radiation absorbed by the vegetation (fPAR), land cover, and leaf area index (LAI), both NPP products rely on productivity and respiration models (Heinsch et al., 2003; Knorr, 2000; Knorr & Kattge, 2005). Evaluation studies have demonstrated the validity of MODIS NPP in boreal and temperate forests, although relying on a limited number of test sites (Turner et al., 2005, 2006; Zhao et al., 2005), whereas BETHY/DLR GPP and NPP have been validated for Europe using FLUXNET (Wißkirchen et al., 2013) and national forest inventory data (Tum, Buchhorn, Günther & Haller, 2011). The radar remote sensing based biomass product takes into account above‐ as well as belowground vegetation carbon stocks, applying information on wood density and allometric relationships (derived from forest inventory databases) to estimates of stem volume from remote sensing. A corresponding uncertainty estimate integrates the uncertainty of the underlying remote sensing and inventory data. The high accuracy (r² = .70–.90) of this biomass product with respect to upscaled forest inventory biomass has been demonstrated at regional scales (Thurner et al., 2014).

2.4. Controls of vegetation carbon turnover rate

Climate variables considered as influencing k include the number of icing days, number of frost days, and maximum length of warm–dry periods. These are selected as they are related to observation‐based k in boreal and temperate forest transects (Thurner et al., 2016; for transect definition see Appendix S1). Icing days are defined as the annual number of days with a daily maximum temperature below 0°C, whereas frost days are the annual number of days with a daily minimum temperature below 0°C. We refer to warm–dry periods as both warm (Tmax ≥ 10°C) and dry (without precipitation) consecutive days and derive their maximum length for each year. Long‐term average values (1975–2004) are calculated for all of these variables based on daily bias‐corrected HadGEM2‐ES climate data (Collins et al., 2011) at .5° resolution.

The applicability of observation‐based relationships between k and climate variables (Thurner et al., 2016; see Appendix S2) to model simulations is evaluated by their modelling efficiency (MEF; Nash & Sutcliffe, 1970), defined as follows:

$$\mathrm{MEF}=1-\frac{\sum {(isimip-\mathrm{obs})}^2}{\sum {(isimip-\mathrm{mean}(isimip))}^2}$$

where isimip is a modelled value of k and obs is its value calculated from the observation‐based relationship. Negative MEF indicates that the mean of the modelled k values is a better predictor than the k calculated from the observation‐based relationship, while a MEF of 1 indicates a perfect match between model and observations (Nash & Sutcliffe, 1970).

3. Results

3.1. Spatial patterns of turnover rate k

While increasing spatial gradients in k have been detected towards the northern edges of boreal and the southern edges of temperate forests using observation‐based estimates (Thurner et al., 2016), spatial patterns in k are very different between models (Fig. S3.1). Across all models, the spatial variation in k is more strongly related to the spatial variation in biomass than to the spatial variation in NPP, in both boreal and temperate forests (Appendix S4 and Fig. S3.2 and Fig. S3.3). Comparing the ensemble mean of ISI‐MIP models with the observation‐based k (Figure 1), we find that the GVMs simulate lower k across almost the entire northern hemisphere boreal and temperate forests. In most of the selected boreal forest transects (b1, b3, and b4 out of b1–b4; cf. Appendix S1), the GVMs show an increase in k towards the north, similar to the observation‐based spatial patterns. Nevertheless, the relative underestimation of the model ensemble mean with respect to the observation‐based k becomes more pronounced along these gradients as well. In contrast, in the selected temperate forest transects (t1–t4) the GVMs do not reproduce the observed increase in k towards the south. Thus, the relative underestimation of modelled k compared to the observation‐based estimate is more severe in the south of the transects.

Figure 1.

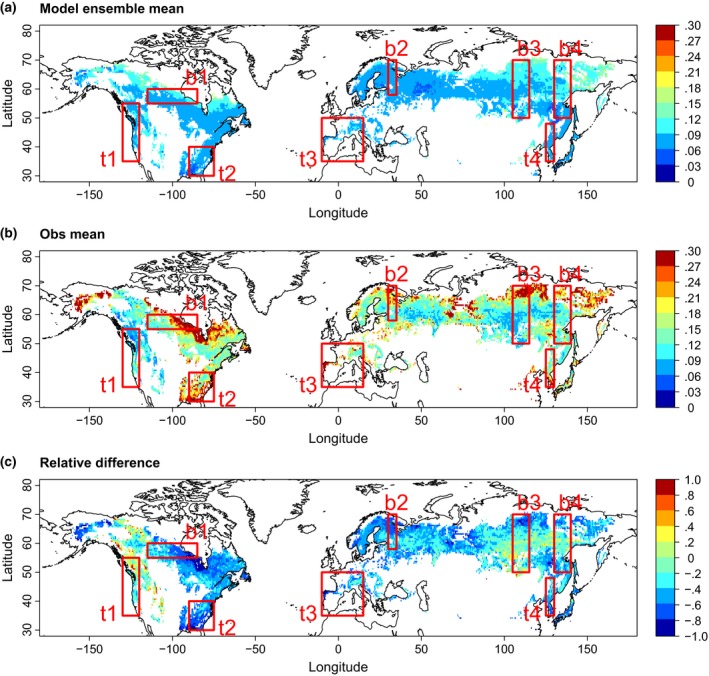
Spatial patterns of forest k [yr⁻¹] as the ratio of NPP to biomass (a) simulated by GVMs participating in ISI‐MIP (ensemble mean of HYBRID4, JeDi, JULES, LPJml, ORCHIDEE, SDGVM, and VISIT) and (b) based on satellite data (Obs mean; using an average of MODIS and BETHY/DLR NPP products and observation‐based biomass from Thurner et al. 2014). The relative difference of (a) with respect to (b) is shown in (c). Only areas with at least 40% forest cover are considered. Red boxes show selected transects (see Appendix S1): b1 Canada, b2 Karelia/Western Russia, b3 Central Siberia/Baikal, b4 Eastern Siberia, t1 Western North America, t2 South‐Eastern North America, t3 South‐Western Europe, t4 North‐Eastern China/Korea

3.2. Comparison of modelled and observation‐based k, NPP, and biomass at biome level

At a biome level, all models but HYBRID4 agree well with the observation‐based estimates of average NPP and are usually within or close to the range defined by MODIS and BETHY/DLR (Figure 2b). In contrast, biomass is severely overestimated (far beyond the uncertainty range) by all the models except JeDi and VISIT, which very closely match the observation‐based mean biomass in both biomes (Figure 2c). Hence, only the simulations by JeDi and VISIT are well‐matched to the mean observation‐based k (Figure 2a), as they do not exhibit significant deviations from either the observation‐based mean NPP or biomass. Although HYBRID4 compares reasonably to the observation‐based average k in boreal forests, this model is associated with considerable overestimation of both NPP and biomass. HYBRID4 overestimates observation‐based NPP (in boreal forests) and biomass (in both boreal and temperate forests) by more than 100%. Hence, a correction of the NPP simulated by HYBRID4 might suffice to match the observation‐based mean biomass in these biomes. All other investigated GVMs (JULES, LPJml, ORCHIDEE, SDGVM) simulate a mean k which is far below the observation‐based average in both boreal and temperate forests, considering its uncertainty bounds.

Figure 2.

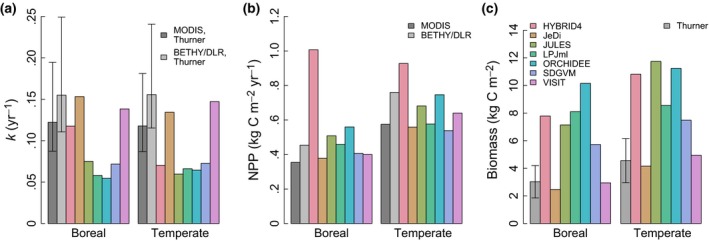
Comparison of observation‐based and simulated (a) mean k, (b) mean NPP, and (c) mean biomass in boreal and temperate forests (cf. Appendix S5). All forest areas at .5° resolution are included, but accounting for nonforest vegetation within these areas. Simulated k, NPP, and biomass are obtained from GVMs participating in ISI‐MIP (HYBRID4, JeDi, JULES, LPJml, ORCHIDEE, SDGVM, VISIT). In (a), the harmonic mean of k has been calculated. Observation‐based k has been derived based on both available NPP products (MODIS and BETHY/DLR), using the biomass product from Thurner et al. (2014). Uncertainty bounds in observation‐based k represent the uncertainty in the biomass product. In (b), observation‐based NPP is available from two products (MODIS and BETHY/DLR). No comparable uncertainty estimates are available for NPP. In (c), observation‐based biomass is obtained from Thurner et al. (2014), including an uncertainty estimate

Spatial correlation analyses show that none of the models can reproduce observation‐based spatial patterns in k in either boreal or temperate forests (Table 2). The Pearson correlation coefficient (r) between mean observation‐based (Obs mean) and simulated k does not exceed .42 (SDGVM) in boreal and .22 (LPJml) in temperate forests, respectively. Also, there are important disagreements between models, the highest correlations between JULES, LPJml, and ORCHIDEE (r = .33–.36) in boreal and between JeDi and VISIT (r = .20) in temperate forests. In many cases, significant negative correlations occur between models and (in temperate forests) between models and observations. Although there are large differences in modelled NPP, spatial correlations with the observation‐based NPP are in general much higher than between simulated and observation‐based k (Table S6.1), except for HYBRID4. In both biomes, the Pearson correlation coefficient between the mean of the NPP products (Obs mean) and some models is ≥ .65 (LPJml and SDGVM in boreal forests; JeDi, JULES, and SDGVM in temperate forests). For biomass, correlations between models and between models and observations are relatively weak (Table S6.2). While in boreal forests SDGVM (r = .72) and ORCHIDEE (r = .58) show the highest agreement with observations, models compare worse in temperate forests, with ORCHIDEE, SDGVM, and VISIT (r = .22–.24) most closely matching the observation‐based biomass.

Table 2.

Spatial correlation between modelled and observation‐based k in boreal (right above the diagonal) and temperate (left below the diagonal) forests. GVMs participating in ISI‐MIP, including HYBRID4, JeDi, JULES, LPJml, ORCHIDEE, SDGVM, and VISIT. k derived from observation‐based NPP, either MODIS, BETHY/DLR, or an average (Obs mean) of both products, and observation‐based biomass. Correlation in terms of the Pearson correlation coefficient and the significance level

MODIS	.93***	.98***	.06***	.03**	.05***	.17***	.31***	.47***	0
.89***	BETHY/DLR	.98***	.04***	.12***	−.07***	.07***	.18***	.35***	.03**
.97***	.98***	Obs mean	.05***	.08***	−.02.	.12***	.24***	.42***	.02
−.39***	−.46***	−.44***	HYBRID4	−.13***	.22***	.08***	.04***	.10***	−.09***
.03	.10***	.07***	−.24***	JeDi	−.28***	−.12***	−.08***	.12***	.05***
−.09***	−.04*	−.07***	.13***	−.20***	JULES	.36***	.33***	.05***	.03*
.17***	.25***	.22***	−.25***	.05**	0	LPJml	.33***	.21***	.03*
.11***	.13***	.13***	−.09***	.02	0	0	ORCHIDEE	.20***	.01
.05**	.03.	.04*	−.04*	−.24***	−.02	.15***	.13***	SDGVM	−.08***
.05**	.07***	.06***	−.03.	.20***	−.03.	−.16***	.04*	−.07***	VISIT

The significance level is quantified by the p‐value: ‘***’ p ≤ .001, ‘**’ .001 < p ≤ .01, ‘*’ .01 < p ≤ .05, ‘.’ .05 < p ≤ 1, ‘ ’ p > .1.

3.3. Spatial relationships between k and climate variables

Observation‐based k was previously shown to increase with the number of icing days in boreal forests (Thurner et al., 2016; cf. Appendix S2). This relationship is hardly reproduced by any of the models in the selected boreal forest transects (Figure 3). The always negative MEF values (Fig. S7.1) indicate that observation‐based k = f(icing days) relationships are not suitable to predict the modelled k. Although all models show deviations from observation‐based relationships, in most models simulated k is positively correlated with icing days in some boreal forest transects (r > .3 for JULES in all transects; HYBRID4 in b2; JeDi in b3 and b4; LPJml in b4; ORCHIDEE in b1, b3, and b4; SDGVM in b1, b2, and b4). In general, NPP decreases slightly as the number of icing days increases, whereas the decrease in biomass is more pronounced in both models and observation‐based products. NPP simulated by GVMs (except for HYBRID4) is relatively close to the observation‐based NPP, but does not decrease as strongly with increasing icing days. Concerning biomass, the spread between models is relatively larger compared to NPP for their relationship to icing days.

Figure 3.

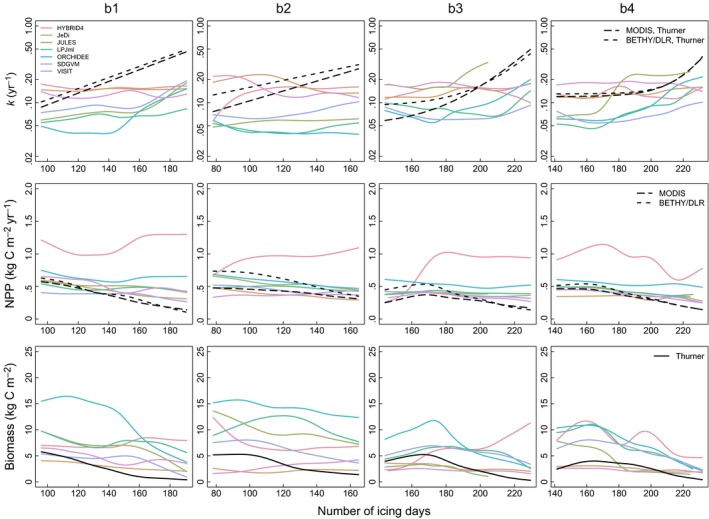
Simulated (coloured lines) and observation‐based (black lines) k, NPP, and biomass as a function of the number of icing days during a year in boreal forest transects (b1 Canada, b2 Karelia/Western Russia, b3 Central Siberia/Baikal, b4 Eastern Siberia). For k and NPP, long‐dashed black lines correspond to the use of MODIS NPP and dashed black lines to the use of BETHY/DLR NPP. Observation‐based biomass has been estimated by Thurner et al. (2014). Exponential functions have been fitted to the observation‐based relationships between k and the climate variable (cf. Appendix S2). All other observation‐based and the simulated relationships between k, NPP, or biomass and the climate variable are represented by smoothing spline fits (Chambers & Hastie, 1992) to the scatter plots (see Appendices S7–S9 for original scatter plots)

The increase in k related to drought in the observation‐based relationships in temperate forest transects is not reproduced by any of the models, with the exception of LPJml (MEF = .208) and SDGVM (MEF = .178) in transect t1. Nevertheless, JULES (t2 and t3), LPJml (t1 and t4), ORCHIDEE (t4), and SDGVM (t1, t3, and t4) show a relationship with r > .3 in some transects (Figure 4 and Fig. S7.2). Usually, NPP is increasing along spatial gradients with longer warm and dry periods. This indicates that dry conditions have little effect on productivity and respiration in most of the models, but also on the observation‐based products. Distinct decreases in biomass in areas with longer warm and dry periods, which are evident in the observation‐based product (in all transects but t1), are hardly visible in modelled biomass (but e.g. to some extent in LPJml).

Figure 4.

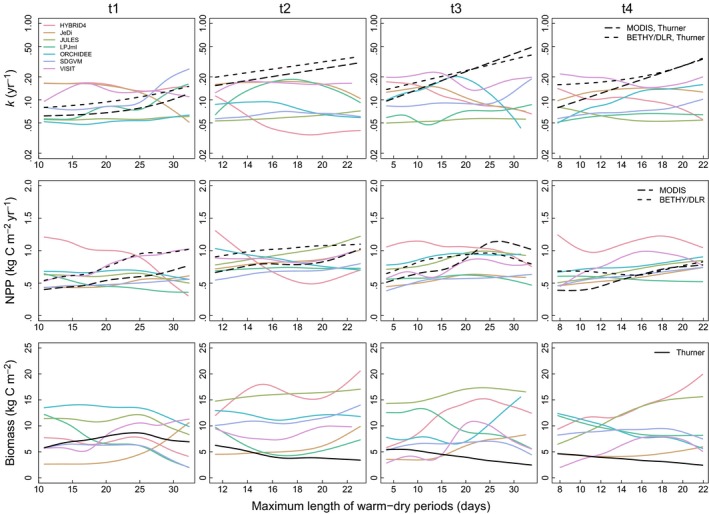
Simulated (coloured lines) and observation‐based (black lines) k, NPP, and biomass as a function of the maximum length of warm–dry periods (in days) during a year in temperate forest transects (t1 Western North America, t2 South‐Eastern North America, t3 South‐Western Europe, t4 North‐Eastern China/Korea). For k and NPP, long‐dashed black lines correspond to the use of MODIS NPP and dashed black lines to the use of BETHY/DLR NPP. Observation‐based biomass has been estimated by Thurner et al. (2014). Exponential functions have been fitted to the observation‐based relationships between k and the climate variable (cf. Appendix S2). All other observation‐based and the simulated relationships between k, NPP, or biomass and the climate variable are represented by smoothing spline fits (Chambers & Hastie, 1992) to the scatter plots (see Appendices S7–S9 for original scatter plots)

None of the investigated GVMs reproduces the observation‐based increase in k related to fewer frost days in temperate forest transects (Figure 5 and Fig. S7.3; MEF < 0). JeDi (t4), JULES (t2 and t3), LPJml (t4), ORCHIDEE (t4), and SDGVM (t4) have r < −.3 in some of the transects, but this might be caused by high correlation between the number of frost days and other climate variables in these areas. Furthermore, in most GVMs, NPP is negatively correlated with the number of frost days, similar to the observation‐based products. These effects of temperature and growing season length on productivity usually propagate to the spatial gradients in biomass simulated by these models, whereas the observation‐based estimates of biomass do not increase with fewer frost days except in t1.

Figure 5.

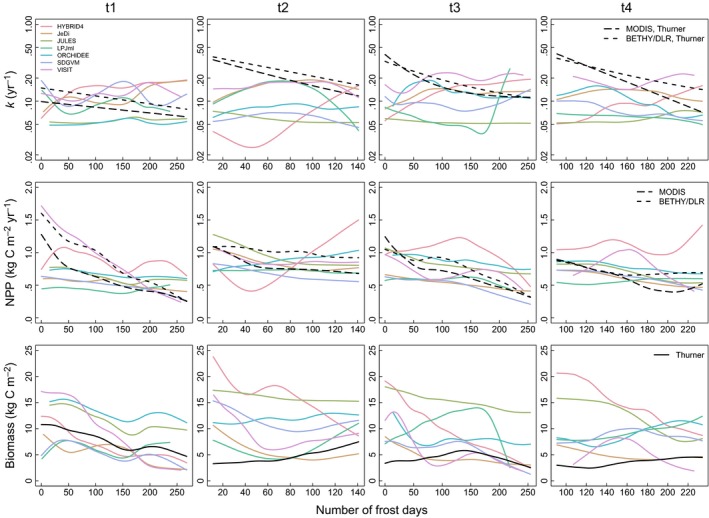
Simulated (coloured lines) and observation‐based (black lines) k, NPP, and biomass as a function of the number of frost days during a year in temperate forest transects (t1 Western North America, t2 South‐Eastern North America, t3 South‐Western Europe, t4 North‐Eastern China/Korea). For k and NPP, long‐dashed black lines correspond to the use of MODIS NPP and dashed black lines to the use of BETHY/DLR NPP. Observation‐based biomass has been estimated by Thurner et al. (2014). Exponential functions have been fitted to the observation‐based relationships between k and the climate variable (cf. Appendix S2). All other observation‐based and the simulated relationships between k, NPP, or biomass and the climate variable are represented by smoothing spline fits (Chambers & Hastie, 1992) to the scatter plots (see Appendices S7–S9 for original scatter plots)

4. Discussion

The performance of the investigated GVMs regarding the spatial patterns of k and its relationship to climate variables is different between models, depending on the ability to reproduce observation‐based NPP and the mortality algorithms they contain. For the first time, remote sensing based biomass together with NPP products has enabled an evaluation of the modelled spatial patterns of biomass and k in northern boreal and temperate forests. Simulated mean NPP at biome level is usually within or close to the range of the two observation‐based estimates (except for HYBRID4). Simulated mean biomass is, however, severely overestimated by most GVMs except JeDi and VISIT. This suggests important shortcomings in the representation and parameterization of mortality processes in current GVMs. Spatial correlation between models and observation‐based products is usually weak (r ≤ .65) for NPP and even weaker for k and biomass, demonstrating that GVMs do not capture the spatial variation in these fundamental carbon stocks and fluxes. Observation‐based spatial relationships between k and climate variables, which are hardly reproduced by the models, suggest that representations of climate‐dependent carbon turnover processes need to be improved in GVMs to correctly simulate spatial patterns in k and biomass. A process‐based understanding of carbon turnover is critical to reduce the uncertainty in the feedback of the forest carbon balance to climate change (Friend et al., 2014). Most of the investigated GVMs currently underestimate k due to missing climate impacts on forest mortality and thus potentially overestimate the negative feedback of boreal and temperate forest ecosystems to climate change (McDowell et al., 2011). This might be especially relevant to temperate forests, where less frost days and longer drought periods are predicted in the future (Sillmann, Kharin, Zwiers, Zhang & Bronaugh, 2013), likely further intensifying large‐scale forest mortality.

4.1. Towards improved vegetation carbon turnover processes in GVMs

Processes such as frost‐induced xylem embolism (Sperry & Sullivan, 1992), desiccation (Sakai & Larcher, 1987), and forest destruction by ice storms (Sun, Gu, Dickinson & Zhou, 2012) are considered to be key mortality mechanisms in northern forest ecosystems (Reichstein et al., 2013). However, direct frost damage effects on mortality are usually not accounted for in GVMs. For instance, among the GVMs participating in ISI‐MIP, only HYBRID4 considered frost stress impacts on the tree carbon balance potentially leading to tree mortality. Due to growth efficiency (in LPJml) and NPP‐dependent mortality rates (in JeDi and SDGVM), some models include indirect effects of low temperatures and of soil water availability in permafrost regions (Beer, Lucht, Gerten, Thonicke & Schmullius, 2007; Beer, Lucht, Schmullius & Shvidenko, 2006) on productivity and mortality. Thus, simulated spatial relationships between k and winter length agree to some extent with observation‐based results in some of the boreal forest transects considered. Among other improvements, a recent study (Zhu et al., 2015) introduced a tree mortality rate increasing linearly with decreasing winter temperature and a broadleaf tree mortality caused by spring frost after bud break in ORCHIDEE, but these improvements were made after the submission of the ISI‐MIP simulations analysed here. Furthermore, cold hardiness and related frost damage have been implemented within the ecosystem model LPJ‐GUESS (Rammig et al., 2010). Besides these examples, frost‐driven mortality usually seems to be underrepresented in current GVMs and in forest ecology research in general, although the basic mechanisms are known (Sakai & Larcher, 1987). In addition, recent fires can cause elevated k in some regions; however, they can hardly explain the observation‐based spatial gradients in k (please refer to Thurner et al., 2016 and corresponding supporting information therein for a more detailed discussion of such aspects). In boreal forests, longer fire return intervals (and thus less impact of fires on long‐term average k) have rather been observed towards their northern boundary (Kharuk, Ranson, Dvinskaya & Im, 2011; Thonicke et al., 2001).

Despite a variety of implemented drought‐related mortality processes, with very few exceptions the investigated GVMs are not able to reproduce observation‐based spatial relationships to drought in temperate forests. We find NPP increasing despite longer periods of drought in most of the models, but also in the observation‐based products, indicating missing or insufficient controls of productivity and respiration by the water cycle. Concerning mortality processes, soil or litter moisture affects leaf turnover (HYBRID4, ORCHIDEE) or fire (LPJml, SDGVM, VISIT) in some models, and indirect impacts of water availability are implemented in terms of NPP, growth efficiency, or carbon balance dependent mortality (HYBRID4, JeDi, LPJml, SDGVM). However, further hydrological impacts on mortality are usually not considered by the investigated GVMs, most importantly direct drought effects such as carbon starvation (only in HYBRID4) or hydraulic failure (Hartmann, Ziegler, Kolle & Trumbore, 2013; McDowell et al., 2011) or drought‐favoured susceptibility to insect and pathogen epidemics (Raffa et al., 2008; Williams et al., 2010) and windthrow (Schlyter, Stjernquist, Bärring, Jönsson & Nilsson, 2006). In addition, integrating fire modules into GVMs is essential to correctly account for the response of long‐term fire return intervals to moisture conditions (Thonicke et al., 2001). Also, for ecosystem carbon turnover time, it has been shown recently that Earth system models do not fully capture covariations with precipitation, again indicating missing feedbacks of water limitations on carbon turnover processes (Carvalhais et al., 2014).

Observation‐based spatial relationships between k and winter length have led to the hypothesis of effects of insect population dynamics on carbon turnover in temperate forests (Thurner et al., 2016). Further research is required to directly assess the impact of insect outbreaks at large scales and to separate these effects from direct drought impacts, which is, however, complicated due to their interaction (Raffa et al., 2008; Williams et al., 2010). Overall, none of the investigated GVMs explicitly represents the effects of winter length and temperature on the survival of insect populations, which in turn would affect forest mortality. There are also no other processes implemented in these models which could cause increased mortality rates as a direct consequence of fewer frost days. Making turnover processes in GVMs depend on climate conditions favouring insect epidemics can serve as a proxy to reproduce the large‐scale spatial impact of these mortality agents. The explicit incorporation of the life cycle of insects into GVMs would be the ultimate step to be taken. Forestry research on this problem is already ongoing, and available conceptual frameworks and models representing insect population dynamics (e.g. Kurz et al., 2008; Logan et al., 2003; Raffa et al., 2008; Régnière & Bentz, 2007) should be evaluated as regards integrating them into GVMs. This would require the adjustment of processes and parameters in order to cover region‐specific differences in insect populations and their dynamics. Finally, other interacting effects of different processes and their importance at global scale also need to be investigated. For instance, first attempts at coupled fire and insect outbreak models have been made (Chen‐Charpentier & Leite, 2014). In addition, forest management and its influence on mortality rates should be improved in GVMs to better represent present‐day turnover rates. One example is the effect of human activities in fire management (Le Page, Morton, Bond‐Lamberty, Pereira & Hurtt, 2015).

4.2. The turnover rate concept – Interpretation and uncertainty

When interpreting spatial patterns of k, note that NPP directly influences biomass accumulation. In the absence of climate‐dependent turnover processes, this leads to the propagation of any biases in climate‐driven NPP patterns to biases in biomass. Thus, spatial differences in the NPP/biomass ratio can be explained by the effects of mortality processes on biomass possibly confounded by differences in the ecosystem state (steady state vs. succession), the potential impact of nonforest vegetation and forest management on k, the uncertainty in modelled NPP and effects of phenology on turnover rates. Our definition of turnover rate and its estimation based on observations include both complete mortality of individual trees and litterfall.

Elevated k in areas of very low biomass might be influenced by a possibly higher contribution of nonforest vegetation within such grid cells. This potential effect might correlate with the investigated climate variables and thus influence the simulated relationships between k and climate. However, by applying a forest cover threshold and by masking out very low biomass areas, we attempted to minimize the influence of nonforest vegetation and also ecosystem state on our results. Apart from disturbances, differences in the ecosystem state between grid cells can be caused by recent shifts in the PFT or plant growth strategy composition in DGVMs (including HYBRID4, JeDi, JULES, LPJml). For example, in LPJml, mortality of PFTs occurs if long‐term climate exceeds climatic tolerances, whereas a short‐term exceedance of a maximum temperature threshold already leads to mortality of boreal forests in this model. In addition, DGVMs usually simulate a potential natural vegetation distribution and thus do not account for land use (e.g. agriculture or forest management), which considerably accelerates biomass turnover in temperate biomes, but to a lesser extent in boreal biomes (Erb et al., 2016). The differences in the spatial patterns in k between observation‐based estimates and the other GVMs (ORCHIDEE, SDGVM, VISIT), which prescribe the vegetation distribution based on observed land cover, are likely to be less affected by the influence of ecosystem state and nonforest vegetation.

Furthermore, the impact of forest management on NPP and biomass can affect our results in some regions (Erb et al., 2016). While forest management contributes to the observation‐based NPP, biomass, and k, it is not considered by the ISI‐MIP models which assume potential natural forests. In general, forest management aims to increase NPP and involves reductions in biomass compared to natural forests, but the observed spatial patterns are not that clear at continental to global scales (Ciais et al., 2008; Noormets et al., 2015). The neglect of management effects in the investigated GVMs could thus partly explain the overestimation of biomass compared to the observations and might also lead to underestimation of simulated k in managed forests. Nevertheless, forest management cannot explain observation‐based spatial gradients in k (Thurner et al., 2016) and the spatial patterns in the deviations of modelled from observation‐based k (Appendix S10).

Concerning the uncertainty in NPP components, there are still important open research questions on the dependence of plant respiration (e.g. Atkin & Tjoelker, 2003; Piao et al., 2010; Smith & Dukes, 2013) and allocation fractions to carbon pools (e.g. Friedlingstein, Joel, Field & Fung, 1999; Litton, Raich & Ryan, 2007; Wolf, Field & Berry, 2011) on environmental conditions, especially at the spatial and temporal scales relevant to GVMs. For example, the ratio of biomass production to GPP is suggested to be related to nutrient availability (Vicca et al., 2012) and management (Campioli et al., 2015). Carbon allocation determines the ratio of carbon pools having different turnover times (i.e., living tissue pools with shorter turnover times vs. woody vegetation pools with longer turnover times) and hence inherently contributes to faster or slower turnover not directly related to mortality. Our estimate of turnover rate integrates over both living tissue and woody vegetation components. In contrast to plant respiration and carbon allocation, the spatial pattern of GPP and its relation to climate are relatively well known at a global scale (Beer et al., 2010; Luyssaert et al., 2007), but there is still considerable uncertainty in simulated GPP between models and their comparison to observations (Piao et al., 2013; Schaefer et al., 2012).

Furthermore, climate‐dependent phenology can contribute to overall carbon turnover rates. This is to some extent the case in HYBRID4, JeDi, JULES, LPJml, and ORCHIDEE, where soil moisture stress and/or low temperatures influence leaf longevity and turnover. The inclusion of a limitation of phenology by cold temperatures, heat stress, light, and water availability has been shown to improve biomass spatial patterns simulated by LPJml compared to the original model version used in ISI‐MIP (Forkel et al., 2014). In addition to direct effects on leaf turnover, phenology can also influence mortality indirectly through impacts on productivity (Xia et al., 2015), carbon allocation, and the vegetation distribution in DGVMs. Nevertheless, as long as climate‐related mortality processes are not considered, a climate‐dependent phenology alone does not enable models to correctly reproduce long‐term carbon dynamics.

Despite all these potential confounding factors, the difference in spatial patterns between k calculated as the ratio of NPP to biomass (as presented here) and k derived from the carbon efflux from vegetation carbon stocks is small (see Appendix S11). The agreement between k derived from the two different methods is very high for all models in terms of correlations (r > .95) and MEF (> 0.9). Furthermore, for all models the differences from observation‐based values of k are more strongly related to errors in biomass than errors in NPP in boreal and temperate forests (Appendix S12). These results strongly support the reliability of our interpretation of the spatial patterns in k in terms of turnover processes.

4.3. Uncertainties in the observation‐based products

In this study, we compared GVM simulations of NPP and biomass (and their ratio, k) to observation‐based estimates. The application of remote sensing based products allows to capture turnover processes acting at spatial and temporal scales which are highly relevant for an appropriate evaluation of k simulated by GVMs. Both GVM simulations and observation‐based products account for above‐ and belowground NPP and biomass. Nevertheless, the consideration or neglect of specific NPP components (Luyssaert et al., 2007) in different models and observation‐based products may contribute to the differences between them. In particular, belowground NPP (and also belowground biomass) is difficult to measure and thus relatively uncertain (Clark et al., 2001). It is noted that the observation‐based NPP products, although their spatial variation is mainly driven by remote sensing observations, themselves involve models of productivity and respiration with their own uncertainty and sensitivity to environmental drivers.

The uncertainty estimate given for biomass is based on a conservative approach and has to be interpreted as an upper bound as a perfect correlation was assumed (i) between the uncertainties in the underlying biomass compartments (stem, branches, foliage, root biomass) and (ii) between the uncertainties in all grid cells (cf. Thurner et al., 2014). In contrast to the rigorously estimated uncertainty in biomass (30–40% in most areas; Thurner et al., 2014), a comparable uncertainty measure is unfortunately not available for the NPP products. Instead, we used the two different NPP products to estimate two different observation‐based turnover rates to represent the variation of available observation‐based NPP. Nonetheless, a wrong representation of processes in the algorithms underlying these products could lead to potential biases that we cannot currently quantify. For further discussion of the limitations of the observation‐based products, the reader is referred to Thurner et al. (2016). Differences between simulated and observation‐based NPP, biomass, and k have been interpreted as shortcomings of the GVMs to reproduce observation‐based biome averages and spatial relationships to climate, but may also be partly due to the uncertainty in the observation‐based products and related assumptions.

The robustness of the presented approach with respect to the influence of interannual variability could be improved by a longer overlap in NPP from ISI‐MIP simulations (up to 2004) and from observation‐based products (the MODIS and BETHY/DLR time series starting in 2000). However, the agreement between modelled k derived for different time spans (1995–2004 vs. 2000–2004) is very high for all models in terms of relative differences, correlations, and spatial variations (Appendix S13). The agreement in observation‐based k is very high for different time spans (2000–2004 vs. 2000–2010), but lower for different NPP products (BETHY/DLR vs. MODIS; Appendix S14). The influence of the difference in time when biomass was estimated between models (2004) and observation (2010) on our findings is considered relatively small at the applied spatial scale.

In conclusion, observation‐based findings are reproduced by the ISI‐MIP models only to a limited extent. In addition to important differences in the spatial patterns of simulated productivity, these results demonstrate the high uncertainty in carbon turnover processes accounted for by GVMs and show the need for improvements of models in this direction. Further research should concentrate on incorporating frost damage effects and the trade‐off between growth and frost adaptation in boreal forests, whereas direct effects of drought and insect epidemics on mortality may need to be considered in temperate forests to improve the agreement with observation‐based estimates of k and biomass.

Supporting information

 

Thurner M, Beer C, Ciais P, et al. Evaluation of climate‐related carbon turnover processes in global vegetation models for boreal and temperate forests. Glob Change Biol. 2017;23:3076–3091. https://doi.org/10.1111/gcb.13660