Abstract
A MATLAB toolbox for the efficient estimation of the threshold, slope, and lapse rate of the psychometric function is described. The toolbox enables the efficient implementation of the updated maximum-likelihood (UML) procedure. The toolbox uses an object-oriented architecture for organizing the experimental variables and computational algorithms, which provides experimenters with flexibility in experimental design and data management. Descriptions of the UML procedure and the UML Toolbox are provided, followed by toolbox use examples. Finally, guidelines and recommendations of parameter configurations are given.
Keywords: Psychometric function, Adaptive procedure
At the core of psychophysics is the quantification of the relationship between changes in physical stimuli and changes in perception. In a typical psychophysical experiment, observers perform detection or discrimination tasks. As the physical property of the stimulus (the signal intensity) is manipulated, the task performance—for example, in terms of proportion correct, systematically changes. The function that summarizes the relationship between the signal intensity and proportion correction is the psychometric function (e.g., Urban, 1910; see Klein, 2001, for a review), which typically exhibits a sigmoidal shape. The estimation of the psychometric function is fundamental to psychophysical experimentation, and therefore, software is available to fit the psychometric function to psychophysical data using a variety of methods.1
When considering alternative forms of the psychometric function, both the dependent variable (proportion correct, proportion of a particular response, etc.) and the shape of the function are key factors. The shape of the psychometric functions may be described parametrically or nonparametrically (e.g., Poppe, Benner, & Elze, 2012; Zchaluk & Foster, 2009), that is, the psychometric function can be modeled using an analytical function whose shape is determined by a set of model parameters or can be model-free and characterized by smoothing the dependent variables across discrete signal intensities. For parametrically described psychometric functions, a variety of parameterization have been used, including Gaussian, Weibull, and logistic cumulative distributions. (e.g., Treutwein & Strasburger, 1999). Two commonly used formulations are the logistic and Weibull (cumulative density) functions. The logistic psychometric function is given by
| (1) |
where α is a threshold parameter indicating the center of the psychometric function’s dynamic range; β is related to the slope of the function; γ is the proportion correct at chance levels of performance, which sets the lower bound of the psychometric function; and λ reflects the upper bound of the psychometric function. Another frequently assumed form of the psychometric function, the Weibull psychometric function is given by (e.g., Harvey, 1986):
| (2) |
where, on a logarithmic axis, α is the threshold parameter and β is the slope/spread parameter; the parameters γ and λ are as in Eq. 1.
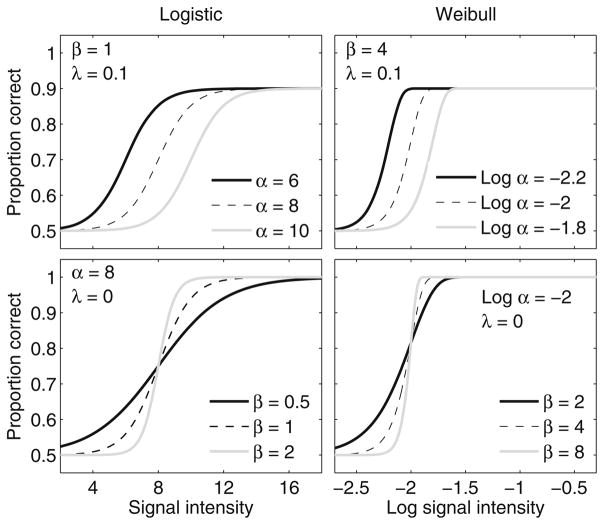
Figure 1 shows the effects of manipulating the parameters of the logistic and Weibull psychometric function on both a linear and a logarithmic abscissa. As the threshold parameter α increases (upper panels), the psychometric functions shift to higher signal intensities. As the slope parameter β increases (lower panels), the psychometric functions become steeper. For the upper panels, the value of λ is set to .1, whereas for the lower panels, the value of λ is 0. Comparing the upper and lower panels, it is evident that the value of λ determines the distance between the upper asymptote of the function and one. When λ = 0, the psychometric function approaches one as the signal intensity increases, whereas when λ > 0, the proportion correct fails to reach one even at very high signal intensities. The λ parameter is referred to as the “lapse rate,” indicating the proportion of times that the listener’s attention has lapsed.
Fig. 1.
Logistic and Weibull formulations of the psychometric functions are presented in the left and right panels, respectively. For these examples, the chance proportion correct without a signal was .5 (i.e., γ = .5). For the top panels, the values of β and λ are fixed, and the different curves reflect differences in α. For the bottom panels, the values of α and λ are fixed, and the different curves indicate differences in the value of β
The method of constant stimuli, which dates to Fechner (Treutwein, 1995), is a common data collection method used to estimate the psychometric function. By this method, several values of signal intensity are selected and then stimuli are presented at these signal intensities in quasi-random order until a pre-determined number of responses are collected at each of the signal intensities. The proportion correct as a function of the signal intensity is computed and the psychometric function is estimated by fitting a function to the resulting data (e.g., Fründ, Haenel, & Wichmann, 2011; Treutwein & Strasburger, 1999; Wichmann & Hill, 2001a, 2001b). One shortcoming of the method of constant stimuli is that the data collection can be time-consuming, especially when the underlying psychometric functions have shallow slopes or high lapse rates. Moreover, because the signal intensities to be tested have to be determined before data collection, it is difficult to assess if the selected values of signal intensity are appropriate. When inappropriate signal intensities are used, the parameters of the psychometric function may be poorly estimated even if a large number of trials are run.
Because the estimation of the psychometric function can be time-intensive, adaptive methods have been developed to efficiently estimate elements of the psychophysical function, such as the threshold and the slope. Adaptive procedures are rule-based procedures for which the stimulus intensity for the upcoming trial depends on the stimuli and responses from previous trials. Both nonparametric and parametric adaptive procedures are available. One example of a nonparametric procedure is the transformed up–down procedure of Levitt (1971), although there are many others (Derman, 1957; Durham & Flournoy, 1995; Garcia-Perez, 1998; Kaernbach, 1991; Rose, Teller, & Rendleman, 1970; Taylor, 1971; Taylor & Creelman, 1967; Wetherill & Levitt, 1965). The transformed up–down procedure estimates the signal intensity associated with a target percent correct on the psychometric function. For the 2-down, 1-up procedure the signal intensity is increased following a single incorrect response and decreased following two consecutive correct responses. The analysis of a run of trials provides an estimate of the 71 % correct point on the psychometric function.
In addition to nonparametric adaptive procedures, several adaptive parametric procedures are available that efficiently estimate the psychometric function’s parameters (e.g., Green, 1990; Hall, 1981; Harvey, 1986; King-Smith & Rose, 1997; Kontsevich & Tyler, 1999; Lam, Dubno, Ahlstrom, He, & Mills, 1997; Laming & Marsh, 1988; Watson & Pelli, 1983; see Leek, 2001, or Treutwein, 1995, for reviews and evaluations of both nonparametric and parametric adaptive procedures). Like nonparametric procedures, these procedures revise the signal intensity depending on the stimuli and responses from past trials. In contrast to the nonparametric methods, a parametric form of the psychometric function is assumed and using maximum-likelihood or Bayesian estimation methods, the stimuli are chosen to provide an estimate of a parameter(s) of the assumed psychometric function. How the procedure proceeds depends on what constitutes a “reasonable estimate” of the parameter; different criteria such as minimizing the expected variance in the psychometric-function parameter, minimizing the uncertainty in the parameter estimate, and so forth, may be used. The best point(s) on the psychometric function that achieves the criterion of interest is sometimes referred to as the “sweet” points, which dictates the next stimulus to be tested.
In the maximum-likelihood (ML) adaptive parametric procedure described by Green (1990), stimulus sampling occurs at the sweet point that minimizes the expected variance of the estimation of α, the threshold. However, if one is interested in estimating multiple parameters needed to specify the psychometric function (e.g., α, β, and λ in Eqs. 1 and 2), using a single sweet point associated with the parameter α can lead to biased estimates of β (Kaernbach, 2001; Leek, Hanna, & Marshall, 1992) and λ (Gu & Green, 1994). To minimize the expected variance for the estimate of β two sweet points are needed, close to the lower and upper asymptotes of the psychometric function, respectively (Brand & Kollmeier, 2002; Kaernbach, 2001; King-Smith & Rose, 1997). For λ, the sweet point is associated with the largest possible signal intensity (Shen & Richards, 2012). For the logistic and Weibull forms of the psychometric function, the sweet points for the parameters α, β, λ, and γ can be expressed analytically (Shen & Richards, 2012), providing the basis of the generalization of the ML procedure described by Green to estimate not just α but also β, λ, and γ (Shen & Richards, 2012). Indicating the resulting procedure’s similarity to Green’s ML procedure, Shen and Richards referred to the procedure as the “updated maximum-likelihood procedure” (UML). This descriptor is somewhat of a misnomer because, like Green’s original ML procedure, the procedure might incorporate prior distributions, and thus may be better described as a Bayesian procedure.
For a psychometric function associated with logistic or Weibull distributions with parameters α, β, and λ (assuming the value of γ is fixed at the expected proportion correct with no stimulus), four sweet points are defined: one for α, two for β, and one for λ. Because these sweet points are known, the decision as to the next stimulus to present depends on which sweet point is to be sampled. Shen and Richards (2012) reported simulations using alternative sweet-point sampling strategies. For one strategy, the sweet point is chosen using a 2-down, 1-up rule. By this rule, following two consecutive correct responses the sweet point to be tested on the next trials is the one lower than the current sweet point. After a single incorrect response, the next sweet point is the one higher than the current sweet point. This is similar to the transformed up–down procedure (Levitt, 1971) except that the manipulation of the signal intensity is based on sweet points. Other strategies, such as the random choice among sweet points, may also be used (Shen & Richards, 2012). Whichever sampling rule is chosen, the estimate of the psychometric function is updated following each experimental trial, as are the estimates of the sweet points. Therefore, even if the same sweet point is sampled on two consecutive trials, the corresponding signal intensities may not be the same.
Because multiple sweet points are sampled, the UML procedure is capable of efficiently estimating multiple parameters of the psychometric function. Because the lapse rate (the λ parameter) is estimated in addition to the threshold and slope parameters, the estimates of the α and β parameters are less likely to be biased due to a subject’s lapses of attention. Moreover, one of the drawbacks of the original maximum-likelihood procedure is that the signal intensity often jumps dramatically from trial to trial at the beginning of an adaptive track, potentially confusing subjects and prolonging the learning of a novel experimental task. The UML procedure with an up–down rule overcomes the difficulty in two ways. First, the up–down sweet-point selection rule limits the changes in signal intensity between consecutive trials. Second, the UML procedure allows the specification of the prior distributions for the psychometric function’s parameters before data collection, which promotes fast convergence of the parameters and avoids large jumps of signal intensity at the beginning of an adaptive track (Treutwein, 1995).
Using computer simulations, Shen and Richards (2012) showed that the UML procedure outperformed the original maximum-likelihood procedure (Green, 1990) when multiple psychometric-function parameters are desired (see also Leek et al., 1992). In a recent study, Shen (2013) measured the psychometric function for an auditory gap-detection task using three adaptive psychophysical procedures: the staircase procedure (Levitt, 1971), the UML procedure (Shen & Richards, 2012), and the entropy-based Bayesian procedure proposed by Kontsevich and Tyler (1999). The results indicated that when the expected lapse rate was low and the number of trials fixed, all three procedures appeared to provide good estimates of the underlying psychometric function. However, when the expected lapse rate was high, the UML procedure was superior to the other two procedures. Therefore, both simulation and behavioral data suggested the usefulness of the UML procedure, especially when high lapse rates are expected from the subjects.
The UML procedure both directs data collection by its choice of the sweet points and provides an estimate of the underlying psychometric function. Its primary function, however, is to direct data collection. In most instances, it is advantageous, post-hoc, to fit the collected data to psychometric functions using algorithms designed for that purpose (e.g., the Psignifit3 Toolbox; Fründ et al., 2011).
Here, we describe a software toolbox for the implementation of the UML procedure. The implementation/architecture of the UML Toolbox is described, instructions regarding the use of the toolbox are provided and an example of the use of the toolbox is discussed. Suggestions for the configuration of the UML procedure are also provided. It should be noted that the UML Toolbox presented here is modest in scope in that only the UML procedure is implemented—that is, software for stimulus generation, a large number of alternative data collection procedures, and so forth, are not provided. Several toolboxes are available that implement a variety of adaptive psychophysical procedures. For example, for the MATLAB environment, the PsychToolbox (Brainard, 1997; Pelli, 1997) includes the QUEST procedure (Watson & Pelli, 1983) and the Ψ procedure (Kontsevich & Tyler, 1999); the Palamedes toolbox (Prins & Kingdom, 2009) includes the transformed up–down (Levitt, 1971), bestPEST (Lieberman & Pentland, 1982), QUEST, and Ψ procedures; and the MLP toolbox (Grassi & Soranzo, 2009) includes the transformed up–down, PEST (Taylor & Creelman, 1967), and maximum-likelihood (Green, 1990) procedures. Thus, guidelines for choosing among various adaptive procedures/toolboxes will be discussed.
The architecture of the UMLToolbox
The UML Toolbox can be downloaded from http://hearlab.ss.uci.edu/UML/uml.html, according to the conditions of the GNU General Public License.
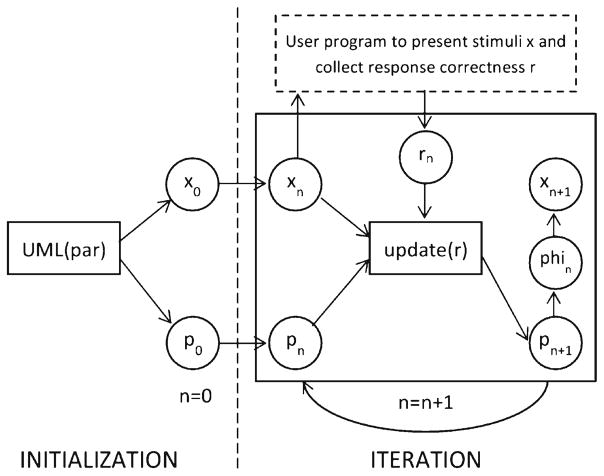
Software routines for the implementation of the UML procedure were developed using MATLAB2 and are collectively presented here as the UML Toolbox. To allow for a flexible and intuitive organization of the experimental variables and the computational algorithms, a UML object is introduced. Each UML object is a data structure that includes several variables and methods. The variables within the data structure store the parameters (e.g., estimates of the psychometric-function parameters), trial-by-trial data (e.g., signal intensity and the correctness of subjects’ responses), internal parameters (e.g., the counter for the trial number), and so forth. The methods within the data structure conduct operations on the variables, including setting and updating the variable values. Table 1 lists the available variables and methods. Figure 2 illustrates the cornerstone variables (in circles) and methods (in rectangles) associated with the UML object for a psychophysical experiment.
Table 1.
Variables and methods for the UML object
| Variables | Comments |
|---|---|
| uml.x | Signal intensity |
| uml.xnext | Next signal intensity, based on previous trials |
| uml.p | Current estimate of the posterior parameter distribution |
| uml.phi | Estimates of the psychometric- function parameters |
| uml.r | Subject’s binary responses in terms of correctness |
| uml.par | Data structure containing parameter space configuration |
| uml.n | Current trial number |
| uml.phi0 | Parameters of the psychometric function for a virtual observer (used for simulation only) |
| uml.userdata01 | Reserved for user-defined data |
| uml.userdata02 | Reserved for user-defined data |
| uml.userdata03 | Reserved for user-defined data |
| uml.userdata04 | Reserved for user-defined data |
| Methods | Comments |
| Initialization: | |
| uml = UML(par) | Construct a UML object |
| uml.setNdown(ndown) | Set the n-down, 1-up sweet-point selection rule |
| uml.setX0(x0) | Set the initial presentation level |
| Iteration: | |
| uml.update(r) | Update the stimulus strength x, depending on response correctness r |
| Simulation: | |
| uml.setPhi0(phi0) | Set the parameter uml.phi0 |
| r = uml.simulateResponse(x) | Generate a response, and indicate correctness (r) from the virtual observer |
| Other: | |
| conf = uml.getConf(percent) | Return the confidence limits of the parameters |
| uml.plotP() | Plot the posterior parameter distribution |
Fig. 2.
Schematic of an experiment constructed using the UML Toolbox
A psychophysical experiment is conceptualized as unfolding in two core phases: (a) initialization and (b) iteration. During the initialization phase (left of the vertical dashed line in Fig. 2), the experimental configuration is initialized, and the prior distribution for each of the psychometric-function parameters is established. When a new UML object is constructed using the constructor uml=UML (par) , variables are generated and their initial values are set. The variable uml.p stores the current posterior probability distributions of the parameters; at initialization, it holds the prior distribution. The variable uml.xnext stores the optimal signal intensity to test for the next trial, on the basis of the posterior distribution. The variables uml.x, uml.r, and uml.phi store the signal intensity, behavioral responses, and parameter estimates from all past trials, respectively. The variables uml.x and uml.r are column vectors, with each row indicating a single trial. The variable uml.phi is a matrix in which the parameter estimates from different trials are arranged in rows and the parameter estimates for α, β, γ, and λ, in that order, are arranged into four columns. The variables uml.x, uml.r, and uml.phi are initialized as empty variables. The parameter γ indicates chance-level performance and is set to a fixed value by the experimenter (e.g., γ = .5 for a two-alternative, forced choice task).
During the iteration phase (to the right of the vertical dashed line in Fig. 2), the variables are updated after each trial using the method update (r). This method proceeds as follows: First, the value stored in is uml.xnext appended to the final row in the variable uml.x; that is, it has become the most recent signal intensity tested. The response correctness r from the current trial (as input to the function) is appended to the final row in the variable uml.r. Then, the likelihood function for the parameters for the current trial is calculated on the basis of r. Using the likelihood function, the posterior parameter distribution uml.p is updated according to Bayes’s theorem. Next, the maximum of the posterior parameter distribution provides interim parameter estimates. The new parameter estimates are appended to the final row in the variable uml.phi. Sweet points are then derived from the interim estimate of the psychometric function, and the signal intensity for the next trial’s stimulus uml.xnext is computed.
Given the construct of the UML object, programming a new experiment involves two steps. First, before data collection begins, a UML object is constructed using the method uml=UML (par). Next, a loop is used to (a) iteratively collect the correctness of responses and (b) update the variables stored in the UML object (using the method update(r)). When a UML track terminates (e.g., when a certain number of trials is reached), the final posterior parameter distribution is accessible from the variable uml.p.
Using the UMLToolbox
Initialization
At the outset of an experiment, a UML object is constructed by
uml=UML(par);
where UML is the constructor method. The constructor takes an input argument, par, which is a data structure in a predefined format that includes the parameters set by the experimenter. The file exp_config.m included in the toolbox provides an example of defining the input argument par for the UML constructor. The steps are as follows. First, the choice of the psychometric-function model, either a logistic or a Weibull function, is specified:
par.model = ‘weibull’; % Weibull function.
or
par.model = ‘weibull’; % Weibull function.
Besides the type of the model for the psychometric function, the user can also specify how the parameters are estimated from the posterior distribution. Either the mean or the mode of the posterior distribution can be chosen as the reported parameter estimate:
par.method = ‘mean’;
or
par.method = ‘mode’;
Next, the n-down, 1-up rule for selecting the sweet point and the initial signal intensity are set:
par.ndown = 2; % n-down, 1-up sweet-point selection par.x0 = 30; % the initial signal intensity.
For the example above, a 2-down, 1-up algorithm is chosen, and the initial signal intensity is 30 (arbitrary units). Higher overall proportion-correct scores are expected for larger values of par.ndown (Levitt, 1971) meaning that the choice of par.ndown impacts the distribution of the sweet points ultimately sampled. The initial signal intensity is the signal intensity on the first trial, as well as the sweet point for λ.
Once these experimental variables are set, the parameter space for the psychometric function is established. Both the logistic and Weibull models of the psychometric function include four parameters (α, β, γ, and λ). The parameter γ is a constant set by the experimenter equal to the chance proportion correct expected from the experimental design.
The parameters α, β, and λ require the specification of their ranges, gradations, and prior distributions. For example, the α parameter space might be set as follows:
par.alpha = struct(... ‘limits’, [−10 30],... % the value range ‘N’, 61,... % number of potential values ‘scale’, ‘lin’,... % ‘lin’ or ‘log’ spacing ‘dist’, ‘norm’,... % prior distribution: ‘norm’ for normal ... % distribution or ‘flat’ for uniform ... % distribution ‘mu’, 0,... % mean of the prior ‘std’, 10... % standard deviation of the prior );
Here, the α parameter space contains 61 potential values, linearly spaced between −10 and 30. The prior probability for α is given by a normal probability density function with mean par.alpha.mu and standard deviation par.alpha.std. In addition to a normally distributed prior, the user can choose a prior with all potential values of α having equal probability by setting the variable par.alpha.dist to ‘flat’. When a flat prior is chosen the variables par.alpha.mu and par.alpha.std are ignored. The prior distributions for the β and λ parameters are configured using the same procedure.
The ranges of the parameters should be sufficiently large so that the probability of the “true” parameter being outside the range is negligible. For the Weibull formulation of the psychometric function, α must be larger than zero and β must be larger than one.
Two aspects of the initialization process deserve note. First, if the number of potential values in the β or λ parameter space ( par.beta.N or par.lambda.N) is assigned a value of one, the parameter will be fixed as specified by the first element in par.beta.limits or par.lambda.limits, respectively. This means that the parameter is not estimated, and the associated sweet point(s) are removed from the sampling strategy. For example, if both par.beta.N and par.lambda.N are set to one, the procedure will sample stimuli at the single sweet point associated with α (essentially the original maximum-likelihood procedure by Green, 1990). Second, if the potential values for a given parameter are logarithmically spaced and the prior distribution is set to be normally distributed, the fields ‘mu’ and ‘std’ correspond to geometric mean and geometric standard deviation of the distribution.
Running an experiment
Once the experimental configuration is set, an experiment can be programmed using a simple two-step process: initialization and iteration. To carry out a typical experiment, the following MATLAB script can be used:
uml = UML(par);
ntrials = 100;
for i = 1: rntrials
r = User_Function(uml.xnext);
uml.update(r);
end
In the example above, a UML object uml (the left side of the vertical dashed line in Fig. 2) is generated using the constructor UML (par). Then, a for loop is used to collect data during the iteration phase (the right side of the vertical dashed line in Fig. 2). The total number of trials is specified by the variable ntrials. Within the for loop, on each trial, the correctness of the subject’s response is collected by a user-defined function User_Function (uml.xnext), the UML object is updated, and the signal’s strength for the next trial is set using the method uml.update (r). The variable uml.xnext stores the signal intensity for the next trial, unless it is the first trial, in which case, the initial signal intensity is stored. The user-defined function (the dashed box in Fig. 2) can take any function name that the experimenter prefers. It should be a function that takes uml.xnext as the input argument, presents the stimulus at the signal intensity to the subject, and collects a response from the subject. The response is returned as an output argument, r, in terms of correctness with a value of 1 for a correct response and 0 for an incorrect response.
Once the response correctness is known, the method uml.update (r) updates several variables held in the UML object. These variables include the trial counter uml.n, the posterior parameter distribution uml.p, the parameter estimates uml.phi, the sweet points uml.swpts, the signal intensity for the next stimulus presentation uml.xnext, the signal intensity uml.x, and the overall proportion correct uml.PC. These variables are accessible both within the experimental loop (for online data peeking) and after the experiment is finished (for data storage). The stimulus presentation, the subject’s responses, and parameter updating continues until the total number of trials ( ntrials, in the example above) is reached.
Experiment simulations
The UMLToolbox includes software routines that simulate a virtual observer who responds in accordance with a “true” psychometric function specified by the variable phi0. Such Monte Carlo simulation experiments are useful to evaluate the role that changes in the prior distribution plays on the rate of parameter convergence, to determine plausible parameter ranges that might be used in an experiment, and so forth. The process is similar to that for a “real” experiment, except that a virtual observer replaces the user-defined stimulus generation and data collection scripts (dashed box in Fig. 2). Below is an example for a virtual observer whose psychometric function is logistic:
uml = UML(exp_config());
uml.setPhi0([10,1.6,0.5,0.05]);
ntrials = 200;
for i = 1:ntrials
r = uml.simulateResponse(uml.xnext);
uml.update(r);
uml.plotP();
end
The simulation is accomplished using the methods setPhi0 (phi0) and simulateResponse (x). In the initialization phase, the method set Phi0 (phi0) takes a four-element array phi0 as the input argument, which specifies the values for the parameters (α, β, γ, and λ, in that order) of the “true” underlying psychometric function. This method stores these values as the variable uml.phi0 in the UML object. In the iteration phase, the method simulateResponse (x) takes the signal intensity and generates responses according to the “true” psychometric function with the parameters stored in uml.phi0. The method uml.plotP ( ) in the for loop plots the posterior parameter distribution after each trial.
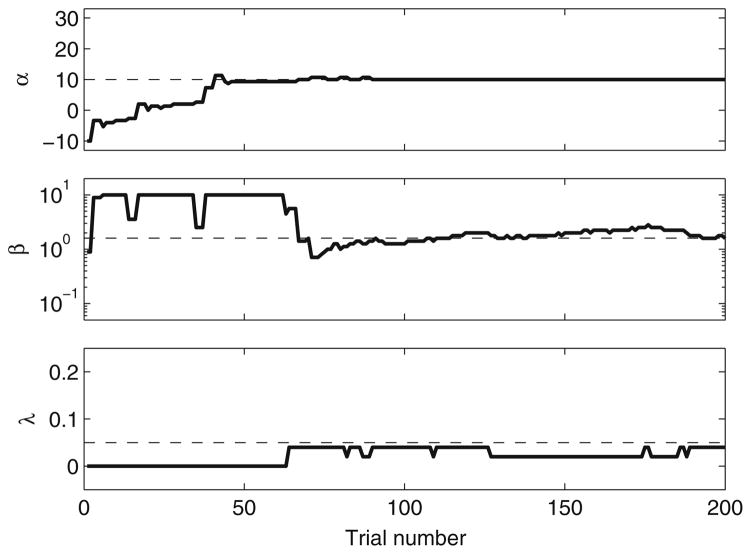
Figure 3 plots the trial-by-trial estimates of the parameters α, β, and λ (top to bottom panels) of the logistic function, from the script outlined above. In this simulation, the 61 potential values for the α parameter were linearly spaced between −10 and 30; the 41 potential values for β were logarithmically spaced between 0.1 and 10; and the 11 potential values for λ were linearly spaced between 0 and .2. Flat priors were used for all three parameters.
Fig. 3.
Estimates of the parameters for a virtual observer’s psychometric function as a function of the number of trials. The top, middle, and bottom panels plot the results for α, β, and λ, respectively. The “true” values for the simulated observer’s parameters α0, β0, and λ0 (10, 1.6, and .05, respectively) are indicated using dashed lines. After 200 trials, the estimated parameters were 10, 1.58, and .04, respectively
The parameters α and λ converged quickly. After approximately 60 trials, the estimates were close to the “true” parameters for the virtual observer. The slope parameter β, however, was slower to converge to the “true” value. The pattern of results shown in Fig. 3 is typical, in that α usually converges more rapidly than β. Shen and Richards (2012) found that 200 trials typically sufficed for the convergence of the psychometric-function parameters, but more trials might be needed if the slope of the psychometric function were very shallow or if the lapse rate were large.
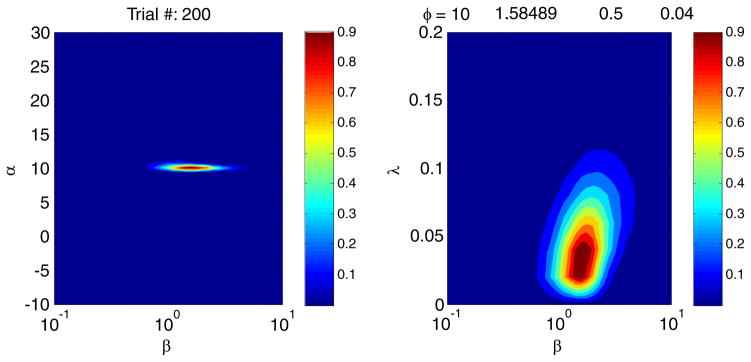
Figure 4 shows the posterior distributions after 200 trials for α (left) and λ (right) as a function of the value of β using the method uml.plotP ( ). After 200 trials, the maximum of the posterior distribution—that is, the final parameter estimate (α = 10.0, β = 1.58, and λ = .04)—was in good agreement with the “true” parameter tuple (α0 = 10, β0 = 1.6, and λ0 = .05).
Fig. 4.
Posterior distributions for the simulation described for Fig. 3 are plotted using uml.PlotP ( ). The log probabilities of the values of α, β, and λ after 200 trials are projected onto two planes. For the left panel, the abscissa is the value of β, the ordinate is the value of α, and the title indicates the number of trials. For the right panel, the abscissa is the value of β, the ordinate is the value of λ, and the title indicates vector uml.phi, containing the current estimates of the α, β, γ, and λ parameters of the psychometric function
Data management
The UML object intrinsically organizes all relevant variables and methods concerning the adaptive track in one place. After data collection, one can store the data into files by simply saving the UML object. For example, for hypothetical subject obs01, the command
save obs01_expdata.mat uml;
will save the UML object ( uml) into a file named obs01_expdata.mat.
Another advantage of the UML object is that UML objects can be concatenated into arrays or matrices just as other data structures in MATLAB. For example, one experiment might have multiple conditions, with a unique psychometric function being estimated in each condition. In such a situation, an array of UML objects can be generated with each element in the array corresponding to a UML object. Consider an experiment with three separate conditions, in which the three conditions are to be tested using the following protocol. First, the order of the three conditions is drawn at random order with 50 trials per condition. Then, the process is repeated three times, yielding 200 trials for each condition. This protocol can be realized using the following script.
protocol =[312312312312];
uml(1:3) = UML(par);
for iblock = 1:length(protocol)
idx = protocol(iblock);
for i = 1:50
r = User_Function(uml(idx).xnext);
uml(idx).update(r);
end
end
In this example, the experimental protocol—that is, the sequence indicating the order in which the three conditions are tested—is held in the variable protocol. During the initialization phase, an array of UML objects is created. Once the data collection begins, the blocks of 50 trials are tested following the sequence specified in protocol. For each block, data are collected iteratively as in the previous examples. Note that each UML object stores the status of the corresponding adaptive track, so that data collection is easily resumed after interruption. This potential of arrays of UML objects allows for a wide variety of experimental protocols.
In many cases, it may be helpful to store trial-by-trial experimental information in addition to the predefined variables available in the UML object provided in the UML Toolbox. In such circumstances, the experimenter can make use of the reserved variable names userdata0l, userdata02, userdata03, and userdata04. These variables are initialized as empty arrays, but they can be manually updated to store any user-defined data. For example, the experimenter might want to save the trial-by-trial reaction times. This can be achieved as follows:
uml = UML(par);
for i = 1:100
[r, rt] = User_Function(uml.xnext);
uml.update(r);
uml.userdataOl(end+1) = rt;
end
The user-defined function returns both the response correctness, r, and reaction time, rt. The command uml.userdata01 (end+1) = rt appends the reaction time data on each trial to the end of the variable uml.userdata01. Consequently, when data collection is complete, the trial-by-trial reaction time is retrievable from uml.userdata01.
Considerations regarding the configuration of the UML procedure
As we described previously, constructing an experiment using the UML Toolbox starts with the configuration of the procedure. This includes specifying the parameter-estimation method, the up–down rule for sweet-point selection par.ndown, the range and gradation of the parameter space, and the prior distributions. Therefore, these experimental parameters have to be set before data collection. Although the UML procedure is relatively robust to the changes in the experimental configuration, it is beneficial to choose parameters that provide efficient data collection. Here, guidelines for setting various experimental parameters are provided.
Choosing the parameter estimation method
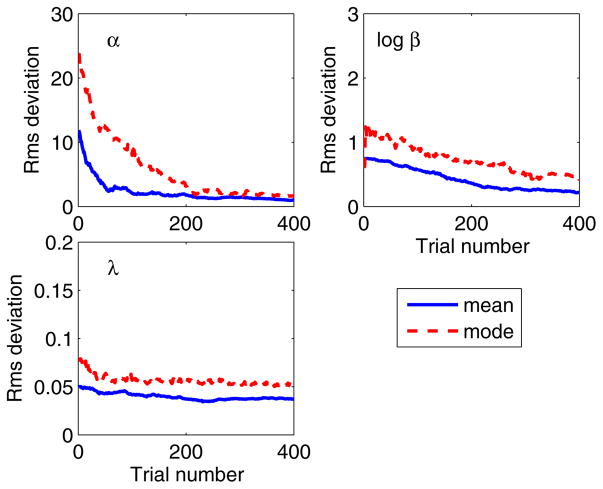
The par.method variable specifies whether the mean or the mode of the posterior parameter distribution should be used as the parameter estimates. The original maximum-likelihood procedures (e.g., Green, 1990; Hall, 1968; Harvey, 1986) use the mode of the posterior distribution for parameter estimation. However, for Bayesian adaptive procedures similar to the present UML procedure, Emerson (1986a, 1986b) and King-Smith, Grigsby, Vingrys, Benes, and Supowit (1994) showed that the mean yielded better precision in the parameter estimates than the mode. To determine whether this also holds for the UML procedure, a simulation was conducted. In this simulation, 100 virtual observers were constructed who responded according to “true” psychometric functions (defined by “true” parameters α0, β0, and λ0). For each virtual observer, the true logistic psychometric function had an α0 drawn at random from a uniform distribution ranging from −30 and 10, log β0 drawn from a uniform distribution ranging from −1 and 1, and λ0 drawn from a uniform distribution ranging from 0 and .15. For half of the virtual observers, the psychometric function parameters were estimated using the mean of the posterior distribution and for the other half the mode was used. For all simulated tracks, a 2-down, 1-up sweet-point selection rule was used, and flat priors were used for all three parameters [α, log β, and λ].
Figure 5 plots the root-mean-squared (rms) deviation between the estimated and “true” parameters as a function of trial number for each estimation method (different colors) and for each parameter (different panels). The rms deviation was used as a single measure for the performance of the UML procedure, because it captures both the bias and the variability in the estimates. For all three parameters, the rms deviation was smaller when the mean of the posterior distribution was used. The advantage of using the mean over the mode was especially evident for the slope and lapse parameters (upper right and lower left panels) and for the first 200 or so trials for the α parameter (upper left panel). Therefore, we recommend that the parameter estimation method par.method be set to as ‘mean’ the default setting. This setting was used for all simulation results in the following sections.
Fig. 5.
Effect of the parameter estimation method on the convergence of the parameter estimates. Either the mean (solid curves) or the mode (dashed curves) of the posterior parameter distribution is used to obtain the parameter estimates. The rms deviation for 50 randomly chosen virtual observers is shown as a function of trial number for both methods and for three psychometric-function parameters
Choosing a sweet-point selection rule
The par.ndown variable controls the sweet-point selection rule in the UML procedure. For an n-down, 1-up rule, the stimulus would be sampled at one sweet point lower than the current sampling point following n consecutive correct responses, and sampled at one sweet point higher following a single incorrect response. This rule is similar to the one used for the transformed up–down staircase procedure (Levitt, 1971). The purpose of implementing an up–down sweet-point selection rule was to ensure suprathreshold signal intensities at the beginning of a UML track and to avoid drastic changes in signal intensity across adjacent trials. Therefore, including the up–down sweet-point selection rule helps inexperienced observers learn the experimental task quickly.
As was shown by Levitt (1971), the value of n corresponds to the expected overall proportion correct, such that the proportions correct are expected to be .71, .79, .84, and .87 for n values of 2, 3, 4, and 5, respectively. Therefore, the variable par.ndown can be chosen to support the experimenter’s preference regarding the expected overall proportion correct. Usually, the choice of par.ndown between 2 and 5 does not have a significant impact on the rate of convergence for the psychometric-function parameters. However, if the upper asymptote of the psychometric function is relatively low, using high values for par.ndown may undermine the efficiency of the UML procedure. For example, if the upper asymptote is at .8 (λ = .2), a 5-down, 1-up sweet-point selection rule will push the focus of sampling toward a proportion correct of approximately .87. As a result, almost all stimuli would be sampled at the λ sweet point and seldom at lower sweet points, leading to poor estimates of the psychometric function.
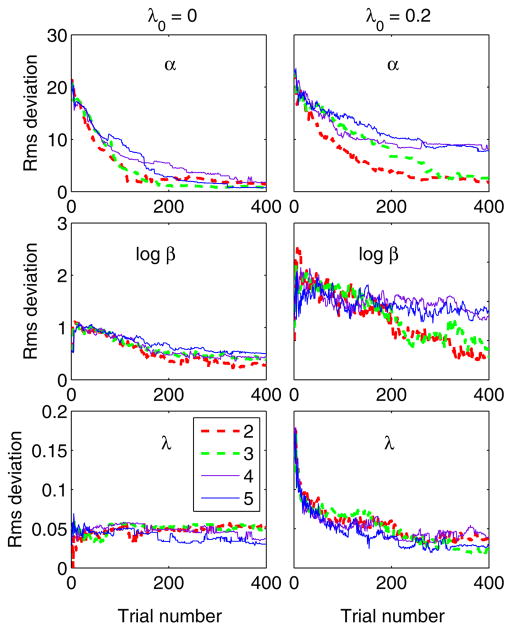
To illustrate the interaction between par.ndown and the lapse rate, simulations were conducted for two groups of virtual observers. The two groups corresponded to λ0 values of 0 and .2. For each group, 50 virtual observers were defined. The threshold and slope parameters of the psychometric function (α0 and β0) were drawn at random from the range of the α and β parameter spaces. The 50 values of α0 were drawn from a uniform distribution ranging from −10 to 30 on a linear scale, and the values of β0 were drawn from a uniform distribution ranging from 0.1 to 10 on a logarithmic scale. For each virtual observer, the psychometric function was estimated using the UML procedure and the deviations of the estimated parameters (α, log β, and λ) from the “true” parameters (α0, log β0, and λ0) were calculated. The rms deviations across the 50 observers as a function of the trial number were plotted and used to quantify the convergence for α, log β, and λ. This process was repeated for the two values of λ0 and par.ndown values of 2, 3, 4, and 5.
The simulation results are summarized in Fig. 6. The simulated rates of convergence for α, log β, and λ are shown in the top, middle, and bottom panels, respectively. The left panels are for a λ0 of 0, and the right panels are for a λ0 of .2. Different line types are for different values of par.ndown (legend). For a λ0 of 0, the rms deviations for all three parameters decreased toward zero as the trial number increased, and the rates of convergence were similar across the four values of par.ndown. When the λ0 was .2, although similar convergence rates for λ were observed for all values of par.ndown (bottom right panel), for α and β (upper and middle right panels) better accuracy and faster convergence were observed for smaller values of par.ndown. The poor estimates of α and β with larger par.ndown values reflected the fact that too few stimuli were sampled at the sweet points associated with the α and β parameters. Therefore, when little is known about the lapse rate, it is recommended that par.ndown a value of 2 be used as the default value. For all simulations presented in the subsequent discussion, a 2-down, 1-up sweet-point selection rule was used.
Fig. 6.
Effect of an n-down, 1-up sweet-point selection rule on the convergence of the psychometric-function parameters. The rms deviations for 50 randomly chosen virtual observers are shown as a function of trial number for λ0s of 0 (left panels) and .2 (right panels). The values of n evaluated were 2, 3, 4, and 5, which are indicated using red (dashed), green (dashed), violet (thin), and blue lines
Establishing the parameter space
Creating the parameter space using the UML Toolbox is equivalent of setting a three-dimensional grid. Each node in the grid represents a unique combination of the potential α, β, and λ values. During the iteration phase of the UML procedure, after each trial the mean or mode of the posterior distribution evaluated in the discrete parameter space is taken as the interim estimate of the psychometric function. When little is known about the expected values for the psychometric-function parameters, it is beneficial to set a large range for the parameter space to ensure the parameters to be estimated are situated within the space. When the experimenter has a priori information regarding the expected parameter values, narrowing the range of the parameter space may reduce computational time.
Once the range of the parameter space is determined, the number of potential values along the α, β, and λ dimensions are set. Denser gradations for the parameters would lead to more accurate estimates of the psychometric function. However, it is impractical to use extremely large numbers of potential values for the parameters given time and/or computational constraints. To evaluate the influence of parameter gradation on the efficiency of the UML procedure, a series of simulations was conducted. As for the simulations described previously, α was defined between −10 and 30 (linear scale), β was defined between 0.1 and 10 (logarithmic scale), and λ was defined between 0 and .2 (linear scale). In three separate conditions, the numbers of potential values for α, β, and λ were systematically varied from 5 to 40. For each test condition, the simulation was repeated for 200 virtual observers, with the “true” parameters being drawn at random from the defined parameter space. The rms deviations between the ultimate parameter estimates and the “true” parameter values across the 200 virtual observers were calculated to quantify the efficiency of the UML procedure.
The resulting rms deviations for the three parameters after 200 and then 400 trials are listed in Table 2. When the numbers of potential values were manipulated for β and λ the accuracy of the estimates for all three parameters did not exhibit systematic dependencies on the gradation of either the β or the λ parameter range. In contrast, the rms deviations for all three parameters tended to decrease as the number of potential α values was increased from 5 to 40. Overall, the UML procedure is robust against manipulations of the β and λ gradations, but the experimenter is advised to use at least 20 potential values of α. If the user intends to fit the psychophysical data using software external to the UML Toolbox, similar simulations might be run to evaluate the role of the parameter space gradation on convergence for that larger data-collection/model-fitting environment.
Table 2.
Effect of the parameter space gradation on the root-mean-squared (rms) deviations from the parameter estimates to the “true” parameter values across 200 simulated virtual observers
| rms Deviations
|
|||||||
|---|---|---|---|---|---|---|---|
|
α
|
log β
|
λ
|
|||||
| 200 | 400 | 200 | 400 | 200 | 400 | ||
| Number of potential α values | 5 | 4.3 | 3.7 | 1.6 | 1.4 | .067 | .061 |
| 10 | 3.1 | 1.9 | 1.4 | 1.1 | .058 | .053 | |
| 20 | 2.6 | 1.9 | 1.4 | 0.9 | .058 | .048 | |
| 40 | 3.9 | 2.5 | 1.3 | 0.9 | .055 | .048 | |
| Number of potential β values | 5 | 3.8 | 1.6 | 1.4 | 0.9 | .047 | .038 |
| 10 | 3.2 | 1.8 | 1.4 | 0.8 | .052 | .043 | |
| 20 | 3.8 | 1.7 | 1.5 | 0.9 | .053 | .047 | |
| 40 | 4.7 | 2.2 | 1.4 | 0.9 | .049 | .044 | |
| Number of potential λ values | 5 | 2.4 | 2.0 | 1.5 | 0.9 | .055 | .050 |
| 10 | 3.8 | 1.4 | 1.4 | 0.8 | .051 | .042 | |
| 20 | 2.7 | 1.6 | 1.5 | 0.8 | .049 | .046 | |
| 40 | 3.1 | 1.6 | 1.5 | 0.9 | .049 | .038 | |
Results are shown at the end of 200 and 400 trials
Setting up the prior parameter distributions
The UML Toolbox provides the experimenter with the opportunity to configure the prior distribution for each parameter. The prior distribution reflects the experimenter’s a priori belief regarding the expected ranges for the parameters. Should the experimenter prefer not to make assumptions regarding the relative likelihood of particular parameters across the range of the parameter space, a flat prior can be used (noting the range of the parameter space is itself a form of a prior distribution). Invoking informative prior distributions is appropriate when the experimenter has some knowledge regarding the parameters to be estimated. Well-chosen prior distributions typically lead to faster convergence of the parameter estimates and may be essential when subjects are available only for a short time period.
Shen and Richards (2012) systematically manipulated the standard deviations of the prior distributions in a simulation study. They showed that when the assumed means of the priors and the “true” psychometric-function parameters were slightly mismatched, priors that were too broad or too narrow led to increases in the rms deviations for α and hence inaccurate threshold estimates. In contrast, the rms deviations for α were minimal when moderate values of the standard deviations were implemented into the priors. On the basis of these observations, a reasonable rule of thumb is that priors with standard deviations between one-half and one-quarter of the range of the parameter space produce satisfactory results.
Comparing UML to other adaptive procedures
The UML Toolbox presented here is one of many software toolboxes that implement adaptive procedures. For example, the MATLAB toolbox PsychToolbox (Brainard, 1997; Pelli, 1997) currently includes the QUEST procedure (Watson & Pelli, 1983) and the Ψ procedure (Kontsevich & Tyler, 1999). Another comprehensive MATLAB toolbox, Palamedes (Prins & Kingdom, 2009) includes the transformed up–down (Levitt, 1971), bestPEST (Lieberman & Pentland, 1982), QUEST, and Ψ procedures. The MLP toolbox developed by Grassi and Soranzo (2009) includes the transformed up–down, PEST (Taylor & Creelman, 1967) and the maximum-likelihood (Green, 1990) procedures. Outside of the MATLAB environment, adaptive psychophysical procedures are also available in the PsychoFit toolbox by Harvey (1986, 1997) written in C/C++, the YAAP toolbox by Treutwein (1997) written in Modula-2, and the Psychophysica toolbox by Watson and Solomon (1998) as Mathematica notebooks.
The various adaptive procedures currently available in the above-mentioned toolboxes can be classified into three categories: (1) nonparametric staircase procedures (e.g., the transformed up–down procedure), (2) Bayesian procedures that minimize variance in parameter estimates (e.g., the maximum-likelihood, QUEST, and bestPEST procedures), and (3) Bayesian procedures that minimize the expected entropy of the posterior parameter distribution (e.g., the Ψ procedure). The UML procedure belongs to the category of Bayesian minimum-variance procedures. Among the members of this second category, the original maximum-likelihood procedure (as in Hall, 1968; Harvey, 1986; and Green, 1990) did not recommend the use of prior distributions whereas the QUEST procedure (Watson & Pelli, 1983) uses a Bayesian framework including the specification of the priors for the psychometric-function parameters. The Best PEST procedure (Lieberman & Pentland, 1982) begins with a staircase procedure and switches to the QUEST procedure after a criterion number of reversals are reached. Although the QUEST-based procedures are efficient for estimating performance thresholds, when both the threshold and slope of the psychometric function are simultaneously estimated, the results are subject to biases (Kaernbach, 2001; Otto & Weinzierl, 2009). For these procedures that minimize the variance of the parameter estimates, the estimation of multiple psychometric-function parameters requires sampling at the multiple sweet points on the psychometric function. However, the above-mentioned toolboxes do not currently include procedures that sample multiple sweet points (e.g., ZEST [King-Smith et al., 1994] and UML [Shen & Richards, 2012]). The current UML Toolbox provides an implementation of the UML procedure, which could be advantageous over other minimum-variance Bayesian adaptive procedures when multiple psychometric-function parameters are of interest to the experimenter.
Kontsevich and Tyler (1999) and Prins (2012a, 2012b, 2013) have demonstrated that minimum-entropy Bayesian procedures, forming the third category described above, can be used to simultaneously estimate multiple parameters of the psychometric function. Shen (2013) compared the performance of the Ψ and UML procedures using an auditory gap detection task and a logistic model for the psychometric function. The two procedures sampled stimuli in similar regions, and the resulting parameter estimates were comparable. When high lapse rates were expected from the observers, the estimates from the UML procedure were more reliable than the Ψ procedure. However, it is possible to modify the original minimum-entropy algorithm and improve its robustness against high lapse rate (see Prins, 2012b, 2013).
To illustrate how the various adaptive procedures might differ, simulations were carried out. A virtual observer was modeled using a Weibull psychometric function with “true” parameters of log α = −2, β = 3.5, γ= .5, and λ= .02. Three procedures were compared: the QUEST, UML, and Ψ procedures as implemented in the PsychToolbox (Brainard, 1997; Pelli, 1997), the UML Toolbox, and the Palamedes toolbox (Prins & Kingdom, 2009), respectively. All simulations were conducted in MATLAB. Identical prior distributions were used for the threshold parameter α in all three procedures, which assumed a normal distribution for log α with a mean of −1 and a standard deviation of 2. Additionally, the UML and Ψ procedures shared the same prior distributions for the slope parameter β and the lapse parameter λ. The β prior was a normal distribution on the log scale, it had a mean of 0.5 and a standard deviation of 1 for log β. The λ prior was uniformly distribution on the linear scale, between 0 and .2. For each procedure, 200 tracks were simulated with each track containing 200 trials.
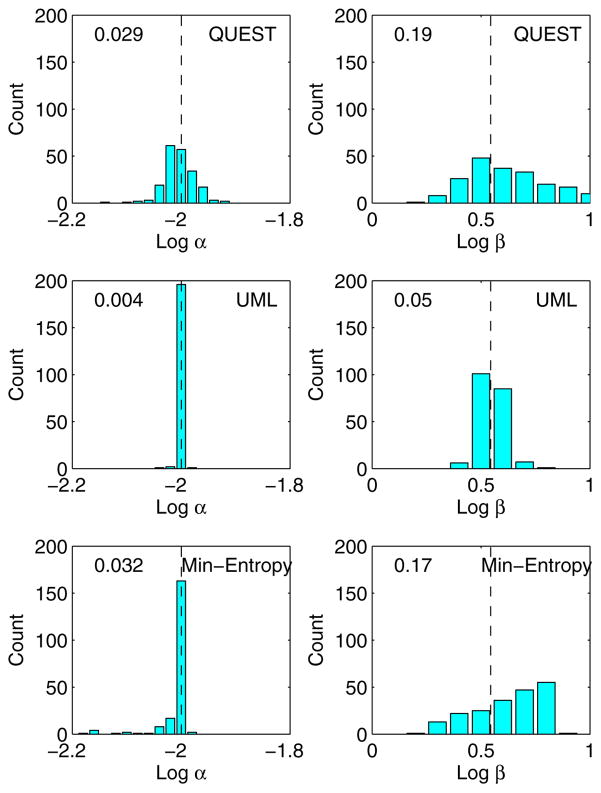
Histograms of the estimated threshold parameter α and slope parameter β at the end of each track are plotted in Fig. 7. The rms error relative to the “true” value is given for each procedure and for each parameter. As expected, because the QUEST procedure focused stimulus sampling to a single target location on the psychometric function, it provided reliable estimates of α (top left panel), but failed to provide an accurate estimate of β (top right panel). For the UML (middle panels) and Ψ (bottom panels) procedures, the parameter estimates varied less among different simulated tracks than with the QUEST procedure. However, the Ψ procedure occasionally generated poor estimates of α, and the estimate of β was biased. As a result, the rms errors for the UML procedure were the smallest among the three procedures in this particular example.
Fig. 7.
Histograms of the α (left) and β (right) estimates from 200 Monte-Carlo simulated tracks. Results are shown separately for the QUEST (top), UML (middle), and minimum-entropy (bottom) procedures, as implemented in the PsychToolbox, the UML Toolbox, and the Palamedes toolbox, respectively. The Weibull psychometric function used to generate simulated responses was determined by the “true” parameters: log α = −2, β = 3.5, γ= .5, and λ= .02. The “true” values for log α and log β are indicated as vertical dashed lines in each panel. The number inside each panel indicates the rms error of the estimates relative to the “true” value
To generalize the results presented above, additional simulations were run in which each of the 200 tracks was based on a randomly drawn psychometric function (e.g., 200 different “virtual observers”), with each virtual observer being tested for the three procedures. The “true” psychometric functions (defined by “true” parameters α0, β0, and λ0) were Weibull functions with log α0 drawn from a uniform distribution ranging from −3 to 3, β0 drawn from a uniform distribution ranging from 1 to 8, and λ0 drawn from a uniform distribution ranging from 0 to .15. The priors for all three parameters and the configurations for the procedures were identical to those used to generate the results in Fig. 7.
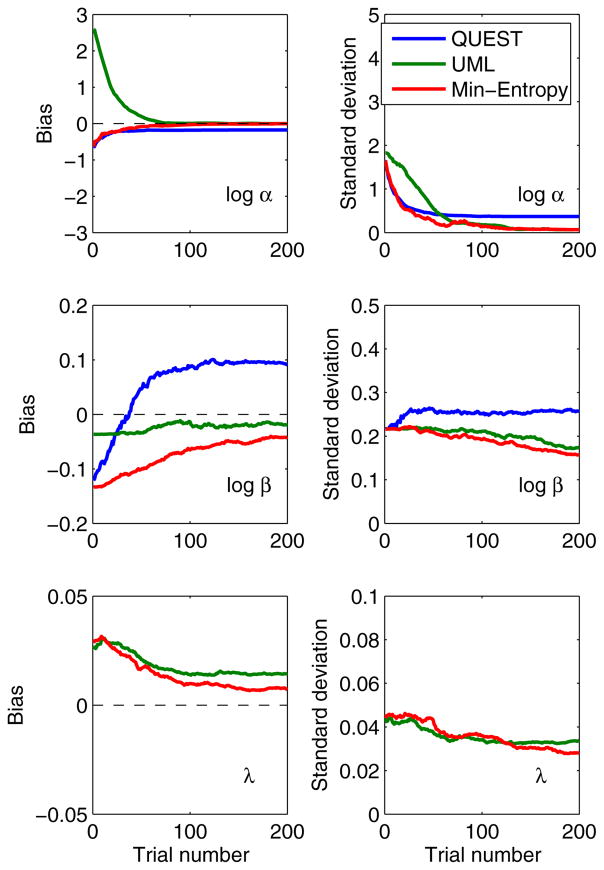
Figure 8 plots the bias (left) and the standard deviations (right) of the estimated parameters as functions of trial number for the three procedures (different colors) and for each of the three parameters (different panels). Because the QUEST procedure implemented in the PsychToolbox does not provide lapse estimates, only the results for the UML and Ψ procedures are shown in the bottom panels. For the threshold parameter (top panels), the bias and standard deviation were smaller for the QUEST and Ψ procedures than for the UML procedure during early trials, indicating better performance. After 100 trials, the bias and standard deviations for the UML were similar to those for the Ψ procedure, and both of these procedures outperformed the QUEST procedure. For the slope parameter (middle panels), the estimate was biased and did not converge for the QUEST procedure, whereas the UML and Ψ procedures gradually converged. The UML procedure exhibited less bias but a larger standard deviation than did the Ψ procedure. For the lapse parameter, the bias and standard deviation were similar for the UML and Ψ procedures for the first 100 or so trials, after which the Ψ procedure outperformed the UML procedure. In summary, the results suggest that, as expected, the QUEST procedure is not appropriate for estimating multiple model parameters simultaneously, and that the Ψ procedure outstrips the UML procedure in terms of the accuracy of α estimates on early trials.
Fig. 8.
The bias (left panels) and standard deviations (right panels) of the parameter estimates using the QUEST, UML, and minimum-entropy procedures, as implemented in the PsychToolbox, the UML Toolbox, and the Palamedes toolbox, respectively. The results are based on 200 simulated virtual observers, with the parameters for their Weibull psychometric function being drawn independently
The modest disadvantage of the UML procedure relative to the Ψ procedure is expected. As compared to the Ψ procedure, the efficiency of the UML procedure is compromised by not allowing the signal intensity to jump directly to the optimal sampling location in the stimulus space. However, for the UML procedure, the listener is exposed to several suprathreshold, high-intensity stimuli at the beginning of a UML track, and the changes in the signal intensity are as easy to follow as for the staircase procedure. These factors lead to reduced time for subject training and could be extremely important when applying Bayesian adaptive procedures to clinical applications.
Summary
The UML procedure provides an efficient way of estimating multiple parameters of the psychometric function, including the threshold, slope, and lapse rate, simultaneously. The UML Toolbox presented here allows for the straightforward implementation of the UML procedure in MATLAB. Using the toolbox, experimenters with little programming experience can easily set up an experiment and carry out data collection. The object-oriented organization enables highly flexible experimental protocol and user-friendly data management schemes. As the default setting, it is recommended that the experimenter use the mean of the posterior distribution for parameter estimation, a 2-down, 1-up sweet-point selection rule, a parameter grid with at least 20 potential values for the threshold parameter, and prior distributions with a standard deviation between one-half and one-quarter of the range of the parameter space.
Acknowledgments
This work was supported by NIH NIDCD Grant No. R21 DC010058, awarded to the third author. We acknowledge Sierra N. Broussard’s assistance in running several computer simulations.
Footnotes
A well-organized list of software available for the analysis of psychophysical functions, as well libraries/toolboxes for the collection of psychophysical data is available at http://visionscience.com/documents/strasburger/strasburger.html.
Although the current toolbox was developed for the MATLAB environment, all source codes are contained in the toolbox and can be modified into other programing environments or languages.
Contributor Information
Y. Shen, Department of Cognitive Sciences, University of California, 3151 Social Sciences Plaza, Irvine, CA 92697-5100, USA
V. M. Richards, Department of Cognitive Sciences, University of California, 3151 Social Sciences Plaza, Irvine, CA 92697-5100, USA
W. Dai, Department of Computer Science, University of California, Irvine, CA, USA
References
- Brainard DH. The psychophysics toolbox. Spatial Vision. 1997;10:433–436. doi: 10.1163/156856897X00357. [DOI] [PubMed] [Google Scholar]
- Brand T, Kollmeier B. Efficient adaptive procedures for threshold and concurrent slope estimates for psychophysics and speech intelligibility tests. Journal of the Acoustical Society of America. 2002;111:2801–2810. doi: 10.1121/1.1479152. [DOI] [PubMed] [Google Scholar]
- Derman C. Non-parametric up-and-down experimentation. Annals of Mathematical Statistics. 1957;28:795–798. doi: 10.1214/aoms/1177706895. [DOI] [Google Scholar]
- Durham SD, Flournoy N. Up-and-down designs I: Stationary treatment distributions. In: Flournoy N, Rosenberger WF, editors. Adaptive designs: Papers from the Joint AMS–IMS–SIAM Summer Conference; Mt. Holyoke College, South Hadley, MA. July 1992; Hayward, CA: Institute of Mathematical Statistics; 1995. pp. 139–157. [Google Scholar]
- Emerson PL. Observations on maximum likelihood and Bayesian methods of forced choice sequential threshold estimation. Perception & Psychophysics. 1986a;39:151–153. doi: 10.3758/bf03211498. [DOI] [PubMed] [Google Scholar]
- Emerson PL. A quadrature method for Bayesian sequential threshold estimation. Perception & Psychophysics. 1986b;39:381–383. doi: 10.3758/bf03203007. [DOI] [PubMed] [Google Scholar]
- Fründ I, Haenel NV, Wichmann FA. Inference for psychometric functions in the presence of non-stationary behavior. Journal of Vision. 2011;11(6):16. doi: 10.1167/11.6.16. [DOI] [PubMed] [Google Scholar]
- Garcia-Perez MA. Forced-choice staircases with fixed step sizes: Asymptotic and small-sample properties. Vision Research. 1998;38:1861–1881. doi: 10.1016/s0042-6989(97)00340-4. [DOI] [PubMed] [Google Scholar]
- Grassi M, Soranzo A. MLP: A MATLAB toolbox for rapid and reliable auditory threshold estimation. Behavior Research Methods. 2009;41:20–28. doi: 10.3758/BRM.41.1.20. [DOI] [PubMed] [Google Scholar]
- Green DM. Stimulus selection in adaptive psychophysical procedures. Journal of the Acoustical Society of America. 1990;87:2662–2674. doi: 10.1121/1.399058. [DOI] [PubMed] [Google Scholar]
- Gu X, Green DM. Further studies of a maximum-likelihood yes–no procedure. Journal of the Acoustical Society of America. 1994;96:93–101. doi: 10.1121/1.410378. [DOI] [PubMed] [Google Scholar]
- Hall JL. Maximum-likelihood sequential procedure for estimation of psychometric functions [Abstract] Journal of the Acoustical Society of America. 1968;44:370. doi: 10.1121/1.1970490. [DOI] [PubMed] [Google Scholar]
- Hall JL. Hybrid adaptive procedures for the estimation of psychometric functions. Journal of the Acoustical Society of America. 1981;69:1763–1769. doi: 10.1121/1.385912. [DOI] [PubMed] [Google Scholar]
- Harvey LO., Jr Efficient estimation of sensory thresholds. Behavior Research Methods, Instruments, & Computers. 1986;18:623–632. [Google Scholar]
- Harvey LO., Jr Efficient estimation of sensory thresholds with ML-PEST. Spatial Vision. 1997;11:121–128. doi: 10.1163/156856897X00159. [DOI] [PubMed] [Google Scholar]
- Kaernbach C. Simple adaptive testing with the weighted up–down method. Perception & Psychophysics. 1991;49:227–229. doi: 10.3758/BF03214307. [DOI] [PubMed] [Google Scholar]
- Kaernbach C. Slope bias of psychometric functions derived from adaptive data. Perception & Psychophysics. 2001;63:1389–1398. doi: 10.3758/bf03194550. [DOI] [PubMed] [Google Scholar]
- King-Smith PE, Grigsby SS, Vingrys AJ, Benes SC, Supowit A. Efficient and unbiased modifications of the QUEST threshold method: Theory, simulations, experimental evaluation and practical implementation. Vision Research. 1994;34:885–912. doi: 10.1016/0042-6989(94)90039-6. [DOI] [PubMed] [Google Scholar]
- King-Smith PE, Rose D. Principles of an adaptive method for measuring the slope of the psychometric function. Vision Research. 1997;37:1595–1604. doi: 10.1016/s0042-6989(96)00310-0. [DOI] [PubMed] [Google Scholar]
- Klein SA. Measuring, estimating, and understanding the psychometric function: A commentary. Perception & Psychophysics. 2001;63:1421–1455. doi: 10.3758/bf03194552. [DOI] [PubMed] [Google Scholar]
- Kontsevich LL, Tyler CW. Bayesian adaptive estimation of psychometric slope and threshold. Vision Research. 1999;39:2729–2737. doi: 10.1016/s0042-6989(98)00285-5. [DOI] [PubMed] [Google Scholar]
- Lam CF, Dubno JR, Ahlstrom JB, He NJ, Mills JH. Estimating parameters for psychometric functions using the four-point sampling method. Journal of the Acoustical Society of America. 1997;102:3697–3703. doi: 10.1121/1.420155. [DOI] [PubMed] [Google Scholar]
- Laming D, Marsh D. Some performance tests of Quest on measurements of vibrotactile thresholds. Perception & Psychophysics. 1988;44:99–107. doi: 10.3758/bf03208701. [DOI] [PubMed] [Google Scholar]
- Leek MR. Adaptive procedures in psychophysical research. Perception & Psychophysics. 2001;63:1279–1292. doi: 10.3758/bf03194543. [DOI] [PubMed] [Google Scholar]
- Leek MR, Hanna TE, Marshall L. Estimation of psychometric functions from adaptive tracking procedures. Perception & Psychophysics. 1992;51(3):247–256. doi: 10.3758/bf03212251. [DOI] [PubMed] [Google Scholar]
- Levitt H. Transformed up–down methods in psychoacoustics. Journal of the Acoustical Society of America. 1971;49(2 Pt 2):467–477. doi: 10.1121/1.1912375. [DOI] [PubMed] [Google Scholar]
- Lieberman HR, Pentland AP. Microcomputer-based estimation of psychophysical thresholds: The Best PEST. Behavior Research Methods & Instrumentation. 1982;14:21–25. doi: 10.3758/BF03202110. [DOI] [Google Scholar]
- Otto S, Weinzierl S. Jahrestagung der Deutschen Gesellschaft für Akustik. Rotterdam, The Netherlands: Deutsche Gesellschaft für Akustik; 2009. Comparative simulations of adaptive psychometric procedures; pp. 1276–1279. [Google Scholar]
- Pelli DG. The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spatial Vision. 1997;10:437–442. doi: 10.1163/156856897X00366. [DOI] [PubMed] [Google Scholar]
- Poppe S, Benner P, Elze T. A predictive approach to nonparametric inference for adaptive sequential sampling of psychophysical experiments. Journal of Mathematical Psychology. 2012;56:179–195. doi: 10.1016/j.jmp.2012.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prins N. The adaptive psi method and the lapse rate. Journal of Vision. 2012a;12(9):322. doi: 10.1167/12.9.322. [DOI] [PubMed] [Google Scholar]
- Prins N. The psychometric function: The lapse rate revisited. Journal of Vision. 2012b;12(6):25. doi: 10.1167/12.6.25. [DOI] [PubMed] [Google Scholar]
- Prins N. The psi-marginal adaptive method: How to give nuisance parameters the attention they deserve (no more, no less) Journal of Vision. 2013;13(7):3. doi: 10.1167/13.7.3. [DOI] [PubMed] [Google Scholar]
- Prins N, Kingdom FAA. Palamedes: MATLAB routines for analyzing psychophysical data. 2009 www.palamedestoolbox.org.
- Rose RM, Teller DY, Rendleman P. Statistical properties of staircase estimates. Perception & Psychophysics. 1970;8:199–204. [Google Scholar]
- Shen Y. Comparing adaptive procedures for estimating the psychometric function for an auditory gap detection task. Attention, Perception, & Psychophysics. 2013;75:771–780. doi: 10.3758/s13414-013-0438-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Y, Richards VM. A maximum-likelihood procedure for estimating psychometric functions: Thresholds, slopes, and lapses of attention. Journal of the Acoustical Society of America. 2012;132:957–967. doi: 10.1121/1.4733540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor MM. On the efficiency of psychophysical measurement. Journal of the Acoustical Society of America. 1971;49:505–508. doi: 10.1121/1.1912379. [DOI] [PubMed] [Google Scholar]
- Taylor MM, Creelman CD. PEST: Efficient estimates on probability functions. Journal of the Acoustical Society of America. 1967;41:782–787. [Google Scholar]
- Treutwein B. Adaptive psychophysical procedures. Vision Research. 1995;17:2503–2522. [PubMed] [Google Scholar]
- Treutwein B. YAAP: Yet another adaptive procedure. Spatial Vision. 1997;11:129–134. [PubMed] [Google Scholar]
- Treutwein B, Strasburger H. Fitting the psychometric function. Perception & Psychophysics. 1999;61:87–106. doi: 10.3758/bf03211951. [DOI] [PubMed] [Google Scholar]
- Urban FM. The method of constant stimuli and its generalizations. Psychological Review. 1910;17:229–259. [Google Scholar]
- Watson AB, Pelli D. QUEST: A Bayesian adaptive psychometric method. Perception & Psychophysics. 1983;33:113–120. doi: 10.3758/BF03202828. [DOI] [PubMed] [Google Scholar]
- Watson AB, Solomon JA. Psychophysica: Mathematica notebooks for psychophysical experiments. Spatial Vision. 1998;10:447–466. doi: 10.1163/156856897x00384. [DOI] [PubMed] [Google Scholar]
- Wetherill GB, Levitt H. Sequential estimation of points on a psychometric function. British Journal of Mathematical and Statistical Psychology. 1965;18:1–10. doi: 10.1111/j.2044-8317.1965.tb00689.x. [DOI] [PubMed] [Google Scholar]
- Wichmann FA, Hill NJ. The psychometric function: I. Fitting, sampling, and goodness of fit. Perception & Psychophysics. 2001a;63:1297–1313. doi: 10.3758/BF03194544. [DOI] [PubMed] [Google Scholar]
- Wichmann FA, Hill NJ. The psychometric function: II. Bootstrap-based confidence intervals and sampling. Perception & Psychophysics. 2001b;63:1314–1329. doi: 10.3758/BF03194545. [DOI] [PubMed] [Google Scholar]
- Zchaluk K, Foster DH. Model-free estimation of the psychometric function. Attention, Perception, & Psychophysics. 2009;71:1414–1425. doi: 10.3758/APP.71.6.1414. [DOI] [PMC free article] [PubMed] [Google Scholar]