Enhancement of accuracy in shape sensing of surgical needles using optical frequency domain reflectometry in optical fibers

Abstract

We demonstrate a novel approach to enhance the precision of surgical needle shape tracking based on distributed strain sensing using optical frequency domain reflectometry (OFDR). The precision enhancement is provided by using optical fibers with high scattering properties. Shape tracking of surgical tools using strain sensing properties of optical fibers has seen increased attention in recent years. Most of the investigations made in this field use fiber Bragg gratings (FBG), which can be used as discrete or quasi-distributed strain sensors. By using a truly distributed sensing approach (OFDR), preliminary results show that the attainable accuracy is comparable to accuracies reported in the literature using FBG sensors for tracking applications (~1mm). We propose a technique that enhanced our accuracy by 47% using UV exposed fibers, which have higher light scattering compared to un-exposed standard single mode fibers. Improving the experimental setup will enhance the accuracy provided by shape tracking using OFDR and will contribute significantly to clinical applications.

1. Introduction

Device tracking is an extremely active and well established field in the field of biomedical image-guidance, dating back to the 1980`s with stereotactic systems to navigate medical instruments within the human body during procedures. In this regards, current technologies for tracking surgical instruments during image-guided intervention have significant limitations. For example, magnetic resonance imaging (MRI) is less accessible and time consuming, computed tomography exposes the patient to increased radiation levels and ultrasound (US) provides poor image contrast, has a limited depth of field and is mostly limited to 2D images [1, 2]. 3D images can be obtained with US devices but require additional tracking systems (ex. electromagnetic tracking systems (EMTS)) and complex data processing [3–5]. Combined EMTS and optical tracking systems (OTS) offer sufficient levels of accuracy to achieve precise targeting (between 0.8mm and 1.8mm) [6]. However, considering EMTS is MRI incompatible and can undergo distortions if metallic instruments are nearby [7, 8], an OTS is mostly used for tracking a dynamic reference frame while another tracking system is simultaneously used for shape tracking [9, 10]. These limitations on current navigation systems have motivated the development of new tracking approaches strictly based on optical fibers which could be directly inserted inside the minimally invasive surgical tool. Recently, three-dimensional (3D) shape tracking of minimally invasive surgical instruments such as endoscopes, needles and catheters using embedded optical fibers have been the focus of many studies over the past few years [1–6], as it can provide real-time navigation of instruments inside the body without the constraints of the previously stated technologies. Indeed, visualization of the environment is still important to relate the sensed needle tip position and shape in real-time with respect to the patient’s anatomy provided by CT, MRI or ultrasound imaging, and this demands the need for registration with preoperative imaging. To address this issue, an approach have been previously demonstrated [11] to register (or align) optical shape sensing devices with preoperative MRI images with no electromagnetic interference, and no reliance on the MR imager itself, allowing for accurate real-time tool shape detection with respect to the patient’s anatomy. This approach shows an integrated navigation system which offers the environment to the sensed needle and it can be adapted for the approach describe in this manuscript (OFDR). One of the main assets of technics based on optical fibers for shape tracking during image guided interventions is that imaging can be done before instead of during the procedure.

Therefore, medical applications have incorporated FBGs in biopsy needles [12], catheters and other minimally invasive tools for shape detection and force sensing [13]. Medical robotics for image guided prostate biopsies has also used shape sensing to track needle deflections during insertions [14]. To do so, FBGs are used to sense the strain locally, which is directly related to the curvature radius of the fiber. To orientate the curvature radius in the laboratory frame, at least three fibers are used glued in a particular geometry (linear [15, 16], triangular [12, 17, 18] or square [19] cross-section) in order to get two or three degrees of freedom. A simplified design implying a multicore fiber has been proposed and demonstrated accurate results [1]. The difference in the curvature radius of the three fibers allows one to reconstruct the surgical instruments shape based on geometric assumptions alone.

To the best our knowledge, in experiments using needles and strain sensors based on FBGs, the highest accuracy reached for tip tracking is ~0.3mm for single axis tip displacements of ± 15mm [12]. To reach this precision, three fibers were used, each containing 2 FBGs separated by 63mm each inside a 15cm long needle. A precision of 0.74 – 1.2 mm [2, 14, 18, 20] were obtained using different needles length and different numbers of FBG sensors spaced out at various distances along the fibers. However, shape tracking of the entire device can be of clinical value especially during vascular interventions for catheter tracking. In this regard, the main limitation of FBGs based shape sensors for needle shape tracking is the limited number of FBGs that can be integrated without hindering device efficiency. As the number of FBGs is limited, they need to be spaced out over the whole needle length, providing discrete measurements only and approximations are therefore needed to extrapolate the entire needle shape. Those approximations are normally applied on single-axis curvature, limiting this technique to basic shapes. Also, writing FBGs enhance the fragility of fibers, which could have an impact for flexible devices such as catheter.

In this regards, the use of OFDR to reconstruct the whole shape of the surgical tool avoids having to rely on approximations and assumptions and can reconstruct any shape with potentially improved precision as single-axis bending with FBGs. Indeed, OFDR is a truly distributed sensing technic with a tunable sensing resolution that can reach values above 1cm, which is much better than FBG measurement where those are usually spaced by several centimeters. Moreover, in 2007, Duncan et al. [21] compared the FBG and OFDR strain sensing approaches for general shape tracking of optical fibers showing an improve in precision with the OFDR method. First, an array of 110 FBGs equally distanced was used and an accuracy of 1.9mm was achieved. Using OFDR, the precision of the reconstructed shape has been shown to be 0.3mm. Also, Loranger et al. [22] recently showed that Rayleigh scatter, on which strain measurements using OFDR is based, can be considerably enhanced by exposing fibers to a focused UV light. Therefore, this paper investigates the possibility of using high scatter UV exposed fibers to perform shape reconstruction of a typical biopsy needle (19 gauge (G)). To do so, a custom made setup was built to assemble three fibers in an equidistant geometry. The fibers were then embedded in the needle, to which increasing levels of deflections were applied to simulate needle bending. Finally, the shape of the needle was reconstructed according to the strain values measured by OFDR and the precision was evaluated using Euler-Bernoulli beam theory to determine the theoretical needle shape.

2. Theory

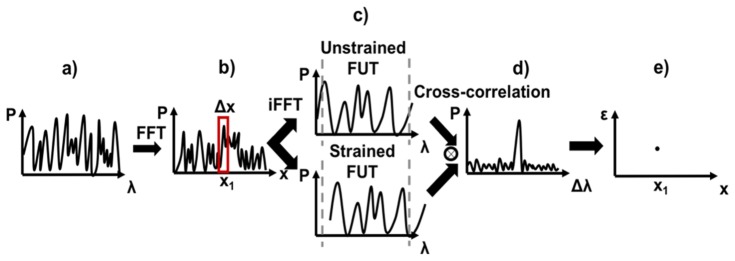
The OFDR method uses a frequency swept laser for the interrogating of the three fibers under test (FUT), successively. The backscatter signal of each FUT is then detected and analyzed in the frequency domain (Fig. 1(a)). By using interferometric measurements, one can retrieve the strain along the fibers. In fact, as schematically shown in Fig. 1, a Fast Fourier Transform (FFT) is performed to evaluate the intensity of the backscatter signal as a function of the position along the fiber under test (Fig. 1(b)). Then, a small section (which corresponds to the spatial resolution (Δx) of the strain sensor) of this signal is selected by an inverse FFT to evaluate the frequency response of this specific section (Fig. 1(c)). By comparing this frequency response of the fiber under strain and with the unstrained fiber, the local strain can be determined. To do so, a cross-correlation of the strained and the unstrained spectra were performed (was actually done directly in the time domain, as cross-correlation is a harder operation). The corresponding cross-correlation spectra allows one to evaluate precisely the spectrum drift between the reference and the measurement in the selected gauge length (Fig. 1(d)). The spectral drift is proportional to the strain (or temperature), so that the local strain or temperature can be calculated easily (Fig. 1(e)). In order to obtain a truly-distributed strain sensor, this process is repeated for each section of the FUT, successively. This data processing is entirely done by an Optical Backscattering Reflectometer (OBR, LUNA Inc.). After selecting the desired length of the FUT and its position along the setup, the desired gauge length (spatial resolution) (Δx) and the sensor spacing (δx), the OBR provides distributed strain values along the desired region of the FUT.

Fig. 1.

Qualitative illustration of the data process to use OFDR as a distributed strain sensor. a) represents de spectrum of the backscattering signal. b) is the intensity backscattered along the fiber, resulting from a FFT of a). c) is the spectrum of the selected region of interest define by the spatial resolution (Δx), resulting from an inverse FFT. d) is the crosscorrelation (applied in the time domain) obtain by comparing the spectra of the unstrained and strained FUT. e) represents the strain values at the determined (graph b) region of interest on the fiber.

A derivation from Maxwell’s equations can link permittivity fluctuation (Δε(z)) and optical field at the detector Ψ_d(β) as shown in Eq. (1) [23]. These fluctuations are determined by molecular and structural defects within the material from the amorphous nature of glass and its fabrication process. Although these defects are randomly distributed, they are static and do not change over time at room temperature, thus become a natural and permanent imprint at a given temperature, which can be used as a reference for sensing. In Eq. (1), $\beta$ is the spatial frequencies swept by the laser, $E_0$ is the amplitude of the electric field, z is the position along the FUT and r is the reflection coefficient of a reference reflector placed on purpose to retrieve the phase of the signal with higher precision.

$${\Psi }_d(\beta )=\frac{E_0\beta }{2i}{\displaystyle {\int }_{-\infty }^{\infty }\frac{\Delta \epsilon (z)}{\epsilon }}{e}^{2i\beta z}dz+r{E}_0{e}^{2i\beta z}$$ (1)

According to Eq. (1), the detected signal has the signature of the Fourier transform of permittivity fluctuations, which are random but static. Detailed derivation of this signal for temperature and strain measurement has been presented by Froggatt et al. [24]. The major limitation of strain sensing using OFDR is the relation between the strain sensitivity ($\Delta \epsilon$) and the spatial resolution ($\Delta x$). While one would like to minimize the resolution (gauge length as shown in Fig. 1(b)), this would come at a sacrifice of the frequency resolution, hereby strain resolution. Here, λ is the wavelength scanned and n is the core refractive index.

$$\Delta x\Delta \epsilon =\frac{\lambda }{4n}$$ (2)

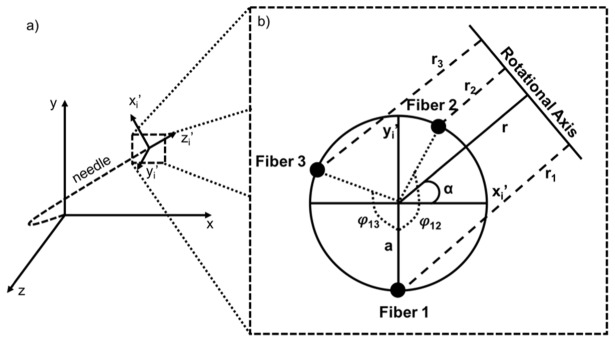
Once the OFDR is performed to evaluate the strain distributed along each fiber, a geometrical model proposed by Froggatt et al. [24] is used to evaluate the position of the fiber triplet in the laboratory frame. The idea is to divide the triplet into many (i) segments and evaluate the position of the segment tip in its own frame (x_i’,y_i’,z_i’). Then, we use geometrical assumption to find the angle (α_i) between the x_i’ axis and the rotational axis of this segment, as shown in Fig. 2. Assuming a_ij is the distance between the triplet center and the core of fiber j, φ_ijk is the angle between the core of fiber j and k (j and k = {1,2,3}, k≠j) and r_i is the distance between the triplet center and the rotational axis of this segment, Eq. (3) and Eq. (4) can be obtained (see [24] for further details).

Fig. 2.

a) Illustration of a deflected needle separated in i-segments. Each segment is defined within its own (x_i’,y_i’,z_i’) frame can then be expressed in the laboratory frame (x,y,z). b) Schematic of a (x_i’,y_i’,z_i’) frame cross-section showing the angle between x_i’ and the rotational axis (α_i), the distance between the center of the fiber triplet and the rotational axis (r_i) as well as the angle between each fiber (φ_ijk), Figure adapted from [24].

$$\tan ({\alpha }_i)=\frac{{\epsilon }_{i13}\sin ({\varphi }_{i12})+{\epsilon }_{i12}\sin ({\varphi }_{i13})}{{\epsilon }_{i23}-{\epsilon }_{i13}\cos ({\varphi }_{i12})+{\epsilon }_{i12}\cos ({\varphi }_{i13})}$$ (3)

$$r_i=\frac{a_i}{{\epsilon }_{i12}}\left({\sigma }_{i1}\sin \left({\alpha }_i+{\varphi }_{i12}\right)-{\sigma }_{i2}\sin \left({\alpha }_i\right)\right)$$ (4)

Note that ${\epsilon }_{ijk}={\epsilon }_{ik}-{\epsilon }_{ij}$ and ${\epsilon }_{ik}$ is the strain of fiber k measured on segment i. Also, ${\sigma }_{ik}=1+{\epsilon }_{ik}\approx 1$since ${\epsilon }_{\mathrm{ik}}$is in the microstrain order of magnitude $(\sim \mu \epsilon )$. Using these two values (α_i and r_i), the position of the segment tip in its own frame (x_i’,y_i’,z_i’) can be evaluated. Then, by applying a succession of projections and using rotational matrices, one can express these results in the laboratory frame (x_i,y_i,z_i). Since ${\sigma }_{ik}\approx 1$and since only the strain differences between fibers is considered (${\epsilon }_{ijk}={\epsilon }_{ik}-{\epsilon }_{ij}$), temperature variations have very low impact on the reconstructed shape. Indeed, any offset in the measured strain caused by temperature fluctuations is cancelled when is being evaluated assuming each fiber experiences the same temperature at a specific location (i).

3. Method

As discussed, in order to perform 3D shape tracking, three fibers have to be fixed together to form a fiber triplet. For comparison purposes, triplets should be identical, which is why a specific assembly setup was built, as shown in Fig. 3(a), to ensure repeatability. As shown in the schematic, three fibers placed in a triangular geometry are forced to pass through the two plates in the middle containing holes that are just large enough to accommodate the fibers. This forces the fibers to stay in this particular geometry. Then, UV curing glue drops are applied slowly as the middle plates move further apart. The glue is cured meanwhile using a UV lamp.

Fig. 3.

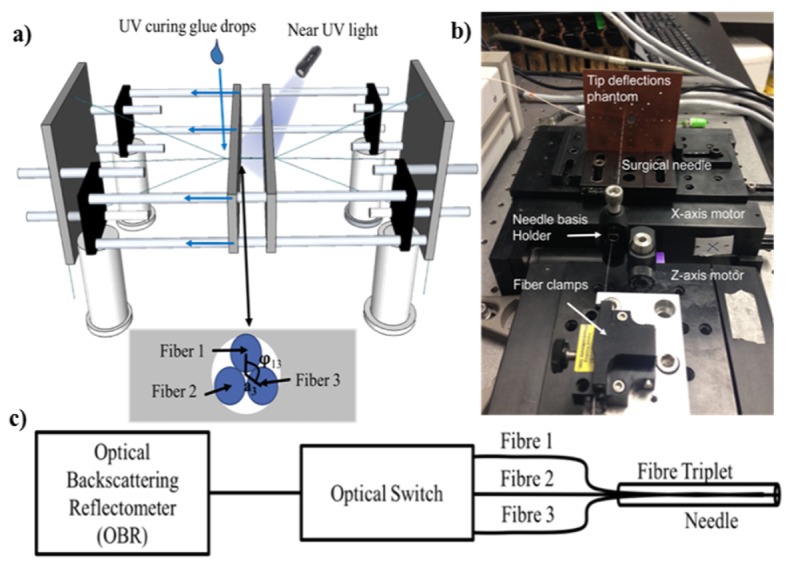
a) Schematic of the custom setup built to glue 3 fibers into a fiber triplet. b) Experimental setup used to induce a controlled deflection on the needle. c) Schematic representation of all the instruments used during measurements.

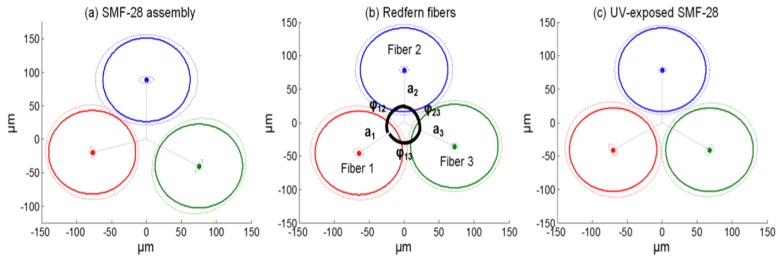
As shown in Eq. (3) and Eq. (4), the geometrical parameters of the fabricated fiber triplet need to be well known to perform shape reconstruction. Characterization of the fibers triplets’ geometry along the entire sensor fiber is therefore crucial to achieving precise measurements. A characterization method proposed by Roesthuis et al. [20] was implemented to evaluate the relative position between the fibers over the entire lengths of the fibers in the triplet. The idea of this technic is to bend the needle in a predictable shape by fixing its basis axis and moving the tip by a known distance. Then, the strain is measured as the needle (or the fibers) rotate around its own axis. As rotation occurs, each fiber will see a sinusoidal strain variation. The phase between each of the sine functions determines the angle of each fiber with respect to a relative center (φ_ij), while the amplitude determines the distance of each core with that center (a_i). Figure 4 summarized these values for each fiber triplet studied, i.e. one triplet formed with SMF-28, another one formed with Redfern (Germanium-Boron doped, high NA) photosensitive fibers and the last one formed with UV exposed deuterium-loaded SMF-28 (UVE-SMF-28), as proposed by Loranger et al. [22]. We can see that the fibers are not exactly positioned at 120° from each other (especially the SMF-28 assembly), but it is not a problem since the exact relative position can be evaluated and used in the shape reconstruction algorithm.

Fig. 4.

Characterization of each fiber triplets used for shape sensing. The full lines represent the measured value and the dashed lines are acting as error bars. The ideal (and aimed) configuration would be 120° between each fiber (from each core to the triplet center).

Once these triplet properties have been measured, one can use the geometric model suggested by Froggatt and Duncan [24] to progressively reconstruct the needle’s shape using the strain measured in all three fibers. In order to compare our results with theoretical values, the needle had to be bent in a repeatable way and its shape had to be easily predictable using Euler-Bernoulli Beam-Theory. The setup used (Fig. 3(b)) fulfills these requirements since the tip-deflection phantom allows one to move the needle tip in different directions and distances from the unstrained position. The fiber was displaced using precision motors and a phantom consisting of a plate with small holes (Figs. 3(b) and Fig. 5(b)) distributed on the surface was used to position and move the fiber. Normally, the fiber triplet should be glued in the needle to prevent the inside rotation of the triplet. However, in our case, the triplet could not be glued to the needle, as many triplets had to be characterized on our surgical testing needle.

Fig. 5.

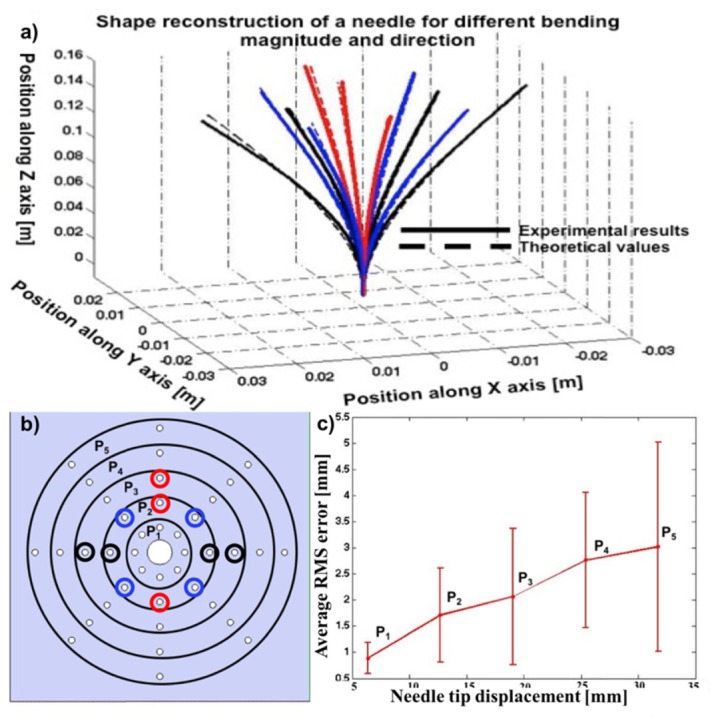
a - Needle shape reconstruction using the SMF-28 triplet. Each line corresponds to a specific hole circled in the tip displacement phantom (b). c – Precision reached (average RMS errors) on shape sensing as a function of the distance from the unstrained tip position. The error bars shown illustrate variation of the error from different holes.

As shown in Fig. 3(c), a commercial OBR system from LUNA was used for the OFDR measurement and data analysis for strain recovery. Each acquisition was done as fast as the system allows (~0.5Hz) and an optical switch was used to scan each fiber of the triplet in sequence. Further data processing for needle shape reconstruction considering the triplet characteristics as shown in Fig. 4 was done by our own software.

3. Results and discussion

Demonstration of shape reconstruction

After characterization of the fiber triplet, the shape reconstruction performance was tested. Figure 5(a) shows the reconstructed shape of the needle according to the corresponding holes on the phantom (Fig. 5(b)). Figure 5(c) shows the precision reached for the triplet made of standard SMF-28. Only a few results are shown in Fig. 5(a) for visualization purposes. Each curve corresponds to one particular tip displacement as the needle is placed inside the corresponding hole in the phantom shown in Fig. 5(b).

To make sure that this approach could be used for more complex needle deformations, Fig. 6 illustrates results on three arbitrary shapes, including one with 2 deflection points (red line). This figure clearly shows that shape reconstruction remains efficient and accurate (~1mm of RMS error). In this case, the evaluation of the RMS error was done manually using millimetric paper. Since this validation method is less rigorous than using Euler-Bernoulli Beam Theory, other results all have been acquired using single tip displacement to ensure repeatability on the needle deflection. Nevertheless, it is clear here that shape reconstruction could have been done on various needle deformation.

Fig. 6.

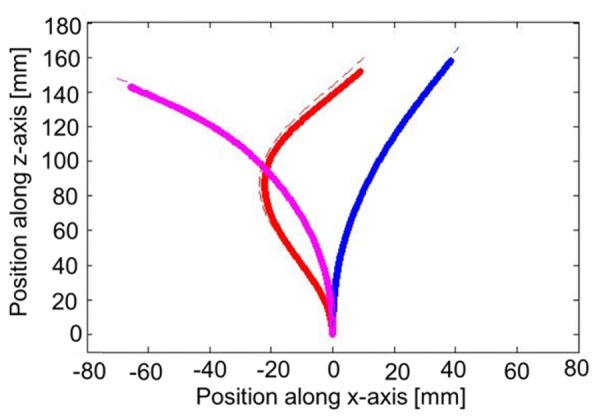
Demonstration of the shape tracking efficiency on three different arbitrary needle shape, including one with 2 deflection points (red line). The dash lines represent the expected shape evaluated using millimetric paper and the full lines are resulting from shape reconsctruction using OFDR.

Optimizing fiber backscatter

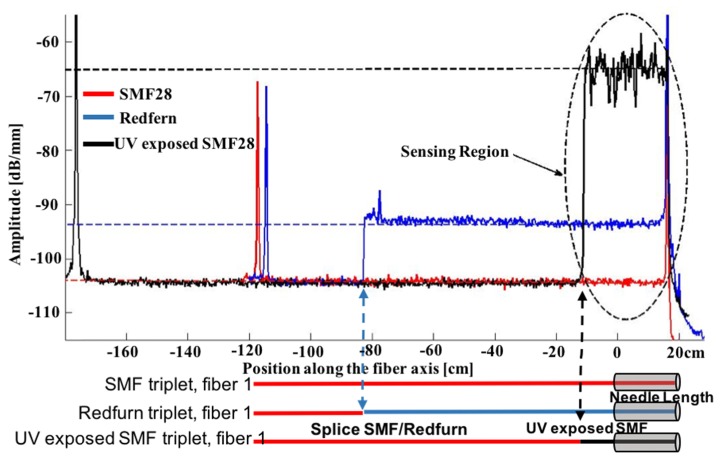
As described earlier, shape reconstruction has been also performed on triplets made from different types of fiber. Since distributed strain sensing based on OFDR relies on the analysis of the backscattered signal, we investigated the possibility of using high scatter fibers. Figure 7 shows the amplitude of the backscatter signal of the three types of fibers studied, which are standard single mode fiber (SMF-28), Germanium-boron doped fiber (Redfern) and hydrogen-loaded SMF-28 exposed to a focused UV beam (UVE-SMF-28). As expected, the backscattered signal in Redfern fibers is near ~10X higher than in SMF-28. This is mainly due to the presence of dopant inside the fiber core and to the larger numerical aperture (NA) which collects more of the back-scattered light. However, as predicted by Loranger et al. [22], UV exposed fibers (Hydrogen-loaded SMF-28 in this case) show a radical increase in the backscattered signal of about ~6300 times (~37dB). Contrary to the previous report on UV-exposed Rayleigh enhancement caused by the creation of color centers (defects) yielding a Rayleigh enhancement of ~20-25 dB [22], the fiber studied here actually had a strong and chirped (~5 nm) FBG written with a Bragg wavelength outside the scanned bandwidth for the distributed sensing. Scanning the laser close to the spectrum of the FBG allows a much higher signal, but limits the sensing length as the signal is quickly attenuated. Also, this reduces the effective scanning bandwidth to ~10 nm (even if 40 nm bandwidth is scanned) as the FBG’s side-band reflection decreases quickly, thus reducing the effective resolution. Both of these issues are not relevant in the case of needle reconstruction: the short length (10-20 cm) involved here does not suffer from attenuation and the resolution obtained (~με) with the shorter bandwidth is more than sufficient. The FBG was made by a direct writing scheme at 25 µm/s with a Talbot interferometer [25] using the fourth harmonic (λ = 266nm) of a Q-switched Nd:YAG laser with 100mW of power.

Fig. 7.

Backscattering amplitude as a function of the position along the fibers used measured for all three type of fiber. Underneath the graph, a scheme shows the positions where two different type of fibers are spliced together, explaining the abrupt peaks in the signal measured. The other peaks are due to reflections at fiber connectors (FC-APC).

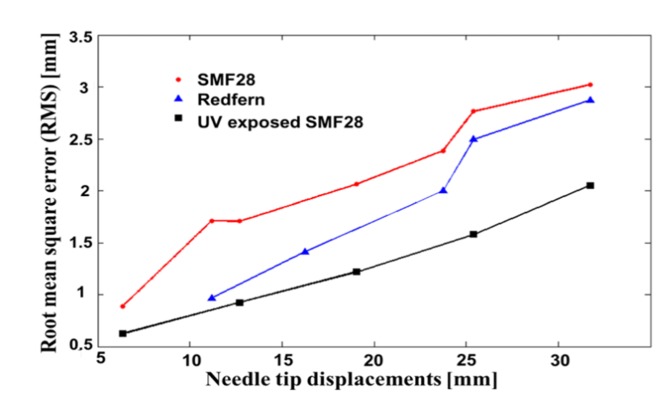
The precision is significantly enhanced when the fibers used have higher backscatter as shown in Fig. 8. The maximum precision reached is 0.9 ± 0.3 mm using standard SMF-28, which is not far from the higher precision reached with the FBGs’ approach (0.3 mm [16]). However, using Redfern fibers with a backscatter signal ~10X higher than SMF-28, an average accuracy enhancement of ~20% (considering all the curvatures studied) was achieved. More specifically, Redfern showed a precision of 44% higher for tip displacement of 11.34 mm (corresponding to a maximum curvature radius of 1.51m⁻¹). For tip displacements higher than ~24mm (curvature higher than ~3.2m⁻¹), the enhancement lowered to 17%, which is still significantly better than other published techniques to conclude the efficiency of this approach.

Fig. 8.

Comparison of the precision reached for all three type of triplet used, which is SMF-28, Germanium-boron doped fiber (Redfurn) and UV exposed hydrogen loaded SMF-28.

Moreover, for the UVE-SMF-28, which as a backscatter signal ~6300X higher than SMF-28, the average enhancement in the obtained accuracy is ~39%, reaching 47% for a needle curvature of 1.7m⁻¹. The best precision reached is 0.6 ± 0.2 mm and has been obtained using UVE-SMF-28 with a tip displacement of 6.35mm (0.85m⁻¹).

Optimizing the gauge length

According to Eq. (2), the spatial resolution achieved during strain sensing can have a significant impact on the accuracy for shape tracking. Therefore, we investigated the attainable accuracy using various spatial resolutions (gauge length) for all three type of triplets studied. During these experiments, the needle tip was displaced along the horizontal axis while changing the gauge length (Δx) as shown in Fig. 9. The large error for short gauge lengths (Δx < 0.4 cm) is a Fourier transform limitation as shown in Eq. (2). For longer gauge lengths (Δx > 4 cm), the strain sensitivity improves but the needle curvature cannot be correctly resolved since the gauge length is too large. However, between these two extreme values, Fig. 9 demonstrates that the choice of the spatial resolution seems to have very little impact on the precision reached during shape tracking.

Fig. 9.

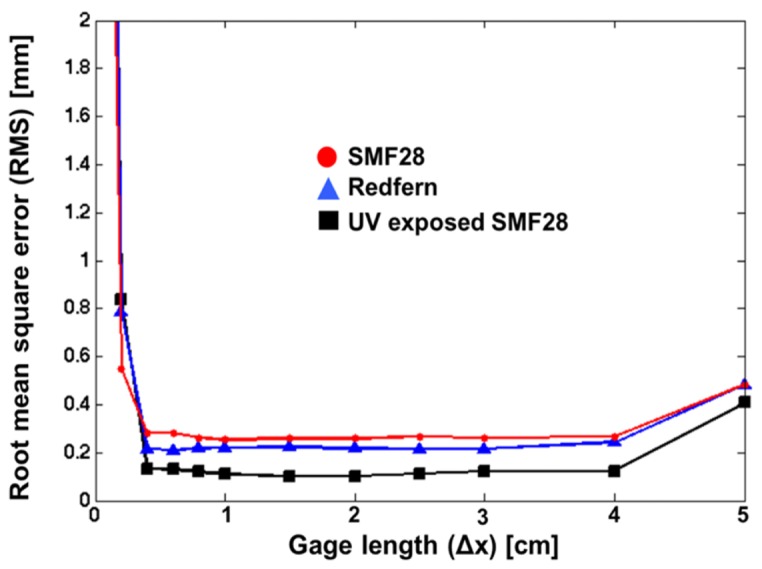
Analysis of the spatial resolution impact regarding shape sensing precision.

4. Conclusion

Accurate shape tracking of surgical needles was achieved using OFDR based true-distributed strain sensing. To do so, an optical backscatter reflectometer was used for strain measurements. Then, the geometrical model suggested by [24] combined with the approach suggested by [14] were used to obtain fiber triplets characteristics leading to shape tracking based on strain measurements. Measurements on three different types of fiber triplets (SMF-28, Hydrogen-loaded Germanium-Boron doped fibers (Redfern) and Hydrogen-loaded UV exposed SMF-28 (UVE-SMF-28)) were performed in order to correlate the attainable accuracy with the scatter level in the fibers. We thus demonstrated that higher scatter fiber leads to better shape tracking accuracy. Indeed, an average enhancement of 20% was observed by comparing Redfern with SMF-28 fiber. This enhancement increases to 39% for the higher scatter UVE-SMF-28 fiber.

Statistically, the best precision reached, using a gauge length of Δx = 1cm with the UVE-SMF-28 triplet, is 0.6 ± 0.2 mm, which is slightly above the best accuracy listed in the literature using FBG based strain sensors (0.3mm [16]). However, it is still really promising considering that the accuracy can be optimized using fibers with high scatter properties. Also, it is important to note that our distributed fiber triplet is a far more easily replaceable and of inexpensive construction compared to FBG based systems, which are very costly and difficult to construct. In view of potential breakage of the sensor, our device does not require the writing of matched gratings, nor the accurate placement of FBGs at certain locations, but merely the use of UV pre-exposed fiber in the fiber triplet for enhanced performance. In addition, since this technique is able to reconstruct complex shape, which is much more difficult and potentially extremely costly with FBGs, it is promising for many potential applications. In this regards, it is clear that shape sensing using OFDR and UV exposed fibers is a step towards the enhancement of accuracy in shape sensing inside minimally invasive surgical tools, which is also a step in the direction of surgical interventions obviating the simultaneous use of other external imaging tools such as CT, MRI or ultrasound imaging. Moreover, by optimizing even more the accuracy of such devices, one can possibly imagine a single multi-purpose probes including few fibers used to acquire images of the targeted area simultaneously as fibers triplet are used to guide the probes in-vivo through to body.

In this regards, many improvements can be made on the experimental setup in order to enhance the accuracy. Amongst these improvements, fixing the triplets inside the needle would be the simplest and more efficient one, since it would prevent the triplet from moving in between measurements inducing unwanted errors. Also, increasing the distance between each fiber core would increase precision, but would reduce flexibility.

Funding

Fonds de recherche Nature et Technologies du Québec FRQNT (B2); Canada Research Chair in Medical Imaging and Assisted Interventions; Canada Research Chairs on Future Photonics Systems.