Changes in optical properties of electroporated cells as revealed by digital holographic microscopy

Abstract

Changes in optical and shape-related characteristics of B16F10 cells after electroporation were investigated using digital holographic microscopy (DHM). Bipolar rectangular pulses specific for electrochemotherapy were used. Electroporation was performed in an “off-axis” DHM set-up without using exogenous markers. Two types of cell parameters were monitored seconds and minutes after pulse train application: parameters addressing a specifically defined area of the cell (refractive index and cell height) and global cell parameters (projected area, optical phase shift profile and dry mass). The biphasic behavior of cellular parameters was explained by water and mannitol dynamics through the electropermeabilized cell membrane.

1. Introduction

The electroporation procedure represents a platform technology for multiple biological and industrial applications. It is based on the application of electrical pulses which induces permeabilization of cell membranes. Depending on the pulse characteristics (microsecond and nanosecond pulses of various amplitudes) the membrane of cell or cell organites become permeable, allowing various substances to go in or out of the cell [1–3]; many applications such as electrochemotherapy [4–7], gene electrotransfer [8] and cancer vaccination [9–11], cellular electrofusion [12] and electroablation [13, 14] have been developed in the last decade. In food and biomass industry, electroporation was successfully implemented for food preservation [15, 6] and for quality increase and energy savings in biomass processing [17, 18].

In parallel with the fast development of applications there is a constant interest in fundamental research, since the intrinsic mechanisms of electroporation are still under debate [19]. Cellular and molecular changes occurring during electroporation process and cell recovery are not yet well understood and described in detail, due to their fast dynamics and difficult access by sensitive optical and electric techniques. The efficiency improvement of the medical applications requires however a better understanding of physical events arising in electroporated cells during and after pulse application.

Optical methods may offer significant information regarding the cell morphological changes accompanying electroporation. Here we propose the use of Digital Holographic Microscopy (DHM) as an innovative technique for the study of cellular modifications subsequent to electroporation. DHM has been already validated on biological samples [20, 21] and is nowadays used to study various samples of interest in medicine, material science, microdevice characterization or technical inspection [22–26]. By taking advantage of the high spatio-temporal resolution of quantitative phase imaging by DHM, this method was used to evaluate the dynamics of the damages production and repair following laser microsurgery and cell optical micromanipulation [27, 28]. DHM allows mapping the refractive indices of a single cell. Tomographic phase microscope was further on developed for performing refractive index measurements of substrate-attached cells or multicellular organisms, and the time-dependent changes of the indices within the cell [29].

DHM may be used for image reconstruction of transparent samples after one single image acquisition, in fraction of seconds, without using any kind of labels or contrast chemicals. The physical principle of the method is based on the phase shifts introduced in the wavefront of a laser beam diffracted by the specimen, due to different optical path lengths in each point of the sample. When this beam interferes with the reference beam, their superposition produces the holographic image, which contains phase shift values of the specimen in each point. Further, the reconstruction using scalar diffraction theory, Fourier analysis and specific image processing techniques retrieves information about the shape and optical properties of the sample [30]. Living cells in their natural liquid environment can be thus characterized with preservation of cell viability. DHM represents a non-destructive, non-invasive, marker-free technique with nanometric resolution along laser beam propagation axis [31, 32].

In this paper we focused on monitoring the changes induced by electroporation in the optical and shape characteristics of murine melanoma B16F10 cells. Using DHM in the “off-axis” configuration and the decoupling procedure we evaluated the refractive index and the height of the living cells before and after pulse delivery. For 10 minutes after pulse application we monitored two types of cell parameters: those addressing a specifically defined area of the cell (refractive index and cell height) and global cell parameters (projected area, optical phase shift profiles and dry mass).

2. Materials and methods

2.1 Cell culture

B16F10 murine melanoma cells were cultured in high glucose Dulbecco’s modified Eagle’s medium, containing 1 mM L-glutamine, supplemented with 10% fetal bovine serum, in a 37°C and 5% CO₂ incubator (Heracell 150i, Thermo Scientific, USA). All culture products were purchased from Sigma Aldrich Chemie GmbH, Germany. 24 h prior to experiments the cells were harvested by trypsination (0.5% Porcine Trypsin EDTA, Gibco, EU) and seeded at 5−10 × 10⁴ cells/ml in optical glass bottom chambers (µ-Slide 2 wells, Ibidi, Germany). At the moment of the holographic experiments, the cells were covering only 20 to 30% of the chamber (Fig. 1(c)); this low cellular density avoids cells superposition and insures a homogenous electric field in the area of the cell which is to be observed. This allows also separate digital processing for one single cell.

Fig. 1.

(a) L-shape stainless steel plate electrodes; (b) electroporation pulse profile: a train of four pulses was applied with a frequency of 1 kHz; (c) attached cells at 20-30% covering density, allowing separate analyses of a single cell; (d) membrane electropermeabilization checked by Propidium Iodide; accumulation of the fluorescent probe witnesses for the permeabilization of the cell membrane.

2.2 Chemicals

Two cell-bathing solutions were used during the experiments:

i/ solution M: 300 mM mannitol (Aldrich Chemistry, France) solution of conductivity up to 0.001 S/m and 305 ± 10 mOsmol, prepared using ultrapure water (18.2 MΩ × cm at 25°C, Smart2Pure Ultrapure Water Systems, TKA, Germany). The pH of the solution was adjusted at 7.2 by adding 20 µl NaOH 1M to 500 ml solution M (final sodium concentration 40 µM).

ii/ solution D: Dulbecco’s Modified Eagle Medium without Phenol Red, with 1g/l D-glucose and Pyruvate (Gibco Invitrogen, USA). The measured osmolarity (Osmomat 030, Gonotec, Germany) of this solution was found to be 298 ± 2 mOsmol.

The refractive indices of these solutions were measured with an Abbe refractometer (Novex, Holland): n_M = 1.3412 ± 0.0003 and n_D = 1.3356 ± 0.0002.

For electroporation tests, Propidium Iodide (PI) (Fluka Biochemica, USA) solution was used (0.15 µM final concentration). The PI stock solution (75 mM) preserved in dark at 4°C, was prepared in ultrapure water.

2.3 Cell electroporation protocol

Electroporation of the attached cells was performed in M solution, in the Ibidi cell chamber, using a pulse generator (ELECTRO cell B10, Betatech, France). We applied a sequence of four bipolar rectangular pulses (1 kV/cm electric field intensity for both positive and negative pulses, with time characteristics described in Fig. 1(b)). L-shaped stainless steel plate electrodes, touching the chamber bottom, were used; the distance between electrodes was 0.5 cm (Fig. 1(a)). The cell electroporation was checked by penetration of fluorescent dye Propidium Iodide [33] (Fig. 1(c) and 1(d)).

2.4 Acquisition and processing of holographic images

2.4.1 Experimental procedure

The experimental setup for digital holography is based on the Mach-Zehnder interferometer in “off-axis” configuration, working in transmission, suitable for transparent samples [34]. In our experimental set-up the angle between the reference and object beams was trimmed to improve the lateral resolution by setting the interfringe at an optimum value of 8−12 pixels.

We used a double stabilised HeNe laser operating at 632.8 nm (Spectra Physics) and a CCD camera for image acquisition (Pike, F421C equipped with a 2048 × 2048, 6.7 pixel pitch Kodak sensor). A 40X (N.A = 0.85) microscope objective (Nikon) ensured a lateral resolution of 0.9 µm, allowing an optical field of about 200 μm diameter.

A set of 13 holograms was recorded on every chosen single cell (a sample of such hologram is shown in Fig. 2(a). The first two holograms of the same cell were recorded in D and M solutions, respectively. The change of the liquids was done using a manual perfusion system without removing the chamber from the DHM set-up, avoiding thus any displacement of the cell. Then, the electroporation pulse sequence described in Fig. 1(b) was applied. The 3rd holographic image was recorded 2 seconds after pulse delivery, in M solution. Subsequent holograms of the cell were recorded every minute during 10 minutes after the pulse delivery. Electroporation and image acquisition were carried on at room temperature.

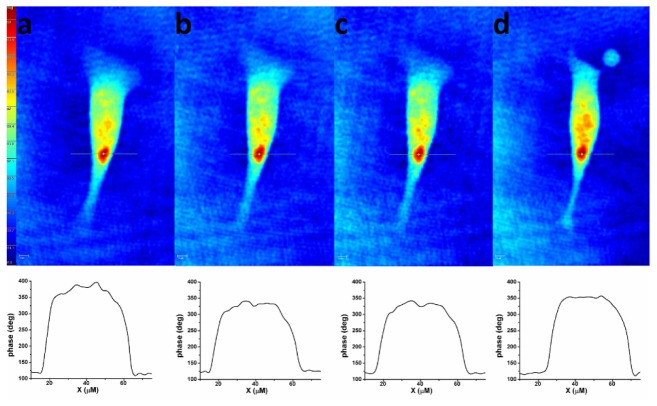
Fig. 2.

Experimental and numerical steps of the holographic image acquisition and processing: (a) hologram, (b) and (c) reconstructed quantitative phase images, (d) cross section through the reconstructed quantitative phase image.

2.4.2 Image processing and computation of local parameters (height and refractive index)

The image reconstruction was performed using dedicated commercial software KOALA^R [35]. The procedure consists in following the standard routines of the software [30], producing a quantitative phase image of the cell (an image which attributes a phase shift value to every pixel) (Fig. 2(b) and 2(c)). The optical phase shift profile (Fig. 2(d)) was drawn along a direction parallel to the applied electric field and passing through the point of maximum phase shift of the image.

The phase shift depends on both the height and the refractive index of the cell in each pixel of the image. To resolve individually these values, a so-called decoupling method was proposed [36], based on recording two holograms of the same region in two liquids with slightly different refractive indices. We used in our experiment the D and M solutions as described in 2.4.1, obtaining two phase shift images characterised in each (x,y) coordinates by optical phase shift values Δφ_D(x,y) and Δφ_M(x,y), respectively:

$$\Delta {\phi }_D(x,y)=\frac{2\pi }{\lambda }\left[n(x,y)-n_D\right]h(x,y)$$ (1)

$$\Delta {\phi }_M(x,y)=\frac{2\pi }{\lambda }\left[n(x,y)-n_M\right]h(x,y)$$ (2)

where λ = 632.8 nm is the laser wavelength, h is the height and n is the refractive index of the cell in the point of (x,y) coordinates.

Equations (1) and (2) were used to obtain the values for n(x,y) and h(x,y) in each investigated (x,y) point:

$$h(x,y)=\frac{\frac{\lambda }{180}\left[\Delta {\phi }_D(x,y)-\Delta {\phi }_M(x,y)\right]}{\frac{2\pi }{\lambda }\left(n_M-n_D\right)}$$ (3)

$$n(x,y)=\frac{n_D\Delta {\phi }_M(x,y)-n_M\Delta {\phi }_D(x,y)}{\Delta {\phi }_M(x,y)-\Delta {\phi }_D(x,y)}$$ (4)

These equations were first applied to the pair of holograms acquired in D and M solutions before the electric pulse delivery (in this case, n and h parameters are referred to as n_BP and h_BP). Then, they were solved using the following pairs of holograms: the same hologram acquired in the initial D solution, paired with those acquired in the M solution at 2 seconds, 1, 2, 3…7 min after the pulse sequence delivery (here, n and h parameters are referred to as n_AP and h_AP).

For cellular data extraction, MATLAB codes were developed (adapted for this series of holograms processing). For decoupling procedure, these codes identified an area of 3x3 pixels in the region characterized by the maximum phase shift. Average values of n(x,y) and h(x,y) corresponding to this region were computed using Eqs. (3) and (4).

The n and h parameters were computed from pairs of holograms acquired before and after pulse delivery, assuming thus the risk of supplementary errors but with the major benefits of monitoring the evolution of the same cell a longer time after electroporation.

For decoupling computations only holograms recorded until the minute 7 were used. For longer periods, the decoupling procedure based on the initial hologram is no longer reliable, mainly due to a possible cell displacement.

2.4.3 Computation of phase-based parameters: projected area, optical phase shift profile and dry mass

Using the quantitative phase profile of the cell, without decoupling procedure, various parameters may be computed offering information about cell structure and shape [37], cell volume changes and cell dry mass dynamics [38]. Based on our reconstructed images from the experimentally recorded holograms, we determined cell projected area (A) and averaged optical phase shift profile (OPS). In order to calculate the projected area of cells, MATLAB codes were developed for the cellular edge detection and cell contour drawing [39]. Cell surface area was computed as the sum of all pixels inside this contour; the dimension of one pixel was previously established by an independent calibration procedure, using an objective micrometer. By summation of the phase values inside the cell contour, divided by the number of pixels within this contour, the averaged optical phase shift profile of the cell was obtained. Dry mass (DM) was calculated according to a method described by Popescu et al as a surface integral of the phase shift on the whole cell area [40].

2.5 Statistical analysis of data

Thirteen independent experiments with decoupling procedure (described in 2.4.2) were performed, among which 7 were on electroporated cells and 6 on controls (to which no pulses were delivered). Computer software Origin Lab v.8.0 was used to plot the data and evaluate the statistical significance of differences between the electroporated cells and controls (Mann-Whitney two samples non-parametric test). Differences were considered as significant at p < 0.05. The data were plotted as relative variation of refractive index, cell height, projected area, averaged optical phase shift profile and dry mass with respect to the values of these parameters before the moment of electric pulse delivery. Graphical representations in Fig. 4 and Fig. 5 are “box and whiskers” type, in which boxes include percentiles 25–75, whiskers are outliers, middle horizontal line is the median and the small square in the box is the mean.

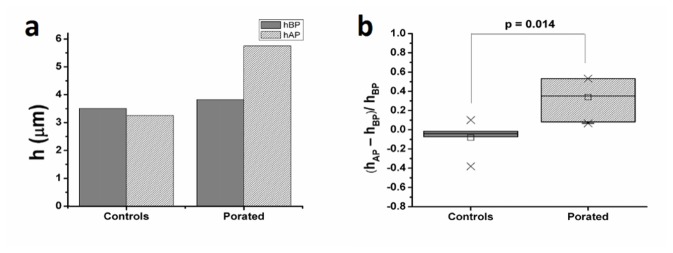
Fig. 4.

Variation of cellular height observed at 2 s after pulse delivery (h_BP - height of the cell before electroporation, h_AP - height of the cell after electroporation). For the decoupling procedure we have used the hologram taken in D solution before pulse application: (a) example of typical variation of cell height as calculated on one cell; (b) relative variation of cellular height computed on all thirteen experiments.

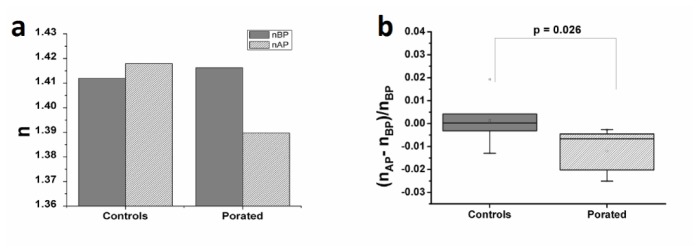
Fig. 5.

Variation of cellular refractive index at 2 seconds after pulse delivery (n_BP - refractive index of the cell before electroporation, n_AP - refractive index of the cell after electroporation). For the decoupling procedure we have used the hologram taken in D solution before pulse application: (a) example of typical variation of cell refractive index as calculated on one cell; (b) relative variation of cellular refractive index computed on all thirteen experiments.

3. Results

Figure 3 presents a set of consecutive holographic phase images of a B16F10 cell, acquired in D and M solutions before electroporation and at different time moments after pulse delivery. Optical phase shifts are codified in colors (blue represents the smallest phase shift, red the highest one). Changes in optical phase shift values reflecting variations in cellular shape and refractive index are observed after pulse delivery.

Fig. 3.

Consecutive holographic phase images of an attached B16F10 cell in two different solutions (D and M) at different time moments. Top: (a) hologram acquired in solution D before the electric pulse delivery, (b) hologram acquired in solution M before the electric pulse delivery, (c) hologram acquired in solution M at 2 seconds after pulse delivery, (d) hologram acquired in solution M at 10 minutes after pulse delivery. Bottom: phase shift profiles along cross sections through the point of maximum phase shift corresponding to each hologram.

3.1 Cellular height and refractive index variation

Using the decoupling procedure, the height and refractive index of each cell were calculated in a square area of 3x3 pixels within the region of maximum phase shift, identified with the MATLAB codes described in section 2.4.2. Both parameters were presented using their relative variations between 2 seconds, 1, 2…7 min after pulse delivery (referred as h_AP and n_AP) and the moment before pulse delivery (h_BP and n_BP). Before pulse delivery, the height of the cells was ranging from 2.87 to 14.61 µm depending on the cell shape. The average refractive index was found n_BP = 1.3929 ± 0.0263.

At 2 seconds after pulse delivery, a statistically significant modification of the cell height was observed (the average height of the electroporated cells increased by 33%, p = 0.014). In the same time interval, the average height of controls decreased by 6.7% (Fig. 4(b)).

At the same time (2 seconds after pulse application), the refractive index showed a statistically significant decrease (the average value dropped by 1.2% in electroporated cells (p = 0.026) while in controls there was a small increase of 0.1%) (Fig. 5(b)).

Due to the intrinsic inhomogeneity of cells in culture (i.e. cell cycle phase), the absolute thickness and refractive indices were dispersed. In Fig. 4(a) and Fig. 5(a), examples of typical results on one single cell are given. In order to evidence the effect of the applied electric field pulses on cells thickness and refractive indices, the relative variation of these parameters was computed (illustrated in Figs. 4(b) and 5(b)).

In the next 7 minutes after the initial drop (Fig. 6 inset), the refractive index showed a constant tendency to recover (Fig. 6), reaching the controls value after about 4 minutes. In control cells, the refractive index remained roughly constant; the slight increase observed in our recording may be attributed to the conditions in which the cells were kept during the experiment.

Fig. 6.

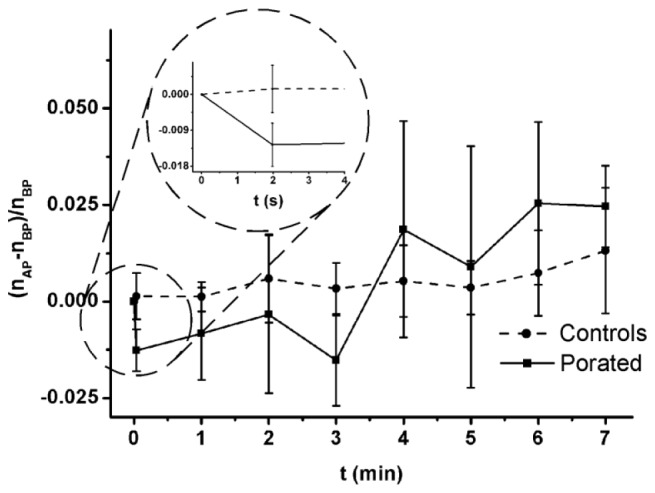
Relative variation of cell refractive index during the 7 minutes following the pulse delivery. The inset shows the evolution of the relative refractive index within 2 seconds after poration (n_BP - refractive index of the cell before electroporation, n_AP - refractive index of the cell after electroporation).

3.2 Cell projected area, optical phase shift profile and dry mass evolution

By processing the quantitative phase images, we computed (as described in 2.4.3) three parameters related to the whole cell morphology: cellular projected area (A), averaged optical phase shift profile (OPS) and dry mass (DM). Evolution of all parameters is shown as the relative variation of their values at 2 seconds, 1, 2 …10 min after pulse delivery (referred as A_AP, OPS_AP and DM_AP) and at the moment before pulse delivery (A_BP, OPS_BP and DM_BP) (Fig. 7).

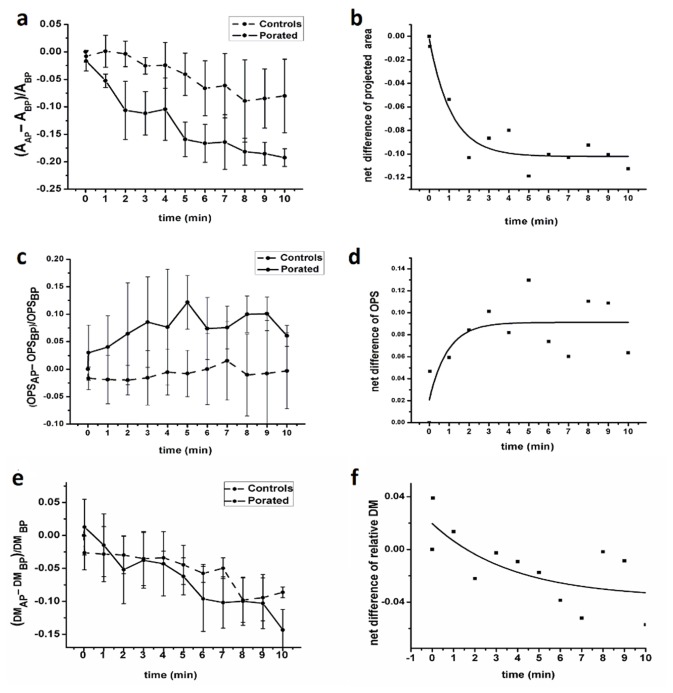
Fig. 7.

Relative variation of cellular projected area (a), averaged optical phase shift (c) and dry mass (e) after pulse delivery. Panels (b), (d) and (f) present these parameters after subtracting the controls (dots) and the exponential fit (line) of their time behavior (A_BP - projected area of the cell before electroporation, A_AP - projected area of the cell after electroporation, OPS_BP - averaged optical phase shift profile of the cell before electroporation, OPS_AP - averaged optical phase shift profile of the cell after electroporation, DM_BP - averaged dry mass of the cell before electroporation, DM_AP - averaged dry mass of the cell after electroporation).

A time-dependent decrease of projected area was observed as an effect of pulse application (Fig. 7(a)). At the end of the 10 minutes, the projected area of porated cells dropped by 19.5 ± 1.6% while the projected area of controls dropped by only 8.4 ± 6.7%. In the same time interval, OPS increased by 6 ± 1%, compared to 0.5 ± 0.3% increase in controls (Fig. 7(c)). Concerning the dry mass, no obvious changes were observed when electroporated cells were compared to the controls (Fig. 7(e)). As can be seen in Fig. 7(f), the relative dry mass change was in the limits of less than ± 4%, which is within the sensitivity limits of our experiments.

It appeared that the control cells were also undergoing progressive changes of the projected area and averaged optical shift profile, being exposed to the same unfriendly conditions during the experiment: immersion in mannitol solution, no CO₂/temperature control. However, the changes recorded in the porated cells were much more significant than those observed in controls.

By subtracting the area of the porated cells from that of the controls at each moment of time, one may observe the net response of the cells to pulse application, in terms of projected area (Fig. 7(b)). A similar computation of the OPS shows the evolution of the averaged optical phase shift profile caused by the pulse delivery (Fig. 7(d)).

As seen in Fig. 7(b) and 7(d), at 3 to 4 min after pulse delivery, the relative variation of cell projected area and the averaged optical phase shift profile became the same in porated and control cells (plateaus). This leads to the conclusion that the maximum impact of pulse train application is present within first 3 min after pulse application. From minutes 4 to 10, the porated cells’ area and averaged optical phase shift profile behave similar to those of controls.

4. Discussion

Using DHM, a technique which avoids a cell damage induced by fluorescent or any other exogenous marker, we observed the changes in cell shape and refractive index of electroporated cells in the time interval 2 s–10 min after pulse application.

There were two categories of parameters obtained from our experimental data: parameters addressing a specifically defined area of the cell (refractive index and cell height in the region of maximum phase shift) and global cell parameters (projected area, averaged optical shift profile and dry mass). It is worth to note the biphasic behavior of the cellular parameters. The refractive index drops in the first 2 s after pulse application and recovers within next 3 min (Fig. 6). The projected area and averaged optical phase shift profile show a fast evolution within first 4 minutes after pulse, followed by a steady progression at the same rate as in controls (Fig. 7).

A similar biphasic behavior was observed by Nesin et al when electroporating GH3 cells immersed in solutions containing various PEGs and sugars of different molecular weight (mannitol including) [41]. These authors have used fifty 60 and five 600 ns pulses but found no statistically significant difference between the cell volume changes in these two electroporation conditions. They monitored the cell volume changes at some minutes after pulse application, by recording confocal images followed by 3D reconstruction of different cell sections on z axis. Their findings reported for GH3 cells were consistent with their earlier observations on cell volume changes in CHO-K1cells, NG108 neuroblastoma cells and U-937 monocytes [42]. These similarities encourage the idea that osmotically driven phenomena generate similar effects in different cell lines and the results obtained by different research groups on different cell lines may be compared.

Based on our observations and computations, and according to observations of other authors [1, 19, 41, 43–45], the following scenario of the cellular events consecutive to pulse application may be outlined: immediately after pulse delivery (2 seconds in our recordings) the small intra- and extracellular solutes will travel freely across the plasma membrane of the porated cell, in order to attain the electrochemical and osmotic equilibrium. The larger intracellular solutes (unable to pass through membrane pores) remain trapped inside, creating additional osmotic pressure and attracting water to cause cell swelling. It may be thus assumed that the cell height increase and the refractive index decrease we have observed immediately after the pulse (2 s after pulse application) correspond to a cell swelling due to water entering the cell. The details of this process may be described as follows: once the membrane is permeabilized, two main transfer processes may occur according to different chemical gradients: ion leakage from the cell (in our experimental conditions the ionic concentration outside the cell is almost negligible) and mannitol penetration into the cell, the latter being much slower due to the large size of the mannitol molecule compared to ions.

Both processes are accompanied by water translocation: an initially fast process of water penetration (associated with ion leakage and aiming to dilute the intracellular concentration of non-permeable macromolecules) and a much slower process of water leakage (to compensate the mannitol concentration outside the cell). The overall effect is that during and immediately after pulse application, water penetration prevails (leading to cell swelling) while after a period, water leakage becomes more important, determining the cell coming back to its initial dimensions. This means that the time-profile of water content of the cell presents a peak-value during or at very short time after poration, which in turn, explains the decreased value of refractive index as well as the increased value of the cell height described in paragraph 3.1 and Figs. 4(b) and 5(b). In the following minutes, in which the water leakage prevails, the resulting cell shrinking makes the refractive index turning back to the initial value (at 3 to 4 min after pulse delivery) (Fig. 6) accompanied by the decrease of the cell projected area (Fig. 7(a)). A similar evolution in phase image computed parameters (cell projected area and optical phase shift profile) was observed by Popescu et al [40] when the cell was contracting due to water efflux in a hyperosmolar solution; the observed decrease of the cell volume and cell projected area were associated with recorded increase of the optical phase shift.

Cells observation by classical optical microscopy we have made, showed that, after pulse delivery, their projected area is progressively decreasing (by up to 20%), in parallel with their retraction and partial detachment from the chamber bottom (data not shown).

In the above outline, we tried to describe and explain the observed changes in cell parameters, based only on the osmotically driven processes generated by electropulses application. It must be however taken into consideration that in the time interval of our observation, the pulsed cells have already triggered their repair mechanisms, which may last minutes or even hours [33, 46–49]. According to the steps of electropermeabilization kinetics described by Teissie et al [50], our recordings address the “resealing step”, which is driven by the cell metabolism. The cellular events associated to the repair phase are also reflected by the time evolution of the global parameters (A and OPS) we have measured (Fig. 7(b) and 7(d)).

The 1.2% decrease of the refractive index observed at 2 s after pulse application represents a significant change of this parameter. The same order of variation in the refractive index of neural cells exposed to osmotic stress was observed by Rappaz et al [20]; the authors attributed this decrease to the osmotically-driven water penetration into the cell. This explanation may also stand for phenomena observed in our electroporation experiments. Moreover considering the physical characteristics of the electric pulses (short duration, bipolar) any net electrophoretic movement of large molecules across the cell membrane was not to be supposed. The only expected mass exchange occurring during the transient permeabilization can be attributed to small molecules/ions movement due to the electrochemical gradient across the membrane, which does not affect the dry mass of the cell (Fig. 7(f)), the variation of the cellular dry mass being usually attributed to protein content modifications [40, 51].

The absolute values of the refractive indices calculated before the pulse application (1.3929 ± 0.0263) are in good agreement with the values found by other authors for cancer cells [52, 53]. The advancements in detection techniques [54] allow not only high resolution mapping of refractive index of normal and cancerous cells, but comparison of cancer cells from the same source. Various research studies have presented the refractive index evolution during cell cycle stages, mainly in cancer cells characterized by abnormal cell cycles and increased proliferation rates (see summarizing overview on the issue by Liu et al [55]). In our experiments the cells were not synchronized in culture or selected on morphological features suggestive for a certain cell cycle stage (before pulse delivery, the height of the cells was ranging from 2.87 to 14.61 µm). In order to evidence the effect of the applied electric field pulses the data were plotted as relative variation with respect to the values of each parameter before the moment of electric pulse delivery, and after that the evolution of the control and electroporated cells were compared. It is worth to note that within this context of inhomogeneity of cell cycle stage, the cells reacted similarly to the electroporation pulses.

Regarding the possibilities to improve the technique, it is worth mentioning that the decoupling procedure, which consists in the change of cells immersion liquid, implies the risk of cell moving and/or detachment; this is a major limitation in the data quality. We have used for data processing only experiments in which no such event occurred. This drawback may be overcome by using the dual-wavelength DHM technique, which would also allow determining the refractive index and cellular height in real time [56].

We also have to note that although we have observed a biphasic evolution of the measured local and global parameters, they cannot be however compared ad literam since the projected area and optical phase profile we have determined, are averages for the whole cell, while the height and refractive index describe the cell properties in a small particular area and could show a different trend if averaged on the whole cell.

5. Conclusions

Digital Holographic Microscopy appears to be a valuable tool for monitoring cell dynamics during and after electroporation. In our recordings, cell refractive index and shape changes could be monitored at seconds and minutes after pulse application. These changes are accompanying and are the result of the phenomena produced in cell membrane by the electric field during pulse application as well as by the metabolic response of the cell within the cellular recovery and membrane resealing processes.

DHM may be used for the study of fast processes arising during the pulse application as well as at micro and milliseconds after pulse if a high-speed camera is used; it allows monitoring the processes occurring in a broad range of time scales. In DHM, no scanning is necessary (as it is the case in confocal or atomic force microscopy), the cell image being recorded in fractions of seconds.

Another remarkable advantage of the DHM is that it may provide a spatial resolution of parameters at single cell level. In this paper, we computed the refractive index value in a limited cell area corresponding to the maximal phase shift. Using the same procedure, different phase profiles may be investigated providing time-resolved refractive index and height maps of the cell as well as the cell volume evolution during the electroporation and recovery processes. This approach opens a broader perspective in following up and understanding the cellular changes induced by electroporation.

Funding

Romanian Ministry of Education (PhD fellowship attributed to Violeta L. Calin, contract no. 24450/01.10.2013).