FISH-ing for captured contacts: towards reconciling FISH and 3C

Abstract

Chromosome conformation capture (3C) and fluorescence in-situ hybridization (FISH) are two widely-used technologies that provide distinct readouts of 3D chromosome organization. While both technologies can assay locus-specific organization, how to integrate views from 3C, or genome-wide Hi-C, and FISH is far from solved. Contact frequency, measured by Hi-C, and spatial distance, measured by FISH, are often assumed to quantify the same phenomena and used interchangeably. Here, however, we demonstrate that contact frequency is distinct from average spatial distance, both in polymer simulations and in experimental data. Performing a systematic analysis of the technologies, we show this distinction can create a seemingly-paradoxical relationship between 3C and FISH, both in minimal polymer models with dynamic looping interactions and in loop extrusion simulations. Together, our results indicate that cross-validation of Hi-C and FISH should be carefully designed, and that jointly considering contact frequency and spatial distance is crucial for fully understanding chromosome organization.

The bewilderments of the eyes are of two kinds, and arise from two causes, either from coming out of the light or from going into the light

-- Plato, The Republic, Book VII

Introduction

While genomes are often considered as one-dimensional sequences, they are also physically organized in three-dimensions inside the cell nucleus, with far-reaching consequences^1–4. One of the many important implications relates to gene regulation: regions of regulatory DNA are often very far away in the linear genomic sequence from the genes they regulate, yet their regulatory interactions are presumed to rely on direct encounters in three-dimensional space. Ideally, one would be able to follow the exact spatial position of two interacting loci in real time, while simultaneously assaying their functional state and the consequences of their encounters, such as RNA production. However, no method currently exists that allows both directly tracing chromosomes with nucleosome-level spatial resolution, let alone in living cells; current methods are indirect readouts of chromosomal organization. Below we focus on two widely used techniques for assaying chromosomes, DNA-FISH and chromosome conformation capture.

Chromosome conformation capture (3C) techniques have become popular for their high-throughput ability to connect spatial information to the genomic sequence^2–5. 3C-based approaches use crosslinking and ligation to capture the information that two genomic loci were spatially proximal. Moreover, 3C techniques are readily generalized to genome-wide scale, usually termed Hi-C⁶; here we refer to the contact frequency from Hi-C and 3C interchangeably. Importantly, while 3C records whether two loci were in contact in some fraction of cells in the population, it does not record where in the nucleus this contact occurred. Also, 3C is usually performed on large populations of cells. This is advantageous in that 3C can assay both very frequent and very rare events, as the large population allows for a large dynamic range. However, information regarding cell-to-cell variability is not available in population-average maps of chromosomal contact frequencies^7,8.

Fluorescence in-situ hybridization (FISH) technologies are appreciated for their ability to specifically determine the spatial position of sets of chromosomal loci by imaging⁹. FISH is based on optically labeled probes that hybridize to complementary regions of chromosomes. Importantly, as an imaging-based approach, FISH is intrinsically able to probe cell-to-cell variability and directly record spatial position inside the nucleus. Many different labeling approaches have been considered, including labeling pairs of loci (two-loci FISH)¹⁰, as well larger contiguous regions¹¹, and even whole chromosome painting^12–14. High-throughput^15,16 and super-resolution^17–19 FISH approaches are currently in development. Still, obtaining high-resolution pairwise distance distributions for all pairs of loci, i.e. constructing a pairwise distance map similar to a genome-wide Hi-C contact map, currently remains out of reach. For further experimental background on the connection between FISH and Hi-C, see (Giorgetti and Heard, 2016)²⁰.

In studies that primarily rely on 3C-based approaches, FISH is often performed on a subset of loci as a validation. Typically, for loci at increasing genomic separations, their average FISH spatial distance increases and 3C contact frequency decreases^6,21–23. Additionally, for a limited set of tested pairs of loci, it was found that loci in the same A/B compartment contact each other frequently and are on average closer⁶, with similar findings for loci in the same TAD^24,25. Moreover, spatial distance and contact frequency are largely correlated at the ~300kb–10Mb scale²⁶. However, this does not strictly seem to be the case for all loci⁸, and can even lead to seemingly-paradoxical observations when comparing FISH and 3C^20,27.

Due to the stochastic and variable nature of chromosome folding in vivo, polymer models provide a useful framework for interpreting 3C or FISH data^8,28. Modeling efforts naturally started with homopolymer models, which assume the chemical equivalence of all monomers (i.e. no sequence specificity for chromosomal interactions or folding²⁸). Homopolymer models are highly studied in the physics literature, and are often more amenable to analytical understanding. In the majority of homopolymer models, the further apart two monomers are along the polymer chain, the further apart they are in space, and the less frequently they are in contact; this leads to an often-useful, but potentially misleading, heuristic that the two quantities are directly related (Supplemental Note). As measuring contact frequency was largely inaccessible in polymer systems prior to 3C for chromosomes, the concordance or discordance of contact frequency and spatial distance has received less attention in the polymer physics literature. Nevertheless, chromosomes in-vivo are generally better described by models with additional locus-specific folding mechanisms^8,28.

Here we demonstrate how 3C and FISH generally probe different aspects of spatial chromosome organization. We first illustrate how spatial distance and contact frequency can display a seemingly-paradoxical relationship in currently available experimental data, focusing on the simplest two-locus labeling approach for FISH, as it is most directly comparable to 3C. We then study the connection between contact frequency and average spatial distance in a simple polymer model; these simulations show that a minimal assumption, introduction of a single dynamic loop between two loci, can break the typical relationship between contact frequency and average spatial distance. We then consider polymer simulations with loop extrusion, and find that this process can also affect contact frequency and spatial distances to greatly different degrees. Together our results show how seemingly-paradoxical relationships between contact frequency and spatial distance can easily emerge in experimental data for physical reasons, demonstrate that cross-validation of Hi-C and FISH must be very carefully considered, and argue that jointly considering contact frequency and spatial distance will underlie further understanding of chromosome organization in-vivo.

Results

3C and FISH probe different aspects of spatial organization

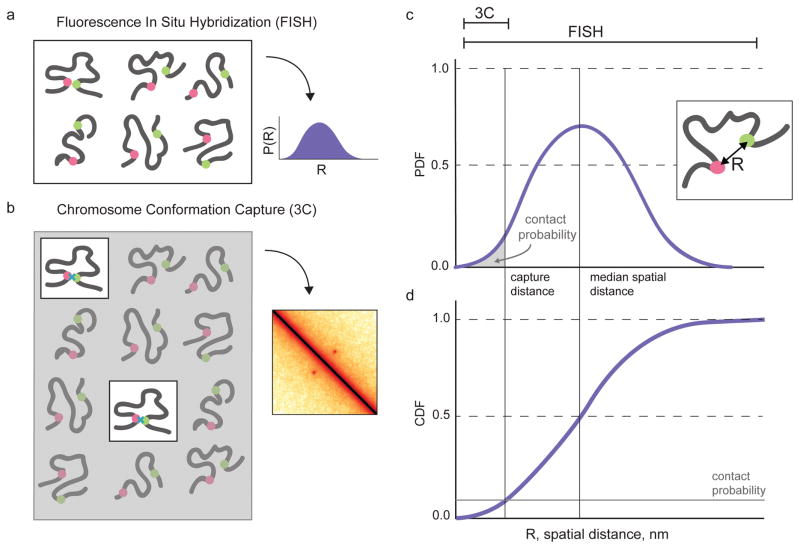
To investigate the connection between 3C and FISH we focused on the simplest case of both methods, where each method probes the relationship between a pair of loci (Fig 1a,b). A common design for FISH experiments involves labeling a pair of genomic loci to directly visualize their distances in a population of cells (Fig 1a). This experimental design allows the measurement of the probability density function (PDF) of spatial distances between a pair of loci (Fig 1c). Results from such experiments are often shown as cumulative distribution functions (CDFs, Fig 1d) as these do not require binning or density estimation steps to obtain relatively smooth curves for limited numbers of cells. In contrast with FISH, 3C experiments capture rare contacts that occur when these loci are closer than the capture radius imposed by crosslinking and ligation (Fig 1b). Roughly, 3C measures the integral of the spatial distance PDF up to the capture radius (Fig 1c), or, equivalently, the value of the CDF at the capture radius (Fig 1d)²⁰. Since such small distances are relatively rare, imaging many cells is certainly a requirement for directly comparing 3C contact probabilities with distances measured by FISH.

Figure 1. Illustrated relationship between 3C and FISH.

a. FISH obtains information for all cells in a population to build up a full distribution of pairwise distances between labeled loci. b. 3C-based approaches (including 4C, 5C, Hi-C) capture contacts from the small fraction of cells where two loci are within the capture radius. c,d. Illustration of a PDF and CDF pairwise spatial distance, R, between two loci for a large population of cells. Theoretically, FISH can measure the full pairwise spatial distance distribution. 3C captures contacts that occur at distances less than the capture distance, indicated by the area under the PDF up to the capture distance, or the value of the CDF at the capture distance.

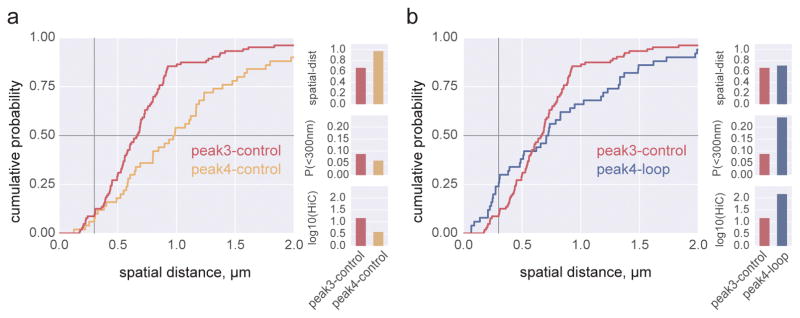
We further examined the connection between 3C and FISH by considering recent publicly-available Hi-C data²³. This publication performed high-resolution Hi-C experiment and uncovered several thousands of CTCF-mediated chromosomal loops in the Hi-C data. As a validation of the loops by FISH, they report CDF FISH plots for four pairs of ‘loops’ and ‘control’ loci at matched genomic separations (e.g. peak1-loop and peak1-control, re-plotted in Supplemental Fig 1) for the same cell type. As part of the validation, the authors reported that for each of the loop-control pairs of loci, the median spatial distance changed concordantly with the Hi-C signal²³. While this holds, we also found that this was not always the case when we compared loops and controls from different pairs. Indeed, we found a seemingly-paradoxical relationship between peak4-loop and peak3-control (Fig 2); peak4-loop has higher contact frequency despite being further away on average than peak3-control. Nevertheless, the change in the value of the CDF at small distances actually was in agreement with Hi-C, suggesting that this short-range behavior of the CDF is more closely connected with contact frequency²¹. A similar situation is observed for peak4-loop and peak2-control. In contrast, for all control-control pairs of loci, the median spatial distance changed concordantly with the Hi-C signal. We note that seemingly-paradoxical pairs involved comparisons between a loop and a control.

Figure 2. Experimental data demonstrate the complex relationship between Hi-C and FISH.

a. comparison between a pair of typical loci shows increased spatial distance and decreased Hi-C counts. b. comparison between a pair of loop loci and a control pair shows increased spatial distance, but increased Hi-C counts. FISH and Hi-C data re-plotted from (Rao et al, 2014) for GM12878 cells (Supplemental Table 1). Horizontal grey line intersects the median spatial distance, vertical grey line intersects the probability of an observation less than 300nm, P(<300nm). Bar plots show median spatial distance, P(<300nm), and log10(corrected Hi-C counts).

Together, these observations suggest that locus-specific chromosome organization in vivo can be an important reason why average spatial distance and contact frequency could behave divergently. They additionally argue that to reconcile this divergence and cross-validate observations from 3C, it will be necessary to obtain the full spatial distance distribution from FISH, including very short distances. Given the currently limited availability of high-resolution matched experimental Hi-C and FISH data, we turned to polymer models to study the relationship between spatial distance and contact frequency, where these two quantities can be unambiguously calculated for any desired pairs of loci from the same set of conformations.

Simulations can reconcile contact frequency and spatial distances

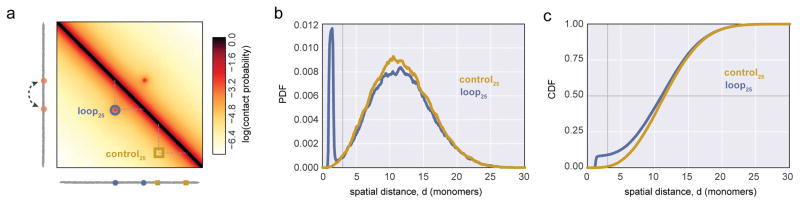
To understand the minimal set of assumptions that can decouple contact frequency from average spatial distance, we investigated both of these quantities in equilibrium polymer simulations of a single dynamic chromatin loop (Fig 3). Following (Doyle et al., 2014), where we investigated the effect of a fixed chromatin loop²⁹, we modeled chromatin as a semi-flexible polymer fiber with excluded volume interactions, (Methods, Supplemental Note). We performed simulations using OpenMM^30,31, and calculated simulated contact maps (Fig 3a), spatial distance distributions (Fig 3b,c), and average spatial distance maps (Supplemental Fig2b) from the simulated ensemble of conformations.

Figure 3. Simulations demonstrate the effect of introducing a single dynamic loop on contact maps, and spatial distance distributions.

a. Contact frequency map for a polymer with a specifically interacting dynamic 25kb loop, indicated as a dashed arc between two loop bases in orange. Two locations for simulated FISH (control₂₅ yellow square, and loop₂₅ blue circle) are indicated on the contact map. loop₂₅ indicates the loci at the loop bases, and control₂₅ indicates an equally spaced pair of control loci, without any specific interactions. b. PDF of spatial distances for the loop and control pairs of loci (colors as in a). c. CDFs for indicated loci; vertical grey line intersects contact frequency, horizontal grey line intersects median distance.

We imposed the dynamic looping interaction using a short-ranged attractive force. Monomers at the base of the 25kb dynamic loop interacted with attractive energy (4kT, unless noted) when they were closer than a distance of 2 monomer diameters; for other monomers the attractive part of the potential was set to be negligibly small (0.1kT). This pairwise interaction potential could arise from direct molecular interactions, and the two monomers involved in the dynamic looping interaction can be thought of as hard spheres that stick to some degree upon coming into contact, following a stochastic encounter in 3D (for review^8,32). In our simulations, the dynamic looping interaction is clearly visible in the contact frequency map, but is faint in a map of average spatial distances (Supplemental Fig 2a,b). Interestingly, the PDF of spatial distances for monomers at the base of the dynamic loop and control monomers (Fig 3b) appeared quite similar, apart from a sharp peak at short distances for the monomers at the loop base.

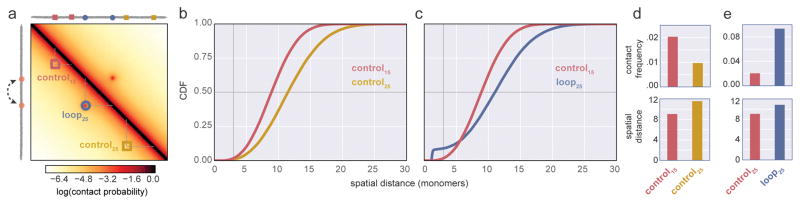
For typically-considered polymer systems of indistinguishable monomers, mean spatial distance and contact probability are generally inversely related (Supplemental Note). However, our simulations demonstrate that even a minimal modification, introduction of a single dynamic loop, changes this typical behavior (Fig 4). While a comparison between control loci of separation 15kb or 30kb displays the typical monotonic behavior over all genomic separations (Fig 4b), an apparent paradox emerges when comparing the control loci separated by 15kb with the 25kb dynamic loop (Fig 4c). While the 25kb dynamic loop is further apart on average, it displays a higher contact frequency. This behavior can emerge because contacts are rare events, and therefore contact frequency can increase many-fold without large changes in the average distance (Supplemental Fig 2d,e). Similar behavior emerges in simulations for a range of parameter values of chromatin stiffness, chromatin density, dynamic loop attraction strength, and loop size (Supplemental Fig 3). Consideration of dynamic loop models as equilibrium ensembles of conformations provides further support for the widespread possibility of seemingly-paradoxical pairs (Supplemental Note). Together, our show how, even in a particularly simple case, seemingly-paradoxical relationships can emerge between spatial distance and contact frequency, arguing for caution when designing comparisons between FISH and 3C.

Figure 4. Simulations highlight the complex relationship between contact frequency and median spatial distance.

a. Contact frequency map for a polymer with a specifically interacting dynamic 25kb loop, as in Figure 3, indicated as a dashed arc between two loop bases in orange. Three locations for simulated FISH (control₁₅, red square; control₂₅ yellow square, and loop₂₅ blue circle) are indicated on the contact map; control₁₅ and control₂₅ indicate regions without specific interactions between monomers. b,c. CDFs for indicated loci; vertical grey line intersects contact frequency, i.e. the probability of distance <=3, horizontal grey line intersects median spatial distance. d,e. changes in contact frequency for indicated loci, and median spatial distance for indicated loci pairs (Supplemental Table 2). Note that loop₂₅ has a higher contact frequency, but larger median spatial distance, than control₁₅.

Simulations illustrate how experimental limitations could impact validation of a dynamic loop

We next investigated how possible experimental limitations to either FISH or 3C can impact our ability to ascertain the presence of this simulated looping interaction, as each approach has limitations as compared with the idealized representation in Figure 1 and in polymer simulations.

In FISH experiments, assaying a finite number of cells both imposes uncertainty on the PDF and makes the probability of rare events difficult to estimate. Consistently, it is more difficult to reliably detect changes in contact frequency than median spatial distance in simulations (Supplemental Fig 4). As contact frequencies are often quite low, this indicates that consistent validations of Hi-C by FISH would require larger populations of cells than typically used in FISH experiments.

For FISH, additional uncertainty can be imposed by factors including: probe size, chromatin movement during denaturation and hybridization, background noise, and ambiguities arising from the presence of homologous chromosomes (for review²⁰). In simulations, we considered how the first two factors might affect spatial distance distributions of loop and control loci (Supplemental Fig 5). To simulate the impact of probe sizes, we considered the pairwise distributions between centroids of chosen regions, rather than an exact pair of monomers. To simulate uncertainty or perturbation of relative distances due to chromatin movement during the FISH protocol, we simulated probe localization uncertainty by adding Gaussian noise to each set of simulated set of probe distances. Interestingly, we find that even a small uncertainty or imprecision in the spatial localization of probes during FISH makes the existence of a dynamic looping interaction much more difficult to ascertain, whereas larger probe sizes had a relatively smaller impact on the spatial distributions (Supplemental Fig 5).

In a 3C experiment, whether two loci in close spatial proximity in a given cell are recorded as a contact depends on the effective capture radius. The capture radius can be influenced by a number of factors, including restriction efficiency, restriction frequency, and the details of crosslinking, which may depend on the particular complement of DNA-associated proteins at a given genomic locus^33–35. Indeed, our simulations show that a larger contact radius for simulated 3C can also obscure the existence of a dynamic looping interaction (Supplemental Fig 5). Additional measurement noise may also come from library complexity, sequencing depth, and ligations in solution^{23,33,35–37}, which could all obscure the detection of looping interactions in 3C-based methods (for review³⁶).

Together, these simulated perturbations to the idealized FISH and 3C protocols illustrate how considering many experimental details will be required to fully reconcile observations from FISH and Hi-C.

Loop extrusion simulations can display divergent contact frequency and spatial distance

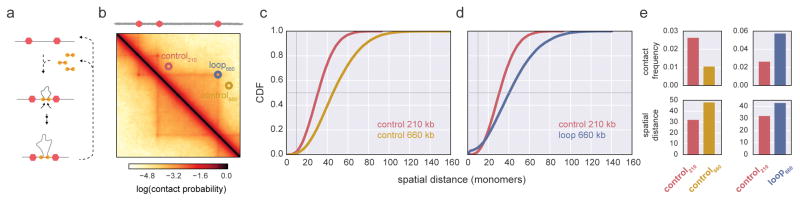
After considering spatial distance and contact frequency in this minimal model, we then considered their relationship in simulations of loop extrusion, recently proposed by us³⁸ and others^39,40 as explaining key aspects of interphase chromosome organization. Loop extrusion provides a mechanism for explaining the formation of TADs and loops in mammalian Hi-C maps, making it a subject of recent interest^41–45. To consider genomic scales similar to the loop-control pairs from (Rao & Huntley et al., 2014) considered above, we simulated a genomic region containing several TADs of 210–870kb, with parameters of the chromatin fiber as defined in (Fudenberg & Imakaev et al., 2016), our previous study of interphase loop extrusion³⁸. For each loop at the corner of every TAD, we considered a matched control at the same genomic separation, but offset by 100kb.

The dynamics of loop extrusion are governed by key parameters: processivity, separation, and extrusion speed^38,46. In simulations, we found that certain combinations of these parameters led to loop-control pairs with seemingly-paradoxical relationships (Fig 5). Such relationships could emerge because, similarly to the minimal dynamic loop model considered above, certain regimes of loop extrusion can greatly increase contact frequency between subsequent boundary elements while minimally altering average spatial distance (Supplemental Fig 6). In our simulations, the number of seemingly-paradoxical pairs increased with larger separation, and also for slower SMC translocation (Supplemental Fig 6). Interestingly, the best-fitting parameters from the sweep in (Fudenberg & Imakaev et al., 2016) did not produce seemingly-paradoxical pairs for the considered TAD sizes. However, simply making SMC translocation slower was sufficient to create seemingly-paradoxical pairs, while having little effect on the simulated contact map (Supplemental Fig 7). This indicates that perturbing loop extrusion dynamics could alter average FISH distances while having little effect on Hi-C contact maps, and thus using Hi-C alone to infer mechanisms of chromosomal folding may be insufficient.

Figure 5. Loop extrusion simulations can display divergent contact frequency and spatial distance.

a. illustration of loop extrusion dynamics: loop extruding factors translocate along the chromatin fiber, forming progressively larger loops, until dissociating or becoming halted at a boundary element (red hexagons). b. Region of a simulated contact frequency map at 6kb resolution, showing TADs of sizes 210kb and 660kb for loop extrusion parameters processivity 240kb; separation 480kb, relative velocity 20,000. Three locations for simulated FISH (control₂₂₀, red; control₆₆₀ yellow, and loop₆₆₀ blue) are indicated on the contact map. c,d. CDFs for indicated loci; vertical grey line intersects contact frequency, i.e. the probability of distance <=10, horizontal grey line intersects median spatial distance. e. changes in contact frequency for indicated loci, and median spatial distance for indicated loci pairs (Supplemental Table 3). Note that loop₆₆₀ has a higher contact frequency, but is further away on, than control₂₂₀.

Discussion

Our results illustrate that while median spatial distance and contact frequency are often inversely proportional, they are far from equivalent. Indeed, our simulations show that a relatively minor assumption-- the existence of a dynamic looping interaction between two loci-- clearly breaks the equivalence between these two quantities. In particular, we show that there is great freedom to make large shifts in contact frequency with small shifts to median spatial distance, since contacts between distal chromosomal loci are generally rare events. We then show that loop extrusion can similarly break the typical correspondence between median spatial distance and contact frequency. Together, our simulations demonstrate that our expectation in-vivo should be a non-trivial relationship between contact frequency and spatial distance, and that Hi-C and FISH data together will be necessary to better understand chromosome organization.

Given these factors, 3C experiments cannot be simply validated (or invalidated) by FISH, without carefully considering technical details of the two methods. Indeed, efforts to integrate results from these technologies will need to carefully address unknowns of the 3C capture radius and FISH localization uncertainty, in addition to assaying sufficiently large numbers of cells to populate the small distance portion of the FISH distribution. While here we limit ourselves to considering the relatively simple comparison between 3C and two-loci FISH, many other comparisons would be valuable in future work, including how to best integrate information obtained from contiguously stained regions^11,17 with Hi-C experiments.

In addition to the implications for validation, our results also caution against certain modeling approaches. In particular, our results show how a common strategy of simply transforming ensemble average 3C contact frequencies into spatial distances ultimately leads to inconsistent models of chromosomal organization (for review⁸).

Nevertheless, our results also demonstrate how polymer modeling can in principle be used to reconcile FISH spatial distances and 3C/Hi-C contact frequencies. This is because both quantities are readily calculable from an ensemble of simulated polymer conformations. One of the central goals of the recently-formed 4DN consortium is to systematically compare Hi-C and high-throughput high-resolution imaging data and understand any potential discrepancies (https://commonfund.nih.gov/4DNucleome/overview). As this matched data becomes available, systematically comparing polymer models to both Hi-C and imaging data will be an essential step towards understanding principles of chromosomal organization.

Online Methods

Polymer Simulation Overview

Polymer models were simulated with OpenMM^30,31, a high-performance GPU-assisted molecular dynamics software (https://simtk.org/home/openmm). We used an in-house openmm-polymer library (publicly available http://bitbucket.org/mirnylab/openmm-polymer).

Dynamic loop Simulations

Dynamic loop simulations were performed as in (Doyle et al., 2014), albeit with a dynamically interacting loop rather than a static loop, implemented as described below. Following (Doyle et al., 2014), we modeled chromatin as a semi-flexible polymer fiber with excluded volume interactions, where spherical monomers of 15nm diameter represent ~500bp, or approximately three nucleosomes. Adjacent monomers were connected by harmonic bonds with a potential U = 25*(r – 1)² (here and below, energy is in units of kT). The stiffness of the fiber was modeled by a three point interaction term, with the potential U = k*(1-cos(α)), where α is an angle between neighboring bonds, and k is a parameter controlling stiffness, here set to 1kT.

To model the dynamic loop considered in the present work, we used a Lennard-Jones (LJ) potential U = 4ε_ij * (1/r¹² − 1/r⁶) where ε_ij was set to 4kT for the monomers at the base of the dynamic loop (i,j), and was set to negligibly small otherwise (ε = 0.1kT). We initialized our simulations as a system of 8 compact rings (see⁴⁷), and used periodic boundary conditions to achieve a density of 0.10 (in the middle of the estimated range for mammalian cells⁴⁸).

We then simulated 50 runs of this system using Langevin Dynamics, for 10e8 time steps. For the fiber lengths considered here, polymer simulations reached equilibrium in less than 1e7 time steps; this was confirmed by observing that monomer displacement saturates after about 5e6 blocks. Conformations were saved every 1e5 time steps and an equilibrium ensemble of 900 conformations obtained after the initial equilibration was used for our analysis. An Andersen thermostat was used to keep the kinetic energy of the system from diverging using a time step that ensured conservation of kinetic energy.

To obtain simulated contact maps, we first found all contacts within each polymer conformation, and then aggregated these contacts for all pairs of monomers. A contact was defined as two monomers being at a distance less than 3 monomer diameters. To obtain simulated FISH distributions, we calculated a list of spatial distances for a chosen set of loci, and built a histogram of distances starting at 0 in bins of 0.1 monomers. To display PDFs this histogram was then smoothed with a moving average window with a size of 0.7 monomers.

Loop extrusion simulations

Loop extrusion simulations were performed as in (Fudenberg & Imakaev et al., 2016) with slight modification to the sizes and number of TADs, and an upgraded loop-extruding factor (LEF) simulation engine.

To better span the genomic size range of TADs and loops probed by FISH in (Rao et al., 2014), we considered simulations of a 6Mb region, with 10,000 monomers, 12 TADs, and monomers representing 600bp as in (Fudenberg & Imakaev et al., 2016). These TADs were separated by 11 boundary elements that stalled loop extrusion, positioned at monomers: 750, 1550, 1900, 3000, 3650, 4300, 5750, 6550, 6900, 7550, 9000. We used the same fiber stiffness and the same volume density as in the best-fitting model in (Fudenberg & Imakaev et al., 2016): density of 0.2 and stiffness of 2; where values of parameters are as defined as previously.

In the updated the loop-extruding factor (LEF) simulation engine, simulations do not need to be re-initialized between each subsequent step of loop extrusion. Instead, simulations are done in blocks of 100 loop extrusion steps. At the start of each block, all LEF-mediated bonds that would occur in the next 100 loop extrusion steps were initialized, and all but current (step=0) bonds were given a strength of zero. Current bonds were given the same strengths as previously. Langevin Dynamics (LD) was then advanced by a certain number of LD timesteps, reflecting the relative velocity of loop extrusion (1000, 5000, 20000 used in this manuscript). After that, strengths of the bonds were adjusted such that only bonds that exist at step=1 of loop extrusion have non-zero strengths. This allowed us to avoid restarting simulations between subsequent extrusion steps, and do so only every 100 extrusion steps. The new engine lead to significant performance improvement, as it eliminated the necessity to frequently restart simulations. The reason or this update scheme, with blocks of 100 LEF steps, is that OpenMM does not allow addition or removal of bonds once a simulation is initialized, but does allow for changing bond strengths. The new engine also allowed us to advance loop extrusion by only one step at a time (4 steps were used previously to decrease the number of restarts). This additionally allows higher-fidelity simulations of loop extrusion, with less abrupt motion of the polymer after updating the positions of bonds imposed by loop extrusion. The new loop extrusion engine was added to the example folder of the openmmlib package (http://bitbucket.org/mirnylab/openmm-polymer).

We performed simulations for three different loop extrusion speeds: 1000, 5000, and 20000 LD steps per LEF step. Simulations with 1000 LD steps were run for 2,000,000 blocks of LD; simulations with 5000 steps were run for 500,000 blocks of LD, and simulations with 20,000 steps were run for 250,000 blocks of LD. We obtained every 20th block for the simulation with 20 steps, and every 5th block for other simulations, yielding 100,000 total conformation for simulations with 1000 and 5000 LD steps per LEF step, and 50,000 conformations for 20,000 LD steps. Contact maps were built using capture radius of 10 monomers. Simulated FISH distributions were calculated as above.

Experimental data

FISH CDFs corresponding to (Rao & Huntley et al., 2014) were obtained from https://groups.google.com/forum/#!topic/3d-genomics/0TI5sz4TyF4 from their UPDATED spreadsheet. Published publicly-available Hi-C data (Rao & Huntley et al., 2014), GEO accession GSE63525, was re-processed, filtered, and iteratively corrected using hiclib http://mirnylab.bitbucket.org/hiclib/ ⁴⁹.