Inconsistency Between Univariate and Multiple Logistic Regressions

Summary

Logistic regression is a popular statistical method in studying the effects of covariates on binary outcomes. It has been widely used in both clinical trials and observational studies. However, the results from the univariate regression and from the multiple logistic regression tend to be conflicting. A covariate may show very strong effect on the outcome in the multiple regression but not in the univariate regression, and vice versa. These facts have not been well appreciated in biomedical research. Misuse of logistic regression is very prevalent in medical publications. In this paper, we study the inconsistency between the univariate and multiple logistic regressions and give advice in the model section in multiple logistic regression analysis.

1. Introduction

Many medical studies have binary primary outcomes. For example, to study the treatment effect of a new intervention on patients with severe anxiety disorders, patients are randomized to the new intervention or treatment as usual (control) groups. The outcome is significant clinical improvement (yes or no) within a period such as 12 months. For this kind of outcome, we use 1 (0) to denote the occurrence or success (no occurrence or failure) of the outcome of interest such as significant (no significant) clinical improvements. The treatment effects can be measured by the difference or ratio of success rates in the two groups. Pearson’s chi-square test (or Fisher’s exact test) can be easily used if the treatment effect of the treatment method is better than the current method.

It is not uncommon that treatment effect is confounded by differences between treatment groups such as age, medication use and comorbid conditions. If such confounding covariates are categorical, such as gender and smoking status, contingency table methods can be easily used to study treatment differences. For continuous covariates such as age, although still possible to apply such methods by categorizing them into categorical variables, results depend on how continuous variables are categorized such as the number of end cut-points for categories.

The multiple logistic regression^[1] provides a more objective approach for studying effects of covariates on the binary outcome. It addresses both categorical and continuous covariates, without imposing any subjective element to categorize a continuous covariate. Coefficients of continuous as well as noncontinuous covariates, which are readily obtained using well-established estimation procedures such as the maximum likelihood, have clear interpretation. Also, its ability to model relationships for case-control studies has made logistic regression one of the favorite statistical models in epidemiologic studies.^[2]

Model selection offers advantages of increasing power for detecting as well as improving interpretation of effects of covariates on the binary outcome, especially when there are numerous covariates to consider. Here is how model selection was carried out in multiple logistic regression in a paper recently published in JAMA surgery^[3]:

‘Associations between preoperative factors and adenocarcinoma or HGD were determined with univariate binary logistic regression analysis. Variables with statistically significant association on univariate analysis were included in a multivariable binary logistic regression model.’

Such a univariate analysis screening (UAS) method to select covariates for multiple logistic regression has been widely used in research studies published in top medical journals^[4-6] since it seems very intuitive, reasonable, and easy to understand. In this paper we take a closer look at this popular approach and show that the UAS is quite flawed, as it may miss important covariates in the multiple logistic regression and lead to extremely biased estimates and wrong conclusions. The paper is organized as follows. In Section 2 we give a brief overview of the logistic regression model. In Section 3 we study the relationship between the univariate regression analysis, the basis for selecting covariates for further consideration in multiple logistic regression, and the multiple logistic regression model. In Section 4 we use the theoretical findings derived, along with simulation studies, to show the flaws of the UAS. In Section 5, we give our concluding remarks.

2. Logistic regression model

We use Y=1 or 0 to denote ‘success’ or ‘failure’ of the outcome. Here ‘success’ and ‘failure’ only indicate two opposite statuses and should not be interpreted literally. For example, if we are interested in the relation between the exposure of high density of radiation and cancer, we can use Y=1 to denote that the subject develops cancer after the exposure. Aside from the outcome, we also observe some factors (covariates) which may have significant effects on the outcome, denoting them by X₁ X₂, ..., X_p. The relation between the outcome and the covariates is characterized by the conditional probability distribution of Y given X₁ X₂, ... X_p. In multiple logistic regression, the conditional distribution is assumed to be of the following form

(1)

where β₁β₂ ... β_p ≠ 0. This is the model on which our following discussions will be based. The covariates may include both continuous and categorial variables. A more familiar equivalent form of (1) is

where the left hand side is called the conditional logodds.

Given a random sample, the parameters (β₀, β₁, …,β_p) in (1) can be easily estimated by maximum likelihood estimation (MLE) method, see for example.^[7,8]

3. Univariate regression model

Suppose we are interested in the marginal relation between the outcome and a single factor X₁, i.e. we need to find Pr{Y = 1|X₁}.

From the property of conditional expectation^[9] we know that

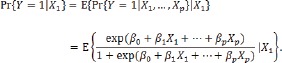(2)

If the joint distribution of X₁, X₂,…,X_p is unknown, generally it is impossible to find the analytical form of (2). In this section we consider the univariate regression model with following some specific distributions.

3.1 Univariate regression with categorical covariate

First assume X₁ is a 0-1 valued covariate. For example, in the randomized clinical trial, we can use X₁ as the group indicator (=1 for the treatment group and for the control group). It is easy to prove that there exist unique constants α₀ and α₁ such that

(3)

where both α₀ and α₁ are functions of β₀, β₁ …,β_p. Usually the form of these functions are complex as they depend on the joint distribution of X₁ X₂,…,X_p There is no obvious qualitative relation between α-t in (3) and β₁ in (1).

Equation (3) indicates the marginal relation between Y and X₁ still satisfies the logistic regression model, and

which means that α-t in (2) is the log odds ratio. Furthermore, if X₁ is independent of (X₁, X₂, ..., X_p), we can prove that (i) a₁>0 if and only if P₁>0, (ii) α₁<0 if and only if P₁<0, and (iii) a₁=0 if and only if P₁=0. The independent assumption is true for completely randomized clinical trials. However, it seldom holds in practice, especially in observational studies.

Now assume X₁ is a covariate with k-categories, denoted by 1, ... k. Let Z_j=1{X₁=j}. We can also prove that there exist constant α₀, α₁ …,α_(k-1) such that

All those parameters have similar interpretation as in the binary case.

This section shows that for categorical covariate, the univariate regression still has the form of logistic regression. However, the interpretation of the parameter is different from that in multiple logistic regression.

3.2 Univariate regression with continuous covariate

Assume X₁ is a continuous covariate, for example, the age of the patient. We want to know if Pr{Y=1|X₁} can be written in the (3) if (1) is the true multiple logistic regression model. Before answering this question, let’s us take a look a the following example.

Example 1. Suppose there are only two covariates in the multiple logistic regression model (1), where X₁ is a continuous covariate with range R, X₂ is 0-1 valued random variable with Pr{X₂=1}=1/2, and X₁ and X₂ are independent. We further assume β₀=β₁ =β₂=1 in (1). Then

If (3) is true, then we should have

(4)

Let X₁→∞ in (4) we have a₁=1. Let X₁=0 in (4) we have

However, if X₁=1 in (4), then

Since these two solutions of a₀ do not match, model (3) does not hold.

This example shows that, for continuous covariate X₁, the regression of Y on X₁ does not in general satisfy the univariate logistic regression model even if X₁ is an essential component in the multiple logistic regression. Hence, the univariate logistic regression model should not be used to estimate the marginal relation between the outcome and a continuous covariate.

4. Inconsistency between univariate and multiple logistic regressions

In Section 3 we show that in multiple logistic regression, the univariate regression of the outcome on each individual covariate may not satisfy the logistic regression any more. This fact has serious implications for model selection and interpretation of results in data analysis. In this section, we demonstrate this important issue using simulation studies.

4.1 Significant effect in multiple but not in univariate logistic regression

In this section we show an example where a continuous covariate is a necessary part in the multiple logistic, but the univariate regression indicates that the covariate has no effects in the univariate regression. The following preliminary result will be used in our discussion.

Lemma 1. Suppose c is a positive constant and the random variable × has standard normal distribution. Then E[X/(1+cexp(θX))]=0 if and only if θ=0.

The proof of this result is available from authors upon request.

Example 2. Let X₂ and X₃ be independent random variables with standard normal distributions, and X₁=X₂+2X₃. Consider the following multiple logistic regression model

(5)

where α₁=-α₂/5,α₂≠0. Using the result in Lemma 1 we can prove that if

(6)

then θ₁=0.

What does this result mean within the current context? Although X₁ and X₂ both are in the multiple logistic regression, if their coefficients satisfy the condition (5), the regression of Y on X₁ is no longer a univariate logistic regression. Moreover, if (Y_i1, X_i1, X_i2), i=1,…, n is a random sample from (5), X₁ and X₂ will become increasingly significant in the multiple logistic regression, but X₁ will remain nonsignificant regardless of sample size, as illustrated by the following simulation results.

The data was generated according (5) with a₀=1, a₁=-3/5,a₂=3. Shown in Table 1 are the estimates and standard deviations of the coefficient of X₁ in both univariate and multiple logistic regression after 10,000 Monte Carlo (MC) replicates. The parameters were estimated by MLE. For a wide range of sample sizes, the maximum likelihood estimator of the coefficient of X₁ in the multiple logistic regression was very close to the true value, and the standard errors decreased with the sample size, as expected. However, the estimated coefficient in the univariate analysis was consistently close to 0 in all cases.

Table 1.

Estimate of regression coefficient of X₁ in Example 2

n	Univariate regression				Multiple regression
	Estimate	SD	p-value>0.2	p-value>0.1	Estimate	SD
100	-0.0042	0.0983	0.7963	0.8991	-0.6533	0.2103
200	-0.0015	0.0674	0.7952	0.898	-0.6173	0.1308
500	-0.0004	0.0429	0.791	0.889	-0.6085	0.0828
1,000	-0.0009	0.0284	0.801	0.907	-0.6056	0.0566
1,500	-0.0002	0.0239	0.799	0.902	-0.6046	0.0465
2,000	-0.0004	0.0205	0.809	0.905	-0.6027	0.0392

Table 1 also reports the chance that p-value is >0.2 (or >0.1) in the univariate logistic regression. It shows that although X₁ is a necessary part of the multiple logistic regression, X₁ will most likely be excluded from the multiple logistic regression, if the cutoff of the p-value is set at 0.2 (or 0.1).

Reported in Table 2 are the estimates of the coefficient of X₂ in the logistic regression if X₁ is mistakenly excluded due to UAS method. The true coefficient of X₃ is 3 in the multiple logistic regression, but the estimated coefficient of X₂ became extremely biased if X₁ was excluded.

Table 2.

Estimates of coefficients of X₂ in logistic regression with X₁ being removed in Example 2

n	Coefficient of X2 (α2=3)
	Estimate	SD
100	2.0243	0.4268
200	1.9843	0.2903
500	1.9579	0.1789
1,000	1.9556	0.1231
1,500	1.9498	0.1040
2,000	1.9495	0.0857

Taken together, the results show that the UAS not only most likely misses some important covariates in the multiple logistic regression, but also leads to severely biased estimates of effects of other covariates on the response.

4.2 Significant effect in univariate but not in multiple regression

In this section we show a case where a continuous covariate has significant effect in the univariate regression, but is not significant if it is included in the multiple regression.

Example 3. Suppose X₁, X₂, X₄ and ε are independent standard normal random variables, and X₃=X₁+X₄. Consider the following multiple logistic regression model

(7)

where α₁ α₂≠0.

In the simulation study, the data was generated according model (7) with α₀=0,α₁=2,α₂=1. Shown in Table 3 are the estimates of the coefficient of X₃ in both univariate and multiple linear regression (with X₁,X₂ and X₃ as covariates) after 10000 replicates. For all sample sizes, X₃ shows very significant effect on Y in the univariate regression, but no significant effect in the multiple logistic regression.

Table 3.

Estimate of the regression coefficient of X₃

n	Univariate regression		Multiple regression
	Estimate	SD	Estimate	SD
100	0.7120	0.2012	0.0130	0.3079
200	0.6907	0.1320	-0.0021	0.1953
500	0.6787	0.0800	-0.0039	0.1221
1,000	0.6777	0.0588	0.0005	0.0865
1,500	0.6772	0.0463	-0.0012	0.0681
2,000	0.6771	0.0400	0.0000	0.0602

5. Discussion

Although the logistic regression is a very powerful analytical method for binary outcome, the results from the univariate and multiple logistic regressions tend to be conflicting. A covariate may show very significant effect in the univariate analysis but has no role in the multiple logistic regression model. On the other hand, a covariate may be an essential part of the multiple logistic regression but shows no significant effect on the outcome in the univariate regression. The UAS method uses the univariate analysis as an initial step to select covariates for further consideration in the multiple regression. This method may mistakenly exclude important covariates in the multiple logistic regression and lead to extremely biased estimates of the effects of other covariates in the multiple model. Hence the UAS is not a valid method in model selection. It should be removed from the tool kits of biomedical researchers and even some PhD statisticians. Formal model selection methods based on solid theory, such as Akaike’s information criterion (AIC) and Schwarz’ Bayesian information criterion (BIC) discussed in ^[10] should be implemented in all regression analyses.

Biography

Hongyue Wang obtained her BS in Scientific English from the University of Science and Technology of China (USTC) in 1995, and PhD in Statistics from the University of Rochester in 2007. She is a Research Associate Professor in the Department of Biostatistics and Computational Biology at the University of Rochester Medical Center. Her research interests include longitudinal data analysis, missing data, survival data analysis, and design and analysis of clinical trials. She has extensive and successful collaboration with investigators from various areas, including Infectious Disease, Nephrology, Neonatology, Cardiology, Neurodevelopmental and Behavioral Science, Radiation Oncology, Pediatric Surgery, and Dentistry. She has published more than 80 statistical methodology and collaborative research papers in peer-reviewed journals.