EARLY, LATE OR NEVER? WHEN DOES PARENTAL EDUCATION IMPACT CHILD OUTCOMES?

Abstract

We estimate the causal effect of parents’ education on their children’s education and examine the timing of the impact. We identify the causal effect by exploiting the exogenous shift in (parents’) education levels induced by the 1972 minimum school leaving age reform in England. Increasing parental education has a positive causal effect on children’s outcomes that is evident in preschool assessments at age 4 and continues to be visible up to and including high-stakes examinations taken at age 16. Children of parents affected by the reform attain results around 0.1 standard deviations higher than those whose parents were not impacted.

It is a consistent finding across numerous countries that individuals with higher levels of schooling have children who also attain higher levels of schooling. There are two main sources of this intergenerational correlation and distinguishing between them is of considerable importance. The first explanation of the intergenerational link is a selection story – characteristics that lead parents to select into higher levels of education may also impact their abilities in child-raising or be related to other genetic and environmental factors shared with their children that will lead the children to also achieve higher levels of education. The second explanation is a causal story – as a result of attaining more education, the parents with high levels of schooling provide a better childhood experience and educational environment and consequently their children do better in school. The design of policy to improve intergenerational mobility, which is arguably the top social policy goal of the current UK government, will differ according to the extent of causation in the link between education levels in successive generations of a family. As the UK has raised the Participation Age (full-time education or employment with a vocational apprenticeship) to the age of 18 in 2015, examining the intergenerational effects on mobility of raising educational participation among the lower achieving tail is timely. The empirical challenge is to differentiate between these two mechanisms and identify whether there is a causal effect of parental education on child outcomes or whether the intergenerational correlation is purely an artefact of selection.

There have been a number of recent studies using a range of techniques to isolate the causal effect of parental education (see Holmlund et al., 2011, for a reconciliation study for the main techniques used). Oreopoulos et al. (2006), Chevalier (2004), Black et al. (2005), Chevalier et al. (2005), Carneiro et al. (2008) and Maurin and McNally (2008) and all use instrumental variables techniques with a variety of instruments and with quite diverse results. Few studies go on to assess the age at which the intergenerational education transmission emerges and the relative scale of effects across literacy and numeracy. Here, we use a rich cohort dataset – the Avon Longitudinal Study of Parents and Children (ALSPAC) – and exploit the fact that a proportion of the parents in the data were impacted by the most recent raising of the minimum school leaving age (RoSLA) in England which occurred in 1972.¹ This policy change provides an exogenous increase in education for a cohort of the ALSPAC parents, focused on the lower achieving tail of educational attainment and in the age range 30–38 at the time of the child’s birth. The high frequency longitudinal nature of the data allows us to also examine the timing of impacts throughout the child’s life, from early development indicators (18–30 months) and preschool assessments through various assessments during the school years to the final examinations at the end of the compulsory schooling period. Moreover, the richness of the data also allows us to look separately at results in literacy and those in Mathematics. Importantly, the structure of the ALSPAC data allows us to identify the causal impact of the policy separately from the effect of the age of the child’s parents at the time of the child’s birth.

Our results suggest that increasing parental education has a positive causal effect on children’s outcomes that is evident at age 4 and continues to be visible up to and including the high stakes examinations taken at age 16. Children of parents affected by the reform gain results approximately 0.1 standard deviations higher than those whose parents were not impacted. Focusing on the lower educated parents where we would expect there to be more of an impact, the effect is larger: children of affected parents gaining results approximately 0.15 standard deviations higher. There are no marked differences in the extent of elevated performance between literacy and numeracy scores.

The article proceeds as follows: in Section 1 we review the recent literature on the causal effect of parents’ education on child outcomes, before Section 2 describes the ALSPAC data. Section 3 outlines our empirical strategy, Section 4 presents the results before Section 5 discusses the findings and concludes.

1. Previous Literature

The majority of the recent literature on the intergenerational transmission of education can be categorised into three approaches to identifying the causal effect:

1. twin studies;

2. adoption studies; and

3. instrumental variables.

1.1. Twin Studies

The foundation of the twin approach is that by comparing the education outcomes of children born to identical twin sisters, the effect of the mother’s education on the child’s education can be inferred net of any genetic influences. Behrman and Rosenzweig (2002) first applied this approach using US data and found that the effect of father’s education is more important than that of the mother’s. This finding has been replicated in twin studies (using both identical (monozygotic, MZ) and non-identical (dizygotic, DZ) twins) in Scandinavian countries (see Holmlund et al. (2011) for Sweden, and Pronzato (2012) for Norway). However, Antonovics and Goldberg (2005) show the sensitivity of Behrman and Rosenzweig’s conclusion to data coding and sample inclusion criteria, concluding themselves that there is not a dramatic difference in the importance of maternal and paternal schooling. There are, however, problems with the twin study methodology. It requires that twins are identical bar their difference in education which is assumed to be unrelated to any unobserved differences between the twins. This seems a very strong assumption as it appears highly unlikely that twins choose different levels of education for purely random reasons – there must be some reason why one twin gets a different level of education to the other and whatever leads to the difference cannot be assumed to be irrelevant for other later outcomes. In addition, only one parent’s unobservables (the one with a twin) can be controlled using in this strategy. Moreover, it is hard to know how to control for the observable characteristics of the spouse. These may reflect the education decision but there may remain bias resulting from assortative mating on the unobservable characteristics that lie behind the decision to increase education levels. Overall the twin methodology has serious problems and it is not clear how reliable resulting estimates can be.

1.2. Adoption Studies

Compared with twin studies as a methodology, adoption studies reduce the bias in the causal estimates by eliminating the genetic link between both parents and the child – whereas twin studies can difference out genetic factors for just one parent. The adoption estimates capture the non-genetic effect of parental education but will remain (upwardly) biased since they also contain the effect of parental nurturing skills which differ between parents and are likely to be (positively) correlated with but not wholly driven by education level. The adoption strategy is exploited by inter alia Sacerdote (2007) and Plug (2004). Examining the outcomes of Korean adoptees in the US, Sacerdote (2007) finds that an additional year of maternal education for the adopting mother increases the adoptee’s years of schooling by approximately 0.1 years and increases the probability of the adoptee having a four-year college degree by 2 percentage points. Plug, using US data, finds that genetic factors account for approximately 50% of the mother’s education effect and 30% of the father’s – echoing the twin study findings that father’s education is more important causally for children’s outcomes. In fact, when both parents’ education is included in the model, only the effect of father’s education is significant, suggesting that the mother’s education effect is wholly accounted for by genetic and assortative mating factors. Holmlund et al. (2011) also examine estimates using adoptees in Sweden and in contrast find equally important effects for mothers and fathers though in each case including spouse’s education sees the coefficients halve in size and become insignificant. As acknowledged by authors using this strategy, the correlation between parents’ and children’s educational outcomes can still be because of non-genetic factors that are shared by both the parents and the children, with the transmission via parenting style, ethos and values and the result that both parents and children select levels of education on these unobservables. In addition, the sample sizes typically available even in registry datasets are small and the placement of adoptee children may not be random.

1.3. Instrumental Variable Studies

Arguably the most clear cut strategy for isolating the true causal effect of parental education on child education is instrumental variables. In this case, the biases from both the genetic and environmental transmission factors that confound OLS estimates are removed, since the variation in parental education is orthogonal to unobservables. The majority of IV strategies rely, as we do, on changes in compulsory schooling requirements which induce certain cohorts of relatively low educated young people to increase their schooling relative to the previous cohorts. These changes are involuntary increases in schooling for a group who are likely to be drawn from those with lower prior educational attainment and a less positive attitude toward education. Other IV strategies which focus on unanticipated variations in opportunities for continuing education to the graduate level, such as Carneiro et al. (2008), are likely to be drawing inference from a very different part of the educational attainment distribution and there is no a priori reason why the effects should be similar across these groups. The ‘local average treatment effect’ identified at the low education part of the distribution is likely to be more important in policy terms where policy makers are concerned with low intergenerational mobility or low income in the second generation.

Oreopoulos et al. (2006) exploit changes in compulsory schooling requirements across US states over time to identify the causal effect of parents’ education on children’s probability of repeating a school grade or dropping out of high school – each are reduced by 2–4 percentage points for an additional year of education for either parent. Black et al. (2005) similarly exploit a two-year increase in the compulsory schooling required by law in Norway, introduced at different times across different regions during the 1960s and early 1970s. There are, however, few causal effects identified, suggesting that selection explains most of the cross-sectional correlation. The exception is for mothers and their sons, where a year increase in schooling for low educated women increases their son’s subsequent schooling by one tenth of a year. On their full sample, Holmlund et al. (2011) find results of a similar magnitude for Swedish data, again exploiting a compulsory school leaving age reform, though they find that the coefficient on father’s education is also significant and almost as large. Restricting the sample to just the lower educated parents where the reform should impact the most, the coefficients are incongruously smaller and only the mother’s is significant and only when the partner’s education is excluded from the regression.

Within the UK, a number of studies have exploited both the 1947 (to age 15) and the 1972 (to age 16) RoSLA to identify the intergenerational transmission of education. The combination of the NCDS 1958 birth cohort study and the 1947 RoSLA has been exploited by two studies looking at child cognitive and non-cognitive development indicators, as opposed to educational qualifications. Sabates and Duckworth (2010) estimate the impact of increasing mothers’ schooling on children’s relative rank within cohort along four dimensions of development: two cognitive, two behavioural. They find that amongst mothers who only attain the compulsory years of education, increasing schooling by one year positively impacted on the mathematics attainment of their children. There were no significant impacts on reading or on behavioural outcomes, though it is difficult to identify effects in the small estimation sample of only 467 children available around the education discontinuity. Silles (2010) examines the impact of fathers’ as well as mothers’ education on child’s percentile rank in cognitive and non-cognitive outcomes at ages 7, 11 and 16. Despite large correlations between parental education and child cognitive development in the OLS estimates, the large standard errors on the IV estimates make them too imprecise to identify any significant effects. One problem here is that identification in this context relies on comparing successive cohorts of parents, only one of which was affected by the schooling reform. When the children are from a cohort study and born at almost the same time, this can lead to the treatment effect becoming confounded with the age of the parent at the child’s birth, which may exert an independent effect on child outcomes. This may cause a problem for studies using the NCDS, for example, where all children were born in a single week of 1958.

The 1972 RoSLA that we exploit has also been utilised to identify causal effects of parental education by Chevalier (2004) and Chevalier et al. (2005). The former uses the Family Resources Survey, and finds that the causal impact of an additional year of parental schooling on the probability of the child remaining in school post-16 is roughly equal at 8 percentage points for either parent, though significant only at the 10% level. Chevalier et al. use the UK Labour Force Survey to examine the impact of parental education and income on the probability of a child remaining in school post-16 and also on the probability of attaining five or more GCSEs graded A to C (a standard measure of educational achievement in the UK). Despite large effects of parental education on the children’s educational outcomes in the OLS, when instrumenting both education and parental permanent income, the parental education effects become non-significant. Both of these studies are limited by the child outcome variables available in the respective datasets.

The US study most similar to our own is that by Carneiro et al. (2008) using data from the children born to women in the National Longitudinal Survey of Youth (NLSY). The authors are able to look at outcomes at different stages of the children’s upbringing and consider both reading/literacy and mathematics results at these ages. The identification strategy relies on differences in the availability and costs of higher education and therefore the education margin examined is quite different to the one that we study. Moreover, only maternal education is known thus the estimated education effects will combine the direct effect plus any impact via assortative mating. Carneiro et al. find that for children of white mothers, an additional year of maternal education increases child reading and mathematics test scores at age 7–8 by 0.075 and 0.1 standard deviations respectively. By age 12–14, the effects are smaller and not significant. A year increase in maternal education also causally reduces the probability of grade repetition by just under 3 percentage points at each age, tallying with the finding of Oreopoulos et al. (2006). For children of black mothers, the results are similar, though the mathematics and reading impacts remain significant at age 12–14 and are stronger. Maurin and McNally (2008) also examine the higher education margin, exploiting the French student uprising of 1968 to instrument for higher education access. The student protests disrupted the education system to such an extent that the usual examination procedures were curtailed during 1968; in particular the baccalauréat which if passed guarantees a place in university, was assessed using just oral examinations on a single day rather than the usual series of oral and written examinations. As a result there was a 30% increase for this cohort in the number of people attaining the qualifications to access University. Exploiting this exogenous increase in higher education, Maurin and McNally find that increased paternal education significantly reduces the probability of a child being held back a grade.

In addition, there are a small number of papers that pursue alternative identification strategies. Ermisch and Francesconi (2001) provide a theoretical model of investment by parents in the education of their children and propose conditions under which the cross-sectional associations between parents’ and children’s schooling can be interpreted causally. Amongst poorer parents where the authors’ model suggests the education effects are causal, the estimates suggest a strong influence of both parents’ education. It is clear from reviewing the recent literature that there is not a consensus regarding the causal effect of parents’ education on the education of their children – even amongst studies employing the same identification strategy. Holmlund et al. (2011) suggests that the underlying causal parameter identified by each differing method is the same, with differences in estimates owing to country and time specific factors, which needs to be borne in mind when considering the wider applicability of our findings here. There are also unresolved issues over the timing of any causal effects within the upbringing of the child and also the areas affected – is any causal effect felt early on in life or is it only apparent at later school years? Moreover, is the effect universal across all subjects or specific to certain educational domains?

2. Data

As alluded to above, our data come from the ALSPAC,² which is a cohort dataset comprising children who were expected to be born between 1 April 1991 and 31 December 1992 in the Avon area, a former administrative area in the South West of England which includes the city of Bristol and a number of smaller towns and the rural area around the city. All mothers in Avon with children due during this period were invited to join the study, resulting in 13,971 live children at 12 months, from 13,801 mothers. Additionally, eligible children who were found in the national pupil census data but who were not in the core ALSPAC sample were invited to join the study. In total we have a potential maximum of 19,966 children who would represent a full census of children born in the study area in the applicable window.³ The ALSPAC mothers in total, mirror the national picture in terms of timing of fertility: for 1991 and 1992 the national averages of age of mother across all birth parities were 27.7 and 27.9 respectively, which compares with 27.9 for the ALSPAC mothers (Office for National Statistics, 2012b). The national average completed fertility for the cohorts of women corresponding to our main sample is between 1.98 and 2.02 (Office for National Statistics, 2012a) which is below the average in our sample (2.51) thus compared to the national picture our sample mothers have slightly larger families on average. The median birth parity for the children in our sample is 2 (mean 2.1), therefore, on average, these are the second born child in families with 2 or 3 children. With regard to childbearing of women of lower education in the 30–38-year-old bracket, we can compare the British Household Panel Survey where 36.4% of women who have O-levels or less have a child during these years – thus this combination of lower education and childbearing in this age range is quite common.

The data from the study includes information from survey questionnaires completed by the mothers, the mothers’ partner and the study children at various points during the children’s lives – from pre-birth through to late teenage years. Further to the main questionnaires, there were several ‘clinics’ at different ages, during which children completed various types of tests and questionnaires. Data from administrative sources have also been linked in, including the National Pupil Database and the Annual School Censuses, at school and pupil level giving test results for all Key Stages and Entry Assessment.

The Key Stages in the English schooling system are formal assessments, externally set and marked, which are taken by children in all state schools, for this age cohort, at ages 7 (Key Stage 1), 11 (KS2), 14 (KS3) and 16 (KS4).⁴ The KS4 assessments include GCSE examinations and also other more vocational qualifications (Appendix Table A8 shows how academic qualifications correspond to the National Vocational Qualifications equivalence scale). These data can be explored in different forms, specifically, we use KS4 points (the sum of all GCSE-equivalent points for all age 16 qualifications), the total points for GCSEs only so that vocational qualifications are excluded, the total points for traditional academic GCSEs,⁵ the score for Mathematics GCSE and the score for English Language GCSE (as a measure of literacy).

At the earlier ages we also look assessments of English and Mathematics separately and a combined overall test score. For KS1 (age 7) the assessments are reading, writing and mathematics. We combine the reading and writing scores into an overall ‘literacy’ measure. We also have information on the child’s school entry assessment scores: these measures are teacher-assessed in the child’s first term of Reception class (normally four years of age), generally in late October/early November so the child has been in school for only one or two months. These assessments were not compulsory nationally at the time the ALSPAC children were entering school, however, the same system was used in about 80% of schools in the Avon area at that time. We create an entry assessment total score by combining results for reading, writing, language and mathematics; we also look at mathematics and literacy scores separately.

We also have a number of outcomes that are not measures of formal education. One such outcome is a measure of IQ. This is taken from the Focus 8+ Clinic, to which all ALSPAC study children were invited at around eight years of age. The children were measured using the Wechsler Intelligence Scale for Children, specifically the WISC-III^UK, which was the most up-to-date at the time of the clinic. We use the total score, a sum of 10 subscales⁶ (split into verbal and performance categories) which are age- adjusted and also just performance IQ, which is thought to capture the more innate ‘fluid intelligence’ dimension of IQ. Finally we have mother-reported measures of child development in several areas from the early child-focused questionnaires. We use gross and fine motor skills scores which are averages of scores taken from questionnaires when the child is aged 18 and 30 months, scaled between 0 and 100. We do not adjust the scores for age but we do include age when measured in regressions as controls when using these dependent variables.

For the parents the education data are more restricted. There is no information regarding the age parents left full-time education or indeed an IQ type test but there are qualifications achieved. We construct three different (0,1) qualification indicators capturing whether the parent has any qualifications,⁷ has any O-levels (the examinations preceding GCSE and taken at age 16) and has any A-levels. Unfortunately there was no information on the number of each type of qualification or grades, hence our focus on the impact of the RoSLA on the broad level of qualification attainment of the parents. The increase in education experienced as a result of the RoSLA will be felt in terms of both years in education and in qualifications attained at the end of the extra year in education resulting from the reform. Thus, we do not directly observe the full extent of the RoSLA impact on parental education within the ALSPAC study but only in the domain of qualifications. We show the size of the change in terms of the proportion of the population that stayed on for the extra year using other data sources.

Table 1 contains summary statistics for the parents in our main estimation sample (±3 years around the RoSLA). These are the characteristics of the parents who are either treated or untreated, that is they are born within the ±3 years around 1 September 1957, and so are considered to be comparable with respect to the treatment effect. We see from Table 1 that the fathers are on average slightly more educated than the mothers with fewer having no or low qualifications and more having A-levels and above. More of the mothers have teaching or nursing qualifications as we may predict. The lower part of the Table shows that the ALSPAC fathers in the treatment zone are slightly older than the mothers but the difference can only be small given that by definition of inclusion in the treatment zone these parents must be born within ±3 years of RoSLA.

Table 1.

Summary Statistics for Parents in the Treatment Zone

		Mothers				Fathers
Total number		3,550				2,815
Education		N		Proportion		N		Proportion
Education info missing		552		0.155		125		0.044
Education info non-missing		2,998		0.845		2,690		0.956
				Proportion			Proportion
Highest education level:				…of educ non-missing	…of total		…of educ non-missing		…of total
No qualifications				0.100	0.084		0.095		0.091
Less than O-Level (CSE, intermediate C&G)				0.118	0.100		0.072		0.069
O-level or equivalent (Final C&G, apprenticeship)				0.263	0.222		0.250		0.239
A-level or equivalent (State Enrolled Nurse, full C&G)				0.175	0.148		0.259		0.248
State Registered Nurse or teaching qualification				0.100	0.085		0.017		0.016
Degree				0.244	0.206		0.307		0.293
Total				1.000	0.845		1.000		0.956
Age at ALSPAC child’s birth	N		Mean	SD	Minimum				Maximum
Mother	3,550		33.31	1.72	30				38
Father	2,815		33.50	1.72	30				38

Note. Main estimation sample window: parent must be born in the ±3 years around 1 September 1957.

Table 2 contains summary statistics for the children of parents in the ±3 years sample, both the overall measures and broken down by the education level of the parents. The final column (‘full sample’) shows that just over half of the sample are in the cohort that took their GCSEs in 2008.⁸ Moving from parental education group 1, which represents children of parents with no or only low qualifications between them, to education group 4 which represents children of parents who both either have a degree or equivalent, there is a clear parental education gradient in child outcomes. For example, moving from children of the lowest educated parents to children of the highest increases the average Key Stage 4 (age 16 examinations) score from 350.65 to 502.35 which is equivalent to an additional three GCSEs at the top grade (A). Similar gradients exist for each of the education measures and IQ. Fine motor skills averaged at age 18 and 30 months, which is a developmental indicator that is correlated with later educational outcomes, exhibits a small gradient, however, gross motor skills recorded at the same points and which is not strongly related to later outcomes is almost constant across parental education groups.

Table 2.

Summary Statistics for Children in the Main Estimation Sample

	Parental education group
	1 (least educated)		2		3		4 (most educated)		Full sample
	Mean	N	Mean	N	Mean	N	Mean	N	Mean	SD	N
Child/young person is female (dummy)	0.49	1,000	0.46	742	0.48	1,314	0.48	1,322	0.48	0.50	4,967
Child/young person’s age within school year	6.30	1,000	6.17	742	6.15	1,314	6.37	1,322	6.28	3.71	4,967
Key Stage 4 score	350.65	880	402.11	673	449.99	1,082	504.59	977	423.76	146.29	4,094
GCSE total score	257.72	889	319.41	673	377.81	1,089	447.26	978	347.42	143.20	4,116
GGSE total score (academic subjects)	177.08	835	210.05	659	253.55	1,067	301.91	971	235.87	98.07	3,985
Fine motor skills (18 and 30 months)	80.54	897	82.20	707	83.52	1,252	83.65	1,261	82.64	9.42	4,209
Gross motor skills (18 and 30 months)	84.04	896	84.45	707	83.98	1,252	82.54	1,261	83.59	10.91	4,208
IQ, aged 8	96.45	486	101.23	464	107.35	900	114.48	960	106.66	16.62	2,877
Performance IQ, aged 8	93.13	488	97.03	466	101.92	903	107.15	961	101.22	17.13	2,886
Entry assessment score	19.84	741	21.01	539	21.81	804	22.80	631	21.15	3.29	3,123
Key Stage 1 score	8.09	878	9.31	635	10.43	975	11.74	827	9.68	3.74	3,791
Key Stage 2 score	78.82	888	84.20	682	88.08	1,132	92.56	1,062	85.73	12.13	4,253
Key Stage 3 score	98.33	833	107.66	634	114.07	966	124.04	771	109.81	20.13	3,639
Entry Assessment Literacy score	4.77	741	5.04	539	5.21	804	5.40	631	5.06	0.79	3,122
Key Stage 1 literacy score	2.62	877	3.00	635	3.40	974	3.83	827	3.14	1.30	3,789
Key Stage 2 English score	25.62	883	27.42	679	28.86	1,124	30.40	1,055	28.01	4.76	4,224
Key Stage 3 English score	40.68	748	46.06	610	51.64	936	60.05	760	49.06	17.02	3,442
English language GCSE	37.30	812	40.24	651	43.85	1,061	48.21	967	42.43	9.10	3,931
Entry assessment mathematics score	4.99	740	5.31	539	5.61	804	5.94	631	5.40	1.11	3,120
Key Stage 1 mathematics score	2.85	877	3.31	633	3.63	975	4.08	827	3.40	1.36	3,786
Key Stage 2 mathematics score	25.55	883	27.61	676	28.84	1,128	30.49	1,053	28.05	4.87	4,217
Key Stage 3 mathematics score	75.20	796	81.88	624	87.07	945	96.22	761	84.52	21.95	3,536
Mathematics GCSE	34.11	819	38.84	647	43.07	1,038	47.97	894	40.84	11.00	3,837
GCSE Cohort 2007	0.21	1,000	0.20	742	0.20	1,314	0.16	1,322	0.19	0.39	4,967
GCSE Cohort 2008	0.55	1,000	0.58	742	0.50	1,314	0.44	1,322	0.51	0.50	4,967
GCSE Cohort 2009	0.12	1,000	0.13	742	0.12	1,314	0.14	1,322	0.13	0.34	4,967
GCSE Cohort Miss	0.11	1,000	0.09	742	0.17	1,314	0.26	1,322	0.17	0.38	4,967

Notes. Sample window ±3 years around 1 September 1957. The four parental education groups are defined as follows: each parent given score ranging from 0 = no qualifications or below GCSE qualifications, 1 = GCSEs, 2 = A Levels, 3 = Degree. The parental education group is the combined parents score: group 1 = 0 or 1, 2 = 2, 3 = 3–4 and group 4 = 5–6.

3. Empirical Strategy

In England and Wales, compulsory schooling laws apply nationwide and govern the mandatory age by which children must start school and the minimum age⁹ at which individuals are no longer required to be in full-time education. The most recent change to the minimum school leaving age came into effect from 1 September 1972¹⁰ and required individuals to remain in school until the end of the academic year in which they turn 16 – a one-year increase from the previous requirement. The law change therefore affected all individuals turning 15 on or after 1 September 1972 and was binding on anyone wishing to leave at the earliest opportunity.¹¹ The educational impact of the law change was substantial: Figure 1 shows the mean age of leaving full-time education for men and women for the 10 cohorts immediately before and after RoSLA, using data from the UK Labour Force Survey. While there is a general upward trend both before and after the RoSLA, there is a discrete jump in the average years of schooling by just under one-third of a year for both men and women as a result of RoSLA (implying that just under one-third of the cohort were bound by the reform). Moreover, as Figure 2 illustrates, the proportion that left school without any qualifications dropped sharply while the proportion leaving with one or more level 1 (below O-Level) or level 2 (O-Level) qualifications increased. There is no impact on A-level qualifications (which are level 3 qualifications normally sat at age 18) or higher, which suggests that the impact of RoSLA was limited to the lower end of the education distribution, with no ripple effect further up (see Chevalier et al., 2004; for further evidence of this). Table 3 quantifies the pattern illustrated in the Figures and shows the pattern by gender, comparing the three-year trends pre and post-policy in mean years of schooling, the proportion who left school by age 15 and the proportion of each cohort holding various levels of qualifications, with the change in these measures induced by RoSLA. Clearly at the national level there is a significant, discontinuous education impact at the point of RoSLA with particular impact on those leaving school at age 16 or younger.¹² Thus the treatment here involves both a years of education effect, about a third of year on average, and an effect on qualifications at a little under a ten percentage point increase in the proportion with any qualifications.

Fig. 1. Mean Age Left Full-time Education, By Birth (School) Cohort and Sex Source.

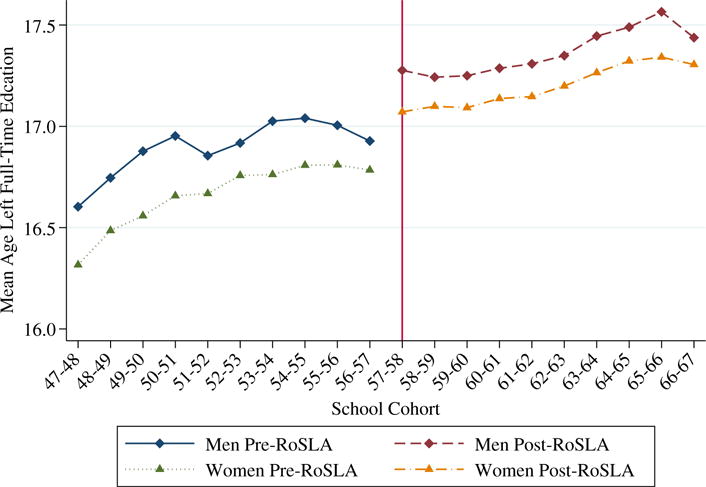
Source. Quarterly Labour Force Survey, pooled 1993q1 to 2010q2.

Fig. 2. Qualification Attainment Levels in NVQ Equivalence Scale, By Birth (School) Cohort Source.

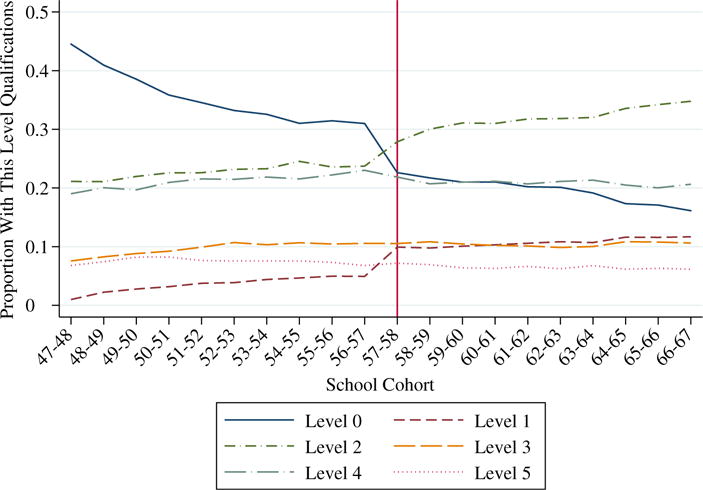
Source. Quarterly Labour Force Survey, pooled 1993q1 to 2010q2.

Table 3.

The Impact of RoSLA on Educational Attainment: Comparison of Trends

		All individuals			Those leaving aged 16 or younger
		1953/4 to 1955/6	1956/7 to 1957/8	1958/9 to 1960/1	1953/4 to 1955/6	1956/7 to 1957/8	1958/9 to 1960/1
		Δ3 years pre-policy	Δ at policy	Δ3 years post-policy	Δ3 years pre-policy	Δ at policy	Δ3 years post-policy
Mean age center full time education (years)	Men	0.029	0.287	0.001	–	–	–
	Women	0.014	0.272	0.040	–	–	–
Proportion center school by 15	Men	−0.023	−0.203	0.005	–	–	–
	Women	−0.017	−0.250	0.010	–	–	–
Proportion with..…No quals	Men	−0.013	−0.063	−0.009	−0.028	−0.129	−0.034
	Women	−0.009	−0.109	−0.004	−0.008	−0.178	−0.003
..…NVQ Level 1 quals	Men	0.002	0.037	0.011	0.006	0.072	0.012
	Women	0.010	0.066	−0.001	0.013	0.103	0.000
..…NVQ Level 2 quals	Men	0.008	0.029	0.012	0.024	0.064	0.016
	Women	−0.003	0.057	0.005	0.008	0.089	0.013
..…NVQ Level 3 quals	Men	0.002	−0.004	−0.008	0.001	0.002	0.000
	Women	0.000	0.004	−0.004	−0.006	0.000	−0.002
..…NVQ Level 4 quals	Men	0.002	−0.009	0.001	0.001	−0.011	0.006
	Women	0.005	−0.015	0.009	−0.002	−0.014	−0.004
..…NVQ Level 5 quals	Men	−0.002	0.010	−0.007	−0.003	0.002	0.001
	Women	−0.003	−0.003	−0.006	−0.004	0.000	−0.003

Notes. Comparison of trends pre-policy and post-policy with the impact at the time of the policy. Calculations using the Quarterly Labour Force Survey pooled from 1993ql to 2010q2. Relatively high values are italicised.

A number of studies have exploited this exogenous increase in education to estimate the causal impact of education on inter alia wages (Harmon and Walker, 1995; Grenet, 2013), employment (Dickson and Smith, 2011), health (Silles, 2009; Clark and Royer, 2013) and crime (Machin et al., 2011). The estimated impacts of the RoSLA are substantial for wages, employment and crime, though there is mixed evidence regarding any effect on health. In each case the estimates are interpreted as ‘local average treatment effects’¹³ as the policy impact is limited – as illustrated above – to the lower part of the education distribution: there was no impact of the reform on educational attainment further up. Similarly, we are interested in investigating the causal effect of parental education on child outcomes amongst parents with low levels of education – a group whose children are most at risk of poor economic outcomes. Therefore though the estimated effects may be different to the average treatment effect, the LATE we estimate is arguably the most important for policy.

The availability of information on the date of birth and the qualifications of both parents provides an additional dimension to the ‘treatment’ of study children, which is determined by whether none, one or both of their parents were impacted by the RoSLA. One potential issue with including information on both parents is the possibility that the RoSLA treatment of the mother (father) may have an impact on the partner that they choose or on the stability of the relationship. For this reason we do not condition on the characteristics of each partner, rather we allow the education of the mother and father to be shocked in the same way by the RoSLA event – which was exogenous to both the mother and the father of the child. There are two possible threats to this strategy: first, if the RoSLA affected the probability of relationships remaining intact and/or the probability of information on the father being available at all. Second, if education affected the age of the partner chosen in which case father’s treatment status would be endogenous to mothers and vice-versa. We can check both of these things in our data. The results show (see Table 6b and Figures A1–A4) that the likelihood of the mother and father being together until the child is at least 12, the mother changing partner at all or the father information being missing is unaffected by the treatment. Moreover, the age gap between partners is unaffected by the RoSLA treatment – whether we look at mothers who are treated or fathers. Additional support comes from the other balancing tests reported in Table 6, which also suggest that the level of qualifications of the father (mother) is not significantly different between the treated and untreated mothers (fathers). We therefore proceed on the assumption that each partners’ treatment status is exogenous and that considering fathers as well as mothers does not bias the estimates.¹⁴

Table 6.

Balancing Tests of Characteristics of Treated Versus Non-treated Parents

		±1 year window, means				6-year bandwidth RDD estimates
		Untreated	Treated	Difference	Difference	SE	N
Panel (a): child and grandparent characteristics
Mother age at first birth	Mother	30.60 310	30.14 369	−0.461	−0.278	0.285	4,820
Birth order	Mother	2.11 384	2.06 457	−0.046	0.032	0.059	5,817
	Father	1.99 391	1.96 490	−0.024	−0.002	0.052	5,176
No. siblings	Mother	1.45 249	1.57 290	0.123*	0.093*	0.052	3,678
	Father	1.48 259	1.48 329	−0.005	0.030	0.048	3,388
(Grand)mother education	Mother	0.18 488	0.18 600	−0.009	−0.002	0.020	7,515
	Father	0.18 413	0.19 526	0.010	0.000	0.021	5,560
(Grand)father education	Mother	0.18 488	0.18 600	−0.003	−0.002	0.020	7,515
	Father	0.18 413	0.21 526	0.026	0.020	0.021	5,560
Child IQ	Mother	107.908 272	108.024 338	0.116	−0.041	1.154	4,098
	Father	108.32 275	106.207 348	−2.113	−1.614	1.104	3,650
Child ‘performance IQ’	Mother	102.04 273	102.425 339	0.384	−0.425	1.195	4,112
	Father	102.964 275	101.075 348	−1.889	−1.446	1.131	3,658
Panel (b) : relationship characteristics
Difference in age between parents (months)	Mother	14.13 312	20.67 364	6.545	4.030	3.792	4,657
	Father	37.41 412	33.76 525	−3.650	−1.834	2.303	5,544
Same father throughout childhood as for treatment DoB	Mother	0.539 488	0.517 600	−0.022	−0.001	0.026	7,515
Mum’s relationship changes after birth of child	Mother	0.051 488	0.057 600	0.005	0.002	0.012	7,515
No information on mother’s relationships	Mother	0.410 488	0.427 600	0.017	−0.001	0.025	7,515
Father of ALSPAC child has qualifications	Mother	0.732 488	0.728 600	−0.003	0.006	0.023	7,515
Father of ALSPAC child has O-levels	Mother	0.555 488	0.575 600	0.020	0.035	0.026	7,515
Father of ALSPAC child has A-levels	Mother	0.408 488	0.407 600	−0.001	0.026	0.025	7,515
Father of ALSPAC child has above A-levels	Mother	0.488 488	0.493 600	0.006	0.017	0.026	7,515
Mother of ALSPAC child has qualifications	Father	0.903 413	0.918 526	0.015	0.023	0.016	5,560
Mother of ALSPAC child has O-levels	Father	0.746 413	0.787 526	0.041	0.041*	0.024	5,560
Mother of ALSPAC child has A-levels	Father	0.383 413	0.411 526	0.028	0.024	0.027	5,560
Mother of ALSPAC child has above A-levels	Father	0.462 413	0.494 526	0.032	0.030	0.027	5,560

Notes.

^*p < 0.10,

^**p < 0.05,

^***p < 0.01.

Regression discontinuity estimates use local linear regression, rectangular kernel.

We proceed by initially estimating the reduced form impact of the RoSLA on both parents’ qualifications ((1) below) to illustrate the first stage effect which is a pre-requisite for there being a causal effect on child outcomes via the parents’ education. For the dependent variable Q_j we consider three different (0, 1) qualification indicators: has any qualifications, has any O-levels and has any A-levels; in all cases the subscript j refers to the parent. The indicator RoSLA_j is a dummy variable for being born on or after 1 September 1957 and the vector X_1j contains either a linear or a quadratic term in the month of birth of the parent. Equation (1) is estimated using a linear probability model.

$$Q_i={\mathit{X}}_{1j}^{\prime }{\mathit{\beta }}_1+{\gamma }_1\mathit{\text{RoSL}}{A}_j+{\epsilon }_j.$$ (1)

Compulsory school reforms lend themselves to analysis by regression discontinuity methods, however given the information on both parents’ treatment, it would not be a standard implementation of RD due to there being both the mother and the father potentially affected by the treatment, effectively two running variables. One approach would be to focus only on mothers (or fathers) and implement a standard RD design.¹⁵

However, apart from the requirement to focus on one parent at a time, the more important reason for not using RD designs is the unique characteristic of the ALSPAC data that allows us to identify separately the treatment effect (born in or after September 1957 and therefore subject to a one-year increase in compulsory schooling requirement) and the effect of the age of the mother (and father) at the time of the child’s birth.

Previous studies have not been able to separate out the effect of treatment from the age of the parent(s) at child’s birth, on account of the children in other cohort studies all being born within the same week. This mechanically confounds the treatment and the age of the parent(s) at the time of the child’s birth. When we implement a design in which we treat the continuous variable mother’s month of birth as the running variable and compare children born to mothers in a certain bandwidth around the treatment threshold, we are not able to control for the age of the mother at the time of the child’s birth. As ALSPAC children in our data are born between April 1991 and January 1993, this means that even in our sample of mothers born within ±1 year of the treatment threshold this translates to a three years and 7 month range of ages of the mother at time of child’s birth.¹⁶ There may be physiological reasons why younger child bearing may impact child development and outcomes or there may be an impact of lower life-experience amongst younger mothers that affects their parenting skills and may carry through to child educational outcomes. Therefore it is important in our empirical strategy to control especially for the age of the mother at the child’s birth in order to prevent the treatment effect being confounded with the effect of bearing the child at a younger age. This analysis applies equally for fathers. The results below bear this out indicating, for example, that for each additional year of age of the mother at the time of the child’s birth, Key Stage 4 results increase by approx. 6 points – equivalent to one grade higher on one GCSE examinations.

For the reduced form estimates we estimate the effect of RoSLA for each parent on the child outcomes, S_i (see (2) below), controlling flexibly for the age of the mother and father at the child’s birth, in addition to including controls in X_2i for child demographic characteristics: gender, month of birth, and school cohort. In the regressions for the tests/examinations undertaken in school we also include the measure of child’s performance IQ, which is thought to be the best measure of innate ability. In our study this is never significantly affected by our treatment, which is re-assuring and provides an important check that our main results are not reflecting parental selection. However, as the point estimates for our treatment on IQ are positive, the inclusion of performance IQ as a control means we are not at risk of an upward bias in the magnitudes we estimate for the RoSLA treatment.¹⁷ Results are robust to the inclusion of the interaction of the individual parent treatment dummies though this interaction term is rarely significant and so in the interests of parsimony is not included in our main specification.¹⁸ The subscript i refers to the child, though the variables themselves in some cases are characteristics of child i’s parents. The particular outcomes that we examine are various education outcomes from national tests at ages 7, 11, 14 and 16 along with school entry assessment (age 4), very early measures of development (18 and 30 months old) and IQ measured at age 8:

$$S_i={\mathit{X}}_{2i}^{\prime }{\mathit{\beta }}_2+{\gamma }_2\mathit{\text{RoSLA}}\mathbf{\_}{M}_i+{\gamma }_3\mathit{\text{RoSLA}}\mathbf{\_}{F}_i+\mathit{\text{AgeMot}}{h}_i\times {\mathit{M}}_i^{\prime }{\mathit{\delta }}_1+\mathit{\text{AgeFat}}{h}_i\times {\mathit{F}}_i^{\prime }{\mathit{\phi }}_1+u_{1i},$$ (2)

in which RoSLA_M_,i and RoSLA_F_,i are the mother and father RoSLA treatment dummies respectively. As noted above, it is important that we control for the age of the mother and father at the child’s birth in order to prevent the treatment effect being confounded with the effect of bearing the child at a younger age. The vector M_i contains three dummy variables indicating whether the mother was born before the sample treatment window, during the window or after the window. The specification allows a different slope for the age of mother at the time of the child’s birth (AgeMoth_,i) for mothers born before, during and after the sample treatment window as AgeMoth_,i is interacted with M_i Allowing a different quadratic shape of the mothers’ age effect for before, during and after window does not alter the results and so in the interest of parsimony only the linear age splines are used. Similarly for fathers, the F_i vector contains a dummy for whether the father was born before the sample treatment window, during the window or after the window and this is interacted with the age of the father at the time of the child’s birth (AgeFath_,i). Unlike in other cohort studies, the children in ALSPAC are born in a window that spans two calendar years, which means that they are placed into three different school years.¹⁹ This is an important feature of the data as it means that the results are not being driven by cohort specific idiosyncratic factors.

Clearly the younger parents in the sample will be treated and the oldest parents in the sample will be untreated, however there is a range of ages where it is the case that the parent may have been treated or may not. Figure 3 illustrates this: the youngest parent in the data who is untreated was born in August 1957 (the last month of birth for which the individuals faced a minimum school leaving age of 15) and had their child in April 1991 and so was 33 years and 8 months old at the time of the child’s birth. The oldest parent in the data who is treated was born in September 1957 (the first month of birth for which the RoSLA is in effect) and had their child in December 1992 and so was 35 years and 3 months old when the child was born. Therefore any parent who is older than 35 years and 3 months is definitely untreated, while any parent younger than 33 years and 8 months is definitely treated – however, the treatment status of any parent in between these ages may not be inferred from their age at the birth of the study child.

Fig. 3.

Schematic Representation of the Overlap in Age Range for Treated and Untreated Parents

Table 4 shows that depending on the sample used there are approximately 800–900 mothers who fall in this age range at the time of the child’s birth, with about 100 fewer fathers in this range – as we would expect since fathers are on average slightly older than mothers. Amongst the parents in this age range who may be treated or untreated, just over half (52%) of the mothers are treated as are around 60% of the fathers. Therefore there is a 19 month range of ages that identify the treatment effect separately from the effect of parents’ age at child’s birth and a fairly even split between treated and non-treated within this age range. Figure A1 in illustrates the density of parents’ age at child’s birth for mothers and fathers separately, with the vertical lines delineating the areas in which the parent is definitely treated, definitely untreated and the ambiguous 19-month range in between.

Table 4.

The Breakdown of Treated Versus Untreated for Parents Whose Age at Child’s Birth Does Not Map Directly Into Treatment Status

	±1 year window			±3 year window or ±6 year window
	Untreated	Treated	Total	Untreated	Treated	Total
Mothers	375   48.45%	399   51.55%	774 100.00%	451   47.83%	492   52.17%	943 100.00%
Fathers	292   41.24%	416   58.76%	708 100.00%	336   39.34%	518   60.66%	854 100.00%

Notes. The 19 month range in parents’ age at child’s birth within which parents may be treated (born on or after 1 September 1957) or untreated (born prior to 1 September 1957) is not fully captured by the restriction that parents are born within ±1 year of September 1957. However, all parents whose age at child’s birth places them in the 19 month range are born with ±3 years of September 1957, hence by definition they are all born within ±6 years of September 1957 and so the numbers of these samples are the same.

In order to capture the treatment effect as tightly as possible, we restrict our focus to parents’ born in short windows around the date of the policy change. In choosing the size of the window there is a trade-off between comparing parents born just before and just after the reform (which reduces any bias introduced to the treatment effect estimate when moving further away from the time of the policy change) and increasing the sample size (which improves precision of the estimates). Closing to less than one-year either side of the discontinuity would not be advisable since in this case the comparison becomes between the older-within-school-cohort treated individuals and the younger-within-school-cohort untreated individuals, confounding the treatment effect estimate with the well-known age-within-school-cohort effect (Crawford et al., 2010). We consider windows of ±1 year, 3 years or 6 years around the policy change and all of our results are robust to the choice of sample window. To be included in the sample, a child must have at least one parent who was born within the sample window. If a parent is born outside the sample window then that parent is ineligible to be considered as either treated or not (in which case only their age at time of child’s birth is controlled). If they are born within the sample window and before September 1957 they are untreated and if they are in the window and born on/after 1 September 1957 they are treated.

Therefore each child’s treatment status is either no, one (which can either the mother or father), or both parents treated. This is captured in (2) by the two (0,1) RoSLA treatment dummies. The estimated coefficient on RoSLA_M_,i (RoSLA_F_,i) captures the intention to treat impact of increasing the education of the mother (father) by RoSLA. If both parents are born outside of the treatment window then that child is excluded from the sample. Single parents are included in the data, identified by a dummy variable, while another dummy variable is included to pick up the effect of the other parents’ information being missing; moreover if the current partner is not the same as when the child was born we exclude these parents (mostly fathers) from the treatment such that we do not consider the treatment status of the mother’s partner who arrived in the household later in the ALSPAC child’s childhood.

Table 5 illustrates the treatment matrix for the main estimation sample ±3 years around the RoSLA policy change for our data which is discussed in detail in the next Section. Horizontally along the top of the Table, the fathers of ALSPAC children are partitioned according to when they were born, while the mothers are partitioned down the left side of the Table. The numbers on the right of each cell indicate the number of children in this category and, for the categories that comprise our estimation sample (highlighted cells), the number on the left gives the number of parents treated for children in this category. As outlined above, any parent born outside the window ±3 years either side of 1 September 1957 (for the main sample, ±1 year either side or ±6 years either side for the robustness check samples) is not included in the treatment variable and, if both parents fall outside of the window, then the child is thus excluded from the sample. Thus only children in the highlighted cells are included in our main estimation sample. There are 262 ALSPAC children for whom both their mother and father were born more than 3 years before RoSLA and so these children are not in our main estimation sample. There are, however, 274 children whose father was born more than 3 years before RoSLA but whose mother was born in the 3 years pre-RoSLA and so these children are included as part of the pre-RoSLA comparison group. There are 505 children for whom both parents were born in the first 3 years post-RoSLA and so these children are ‘doubly’ treated. In total, for the main estimation sample there are 4,967 children who have one or more parents within the treatment window. Of these 1,477 are untreated, 2,985 have one parent treated and, as noted, 505 have both parents treated.²⁰ Some 4,046 observations have no data on mother’s or father’s date of birth, these are almost all drawn from the additional supplement sample identified at age 4 on entry into school. However, there are also a sizeable number of cases where the father’s date of birth was not recorded with enough accuracy to isolate definitively treatment status. These are disproportionately associated with younger mothers and are thus outside our treatment window.

Table 5.

Treatment Matrix for the ±3 Year Sample

±3 year window		Fathers
		Pre-Sample		Pre-RoSLA		Post-RoSLA		Post-Sample		Missing
		(a)	(b)	(a)	(b)	(a)	(b)	(a)	(b)	(a)	(b)	Total
Mothers	Pre-Sample		262	0	46	1	23		31		261	623
	Pre-RoSLA	0	274	0	241	1	116	0	91	0	450	1,172
	Post-RoSLA	1	287	1	351	2	505	1	298	1	891	2,332
	Post-Sample		314	0	369	1	1,011		4,519		5,514	11,727
	Missing		21	0	6	1	8		31		4,046	4,112
	Total		1,158		1,013		1,663		4,970		11,162	19,966
Treatment			0			1			2			Total
N		1,477				2,985		505				4,967

Notes. Map of treatment status for children according to number of parents treated by the 1972 raising of the school leaving age reform. Parents have to be born within ±3 years of 1 September 1957 to be eligible for a treatment status. Rows indicate mothers’ status, columns indicate fathers’ status. Figures in columns labelled (b) represent total number of children in the cell. The shaded cells indicate children included in the sample (i.e. those with one or both parents born within ±3 years of 1 September 1957); the figures in columns labelled (a) represent the number of the child’s parents who are treated. The lower panel of the Table shows the breakdown of parental treatment status for the children included in the sample.

We later consider a narrower definition of the treatment, focusing in on the part of the education distribution where the treatment is actually biting, that is, less educated parents. For these regressions we redefine the treatment variable such that only those parents with less than A-level qualifications are considered at risk of treatment. As stated earlier, to be included in the sample, a child must have at least one parent born within the treatment window and now the additional stipulation is that this parent must also have less than A-level qualifications. We include a control to capture the A-level qualifications of the other parent if the other parent is higher educated.²¹ The RoSLA_M_,i and RoSLA_F_,i variables can still take the values of (0, 1) depending on the education level and date of birth of each parent; for example, both will be 1 if both parents are born after the RoSLA threshold date and within the treatment window and neither has A-level qualifications.

There may be a concern that those parents born either side of the policy change are different in observable and unobservable ways that would confound the estimated treatment effects. This may be of concern if the increase in education altered fertility patterns of parents and hence whether they can be in our study data. To assess this possibility Table 6 contains balancing tests of the difference between the treated and non-treated parents in terms of their fertility, demographic and relationship characteristics. These are shown in two ways: first, via mean differences for the parents in the ±1 year window around the treatment threshold, bearing in mind that there is a great deal of overlap in the age of parents at the birth of the ALSPAC child for the treated and untreated parents in this window. Second, by regression discontinuity estimates of the impact of RoSLA on the parents’ characteristics, using a 6-year bandwidth around the treatment threshold.²² With respect to mother’s age at first birth, the birth order of the ALSPAC child and the completed fertility of the ALSPAC child’s parents (measured by the number of siblings the ALSPAC child has), in the ±1 year sample there is only a statistically significant difference between the treated and untreated in the completed fertility of the ALSPAC mothers. Moreover, despite statistical significance the magnitude of the difference is small (0.1 children). These findings are confirmed in the RD estimates. It is clear that any differences in means are small and it is also the case that for all of our estimation samples that the median birth-order (2) and number of siblings (1) is identical for the treated and untreated parents.

The UK literature on the effect of this RoSLA on fertility is unanimous in its findings. Geruso et al. (2011) pool data from a large number of labour force surveys along with live birth records, abortion records and the 1971 longitudinal study and, exploiting the same 1972 RoSLA in England and Wales that we do, examine the causal effect of education on fertility. Their findings indicate that the only effect of RoSLA was to reduce the incidence of teenage fertility amongst 16 and 17 year olds, with no impact at age 18 and 19 or older. Overall the authors cannot reject that the additional education had no effect on post-teen fertility and no impact on completed fertility. The effects are estimated for narrow confidence intervals strongly suggesting no effect on overall fertility. Teenage pregnancy is a very small proportion of all pregnancies and age 16 and 17 pregnancies are only a part of teen fertility. Wilson (2014) carries out a similar analysis of the 1972 RoSLA reform and echoes the results of Geruso et al. finding no impact on fertility beyond age 20 hence this evidence suggests that for the cohorts of women that we are looking at, the additional education induced by RoSLA would have a minimal impact on the composition of our sample via a timing of fertility effect or a change to completed fertility. Thus we would not expect to find any effect on fertility among mothers in our sample who are in their early to mid-thirties at the time of the child’s birth.

The middle Section of Table 6a compares the pre and post-treatment parents with respect to their own parents’ education (i.e. the ALSPAC children’s grand-parents), measured in terms of whether they hold O-levels or not. For the ALSPAC mothers in our ±1 year sample there is no difference at all in their parents’ education between the treated and untreated and for fathers any differences are small and not statistically significant. This is also true in the RD estimates, thus the educational backgrounds of the treated and untreated ALSPAC parents seem to be well balanced.

The final part of Table 6a compares the IQ of the children of untreated versus treated parents. There are no significant differences in IQ for the children of ALSPAC mothers nor for children of ALSPAC fathers in the ±1 year sample, nor in the RD estimates. Moreover, looking at ‘performance IQ’ which is thought to capture the more innate element of IQ (‘fluid intelligence’), again there are no differences between children of treated and untreated parents whether we look in the ±1 year sample mean differences or the wider RD estimates. These tests provide evidence that there is not an underlying difference in innate ‘ability’ between the children of treated and untreated parents.

Table 6b presents balancing tests relating to the characteristics of the relationships of the pre and post-treatment couples. As detailed above, these tests show no difference in the parental age gap or the stability of the relationship on account of the treatment, nor is the level of qualifications of the father (mother) significantly different between the treated and untreated mothers (fathers).

In summary, the results of these balancing tests give us confidence that there is not selection into treatment on observable characteristics of the parents nor are the children of treated parents different in their more innate characteristics from the children of the untreated parents. Therefore, given the nature of the exogenous policy change, there is no reason to suspect that there is selection on unobservables either, hence the treatment variables should be unbiased estimates of the intention-to-treat impact of RoSLA on child outcomes.

4. Results²³

4.1. The Impact of RoSLA on Parents’ Education

To illustrate that the national impact of the RoSLA on the education distribution is mirrored amongst the ALSPAC parents, Table 7 shows the results for the reduced form (1) estimates, using each of our three measures of educational attainment for the parents. The upper panel (a) refers to the full sample, whereas the lower panel refers to the sample when we restrict to only including parents who have less than A-level qualifications in the definition of the treatment variable.

Table 7.

The Impact of RoSLA on Parents’ Qualifications, Main Estimation Sample: Parents Born in ±3 Year Window Around 1 September 1957

	(1)	(2)	(3)	(4)	(5)	(6)
	Any qualifications	O-levels	A-levels	Any qualifications	O-levels	A-levels
Panel (a): full sample
RoSLA dummy	0.044*** (0.016)	0.065*** (0.024)	0.028 (0.027)	0.039** (0.016)	0.060** (0.025)	0.009 (0.027)
Parent’s DOB in months	0.000 (0.000)	−0.001* (0.001)	−0.002*** (0.001)	0.017* (0.010)	0.002 (0.015)	0.031* (0.017)
Parent’s DOB in months squared				−0.002 (0.001)	−0.001 (0.002)	−0.006*** (0.002)
Constant	0.866*** (0.010)	0.734*** (0.016)	0.506*** (0.018)	0.844*** (0.017)	0.716*** (0.026)	0.432*** (0.029)
R2	0.007	0.001	0.004	0.008	0.002	0.005
Observations	5,512	5,512	5,512	5,512	5,512	5,512
	(1)		(2)	(3)		(4)
	Any qualifications		O-levels	Any qualifications		O-levels
Panel (b): sample restricted to parents with less than A-level qualifications
RoSLA dummy	0.111*** (0.033)		0.116*** (0.041)	0.109*** (0.034)		0.21*** (0.042)
Parent’s DOB in months	0.001 (0.001)		−0.001 (0.001)	0.001 (0.002)		−0.002 (0.003)
Parent’s DOB in months squared				−0.000 (0.000)		0.000 (0.000)
Constant	0.680*** (0.021)		0.459*** (0.026)	0.672*** (0.034)		0.477*** (0.042)
R2	0.025		0.008	0.025		0.008
Observations	2,479		2,479	2,479		2,479

Column (1) of panel (a) shows that the impact of RoSLA is to significantly increase the proportion of individuals with any qualifications by 4.4 percentage points and the proportion with O-levels by 6.5 percentage points, both significant at the 1% level. This is in line with the national picture for men, though the ALSPAC women appear not to have increased qualification levels as much as the national average. These estimates are robust to the inclusion of a higher order polynomial in parents’ date of birth (in months), the impact coefficients altering slightly to 3.9 percentage points for any qualifications, 6.0 percentage points for O-levels (as shown in columns (4) and (5) respectively).²⁴ As with the national picture, there is no impact on the proportion holding A-level qualifications – whether we use a linear (column (3)) or a quadratic (column (6)) trend in parent’s date of birth. This is important as later we will narrow the focus to the impact on parents with less than A-level qualifications on the basis that this is where the main impact of RoSLA is felt.

Imposing the restriction, panel (b), the impact of RoSLA is increased as we would expect to be the case. Now the increase in any qualification holding is 11.1 percentage points and 11.6 pp for holding O-levels, each significant at the 1% level. Allowing a quadratic in parent’s month of birth very slightly changes these impacts to 10.9 pp and 12.1 pp respectively. Thus the impact of RoSLA on parental qualifications is sizeable, especially when we focus on the part of the education distribution where the effect is most keenly felt. Moreover, given that the effect on qualifications amongst the ALSPAC parents closely mirrors the national impact on qualifications, we can surmise that a similar proportion of the parents were bound by the reform in terms of each time spent in education – around one-third receiving an extra year of education. All of these results in Table 7 are confirmed in Table 8 where we present regression discontinuity estimates of the impact of RoSLA on qualifications for various bandwidths around the discontinuity.

Table 8.

The Impact of RoSLA on Parents’ Qualifications, RDD Estimates of the Effect of Being Born After 1 September 1957 and thus Subject to RoSLA

	Any qualifications	O-levels	A-levels
Panel (a) : full sample
Bandwidth 3 years N = 5,512	0.040* (0.017)	0.063* (0.025)	0.014 (0.027)
Bandwidth 6 years N = 11,429	0.056*** (0.012)	0.049** (0.018)	0.014 (0.020)
Bandwidth 10 years N = 17,421	0.053*** (0.011)	0.065*** (0.015)	0.007 (0.016)
	Any qualifications		O-levels
Panel (b): sample restricted to parents with less than A-level qualifications
Bandwidth 3 years N = 2,479	0.109** (0.036)		0.119** (0.041)
Bandwidth 6 years N = 5,685	0.128*** (0.026)		0.090** (0.030)
Bandwidth 10 years N = 9,747	0.128*** (0.022)		0.114*** (0.025)

Notes.

^*p < 0.10,

^**p < 0.05,

^***p < 0.01.

Local linear regression, rectangular kernel.

4.2. The Impact of RoSLA on Children’s Education

The results from estimating the impact of RoSLA on children’s age 16 outcomes are displayed in Table 9 for the three different windows around the policy change: ±1 year, ±3 years and ±6 years. The KS4 outcomes are graded on the same equivalence scale which ranges from the lowest grade G which is worth 16 points, through increments of 6 points per grade to the highest grade A* being worth 58 points. The mean and standard deviation of each outcome variable are displayed in the Table to give a sense of scale, as is each treatment effect as a proportion of a standard deviation, to allow comparison across later measures, such as the other KS outcomes.

Table 9.

The Impact of RoSLA on Child Key Stage 4 (Age 16) Outcomes, Three Windows Around the Policy Change

	1 year window			3 year window			6 year window
	Key stage 4 score	GCSE total score	GCSE academic total	Key stage 4 score	GCSE total score	GCSE academic total	Key stage 4 score	GCSE total score	GCSE academic total
RoSLA treatment of mother	22.046** (9.039)	14.980* (8.590)	10.622* (5.899)	17.274*** (6.146)	18.872*** (5.891)	12.295*** (4.046)	16.380*** (6.009)	22.900*** (5.731)	13.746*** (3.873)
RoSLA treatment of father	23.546** (9.714)	20.194** (9.227)	11.732* (6.347)	20.027*** (6.777)	20.369*** (6.499)	12.037*** (4.455)	23.318*** (6.445)	19.751*** (6.153)	14.580*** (4.146)
Mother’s age at child’s birth: pre-window	5.993*** (1.803)	6.309*** (1.713)	4.341*** (1.180)	5.837*** (1.188)	6.569*** (1.138)	4.896*** (0.785)	3.916*** (1.020)	5.251*** (0.974)	3.367*** (0.653)
Mother’s age at child’s birth: in window	7.412*** (1.883)	8.049*** (1.789)	5.090*** (1.232)	6.975*** (1.206)	7.495*** (1.154)	5.403*** (0.796)	4.364*** (0.833)	6.299*** (0.793)	4.298*** (0.537)
Mother’s age at child’s birth: post-window	7.808*** (2.143)	8.133*** (2.036)	5.411*** (1.402)	7.925*** (1.498)	8.160*** (1.433)	6.027*** (0.988)	4.730*** (1.157)	6.974*** (1.102)	4.770*** (0.745)
Father’s age at child’s birth: pre-window	0.815 (1.697)	2.157 (1.616)	1.996* (1.108)	1.723 (1.122)	2.200** (1.078)	1.044 (0.739)	1.494* (0.782)	1.108 (0.746)	1.354*** (0.502)
Father’s age at child’s birth: in window	1.402 (1.939)	2.823 (1.846)	2.497** (1.264)	2.694** (1.304)	3.348*** (1.253)	1.602* (0.859)	2.340** (0.930)	1.936** (0.888)	2.058*** (0.598)
Father’s age at child’s birth: post-window	1.275 (2.209)	2.733 (2.103)	2.537* (1.440)	2.689* (1.631)	3.456** (1.567)	1.506 (1.073)	1.953 (1.310)	1.245 (1.251)	1.974** (0.841)
R2	0.195	0.230	0.249	0.197	0.225	0.247	0.180	0.212	0.236
Observations	1,523	1,531	1,481	4,094	4,116	3,985	7,570	7,621	7,378
Outcome mean	430.9	358.02	243.09	423.76	347.42	235.87	416.82	337.31	227.91
Outcome SD	145.65	141.86	97.05	146.29	143.2	98.07	147.87	144.32	97.41
Treatment as % of SD (mum only)	15.14	10.56	10.95	11.81	13.18	12.54	11.08	15.87	14.11
Treatment as % of SD (dad only)	16.17	14.24	12.09	13.69	14.22	12.27	15.77	13.69	14.97
Treatment as % of SD (both)	31.30	24.80	23.03	25.50	27.40	24.81	26.85	29.55	29.08
Treatment joint significance p-value	0.003	0.019	0.035	0.000	0.000	0.000	0.000	0.000	0.000

Notes

^*p < 0.10,

^**p < 0.05,

^***p < 0.01.

Additional controls included: child gender, month of birth, GCSE cohort, parent foreign qualifications, single mother dummy, father missing info dummy, child performance IQ.

The first thing of note in Table 9 is that the RoSLA treatment variables for mother and father are significant in all windows and for all outcomes. Secondly, comparison of the separate RoSLA treatment coefficients for the mother and the father finds that they are almost always very close to each other and in no case could we rule out that they are the same. Comparison of the coefficients in columns (1), (4) and (7) for KS4 total score, those in columns (2), (5) and (8) for GCSE total score and those in (3), (6) and (9) for the more academic GCSE qualifications, show that the point estimates for the treatment impacts across the different sample windows and very close to each. For each parent affected by RoSLA, the child’s KS4 total score is raised by between 12 and 20 points – which is the equivalent of two to three GCSEs grades. Including only GCSEs – therefore excluding the vocational equivalent qualifications – the treatment impact is very similar, approximately 18–20 points. When we focus just on the traditional academic subject GCSEs the impact is smaller, at around 12 points, which is two GCSE grades. The impacts as a proportion of the outcome variable standard deviation are shown in the lower rows of Table 9. For each KS4 outcome the impact of mother treatment is around 12% of a standard deviation, while for fathers it is slightly higher at 14% of a standard deviation. For all outcomes, in all windows the test of the joint significance of the two parental RoSLA treatment dummies has a p-value of 0.035 or less.

The impact of mother’s age at the time of the child’s birth is significant whether the mother was born before, during or after the treatment window, with the age impact higher for the younger mothers in all cases – we find, as we would expect, that amongst younger parents the slope of the age effect is steeper. Summarising the broad pattern, for mothers who are born before or within the treatment window an additional year of age at child’s birth increases these age 16 outcomes byjust under one GCSE grade (5–6 points) on average, whereas for the younger mothers the additional year increases these outcomes byjust over one grade (6–7 points). The age of the father at the time of the child’s birth is much less significant, only really having an impact for fathers born within the treatment window with each additional year of age adding approximately 2–3 points to KS4 outcomes.

The impact of the RoSLA treatment on the high stakes age 16 examinations is clear with the RoSLA raising attainment by just over 0.1 standard deviations per parent across the alternative examination metrics; now we turn to looking at earlier assessments. Table 10 contains the estimates of the RoSLA treatment impacts on early development indicators: IQ and performance IQ, school entry assessment and the Key Stage scores at ages 7, 11 and 14 (KS1, 2 and 3 respectively). We focus on the ±3 years window here as being representative of the alternative lengths of window considered. Gross motor skills is not strongly correlated with later educational outcomes and it is interesting that column (2) of Table 10 shows that there is actually a negative impact of the mother being RoSLA treated for this outcome. Fine motor skills however are predictive of later outcomes but there is no significant impact of RoSLA treatment on this outcome though the point estimates for mother and father treatment are positive (column (1)). ‘Performance IQ’ which is a component of the Wechsler Intelligence Scale for Children IQ measure that we use, is thought to capture the more innate element of IQ and as such this should not be malleable to the intervention of increased parental education. As is clear in Table 2, this IQ measure is graded by parental education, however, we see in Table 10 that there is no impact of either parent being RoSLA treated on this measure, nor on the wider total IQ measure. This is re-assuring as we would expect as parental education does not influence innate child intelligence and supports the evidence from the balancing tests, showing that there is not an underlying difference between the children of parents either side of the treatment line in the more innate performance IQ.

Table 10.

The Impact of RoSLA on Outcomes Throughout Childhood, ±3 Year Window

	Fine motor skills (18 and 30 months)	Gross motor skills (18 and 30 months)	IQ, aged 8	Performance IQ, aged 8	Entry assessment score	Key Stage 1 score	Key Stage 2 score	Key Stage 3 score
RoSLA Treatment of mother	0.183 (0.431)	−0.909* (0.506)	1.029 (0.933)	1.240 (0.968)	0.475*** (0.149)	0.345** (0.154)	1.395*** (0.486)	1.535* (0.860)
RoSLA treatment of father	0.160 (0.441)	−0.794 (0.517)	−0.068 (0.931)	0.021 (0.967)	0.122 (0.167)	0.576*** (0.171)	1.145** (0.530)	2.477*** (0.944)
Mother’s age at child’s birth: pre-window	0.012 (0.079)	−0.202** (0.093)	0.789*** (0.181)	0.723*** (0.188)	0.105*** (0.029)	0.085*** (0.029)	0.451*** (0.094)	0.623*** (0.164)
Mother’s age at child’s birth: in window	0.020 (0.082)	−0.174* (0.096)	0.880*** (0.188)	0.825*** (0.195)	0.116*** (0.029)	0.096*** (0.029)	0.529*** (0.096)	0.724*** (0.165)
Mother’s age at child’s birth: post-window	0.035 (0.102)	−0.190 (0.119)	0.929*** (0.231)	0.921*** (0.240)	0.148*** (0.036)	0.112*** (0.036)	0.597*** (0.119)	0.799*** (0.206)
Father’s age at child’s birth: pre-window	−0.067 (0.072)	−0.231*** (0.084)	0.070 (0.152)	0.044 (0.158)	0.033 (0.027)	0.080*** (0.028)	0.181** (0.086)	0.340** (0.154)
Father’s age at child’s birth: in window	−0.064 (0.084)	−0.263*** (0.098)	0.156 (0.177)	0.116 (0.184)	0.048 (0.031)	0.097*** (0.033)	0.269*** (0.100)	0.498*** (0.180)
Father’s age at child’s birth: post-window	−0.088 (0.104)	−0.285** (0.122)	0.101 (0.219)	0.081 (0.228)	0.050 (0.039)	0.111*** (0.041)	0.287** (0.125)	0.539** (0.225)
R2	0.037	0.013	0.056	0.040	0.281	0.274	0.242	0.267
Observations	4,209	4,208	2,877	2,886	3,123	3,791	4,253	3,639
Outcome mean	82.64	83.59	106.66	101.22	21.15	9.68	85.73	109.81
Outcome SD	9.42	10.91	16.62	17.13	3.29	3.74	12.13	20.13
Treatment as % of SD (mum only)	1.94	−8.33	6.19	7.24	14.47	9.22	11.49	7.62
Treatment as % of SD (dad only)	1.70	−7.28	−0.41	0.12	3.71	15.39	9.44	12.31
Treatment as % of SD (both)	3.64	−15.62	5.78	7.36	18.18	24.61	20.93	19.93
Treatment joint significance p-value	0.846	0.049	0.545	0.438	0.004	0.000	0.001	0.005

Notes.

^*p < 0.10,

^**p < 0.05,

^***p < 0.01.

Additional controls included: child gender, month of birth, GCSE cohort, parent foreign qualifications, single mother dummy, father missing info dummy. Child age in months is included as an additional covariate for the early development scores. Child performance IQ included as a control in Entry Assessment and Key Stage test score regressions.

Columns (5) to (8) of Table 10 show that it is in the education measures assessed within school that the RoSLA treatment impact starts to become significant. These assessments are marked according to their own non-comparable scales, so the treatment impact is converted to the proportion of a standard deviation of the outcome variable in the last rows of the Table. The entry assessment is carried out when children are aged 4 or just turned 5 and have been in school for just one or two months. There is a significant impact of mothers’ RoSLA treatment on this measure, 14% of a standard deviation higher results for children of mothers affected by RoSLA. The size of impact is comparable for the KS1 and KS2 scores, both statistically significant, with only the KS3 score impact smaller though still marginally significant. For fathers, the KS1, KS2 and KS3 results show a significant RoSLA impact, with similar magnitude to the mother impact, around 10% of a standard deviation. As with the KS4 results, mother’s age at the time of the child’s birth is significant for all outcomes and with a steeper gradient for younger mothers. Again father’s age effect generally has a smaller magnitude and like for mothers has a steeper slope for the younger fathers. Unlike Carneiro et al. (2008) we find no fading of the impact of parents’ education as children age.

Table 11 considers separately results for English/literacy, columns (1) to (5), and Mathematics, columns (6) to (10). For English/literacy, the impact of mothers’ RoSLA treatment is evident at school entry (effect size 19% of standard deviation) and in all of the Key Stage assessments (age 7, 11, 14 and 16), with each of these assessments having an effect size of approximately 8% of a standard deviation. For fathers the effects are significant for the Key Stage assessments at 9–13% of a standard deviation. For mathematics scores the mother effects are consistent at 9% of standard deviation for entry assessment, KS1, KS2 and KS4, all significant. For fathers the effects are significant at every stage from KS1 upwards and of sizes between 10% and 16% of a standard deviation. Overall the father effects tend to be slightly higher, and for each parent there are no stark differences between the impact on English and mathematics test scores.

Table 11.

The Impact of RoSLA on Child English/Literacy and Mathematics Outcomes Throughout Childhood, ±3 Year Sample Window

	Entry assessment literacy	Key stage 1 literacy score	Key stage 2 English score	Key stage 3 English score	English language GCSE	Entry assessment mathematics	Key Stage 1 mathematics score	Key Stage 2 mathematics score	Key Stage 3 mathematics score	Mathematics GCSE
RoSLA treatment of mother	0.146*** (0.037)	0.117** (0.055)	0.392** (0.197)	1.324* (0.781)	0.802** (0.394)	0.106** (0.052)	0.111** (0.056)	0.483** (0.200)	0.530 (1.027)	1.135** (0.477)
RoSLA treatment of father	0.047 (0.041)	0.170*** (0.061)	0.410* (0.214)	1.944** (0.849)	1.199*** (0.434)	0.041 (0.058)	0.230*** (0.063)	0.478** (0.219)	2.907*** (1.123)	1.770*** (0.524)
Mother’s age at child’s birth: pre-window	0.027*** (0.007)	0.024** (0.010)	0.142*** (0.038)	0.687*** (0.150)	0.353*** (0.077)	0.030*** (0.010)	0.035*** (0.011)	0.152*** (0.039)	0.297 (0.195)	0.374*** (0.092)
Mother’s age at child’s birth: in window	0.030*** (0.007)	0.028*** (0.010)	0.177*** (0.039)	0.683*** (0.152)	0.380*** (0.078)	0.035*** (0.010)	0.040*** (0.011)	0.176*** (0.039)	0.443** (0.198)	0.449*** (0.093)
Mother’s age at child’s birth: post-window	0.039*** (0.009)	0.032** (0.013)	0.196*** (0.048)	0.728*** (0.189)	0.406*** (0.096)	0.042*** (0.012)	0.047*** (0.013)	0.200*** (0.049)	0.439* (0.247)	0.496*** (0.116)
Father’s age at child’s birth: pre-window	0.014** (0.007)	0.022** (0.010)	0.054 (0.035)	0.253* (0.138)	0.155** (0.072)	0.012 (0.009)	0.036*** (0.010)	0.061* (0.036)	0.415** (0.183)	0.157* (0.087)
Father’s age at child’s birth: in window	0.018** (0.008)	0.027** (0.012)	0.088** (0.041)	0.355** (0.161)	0.205** (0.084)	0.019* (0.011)	0.044*** (0.012)	0.088** (0.042)	0.505** (0.214)	0.228** (0.101)
Father’s age at child’s birth: post-window	0.023** (0.010)	0.030** (0.015)	0.082 (0.051)	0.325 (0.202)	0.199* (0.105)	0.016 (0.014)	0.052*** (0.015)	0.094* (0.052)	0.615** (0.268)	0.220* (0.126)
R2	0.245	0.245	0.198	0.205	0.184	0.240	0.265	0.211	0.149	0.202
Observations	3,122	3,789	4,224	3,442	3,931	3,120	3,786	4,217	3,536	3,837
Outcome mean	5.06	3.14	28.01	49.06	42.43	5.40	3.40	28.05	84.52	40.84
Outcome SD	0.79	1.30	4.76	17.02	9.10	1.11	1.36	4.87	21.95	11.00
Treatment as % of SD (mother only)	18.60	8.97	8.25	7.78	8.81	9.60	8.17	9.90	2.41	10.32
Treatment as % of SD (father only)	5.97	13.04	8.62	11.43	13.17	3.73	16.93	9.80	13.25	16.09
Treatment as % of SD (both)	24.58	22.01	16.87	19.21	21.98	13.33	25.10	19.71	15.66	26.40
Treatment joint significance p-value	0.000	0.001	0.018	0.014	0.002	0.084	0.000	0.004	0.028	0.000

Notes.

^*p < 0.10,

^**p < 0.05,

^***p < 0.01.

Additional controls included: child gender, month of birth, GCSE cohort, parent foreign qualifications, single mother dummy, father missing info dummy, child performance IQ.

4.3. The Impact of RoSLA on the Education of Children with Lower Educated Parents

We now restrict our focus to children of parents with lower levels of education – the parents most likely to be impacted by the RoSLA. As outlined above, to do this we redefine the treatment variable such that only those who attain less than A-levels are considered ‘at risk’ of RoSLA treatment – as before, provided they are born within ±3 years around 1 September 1957. Therefore, if both of a child’s parents have A-level education or higher then that child is excluded from the sample, whereas if one parent is considered at risk of treatment but the other is not and has A-levels or higher, this is controlled for in the regression. Though the partner having A-level or higher qualifications could be considered an outcome of the treatment, the balancing tests suggest there is no impact of RoSLA on partner qualifications and so we proceed on this basis, though acknowledging the possible (downward) bias in the estimated coefficients.

Table 12 considers the age 16 outcomes – KS4 total, GCSE total and GCSE academic subjects’ total for this reduced sample. We know from the lower panel of Tables 7 and 8 that the impact of RoSLA on qualification holding amongst parents in this sample was approximately double the impact for the larger sample and we see a sizeable increase in impact in the reduced form estimates on child outcomes. The mother and father RoSLA treatment effects now range from 14% to 21% of a standard deviation, compared with 12–14% for the results in Table 9. The largest impact is on the broader KS4 total scores which include vocational qualifications, with the father treatment having a particularly strong effect here (21% of a standard deviation). The effect on GCSE total score is equivalent to an increase of one grade for three GCSEs for each parent treated. In each column we see the strong, positive effect of one parent having A-levels equivalent or higher education on child outcomes. Tables A3 and A4 show the effect of RoSLA treatment on the results at different points in the children’s education progress, and separate picture for Mathematics and literacy, after selecting on parents in the treatment window without A-levels. The impacts on fine or gross motor skills mirror those in the full sample, and as with that sample there are no impacts on IQ or performance IQ. Each of the assessments from school entry onwards do show positive point estimates though in these smaller samples there are fewer significant effects, KS1 (age 7) apart where the father effect is strongly significant and at 22.8% of standard deviation is approximately one-and-a-half times the effect size compared with the full sample. The pattern for English and mathematics is largely the same as the full sample Table, though it is notable that while the mother effect sizes do not change substantially where significant, for fathers the significant effects are all higher, up to one-and-a-half times the size compared to the full sample, hinting that father’s treatment is particularly important for this albeit selected sample.²⁵

Table 12.

The Impact of RoSLA on Child Key Stage 4 (Age 16) Outcomes Parents With Lower Levels of Education, ±3 Year Sample Window

	Key stage 4 score	GCSE total score	GCSE academic total
RoSLA treatment of mother	22.246*** (7.805)	21.910*** (7.198)	8.520* (4.733)
RoSLA treatment of father	30.585*** (9.772)	22.698** (9.005)	12.895** (5.894)
Mother has A levels, equivalent or higher	49.698*** (10.498)	64.749*** (9.703)	39.148*** (6.289)
Father has A levels, equivalent or higher	50.883*** (8.521)	61.733*** (7.868)	42.068*** (5.144)
Mother’s age at child’s birth: pre-window	4.336*** (1.527)	4.254*** (1.409)	2.469*** (0.930)
Mother’s age at child’s birth: in window	6.517*** (1.496)	6.309*** (1.378)	3.650*** (0.910)
Mother’s age at child’s birth: post-window	7.801*** (1.851)	7.502*** (1.706)	4.456*** (1.125)
Father’s age at child’s birth: pre-window	1.801 (1.425)	2.302* (1.318)	1.246 (0.860)
Father’s age at child’s birth: in window	2.692 (1.692)	3.313** (1.564)	1.563 (1.022)
Father’s age at child’s birth: post-window	3.076 (2.095)	4.081** (1.937)	1.938 (1.263)
R2	0.176	0.205	0.235
Observations	2,452	2,467	2,359
Outcome mean	385.52	302.04	205.03
Outcome SD	147.43	138.85	90.97
Treatment as % of SD (mum only)	15.09	15.78	9.37
Treatment as % of SD (dad only)	20.75	16.35	14.17
Treatment as % of SD (both)	35.83	32.13	23.54
Treatment joint significance p-value	0.000	0.000	0.022

Notes.

^*p < 0.10,

^**p < 0.05,

^***p < 0.01.

Additional controls included: child gender, month of birth, GCSE cohort, parent foreign qualifications, single mother dummy, father missing info dummy, child performance IQ.

5. Discussion and Conclusions

The causal impact of parental education on children has potentially important policy implications for intergenerational mobility, especially among lower educated parents. Yet the available evidence from twin, adoptee and policy change studies is inconclusive. Using high frequency, high quality data from the Avon area of the UK we explore the impact of the 1972 Raising of the School Leaving Age (RoSLA) on parents’ qualifications and child educational outcomes throughout childhood. In summary, the findings suggest that the RoSLA treatment of parents impacts on child outcomes from school entry onwards and that the effect does not massively increase between the entry assessment and the examinations taken at the end of the compulsory schooling period. For age 16 outcomes the impact sizes are comparable whether it is the mother or the father who is treated by RoSLA. In earlier assessments there are more significant mother’s treatment effects but where father’s treatment is significant it tends to have a slightly larger effect, though still very similar magnitude. There is some variation in impact size over the years but overall the impact seems to be significant at the start of school and then steady, without any strong increase in impact size exhibited. This remains the case when we look at results separated by English/literacy and mathematics, with the father effects being slightly larger particularly at older ages.

There is no impact of RoSLA treatment on children’s IQ nor on their ‘performance IQ’ which is re-assuring as this captures a more innate measure of ability. This and the raft of balancing tests on parent, child and grandparents’ characteristics give confidence that there are no selection effects across our treatment and control groups and the effects are causal with parents born in the treated post-reform years seeing gains equal to just over 0.1 standard deviations in test scores and qualifications achieved. The ‘complier’ group who identify our results are those who have both lower levels of education and who are having children in their early to mid-30s. Child bearing in this group is quite common, especially for men but also for women: for example, figures from the British Household Panel Survey suggest that amongst the cohort of women born between 1952 and 1962, who have O-levels or lower qualifications, 36.4% have a child between the ages of 30 and 38²⁶ i.e. the range of ages for our main estimation sample. Thus it is not the case that low educated women complete their fertility before their 30s.

Importantly, the structure of the ALSPAC data – with children born over two calendar years – allows the treatment effect of RoSLA to be separately identified from the age of the parents at the time of the child’s birth and the results demonstrate the importance of separating these effects. As we do not have years of completed education for the parents in the ALSPAC data, we cannot compute the Wald estimate of the effect of an additional year of education on child outcomes. However, the UK literature on the 1972 RoSLA consistently estimates a ‘first stage’ effect of 0.33 additional years of schooling for the affected cohort – implying around 1/3 were bound by the reform. Taking a two sample two stage least squares approach and using this figure along with our reduced form results would imply a ‘local average treatment effect’ impact of a 0.3 standard deviation increase in test scores for children with a parent who gained an additional year of education due to RoSLA. This is a non-trivial impact and appears from school entry and remains throughout the school career.

The policy implications of these results are important with the UK having recently implemented a Raising of the Participation Age (that is in full-time education or a job with an apprenticeship) to age 18 in 2015, as they suggest a positive impact on the educational attainment of the next generation results from increasing the schooling of individuals who wish to leave school at the first opportunity. These (future) parents who have low tastes for education or binding credit constraints identify the parental education effect, hence it is a ‘local average treatment effect’. However, from a policy point of view this is an extremely important LATE as this group of individuals are most at risk of failing to achieve their own potential and a similar risk applies to the children that they go on to have. This is in line with previous findings, for example Carneiro et al. (2008) find effects of a similar magnitude in the US, albeit here our magnitudes are somewhat larger.

The mechanisms through which parental education causally affects children’s outcomes – the ‘why’ question – remains a very important question for future research to answer. Del Bono et al. (2016) shed some light on the question, examining the importance of maternal time inputs for child human capital development. Using data from the UK Millennium Cohort Study, they find that more time spent by mothers with their children in the early years leads to greater cognitive and non-cognitive outcomes at age 7. Moreover, they find a strong, positive relationship between maternal education and their ‘educational time’ input in the children’s early years – suggesting that parental time allocation towards educational activities is one mechanism through which parental education translates into child outcomes. Similarly, Del Boca et al. (2016) use data from the Panel Study of Income Dynamics and its Child Development Supplements to examine the impact of different potential policy interventions on child development, modelling how policies affect household behaviour and subsequent child ‘quality’. The findings suggest that policies that distort the input mix into the child quality production function away from parental time investments (and towards investment in child-related goods) are less effective. This again points towards the importance of the parental time investment channel and would support the notion that part of the reason why children of more educated parents achieve better outcomes relates to the greater time invested in their children by more educated parents. Carneiro and Ginja (2016) also shed light on this question using data from the NLSY 1979 and the Children of the NLSY. They illustrate the differential response of parental inputs to income fluctuations, depending on the education of the mother. In contrast to lower educated parents, college-educated mothers do not alter their investments in their children in response to changes in income, controlling for an extensive set of demographics and other observable determinants of income. The measures of investment include an index of time and child-related goods, the Home Observation Measurement of Environment (HOME) index and the two components used to construct this index: cognitive stimulation and emotional support. They also find a strong relationship between the HOME index and child outcomes. Given the positive relationship between parental education and the home environment, and the effect of education to insure against income shocks, this hints at additional channels – other than parental time – through which education in one generation transmits to the next.

Nevertheless, many questions remain for future research regarding the educational transmission mechanisms and the relative importance of parental time investments versus other inputs such as child-related goods and the home environment, with important implications for the design of education and family-related policy.

Appendix A. Further results, robustness to choice of model specification and additional information

Table A1.

Regression Discontinuity Estimates of the Impact of RoSLA on Child Key Stage 4 (Age 16) Outcomes, Mothers, Various Bandwidths

Bandwidth	Key Stage 4 score	GCSE total score	GCSE academic total
1-year
Coefficient	23.668	−5.555	3.216
SE	(20.867)	(19.742)	(13.454)
N	865	868	842
2-year
Coefficient	21.572	7.615	5.434
SE	(14.118)	(13.529)	(9.267)
N	1,863	1,870	1,814
3-year
Coefficient	18.360	6.361	10.865
SE	(11.593)	(11.157)	(7.678)
N	2,856	2,879	2,784
4-year
Coefficient	9.221	4.884	4.460
SE	(9.953)	(9.679)	(6.665)
N	3,904	3,930	3,800
5-year
Coefficient	11.071	6.766	5.567
SE	(9.088)	(8.803)	(6.030)
N	5,028	5,062	4,896
6-year
Coefficient	10.557	8.033	5.366
SE	(8.427)	(8.204)	(5.615)
N	6,188	6,229	6,025

Notes.

^*p < 0.10,

^**p < 0.05,

^***p < 0.01.

RDD estimated using local linear regressions either side of the discontinuity, rectangular kernel.

Table A2.

Regression Discontinuity Estimates of the Impact of RoSLA on Child Key Stage 4 (Age 16) Outcomes, Fathers, Various Bandwidths

Bandwidth	Key Stage 4 score	GCSE total score	GCSE academic total
1-year
Coefficient	9.545	15.457	21.387
SE	(20.516)	(19.798)	(14.114)
N	796	800	777
2-year
Coefficient	18.509	15.185	10.483
SE	(14.058)	(13.840)	(9.809)
N	1,561	1,570	1,530
3-year
Coefficient	13.824	8.157	2.557
SE	(11.555)	(11.450)	(8.176)
N	2,349	2,360	2,305
4-year
Coefficient	13.682	6.017	3.119
SE	(10.065)	(10.041)	(7.173)
N	3,151	3,164	3,099
5-year
Coefficient	17.754*	10.392	7.784
SE	(9.096)	(9.077)	(6.429)
N	3,937	3,953	3,872
6-year
Coefficient	17.084**	12.003	6.606
SE	(8.356)	(8.322)	(5.923)
N	4,710	4,729	4,633

Notes. RDD estimated using local linear regressions either side of the discontinuity, rectangular kernel.

^*p < 0.10,

^**p < 0.05,

^***p < 0.01.

Table A3.

The Impact of RoSLA on Child Outcomes Throughout Childhood, Parents With Lower Levels of Education, ±3 Year Sample Window

	Fine motor skills (18 and 30 months)	Gross motor skills (18 and 30 months)	IQ, aged 8	Performance IQ, aged 8	Entry Assessment score	Key Stage 1 score	Key Stage 2 score	Key Stage 3 score
RoSLA treatment of mother	−0.246   (0.610)	−0.983   (0.705)	−0.133   (1.253)	0.006   (1.342)	0.283   (0.183)	0.395**   (0.192)	0.926   (0.641)	1.351   (1.045)
RoSLA treatment of father	0.602   (0.680)	−1.517*   (0.785)	0.841   (1.348)	1.201   (1.448)	0.282   (0.227)	0.853***   (0.240)	1.309*   (0.795)	1.961   (1.302)
Mother has A levels, equivalent or higher	1.840**   (0.715)	−1.615*   (0.825)	8.329***   (1.334)	7.697***   (1.430)	0.620**   (0.249)	0.923***   (0.262)	3.166***   (0.858)	5.343***   (1.396)
Father has A levels, equivalent or higher	2.445***   (0.596)	0.416   (0.688)	6.107***   (1.188)	4.653***   (1.272)	0.600***   (0.202)	1.213***   (0.216)	4.181***   (0.696)	7.845***   (1.136)
Mother’s age at child’s birth: pre-window	−0.048   (0.113)	−0.075   (0.130)	0.669***   (0.242)	0.682***   (0.260)	0.074**   (0.037)	0.036   (0.037)	0.189   (0.127)	0.360*   (0.204)
Mother’s age at child’s birth: in window	−0.069   (0.111)	−0.139   (0.128)	0.685***   (0.242)	0.644**   (0.260)	0.079**   (0.035)	0.076**   (0.036)	0.295**   (0.123)	0.524***   (0.198)
Mother’s age at child’s birth: post-window	−0.068   (0.137)	−0.138   (0.158)	0.812***   (0.294)	0.793**   (0.316)	0.098**   (0.044)	0.094**   (0.045)	0.356**   (0.152)	0.661***   (0.246)
Father’s age at child’s birth: pre-window	−0.039   (0.099)	−0.300***   (0.114)	0.038   (0.197)	0.037   (0.212)	0.039   (0.032)	0.086**   (0.035)	0.190*   (0.113)	0.223   (0.190)
Father’s age at child’s birth: in window	−0.028   (0.117)	−0.290**   (0.136)	0.015   (0.234)	0.025   (0.251)	0.058   (0.039)	0.103**   (0.042)	0.260*   (0.135)	0.334   (0.225)
Father’s age at child’s birth: post-window	−0.032   (0.145)	−0.335**   (0.168)	0.060   (0.287)	0.083   (0.308)	0.070   (0.048)	0.128**   (0.052)	0.297*   (0.167)	0.409   (0.279)
R2	0.047	0.029	0.090	0.068	0.250	0.239	0.202	0.234
Observations	2,186	2,185	1,373	1,381	2,008	2,358	2,498	2,285
Outcome mean	81.69	83.91	101.38	97.31	20.48	8.82	82.27	104.17
Outcome SD	10.00	11.44	16.10	17.11	3.27	3.73	12.43	19.70
Treatment % of SD (mum)	−2.46	−8.59	−0.83	0.03	8.65	10.57	7.45	6.86
Treatment % of SD (dad)	6.02	−13.26	5.22	7.02	8.63	22.83	10.53	9.95
Treatment % of SD (both)	3.56	−21.85	4.40	7.05	17.28	33.40	17.98	16.81
Treatment joint significance p-value	0.612	0.066	0.813	0.708	0.154	0.000	0.104	0.155

Notes.

^*p < 0.10,

^**p < 0.05,

^***p < 0.01.

Additional controls included: child gender, month of birth, GCSE cohort, parent foreign qualifications, single mother dummy, father missing info dummy. Child age in months is included as an additional covariate for the early development scores. Child performance IQ included as a control in Entry Assessment and Key Stage test score regressions.

Table A4.

The Impact of RoSLA on Child English/Literacy and Mathematics Outcomes, Parents With Lower Levels of Education, ±3 Year Sample Window

	Entry Assessment literacy	Key Stage 1 literacy score	Key Stage 2 English score	Key Stage 3 English score	English language GCSE	Entry Assessment maths	Key Stage 1 maths score	Key Stage 2 maths score	Key Stage 3 maths score	Maths GCSE
RoSLA treatment of mother	0.120***   (0.045)	0.115*   (0.068)	0.011   (0.257)	0.799   (0.924)	0.665   (0.504)	0.063   (0.062)	0.165**   (0.071)	0.397   (0.264)	0.236   (1.250)	0.973   (0.599)
RoSLA treatment of father	0.111**   (0.056)	0.263***   (0.084)	0.393   (0.319)	1.835   (1.142)	0.966   (0.631)	0.089   (0.077)	0.322***   (0.089)	0.587*   (0.328)	2.093   (1.551)	2.139***   (0.744)
Mother has A levels,equivalent or higher	0.141**   (0.061)	0.311***   (0.092)	1.026***   (0.344)	4.854***   (1.211)	3.303***   (0.669)	0.193**   (0.085)	0.302***   (0.097)	1.006***   (0.353)	3.107*   (1.656)	3.557***   (0.795)
Father has A levels,equivalent or higher	0.149***   (0.050)	0.411***   (0.076)	1.316***   (0.279)	5.489***   (0.995)	2.875***   (0.546)	0.232***   (0.069)	0.407***   (0.080)	1.600***   (0.286)	8.406***   (1.356)	5.083***   (0.649)
Mother’s age at child’s birth: pre-window	0.022**   (0.009)	0.001   (0.013)	0.048   (0.051)	0.310*   (0.183)	0.163   (0.101)	0.020   (0.013)	0.033**   (0.014)	0.080   (0.052)	0.213   (0.243)	0.164   (0.117)
Mother’s age at child’s birth: in window	0.022**   (0.009)	0.017   (0.013)	0.092*   (0.049)	0.433**   (0.178)	0.254***   (0.097)	0.024**   (0.012)	0.041***   (0.013)	0.109**   (0.050)	0.408*   (0.238)	0.328***   (0.115)
Mother’s age at child’s birth: post-window	0.028***   (0.011)	0.021   (0.016)	0.103*   (0.061)	0.504**   (0.219)	0.304**   (0.120)	0.028*   (0.015)	0.051***   (0.017)	0.136**   (0.062)	0.524*   (0.295)	0.399***   (0.142)
Father’s age at child’s birth: pre-window	0.015*   (0.008)	0.023*   (0.012)	0.083*   (0.045)	0.207   (0.165)	0.186**   (0.093)	0.015   (0.011)	0.040***   (0.013)	0.031   (0.047)	0.286   (0.226)	0.161   (0.108)
Father’s age at child’s birth: in window	0.021**   (0.009)	0.027*   (0.015)	0.112**   (0.054)	0.262   (0.196)	0.223**   (0.110)	0.022*   (0.013)	0.050***   (0.015)	0.048   (0.056)	0.371   (0.268)	0.213*   (0.129)
Father’s age at child’s birth: post-window	0.027**   (0.012)	0.034*   (0.018)	0.118*   (0.067)	0.251   (0.242)	0.251*   (0.136)	0.023   (0.016)	0.061***   (0.019)	0.052   (0.069)	0.508   (0.332)	0.229   (0.159)
R2	0.226	0.219	0.171	0.187	0.172	0.214	0.228	0.173	0.109	0.179
Observations	2,007	2,356	2,479	2,119	2,316	2,005	2,353	2,476	2,203	2,313
Outcome mean	4.92	2.85	26.79	44.62	39.69	5.18	3.13	26.84	80.23	37.58
Outcome SD	0.79	1.30	4.87	16.26	9.24	1.09	1.37	5.00	21.43	10.98
Treatment as % of SD (mum only)	15.25	8.83	0.23	4.91	7.20	5.82	11.98	7.93	1.10	8.86
Treatment as % of SD (dad only)	14.12	20.24	8.07	11.28	10.46	8.19	23.44	11.73	9.77	19.48
Treatment as % of SD (both)	29.37	29.08	8.30	16.20	17.65	14.01	35.42	19.66	10.87	28.34
Treatment joint significance p-value	0.005	0.002	0.467	0.205	0.144	0.326	0.000	0.075	0.400	0.006

Notes.

^*p < 0.10,

^**p < 0.05,

^***p < 0.01.

Additional controls included: child gender, month of birth, GCSE cohort, parent foreign qualifications, single mother dummy, father missing info dummy, child performance IQ.

Table A5.

Estimates of the Impact of RoSLA Treatment on Child Key Stage 4 (age 16) Outcomes, Combined Treatment Variable, All and Lower Educated Parents ± 3 Year Sample Window

	All parents			Parents with lower education
	Key Stage 4 score	GCSE Total score	GCSE academic total	Key Stage 4 score	GCSE total score	GCSE academic total
RoSLA treatment (0, 1, 2 parents treated)	18.523*** (4.427)	19.551*** (4.246)	12.178*** (2.914)	25.451*** (6.231)	22.213*** (5.744)	10.210*** (3.780)
Mother has A levels, equivalent or higher				50.976*** (10.328)	64.869*** (9.547)	39.819*** (6.185)
Father has A levels, equivalent or higher				49.551*** (8.293)	61.608*** (7.658)	41.360*** (5.003)
Mother’s age at child’s birth: pre-window	5.945*** (1.130)	6.628*** (1.082)	4.886*** (0.747)	4.571*** (1.488)	4.276*** (1.372)	2.591*** (0.907)
Mother’s age at child’s birth: in window	7.081*** (1.151)	7.552*** (1.101)	5.393*** (0.760)	6.750*** (1.456)	6.332*** (1.340)	3.771*** (0.887)
Mother’s age at child’s birth: post-window	8.087*** (1.391)	8.249*** (1.331)	6.011*** (0.918)	8.194*** (1.759)	7.540*** (1.620)	4.660*** (1.071)
Father’s age at child’s birth: pre-window	1.594 (1.032)	2.129** (0.991)	1.056 (0.679)	1.451 (1.330)	2.269* (1.229)	1.063 (0.802)
Father’s age at child’s birth: in window	2.554** (1.214)	3.271*** (1.166)	1.615** (0.799)	2.308 (1.596)	3.277** (1.474)	1.361 (0.964)
Father’s age at child’s birth: post-window	2.496* (1.492)	3.350** (1.433)	1.524 (0.981)	2.548 (1.946)	4.030** (1.798)	1.661 (1.174)
R2	0.197	0.225	0.247	0.175	0.205	0.235
Observations	4,094	4,116	3,985	2,452	2,467	2,359
Outcome mean	423.76	347.42	235.87	385.52	302.04	205.03
Outcome SD	146.29	143.20	98.07	147.43	138.85	90.97
Treatment as % of SD	12.66	13.65	12.42	17.26	16.00	11.22

Notes.

^*p < 0.10,

^**p < 0.05,

^***p < 0.01.

Additional controls included: child gender, month of birth, GCSE cohort, parent foreign qualifications, single mother dummy, father missing info dummy, child performance IQ.

Table A6.

Estimates of the Impact of RoSLA Treatment on Child Outcomes Throughout Childhood, Combined Treatment Variable ± 3 Year Sample Window

	Fine motor skills (18 and 30 months)	Gross motor skills (18 and 30 months)	IQ, aged 8	Performance IQ, aged 8	Entry Assessment score	Key Stage 1 score	Key Stage 2 score	Key Stage 3 score
RoSLA treatment (0, 1, 2 parents treated)	0.172 (0.297)	−0.853** (0.348)	0.479 (0.634)	0.630 (0.658)	0.317*** (0.107)	0.449*** (0.111)	1.280*** (0.349)	1.964*** (0.619)
Mother’s age at child’s birth: pre-window	0.011 (0.075)	−0.197** (0.088)	0.738*** (0.169)	0.666*** (0.176)	0.092*** (0.028)	0.093*** (0.028)	0.441*** (0.089)	0.659*** (0.156)
Mother’s age at child’s birth: in window	0.019 (0.078)	−0.169* (0.091)	0.830*** (0.177)	0.769*** (0.184)	0.103*** (0.027)	0.104*** (0.028)	0.519*** (0.091)	0.758*** (0.158)
Mother’s age at child’s birth: post-window	0.034 (0.094)	−0.183* (0.110)	0.854*** (0.212)	0.838*** (0.220)	0.128*** (0.033)	0.125*** (0.034)	0.581*** (0.110)	0.853*** (0.192)
Father’s age at child’s birth: pre-window	−0.066 (0.067)	−0.236*** (0.078)	0.114 (0.142)	0.093 (0.148)	0.049** (0.025)	0.069*** (0.026)	0.192** (0.080)	0.298** (0.142)
Father’s age at child’s birth: in window	−0.063 (0.079)	−0.268*** (0.092)	0.203 (0.167)	0.168 (0.173)	0.065** (0.029)	0.085*** (0.031)	0.281*** (0.094)	0.452*** (0.168)
Father’s age at child’s birth: post-window	−0.087 (0.096)	−0.293*** (0.113)	0.166 (0.203)	0.154 (0.211)	0.075** (0.036)	0.095** (0.038)	0.304*** (0.115)	0.474** (0.206)
R2	0.037	0.013	0.056	0.039	0.280	0.274	0.242	0.267
Observations	4,209	4,208	2,877	2,886	3,123	3,791	4,253	3,639
Outcome mean	82.64	83.59	106.66	101.22	21.15	9.68	85.73	109.81
Outcome SD	9.42	10.91	16.62	17.13	3.29	3.74	12.13	20.13
Treatment as % of SD	1.82	−7.82	2.88	3.68	9.64	11.99	10.55	9.76

Notes.

^*p < 0.10,

^**p < 0.05,

^***p < 0.01.

Additional controls included: child gender, month of birth, GCSE cohort, parent foreign qualifications, single mother dummy, father missing info dummy. Child age in months is included as an additional covariate for the early development scores. Child performance IQ included as a control in Entry Assessment and Key Stage test score regressions.

Table A7.

Estimates of the Impact of RoSLA Treatment on Child Outcomes Throughout Childhood, Combined Treatment Variable, Lower Educated Parents ± 3 Year Sample Window

	Fine motor skills (18 and 30 months)	Gross motor skills (18 and 30 months)	IQ, aged 8	Performance IQ, aged 8	Entry Assessment score	Key Stage 1 score	Key Stage 2 score	Key Stage 3 score
RoSLA treatment (0, 1, 2 parents treated)	0.130 (0.464)	−1.220** (0.536)	0.315 (0.955)	0.554 (1.024)	0.282* (0.146)	0.573*** (0.153)	1.074** (0.513)	1.586* (0.837)
Mother has A levels, equivalent or higher	1.975*** (0.700)	−1.700** (0.808)	8.487*** (1.302)	7.889*** (1.398)	0.620** (0.245)	0.989*** (0.258)	3.223*** (0.845)	5.435*** (1.375)
Father has A levels, equivalent or higher	2.319*** (0.581)	0.496 (0.670)	5.950*** (1.153)	4.462*** (1.235)	0.600*** (0.197)	1.141*** (0.211)	4.120*** (0.678)	7.750*** (1.108)
Mother’s age at child’s birth: pre-window	−0.023 (0.109)	−0.090 (0.126)	0.701*** (0.235)	0.721*** (0.252)	0.074** (0.036)	0.049 (0.037)	0.200 (0.123)	0.377* (0.198)
Mother’s age at child’s birth: in window	−0.045 (0.108)	−0.154 (0.125)	0.717*** (0.235)	0.683*** (0.253)	0.079** (0.034)	0.089** (0.035)	0.306** (0.119)	0.541*** (0.194)
Mother’s age at child’s birth: post-window	−0.028 (0.130)	−0.164 (0.150)	0.863*** (0.280)	0.855*** (0.300)	0.098** (0.041)	0.115*** (0.042)	0.375*** (0.144)	0.689*** (0.234)
Father’s age at child’s birth: pre-window	−0.070 (0.093)	−0.281*** (0.108)	0.005 (0.188)	−0.004 (0.201)	0.039 (0.030)	0.067** (0.033)	0.175* (0.106)	0.198 (0.177)
Father’s age at child’s birth: in window	−0.061 (0.112)	−0.269** (0.129)	−0.022 (0.225)	−0.021 (0.241)	0.058 (0.036)	0.082** (0.039)	0.243* (0.128)	0.306 (0.212)
Father’s age at child’s birth: post-window	−0.079 (0.137)	−0.306* (0.158)	0.009 (0.271)	0.019 (0.291)	0.070 (0.045)	0.099** (0.048)	0.274* (0.156)	0.370 (0.259)
R2	0.046	0.029	0.089	0.067	0.250	0.239	0.202	0.234
Observations	2,186	2,185	1,373	1,381	2,008	2,358	2,498	2,285
Outcome mean	81.69	83.91	101.38	97.31	20.48	8.82	82.27	104.17
Outcome SD	10.00	11.44	16.10	17.11	3.27	3.73	12.43	19.70
Treatment as % of SD	1.30	−10.66	1.96	3.24	8.64	15.33	8.64	8.05

Notes.

^*p < 0.10,

^**p < 0.05,

^***p < 0.01.

Additional controls included: child gender, month of birth, GCSE cohort, parent foreign qualifications, single mother dummy, father missing info dummy. Child age in months is included as an additional covariate for the early development scores. Child performance IQ included as a control in Entry Assessment and Key Stage test score regressions.

Table A8.

National Vocational Qualifications Equivalent Qualifications Classification

NVQ equivalent	Academic qualification
Level 0	No nationally recognised academic qualifications
Level 1	CSE below grade 1, GCSE below grade C
Level 2	CSE grade 1, O-levels, GCSE grade A–C
Level 3	A-levels, A/S levels, SCE Higher, Scottish certificate of sixth year studies, international baccalaureate
Level 4	First/foundation degree, other degree, diploma in higher education
Level 5	Higher degree

Fig. A1.

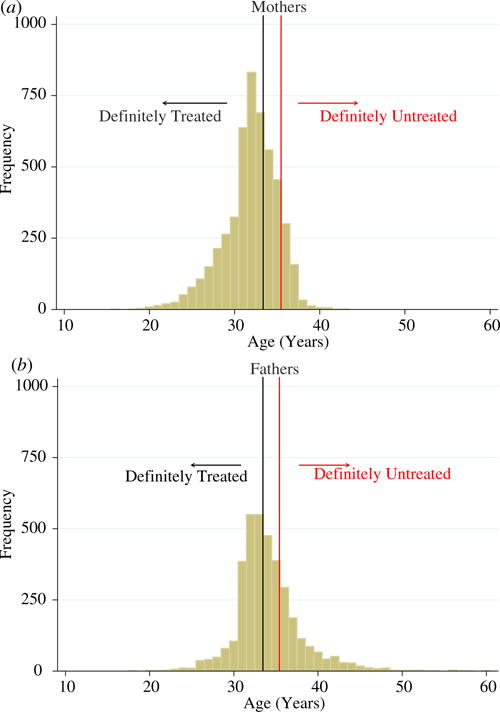
Age of Parent at Child’s Birth and Mapping to RoSLA Treatment Status, by Parent

Fig. A2. Balancing Tests – Mother’s Fertility Characteristics.

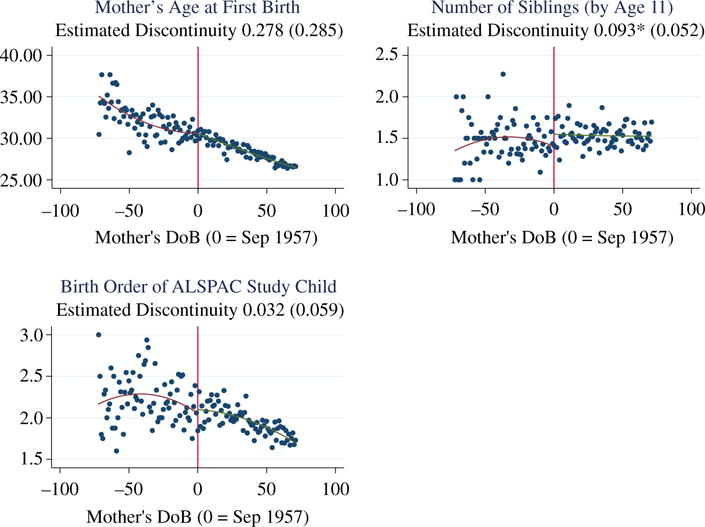
Notes. *p < 0.10, **p < 0.05, ***p < 0.01.

Fig. A3.

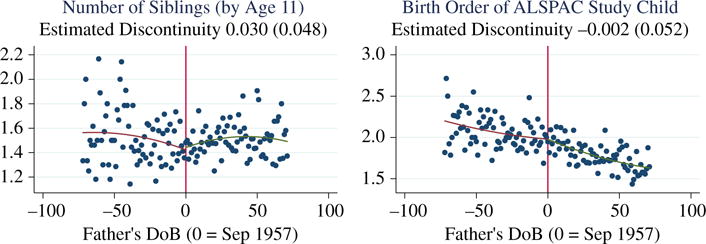
Balancing Tests – Father’s Fertility Characteristics

Fig. A4.

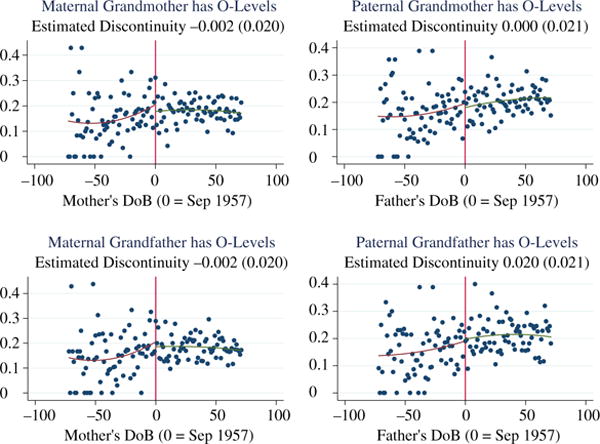
Balancing Tests – Grandparent Education

Fig. A5. Balancing Tests – Parental Relationship Characteristics.

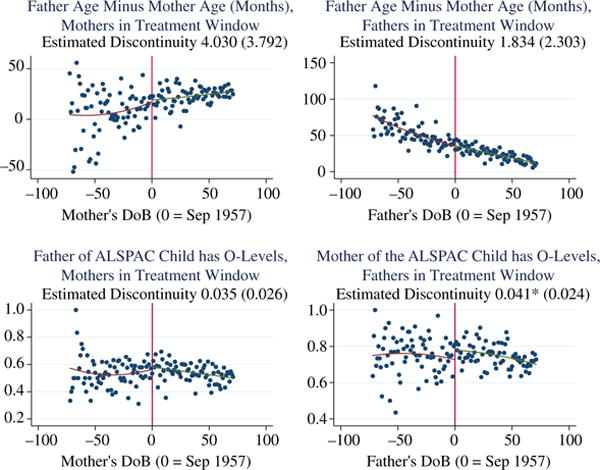
Notes. *p < 0.10, **p < 0.05, ***p < 0.01.

Fig. A6.

Balancing Tests – Parental Relationship Characteristics and Information Availability

Appendix B

Avon Longitudinal Study of Parents and Children

Data S1.