Abstract
The concept of a “power stroke”—a free-energy releasing conformational change—appears in almost every textbook that deals with the molecular details of muscle, the flagellar rotor, and many other biomolecular machines. Here, it is shown by using the constraints of microscopic reversibility that the power stroke model is incorrect as an explanation of how chemical energy is used by a molecular machine to do mechanical work. Instead, chemically driven molecular machines operating under thermodynamic constraints imposed by the reactant and product concentrations in the bulk function as information ratchets in which the directionality and stopping torque or stopping force are controlled entirely by the gating of the chemical reaction that provides the fuel for the machine. The gating of the chemical free energy occurs through chemical state dependent conformational changes of the molecular machine that, in turn, are capable of generating directional mechanical motions. In strong contrast to this general conclusion for molecular machines driven by catalysis of a chemical reaction, a power stroke may be (and often is) an essential component for a molecular machine driven by external modulation of pH or redox potential or by light. This difference between optical and chemical driving properties arises from the fundamental symmetry difference between the physics of optical processes, governed by the Bose–Einstein relations, and the constraints of microscopic reversibility for thermally activated processes.
Keywords: Brownian motors, energy landscapes information ratchet, microscopic reversibility, molecular machines
Graphical Abstract
1. Introduction
One of the most important features of a living system is its ability to harvest energy from the environment to do work and to form structure. These tasks are accomplished in biological systems by molecular machines such as myosin and kinesin,[1,2] the FoF1 ATP synthase,[3] the bacterial flagellar motor,[4] the ribosome,[5] and various DNA and RNA processing enzymes,[6] among many others. Recent work has described great progress in accomplishing the synthetic imitation of some of these remarkable devices.[7–13] At first glance, it would seem that a physical theory for molecular machines must be extremely complicated and requires a strong focus on the fact that the chemical driving forces that provide the energy to fuel the machines are very far from thermodynamic equilibrium.[14] In fact, however, the “physics” of a chemically driven molecular machine—its equation of motion—is very simple:[15]
| (1) |
In Equation (1), r⃗ is the vector comprising the relevant degrees of freedom of the machine, γ is the coefficient of viscous friction, f⃗(t) is random thermal noise, the components of which are given by independent normalized Gaussian distributions, and −∇U(r⃗) is the force due to the gradient of a single, time-independent, potential energy surface, U(r⃗).
Equation (1) reflects an important assumption about the regime of motion in which a molecular machine carries out its function, that is, the assumption that the velocity (NOT acceleration) of each relevant degree of freedom is proportional to the force that causes it. This is the regime in which Onsager derived his reciprocal relations,[16] and is also the regime in which the Onsager–Machlup thermodynamic action theory[17] is valid. The inertial force is very small (negligible) in comparison to the viscous drag force , and hence does not appear in Equation (1). This regime of motion was explored beautifully by Purcell in his paper “Life at Low Reynold’s Number”.[18] The effect of the solvent is modelled in terms of the viscous drag coefficient, γ, and thermal noise, , with a fluctuation dissipation relation between the viscous drag coefficient and the amplitude of thermal noise, γD = kBT. All energies in this paper are given in units of the thermal energy kBT, where kB is Boltzmann’s constant and T is the Kelvin temperature.
It is important to note that Equation (1) describes a mechanical equilibrium theory—the average net force is zero, , about which there is Gaussian distributed thermal noise f⃗(t). All of the information about how the structure relates to the mechanism is contained in the energy function U(r⃗). In the zero noise limit, the system would inexorably find a local energy minimum and remain there forever. The transitions between minima that are necessary for the molecular machine to carry out its function require thermal noise, and hence all chemically driven molecular machines in water, the functions of which are described by Equation (1), are properly termed “Brownian Motors”.[19–21]
The Langevin equation [Eq. (1)] expresses completely the “physics” of a chemically driven molecular machine. Many authors, however, seem to be looking for a description in terms of classical mechanics,[6] and this is what cannot be given, for the simple reason that the problem of mechano-chemical coupling by an enzyme is NOT a problem of classical mechanics. It makes almost as little sense to seek a mechanical description of the coupling between a chemical reaction and the motion of a molecular machine in water as it does to seek a mechanical description of the diffraction of an electron. Quantum mechanics is of course fundamentally not mechanical but rather probabilistic, whereas the thermodynamics and kinetics of molecular machines are only practically probabilistic rather than mechanical. In a full molecular dynamics simulation involving all degrees of freedom of both the protein and of the molecules in the solution, the dynamics would be described by Newton’s equations of motion in which acceleration and not velocity appear, but the impracticality of a classical mechanical description in terms of Newton’s equations (or Lagrange’s or Hamilton’s) is overwhelming. There are 1018–1020 collisions[22] each second between water molecules and a molecular machine like myosin, the flagellar motor, or kinesin, and any attempt to model the system in terms of Newton’s equations for longer than a few picoseconds is doomed to failure.
The principle of microscopic reversibility[23] provides a solid foundation for development of a thermodynamic theory for molecular machines. For an over-damped system described by Equation (1), Bier et al.[24] used the Onsager–Machlup thermodynamic action theory[17] to derive Equation (2):
| (2) |
for motion on a potential energy surface U(r⃗) where r⃗′ and r⃗″ are two arbitrary points. Both the numerator and the denominator on the left hand side of Equation (2) depend on the path r(t) and on the interval tf, and is a state function that depends only on the difference in the energies of the initial and final states and on the temperature, which is subsumed in our energy units kBT. The ration in the third identity has been enclosed in brackets as only the ratio makes sense—the notation P(r′ → r″) alone makes little sense without specification of r(t)and of tf Because the ratio is a state function, the identity holds also for the ratio of the integrals of the numerator and denominator over all r(t)and tf. Note that Equation (2) can also be very easily derived by using the principle of detailed balance at equilibrium. Although this derivation uses knowledge of the behavior of the system at equilibrium, Equation (2) itself, while requiring mechanical equilibrium, holds arbitrarily far from thermodynamic equilibrium.[25]
Although the physics and physical chemistry of chemically driven molecular machines are actually quite simple, the mechanism by which these tiny machines work is contrary to our macroscopic experience, to the way light-driven molecular machines are shown to work, and to expectations based on experimental responses following external changes in the environment. It is the deviation from what we perceive to be “common sense”, and even from what seems to be supported by experimental observation, that leads to much confusion in the literature. To firm up the understanding of what Equations (1) and (2) tell us about the mechanism of molecular motors and rotors, let us consider a specific example involving recent computational work on the F1 ATPase, a component of the FoF1 ATP synthase found in the mitochondria. This molecular machine uses a proton electrochemical gradient to provide the energy for synthesis of ATP, the major storage form of chemical energy in a cell.[3]
2. F1 ATPase, an ATP-Driven Molecular Rotor
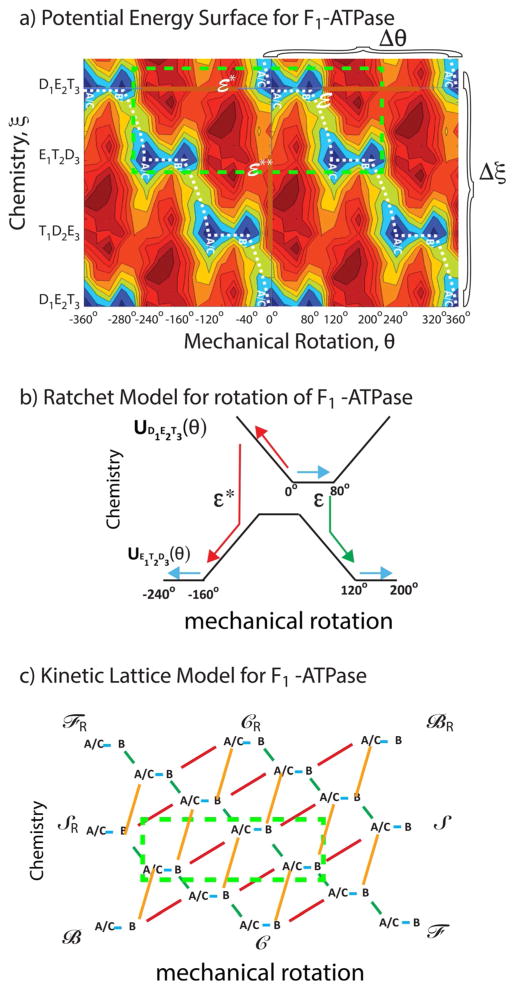
In principle, there may be many degrees of freedom incorporated in the vector r⃗ in Equation (1), but as Bier and Astumian,[26] and contemporaneously Marcello Magnasco,[27] suggested (see also ref. [28]), and as elaborated by Keller and Bustamante,[29] the problem often reduces to coupling between only two effective coordinates: one describing the mechanical motion—rotation in the cases of the F1 ATPase and the bacterial flagellar motor, or translation in the cases of kinesin, myosin V, and other molecular walkers; and one describing the chemical reaction—proton transport or ATP hydrolysis. For the purposes of this discussion, let us consider a mechanical coordinate θ and a chemical coordinate ξ such that r⃗(t) = (θ(t), ξ(t))T, where superscript T denotes transpose. This approach is well illustrated by recent work on the F1 ATPase[30] where Mukherjee and Warshel have computationally investigated the energy of F1 ATPase in many of its possible rotational and chemical state dependent conformations. Their key result is shown in the potential energy landscape in Figure 1a, where the horizontal axis represents mechanical rotation of F1 ATPase, and the vertical axis represents the transitions between the different chemical states.
Figure 1.
a) Energy landscape for the F1 ATPase from the work of Warshel and Mukherjee.[30] The fundamental periods Δξ and Δθ for which U(ξ, θ)=U(ξ ± iΔξ, θ ± jΔθ) with i,j = any integers, are shown. b) A “ratchet” representation in terms of two 1D energy profiles with transitions between them for the two chemical states D1E2T3 and E1T2D3 from −240° to +200° (the area enclosed in the bright green dashed box in Figure 1a). The remarkable and salient point is that the mechanism shown by the green arrows (clockwise rotation of 120°) seems by common sense to be far more likely than that shown by the red arrows (counterclockwise rotation by 160°), but, in fact, if ε*=ε these two processes are equally likely, and if ε*<ε counterclockwise rotation (red path) is more likely than clockwise rotation (green path). c) A kinetic lattice model describing the potential energy landscape, where green indicates transition over the barrier (saddle point) ε and red indicates transition over the energy barrier (saddle point) ε*. The dashed box illustrates the part of the kinetic lattice corresponding to the region enclosed in the bright green box in Figure 1a. Four different cycles and their microscopic reverses can be identified, ℱ/ℱR in which clockwise rotation is coupled to ATP hydrolysis, ℬ/ℬR in which counterclockwise rotation is coupled to ATP hydrolysis, 𝒮/𝒮R (slip) in which rotation occurs uncoupled to chemistry, and 𝒞/𝒞R (futile cycling) in which chemistry occurs uncoupled to roation.
The energy surface shown in Figure 1a is an equilibrium picture of the system—there is no net tilt along either the chemical or the mechanical coordinate. Even so, the landscape tells us much of what we need to know about the coupling. The deep zigzag energy valley in blue for the wells (states) and green for the saddle points (transition states) is the hallmark signature of a Brownian motor.[28] This pattern shows that under circumstances where it is more likely to bind ATP and release ADP and Pi (Pi = inorganic phosphate) than it is to bind ADP and Pi and release ATP (i.e., where the chemical potential of ATP is higher than that of ADP and Pi) there will be net clockwise (positive) rotation in the absence of an applied torque. The most probable pathway through this energy landscape, indicated by the white dashed line, is a clear visual indication of the coupling, even without explicitly including the chemical free energy released during the process. The motion on this two dimensional energy landscape can be described using the Langevin equation, Equation (1), where boundary conditions incorporate the effect of having ATP in excess and ADP in deficit of their equilibrium amounts.
The mechanism can also be viewed in several other ways. In Figure 1b the energy profiles for two chemical states, D1E2T3 and E1T2D3, are shown schematically as a function of the rotational angle between −240° and + 200° with chemical transitions between the two states. This is a typical “ratchet” model in which mechanical motion is described along the horizontal axis and the effect of chemistry is modeled in terms of transitions between these horizontal energy landscapes for the mechanical motion. The behavior of the system can be modeled based on this description by reaction–diffusion equations. In early descriptions using this approach, the constants describing the transition rates between the potentials were assigned in consistency with the principle of microscopic reversibility.[28,31] Unfortunately many subsequent authors have adopted similar approaches but where the transition constants are assigned in a way unconstrained by microscopic reversibility, resulting in extremely misleading and incorrect interpretations.
One can also model the molecular machine in terms of a random walk on a lattice of states as shown in Figure 1c. Two periods of the kinetic lattice model representing the energy minima as states (A/C, B) and the saddle points as transitions—red for those involving the energy barrier (saddle point) ε*, green for those involving the energy barrier ε, and orange for those involving the energy barrier ε**—are shown on the right. The motion of the motor can be described as a random walk on this lattice of states.[28] Downward transitions are strongly favored when ATP is in excess and ADP is in deficit of their equilibrium amounts, but the most probable downward transition is determined by the relative barrier heights. As with the reaction–diffusion approach, applying the constraints of microscopic reversibility assures consistency with the underlying model governed by Equation (1).
It is not useful to describe the effect of a chemical gradient in terms of a tilt along the vertical axis in Figure 1a when one attempts to understand the microscopic picture of the binding, release, and chemical processes and how they relate to the conformational changes, although such phenomenological models could offer heuristic insight in comprehending the mechanism. Binding of a ligand such as ATP is purely local. The chemical potentials of ATP, ADP, and Pi in the bulk do not influence in any way the internal energies of the protein (although they influence the free energy of the overall state). In reaction–diffusion or kinetic models, the effect of concentration is handled consistently by allowing the rates of processes in which ATP, ADP, or Pi are bound to be proportional to the concentrations (or more correctly, activities) of [ATP], [ADP], or [Pi], respectively. The best description of the effect of the chemical potential difference, , between reactant and product is the phrase “mass action” as used by Guldberg and Waage[32] in the second half of the 19th century. It is perhaps a bit more sensible to describe the effect of an applied torque as a tilt between the initial and final point of the mechanical coordinate, θ, once the chemical potential is added[33,43] but the torque will influence both the net tilt, and also distort the local features (e.g., well and saddle point energies) of the energy surface.
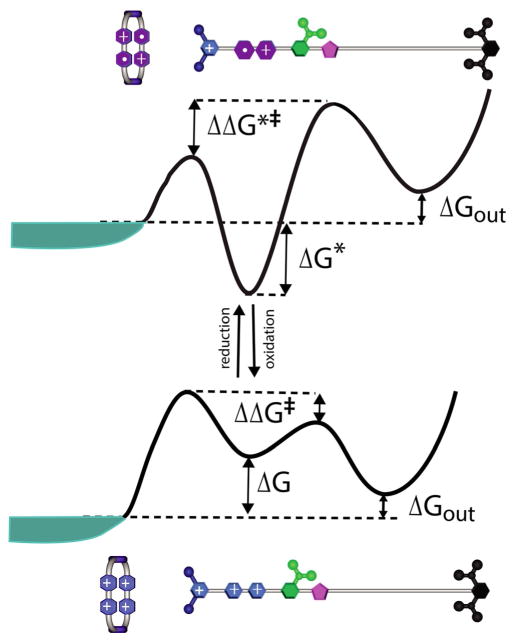
It is possible to get useful insight into the applied torque or the applied force against which the motor can do work by adding the chemistry (free energy in the standard state plus the concentration effect, which is equivalent to the chemical potential) to the conformational free energy profile to model the action of the motor[30,33–35] in the presence of ATP in excess of its equilibrium amount. In this representation, the effect of concentration appears as a reduction of the state energies and also of the effective activation barrier when going from an unbound state to a bound state along the functional pathway (see Figure 4). This approach allows for Monte Carlo or Langevin dynamics simulations on the simplified functional surface, thus eliminating the need for simulations with many particles.[36]
Figure 4.
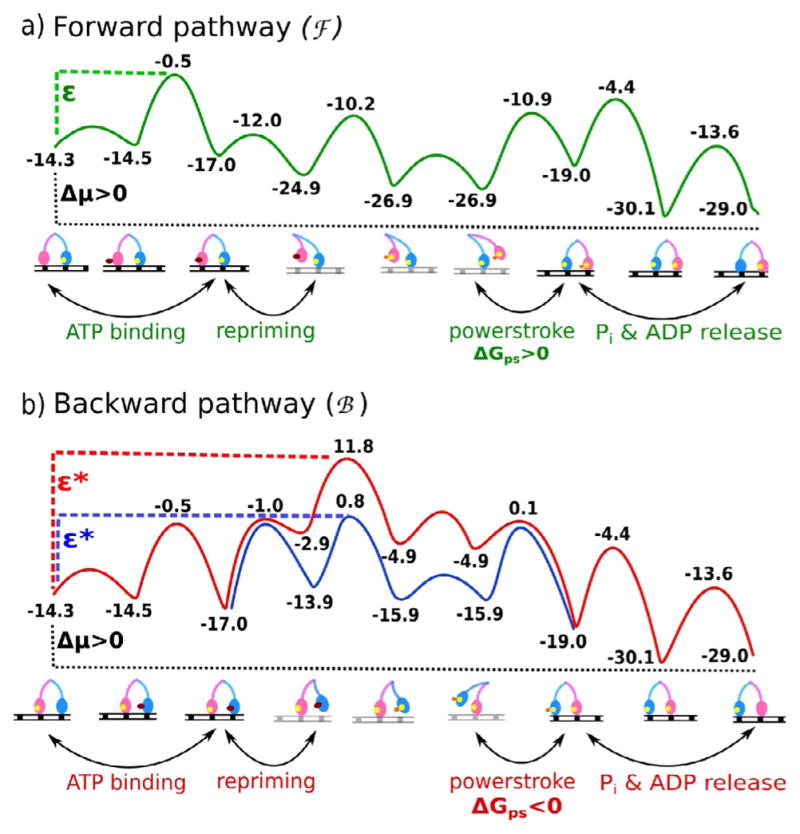
Energy profiles for the a) forward functional (plus end directed) pathway (green curve) and b) the backward (minus end directed) pathway (red or blue curves) for two-headed myosin V walking on actin are shown (adapted from ref. [35]). The computational results suggest that the “power stroke” in the forward pathway is endergonic (ΔGps>0), whereas that in the backward pathway is exergonic (ΔGps<0). The forward pathway nevertheless is strongly preferred over the backward pathway because the highest activation barrier in the backward path is much higher than the highest barrier in the forward pathway (green compared with red curve), Δε=ε−ε*. Even when one considers that the energetically costly conformational change in one leg of myosin V is compensated completely by the downhill conformational change in the other leg, still the system goes through the blue curve where ε*>ε, although Δε is much lower than that for the red curve. It should be noted that a complete and simultaneous compensation of the conformational changes in the two legs is unlikely to occur and myosin V most likely adopts a much high energy pathway for back stepping (i.e., red curve).
We can also circumvent the necessity of considering many of the local details of energy coupling by focusing on how the energy surface relates to complete cycles of the machine[37] in which some number of ATPs are hydrolyzed/synthesized, and the motor makes some number of complete rotations in the clockwise/counterclockwise direction.
3. Non-Equilibrium Thermodynamics of Molecular Machines
In every completion of a random walk from (θ +iΔθ, ξ + jΔξ) to [θ + (i + 1)Δθ, ξ + (j + 1)Δξ], the F1 ATPase undergoes a +Δθ (clockwise) rotation and hydrolyses three ATPs (i.e., completes a step on the chemical axis of Δξ). This process is labeled ℱ. In the reverse process, (θ + iΔθ, ξ + jΔξ) to [θ + (i − 1)Δθ, ξ + (j − 1)Δξ], termed ℱR, the F1 ATPase undergoes a −Δθ (counterclockwise) rotation and synthesizes three ATPs. In every completion of a walk from (θ + iΔθ, ξ + jΔξ) to [θ + (i − 1)Δθ, ξ + (j + 1)Δξ], the F1 ATPase undergoes a −Δθ (counterclockwise) rotation and hydrolyses three ATPs. This process is labeled backward, ℬ. In the reverse (completion of a walk from (θ + iΔθ, ξ + jΔξ) to [θ + (i + 1)Δθ, ξ + (j − 1)Δξ]), termed ℬR, the F1 ATPase undergoes a +Δθ (clockwise) rotation and synthesizes three ATPs. There are also processes involving uncoupled ATP hydrolysis (futile cycling, 𝒞/𝒞R) and processes involving rotation without ATP hydrolysis/synthesis (slip, 𝒮/𝒮R). These possibilities are illustrated explicitly in the kinetic lattice model of Figure 1c.
The ratio of the probability for any process and its microscopic reverse is a thermodynamic identity. For the complete cycles shown in Figure 1b these identities can be written as Equation (3):[37]
| (3) |
where the “generalized thermodynamic forces” for the F1 ATPase, Xθ = 𝒯Δθ and Xξ = 3Δμ, are the mechanical work and chemical work done in moving a period Δθ and Δξ, respectively, and where 𝒯 represents the applied torque. Under physiological conditions for hydrolysis of ATP Δμ≈70 kJ mol−1. The relative likelihood for ATP to bind and for ADP and Pi to dissociate versus the likelihood for ADP and Pi to bind and ATP to dissociate—that is, the effect of Δμ on the process—is incorporated in the factor eXξ appearing in both ratios Pℬ/PℬR and Pℱ/PℱR. The net probability for completion of a clockwise rotation, PΔθ,net, and for ATP hydrolysis, PATP,net, are given by Equations (4a) and (4b):
| (4a) |
| (4b) |
Using Equations (3), and recognizing that the currents (fluxes) can be written as the products of the net probabilities and a common inverse time constant, τ−1, we get Equations (5a) and (5b):
| (5a) |
| (5b) |
where Jθ and Jξ are the currents in units of steps of angle Δθ per unit time and stoichiometric conversions (ATPs hydrolyzed) per unit time, respectively. The controlling factor for the coupled transport is the ratio Pℬ/Pℱ = q eXθ, where q ≈ eΔε/kBT is governed solely by the difference in activation barriers for the ℬ and ℱ paths. The four paths Pℬ, PℬR, Pℱ, and PℱR are related by symmetry[38] and determine completely the terms labeled “coupled transport”. Plots of the fluxes normalized by the flux at zero applied torque are shown in Figure 2.
Figure 2.
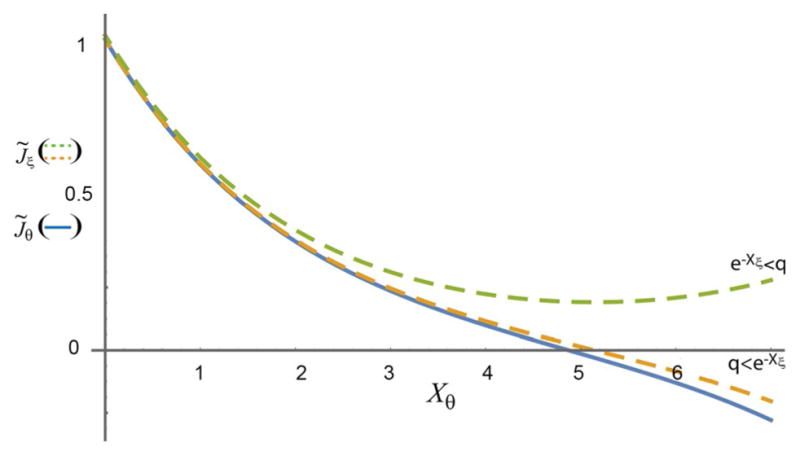
Plots of the coupled transport terms in Equation (5a) (solid blue line) and Equation (5b) (dashed lines) are shown for q = e−7 and e−Xξ = e−5 (dashed green curve) and q = e−5 and e−Xξ = e−7 (dashed orange curve) with .
When e−Xξ ≫ q, the system is under thermodynamic control. Forcing the motor backwards by an applied torque causes the motor to move over the low barriers, but in the reverse direction, resulting in synthesis of ATP. This regime, also known as tight coupling, is the regime that is often considered in literature on the thermodynamics of molecular machines, and seems to be the case for the F1 ATPase.
When e−Xξ ≪ q, the system is under kinetic control. In this case, forcing the motor backward by an applied torque causes a transition over the higher barriers to carry out increased ATP hydrolysis. This possibility was pointed out by Bier and Astumian[28] and given experimental support by Nishiyama, Higuchi, and Yanagida[39] and by Carter and Cross[40] for kinesin in particular.
3.1. Response of a Molecular Machine to External Load
Equation (5a) can be rewritten in a very simple form as Equation (6):
| (6) |
where r0 is given by Equation (7):
| (7) |
The term r0eXθ is the ratio of backward/counterclockwise (Pℬ + PℱR + P𝒮R) to forward/clockwise (Pℱ + PℬR + P𝒮) steps/rotations and C = τ−1(Pℱ + PℬR + P𝒮) is a kinetic pre-factor. Taking a simple Boltzmann expression, C = C0 ea Xθ, Equation (6) can be cast in dimensionless form as Equation (8):
| (8) |
where X̃θ is the generalized mechanical “force” normalized by the stopping force (the force at which r0eXθ = 1), and J̃θ is the flux normalized by the flux evaluated with Xθ = 0. The normalized flux, J̃θ, is shown as a function of X̃θ for several values of “a”.
As a point of comparison, the hyperbolic expression J̃θ = K(1 − X̃θ)/(K + X̃θ) proposed by Hill[41] to model the shortening force versus velocity curves for muscle is shown as a dashed curve in Figure 3.
Figure 3.
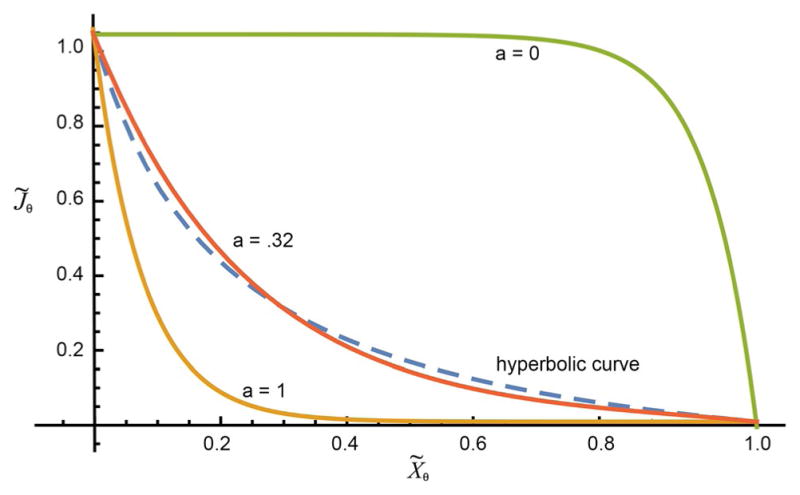
Plots of Equation (7) (solid curves) with r0 = e−13 for three different values of a. The hyperbolic curve J̃θ = K(1 − X̃θ)/(K + X̃θ) proposed by Hill, with K = 0.2 as used by Hill to fit experimental data obtained for the force versus velocity curve of muscle, is shown as the dashed blue curve.
A simple mathematical analysis of Andrew Huxley’s early mechanistic model of muscle[42] can be cast into the hyperbolic form proposed as a phenomenological fit to the data. However, when we analyze Huxley’s model,[42] taking rate constants that are consistent with microscopic reversibility, the result is of the form of Equation (8)[43] and not of the hyperbolic form of Hill.[41]
3.2. Rethinking the Terms “Torque Generation” and “Force Generation”
When we say that Joseph Priestly was the first chemist to generate oxygen we mean that he could bottle it, stopper the bottle, and send the bottled oxygen to other labs. The use of the term energy generation is similarly meaningful, the storage form of energy being potential energy. There is, however, no equivalent potential torque or force. It is neither possible to store, nor to produce and consume torque, and it is certainly not correct to describe torque or force as a “product of a reaction”.[44]
In a recent paper on the FoF1 ATP synthase, Mukherjee and Warshel[45] referred to the “experimentally observed torque”, which essentially implies the torque inferred from the experimentally observed rotational motion, and not torque as a direct observable of the single molecule experiments. The imprecision of the phrase highlights an important difference between the macroscopic world of our experience and the molecular world in which even large macromolecular complexes such as the flagellar motor, actinomyosin (muscle), and FoF1 ATP synthase carry out their functions. If a macroscopic, or even a mesoscopic, object is observed to undergo persistent rotation, the inference that there is an underlying mechanical torque causing the rotation is absolutely secure. On the other hand, in the microscopic world, gating, as in the original presentation of an information ratchet,[46,47] can lead to persistent rotational motion even if the mechanical torque along the reaction path, , is zero or negative.
It is tempting to characterize molecular rotors according to whether there is or is not a local mechanical torque as the rotor moves, but this distinction leads to confusion. On the energy scale of the coarse-grained molecular landscape of F1 ATPase shown in Figure 1a, UA/C is comparable to UB, but the direction of motion does not depend on whether UA/C > UB or UB > UA/C (or in general, on the relative energies of any of the states—the energy minima—of the system). With UA/C > UB, we could perhaps seemingly justify words such as “deposition of chemical energy results in lifting the system energetically from B to the pre-power stroke state A/C from which the system executes the power stroke A/C→B, thereby generating torque and causing rotation”. However, when UB > UA/C, the mechanism remains fundamentally the same, but transitions along the mechanical coordinate are predominately energetically uphill. Irrespective of whether UA/C > UB or UB > UA/C the mechanism by which rotational motion occurs is that of an information ratchet[45,46] where ATP binding/release is fast, and ADP binding/release is slow at some values of θ and ATP binding/release is slow, and ADP binding/release is fast at other values of θ. This gating, combined with ever-present thermal noise, is sufficient to drive the experimentally observed rotation. For chemical driving, the mechanical torque on the equilibrium potential is simply irrelevant for determining the direction, stopping force, and maximal efficiency of the motor. It should be additionally noted that gaining a thermodynamically robust understanding of the directionality or gating mechanism of molecular motors is not possible through the application of external forces or torque, as adopted by many as a preferred route to perform forced-molecular dynamics simulations of biological systems. Investigations of the relaxations of a deterministic elastic network model following sudden changes of the constraints applied to atoms at the active site or to those involved in allosteric conformational changes of a protein are similarly unhelpful with regard to understanding the thermodynamics of mechano-chemical coupling by a molecular machine. Conversely, our analysis shows that by revealing the underlying nature of the relative energies of the various possible pathways, that is, by constructing a detailed free-energy surface for the most relevant mechanical and chemical degrees of freedom, one can proceed towards a holistic understanding.
Using the example of F1 ATPase and Figure 1a, we see that the direction of motion is independent of the energies of the states (minima on the energy landscape); so what feature of the energy landscape actually controls the direction of motion? Using our mind’s eye, we see that the transformation ε* ↔ ε, which switches between red and geen in the kinetic lattice picture, does, in a visually clear way, change the sense of rotation—the minimum energy zigzag valley runs between the lower left and upper right hand corners when ε* < ε. Thus, we conclude that the directionality is controlled by the relative energies of the barriers and not by the energies of the states. Another recent study has revealed the molecular origins of ε and ε*, showing that mutations of certain parts of the F1 ATPase rotary subunit can lead to the destruction of the zigzag path by effectively putting ε≈ε*. This leads to systems where the mechanical rotation is uncoupled from the chemical steps, thereby generating a futile molecular motor incapable of showing directional motions powered by ATP hydrolysis.[45]
3.3. Mechano-Chemical Coupling—An Overview
The single parameter describing mechano-chemical coupling is q ≈ eΔε/kBT where Δε is the difference in activation energy for a “functional” forward process, ℱ, in which substrate is converted to product concomitant with a forward step, and a backward process, ℬ, in which substrate is converted to product concomitant with a backward step. A more precise expression as the exponential of the difference of the Onsager–Machlup thermodynamic actions can be calculated from the equilibrium energy landscape, with arbitrary stoichiometry,[38] but in the simplest case (such as that shown in Figure 1a) the processes are controlled by single rate-limiting barriers so Δε is very easily defined. At equilibrium, of course, completion of a forward cycle ℱ is exactly as likely as completion of its microscopic reverse ℱR, and completion of a backward cycle ℬ is as likely as completion of its microscopic reverse ℬR so there is no net transport, in consistency with the second law of thermodynamics. Away from chemical equilibrium, however, ℱ is more likely than ℱR, and ℬ is more likely than ℬR. In this case, the structural bias by which ℱ is more likely than ℬ comes to the forefront and we have net clockwise rotation powered by hydrolysis of ATP.
As an example of this perspective, consider the recent computational model for the overall functional cycle of myosin V.[34] The authors show that the free energy of the pre-“power stroke” state is 11 kCal mol−1 lower than the post-“power stroke” state for the forward functional cycle (ℱ) of myosin V in which an ATP is hydrolyzed and myosin moves one step toward the “plus” end of actin—energy is absorbed, not released in the process termed the “power stroke”. In the backward, non-functional cycle (ℬ) in which an ATP is hydrolyzed and the myosin moves one step toward the “minus” end of actin, the free energy of the pre-“power stroke” state is 15 kCal mol−1 (or by a different pathway 3 kCal mol−1) higher in energy than the post-“power stroke”—energy is released in the step labelled “power stroke” in the backward non-functional cycle. Thus, according to a power stroke model, myosin V should move toward the “minus” end of actin, but in fact experimental observation shows that myosin V moves toward the “plus” end of actin. Mukherjee and Warshel[34] show that the energy barrier in the forward functional direction is lower than the energy barrier in the backward direction, and that it is this kinetic difference in activation barriers that governs the direction—that is, myosin V functions as an information ratchet. In Figure 4, schematic energy diagrams inspired by those of Mukherjee and Warshel[34] are shown to illustrate that the direction of motion is kinetically selected based on the relative heights of the maximum energy barriers rather than by the energy released (absorbed) by the power stroke.
When the chemical reaction is away from thermodynamic equilibrium (Xξ≠0), q is unchanged, but there is net mechanical flux Jθ because (1 − e−Xξ)≠0, and the flux is proportional to a time constant, τ−1. The flux arises because of mass action,[32] and any attempt to describe coupling in terms of causal language is doomed to failure.[23] The equilibrium free-energy surface defines q, and the flux is given by Jθ = τ−1(1 − q)(1 − e−Xξ). The time constant, τ−1, does not depend thermodynamically on Xξ, but it does depend kinetically on the absolute concentrations of substrate and product as a saturable function of the concentration.
Both of the positive definite coefficients q and τ−1 depend on the applied torque (or force), 𝒯, kinetically since not only does 𝒯 influence the net tilt along the mechanical axis, Xθ, but it may also distort the energy landscape, and hence εℱ, εℬ, and Δε may all depend on 𝒯. The dependence of q and τ−1 on 𝒯 is important for fitting kinetic data, but the thermodynamic dependence of the coupled system on 𝒯 is captured in the terms that involve Xθ.
Equations (6) and (8) are exact rewritten forms of Equation (5a) and are convenient for examining the velocity versus torque response of a molecular machine. Equation (8) in particular highlights the fact that the thermodynamic theory based on trajectories[37] fits the data that had previously been described by using Hill’s hyperbolic expression for the force–flux relation.[41]
4. Irrelevance of the Power Stroke for Chemically Driven Motors
From the above analysis we see that the internal energy released in any single transition between states is irrelevant for determining the intrinsic directionality, the stopping force, and the optimal efficiency of any chemically driven motor.[37,43,48,49] Even so, the concept of the “power stroke” for chemically driven molecular machines stubbornly persists in the literature. There are perhaps two reasons for this persistence. First, the power stroke is unarguably an important determinant of the directionality of light-driven motors,[50] the rate constants of which do not obey microscopic reversibility, and of motors driven by external modulation of thermodynamic parameters such as electric field strength, pH, and redox potential.[7] Second, the diagrams by which the power stroke models are explained are very persuasive from the perspective of macroscopic mechanical intuition.[51,52] First, let us consider a heuristic model as shown in Figure 5, which illustrates how random fluctuations can be used in synergy with externally supplied energy or information to drive directed motion.
Figure 5.
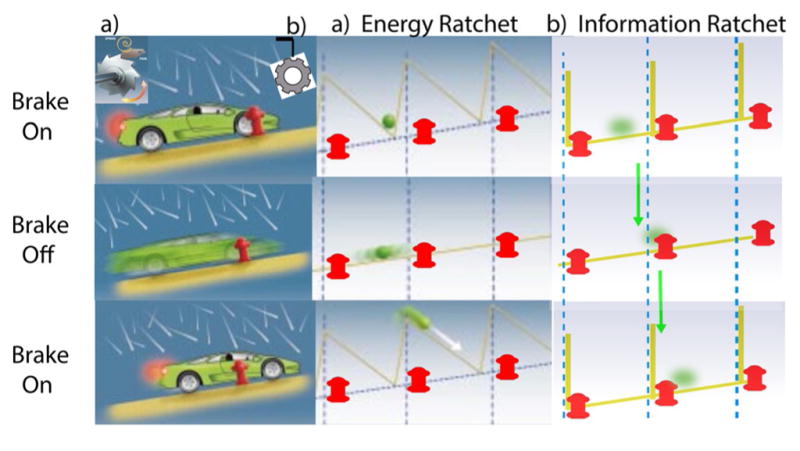
Schematic illustration of how random energy from a hail storm can make it possible for a very small car to drive uphill given an appropriate brake design (adapted from ref. [8b]). There are two possible mechanisms shown, a) an energy ratchet and b) an information ratchet. The car is modeled as a small green sphere in each, where the fire hydrants act as fiduciary markers. a) In the energy ratchet, the car is equipped with a special brake modelled after a mechanical ratchet shown in the upper left hand corner. When the brake is on, the car is forced into the notch of the ratchet just to the rear of the fire hydrant. When the brake is released, the car tends to roll backward but because of the hail the car also jitters back and forth. Owing to the asymmetry of the ratchet teeth it is more likely for the car to initially move forward past the hydrant to its front than backward past the hydrant to its rear, although eventually the car will move downhill if the brake is kept off for a long time. Reapplying the brake, however, at intermediate times when the car is more likely to have moved the short distance forward past the hydrant to the front than the long distance backward past the hydrant to the rear, forces the car on average forward to the next notch to the front. This process can be repeated, resulting in net uphill motion of the car. Note that the energy comes not from the hail itself, but from the effort expended by the driver in applying the brake—that is, from a power stroke. This mechanism does not require the driver to observe the position of the car in determining whether to apply or release the brake, but only to make sure the brake is not kept off for too long. b) An alternate method involves the driver observing the position of the car relative to the hydrants. If the driver releases the brake only when the car is near the hydrant in front, and applies the brake whenever the car is near the hydrant to the rear, the car inexorably moves uphill, even with a very simple brake that simply prevents slippage and where no force needs be exerted when applying the brake. Here, the car moves uphill by virtue of the information obtained to determine when to apply and release the brake.
4.1. Simple Model for Using a Ratchet to Harness Random Energy to Drive Directed Motion
Imagine a small car subject to a violent hail storm.[8b] The random pushes resulting from the hail can be exploited to move the car uphill by use of a specially designed ratchet brake as shown in Figure 5a. When the brake is engaged, the car is locked in place at the notch of the ratchet as shown. When the brake is released, the car on average rolls backward (and the ratchet gear rotates counterclockwise), but because of the hail it sometimes moves forward, rotating the ratchet gear clockwise. The asymmetry of the ratchet brake is such that the distance to move forward to where the brake, when depressed, will catch on the next tooth in the clockwise direction is much smaller than the distance to move backward to where the brake will catch on the next tooth in the counterclockwise direction. If the hill is not too steep and the ratchet is designed correctly, on average depressing the brake after a short period of having released it, will apply a torque that moves the car forward, uphill. This cycle can be repeated to move the car uphill when the driver applies and releases the brake at set intervals without the need to use any knowledge of the cars position to determine what to do.
The work of moving the car uphill is done by the driver depressing the brake pedal. The hail, without which the mechanism fails, simply serves to allow the car to move randomly uphill or downhill when the brake is released. This mechanism has been termed an energy ratchet, and the action of the driver in pressing the brake can be very reasonably described as a power stroke. An alternate mechanism termed an information ratchet (Figure 5b) is in many ways even simpler than the energy ratchet.
If the driver observes the position of the car relative to a periodic array of fire hydrants that serve as fiduciary points and applies the brake only when the car is in such a position that the brake will catch on the next clockwise notch of the ratchet, the car can be moved very reliably uphill. Remarkably, the design of the brake can be simplified to where the cogs teeth are simple rectangular cutouts. When the pawl is engaged, the car remains free to diffuse but only within a limited range. If the driver releases the brake only when in the forward most part of the cog’s constrained diffusive range and applies the brake after the cog has rotated forward past the next tooth, the car inexorably moves forward even though at no time does the driver perform any force times distance work. In this case, the energy for the uphill motion comes from the hail, but this is allowed by the information used by the driver in deciding when to apply and release the brake. The driver plays the role of Maxwell’s demon.[9,23,31]
To understand the relevance of these models to real molecular machines, it is necessary to incorporate physically consistent descriptions of a molecule rather than of a car, of thermal noise instead of a hail storm, and of allosteric interactions rather than of an observant driver, and to explicitly describe how the binding substrate and release of product effectively applies and then releases the brake. In other words, one must have in hand a quantitative free energy description of the chemical state dependent conformational changes calculated from the atomistic 3D structure of biological motors and then scrutinize the nature of the motor through the lens of microscopic reversibility. When this is done, one sees that the energy ratchet mechanism cannot operate when powered by an autonomous exergonic chemical reaction, but that the information ratchet can, and that the presence or absence of a power stroke is irrelevant for determining the direction and thermodynamics of the molecular machine.
Now, with this in mind, let us examine a supposed power stroke mechanism from the literature that has been used to describe the flagellar rotary motor,[52] and that is very similar to an earlier mechanism for muscle.[51]
4.2. Power Stroke Models in the Literature
A diagram inspired by work on the flagellar rotor[52a] is shown in Figure 6, where in the original illustration the authors included only the mechanism indicated by the solid arrows in the shaded windows. The slope of the potential is a trompe l’oeil that fools the naïve reader into accepting the implicit idea that the transitions labelled “power strokes” are important for determining the direction of the motor.[48] The mechanism, known as a shift ratchet, seems to have been inspired by analogy with a mechanical escapement mechanism rather than a simple brake as discussed in Figure 5. A huge difference between a mechanical escapement mechanism and a braking mechanism is that, seemingly, no diffusion is required for directed motion by the escapement. Unfortunately, this description, when applied to molecules, leads to a falsely mechanical perspective of motion in which biological rotary motors have been described as the “world’s smallest wind-up toy”.[52b] Bluntly put, attempts to analyze the behavior of molecular machines in terms of mechanical devices without consideration of fundamental thermodynamic principles is futile. Fortunately, the principle of microscopic reversibility provides a solid platform from which to launch a detailed analysis of the mechanisms by which molecular machines carry out their functions.
Figure 6.
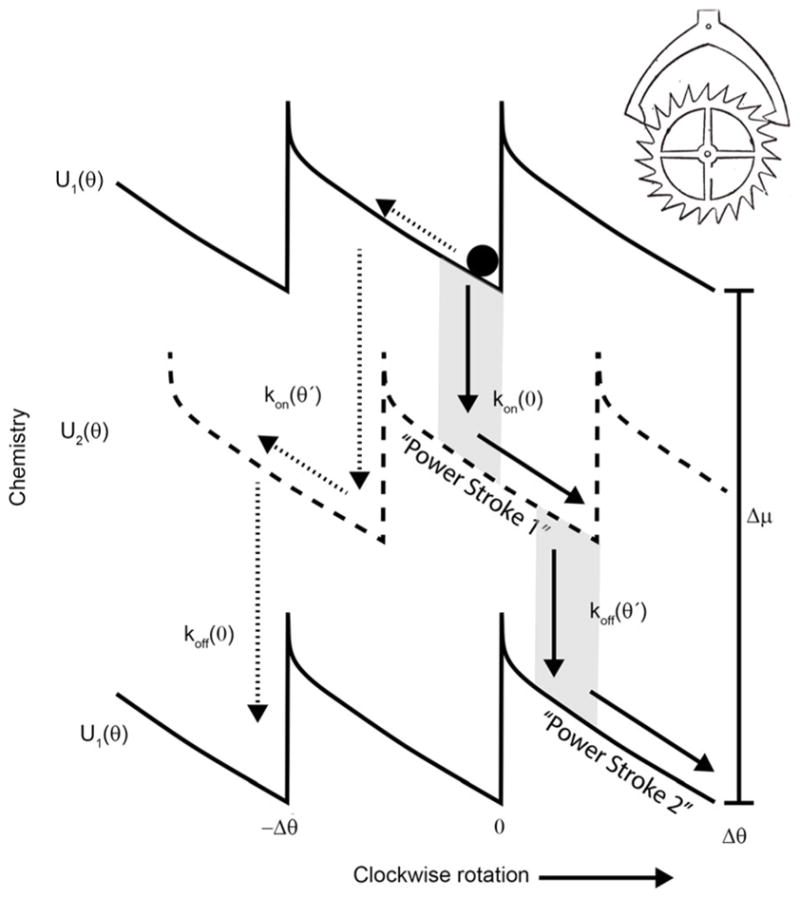
A ratchet mechanism inspired by a paper on the bacterial flagellar motor[52a] is formally similar to a mechanical escapement (upper right hand corner). Similar pictures have been given for many other molecular machines, including myosin moving on actin.[51] Only the solid arrows are shown for the mechanism in the figure by Xing et al.[52] where kon and koff are described as rates for composite conformational transition and proton association from the periplasm or dissociation to the cytoplasm, respectively. The figure is a trompe l’oeil that leads the naive reader to the conclusion that the slope of the potential dictates the direction of motion and other thermodynamic properties. In fact, the slope does not dictate the direction of rotation—the direction of motion is determined by selection between the pathway to the right shown by the solid arrows and the pathway to the left indicated by the dotted arrows, a selection dictated by the θ dependence of the specificities for binding/release of proton to the cytoplasm/periplasm.[42,48]
When we carefully analyze the dynamics of the system in light of microscopic reversibility, we find that if the specificities for the reactions are the same at θ = θ′ and at θ = 0, the macroscopically implausible, and deterministically impossible, pathway shown by the dotted arrows is just as likely as the process shown by the solid arrows, and hence the machine does not, on average, rotate at all.[28] Further, when the specificity for proton to/from periplasm is greater at θ = θ′ than at θ = 0, and the specificity for proton to/from cytoplasm is greater at θ = 0 than at θ = θ′, the system undergoes, on average, counterclockwise rotation!
To better understand what governs the directionality of a molecular machine, consider the model shown in Figure 7a where the system undergoes switching between two potentials, U1(θ) and U2(θ).[28] If the transitions between U1(θ) and U2(θ) are caused by some external modulation, with, for example, αf(θ)= αr(θ) = βf(θ) = βr(θ) = Γ for all θ, the directionality is indeed controlled by the slope of the potentials.
Figure 7.
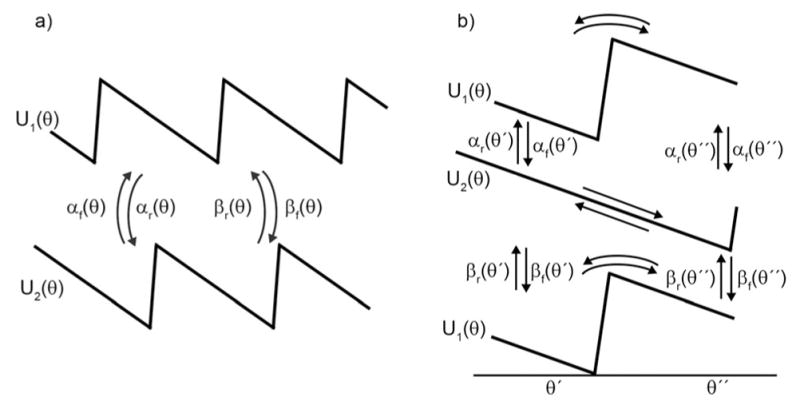
a) Illustration of a catalytically driven shift ratchet. The clear implication is that the slope of the potential dictates the direction of motion. For a system in which the flipping between the two potentials is accomplished externally by, for example, an applied electric field, this is in fact the case. b) However, when the flipping between the two potentials is mediated by the binding of substrate and release of product in a catalytic process, the rate constants are constrained by microscopic reversibility and we see that the direction of motion is governed not by the slopes of the potentials but by the θ dependence of the chemical specificities.[28]
4.3. Enforcing the Constraints of Microscopic Reversibility
The situation is very, very different when the driving is mediated by catalysis of a chemical reaction such as hydrolysis of ATP (as in the F1 ATPase), or by transport of protons across a membrane from high to low chemical potential (as in the bacterial flagellar motor and the Fo portion of the ATP synthase).[28] In these cases, the rate constants are constrained by the principle of microscopic reversibility. One constraint of microscopic reversibility is immediately evident from Equation (9):
| (9) |
for any θ. By use of Equation (2), a second constraint can be derived from the picture involving two arbitrary values of θ—θ′ and θ″—shown in the expanded view in Figure 7b. Irrespective of whether the system is at or away from thermodynamic equilibrium, the forward and microscopically reverse trajectories that begin and end at the exact same point must have equal probabilities.
| (10) |
with an analogous equation holding for the β coefficients. From Equation (10) and Equation (2) it is straightforward to derive Equation (11):
| (11) |
for any pair θ′, θ″. From Equations (9) and (11) we can derive another relationship that will prove useful [Eq. (12)]:[49]
| (12) |
where we have introduced the chemical specificities , which are independent of the energies U1(θ) and U2(θ) Using Equation (9), we have .
Imposing the constraints of microscopic reversibility, Equations (9) and (11), on the rate constants ensures that any reaction diffusion or kinetic model involving states and transitions between them is consistent with an underlying model in which over-damped motion occurs on a single time-independent energy surface. The constraint given in Equation (10) is the discrete equivalent of the requirement that the force field derived as the gradient of the potential be curl free, that is, that ∇ × ∇U(ξ, θ)=0. The transitions between the states occur because of thermal noise as described by Equation (1) and hence the machine functions as a “Brownian motor”. To better illustrate this point, the ratchet mechanism shown in Figure 7a is redrawn in Figure 8a where the α and β transitions are shown vertically as in Figure 7b rather than as a cycle as in Figure 7a. Potential energy surfaces obtained by specifying the energies Ui(±jΔθ/2), Ui(±jΔθ), i = 1,2 and transition-state energies εi(±jΔθ/2), εi(±j Δθ), i = α, β, for integer j, with linear extrapolation between the specified energies, are shown in Figure 8b and 8c. For simplicity, we take εα(±jΔθ) = εβ(±jΔθ/2) = ε and εβ(±jΔθ) = εα(±jΔθ/2) = ε*.
Figure 8.
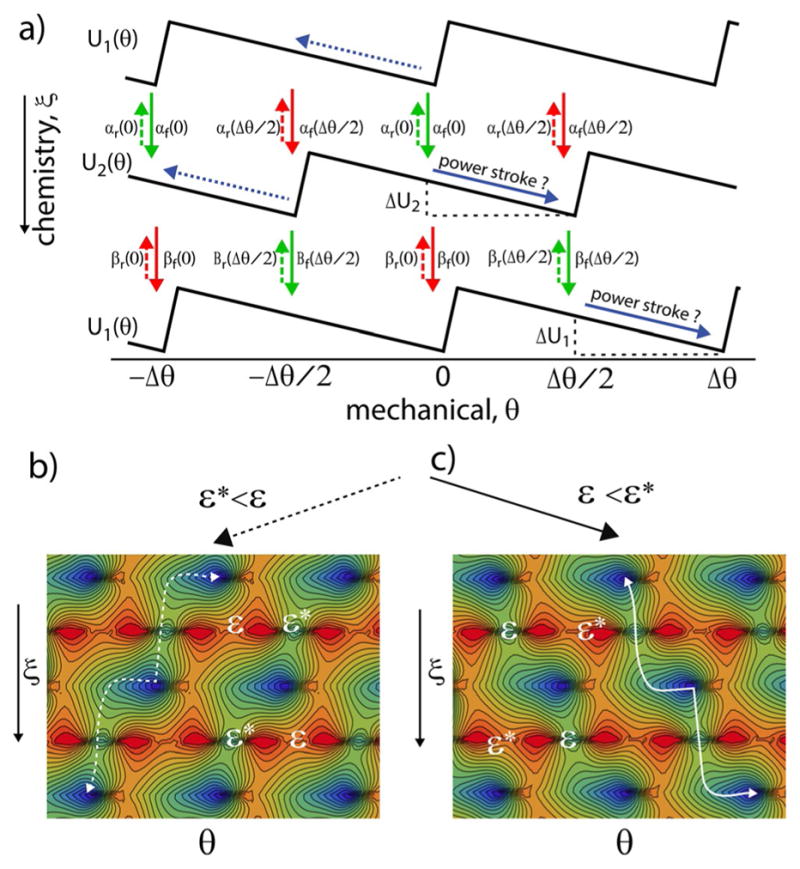
a) Schematic picture of how a chemical process can drive directed mechanical motion. The mechanism illustrated with the solid arrows involves two “power strokes”, downhill “slides” on the slopes of U1 and U2. The mechanism with the dotted blue arrows looks impossible from the point of view of macroscopic physics, but when the activation energies for the chemical processes are equal, ε = ε*, the mechanism with dotted blue arrows in which the motor steps left is just as likely as the mechanism involving the solid blue arrows in which the motor steps right. b) and c) Potential energy surfaces for the ratchet mechanism in Figure 7a for the cases ε* < ε and ε < ε*, respectively, where the most probable trajectories are shown by the white dashed and solid curves.
Let us compare two processes: one in which the system undergoes chemical reaction from U1 to U2 at θ=0, moves from θ=0 to θ = +Δθ/2 on U2 (power stroke 1), undergoes chemical reaction from U2 to U1 at +Δθ/2, and then moves from + Δθ/2 to + Δθ while on U1 (power stroke 2), completing a forward step; and another in which the system moves from θ=0 to θ=−Δθ/2 on U1 (un-power stroke 2?), undergoes chemical reaction from U1 to U2 at θ=−Δθ/2, moves from −Δθ/2 to −Δθ while on U2 (un-power stroke 1?), and undergoes chemical reaction from U2 to U1 at −Δθ, thus completing a backward step. The ratio of the probability for a backward step and a forward step is given by Equation (13):
| (13) |
where we have used periodicity to deduce the identities P1(−Δθ/2 ← 0) = P1(Δθ/2 ← Δθ) and P2(−Δθ ← −Δθ/2) = P2(0 ← Δθ/2). Using Equations (2), (9), (11), and (12) we find:[49]
| (14) |
where we identify q = s(0)s−1 (Δθ/2), and where vuc = [s−1 (Δθ/2)+s(0)e−Xξ. The salient point of Equation (14) is that the ratio of forward to backward steps depends only on the chemical specificities and the generalized thermodynamic “forces”, Xξ and Xθ, and not on the energies of the states.
4.4. A Cautionary Tale
It is easy to become confused, however. If we take simple, plausible, expressions for the rate coefficients αf(θ) = βf(θ) = eXξ/4 and αr(θ) = βr(θ) = e−Xξ/4 for all θ, an assignment that is clearly in agreement with constraint Equation (9), and where we blithely assert that Xξ parametrizes the deviation from equilibrium, we find mathematically that in the limit Xξ ≫ 0, we seem to have Equation (15):
| (15) |
where
ΔU1 + ΔU2 ≡ [U1(Δθ/2) − U1(Δθ)] + [U2(0) − U2(Δθ/2)]. This result seemingly supports the power stroke model since ΔU1 + ΔU2 is the energy dissipated in the two “power strokes” in the mechanism of Figure 7a. Hill, Eisenberg, and Chen,[51] based on a similar picture, asserted that the maximum efficiency for a molecular machine is . However, the θ independent assignment of the rate constants violates the constraint imposed by Equation (11) and this assignment is not consistent with a mechanism for autonomous chemical driving. The efficiency for chemically driven motors is not controlled by (ΔU1 + ΔU2) but by the chemical specificities,[49] and in the limit that q ≪ e−Xξ the efficiency approaches unity when Xθ → Xξ irrespective of the value of (ΔU1 + ΔU2].[48]
It is perhaps worthwhile to step back and recognize from Equation (13) possible limiting cases. When Xξ is very large the transition constants for the dashed red and green arrows can be ignored in favor of those for the solid red and green arrows. It is also reasonable to take the approximation where the transitions for the red arrows are kinetically blocked such that the transition constants for the red arrows can be ignored in favor of those for the green arrows. It is not, however, reasonable to take both approximations, as is done implicitly in Figure 4b of Xing et al.,[52] since this leads to division by zero in Equation (13) for r.
There is an unfortunate tendency in the literature for authors to incant the words “far from equilibrium” several times and then proceed to assign rate constants ad libatum with no attention whatsoever to the fundamental physical principles such as microscopic reversibility that govern the dynamics of the system. It is not clear what, if any, contribution is made by such unconstrained “theoretical” analysis.
A similar point has been made with regard to hypothetical mechanisms for evolution of homochirality (mechanism for the establishment of a preponderance of L or D isomers from a racemic mixture) in biological systems where hypotheses ungrounded by microscopic reversibility were described, accurately, if unflatteringly, as “if pigs could fly” chemistry.[53] The problem with regard to flying pig proposals such as the power stroke is that from a macroscopic perspective the power stroke seems to follow from common sense, and indeed the power stroke is important for externally and optically driven motors. Nevertheless, the assertion of the importance of a power stroke for molecular machines driven by catalysis of a chemical reaction is just plain wrong.
4.5. Motion on an Energy Landscape
The 2D energy landscapes derived from the model in Figure 7a are shown in Figure 7b for ε* < ε, and in Figure 7c for ε < ε*. The white dashed and solid lines are the paths of least thermodynamic action as calculated[48] from Onsager and Machlup’s theory.[17] In Onsager and Machlup’s derivation of the thermodynamic action, the probability for any trajectory involves a rather complicated pre-factor in addition to the exponential of the energy difference between the initial and final points on the trajectory. The key to obtaining Equation (2) is recognizing that this pre-factor is direction independent and hence cancels in the ratio of the probability for any trajectory and its microscopic reverse.[24]
A common objection to the use of Onsager–Machlup thermodynamic action theory for molecular machines is the claim that Onsager’s theory is only valid near equilibrium in the linear regime. Indeed, Onsager and Machlup explicitly state that “The essential physical assumption about the irreversible processes is that they are linear; that is, that the fluxes depend linearly on the forces that ”cause“ them”.[17] This situation, however, is the case with all over-damped systems obeying Equation (1) in which the linearity between the velocity, , and the force that causes it, −∇U(r⃗), is manifest. The required equilibrium is the mechanical equilibrium by which acceleration can be ignored for trajectories of single molecules. There is no requirement that the overall system be near thermodynamic equilibrium. The results of our analysis, such as Equations (5a) and (5b), remain valid for large generalized thermodynamic “forces” Xθ and Xξ because the underlying process, described at the single-molecule level by Equation (1), is in mechanical equilibrium.
Although the power stroke is irrelevant for the thermodynamics of chemically driven molecular machines, a power stroke can be, and often is, essential for light-driven molecular machines. We can understand this fundamental difference between light-driven and thermally activated processes in the context of binding of CO to myoglobin, an extremely well-studied process.
5. Microscopic Reversibility and the Physics of Ligand Binding to Proteins
Molecular dynamics simulations have shown that a CO molecule can arrive at the binding site of myoglobin by diffusing through the bulk of the protein.[54] Any specific realization of this process is of course very unlikely. The microscopic reverse of the process where CO leaves the binding site by diffusing through the protein is also very unlikely, but the ratio of the probability for the forward and microscopic reverse of these rare trajectories is exactly the same as the ratio of the probabilities for any other, possibly far more likely, binding/unbinding pathway. This is the essence of microscopic reversibility reflected in Equation (2), and which is stated by IUPAC as:[55]
“In a reversible reaction, the mechanism in one direction is exactly the reverse of the mechanism in the other direction. This does not apply to reactions that begin with a photochemical excitation.”
Early experiments on dissociation of CO from myoglobin seemed to challenge this fundamental principle. In the mechanism for association, CO diffuses to the iron-containing binding site of the deoxy form, deoxyMb, of the protein and there interacts with the iron in the high-spin, out-of-plane state. The iron undergoes a local configuration change to the in-plane low-spin form, followed by a global conformational change to the bound form MbCO. An essential feature is that the myoglobin conformational change starts locally and propagates globally, consistent with our experience in the macroscopic world in which waves propagate away from a source of excitation as in water, see Figure 9.
Figure 9.
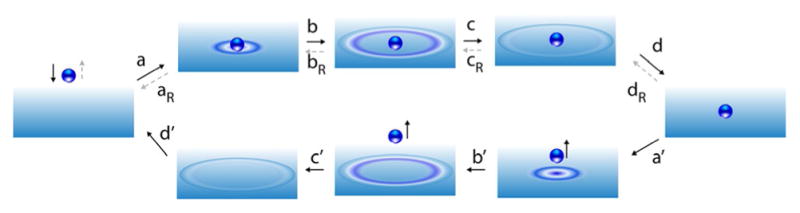
When a neutral density ball falls on a viscous liquid (a) waves propagate outward from the ball (b,c,d) until finally the liquid, with the ball resting on it, is quiescent. If the ball is removed from the surface by some external means (a′), waves once again propagate outward from where the ball had been (b′,c′,d′), until finally the liquid is again quiescent. This backward mechanism is very different than the microscopic reverse mechanism (gray dashed arrows) for removal of the ball from the surface in which waves spontaneously propagate inward toward the ball (dR,cR,bR) until finally the energy of the wave coalesces at the ball, propelling the ball away from the surface. The external removal of the ball corresponds molecularly to photo-dissociation,[56] external changes to thermodynamic parameters[57] (electric field strength, pressure, pH, or redox potential), or to computational disapparition.[58] From the macroscopic or even mesoscopic perspective, the process dR → cR → bR → aR seems remarkably unlikely, requiring as it does energy to spontaneously concentrate from many degrees of freedom to the single degree of freedom of the ball. Even so, this is the most likely mechanism for thermally activated dissociation as required by the principle of microscopic reversibility.
Frauenfelder and colleagues[56] studied the dissociation of CO, finding the mechanism to first involve dissociation of CO from the in-plane MbCO. Then, the iron undergoes a local configuration change to the out-of-plane high-spin iron state, followed by a global change to the deoxyMb form. Once again, the local to global progression is consistent with experience based on removing an object from quiescent water. These results led Frauenfelder and colleagues to argue that “Binding or dissociation of a ligand at the heme iron causes a protein quake.” However, although the local to global progression for both binding and dissociation is consistent with macroscopic experience, it is not consistent with microscopic reversibility, according to which the thermal dissociation of CO must be preceded by a global to local “unquake” followed by dissociation of CO. The critical point is that the experiments of Ansari et al.[56] were carried out by flash photolysis with photochemically induced desorption, a distinction that changes everything (Figure 10).
Figure 10.
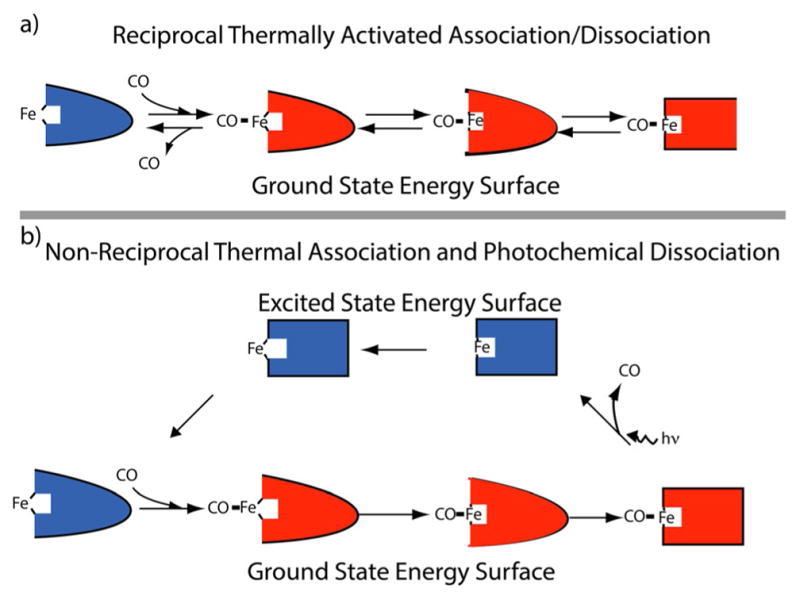
Illustration of the difference between a) equilibrium, thermally activated, dissociation in which the most probable path for dissociation of CO is the microscopic reverse of that for association of CO and b) photolysis induced dissociation of CO in which the dissociation is not the microscopic reverse of association.
The appearance of a non-reciprocal cycle—a situation where the dissociation of CO is not the microscopic reverse of the association of CO—is of paramount importance for understanding the operation of a molecular machine. Such a cycle is necessary for the generation of directed motion, and is at the heart of the mechanism for all molecular machines. There are several excellent reviews that discuss the hydrodynamics by which non-reciprocal shape changes lead to directed motion.[59,60] Such a non-reciprocal cycle can result either from optical or external driving, or from driving by catalysis of a non-equilibrium chemical reaction, but the design principles by which a molecular motor can use these two types of energy are totally different.
5.1. Seeing the Light versus Feeling the Heat
Unfortunately, there is a strong tendency in the literature to analogize chemical driving with optical driving. Indeed, in popular animations of kinesin and myosin, which are widely available on the web, the ATP hydrolysis step is denoted by a flash of light. This analogy, however, is seriously misleading and tends to gloss over a very important symmetry difference between thermally activated transitions and optically induced transitions.
The immediately apparent difference between optically and chemically driven processes is quantitative—hydrolysis of a molecule of ATP under physiological conditions can provide around 20 kBT energy whereas a single photon of green light can provide around 100 kBT of energy. A seemingly natural assumption is that a chemically driven molecular machine can approach the behavior of a similar optically driven molecular machine in the limit that the reaction being catalyzed is very, very far from equilibrium. This natural assumption, however, is wrong.
The essential difference between light-driven and thermally activated processes is based on a fundamental symmetry difference between the Bose–Einstein relations[61] and microscopic reversibility. According to the Bose–Einstein relations, the transition coefficient for absorption is identical to the transition coefficient for stimulated emission if the degeneracies of the ground and excited states are the same. In contrast, the microscopic reversibility [Equation (2)] that holds for all thermally activated processes requires that the ratio of forward and reverse transition coefficients be proportional to the exponential of the energy difference between starting and ending states. Thus, the description of a chemical process as driving a reaction between a “ground state” N-dimensional energy surface and an “excited state” N-dimensional energy surface[62] is problematic and can lead to seriously incorrect conclusions. Instead, the effect of substrate binding and catalysis of a chemical reaction must be described in terms of motion on a single (N+1)-dimensional energy surface (see Figure 8a–c). The conclusions based on these two very different pictures can be tremendously different, and correspond to the difference between light-activated and thermally activated processes.[42,48] In a photochemical process, light absorption and emission is followed by a non-equilibrium relaxation of the conformational state of a protein and controlled by the exothermicity, the reorganization energy, and leakage to the original ground state.[63] The resulting transitions are described by Ansari et al.[56] as “functionally important motions”. The relaxation of the protein on either the ground- or excited-state surfaces can, in the case of flash photolysis, be well described as a “power stroke” that can result in mechanical motion.
In contrast, the internal degrees of freedom of the protein remain in equilibrium at every instant during catalysis of even a very strongly exergonic reaction.[23] For example, in ATP hydrolysis an ATP diffuses to the active site of the enzyme (an ATPase), binds, and undergoes conversion to ADP+Pi at the active site, and then ADP and Pi dissociate and diffuse away. The reverse, in which ADP and Pi diffuse to the active site, bind, and undergo in situ conversion to ATP, which then dissociates and diffuses away, results in ATP synthesis. As far as the individual protein is concerned, both of these are equilibrium processes. The character of the motion of the protein is independent of the chemical potentials of ATP, ADP, and Pi in the bulk. Any thermodynamic disequilibrium in the bulk is manifest only in a change of the relative frequencies of trajectories leading to hydrolysis versus those leading to synthesis, and not to a change in the character of the protein motion. The chemical potential difference acts to impose a preferred direction of reaction by mass action.[32] It is very misleading to characterize the effect of ATP as delivering “violent kicks”[64a] to the enzyme that catalyzes its hydrolysis, and proposal of chemoacoustic waves[64b] (in analogy with the photo-acoustic effect) as a mechanism for enhanced diffusion of enzymes is ill-founded.
5.2. Why the Power Stroke Model is Correct for Light-Driven Processes and Wrong for Chemically Driven Processes
Consider a simple model for the light-driven pumping of protons by bacterio-rhodopsin.[65]
When used to describe light-driven processes, a drawing such as Figure 11 represents a process in which external energy from light is used to cause transitions between a “ground-state” energy surface (shown in blue) and an “excited-state” energy surface (shown in red). The transitions on either the ground or excited energy surfaces are thermally activated processes where the ratios of the forward and backward rate constants have the standard interpretations [Eq. (16)]:
| (16) |
Figure 11.
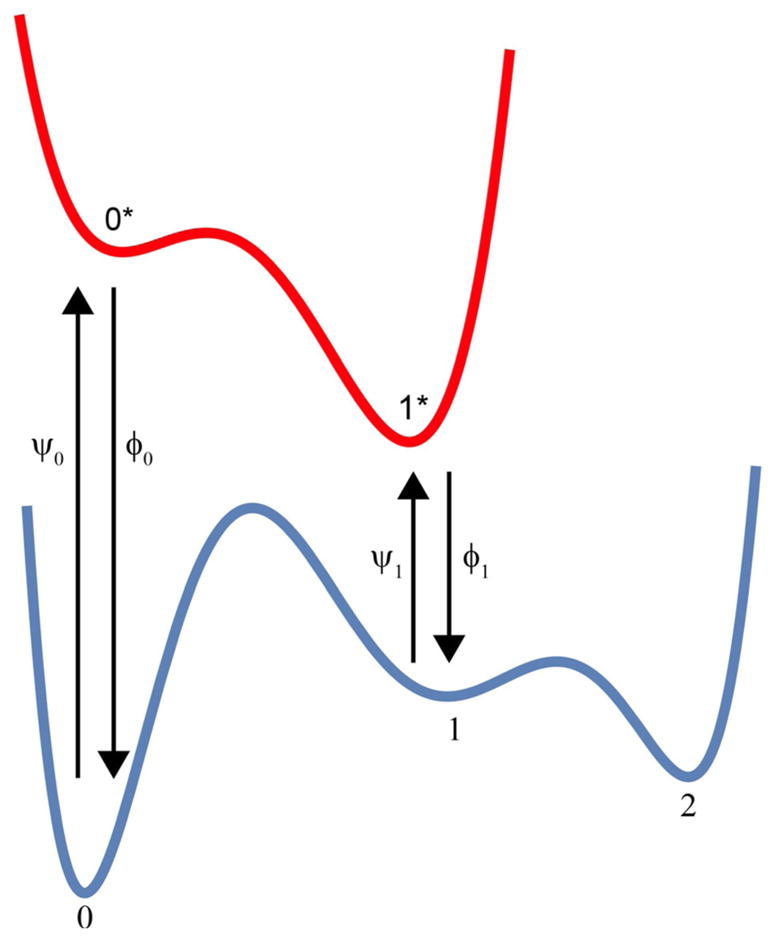
Schematic figure used to illustrate how input energy can be used to maintain a non-equilibrium steady state in which the relative concentrations in states 2 and 0 are not given by a Boltzmann expression.
It is a simple matter to calculate the concentrations (or probabilities) of the five “states” (0,1,2,0*,1*) as a function of time given arbitrary initial conditions, and simpler still to calculate steady-state levels. If we take the barrier between states 0 and 1 to be very high, the approximate ratio of the steady-state levels of states 2 and 0 can be written down by inspection as Equation (17):
| (17) |
In light that is very bright at both the frequency and , we obtain from the Bose–Einstein relations that if the degeneracies of states 0 and 0* and 1 and 1* are the same. In this case, the optically driven steady-state ratio between states 2 and 0 is given by Equation (18):
| (18) |
The transitions 0* → 1* and 1 → 2 can be very reasonably described as “power strokes” and the energy released in these power strokes is necessary to allow light energy to maintain a non-equilibrium steady state.
We can contrast this with the equilibrium case where there is no light and where all transitions occur on the ground-state surface, in which case Equation (19) applies:
| (19) |
The ratio at steady state in bright light is changed from that at equilibrium by a factor eΔG0*1*−ΔG01. This condition holds also if the optical densities for a black-body radiator at the same temperature as the molecular machine are used in the Bose–Einstein relations,[61] as shown by Astumian.[48]
What happens, though, if the transitions are caused, not by light, but by the binding of a ligand, L. In this case, the vertical transitions must be interpreted as thermally activated processes, where we can take the red energy surface to be that for the ligand bound protein and the blue surface for the unbound form, and where Equation (20) applies:
| (20) |
It is important to note that although the figure does not change depending on whether the transitions between the surfaces are caused by light or by binding of a ligand, the interpretation must change entirely. This understanding is very important when interpreting diagrams such as those used to describe, for example, Marcus theory for electron transfer reactions.[66] As noted, an optically driven system must be interpreted as a process in which transitions are driven between two separate energy surfaces. However, for a system involving ligand binding/dissociation (or any system driven by internal processes), the transitions between two effectively 1D energy surfaces are mediated by thermally activated binding, and dissociation can be described as diffusive motion on a single 2D energy surface by Equation (1).
Now, when we calculate the steady state in the presence of ligand, we find Equation (21):
| (21) |
In other words, the steady state when the transitions between the two surfaces are mediated by a single thermally activated process (binding/dissociation of a ligand) is just the equilibrium state. This should not be a surprise, but it is comforting that the math works out correctly.
This being the case, how can catalysis of a chemical reaction such as ATP hydrolysis support a non-equilibrium steady state? Without specifying the details of the chemical mechanism, let us consider ψ0 = (αf,0 + βr,0), ψ1 = (αf,1 + βr,1), ϕ0 = (βf,0 + αr,0), and ϕ1 = (βf,1 + αr,1) where, by microscopic reversibility Equations (22) and (23) apply:
| (22) |
and
| (23) |
When these relations are inserted into the expression for the steady-state ratio between state 2 and 0, we find Equation (24):
| (24) |
where and .
Both ATP hydrolysis and light absorption can support a non-equilibrium steady state, but there is a huge difference in the design principle. For a light-driven process, it is necessary that ΔG0*1* ΔG01, whereas for a chemically driven process this is not necessary at all. What is necessary is that s1 s0, that is, the kinetic specificities be such that state 0 is specific for ATP (i.e., ATP binding/release is fast and ADP and Pi binding/release is slow in state 0) and state 1 is specific for ADP and Pi (i.e., ATP binding/release is slow and ADP and Pi binding/release is fast in state 1).
5.3. Spectroscopy and Dynamical Contributions to Enzyme Catalysis
Because of the fundamental difference in the symmetry constraints for optical versus thermal transitions, it is imperative to be especially careful in interpreting results based on spectroscopic investigations of proteins. In recent work, several groups have shown that light can induce slightly under-damped collective motion in a protein,[67,68] lysozyme, where the frequency of vibration is influenced by whether the protein is or is not bound by a ligand. These very interesting results, unfortunately, have led to over-the-top descriptions in press releases from the two groups’ respective home institutions in which proteins are described as “ringing like bells” while “playing the symphony of life”. High frequency (1–10 THz) modes of motion certainly exist in proteins and these may well involve collective dynamics of many degrees of freedom, and may be somewhat under-damped when excited by light. In the experiments, the damping frequency was found to be about half the value of the oscillator frequency, around 2 THz. These results seem to support earlier proposals that there may exist “protected” degrees of freedom that store energy and that are important for catalysis and for chemo-mechanical energy coupling.[69]
To better understand whether this proposal is reasonable, let us consider the implications of the recent spectroscopic results on proteins in the context of a molecular dynamics investigation of a small molecule molecular machine, a molecular rotor (diethyl sulfide) on a gold surface driven by a terahertz oscillating electric field applied normal to the surface.[70] This work was inspired by experimental studies of thioether molecular rotors.[71,72] The THz ac field causes rapid (gigahertz) directional rotation of the diethyl sulfide as assessed by molecular dynamic simulations, where the directionality is governed by the chirality of the diethyl sulfide. The frequency response was fit with a simple Brownian oscillator model coupled with a parametric resonator. A librational frequency[70] of 2.4 THz, with a damping frequency of 1.2 THz was used to fit the molecular dynamics simulation of the high-frequency rotation induced by the driving. These values are very close to the oscillator and damping frequencies found for lysozyme. While there is certainly some inertia, as evident from a few rotations (<2) being completed after the field was turned off, the rotation was completely damped within a picosecond (see also ref. [73] for a similar discussion on the possible role of dynamics on enzyme catalysis). The most appropriate onomatopoeia for the tintinnabulation of this particular bell would be, perhaps, “thunk”, not to be confused with the past tense of think, an action with which the description of a protein as a ringing bell has no relationship.
The source of the damping for diethyl sulfide on the gold surface is dielectric friction resulting from the interaction between the electrons of the diethyl sulfide with those of the gold atoms that make up the surface. Since electrons and other charged particles are ubiquitous in molecules, the dielectric friction probably sets an insurmountable fundamental limit for the damping coefficient. Further, as noted above, the catalysis of even a highly exergonic reaction is, from the perspective of an individual protein molecule, a mechanical equilibrium process.
Olsson, Parson, and Warshel[74] and Kamerlin and Warshel[75] have reviewed the literature searching for evidence for “dynamical contributions to enzyme catalysis” and found that within all of the reasonably defined dynamical effects proposed by various groups, none contributes to catalysis. Further, there is a fundamental reason—microscopic reversibility—that no enzyme carrying out its function in the ground state can exploit dynamical effects to store and harness energy. This recent conclusion is consistent with that of Stackhouse et al.[76] who summarize the results of their experiments in the abstract to their 1985 paper, “no evidence was found to support a significant contribution to the rate of catalysis by dynamic funneling of vibrational energy within the protein molecule”.
6. Microscopic Reversibility and Motor Cycles
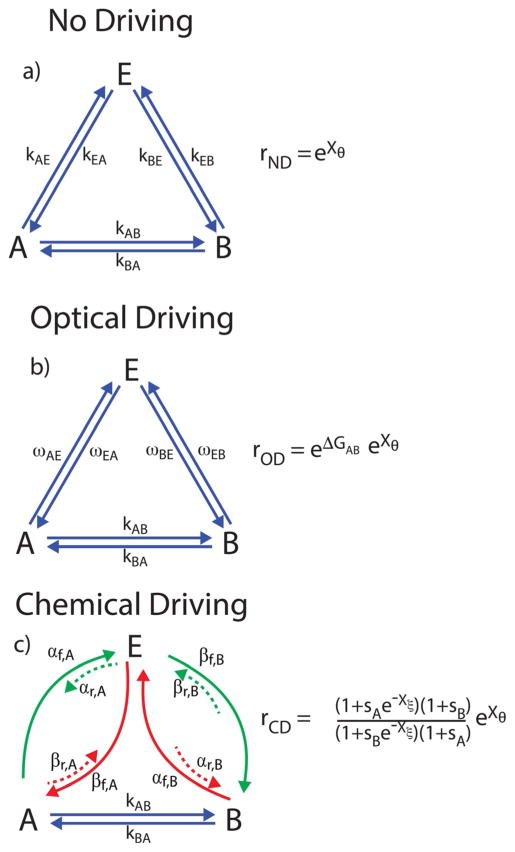
Many models for molecular machines involve kinetic cycles. One of the simplest non-trivial examples is the three-state triangle reaction discussed by Onsager in his paper on reciprocal relations in chemistry.[14] This “triangle reaction” is shown in Figure 12 for three cases, a) no driving; b) optical driving; and c) chemical driving, where an external load tends to drive counterclockwise cycling when Xθ 0. The ratio of the probabilities for completion of a counterclockwise and clockwise cycle is equal and the ratio of the products of the net clockwise rates and net counterclockwise rates are shown for the three cases of no driving (ND), optical driving (OD), and chemical driving (CD).
Figure 12.
Triangle reaction with an external load Xθ and: a) no external driving (ND); b) optical driving (OD); and c) chemical driving (CD). The ratio, r, is the probability of a counterclockwise cycle divided by the probability of a clockwise cycle, and is calculated as the ratio of the product of the counterclockwise rates divided by the product of the clockwise rates. In very bright light, the optical transition coefficients obey the simple relation ωAE ≈ ωEA and ωBE ≈ ωEB. In contrast, the ratio of each forward and reverse rate constant for each pair of processes that are microscopic reverses of one another must be proportional to the exponential of the free-energy difference of the states they connect [see Eq. (2)].
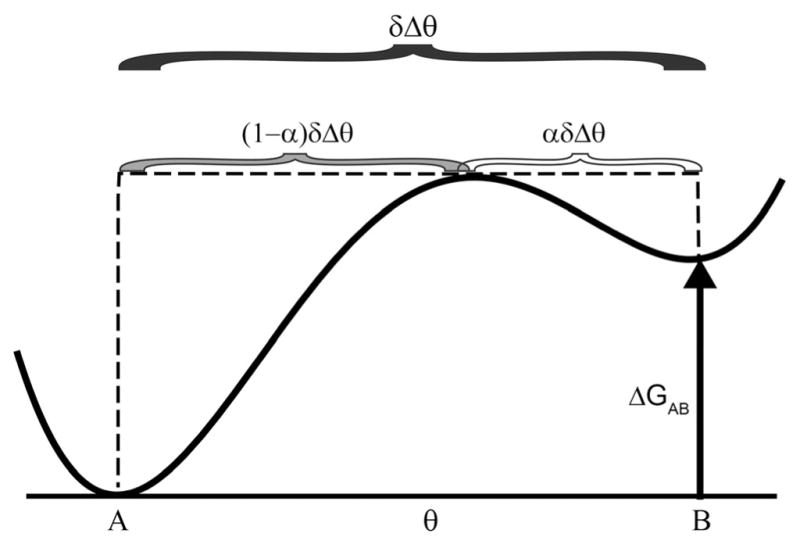
An equilibrium, no driving, realization of the triangle reaction is the isomerization reaction between 1-butene, cis-2-butene, and trans-2-butene.[23] In this case, r0,ND = eXθ (with Xθ = 0) and the probability for a clockwise cycle is the same as the probability for a counterclockwise cycle as emphasized by Onsager.[16] For an optically driven molecular machine, Lehn[77] proposed a triangle mechanism for optical conversion between the anti and syn forms of imines. In the ground state, the imine is aromatic and hence planar, but in the excited state the molecule cannot be planar. If the free energies of the anti and syn are different (ΔGAB≠0) and the molecule is on a surface, constant illumination will result in steady-state cycling. In this case, rOD = eΔGABeXθ and the optically driven transitions A⇄E and B⇄E sustain a non-equilibrium steady state where clockwise or counterclockwise cycling occurs when Xθ = 0, depending on whether ΔGAB is positive or negative.
There are many realizations of chemically driven triangle reactions including enzyme-catalyzed isomerization,[78] ion channels,[79] muscle contraction,[80] and the bacterial flagellar motor.[81] For all of these cases, where , i = A, B. Energy from the catalyzed non-equilibrium (Xξ≠0) chemical reaction sustains a non-equilibrium steady state if, and only if, sA≠sB. The direction of cycling, and the external force necessary to cause the cycling rate to be zero, is determined by the chemical specificities, and , but is independent of ΔGAB. This recognition is the basis of the assertion that the power stroke is irrelevant for chemically driven molecular machines.[48]
6.1. Deconstructing the “Power Stroke”
The rate of cycling for a chemically driven motor is given by Equation (6), Jθ = C(1 − rCD). The kinetic pre-factor C is a complicated function of all of the rate constants, but it is positive and definite and so the stopping force and direction of cycling are determined solely by rCD. The pre-factor C depends kinetically on the applied torque, T, and is important for fitting torque versus angular velocity data, but has no bearing on the relevance of a power stroke for the mechanism.
Berry and Berg[81] showed that the shape of the torque–angular velocity curve observed for the bacterial flagellar rotor (similar to the shape in Figure 3 with a=0) is best fit with rate constants in which most of the physical rotation occurs in the transition A⇄B. An energy diagram for this transition is shown in Figure 13
Figure 13.
Anatomy of a “power stroke”. In clockwise cycling, the motor moves through the transition B → A. Seemingly, the energy ΔGAB provides the power for the power stroke and according to Howard[82] allows the motor to do work against an applied force or applied torque provided ΔGAB Xθ, with a maximum efficiency[51] of ηmax = ΔGAB/Xξ. This analysis is correct for an optically driven machine, but is totally wrong for a chemically driven motor. In the thermodynamic control limit, irrespective of whether ΔGAB is positive, negative, or zero, a chemically driven motor can do work against an applied force or applies torque provided Xξ Xθ, and the maximum eddiciency is bounded only by unity.
The results from Berry and Berg[81] are consistent with δ ≈ 1 and α ≈ 0, that is, with a situation in which most of the motion occurs in the B⇄A transition, and where most of the torque dependence is absorbed in the rate constant kAB. These fit parameters are very interesting with regard to understanding how the structure of the motor determines its function. The assertion that this result suggests that the motor operates by a “power stroke” mechanism is, however, a non sequitor. The fraction of the step, Δθ, taken in any transition has nothing to do with whether a power stroke is important for the mechanism. The further assertion that the fact that most of the mechanical motion occurs in the transition A⇄B indicates that this transition “dissipates most of the available free energy” is wrong, as can be recognized from the fact that the experimentally observed angular velocity versus applied torque can be fit whether ΔGAB is positive, negative, or zero. It is not necessary that the load against which a chemically driven machine works be less than ΔGAB as claimed by Howard.[82] Further, the concept of identifying a fraction of the dissipation with a single transition is misguided as pointed out by Hill and Eisenberg who conclusively demonstrated that for chemically driven motors, as opposed to light-driven motors, free energy dissipation is a property of the cycle as a whole and cannot be assigned to one or a few transitions within the cycle.[83]
7. Dissipation-Driven Assembly of Non-Equilibrium Structures
7.1. Enzymes Use Input Energy to Drive a Reaction Away from Equilibrium
It is often claimed in the literature that having the product of counterclockwise rate constants equal the product of clockwise rate constants (kAEkEBkBA = kBEkEAkAB for the cycle in Figure 12a) is sufficient to guarantee that the flux Jθ is zero. This is not true in the presence of external fluctuations that cause the rate constants to depend on time. If, for example, and the condition kAEkEBkBA = kBEkEAkAB holds at every instant and yet the system undergoes clockwise flux. The rate of cycling is dependent on the details of ψ(t). Indeed, many molecular systems, both biological and non-biological, can harvest energy from oscillating,[84] or even noisy,[85a,b] external perturbations to generate order and to do work, thereby driving a system away from equilibrium.[86]
A simple illustration is shown in Figure 14 where oscillation of the free energy of an intermediate state and a kinetic barrier for a Michaelis–Menten enzyme can cause the enzyme to drive the catalyzed reaction away from equilibrium.[86]
Figure 14.
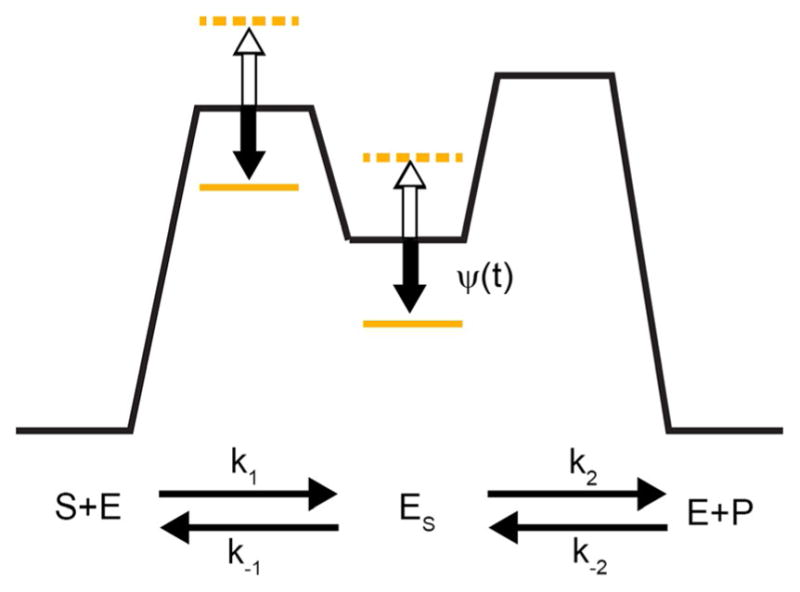
Kinetic barrier model for an enzyme. Under the influence of an external driving, ψ(t), which changes the energy of the intermediate ES and the kinetic barriers (transition states) the enzyme can drive the reaction S⇄P away from rather than towards equilibrium.
The rate constants are given by the expression , i = ±1, 2, where zi are parameters of the enzyme such as activation volume when the external perturbation, ψ(t), is pressure; or dipole moment of activation when the external perturbation, ψ(t) is electric field strength, etc.
For high-frequency externally imposed oscillations, the “steady-state” concentration gradient is given by Equation (25):[86]
| (25) |
where the over-bar indicates a time average, and where Keq is the time-independent equilibrium constant for conversion of substrate S to product P. In Figure 14, z1 = −z2 = z, and z−1 = z−2 = 0, so the steady-state concentration ratio is different from the equilibrium ratio by a factor . For the case shown (and in general when z1 + z2 + z−1 + z−2 = 0), the overall equilibrium constant for the catalyzed reaction, Keq, is independent of the external driving parameter ψ(t). The input electric energy is and for large, high-frequency perturbation, the efficiency can approach 100 %.[86]
An important point to note is that the enzyme itself provides a mechanism for pumping energy into the system—the equilibrium constant of the catalyzed reaction itself, does not depend on ψ. The conclusion can be dramatically emphasized by considering a situation with μS = μP in the presence of a high-frequency oscillating or fluctuating perturbation ψ(t) but without the enzyme. Because there is no mechanism to absorb energy from ψ(t), the system is in overall thermodynamic equilibrium. Then, when we add a small amount of the enzyme—a catalyst—the reaction spontaneously moves away from equilibrium until a concentration ratio given by Equation (25) is reached because the enzyme absorbs and harnesses energy from ψ(t), a source of energy that could not be utilized in the absence of the enzyme, to attain and maintain a non-equilibrium steady state.
We can better understand the effect of an external fluctuating perturbation in the context of a simple kinetic model in which ψ(t) is taken to fluctuate between its maximal (+ψ) value given by the dashed orange line and minimal (−ψ) value given by the solid orange line (Figure 14) with a Poisson distributed lifetime, Γ, at each value,[57] .
For sufficiently large Γ and ψ, the dominant mechanism is with an effective “equilibrium” constant of (Figure 15).
Figure 15.
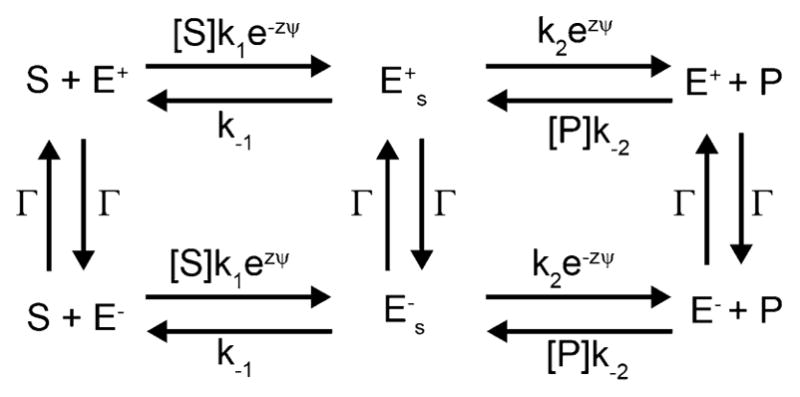
Kinetic mechanism for an enzyme, describing the effect of externally driven Poisson fluctuations between two states, ±ψ. The fluctuations can drive the reaction S ⇌ P away from equilibrium.[57]
These and similar ideas on the effects of external perturbations[87,88] have led to recent advances in the design and synthesis of molecular machines, including those that use dissipation of energy to achieve self-assembly.[89,90] One system, in particular, on which we shall focus, has been termed a synthetic molecular pump, where externally driven oscillations of the redox potential leads to formation and maintenance of a strongly disfavored non-equilibrium structure.[10,91]
7.2. The Demon is in the Details
In Figure 16 we consider a ring molecule [cyclobis(paraquat-p-phenylene) (CBPQT)] interacting with a dumbbell-shaped rod molecule, a bistable [2]pseudorotaxane with a bipydidinium recognition site, a 2-isopropyphenyl (IPP), shown in green, as a steric barrier, with one end capped by charged 3,5-dimethyl pyridinium (PY+) and the other end capped by a bulky stopper group (shown in black on the right hand side of the dumbbell) that provides an insurmountable barrier to the CBPQT ring. The IPP is connected through a triazole to a ring collecting oli-gomethylene chain that is terminated by the bulky stopper group. The ring collecting chain can, in principle, be occupied by several of the CBPQT rings, but this would be a very high energy and low entropy structure since even one ring has a higher energy (by ΔGout) on the ring than in the bulk.
Figure 16.
Illustration of a synthetic molecular pump. The energy profiles for a ring under both reducing (top) and oxidizing (bottom) conditions are shown, where the overall free-energy difference between having a ring on the collection site is the same irrespective of whether the ring is oxidized (CBPQT4+) or reduced (CBPQT2(•+)).
Under either reducing or oxidizing conditions, only a very small fraction of the collecting chains will be occupied by even a single ring, and the ratio of occupied (assembled, [A]) to unoccupied (disassembled [D]) forms is given by the equilibrium expression . However, repetitively changing between oxidizing and reducing conditions pumps a ring onto the collecting chain with almost unity certainty, and a second cycle can even place a second CBPQT ring on the collecting chain to form a highly non-equilibrium structure.[91] Energy is dissipated each time the redox potential is changed, and some of this energy can be used for assembling non-equilibrium structures. The mechanism can be considered in analogy with the action of a molecular “demon”,[31,47,92,93] which selects a path that leads to an ordered structure over another path that leads to a disordered structure, as illustrated in Figure 17.
Figure 17.
Illustration of a molecular demon that selectively shepherds a ring in an intermediate state to assemble rather than disassemble even though the assembled state is higher in energy. The demon can operate either as a blind energy ratchet (Smoluchowski demon), raising and lowering the energies of states and barriers irrespective of the state of the molecule, or as a sighted information ratchet (Maxwell demon), raising and lowering barriers depending on the state of the molecule. The design principles necessary for synthetic implementation of the two types of “demons” are very different.[10,49]
External modulation of the redox potential allows the system to act as a Smoluchowski’s energy demon or energy ratchet (Figure 18a) whereas catalysis of a non-equilibrium chemical reaction can power a Maxwell’s information demon or information ratchet (Figure 18b).
Figure 18.
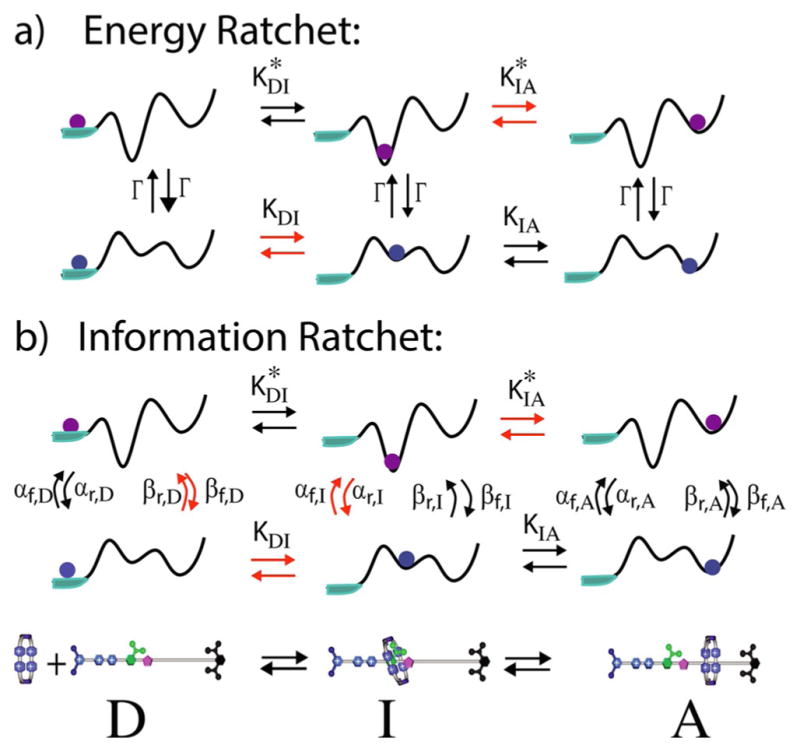
Driving by a) an external fluctuation that results in an energy ratchet mechanism; and by b) an energy-releasing catalyzed reaction that results in an information ratchet mechanism.
The steady-state ratio [A]/[D] for both mechanisms can be easily calculated, and the task becomes particularly simple when the transitions denoted by the red arrows are taken to be very slow. For the energy ratchet, Figure 18a this can be calculated as the product of the “equilibrium” constants along the path D⇄D*⇄I*⇄I⇄A to give Equation (26):
| (26) |
The transitions D*→I* in the reduced state and I → A in the oxidized state are both power strokes with equilibrium constants greater than unity, so the external modulation between reducing and oxidizing conditions supports a non-equilibrium steady state in which it is more likely for the collecting chain to be occupied than not despite the unfavorable ΔGout.
The power strokes for this pump are absolutely essential. Absent the increase in the energy of the complex between the ring and recognition site in the oxidized state relative to the reduced state the mechanism fails. Similar ideas have been used in the design of light-driven motors,[89,94,95] where the power stroke is also essential. When considering from a theoretical standpoint how to turn these mechanisms into autonomous chemically driven motors, it soon became apparent that, because the principle of microscopic reversibility constrains the transition constants of the exergonic catalyzed reaction, a power stroke is not sufficient to allow the energy released by the reaction to drive pumping.[10] Even more surprisingly, perhaps, the power stroke is not even necessary. This can be seen by calculating the product of the ratios of the forward and reverse rates for the path D⇄D*⇄I*⇄I⇄A in the mechanism shown in Figure 18b to obtain Equation (27):
| (27) |
By applying the constraints of microscopic reversibility
| (28) |
and
| (29) |
to Equation (27), we obtain Equation (30):
| (30) |
where and .
The presence or absence of a power stroke is, simply put, irrelevant in the information ratchet mechanism by which all chemically driven molecular motors function. The essential requirement is seen to be a mechanism for gating the catalysis such that reaction with substrate is fast and reaction with product slow in one state of the mechanical cycle, and reaction with substrate slow and reaction with product fast in a different state of the mechanical cycle. This is achieved in Figure 18b when sD ≪ 1 ≪ sI. This gated specificity assures that the mechanical and chemical steps are interleaved with one another, a condition that, combined with Xξ 0 for the catalyzed reaction, is both necessary and sufficient to assure directional pumping of the rings onto the collecting chain.
The energy ratchet is a power stroke mechanism—if ΔG* and ΔG are both zero, there is no enhancement of the assembled structure versus the disassembled structure. In contrast, although there may be power strokes, an information ratchet is not a power stroke mechanism. The enhancement of the assembled structure versus the disassembled structure is independent of ΔG* and ΔG and is governed solely by the specificities. We can better understand the constraints of microscopic reversibility by considering a kinetic lattice model of the information ratchet as shown in Figure 19.
Figure 19.
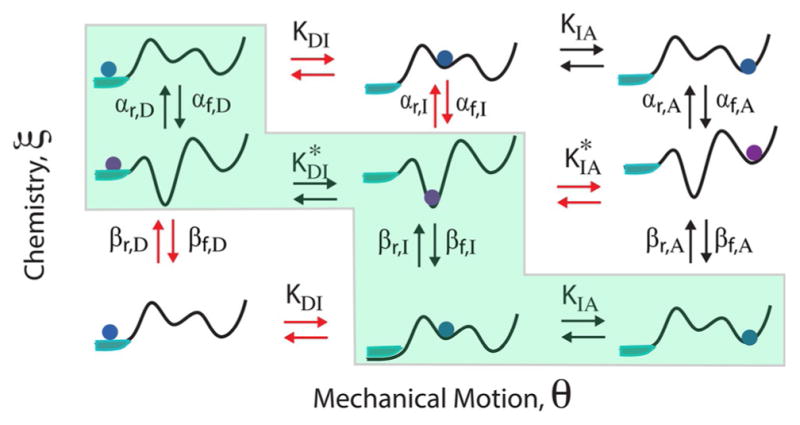
A kinetic lattice model to describe the mechanism of using energy released by catalysis of a chemical reaction to pump a ring from the bulk onto a high-energy collecting site. The green zigzag path denotes the desired mechanism for coupling.
This mechanism is very similar to that described by Jencks for a Ca ATPase ion pump,[96] and was proposed explicitly by Astumian and Derenyi for understanding ATP-driven ion pumping by membrane ATPases.[45] A similar picture was given very recently by Alhadeff and Warshel[97] for a sodium/proton anti-porter. The mechanism in Figure 19 is an information ratchet because the essential requirement is that the specificity of the catalytic active site is controlled by the mechanical state of the ring. A chemically driven information ratchet has recently been synthesized by Leigh and colleagues.[98] The key design criterion for the autonomous chemically driven information ratchet is that the transitions leading off of the coupled pathway be slow, indicated here by the red arrows. Given this, mass action resulting from the non-equilibrium chemical reaction driving the system from top to bottom leads to a significant enhancement in the amount of the assembled product at the steady state as shown in Equation (30).
The essential difference between an energy ratchet, which describes the effect of external and optical driving, and an information ratchet, which describes the operation of an autonomous chemically driven molecular machine, is microscopic reversibility. The constraint Equation (29) can be rewritten as:
| (31) |
Equation (31) represents the discrete equivalent of the curl-free condition ∇ × ∇U(θ, ξ) = 0 for the gradient of the underlying potential. From the point of view of a single molecular machine, chemo-mechanical coupling is an equilibrium process in which the internal degrees of freedom of the protein or macromolecule remain in equilibrium at every instant. The coupled processes can be described as motion on a single time-independent multi-dimensional energy landscape. Thermodynamic disequilibrium in the bulk is manifest by changes in the frequency of carrying out forward and reverse trajectories on this landscape (i.e., by mass action), but not by a change in the character of the motion of the machine from the equilibrium case. The constraints of microscopic reversibility ensure that kinetic and reaction diffusion models for molecular motors and pumps are consistent with an underlying picture of diffusive motion on a single potential energy surface as described by Equation (1).
8. Conclusion
In their 1981 discussion of why “free energy transduction cannot be localized at some crucial part of the enzymatic cycle”,[83] Eisenberg and Hill observed that the disagreement in the field regarding this point was only conceptual. Nevertheless, they argued, resolution of the controversy was important because of the great amount of intellectual and experimental effort devoted to finding the crucial step (power stroke?) and energized state (pre-power stroke state?) in the overall mechanism. Hill and Eisenberg point out that the basic idea—that there is a crucial step—is wrong and that free energy transduction by chemically driven molecular machines must be understood in terms of the cycle as a whole.
Science has progressed to the point where it is possible to study biomolecular machines at the single-molecule level,[1–6] and even to synthesize molecular machines.[7–13] The controversy highlighted by Hill and Eisenberg 35 years ago now has very practical implications—the chemical requirements for synthetic design of an energized state, the escape from which is driven by a power stroke, are very different than the requirements necessary to achieve gating of a catalyzed reaction depending on the state of the catalyst.
The necessity of the power stroke for light-driven and externally driven processes may explain why experiments often find that there are in fact strongly exergonic conformational changes in the mechanisms of molecular machines. In the earliest stages of evolution, the machines necessary to carry out transport, pumping, and other essential tasks may well have been driven by light, or by periodic changes in the thermodynamic parameters of the system, for example, by circulation in a temperature gradient near a thermal vent. Subsequent evolution developed allosteric gating mechanisms to allow for utilization of energy from a catalyzed chemical reaction, but there was never pressure to eliminate the vestigial “power stroke” from the operation of the precursor molecular machines that evolved to become muscle, flagella, kinesin, dynein, FoF1 ATP synthase, etc. Thus, experimentalists, when seeking the structural origins of the power stroke, do indeed often find strongly exergonic conformational changes in the mechanisms of many biomolecular motors to which they can point. The pseudo-deterministic models invoking these power strokes are very attractive and persuasive from a macroscopic perspective. It is only by examining the mechanisms through the lens of microscopic reversibility that we are able to see that in fact the naive conclusions regarding the importance of the power stroke for chemically driven motors and pumps are not correct. The directionality and thermodynamic properties are instead governed solely by chemical gating—the ability of the molecular complex to discriminate different mechanical states of the motor. One of the most important agendas for development of autonomous chemically driven molecular machines is achieving better control of allosteric mechanisms by which gating can be achieved.[99–102] It can be expected that the ongoing efforts devoted to the design and construction of synthetic molecular pumps and motors will result both in better understanding of biomolecular machines, and in the development of remarkable tools for organizing complex matter,[103] for developing networked nanoswitches for catalysis,[104] and for harnessing the power of molecule-by-molecule assembly.[105]
Physical Perspectives on Molecular Machines
Molecular machines can be understood in terms of their free-energy landscape, not by analogy with macroscopic mechanical devices.
Directionality of chemically driven molecular machines operating under the thermodynamic constraints of reactant and product concentrations is governed by barrier heights (transition states), not by well depths (state free energies).
Thermal noise is essential to the operation of chemically driven molecular machines, although the free energy barriers of the relevant coupled allosteric changes dictate directionality.
Enzymes, including chemically driven molecular machines, operate at mechanical equilibrium.
Microscopic reversibility provides a fundamental thermodynamic grounding for development of a theory of chemically driven molecular machines.
Light-driven processes are fundamentally different to thermally activated processes, and analogy between the two can lead to seriously incorrect conclusions.
The presence or absence of a power stroke (an exergonic conformational change) is irrelevant for determining the direction and thermodynamics of chemically driven molecular machines.
In contrast, optical and externally driven molecular machines can (and often do) operate by a power stroke mechanism.
The best description of the overall mechanism by which an exergonic reaction is coupled to drive mechanical motion is “mass action”.
A complete understanding of the mechanism of a molecular motor can be gained only by viewing the chemo-mechanical cycles holistically. Experiments on parts of the cycle can fill in the details, but over-interpretation often leads to erroneous conclusions, especially when analogies are drawn with macroscopic elements.
Acknowledgments
This work was supported by the National Science Foundation (grant MCB-1243719), National Institute of Health (R01-AI055926), and National Cancer Institute (grant 1U19CA105010). We also thank the University of Southern California High Performance Computing and Communication Center (HPCC) for computational resources.
Biographies
 Dean Astumian received his Ph.D. from the University of Texas at Arlington. Following staff positions at the NIH and NIST, he moved to the University of Chicago as Assistant then Associate Professor, and then as Full Professor to the University of Maine. He is a fellow of the American Physical Society, and he received the Galvani Prize of the Bioelectrochemical Society, a Humboldt Prize in 2009, and the Feynman Prize in 2011. His research focus is on kinetic mechanisms and thermodynamics of molecular motors.
Dean Astumian received his Ph.D. from the University of Texas at Arlington. Following staff positions at the NIH and NIST, he moved to the University of Chicago as Assistant then Associate Professor, and then as Full Professor to the University of Maine. He is a fellow of the American Physical Society, and he received the Galvani Prize of the Bioelectrochemical Society, a Humboldt Prize in 2009, and the Feynman Prize in 2011. His research focus is on kinetic mechanisms and thermodynamics of molecular motors.
 Shayantani Mukherjee obtained her Ph.D. from Jadavpur University in Computational Biology while working as a Research Fellow at the Saha Institute of Nuclear Physics in Kolkata, India. She then moved to Michigan State University as a Post Doctoral Fellow and is currently a Research Associate at the University of Southern California. Her research interests are in elucidating structure–function relationships of biological macromolecules, molecular motors, and kinetics and thermodynamics of complex cellular processes.
Shayantani Mukherjee obtained her Ph.D. from Jadavpur University in Computational Biology while working as a Research Fellow at the Saha Institute of Nuclear Physics in Kolkata, India. She then moved to Michigan State University as a Post Doctoral Fellow and is currently a Research Associate at the University of Southern California. Her research interests are in elucidating structure–function relationships of biological macromolecules, molecular motors, and kinetics and thermodynamics of complex cellular processes.
 Arieh Warshel was born in 1940 in Kibbutz Sde-Nahum, Israel. He received a B.Sc. from the Technion in 1966 and a Ph.D. from the Weizmann Institute in 1969. He is currently Distinguished Professor and the Dana and David Dornsife Chair in Chemistry at the University of Southern California. Dr. Warshel has pioneered computer simulations of the functions of biological molecules, and he and his group continue to push the frontiers in the area. Dr. Warshel received numerous awards including the Nobel Prize in Chemistry in 2013. He is a member of the National Academy of Science and an honorary member of the Royal Society of Chemistry and the holder of several honorary degrees.
Arieh Warshel was born in 1940 in Kibbutz Sde-Nahum, Israel. He received a B.Sc. from the Technion in 1966 and a Ph.D. from the Weizmann Institute in 1969. He is currently Distinguished Professor and the Dana and David Dornsife Chair in Chemistry at the University of Southern California. Dr. Warshel has pioneered computer simulations of the functions of biological molecules, and he and his group continue to push the frontiers in the area. Dr. Warshel received numerous awards including the Nobel Prize in Chemistry in 2013. He is a member of the National Academy of Science and an honorary member of the Royal Society of Chemistry and the holder of several honorary degrees.
References
- 1.Schliwa M, Woehlke G. Nature. 2003;422:759–765. doi: 10.1038/nature01601. [DOI] [PubMed] [Google Scholar]
- 2.Vale RD, Milligan RA. Science. 2000;288:88–95. doi: 10.1126/science.288.5463.88. [DOI] [PubMed] [Google Scholar]
- 3.Boyer PD. Annu Rev Biochem. 1997;66:717–749. doi: 10.1146/annurev.biochem.66.1.717. [DOI] [PubMed] [Google Scholar]
- 4.Berg HC. Annu Rev Biochem. 2003;72:19–54. doi: 10.1146/annurev.biochem.72.121801.161737. [DOI] [PubMed] [Google Scholar]
- 5.Moore PB. Annu Rev Biophys. 2012;41:1–19. doi: 10.1146/annurev-biophys-050511-102314. [DOI] [PubMed] [Google Scholar]
- 6.Bustamante C, Cheng W, Mejia YX. Cell. 2011;144:480–497. doi: 10.1016/j.cell.2011.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Abendroth JM, Bushuyev OS, Weiss PS, Barrett CJ. ACS Nano. 2015;9:7746–7768. doi: 10.1021/acsnano.5b03367. [DOI] [PubMed] [Google Scholar]
- 8.a) Coskun A, Banaszak M, Astumian RD, Stoddart JF, Grzybowski BA. Chem Soc Rev. 2012;41:19–30. doi: 10.1039/c1cs15262a. [DOI] [PubMed] [Google Scholar]; b) Astumian RD. Sci Am. 2001;285:56–64. doi: 10.1038/scientificamerican0701-56. [DOI] [PubMed] [Google Scholar]
- 9.a) Erbas-Cakmak S, Leigh DA, McTernan CT, Nussbaumer AL. Chem Rev. 2015;115:10081–10206. doi: 10.1021/acs.chemrev.5b00146. [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Kay ER, Leigh DA, Zerbetto F. Angew Chem Int Ed. 2007;46:72–191. doi: 10.1002/anie.200504313. [DOI] [PubMed] [Google Scholar]; Angew Chem. 2007;119:72–196. [Google Scholar]
- 10.Cheng C, McGonigal PR, Stoddart JF, Astumian RD. ACS Nano. 2015;9:8672–8688. doi: 10.1021/acsnano.5b03809. [DOI] [PubMed] [Google Scholar]
- 11.Sengupta S, Ibele ME, Sen A. Angew Chem Int Ed. 2012;51:8434–8445. doi: 10.1002/anie.201202044. [DOI] [PubMed] [Google Scholar]; Angew Chem. 2012;124:8560–8571. [Google Scholar]
- 12.Feringa BL. J Org Chem. 2007;72:6635–6652. doi: 10.1021/jo070394d. [DOI] [PubMed] [Google Scholar]
- 13.Kottas GS, Clarke LI, Dominik Horinek A, Michl J. Chem Rev. 2005;105:1281–1376. doi: 10.1021/cr0300993. [DOI] [PubMed] [Google Scholar]
- 14.Julicher F, Ajdari A, Prost J. Rev Mod Phys. 1997;69:1269–1281. [Google Scholar]
- 15.Astumian RD. Phys Chem Chem Phys. 2007;9:5067–5083. doi: 10.1039/b708995c. [DOI] [PubMed] [Google Scholar]
- 16.Onsager L. Phys Rev. 1931;37:405–426. [Google Scholar]
- 17.Onsager L, Machlup S. Phys Rev. 1953;91:1505–1512. [Google Scholar]
- 18.Purcell EM. Am J Phys. 1977;45:3–11. [Google Scholar]
- 19.Astumian RD. Science. 1997;276:917–922. doi: 10.1126/science.276.5314.917. [DOI] [PubMed] [Google Scholar]
- 20.Astumian RD, Hänggi P. Phys Today. 2002;55:33–39. [Google Scholar]
- 21.Reimann P. Phys Rep. 2002;361:57–265. [Google Scholar]
- 22.Chandrasekhar S. Rev Mod Phys. 1949;3:114–126. [Google Scholar]
- 23.Astumian RD. Nat Nanotechnol. 2012;7:684–688. doi: 10.1038/nnano.2012.188. [DOI] [PubMed] [Google Scholar]
- 24.Bier M, Derényi I, Kostur M, Astumian RD. Phys Rev E. 1999;59:6422–6432. doi: 10.1103/physreve.59.6422. [DOI] [PubMed] [Google Scholar]
- 25.Astumian RD. Am J Phys. 2006;74:683–688. [Google Scholar]
- 26.Astumian RD, Bier M. Phys Rev Lett. 1994;72:1766–1769. doi: 10.1103/PhysRevLett.72.1766. [DOI] [PubMed] [Google Scholar]
- 27.Magnasco M. Phys Rev Lett. 1994;72:2656–2659. doi: 10.1103/PhysRevLett.72.2656. [DOI] [PubMed] [Google Scholar]
- 28.Astumian RD, Bier M. Biophys J. 1996;70:637–653. doi: 10.1016/S0006-3495(96)79605-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Keller D, Bustamante C. Biophys J. 2000;78:541–556. doi: 10.1016/S0006-3495(00)76615-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mukherjee S, Warshel A. Proc Natl Acad Sci USA. 2011;108:20550–20555. doi: 10.1073/pnas.1117024108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Astumian RD, Derényi I. Eur Biophys J. 1998;27:474–489. doi: 10.1007/s002490050158. [DOI] [PubMed] [Google Scholar]
- 32.Voit EO, Martens HA, Omholt SW. PLoS Comput Biol. 2015;11:e1004012. doi: 10.1371/journal.pcbi.1004012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mukherjee S, Bora RP, Warshel A. Q Rev Biophys. 2015;48:395–403. doi: 10.1017/S0033583515000050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mukherjee S, Warshel A. Proc Natl Acad Sci USA. 2012;109:14876–14881. doi: 10.1073/pnas.1212841109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Mukherjee S, Warshel A. Proc Natl Acad Sci USA. 2013;110:17326–17331. doi: 10.1073/pnas.1317641110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Burykin A, Kato M, Warshel A. Proteins Struct Funct Bioinf. 2003;52:412–426. doi: 10.1002/prot.10455. [DOI] [PubMed] [Google Scholar]
- 37.Astumian RD. Biophys J. 2010;98:2401–2409. doi: 10.1016/j.bpj.2010.02.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.a) Astumian RD. Phys Rev E. 2007;76:020102. doi: 10.1103/PhysRevE.76.020102. [DOI] [PubMed] [Google Scholar]; b) Astumian RD. Phys Rev E. 2009;79:021119. doi: 10.1103/PhysRevE.79.021119. [DOI] [PubMed] [Google Scholar]
- 39.Nishiyama M, Higuchi H, Yanagida T. Nat Cell Biol. 2002;4:790–797. doi: 10.1038/ncb857. [DOI] [PubMed] [Google Scholar]
- 40.Carter NJ, Cross RA. Nature. 2005;435:308–312. doi: 10.1038/nature03528. [DOI] [PubMed] [Google Scholar]
- 41.Hill AV. Proc R Soc London Ser B. 1938;126:136–195. doi: 10.1098/rspb.1949.0019. [DOI] [PubMed] [Google Scholar]
- 42.Huxley AF. Prog Biophys Biophys Chem. 1957;7:255–318. [PubMed] [Google Scholar]
- 43.Astumian RD. Top Curr Chem. 2015;369:285–316. doi: 10.1007/128_2015_644. [DOI] [PubMed] [Google Scholar]
- 44.Bustamante C, Chemla YR, Forde NR, Izhaky D. Annu Rev Biochem. 2004;73:705–748. doi: 10.1146/annurev.biochem.72.121801.161542. [DOI] [PubMed] [Google Scholar]
- 45.Mukherjee S, Warshel A. Proc Natl Acad Sci USA. 2015;112:2746–2751. doi: 10.1073/pnas.1500979112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Astumian RD. Appl Phys A. 2002;75:193–206. [Google Scholar]
- 47.Derényi I, Bier M, Astumian RD. Phys Rev Lett. 1999;83:903–906. [Google Scholar]
- 48.Astumian RD. Biophys J. 2015;108:291–303. doi: 10.1016/j.bpj.2014.11.3459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Astumian RD. Annu Rev Biophys. 2011;40:289–313. doi: 10.1146/annurev-biophys-042910-155355. [DOI] [PubMed] [Google Scholar]
- 50.Conyard J, Addison K, Heisler IA, Cnossen A, Browne WR, Feringa BL, Meech SR. Nat Chem. 2012;4:547–551. doi: 10.1038/nchem.1343. [DOI] [PubMed] [Google Scholar]
- 51.Hill TL, Eisenberg E, Chen YD, Podolsky RJ. Biophys J. 1975;15:335–372. doi: 10.1016/S0006-3495(75)85823-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.a) Xing J, Bai F, Berry R, Oster G. Proc Natl Acad Sci USA. 2006;103:1260–1265. doi: 10.1073/pnas.0507959103. [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Berry RM. Curr Biol. 2005;15:R385–R387. doi: 10.1016/j.cub.2005.05.004. [DOI] [PubMed] [Google Scholar]
- 53.Blackmond DG. Angew Chem Int Ed. 2009;48:2648–2654. doi: 10.1002/anie.200804566. [DOI] [PubMed] [Google Scholar]; Angew Chem. 2009;121:2686–2693. [Google Scholar]
- 54.Case DA, Karplus M. J Mol Biol. 1979;132:343–368. doi: 10.1016/0022-2836(79)90265-1. [DOI] [PubMed] [Google Scholar]
- 55.International Union of Pure and Applied Chemists (IUPAC) Compendium of Chemical Terminology. http://goldbook.iupac.org.
- 56.Ansari A, Berendzen J, Bowne SF, Frauenfelder H, Iben IE, Sauke TB, Shyamsunder E, Young RD. Proc Natl Acad Sci USA. 1985;82:5000–5004. doi: 10.1073/pnas.82.15.5000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Astumian RD, Chock PB, Tsong TY, Westerhoff HV. Phys Rev A. 1989;39:6416–6435. doi: 10.1103/physreva.39.6416. [DOI] [PubMed] [Google Scholar]
- 58.Cressman A, Togashi Y, Mikhailov AS, Kapral R. Phys Rev E. 2008;77:050901. doi: 10.1103/PhysRevE.77.050901. [DOI] [PubMed] [Google Scholar]
- 59.Lauga E. Soft Matter. 2011;7:3060–3065. [Google Scholar]
- 60.Sakaue T, Kapral R, Mikhailov AS. Eur Phys J B. 2010;75:381–387. [Google Scholar]
- 61.Einstein A, Ehrenfest P. Z Phys. 1923;19:301–306. [Google Scholar]
- 62.Bai X, Wolynes PG. J Chem Phys. 2015;143:165101. doi: 10.1063/1.4933424. [DOI] [PubMed] [Google Scholar]
- 63.Warshel A, Schlosser DW. Proc Natl Acad Sci USA. 1981;78:5564–5568. doi: 10.1073/pnas.78.9.5564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.a) Liphardt J. Nat Phys. 2012;8:638–639. [Google Scholar]; b) Riedel C, Gabizon R, Wilson CAM, Hamadani K, Tsekouras K, Marqusee S, Pressé S, Bustamante C. Nature. 2015;517:227–230. doi: 10.1038/nature14043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Warshel A. Methods Enzymol. 1986;127:578–587. [Google Scholar]
- 66.Marcus RA. Rev Mod Phys. 1993;65:599–610. [Google Scholar]
- 67.Turton DA, Senn HM, Harwood T, Lapthorn AJ, Ellis EM, Wynne K. Nat Commun. 2014;5:3999. doi: 10.1038/ncomms4999. [DOI] [PubMed] [Google Scholar]
- 68.Acbas G, Niessen KA, Snell EH, Markelz AG. Nat Commun. 2014;5:3076. doi: 10.1038/ncomms4076. [DOI] [PubMed] [Google Scholar]
- 69.McCammon JA, Wolynes PG, Karplus M. Biochemistry. 1979;18:927–942. doi: 10.1021/bi00573a001. [DOI] [PubMed] [Google Scholar]
- 70.Neumann J, Gottschalk KE, Astumian RD. ACS Nano. 2012;6:5242–5248. doi: 10.1021/nn301001s. [DOI] [PubMed] [Google Scholar]
- 71.Tierney HL, Murphy CJ, Jewell AD, Baber AE, Iski EV, Khodaverdian HY, McGuire AF, Klebanov N, Sykes ECH. Nat Nanotechnol. 2011;6:625–629. doi: 10.1038/nnano.2011.142. [DOI] [PubMed] [Google Scholar]
- 72.Michl J, Sykes ECH. ACS Nano. 2009;3:1042–1048. doi: 10.1021/nn900411n. [DOI] [PubMed] [Google Scholar]
- 73.Pisliakov AV, Cao J, Kamerlin SCL, Warshel A. Proc Natl Acad Sci USA. 2009;106:17359–17364. doi: 10.1073/pnas.0909150106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Olsson MHM, William A, Parson W, Warshel A. Chem Rev. 2006;106:1737–1756. doi: 10.1021/cr040427e. [DOI] [PubMed] [Google Scholar]
- 75.Kamerlin SCL, Warshel A. Proteins Struct Funct Bioinf. 2010;78:1339–1375. doi: 10.1002/prot.22654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Stackhouse J, Nambiar KP, Burbaum JJ, Stauffer DM, Benner SA. J Am Chem Soc. 1985;107:2757–2763. [Google Scholar]
- 77.Lehn JM. Chem Eur J. 2006;12:5910–5915. doi: 10.1002/chem.200600489. [DOI] [PubMed] [Google Scholar]
- 78.Eisenmesser EZ, Bosco DA, Akke M, Kern D. Science. 2002;295:1520–1523. doi: 10.1126/science.1066176. [DOI] [PubMed] [Google Scholar]
- 79.Richard EA, Miller C. Science. 1990;247:1208–1210. doi: 10.1126/science.2156338. [DOI] [PubMed] [Google Scholar]
- 80.Seow CY. J Gen Physiol. 2013;142:561–573. doi: 10.1085/jgp.201311107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Berry RM, Berg HC. Biophys J. 1999;76:580–587. doi: 10.1016/S0006-3495(99)77226-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Howard J. Curr Biol. 2006;16:R517–R519. doi: 10.1016/j.cub.2006.06.045. [DOI] [PubMed] [Google Scholar]
- 83.Hill TL, Eisenberg E. Q Rev Biophys. 1981;14:463–511. doi: 10.1017/s0033583500002468. [DOI] [PubMed] [Google Scholar]
- 84.Liu DS, Astumian RD, Tsong TY. J Biol Chem. 1990;265:7260–7267. [PubMed] [Google Scholar]
- 85.a) Astumian RD, Chock PB, Tsong TY, Chen YD, Westerhoff HV. Proc Natl Acad Sci USA. 1987;84:434–438. doi: 10.1073/pnas.84.2.434. [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Xie TD, Marszalek P, Chen YD, Tsong TY. Biophys J. 1994;67:1247–1251. doi: 10.1016/S0006-3495(94)80594-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Astumian RD, Robertson B. J Am Chem Soc. 1993;115:11063–11068. [Google Scholar]
- 87.Astumian RD. Phys Rev Lett. 2003;91:118102. doi: 10.1103/PhysRevLett.91.118102. [DOI] [PubMed] [Google Scholar]
- 88.Astumian RD. Proc Natl Acad Sci USA. 2007;104:19715–19718. [Google Scholar]
- 89.Ragazzon G, Baroncini M, Silvi S, Venturi M, Credi A. Nat Nanotechnol. 2015;10:70–75. doi: 10.1038/nnano.2014.260. [DOI] [PubMed] [Google Scholar]
- 90.Tretiakov KV, Szleifer I, Grzybowski BA. Angew Chem Int Ed. 2013;52:10304–10308. doi: 10.1002/anie.201301386. [DOI] [PubMed] [Google Scholar]; Angew Chem. 2013;125:10494–10498. [Google Scholar]
- 91.Cheng C, McGonigal PR, Schneebeli ST, Li H, Vermeulen NA, Ke C, Stoddart JF. Nat Nanotechnol. 2015;10:547–553. doi: 10.1038/nnano.2015.96. [DOI] [PubMed] [Google Scholar]
- 92.Chatterjee MN, Kay ER, Leigh DA. J Am Chem Soc. 2006;128:4058–4073. doi: 10.1021/ja057664z. [DOI] [PubMed] [Google Scholar]
- 93.Feld GK, Brown MJ, Krantz BA. Protein Sci. 2012;21:606–624. doi: 10.1002/pro.2052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Bauer J, Hou L, Kistemaker JCM, Feringa BL. J Org Chem. 2014;79:4446–4455. doi: 10.1021/jo500411z. [DOI] [PubMed] [Google Scholar]
- 95.Li H, Cheng C, McGonigal PR, Fahrenbach AC, Frasconi M, Liu WG, Zhu Z, Zhao Y, Ke C, Lei J, Young RM, Dyar SM, Co DT, Yang YW, Botros YY, Goddard WA, III, Wasielewski MR, Astumian RD, Stoddart JF. J Am Chem Soc. 2013;135:18609–18620. doi: 10.1021/ja4094204. [DOI] [PubMed] [Google Scholar]
- 96.Jencks WP. Annu Rev Biochem. 1997;66:1–18. doi: 10.1146/annurev.biochem.66.1.1. [DOI] [PubMed] [Google Scholar]
- 97.Alhadeff R, Warshel A. Proc Natl Acad Sci USA. 2015;112:12378–12383. doi: 10.1073/pnas.1516881112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Alvarez-Pérez M, Goldup SM, Leigh DA, Slawin AMZ. J Am Chem Soc. 2008;130:1836–1838. doi: 10.1021/ja7102394. [DOI] [PubMed] [Google Scholar]
- 99.Henkelis JJ, Blackburn AK, Dale EJ, Vermeulen NA, Nassar MS, Stoddart JF. J Am Chem Soc. 2015;137:13252–13255. doi: 10.1021/jacs.5b08656. [DOI] [PubMed] [Google Scholar]
- 100.Share AI, Parimal K, Flood AH. J Am Chem Soc. 2010;132:1665–1675. doi: 10.1021/ja908877d. [DOI] [PubMed] [Google Scholar]
- 101.Makhlynets OV, Raymond EA, Korendovych IV. Biochemistry. 2015;54:1444–1456. doi: 10.1021/bi5015248. [DOI] [PubMed] [Google Scholar]
- 102.Deckert K, Budiardjo SJ, Brunner LC, Lovell S, Karanicolas J. J Am Chem Soc. 2012;134:10055–10060. doi: 10.1021/ja301409g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Lehn JM. Angew Chem Int Ed. 2013;52:2836–2850. doi: 10.1002/anie.201208397. [DOI] [PubMed] [Google Scholar]; Angew Chem. 2013;125:2906–2921. [Google Scholar]
- 104.Schmittel M. Chem Commun. 2015;51:14956–14968. doi: 10.1039/c5cc06605k. [DOI] [PubMed] [Google Scholar]
- 105.Kassem S, Lee A, Leigh DA, Markevicius A, Sola J. Nat Chem. 2016;8:138–143. doi: 10.1038/nchem.2410. [DOI] [PubMed] [Google Scholar]