Cation-selective channel is regulated by anions according to their Hofmeister ranking

Abstract

Specificity of small ions, the Hofmeister ranking, is long-known and has many applications including medicine. Yet it evades consistent theoretical description. Here we study the effect of Hofmeister anions on gramicidin A channels in lipid membranes. Counterintuitively, we find that conductance of this perfectly cation-selective channel increases about two-fold in the H₂PO₄⁻<Cl⁻≈Br⁻≈NO₃⁻<ClO₄⁻<SCN⁻ series. Channel dissociation kinetics show even stronger dependence, with the dwell time increasing ~20-fold. While the conductance can be quantitatively explained by the changes in membrane surface potential due to exclusion of kosmotropes from (or accumulation of chaotropes at) the surface, the kinetics proved to be more difficult to treat. We estimate the effects of changes in the energetics at the bilayer surfaces on the channel dwell time, concluding that the change would have to be greater than typically observed for the Hofmeister effect outside the context of the lipid bilayer.

Ion specificity and, in particular, the distinctive effects of anions in salt-induced protein precipitation have been known since the 1880’s, when Franz Hofmeister established the ranking of anions in their ability to regulate egg yolk protein water solubility ^[1]. Experimental and theoretical studies have given a detailed empirical picture of the phenomenon, the nature of the ionic interactions with the surfaces leading to the Hofmeister effect is still under debate ^[2]. The only consensus is that it cannot be explained by standard theories of electrolytes. For example, bromide is unique in that its salts were recognized as a drug to treat epilepsy a couple of dozen years before Hofmeister’s studies ^[3] and they are still in use to treat specific types of refractory seizures in children ^[4], but the mechanism of their action remains elusive.

Graphical Abstract

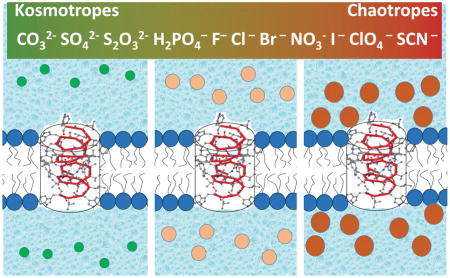
Hofmeister effect studied with a nanopore in a neutral lipid membrane. Rather unexpectedly, we find that conductance of a purely cation-selective peptide pore is regulated by anions in correlation with their position in the Hofmeister series. Moreover, the pore conformational dynamics are highly sensitive to the anion species. We relate both effects to preferential depletion of kosmotropic anions (accumulation of chaotropic anions) at the membrane-water interface.

The Hofmeister ranking of salts has been a frequent target of biological studies (see ^[5] and ^[2a] for recent reviews), including channel-facilitated membrane transport ^[6]. In the present work, we take advantage of arguably the simplest ion transport model of modern biophysics – the channel formed by a linear pentadecapeptide, gramicidin A (grA) ^[7]. We find that the conductance of this perfectly cation-selective channel is sensitive to anion type in correlation with its position in the Hofmeister series. The conductance increases nearly by a factor of two from KH₂PO₄ to KSCN in 200 mM solutions. The effect on the channel dwell time is even more pronounced.

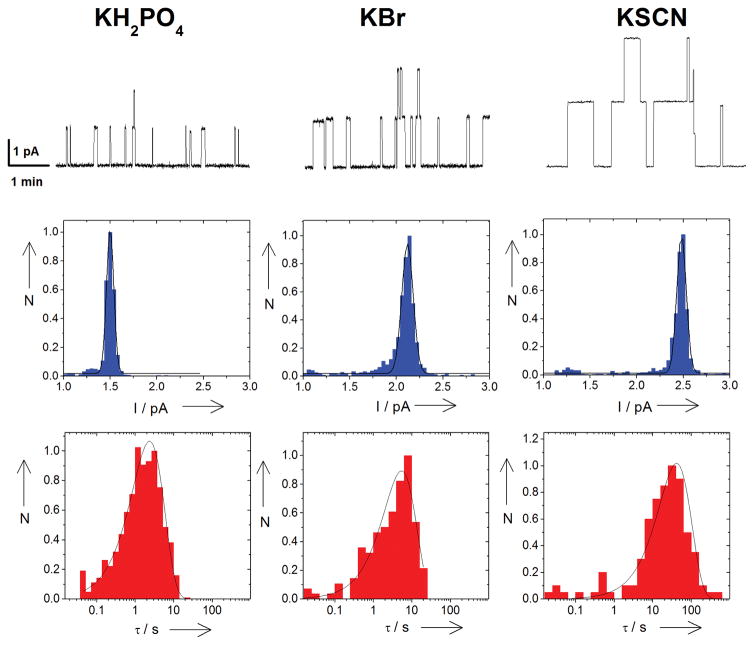
Upper row of Figure 1 shows three samples of 5 minute recordings of ion currents through a bilayer with spontaneously associating and dissociating grA channels bathed by potassium salts with different Hofmeister anions. Both channel conductance and dwell time depend on the anion species. At the constant voltage of 100 mV applied to the membrane, the current through the channel is significantly larger in KSCN than in KH₂PO₄. KSCN enhances channel stability: substantially longer dwell times are observed than those with KH₂PO₄. Examples of the statistical analyses of these raw data are shown below as ion current histograms (middle row) and log-binned dwell time histograms (bottom row).

Figure 1.

Upper row: Records of ion currents through single grA channels in DPhPC bilayers demonstrate that both channel conductance and dwell time depend on the anion species. Middle: Current histograms (normalized event counts, N, vs channel current, pA) fitted by Gaussian distributions. Bottom: Dwell time (τ, s) log-binned histograms fitted by single exponential distributions. Salt concentrations are 200 mM, transmembrane voltage is 100 mV.

Results of the statistical analysis of channel conductance are given in Figure 2. They demonstrate a good correlation with the anion position in the original Hofmeister series ^{[1, 5]}, showing conductance increase from KH₂PO₄ to KSCN. Importantly, the channel stays cation-selective for all these salts. The inset in Fig. 2 shows that for both KH₂PO₄ and KSCN, the most kosmotropic and most chaotropic anions, respectively, used in the present study, the reversal potentials measured at asymmetric salt conditions have the values expected for an ideally cation-selective channel.

Figure 2.

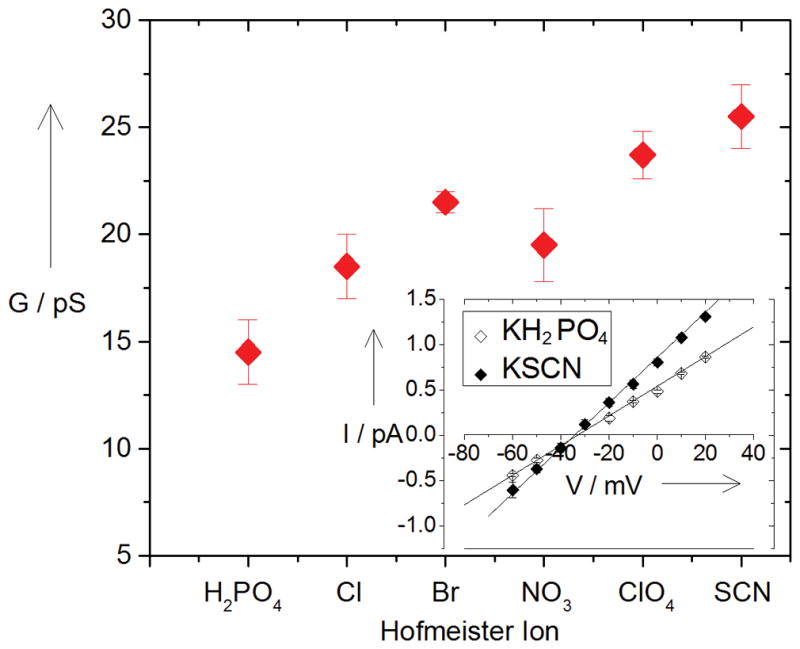
Statistical analysis of currents, examples of which are shown in Fig. 1, demonstrates an about two-fold increase in the channel conductance (G, pS) along the series KH₂PO₄ < KCl ≈ KBr ≈ KNO₃ < KClO₄ < KSCN. Inset: Measurements of the current (pA) reversal potentials (mV) for 0.5 M vs 0.1 M (cis vs trans) solutions of KH₂PO₄ and KSCN. Obtained transport numbers for cations (t+) are t+ = 1.00 ± 0.03 for KH₂PO₄ and t+ = 0.97±0.03 for KSCN.

We now rationalize the dependence of the conductance of this perfectly cation-selective channel on anion species-dependent changes in the membrane surface potential, similarly to those observed for the water-air interface ^[8]. To independently verify such a possibility we first measured zeta potentials of small unilamellar liposomes of the same lipid composition as that used for the bilayers as a function of salt concentration for KSCN and KH₂PO₄. Figure 3 shows that for 200 mM solutions of the two salts, the potentials differ significantly, with KSCN at −25 mV and KH₂PO₄ about +5 mV.

Figure 3.

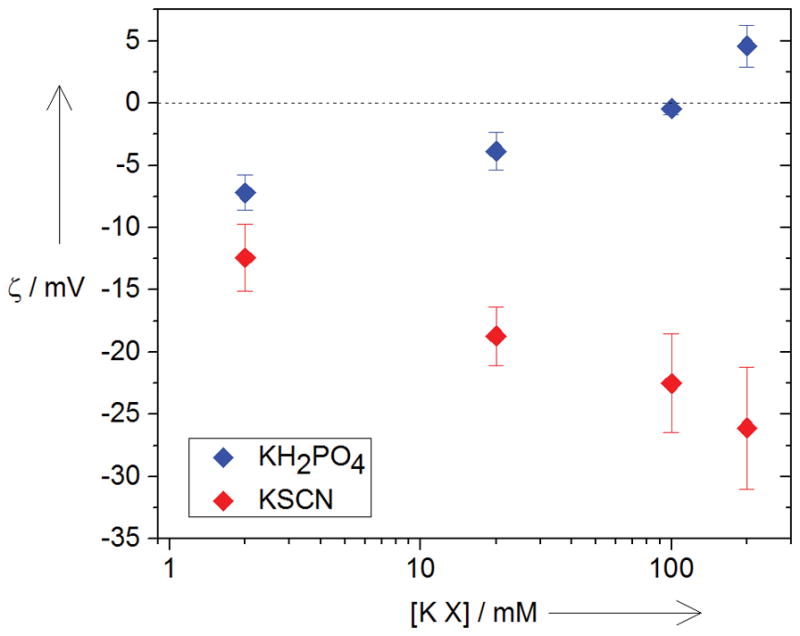
Zeta potentials (ζ, mV) of small unilamellar liposomes as functions of salt concentration show effects of opposite signs for KH₂PO₄ and KSCN.

The 30 mV difference in zeta potentials is sufficient to affect channel conductance. This conclusion follows from studies that explored the effect of the surface charge on conductance of various ion-selective channels ^[9].

Membrane Surface Electrostatics

Theoretical analysis of the relation between channel conductance and bilayer surface electrostatics is complicated by channel geometry and the possibility of lipid-induced changes in channel conformation that are not directly related to the lipid charge, as demonstrated for the BK Ca²⁺–activated potassium channel ^[10]. Nevertheless, in many cases electrostatic considerations work well even at the quantitative level ^[9e]. One study ^[11] analyzed several alternative ways to evaluate the surface charge effect by assuming that the channel conductance is proportional to the concentration of permeant cations at its entrance.

We use the approach in which the surface potential is multiplied by the Debye screening factor, shown to work best if an effective separation was chosen as a = 4Å ^[11]. Following this approach we relate the measured channel conductance g⁽ⁱ⁾ to the surface potential ${\psi }_0^{(i)}$ in the presence of anion species i as

$$g^{(i)}\propto exp\left[-\frac{e{\psi }_0^{(i)}}{k_{B}T}exp\left(-a\sqrt{2e^{2}c/k_{B}T\epsilon {\epsilon }_0}\right)\right],$$ Eq 1

where k_B and T are the Boltzmann constant and absolute temperature, respectively, c is salt concentration, e is the absolute value of electron charge, and εε₀ is dielectric constant of water. Thus, for the difference in potentials $\mathrm{\Delta }{\psi }_0^{(i,j)}$ that is necessary to account for the ratio g⁽ⁱ⁾/g^(j) of channel conductances in the presence of anion species i and j we have

$$\mathrm{\Delta }{\psi }_0^{(i,j)}=\frac{k_{B}T}{e}exp\left(a\sqrt{2e^{2}c/k_{B}T\epsilon {\epsilon }_0}\right)ln\frac{g^{(i)}}{g^{(j)}},$$ Eq 2

The predicted differences in the membrane surface potentials in the presence of 200 mM potassium salt solutions are given in Table 1. The potential in KCl was used as a reference because it gives the smallest modification of the surface potential ^{[8, 12]}.

Table 1.

Predicted differences of surface potential in the presence of 200 mM K salts

Anion	H2PO4−	Cl−	Br −	NO3−	ClO4−	SCN −
Δψ0, mV	+14.2±5.0	0	−6.8±3.1	−2.4± 3.9	−11.2±3.1	−15.0±2.6

Thus, the surface potential reports on non-electrostatic interactions between anions and membrane. It changes from +14 mV to −15 mV along the series H₂PO₄⁻ > Cl⁻ ≈ Br⁻ ≈ NO₃⁻ > ClO₄⁻ > SCN⁻. In particular, for KH₂PO₄ vs. KSCN the difference is close to 30 mV, in satisfactory agreement with the measured liposome zeta-potential difference (Fig. 3). Thus, accumulation of chaotropic anions at the bilayer surface, with a similar sequence also found for supported membranes ^[2b], produces a negative potential that increases channel conductance relative to its value in KCl; the cosmotropes, which (relatively) prefer bulk water to the bilayer surface, have the opposite effect.

Bilayer Mechanics

The elastic properties of lipid bilayers are recognized as important factors in regulation of the functions of membrane-embedded proteins ^[13]. According to the hydrophobic mismatch idea ^[13a–e], the difference between the hydrophobic “thickness” of the protein and the bilayer creates a bilayer deformation with an energetic penalty. Protein conformational transitions that change protein thickness also change the bilayer deformation and thus change the free energy balance that governs the protein functional properties. Modeling the major contributions to the deformation energy requires the monolayer compressibility K_A, bending modulus k_c, and surface tension. Changes in bilayer mechanics have a profound effect on the dwell time of the grA dimer and are shown to dominate dissociation kinetics ^[7]. Membrane mechanical parameters can be manipulated by the choice of different lipids or varying pH ^[14]. In the present study this is achieved by using different anions of the Hofmeister series.

Figure 4 shows the change in the channel dwell time (τ, s) as a function of anion species. The effect is much more extensive than that on the channel conductance. It is seen that substitution of H₂PO₄⁻ by SCN⁻ increases the dwell time by more than an order of magnitude.

Figure 4.

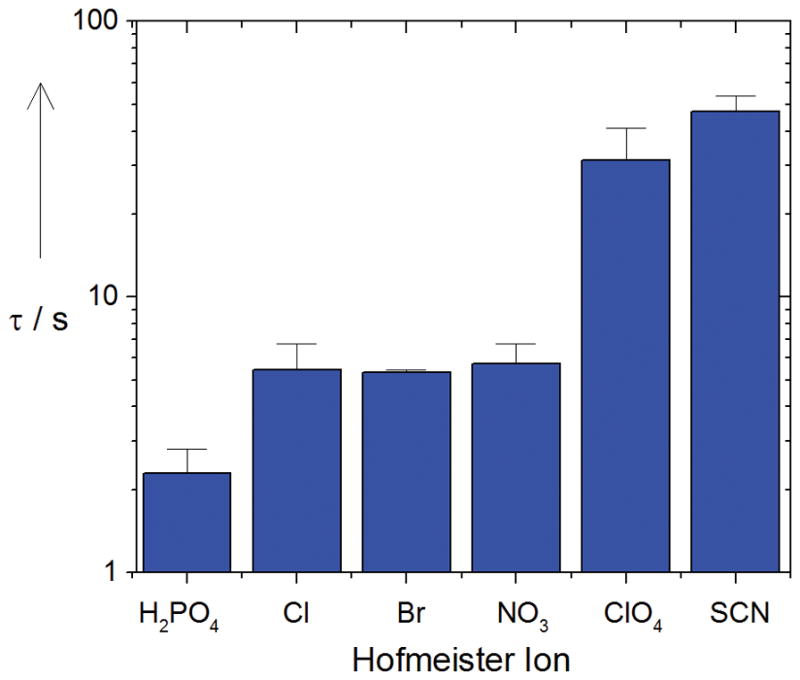
Channel dwell times increase about 20-fold along the series KH₂PO₄ < KCl ≈ KBr ≈ KNO₃ < KClO₄ < KSCN.

Change of bilayer mechanical properties with surface pressure

Andersen and coworkers have described the dependence of the channel dwell time on bilayer material properties ^[15]. The dimer and transition state for dissociation have different effective mismatch Δh and Δh − δ, respectively. The phenomenological model of the free energy, F is ^[16]:

$$F=H{(\mathrm{\Delta }h)}^2,$$ Eq 3

with H an experimentally determined force constant. The change in F between the transition state (t.s.) and dimer state is:

$$\mathrm{\Delta }{E}_{\text{def}.,\mathrm{t}.\mathrm{s}.}=H{(\mathrm{\Delta }h-\delta )}^2-H{(\mathrm{\Delta }h)}^2=H\delta (\delta -2\mathrm{\Delta }h)$$ Eq 4

The value must be ~ 2 kcal/mol to achieve a factor of 20 in dwell times between ions at the opposite ends of the Hofmeister scale

A molecular theory for how anions associated with the surface could affect bilayer properties (e.g., H) is provided by Evans’ application of polymer brush theory ^[17]. In this model, two competing forces determine the thickness and stiffness of the bilayer. First, the positive surface pressure Π shrinks the leaflet surface area to lessen polar/apolar surface exposure. Second, tail entropy favors larger surface area for which they are less confined. The effect of the anions near the surface is to modify the value of Π, for example, by reducing the magnitude of the hydrophobic effect. Polymer brush theory relates the degree of tail confinement (as a result of Π) to compressibility that directly changes H. In the Supporting Information, polymer brush theory is applied to determine that a 12.1 mN/m change in the surface pressure is necessary for this molecular explanation. Experimental and theoretical studies of salt influence on the water-air and water-oil interface tension ^{[12, 18]} demonstrate that, indeed, the tension is sensitive to anion species, but the maximum change for 0.2 M monovalent salt concentrations is under 0.5 mN/m. For this explanation the effect must be dramatically stronger for amphiphilic surfaces compared to oil.

Literature concerning the mechanisms of grA channel sensitivity to different parameters of the environment is vast. In our treatment we limited ourselves to those that are carefully quantified. Still other possibilities to consider may include regulation of the dwell time by the membrane dipole potential ^[19] and by peptide-lipid headgroup interactions ^[20], which could be differently modified by the anionic species used in the present work.

Conclusions

We used grA channel as a nanopore probe to study effects of Hofmeister anions on membrane and membrane-peptide interactions. It turns out that both the conductance of this perfectly cation-selective channel and its dwell time depend on the anions according to their position in the “direct Hofmeister series” ^[2c]. While the two-fold change in conductance along the series can be satisfactory explained, and even quantified, the mechanism of the 20-fold change in the rate of channel dissociation remains unclear. The salt-induced change in membrane mechanics and the stabilizing action of the occupancy of the channel by permeating cations ^[21], seem to account only for a much smaller, well under factor of 2, change of the rate. Thus, though this simple biophysical reasoning predicts correctly the trend of the changes in dwell times, it does not give the magnitudes of the changes, which suggest that more specific effects are involved. One of the possibilities is that the effect may be much stronger for lipid surfaces compared to oil or air. We believe that our results are of importance for further progress in understanding of ion specificity, which manifests itself in many physicochemical and biological phenomena ^[2a] including the more than century-old medical applications ^[3–4].