Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Aug 12;16(9):5333–5339. doi: 10.1021/acs.nanolett.6b01060

Radiatively Limited Dephasing and Exciton Dynamics in MoSe2 Monolayers Revealed with Four-Wave Mixing Microscopy

Tomasz Jakubczyk †,‡, Valentin Delmonte †,‡, Maciej Koperski §,∥, Karol Nogajewski §, Clément Faugeras §, Wolfgang Langbein ⊥, Marek Potemski §, Jacek Kasprzak †,‡,*
PMCID: PMC5518748  PMID: 27517124

Abstract

graphic file with name nl-2016-010607_0008.jpg

By implementing four-wave mixing (FWM) microspectroscopy, we measure coherence and population dynamics of the exciton transitions in monolayers of MoSe2. We reveal their dephasing times T2 and radiative lifetime T1 in a subpicosecond (ps) range, approaching T2 = 2T1 and thus indicating radiatively limited dephasing at a temperature of 6 K. We elucidate the dephasing mechanisms by varying the temperature and by probing various locations on the flake exhibiting a different local disorder. At the nanosecond range, we observe the residual FWM produced by the incoherent excitons, which initially disperse toward the dark states but then relax back to the optically active states within the light cone. By introducing polarization-resolved excitation, we infer intervalley exciton dynamics, revealing an initial polarization degree of around 30%, constant during the initial subpicosecond decay, followed by the depolarization on a picosecond time scale. The FWM hyperspectral imaging reveals the doped and undoped areas of the sample, allowing us to investigate the neutral exciton, the charged one, or both transitions at the same time. In the latter, we observe the exciton–trion beating in the coherence evolution indicating their coherent coupling.

The identification of atomically thin solids1 resulted in the development of the intriguing physics of graphene, followed by the emerging technological applications.2,3 Also, it stimulated a rapid progress in fundamental studies of thin films extracted from other than graphite layered materials, such as semiconducting transition metal dichalcogenides (S-TMDs). The bandgap of S-TMDs converts from indirect to direct, when reducing the material thickness to a single monolayer,4 enabling exceptionally strong excitonic transitions. Owing to the breakdown of out of plane translational symmetry for two-dimensional systems, the coupling of excitons with light is boosted,5 resulting in their short radiative lifetime and thus increased oscillator strength μ. Excitons in S-TMD monolayers display large binding energies EB of several hundreds of meV6−9—an increase by 1–2 orders of magnitude with respect to a typical semiconductor quantum well.10,11 The observed excitonic absorption in S-TMDs reaches the values as high as 10%,12 illustrating an exceptionally strong μ in these systems and implying a radiative lifetime in the subpicosecond (subps) range,13 as recently observed in monolayers of WSe214,15 and other emerging two-dimensional systems, namely, nanoplatelets.27 The robust coupling with light is attractive in prospective applications, especially for photodetectors.3 It is also appealing in optical fundamental studies, for instance in polaritonics16 and nonlinear spectroscopy.15,17,19

The large μ in S-TMDs gives rise to a giant nonlinear optical response, which is investigated in this work via three-pulse four-wave mixing (FWM) microspectroscopy. This approach offers a direct access to the exciton coherence and population dynamics with a time resolution limited only by the duration of the laser pulses, which resonantly excite targeted optical transitions. Indeed, time-resolved nonresonant photoluminescence measurements,18 offer insufficient time-resolution to infer subps evolution and involve complex relaxation pathways. Instead, resonant experiments,15,19 also investigating internal transitions14 occurring in the THz domain, have recently revealed ultrafast radiative recombination of the exciton ground state in WSe2.

In this work, we show that the optical dephasing time T2 of the neutral exciton transition (EX) in a monolayer of MoSe2 is intrinsically limited by the EX ultrafast radiative recombination T1. In contrast to previous works inferring optical coherence in S-TMDs,15,19 we take advantage of the microspectroscopy approach, employing the laser beams focused down to the diffraction limited size of 0.7 μm (full width at half-maximum, fwhm). Such implementation is used to perform the FWM hyperspectral imaging,20 which discriminates the exciton charge state across the sample and helps to reveal the striking features of coherent coupling between the neutral and charged excitons. We demonstrate that the EX linear response inferred via microreflectance is affected by the inhomogeneous broadening ξ also on a subμm scale, evidenced by the photon echo formation in the FWM transients.21 The analysis of the FWM delay dependence yields T2 ≃ 2T1, occurring on a subps time scale. A spatially resolved study shows that T2 depends on the local disorder varying on a subμm scale. From the temperature-dependent homogeneous line width, we determine the dephasing due to phonon interaction. We also monitor the density dynamics of excitons, which is governed by the interplay between bright states within the light cone and various available dark states.

Sample and Experiment

The investigated MoSe2 monolayerw were fabricated by means of polydimethylsiloxane-based exfoliation of bulk crystals, purchased from HQ Graphene, and transferred onto a Si/SiO2 substrate. Relatively large monolayer flakes of up to (50 × 50) μm2 size have been obtained and placed in an optical He-flow cryostat.

To infer both the coherence and the population dynamics of excitons, we retrieved their FWM by implementing a three-beam configuration20 of the heterodyne spectral interferometry.21 This technique has been proven as an efficient detection scheme of optical nonlinearities in a solid, until now only employed to retrieve wave mixing signals generated by individual transitions in semiconductor quantum dots.20,21,25 FWM is an optical polarization created with short, resonant driving pulses; 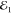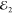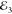Inline graphic, Inline graphic and Inline graphic, as depicted in Figure 1 a. In the third-order (χ(3)) regime its amplitude is proportional to 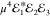Inline graphic. Thus, owing to a large μ, a dramatic enhancement of FWM is expected in MoSe2 monolayers. Note that the * stands for the complex conjugate, which is the origin of the FWM rephasing in inhomogeneously broadened systems,21 generating the photon echo (as also sketched in Figure 1a), which acts as a probe of the microscopic dephasing.

Figure 1.

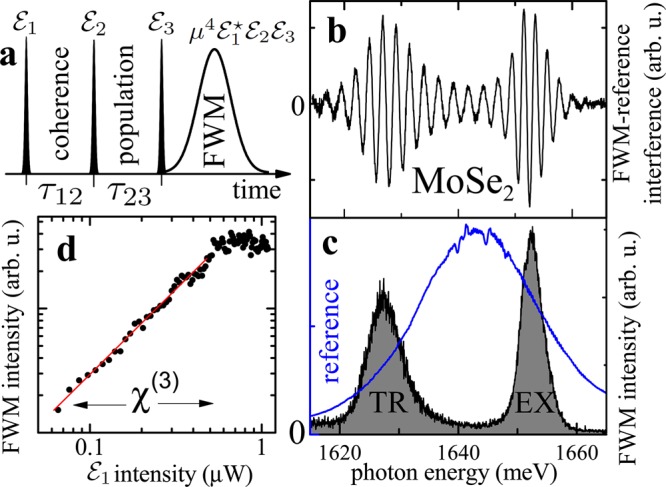
Figure 1

Open in a new tab

Four-wave mixing spectroscopy of the MoSe2 monolayer. (a) Pulse sequence employed in FWM experiments and related observables. (b) FWM spectral interferogram obtained on the flake position displaying the exciton (EX) and trion (TR) transitions. (c) FWM intensity (black) retrieved from (b) via spectral interferometry. Inline graphic is shown with a blue line. (d) Spectrally integrated FWM intensity of EX as a function of Inline graphic intensity, showing the driving range yielding the χ(3) regime of the FWM.

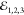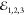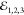Micro-FWM spectroscopy requires the colinear arrangement of the driving fields Inline graphic, which is enabled by phase-selecting the signal through optical heterodyning.21 By employing acousto-optic modulation, Inline graphic are frequency up-shifted by radio-frequencies, introducing controlled phase-drifts in their respective pulse trains generated by a Ti:sapphire femtosecond laser. 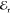After acquiring the delays τ12 and τ23, introduced by a pair of mechanical delay lines, Inline graphic are recombined into a common spatial mode and are focused on the sample with the microscope objective. 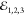The reference beam Inline graphic, used in the heterodyne mixing and interferometric detection, is also focused at the sample, yet is vertically displaced with respect to Inline graphic by around 12 μm.

The time-ordering of the pulses is presented on Figure 1 a: measuring time-integrated FWM detected at the Ω3 + Ω2 – Ω1 heterodyne frequency, as a function of τ12 (τ23), yields the coherence (population) dynamics of an optical transition. The FWM signal is measured in reflectance, attaining a shot-noise detection limit and rejecting the resonant driving fields 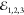Inline graphic with 106 (1012) selectivity in field (intensity). The interference between the heterodyned signal and 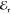Inline graphic is spectrally resolved with an imaging spectrometer. Further details regarding the current experimental implementation are given in ref (20).

In Figure 1b we present a typical spectral interference between 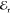Inline graphic and the FWM at a temperature T = 5 K for τ12 = 0. The FWM intensity is retrieved by spectral interferometry and shown in Figure 1c. The signal consists of two transitions identified as the ground state–exciton (EX) and the single electron–trion transitions (TR).22 In Figure 1 d we present the FWM intensity of EX as a function of 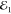Inline graphic intensity demonstrating a linear dependence in the χ(3) regime, as expected. 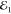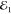Note that the FWM can be driven with a Inline graphic intensity as low as a few tens of nW, corresponding to a few hundreds of photons per pulse Inline graphic and generating a low carrier density, less than 109/cm2. Such density is far below the saturation density23 estimated at around 1013/cm2. In our study, we therefore consider the creation of excitons with K ∼ 0 center of mass momentum, which appear at the K+ and K–, points of the Brillouin zone of the S-TMD crystal. Those excitons can either decay radiatively or disperse out of the light cone (K > nω/c) via phonon scattering. The latter process occupies dark exciton states, which relax back to K < nω/c on a pico-second time scale and eventually recombine. Further relaxation pathways are scattering electrons and holes between the K-points.

Hyperspectral Imaging

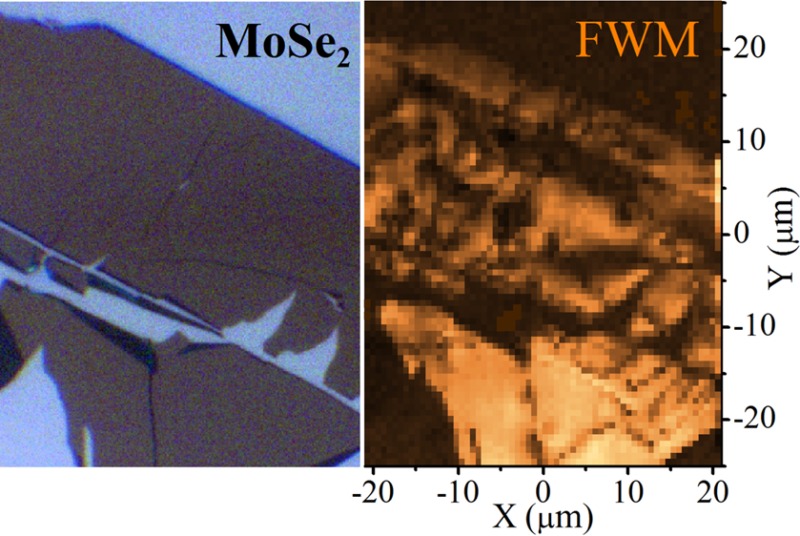
An image of the studied MoSe2 monolayer is shown in Figure 2 and in the Table of Contents graphics. The microspectroscopy approach enables to perform FWM hyperspectral imaging,20,25 allowing us to identify regions of the flake dominated by the FWM of EX or TR (see Figure 2b and c). Clearly, the two images are complementary, which permits to distinguish regions of different resident carrier concentration. In the following experiments, the performed imaging allowed us to selectively address EX or TR or to drive simultaneously both transitions.

Figure 2.

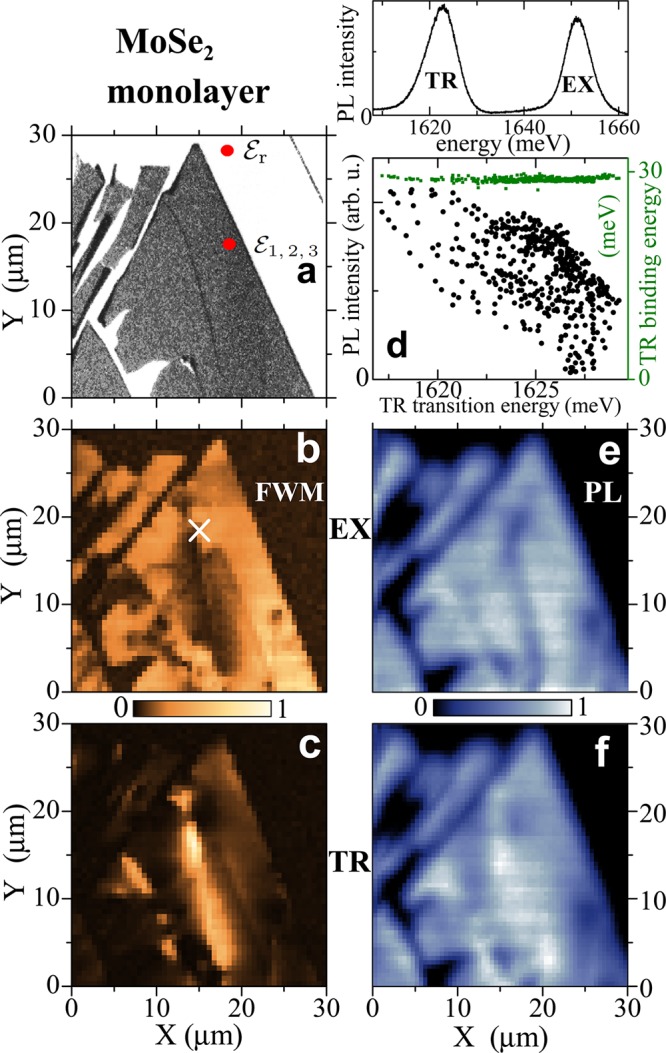
Figure 2

Open in a new tab

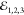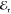Hyperspectral mapping of the MoSe2 monolayer. (a) Optical contrast of the sample observed in reflectance. Red dots indicate Inline graphic and Inline graphic. (b–c) Spatial imaging of the FWM amplitude, spectrally averaged over the exciton (b) response, centered at ∼1650 meV and the trion (c) at ∼1625 meV. Heterodyning at the FWM frequency Ω3 + Ω2 – Ω1 with τ12 = τ23 = 50 fs, T = 6 K. (d) Top: A typical PL spectrum, nonresonantly excited at ∼1750 meV (∼710 nm) with ≃0.1 μW average power arriving at the sample surface, displaying bright emission from EX and TR, with integrated count rate of 350 kHz for each transition. Bottom: Correlation between the PL intensity of the TR (black) and its binding energy (green), as a function of its transition energy. (e–f) PL imaging of TR and EX, respectively. Excitation conditions as in d. Linear color scale, as shown by horizontal bars.

Performing microspectroscopy also permits to locally address subμm regions of smaller spectral inhomogeneous broadening with respect to the total area of the flake. To exemplify this, we have performed a statistical analysis of the microphotoluminescence (PL) hyperspectral imaging. Similarly as in Figure 1 c, confocally detected PL spectra yield EX and TR transitions, as displayed at the top of Figure 2d. We observe particularly bright emission, with a photon flux per second of 108–109, indicating a high quantum yield.

For every spatial position, we have determined the integrated intensity for both transitions and their center energies. For the latter, we observe the spread over ξ ≃ 10 meV, as displayed at the bottom of Figure 2 d. Interestingly, despite this large, macroscopic ξ, the trion binding energy Δ remains well-defined, Δ = (28.8 ± 0.3) meV. We note that the lower the TR transition energy, the higher its intensity is measured. In our understanding this reflects the distribution of residual electrons in the sample. Interestingly, however, such correlation is not observed for EX, i.e., the EX intensity is not sensitive to the apparent changes in the charge density in our sample.

In Figure 2 e and f we present the PL imaging spectrally integrated over EX and TR transition, respectively. By comparing it with Figure 2 b and c, we point out two advantages of our original FWM imaging with respect to the routinely performed PL one. First, owing to the third-power scaling of the FWM intensity with the excitation power, combined with heterodyning with 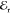Inline graphic, the spatial resolution in the FWM imaging is enhanced26 up to 0.3λ/NA ≈ 360 nm, surmounting the standard diffraction limit by a factor of 2. Second, the FWM yields a significantly improved imaging selectivity of EX and TR across the flake. In fact, different properties are inferred in both experiments. The FWM directly probes μ of the resonantly generated excitons at the K-points of the valleys. Instead, the nonresonant PL reflects more complex carrier relaxation along the valleys toward their K-points, prior to the exciton formation, followed by their radiative recombination.

Coherence Dynamics

The strength of the FWM spectroscopy in assessing the coherence in solids lies in its capability to separate homogeneous (γ) and inhomogeneous (ξ) contributions of the transition’s spectral width. In particular, in a presence of ξ, the time-resolved FWM amplitude exhibits a photon echo,15,27 which decays as exp(−2τ12/T2). Hence, to investigate the exciton coherence dynamics, we measured FWM as a function of τ12. Time-resolved FWM amplitude of the EX transition, displayed in Figure 3a, clearly demonstrates formation of the photon echo. From its temporal width we estimate the local ξ to be in a few meV range. Figure 3b shows the time-integrated FWM as a function of τ12. The data are modeled by a convolution of a Gaussian profile with an exponential decay. The former exhibits the fwhm width of 0.15 ps, reflecting duration of 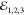Inline graphic impinging the sample. Instead, from the latter we retrieve at T = 6 K the dephasing time T2 = 2ℏ/γ = 620 ± 20 fs, and thus γ ≃ 2.1 meV (fwhm). For simplicity, the dynamics owing to the echo formation process close to zero delay has been here disregarded. The homogeneous broadening γ is around twice smaller than the transition line width directly measured via microreflectivity, as shown in the inset of Figure 3b and also in FWM (see Figure 1c). We thus conclude that the line-shape remains affected by the inhomogeneous broadening ξ, even though a subμm area is probed.

Figure 3.

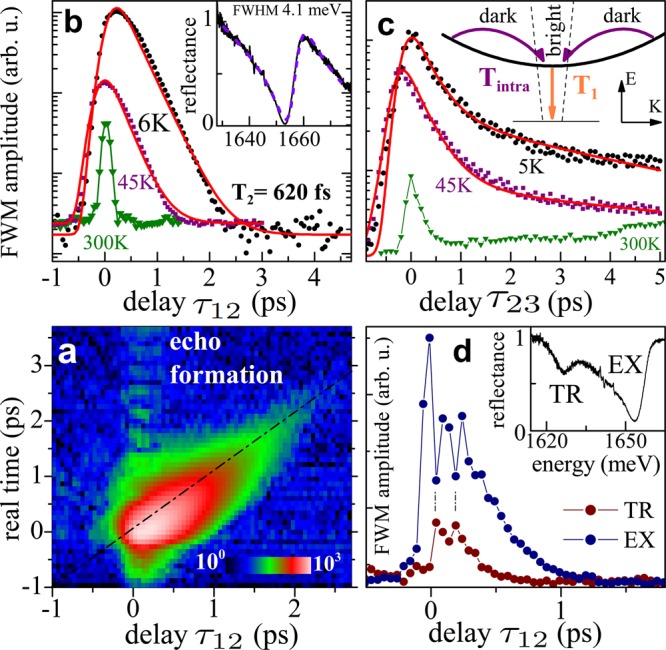
Figure 3

Open in a new tab

Exciton dynamics in the MoSe2 monolayer inferred with FWM microscopy. (a) Time-resolved FWM amplitude as a function of τ12, showing the formation of a photon echo: a Gaussian signal with a maximum for t = τ12. Logarithmic color scale is given by the color bar. (b) FWM amplitude as a function of τ12 retrieved from the EX at T = 6, 45, and 300 K given by black circles, purple squares, and green triangles, respectively. The simulations yielding T2 ≃ 620 and 520 fs are given by red traces. Inset: reflectance measured at T = 6 K yielding 4.1 meV fwhm. (c) Cartoon of the considered radiative recombination and intravalley relaxation processes is presented in the inset. The initial dynamics of the EX population measured at 5, 45, and 300 K, color coding as in b. The results yield radiative lifetime T1 and relaxation time Tintra (see main text). (d) τ12 dependence of the FWM amplitude when simultaneously driving the EX (blue) and TR (brown) transitions, revealing a beating with 140 fs period, and thus indicating EX–TR coherent coupling. The location of the excitation is marked with a cross in Figure 2 b, while the corresponding microreflectance spectrum is given in the inset.

With increasing temperature, T2 is expected to decrease,15 owing to phonon scattering. This is highlighted in Figure 3 b. At T = 45 K the dephasing accelerates, and we measure T2 = 520 ± 40 fs. At ambient temperature the dephasing occurs at a time scale faster than 100 fs and is not resolved by our setup, although a pronounced FWM is still measured. We note that for the TR transition at T = 6 K we find T2 = (460 ± 30) fs and similar inhomogeneous broadening as for EX, also generating a photon echo as in Figure 3c (not shown). This shorter dephasing of the charged exciton is tentatively interpreted in terms of the final state damping, due to the energy distribution of final state energies of the leftover electron.

In Figure 3c we present the coherence dynamics measured at the boundary of the doped and undoped regions of the flake, marked with a cross in Figure 2d, such that the FWM of both EX and TR is driven in tandem. We observe a beating, withstanding on both transitions during initial positive delays τ12, up to around 700 fs when the TR coherence virtually vanishes. The beating period of ζ = 140 fs (marked with a pair of vertical lines), well corresponds to the EX–TR binding energy Δ = 2πℏ/ζ ≃ 29 meV and thus indicates their coherent coupling.28,29

To gain a deeper understanding of the exciton ultrafast dynamics, we have combined the enhanced spatial and temporal resolution of our experiment and we have performed spatially resolved dephasing study at T = 6 K. Within an area of 8 μm × 8 μm, displaying uniquely the EX transition, we have scanned the coherence dynamics with a spatial step of 0.66 μm. The analysis of the obtained statistics of dephasing, reveals variations of T2 within the probed area from around 0.5 ps up to 1.5 ps. Interestingly, the locations on the flake yielding the shortest T2 also display the broadest photon echo, and thus the smallest ξ. Conversely, the longest T2 is measured on the areas characterized by a larger ξ, and thus showing the narrowest photon echo, here limited by the temporal duration of the laser pulses. An example of such two representative cases is displayed in Figure 4a and b. The spatially resolved dephasing experiment indicates that T2 is governed by a local disorder, realizing various localization potentials. The resulting spatially dependent coherence volume of EX has a direct impact on its radiative lifetime T1: the fastest recombination is expected at the areas of the smallest ξ, as indeed measured.

Figure 4.

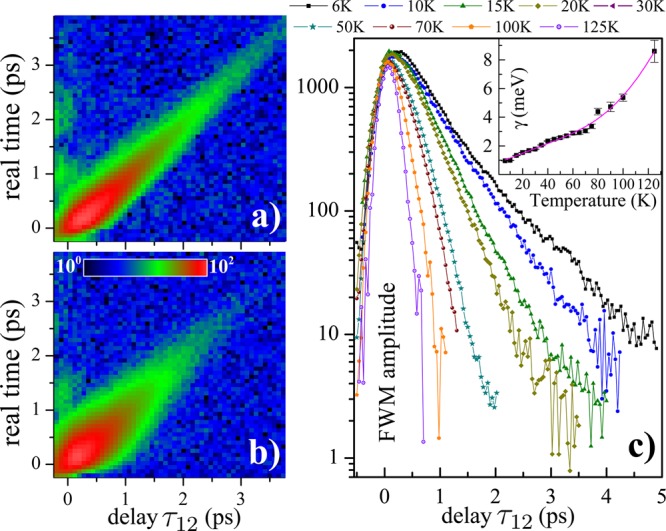
Figure 4

Open in a new tab

Impact of a local disorder and temperature on the exciton dephasing in the MoSe2 monolayer. (a) Time-resolved FWM amplitude, measured on the location displaying a larger ξ, showing a temporarily narrowed photon echo. The observed increased dephasing time with respect to Figure 3 attributed to a localization induced increase of the radiative lifetime T1. (b) As in panel a but measured on the area showing a broader echo and thus smaller ξ. A weaker localization yields a shorter T1 = T2/2 than in panel a. Logarithmic color scale over 2 orders of magnitude. (c) FWM amplitude dynamics as a function of temperature measured on the area as in a. Above T = 125 K the dephasing is faster than the temporal resolution of the experiment. The temperature-dependent homogeneous broadening γ = 2ℏ/T2 (inset) indicates the phonon-induced dephasing mechanism. For clarity, the fits are not shown.

In Figure 4c we present the coherence dynamics on the chosen area exhibiting an increased T2, measured from 6 to 150 K. The data clearly show a gradual decrease of T2 with temperature from 1.4 to 0.2 ps, respectively, adding to the measurements shown in Figure 3b. The retrieved γ = 2ℏ/T2 is plotted in the inset. It can be modeled with a linear dependence and an additional bosonic term:41 γ(T) = γ0 + aT + b/(exp(E1/kBT) – 1). The linear term (γ0 = 0.78 ± 0.11 meV, a = 0.03 ± 0.003 meV/K) is due to low energy acoustic phonons. The latter term, with the energy E1 = 43 ± 4 meV and b = 187 ± 75 meV, could be attributed to thermal activation of higher energy optical phonons.41 The phonon dephasing mechanisms are therefore similar as in semiconductor quantum wells.

Population Dynamics

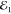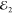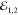In the following, the FWM is employed to infer the EX population dynamics after their resonant and selective excitation in a given valley (Inline graphic and Inline graphic, denoted as Inline graphic, are cocircularly polarized). They arrive at the flake with virtually no delay generating exciton population. Owing to the large μ, the excitons exhibit fast radiative decay. Nevertheless, they still experience scattering24 for instance induced by defects, disorder and phonons, which can efficiently redistribute them out of the light cone (marked with dashed lines in the inset of Figure 3c), toward K > nω/c. This type of scattering is particularly efficient in S-TMDs: due to heavy masses (and thus flat bands at the bottom of the branches) and large γ, the excitons’ center of mass scatter out of the light cone at practically no cost in energy. As a result, the major part of the created population instantly decays with its radiative lifetime T1, while the remaining part spreads along the dispersion branch populating dark states (i.e., outside the light cone). Also a part of these excited excitons eventually relax toward the bottom of the valley with a characteristic time Tintra and recombine radiatively, as depicted in Figure 3c. In the dynamics probed with FWM, we disregard the influence of strongly localized, quantum-dot like states, due to their small density and we disregard nonradiative Auger processes,14 as we operate at low exciton densities.

The FWM therefore probes all the above-mentioned processes via τ23 dependence. This is shown in Figure 3c, for the EX (obtained the same spatial position as in Figure 3b) for driving upon cocircular polarization of 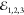Inline graphic. The data are modeled with a double exponential decay convoluted with the Gaussian laser pulse, showing temporal width of 0.16 ps (fwhm). From the initial decay we retrieve the exciton lifetime of T1 = 390 ± 20 fs, while the FWM for further delays τ23 yields the intravalley relaxation time of Tintra = 4.3 ± 0.6 ps. At T = 45 K we measure instead T1, Tintra = 0.42 ± 0.01, 6.84 ± 0.38 ps. An increase of Tintra with temperature is attributed to Boltzmann distribution of excitons, allowing for reaching higher energies and K-vectors out of the light cone, and also to access different dark states offered by the structure of the valley excitons.

A physical picture arising from the FWM experiment at low temperature is that the initial exciton decay with the time T1, covering an order of magnitude in amplitude (see Figure 3c), is due to the radiative recombination, while the nonradiative processes are of minor impact, as they are not faster than the Tintra (we assume they have the same dynamics for both bright and dark excitons). Importantly, comparing the T1 with T2 times, we conclude that the dephasing is principally due to the radiative decay, nearing to the radiative limit. Observation of the radiatively limited dephasing is a prerequisite for implementing more advanced optical coherent control schemes in S-TMDs.

We point out that the dynamics of the secondary, incoherent excitons—here probed by τ23 dependence of FWM—is particularly complex and might be influenced by a set of unconventional features present in S-TMDs. One should bear in mind coupling with and scattering toward counter-polarized K-valleys and spin-split bands, relevant in formation of exciton complexes. In fact, triple degeneracy of the K-valleys, enables various configurations for bright and dark exciton states, as previously considered for other systems hosting multiexcitons.30,31 We also point out exotic dispersion relations for the center-of-mass momentum.32 Thus, we refrain from firm interpretation and first-principle modeling of the secondary exciton dynamics, displayed in Figure 5 on a 100 ps time scale.

Figure 5.

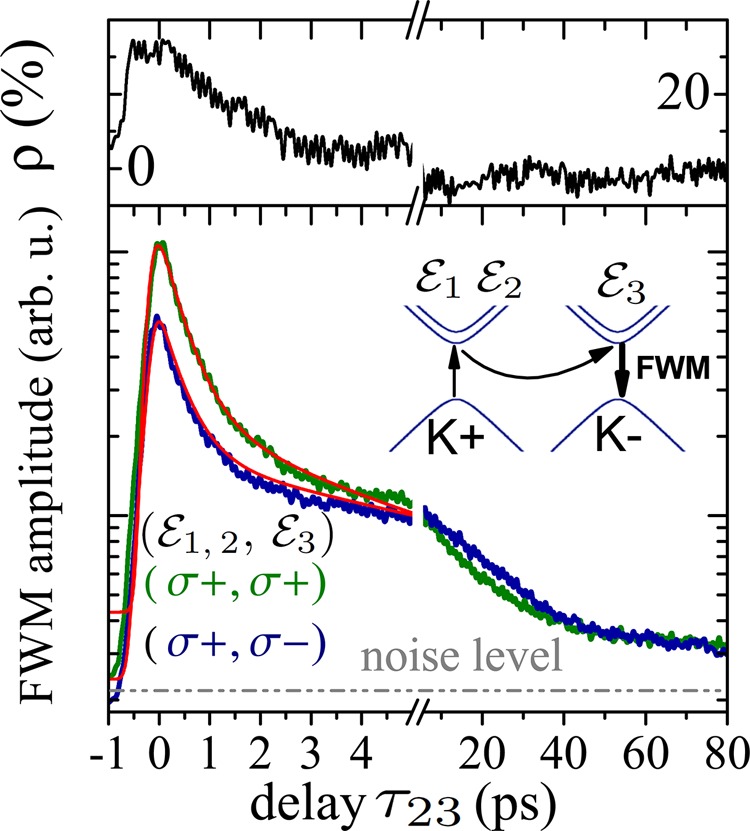
Figure 5

Open in a new tab

Intervalley population dynamics in the MoSe2 monolayers investigated with the polarization-resolved driving of the FWM. Bottom: FWM amplitude versus τ23 of the EX transition obtained at T = 6 K upon co- (green trace) and cross-circular (blue trace) setting of 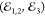Inline graphic. The modeling, as in Figure 3c, is displayed as red lines. Equivalent dynamics have been measured (not shown) for a counter-polarized driving (σ+ → σ−). Inset: Rationale of the intervalley dynamics probed with FWM using polarization-resolved driving: 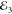Inline graphic induces the FWM signal in a given valley, which originates from the population generated in the counter- or copolarized valley, by setting counter- or cocircular 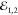Inline graphic, respectively. Top: τ23 delay dependence of the measured circular polarization degree, ρ(τ23). We measure ρ(τ23) of several tens of percent for initial delays τ23, followed by a total depolarization of the FWM, generated by the secondary exciton population (see the main text).

Intervalley Dynamics

Below, we present the FWM results obtained upon polarization-resolved driving, employed to investigate exciton scattering between counter-polarized valleys, and thus testing the robustness of the pseudospin degree of freedom. The reciprocal space of TMD monolayers displays nonequivalent bands with the extrema at K-points,33−35 labeled as K+ and K–. The dipole-allowed transitions in these two valleys can be selectively addressed by circularly polarized light, σ+ and σ–, respectively. The light helicity is therefore considered as an asset to drive, manipulate, and read the state of the valley subspaces. The valley polarization,34 although protected by the strong spin–orbit splitting in the valence band, decays mainly due to the to electron–hole exchange interaction.36,37 Since the stability of this degree of freedom is required in prospective applications of TMDs, intense efforts are currently devoted to study its dynamics and to reveal the mechanisms that govern it,38 in particular in a presence of spin-forbidden transitions.12,39,40,42−44

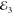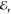To infer the exciton intervalley dynamics, we implemented polarization-resolved excitation of the FWM signal. Specifically, Inline graphic and Inline graphic are set as cocircular. Instead, the circular polarization of 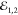Inline graphic is opposite, such that FWM probes the conversion of the exciton population between K+ and K– valleys,35 as depicted in Figure 5. 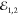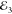Instead, to probe the exciton dynamics in the same valley, we set the cocircular polarization of Inline graphic and Inline graphic. The measurement is presented in Figure 5 (bottom). As in Figure 3 c, we observe an initial fast decay of the radiatively recombining excitons within the first picoseconds and subsequent recombination of the secondary excitons. The early dynamics for both polarization configuration is not the same during initial several picoseconds of τ23. Instead, for longer delays, τ23 > 10 ps, the measured FWM (generated by the secondary excitons) is the same for both driving configurations.

We calculate the FWM circular polarization degree, which we define as 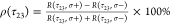Inline graphic, where R denotes the spectral FWM amplitude. The resulting ρ(τ23) is plotted at the top of Figure 5. We thus do observe a significant pseudospin polarization around zero delay, ρ(τ23) ≃ 0) ≃ 30%, which however vanishes extremely rapidly, within around 5 ps, such that ρ(τ23) = 0 for τ23 > 10 ps. We therefore show that under resonant excitation it is possible to generate valley-polarized excitons in MoSe2 monolayers, but confirm their rapid depolarization. This result brings new input toward a firm understanding of an intriguingly weak efficiency of optical pumping in MoSe2 monolayers, as opposed to other S-TMDs.45 The circular polarization degree, relevant for valleytronics applications, could be stabilized by using magnetic fields38 or by fabricating more involved heterostructures46,47 based on S-TMDs.

When analyzing Figure 5 it is worth noting a large fraction of the FWM response within initial several picoseconds for both polarization configurations, as compared to the subsequent dynamics. This shows that the exciton density is mainly removed radiatively within the subps radiative lifetime T1, as discussed before.

Conclusions

By performing FWM spectroscopy, we have demonstrated a giant, optical, coherent, nonlinear response of exciton transitions in MoSe2 monolayers. We find an increase in the FWM amplitude by 2 orders of magnitude, as compared to a high-quality CdTe semiconductor quantum well (not shown), emitting at the similar wavelength and excitation power. Taking advantage of the microscopy approach, we have performed the hyperspectral imaging, which allowed us to accurately determine the areas yielding FWM responses of either neutral or charged excitons, or both. Electrical gating of such structures could enable spectral control of coherent responses from TMDs, providing insights into the mutual influence of TR and EX onto their dynamics. Using two-beam FWM microspectroscopy, we have measured the excitons’ coherence evolution, accessing dephasing times T2, which turn out to be intrinsically limited by the radiative lifetime. The inhomogeneous broadening on a subμm range is reduced by an order of magnitude with respect to the size of the flake, although still gives rise to the photon echo. We have also shown that T2 spatially varies across the flake, as the T1 is governed by the local disorder, determining the exciton localization. Microscopic measurement of the FWM response is therefore required to accurately assess these parameters. Prospective experiments, exploiting two-dimensional FWM spectroscopy, will ascertain coupling mechanisms between exotic valley–exciton species offered by S-TMDs. Our approach could be used to retrieve coherent responses of the localized exciton states in S-TMDs,48 which are expected to exhibit ultralong dephasing.49 Finally, by exploiting polarization-resolved, three-beam FWM we assessed the exciton population dynamics, revealing the interplay between the subps radiative decay T1 and the intravalley relaxation Tintra of the excitons scattered toward the dark states, revisiting the light–matter coupling in two-dimensional systems.5

Acknowledgments

We acknowledge the support by the ERC Starting Grant PICSEN contract no. 306387 and the ERC Advanced Grant MOMB contract no. 320590. We thank G. Nogues and M. Richard for helpful remarks on the manuscript. We also acknowledge the support from Nanofab facility of the Institute Néel, CNRS UGA.

The authors declare no competing financial interest.

References

  1. Novoselov K. S.; Geim A. K.; Morozov S. V.; Jiang D.; Zhang Y.; Dubonos S. V.; Grigorieva I. V.; Firsov A. A. Science 2004, 306, 666–669. 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
  2. Fiori G.; Bonaccorso F.; Iannaccone G.; Palacios T.; Neumaier D.; Seabaugh A.; Banerjee S. K.; Colombo L. Nat. Nanotechnol. 2014, 9, 768–779. 10.1038/nnano.2014.207. [DOI] [PubMed] [Google Scholar]
  3. Koppens F. H. L.; Mueller T.; Avouris P.; Ferrari A. C.; Vitiello M. S.; Polini M. Nat. Nanotechnol. 2014, 9, 780–793. 10.1038/nnano.2014.215. [DOI] [PubMed] [Google Scholar]
  4. Mak K. F.; Lee C.; Hone J.; Shan J.; Heinz T. F. Phys. Rev. Lett. 2010, 105, 136805. 10.1103/PhysRevLett.105.136805. [DOI] [PubMed] [Google Scholar]
  5. Deveaud B.; Clérot F.; Roy N.; Satzke K.; Sermage B.; Katzer D. S. Phys. Rev. Lett. 1991, 67, 2355. 10.1103/PhysRevLett.67.2355. [DOI] [PubMed] [Google Scholar]
  6. Ye Z.; Cao T.; O’Brien K.; Zhu H.; Yin X.; Wang Y.; Louie S. G.; Zhang X. Nature 2014, 513, 214–218. 10.1038/nature13734. [DOI] [PubMed] [Google Scholar]
  7. Chernikov A.; Berkelbach T. C.; Hill H. M.; Rigosi A.; Li Y.; Aslan O. B.; Reichman D. R.; Hybertsen M. S.; Heinz T. F. Phys. Rev. Lett. 2014, 113, 076802. 10.1103/PhysRevLett.113.076802. [DOI] [PubMed] [Google Scholar]
  8. Wang G.; Marie X.; Gerber I.; Amand T.; Lagarde D.; Bouet L.; Vidal M.; Balocchi A.; Urbaszek B. Phys. Rev. Lett. 2015, 114, 097403. 10.1103/PhysRevLett.114.097403. [DOI] [PubMed] [Google Scholar]
  9. Olsen T.; Latini S.; Rasmussen F.; Thygesen K. S. Phys. Rev. Lett. 2016, 116, 056401. 10.1103/PhysRevLett.116.056401. [DOI] [PubMed] [Google Scholar]
  10. Leavitt R. P.; Little J. W. Phys. Rev. B: Condens. Matter Mater. Phys. 1990, 42, 11774. 10.1103/PhysRevB.42.11774. [DOI] [PubMed] [Google Scholar]
  11. Andreani L. C. In Confined Electrons and Photons: New Physics and Applications; Burstein E., Weisbuch C., Eds.; Nato Science Series: B Physics; Plenum Press: New York, 1995; Vol. 340; pp 57–112. [Google Scholar]
  12. Arora A.; Koperski M.; Nogajewski K.; Marcus J.; Faugeras C.; Potemski M. Nanoscale 2015, 7, 10421–10429. 10.1039/C5NR01536G. [DOI] [PubMed] [Google Scholar]
  13. Palummo M.; Bernardi M.; Grossman J. C. Nano Lett. 2015, 15, 2794. 10.1021/nl503799t. [DOI] [PubMed] [Google Scholar]
  14. Poellmann C.; Steinleitner P.; Leierseder U.; Nagler P.; Plechinger G.; Porer M.; Bratschitsch R.; Schüller C.; Korn T.; Huber R. Nat. Mater. 2015, 14, 889–893. 10.1038/nmat4356. [DOI] [PubMed] [Google Scholar]
  15. Moody G.; Dass C. K.; Hao K.; Chen C.-H.; Li L.-J.; Singh A.; Tran K.; Clark G.; Xu X.; Berghaüser G.; Malic E.; Knorr A.; Li X. Nat. Commun. 2015, 6, 8315. 10.1038/ncomms9315. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Liu X.; Galfsky T.; Sun Z.; Xia F.; Lin E.-C.; Lee Y.-H.; Kéna-Cohen S.; Menon V. M. Nat. Photonics 2014, 9, 30–34. 10.1038/nphoton.2014.304. [DOI] [Google Scholar]
  17. Malard L. M.; Alencar T. V.; Barboza A. P. M.; Mak K. F.; de Paula A. M. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 201401. 10.1103/PhysRevB.87.201401. [DOI] [Google Scholar]
  18. Lagarde D.; Bouet L.; Marie X.; Zhu C. R.; Liu B. L.; Amand T.; Tan P. H.; Urbaszek B. Phys. Rev. Lett. 2014, 112, 047401. 10.1103/PhysRevLett.112.047401. [DOI] [PubMed] [Google Scholar]
  19. Hao K.; Moody G.; Wu F.; Dass C. K.; Xu L.; Chen C.-H.; Li M.-Y.; Li L.-J.; MacDonald A. H.; Li X. Nat. Phys. 2016, 12, 677. 10.1038/nphys3674. [DOI] [Google Scholar]
  20. Fras F.; Mermillod Q.; Nogues G.; Hoarau C.; Schneider C.; Kamp M.; Höfling S.; Langbein W.; Kasprzak J. Nat. Photonics 2016, 10, 155. 10.1038/nphoton.2016.2. [DOI] [Google Scholar]
  21. Langbein W.; Patton B. Phys. Rev. Lett. 2005, 95, 017403. 10.1103/PhysRevLett.95.017403. [DOI] [PubMed] [Google Scholar]
  22. Wang G.; Palleau E.; Amand T.; Tongay S.; Marie X.; Urbaszek B. Appl. Phys. Lett. 2015, 106, 112101. 10.1063/1.4916089. [DOI] [Google Scholar]
  23. Jones A. M.; Yu H.; Ghimire N. J.; Wu S.; Aivazian G.; Ross J. S.; Zhao B.; Yan J.; Mandrus D. G.; Xiao D.; Yao W.; Xu X. Nat. Nanotechnol. 2013, 8, 634. 10.1038/nnano.2013.151. [DOI] [PubMed] [Google Scholar]
  24. Langbein W.; Runge E.; Savona V.; Zimmermann R. Phys. Rev. Lett. 2002, 89, 157401. 10.1103/PhysRevLett.89.157401. [DOI] [PubMed] [Google Scholar]
  25. Kasprzak J.; Patton B.; Savona V.; Langbein W. Nat. Photonics 2011, 5, 123. 10.1038/nphoton.2011.13. [DOI] [Google Scholar]
  26. Langbein W. Rivista del nuovo cimento 2010, 33, 255–312. [Google Scholar]
  27. Naeem A.; Masia F.; Christodoulou S.; Moreels I.; Borri P.; Langbein W. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 121302. 10.1103/PhysRevB.91.121302. [DOI] [Google Scholar]
  28. Singh A.; Moody G.; Wu S.; Wu Y.; Ghimire N. J.; Yan J.; Mandrus D. G.; Xu X.; Li X. Phys. Rev. Lett. 2014, 112, 216804. 10.1103/PhysRevLett.112.216804. [DOI] [Google Scholar]
  29. Hao K.; Xu L.; Nagler Ph.; Singh A.; Tran K.; Dass Ch.; Schuller Ch.; Korn T.; Li X.; Moody G. Nano Lett. 2016, 16, 5109. 10.1021/acs.nanolett.6b02041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Masia F.; Langbein W.; Moreels I.; Hens Z.; Borri P. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83, 201305. 10.1103/PhysRevB.83.201309. [DOI] [Google Scholar]
  31. An J. M.; Franceschetti A.; Zunger A. Nano Lett. 2007, 7, 2129. 10.1021/nl071219f. [DOI] [Google Scholar]
  32. Qiu D. Y.; Cao T.; Louie S. G. Phys. Rev. Lett. 2015, 115, 176801. 10.1103/PhysRevLett.115.176801. [DOI] [PubMed] [Google Scholar]
  33. Xiao D.; Liu G.-B.; Feng W.; Xu X.; Yao W. Phys. Rev. Lett. 2012, 108, 196802. 10.1103/PhysRevLett.108.196802. [DOI] [PubMed] [Google Scholar]
  34. Jones A. M.; Yu H.; Ghimire N. J.; Wu S.; Aivazian G.; Ross J. S.; Zhao B.; Yan J.; Mandrus D. G.; Xiao D.; Yao W.; Xu X. Nat. Nanotechnol. 2013, 8, 634–638. 10.1038/nnano.2013.151. [DOI] [PubMed] [Google Scholar]
  35. Xu X.; Yao W.; Xiao D.; Heinz T. F. Nat. Phys. 2014, 10, 343–350. 10.1038/nphys2942. [DOI] [Google Scholar]
  36. Yu T.; Wu M. W. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89, 205303. 10.1103/PhysRevB.89.205303. [DOI] [Google Scholar]
  37. Glazov M. M.; Amand T.; Marie X.; Lagarde D.; Bouet L.; Urbaszek B. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89, 201302. 10.1103/PhysRevB.89.201302. [DOI] [Google Scholar]
  38. Smoleński T.; Goryca M.; Koperski M.; Faugeras C.; Kazimierczuk T.; Nogajewski K.; Kossacki P.; Potemski M. Phys. Rev. X 2016, 6, 021024. 10.1103/PhysRevX.6.021024. [DOI] [Google Scholar]
  39. Zhang X.-X.; You Y.; Zhao S. Y. F.; Heinz T. F. Phys. Rev. Lett. 2015, 115, 257403. 10.1103/PhysRevLett.115.257403. [DOI] [PubMed] [Google Scholar]
  40. Wang G.; Robert C.; Suslu A.; Chen B.; Yang S.; Alamdari S.; Gerber I. C.; Amand T.; Marie X.; Tongay S.; Urbaszek B. Nat. Commun. 2015, 6, 10110. 10.1038/ncomms10110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Horzum S.; Sahin H.; Cahangirov S.; Cudazzo P.; Rubio A.; Serin T.; Peeters F. M. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 125415. 10.1103/PhysRevB.87.125415. [DOI] [Google Scholar]
  42. Wang G.; Robert C.; Suslu A.; Chen B.; Yang S.; Alamdari S.; Gerber I. C.; Amand T.; Marie X.; Tongay S.; Urbaszek B. Nat. Commun. 2015, 6, 10110. 10.1038/ncomms10110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Echeverry J. P.; Urbaszek B.; Amand T.; Marie X.; Gerber I. C. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93, 121107. 10.1103/PhysRevB.93.121107. [DOI] [Google Scholar]
  44. Withers F.; Del Pozo-Zamudio O.; Schwarz S.; Dufferwiel S.; Walker P. M.; Godde T.; Rooney A. P.; Gholinia A.; Woods C. R.; Blake P.; Haigh S. J. Nano Lett. 2015, 15, 8223–8228. 10.1021/acs.nanolett.5b03740. [DOI] [PubMed] [Google Scholar]
  45. Dery H.; Song Y. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 125431. 10.1103/PhysRevB.92.125431. [DOI] [Google Scholar]
  46. Rivera P.; Schaibley J. R.; Jones A. M.; Ross J. S.; Wu S.; Aivazian G.; Klement P.; Seyler K.; Clark G.; Ghimire N. J.; Yan J.; Mandrus D. G.; Yao W.; Xu X. Nat. Commun. 2015, 6, 6242. 10.1038/ncomms7242. [DOI] [PubMed] [Google Scholar]
  47. Rivera P.; Seyler K. L.; Yu H.; Schaibley J. R.; Yan J.; Mandrus D. G.; Yao W.; Xu X.. arXiv:1601.02641, 2016. [Google Scholar]
  48. Koperski M.; Nogajewski K.; Arora A.; Cherkez V.; Mallet P.; Veuillen J.-Y.; Marcus J.; Kossacki P.; Potemski M. Nat. Nanotechnol. 2015, 10, 503–506. 10.1038/nnano.2015.67. [DOI] [PubMed] [Google Scholar]
  49. Schaibley J. R.; Karin T.; Yu H.; Ross J. S.; Rivera P.; Jones A. M.; Scott M. E.; Yan J.; Mandrus D. G.; Yao W.; Fu K.-M.; Xu X. Phys. Rev. Lett. 2015, 114, 137402. 10.1103/PhysRevLett.114.137402. [DOI] [PubMed] [Google Scholar]

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES