Cell mechanics: a dialogue

Abstract

Under the microscope, eukaryotic animal cells can adopt a variety of different shapes and sizes. These cells also move and deform, and the physical mechanisms driving these movements and shape changes are important in fundamental cell biology, tissue mechanics, as well as disease biology. This article reviews some of the basic mechanical concepts in cells, emphasizing continuum mechanics description of cytoskeletal networks and hydrodynamic flows across the cell membrane. We discuss how cells can generate movement and shape changes by controlling mass fluxes at the cell boundary. These mass fluxes can come from polymerization/depolymerization of actin cytoskeleton, as well as osmotic and hydraulic pressure-driven flow of water across the cell membrane. By combining hydraulic pressure control with force balance conditions at the cell surface, we discuss a quantitative mechanism of cell shape and volume control. The broad consequences of this model on cell mechanosensation and tissue mechanics are outlined.

1. Introduction

In a cluttered corridor of a rather drab-looking concrete laboratory tower, a young graduate student, S, is walking briskly, immersed in thought. She is on her way to a meeting with her mentors, still dressed in a stained lab coat and clutching safety glasses. These weekly meetings are a part of her interdisciplinary training program, where researchers from physics and cell biology are brought together to tackle basic biophysics questions. Today, she just completed a round of laboratory experiments, and now her mind is brimming with excitement and questions. The door is open, and in seconds she is in the office of biology professor B.

Her co-mentors, physics professor P together with B, are already seated at the small conference table. S gives a slight nod in their direction and sits down.

S: This week, I performed live cell microscopy experiments on different types of eukaryotic cells. I was able to capture images of several fluorescently labeled cytoplasmic proteins and the cell membrane. What I saw was fascinating! Cells seem to have a mind of their own, and can take on variety of shapes and sizes. Cells can also migrate and change shapes at different stages of their cell cycle (figure 1). What are the molecular components that allow cells to behave this way? Cytoplasmic proteins I observed also can move and form patterns that are correlated with the cell shape and cell movement. Do we understand how cells control their shape and movement?

Figure 1.

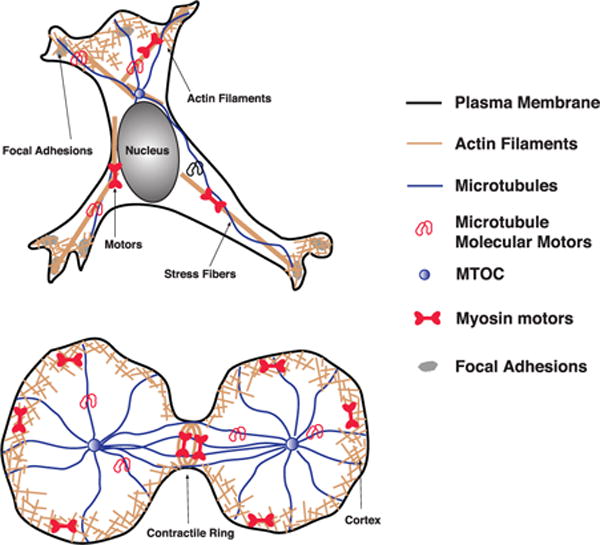
Living animal cells must move and deform to accomplish essential processes such as cell division or cell motility. These active movements are thought to be generated by cytoskeletal filaments and molecular motors within the cell. Motors such as myosin can generate contractile forces within actin networks. Actin filaments can also polymerize, and together with actin binding proteins to form loose open networks such as the lamellipodium, or bundled structures such as stress fibers. These structural elements in the cell can all influence the shape and movement of cell boundaries.

B: These are of course key questions in understanding how cells work. We now know the genetic sequences of many organisms, and it is fairly straightforward to find out the protein content (the proteome) of a given cell type [1]. But how these expressed proteins are organized and controlled to perform essential cell functions like movement and division are still not clear. There is a lack of quantitative models that adequately address phenomena at the cell scale. From experiments, it is also apparent that there are higher-order mechanical structures in the cell. For instance, we know that the cytoplasm of the cell is not a structureless liquid. There are complex micron-sized assemblies such as cross-linked actin filament networks, microtubules and intermediate filaments [2–7]. These filaments are very dynamic, undergoing cycles of polymerization and depolymerization, regulated by other proteins. In addition, organelles such as the nucleus, mitochondria and endoplasmic reticulum have dynamic and distinct shapes as well [8]. Several different types of molecular motors also work together with the cytoskeleton filaments to generate movement and transport within the cell [9–11].

S: So how do cells uses these elements to actively move, divide and change shape?

2. Forces and conservation laws

P: Newton’s laws state that motion is related to forces. In the context of cells, we clearly see a lot of movement, and forces can be generated in several ways. Molecular motors can directly provide forces derived from small molecules such as ATP or GTP. These motor molecules make small (nanometer-sized) conformational changes during the ATP hydrolysis cycle [11–13]. When many of these molecules sum up their forces, large cell-scale forces are developed. But there are other ways of generating forces as well. From fundamental conservation laws, mass transport is connected to momentum flux and therefore movement. For a continuous material with density ρ, fundamental mass conservation is [14, 15]

$$\frac{\partial \rho }{\partial t}+\nabla \cdot \mathbf{g}=J$$ (1)

where g = ρv is the momentum density and v is the spatial velocity field. J is a source (or sink) term coming from an external mass flux. For simplicity, let us consider the cell as a 1D continuum strip of material with length L (figure 2(A)), and the mass flux can come from material outside of the cell or added from the cytoplasmic fluid phase. There is new mass added at the front x = x₂, and mass is removed at the back, x = x₁. Therefore the source term can be written as J=J₂δ(x−x₂) − J₁δ(x−x₁) If the material density ρ is constant, then the mass conservation equation is simply

$$\rho \frac{\partial v_x}{\partial x}=0$$ (2)

for x∈(x₁,x₂) implying that the velocity field inside (x₁,x₂) is a constant. However, from overall mass conservation (x₁,x₂) must be changing. Since the overall mass balance within the domain is

$${\displaystyle {\int }_{x_1}^{x_2}\rho \frac{\partial v_x}{\partial x}\mathrm{d}x=J_2-J_1}$$ (3)

where L = x₂ − x₁ is the length of the strip, this gives a condition for the boundary velocities

$$v(x_2)-v(x_1)={\dot{x}}_2-{\dot{x}}_1=\frac{J_2-J_1}{\rho }.$$ (4)

The actual constant velocity field within the domain is not known, and must be determined from another condition. In cases where material points are fixed in space such as from adhesions to stationary substate (figure 2(A)), then ν(x,t) = 0 within the domain, and the only points that are moving are the boundaries, giving velocity conditions for individual boundaries: ${\dot{x}}_{1,2}=J_{1,2}/\rho$. Thus, from mass fluxes alone, we can get motion!

Figure 2.

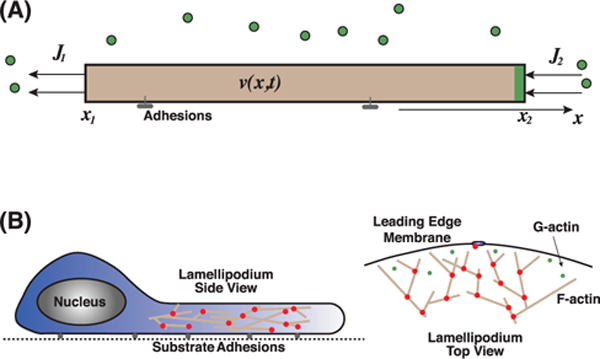
(A) Mass conservation is related to cell boundary movement. There is a velocity field, v(x, t ), within the shaded region representing the material in consideration. The boundary of the material can move from mass fluxes at the boundary J_1,2. Cells build actin filaments from actin monomers; therefore the actin network can extend and retracting according monomer fluxes. (B) For a moving cell with a flat and broad lamellipodium, there is a polymerizing actin network at the leading edge. Mass flux of actin monomers (G-actin) increases F-actin network mass and drives membrane protrusion.

Note that this problem becomes more complicated in 2D, when there are two unknown velocity fields v = (v_x,v_y). In this case, other conservation laws must come into play in order to obtain a solution. The momentum density also satisfy momentum conservation (Newton’s 2nd Law) [14, 15], therefore

$$\frac{\partial \mathbf{g}}{\partial t}+\nabla \cdot (\mathbf{g}\otimes \mathbf{v})-\nabla \cdot \mathbf{\sigma }=0$$ (5)

where σ is now the momentum current tensor, or the stress tensor. In the low Reynolds number limit that is appropriate for the cellular scale, we can neglect the nonlinear term (2nd term) [16]. The momentum current tensor contains information about mechanical forces on a small volume element in the material. In order to mathematically solve the coupled equations (1) and (5), is it necessary to introduce a constitutive law, i.e. a relationship between σ and the velocity field v. This constitutive relationship depends on the type of material, and the microscopic molecular structure. This relationship can also be measured experimentally.

Without complicating things, in the simplest picture, mass fluxes J are sufficient to push the cell boundary and generate cell shape changes.

B: In the cell, there are multiple sources of mass flux. One possibility is from polymerization and depolymerization of actin cytoskeleton or microtubule cytoskeleton. From experiments, it has been shown that the actin cytoskeletal network is important for cell shape and cell movement [17–19]. New actin networks in the cell are formed from monomers (G-actin) that polymerizes into actin filaments.

S: Ahh, that means by controlling where and when actin polymerization and depolymerization happens (figure 2(B)), the cell can control its motion and generate forces!

B: Precisely. It is known from experiments on cells on 2D substrates that by depolymerizing the actin cytoskeletal network using drugs such as Latrunculin A/B, cells no longer can change shape or move on 2D flat substrates [20, 21]. Therefore, actin is necessary for 2D migration. From extensive studies on the shape of rapidly migrating cells, we now have very sophisticated models of how actin network dynamics generate the shape of moving cells [22–24]. Features such as myosin contraction, diffusion of G-actin in the cytoplasm and detailed branched structure of the actin network has been incorporated [25]. So we know a lot about how actin drives cell movement.

S: In order to predict how cells move and change shape, we need information on the stress tensor in equation (5), right? A constitutive law as you described?

3. Actin cytoskeleton mechanics

P: You are absolutely right. There has been a lot of work in this area, trying to understand properties of the actin cytoskeleton [26–30].

B: From a biological perspective, the actin network plays a crucial role in a cell’ s morphology, migration and force production [31–33]. In mammalian cells, a large portion of actin is located within a cell cortex, which is just below the plasma membrane [33–37]. It is within this actin rich cortex that F-actin interacts with molecular motors and actin crosslinking proteins [38–40].

P: There has been also a lot of work on structural composition of actin networks in cells. For example, actin crosslinking proteins such as α-actinin, cortexilin, and fascin are important proteins in forming actin networks [41–43]. In addition to exerting active forces, myosin also forms mini-filaments that cross-links F-actin [44]. Branch forming proteins such as Arp2/3 generate a mesh-like network [45]. Speckle microscopy has been developed to measure movement of individual actin monomers [46–48]. So far, hundreds of actin-binding proteins have been identified. These proteins seem to regulate all aspects of the actin network, including polymerization, depolymerization, cross-linking and mechanical rigidity. Thus, to by-pass the molecular complexity, a constitutive model is an useful approach to describe the actin network mechanics. In such a constitutive model, molecular components will influence the mechanical moduli, but the mathematical relationship between kinematic variables and stress remains similar.

There are several broad classes of constitutive models. Of course, solids and fluids are already familiar, the primary difference being that solids can sustain shear stress at static mechanical equilibrium while fluids cannot. Actin networks are examples of semi flexible polymer networks [49–52]. These networks are viscoelastic, meaning that they retain some properties of solids and fluids. However, it is important to keep in mind that actin networks in cells are viscoelastic fluids. Therefore, the stress at long times is only a function of deformation rate:

$$\mathbf{\sigma }={\sigma }_0\mathbf{I}+\mu (\nabla {\mathbf{v}}_n+{(\nabla {\mathbf{v}}_n)}^T)$$ (6)

where I is the identity tensor and v_n is the spatial velocity field of the actin network. μ is the shear viscosity of the network. The diagonal part of the stress tensor acts like a pressure, but the shear part (off-diagnol) vanishes when v_n = 0 or when v_n is spatially constant. This is the long time behavior of actin networks.

The dynamic nature of the cross-linking proteins and accessory proteins that depolymerize actin allow the cell to tune the mechanical properties of its actin network [53–55]. When cross-linking proteins bind to filaments they contribute to the elasticity within the meshwork and when they unbind they allow the filaments to slide past one another, thus contributing to the development of shear stress (figure 3). The elastic behavior of the network is modeled by a Young’s modulus, E. When it is combined with the viscosity μ, a relaxation time scale τ=E/μ emerges. After an initial step perturbation or deformation, τ is the time scale which the material still retains some elastic characteristics. After τ, the material behaves as a fluid and flows. For actin in the cytoplasm, τ is about 10 s [56, 57].

Figure 3.

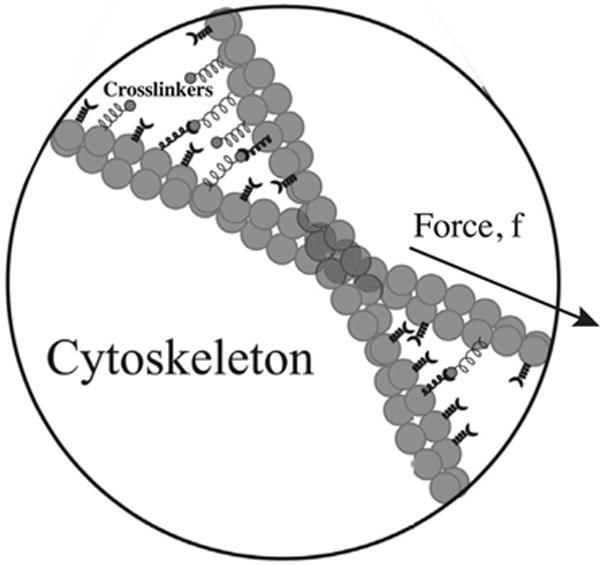
Actin cytoskeletal network behaves as a viscoelastic fluid, primarily due to force-dependent binding and unbinding of cross-linker proteins and filament depolymerization. When forces are applied to filaments, cross-linker dynamics acts as a viscous friction between filaments at time scales longer than cross-linker binding rates. The network flows under force, giving a constitutive relationship as in equation (6).

S: Okay, so measurements show that the viscosity of actin network, μ, is about 1000 times higher than that of water [26, 58, 59].

P: Correct. It is also important to note that a single time scale as described above is a simplification. Rheological properties of actin network also depend on other factors like filament stiffness, filament bending and entropic fluctuations. There are multiple time scales in the viscous behavior [60, 61]. In the simplified case of rigid filaments with dynamic cross-links, the force-velocity behavior of filaments sliding with respect to each other resembles viscous friction, and the friction coefficient can be explicitly related to cross-linker binding kinetics and linker stiffness [62–64]. Furthermore, when forces are applied to the network, the mutual sliding friction tend to align the filaments and generate large actin bundles, so-called stress fibers [65, 66]. These stress fibers tend to attach to substrates through integrin focal adhesions [67–69]. The movement of adhesions depend on substrate stiffness [62].

B: Myosin molecular motors also add to the fluidity of the actin network. The heads of myosin motors bind F-actin and utilize ATP hydrolysis to generate force to move toward the positive end of actin filaments [39, 44]. This movement also slides filaments with respect to each other and further fluidizing the network [39, 52]. Indeed, activities of small myosin assemblies is responsible for the contractile nature of actin networks in cells. If the contraction is isotropic, the contractile stress can be modeled as an active part of σ₀ in equation (6). The contraction acts as a negative pressure, i.e.

$${\sigma }_0={\sigma }_p-{\sigma }_a$$ (7)

where σ_p is the passive pressure in the actin network and σ_a is the negative pressure from active contraction of myosin. σ_a depends on energy input, such as ATP hydrolysis [32, 70], and signaling pathways that controls concentrations of myosin [71–73]. In order for sustained network contraction by myosin to occur, it is not sufficient to only have filament sliding, since the sliding movement does not decrease overall network volume. It is shown that buckling of actin is also necessary for contraction [74, 75]. In addition, filaments under mechanical compression should also depolymerize faster [76]. This elevated depolymerization in compressed networks allows recycling of G-actin and sustained contractile stress generation by myosin. Finally, network contraction can result not just from myosin motor activity, but also from passive crosslinking. Actin cross-linkers such as α-actinin can directly cause network contraction [64, 77], simply from favoring closer filament-filament interaction.

P: There is a growing body of literature on the active behavior of the actin cytoskeleton, including non-isotropic networks and active chiral behavior [78–81]. In these more complex scenarios, the stress depends on possible nematic order in the network and active stresses are not necessarily isotropic [70]. As one can imagine, studying the actin network within a cell is difficult due to the presence of other structures within the cell. Researchers have therefore been using reconstituted actin works in vitro to further investigate the behavior of the actin cytoskeleton [54, 61, 62, 82–86].

S: Ok, but the cytoplasm is more complex than just the cytoskeleton right? What about the water phase? I recently read that water is apparently 70% of the cell mass content [87], and the cytoplasm is a porous material where water can flow [88]. Are there other mass fluxes that are important for cell shape and mechanics?

4. Water dynamics in cells

P: Indeed, in addition to cytoskeletal polymerization, the cell can passage water through the cell membrane directly, or through the membrane water channel aquaporin [89, 90]. The direction and magnitude of the water flux depend on the water chemical potential difference, Δμ, across the cell membrane, which is influenced by both the hydrostatic pressure difference, ΔP, and the osmotic pressure difference, ΔΠ [91]:

$$J_{\text{water}}\propto \mathrm{\Delta }\mu =-\alpha (\mathrm{\Delta }P-\mathrm{\Delta }\prod ).$$ (8)

Here α is a permeation constant proportional to aquaporin density. Since this flux depends on two kinds of pressures, mechanical forces that influence ΔP and solute concentration changes that influence ΔΠ will both drive water flow across the membrane (figure 4). Therefore, mechanics and chemical contents inside and outside of the cell determine water flow.

Figure 4.

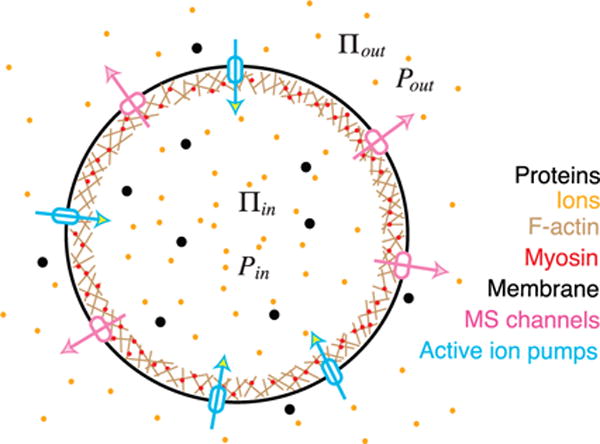
Cell pressure and volume regulation. There is typically an elevated cytoplasmic osmotic pressure (Π_in) as compared to the extracellular environment (Π_out). Therefore, hydrostatic pressure inside the cell is higher: P_in > P_out. The hydrostatic pressure difference is largely sustained by tension in the actin cortex underneath the membrane. When the osmotic pressure difference changes, this causes a change in the hydrostatic pressure difference and a change in cortical/membrane tension. Cells will re-adjust its osmotic content by opening and closing ion channels and pumps, and re-adjust cortical tension. When the cell experiences mechanical forces, the hydrostatic pressure difference changes, and cause the same chain of osmolyte flux and actomyosin tension change. It is unclear whether the cell maintains a constant osmotic pressure difference in all conditions.

B: This water flux has been studied in various physiological contexts, including coupled transport of water and salt across epithelia [92]. Indeed, aquaporin was discovered in kidney epithelium cells and every day your kidney re-absorbs 180 liters of water from blood that leaks into the glomerulus [93]. For cells, water flux also plays a role in membrane blebbing [94, 95], and the ameboid mode of cell migration [96, 97], where extruded blebs is refilled with cytoskeleton, and the cell can move by repeated development of blebs [36, 98–100]. Outside of physiological situations, osmotic effects can drive microfluidic pumping [101] and has been proposed as a way to generate energy [102, 103].

S: So water can flow in and out of the cytoplasm. Does this mean that the cell size increases when there is net water flux into the cell? How fast can the cell size change? What are the factors influencing the cell size?

4.1. Cellular pressure/volume regulation: a qualitative description

P: Yes, water permeation is an important element in the regulation of cell volume [104]. Mathematically, on the time scale of water flow, we have [105],

$$\frac{\mathrm{d}V}{\mathrm{d}t}=A{J}_{\text{water}}=-A\alpha (\mathrm{\Delta }P-\mathrm{\Delta }\prod ).$$ (9)

where V and A are the volume and surface area of the cell, respectively. Here, the hydrostatic pressure difference ΔP is mechanically balanced by cell surface tension and surface curvature. We will discuss the precise force balance conditions a little later. The osmotic pressure difference, ΔΠ=Π_in − Π_out depends on concentration of solutes inside and outside of the cell. Potentially there is larger concentrations of solutes in the cell, therefore Π_in > Π_out. Note that the osmotic pressure is an entropic force, arising from entropy of mixing [106], and therefore does not depend on molecular details. Π_in ≈ R_ATc_in=R_AT(n+N_p)/V, where n is the number of small transportable ions and molecules such as Na⁺, K⁺, Cl⁻ and ${\text{HCO}}_3^{-}$ in the cytoplasm. N_p is the number of untransportable proteins and macromolecules in the cytoplasm, and R_a is the gas constant and T is the temperature. Note this estimate of the osmotic pressure is valid for simple solutes in dilute solutions, and additional corrections could be necessary for complex cytoplasmic environments.

B: The cell of course actively controls both the protein content N_p, and the ion content, n. For ions, there are many ionic species to consider. Na⁺, K⁺, and Cl⁻ are the most abundant ones, each with concentrations in the 100 mM range. But Ca²⁺, H⁺, ${\text{HCO}}_3^{-}$, and other small organic molecules are also involved. Transport of sugars and other small nutrients are obviously needed for increasing N_p. Ions flow across the cell membrane both passively and actively. Passive ion channels allow ions to flow according to the chemical potential difference of each ionic species. Active ion pumps can transport ions against the chemical potential gradient; and the pumping process requires energy input. Some common pumps and co-transportors include Na/K pump [107], Na-K-Cl cotransport [108], and Na/H exchanger [109, 110]. These channels and pumps are essential for cells to maintain intracellular osmolyte concentrations.

P: These ion channels and pumps work on relatively fast time scale (~s). We can describe cell volume regulation on this time scale by considering water and ion fluxes in mathematical models. If osmolarity and cell mechanical behavior are the main concerns, we can consider simplified models with neutral osmolytes [105]. Equation (9) implies that at equilibrium, the hydrostatic pressure difference is equal to the osmotic pressure difference: ΔP = ΔΠ, and the water content does not change. One can induce water flow and cell volume change by applying osmotic shock [111], i.e. changing ∏_out, or by changing the hydrostatic pressure difference either by changing P_out [112] or applying mechanical forces to the cell. When the extracellular osmolarity varies, the ion flux across the membrane changes, leading to an increase or decrease of intracellular ions within a few minutes. This process changes the volume of the cell, primarily from ion fluxes driving water flow. From experiments, it is known that cells can adapt to osmotic shocks, and the cell volume can recover within tens of minutes [111]. The cell volume change also depends on the mechanical stress in the actomyosin cortex, which directly influences ΔP. The coupled water and ion fluxes together with cortical contraction are responsible for the volume recovery [105, 111]. Note that water fluxes are equally influenced by both hydrostatic pressure and osmotic pressure (equation (9)). Therefore, mechanical response of the cell on the time scale of minutes is also influenced by water and ion dynamics as well as actomyosin dynamics.

B: On longer time scales, tens of minutes to hours, cell volume is determined by changes in N_p, or the total protein content of the cell. Cells actively import molecules and nutrients to grow. And over the cell cycle, the cell volume roughly doubles [113–115]. Indeed, one possibility is that the osmotic regulation system roughly keeps a constant osmolyte concentration in the cell, and therefore N_p and volume should increase at the same rate [116]. The regulation of N_p is an important aspect of the cell cycle and signaling pathways are involved in this regulation [117–119]. A full quantitative picture is still not clear. It is evident that these pathways must also couple with ionic fluxes, actin cytoskeleton and myosin contraction. More work is needed to understand this area.

S: Huh, cell volume regulation is quite complex! I guess it makes sense since the cell volume determines the concentration of everything in the cell. The cell has to get that right. Coupling with water dynamics is also interesting. Water fluxes are clearly important in the kidney. Are there other situations where water fluxes has an important role?

4.2. Water-driven cell migration—an osmotic engine

P: It’s a good question. So far, we have discussed how isotropic (i.e. spatially uniform) water flux can lead to cell volume increase and decrease. If the water flux is spatially varying, this mass flux can lead to cell movement, exactly in the same manner as depicted in figure 2(A). For cells confined in a 1D narrow channel, it was discovered experimentally that cells can move without actin or myosin [21, 120]. Therefore, we can neglect their contribution to mass fluxes. In this case, the cell moves by permeating water through the cell: the so-called osmotic engine model (OEM, figure 5) [121]. This concept has been proposed sometime ago [122–124], and it is possible because, for a polarized cell, the intracellular osmolyte concentration is non-uniform. This allows an influx of water at the leading edge of the cell and an efflux at the trailing edge. When the intracellular fluid is stationary with respect to a fixed frame, the polarized water flux drives cell migration through the extension of cell membrane (figure 5(A)).

Figure 5.

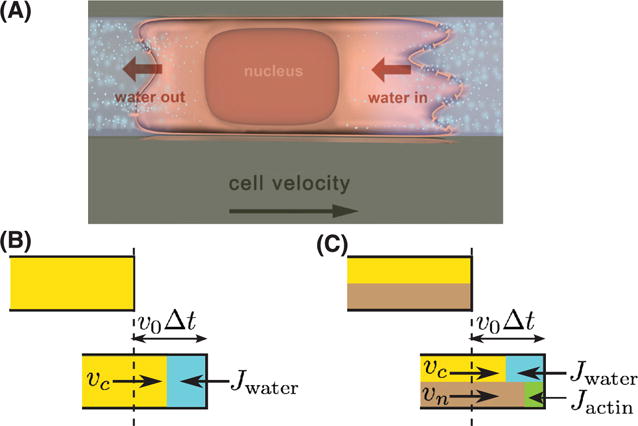
Directional water flux, like actin polymerization flux, can drive cell movement. (A) Cells in confined environments can generate water influx at the leading edge and water efflux at the trailing edge. The water flux is connect with directional ionic flows. (B) Fluid flux gives a quantitative kinematic condition for the cell boundary: equation (10). Here v_c is the fluid velocity in the cytoplasm and v₀ is the velocity of the cell leading edge. In time Δt, the new volume element is v₀Δt which is equal to the sum of v_cΔt and J_waterΔt. (C) If the cytoplasm is considered as a 2-phase fluid, the fluid phase only occupies a fraction of the cell volume θ_c. In this case, the new volume is given by a combination of v_c, actin velocity v_n, and J_water and J_actin (equation 11).

B: In order to develop the gradient of osmolytes in the cell, it is important to have a polarized distribution of ion channels and pumps in the cell. In the experiments of [121], they studied cancer cells migrating in 1D confined channels, a situation mimicking cancer metastasis in tissues. They observed that the cell has an elevated concentration of Na/H exchanger at the leading edge [121].

B: The interesting aspect is that the cell appears to be able to move with and without actin [120, 121]. The cell speed in actin-dependent motility appears to be faster, and the osmotic engine appears to be slower. Therefore, the cell seems to have two different gears, possibly for different environmental conditions. Water fluxes can also come from asymmetric external hydrostatic pressures, which also can drive cell migration [125].

S: Ions have electrical charges. Therefore, is it correct to consider neutral osmolytes in the OEM?

P: Only in a simplified phenomenological manner. In general we need to consider charged ionic species and the associated electric fields and voltage gradients [107, 126, 127]. This is true for both cell volume regulation and OEM. When transmembrane voltages are introduced, there is then a natural coupling between the osmotic engine model and cell migration under external electric fields (electro-motility) [128].

B: Electro-motility has been experimentally explored in 2D cells [129, 130]. Cells can go to either the cathode or the anode, and this ‘galvanotaxis’ appears to be cell-type dependent. Again, just as in the osmotic engine case, polarization of the cell plays an important role. It is not clear how cells turn these external electrical signals into spatial arrangements of various proteins in the cell. In general, actin and myosin are perhaps involved in both polarization dynamics and driving motility, and in the case of galvanotaxis, cell polarization maybe organized by downstream signal pathway from the electric signals [129].

P: In 2D the story could be more complicated. The water flux across the membrane now can come from any direction; it is the spatial distribution of water flux that determines cell shape and movement. In addition, we also need to consider the intracellular fluid dynamics [94, 131]. But in 1D, the story is simpler. We can think of 1D cells with non-zero intracellular fluid velocity. In this case, as shown in figure 5(B), both the intracellular fluid velocity, v_c, and water flux, J_water, contribute to the cell migration. At the leading edge of the cell, we have a simple relation for the leading edge velocity

$$v_0=J_{\text{water}}+v_c.$$ (10)

This velocity condition is again a result of mass conservation.

B: Absolutely. Experimental observation shows that knocking out aquaporins in cells reduces cell migration speed [121, 132]. In many cases water flux and actin polymerization probably work together to facilitate cell migration. Although the exact details require further elucidation.

4.3. Actin and water together? A two-phase model of the cytoplasm

P: Yes. Indeed, for the general cell migration case, we can consider a two-fluid-phase model to understand physical elements giving rise to cell velocity. Let’s still consider a 1D cell. Let the volume fraction of the fluid (actin network) phase be θ_c (θ_n).θ_c+θ_n= 1 by volume conservation. Since now the fluid only occupies a fraction of the total mass of the cell, as illustrated in figure 5(C), then the velocity of the cell leading edge is related to the velocity of the fluid and fluxes by

$$v_0=J_{\text{water}}+J_{\text{actin}}+{\theta }_c{v}_c+{\theta }_n{v}_n$$ (11)

whereJ_actin is the mass flux of new actin polymerizing at the cell boundary.J_actin depends on the G-actin concentration and the density of polymerizing actin ends. Now we observe that the water flux and actin polymerization add constructively to the velocity of the leading edge, as seen in the experiments [133]. Note that all the variables in entire system are potentially coupled,J_water,J_actin, v_c, and v_n could all depend on each other.

S: That’s interesting! The actin phase and the water phase are coupled. Does this mean that water flux is always necessary during cell migration?

B: The kinematic relationship in equation (11) is clear, but how the actin and water velocities are regulated is unclear. The regulation of these kinematic variables has to do with mechanisms of cell polarization, and it is known that in addition to chemical factors, mechanical factors such as the cell membrane tension are involved [25, 134]. Actin perhaps is involved in setting up a polarized cell as well as contributing to membrane velocity. The answer is still out there.

5. Cell volume and cell shape dynamics: a quantitative view

P: In order to examine the combined contributions of actomyosin dynamics and osmotic flow in cell mechanics, it is useful to develop a quantitative description of forces and flows in cell volume regulation and cell shape change. To start we have to consider how mechanical forces are balanced at the cell surface for different cell geometries. This force balance requires us to consider the cell membrane, the actomyosin cortex, active contraction and polymerization, and potential water flows across the membrane. Using a continuum mechanics approach, it is possible to get an order of magnitude estimates of these contributions to the steady state cell shape.

5.1. Cell surface force balance

P: To see how the details work, we can focus on a small section of the cell surface which includes the membrane and the actomyosin cortex underneath (figure 6). Since the cortex is permeable to water, at steady state the hydrostatic pressure within the cortex is relatively uniform. At mechanical equilibrium, the total force acting on the membrane surface element S enclosed by C is zero (figure 6(A)), and we have

$$0={\displaystyle {\int }_S\mathbf{\sigma }\cdot \mathbf{n}\mathrm{d}S+{\displaystyle {\int }_S\mathrm{\Delta }P\mathbf{n}\mathrm{d}}S+{\displaystyle {\int }_{C}T\mathbf{m}\mathrm{d}l}}$$ (12)

where σ · n is the total force acting on the surface element S from the actomyosin network. σ is the mechanical stress in the cortex. T is the membrane tension, and the last term can be shown to be:

$${\displaystyle {\int }_{C}T\mathbf{m}\mathrm{d}l}={\displaystyle {\int }_S\nabla T-T\mathbf{n}(\nabla \cdot \mathbf{n})\mathrm{d}S}$$ (13)

where the right hand side is the total force from membrane tension. Therefore, within the continuum framework, force balance gives an explicit relationship between actomyosin activity, cell hydrostatic pressure and membrane tension.

Figure 6.

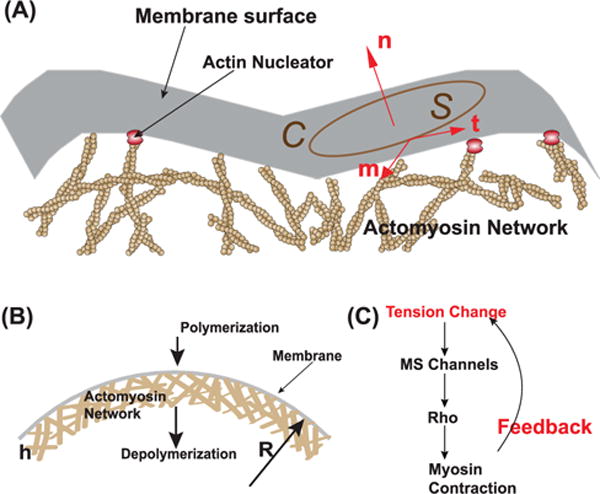
(A) Schematic illustration of mechanical forces on a membrane element S. This element experiences forces from stress in the actin cortex below, membrane tension in plane of the membrane, and hydrostatic pressure that acts normal to the membrane. (B) When actin polymerization and myosin contraction are consider, we can estimate the stress in the cortex. The sum of mechanical forces yields force balance condition equation (14). (C) Myosin contraction in the cortex is regulated by signaling networks. Mechanosensitive channels can sense membrane tension change, and activation myosin contraction relatively quickly.

S: Ok, what is the stress in the actomyosin cortex, σ? How do we compute it?

B: Within the cytoskeleton network, actin actively polymerizes near the cell membrane and depolymerizes some distance from the membrane. This continuous mass flux generates an actin flow, and maintains a relatively constant cortical thickness, h ~ 200–500 nm [135]. As discussed earlier, myosin actively applies a contractile stress tangential to the membrane surface. Therefore, the total stress is σ=σ_p+σ_active, and σ_active = −σ_a(t ⊗ t+m ⊗ m), where we have assumed that the myosin-generated stress is isotropic: equal in both t and m directions. The negative sign in front of σ_a indicates that it is contractile. Since signaling networks can control the activation of myosin (figure 6(C)), σ_a is proportional to the amount of activated myosin, M: σ_a = K_maxM, in which K_max is the maximum contractile stress when 100% of myosin is activated. K_max is a function of protein expression, and therefore can be assumed to be a constant over a short period of time (<hours).

P: σ_passive can be estimated using the constitutive relation in equation (6). The results are straightforward [116], and we find that the passive stress within the network is relatively small when compared with the contractile stress and hydrostatic pressure, and the normal component of the force balance obtained from dotting equation (12) with n becomes

$$\mathrm{\Delta }P-(T+{\sigma }_{a}h)(\nabla \cdot \mathbf{n})=0.$$ (14)

The tangential component is also interesting, and depending on the spatial variations in σ, there could be membrane flow and tension gradients. Geometrically, ∇ · n = 2H where H is the cell surface mean curvature [136]. Therefore we see that the active stress in the cortex and the membrane tension both balance the hydrostatic pressure difference. Also, from our discussions earlier, if the cell is steady and there is no net water flow across the membrane, i.e. ΔP = ΔΠ, which means that osmotic pressure is related to membrane and cortical tension.

B: Another good thing about equation (14) is that it is essentially exact for rapid cortical turnover. Other cortical components like actin cross-linkers, Arp2/3 and bundling proteins may change the viscosity of the actin network, and could introduce a passive stress contribution in equation (14). Proteins like spectrin may further help to stiffen the cortex and generate elastic behavior [137]. But the general form of equation (14) still remains the same, only the passive stress contribution may change.

S: So we have local force balance for a stationary cell. What does this say about cell volume and cell shape?

P: The force balance equation is sufficient to determine the overall cell shape! Since ∇ · n is related to the mean curvature, we can relate the cell geometry to forces at the cell surface. For a spherical cell, ∇ · n = 2/R, where R is the cell radius. For other geometries, computation of the complete cell shape is possible from equation (14). We can discuss this a little later.

B: Moreover, equation (14) gives us a good view on how active regulation of myosin activity contributes to cell volume adjustment (figure 6(C)). σ_a depends on active chemical regulation of myosin. Some details on this are fuzzy, but studies suggest that mechanosensitive transmembrane protein is responsible for Rho activation, a crucial signal upstream for activating myosin. For example, mechanosensitive Ca²⁺ channel, such as TRPV4, can directly activate Rho [138, 139]. These mechanosensitive ion channels are membrane tension sensitive. Estimates have shown that membrane tension at steady state is low, in the order of 0.01 pN nm⁻¹ [140, 141]. However, if there is a sudden changes in cell mechanical and chemical environment, such as during a osmotic shock or changes in mechanical force, the membrane tension can increase dramatically. The jump in membrane tension opens these mechanosensitive channels, and signals to the cell to activate Rho and myosin contraction. Since equation (14) is correct at times scales of tens of seconds, changes in σ_a re-adjusts ΔP and T, so that overall cell volume can adapt to change.

5.2. Dynamic control of cell volume and pressure

P: The sequence of events described by B can be put in mathematical form. We will limit our discussion to spherical cells where everything is spatially uniform. The first equation describes the total water content of the cell,

$$\frac{\mathrm{d}R}{\mathrm{d}t}=-\alpha (\mathrm{\Delta }P-\mathrm{\Delta }\prod ).$$ (15)

Here ΔΠ = R_AT(n + N_p)/V − R_ATc_out where c_out is the extracellular concentration. From what we know about ion channels, n changes much faster than N_p, therefore we have

$$\frac{\mathrm{d}n}{\mathrm{d}t}=A(I_{\text{active}}+I_{\text{passive}})$$ (16)

where I_active could be the flux through the active ion pumps and I_passive is the flux through passive ion channels. The functional forms of I_{pssive,active} will depend on specific channels, and could depend on T and membrane electrical potential ϕ_m, and (c_in, c_out) where c_in,_out are concentrations inside and outside of the cell. For example, for the Na/K exchanger, which is an ATP-driven ion pump that exchanges 3Na⁺ with 2K⁺ ions, the flux depends on both intracellular and extracellular Na⁺ and K⁺ concentrations. The flux expression has been proposed, and is dependent on transmembrane voltage, ϕ_m [126]. Na⁺ flux is coupled to Cl⁻ flux through Na-K-Cl co-transporters [108].

The remaining quantity to define is ΔP which according to equation (14) is

$$\mathrm{\Delta }P=\frac{2(T+{\sigma }_{a}h)}{R}.$$ (17)

This introduce unknowns T and σ_a If σ_a is governed by a feedback signaling mechanism then

$$\frac{\mathrm{d}{\sigma }_a}{\mathrm{d}t}=K_{max}\frac{\mathrm{d}M}{\mathrm{d}t}=K_1(T,c_{\text{in}})(1-M)-K_{2}M$$ (18)

where K_1,2 are phosphorylation/dephosphorylation rate constants. From properties of the signaling network, K_1,2 can depend on membrane tension and ion concentrations inside the cell. It is also possible that shear stress within the cortex could signal to myosin, and K₁ depend on σ_p, or myosin intrinsic mechanosensitivity [142]. Finally, membrane tension can be described by another constitutive relation, e.g.

$$T\propto (A-A_0)$$ (19)

where A₀ is the unstretched membrane area, and A would be the current membrane area. A would be a function of R. Note that in cells, the membrane is likely highly folded, therefore the actual constitutive law must incorporate entropic elasticity, and the relationship between A and R maybe complicated [143, 144].

Equations (15)–(19) are a closed set of dynamic equations that describe changes in (R, n, σ_a, T) for given parameters (N_p,A₀, K_max, c_out) and associated flux constants in α and I_{passive, active}. This system of equations has a steady state (R_ss, n_ss, σ_a,ss, T_ss), which are the homeostatic values of these quantities in the cell. This steady state should be stable against perturbations, and the phase space region around the steady state will describe how cells responds to changes in variables such as N_p and c_out.

S: Does this mean that we can predict cell volume for a given condition?

P: Precisely.

B: The details are significantly more complicated than described here. First, there are multiple types of permeable ions, at least Na⁺, K⁺ and Cl⁻ are involved. Ca²⁺ is another secondary messenger. Furthermore, flux equations for I_{passive.active} are generally not known. Since ions are charged, membrane potential ϕ_m also comes into play [128]. Since ionic species are coupled through co-transporters, flux couplings become very complicated. It is likely that cells have compensatory mechanisms when fluxes are disrupted. Currently there are no predictive models of ionic flux balance in cells.

S: So this problem is not completely understood at all!

5.3. Adherent cells: a test of the model

P: Spherical cells are not very common. But further verification of these ideas can come from examining adherent cells: cells that are growing on flat substrates. Let us consider a static axisymmetric cell confined on a circular substrate (figure 7). At steady state, T ≪ σ_ah. Equation (14) then becomes: (∇ · n)⁻¹ = hσ_a./ΔP For the coordinate system defined in figure 7(A), D, which describes the shape of the adherent cell, is a function of θ. ∇ · n can be expressed as a function of D(θ), we therefore have

$$\frac{2D{\prime }^2+D^2-D{D}^{″}}{{(D^2+D{\prime }^2)}^{3/2}}+\frac{1+D\prime D{\prime }^{-1}\tan \theta }{{(D^2+D{\prime }^2)}^{1/2}}=\frac{\mathrm{\Delta }P}{{\sigma }_{a}h}$$ (20)

where D′ = ∂D/∂θ and D″=∂²D/∂θ². This is a nonlinear 2nd order ODE, therefore two boundary conditions (BCs) are needed to determine the cell shape. One of the BC is the adhered size, R₀, which sets D(θ = 0) = R₀. The other BC can be obtained by assuming the cell surface is smooth at θ = π/2. Notice σ_a, h all can be functions of θ, but if they are constants, then there is a single size parameter r₀ = 2hσ_a/ΔP. In this case, if R₀ = r₀, the cell is a prefect hemisphere. If R₀ > r₀, the cell will be stretched at the top, with a flatter region near the substrate. Figure 7 shows some computed cell shape for different adhesion size R₀. The result predicts that for the same r₀, cells with larger spread area tend to have larger volume (figure 7(B)).

Figure 7.

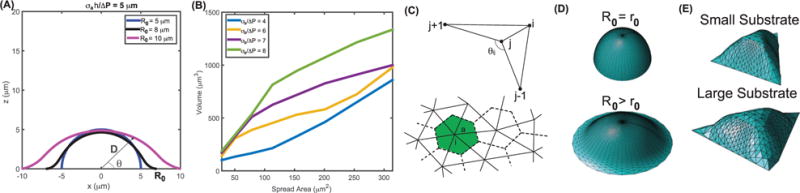
(A) Computed 3D shapes of adherent cells for different substrate adhesion size, R₀. The cell surface is described by the function D(θ) (inset). Equation (20) predicts that the cell shape varies with increasing R₀. (B) Cell volume increases as substrate size increases. The critical parameter governing the volume-area correlation is σ_a/ΔP. (C) Mean curvature can be approximately computed using triangular surfaces using equation (21). The triangulated surface can describe cell shape in arbitrary geometry. ((D), (E)) Computed 3D cell shapes using triangulation of cell surface for cells on circular and triangular substrates. Here r₀ = 2σ_ah/ΔP.

S: It seems that equation (14) can predict at lot of features of the cell. But you only mentioned about suspended or axisymmetric cell shape. What about non-axisymmetric cells?

P: Of course, equation (14) is applicable for all types of cells under any condition. But the distribution of σ_a is in general a function of space, and depends on local signaling activity of Rho, Rac GTPases. If we can measure hσ_a/ΔP as a function of space, then we can compute the cell shape for any adhesion geometry. For example, by triangulating the cell surface, we can compute the local mean curvature around the ith vertex as (figure 7(C)) [146, 147]

$$H_i=\frac{1}{4a_i}{\displaystyle \sum _j\left[\tan \left(\frac{{\theta }_{ij}}{2}\right)+\sin \left(\frac{{\theta }_{ij}}{2}\right)\right]l_{ij}}$$ (21)

where a_i is the area around the vertex, and the sum is over j vertices connected to the i-th vertex. l_ij and θ_ij are the length of the connecting edge and the angle between triangles sharing the edge, respectively. Using a weak form of equation (14), we can compute the shape of the cell surface for a given hσ_a/ΔP for any substrate geometry (figure 7(C)).

The other unknown is ΔP, which if there are no protein and ionic gradients, ΔP should be spatially uniform. But we do not know whether it remains constant in all conditions. There has been efforts to measure intracellular ΔP [145]. In general, the right hand side of equation (20) is not clear, and generally depends on θ.

S: Ok, but why are we interested in cell shape dependence on substrate geometry? How would this influence important biological functions?

B: We know that substrate properties can influence many aspects of cell function [68, 148, 149]. For example, cell cycle progression seems to depend on substrate stiffness [150]. R₀ seems to change depending on cell substrate properties. These changes also seem to influence mesenchyemal stem cell differentiation [151]. Therefore, many essential cell functions depend on substrate stiffness and substrate adhesion [67]. Extracellular matrix stiffness also influences cell migration and cancer metastasis [152], the list goes on… Indeed, gene expression profiles are changed depending on substrate adhesion and substrate stiffness [153]. From mechanics alone, we see that cell volume and cell shape depend on substrate adhesion and geometry. And since cell volume will influence all kinds of protein concentrations, there could be a physical basis to these biological changes [154]. There are lots of questions in this direction and further work is needed

5.4. Higher order models: cell and tissue mechanics

S: We see that water flux is influenced by hydrostatic and osmotic pressures equally. Therefore, it should be possible to drive water flow from externally applied mechanical forces too, right?

P: This is correct! In equation (14), if there is an externally applied mechanical force to the cell F_ext, it simply adds to the force balance equation and modifies it to

$$\mathrm{\Delta }P-(T+{\sigma }_{a}h)(\nabla \cdot \mathbf{n})=-{\mathbf{F}}_{\text{ext}}\cdot \mathbf{n}.$$ (22)

This says that the hydrostatic pressure difference can be changed by externally applied mechanical force. A change in ΔP leads to water flux, and changes in osmotic pressure as well. Therefore, a complex response is initiated when an external force is applied to the cell [105, 155]. The response depends on the rate of deformation: since water flows across the membrane slowly, a rapidly applied force will generate deformations that essentially preserves the cell volume [105]. Alternatively, if the deformation is slow, then water will flow, leading to cell volume change. It appears that the relevant deformation time scale is μm s⁻¹ [105, 116]. With this time scale or slower, cells can change volume significantly.

B: This time scale of deformation is important. During organismal development, most shape changes occur slowly. Therefore mechanical forces in developing tissues must influence water dynamics in cells and tissues [156–159].

S: In some of my readings, there are already proposed models for tissue mechanics. For example, an approach that relates cell volume and surface area with a ‘mechanical energy’ has been popular [160–166] (figure 8):

$$E={\displaystyle \sum _J\frac{1}{2}{k}_c{(V_J-V_0)}^2+\mathrm{\lambda }{A}_J^2}-{\displaystyle \sum _{J,J\prime }\mathrm{\gamma }{A}_{J,J\prime }}$$ (23)

where the first sum is over cells, and the second sum is over cell-cell interfaces. The first term models cell volume change with respect to a reference V₀. The second term is a contractility term, describing the propensity to shrink the cell surface area from myosin activity. The last term is a surface energy term. The surface energy term may model cell-cell contact energy arising from chemical bonds such as E/N Cadherins [167]. This model has used to describe cell motility in the confluent epithelium [163, 168, 169], and it has been shown that different combinations of surface energy term and contractility can lead to a jamming transition, i.e. a possible lost of global cell mobility within the epithelium [169]. How do we interpret this model, since the cell is an active object that does not obey energy conservation principles?

Figure 8.

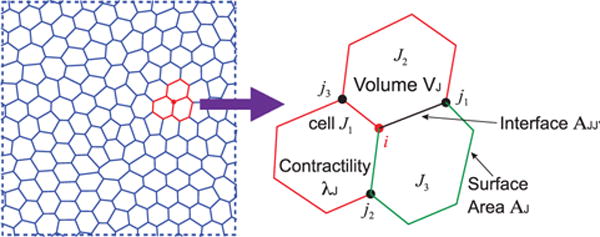
Epithelial cell layer mechanics. When cells form a confluent layer, the shape and forces within the tissue can be described by an energy formulation of the vertex model (equation (23)). The energy function describes cell-cell adhesion, cell volume change and cell surface contractility, and can be understood as a Lyapunov function of the shape and volume dynamical system described by equations (15)–(19).

P: Well, this is a very interesting point. This is a phenomenological model that roughly describes cell shape and volume dynamics using an energy. It could be interpreted as a Lyapunov function of the dynamical systems model, equations (15)–(19). Lyapunov function is an energy-like function that describes phase space flow near the steady state fixed point [170]. This function is generally difficult to find. For cells in normal physiological situations, since it actively controls its cell shape and volume, the steady state fixed point must be stable, and a Lyapunov function likely exists. In other contexts, the system may exhibit interesting limit cycle dynamics [171, 172] Therefore it would be interesting to connect the cell volume and cell shape model at the single cell level to the multi-cellular model in equation (23).

In addition, a continuum model for the tissue layer can be built from a discrete model in equation (23). Indeed, the material described by equation (23) can behave as a jammed solid or a fluid [166]. At long times, cell division and apoptosis relieves shear stress and overall tissue again behaves as a fluid [173].

6. Conclusions and perspectives

S: So mechanics has a lot to do with how cells move and control their size and shape. How cells generate force and respond to applied force depends on functions of cytoskeleton as well as water flow.

B: This is good, but the next level of question for biology is how these mechanical forces and cell shape information are integrated to gene expression and epigenetic modification. For example, we know that when mechanical forces are applied to the cell, the cell responds at the seconds time scale by opening and closing ion channels and pumps. At the minute time scale, signaling molecules such as Rho, Rac and ROCK integrates this information to regulate cytoskeleton activity and motor function [71, 174]. At time scales longer than minutes, however, we observe transcription factor movement across the nuclear envelope, and gene expression profiles of the cell starts to change [153, 175, 176]. Ultimately, these changes will modify cell cycle dynamics, and perhaps even the cell phenotype. Therefore, the connection between cell mechanics and genetic regulation is the critical step in advancing biology.

P: This is absolutely right. The connection between mechanics, forces and genes ultimately underlies organismal development, tissue morphogenesis and disease biology [151, 177]. Often, there is a circular loop between mechanics and genes. Transcriptional changes alter cell force generation; this then of course changes the cell organization, shape and motility, which further alter gene activity (figure 9(A)). The opposite loop can also occur: when forces and mechanics experienced by cells change, this could alter signaling pathways and modify gene activity, which then leads to protein expression change and alterations in cell force production and shape. Biology is probably best explained when we consider forces and mechanics, together with genes as a combined system.

Figure 9.

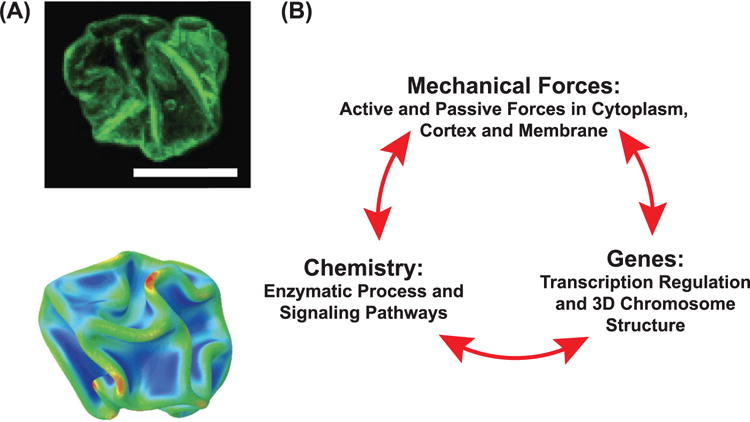
(A) Nuclear shape and volume is directly impacted by cell mechanics. The upper image is of a crumpled nucleus when a tissue cell is detaching from the substrate. The lower image is a computational analysis of an elastic shell undergoing crumpling transition when the pressure difference across the shell is increasing. (B) Mechanistic models that describe cell dynamics must incorporate cell mechanics, biochemistry and gene expression together in a single picture. These systems interact with each other and give rise to complex cell behavior in biological contexts.

B: P makes an excellent point. Some preliminary evidence could link cell mechanics with gene expression. For example, by changing the substrate size, the variable R₀ in figure 7, an important transcription factor can change its localization between the cytoplasm and the nucleus [175]. We also know that the genome of the cell is organized and folded in a reasonably well defined 3D structure [178, 179]. The topology of this 3D structure seems to determine the epigenetic state of the cell. Indeed, genetic material itself seems to be a mechanically active material [180]. Mechanical forces of course, can alter the structure of biological molecules as well as chromatin [181–184]. It is reasonable to consider how forces might directly alter 3D chromatin organization, and some studies have demonstrated that there is a connection between nuclear mechanics and cytoskeletal mechanics [185–188]

P: Indeed, there seems to be experimental evidence that links cell volume with cell nuclear volume and shape (figure 9(B)). When cell volume decreases, the nuclear volume also shrinks [189]. Cytoskeletal networks are also physically connected to the nuclear envelop, and actively exert forces to shape the nucleus [185, 186, 188, 190–192]. This would compact the chromatin loops and change transcriptional program. Of course, mechanosensory molecules such as membrane channels, Rho, myosin and actin network itself may also directly communicate with nuclear transport and transcriptional factor localization, leading to direct connection between genes and cell mechanics.

S: Ahh, so many things to consider in order to understand biological organization. Where can physical models help?

B: From a biologist perspective, mathematical modeling provides a framework to think about functional relationship between measurable quantities. For example, a relationship between cell size and cell cortical tension is predicted by equation (14). We can then check this by measuring cell size and myosin activity. It is not necessarily possible to achieve quantitative prediction, but it is absolutely necessary to make predictions about how things maybe related to each other. These functional relationships are also opportunities for us to test the model.

P: From the modeling perspective, models are only as good as their assumptions! Therefore, experimental work that test assumptions are valuable. Some of the modeling assumptions are not easily understood, or even noticed! Therefore, in addition to testing functional relationships provided by the models, another way to test models is to simply test assumptions of the model, implicit or otherwise!

S: Great, let me get back to the lab and checkout what we talked about today. Next week, I will come back and show you what I find, and I’m sure I will have more questions!