A thermodynamic paradigm for solution demixing inspired by nuclear transport in living cells

Abstract

Living cells display a remarkable capacity to compartmentalize their functional biochemistry. A particularly fascinating example is the cell nucleus. Exchange of macromolecules between the nucleus and the surrounding cytoplasm does not involve traversing a lipid bilayer membrane. Instead, large protein channels known as nuclear pores cross the nuclear envelope and regulate the passage of other proteins and RNA molecules. Beyond simply gating diffusion, the system of nuclear pores and associated transport receptors is able to generate substantial concentration gradients, at the energetic expense of guanosine triphosphate (GTP) hydrolysis. In contrast to conventional approaches to demixing such as reverse osmosis or dialysis, the biological system operates continuously, without application of cyclic changes in pressure or solvent exchange. Abstracting the biological paradigm, we examine this transport system as a thermodynamic machine of solution demixing. Building on the construct of free energy transduction and biochemical kinetics, we find conditions for stable operation and optimization of the concentration gradients as a function of dissipation in the form of entropy production.

Demixing of solutions is a difficult thermodynamic problem with important practical consequences [1]. Examples include the desalination of seawater, medical dialysis, and chemical purification. In all of these processes, free energy is consumed in order to balance entropy of mixing. Typical engineering approaches to demixing involve application of hydrostatic pressure (reverse osmosis), solution exchange (dialysis), or phase change (crystallization or distillation) [2, 3]. In this context living cells adopt a fundamentally diffierent paradigm by establishing and maintaining concentration gradients at steady-state under a fixed set of intrinsic thermodynamic parameters. This recalls the similar capacity to operate mechanochemical motors isothermally [4, 5].

A prominent example of molecular separation is the eukaryotic cell nucleus, wherein the concentrations of many proteins and RNA differ significantly from those in the cell body (cytoplasm). These gradients are maintained by a transport system that shuttles molecular cargo in and out via large protein channels known as nuclear pores [6, 7]. This system has been under intensive study in the biological [8–12] and biophysical [13–17] literatures, with particular emphasis on single-molecule interactions at the pore itself [18–21]. Simple thermodynamic considerations make clear that equilibrium pore-molecule interactions are insufficient to support concentration gradients in solution. Demixing between two compartments cannot occur spontaneously, but must be coupled to a free energy source [22]. At the same time, demixing does not require rectified translocation [23]. Concentration gradients may be established in the presence of a balanced, bi-directional exchange [14, 24, 25].

Nuclear pores represent an unusual transporter in that there is no membrane to cross. Water, ions, and small molecules diffuse freely across the nuclear envelope to equilibrate between the two compartments. Generally, the permeability drops between molecular weight 20 kDa and 40 kDa [26, 27]. Transport of larger macromolecules relies on a special class of proteins, called transport receptors (i.e. “importin”), that usher their cargoes across the nuclear pores by virtue of specific interactions with the channel components. Recognition between importins and their molecular cargo depends on the presence of particular amino acid sequences known as nuclear localization signals (NLS) [8, 28, 29]. The affinity between importin and cargo is regulated by a small GTP-binding protein called Ran [30, 31]. When associated with GTP (RanGTP), Ran binds strongly to importin in a manner that is competitive to NLS binding. By contrast, Ran associated with GDP (RanGDP) binds importin very weakly. Ran interconverts between these two forms through GTP hydrolysis and GTP/GDP exchange, facilitated by the GTPase Activating Protein (RanGAP) and the Guanosine Exchange Factor (RanGEF), respectively [32]. RanGAP is structurally bound to the cytoplasmic face of the nuclear pore and RanGEF is bound to chromatin. Their activities generate a high concentration of RanGTP in the nucleus and RanGDP in the cytoplasm (see FIG. 1).

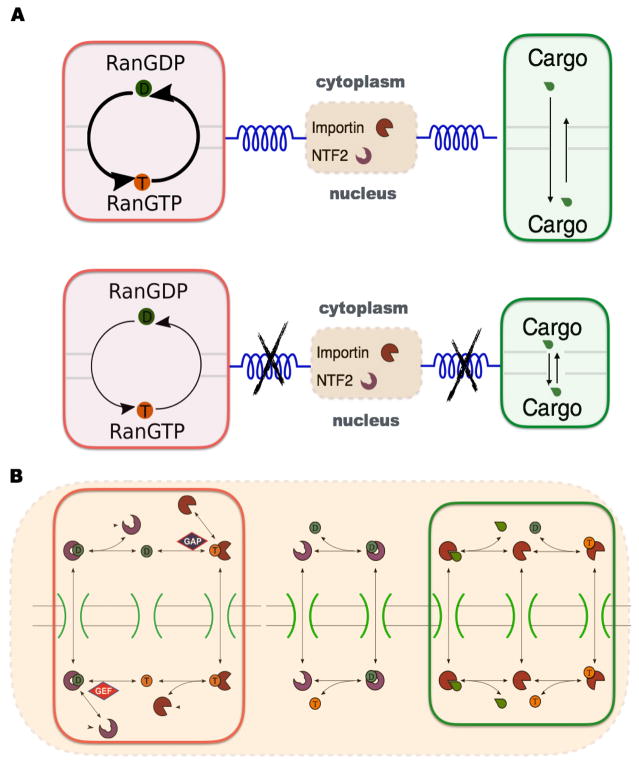
FIG. 1.

(Color online) Demixing of cargo across the nuclear membrane is driven by Ran coupled to NTF2 and importin system. (A) With such coupling (upper panel), nuclear cargo accumulation is favored and Ran GTP/GDP exchange cycle proceeds faster than without coupling (lower panel). The thickness of arrowed curves in Ran cycle indicates the strength of reaction flux while the length of the arrowed lines in cargo transport represents the rate at which the underlying processes occur. (B) Details of molecular demixing machine in the context of nuclear transport. Species labels as above. In both panels, reactions corresponding to Ran cycle and cargo transport are highlighted by red and green boxes, respectively. The orange dashed box includes all reactions coupled by the importin-NTF2 system. See also Fig S1 in the Supplementary Material.

Demixing is powered by transducing free energy from GTP hydrolysis through the interactions of transport receptor with Ran. The transport machinery has been formulated in terms of coupled chemical kinetics [23, 33, 34] but the energetics have not yet been addressed. In particular, we ask: How does the rate of dissipation (energy consumption) relate to the achieved concentration gradient? What is the proper definition of transport efficiency? Is there an optimal working point given the nonequilibrium nature of this cellular machine? To address these questions, it is helpful to reformulate the problem in a thermodynamic language. For consistency with the literature we retain the biological nomenclature, yet the aim is to understand the natural engineering in a more abstract sense that might ultimately be implemented synthetically.

In the thermodynamic formulation, a central role is played by energy transduction in a “futile cycle” among the components (see FIG. 1). This is roughly analogous to heat flow in a Carnot cycle. The importin receptor binds RanGTP, and a second receptor known as nuclear transport factor 2 (NTF2) binds specifically RanGDP. The forward cycle takes RanGTP out to the cytoplasm with importin and RanGDP back to the nucleus with NTF2. Detailed balance is broken by the distribution of RanGAP and RanGEF as described above, so that the reverse cycle is scarcely populated.

Free energy from the Ran cycle is transduced by importin to bias the steady-state free cargo concentrations in the nuclear and cytoplasmic compartments. Details of the underlying biochemical reactions are shown in FIG. 1B and can be modeled on the basis of mass action. The corresponding kinetic parameters can be found from the literature or estimated from simple scaling arguments (see FIG. S1 and Supplementary Material for details of the kinetic model). Numerical solutions are obtained by solving all the coupled rate equations using a standard Runge-Kutta method (The code used for simulation is available in the Supplementary Material). We emphasize that the present aim is not so much to model the biological implementation as to explore the generic operation of the thermodynamic machine. Relations between parameters are therefore more important than specific values.

Energetics enter the model via the charging of Ran with GTP and its subsequent hydrolysis to GDP (reactions 5 and 2 in FIG. S1, respectively). The flux through these two reactions must be equal in steady state. Energy is drawn from the non-equilibrium ratio of free GTP to GDP, θ, which is maintained by cellular metabolism and defines an effective “free energy” F_θ:= k_BT log (θ). A typical value of θ is roughly a few tens to a hundred [32, 35]. Independent of the complex operational details of RanGEF and RanGAP with associated co-factors, we can look at the steady states and relate the reactions to θ. (See Supplementary Material for details.) On the nuclear side, the complex NTF2-RanGDP exchanges for NTF2 and RanGTP. The dissociation constant K_D (forward divided by reverse flux) can be shown to be proportional to θ. Conversely, on the cytoplasmic side the corresponding K_D is proportional to 1/θ. As a result, any enhancement of flux through the futile cycle in the forward reaction conferred by increasing θ (i.e. reaction 5 in FIG. S1C) is balanced by the contradicting counterpart in preventing RanGTP release (i.e. reaction 2 in FIG. S1C).

A useful measure of cargo demixing is the nuclear localization ratio, NL, defined as the ratio between nuclear and cytoplasmic cargo concentrations: [C]_nu/[C]_cyto. This ratio defines a chemical potential, Δμ = −k_BT log [C]_nu/[C]_cyto, that measures the excursion from equilibrium. FIG. 2A shows NL as a function of importin and NTF2 concentrations. The most striking feature is that NL is maximum for intermediate levels of importin. The importin concentration at which NL is maximized, [Im*], grows with the total cargo load, [C]_tot (see FIG. 2B). Furthermore, [Im*] is largely independent of NTF2 concentration for different cargo concentration considered (see FIG. S5). This suggests an inherent optimization.

FIG. 2.

(Color online) Phase diagram of nuclear localization. (A) The cargo nuclear localization NL:= [C]_nu/[C]_cyto, represented by different color shadings, is obtained by varying the total importin and total NTF2 concentrations while keeping overall cargo level fixed at [C]_tot = 100 nM. (B) A family of curves shows NL for several cargo concentrations as a function of importin concentration with [NTF2]_tot = 100 nM. The 1D curve for [C]_tot = 100 nM is a cut across the plot of panel A. The total concentration of Ran is [Ran]_tot=75 nM. Locations of NL maximum are marked by diamonds (see FIG. 4C as well). Kinetic rate constants used are given in the Supplementary Material.

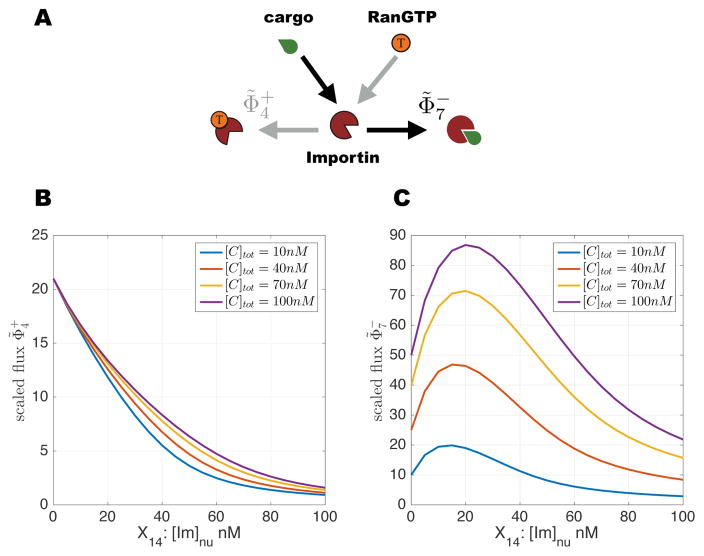
At first sight it is surprising that augmenting the importin concentration, which increases the number of molecules that can transport cargo to nucleus, may decrease the localization ratio. The optimal dependence of NL on importin reflects the dual role importin plays as the inbound carrier of cargo protein as well as the outbound carrier of RanGTP. Powering the futile cycle requires that importin bind RanGTP, whereas cargo transport requires importin to bind cargo. This establishes a binding competition in the nucleus that is a characteristic feature of protein import (FIG. 3A). In spite of the higher affinity of RanGTP for importin, the cycle analysis shows that importin in the nucleus binds cargo more rapidly. As seen in FIG. 3BC, NL is maximized close to the point at which the difference between the reaction fluxes of importin-cargo formation ( ${\mathrm{\Phi }}_7^{-}:={\stackrel{\sim }{\mathrm{\Phi }}}_7^{-}{[Im]}_{nu}=(k_7^{-}{[C]}_{nu}){[Im]}_{nu}$) and importin-RanGTP formation ( ${\mathrm{\Phi }}_4^{-}:={\stackrel{\sim }{\mathrm{\Phi }}}_4^{+}{[Im]}_{nu}=(k_4^{+}{[\mathit{RanGTP}]}_{nu}){[Im]}_{nu}$) is maximal. Intuitively, this is the realm where importin can bind cargo effectively while maintaining its coupling to the reaction cycle that transduces energy for cargo transport.

FIG. 3.

(Color online) Competition between RanGTP and cargo to bind importin: (A) Schematic of the two competing reactions: (B) Reaction flux for importin-RanGTP formation ${\stackrel{\sim }{\mathrm{\Phi }}}_4^{+}~k_4^{+}[\mathit{RanGTP}]$ and (C) that for importin-cargo formation ${\stackrel{\sim }{\mathrm{\Phi }}}_7^{-}~k_7^{-}{[C]}_{nu}$. Fluxes are scaled by [Im]_nu (see text). Parameters as in FIG. 2

To understand the thermodynamics of nuclear transport, we formulate the transport system as a nonequilibrium Markov process. Since a nonequilibrium steady state (NESS) necessarily breaks detailed balance in the underlying Markov process, the system has a nonzero entropy production [22, 36, 37]. This is the energy per unit time required to maintain the NESS, with units of power. Following the Schnakenberg description, the EP for a NESS is given by [38]

$$EP=k_{B}T\sum _{i,j}{P}_i^{SS}W(i,j)log\frac{W(i,j)}{W(j,i)},$$ (1)

where $P_i^{SS}$ is the steady state probability distribution of state i while W (i, j) denotes the transition probability from state i to state j. Concretely, $P_i^{SS}$ is the fraction of reactants that participate in the transition reaction starting from state i while W (i, j) can be calculated from the relevant reaction fluxes. Note that the summation in Eq. (1) is over all links of the reaction network, though this is equivalent to summing over all links pertaining to Ran futile cycle (See Supporting Material for details).

This entropy production provides a direct measure of the power input to the underlying biochemical circuit. FIG. 4A shows EP for various importin and NTF2 concentrations. FIG. 4B adds various cargo concentrations for a fixed level of [NTF2]. In each case, as the importin concentration increases, EP first drops to a minimum and then peaks before slowly decaying. Note that the minimal dissipation (entropy production) tracks closely with the value at which the NL ratio peaks (see FIG. 4C). These conditions define an optimal efficiency of the demixing machine. With further increasing importin concentration, the futile cycle decouples from cargo translocation and EP increases. At a still higher concentration, EP peaks and then decreases. This can be understood qualitatively as a short circuit via reaction 8, where importin moves between compartments carrying neither cargo nor RanGTP. As seen in FIG. 4D, for such high importin levels the corresponding flux Φ₈ exceeds that of the RanGTP loading to importin, Φ₄.

FIG. 4.

Phase diagram of entropy production. (A) Entropy production is plotted as a 2D function of NTF2 and importin, at fixed cargo concentration [C]_tot = 100 nM. Compare with FIG. 2A. (Note that both axes extend down to 5 instead of 0 to avoid numerical divergence.) (B) A family of curves shows the entropy production for several cargo concentrations as a function of importin concentration; NTF2 concentration fixed at [NT F2]_tot = 100 nM. The 1D curve for [C]_tot = 100 nM is a cut across the plot of panel A. Compare with FIG. 2B. The peaks and troughs of these curves are marked by squares and circles, respectively. (C) Locations of entropy production maximum/minimum (square/circle) and that of nuclear localization maximum (diamond). The importin concentration at which EP is minimum is close to but always less than [Im*], where NL is maximum. Thus, one strategy for maximizing the efficiency of demixing is to have the futile cycle operate in regime where its entropy production is minimized. (D) At very high importin concentration, EP decreases. This reflects a loop around the energetic reaction Φ₄ via the reversible re-action Φ₈. Here [NT F 2]_tot=100 nM, as in the panel B. In all panels, [Ran]_tot = 75 nM. The kinetics constants used are the same as in FIG. 2 and 3 (see SM Section II).

To the best of our knowledge the optimal steady-state has not been observed experimentally. The kinetic rate of nuclear protein uptake was found to be reduced by microinjection of importin receptor to live cells; rate equation simulations done in parallel also pointed to the dual role of importin (FIG. 3A) [39]. Steady-states were not reported in that study, however. Other possible experimental tests include titration of importin protein to nuclei reconstituted in vitro in Xenopus egg extract and optical activation of importin receptors, similarly to induction of nuclear transport by NLS activation [40]. An important point in comparison with literature is that we have considered a single, collective “cargo” for transport. In reality, multiple cargoes compete for binding to relatively few but promiscuous transport receptors. This competition leads to a partitioning according to equilibrium binding affinities and may lead to vastly different kinetics. However the steady-state NL ratio (in solution) is independent of the affinity, reflecting thermodynamic control and equilibration of the chemical potentials [24, 25, 34]. Consistent with this paradigm, in which a net accumulation occurs together with a balanced bidirectional flux, the simulations show that the nuclear and cytoplasmic concentrations of the importin-cargo complex (X₄ and X₁₁, respectively) equilibrate in steady-state. It is also interesting to note that RanGTP loading onto importin (reaction 4) was identified in the earlier analysis as the primary rate-limiting step in accumulation kinetics [34].

In summary, we have analyzed the biological paradigm for nuclear transport from a thermodynamic point of view. Building upon prior understanding that protein cargo demixing is facilitated by hydrolysis of GTP, we draw the connection between consumption of chemical energy and maintenance of the cargo concentration gradient at non-equilibrium steady states. We show that the efficacy of nuclear localization ratio peaks at intermediate importin level, which is not far from the power consumption (entropy production) minimal. It is likely that the cell maintains an importin concentration at an advantageous level with respect to these operating points defined by the thermodynamic analysis. Interestingly, the system as configured is robust to the quality of the chemical energy source, in the sense that the NL ratio is almost independent of the GTP:GDP ratio θ when θ> ≳ 20, FIG. S4. A thermodynamic definition of the system efficiency remains elusive, however. Whereas conventional efficiency of an engine is a dimensionless ratio of mechanical to thermal power, in the NESS a constant free energetic gradient (chemical potential in the present case) is maintained by a constant power input. The ratio has units of time. This could be renormalized sensibly by a characteristic remixing time, e.g., the permeability of the nuclear pores to the cargoimportin complex. There is no guarantee of a bound at unity, however, so the definition remains ad hoc, a useful figure of merit. It is also interesting to contrast the competitive interactions between receptor and RanGTP in nuclear protein accumulation (import) with the cooperative interactions in nuclear protein depletion (export). While these are often considered as simple inverse processes, they differ in this essential aspect [41].

This work is part of a larger literature that seeks to examine basic biophysical processes from a thermodynamic perspective. It is now clear that thermodynamics fundamentally constrains the ability of cells to perform various task ranging from detecting external signals [42–44], to adaptation [45], to making fidelity decisions [37], generating oscillatory behavior [46], and of course generating forces and dynamic structures [47–49]. In all these examples, it is possible to map these tasks to Markov processes and compute the corresponding entropy production rate. This suggests that there may be general theorems about thermal efficiency in cells that are independent of the particular task under consideration [36, 50–52]. It will be interesting to explore if this is actually the case and to see if these principles can be applied to synthetic biology and ultimately biomimetic engineering [50].