Arbitrary waveform modulated pulse EPR at 200 GHz

Abstract

We report here on the implementation of arbitrary waveform generation (AWG) capabilities at ∼200 GHz into an Electron Paramagnetic Resonance (EPR) and Dynamic Nuclear Polarization (DNP) instrument platform operating at 7 Tesla. This is achieved with the integration of a 1 GHz, 2 channel, digital to analogue converter (DAC) board that enables the generation of coherent arbitrary waveforms at K_u-band frequencies with 1ns resolution into an existing architecture of a solid state amplifier multiplier chain (AMC). This allows for the generation of arbitrary phase- and amplitude-modulated waveforms at 200 GHz with > 150 mW power. We find that the non-linearity of the AMC poses significant difficulties in generating amplitude-modulated pulses at 200 GHz. We demonstrate that in the power-limited regime of ω₁ < 1MHz phase-modulated pulses were sufficient to achieve significant improvements in broadband (>10MHz) spin manipulation in incoherent (inversion), as well as coherent (echo formation) experiments. Highlights include the improvement by one order of magnitude in inversion bandwidth compared to that of conventional rectangular pulses, as well as a factor of two in improvement in the refocused echo intensity at 200GHz.

Graphical abstract

1. Introduction

High field Electron Paramagnetic Resonance (EPR) is an established technique that has provided important insights in many material and biological applications. The use of advanced pulsed and multidimensional EPR techniques at high magnetic fields, despite its obvious prospects, is hampered by the limited available microwave power at frequencies above W-band (>100 GHz) where high-power amplifiers >150mW are not available, or are prohibitively expensive. The limited microwave power available for high-field EPR results in low nutation frequency ω₁ values of at most 4.2 MHz at 180 GHz and 2.1 MHz at 275GHz, even when using an efficient T₀₁₁ single mode resonator.[1,2] This hampers the feasibility or quality of important pulsed EPR experiments, including double electron-electron resonance (DEER) at high fields. The low ω₁ available at high field / frequency of a few MHz is in stark contrast to the 70 MHz ω₁ routinely achieved at X-band frequencies where DEER and other pulsed EPR experiments are routinely performed.

EPR experiments are typically limited by the available pulse bandwidth, hence the push for higher power and shorter pulses. Amplitude and phase modulated microwave pulses, generated by an arbitrary waveform generator (AWG), have proven a viable solution to the limitations in the available pulse bandwidth. AWG-generated waveform-modulated pulses allow for high level of control over spin manipulations which results in a dramatically improved pulse performance at a given microwave power. Owing to such capabilities, AWG pulses have been successfully applied for decades in nuclear magnetic resonance (NMR),[3–5] and have become integral to virtually all modern NMR spectroscopy and imaging experiments. In contrast, only recent advances in high speed electronics permitted the implementation of AWGs in pulsed EPR experiments.[6–9] There are numerous recent applications detailing the use of AWGs in pulsed EPR experiments at conventional, X-band (∼9.5 GHz) and Q-band (∼35 GHz), frequencies that showcase the gains afforded by arbitrary amplitude and phase modulation of microwave pulses [7,9–14]. However, AWG-controlled pulsed EPR at higher frequencies have not been demonstrated to date.

The application of AWGs to pulsed EPR spectroscopy is expected to have an even greater impact at higher magnetic fields. The rational is two-fold: (1) the available microwave power (50-200 mW) and thus the pulse bandwidth (∼ 1 MHz) is significantly less compared to lower microwave frequencies and (2) the EPR spectral width is typically much wider due to the increased g-factor resolution. For instance the spectral width of a simple nitroxide radical is ∼ 1 GHz at 7 T and spans a few GHz or more for common transition metal ions. This discrepancy between the typical pulse excitation bandwidth (∼1MHz) and the width of the EPR spectra (∼few GHz) significantly limits the sensitivity of high field pulse EPR experiments, as well as presents an opportunity for significant sensitivity gains by AWG implementation. The cost of overcoming the pulse bandwidth limitation without increasing microwave power is an increased pulse length. This poses a limitation on the shaped-pulse utility for systems with short relaxation times (compared to the required pulse length) or strong electron spin-spin couplings (compared to the inverse pulse length), and requires a compromise between the length of the best performing shaped pulse and the relaxation time or the electron spin-spin coupling strength.

To this end we integrate a homebuilt AWG system with 1GHz bandwidth into a 200GHz microwave bridge with dual EPR and Dynamic Nuclear Polarization (DNP) capabilities for the purpose of confronting the pulse bandwidth limitation [15]. We implement the AWG into the 12 GHz pulse forming network of the microwave bridge. The AWG features two digital to analog converter (DAC) boards that drive the I and Q channels of an IQ mixer. The IQ mixer mixes the DAC outputs with the 12 GHz microwave. The output microwave pulses are then up-converted to 200 GHz by an amplifier multiplier chain (AMC). This design achieves amplitude and phase modulation at 200 GHz, similar to other systems designed for rotational spectroscopy at sub-THz frequencies. [16,17]

In the following we describe the integration of the AWG unit into a 200 GHz solid-state source powered EPR / DNP spectrometer platform. We showcase broadband manipulation of up to 20 MHz bandwidth of the EPR spectrum at 200 GHz using phase-modulated chirp pulses that largely exceeds the bandwidth possible with standard rectangular pulses at the available microwave power. Using phase modulated pulses we demonstrate broadband inversion and coherent echo formation on electron spins in a BDPA / poly styrene mixture, and in the P1 centers of a ¹³C enriched diamond sample. Finally, we present the performance and limitations of the 200GHz IQ mixer and AMC-based microwave bridge for generating both amplitude and phase modulated pulses.

2. Results

2.1 Hardware setup and design

The conventional approach for implementing arbitrary phase and amplitude modulated pulses at X-band frequencies is to mix the arbitrary waveform with a carrier frequency at (or close to) the final operating X-band frequency of around 9.5 GHz using an IQ mixer.[7,8] The drop in power due to insertion loss of the 12 GHz IQ mixer (∼7-9dB) is compensated for by further amplification after mixing, culminating in the final high-power amplification stage of the ∼1kW TWT amplifier. However, the absence of a microwave amplifier operational at high frequencies (> ∼100GHz) prevents us from replicating this approach at 200GHz, where the power drop due to the insertion loss of a ∼200GHz mixer cannot be compensated for by subsequent amplification. Instead, we integrate the AWG into the spectrometer at the ∼12 GHz base frequency, before the AMC. To achieve this, an additional channel that includes the IQ mixer for mixing the AWG waveform with the 12GHz base signal was added to the pulse-forming unit of our spectrometer. The schematics of the pulse-forming unit is presented in figure 1, with the IQ mixer used for AWG integration shown on top right of the figure.

Figure 1.

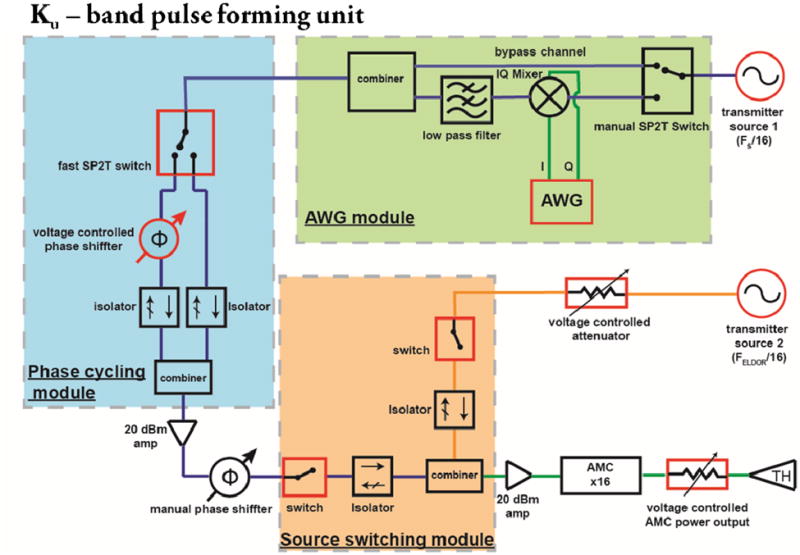
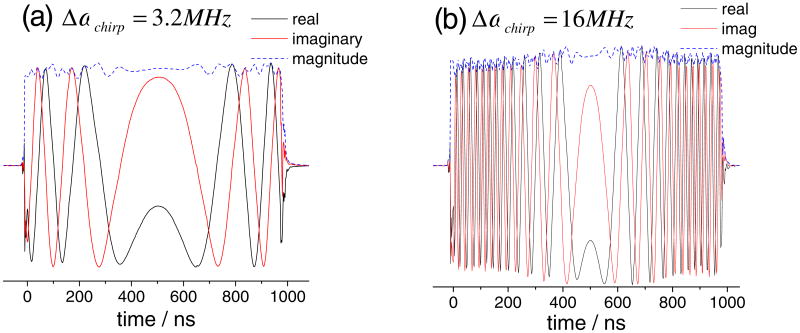
(a) Schematics of the K_u-band pulse forming unit. Devices highlighted in red are computer controlled using Specman4EPR software. Experimental ∼200GHz full amplitude 1μs chirp pulse with (b) Δν_chirp = 3.2MHz and (c) Δν_chirp = 16MHz

The overall design of the 200 GHz quasi optics (QO) bridge for dual EPR and DNP operation was described in detail in a recent publication.[15] The system utilizes three digitally programmable, continuous wave (CW) ∼12GHz synthesizers to operate (i) the main microwave transmitter channel source for pulsed and CW EPR and (ii) the second transmitter channel for pump-probe Electron Double – Resonance (ELDOR) experiments, as well as (iii) to generate the LO (local oscillator) reference for the 200GHz sub-band mixer in the heterodyne receiver system. The microwave output of the main ∼12 GHz CW transmitter source (i) is sliced, and if desired mixed, with coherent AWG waveforms produced with a fast (1 GHz) DAC board for phase and amplitude modulation. The generation of this ∼12 GHz AWG waveform occurs in the pulse-forming unit before it is sent to the ×16 amplifier multiplier chain (AMC) chain to produce the pulsed and shaped output at 200 GHz. The induction mode-selected 200GHz EPR signal is routed via the QO bridge to the 200GHz sub-band mixer, where it is down-converted to an intermediate frequency of 3GHz. The 3GHz signal is amplified using a 46dB gain low-noise amplifier, before being down converted to a DC signal by mixing with a coherent 3GHz signal from a reference arm, and then digitized for detection.

2.2 Pulse forming unit

The pulse forming unit operating at ∼12GHz frequency consists of three main modules (figure 1). In the AWG module (highlighted in green in figure 1) the CW signal from the transmitter source is mixed, using the IQ mixer (IQ0618LXP by Marki microwave), with the AWG waveform. The digital to analog converter (DAC) board used for arbitrary waveform generation in this work consists of an Ethernet accessible FPGA board (Altera Stratix II by Altera) that drives two independent DAC boards with 14-bit resolution and 1 GHz bandwidth that form two analog output channels that are used to produce the real and imaginary DC - 1 GHz waveforms. In addition, there are three digital ECL (emitter-coupled logic) channels synchronized with the analog ones, by virtue of operating at the same high frequency clock, which can be used to trigger / control other devices, such as microwave switches and digitizers. The AWG can be set to generate the programmed waveform, either immediately after finishing the data transfer or upon receiving an external trigger. This DAC board was previously used in a digital X-band EPR spectrometer constructed in our lab[8] and was designed by the Martinis group at UCSB[18]. The shaped ∼12GHz waveform output after the IQ mixer passes through a low pass filter (FLP-1740 by Marki microwave), mainly to suppress the leakage signal at the 2^nd harmonic of the carrier frequency (∼24GHz). It is important to ensure careful calibration of the power level of the shaped pulses such that the input power of the full-amplitude shaped pulse is sufficient to operate the AMC at saturation while the leakage at carrier and image frequencies is below the power threshold for engaging the AMC. Subsequently the shaped signal is routed into the phase cycling unit (highlighted in blue in figure 1). The manually selectable bypass channel, selected by a manual SP2T switch, (SM-2min by RLC electronics) in the AWG module is installed to carry out experiments that do not require AWG operation with the same transmitter source as used for AWG, and to maintain backward compatibility with existing pulse sequences and operating procedures. The bypassed signal is routed into the same phase cycling module as the shaped signal.

The signal generated from the AWG module is routed via a fast <10ns SP2T (F9120AH by General Microwave) switch to either a bypass channel (0° phase shift) or through a voltage controlled phase shifter hardware that is set nominally for an 11.25° phase shift at the ∼12GHz operating frequency, thus resulting in a 180° degree phase shift at ∼200GHz (following ×16 multiplication in the AMC). While phase cycling can of course be achieved without relying on an analogue phase shifter unit by digitally reprogramming the waveform produced by the AWG, it is beneficial to retain the hardware-based phase cycling capability, especially when delays associated with AWG data transfer rates become significant. The source switching module (highlighted in orange in figure 1) is designed to allow for quick (∼10ns) switching between the main and the ELDOR source (transmitter source 2) to allow for pulsed double-resonance experiments. The two SPST switches used in the source switching module are identical (SWM-DJV-1DT-2ATT by American Microwave Corporation) with a 1ns rise and fall time. In principle the AWG eliminates the need for a dedicated ELDOR source to generate multiple frequencies. However, this functionality is retained for experiments that require long ELDOR pulses that exceed the 15 μs memory limit of the current AWG module.

2.3 Timing and software control

To properly integrate the pulse shaping capabilities into the pulsed EPR spectrometer, it is necessary to accurately synchronize (preferably to <1ns) the (i) waveform generation by the DAC, (ii) microwave switch operations: the SP2T switch in the phase cycling module and the two switches in the source switching module, and (iii) digitizer triggering for detection (not shown on the schematic). In the previously debuted digital X-band AWG spectrometer developed in the Han lab[8], precise switch and detector synchronization with the waveform generation and transmission were achieved by utilizing three auxiliary ECL digital channels available on our DAC board to operate all microwave switches, as well as to trigger the oscilloscope that was used to digitize the signal. These ECL channels are timed to the same precise 250MHz internal (on board) clock to time the generation of the arbitrary waveform, therefore avoiding any synchronization issues between waveform generation and device triggering. However, the number of currently available ECL channels (three) is not sufficient to operate the three switches in the 200GHz setup, as well as trigger the digitizer in the more complex 200GHz spectrometer. Thus, an alternative control scheme was implemented. Specifically, the microwave bridge is now controlled by a 24 channel PulseBlasterESR-Pro (PB) TTL pattern generation board (SpinCore Technologies Inc) that handles the overall timing of the experiment. The PB controls the hardware timing of all three mw switches, externally triggers the DAC board for waveform generation, and the triggers the digitizer for signal detection. The drawback of this method of timing control is a 4ns jitter in the timing of the AWG waveform output relative to the timing of the mw switches and the digitizer that are now all directly controlled by the PB. This jitter is a consequence of the PB and AWG operating on different internal clock frequencies of 300 MHz and 250 MHz, respectively. Waveform generation by the DAC board starts in sync with the 250MHz clock cycle. By virtue of the PB and AWG boards not having their internal clock cycles synchronized, a PB trigger can be received any time during the 4ns clock cycle of the AWG, and thus resulting in a <4ns jitter that generates uncertainty in the position of the waveform relative to the time of the trigger received by the AWG. Currently, this does not present a problem given the maximum excitation bandwidth used in this work of 20MHz which corresponds to an echo widths of > 50ns and with < 4ns jitter does not cause a significant broadening problem. If needed achieving more precise timing in the future is rather straightforward, since it is possible to operate the relevant mw switches and digitizer trigger using the auxiliary ECL channels available on the AWG board, and leave the less critical timing to be controlled by the PB board. However, an advantage of the current combined configuration, where the AWG is operating in slave mode relative to PB, is that it allows for the generation of pulse sequences that exceed the 15 μs memory limit of the currently available AWG, as long as only part (<15us) of the pulse sequence involves shaped pulses (see SI). In the future, the installment of an AWG with greater memory than 15 μs will alleviate such limitations.

The overall software control of the 200 GHz spectrometer, including arbitrary waveform generation for shaped pulses, is carried out using the Specman4EPR software[19] (FeMi Instruments, LLC). In its current implementation the software includes a library of several standard parameterized shaped pulses and a possibility to load user-generated waveforms. For operation using standard parameterized shaped pulses the waveform parameters are accessible as user-defined variables in the experiment, thus allowing for easy and real-time adjustment and optimization of the pulse shapes. To deal with non-standard waveforms it is possible to load user-defined waveforms directly into the Specman4EPR software that were generated with other programs (e.g. MATLAB, Python, Mathematica) and saved as ASCII files. The user-defined waveforms can be interpolated to a given pulse duration, additionally the offset from the carrier frequency, as well as the phase of the user-defined pulse can be adjusted by the user. In addition to generating waveforms for shaped pulses and controlling the overall timing of the experiment, the SpecMan4EPR software also controls the frequency of the two digitally programmable transmitter sources, the voltage controlled phase shifter in the phase cycling module, the voltage controlled attenuator in the ELDOR channel (located between the transmitter source II and preceding the source switching module), and the overall intensity of the AMC output. The output power of the AMC is regulated via changes in voltage applied to user controlled attenuation (UCA) port of the AMC chain; this is schematically depicted as a separate attenuator following the AMC in figure 1). All devices that are controlled via the SpecMan4EPR software are highlighted with a red border in figure 1. The variable voltage used to control the voltage controlled phase shifter, the voltage controlled attenuator of the ELDOR source and voltage controlled AMC output is provided by the USB-6001 DAQ (National Instruments).

2.4 Spectrometer performance

2.4.1 Phase modulated chirp pulses

Figure 2 shows the pulse profile of two 1μs long chirp pulses at a carrier frequency of 197.549 GHz, as captured using the ∼200 GHz super heterodyne detector. The QO bridge has a built-in ∼35 dB isolation of, the usually unwanted, reflected signal from that of induction-mode signal that is the desired EPR signal for detection. This configuration allows us to capture the high-power pulse shape in real-time with the ∼35db attenuation of the pulse ensuring that no damage is caused to the detector when used as configured for detection of the induction mode EPR signal. The phase profile, θ_pulse (t) , of a linear chirp pulse with arbitrary offset from the carrier frequency is given by:

Figure 2.

Experimentally acquired waveforms for 1μs long chirp pulses at 197.549GHz as acquired via the leak into the induction mode using phase sensitive detector.

$${\theta }_{\mathit{\text{pulse}}}\left(t\right)=\left(\left({\omega }_{\mathit{\text{offset}}}-\frac{\Delta {\omega }_{\mathit{\text{chirp}}}}{2}\right)t+\frac{k{t}^2}{2}\right)$$ (1)

Where ω_offset is the offset frequency from the carrier, Δω_chirp is the bandwidth of the chirp pulse, k is the chirp sweep rate (in MHz/μs) and t is the time variable in μs. For a given pair of Δω_chirp and pulse length t_p the chirp sweep rate is given by:

$$k=\frac{\Delta {\omega }_{\mathit{\text{chirp}}}}{t_p}$$ (2)

For the two pulses displayed in figure 2, the parameters used were t_p = 1μs and ω_offset= 0; the two pulses displayed in figure 2a and b differ by their Δω_chirp values of 3.2MHz and 16MHz, respectively. The frequency profile is symmetric relative to the center frequency of the pulse. At the center of the pulse, the instantaneous frequency of the pulse coincides with the frequency of the carrier at the reference frame of the carrier, yielding $\frac{\mathrm{d}{\theta }_{\mathit{\text{pulse}}}\left(t\right)}{\mathrm{d}t}=0$. The instantaneous frequency is increasing towards each end of the pulse, as evident by the increasing frequency of the oscillations for both pulses. As expected the frequency increase is higher for the pulse in figure 2b compared to the one in figure 2a due to a higher Δω_chirp. The high frequency oscillations in the amplitude of the chirp pulses seen in figure 2 (blue trace) are largely due to imperfections of the 12GHz IQ mixer of the pulse forming unit and 3GHz IQ mixer in the intermediate frequency stage of the receiver.

2.4.2 Non-coherent spin manipulation (adiabatic inversion)

Phase-modulated linear chirp pulses can perform inversion of the magnetization over a very large bandwidth which, excluding the edge effects and relaxation, is equal to the width of the chirp pulse (Δω_chirp) and is commonly referred to as an adiabatic passage pulse. During the course of an adiabatic passage (from low to high frequency) the effective B₁ magnetic field vector in the rotating frame changes from being aligned along the +z direction (pulse frequency is below resonance) to being in the x-y plane (on resonance) and finally to being aligned along the -z direction (pulse frequency is above the resonance).

When the adiabaticity condition:

$$\frac{k{T}_2}{{\omega }_1}\gg 1\gg \frac{k}{2\pi {\omega }_1^2}$$ (3)

is fulfilled, the electron spin magnetization vector will stay aligned parallel (or antiparallel in the case of the sweep from high to low frequency) with the direction of the effective B₁ magnetic field vector, resulting in the inversion of its direction at the end of the pulse. Here, ω₁ is the nutation frequency of the B₁ magnetic field vector, k the chirp sweep rate and T₂ the transverse electron spin relaxation time. The right side of eq (3) ensures that the change in the direction of the magnetic field vector is adiabatic so the magnetization vector can follow the magnetic field vector. Given this relationship the chirp rate k can be increased when higher microwave power (higher ω₁) is available, and thus for a given pulse length the inversion bandwidth Δω_chirp can be increased without compromising the adiabaticity.

Fulfilling the left side of eq (3) ensures that the passage through the x-y plane is rapid enough so that no significant dephasing occurs while the magnetization resides in the x-y plane. The adiabaticity is minimal exactly on resonance where the magnitude of the effective magnetic field vector is the smallest. It follows that the dependence of the inversion efficiency is conveniently described using the on-resonance adiabaticity, also known as critical adiabaticity (Q_crit) [4,20] For a linear frequency sweep with constant irradiation strength, ω the on-resonance or critical adiabaticity is given by. [4,20]

$$Q_{\mathit{\text{crit}}}=\frac{2\pi {\omega }_1^2}{k}$$ (4)

From eq (4) it follows that for high fidelity inversion the requirement can be simplified as Q_crit ≫ 1 since it ensures the right side of eq (3) is fulfilled for the entire adiabatic pulse.

For a non-resonant setup (no mw cavity) as described here the ∼150mW output of the AMC at 200GHz results in a nutation frequency of ω₁ ≈ 0.6 - 0.8MHz for non-lossy thin samples such as diamond. In practice when setting Q_crit = 5, the “adiabatic” chirp rate for our setup becomes $k=\frac{2\pi {\omega }_1^2}{5}\approx 0.45-0.8\frac{\text{MHZ}}{\text{μs}}$. Since slight reduction of the critical adiabaticity Qcrit < 5 can still be tolerated and it is more beneficial to have a faster chirp rate to diminish effects of relaxation decay during the pulse. We chose the maximum chirp rate for our inversion experiments to be k = 1MHz / μs. The situation is different for higher volume samples where the sample thickness exceeds the 200 GHz wavelength (1.5mm). In this case lower nutation frequencies and larger ω₁ inhomogeneity were observed. For 1% BDPA in o-terphenyl sample the nutation frequency was ω₁ = 0.35 ± 3 MHz, determined by the analysis of the nutation and square pulse inversion experiments as detailed in the SI.

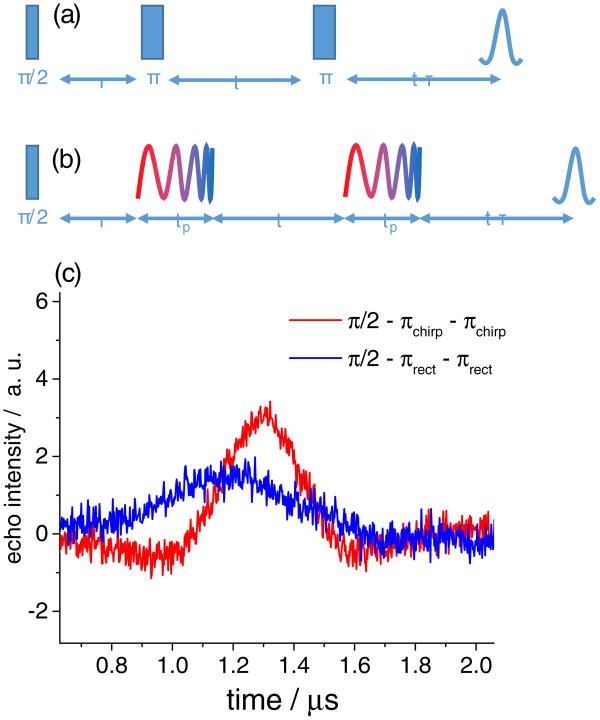
To experimentally measure the inversion profile of a chirp pulse we used a three-pulse experiment (figure 3a), where the effect of the chirp pulse (first pulse) is monitored by changes in the echo produced by the last two pulses. The experimentally detected inversion profiles obtained for 1% BDPA in o-terphenyl sample (frequency swept EPR spectrum is presented in figure S2 of the SI) using a 10 μs long chirp pulses for Δω_chirp = 10, 6 and 2 MHz are shown in figure 3b as black red and green curves, respectively. The inversion profile obtained for a 1 μs (π) pulse is shown as blue dashed line for comparison. Figure 3c shows similar inversion experiments performed on a center line of a P₁ center in 10% ¹³C enriched diamond (frequency swept EPR spectrum is presented in figure S2 of the SI) using a 10 μs long chirp pulses with Δω_chirp = 10 and 5 MHz as red and black curves, respectively. The vertical dashed lines denote the nominal bandwidth of these two chirp pulses. It is evident that broadband spin manipulation is successfully achieved over the whole Δω_chirp bandwidth in both cases.

Figure 3.

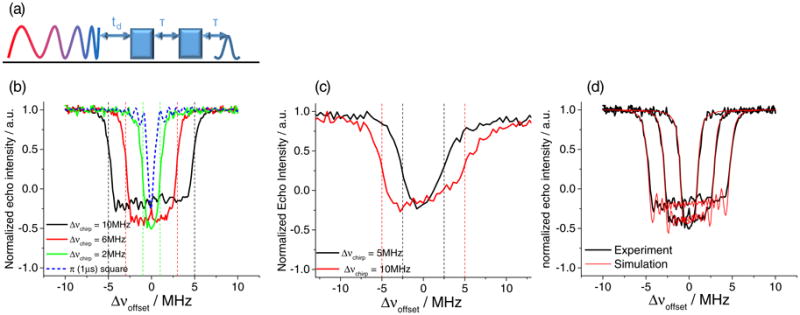
Pulse sequence used for measuring inversion profile of a chirp pulse. (a) Experimental inversion profiles of a 10μs chirp pulse for BDPA in o-terphenyl sample (b) and P1 center of diamond (c). Vertical dashed lines denote the nominal Δω_chirp for each pulse bandwidth respectively. Overlay of experimental and simulated data for BDPA in o-terphenyl sample (d) Experimental parameters BDPA sample: t_p = 500 ns; τ = 800 ns; t_d = 2.4 μs; Frequency 197.589GHz; Diamond sample: t_p = 400 ns; τ = 800 ns; t_d = 500 ns; Frequency 197.529GHz.

The electron spin relaxation times for the BDPA sample are T₁ = 260 μs and phase memory time T_m = 3.3 μs, and for the diamond sample are T₁ = 115 μs and phase memory time T_m = 800 ns, as measured by saturation recovery and two-pulse echo decay experiments, respectively. Substituting the above values for T_m in place of the T₂ into eq (3) reveals that the left side of the equation is not fulfilled for k ≈ 1 MHz and ω1 < 1 MHz for both BDPA and diamond samples.

Consequently, we expect significant reduction of the inversion efficiency due to the transverse relaxation (T₂) during the pulse. Indeed, as expected, from not fulfilling the left side of eq(3) a complete inversion is not achieved due to signal loss from the dephasing. Nevertheless, to illustrate the gain in inversion efficiency achieved with the broadband chirp pulses we plotted, the inversion profile of a 1 us rectangular (π) pulse a blue dashed line on figure 3b. It is clear that the inversion profile width of the 10 MHz chirp pulse exceeds that of the rectangular π pulse by approximately one order of magnitude without compromising the inversion efficiency. This is of course at the expense of the longer 10 μs versus 1 μs pulse length. For EPR experiments such as DEER, where maximizing the overall change in the magnetization (ΔM_z) for all spin packets over a broad bandwidth is of interest such chirp pulses will be clearly beneficial, granted higher microwave power (higher ω₁) becomes available at 200 GHz, as demonstrated for X-band an Q-band experiments.[6,7]

For the diamond sample (frequency swept EPR spectrum is presented in the SI) the shape of the inversion profiles is visibly skewed. This is the effect of T₁ relaxation. For the diamond sample the length of the pulse (10 μs) is not negligible relative to the T₁ relaxation time (115 μs), so that the spin packets that were affected in the beginning of the chirp pulse have more time to relax back to equilibrium before they are detected by an echo compared to spin packets that are affected at the end of the chirp pulse. Note that the chirp pulse sweep direction was from positive to negative offset frequency.

As expected for the BDPA sample the slope of the inversion profile is much more gradual due to a reduced effect of the T1 relaxation (T₁ = 260 μs) during the 10 μs pulse.

Interestingly, for the BDPA sample, 5 MHz and 2 MHz chirp pulses show better on-resonance inversion efficiency compared to the monochromatic rectangular pulse. This is despite longer time between inversion and detection for the chirp versus rectangular pulse. To understand this effect and to quantitatively access the performance of our phase-modulated pulses, we compare the experimental data to simulated results for a S=1/2 system including the effects of the T₂ and T₁ relaxation times. The results of these simulations, overlaid with the experimental data are presented on figures 3c for BDPA sample and in figure S2 for the diamond sample. The simulation procedure is detailed in the SI. For a much larger BDPA sample a ω₁ inhomogeneity was taken into account explicitly as detailed in the SI, it was neglected for the much smaller and thinner diamond sample. For the latter the ω₁ intensity was estimated from a nutation experiment that was published previously.[15] Notably for both BDPA and diamond samples we had to use T₂ > T_m in the simulations to arrive at a good agreement with the experimental data. This is not surprising since the T_m measurement provides only a lower limit for T₂. This is attributed to either effects of instantaneous diffusion[21] or to the need to use a rotating frame relaxation time (T_1ρ) [22] which accounts to the fact that relaxation with and without on-resonance mw irradiation is different.

2.4.3 Coherent spin manipulation (broadband echoes)

The next level of complexity in experiments employing broadband arbitrary shaped pulses are experiments that involve coherent manipulation of the electron spins. An echo experiment relying on broadband linear chirp pulses is such an experiment. Such two chirp-pulse echo sequences were introduced in the late eighties by Bohlen and Bodenhausen in NMR, [5] and independently by Kunz in magnetic resonance imaging (MRI).[23] This pulse sequence was recently implemented in EPR for broadband echo and FT EPR.[24] The pulse sequence for a two-chirp pulse echo experiment is shown in the insert of figure 5a. To ensure simultaneous refocusing of all the spin packets within the chirp pulse bandwidth, the length of the (2^nd) refocusing pulse is set to be half the length of the (1^st) excitation pulse. To ensure optimal excitation and refocusing of spins in an ideal case, the B₁ intensity should be adjusted separately for each pulse.[5,23-25]

Figure 5.

Refocused echo with all rectangular pulses (a) and chirp refocusing pulses (b). Refocused echoes as measured on the 3.4nm Gd³+ ruler molecule using pulse sequence in (a) blue trace and pulse sequence in (b) red trace (c). Experimental Parameters: temperature 10 K; frequency 192.51 GHz; π/2 = 187.5 ns; π = 375 ns; π_chirp = 1 μs; Δω_chirp = 4MHz; τ = 1 μs; t = 6 μs; t_p = 1 μs; repetition time 100 μs;

For the broad-band echo experiments presented here, while we adhere to this pulse length requirement of the Bohlen-Bodenhausen echo, we avoided changes in the pulse amplitude given hardware limitations, and instead utilized all available mw power for both broadband excitation and refocusing pulses. This approach is a compromise where the excitation and / or refocusing is not complete, but still allows for generation of broadband echoes.

The experimentally detected broadband echoes generated with chirp pulses with Δω_chirp = 5, 10, and 20MHz bandwidth are shown on figure 4a. The pulse length were 2t_p = 1μs for the excitation and t_p = 0.5μs for the refocusing pulse. This choice for pulse length was governed by a compromise between an increase of excitation and inversion efficiencies by increasing adiabaticity and minimizing signal loss due to relaxation. As expected, the echoes generated with the chirp pulses corresponding to larger bandwidths are narrower in the time domain, corresponding to a larger excitation bandwidth in the frequency domain. The corresponding simulations (figure 4b) assume an inhomogeneously broadened EPR line defined by a Gaussian with a FWHM = 10 MHz and the experimentally measured T₁ and T₂ relaxation times. Good agreement between the experiments and simulations show that, given the limitations of employing equal amplitudes for the broadband pulses, we were able to achieve coherent broadband manipulation of spins at 200GHz.

Figure 4.

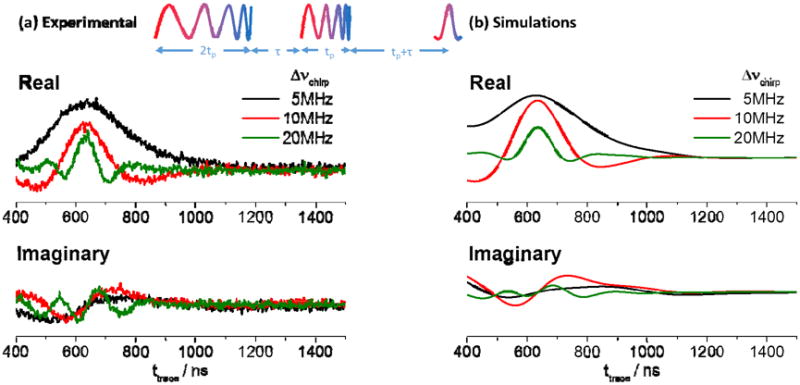
Experimental (a) and simulated (b) broadband echo profiles generated with the Bohlen Bodenhausen echo sequence shown in the insert of (a). Experimental paramters t_p = 500ns; τ =200ns

For completeness, we discuss the theoretical efficiency of the excitation and refocusing pulses in our experiments. The refocusing pulse is half the length of the excitation pulse (2t_p = 0.5 μs for π and t_p = 1 μs for π/2 pulses in the presented experiments). A proper refocusing π chirp pulse requires higher critical adiabaticity of Q_crit ≫ 1 than a π/2 excitation pulse where the requirement is Q_crit = 2ln(2)/π ≈ 0.44.[20] Since Q_crit is given by eq 4, it follows that a much higher ω₁ amplitude is required for efficient refocusing than for efficient excitation. Therefore, in the case of limited mw power, as is mostly the case for high field experiments at frequencies such as 200 GHz, we expect better performance from our excitation pulses than from the refocusing ones. Indeed when calculating Q_crit for ω₁ = 1MHz and tp_π = 0.5 μs refocusing pulses, we obtain Q_crit ≈ 0.6, 0.3 and 0.16 for Δω_chirp = 5, 10 and 20MHz, respectively, which is smaller than a requirement for efficient refocusing of Q_crit ≫1 meaning that efficient refocusing is not achieved with our settings. In contrast the same calculation results in Q_crit ≈ 1.3, 0.6 and 0.3 for ω₁ = 1MHz and tp_π/2 = 1μs excitation pulses - rather close to the required value of Q_cri ≈ 0.44 for an ideal excitation pulse. It is thus apparent that the refocusing efficiency is a limiting factor in the formation of broadband echoes in our experiments. This limitation becomes more severe with increasing Δω_chirp, which explains the reduction in echo intensity with increasing Δω_chirp observed both in the experimentally detected echoes and the corresponding simulations, shown in figure 4.

We find that the real gain from using full-amplitude wideband chirp pulses comes in a refocused echo sequence (figure 5a) where replacing the last two π pulses by broadband chirp pulses (figure 5b) improves the refocusing efficiency by a factor of ∼2 as shown on figure Figure 5b. In this experiment the additional phase acquired by the spins due to the first π pulse is refocused by the second π pulse resulting in the sharp echo resulting from all the excited spins. The refocused echo experiments were performed on a |- ½> - |½> transition of a 3.4nm Gd³⁺ ruler molecule (See SI for sample preparation details) with experimental details given in the figure caption. Note that these experiments benefit from 4 times higher nutation frequency due to the high (S=7/2) spin of the Gd³⁺ that allow for a 16 fold improvement in adiabaticity of the chirp pulses compared to that of a S=1/2 spin system. The inter-pulse delays were kept the same between the two refocused echo experiments so the intensity of the echo in the sequence employing broadband chirp pulses is higher despite having 1.25 μs longer echo time. The reason for that is twofold. First, when equal amplitude rectangular pulses are used in the refocused echo sequence the bandwidth of the two times longer π pulses is smaller and does not allow for refocusing of the whole bandwidth excited by a shorter π/2 pulse The broader bandwidth chirp pulses circumvent this limitation and allow for more efficient refocusing of the magnetization excited by the rectangular π/2 pulse. Secondly, two adiabatic chirp pulses applied back to back are less sensitive to variations in ω₁ and thus together result in a more robust refocusing of the echo.[26] The observed gain is present despite the critical adiabaticity for these chirp pulses with Δω_chirp = 4MHz and t_p = 1 μs of only Q_crit = 2.25 eq(4) calculated for a nominal nutation frequency of ω₁ = 1.2 MHz that is below the accepted threshold value of Q_crit > 5.

2.5 Amplitude and phase modulated pulses

2.5.1 Characterization of the AMC response

To explore the potential of generating truly arbitrary shaped pulses that are both phase and amplitude modulated we characterized the response of the IQ mixer-based pulse forming unit and 200GHz AMC for both phase and amplitude modulated input waveforms. To achieve amplitude modualtion it is necessary to account for the nonlinear response of the AMC. The nonlinearity of the AMC response prevents the correction of the output using a simple transfer function—an approach already employed for the correction of the resonator response at X-band. [8,10,27] Nevertheless, even for a non-linear AMC response it should be possible to come up with a calibration routine if the hardware response is deterministic. Such correction procedure can potentially allow for generation of the pre-distorted input waveform that will result in a desired output after the AMC. When characterizing the performance of the AMC it became apparent that the amplitude / phase response of the AMC is strongly dependent on the length of the microwave pulse. This was attributed to the transient heating of the AMC components that lead to different extent of amplitude and phase distortion depending on the length of the pulse, probably due to a different maximum temperature that the internal components of the AMC had reached. To minimize these heating artifacts, all experiments described in this section were performed in a “quasi CW” mode, where the AMC was driven continuously on- or off-resonance. Thus, instead of turning off the microwave output between the pulses we used a second transmitter source (transmitter source 2 in figure 1) to fill in and continuously drive the AMC at 1GHz off-resonance. Using this approach the AMC is always kept in a “hot” state and variations in temperature of the internal AMC components is presumably minimized. This is illustrated in figure 6a where the second source is turned on during the “idle” phase of the pulse sequence and off during the “pulsing” part when the shaped pulse is generated.

Figure 6.

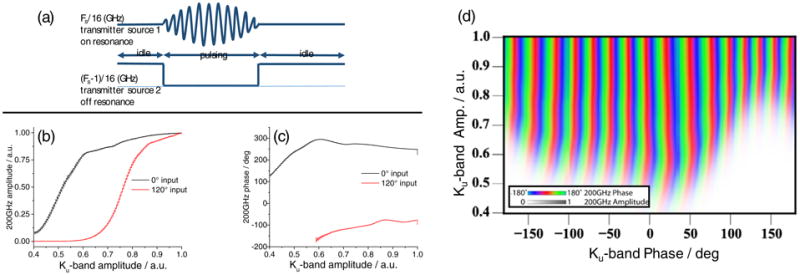
Illustration of the Quasi-CW shaped pulse generation. (a) Experimental amplitude (b) and phase (c) outputs of the AMC for a “ladder” waveform used as an input with 0 and 120 degrees phase. Experimental phase / amplitude calibration table as measured at 197.549 GHz. (d) Color denotes the phase of the AMC output and opacity denotes the amplitude.

With the heating artifacts accounted for to “first order” we proceeded into experimentally characterizing the response of the AMC to an input with variable phase and amplitude. For this purpose we recorded the output of the AMC chain with a 12.8μs long “ladder” waveform that consisted of 128 100 ns long steps of increasing amplitude. An example of an AMC output (at 197.549GHz) for such a “ladder” waveform input is presented as a black trace in figure 6b and 6c for amplitude and phase response respectively. Note that ideal, non-distorted response would be linear in amplitude and flat in phase, which is not the case. To further demonstrate the challenges associated with using AMC for phase and amplitude modulated pulses we show the response of the AMC for the same input “ladder” waveform with a phase rotated by 120 degrees. The response is shown as red traces on figure 6b and 6c for amplitude and phase respectively and is notably different from the one shown in black for a 0 degree phase input. This phase dependence is not expected for an ideal AMC input and is most likely due to non-idealities in the IQ mixer-based pulse forming unit, causing insufficient image rejection, local oscillator (LO) leakage and higher order harmonics in the mixer output. This conjecture is supported by the observation that when the desired signal from the K_u-band IQ mixer is strong (>0.85) the 200GHz phase profile is largely flat, as expected (figure 6c). In other words, the AMC response is largely devoid of the mutual phase-amplitude interdependence. For lower amplitude signals (from the K_u-band IQ mixer) the spurious output from the IQ mixer becomes more significant compared to the desired output, resulting in a non-linear response of the AMC that manifests itself as mutual interdependence of the phase and amplitude response of the AMC.

This is especially pronounced in a full response table that shows the complete phase-amplitude response of our setup that was acquired by stepping the phase of the input “ladder” waveform through 360° phase rotations in 128 increments and recording the output of the AMC. The complete phase-amplitude response is shown in figure 6d where the color encodes the phase and the opacity encodes the intensity of the output AMC signal. This responce table was used to calculate a pre-distorted input waveform that accounts for both amplitude and phase response of the AMC to the non-ideal IQ mixer output of the pulse forming unit. See SI for details. As expected, due to ×16 phase multiplication of the AMC chain the output phase is periodic, undergoing a full 360° revolution for every θ_input = 360°/16 = 22.5°. This redundancy was taken into account when designing an algorithm for calculating the pre-distorted low frequency input waveform to obtain the target high-frequency waveform based on the experimental calibration data.

2.5.2 Performance of the pre-distorted phase-amplitude modulated pulses

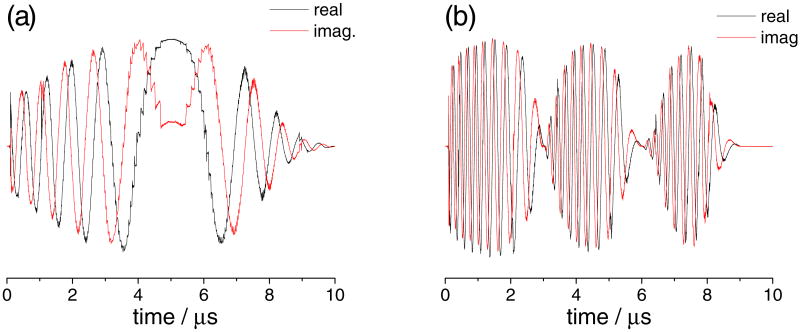
The experimentally measured amplitude and phase modulated pulse, resulting from a calculated pre-distorted input waveform, is presented in figure 7a. The predistorted input waveform was designed to produce a half-sine apodized chirp pulse with Δω_chirp = 2 MHz and Δω_offset = 0 MHz at 197.549 GHz the sampling for this waveform was reduced to 100ns to save on the memory and computation time. The experimental AMC output, while not perfect, clearly resembles this target waveform. The most apparent deviation in this pulse is its asymmetry, in which the right side of the pulse has the expected shape while the left side displays a large distortion, mainly in amplitude. The most likely cause of this distortion is, again, transient heating effects of some AMC component(s) which could not be completely avoided even employing the “quasi CW” approach. Another imperfection in the experimental waveform is the phase wrappings that are especially apparent in the center of the waveform where the frequency is lowest and the amplitude maximal. These artifacts are attributed to the insufficient resolution of the 128 × 128 lookup table that did not provide fine enough resolution to account for all of the small variations in the waveform. This problem can be easily improved by increasing the number of increments in the experiment used to acquire the lookup table. This potential improvement was not pursued, since it became apparent that the more significant shortcoming of the asymmetry artifact cannot be corrected using the calibration table approach.

Figure 7. Experimentally acquired amplitude and phase modulated 197.549GHz waveforms where the pre-distorted waveforms designed to produce a 10 μs long half sine apodized chirp pulse Δω_chirp = 2 MHz and Δω_offset = 0 MHz (a) and three repeats of the 3 μs half sine apodized pulse with Δω_chirp = 2 MHz and Δω_offset = -3 MHz (b).

As the target waveform for the half sine apodized pulse at Δω_offset = 0 is symmetric, the asymmetry in the experimental pulse amplitude profile in figure 7a suggests that there is a few μs long transient response that must be responsible for the distortion, and is not accounted for by the calibration procedure. To verify whether this transient response is due to heating of the AMC components that is not sufficiently corrected for by the “quasi CW” approach, we recorded the output of the AMC chain for a three consecutive repeats of 3μs long, half sine apodized, chirp pulses with Δω_chirp = 2 MHz and Δω_offset = -3 MHz offset from the carrier. The input waveform was generated according to the same procedure outlined in the SI and three consecutive repeats of the same input waveform were used as input to the AMC chain. The experimental high-frequency AMC output is shown in figure 7b. It is apparent that while the phase profile, manifested as change in instantaneous frequency, is well reproduced in all three repeats of the waveform, the amplitude apodization profile is different for every repeat of the pulse. This clearly demonstrates that the transient effects cannot be entirely accounted for by a single calibration table due to the hysteresis in the hardware that occurs on a μs timescale. It is important to note that the AMC response is deterministic and reproducible with consecutive repeats of the same input pulse sequence resulting in the same AMC output granted that the AMC was allowed to cool down, typically for a few milliseconds. Clearly a static calibration table was not sufficient for generation of a pre-distorted waveform that could account for all the transient effects present in the AMC. Consequently, with the currently available experimental capabilities, amplitude-modulated pulses did not show improvement in inversion efficiency or selectivity over non-apodized chirp pulses. Potential approaches for improving the spectrometer performance for amplitude-modulated pulses require improvements in suppression of the spurious mixer outputs that is possible to achieve either by calibration of the IQ-mixer and adjusting the I and Q waveforms accordingly, or alternatively by redesigning the pulse forming unit such that the spurious signals are further suppressed in the hardware. Furthermore, transient heating effects of the AMC can be potentially accounted for with a feedback procedure that allows for design of the waveform for a complete pulse sequence rather than an individual pulse. Such developments are work in progress.

3. Summary and conclusion

We have demonstrated that accurate constant-amplitude, arbitrary phase-modulated, pulses can be generated at 200GHz using our existing EPR/DNP microwave bridge that is based on a K_u-band CW source pulse forming unit and ×16 AMC from Virginia Diodes Inc. Addition of arbitrary phase-modulated pulse capability significantly extends the spectrometer's ability to manipulate the electron spins in pulsed EPR and DNP experiments. Specifically, we demonstrated that spins can be manipulated, inverted and excited, over bandwidths that exceeds what is possible with conventional square pulses and available ω₁ strengths by more than an order of magnitude. Specifically, adiabatic inversion of up to 10MHz bandwidth using ω₁ ≤ 1MHz was demonstrated at 200 GHz relying on a ∼150 mW microwave power output and a non-resonant sample holder. This gain of course comes at the expense of having to use longer pulses which poses limitation on samples with short relaxation times and necessitates the compromise between the pulse length and the performance. The excellent agreement obtained for the theoretically expected and experimentally measured pulse performances demonstrate the sufficient accuracy of the 200 GHz phase-modulated waveforms generated using the 200 GHz EPR/DNP microwave bridge. The accuracy of these arbitrary phase-shaped pulses is substantiated by demonstration of effective coherent spin manipulation over a large bandwidth. Again, excellent agreement was achieved between experimental and simulated broadband echoes generated using the Bohlen-Bodenhausen echo scheme. Coherent echo formation was demonstrated for excitation bandwidths up to 20MHz. The overall efficiency of the excitation and refocusing pulses was analyzed using the critical adiabaticity parameter. We showed that the main limitation is the low ω₁ intensity that is insufficient to achieve the required adiabaticity and is a limiting factor for efficient refocusing over larger bandwidths in our experiments. However, the available ω₁ intensity appears to be sufficient for efficient broadband excitation (π/2 chirp) pulses that require much smaller critical adiabaticity. Ideally for efficient echo formation using the Bohlen Bodenhausen sequence, ω₁ is increased for the refocusing π pulse to achieve higher adiabaticity. This was not possible at 200 GHz with the currently available microwave power in a non-resonant setup. For experiments performed on a central -½ – ½ transition of a high spin (S=7/2) Gd³⁺ where we benefitted from four times higher effective nutation frequency we were able to show that refocused echo amplitude can be increased by a factor of ∼2 by substituting the monochromatic π pulses by their chirp counterparts.

We furthermore learn that while it should be possible, it is not straightforward with the currently available AMC-based 200 GHz microwave bridge to achieve accurate amplitude modulation using the same approach of varying the input waveform at the, K_u-band frequency stage. Indeed, reducing the amplitude of the input, low frequency (K_u-band), waveform to the AMC does not result in the linear reduction in the amplitude of the AMC output, but rather in a nonlinear amplitude response accompanied with large distortions in the waveform phase. A calibration procedure that is aimed at accounting for the nonlinear behavior of the AMC proved to be only partially successful, with the resulting amplitude and phase modulated pulses distorted in their amplitude profiles. These artifacts were traced down to a transient heating response of the AMC, where the phase and amplitude response depends on the particular heating history of the AMC, namely not only on the pulse to be produced, but rather on the whole preceding waveform. Since our hardware allows for accurate measurement of the 200GHz pulse waveforms (within the ∼200MHz detector bandwidth) we anticipate that real time correction of the waveforms using a feedback loop is possible. In this case the waveform will be optimized in the context of the preceding pulse sequence, and thus take into account the transient AMC response. Such efforts are in progress and worthwhile of developments, given that the possibility to generate both amplitude and phase modulated pulses will significantly increase the repertoire of useful pulse shapes for EPR and DNP, such as popular sech/tanh pulses commonly used for band-selective inversion.

The integration of the AWG hardware into the 200GHz EPR / DNP system described here allows for the generation of accurate phase-modulated pulses, and thus opens new frontiers for high field EPR. In fact, phase-only-modulated pulses are not necessarily limiting, especially in the case of low ω₁ intensity compared to the desired excitation bandwidth as is found for many high-field EPR instruments. For example, it was shown that pulses numerically optimized for maximum inversion bandwidth are full amplitude phase modulated ones,[28] as are the pulses optimized for maximum excitation and inversion bandwidths using optimal control theory.[29,30] In fact One potential approach to increase the performance of the high field pulsed EPR is to design dedicated phase-only-modulated pulses that aim at specific task such as broadband or band-selective excitation, inversion, refocusing etc. Optimal control theory provides a convenient and powerful platform for developing such pulses, where a constraint for the absence of amplitude modulation can be straightforwardly implemented.[29,31]. Such approaches for increasing the performance of 200GHz pulse EPR are being explored and will be the subject of future reports.

Arbitrary waveform generated pulsed EPR is demonstrated at 200GHz

High fidelity phase-modulated pulses are generated using solid-state 200GHz Amplifier Multiplier Chain

AWG integration allows for order of magnitude improvements in bandwidth for 200GHz pulsed EPR