Abstract
Water dynamics in the hydration shell of the peripheral membrane protein annexin B12 were studied using MD simulations and Overhauser DNP-enhanced NMR. We show that retardation of water motions near phospholipid bilayers is extended by the presence of a membrane-bound protein, up to around 10 Å above that protein. Near the membrane surface, electrostatic interactions with the lipid head groups strongly slow down water dynamics, whereas protein-induced water retardation is weaker and dominates only at distances beyond 10 Å from the membrane surface. The results can be understood from a simple model based on additive contributions from the membrane and the protein to the activation free energy barriers of water diffusion next to the biomolecular surfaces. Furthermore, analysis of the intermolecular vibrations of the water network reveals that retarded water motions near the membrane shift the vibrational modes to higher frequencies, which we used to identify an entropy gradient from the membrane surface towards the bulk water. Our results have implications for processes that take place at lipid membrane surfaces, including molecular recognition, binding, and protein-protein interactions.
Graphical Abstract
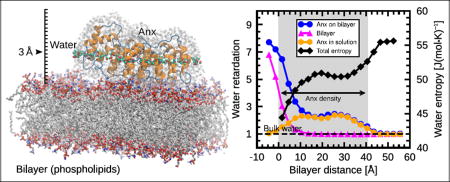
Introduction
Biomolecules and their surrounding solvent shells are structurally and dynamically coupled.1,2 The retardation of water molecules in the vicinity of biomolecules can be relevant to their function, as slowed-down diffusion can keep binding partners in place and ease recognition and reaction.3–5 Membrane proteins often comprise soluble domains that extend into the solvent, similar to peripheral membrane proteins that are located directly on the membrane surface. Membrane-bound proteins mediate a wide range of cellular functions by interacting with their partners in a region where water properties are strikingly different from the bulk. The distinct hydration environment around a membrane-bound protein is illustrated in a recent experimental report showcasing a water diffusivity gradient perpendicular to the lipid membrane surface around the peripheral membrane protein annexin B12 (Anx).6 This sustained gradient of hydration water diffusion was utilized to determine a membrane-bound protein’s secondary structure and location at the water/membrane interface.6 The key outstanding question we wish to answer in this work is: What is the molecular basis for the strong gradient of water motion seen around proteins associated with phospholipid membrane surfaces?
The effects of bare phospholipid membranes on water dynamics have been studied by a variety of experimental and theoretical approaches.7–9 Molecular dynamics (MD) simulations show cooperative motions of phospholipids and their hydration waters,10 with dynamic coupling involving several hydration layers above the membrane. Both perpendicular and lateral diffusion of water is slowed down near DPPC bilayers,11 with retarded diffusion dynamics observed up to around 10 Å away from the lipid head groups. The importance of coupled biomolecule/hydration water dynamics has also been highlighted for the purple membrane12,13 as a prototype for biological membranes, which generally comprise many lipid and protein species, and are thus more complex than model bilayers.
Here, we focus on annexin B12 (Fig. 1) as a model for membrane-associating proteins. Anx binds to anionic phospholipid membranes in a Ca2+-dependent manner.14 Investigations revealed that the hydration water of membrane-bound Anx conforms to the membrane environment, extending the retardation of water diffusion even up to 40 Å above the phosphate groups.6 In this study, we set out to dissect the contributions from the membrane and the protein. For this purpose, MD simulations are employed concurrently with Overhauser dynamic nuclear polarization (ODNP)-enhanced NMR relaxometry measurements of Anx to gain detailed atomic-level insights into diffusional water dynamics, intermolecular vibrations of the water network, as well as the spatial variation in local water entropy. Our MD simulations of membrane-bound Anx show that, at short range, the effect of the phospholipid membrane on water dynamics dominates over that of the protein, and that the two effects are captured by a simple model that assumes additivity of the protein- and membrane-related activation energies for the diffusivity of water molecules next to these two biomolecular surfaces. By comparing different membranes, we show that electrostatic forces due to the polar lipid head groups are responsible for the observed strong water retardation, whereas the net charge of the lipid head groups and counter-ion gradient have negligible effects. Finally, we observe no significant correlation between the chemical nature of the individual amino acids (apolar, polar, charged) and water retardation near a specific protein residue. Thus, the average distance to the water/membrane interface is a good predictor of water dynamics at a particular position in a membrane-bound protein. Accompanying the retardation of water molecule diffusion, we observe frequency shifts in the spectra of intermolecular vibrations in the water hydrogen bond network. Increased vibrational frequencies and slowed down diffusion indicate a rigidification of the local hydrogen bonding environment, from which we derive a decrease of the local water entropy within the 2PT framework.15
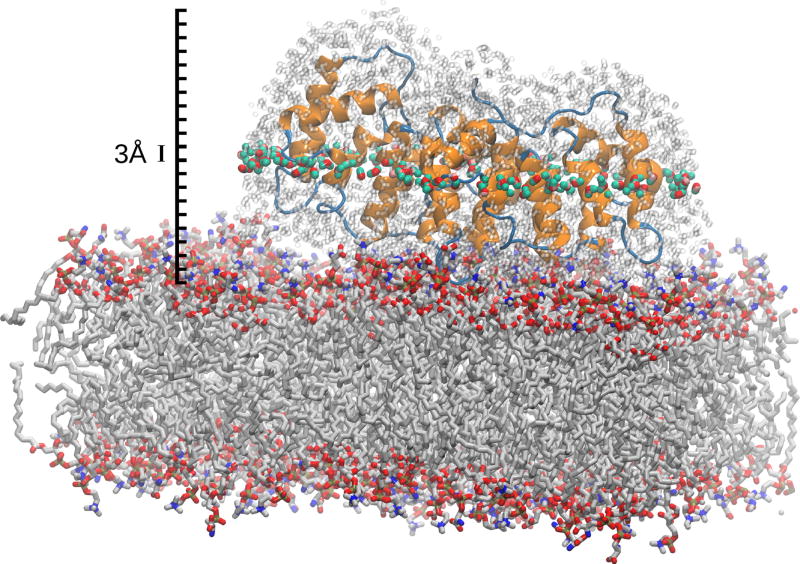
Figure 1.
Anx bound to a phospholipid bilayer. For the analysis of water dynamics, water molecules within 5 Å of Anx (shown in grey) are divided into 3-Å slabs according to their distance to the membrane; one such slab is highlighted here. The system is fully solvated, but only waters within 5 Å of Anx are shown for clarity. Likewise, only a fraction of the 512 lipid molecules that are present in the simulation are shown.
Methods
ODNP-enhanced NMR relaxometry
Overhauser dynamic nuclear polarization (ODNP) is an NMR relaxation technique that reports on local water dynamics within 5–10 Å of a spin label, containing an unpaired electron, that can be attached to a site on the surface of a biomolecule of interest.16–18 ODNP measures the dipolar coupling factor (ξ) between the unpaired electron spin located near the biomolecular surface and the proton spin of the surrounding solvent water. The dipolar coupling factor is dependent on the correlation time (τ) of inter-spin motion between the electron and nuclear spin. Thus, with this technique, it is possible to extract the local motion of solvent molecules relative to the biomolecular surface.
We attached a nitroxide spin label (S-(1-oxyl-2,2,5,5-tetramethyl-2,5-dihydro-1H-pyrrol-3-yl)methyl methanesulfonothioate), which contains an unpaired electron, to a cysteine residue on Anx. We generated eleven single cysteine variants of Anx by site-directed mutagenesis as described previously19 and measured the dipolar coupling factor from each spin-labeled variant individually. The dipolar coupling factor (ξ) was calculated experimentally by the cross-relaxation (kσ) and self-relaxation (kρ) rates:20,21
| (1) |
| (2) |
| (3) |
where C is the molar concentration of the electron spin, E(p) is the proton enhancement as a function of microwave power, T1(p) is the proton spin lattice relaxation time constant as a function of microwave power, S is the saturation factor of the electron spin (which is in this case 1),22 ωH and ωe are the proton and electron Larmor frequencies, respectively, and T1,0 is the proton spin lattice relaxation time constant in the absence of a spin label. The relaxation rate kσ is calculated from extrapolating Eq. 2 to infinite power.20 The correlation time was calculated from the coupling factor by interpolating Eq. 4 given by the dipolar Hamiltonian20,21,23 and using the spectral density function J(ω, τ) given by the FFHS model:24
| (4) |
The spectral density function is a function of the transition frequency (ω) and the dipolar correlation time (τc). The dipolar correlation time is considered equivalent to the translational diffusion correlation time,
| (5) |
in which d is the distance of closest approach between the unpaired electron spin and the adjacent water molecules, Dwater is the diffusion coefficient of local water and Dsurface is the diffusion coefficient of the surface-tethered spin label. The diffusion of the water is typically orders of magnitude faster than the diffusion of the spin label, such that the relationship simplifies to τc = d2/Dwater.
The retardation factors of the site-specific correlation times are defined as ρsite = τsite/τbulk. τbulk was measured from free spin labels dissolved in the buffer solvent. Given that the local water diffusion coefficient is proportional to the mean squared displacement (MSD), the retardation factor obtained from the correlation times corresponds to the one directly computed from the MSDs, ρsite = MSDbulk/MSDsite, as obtained from our MD simulations (see below).
Anx was dissolved in Tris buffer (20 mM Tris and 150 mM NaCl at pH 7.4). C, the concentration of the electron spin attached to Anx, as used in equations 2 and 3, was determined by the double integral of the cw-electron paramagnetic resonance (EPR) spectrum. The Anx concentration was in the 100–400 µM range.
Anx samples (3.5 µl) were loaded into a 0.6 mm inner diameter, 0.84 mm outer diameter quartz capillary, and sealed at one end with Critoseal and at the other end with capillary wax. The capillary was loaded into a homebuilt NMR probe and placed inside a Bruker TE102 X-band cavity. 1H NMR measurements were performed using a Bruker Avance 200 NMR spectrometer. The magnetic field for ODNP experiments was 0.35 Tesla. The ODNP measurements were performed at room temperature. During the ODNP measurements, the samples were continuously irradiated at the EPR transition frequency of 9.8 GHz using a home-built 8–10 GHz amplifier.25 The proton NMR signal enhancement E(p) was determined by the intensity of the free induction decay following a single excitation pulse as a function of microwave power, p. The proton NMR T1(p) was measured by an inversion recovery experiment performed at multiple powers that span the same range as the measurement of the NMR signal enhancement.26 The proton NMR T1,0 was measured by inversion recovery as well. Air was continuously flowed over the sample during the experiment to avoid thermal decomposition of the sample. The error reported is from the standard deviation obtained from two to three repeated measurements.
MD simulations
We started from an X-ray crystal structure of Anx27 and a pre-equilibrated lipid bilayer to build the simulation systems (Table 1) for membrane-bound Anx, Anx in solution, and pure membranes (i.e., in absence of Anx). We used the all-atom Slipids force-field28,29 for the lipids, and neutralized the net charge of the systems with Na+Cl− counter-ions. The Amber99SB*-ILDNP force-field30–33 was used for Anx, which was positioned on the membrane according to experimental reports.6 The TIP4P/200534 water model was used since it correctly captures the experimental diffusion coefficient of bulk water. All simulations were carried out with GROMACS 5.0.5.35 Further simulation details are given in the supporting information.
Table 1.
MD simulation systems.
| Name | [Na+] mM |
[Cl−] mM |
Notes |
|---|---|---|---|
| Anx on DOPC/DOPS (7:3) bilayer | 120 | 0 | Zwitterionic and anionic lipids |
| Anx on DOPC/DOPS (7:3) bilayer, TIP3P | 120 | 0 | Water model control |
| Anx on DOPC bilayer | 4 | 0 | Zwitterionic lipids only |
| Anx on DOPC bilayer + Na+/Cl− | 60 | 60 | Control for ion gradient effects |
| Anx on hydrophobic bilayer | 4 | 0 | Artificial hydrophobic bilayer |
| Anx on restrained DOPC bilayer | 4 | 0 | Control for position restraints |
| Anx in solution | 4 | 0 | Control for additivity |
| Hydrophobic Anx in solution | 0 | 0 | Control for protein electrostatics |
| DOPC/DOPS (7:3) bilayer | 120 | 0 | Control for additivity |
Each system was subjected to 100 ns of MD simulation. For all Anx-containing systems, this was preceded by a 10 ns equilibration during which all protein heavy atoms were position-restrained by harmonic potential energy functions with force constants of 1000 kJ mol−1nm−2. Coordinates were recorded every 10 ps. The binding mode of Anx on the bilayer stabilized after about 30 ns to a position that is consistent with previous EPR measurements (Fig. S1).19 The structural integrity of Anx was assessed by Cα-RMSD with respect to the starting (X-ray) structure, which remained stable at ca. 1.5–2.0 Å (Fig. S2). For details of the analysis of protein position and stability, see supporting information.
For each system under study, 20 additional 1-ns simulations were then initiated, with coordinates and velocities taken from evenly-spaced trajectory frames from the original simulation (i.e. at 5 ns, 10 ns, 15 ns, …, 100 ns). In these 1-ns simulations, coordinates were recorded every 0.1 ps. This high time resolution in the trajectory is necessary for the analysis of the mean squared displacements (MSDs), as described below.
For computing spectra, we performed 10 independent nVE simulations of 100 ps each for the following three systems: Anx on DOPC/DOPS bilayer, a pure DOPC/DOPS bilayer, and Anx on a hydrophobic bilayer. Energy was well conserved in the nVE simulations (temperature drift less than 2 K during 100 ps). Positions and velocities were recorded every 8 fs.
Finally, we carried out simulations of pure water as a control for bulk water properties, including the VDOS and entropy (see later sections). This system was comprised of 2228 TIP4P/2005 water molecules in a cubic periodic box of approximately 40 Å × 40 Å × 40 Å. The system was pre-equilibrated in the nPT ensemble for 100 ps and then equilibrated for 100 ps in the canonical ensemble. For computation of spectra, we performed a production simulation of 100 ps in the nVE ensemble with the same position and velocity recording frequency as used in all other nVE simulations.
Analysis of water retardation
To analyze changes in dynamics as a function of distance to the membrane, water molecules were partitioned into slabs of 3 Å thickness along the bilayer normal, as illustrated in Fig. 1. The origin is set to the average position of the phosphate head groups in the upper leaflet (see Fig. 2B). The slabs extend from −6 to 57 Å, thus covering the entire range from the membrane-embedded region to the bulk water above the protein. The selection of water molecules in each slab is further restricted by considering only water molecules whose oxygen atom is within 5 Å of any non-hydrogen Anx atom. In slabs more than 5 Å above the protein (distance to the membrane over 45 Å, see Fig. 2B), this distance criterion is increased progressively to continue selecting waters while retaining the slab-wise decomposition. For the pure membrane systems (i.e. without Anx), all water molecules within each slab were considered. For the simulation of Anx in solution (i.e. without the membrane), tumbling was removed by an RMSD-minimizing superposition of Cα atoms using the average protein structure from the bilayer simulation as the reference frame.
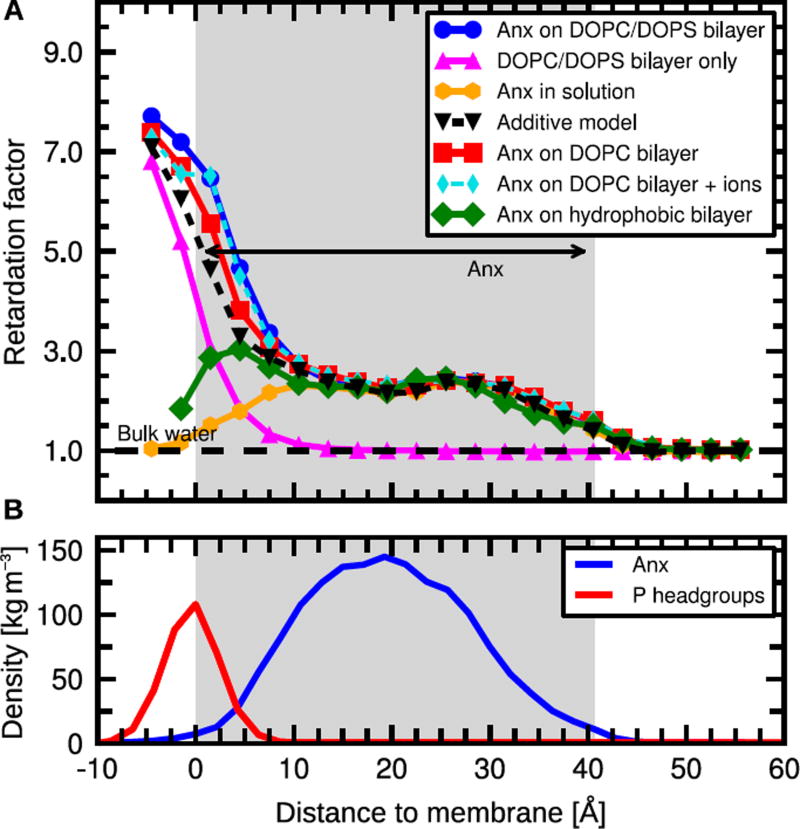
Figure 2.
A: Retardation of translational water dynamics around Anx as a function of distance to the phosphate head groups. B: Anx and phosphate head group mass density; the grey box encloses 90% of Anx mass density. See Figs. S1 and S2 for details of Anx membrane binding and structural stability, and Fig. S3 for MSDs.
Water motion was followed in the short 1-ns trajectories with a 0.1 ps recording frequency. Only the 14 simulations started after the initial 30 ns equilibration time were considered. Each of these were divided into ten non-overlapping blocks of 100 ps length. The lateral MSD was then computed for the selected water molecules in each 100-ps block of each simulation. To ensure that only local water dynamics is captured and to avoid a smearing-out effect due to water molecules leaving their original slab, only MSD values within a time window of 10 ps were considered. The average distance traveled by a water molecule within 10 ps is about 3 Å for bulk water (and correspondingly smaller for the slowed-down water molecules), and hence our analysis is sufficiently local. The MSDs were averaged over all blocks in all simulations, yielding an average for each slab. The retardation factor of water molecules in MD is defined as the ratio of the corresponding MSD value for bulk water over the MSD of this local water, ρsite = MSDbulk / MSDsite. The bulk water MSD value was obtained from a separate simulation of a pure water box. We did not attempt to derive diffusion coefficients from linear fits of the MSD-over-time traces, since we cannot assume linearity on these short (10 ps) time scales, especially not for the strongly retarded water population.
Intermolecular vibrations and water entropy
To study the vibrational spectrum of intermolecular water vibrations, we analyzed the vibrational density of states (VDOS). We obtained the VDOS separately for translational and rotational degrees of freedom via the Fourier transform of time correlation functions (TCF) of the center of mass and angular velocities, respectively:
| (6) |
with the corresponding TCF Ctrans(τ) and Crot(τ):
| (7) |
| (8) |
with the water molecule mass mw, the COM velocity vector vCOM, the moment of inertia Ik of molecular axis k, and the corresponding angular velocity ωk.
The spectrum of COM vibrations reports mainly on intermolecular hydrogen bond bending and stretching modes of the water hydrogen bond network, which result in broad vibrational bands below 100 cm−1 and around 200 cm−1, respectively.36 The spectrum of rotational degrees of freedom reports on librational modes, i.e. hindered rotations of water molecules within the local hydrogen bonding network.37 The sum of the spectrum of all librational modes of water, i.e. hindered rotations around the three distinct molecular axes, results in a broad feature extending from 300 to 1000 cm−1 with a maximum around 500 cm−1.
The VDOS reports on the distribution of kinetic energy over the frequency spectrum. Hence, the prefactor 2/(kBT) normalizes the integral over the VDOS to the corresponding number of degrees of freedom, i.e. the translational and rotational degrees of freedom per rigid water molecule in our simulations.
The zero–frequency response reports on diffusive motion. The zero–frequency response of the translational VDOS is therefore directly related to the diffusion coefficient:
| (9) |
The 2PT methodology proposed by Goddard and co-workers15,38 provides a straight-forward approximate recipe to dissect the translational and rotational VDOS into separate diffusive and vibrational harmonic contributions. This approach allows one to model the diffusive degrees of freedom within the framework of Enskog’s theory of hard sphere (HS) fluids to estimate their contribution to the thermodynamic properties of the liquid as described by Lin and coworkers.38 The remaining VDOS of purely vibrational motions is then simply described as a set of harmonic oscillators (HO), whose thermodynamic properties can be readily obtained from the corresponding partition function. The contributions from the gas– like hard sphere model, describing a fraction and of the translational and rotational degrees of freedom per water molecule, and the contributions from the remaining and solid–like degrees of freedom are treated as additive to obtain the thermodynamic properties of the liquid:
| (10) |
The approach has been shown to accurately reproduce experimental thermodynamic properties of several bulk mono- and poly-atomic liquids.15,38,39
Here, we used this approach to evaluate the thermodynamic properties, in particular the total entropy per water molecule and the separate contributions from translational and rotational degrees of freedom for water around Anx as a function of distance from the lipid bilayer, using the same slab-wise selection of water molecules as in our previous analyses (see above). These molecules were selected based on their position at each time frame of the set of nVE trajectories. COM and angular velocity TCFs were then computed for the following 1.6 ps with the available time resolution of 8 fs. The TCFs for each slab were then averaged prior to Fourier transformation and evaluation of thermodynamic properties.
Results and Discussion
Retardation of water dynamics near the protein and membrane surfaces
Fig. 2 shows the computed retardation of diffusion dynamics of water as a function of the distance to the membrane (the underlying MSDs are shown in Fig. S3 in supporting information). For Anx associated with a mixed DOPC/DOPS bilayer, water molecules in the hydration shell of the protein that are close to the membrane surface (within 10 Å distance or less) are slowed down considerably compared to bulk water by a factor of 3–8 (Fig. 2, blue circles). At distances between 10 and 30 Å, the retardation factor plateaus at around 2.5. Bulk behavior is recovered around 10 Å above the protein (i.e. at about 50 Å distance to the membrane surface), consistent with recent experimental results.6 To separate the effects of the protein and the bilayer on water dynamics, we first consider a bare DOPC/DOPS bilayer in absence of Anx (Fig. 2, magenta triangles). Strong water retardation is observed very close to the membrane, as seen for Anx on a DOPC/DOPS bilayer, but water dynamics reverts to that of bulk water already at a distance of about 10 Å from the membrane surface. This finding is consistent with NMR relaxation dispersion (NMRD) studies,7 which yielded an average retardation of water translational motions of about a factor 3 within a distance range of 10 Å from the phospholipid head groups. Averaged over the same distance range (< 10 Å), our MD-derived retardation factor is 3.7. For comparison, hydration water of Anx free in solution (i.e. in absence of a membrane) exhibits a maximum retardation plateauing at a value of ca. 2.5. The profile is centered around the Anx mass density (Fig. 2, yellow hexagons). This does not imply that residues at the center of the protein slow down water motions more strongly than those at the top or bottom, but is a consequence of the overall protein shape and of considering lateral MSDs. This is shown more clearly by analyzing water dynamics around individual residues (see next section). The overall modest retardation of water dynamics in the hydration shell of Anx in solution by about a factor of 2.5, as obtained from our MD simulations, agrees with NMRD as well as MD simulation data of the hydration dynamics around small soluble proteins.40–45 Much stronger hydration water retardation by several orders of magnitude has been reported from time-dependent Stokes shift spectroscopy;46 however these measurements might also report on collective dynamics involving both hydration water and motions of the protein itself.47 We note that some internal water molecules that are tightly bound within the protein, including the structural waters identified crystallographically, can be considered rigid on the time scale of investigation, and hence are strongly retarded with respect to bulk water, at times by orders of magnitude. However these are only few water molecules that do not strongly contribute to the average retardation factor obtained from our MD simulations.
Remarkably, multiplication of the retardation curves of Anx in solution and the bare DOPC/DOPS bilayer (Fig. 2, black triangles) matches the results of the actual membrane-bound Anx simulation. This finding can be understood by assuming (i) that diffusion of water near the membrane and protein surfaces is an activated process, similar to the reorientation dynamics of water,48 and (ii) that the contributions of the membrane and the protein to the free energy barrier are additive. Thus, and for membrane and protein effects alone, and for the combined effect. Here, ΔG‡ is the activation free energy, and β−1 = kBT. Therefore, we conclude that the observed extension of water retardation up to large distances from the membrane is due to an additive effect of the membrane-associated protein and the lipid membrane on the activation free energy barriers, with no apparent cooperativity between the two contributions. However, water molecules that are very close to the membrane (< 10 Å) are slightly more retarded than expected from the individual protein and membrane contributions, possibly indicating weak cooperativity at short distances from the membrane.
To investigate the underlying mechanisms that govern the observed retardation of water dynamics, we first assessed whether the counter-ion gradient above the anionic lipid bilayer influences water motions. To that end, we simulated Anx on a pure zwitterionic DOPC bilayer with only 4 mM Na+ ions (to ensure a net neutral system) and compared the results to those obtained for Anx on a DOPC/DOPS bilayer, which requires 120 mM Na+ (Table 1). The water retardation profiles in these two systems are highly similar (Fig. 2, red squares for DOPC and blue circles for DOPC/DOPS). Furthermore, to separate the effect of counter-ion concentration from that of the lipid net charge, we simulated Anx on a pure DOPC bilayer with 120 mM Na+Cl−. Again, the results (Fig. 2, cyan diamonds) are very similar to the previous two membrane simulations. Thus, neither the counter-ion gradient nor the lipid net charge is by itself responsible for the pronounced water retardation. This is consistent with previous MD simulations of phosphatidylserine bilayers49 that showed that the Na+ ions are preferentially located next to the carboxylate groups, and thus effectively neutralize the anionic lipid charges.
Next, we investigated to what extent water retardation is due to geometric confinement of the motional freedom of water near an extended surface, or to electrostatic interactions, including hydrogen bonding of water molecules with the lipid head groups. To do so, we simulated Anx on an artificial, uncharged membrane that was created by setting all partial charges of the lipids to zero and applying position restraint potentials on lipid atoms to maintain the bilayer structure (see supporting information). In the following, for simplicity, we refer to this membrane as a hydrophobic membrane. Compared to the conventional DOPC/DOPS and DOPC bilayers, this hydrophobic membrane has a much smaller effect on water dynamics near Anx (Fig. 2, green diamonds). Friction due to electrostatic forces is therefore the primary cause of the observed retarded water dynamics. However, a moderate retardation by a factor 2–3 is still observed at short distances from the membrane, indicating that electrostatics alone do not completely account for the retardation of water dynamics near the membrane surface. We ascribe this residual slow-down of water near the hydrophobic membrane to geometric confinement experienced by the water molecules that are in the hydration shell of Anx and also close to the impermeable two-dimensional membrane surface.
To further validate these results, we carried out additional control simulations (Table 1). First, to test the influence of the position restraints applied to the hydrophobic membrane, we simulated Anx on a position-restrained DOPC bilayer with normal partial charges. The results (Fig. S4, yellow diamonds) show that the position restraints have little effect on the translational motion of water. Finally, to confirm that water retardation is caused by electrostatic friction, we simulated Anx in solution, i.e., in absence of a membrane, this time with all partial charges of Anx set to zero (position restraints were applied on Anx atoms to maintain structural integrity of the protein, see supporting information). Fig. S4 (grey squares) shows that in this case, the effect of the protein on water retardation is abolished. Water behaves almost bulk-like all around the system, again verifying that electrostatic interactions are the key modulator of the retardation of water dynamics. Additional controls comparing 3D and lateral diffusion and the effects of equilibration time and the choice of water model were performed (see Fig. S4), validating our conclusions.
Water dynamics around individual protein residues
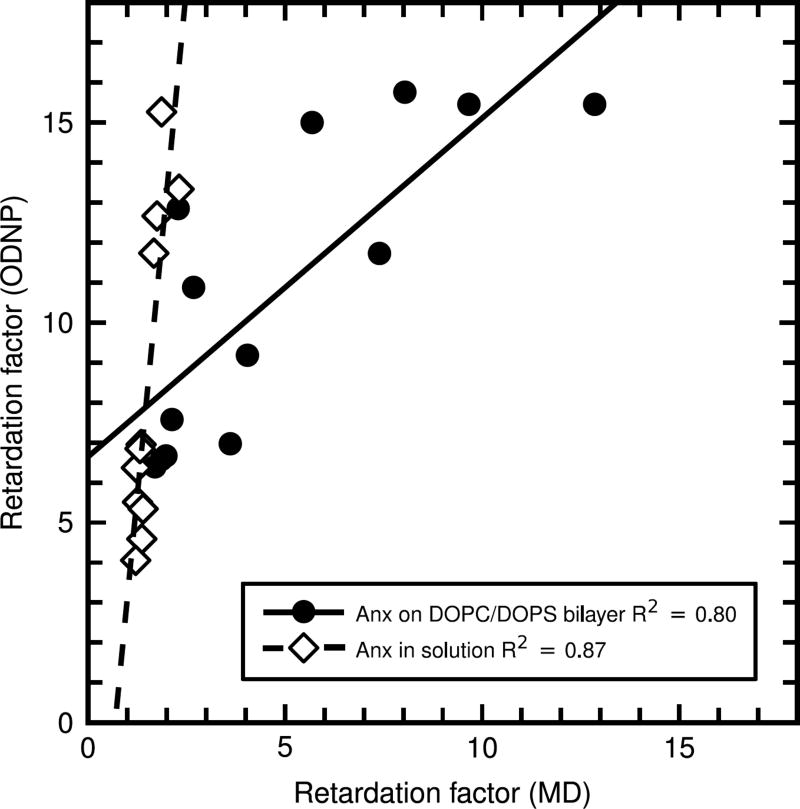
Next, we investigated hydration water dynamics around individual Anx residues. This was done as an independent check and complement of our above slab-wise analysis, which provides an average around the entire perimeter of the protein, but not around single residues. In addition, the single residue analysis enables a more direct comparison of MD and ODNP-enhanced NMR results, since the latter technique probes local water dynamics around spin labels attached to individual residues. Experimentally, we measured water dynamics around eleven spin-labeled Anx residues by ODNP (Table S1). These measurements were carried out with Anx in solution; ODNP data for the same residues of membrane-bound Anx have been reported previously.6 To allow for comparison with our MD results, we computed the retardation factor of water molecules in the vicinity of each of these residues in our simulations of Anx on a DOPC/DOPS bilayer and Anx in solution. Only waters whose oxygen atom is within 5 Å of at least one non-hydrogen atom of the residue were considered. Fig. 3 and Table S2 compare the retardation factors derived from ODNP experiments and MD simulations. The results obtained from the experimental and computational measurements are highly correlated, both for Anx in solution (R2 = 0.87) and membrane-bound Anx (R2 = 0.80). However, while the linear relationship between the two datasets is obvious, the absolute values of the experimental and computed retardation factors are different. The MD simulations give direct access to the MSDs and hence the translational dynamics of water molecules. Since spin labels are not present in our simulations, possible effects related to the spin label itself cannot be captured. The ODNP experiments, by contrast, probe the dipolar relaxation between the unpaired electron of the spin label and the water 1H nuclei. This relaxation is modulated by motions of water with respect to the electron spin label and hence closely linked to the MSDs (τsite ∝ MSD−1), thus allowing comparison with our MD results. In addition, the good correlation between the retardation factors derived from ODNP (in the presence of a spin label) and MD (no spin label) shows that the spin label itself does not determine the local water dynamics in its vicinity, but merely probes it. In conclusion, we consider it unlikely that the presence or absence of a spin label can explain the difference between the absolute values of the retardation factors derived from the two techniques. Thus, in the following, we consider alternative explanations.
Figure 3.
Retardation factors around selected solvent-exposed Anx residues (see Table S2) from MD simulations and ODNP measurements of Anx on a DOPC/DOPS bilayer and Anx in solution. The dashed and solid lines show linear fits.
Fig. 3 shows that the retardation factors derived from ODNP are systematically larger than the ones from MD. One possible explanation reason is that in ODNP water molecules within the first solvation shell of the spin label (at < 3.5 Å) contribute much more strongly due to the r−6 dependence of the dipole-dipole interaction. In contrast, the retardation factor from MD is obtained by weighting equally all water molecules within 5 Å of the residue. Analyzing only water within 3 Å of the residues increases the MD retardation factors (by about 20%, Table S2). Another, potentially important effect is the relative contribution of strongly bound versus weakly bound water molecules. The population of strongly bound waters is typically rather small,44 and do not contribute much to our MD-derived retardation factors (which report on dynamics on the 10 ps time scale, see above). For the ODNP-derived retardation factors, however, water molecules that are bound to a specific residue for times comparable to or longer than the protein tumbling time are weighted more strongly. This argument is consistent with our finding that the retardation factors from MD and experiment nearly quantitatively agree for bare phospholipid membranes, that NMRD studies have found to harbor less strongly bound water compared to protein surfaces.7 Finally, force field inaccuracies could also contribute to the observed difference between MD and ODNP. Although the TIP4P/2005 water model used here reproduces the experimental self-diffusion coefficient of bulk water, it may not perfectly capture the time scale of water diffusion in the vicinity of a biomolecular surface. In summary, the present work focuses on trends rather than a quantitative comparison of the absolute values, which would require an accurate theoretical description of the actual NMR experiments. This will be subject of future work.
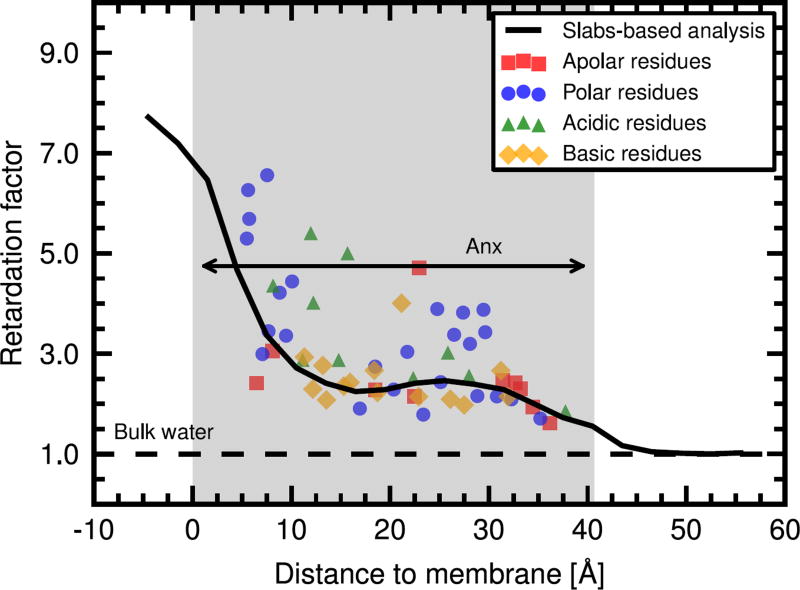
Next, from our MD simulations, we analyzed the hydration dynamics around 61 additional residues located at the protein-water interface, thus yielding a total of 72 residues studied (including the previously discussed eleven residues studied both by MD and ODNP). Our objective was two-fold. First, we wanted to test the correlation between local water behavior and the global profile observed for the entire protein (Fig. 2). Second, we wanted to assess the influence of the chemical nature of the amino acid residues (apolar, polar, acidic, basic) on local water dynamics. Fig. 4 shows the resulting retardation factors, color-coded according to residue type. While high variability is observed between individual residues, the trend of the above slab-based analysis is successfully recovered from these measurements of local water dynamics (Fig. 4, black curve). The spread of the data suggests that averaging over several residues is necessary to reliably evaluate distances to the membrane, however. From the experimental point of view, where the distance to the membrane is a priori unknown, one possible approach to mitigate this variability would be to measure ODNP retardation factors for several sequence-consecutive residues. Furthermore, from the data shown in Fig. 4, we found no correlation between residue type and local water dynamics. We therefore conclude that the dominant effects on surface water retardation are due to membrane electrostatics and protein surface topology. This is not to say that interactions between water molecules and protein residues, such as hydrogen bonds, do not play a role as well. However, these could be collectively influenced by the neighboring residues that are located next to a given amino acid on the protein surface, as also highlighted by recent studies of the reorientation dynamics of water around small soluble proteins.44,45,50 In fact, the importance of interactions is underscored by our control simulation of hydrophobic Anx (Fig. S4), which did not show any effects of retarded water dynamics.
Figure 4.
Water retardation around individual residues as a function of distance to phosphate head groups for Anx on a DOPC/DOPS bilayer. The results from the slab-based analysis (Fig. 2) are shown for comparison (black curve).
Vibrations of the water network
To probe how altered diffusivity correlates with changes to the intermolecular vibrations of the water network, we calculated the vibrational density of states (VDOS) for the translational and rotational degrees of freedom of water molecules. At far-infrared frequencies between 0–300 cm−1, the translational VDOS reports on delocalized hydrogen bond bending and stretching vibrations at frequencies below 100 cm−1 and around 200 cm−1, respectively (Fig. 5).51 Hindered rotations (librational modes of water molecules within the hydrogen-bond network) are observed at frequencies between 300 and 1000 cm−1 for the rotational degrees of freedom.
Figure 5.
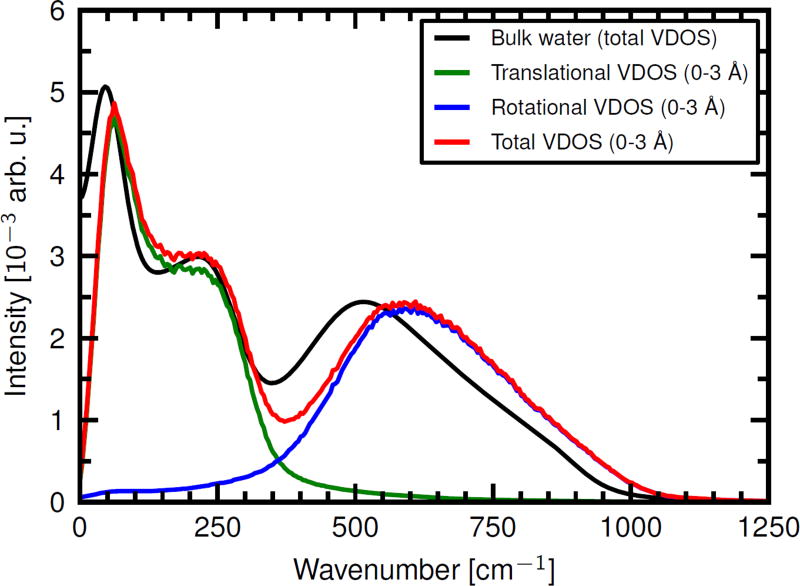
VDOS of bulk water versus water molecules in the slab closest to the membrane in the Anx-on-DOPC/DOPS bilayer system. Shown are the individual total VDOS and, for the protein-bilayer system, the translational and rotational VDOS. All spectra were normalized.
The VDOS of water molecules within slabs of 3 Å thickness along the bilayer normal was analyzed for three different systems: Anx on the mixed DOPC/DOPS bilayer, a bare DOPC/DOPS bilayer (i.e., in absence of protein), and Anx on the hydrophobic membrane. For systems containing Anx, the selected waters were restricted to those whose oxygen atom is within a 5 Å distance to any non-hydrogen Anx atom, as before. The VDOS was computed both from COM-velocities and molecular angular momenta. Fig. 5 compares the VDOS of water molecules around Anx-on-DOPC/DOPS that are within 3 Å of the bilayer with the VDOS of bulk water. A striking observation is the overall blue-shift of the spectrum of hydration water compared to bulk water.
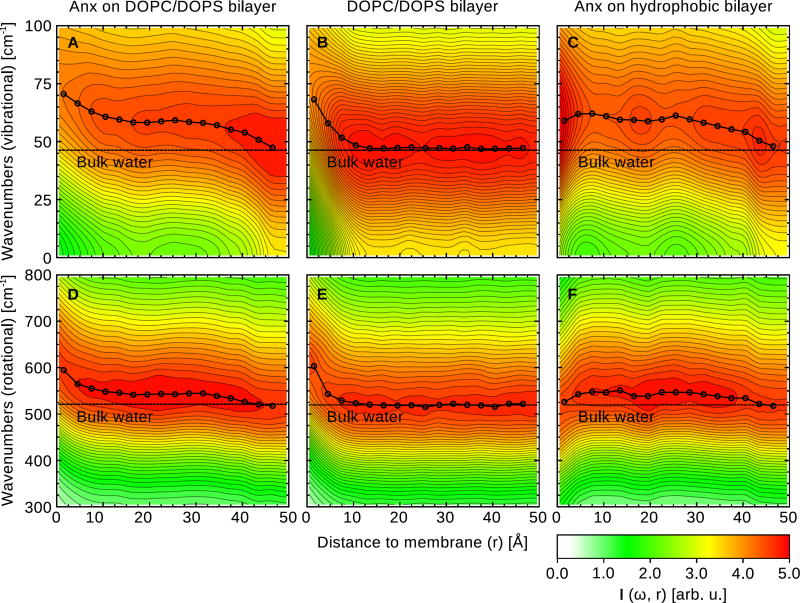
For the COM-VDOS, which describes translational degrees of freedom, we focus our analysis on the H-bond bending peak around 50 cm−1, since it has the highest intensity. Results are shown in Fig. 6A–C. For Anx on the DOPC/DOPS bilayer (Fig. 6A), the bending peak is shifted to higher frequencies as the distance to the bilayer decreases. The peak is shifted by 23 cm−1, from 47 cm−1 to 70 cm−1. The largest shift occurs at distances closer than 10 Å from the phosphate head groups, in agreement with the strong retardation of water found in this region (see Fig. 2). The intensity of the zero frequency response (diffusion) decreases accordingly. Table 2 shows the maximum peak shifts of water near the membrane surface relative to bulk water, both for the H-bond bending band and the libration band. Similarly to the analysis of water diffusivity, we find plateau region in the VDOS for the H-bond bending peak position, which can be attributed to effects of the protein. In addition, the VDOS reveals that the significant frequency shift can be attributed to transfer of intensity from the zero frequency/diffusive mode to higher frequency vibrations. Due to the confinement of water molecules at the water/bilayer (or water/protein/bilayer) interface, diffusive COM motion of water molecules is replaced by vibrational motions of the hydrogen bond network, which can be qualitatively interpreted within the 2PT methodology as a decrease in entropy (see below).
Figure 6.
Top row: Center of mass VDOS of water molecules as a function of distance to the phosphate head groups. Bottom row: Angular momentum VDOS of water molecules as a function of distance to the phosphate head groups. All spectra were smoothed by a Gaussian window function (σ = 20 cm−1) and normalized.
Table 2.
Total shifts of H-bond bending and libration peaks, calculated as the frequency difference Δω between the largest (48–51 Å) and shortest (0–3 Å) distances between water molecules and lipid head groups.
| System | Δωbend [cm−1] | Δωlib [cm−1] |
|---|---|---|
|
| ||
| Anx on DOPC/DOPS bilayer | 23 | 75 |
| DOPC/DOPS bilayer | 21 | 82 |
| Anx on hydrophobic bilayer | 12 | 1 |
For the bare DOPC/DOPS bilayer (Fig. 6B), we find the same pronounced blue-shift of the bending peak at distances less than 10 Å from the bilayer; this shift can therefore be ascribed to an effect of the membrane. By contrast, for Anx on the hydrophobic membrane (Fig. 6C), there is only a weak blue-shift of the low frequency peak. We attribute this effect to geometric confinement, since the retardation of water near the hydrophobic membrane is much less pronounced.
The rotational VDOS is shown in Fig. 6D–F. We observe similar blue-shifts of the libration mode frequency for Anx on the DOPC/DOPS bilayer (Fig. 6D) and the bare DOPC/DOPS bilayer (Fig. 6E). Interestingly, for Anx on the hydrophobic membrane (Fig. 6F), the libration peak of the water close to the membrane is red-shifted with respect to water molecules in the hydration shell of Anx that are further away from the membrane. For those water molecules that are very close to the membrane (0–3 Å), the libration peak is at a frequency comparable to that of bulk water. In this case, the absence of polar and charged lipid head groups and their strong directional interactions with nearby water molecules facilitates rotational tumbling motions of the water molecules, as reflected in the lower frequency. This is in line with our previous finding that water retardation is reduced close to a purely hydrophobic membrane (see Fig. 2), and also agrees with a previous study of water diffusivity near a prototypical hydrophobic amino acid side chain52 and hydrophobic model surfaces.53
Entropy of water near the protein and membrane surfaces
We estimated the total entropy of water and its contributions from translational and rotational degrees of freedom from the computed VDOS using the 2PT method.15,38 From the observed shifts of intensity from zero-frequency responses to higher frequency vibrations, as well as the blue-shifted vibrational bands, we expect a decrease in water entropy. By contrast, a red-shift of the vibrations relative to the water in the hydration shell of the protein, as seen for the librational bands in the vicinity of the purely hydrophobic bilayer, should result in an increase in entropy.
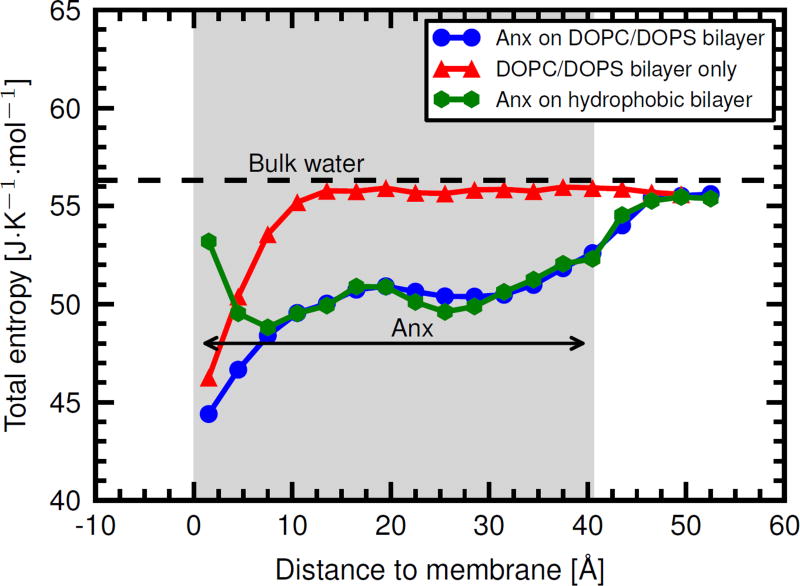
Fig. 7 shows that indeed, the total entropy of water in the hydration shell of the Anx/membrane complex is decreased as compared to the bulk. The entropy of water molecules that are very close to the lipid head groups is about 44 J mol−1 K−1 and thus considerably lower than in the bulk (56 J mol−1 K−1). The additive nature of protein- and membrane-induced effects is apparent also in this analysis, in line with our above discussed results (see Fig. 2). Likewise, the entropy of water in the vicinity of a bare DOPC/DOPS bilayer (i.e. without Anx, red triangles in Fig. 7) is also strongly decreased, up to around 10 Å above the bilayer. This latter result agrees with a recent study of a DPPC bilayer.54 A similar reduction in entropy is not observed on the artificial hydrophobic membrane (Fig. 7, green hexagons). Instead, the entropy of water molecules that are very close to the hydrophobic surface (0–3 Å) is slightly increased, both compared to membrane-distant water molecules in the hydration shell of Anx, and also compared to water molecules that are at a similar close distance (0–3 Å) from the corresponding membrane with realistic (partial) charges.
Figure 7.
Total entropy of water obtained from the total VDOS of water via the 2PT method as a function of distance to the phosphate head groups.
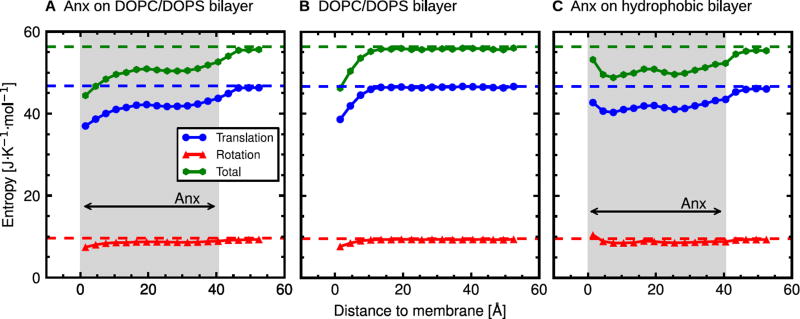
The dissection of the total water entropy into translational and rotational components is shown in Fig. 8. The translational motions (blue) are the major contribution to the total entropy (green); the rotations (red) contribute only about 15–20%. As expected from the vibrational frequency shifts, the increase of water entropy in the vicinity of the hydrophobic membrane (Fig. 8C) can be attributed to both translational and rotational entropies. Despite the weak blue shift of the peak frequency, due to a modified shape of the librational band (Fig. 6F), the rotational entropy of the water molecules in the first hydration layer of the hydrophobic membrane (0–3 Å) is in this case even slightly higher than in the bulk. Changes in thermodynamic properties of interfacial water molecules, including their entropy, can contribute to important biomolecular processes, such as the binding of peripheral membrane proteins or the dimerization of integral membrane proteins with water–soluble domains.
Figure 8.
Total entropy of water and its translational and rotational components. The corresponding bulk water entropies are shown as dashed lines.
Conclusions
We have analyzed in detail the separate contributions of the phospholipid bilayer and protein to the dynamics of water around a membrane-associated protein. The water dynamics measured by ODNP-enhanced NMR experiments correlate with MD simulation data. Electrostatic interactions with the lipid head groups are dominant and strongly retard water dynamics up to about 10 Å above the membrane surface. At larger distances, the more modest retardation effect due to the protein itself takes over, until bulk behavior is reached at around 10 Å above the protein. Membrane- and protein-induced effects on the activation free energy barrier for surface water diffusion are additive. We found no strong residue-specific effects (e.g., hydrophobic versus hydrophilic or charged). Instead, the distance between protein residues and the membrane surface is a reliable predictor of water retardation, at least for distances below 10 Å. We therefore expect water dynamics to be altered in a similar manner around other membrane-bound proteins or protein domains. Our results strengthen the idea that water dynamics can be used as an intrinsic ruler to measure distances to membrane surfaces.6 We have shown that calibrating such a ruler using MD simulations is in principle possible, given that a quantitative link between ODNP and MD can be established. From a more general perspective, this work contributes to a better understanding of the role of lipid membranes in mediating intermolecular interactions, such as molecular recognition and binding events, by shaping hydration water dynamics and entropy.
Supplementary Material
Acknowledgments
This work was funded by the DFG: Cluster of Excellence RESOLV (EXC 1069) and an Emmy-Noether grant to L.V.S.; and by the NIH: GM grants 1R01GM116128-01 to S.H. and 1R01GM115736 to R.L.
Footnotes
Supporting Information Available
Methodological details of simulations, analysis of protein position and stability, mean-square water displacements, additional control experiments, ODNP-enhanced NMR relaxometry measurements, water retardation factors.
This material is available free of charge via the Internet at http://pubs.acs.org/.
References
- 1.Bellissent-Funel M-C, Hassanali A, Havenith M, Henchman R, Pohl P, Sterpone F, van der Spoel D, Xu Y, Garcia AE. Chem. Rev. 2016;116:7673–7697. doi: 10.1021/acs.chemrev.5b00664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bagchi B. Chem. Rev. 2005;105:3197–3219. doi: 10.1021/cr020661+. [DOI] [PubMed] [Google Scholar]
- 3.Levy Y, Onuchic JN. Annu. Rev. Biophys. Biomol. Struct. 2006;35:389–415. doi: 10.1146/annurev.biophys.35.040405.102134. [DOI] [PubMed] [Google Scholar]
- 4.Chaplin M. Nat. Rev. Mol. Cell Biol. 2006;7:861–866. doi: 10.1038/nrm2021. [DOI] [PubMed] [Google Scholar]
- 5.Ball P. Chem. Rev. 2008;108:74–108. doi: 10.1021/cr068037a. [DOI] [PubMed] [Google Scholar]
- 6.Cheng C-Y, Varkey J, Ambroso MR, Langen R, Han S. Proc. Natl. Acad. Sci. U.S.A. 2013;110:16838–16843. doi: 10.1073/pnas.1307678110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hodges MW, Cafiso DS, Polnaszek CF, Lester CC, Bryant RG. Biophys. J. 1997;73:2575–2579. doi: 10.1016/S0006-3495(97)78286-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Berkowitz ML, Bostick DL, Pandit S. Chem. Rev. 2006;106:1527–1539. doi: 10.1021/cr0403638. [DOI] [PubMed] [Google Scholar]
- 9.Berkowitz ML, Vácha R. Acc. Chem. Res. 2012;45:74–82. doi: 10.1021/ar200079x. [DOI] [PubMed] [Google Scholar]
- 10.Das J, Flenner E, Kosztin I. J. Chem. Phys. 2013;139:065102. doi: 10.1063/1.4817322. [DOI] [PubMed] [Google Scholar]
- 11.von Hansen Y, Gekle S, Netz RR. Phys. Rev. Lett. 2013;111:118103. doi: 10.1103/PhysRevLett.111.118103. [DOI] [PubMed] [Google Scholar]
- 12.Wood K, Plazanet M, Gabel F, Kessler B, Oesterhelt D, Tobias DJ, Zaccai G, Weik M. Proc. Natl. Acad. Sci. U.S.A. 2007;104:18049–18054. doi: 10.1073/pnas.0706566104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tobias DJ, Sengupta N, Tarek M. Faraday Discuss. 2009;141:99–116. doi: 10.1039/b809371g. [DOI] [PubMed] [Google Scholar]
- 14.Isas JM, Langen R, Hubbell WL, Haigler HT. J. Biol. Chem. 2004;279:32492–32498. doi: 10.1074/jbc.M402568200. [DOI] [PubMed] [Google Scholar]
- 15.Lin S-T, Blanco M, Goddard WA., III J. Chem. Phys. 2003;119:11792–11805. [Google Scholar]
- 16.Armstrong BD, Choi J, Lopez C, Wesener DA, Hubbell W, Cavagnero S, Han S. J. Am. Chem. Soc. 2011;133:5987–5995. doi: 10.1021/ja111515s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cheng C-Y, Song J, Pas J, Meijer LHH, Han S. Biophys. J. 2015;109:330–339. doi: 10.1016/j.bpj.2015.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Franck JM, Ding Y, Stone K, Qin PZ, Han S. J. Am. Chem. Soc. 2015;137:12013–12023. doi: 10.1021/jacs.5b05813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Isas JM, Kim YE, Jao CC, Hegde PB, Haigler HT, Langen R. Biochemistry. 2005;44:16435–16444. doi: 10.1021/bi051751m. [DOI] [PubMed] [Google Scholar]
- 20.Franck JM, Pavlova A, Scott JA, Han S. Prog. Nucl. Magn. Reson. 2013;74:33–56. doi: 10.1016/j.pnmrs.2013.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hausser K, Stehlik D. Adv. Magn. Reson. 1968;3:79–139. [Google Scholar]
- 22.Robinson H, Bruce, Haas A, Duncan, Mailer C. Science. 1994;263:490–493. doi: 10.1126/science.8290958. [DOI] [PubMed] [Google Scholar]
- 23.Bennati M, Luchinat C, Parigi G, Türke M-T. Phys. Chem. Chem. Phys. 2010;12:5902–5910. doi: 10.1039/c002304n. [DOI] [PubMed] [Google Scholar]
- 24.Hwang L-P, Freed JH. J. Chem. Phys. 1975;63:4017–4025. [Google Scholar]
- 25.Armstrong BD, Lingwood MD, McCarney ER, Brown ER, Blümler P, Han S. J. Magn. Reson. 2008;191:273–281. doi: 10.1016/j.jmr.2008.01.004. [DOI] [PubMed] [Google Scholar]
- 26.Kaminker I, Barnes R, Han S. Methods Enzymol. 2015;564:457–483. doi: 10.1016/bs.mie.2015.06.040. [DOI] [PubMed] [Google Scholar]
- 27.Cartailler JP, Haigler HT, Luecke H. Biochemistry. 2000;39:2475–2483. doi: 10.1021/bi992278d. [DOI] [PubMed] [Google Scholar]
- 28.Jämbeck JPM, Lyubartsev AP. J. Phys. Chem. B. 2012;116:3164–3179. doi: 10.1021/jp212503e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jämbeck JPM, Lyubartsev AP. J. Chem. Theory Comput. 2012;8:2938–2948. doi: 10.1021/ct300342n. [DOI] [PubMed] [Google Scholar]
- 30.Hornak V, Abel R, Okur A, Strockbine B, Roitberg A, Simmerling C. Proteins. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Best RB, Hummer G. J. Phys. Chem. B. 2009;113:9004–9015. doi: 10.1021/jp901540t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lindorff-Larsen K, Piana S, Palmo K, Maragakis P, Klepeis JL, Dror RO, Shaw DE. Proteins. 2010;78:1950–1958. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Aliev AE, Kulke M, Khaneja HS, Chudasama V, Sheppard TD, Lanigan RM. Proteins. 2014;82:195–215. doi: 10.1002/prot.24350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Abascal JLF, Vega C. J. Chem. Phys. 2005;123:234505. doi: 10.1063/1.2121687. [DOI] [PubMed] [Google Scholar]
- 35.Pronk S, Páll S, Schulz R, Larsson P, Bjelkmar P, Apostolov R, Shirts MR, Smith JC, Kasson PM, van der Spoel D, Hess B, Lindahl E. Bioinformatics. 2013;29:845–854. doi: 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hasted J, Husain S, Frescura F, Birch J. Chem. Phys. Lett. 1985;118:622–625. [Google Scholar]
- 37.Walrafen GE. J. Phys. Chem. 1990;94:2237–2239. [Google Scholar]
- 38.Lin S-T, Maiti PK, Goddard WA., III J. Phys. Chem. B. 2010;114:8191–8198. doi: 10.1021/jp103120q. [DOI] [PubMed] [Google Scholar]
- 39.Pascal TA, Lin S-T, Goddard WA., III Phys. Chem. Chem. Phys. 2011;13:169–181. doi: 10.1039/c0cp01549k. [DOI] [PubMed] [Google Scholar]
- 40.Bryant RG. Annu. Rev. Biophys. Biomol. Struct. 1996;25:29–53. doi: 10.1146/annurev.bb.25.060196.000333. [DOI] [PubMed] [Google Scholar]
- 41.Mattea C, Qvist J, Halle B. Biophys. J. 2008;95:2951–2963. doi: 10.1529/biophysj.108.135194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Qvist J, Persson E, Mattea C, Halle B. Faraday Discuss. 2009;141:131–144. doi: 10.1039/b806194g. [DOI] [PubMed] [Google Scholar]
- 43.Abseher R, Schreiber H, Steinhauser O. Proteins. 1996;25:366–378. doi: 10.1002/(SICI)1097-0134(199607)25:3<366::AID-PROT8>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- 44.Sterpone F, Stirnemann G, Laage D. J. Am. Chem. Soc. 2012;134:4116–4119. doi: 10.1021/ja3007897. [DOI] [PubMed] [Google Scholar]
- 45.Fogarty AC, Laage D. J. Phys. Chem. B. 2014;118:7715–7729. doi: 10.1021/jp409805p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pal SK, Peon J, Zewail AH. Proc. Natl. Acad. Sci. U.S.A. 2002;99:1763–1768. doi: 10.1073/pnas.042697899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bagchi B, Jana B. Chem. Soc. Rev. 2010;39:1936–1954. doi: 10.1039/b902048a. [DOI] [PubMed] [Google Scholar]
- 48.Laage D, Hynes JT. Science. 2006;311:832–835. doi: 10.1126/science.1122154. [DOI] [PubMed] [Google Scholar]
- 49.Pandit SA, Berkowitz ML. Biophys. J. 2002;82:1818–1827. doi: 10.1016/S0006-3495(02)75532-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Rahaman O, Melchionna S, Laage D, Sterpone F. Phys. Chem. Chem. Phys. 2013;15:3570–3576. doi: 10.1039/C3CP44582H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Heyden M, Havenith M. Methods. 2010;52:74–83. doi: 10.1016/j.ymeth.2010.05.007. [DOI] [PubMed] [Google Scholar]
- 52.Russo D, Hura G, Head-Gordon T. Biophys. J. 2004;86:1852–1862. doi: 10.1016/S0006-3495(04)74252-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Sedlmeier F, von Hansen Y, Mengyu L, Horinek D, Netz RR. J. Stat. Phys. 2011;145:240–252. [Google Scholar]
- 54.Debnath A, Mukherjee B, Ayappa KG, Maiti PK, Lin S-T. J. Chem. Phys. 2010;133:174704. doi: 10.1063/1.3494115. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.