Abstract
There is an unmet need to accurately identify the locations of innervation zones (IZs) of spastic muscles, so as to guide botulinum toxin (BTX) injections for the best clinical outcome. A novel 3-dimensional IZ imaging (3DIZI) approach was developed by combining the bioelectrical source imaging and surface electromyogram (EMG) decomposition methods to image the 3D distribution of IZs in the target muscles. Surface IZ locations of motor units (MUs), identified from the bipolar map of their motor unit action potentials (MUAPs) were employed as a prior knowledge in the 3DIZI approach to improve its imaging accuracy. The performance of the 3DIZI approach was first optimized and evaluated via a series of designed computer simulations, and then validated with the intramuscular EMG data, together with simultaneously recorded 128-channel surface EMG data from the biceps of two subjects. Both simulation and experimental validation results demonstrate the high performance of the 3DIZI approach in accurately reconstructing the distributions of IZs and the dynamic propagation of internal muscle activities in the biceps from high-density surface EMG recordings.
Keywords: Electromyography (EMG), innervation zone (IZ), motor unit (MU), motor unit action potential (MUAP), surface EMG decomposition, bioelectrical source imaging
1. Introduction
Stroke represents a huge health and economic problem1, with the subsequent incidence of spasticity reported to be 20–40% in post-stroke survivors. This not only has adverse effects on the patients’ quality of life, but it also imposes a substantial burden on the caregivers and the society at large.2 Botulinum neurotoxin (BTX) is considered as the first-line treatment for focal spasticity management.3, 4 Intramuscular BTX injection has proven to be a relatively safe procedure,5 but it may still cause side effects or even severe problems in patients, such as blocking of autonomic nerves, muscle atrophy by anatomical denervation, and immunological reactions.6–9 The occurrence and severity of side effects are dependent on the delivered dose of toxin,10, 11 and it has been clinically shown that the injection of a minimum effective dose reduces the incidence of adverse effects.12 BTX acts on the neuromuscular junction (NMJ) and the effectiveness of the BTX injection depends on the proximity of the injection site to the NMJ.13 Studies have demonstrated that increasing the injection distance by 1cm from the NMJ, indicated by the innervation zone (IZ) of muscles, reduced the effect of BTX by 46%.14 Therefore, it is critical to accurately identify the locations of IZs of the target muscles to guide BTX injections for the best clinical outcome with a minimal dose.
Unfortunately, the location of the IZs varies measurably between muscles and individuals, and currently there is no consensus about techniques which can be used to define IZs for guiding BTX injections for specific patients and particular muscles.15 Clinically, the motor point (MP) is used as the injection site of BTX since it is broadly homologous to the IZ. However, a significant difference between the MP and IZ locations has been reported.15 Bipolar high-density surface Electromyography (EMG) mapping has also been used to localize IZs over the skin surface to improve the BTX injection outcome,14 but the application of this surface localization method is limited by the lack of the depth information of the IZs, particularly due to peripheral adaptive changes including atrophy and fat tissue deposit.16 3D IZ location is therefore needed in order to improve clinical outcomes with minimal treatment dosages and thus minimize side effects.
The bioelectrical activity imaging approach has been well developed and successfully used to localize bioelectrical activities in the brain and the heart from scalp electroencephalogram (EEG) and body surface electrocardiogram (ECG) recordings, respectively17–22. Similar to EEG and ECG recordings, surface EMG signals, which contain important functional information of muscles,23 are composed of the superimposed action potentials of many muscle fibers and are the summation of different motor unit action potentials (MUAPs). Several methods have been developed to localize internal muscle activities from multi-channel recordings of the surface EMG to improve its specificity to particular muscles. The bioelectrical activity imaging approach was first performed with an exhaustive search method based on a single sinusoidal current source model to localize internal muscle activities from surface EMG recordings.24 Later, a distributed tripole model was employed to model muscle activities and a generalized Tikhonov regularization approach was utilized to solve the inverse problem to reconstruct internal muscle activities from multi-channel surface EMG signals.25, 26
We have previously demonstrated the feasibility of imaging internal muscle activities from multi-channel intra-vaginal surface EMG measurements in computer simulation.27 In addition, we also developed a spatiotemporal muscle activity imaging approach to improve the reconstruction accuracy in skeletal muscles by incorporating the spatial and temporal components in the multi-channel surface EMG measurements.28 The feasibility of imaging the muscle activities in the 3D space of the biceps using the weighted minimum-norm (WMN) algorithm was recently verified with multi-channel surface EMG measurements recorded from the upper arm of a healthy subject.27, 29 Those previous studies have demonstrated the feasibility of utilizing bioelectrical activity imaging methods to localize internal muscle activities from noninvasive multi-channel surface EMG recordings, but currently available muscle activity imaging approaches suffer from low accuracy and specificity, which limits their application and prevents them from being utilized to accurately localize muscle IZs.
Composite surface EMG signals can now be decomposed into their constituent MUAP trains.30 A novel 3-dimensional innervation zone imaging (3DIZI) approach has been developed in this study by combining the bioelectrical source imaging and surface EMG decomposition methods to image the distribution of IZs in the 3D space of the biceps, from high-density surface EMG recordings. The 128-channel surface EMG signals were first decomposed into their constituent MUAP trains. The surface location of the IZ of each decomposed motor unit (MU) was identified from the bipolar high-density MUAP trains and was then utilized to constrain the bioelectrical source imaging solution in the 3DIZI approach to improve its 3D localization accuracy. The 3DIZI approach was validated with both simulated surface EMG signals as well as with surface and intramuscular EMG signals simultaneously recorded from the biceps of 2 male subjects. The validation results demonstrated the capability of the proposed 3DIZI approach to accurately localize the IZs in the 3D space of target muscles.
2. Methodology
2.1. Experiment
Simultaneous surface EMG and intramuscular EMG measurements were acquired from the biceps of the two healthy male subjects with a 136-channel Refa (TMSi, Enschede, The Netherlands) according to a protocol approved by the Institutional Review Boards (IRBs) of the University of Houston and the TIRR Memorial Hermann Hospital (Houston, USA). The 128 unipolar channels were employed for surface EMG measurements with two flexible 64-channel surface electrode arrays (TMSi, Enschede, The Netherlands). The electrode array is in 8 × 8 formation with the individual recording probe diameter of 4.5 mm and the center-to-center probe distance of 8.5 mm.
One bipolar channel was employed for simultaneous intramuscular EMG measurements using a sterile needle with fine wire electrodes (VIASYS Healthcare, Madison WI) for the validation purpose. The EMG recording configuration is shown in Fig. 1 (a1) and (b1). The depths of the wire electrodes inserted in the biceps were characterized from the ultrasound images (green circles in Fig. 1 (a2) and (b2): 1.53 cm and 1.50 cm, respectively) obtained from the skin surface of the 1st and 2nd subjects. The locations of electrodes 40, 48, 88 and 96 are marked in Fig. 1(a1) for the 1st subject, and the locations of electrodes 36, 39, 40, 42, 46, 47, 86 and 94 are marked in Fig. 1(b1), in order to better interpret reconstruction results presented in Fig. 6 and Fig. 7.
Fig. 1.
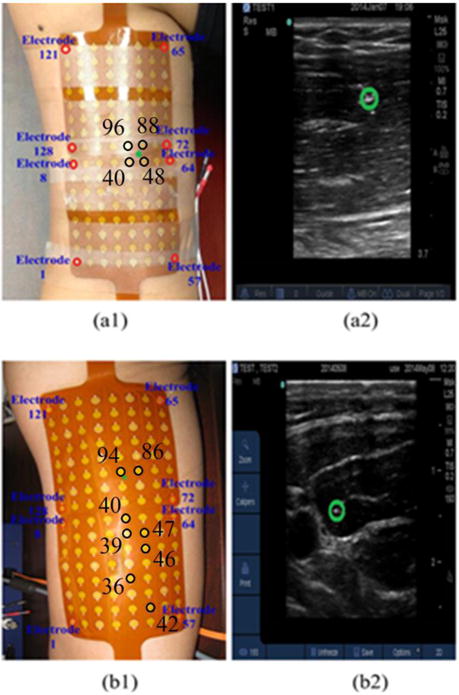
Placement of the surface EMG electrodes and insertion location of the wire electrode (green star) over the (a1) 1st subject’s upper arm and (b1) 2nd subject’s upper arm; Location of the wire electrode (green circle) identified from the ultrasound image of the (a2) 1st subject’s right upper arm and (b2) 2nd subject’s right upper arm.
Fig. 6.
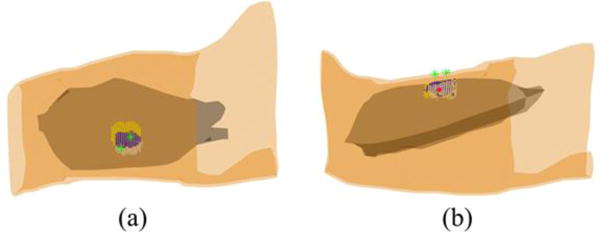
Reconstructed IZs of the MU3 and MU6 of the 1st subject and their overlap zone at the time instant when the MUAP trains were generated. White dots represent the muscle activities generated by MU3 only; yellow dots represent the muscle activities generated by MU6 only; blue dots represent the overlap of the muscle activities generated by both MUs. The two green stars represent the locations of 48th and 96th surface EMG electrodes and the large red dot represents the location of wire electrode inserted in the biceps.
Fig. 7.
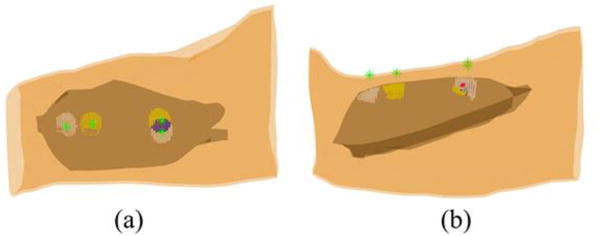
Reconstructed internal muscle activities of MU1 and MU5 of the 2nd subject and their overlap zone at the specific time instant when the 86th and the 94th surface EMG electrodes, closest to the inserted wire electrode, achieved maximum values. White dots represent the muscle activities generated by MU1 only; yellow dots represent the muscle activities generated by MU5 only; blue dots represent the overlap of the muscle activities generated by both MUs. The green stars represent the locations of 42th, 86th, 36th, and 94th surface EMG electrodes and the large red dot represents the location of wire electrode inserted in the biceps.
Subjects were seated comfortably in chairs and their right arm was placed on a table and arranged to lie naturally. The upper arm and forearm were almost parallel to the ground and the palm of the hand was rotated upward, placing the forearm in a supine position. The target area of the skin was well prepared by using an alcohol wipe with mild abrasion. The surface of each EMG electrode in the electrode array was coated with conductive gel to reduce the impedance between the skin and electrodes. Then the two 64-channel surface EMG electrode arrays were placed over the skin of the biceps of the subject and stabilized using medical tape to maintain a good skin-to-electrode contact. The reference electrodes were placed on the dorsum of the left wrist. A sampling rate of 2 kHz per channel was adopted for both surface and intramuscular EMG recordings.
Visual inspection of the signal was performed prior to the data recording to ensure background noise and artifacts were minimized. The subjects were then instructed to perform isometric bicep contraction at 10% MVC level and the surface and intramuscular EMG signals were recorded simultaneously for 30 seconds. The test was repeated for 10 trials for each subject. The ultrasound scanning of the cross-sectional area of the biceps was conducted with a portable B-mode ultrasound scanner (M Turbo, SonoSite, Bothell, WA). A linear probe, with a dynamic frequency range of 6–13MHz, adjustable gains, and a detectable depth over 6 cm was utilized to detect the insertion depth of the intramuscular wire electrode. The probe was kept perpendicular to the skin surface of the biceps region during scanning.
2.2. Surface EMG signal decomposition
Our newly developed K-means clustering and Convolution Kernel Compensation (KmCKC) approach30 was utilized to decompose the 128-channel surface EMG signals into their constituent MUAP trains. Very briefly, the K-mean clustering (KMC) method was firstly utilized to cluster firing times of the same MU via evaluating a distance function. During this process, the initial innervation pulse train (IPT) can be estimated by choosing an appropriate number of clustered groups and time instants so that the time instants fired by a single MU can be gathered into one group as completely as possible. Then, an improved multi-step iterative convolution kernel compensation (CKC) method is employed to update the estimated IPTs to improve the decomposition accuracy in a noisy environment.
2.3. Geometry Model and Source Model
Two realistic geometry upper arm models consisting of the skin, fat, biceps, triceps, compact bone and cancellous bone were constructed from a general magnetic resonance (MR) image data set and modified to match the ultrasound images of the subjects’ upper arms, then meshed into finite element (FE) models with ANSYS 13.0 (ANSYS, Canonsburg, PA), as shown in Fig 2. The upper arm FE model of the first subject consists of 225,462 tetrahedral elements and 39,605 nodes, and the upper arm FE model of the second subject includes 231,421 tetrahedral elements and 40,596 nodes. The conductivity values assigned to the skin, fat, muscle, compact bone and cancellous bone were 4.55×10-4 S/m, 0.0379 S/m, 0.2455 S/m, 0.02 S/m and 0.075 S/m, respectively.31
Fig. 2.
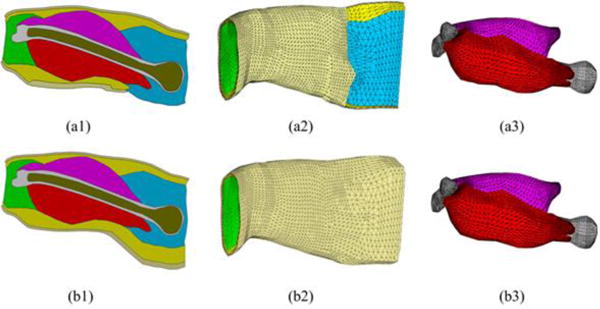
Cross-sectional view of the geometry model for the right upper arm of the 1st subject (a1) and 2nd subject (b1). FE models of the entire upper arm of the 1st subject (a2) and 2nd subject (b2). FE models of the bones and muscles of the 1st subject (c1) and 2nd subject (c2). The different colors indicate different types of tissues involved in the upper arm model: light gold – skin, yellow – fat, red – bicep, magenta – triceps, grey – compact bone, bronze – cancellous bone, green – elbow fill, blue – shoulder fill
The electrical current dipole source model,32 tripole source model,33 quadrupole source model,34 and analytical waveform source model35 have all been used to model action potentials (muscle activities) in EMG studies. Considering the irregular and arbitrary shapes of muscle fiber groups in the human body, a distributed source model27, 36, 37 which has the capability of accurately describing bioelectric activities without requiring any prior assumptions about its shape was employed in the proposed 3DIZI approach. Specifically, a total number of 42,840 and 43,589 dipoles were evenly distributed in the 3D space of the biceps of the first and second subjects, respectively, with a dipole-to-dipole distance of 2 mm. Each dipole had three orthogonal components that need to be determined.
2.4. Bioelectrical source imaging
The linear relationship between the source space and the measurement space can be expressed as27, 36
| (1) |
where Φ=(Φ1, Φ2, ⋯, ΦM)T is the vector of surface EMG measurements, X=(x1, x2, ⋯, x3N)T is the vector representing the strength of the distributed dipoles in the 3D space of the biceps, L = (L1, L2, …, LN) is the transfer matrix and Li is a M×3 matrix that represents the electrical lead field of the ith dipole. The transfer matrix L can be constructed by solving the forward problem.38 M refers to the number of surface recording electrodes over the skin and N refers to the number of dipole sources in the source space. Since the number of surface measurements is much smaller than the number of dipoles, the inverse problem described in Eq. (1) is an under-determined problem. In order to achieve a unique and high-accuracy solution, a surface EMG decomposition informed weighted minimum norm approach was developed and utilized to solve the inverse problem in the 3DIZI approach by minimizing the following equation:
| (2) |
The corresponding inverse solution to above equation can be given as follows:39–41
| (3) |
where W is a 3N×3N weighted matrix which accounts for the undesired depth dependence, λ is the regularization parameter which is determined by means of the L-curve method,42 R is a 3N×3N diagonal source covariance matrix, which assumes that the dipole strengths at different locations are completely independent. Once the surface location of the IZ is identified from the bi-directional propagation pattern of decomposed MUAPs, a cylindrical space is then defined directly underneath the identified surface IZ location and axially pointed to the normal direction of the skin surface. Different factors are assigned to the elements of the R matrix corresponding to the dipoles inside (0.9) and outside (0.1) the cylindrical sub-spaces to constrain the solution to the cylindrical sub-spaces with a higher weighting factor.
The IZ is defined as the region of a MU including the end-plates (neuromuscular junctions) where the MUAPs are generated and propagate in two opposing directions towards the fiber endings. The signals propagating in opposite directions appear with opposite phases in the bipolar MUAP maps. Therefore, the surface position of the IZ of a particular MU can be localized from the bipolar map of the decomposed high-density MUAPs by checking the phases of the propagating signals. The surface location of the IZ can be employed to construct the source covariance matrix R in Eq. (3) to constrain the muscle activity imaging solution in the 3DIZI approach and improve its localization accuracy. A cylinder with the diameter of 20 mm33, 43 is defined directly underneath the identified surface IZ location and axially pointed to the normal direction of the skin surface, and this cylinder will create a cylindrically shaped sub-space in the target muscle space. A high weighting factor (0.9) is assigned to the elements of the R matrix for the dipoles inside the cylindrical sub-space and a low weighting factor (0.1) is assigned to the elements of the R matrix for the dipoles outside of the sub-space.
2.5. Computer simulation
A series of designed computer simulations were conducted based on the FE model of the subject1’s upper arm, presented in Fig. 2 (a2), to evaluate and optimize the performance of the 3DIZI approach in localizing IZs in the 3D space of the biceps. An IZ with different depths was simulated at multiple locations with different noise levels. The depths of the center of the assumed IZs were set at 15, 20, 25, 30, and 35 mm from the surface of the skin.44, 45 At each depth, five different locations were assumed in the biceps along the muscle fiber direction. The IZs were assumed ellipsoidal, with semi-axes length of 5 and 4 mm in parallel and normal to the muscle fiber directions, respectively.33, 43
In order to mimic the measurement noise in the surface EMG signal, different levels of Gaussian white noise (GWN) were added to the noise-free synthetic surface EMG measurement. Previous studies show a SNR of 24.89 dB can be achieved in the recorded surface EMG on biceps with low level muscle activations,46 so the GWNs with SNRs of 30, 25, 20 and 15 dB were considered in our computations. The SNR was defined as ,47, 48 where σs and σn are the respective standard deviations of the synthetic noise-free measurement and the added noise. Thirty sets of independent noise with a mean of zero and standard deviation of σn were generated and added to the synthetic noise-free measurement.
The distance localization error (LE) was employed to evaluate the accuracy of the 3DIZI results. The LE is defined as the spatial distance between the center of the assumed target IZ and that of the reconstructed IZ, which is composed of dipoles with the strength over 60% threshold of the maximal strength value. The mean and standard deviation of LE were calculated based on the reconstruction results of 150 noise-contaminated measurements for each simulated IZ depth where 5 different positions were considered.
3. Results
3.1 Simulation results
Fig. 3 summarizes the mean and standard deviation of the LEs of the reconstructed IZs using the 3DIZI approach from simulated surface EMG signals at five noise levels and five source depths. As we can see, both the mean values and standard deviation of the LEs of the reconstructed IZs increase as the noise level increases. However, there is no significant difference in localization accuracy for different IZ depths at the same noise level. The largest LE among all the IZs reconstructed using the proposed 3DIZI approach is lower than 2.65 mm, which indicates the high accuracy of the 3DIZI approach in localizing IZs in the 3D space of target muscles. Specifically low mean LEs of 0.64, 0.88, 0.99, 1.06, and 1.41mm were achieved for simulated IZs at the depth of 15, 20, 25, 30, and 35 mm respectively with the SNR of 25 dB, which is very close to the SNR of 24.9 dB typically achieved in real surface EMG recordings.44 As an example, The mean LEs of 0.54, 0.59, 0.64, 1.72, and 2.27 mm were achieved for simulated IZs with the depth of 15 mm and with SNR = ∞ (no noise), 30, 25, 20, and 15 dB respectively. Fig. 4 shows the distribution of the IZs in the 3D space of the biceps reconstructed using the proposed 3DIZI approach at the depth of 15 mm (close to the depth of inserted intramuscular wire electrode in our experiment) with the SNR of 25 dB. As we can see, the reconstructed IZs can accurately reflect the locations of assumed target IZs.
Fig. 3.
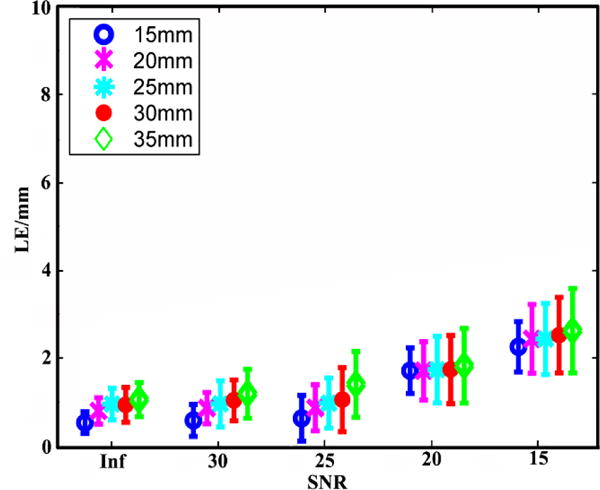
Means and standard deviations of the LEs of the IZ reconstruction results achieved using the 3DIZI approach from simulated surface EMG signals at 5 noise levels and 5 source depths.
Fig. 4.
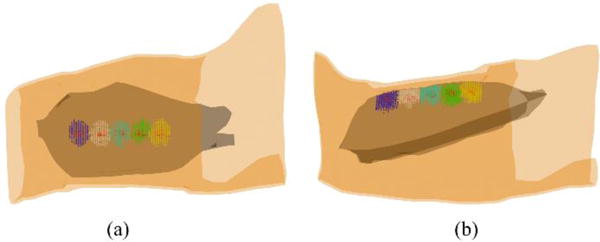
(a) Top view and (b) side view of the distributions of the IZs reconstructed from simulated surface EMG signals with the source depth of 15mm and the SNR of 25 dB. Red dots represent the simulated target IZs and blue, white, light blue, green, and yellow dots represent the reconstructed IZs at different locations of the biceps.
3.2. Experiment results
The K-means clustering and Convolution Kernel Compensation method (KmCKC) that we have developed recently28 was employed to decompose the 128-channel surface EMG signals into their constituent MUAP trains. The correlations between each decomposed MUAP train and the simultaneously recorded intramuscular EMG signals were calculated. A high correlation indicates the MU which generated the MUAPs decomposed from the surface EMG recordings was also recorded by the inserted fine wire electrode simultaneously. The correlation calculation results showed that the 3rd and 6th MUAP trains in Subject 1 and the 1st and 5th MUAP trains in Subject 2 each have a significantly high correlation with their intramuscular EMG signals. The bipolar action potentials of the MU3 and MU6 in the 1st subject are presented in Fig. 5 (a1) and (a2) and the bipolar action potentials of the MU1 and MU5 of the 2nd subject are presented in Fig. 5 (b1) and (b2).
Fig. 5.

Calculated bipolar action potentials of (a1) MU3 and (a2) MU6 of the 1st subject’s biceps; Calculated bipolar action potentials of (b1) MU1 and (b2) MU 5 of the 2nd subject’s biceps. The red rectangles indicate the locations of the IZs correspondingly.
It can be seen from the bipolar map of the decomposed action potentials of the 1st subject presented in Fig. 5 (a1) and (a2), the IZ of the MU3 is located between 48th and 88th surface EMG electrodes and the IZ of the MU6 is located between 40th and 96th surface EMG electrodes. The intramuscular wire electrodes were located in the area enclosed by those four surface EMG electrodes (48th, 88th, 40th, and 96th electrodes). Fig. 6 shows the distributions of the IZs of the MU3 and MU6 reconstructed using the 3DIZI approach from their MUAPs at the time instant when the 48th and the 96th electrodes, which are closest to the IZs of the MU3 and MU6 respectively, achieved their maximum values. The best correlations between the decomposed MUAP trains and paired intramuscular EMG recordings were achieved by the MU3 and MU6 of the 1st subject, which indicates that the muscle activities generated by these two MUs were recorded by both the surface EMG electrodes and the intramuscular wire electrode at the time instant when their MUAPs were generated in their IZs. As we can see from the top view of the reconstruction results presented in Fig. 6, the reconstructed muscle activities cover the surface locations of the IZs of the MU3 and MU6 identified by the 48th, 88th, 40th, and 96th surface electrodes and the wire electrode. It can also be clearly observed from the side view of the reconstruction results that the inserted wire electrode stays in the overlap zone of reconstructed IZs of these two MUs.
The performance of the proposed 3DIZI approach was further tested on the upper arm of the 2nd subject. Similarly, the correlation calculation results show that the decomposed MUAP trains of the MU1 and MU5 have the best correlation with the simultaneously recorded intramuscular EMG signals. The correlation results indicate that muscle activities generated by the MU1 and MU5 were simultaneously recorded by the surface EMG electrodes and the intramuscular wire electrode. The IZ of the MU1 was identified as the position between the 46th and 47th surface EMG electrodes, and the IZ of the MU5 was identified as the position between the 39th and 40th surface EMG electrodes, respectively, by checking the phase changes of the their MUAP trains from their bipolar map in Fig. 5 (b1) and (b2). The intramuscular wire electrode was inserted into the biceps via a location between the 86th and 94th surface EMG electrodes. The muscle activities generated by the MU1 and MU5 were reconstructed using the 3DIZI approach from their MUAPs at the time instant when the 86th and the 94th surface EMG electrodes, which are closest to the inserted wire electrode, achieved their maximum values, as shown in Fig. 7. As we can see, two groups of focal muscle activities symmetric to the IZ were successfully reconstructed. The overlap zone of the reconstructed muscle activities underneath the 94th and 86th surface EMG electrodes fully covers the inserted wire electrode.
4. Discussion
Studies have demonstrated that increasing the injection distance by 1cm from the NMJ as indicated by the IZ of muscles reduced the effect of BTX by 46% in treating muscle spasticity.14 Unfortunately, the location of IZs varies between muscles and individuals, and currently there is no consensus about techniques which can be used to define IZs accurately.15 To bridge this gap, the 3DIZI approach was developed to accurately image the distribution of IZs in the 3D space of the target muscles from high-density surface EMG recordings. The surface location of the IZ of each decomposed MU identified from the bipolar map of their MUAP trains was utilized to constrain the source space of the muscle activity imaging solution in the 3DIZI approach to greatly improve its localization accuracy.
The bipolar high-density surface EMG mapping has been used to localize the IZs of the target muscles over the skin surface.13 High-density surface EMG signals are usually acquired in a monopolar montage with a reference electrode from high-density electrode grids placed over the target muscles. A bipolar electrode montage is then determined by subtracting the consecutive monopolar signals in the direction of the muscle fiber. The position of IZs could be identified over the skin surface from the bi-directional propagation pattern of the MUAPs, resulting in low amplitude and opposite signal polarity on both sides of the endplates in the bipolar montage. However, surface EMG signals are comprised of action potentials produced by the muscle fibers contained in different MUs and it may be challenging to detect the surface IZ locations from the composite surface EMG signals. In this study, the high-density surface EMG signals were first decomposed into their constituent MUAP trains using our newly developed KmCKC approach.30 The surface IZ location can then be clearly identified for each decomposed MU from the bipolar montage of its MUAP trains, as shown in Fig. 5.
The bioelectrical activity imaging approach has been widely used in EEG/ECG source imaging research. However, it is also well known that bioelectrical activity imaging methods suffer from their low spatial resolution because of the ill-posed inverse nature. In the present study, surface locations for IZs identified from the bi-directional propagation properties of their MUAPs were employed as prior constraints in the inverse solver of the 3DIZI approach and greatly improved its performance. The prior constraints were implemented into the 3DIZI approach via incorporating a source covariance matrix R into the minimum norm framework.
Both simulation and experimental results validated the capability of the proposed 3DIZI approach in imaging the distributions of IZs in the 3D space of the biceps. In the computer simulations, an extremely low mean LE of 0.54 mm was achieved by the 3DIZI approach in reconstructing IZs with a depth of 15 mm from skin surface when no noise is considered, which demonstrates the high-performance of the 3DIZI approach in ideal cases. The LEs of 0.64, 0.88, 0.99, 1.06, and 1.41 mm were achieved for simulated IZs at the depths of 15, 20, 25, 30, and 35 mm respectively with the SNR of 25 dB, which is very close to the SNR of 24.9 dB typically achieved in real surface EMG recordings.44 The computer simulation results demonstrate the capability of the proposed 3DIZI approach in imaging the IZ distributions in the 3D space of target muscles with high accuracy. The experimental validation study conducted on the biceps of two male subjects further confirmed the high-performance of the 3DIZI approach in imaging the distributions of IZs in the 3D space of the biceps. In the 1st experiment, the muscle activities generated by the MU3 and MU6 were recorded by both the surface EMG electrodes and intramuscular wire electrode at time instant when their MUAPs were just generated in their IZs. As we can see from Fig. 6, the overlap of the two IZs reconstructed from their MUAPs fully covers the position of the wire electrode inserted into the biceps, which validates the accuracy of the 3DIZI approach in localizing IZs in the 3D space of the target muscles.
The goal of this study is to develop and validate the 3DIZI approach for 3D IZ imaging. It is worthy to note that the proposed 3DIZI approach can also be utilized to image the propagation of the internal muscle activities from the high-density surface EMG recordings. The developed 3DIZI approach was also preliminarily tested for its feasibility in imaging the dynamic bi-directional propagation process of the internal muscle activities, i.e., propagating from the IZ to the two end termination zones.
Figure 8 shows the reconstructed muscle activities of MU5 in the second subject. Three time instants when the 38th, 36th, and 34th surface EMG electrodes achieved maximum values were considered. It can be seen from Fig. 8 that two groups of muscle activities symmetric to the IZ position along muscle fiber direction have been reconstructed at each of these three time instants from the surface EMG recordings for the MU5. For example, one group of muscle activities was reconstructed underneath of the 38th surface EMG electrode at the 1st time instant while the other group of muscle activities was reconstructed underneath of the 96th surface EMG electrode. The 38th and 96th electrodes are located symmetrically about the IZ of MU5 (between 39th and 40th surface electrode). The same phenomena were also observed from the reconstruction results at the other two time instants. It is well known that the MUAP is generated in the IZ (the neuromuscular junction) and propagates bi-directionally toward the tendon. The bi-directional propagation property of MUAP along the muscle fiber was clearly captured by the 3DIZI approach.
Fig. 8.
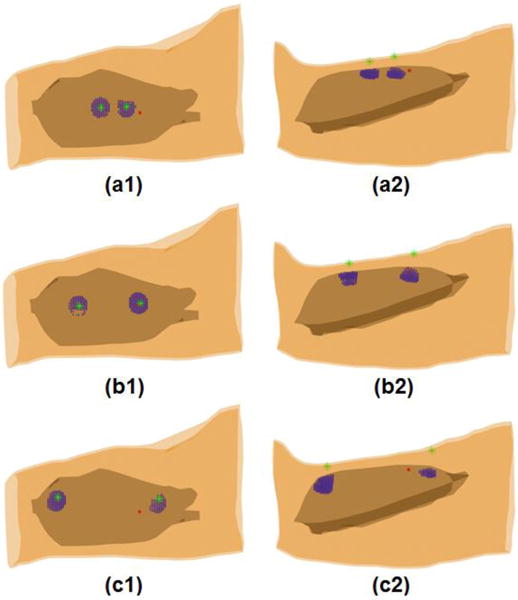
Internal muscle activities reconstructed from the 128-channel surface EMG recordings of the MU5 for the 2nd subject during the bi-directional propagation from the IZ towards the two ends of termination zones. (a1, b1 and c1) Top view and (a2, b2 and c2) side view of the internal muscle activities reconstructed at time instants during the bi-directional propagation process. Blue dots represent the reconstructed internal muscle activities; the green stars represent the locations of the surface EMG electrodes that achieved maximum values and the symmetric electrodes about the IZ; and the large red dot represents the location of the intramuscular wire electrode.
Surface EMG recordings are utilized in the proposed 3DIZI approach for IZ reconstruction. It is well known that surface EMG cannot capture the muscle activities generated by deep MUs. Therefore, one limitation of the 3DIZI approach is that it cannot be used to reconstruct IZs of deep MUs in large muscle groups. Furthermore, the KmCKC algorithm is utilized in the 3DIZI approach for surface EMG decomposition. The KmCKC requires a large number of surface EMG channels in order to satisfactorily decompose surface EMG signals. The number of MUs that can be reconstructed decreases as the number of surface EMG channels decreases. This limitation was overcome in this study by using 128 high density channels for surface EMG acquisition. The KmCKC algorithm used in the proposed 3DIZI approach also favors constant force isometric contraction, which would yield optimal decomposition results. The two subjects tested in our study were instructed to perform constant force isometric contractions in order to achieve the best possible decomposition outcome.
In conclusion, a novel 3D innervation zone imaging (3DIZI) approach was successfully developed to image the distributions of IZs in the 3D space of target muscles. The 3DIZI approach was tested and validated with simulated EMG data as well as with simultaneously recorded high-density surface EMG and intramuscular EMG data. Results demonstrate the highly favorable performance of the 3DIZI approach in accurately reconstructing the distributions of the IZs and the dynamic propagation of internal muscle activities in the 3D space of target muscles from high-density surface EMG recordings at low force isometric contractions.
Acknowledgments
This work was supported in part by NIH K99DK082644, NIH R00DK082644 NIH R24HD050821 and the University of Houston.
Contributor Information
YANG LIU, Department of Biomedical Engineering, University of Houston, 3605 Cullen Blvd, Houston, TX 77004, USA.
YONG NING, Department of Biomedical Engineering, University of Houston, 3605 Cullen Blvd, Houston, TX 77004, USA.
SHENG LI, Department of Physical Medicine and Rehabilitation, University of Texas Health Science Center at Houston, 7000 Fannin St., Houston, TX, USA.
PING ZHOU, TIRR Memorial Hermann Research Center, 1300 Moursund St., Houston, TX, USA.
WILLIAM Z. RYMER, Sensory Motor Performance Program, Rehabilitation Institute of Chicago, 345 East Superior St., Chicago, IL, USA Department of Physical Medicine and Rehabilitation, Northwestern University, 710 North Lake Shore Drive, Chicago, IL, USA.
YINGCHUN ZHANG, Department of Biomedical Engineering, University of Houston, 3605 Cullen Blvd, Houston, TX 77004, USA.
References
- 1.Villar JR, González S, Sedano J, Chira C, Trejo-Gabriel-Galan JM. Improving Human Activity Recognition and its Application in Early Stroke Diagnosis. International Journal of Neural Systems. 2015;0:1–20. doi: 10.1142/S0129065714500361. [DOI] [PubMed] [Google Scholar]
- 2.Zorowitz RD, Gillard PJ, Brainin M. Poststroke spasticity Sequelae and burden on stroke survivors and caregivers. Neurology. 2013;80:S45–S52. doi: 10.1212/WNL.0b013e3182764c86. [DOI] [PubMed] [Google Scholar]
- 3.Crammond DJ. Neurophysiological mapping of muscle endplate location: Precise targeting improves the efficacy of Botulinum neurotoxin injections. Clinical Neurophysiology. 2011;122:1487–1489. doi: 10.1016/j.clinph.2011.01.003. [DOI] [PubMed] [Google Scholar]
- 4.Brashear A, Gordon MF, Elovic E, Kassicieh VD, Marciniak C, Do M, Lee CH, Jenkins S, Turkel C. Intramuscular injection of botulinum toxin for the treatment of wrist and finger spasticity after a stroke. New England Journal of Medicine. 2002;347:395–400. doi: 10.1056/NEJMoa011892. [DOI] [PubMed] [Google Scholar]
- 5.Bakheit AMO. The possible adverse effects of intramuscular botulinum toxin injections and their management. Current drug safety. 2006;1:271–279. doi: 10.2174/157488606777934431. [DOI] [PubMed] [Google Scholar]
- 6.Simpson D, Blitzer A, Brashear A, Comella C, Dubinsky R, Hallett M, Jankovic J, Karp B, Ludlow C, Miyasaki J. Assessment: Botulinum neurotoxin for the treatment of movement disorders (an evidence-based review) Report of the Therapeutics and Technology Assessment Subcommittee of the American Academy of Neurology. Neurology. 2008;70:1699–1706. doi: 10.1212/01.wnl.0000311389.26145.95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Warner SE, Sanford DA, Becker BA, Bain SD, Srinivasan S, Gross TS. Botox induced muscle paralysis rapidly degrades bone. Bone. 2006;38:257–264. doi: 10.1016/j.bone.2005.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dressler D, Eleopra R. Clinical use of non-A botulinum toxins: botulinum toxin type B. Neurotoxicity research. 2006;9:121–125. doi: 10.1007/BF03033929. [DOI] [PubMed] [Google Scholar]
- 9.Klein AW. Complications and adverse reactions with the use of botulinum toxin. Disease-A-Month. 2002;48:336–356. doi: 10.1053/mda.2001.25964. [DOI] [PubMed] [Google Scholar]
- 10.Eleopra R, Tugnoli V, Caniatti L, De Grandis D. Botulinum toxin treatment in the facial muscles of humans Evidence of an action in untreated near muscles by peripheral local diffusion. Neurology. 1996;46:1158–1160. doi: 10.1212/wnl.46.4.1158. [DOI] [PubMed] [Google Scholar]
- 11.Borodic GE, Joseph M, Fay L, Cozzolino D, Ferrante RJ. Botulinum A toxin for the treatment of spasmodic torticollis: dysphagia and regional toxin spread. Head & neck. 1990;12:392–399. doi: 10.1002/hed.2880120504. [DOI] [PubMed] [Google Scholar]
- 12.Brans J, De Boer I, Aramideh M, Speelman J, de Visser BO. Botulinum toxin in cervical dystonia: low dosage with electromyographic guidance. Journal of neurology. 1995;242:529–534. doi: 10.1007/BF00867425. [DOI] [PubMed] [Google Scholar]
- 13.Jahn R. A neuronal receptor for botulinum toxin. Science. 2006;312:540–541. doi: 10.1126/science.1127236. [DOI] [PubMed] [Google Scholar]
- 14.Lapatki B, Van Dijk J, Van de Warrenburg B, Zwarts M. Botulinum toxin has an increased effect when targeted toward the muscle’s endplate zone: a high-density surface EMG guided study. Clinical Neurophysiology. 2011;122:1611–1616. doi: 10.1016/j.clinph.2010.11.018. [DOI] [PubMed] [Google Scholar]
- 15.Guzmán-Venegas RA, Araneda OF, Silvestre RA. Differences between motor point and innervation zone locations in the biceps brachii. An exploratory consideration for the treatment of spasticity with botulinum toxin. Journal of Electromyography and Kinesiology. 2014;24:923–927. doi: 10.1016/j.jelekin.2014.07.012. [DOI] [PubMed] [Google Scholar]
- 16.Gracies JM. Pathophysiology of spastic paresis. I: Paresis and soft tissue changes. Muscle & nerve. 2005;31:535–551. doi: 10.1002/mus.20284. [DOI] [PubMed] [Google Scholar]
- 17.Abeyratne UR, Zhang G, Saratchandran P. EEG source localization: a comparative study of classical and neural network methods. International journal of neural systems. 2001;11:349–359. doi: 10.1142/S0129065701000813. [DOI] [PubMed] [Google Scholar]
- 18.Mosher JC, Spencer ME, Leahy RM, Lewis PS. Error bounds for EEG and MEG dipole source localization. Electroencephalography and clinical Neurophysiology. 1993;86:303–321. doi: 10.1016/0013-4694(93)90043-u. [DOI] [PubMed] [Google Scholar]
- 19.Hämäläinen MS, Ilmoniemi R. Interpreting magnetic fields of the brain: minimum norm estimates. Medical & biological engineering & computing. 1994;32:35–42. doi: 10.1007/BF02512476. [DOI] [PubMed] [Google Scholar]
- 20.Olson LD, Perry MS. Localization of epileptic foci using multimodality neuroimaging. International journal of neural systems. 2013;23 doi: 10.1142/S012906571230001X. [DOI] [PubMed] [Google Scholar]
- 21.Pascual-Marqui RD, Michel CM, Lehmann D. Low resolution electromagnetic tomography: a new method for localizing electrical activity in the brain. International Journal of psychophysiology. 1994;18:49–65. doi: 10.1016/0167-8760(84)90014-x. [DOI] [PubMed] [Google Scholar]
- 22.Liu K, Yu ZL, Wu W, Gu Z, Li Y. STRAPS: A Fully Data-Driven Spatio-Temporally Regularized Algorithm for M/EEG Patch Source Imaging. International Journal of Neural Systems. 2015;0 doi: 10.1142/S0129065715500161. null. [DOI] [PubMed] [Google Scholar]
- 23.Liu J, Li XY, Marciniak C, Rymer WZ, Zhou P. EXTRACTION OF NEURAL CONTROL COMMANDS USING MYOELECTRIC PATTERN RECOGNITION: A NOVEL APPLICATION IN ADULTS WITH CEREBRAL PALSY. International Journal of Neural Systems. 2014;24 doi: 10.1142/S0129065714500221. [DOI] [PubMed] [Google Scholar]
- 24.Jesinger RA, Stonick VL. Processing signals from surface electrode arrays for noninvasive 3D mapping of muscle activity. In: Sixth IEEE, editor. Digital Signal Processing Workshop, 1994. Vol. 1994. IEEE; 1994. pp. IEEE. [Google Scholar]
- 25.Van Den Doel K, Ascher UM, Pai DK. Source localization in electromyography using the inverse potential problem. Inverse Problems. 2011;27:025008. [Google Scholar]
- 26.Van Den Doel K, Ascher UM, Pai DK. Computed myography: three-dimensional reconstruction of motor functions from surface EMG data. Inverse Problems. 2008;24:065010. doi: 10.1109/IEMBS.2008.4649212. [DOI] [PubMed] [Google Scholar]
- 27.Zhang Y, Wang D, Timm GW. A three-dimensional muscle activity imaging technique for assessing pelvic muscle function. Inverse Problems. 2010;26:115018. [Google Scholar]
- 28.Wang J, Zhang Y, Zhu X, Zhou P, Liu C, Rymer WZ. A novel spatiotemporal muscle activity imaging approach based on the Extended Kalman Filter. In: IEEE, editor. Engineering in Medicine and Biology Society (EMBC), 2012 Annual International Conference. IEEE; 2012. pp. IEEE. [DOI] [PubMed] [Google Scholar]
- 29.Liu Y, Ning Y, He J, Li S, Zhou P, Zhang Y. Internal muscle activity imaging from multi-channel surface EMG recordings: A validation study. In: IEEE, editor. Engineering in Medicine and Biology Society (EMBC), 2014 36th Annual International Conference. IEEE; 2014. pp. IEEE. [DOI] [PubMed] [Google Scholar]
- 30.Ning Y, Zhu X, Zhu S, Zhang Y. Surface EMG Decomposition based on K-means clustering and Convolution Kernel Compensation. 2014 doi: 10.1109/JBHI.2014.2328497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lowery MM, Stoykov NS, Taflove A, Kuiken TA. A multiple-layer finite-element model of the surface EMG signal. Biomedical Engineering, IEEE Transactions on. 2002;49:446–454. doi: 10.1109/10.995683. [DOI] [PubMed] [Google Scholar]
- 32.Winter D, Fuglevand A, Archer S. Crosstalk in surface electromyography: theoretical and practical estimates. Journal of Electromyography and Kinesiology. 1994;4:15–26. doi: 10.1016/1050-6411(94)90023-X. [DOI] [PubMed] [Google Scholar]
- 33.Merletti R, Lo Conte L, Avignone E, Guglielminotti P. Modeling of surface myoelectric signals. I. Model implementation. Biomedical Engineering, IEEE Transactions on. 1999;46:810–820. doi: 10.1109/10.771190. [DOI] [PubMed] [Google Scholar]
- 34.Dumitru D. Physiologic basis of potentials recorded in electromyography. Muscle & nerve. 2000;23:1667–1685. doi: 10.1002/1097-4598(200011)23:11<1667::aid-mus2>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- 35.Nandedkar S. Simulation of single muscle fibre action potentials. Medical and Biological Engineering and Computing. 1983;21:158–165. doi: 10.1007/BF02441531. [DOI] [PubMed] [Google Scholar]
- 36.Zhang Y, van Drongelen W, Kohrman M, He B. Three-dimensional brain current source reconstruction from intra-cranial ECoG recordings. NeuroImage. 2008;42:683–695. doi: 10.1016/j.neuroimage.2008.04.263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhang Y, Ding L, van Drongelen W, Hecox K, Frim DM, He B. A cortical potential imaging study from simultaneous extra-and intracranial electrical recordings by means of the finite element method. NeuroImage. 2006;31:1513–1524. doi: 10.1016/j.neuroimage.2006.02.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zhang Y, Zhu S, He B. A second-order finite element algorithm for solving the three-dimensional EEG forward problem. Physics in Medicine and Biology. 2004;49:2975. doi: 10.1088/0031-9155/49/13/014. [DOI] [PubMed] [Google Scholar]
- 39.Liu AK, Belliveau JW, Dale AM. Spatiotemporal imaging of human brain activity using functional MRI constrained magnetoencephalography data: Monte Carlo simulations. Proceedings of the National Academy of Sciences. 1998;95:8945–8950. doi: 10.1073/pnas.95.15.8945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Grech R, Cassar T, Muscat J, Camilleri KP, Fabri SG, Zervakis M, Xanthopoulos P, Sakkalis V, Vanrumste B. Review on solving the inverse problem in EEG source analysis. Journal of neuroengineering and rehabilitation. 2008;5:25. doi: 10.1186/1743-0003-5-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Liu AK, Dale AM, Belliveau JW. Monte Carlo simulation studies of EEG and MEG localization accuracy. Human brain mapping. 2002;16:47–62. doi: 10.1002/hbm.10024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hansen PC. Analysis of discrete ill-posed problems by means of the L-curve. SIAM review. 1992;34:561–580. [Google Scholar]
- 43.Buchthal F, Sten – Knudsen O. Impulse propagation in striated muscle fibers and the role of the internal currents in activation. Annals of the New York Academy of Sciences. 1959;81:422–445. doi: 10.1111/j.1749-6632.1959.tb49325.x. [DOI] [PubMed] [Google Scholar]
- 44.Blok J, Van Dijk J, Drost G, Zwarts M, Stegeman D. A high-density multichannel surface electromyography system for the characterization of single motor units. Review of scientific instruments. 2002;73:1887–1897. [Google Scholar]
- 45.Merletti R, Holobar A, Farina D. Analysis of motor units with high-density surface electromyography. Journal of electromyography and kinesiology. 2008;18:879–890. doi: 10.1016/j.jelekin.2008.09.002. [DOI] [PubMed] [Google Scholar]
- 46.Phinyomark A, Phukpattaranont P, Limsakul C. Fractal analysis features for weak and single-channel upper-limb EMG signals. Expert Systems with Applications. 2012;39:11156–11163. [Google Scholar]
- 47.Bonato P, D’Alessio T, Knaflitz M. A statistical method for the measurement of muscle activation intervals from surface myoelectric signal during gait. Biomedical Engineering, IEEE Transactions on. 1998;45:287–299. doi: 10.1109/10.661154. [DOI] [PubMed] [Google Scholar]
- 48.Zhang X, Zhou P. Filtering of surface EMG using ensemble empirical mode decomposition. Medical engineering & physics. 2013;35:537–542. doi: 10.1016/j.medengphy.2012.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]


