Skip to main content
PMC home page
The ISME Journal logoLink to The ISME Journal
. 2017 Apr 4;11(7):1559–1568. doi: 10.1038/ismej.2017.35

The evolution of bacterial cell size: the internal diffusion-constraint hypothesis

Romain Gallet 1,2,5,*, Cyrille Violle 1,5, Nathalie Fromin 1, Roula Jabbour-Zahab 1, Brian J Enquist 3,4, Thomas Lenormand 1
PMCID: PMC5520153  PMID: 28375214

Abstract

Size is one of the most important biological traits influencing organismal ecology and evolution. However, we know little about the drivers of body size evolution in unicellulars. A long-term evolution experiment (Lenski’s LTEE) in which Escherichia coli adapts to a simple glucose medium has shown that not only the growth rate and the fitness of the bacterium increase over time but also its cell size. This increase in size contradicts prominent ‘external diffusion’ theory (EDC) predicting that cell size should have evolved toward smaller cells. Among several scenarios, we propose and test an alternative ‘internal diffusion-constraint’ (IDC) hypothesis for cell size evolution. A change in cell volume affects metabolite concentrations in the cytoplasm. The IDC states that a higher metabolism can be achieved by a reduction in the molecular traffic time inside of the cell, by increasing its volume. To test this hypothesis, we studied a population from the LTEE. We show that bigger cells with greater growth and CO2 production rates and lower mass-to-volume ratio were selected over time in the LTEE. These results are consistent with the IDC hypothesis. This novel hypothesis offers a promising approach for understanding the evolutionary constraints on cell size.

Introduction

Constraints on evolution can have multiple causes, ranging from specific developmental mechanisms (Maynard-Smith et al., 1985; Brakefield, 2006) to broad biophysical processes (Haldane, 1926; LaBarbera, 1990; Barton and Partridge, 2000). The impact of biophysical constraints on evolution is particularly intriguing as they can shape the phenotypic diversity of life at very broad taxonomic scales, as shown in prominent ecological theories linking morphology and metabolism in metazoans (West et al., 1997, 1999; Enquist et al., 1999). Basic physical traits such as the mass and size of an organism play an important role in these theories. They influence how most biological structures, processes and dynamics covary with each other (Peters, 1983). Here, we focus on the evolution of size in the bacteria Escherichia coli and on how the interplay of different biophysical constraints can drive its evolutionary trajectory.

Studying the allometric scaling between traits across species provides helpful information regarding the origin of biophysical constraint and their impact on the diversification of phenotypes (Enquist et al., 2007). The dependence of a given biological trait, Y, on organismal size, M, is known as allometry. Allometric relationships are often characterized by power laws of the form, Y=Y0Mb, where b is the scaling exponent and Y0 is a normalization constant that may be characteristic of a given taxon (Moses et al., 2008). Identifying allometric relationships has been key to elucidate the evolution of body size across the tree of life (Okie et al., 2013). One of the most debated allometric relationships is between metabolic rate, B, and body size, M. For example, if the scaling of metabolic rate is governed by b<1, increases in size would then decrease the mass-specific metabolism where B/M~M1−b. In many organisms, nutrients cannot simply diffuse through the body, there are some constraints limiting the diffusion and transport of nutrients. Metabolic Scaling Theory hypothesizes that the origin of the allometric exponent b results from selection to maximize resource delivery rates which is constrained by diffusion and transport constraints across hierarchical vascular networks (West et al., 1997, 1999). An open question is if Metabolic Scaling Theory can (i) apply to small, non-vascularized organisms like prokaryotes; and (ii) shed light on the evolution of size in unicellulars.

DeLong et al. (2010) highlighted that metabolic rates and growth rate (Kempes et al., 2012; Kirchman, 2015) appear to have strongly covaried with cell size across prokaryote evolution, but the cause of why these scaling relationships appear to have varied have remained elusive. Two biophysical hypotheses for cell size evolution in bacteria were advanced. First, the ‘external diffusion constraints’ (EDC) hypothesis states that metabolic rates are limited by the rate of nutrient diffusion from the environment to the organism’s body. To increase this diffusion rate, selection will act primarily via changes in the cellular surface-to-volume ratio or cell size (Koch, 1996; Schulz and Jorgensen, 2001; Young, 2006). The growth rate is often limited by the metabolic rate. Hence, higher metabolic rates are expected to be favored by natural selection whenever ecological conditions favors fast growth and fast resource depletion. If the diffusion of nutrients from the environment to the cell is the limiting step (EDC), then a bigger exchange surface (per unit volume of cytosol, that is, a higher surface-to-volume ratio) should be selected. Long-term evolution experiments (LTEEs) performed on microorganisms under various conditions indeed observed an increase in the growth rate associated with a reduction of cell size, resulting in a higher surface-to-volume ratio (Spor et al., 2014; Gounand et al., 2016). Second, the ‘genome size’ hypothesis assumes (1) that bigger cells are required to pack more DNA and (2) that more DNA correlates with higher metabolic or division rates. To explain (2), Delong et al. (2010) hypothesize that bacteria with bigger genomes have more genes and thus supposedly larger biochemical networks, enabling the organism to metabolize a greater diversity of substrates. Another possibility to explain (2) is that the growth rate could be transcription limited. In that case, increasing the number of copies of the genome could favor a higher growth rate. Finally, (2) might occur because cell division rate might increase in cells with active replication forks and during times of DNA replication (Weart et al., 2007).

In their LTEE, Lenski et al. (1991) and Lenski (2001) cultivated E. coli populations for more than 60 000 generations in a simple glucose medium. Along with an increase in fitness and growth rate, a spectacular evolutionary increase in cell size was observed (Lenski and Travisano, 1994). Compared with the ancestral strain, evolved populations were composed of bigger but fewer cells, showing an overall higher total biomass (Vasi et al., 1994). Contrary to the EDC hypothesis, a lower surface-to-volume ratio was selected for. Contrary to the ‘genome size’ hypothesis, changes in cell volume in the LTEE were not accompanied by any substantial change in the genome size or composition (Barrick et al., 2009). Whether bigger cells from the LTEE contained more copies of the genome was not investigated at that time. The difficulty of explaining the evolution of cell size in the longest ongoing evolutionary experiment can be due to: (i) a focus on the evolution of cell volume whereas selection applies on several—probably interacting—traits (for example, cell mass, cell volume, molecular traffic time in the cell); (ii) unidentified constraints acting upon these traits, and (iii) the interplay of different, sometimes opposing, biophysical constraints.

Diffusion time is considered a pivotal constraint that governs the evolution of body size in metazoans. In this paper, we recast theoretical predictions regarding the evolution of cell size and mass in bacteria, introducing inside-to-the-cell diffusion constraints. Based on these predictions, we tested which combinations of biophysical and ecophysiological constraints are at play by specifically tracking the concomitant evolutionary change in per-capita dry mass and volume in one population from the LTEE, sampled at seven time points (between 0 and 40 000 generations). We re-measured relative fitness, maximum growth rate and cell volume (previously measured by Lenski et al.) and measured additional size-related traits (dry mass, dry mass-to-volume ratio, DNA content per cell and volume-to-DNA content ratio) as well as metabolic rates (per-capita CO2 production rate and energetic efficiency). These results are consistent with the internal diffusion constraint (IDC), highlighting that specific biophysical constraints may impact the evolution of cell size in unicellulars.

Materials and methods

Bacterial strains and medium

The E. coli strains REL606, REL1164A, REL2179A, REL4536A, REL7177A, REL8593A and REL10938A used in this study correspond to clones from a single population (Ara-1) in Lenski’s E. coli LTEE (Lenski et al., 1991) sampled at generation 0, 2000, 5000, 10 000, 15 000, 20 000, 40 000 respectively. In order to perform fitness measures, we introduced the cyan fluorescent protein marker (and yellow fluorescent protein for the ancestral strain REL606) at the RhaA locus in each of these seven strains as detailed in Gallet et al. (2012).

All cultures were performed in DM250, that is, Davis minimal medium supplemented with 250 μg ml−1 glucose (7 g K2HPO4, 2 g KH2PO4, 1 g ammonium sulfate, 0.5 g sodium citrate; qsp 1000 ml H2O; pH was adjusted to 7.0 with HCl as necessary, 806 μl of MgSO42− (1m), 1 ml of Thiamine 0.2% and 1.25 ml of glucose 20% were added after autoclaving). DM250 is equivalent to DM25 used by Lenski et al. (1991), but with 10 times more glucose. DM250 was used to increase cell density in the cultures, in order to perform the following measurements with more precision. LB agar plates (10 g tryptone, 5 g yeast extract, 10 g NaCl and 15 g agar per liter of H2O) were used for cell concentration estimation.

Growth rate measurement

In the morning, for each of the seven strains, a colony was inoculated in a 50-ml Falcon tube containing 5 ml of DM250 and incubated at 37 °C with 200 r.p.m. agitation. In the late afternoon, 2 microliters of each culture was inoculated independently in one of the 60 wells at the center of a black 96-well plate (96F—not treated—Nunc), filled with 200 μl of DM250 (four to nine replicated wells/strain/plate). The 96-well plate was incubated at 37 °C in a TECAN Infinite 200 microtiter plate reader (Tecan, Männedorf, Switzerland), and fluorescence measured every 15 min. Maximal growth rate (rmax) were obtained by fitting growth curves with the R grofit package. The whole experiment was replicated three times independently. Our measures of relative rmax were well correlated (r=0.94) to those performed on the 12 populations of the LTEE and reported in Cooper et al. (2001).

Relative fitness measures

The relative fitness of each mutant was estimated by measuring the change in its relative frequency in competition experiments against the ancestor. After an overnight pre-culture, competitions were performed in at least eight independent replicated wells in a 96-well microtiter plate in DM250 at 37 °C. The relative frequency of each competitor was estimated by measuring both cyan fluorescent protein and yellow fluorescent protein fluorescence at the beginning and the end of the assay. For an extended description of this fitness measure, see the Electronic Supplementary Material.

Cell volume measurement

Cell size was estimated by flow cytometry. All strains were first grown overnight in DM250 at 37 °C under 240  r.p.m. The next day, 50 μl of each culture were used to inoculate 5 ml of DM250 in 50 ml falcon tubes. After 4 h incubation at 37 °C under 240 r.p.m., 950 μl of each culture were taken and mixed to 55 μl of formaldehyde 36% (final concentration=2%). The volume of fixed cells was then estimated by their forward scatter (Volkmer and Heinemann, 2011) using a Gallios Beckman Coulter flow cytometer (Brea, CA, USA). In order to minimize potential skewing effects, the mode of forward scatter distributions was used as a descriptive measure of these distributions. The experiment was repeated six times independently. We converted forward scatter values to cell volumes by using three calibration polystyrene beads of volumes: 0.06, 4.19 and 20.6 μm3.

Cell DNA content measurement

The DNA content of individual cells was measured by flow cytometry. Cells in the exponential phase were fixed with ethanol (75% final concentration) and stained with propidium iodide. The average fluorescence of 10 000 single cells was measured. Cell size was also measured concomitantly in order to estimate the volume-to-DNA content ratio. Bacterial cells fixation and staining could have affected the estimation of cell size, compared with the previous estimation of this parameter. Supplementary Figure S1 shows that cell size measurements are strongly correlated.

Cell mass measurement

All strains were grown overnight in 1 l Erlenmeyer flasks containing 110 ml of DM250 at 37 °C under 240 r.p.m. agitation. A hundred milliliter of each culture were placed in two 50-ml Falcon tubes and centrifuged for 25 min at 7830 r.p.m. in an Eppendorf 5430R centrifuge (Hauppauge, NY, USA) at 7 °C. Pellets were re-suspended and placed in 1.5 ml microtubes for an extra centrifugation at 14 680  r.p.m. for 1 min in an Eppendorf 5424 centrifuge. Finally, pellets were re-suspended again in DM250, placed in 10.5 × 9 mm pressed tin capsules (Elemental Microanalysis D1104) and let to dry for at least 48 h at 70 °C. Tin capsules were weighed before and after adding the pellet on a Sartorius MC5 microbalance (1 μg readability). Dried pellet weights (total population biomass) corresponded to our measure of energetic efficiency, that is, the efficiency at which nutrients were converted into biomass. To estimate cell weight, dried pellet weights were divided by the cell number in 100 ml of cultures, which was estimated by optical density (OD) measurement (ODs were converted into cell number with standard curves—one standard curve per strain). The whole experiment was repeated three times independently. An independent experiment was run in order to estimate the number of cells per OD unit in DM250 for each strain (seven independent replicates per strain).

CO2 production rate measurement

The per-capita CO2 production rate (metabolic rate) was also estimated in this experiment. Bacteria were grown overnight in 50 ml Falcon tubes containing 5 ml DM250. The next day, ODs of all seven cultures were measured and 200 μl of each were inoculated in three independent sealed 150 ml plasma flasks containing 20 ml DM250 and closed by a cap. The flasks were incubated in a water bath at 37 °C. Air samples from the headspace of each flask were analyzed after 1 and 3 h incubation to quantify CO2 concentration with a gas chromatograph using a catharometer (VARIAN GC 4900; Walnut Creek, CA, USA). OD was measured just after CO2 measurements to ultimately assess the final number of cells for each sample. The amount of CO2 released during this time allowed calculating CO2 production rate per unit of OD, then per cell, expressed in mol CO2 per cell per second.

Statistical analyses

All analyses were conducted in R (http://www.r-project.org). We analyzed scaling relationships between size-related traits and metabolic rates using log–log relationships to make them comparable with previously reported relationships (DeLong et al., 2010) and more broadly, to infer metabolic hypotheses about the slope of these relationships (West et al., 1997, 2002). Standardized major axis regressions were performed with the R smatr package (Warton et al., 2006, 2012).

Recasting hypotheses for the evolution of bacterial cell size

Let us consider the scaling of metabolic rate M in a bacteria cell of size z. Let us consider that the metabolic rate is limited by glucose processing. We have

graphic file with name ismej201735e1.jpg

Indeed, this rate M has to be proportional to the number of glucose molecules that get in. This uptake can scale or not with the cell surface, depending on the mechanism. If it depends on transporters and if increasing the number of these transporters can be done without increasing cell surface, it is simply proportional to the number of transporters and independent of cell size. If on the contrary, it is necessary to increase cell surface to pack more transporters, or if only diffusion matters, then the uptake is proportional to the surface z2 times a constant c1 (uptake efficiency per unit surface), which provides a mechanism by which increased cell size could be favored. Since, we aim at explaining how larger cells could be favored, we follow the reasoning with this best-case scenario. Then, the rate M must depend on the number of metabolic effectors E that can process glucose (with a constant c2 measuring enzymatic efficiency), times the rate of ‘encounter’ between glucose and effectors. We ignore here the time to produce and maintain these effectors as well as the nutrient uptake necessary to produce them, which is justified since the half-life of those enzymes is much longer than half-life of glucose. The rate of encounter between glucose and effectors can be measured by the inverse of travel time T of the glucose molecule to the enzyme. This travel time depends on the distance that needs to be traveled between the membrane and the effector that will process it. This distance necessarily scales with cell size z: all distances increase in a larger cell. For instance, the mean distance to the membrane of effectors uniformly spread in a spherical cell of radius z is z/4. The mean distance between E uniformly spread effectors is proportional to (z3/E)1/3=zE−1/3. Hence, we note this distance fz, where f represents a size-independent variable that depends on the number and repartition of effectors. As long established (for example, Edelstein-Keshet, 1989), the distance traveled by a diffusive particle scales with the square root of time times a constant c3 (that depends on the diffusion coefficient and the dimensionality), we thus have

graphic file with name ismej201735e2.jpg

Hence metabolic rate is simply

graphic file with name ismej201735e3.jpg

where C is size independent and equal to c1c2c3/f2. Note however that f may include power of E since travel time in the cytosol is likely to decrease with the number of effectors, so that the overall power of E in Equation (3) may be larger than one. This equation indicates that the metabolic rate does not directly depend on cell size since the increased input of glucose that increases with surface (size squared) is offset by the travel time of glucose which is also increasing with the square of size. This is the best-case scenario. When more glucose transporters can be added without the requirement of a larger cell surface, this rate would scale with the inverse of cell surface.

Hence, in the best-case scenario, increased M can be either achieved by a larger constant C or by increasing the number of effectors E, which is expected to increase weight. If there is a cost to build and maintain the membrane (pores, membrane transporters, etc.), it must increase with the surface of the membrane and hence the square of size. As a consequence, without considering variation in C, the expectation is that selection pressures to increase metabolic rates and/or the growth rate would consist in decreasing size (to reduce costs related to the membrane, while achieving the same metabolic rates) and increasing weight (that is, E, the number of effectors), until the marginal fitness benefit of increasing the number of effectors for increased metabolism, becomes equal to the fitness cost of production of new effector, or some spatial limit is reached to simply pack all essential molecules within the cell. There are two broad possible hypotheses to reverse this conclusion and expect an increase in cell size to increase metabolic rate: (1) the space limitation and (2) the IDC scenarios.

The space limitation scenario

Under this scenario, metabolism is limited by the number of effectors. Here, bigger cells would evolve to fit those effectors and the machinery required to produce and maintain them. When transcription is the limiting step, the best way to increase the production of effectors is to increase the number of the copies of the genome. Many bacteria are known to have multiple copies of their chromosomes in the exponential phase, making this hypothesis plausible. Here, cell size would evolve, simply because it is necessary to increase cell size to fit those extra chromosome copies within the cell. These different possibilities all directly assume 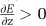Inline graphic and we expect that metabolism increases with cell size.

graphic file with name ismej201735e4.jpg

A consequence of having more metabolic effectors and possibly more DNA is that the mass of the cell should increase as well. Thus, a tight and positive relationship between DNA content, cell volume, cell mass and metabolic rates should be observed. However, DNA content and/or cell weight should increase first in the LTEE and later (or at best concomitantly) cause an adjustment of cell size to maintain a nearly constant mass/volume or DNA content/volume ratio.

The IDC Scenario 1: molecular crowding

Reducing size and/or increasing the number of effectors may also change the physical properties of the cytosol. Increased macromolecular crowding in the cytosol (scaling as E/volume) is known to increase within-cell traffic times (Ellis, 2001; Schulz and Jorgensen, 2001; Golding and Cox, 2006; Ando and Skolnick, 2010). As a first order approximation, let us assume that the glucose diffusion coefficient is linearly varying with E/z3, with a slope c4. Metabolic rates are now becoming dependent on size:

graphic file with name ismej201735e5.jpg

Hence, as long as glucose diffusion coefficient decreases when cytosol concentration (that is, macromolecular crowding) increases (that is, c4<0), metabolic rates are expected to increase with cell size. Diffusion coefficient of small molecules like glucose may not be strongly impacted by macromolecular crowding compared with larger ones (Verkman, 2002). However, the same effect would occur if the metabolic rate is limited by diffusion of macromolecules (RNA, proteins). Overall, in this scenario, the mass-to-volume ratio is expected to decrease through time in the LTEE.

The IDC Scenario 2: cell shape

Glucose travel time can also be altered for other reasons than variation in the diffusion coefficient of glucose. In particular, glucose travel time in the cytosol can also be reduced if metabolic effectors are found closer to the membrane (that is, E(f) becomes smaller), everything else being constant. This might be achieved if, for instance, cell shape varies. Consider that the cell shape is an ellipsoid elongated in one direction, with semi-axes length being (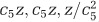Inline graphic), so that it has the same volume as a sphere of radius z. If c5=1, we have a sphere and the average distance of uniformly distributed effectors to the membrane is 0.25, as mentioned above. If c5<1, the cell becomes elongated, and this average distance decreases. For instance, with c5=0.8, such that the cell is twice as long in the elongated direction, this average distance is 0.227. Hence, elongating the cell geometrically reduces the average distance of effectors to the membrane, but this effect is independent of cell size. This scenario would predict more elongated cells, but not necessarily cells with larger volumes, and is therefore not likely to explain increased cell size in the LTEE.

The IDC Scenario 3: cell compartmentalization

Another possibility to increase metabolic rate might be that enzymes can be better packed and immobilized close to the membrane, which would reduce travel distance to effectors, everything else being constant. Here again, the effect is likely to be independent of cell size. However, this ‘compartmentalization’ of effectors closer to membranes might be easier to achieve in a larger, spatially less constrained, cell. For the same reason, micro-compartmentalization and metabolic channeling (Welch and Easterby, 1994; Beg et al., 2007) might be easier to achieve in a larger cell. In both cases, we would have 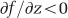Inline graphic and

graphic file with name ismej201735e6.jpg

In this scenario too, there might be a selection pressure to increase cell size in order to achieve a higher metabolic rate. Here, the weight-to-volume ratio is expected to decrease in the LTEE, and if observable, effectors should tend to occur closer to membranes in larger cells.

Results

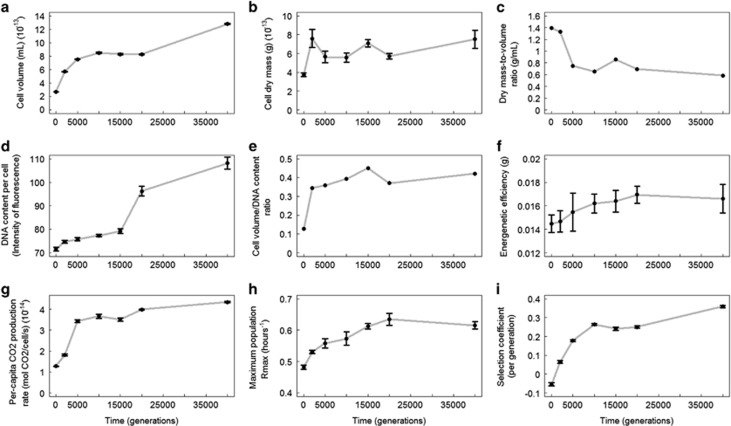
We found an increase in cell volume, cell dry mass, total population biomass, DNA content, volume-to-DNA content ratio, relative fitness, growth rate, per-capita CO2 production rate over the 40 000 generations of the experiment (Figure 1). They increased steadily through time (except for the volume-to-DNA content ratio which started to increase and then stayed relatively constant), with an acceleration between generation 20 000 and 40 000 for cell volume, DNA content and relative fitness. Meanwhile, the cell dry mass-to-volume ratio decreased over time. Growth rate, per-capita CO2 production rate, total population biomass, DNA content and cell volume were positively correlated to fitness while the cell dry mass-to-volume ratio was negatively correlated (Table 1). Cell dry mass increased less consistently than the other measured traits (Figure 1b) and was not correlated to fitness (Table 1).

Figure 1.

Figure 1

Open in a new tab

Trajectories of size-related (a–e), metabolic rates (f, g), maximum population growth rate (rmax) (h) and selection coefficient (i) of the Ara-1 population in the LTEE. Each dot represents mean values (±s.e., when applicable).

Table 1. Matrix of correlations among traits.

  Fitness Growth rate Respiration rate Cell mass Cell volume Mass-to-volume ratio DNA content Volume-to-DNA content ratio Total biomass
Fitness   0.90* 0.97*** 0.54NS 0.96*** −0.94* 0.93* 0.029NS 0.87NS
Growth rate     0.91* 0.52NS 0.82NS −0.83* 0.92* −0.088NS 0.98***
Respiration rate       0.39NS 0.91* −0.98*** 0.88* −0.04NS 0.89*
Cell mass         0.63NS −0.26NS 0.58NS 0.59NS 0.40NS
Cell volume           −0.86NS 0.91* −0.019NS 0.80NS
Mass-to-volume ratio             −0.80NS 0.098NS −0.81NS
DNA content               −0.036NS 0.89*
Volume-to-DNA content ratio                 −0.11NS
Total biomass                  
Open in a new tab

Pearson’s coefficient correlation; NS=not significant; *P<0.01; **P<0.001; ***P<0.0001.

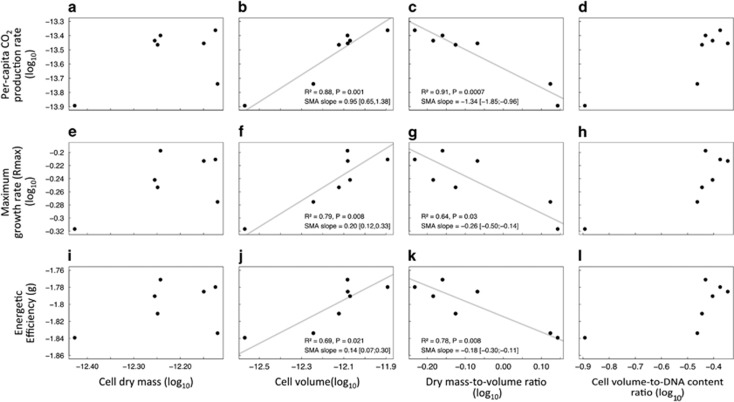
Next, we analyzed scaling relationships between size-related traits and metabolic rates. We found no scaling relationship between per-capita CO2 production rate and cell dry mass (Figure 2a) or per-capita CO2 production rate and cell volume-to-DNA content ratio (Figure 2d). Conversely, we found a significant scaling relationship between per-capita CO2 production rate and cell volume with a scaling slope not different from 1 (Figure 2b). The per-capita CO2 production rate also scaled negatively with the mass-to-volume ratio (Figure 2c). We obtained similar trends with the scaling of maximum population growth rate (rmax; Figures 2e–h) and energetic efficiency (total biomass; Figures 2i–l).

Figure 2.

Figure 2

Open in a new tab

Scaling allometry relationships: size-related traits against CO2 production rate (a–d), maximum population growth rate (rmax) (e–h) and energetic efficiency (i–l). Standardized major axis regressions, appropriated to the analysis of scaling relationships (Warton et al., 2006, 2012), are shown when significant (gray lines). Variables were log-transformed for the study of allometric relationships (see Figure 1 for non-transformed values and unit information).

Discussion

To understand which constraints are directing the evolution of cell size, we tracked the evolution of several key biological traits in the LTEE. These included dry mass, per-capita dry mass-to-volume ratio, total population biomass, DNA content, volume-to-DNA content ratio and CO2 production rate traits that have not been explored previously in the LTEE or other experiments (Hindré et al., 2012). This multi-trait approach allowed us to test our qualitative predictions about the biophysical and ecophysiological constraints that act on the evolutionary trajectory of cell size.

An increase in cell volume, growth rate and relative fitness were previously observed in the LTEE (Lenski and Travisano, 1994; Wiser et al., 2013). Our results confirmed these observations. The fact that growth rate and cell volume were positively correlated to fitness also corroborates previous results showing that both traits are under selection in this experiment (Lenski and Travisano, 1994; Mongold and Lenski, 1996). We attribute the acceleration in the increase of cell size and fitness to the occurrence of a mutator phenotype at generation 26 500 in this population (Wiser et al., 2013). In addition, here we revealed a striking increase in the per-capita CO2 production rate, energetic efficiency, cell mass, DNA content and volume-to-DNA ratio and decrease in cell mass-to-volume ratio over the course of the LTEE. Interestingly, CO2 production rate, energetic efficiency, DNA content, volume-to-DNA content ratio and mass-to-volume ratio were highly correlated to fitness whereas cell mass was not (Table 1).

The selection of a higher growth rate during the LTEE was probably due to the fact that the E. coli strain REL606 had to adapt from a lifestyle where it had to survived in stab cultures, to a new lifestyle where it was competing for glucose in a liquid culture medium (Daegelen et al., 2009). In other words, this bacterial strain had to adapt to a new environment in which growth rate and fast resource consumption was under selection. Investigating scaling relationships between size-related traits and metabolic rates can provide insights into the biophysical and ecophysiological constraints that act on phenotypes (Enquist et al., 2007; Glazier, 2010) and more broadly on the mechanisms that regulate body size evolution (Kempes et al., 2012; Okie et al., 2013). Here, such analysis could help understand why cell size, metabolic rates and fitness correlate positively. Our analyses of metabolic scaling relationships in the LTEE highlighted a volume-based, rather than a mass-based (DeLong et al., 2010), scaling for whole-cell metabolism (cell mass was seldom assessed in previous studies since a dry mass-to-volume ratio of one was systematically used to convert volume to dry mass (DeLong et al., 2010)). However, our results indicate that this assumption is not upheld in the E. coli. We used these metabolic scaling relationships to explore two alternatives, the space limitation and the IDC scenarios.

Under the space limitation scenario, space is the only factor limiting metabolic rates. Thus, if an increase in cell mass (more effectors) and/or DNA content is necessary to reach higher metabolic rates, cell volume should increase accordingly and the mass/volume and/or DNA/volume ratio stay nearly constant. Table 1 shows that cell mass does not correlate significantly with cell volume or metabolic rates which discard the hypothesis that cell size increased to only fit more effectors. However, Table 1 also shows significant positive correlations between DNA content, cell size and metabolic rates (Table 1), which could indicate that the DNA content actually drove the increase in metabolic rates and cell size. Nevertheless, the evolutionary trajectory of the volume-to-DNA content ratio contradicts this conclusion. It shows that between generation 0 and 2000, that is, when the fitness increase was the most important, the volume of the cell increased three times faster than the DNA content. In other words, cell size did not only increase to fit more DNA, but for a different reason. Thus, the space limitation scenario (for DNA or effectors) is not sufficient to explain the increase in cell size that we observe. Overall, while the EDC and the space limitation scenarios seem to be good predictors of cell size of unicellular organisms at the interspecific level (DeLong et al., 2010), our data show that these theories cannot fully explain the evolution of cell size in the LTEE.

As expected under the IDC scenario, we found that cell volume (× 4.76 after 40 000 generations) increased faster than cell mass (× 2.25), indicating that cell volume has not evolved simply to compensate the increase in cell mass. This shift of the cell mass-to-volume ratio scaled with all metabolic rates (CO2 production rate, growth rate and metabolic efficiency) and fitness, suggesting that it was adaptive. This shift—in complete accordance with the predictions given by the IDC—occurred between generation 0 and 10 000, when the fitness and metabolic rates showed the highest increase. Everything else being equal, such a change in the dry mass-to-volume ratio could result in reduced macromolecular crowding in the cytosol (as the cell volume increased faster than the mass, see Equation (5)) or a better packing of metabolic effectors near membranes (as the membrane surface also increased faster than the mass, see Equation (6)). In both cases, such a change would shorten metabolite traffic time and hence increase metabolism and fitness (Beveridge, 1988; Koch, 1996; Schulz and Jorgensen, 2001; Golding and Cox, 2006; Young, 2006; Beg et al., 2007; Ando and Skolnick, 2010; Dill et al., 2011). Thus, we interpret the strong increase in cell volume in the LTEE as resulting from internal diffusion constraints. Under the IDC hypothesis, cell volume would increase to (1) fit more effectors in the cell and (2) to reduce the dry mass-to-volume ratio (by a factor 2.11); two requirements to achieve higher metabolic rates. Selection would favor bigger cells, as packing more effectors than small ones would enable cells to better exploit and deplete glucose. As a result, the cell lag phase would then be reduced. In addition, such cells would have less concentrated cytoplasm allowing faster chemical reactions and higher metabolic efficiency. Further exploration of this idea would require fine-scale within-cell metabolic measures. Studying cell shape variation could also be worth investigating in the light of the theory outlined in this paper. In any case, our findings point to the importance of other physical constraints, rather than the usual constraints based on cell geometry associated with variation in the surface-to-volume ratio. Internal diffusion constraints may be particularly important when selection applies on growth rate, that is, when metabolic rates are important.

Our findings illustrate the combined importance of biophysical and ecophysiological constraints to understand the evolution of morphology (Lynch et al., 2014, and our Figure 3), in addition to the more classical evo-devo constraints (Brakefield, 2006). Biophysical constraints related to allometric relationships are often considered as ‘universal’ constraints in interspecific comparative biology (Enquist et al., 1999; West et al., 1997, 1999, 2002). They also seem to play a key role in the evolution of traits at the intraspecific level, as theoretically envisioned (Shoval et al., 2012). Finally, our findings opens the intriguing possibility that, while body size of metazoans appears mostly constrained by external diffusion in allometry theories (Damuth, 2001; Brown et al., 2004; DeLong et al., 2010; Glazier, 2010), cell size of microbes (bacteria, fungi, algae, etc.) would be constrained in a different way, by a combination of internal and external diffusion constraints. Such a difference is perhaps not entirely unexpected: in metazoans, each cell type has its optimal shape and size to perform a specific function, and increasing body size primarily requires increasing the number of cells. Therefore, the metabolism of metazoans is mostly limited by EDC, and the intensity of this constraint is proportional to the number of cells and vascularization. In unicellular organisms, where body size is the same as cell size, the metabolism is limited by EDC and IDC the effects of which are opposite on cell size. The balance between these two biophysical constraints may differ according to the ecology of the organism, or whether growth rate is under selection or not. Biophysical constraints may also vary between prokaryote and eukaryote unicellulars, since the latter have compartmentalized cytoplasms where reactions are likely to be less dependent on diffusion time in the cytosol. This theory may thus help to explain the differences observed for metabolic scaling with size in these different unicellular organisms (DeLong et al., 2010), which opens a wide range of possible empirical tests.

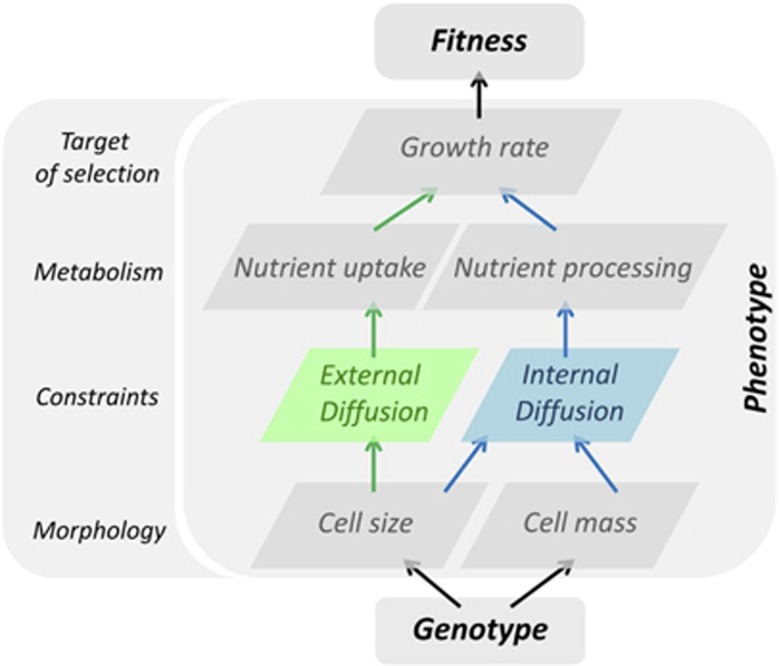
Figure 3.

Figure 3

Open in a new tab

The role of biophysical constraints in the genotype to phenotype to fitness map. Sketch of the cascading effects on metabolism, growth rate and fitness of modification of cell morphology (size, mass). First, cell size modification changes the surface-to-volume ratio and, hence, nutrient uptake (green arrows). This is the consequence of a physical constraint caused by diffusion from/to the external environment. Second, both cell size and cell mass change cell density (blue arrows) and hence internal density that impacts the rate of nutrient processing (internal diffusion constraint due to inner molecular crowding). Both nutrient uptake and processing impact growth rate and fitness.

Acknowledgments

We thank RE Lenski and D Schneider for sharing strains, RE Lenski, J DeLong and T Hindré and the anonymous reviewers for insightful comments on the manuscript and Hervé Isambert for insightful discussions. We thank Bruno Buatois for technical assistance and Marie Pierre Dubois for lab management (UMR 5175 CEFE, Campus CNRS). The CO2 production analysis was performed at the Plateforme d’Analyses Chimiques en Ecologie technical facilities of the LabEx Centre Méditerranéen de l'Environnement et de la Biodiversité. Microbiological experiments were performed at the Service des Marqueurs Génétiques en Ecologie, CEFE. We thank Christophe Duperray for technical assistance on flow cytometry measurements performed at the RIO imaging platform of Montpellier—Institut de Recheche en Biothérapie. BJE was supported by a NSF Macrosystems award EF- 1065861. CV was supported by a Marie Curie International Outgoing Fellowship within the Seventh European Community Framework Program (DiversiTraits project, no. 221060) and by the European Research Council (ERC) Starting Grant Project ‘Ecophysiological and biophysical constraints on domestication in crop plants’ (Grant ERC-StG-2014-639706-CONSTRAINTS). RG and TL were supported by the QuantEvol ERC grant.

Footnotes

Supplementary Information accompanies this paper on The ISME Journal website (http://www.nature.com/ismej)

The authors declare no conflict of interest.

Supplementary Material

Supplementary Information
Click here for additional data file. (30.6KB, docx)

References

  1. Ando T, Skolnick J. (2010). Crowding and hydrodynamic interactions likely dominate in vivo macromolecular motion. Proc Natl Acad Sci USA 107: 18457–18462. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Barrick JE, Yu DS, Yoon SH, Jeong H, Oh TK, Schneider D et al. (2009). Genome evolution and adaptation in a long-term experiment with Escherichia coli. Nature 461: 1243–1247. [DOI] [PubMed] [Google Scholar]
  3. Barton N, Partridge L. (2000). Limits to natural selection. BioEssays 22: 1075–1084. [DOI] [PubMed] [Google Scholar]
  4. Beg QK, Vazquez A, Ernst J, de Menezes MA, Bar-Joseph Z, Barabási A-L et al. (2007). Intracellular crowding defines the mode and sequence of substrate uptake by Escherichia coli and constrains its metabolic activity. Proc Natl Acad Sci USA 104: 12663–12668. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Beveridge T. (1988). The bacterial surface: general considerations towards design and function. Can J Microbiol 34: 363–372. [DOI] [PubMed] [Google Scholar]
  6. Brakefield PM. (2006). Evo-devo and constraints on selection. Trends Ecol Evol 21: 362–368. [DOI] [PubMed] [Google Scholar]
  7. Brown JH, Gillooly JF, Allen AP, Savage VM, West GB. (2004). Toward a metabolic theory of ecology. Ecology 85: 1771–1789. [Google Scholar]
  8. Cooper VS, Bennett AF, Lenski RE. (2001). Evolution of thermal dependence of growth rate of Escherichia coli populations during 20000 generations in a constant environment. Evolution 55: 889–896. [DOI] [PubMed] [Google Scholar]
  9. Daegelen P, Studier FW, Lenski RE, Cure S, Kim JF. (2009). Tracing ancestors and relatives of Escherichia coli B, and the derivation of B strains REL606 and BL21(DE3). J Mol Biol 394: 634–643. [DOI] [PubMed] [Google Scholar]
  10. Damuth J. (2001). Scaling of growth: plants and animals are not so different. Proc Natl Acad Sci USA 98: 2113–2114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. DeLong JP, Okie JG, Moses ME, Sibly RM, Brown JH. (2010). Shifts in metabolic scaling, production, and efficiency across major evolutionary transitions of life. Proc Natl Acad Sci USA 107: 12941–12945. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Dill Ka, Ghosh K, Schmit JD. (2011). Inaugural article: Physical limits of cells and proteomes. Proc Natl Acad Sci USA 108: 17876–17882. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Edelstein-Keshet L. (1989) Mathematical Models in Biology. McGraw-Hill: New York, NY, USA. [Google Scholar]
  14. Ellis RJ. (2001). Macromolecular crowding: an important but neglected aspect of the intracellular environment. Curr Opin Struct Biol 11: 114–119. [DOI] [PubMed] [Google Scholar]
  15. Enquist BJ, Tiffney BH, Niklas KJ. (2007). Metabolic scaling and the evolutionary dynamics of plant size, form, and diversity: toward a synthesis of ecology, evolution, and paleontology. Int J Plant Sci 168: 729–749. [Google Scholar]
  16. Enquist BJ, West GB, Charnov EL, Brown JH, Santa T, Road HP et al. (1999). Allometric scaling of production and life history variation in vascular plants. Nature 401: 907–911. [Google Scholar]
  17. Gallet R, Cooper TF, Elena SF, Lenormand T. (2012). Measuring selection coefficients below 10-3: method, questions, and prospects. Genetics 190: 175–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Glazier DS. (2010). A unifying explanation for diverse metabolic scaling in animals and plants. Biol Rev 85: 111–138. [DOI] [PubMed] [Google Scholar]
  19. Golding I, Cox EC. (2006). Physical nature of bacterial cytoplasm. Phys Rev Lett 96: 98102. [DOI] [PubMed] [Google Scholar]
  20. Gounand I, Daufresne T, Gravel D, Bouvier C, Bouvier T, Combe M et al. (2016). Size evolution in microorganisms masks trade-offs predicted by the growth rate hypothesis. Proc R Soc Lond B Biol Sci 283: 20162272. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Haldane JBS. (1926). On being the right size. Harper’s Mag 1–5. Available at: http://harpers.org/archive/1926/03/.
  22. Hindré T, Knibbe C, Beslon G, Schneider D. (2012). New insights into bacterial adaptation through in vivo and in silico experimental evolution. Nat Rev Microbiol 10: 352–365. [DOI] [PubMed] [Google Scholar]
  23. Kempes CP, Dutkiewicz S, Follows MJ. (2012). Growth, metabolic partitioning, and the size of microorganisms. Proc Natl Acad Sci USA 109: 495–500. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kirchman DL. (2015). Growth rates of microbes in the oceans. Ann Rev Mar Sci 8: 1–25. [DOI] [PubMed] [Google Scholar]
  25. Koch A. (1996). What size should a bacterium be? A question of scale. Annu Rev Microbiol 50: 317–348. [DOI] [PubMed] [Google Scholar]
  26. LaBarbera M. (1990). Principles of design of fluid transport systems in zoology. Science (80-) 249: 992–1000. [DOI] [PubMed] [Google Scholar]
  27. Lenski RE. (2001). Testing Antonovics’ five tenets of ecological genetics: experiments with bacteria at the interface of ecology and genetics. In: Press MC, Huntly NJ, Levin S (eds). Ecology: Achievement and Challenge. Blackwell Science: Oxford, UK, pp 25–45. [Google Scholar]
  28. Lenski RE, Rose MR, Simpson SC, Tadler SC. (1991). Long-term experimental evolution in Escherichia coli. I. Adaptation and divergence during 2000 generations. Am Nat 138: 1315–1341. [Google Scholar]
  29. Lenski RE, Travisano M. (1994). Dynamics of adaptation and diversification—a 10000 generation experiment with bacterial populations. Proc Natl Acad Sci USA 91: 6808–6814. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Lynch M, Field MC, Goodson HV, Malik HS, Pereira-Leal JB, Roos DS et al. (2014). Evolutionary cell biology: two origins, one objective. Proc Natl Acad Sci USA 111: 16990–16994. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Maynard-Smith J, Burian R, Kauffman S, Alberch P, Campbell J, Goodwin B et al. (1985). Developmental constraints and evolution. Q Rev Biol 60: 265–287. [Google Scholar]
  32. Mongold JA, Lenski RE. (1996). Experimental rejection of a nonadaptive explanation for increased cell size in Escherichia coli. J Bacteriol 178: 5333–5334. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Moses ME, Hou C, Woodruff WH, West GB, Nekola JC, Zuo W et al. (2008). Revisiting a model of ontogenetic growth: estimating model parameters from theory and data. Am Nat 171: 632–645. [DOI] [PubMed] [Google Scholar]
  34. Okie JG, Boyer AG, Brown JH, Costa DP, Ernest SKM, Evans AR et al. (2013). Effects of allometry, productivity and lifestyle on rates and limits of body size evolution. Proc R Soc B 280: 20131007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Peters R. (1983) The Ecological Implications of Body Size. Cambridge University press: Cambridge, UK. [Google Scholar]
  36. Schulz H, Jorgensen B. (2001). Big bacteria. Annu Rev Microbiol 55: 105–137. [DOI] [PubMed] [Google Scholar]
  37. Shoval O, Sheftel H, Shinar G, Hart Y, Ramote O, Mayo A et al. (2012). Evolutionary trade-offs, pareto optimality, and the geometry of phenotype space. Science 336: 1157–1160. [DOI] [PubMed] [Google Scholar]
  38. Spor A, Kvitek DJ, Nidelet T, Martin J, Legrand J, Dillmann C et al. (2014). Phenotypic and genotypic convergences are influenced by historical contingency and environment in yeast. Evolution 68: 772–790. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Vasi F, Travisano M, Lenski RE. (1994). Long-term experimental evolution in Escherichia coli. II. Changes in life-history traits during adaptation to a seasonal environment. Am Nat 144: 432–456. [Google Scholar]
  40. Verkman AS. (2002). Solute and macromolecule diffusion in cellular aqueous compartments. Trends Biochem Sci 27: 27–33. [DOI] [PubMed] [Google Scholar]
  41. Volkmer B, Heinemann M. (2011). Condition-dependent cell volume and concentration of Escherichia coli to facilitate data conversion for systems biology modeling. PLoS One 6: e23126. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Warton DI, Duursma RA, Falster DS, Taskinen S. (2012). SMATR 3—an R package for estimation and inference about allometric lines. Methods Ecol Evol 3: 257–259. [Google Scholar]
  43. Warton DI, Wright IJ, Falster DS, Westoby M. (2006). Bivariate line-fitting methods for allometry. Biol Rev 81: 259. [DOI] [PubMed] [Google Scholar]
  44. Weart RB, Lee AH, Chien AC, Haeusser DP, Hill NS, Levin PA. (2007). A metabolic sensor governing cell size in bacteria. Cell 130: 335–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Welch GR, Easterby JS. (1994). Metabolic channeling versus free diffusion: Transition-time analysis. Trends Biochem Sci 19: 193–197. [DOI] [PubMed] [Google Scholar]
  46. West GB, Brown JH, Enquist BJ. (1997). A general model for the origin of allometric scaling laws in biology. Science 276: 122–126. [DOI] [PubMed] [Google Scholar]
  47. West GB, Enquist BJ, Brown JH. (1999). The fourth dimension of life: fractal geometry and allometric scaling of organisms. Science (80-) 284: 1677–1679. [DOI] [PubMed] [Google Scholar]
  48. West GB, Woodruff WH, Brown JH. (2002). Allometric scaling of metabolic rate from molecules and mitochondria to cells and mammals. Proc Natl Acad Sci USA 99: 2473–2478. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Wiser MJ, Ribeck N, Lenski RE. (2013). Long-term dynamics of adaptation in asexual populations. Science (80-) 342: 1364–1367. [DOI] [PubMed] [Google Scholar]
  50. Young KD. (2006). The selective value of bacterial shape. Microbiol Mol Biol Rev 70: 660–703. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (30.6KB, docx)

Articles from The ISME Journal are provided here courtesy of Oxford University Press

RESOURCES