Analysis of Receptor–Ligand Interactions

Molecules have an innate affinity for one another due to electrostatic forces, such as Coulombic attractions, hydrogen bonds, and dispersion forces. The noncovalent interactions that result from this affinity are of particular importance in biological processes, including the catalysis of chemical reactions (by enzymes), neutralization of foreign toxins (by antibodies), and stimulation of cellular activities (by hormones). To initiate these processes, receptors and ligands exchange interactions with solvent and solute molecules for interactions with each other. Much effort is currently being made by biological chemists to understand the molecular details of receptor–ligand interactions, and by medicinal chemis ts to exploit this understanding in developing useful pharmaceutics (1). In addition, organic chemists are attempting to develop s synthetic systems that mimic the biological interactions (2, 3). Each of these efforts requires knowledge of the number of potential binding sites on a receptor and the affinity of each binding site for its ligand. In this article, we describe how this knowledge can be obtained, and draw parallels, when appropriate, to the analysis of the kinetics of enzymatic catalysis (4, 5).

Properties of Receptor–Ligand Interactions

The interactions of all biological receptors with their natural ligands share several properties.

Specificity

Biological receptors generally bind tightly to a single natural ligand. (This specificity need not be absolute. For example, a number of natural toxins, such as α-bungarotoxin, carry out their mischief by binding to the acetylcholine receptor.) Ligand specificity can be readily assessed through a competitive-binding assay. Here, the amount of ligand bound to a receptor is measured in the presence of other putative ligands. If the receptor is indeed specific for the original ligand, the amount of ligand bound is not affected by the presence of the other ligands. For example, the addition of a 1000-fold molar excess of serum albumin does not decrease the amount of diphtheria toxin bound to its cell-surface receptor.

Affinity

Molecules interact noncovalently with other molecules. For example, proteins tend to stick to glass, due in part to polar surfaces interacting with one another. The surface of a cell is also quite polar, due largely to the extensive amount of carbohydrate that extends from membrane proteins and membrane lipids. Consequently, all proteins have some affinity for cell surfaces. Receptor–ligand interactions are distinguished from other noncovalent interactions between molecules by their high affinity.

Saturation

A receptor has a limited number of binding sites, and is therefore saturated at high ligand concentrations. A plot of the concentration of bound ligand versus that of total ligand is curvilinear when all the binding sites are occupied, there is no further increase in binding with increasing ligand concentration (Fig. 1).

Figure 1.

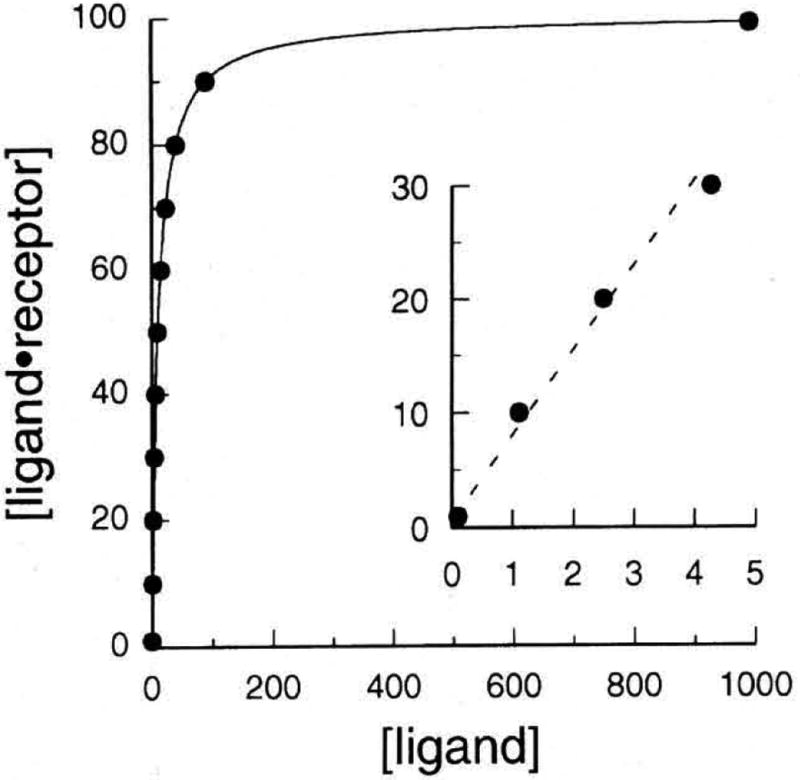
Typical saturation curve for a receptor–ligand interaction. The curve was generated from an interaction with B_max = 100; K_d = 10; F = 0.10, 1.1, 2.5, 3.9, 4.3, 6.7, 10, 15, 23, 40, 90, 990. The insert shows that the binding observed at row concentrations of ligand (F < K_d/2) appears linear and therefore might erroneously be interpreted as nonspecific.

Physiological Response

A meaningful receptor–ligand interaction leads to a physiological response. For example, when glucagon binds to its receptor on adipocytes, the production of fatty acids by hydrolysis of triacylglycerols is enhanced. The extent of this enhancement parallels the amount of glucagon bound to the adipocyte glucagon receptor. Thus, if a receptor is isolated and it binds to glucagon without eliciting a physiological response, then it is not likely to be the glucagon receptor. Not only should binding be correlated with a physiological response, but also the binding and physiological responses should parallel one another. For example, at glucagon concentrations that saturate the adipocyte glucagon receptor, the physiological response—triacylglycerol hydrolysis—is also maximal.

Binding Constants

A binding constant is analogous to the equilibrium constant in a chemical reaction. For example, the binding of a ligand, L, to a receptor, R, can be written

$$\mathrm{L}+\mathrm{R}\underset{k_{\mathbf{\text{off}}}}{\overset{k_{\text{on}}}{\rightleftarrows }}\mathrm{L}·\mathrm{R}$$ (1)

where the association rate constant and dissociation rate constant for this interaction are k_on with units of concentration⁻¹ time⁻¹ and k_off with units of time⁻¹. At equilibrium, the ratio of the concentration of ligand·receptor complex [L·R] to the product of the concentrations of free ligand [L] and free receptor [R] is the equilibrium constant, which is also called the affinity constant or association constant, K_a.

$$K_{\mathrm{a}}=\frac{[\mathrm{L}·\mathrm{R}]}{[\mathrm{L}][\mathrm{R}]}$$ (2)

In biological chemistry, the dissociation constant, K_d is used more frequently. The dissociation constant refers to the reverse of the reaction in eq 1, and is therefore the reciprocal of the association constant.

$$K_{\mathrm{d}}=\frac{1}{K_{\mathrm{a}}}=\frac{[\mathrm{L}][\mathrm{R}]}{[\mathrm{L}·\mathrm{R}]}$$ (3)

The dissociation constant, K_d, should not be confused with the dissociation rate constant, k_off. Rather, K_d is the ratio of the dissociation and association rate constants.

$$K_{\mathrm{d}}=\frac{k_{\text{off}}}{k_{\text{on}}}$$ (4)

The value or K_d is often 10⁻⁹ M or lower for receptor–ligand interactions.

In the Michaelis–Menten model or enzymatic catalysis, the concentration of substrate [S] is much greater than that or enzyme (6). Similarly, in most studies or receptor·ligand interactions, the concentration or ligand is much greater than that or receptor. A difference arises, however, in that [S] is the substrate concentration initially (i.e., when no product is present), but [L] is the free ligand concentration at equilibrium. Despite this difference, the form of the equations that describe each process is identical.

Michaelis–Menten

$$v=\frac{V_{\text{max}}[\mathrm{S}]}{K_{\mathrm{m}}+[\mathrm{S}]}$$ (5)

receptor–ligand

$$[\mathrm{L}·\mathrm{R}]=\frac{{[\mathrm{R}]}_{\text{total}}[\mathrm{L}]}{K_{\mathrm{d}}+[\mathrm{L}]}$$ (6)

The saturation function is the fraction of receptors occupied at equilibrium.

$$\frac{[\mathrm{L}·\mathrm{R}]}{{[\mathrm{R}]}_{\text{total}}}=\frac{[\mathrm{L}]}{K_{\mathrm{d}}+[\mathrm{L}]}$$ (7)

In the context of enzyme kinetics, the saturation function is analogous to v/V_max, which is the fraction of enzyme active sites occupied at steady-state.

Linear Transformations

Binding parameters cannot readily be extracted from the visual inspection of hyperbolic graphs such as that shown in Figure 1. Numerous linear transformations have therefore been used to facilitate the estimation of K_d and [R]_total. Most of these transformations are some form of reciprocal graph, analogous to the widely used Lineweaver–Burk plots of enzymology.

The most popular linear transformation used in the analysis of receptor–ligand interactions is the Scatchard plot (7, 8). The total concentration of receptor is the sum of the concentrations of occupied and unoccupied receptors.

$${[\mathrm{R}]}_{\text{total}}=[\mathrm{R}]+[\mathrm{L}·\mathrm{R}]$$ (8)

Rearranging eqs 2, 3, and 8, we get the Scatchard equation.

$$\frac{[\mathrm{L}·\mathrm{R}]}{[\mathrm{L}]}=\frac{1}{K_{\mathrm{d}}}{([\mathrm{R}]}_{\text{total}}-[\mathrm{L}·\mathrm{R}])$$ (9)

More common terminology is bound or B for [L·R], free or F for [L], and B_max for [R]_total. Substituting these new terms into eq 9, we get

$$\text{ln }{B}_t=\text{ln }{B}_{t=0}-k_{\text{off}}t$$ (10)

Equation 10 has the familiar form of an equation for a line, y = mx + b. A plot of B/F versus B gives a line with a slope of −K_d, x-intercept of B_max, and y-intercept of B_max/K_d (Fig. 2A). Two other common plots for binding data are the Eadie–Hofstee plot, which is simply the inverse of the Scatchard plot with B now plotted versus B/F (Fig. 2B), and the double-reciprocal plot, which is analogous to the Lineweaver–Burk plot (Fig. 2C). These three plots are often used to calculate parameters in receptor–ligand interactions. All three, however, are algebraic manipulations of the same equation and hence contain the same information.

Figure 2.

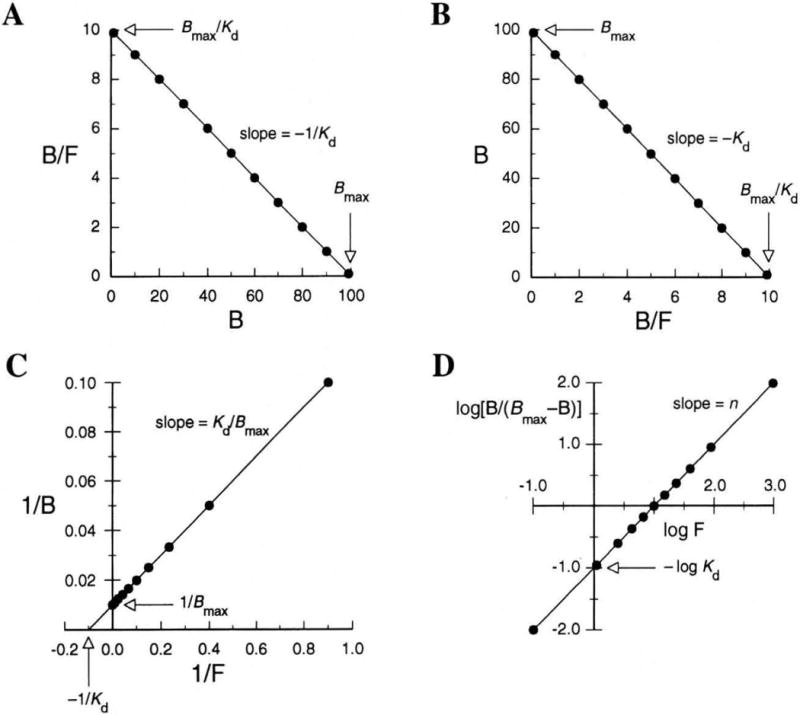
Linear transformations of binding data for the receptor–ligand interaction portrayed in Figure 1. (A) Scatchard plot; (B) Eadie–Hofstee plot; (C) double-reciprocal plot (F = 0.10 not shown); and (D) Hill plot (n = 1).

Linear regression analysis of a linear transformation such as a Scatchard plot weighs data points improperly and can therefore lead to gross errors. The graphs should therefore be used only to obtain initial estimates of the parameters. These estimates can then be used to arrive by iteration at more accurate values for the parameters. Although these plots should not be used to derive the values of the parameters, each is an effective vehicle for displaying binding data and for examining the quality of such data.

Nonlinear Scatchard Plols

The Scatchard plot for the binding of [¹²⁵I]insulin to cultured human lymphocytes is curvilinear, rather than linear (Fig. 3) (9). Three situations lead to such nonlinear Scatchard plots (10–12).

• The binding sites for the ligand may be heterogeneous; the ligand might be binding to one site with a dissociation constant of K_d1 and a second site with a dissociation constant of K_d2.

• The binding of one molecule of ligand may change the affinity or the receptor for the next molecule of ligand (as in the cooperative binding of molecular oxygen to hemoglobin). A Scatchard plot alone cannot distinguish between heterogeneous binding sites and cooperativity (13, 14).

• Certain arrangements of large ligands on lattice-like receptors may limit the access of additional molecules of ligand to free sites on the lattice (as in the binding or polyamines to double-helical DNA). The nonlinear Scatchard plots that arise from lattice binding can be interpreted only by considering special statistical effects (15).

Figure 3.

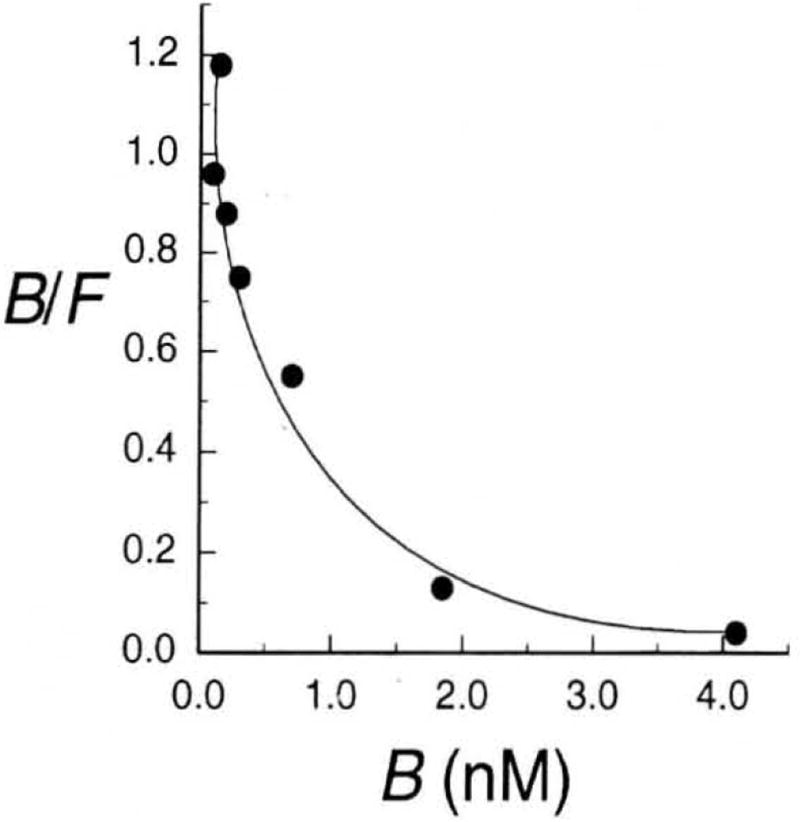
Scatchard plot for the interaction of insulin with its receptor (9).

Cooperativity and receptor heterogeneity can be distinguished by measuring the effect of bound ligand on the value of the dissociation rate constant, k_off. The value of k_off can be measured by allowing ligand and receptor to reach equilibrium, removing free ligand, and then measuring the dissociation of ligand over time. In practice, the decrease in the concentration of bound ligand is usually measured. Initially, this decrease follows first-order kinetics, such that

$$B_t=B_{t=0}{e}^{-k_{\text{off}}t}$$ (11)

or

$$\text{ln }{B}_t=\text{ln }{B}_{t=0}-k_{\text{off}}t$$ (12)

Thus, a plot of ln B_t versus t gives a line with a slope of k_off and y-intercept of ln B_t=0. This type of experiment can distinguish between cooperativity and receptor heterogeneity. If the receptor is heterogeneous, the value of k_off does not vary with the initial extent of receptor saturation. If binding is cooperative, experiments with varying initial extents of receptor saturation give different values of k_off. This method was used to demonstrate negative cooperativity for the binding of insulin to its receptor (8).

In the absence of cooperativity, the saturation function is eq 7. But if the affinity for the receptor is a function of receptor occupancy, the saturation function is

$$\frac{B}{B_{\text{max}}}=\frac{F^n}{K_{\mathrm{d}}+F^n}$$ (13)

If the receptor–ligand interaction has the same cooperativity at all receptor occupancies, then n is the Hill constant (16). Given an accurate estimate of the value of B_max, the value of n can he estimated from a Hill plot, which arises from the Hill equation.

$$\text{log}\frac{B}{B_{\text{max}}-B}=n\text{log }F-\text{log }{K}_{\mathrm{d}}$$ (14)

A plot of log F versus log [B/(B_max − B)] gives a straight line with a slope of n and y-intercept of −log K_d (Fig. 2D). If n = 1, the receptor has a single binding site and, of course, exhibits no cooperativity in its binding of ligand. Nonintegral values of n are consistent with cooperativity.

Numerical Analysis of Hyperbolic Plots

Various computer programs are available for fitting binding data to a hypothetical model (17–20). The general strategy in using these programs is to fit the data to the simplest model compatible with everything that is known about the system. If the fit is not good, then another model should be considered. If the data appear to fit the simplest model, then other models should still be tested to see if they lead to an improved fit. The linear transformations discussed above are useful to provide the initial estimates that enable a computer program to converge upon a solution.

The simplest equation that describes a receptor–ligand interaction has two parameters, such as B_max and K_d in eq 7. Often, nonspecific binding is a significant component of the interaction, and a term is required to describe nonspecific binding (21). If nonspecific binding is assumed to be nonsaturable, then the term is a linear function of ligand concentration, such as K_nsF. Thus, a model describing one saturable binding site plus nonspecific binding has three parameters: B_max, K_d, and K_ns.

$$B=\frac{B_{\text{max}}F}{K_{\mathrm{d}}+F}+K_{\text{ns}}F$$ (15)

If the receptor has two independent binding sites, a term describing each binding interaction must be included in the equation.

$$B=\frac{B_{{\text{max}}_1}F}{K_{{\mathrm{d}}_1}+F}+\frac{B_{{\text{max}}_2}F}{K_{{\mathrm{d}}_2}+F}$$ (16)

A model describing two saturable binding sites and nonspecific binding has five parameters: B_max1, B_max2, K_d1, K_d2, and K_ns. Exceptionally accurate data are required to obtain a meaningful fit for a model with five or more parameters.

A common (and flawed!) method of distinguishing specific from nonspecific binding is to carry out the binding study in the absence and in the presence of a large excess of unlabeled ligand. The binding observed in the presence of the unlabeled ligand is erroneously presumed to be nonspecific binding. Yet, all one is doing is diluting the specific activity of the ligand.

Another problem can arise with the presumption that nonspecific binding is nonsaturable. Nonspecific binding actually describes the binding of a ligand to many saturable sites with a higher K_d. Making the assumption that the sites are not saturable can result in an overestimation of the value of B_max and an underestimation of the value of K_d. This pitfall can be avoided by the use of computer programs to test the validity of each of the models discussed above.

Finally, binding data on receptor–ligand interactions should cover a broad range of ligand concentrations. Obtaining data with ligand concentrations that are an order of magnitude below and above the value of K_d is a good rule of thumb. (The ligand concentrations used to generate Figures 1 and 2 extend to two orders of magnitude below and above the value of K_d.) Although the use of a limited data set may yield an apparently linear Scatchard plot, a graph with data covering a broader range might actually be nonlinear. High sensitivity may be necessary to collect data at low ligand concentrations.

Competition between Ligands

Often one wants to know if two different ligands bind to the same site on a receptor. The most common approach is to carry out a competition experiment in which one ligand is radiolabeled and the other is not. The labeled ligand is usually the one best-characterized and with a known K_d. The concentration of the free, labeled ligand is kept constant at or near the K_d. Varying concentrations of the unlabeled ligand (covering about two orders of magnitude) are simultaneously incubated with the labeled ligand and the receptor.

The equation that describes the binding of the two ligands to the same site on the receptor is identical to that for the competitive inhibition of an enzyme-catalyzed reaction (5).

$$f=1-\frac{B_{[\mathrm{I}]}}{B_{[\mathrm{I}]=0}}=\frac{[\mathrm{I}]}{[\mathrm{I}]+K_{\mathrm{i}}(1+\frac{F}{K_{\mathrm{d}}})}$$ (17)

where f is the fractional inhibition of binding, and [I] is the concentration of free, unlabeled ligand.

Computer analysis of the binding data with eq 17 can be used to determine the value of K_i. Just as a competitive inhibitor of enzymatic catalysis does not affect V_max, a competitive inhibitor of receptor binding (with the same stoichiometry as that of the ligand) does not affect B_max.

Measurement of Binding Parameters

Binding constants are typically measured knowing the concentration of L present in a solution and adding a small amount of R. Then the concentration of L·R is measured using spectroscopy (22) or by separating L·R from L. Several principles must be obeyed during these measurements.

The tracer must be identical to the ligand being traced

In a binding experiment the ligand concentration is assumed to be an independent variable, thus presuming that its concentration has been determined accurately. Because the values of K_d for biological receptors are often 10⁻⁹ M or lower, the determination of ligand concentration usually requires the use of a radioactive tracer or some other sensitive assay. For a radioactive ligand to be a true tracer, it must behave precisely like the ligand being traced. If the binding of the ligand to its receptor has a measurable biological consequence (as the binding of insulin to its receptor stimulates glucose transport), then this consequence can be used to assess the similarity of a radioactive ligand and a nonradioactive ligand.

Measurements of equilibrium-binding parameters must be made at equilibrium

The binding parameters K_d and B_max are thermodynamic, not kinetic, constants. An experiment must be conducted so that the concentration of L·R has sufficient time after mixing Land R to reach equilibrium. The true values of K_d and B_max are independent of time and must be obtained at equilibrium.

Isolation of L·R should not affect the binding equilibrium

Le Chattelier’s Principle dictates that altering the concentration of L or L·R shifts the initial binding equilibrium. Because this shift occurs with time, L·R should be isolated as quickly as possible. Control experiments must be carried out to show that values of K_d and B_max are identical to those obtained from the slower isolation of L·R. Alternatively, the receptor–ligand complex can be covalently cross-linked before separation.

Concentration of free ligand should be adjusted for concentration of bound ligand

In most experiments, the concentration of bound ligand is much lower than that of free ligand so that F ≈ [L]_total. If the concentration of bound ligand is comparable to that of free ligand, then F = [L]_total − B. Also, if the ligand suffers either chemical decomposition or radioactive decay during the course of the experiment, then the value of F must be adjusted accordingly.

Separating Bound from Free Ligand

Several methods are available for separating receptor-bound ligand from free ligand. The impact of the separation on the binding equilibrium must be considered in choosing a particular technique. If the separation is slow (e.g., chromatography or dialysis) or involves extensive dilution (e.g., a rigorous washing step), then it must be demonstrated that the method has no effect on the binding equilibrium.

We have compiled a list of 10 techniques that can be useful for separating a ligand from its receptor (23). The first four require that the ligand and receptor differ greatly in size.

Filtration

Large receptor–ligand complexes can be separated from small, free ligands by filtration. This method is often used in experiments in which the receptor is on the surface of whole cells. The method is technically simple and allows rapid, efficient washing. (The washing steps must not dilute the solution.) Recently, filtration has become much more sophisticated due to the availability of filtration membranes with specific molecular weight cutoffs. These membranes are also available for use in a centrifuge, which greatly speeds the separation.

Gel Filtration

Small ligands can be separated from large receptors by gel filtration. Because this technique is slow, dissociation can occur during separation and perturb the binding equilibrium. Also, the method is impractical for obtaining measurements on large numbers of samples.

Equilibrium Gel Filtration

The binding of a large receptor to a small ligand can be studied by gel filtration catTied out at equilibrium, that is, in the presence of ligand (24). As the receptor emerges from the column, a peak and then a trough appear in the concentration of the ligand (Fig. 4). In theory, the areas under the peak and the trough are each proportional to the fraction of receptor with bound ligand. Often, however, the area of the trough apperu's to be smaller than that of the peak due to diffusion within the column (Fig. 4).

Figure 4.

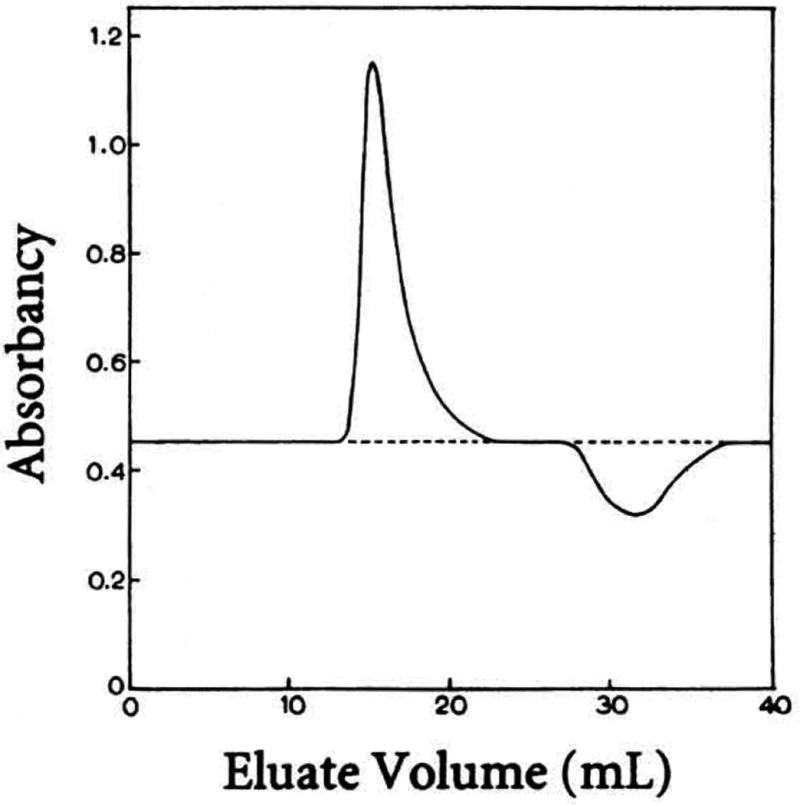
Elution profile of the absorbance at 285 nm accompanying the passage of the protein ribonuclease A through a gel-filtration column, which was equilibrated with the ligand 2′-cytidylic acid (24).

Equilibrium Dialysis

This method requires that the ligand but not the receptor pass freely through a dialysis membrane. The receptor is added to a dialysis bag, which is then sealed and placed in a solution containing free ligand. At equilibrium, the concentration of ligand inside the bag exceeds that outside the bag due only to the affinity of the ligand for the receptor. The following six techniques require that the ligand and receptor differ in a molecular property other than size.

Precipitation

If the receptor–ligand complex and the free ligand have different solubility properties, then they can be separated by differential precipitation. This method has been used in studies of the binding of antigens to antibodies where ammonium sulfate precipitates immunoglobulins while leaving some antigens free in solution.

Affinity Chromatography and Immunoprecipitation

An antibody bound to a resin can be used to separate a ligand from its receptor, either on a column or in batches. Similarly, lectins can be used if the receptor (but not the ligand) is a glycoprotein. Also, if the receptor is coupled to biotin, immobilized avidin can be used due to the extremely high affinity (K_d = 10⁻¹⁵ M) of avidin for biotin (25).

Ultracentrifugation

Ultracentrifugation can be used to separate a ligand from its receptor according to hydrodynamic properties, such as sedimentation rate or buoyant densities. This method is also impractical for large numbers of samples.

Electrophoresis

Gel retardation assays are widely used to study protein binding to DNA and RNA. The migration of a target oligonucleotide is retarded when bound to protein. If carried out carefully, this technique can be used to measure equilibrium binding parameters. A potential concern is the possibility of dissociation during electrophoresis. Dissociation is not often a problem, however, because the value of K_d for the specific complex formed by DNA- and RNA-binding proteins may be as small as 10⁻¹² M, and solution conditions can be adjusted to stabilize the L·R complex, for example, by running the gel in a low salt buffer.

lon-Exchange Chromatography

Molecules flowing through an ion-exchange resin are separated on the basis of charge. An advantage of using ion-exchange resins is that many are inexpensive. For large numbers of samples, it is much more practical to apply this technique in batches.

Activated Charcoal

Small hydrophobic molecules bind to charcoal. This approach is often used to separate free steroid hormones from steroid hormone receptors.

Finally, T. H. Huxley had a germane thought, quoted in ref 8, for those who analyze receptor–ligand interactions.

Mathematics may be compared to a mill of exquisite workmanship, which grinds you stuff of any degree of fineness; but, nevertheless, what you get out depends on what you put in; and as the grandest mill in the world will not extract wheat-flour from peascods, so pages of formulae [or graphs] will not get a definite result out of loose data.