MD simulations identify time scale of conformational changes responsible for conformational selection in molecular recognition of HIV-1 TAR RNA

Abstract

The HIV-1 Tat protein and several small molecules bind to HIV-1 Trans-Activation Responsive RNA (TAR) by selecting sparsely populated but pre-existing conformations. Thus, a complete characterization of TAR conformational ensemble and dynamics is crucial to understand this paradigmatic system and could facilitate the discovery of new anti-virals targeting this essential regulatory element. We show here that molecular dynamics simulations can be effectively used towards this goal by bridging the gap between functionally-relevant timescales that are inaccessible to current experimental techniques. Specifically, we have performed several independent microsecond long molecular simulations of TAR based on one of the most advanced force fields available for RNA, the parmbsc0 AMBER. Our simulations are first validated against available experimental data, yielding an excellent agreement with measured residual dipolar couplings and order parameter S². This contrast with previous MD simulations (Salmon et al., J. Am. Chem. Soc. 2013 135, 5457–5466) based on the CHARMM36 force field, which could achieve only modest accord with the experimental RDC values. Next, we direct the computation towards characterizing the internal dynamics of TAR over the microsecond timescale. We show that the conformational fluctuations observed over this previously-elusive timescale have a strong functionally-oriented character in that they are primed to sustain and assist ligand binding.

Graphical Abstract

INTRODUCTION

The growing number of newly discovered noncoding RNAs raises the demand to explore and characterize their distinct roles in cells.^1–3 An emerging theme is that RNA’s functional complexity is rooted not only in its 3D structure but also in its ability to adaptively acquire very distinct conformations on its own or in response to specific cellular signals.⁴

A paradigmatic case of complex and multilayer RNA dynamics is provided by the HIV-1 Trans-Activation Responsive RNA (TAR). TAR is a 59-nucleotide long RNA located at the 5’-end of viral transcripts.⁵ It activates elongation of transcription of the integrated virus⁶ by forming a complex with the virally encoded HIV-1 Tat protein^7–9 and with human cyclin T1, which recruits the kinase activity of p-TEFb to the HIV-1 promoter. Since viral replication is disrupted by mutations that disfavor the interaction between TAR and its protein partners,¹⁰ the identification of compounds that interact with TAR and prevent formation of the complex with p-TEFb could provide antiviral leads with radically new mechanism of action.^10–12

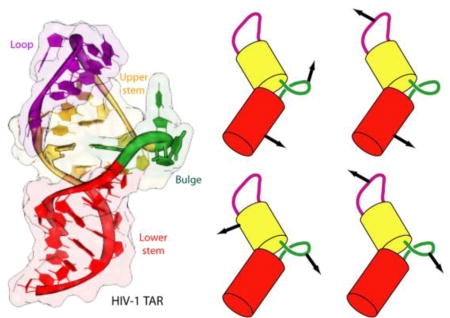
NMR studies^13–21 have established that TAR binds to Tat mimics and small ligands mostly through its “bulge” and the neighboring base pairs, consisting of single stranded nucleotides (NTs) 23–25 separating two helical regions (“upper” and “lower” stems, Fig. 1). In apo TAR, the partial stacking of U23 on A22 and C24 on U23 in the bulge generates a kink between the two stems (Fig. 1).¹⁴ Most ligand-bound complexes (referred to as holo TAR here) overlap with such apo conformation. Few ligands widen instead the major groove and open up the interhelical angle (Tab. S1).^15–17 Hence, ligands binding to TAR can “grab on the fly” a matching TAR conformer as it is spontaneously, yet transiently populated in free TAR,²² suggesting that such ligands use the conformational selection mechanisms for molecular recognition of TAR (Tab. S1).^13,18–21

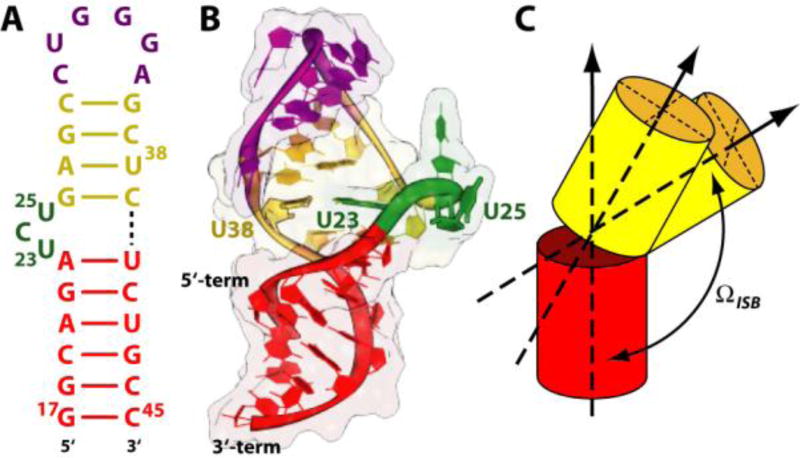
Figure 1.

HIV-1 TAR. Sequence (A) and cartoon representation (B) of the structure obtained from NMR studies.²⁹ The apical loop, bulge and the upper and lower stems are colored in magenta, green, yellow and red, respectively. (C) Cartoon representation of the inter-stem bending (Ω_ISB) angle involved in the movements of the helical stems movement. See Fig. S2 in the Supplementary Information for further details.

In order to understand TAR/ligand recognition mechanism, an in-depth characterization of the internal motions of this RNA is necessary,^23–25 including an understanding of the interplay among relevant time scales. Conformational exchange in TAR has been shown to occur over a very wide range of rates, from ps to ms. As a consequence of this breadth of motional rates, probing experimentally the mechanism of recognition is very challenging.^26–28 On the one hand, the insight provided by NMR in the solution state (solNMR) is limited by the paucity of observables²² as well as by technical difficulties in accessing the ns-µs time scale; residual dipolar couplings can access this motional time scale but the information on rates of motion is lost by averaging and can only be obtained partially and indirectly. On the other hand, solid state NMR (ssNMR) can access this time scale, but the information that can be obtained so far by this approach is limited to relatively few sites that have to be probed individually.

Atomistic molecular dynamics (MD) simulations can obviously complement experimental investigations if they are accurate. These approaches, including the recent multi-µs simulation of apo TAR²⁸ based on the CHARMM36 force field,^30–32 have provided valuable support for the conformational-selection mechanism to explain the interaction between TAR and other ligands. Yet the scope of unbiased atomistic MD simulations in addressing RNA dynamics has been much more limited so far than for proteins, due to imperfections of the parameterizations of the atomistic force field for nucleic acids.^33–36 In the case of TAR, the latter shortcoming, along with the challenges posed by extensive conformational sampling, might be responsible for the modest agreement previously reported for residual dipolar couplings (RDCs) calculated from MD simulations and those observed experimentally.²⁸ Fortunately, recent breakthroughs in force field parameterization indicate that MD simulations of RNA molecules can now be conducted with predictive power. Notably, the latest release of the AMBER force field can accurately reproduce with sub-µs timescale simulations, the structure and conformation of nucleic acids, including, as benchmarks, TAR complexes.^37–39

Here, we build on these technical advances to re-examine the conformational selection hypothesis of TAR-ligand recognition by using advanced computational techniques to reexamine the experimental results. We collected µs-long MD simulations starting from various instances of apo and holo TAR structures depleted of the ligands using the parmbsc0 AMBER force field.³⁷ The viability and effectiveness of the approach for sampling the biologically-relevant conformational space of TAR was established a posteriori by the successful comparison of calculated and experimental RDCs⁴⁰ and order parameter S² values,³⁹ as well as by the consistency of our findings with fluorescence experiments²⁵ and with NMR-based structural information (Tab. S1).^13–21 To the best of our knowledge this represents the first documented instance where such a broad range of TAR experimental data is successfully reproduced by a single set of unbiased MD simulations. Our calculations are consistent with the NMR-based observations that indicate that: (i) Bending and twisting motions of the upper stem, as well as more local motions, occur spontaneously;^13–21 (ii) The structure samples a wide range of inter-helical angles as the upper stem experiences nearly unrestrained motions at intermediate (sub-µs) rates.^41,42 Once fully validated, the numerical approach is used to re-examine the detailed TAR intrinsic dynamics and explore its functionally-oriented character.

METHODS

The simulations of TAR in aqueous solution described herein have been performed following a published protocol.³⁹ The initial structures corresponded to the apo form (PDB ID: 1ANR)¹⁴ and the complex with the cyclo-RVRTRKGRRIRIPP cyclic peptide (L-22, PDB ID: 2KDQ)²⁹ depleted of the ligand. The starting structures were chosen on the basis of the RMSD from the average structure and of the agreement with experimental residual dipolar coupling (RDC) values.⁴⁰ The systems were embedded into truncated octahedrons containing about 13,000 water molecules. Periodic boundary conditions were applied. The solutes and their images were located at a minimum distance of 2.4 nm. The use of large simulation boxes (395–414 nm³) was necessary to eliminate artificial interactions between highly charged molecules at the periodically repeated images.⁴³ Ions were added to reproduce the experimental ion concentration used for NMR structures (50 mM NaCl and 10 mM KCl for the apo and the L-22 bound structure, respectively^14,29). Thus, 40 Na⁺ and 12 Cl⁻ ions and 30 K⁺ and 2 Cl⁻ ions were added to the apo and L-22 bound forms of TAR, respectively. A third condition was prepared by adding 30 K⁺ and 2 Cl⁻ ions to the apo TAR structure. The parmbsc0 AMBER³⁷, the TIP3P model⁴⁴ and Smith and Dang’s force fields⁴⁵ were used for RNA, water and the ions, respectively. The Particle Mesh Ewald method⁴⁶ was used to treat long-range electrostatic interactions with a real space cutoff of 1.2 nm. The simulations were performed using the program GROMACS 4.5.5⁴⁷ with a simulation step of 2 fs. The LINCS algorithm⁴⁸ was applied to constrain all bonds involving hydrogen atoms. NPT conditions were achieved by coupling the systems to a Nosè-Hoover thermostat⁴⁹ at 300 K and a Andersen-Parrinello-Rahman Barostat^50,51 at 1 atm. The same cutoff was also used for the van der Waals interactions. The subdivision of TAR in quasi-rigid domains (QRDs) followed the structure quasi-rigid domain decomposition method (PiSQRD) of ref^52,53. The two highly mobile terminal nucleotides were excluded from analysis. RDCs were calculated by applying the Prediction of ALignmEnt from Structure (PALES)⁵⁴ program onto 10,000 MD snapshots and by averaging the results.

RESULTS AND DISCUSSION

We ran four independent, 1 µs-long atomistic MD simulations starting from different initial conditions. Two simulations (TAR50a and TAR50b hereafter), differing only for the initial velocities, were based on the NMR apo TAR structure at the same ionic strength of the NMR experiments (50 mM NaCl).¹⁴ A third simulation (TAR10a) was based on the NMR TAR structure bound to the cyclic peptide T-22 depleted of the ligand at the ionic strength of NMR experiment (10 mM KCl).²⁹ The last simulation (TAR10b) were based on the NMR apo TAR structure,¹⁴ but with a lower ionic strength than that of experiment (10 mM KCl).

To assess the convergence of the simulated trajectories we considered their projections on the top essential dynamical spaces obtained from a standard covariance analysis. Following Hess’s criterion,⁵⁵ these projections were next compared with those expected for a random reference. The observed negligible overlap (see Table S2) confirms a posteriori adequate sampling of TAR conformations around the equilibrium position. The root-mean-square-deviation (RMSD) from the initial conformations after the first 0.1 µs oscillates between 0.4–0.7 nm (Fig. S3). This RMSD value is compatible with those reported for TAR conformers calculated from replica exchange techniques,³⁸ which can sample conformational space very effectively, but without providing kinetic information. The good match of RMSD values between the two methods demonstrates that coverage of the conformational space accessible to TAR achieved by retaining the full dynamic detail of MD simulations is exhaustive.

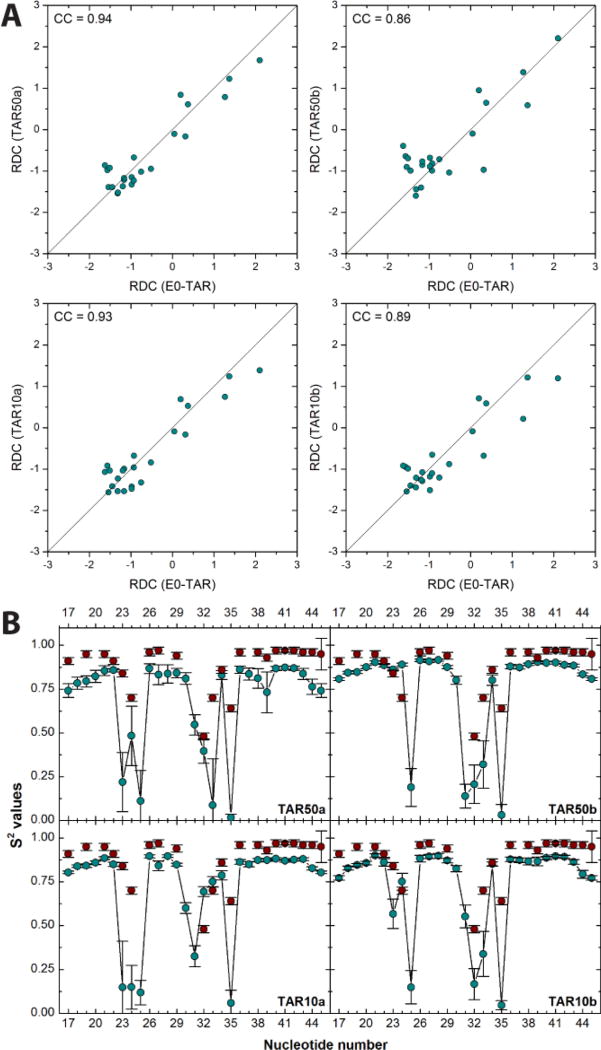
The accuracy of the simulations was established by confronting the calculated RDC^40,a and order parameter S² values with those measured experimentally.³⁹ The Pearson’s correlation coefficients (CCs) between calculated and experimental RDCs are 0.9 (Fig. 2A). To the best of our knowledge, this is the first time that such good agreement is achieved between RDCs extracted from MD simulations of RNA and experimental results.^b The order parameter S² values are also in fair agreement with the experimental data (Fig. 2B). Both techniques confirm that the bulge and the loop in both NMR experiments and computations are the most mobile regions.

Figure 2.

Comparison between NMR data of TAR and four independent, µs-long MD simulations (TAR50a, TAR50b, TAR10a and TAR10b). (A) Correlation plots of experimental RDCs (Hz) from E0-TAR⁴⁰ and the corresponding calculated values. (B) Calculated (blue circles) and experimental³⁹ (red circles) order parameter (S², arbitrary units) values for nucleotides 17–45 of TAR.

The results of Fig. 2 indicate that the four simulations provide similar results, and the same is true for all of the properties calculated in this manuscript. From now on, we report only the result of one simulation based on the apo TAR at 50 mM NaCl (TAR50a). The results of the other three simulations are summarized in the SI.

In order to characterize the large-scale motions of TAR, we find it convenient to identify QRDs, which are approximately rigid, although not static. These are derived by an analysis of the fluctuations of all pairwise nucleotide distances.^52,53 QRDs correspond to regions whose internal geometry is largely fixed (resulting in constant modules of pairwise nucleotide distances) while the relative inter-domain position and orientation changes significantly.

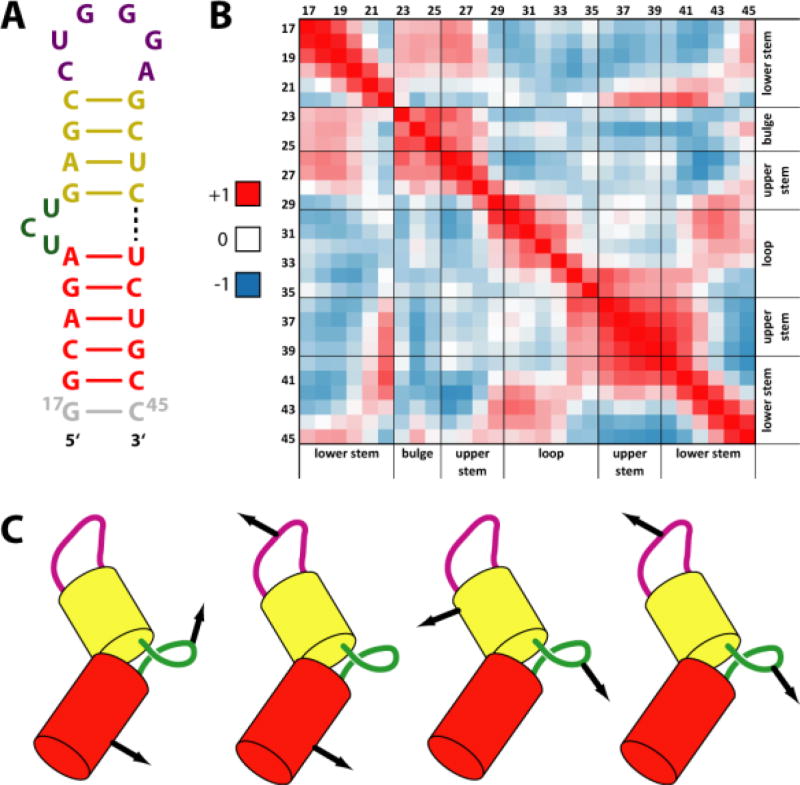
The analysis of the simulation indicates that TAR can be subdivided into four QRDs: the apical loop, the bulge and the upper and lower stems (Fig. 3A). The internal quasi-rigid character (i.e. the highly coordinated motions) of the bulge and apical loop has not been noted before, while that of the helical stems would have been expected a priori based on the structural and dynamics characteristics of helical regions.^25,42

Figure 3.

Quasi-rigid domains (QRDs) of TAR. (A) Calculated QRDs emerging from the MD simulations of TAR50a; additional details can be found in Fig. S9 of supporting information. (B) Residue-by-residue map of correlation matrices for the C4’ atoms of TAR. Red and dark blue regions refer to correlated and anti-correlated movements, respectively. (C) Cartoon representation of correlated and anti-correlated motions of QRDs.

The RMSDs of the upper and lower stems and of the bulge QRDs oscillate between 0.2 and 0.4 nm after a few ns (Fig. S3). The RMSDs of the apical loop QRD indicated a less stable simulation - as confirmed by the root-mean-fluctuations (RMSF, Fig. S5) - and oscillate between 0.2 and 0.5 nm. The motion of the lower stem QRD is correlated with that of the bulge; the motion of the lower and upper stems is anti-correlated with that of the loop, while that of the bulge is anti-correlated with that of the upper stem. The motion of the bulge is anti-correlated to that of the apical loop. In particular, the scissor-like motion of the apical loop relative to the bulge results in a canting of the major groove of TAR in the proximity of the bulge (see Fig. 3C). Bulge rearrangements - monitored as in ref.²⁸ by using the base distance between A22 and U23 - occurs in the hundreds of nanosecond time scale (Fig. S6). Moreover, the correlation plots between the A22-U23 base distance and Ω_ISB show three distinct clusters at both ionic strength (Fig. S7), in agreement with simulations in ref.²⁸.

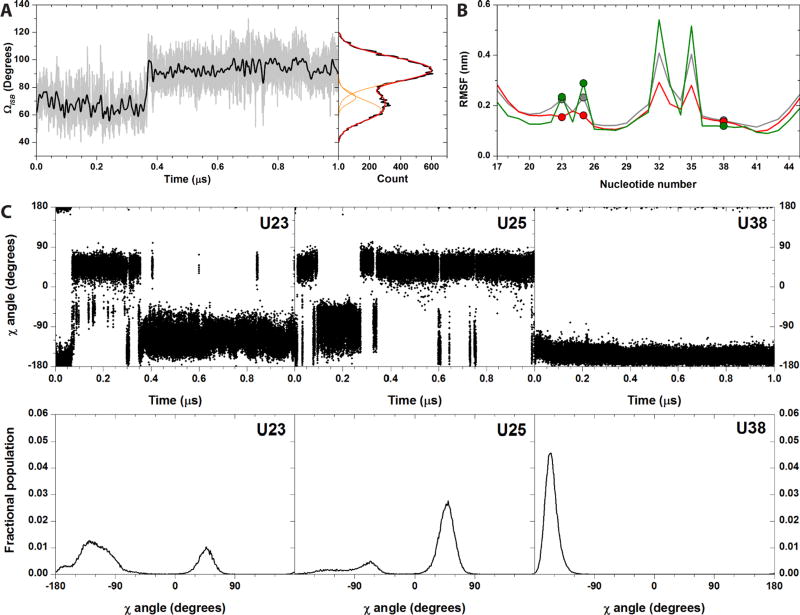
TAR stems experience transient small amplitude motions [inter stems bending angle (Ω_ISB) amplitude < 18°], which occur on a time scale of 1–2 ns, and larger amplitude motions, which occur on the near-µs time scale (Fig. 4A). The overall helical bending motions comprise Ω_ISB values between 40° and 130°, which correspond to conformations within the same range of deposited structure¹⁴ (see SI). Ω_ISB stabilizes around average values (<Ω_ISB>) of ca. 73° for the first 0.15 µs, then decrease to <Ω_ISB> values of ca. 62° (transition amplitude ca. 11°), and finally pass to ca. 92° after ca. 0.36 µs comprising a movement of ca. 20° (Fig. 4A). These observations are consistent with ssNMR data,⁴² which suggest that: (i) the stem’s motions feature small amplitudes base librations in the ns time scale and larger helical twisting and bending in the ns-µs time scale;⁴² (ii) the amplitude of such bending transitions is 13°;⁴² (iii) large transitions occur in ca. 700 ns time scale. Our simulations however differ from conclusions from solution NMR,^22,58 as discussed in detail in Tab. S3.

Figure 4.

Selected properties from the TAR50a MD simulation. (A) Ω_ISB values plotted vs. simulation time (grey line). The black line is obtained by applying a Fast Fourier Transform filter in order to reduce the noise in the data. The right panel reports the distribution of the calculated Ω_ISB angle values (black line). The Gaussian curves used to fit the Ω_ISB distribution are in orange, while the sum of the fitting Gaussians is in red. (B) Calculated RMSFs values of each nucleotide atoms (grey), of the C4’ atoms of each nucleotide (red) and of C5 atoms of each nucleotide (green). RMSF values of U23, U25, and U38 are highlighted by dots in each curve. (C) Time evolution (upper panels) and distribution (bottom panels) of the χ torsional angle of U23, U25 and U38, as observed in the MD simulation TAR50a. Correspondent plots for the TAR50b, TAR10a, and TAR10b simulations are reported in the SI.

Interestingly, in the case of TAR50a and TAR50b simulations, the two trajectories appear to stabilize at inter stem bending values of ca. 62, 73 and 92° (Fig. S12 and S13). In the case of TAR10a and TAR10b, we mainly observed three states comprising Ω_ISB values around ca. 70–71, 84 and 96–97° (Fig. S12 and S13). Thus Ω_ISB angle increases with decreasing ionic strength. Accordingly, it was experimentally observed that decreasing the ionic concentration led to a continuous increase in the average inter-helical bend angle.⁵⁷ Nevertheless, care should be taken when comparing the set of simulations run at 10 mM KCl with experimental NMR structures; since the only available apo TAR structure was determined at 50 mM NaCl ionic strength¹⁴ only the simulations run at the same conditions can be directly compared.

The terminal nucleotides, the bulge (NTs 23–25) and loop residues (NTs 30–36) are the most mobile regions of TAR (Fig. 4B and S5). U38 fluctuates less than U23, which in turn fluctuates less than U25 (Fig. 4B). This order is fully consistent with the ssNMR data.⁵⁹ In the simulations, U23 experiences a large-amplitude intermediate-time scale (hundreds of ns) hopping motion and occupies four distinct conformational states [characterized by base glycosidic angles (χ = O4’-C1’-N1-C2 torsional angle) of ca. −165, −125, −75, and +50° (Fig. 4C and S16–18, left panels)]. U23 further experiences a rapid (few ns) small-amplitude twisting of the base plane of the glycosidic bond. These conclusions are consistent with the ssNMR results.⁴² In the ssNMR experiments, U25 experiences a motion of the backbone away from the intra-helical conformation and a µs time scale large-amplitude twisting of the base.⁴² In our simulations, U25 exchanges between three distinct angular states (χ ca. −130, −60, and +50°, Fig. 4C and S16–18, central panels) on a time scale of tens-hundreds of ns, in fair agreement with ssNMR.⁴² Finally, U38 shows experimentally small-amplitude local motions at a much faster rate with respect to helical motion (ns time scale).⁴² U38 forms H-bonds with A27, and it is also stacked between C37 and C39 for all the simulation time. Moreover, the U38 glycosidic angle populates one single state (χ ca. 160°) with limited motions in the ns timescale (Fig. 4C and Figs. S16–18, right panels). This is fully consistent with the ssNMR data, which shows that U38 experiences small-amplitude local motions at a much faster rate with respect to helical motion (ns time scale).⁴² In conclusion, our results are in good agreement with ssNMR data collected on samples singly labelled at U23, U25 and U38.

The comparison with the simulations in ref.²⁸ is necessarily limited to RDCs, and cannot be extended to all of the available NMR data on TAR (including order parameters S² and time scale of motion of nucleotides) that are only reported in the present study. There are two available RDC’s data sets, measured in different conditions. The first data set is measured in aqueous solution,⁴⁰ consistent with our simulations. The RDCs of the second data set²⁸ are measured using an orienting medium of TAR variants with elongated stems,^c whose structural and dynamics properties may be different from those of native TAR in aqueous solutions. Comparing calculated RDC’s values with the data from ref.⁴⁰ (Fig. 2 and S19) is more meaningful than a comparison with the data of ref.²⁸. Although the latter authors do not report quantitative measures of the correlation between experimental and predicted RDC’s (e.g. correlation coefficients), visual inspection of the correlation plots indicates that our predictions are more accurate.

CONCLUDING REMARKS

RNA’s functional complexity is rooted not only in its intricate 3D structure but also depends on its dynamics. Motions in RNA indeed range from local changes in base-pairing to large-scale collective bending and twisting of helical domain, all of which occur over a range of timescales.⁴ The complex multilayer dynamics of TAR was here addressed by means of four microsecond-long MD simulations with the new AMBER force field. Several order parameters, previously measured in NMR experiments, are quantitatively reproduced with unprecedented agreement by the simulations. Building on the accord between computation and experiment, we investigated the unresolved issue of the typical timescale governing large-scale motions in TAR. On the one hand, the calculations support unambiguously the conclusion that dynamics occurs in the ns-µs time scale (consistent with ssNMR studies), a rate compatible with RNA-ligand binding processes.⁴ This shows that the associated internal dynamics has a functionally-oriented character. On the other hand, by using a suitable multiscale analysis, we conclude that conformational exchange processes relevant to ligand binding (namely transitions between the apo and holo forms) occur in the near-µs time scale. This conclusion is consistent with the findings of ssNMR measurements^41,42,59 that indicate a key role of stochastic hinge-bending motion of TAR occurring in the hundreds of ns time scale for inducing a conformation conducive to Tat binding. The current atomistic simulations extend significantly the insight offered by NMR by elucidating, with unprecedented structural detail, the innate internal dynamics of TAR and its functionally-oriented implications.