Abstract
The optic nerve (ON) is a vital structure in the human visual system and transports all visual information from the retina to the cortex for higher order processing. Due to the lack of redundancy in the visual pathway, measures of ON damage have been shown to correlate well with visual deficits. These measures are typically taken at an arbitrary anatomically defined point along the nerve and do not characterize changes along the length of the ON. We propose a fully automated, three-dimensionally consistent technique building upon a previous independent slice-wise technique to estimate the radius of the ON and surrounding cerebrospinal fluid (CSF) on high-resolution heavily T2-weighted isotropic MRI. We show that by constraining results to be three-dimensionally consistent this technique produces more anatomically viable results. We compare this technique with the previously published slice-wise technique using a short-term reproducibility data set, 10 subjects, follow-up <1 month, and show that the new method is more reproducible in the center of the ON. The center of the ON contains the most accurate imaging because it lacks confounders such as motion and frontal lobe interference. Long-term reproducibility, 5 subjects, follow-up of approximately 11 months, is also investigated with this new technique and shown to be similar to short-term reproducibility, indicating that the ON does not change substantially within 11 months. The increased accuracy of this new technique provides increased power when searching for anatomical changes in ON size amongst patient populations.
Keywords: Magnetic Resonance Imaging, Optic Nerve, Conjugate Gradient Descent, Intensity Model Fitting
1. INTRODUCTION
The human optic nerve (ON) is integral to visual performance as it carries all visual information posterior from the retina to the cortex for visual processing and is thus compromised in a number of diseases, most notably, multiple sclerosis (MS) [1], as well as several forms of optic neuropathy [1, 2]. Optic neuritis is known to be closely linked with MS as 25% of optic neuritis events eventually develop into MS [3]. However, despite this known association there are no current radiological biomarkers which can predict the eventual development of MS or the degree of visual recovery following an optic neuritis event. Therefore, while the ON is essential to visual function, it is challenging to image and quantify due to the fact that it is a small structure which is constantly in motion. The ON is surrounded by a sheath of cerebrospinal fluid (CSF). The size of this CSF sheath has been shown to correlate with intracranial pressure which may be associated with increased mortality and less favorable neurological outcomes [4]. Qualitatively, tools have been developed to visualize ON degradation utilizing high-resolution MRI but automatic quantitative methods are lacking.
Manual or computer-assisted measurements are still the tiresome standard for quantification of the ON. Hickman et al. used manual contouring to measure ON cross-sections in a longitudinal analysis and found patterns consistent with acute inflammation followed by long-term atrophy [5, 6]. These measurements of optic nerve size are often taken at arbitrary points along the length of the ON and thus suffer because they would require significantly more time manually labeling cross sections to investigate local changes along the length of the nerve due to a lack of automated analysis techniques. A more detailed analysis of the ON may reveal anatomical patterns as well as other temporal patterns in disease state evolution. Automated segmentation methods have largely focused on segmenting the ON and CSF as a single structure, deeming it too challenging to measure the two independently [7, 8]. However, a previously presented slice-wise method addressed some of these concerns but yielded results which were useful in aggregate but could be difficult for interpretation on the single subject-level [9, 10]. Therefore, we propose a fully automated, three-dimensionally consistent technique, building upon the previous independent slice-wise technique, to estimate the radius of the ON and surrounding CSF on high-resolution heavily T2-weighted isotropic MRI.
2. METHODOLOGY
Proposed Method
Radius estimation begins with a previously described multi-atlas segmentation method [11], which automatically segments the orbits, optic chiasm and ON including the surrounding CSF for initialization purposes. This method uses 35 manually labeled atlas images, which include both healthy controls as well as ON head drusen, optic neuritis and MS patients. The target image to be segmented is registered to each of the 35 atlas images using an affine registration [12] to achieve a coarse alignment of the eye globes. The globe labels are summed for all 35 atlases to achieve a pseudo-probability map which is thresholded at 0.5 (or 18 atlas images indicating globe for a particular voxel). The centroids of each eye globe are extracted from this coarse hard segmentation and extended 30mm left, right and anteriorly, 40mm superiorly and inferiorly and 60mm posteriorly to define the cropping region. An affine and non-rigid registration of the cropped region to the cropped atlas images results in a more accurate transformation of the atlases to target space [13]. The manual labels of the atlas images are then transformed to the target space using these registrations and are fused using joint label fusion [14]. The segmentation of the ON includes both the ON and surrounding CSF so we must refine our segmentation to separate the two structures and measure them independently. The centroids of the ON label in the coronal plane are used as an initial estimate of the centerline of the ON. A cubic regression is performed to smooth the centerline and fill in any missing slices [15]. Patches are then extracted along this centerline for fitting to the following intensity model.
| (1) |
| (2) |
| (3) |
We begin with a previously described model [16] which can be seen in Equation (1) to fit the ON and CSF sheath in the coronal plane and extract the radii of both. Briefly, the model is a difference of two Gaussian distributions, as defined in Equation (3), which closely resembles the intensity profile of the ON in the coronal plane in our heavily T2-weighted imaging. The covariance matrix in Equation (3) allows for the model to become elliptical to account for off-axis imaging of the ON. The model is fit to the ON in the coronal plane using an iterative conjugate gradient descent optimization method [17].
In the novel variant of the method proposed herein, three-dimensional consistency is enforced through an iterative fitting procedure of this model. The length of the ON is initially fit with the model and each of the eight parameters are smoothed using a 5-element moving window average. Any points falling outside of a threshold n standard deviations away from the regression, nσθ, are considered outliers and those slices are reinitialized with the regression value as their initial parameter values. The error term for the gradient descent is also winsorized at a value of ζ. The tolerance for n and ζ are simultaneously decreased with each iteration until a smooth set of parameters is converged upon.
The model parameters are correlated with the radii of the ON and CSF sheath through a random forest regression[18] using 1 million synthetic training images. Six of the eight model parameters are used for the regression, the centroids are omitted as they are dependent solely on field of view. The standard deviation parameters, [σx,σy], are transformed to be a minimum and maximum term. It was experimentally observed that these terms can interchange for a single radius given the complementary angles of a nerve relative to the imaging plane. By characterizing the terms as a minimum and maximum, we force the radius transformation to be rotationally invariant to the fitting process and improves smoothness of the transformation. The 1 million training images were generated by simulating partial volume effects of imaging two concentric tubular structures with 0.6 mm isotropic voxels using a Monte Carlo simulation. This model is then tilted at randomly selected varying angles relative to the imaging plane and the size of each of the concentric tubes is varied randomly to generate the training set. The regression is validated using tenfold cross validation which shows the predicted radii to correlate with the true underlying simulated radii with an explanatory R-squared greater than 0.95 for both ON and CSF radii.
Data Acquisition
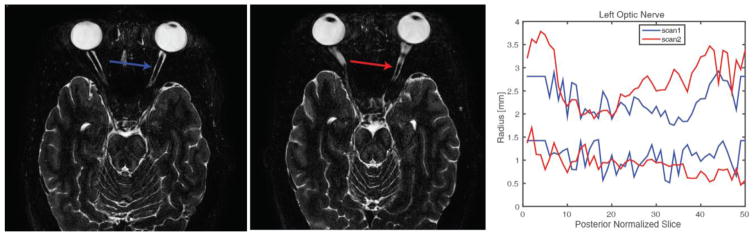
Ten healthy subjects age 24 to 36 years (average: 28.25, median: 27 years, 6 male/4 female) were enrolled in the imaging study, after obtaining consent from the local institutional review board. Imaging was acquired on a 3T Philips Achieva (Philips Medical Systems, Best, The Netherlands) with a 2-channel multi-transmit body coil for transmission and an 8 channel head coil for reception. After tri-planar localization, we acquired all volumes in the axial plane. These images were collected with a Volume ISotropic Turbo spin echo Acquisition (VISTA) imaging sequence with the following parameters: 3D TSE TR = 4000ms, TE = 455ms, α = 90°, FOV= 180 × 180 × 20mm3, acquired resolution = 0.55 × 0.55 × 0.55mm3, reconstructed resolution = 0.35 × 0.35 × 0.35mm3, SENSE factor = 2, fat saturation = SPIR, NSA=2 and total scan time = 7:48. Subjects were scanned with a baseline scan and again within 30 days of the original scan for short-term reproducibility. Inter-scan time was from 4 to 29 days (average: 19.4 days, median: 23 days). Figure 1 shows an example short term scan-rescan image pair. Five of the 10 subjects were also imaged 11 months later for a long-term follow-up scan with the same acquisition scheme.
Figure 1.
An example subject’s short term scan-rescan imaging showing scan 1 (left), scan 2 (middle) 19 days apart shown in radiological standard orientation. The right plot shows the measurement of the left optic nerve for scan 1(blue) and scan 2(red) illustrating the noise in the slice-wise measurements which warrant three-dimensional constraint.
Analysis: Short- and Long-Term Reproducibility
The original slice-wise analysis method [9] and the proposed method are performed on the above data for comparison. The shape of the ON often results in a variable number of coronal slices between individuals and within individuals across different scans. For comparison each ON was interpolated to be the same length as the longest ON in the population, we refer to this as posterior normalized slice. Scan-rescan error is quantified as the absolute difference for each point along the ON. Scale-invariant smoothness (Equation 5) for each method is computed as the standard deviation of the difference between neighboring points scaled by the absolute mean difference of all neighboring points within the nerve. All tests for significance are performed using Wilcoxon sign-rank (p<0.05).
| (4) |
| (5) |
3. RESULTS
Short-Term Reproducibility Results
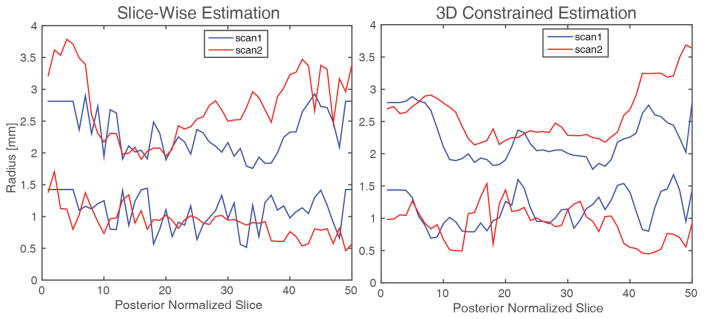
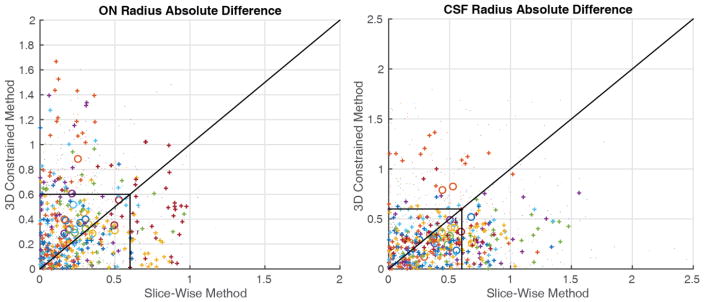
The 3D constrained results are smoother along the length of the ON, as computed by scale-invariant smoothness (p=0.0025), providing more anatomically plausible results since the ON does not change size rapidly. Figure 2 shows a qualitative comparison of the slice-wise results and the 3D constrained results. The 3D constrained results are much smoother along the length of the ON providing more anatomically plausible results since the ON does not change size rapidly. Figure 3 shows the absolute error between the baseline and short term follow-up scans for the aligned ON points. The circles are mean absolute error for a single nerve, with colors representing each subject. The individual points which are dots are the absolute difference between two measurements outside the middle third of the ON, the points which are pluses are the absolute difference between two points within the middle third of the ON again with color corresponding to subjects. The black box indicates error of one voxel and the line of unity separates points with lower slice-wise error (above) and lower 3D constrained error (below). We can see that the majority of the circles and pluses are grouped within the box indicating absolute difference of less than one voxel for the entirety of the nerve and the points within the central third of the ON respectively. There are a large number of CSF sheath measurements (13%) within the central third of the ON which were previously larger than one voxel reproducibility which are now less than one voxel, of the CSF measurements previously outside one voxel nearly all (89%) are now within one voxel.
Figure 2.
Example radius estimation from slice-wise estimation (left) and constrained estimation (right) on the same ON from Figure 1 showing the smoothness of the constrained estimation method results.
Figure 3.
Comparison of scan-rescan absolute error for the ON (left) and CSF (right). Large circles indicate the mean absolute error for a given nerve. Dots indicate individual points between nerves with the color corresponding to each subject. Pluses are individual points between nerves within the central third of the length of the nerve, the area which is most accurately imaged. The lines are drawn along unity and at resolution (0.6mm). Note that pluses tend to be localized within the box indicating reproducibility within a voxel for the central third of the nerve as well pluses being localized below the line of unity indicating the proposed method has lower absolute error between scans.
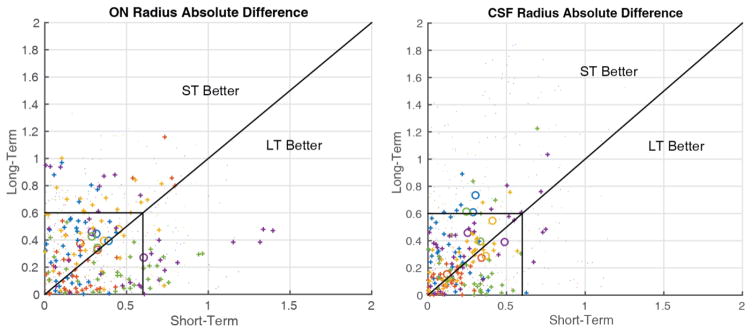
Long-Term Reproducibility
Figure 4 shows a comparison of the short- and long-term reproducibility using the proposed method for the five subjects with long-term follow-up data. The symbols are the same as Figure 3 with circles representing a subject’s ON, pluses indicating individual points within the central third of the ON and dots representing individual points outside the central third. The black box is drawn at resolution and we can see that the majority of points fall within one voxel difference. The subject-wise ON reproducibility, represented by circles, is largely centered along the line of unity indicating that the short- and long-term reproducibility of the ON measurements are similar. While the subject-wise CSF reproducibility trends above the line indicating larger differences between the baseline and long-term follow-up scans than between baseline and the short-term follow-up scans.
Figure 4.
Comparison of short- and long-term scan-rescan absolute error for the ON (left) and CSF (right). Large circles indicate the mean absolute error for a given nerve. Dots indicate individual points between nerves with the color corresponding to each subject. Pluses are individual points between nerves within the central third of the length of the nerve, the area which is most accurately imaged. The lines are drawn along unity and at resolution (0.6mm). Note that pluses tend to be localized within the box indicating reproducibility within a voxel for the central third of the nerve.
4. DISCUSSION
We have demonstrated the superiority of our proposed three-dimensionally consistent ON radius estimation procedure as compared to the previous slice-wise radius estimation procedure in generating anatomically viable results which are reproducible with error of less than the voxel resolution. Future work should address challenges faced in accurately characterizing the anterior ON in the presence of retrobulbar motion and the posterior ON in the presence of frontal lobe CSF to improve characterization along the entire length of the ON. A larger cohort of subjects with long-term follow-ups will be necessary to evaluate the long-term changes in ON morphology with more certainty.
Long-term reproducibility has been shown to be similar to short-term reproducibility indicating that the ON and surrounding CSF do not change substantially within a one year period. Histological studies have shown that there is a slow loss of axons in the optic nerve with normal aging [19–21], but the morphological differences in a 1 year period are expected to be very small based on minimal (if any) change in the optic disk [22–26]. To date, the authors are not aware of studies that have longitudinally followed human optic nerve morphometry in vivo.
The large variability in ON size suggests that a much larger number of subjects will be required to characterize normal ON variability [26]. With a larger set of controls [10] evaluated with this method they could be compared against disease populations, such as acute optic neuritis or MS to investigate possible imaging biomarkers for disease severity or prognosis.
Automatically characterizing the entire ON from globe to chiasm will allow for more meaningful searches for imaging biomarkers by the clinical community possibly revealing latent local changes in the ON which offer prognostic value.
All tools used and developed in this work are available in open source from their respective authors. The ON-CSF measurement code is primarily written in MATLAB (The MathWorks, Inc., Natick, Massachusetts, United States) and bundled into an automated program (i.e., “spider” [27]) that combines these tools using PyXNAT [28] and DAX[29] for XNAT [30] and is available through the NITRC project MASIMATLAB (http://www.nitrc.org/projects/masimatlab).
Acknowledgments
Research reported in this publication was supported in part by the National Institutes of Health R21EY024036, R01EY023240 and 5T32EY007135. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Research was supported by Vanderbilt Vision Research Center NEI Core Grant (P30-EY008126). This project was supported in part by ViSE/VICTR VR3029. The project described was supported by the National Center for Research Resources, Grant UL1 RR024975-01, and is now at the National Center for Advancing Translational Sciences, Grant 2 UL1 TR000445-06. This work was conducted in part using the resources of the Advanced Computing Center for Research and Education at Vanderbilt University, Nashville, TN.
References
- 1.Group ONS. Multiple sclerosis risk after optic neuritis: final optic neuritis treatment trial follow-up. Archives of neurology. 2008;65(6):727. doi: 10.1001/archneur.65.6.727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rizzo JF, III, Andreoli CM, Rabinov JD. Use of magnetic resonance imaging to differentiate optic neuritis and nonarteritic anterior ischemic optic neuropathy. Ophthalmology. 2002;109(9):1679–1684. doi: 10.1016/s0161-6420(02)01148-x. [DOI] [PubMed] [Google Scholar]
- 3.Toosy AT, Mason DF, Miller DH. Optic neuritis. The Lancet Neurology. 2014;13(1):83–99. doi: 10.1016/S1474-4422(13)70259-X. [DOI] [PubMed] [Google Scholar]
- 4.Geeraerts T, Newcombe VF, Coles JP, et al. Use of T2-weighted magnetic resonance imaging of the optic nerve sheath to detect raised intracranial pressure. Critical Care. 2008;12(5):R114. doi: 10.1186/cc7006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hickman SJ, Toosy AT, Jones SJ, et al. A serial MRI study following optic nerve mean area in acute optic neuritis. Brain. 2004;127(Pt 11):2498–505. doi: 10.1093/brain/awh284. [DOI] [PubMed] [Google Scholar]
- 6.Hickman SJ, Brierley CM, Brex PA, et al. Continuing optic nerve atrophy following optic neuritis: a serial MRI study. Mult Scler. 2002;8(4):339–42. doi: 10.1191/1352458502ms809oa. [DOI] [PubMed] [Google Scholar]
- 7.Yiannakas MC, Toosy AT, Raftopoulos RE, et al. MRI Acquisition and Analysis Protocol for In Vivo Intraorbital Optic Nerve Segmentation at 3T. Investigative ophthalmology & visual science. 2013;54(6):4235–4240. doi: 10.1167/iovs.13-12357. [DOI] [PubMed] [Google Scholar]
- 8.Panda S, Asman AJ, Khare SP, et al. Evaluation of multiatlas label fusion for in vivo magnetic resonance imaging orbital segmentation. Journal of Medical Imaging. 2014;1(2):024002–024002. doi: 10.1117/1.JMI.1.2.024002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Harrigan RL, Plassard AJ, Bryan FW, et al. Disambiguating the optic nerve from the surrounding cerebrospinal fluid: Application to MS-related atrophy. Magnetic Resonance in Medicine. 2015 doi: 10.1002/mrm.25613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Harrigan RL, Plassard AJ, Mawn LA, et al. Constructing a statistical atlas of the radii of the optic nerve and cerebrospinal fluid sheath in young healthy adults. :941303–941303-7. doi: 10.1117/12.2081887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Harrigan RL, Panda S, Asman AJ, et al. Robust optic nerve segmentation on clinically acquired computed tomography. Journal of Medical Imaging. 2014;1(3):034006–034006. doi: 10.1117/1.JMI.1.3.034006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ourselin S, Roche A, Subsol G, et al. Reconstructing a 3D structure from serial histological sections. Image and vision computing. 2001;19(1):25–31. [Google Scholar]
- 13.Avants BB, Tustison NJ, Song G, et al. A reproducible evaluation of ANTs similarity metric performance in brain image registration. Neuroimage. 2011;54(3):2033–2044. doi: 10.1016/j.neuroimage.2010.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang H, Suh JW, Das SR, et al. Multi-atlas segmentation with joint label fusion. IEEE transactions on pattern analysis and machine intelligence. 2013;35(3):611–623. doi: 10.1109/TPAMI.2012.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Frohman EM, Dwyer MG, Frohman T, et al. Relationship of optic nerve and brain conventional and non-conventional MRI measures and retinal nerve fiber layer thickness, as assessed by OCT and GDx: a pilot study. Journal of the neurological sciences. 2009;282(1):96–105. doi: 10.1016/j.jns.2009.04.010. [DOI] [PubMed] [Google Scholar]
- 16.Harrigan RL, Plassard AJ, Bryan FW, et al. Disambiguating the Optic Nerve from the Surrounding Cerebrospinal Fluid Sheath in MS-related Atrophy. Magnetic Resonance in Medicine. 2014 doi: 10.1002/mrm.25613. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nocedal J, Wright SJ. Conjugate gradient methods. Springer; 2006. [Google Scholar]
- 18.Breiman L, Friedman J, Stone CJ, et al. Classification and regression trees. CRC press; 1984. [Google Scholar]
- 19.Johnson BM, Miao M, Sadun AA. Age-related decline of human optic nerve axon populations. Age. 1987;10(1):5–9. [Google Scholar]
- 20.Mikelberg FS, Drance SM, Schulzer M, et al. The normal human optic nerve: axon count and axon diameter distribution. Ophthalmology. 1989;96(9):1325–1328. doi: 10.1016/s0161-6420(89)32718-7. [DOI] [PubMed] [Google Scholar]
- 21.Balazsi A, Rootman J, Drance S, et al. The effect of age on the nerve fiber population of the human optic nerve. American journal of ophthalmology. 1984;97(6):760–766. doi: 10.1016/0002-9394(84)90509-9. [DOI] [PubMed] [Google Scholar]
- 22.Bowd C, Zangwill LM, Blumenthal EZ, et al. Imaging of the optic disc and retinal nerve fiber layer: the effects of age, optic disc area, refractive error, and gender. JOSA A. 2002;19(1):197–207. doi: 10.1364/josaa.19.000197. [DOI] [PubMed] [Google Scholar]
- 23.Moya FJ, Brigatti L, Caprioli J. Effect of aging on optic nerve appearance: a longitudinal study. British journal of ophthalmology. 1999;83(5):567–572. doi: 10.1136/bjo.83.5.567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Varma R, Tielsch JM, Quigley HA, et al. Race-, age-, gender-, and refractive error—related differences in the normal optic disc. Archives of Ophthalmology. 1994;112(8):1068–1076. doi: 10.1001/archopht.1994.01090200074026. [DOI] [PubMed] [Google Scholar]
- 25.Jonas JB, Schmidt AM, Müller-Bergh J, et al. Human optic nerve fiber count and optic disc size. Investigative ophthalmology & visual science. 1992;33(6):2012–2018. [PubMed] [Google Scholar]
- 26.Repka MX, Quigley HA. The effect of age on normal human optic nerve fiber number and diameter. Ophthalmology. 1989;96(1):26–32. doi: 10.1016/s0161-6420(89)32928-9. [DOI] [PubMed] [Google Scholar]
- 27.Gao Y, Burns SS, Lauzon CB, et al. Integration of XNAT/PACS, DICOM, and Research Software for Automated Multi-modal Image Analysis. Proc SPIE. 2013;8674 doi: 10.1117/12.2007621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schwartz Y, Barbot A, Thyreau B, et al. PyXNAT: XNAT in Python. Front Neuroinform. 2012;6:12. doi: 10.3389/fninf.2012.00012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Harrigan RL, Yvernault BC, Boyd BD, et al. Vanderbilt University Institute of Imaging Science Center for Computational Imaging XNAT: A multimodal data archive and processing environment. NeuroImage. 2016;124:1097–1101. doi: 10.1016/j.neuroimage.2015.05.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Marcus DS, Olsen TR, Ramaratnam M, et al. The Extensible Neuroimaging Archive Toolkit: an informatics platform for managing, exploring, and sharing neuroimaging data. Neuroinformatics. 2007;5(1):11–34. doi: 10.1385/ni:5:1:11. [DOI] [PubMed] [Google Scholar]