A Bayesian Approach for Population Pharmacokinetic Modeling of Alcohol in Japanese Individuals

Abstract

Background

Blood alcohol concentration data that were previously obtained from 34 healthy Japanese subjects with limited sampling times were reanalyzed. Characteristics of the data were that the concentrations were obtained from only the early part of the time-concentration curve.

Objective

To explore significant covariates for the population pharmacokinetic analysis of alcohol by incorporating external data using a Bayesian method, and to estimate effects of the covariates.

Methods

The data were analyzed using a Markov chain Monte Carlo Bayesian estimation with NONMEM 7.3 (ICON Clinical Research LLC, North Wales, Pennsylvania). Informative priors were obtained from the external study.

Results

A 1-compartment model with Michaelis-Menten elimination was used. The typical value for the apparent volume of distribution was 49.3 L at the age of 29.4 years. Volume of distribution was estimated to be 20.4 L smaller in subjects with the ALDH2*1/*2 genotype than in subjects with the ALDH2*1/*1 genotype.

Conclusions

A population pharmacokinetic model for alcohol was updated. A Bayesian approach allowed interpretation of significant covariate relationships, even if the current dataset is not informative about all parameters. This is the first study reporting an estimate of the effect of the ALDH2 genotype in a PPK model.

Introduction

Alcohol (ethanol) is among the oldest recreational drugs. Population pharmacokinetic (PPK) analysis assumes the presence of interindividual variations in pharmacokinetic (PK) parameters and attempts to explain this in terms of an individual’s characteristics that could affect the PK model parameters. Thus, developing a PPK model of alcohol is essential to understand the effects of an individual׳s characteristics on the time course of alcohol metabolism, and consequently the degree of organ exposure to alcohol, after the ingestion of an alcoholic beverage.

Alcohol is eliminated from the body primarily through oxidization reaction in the liver. It is catalyzed by alcohol-metabolizing enzymes known as alcohol dehydrogenases (ADHs) to acetaldehyde, which is metabolized by aldehyde dehydrogenases (ALDH).¹ There are multiple ADH and ALDH enzymes that are encoded by different genes.² ADH1B is the best-studied ADH gene and has been replicated consistently showing a strong association with the prevalence of alcohol dependence.³ With regard to ALDH, the ALDH 2*2 allele has shown this strong association with alcohol dependence⁴ and is known to encode an almost inactive enzyme.⁵ A genetic variant of ADH1B (ADH1B*2) encodes enzyme with higher activity compared with a wild type (ADH1B*1), and a genetic variant of ALDH2 (ALDH2*2) encodes an essentially inactive ALDH2 enzyme, resulting in acetaldehyde accumulation after drinking alcohol.⁶

We searched PubMed using the query “population pharmacokinetic analysis alcohol AND (breath OR blood)” during August 2016. There were 5 published studies on the PPK of alcohol, including our previous study. Clardy⁷ analyzed the blood alcohol concentration (BAC) data from 55 healthy subjects who consumed 0.12 to 0.93 g ethanol per kilogram body weight and developed a 2-compartment model with first-order absorption and Michaelis-Menten elimination, although contributions of covariates to the interindividual variation of PK parameters were not investigated. Yang et al⁸ reported food ingestion, sex, and body weight as covariates of a 1-compartment model for the BAC data from 184 healthy subjects who consumed 0.5 to 0.7 g/kg ethanol. Lee et al⁹ reported age, body weight, and dissolved oxygen concentration in beverage as covariates of a 1-compartment model with Michalis-Menten elimination for the BAC data from 59 healthy subjects who consumed an average dose of ethanol of 55.39 g. Seng et al¹⁰ investigated genetic polymorphisms in the alcohol-metabolizing enzymes, in addition to demographic characteristics and reported sex, body weight, and genetic polymorphism in ADH1B for a 1-compartment model with Michalis-Menten elimination for 154 healthy subjects who ingested 54 or 36 g ethanol over an hour, together with a standardized light meal to mimic social drinking. Previously, we reported age, body weight, and genotype of ADH1B as covariates by analyzing the BAC data measured in 34 healthy subjects after consuming 17.5 g ethanol during 15 minutes without a meal by a 1-compartment model.¹¹ However, none of these studies succeeded in estimating the effects of the genotype of ALDH2.

The Bayesian approach has been suggested as a valuable tool for information gathering in the context of PPK modeling, which allows the incorporation of prior information into the modeling for current data.12, 13, 14 Our data consist of only the early part of the time-concentration curve and are not informative about all of the parameters for relatively complex models, such as 1- or 2-compartment models with a Michalis-Menten elimination process. It has been suggested that a Bayesian approach to develop a PPK model with informative priors allowed interpretation of a significant covariate relationship, even using poorly informative data.¹²

The objective of this study was to update the PPK model for alcohol. We explored additional significant covariates using our previously obtained BAC data by incorporating the external result of PPK modeling for alcohol using a fully conditional Bayesian estimation.

Materials and Methods

Dataset

A total of 157 BAC observations previously obtained from 34 healthy Japanese subjects (21 men and 13 women) aged 20 to 62 years at ethanol concentrations ranging from 0.0014 to 0.41 g/L¹¹ were reanalyzed. Characteristics of subjects that were surveyed included age, sex, body weight, and genotypes of alcohol-metabolizing enzymes (ADH1B and ALDH2). Of 34 subjects, 21 (62%) carried ALDH2*1/*1 and 13 (38%) carried ALDH2*1/*2. The study was conducted in compliance with the ethical principles originating in or derived from the Declaration of Helsinki. The study protocol was approved by the research ethics committee of the Faculty of Medicine, Osaka University, Japan. Written informed consent was provided by all participants.

Software

The time-concentration data were analyzed using NONMEM 7.3 (ICON Clinical Research LLC, North Wales, Pennsylvania). SAS 9.4 (SAS Institute Inc, Cary, North Carolina) and R version 3.3.1 (R Foundation for Statistical Computing, Vienna, Austria) were used for exploratory analysis in the model-building process and for the model validation.

Bayesian analysis

A fully conditional hierarchical Bayesian analysis was conducted using the NONMEM with $PRIOR NWPRI statement, which allowed priors for the population mean PK (PM-PK) parameter vector $\Theta$ being a normal distribution and the variance of individual PK parameters Ω being an inverse Wishart distribution.¹⁴ The normal prior was specified with mean, $\widehat{\Theta }$, and variance, $\widehat{\Gamma }$. The $\widehat{\Theta }$ value was derived from parameter estimates of the fixed-effect parameters in the previous analysis. The $\widehat{\Gamma }$ value was obtained from the variance of the parameter estimates of the previous analysis, where the off-diagonal elements of $\widehat{\Gamma }$ were assumed to be zero. The inverse Wishart prior was specified with mode $\widehat{\Omega }$ and degrees of freedom (df). The diagonal-element values of $\widehat{\Omega }$ were obtained from estimates of the interindividual variance of PK parameters in the previous analysis and off-diagonal elements were set to be zero, whereas the df was calculated according to the formula recommended by Karlsson.¹⁴

Markov chain Monte Carlo (MCMC) Bayesian estimation was conducted. The maximum number of samples of the burn-in phase was set to 100,000 and a termination test for the burn-in phase of MCMC chains was used. At every 100th iteration, a linear regression was performed on each parameter and an objective function (MCMCOBJ in NONMEM 7.3). If the slope of the linear regression was not statistically different from 0 for all parameters, then the burn-in phase was terminated. The MCMC chain was run for 10,000 samples to make an inference about posterior distributions of the parameters.

Prior information

The prior distributions of parameters were obtained from a report by Seng et al,¹⁰ which was the most preferable among 4 studies conducted before our study because subjects were from Asian populations (Chinese and Indian), and all covariates of the final model (body weight, sex, and the genotype for ADH1B) were obtained from the subjects in our previous study.

Model building

We conducted PPK analysis according to the following steps: Step 1, adoption of external information to the analysis of current dataset, by defining priors from the estimates of PPK parameters and the covariates of the model of Seng et al,¹⁰ which is referred to as the base model in this article; and Step 2, additional covariate modeling was performed. The model developed in Step 2 was named the final model.

After fitting the base model in Step 1, scatter plots showing the relationship between the posterior median value of individual PK parameters and a range of variables were visually investigated to screen for potential covariates. Among 5 characteristics (age, sex, body weight, ADH1B, and ALDH2) of the subjects in our data pool, age, and the genotype of ALDH2 were investigated. This was done because the other 3 variables were included in the base model. Age was modeled as a continuous variable and centered around the median value, and is generally expressed as

$$P={\theta }_P\cdot {\left(covariate/media{n}_{cov}\right)}^{{\theta }_{cov\left(P\right)}}$$ (1)

where $P$ is the population mean PM-PK parameter conditional to a covariate value, ${\theta }_P$ is the typical PK parameter, namely $k_a$ or $V_d/F$ for the covariate equal median, and ${\theta }_{cov\left(P\right)}$ is a covariate scale factor on P. The genotype of ALDH2 was modeled as a dichotomous variable, generally expressed using an indicator variable (IND) being 0 or 1 as

$$P={\theta }_P+{\theta }_{cov}\cdot \mathrm{IND}$$ (2)

where ${\theta }_P$ is the PM-PK value when IND being 0, and ${\theta }_{cov}$ is the change in the parameter value when IND is 1.

Model selection for inclusion of a covariate in the final model was based on a decrease in the mean of the deviance distribution (equivalent to –2 log likelihood), a decrease in the mode of the between subject variance and/or a decrease in the mean of the residual error, and a probability of clinically significant influence on the parameter values, defined as a change in the population parameter of at least 20% between subjects with the lowest and the highest covariate value in the data set.

Base model

The basic PPK model that Seng et al¹⁰ reported was a 1-compartment model with first-order absorption and mixed linear and time-dependent nonlinear (Michaelis-Menten) elimination. In this model, concentration, denoted as C, is expressed as

$$\frac{dC}{dt}=\left(k_a\cdot D\cdot e^{-k_{a}t}-\frac{V_{max}}{K_m+C}\cdot C\right)\cdot \frac{1}{V_d/F}$$ (3)

where $k_a$, D, $V_{max}$, $K_m$, and $V_d/F$ are the first-order absorption rate constant, dose, the maximum metabolic rate, and Michaelis-Menten constant and the apparent distribution volume, respectively. Interindividual variability in PK parameters was modeled by assuming a lognormal distribution, generally described as

$${\theta }_i=\theta \cdot exp\left({\eta }_{{\theta }_i}\right)$$ (4)

where ${\theta }_i$ is the PK parameter of the ith individual, ${\eta }_{{\theta }_i}$ is an interindividual random effect normally distributed with a mean of zero and variance of ${\omega }_{\theta }^2$, and $\theta$ is the PM-PK parameter, represents $k_a$, $V_{max}$, $K_m,$ or $V_d/F$. The details for the model between population PK parameters and covariates are described in Appendix 1. The residual variability was modeled with a proportional error structure, described as

$$C_{ij}^{obs}=C_{ij}^{pred}\cdot \left(1+{\epsilon }_{ij}\right)$$ (5)

where $C_{ij}^{pred}$ is the jth observation of the ith individual predicted by the PK model, $C_{ij}^{obs}$ is the observed concentration, and ${\epsilon }_{ij}$ represents the residual departure of the model from the jth observation from the ith individual. The variable ${\epsilon }_{ij}$ is a normally distributed random variable with a mean of zero and variance of ${\sigma }^2$. All off-diagonals of the population covariance matrix were set to zero.

Model validation

The final model was assessed with goodness-of-fit plots, including visual predictive checks. For visual predictive checks evaluations, 1000 sets of virtual subject groups were created by using bootstrap sampling. Then, individual PK parameters were simulated. To predict ethanol exposures, the concentrations for dense sampling time points were obtained by solving ordinary differential equations using “deSolve” in R software because the elimination process follows Michalis-Menten kinetics. The percentiles of simulated BACs were plotted and compared with the observed data.

Results

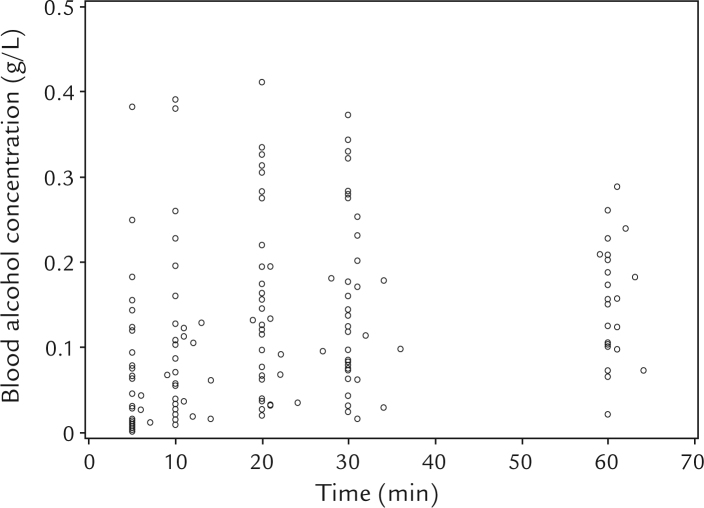
The BACs previously obtained from 34 healthy Japanese subjects (157 observations) were analyzed, and a plot for the BAC versus time after the end of beer consumption is shown in Figure 1. The study population, dosing regimen, sampling plan, and the analysis model are summarized in Table I. We fitted the base model, a 1-compartment model, with Michalis-Menten elimination process that includes sex, body weight, and genotype of ADH2 as covariates. Mean and SD values of priors for the PM-PK parameters and mode of the respective prior for the interindividual variance of the PM-PK parameters were obtained from the parameter estimates of the model reported by Seng et al¹⁰ and are listed in Table II. The study population, dosing regimen, sampling plan, and the analysis model of the study, from which the prior information was obtained,¹⁰ are summarized in Table I. The df for random-effects parameters was calculated and set to 35. The base model was fitted to the current data, and most of the estimated values were in agreement with the priors as shown in the column “Base model” in Table II. Relatively large changes in the posterior distributions of $k_a$ and ${\omega }_{k_a}$ compared to the prior distributions were observed. This seems to be because our data were more informative about $k_a$ and ${\omega }_{k_a}$.

Figure 1.

Scatter plot of blood alcohol concentration versus time after ingestion of alcohol-containing drinks in 34 subjects (157 observations). Four or 5 concentrations were obtained per subject.

Table I.

Study^* designs.

Population	n	Dose	Sampling plan	Basic pharmokinetic model	Reference
Japanese	13 women, 21 men	14 g ethanol (350 mL beer)10 min in the fasted state	5, 10, 20, 30, 60 min postdose	1 compartment	11
Chinese	36 women, 31 men	36† and 56‡ g ethanol	1.5, 2, 2.5, 3,	1 compartment	10
Indian	43 women, 44 men	200† and 300‡ mL (mixture of vodka and orange juice) 1 h with a meal	3.25, 3.5, 3.75, 4, 4.25, 4.5, 4.75, 5, 6 h postdose	Michaelis-Menten elimination

^⁎The current dataset for reanalysis was obtained from study described in reference ¹¹; the priors for population pharmacokinetic parameters were obtained from reference.¹⁰

^†Dose for women.

^‡Dose for men.

Table II.

Parameter estimates of the base model and the final model for alcohol population pharmacokinetic (PK) analysis, and the prior distributions used in the analysis.

	Mean (SD) of normal prior or mode of inverse Wishart prior*	Estimate for parameters (95% CI)
		Base model	Final model
Population mean PK parameters
$k_a$ (1 / h)	4.4 (0.48)	3.3 (2.7 to 4.1)	3.0 (2.4 to 3.9)
$V_d/F$ (L)	50.2 (1.0)	49.7 (47.8 to 51.7)	49.3 (47.4 to 51.2)
$V_{ma{x}_{ADH1B⁎2/⁎1}}$ ($\mathrm{mg}/\mathrm{h})$	7760 (255)	7827 (7327 to 8310)	7790 (7403 to 8264)
$V_{ma{x}_{ADH1B⁎2/⁎2}}$ ($\mathrm{mg}/\mathrm{h})$	8060 (300)	8197 (7660 to 8731)	7966 (7422 to 8483)
$K_m$ ($\mathrm{mg}/\mathrm{L})$	16.2 (6.9)	0.09 (0.01 to 0.47)	0.074 (0.001 to 0.391)
Regression parameters for covariate model
${\theta }_{AGE\left(k_a\right)}$	0.01 (1000)	–	2.7 (2.1 to 3.4)
${\theta }_{AGE\left(V_d/F\right)}$	0.01 (1000)	–	0.52 (0.19 to 0.83)
${\theta }_{ALDH2\left(V_d/F\right)}$ (L)	0.01 (1000)	–	–20.4 (–27.7 to –10.9)
${\theta }_{WT\left(V_d/F\right)}$	0.78 (0.09)	0.80 (0.63 to 0.98)	0.78 (0.60 to 0.95)
${\theta }_{WT\left(V_{max}\right)}$	0.79 (0.06)	0.77 (0.66 to 0.89)	0.78 (0.66, 0.90)
${\theta }_{SEX\left(k_a\right)}$ (1 / h )	–1.9 (0.5)	–1.9 (-2.6 to –1.1)	-1.3 (-2.1, -0.56)
${\theta }_{SEX\left(V_d/F\right)}$ (L)	–11.4 (1.5)	–11.7 (–14.5 to –8.8)	–12.2 (–15.0 to –9.41)
Between-subject variance
${\omega }_{k_a}^2$	0.29	0.66 (0.45 to 0.95)	0.37 (0.24 to 0.55)
${\omega }_{V_d/F}^2$	0.025	0.028 (0.017 to 0.044)	0.029 (0.018 to 0.048)
${\omega }_{V_{max}}^2$	0.026	0.027 (0.017 to 0.042)	0.027 (0.017 to 0.042)
${\omega }_{K_m}^2$	1.04	1.11 (0.69 to 1.77)	1.13 (0.69 to 1.83)
Residual error (%RSE)
σ2	–	0.034 (0.026 to 0.044)	0.028 (0.020 to 0.038)
Structural model for PK parameters and covariates in the base model:
$k_{a_i}=(k_a+{\theta }_{SEX\left(k_a\right)}\times FEMALE)\times exp({\eta }_{k_{a_i}})$
$V_d/F_i=(V_d/F+{\theta }_{SEX\left(V_d/F\right)}\times FEMALE)\times {\left(WT/61.3\right)}^{{\theta }_{WT\left(V_d/F\right)}}\times exp\left({\eta }_{V_d/F_i}\right)$
$V_{ma{x}_i}=V_{ma{x}_{ADH1B⁎2/⁎2}}\times {\left(WT/61.3\right)}^{{\theta }_{WT(V_{max})}}\times exp\left({\eta }_{V_{ma{x}_i}}\right)$†
$K_{m_i}=K_m\times exp\left({\eta }_{K_{m_i}}\right)$
Structural model for PK parameters and covariates in the final model:‡
$k_{a_i}=(k_a+{\theta }_{SEX\left(k_a\right)}\times FEMALE)\times {\left(age/29.4\right)}^{{\theta }_{AGE\left(k_a\right)}}\times exp\left({\eta }_{k_{a_i}}\right)$
$V_d/F_i=(V_d/F+{\theta }_{SEX\left(V_d/F\right)}\times FEMALE+{\theta }_{ALDH2\left(V_d/F\right)}\times ALDH2)\times {\left(WT/61.3\right)}^{{\theta }_{WT\left(V_d/F\right)}}$$\times {\left(age/29.4\right)}^{{\theta }_{AGE\left(V_d/F\right)}}\times exp\left({\eta }_{V_d/F_i}\right)$

%RSE = percent relative standard error of the estimate, equal to SE/parameter estimate □× 100; ALDH2 = 1 for a subject with ALDH2*1/*2; ALDH2 = 0 for a subject with ALDH2*1/*1; FEMALE = 1 for a female subject; $k_a$ and $k_{a_i}$ = the absorption rate and that for ith individual; $K_m$ and $K_{m_i}$ = Michaelis-Menten constant and that for ith individual; ${\theta }_{AGE\left(V_d/F\right)}$= scale factor for age on $V_d/F$; ${\theta }_{AGE\left(k_a\right)}$= scale factor for age on $k_a$; ${\theta }_{ALDH2\left(V_d/F\right)}$= change in $V_d/F$ for ALDH2; ${\theta }_{WT\left(V_d/F\right)}$= scale factor for WT on $V_d/F$; ${\theta }_{WT\left(V_{max}\right)}$= scale factor for WT on $V_{max}$; ${\theta }_{SEX\left(k_a\right)}$= change in $k_a$ for sex; ${\theta }_{SEX\left(V_d/F\right)}$= change in $V_d/F$ for sex; ${\omega }_{k_a}^2$= interindividual variance of $k_a$; ${\omega }_{V_d/F}^2$= interindividual variance of $V_d/F$; ${\omega }_{V_{max}}^2$= interindividual variance of $V_{max}$; ${\omega }_{K_m}^2$= interindividual variance of $K_m$; ${\sigma }^2$= variance of residual in the proportional error model; ${\eta }_i$= interindividual random effect for ith individual. $V_d/F$ and $V_d/F_i$ = the apparent volume of distribution and that for the ith individual; $V_{max}$, $V_{ma{x}_i}$, $V_{\mathit{ma}{\mathit{x}}_{ADH1B⁎2/⁎1}}$ and $V_{ma{x}_{ADH1B⁎2/⁎2}}$= the maximum metabolic rate, that for ith individual, that for subjects carrying ADH1B*2/*1, and that for subjects carrying ADH1B*2/*2; WT = body weight.

^⁎All of values for prior distribution of model parameters except ${\theta }_{AGE\left(k_a\right)}$, ${\theta }_{AGE\left(V_d/F\right),}$ and ${\theta }_{ALDH2\left(V_d/F\right)}$ were from Seng et al.¹⁰

^†$V_{ma{x}_{ADH2⁎2/⁎2}}$ is replaced with $V_{ma{x}_{ADH2⁎1/⁎2}}$ for the subject with $ADH2⁎1/⁎2.$

^‡Structural model for $V_{ma{x}_i}$ and $K_{m_i}$ is the same as those in the base model.

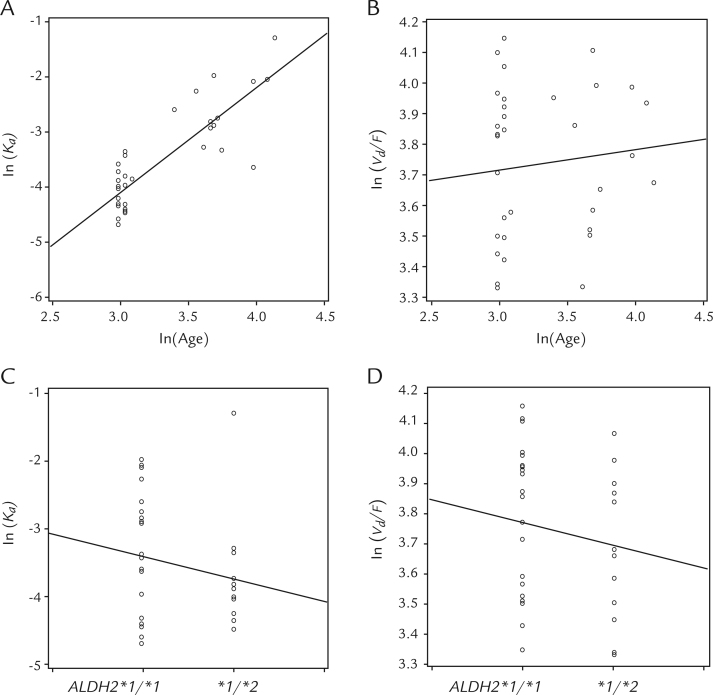
Covariate relationships were investigated for only $k_a$ and $V_d/F$, due to the sparseness of information about the other parameters. Intermediate models in the process of model building are summarized in Table III. Scatter plots of the posterior estimates of individual $k_a$ or the posterior estimates of individual $V_d/F$ versus age or ALDH2 genotype are shown in Figure 2. Among the 4 plots in Figure 2, a trend towards an increase in $k_a$ with advancing age was observed as shown in Figure 2A. The influence of age was modeled by using an exponential model (equation 1). The median age was set to 29.4 years. The informative priors were applied for all of the parameters (as used in the base model) except for ${\theta }_{AGE\left(k_a\right)}$. Prior mean and precision of ${\theta }_{AGE\left(k_a\right)}$ were set to 0.001 and 1,000,000, as a noninformative prior.

Table III.

Pharmacokinetic model building: Effect of addition of covariates to the base model.

Model number and added covariates	Relationship(s)*	Posterior mean
		Deviance	${\sigma }^2$
0: Base model†	–	–1360	0.034
1: Age on $k_a$	$k_a=\theta \times {\left(age/29.4\right)}^{{\theta }_{AGE\left(k_a\right)}}$	–1401	0.034
2: 1 plus age on $V_d/F$	$k_a=\theta \times {\left(age/29.4\right)}^{{\theta }_{AGE\left(k_a\right)}}$	–1401	0.034
	$V_d/F=\theta \times {\left(age/29.4\right)}^{{\theta }_{AGE\left(V_d/F\right)}}$
3: 1 plus ALDH2 on $V_d/F$	$k_a=\theta \times {\left(age/29.4\right)}^{{\theta }_{age\left(k_a\right)}}$	–1412	0.031
	$V_d/F=\left(\theta +{\theta }_{ALDH2\left(V_d/F\right)}\times ALDH2\right)$
4: 1 plus ALDH2 on $k_a$	$k_a=\left(\theta +{\theta }_{ALDH2\left(k_a\right)}\times ALDH2\right)\times {\left(age/29.4\right)}^{{\theta }_{AGE\left(k_a\right)}}$	–1401	0.034
5: 3 plus age on $V_d/F$	$k_a=\theta \times {\left(age/29.4\right)}^{{\theta }_{AGE\left(k_a\right)}}$	–1424	0.028
	$V_d/F=\left(\theta +{\theta }_{ALDH2\left(V_d/F\right)}\times ALDH2\right)\times {\left(age/29.4\right)}^{{\theta }_{AGE\left(V_d/F\right)}}$
6: 5 plus ALDH2 on $k_a$	$k_a=\left(\theta +{\theta }_{ALDH2\left(k_a\right)}\times ALDH2\right)\times {\left(age/29.4\right)}^{{\theta }_{AGE\left(k_a\right)}}$	–1436	0.027
	$V_d/F=\left(\theta +{\theta }_{ALDH2\left(V_d/F\right)}\times ALDH2\right)\times {\left(age/29.4\right)}^{{\theta }_{AGE\left(V_d/F\right)}}$

$k_a$ = absorption rate constant; $V_d/F$ = apparent volume of distribution; ALDH2 = aldehyde dehydrogenase 2; $\theta$ = typical value ofg parameter in the base model; ${\sigma }^2$ = variance of residual error; ${\theta }_{AGE\left(k_a\right)}$ = scale factor for age on $k_a$; ${\theta }_{AGE\left(V_d/F\right)}$ = scale factor for age on $V_d/F$; ${\theta }_{ALDH2\left(V_d/F\right)}$ = change in $V_d/F$ for ALDH2; ${\theta }_{ALDH2\left(V_{max}\right)}$ = change in $V_{max}$ for ALDH2.

^⁎Only the different relationships compared to the base model are presented. The relationships between pharmacokinetic parameters and covariates in the base model are described in the Appendix. ALDH2 = 1 if ALDH2 genotype is *1/*2; ALDH2 = 0 if ALDH2 genotype is *1/*1.

^†The basic compartment model, random effects for pharmacokinetic parameters and the error model are described in Methods.

Figure 2.

Plots of the natural log of estimated individual pharmacokinetic parameters versus covariates. (A) $ln(k_a)$ versus $ln(\mathrm{age})$. (B) $ln(V_d/F)$ versus $ln(\mathrm{age})$. (C) $ln(k_a)$ versus ALDH2 genotype. (D) $ln(V_d/F)$ versus ALDH2 genotype.

When age was added to the base model as a covariate on $k_a$, the posterior mean of deviance decreased from –1360 to –1401 (Table III, model 0 and model 1). The posterior mode of between subject variance for $k_a$, ${\omega }_{k_a}^2$, decreased from 0.66 to 0.35 with the inclusion of age on $k_a$ (data not shown). The probability that age had a clinically significant effect on $k_a$ was more than 0.95, and this covariate was included in the final model. Subsequently, addition of another covariate to model 1 was investigated, as presented in Table III: age on $V_d/F$ as model 2, ALDH2 on $V_d/F$ as model 3, and ALDH2 on $k_a$ as model 4.

Among models 2 to 4, compared with model 1, the posterior deviance decreased most in model 3, from –1401 to –1412 (Table III). Also, the mean of the variance of residual error decreased most in model 3 compared with model 1, from 0.34 to 0.31. Both probability that age had a clinically significant effect on $k_a$ and probability that ALDH2 had a clinically significant effect on $V_d/F$ were more than 0.95, and these 2 covariates were included in the final model. The addition to model 3 of the relationship between age and $V_d/F$ was considered model 5, further followed by addition of the relationship between ALDH2 and $k_a$ as model 6.

From model 3 to model 5, the posterior deviance decreased from –1412 to –1424 and the posterior variance of residual error, ${\sigma }^2$, decreased from 0.31 to 0.28 (Table II). From model 5 to model 6, the posterior deviance decreased from –1424 to –1436 and both the posterior ${\omega }_{k_a}^2$ and the posterior ${\sigma }^2$ decreased. The probability that a covariate candidate had a clinically significant influence on the parameter value exceeded 0.8 in each of 3 relationships included in model 5. However, in model 6, the probability that ALDH2 had a clinically significant effect on $k_a$ was lower than 0.8. Thus, the relationship between ALDH2 and $k_a$ was not included in the final model.

In summary, the relationship of model 5 (Table III) was added to the base model, and this was determined to be the final model. The estimated PPK parameters from the base model are presented in Table II. A typical $k_a$ value was 3.0 hours^–1 for a 29-year-old man and 6.9 hours^–1 for a 40-year-old man. A typical $V_d/F$ value was 49.3 L for a man with a genotype of ALDH2*1/*1, 28.9 L for a man with a genotype of ALDH2*1/*2 when he was aged 29 years and his body weight was 61.3 kg. A typical $V_d/F$ value was 49.3 L for a 29-year-old man and was 57.9 L for a 40-year-old man when his genotype was ALDH2*1/*1 and his weight was 61.3 kg. $V_d/F$ and $k_a$ were estimated to be 12.2 and 1.3 smaller for female subjects than men, respectively.

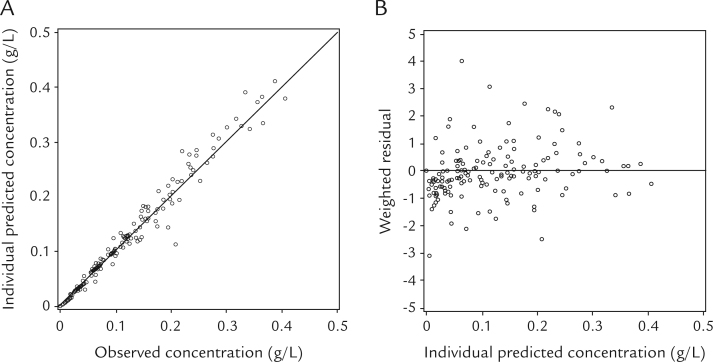
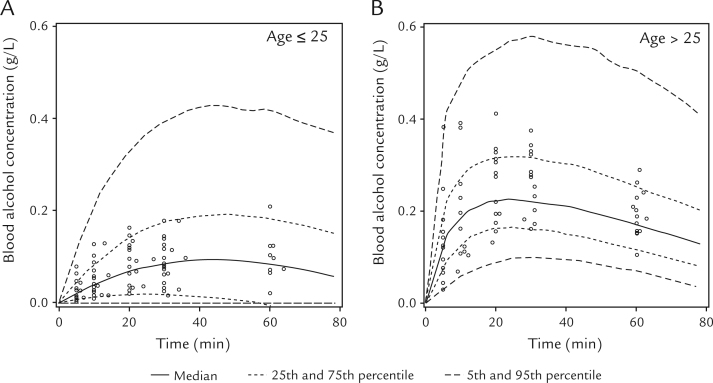
Scatter plots of the individual predicted (IPRED) versus observed concentrations obtained from this model, and the weighted residual versus IPRED concentrations are shown in Figure 3. The correlation between IPRED and observed concentrations was high (Figure 3A), and weighted residual was uniformly distributed within acceptable range (ie, between –5.0 and 5.0) (Figure 3B). The visual predicted check plots of the BAC data versus time-stratified age group are presented in Figure 4. The observed BACs were compared with the percentiles derived from 1000 simulations of individuals from the original data set. As shown in Figure 4, the model describes the data adequately for the different age groups.

Figure 3.

Goodness-of-fit plots for the final model. (A) Individual-predicted versus observed blood alcohol concentrations. (B) Weighted residuals versus individual-predicted blood alcohol concentrations.

Figure 4.

Visual predictive check of the final population pharmacokinetic model stratified by age group. (A) Subjects younger than age 25 years. (B) Subjects older than age 25 years. Circles represent the observed blood alcohol concentration. The solid line denotes the median of 1000 simulated concentrations from the final model, the dotted lines denote 25th and 75th percentiles, and the dashed lines denote 5th and 95th percentiles.

Discussion

Our aim was to update the PPK model for alcohol that included covariates for interindividual variability of PK parameters. In this study, the ALDH2 genotype was identified as an additional covariate by using MCMC Bayesian estimation, which allowed incorporation of parameters of a PPK model reported elsewhere into the current PPK model as informative priors.

A characteristic of our data is that the samples were corrected only before and at 60 minutes after dosing. BACs were observed during the absorption phase and around peak BAC. It was intended to develop a model that explains the interindividual variability of the peak BACs after the consumption of a same amount of ethanol (17.5 g). The range of distribution of the peak BACs in our data was from 0.025 to 0.41 g/L, spanning the BACs of 0.2 to 0.3 g/L at which cognitive function was reported to begin being affected.¹⁵ On the other hand, almost no BAC was observed during the elimination phase. Although the elimination rate of ethanol from the blood was known to be described with the Michaelis-Menten equation,¹⁶ we developed a model using elimination rate $(k_{el})$ and also did not assume interindividual variability for $k_{el}$ because our data were not informative about parameters for Michalis-Menten kinetics, $V_{max}$, and $k_m$. However, the problem remains because it is difficult to determine presently whether the model has clinical predictive validity. In this article, we reported a significant effect of the ALDH2 genotype on $V_d/F$. The relationship between the ALDH2 genotype and $V_d/F$ may sound physiologically inexplicable. This was considered to be also attributable to the lack of concentrations in the elimination phase. This point will be discussed below.

It is known that blood acetaldehyde concentration rises in subjects with the allotype ALDH2*2-encoding inactive enzyme.¹⁷ Ethanol oxidation to acetaldehyde catalyzed by ADH is inhibited by the accumulated acetaldehyde.¹⁸ We considered that a product inhibition of ADH by a high concentration of acetaldehyde was the plausible mechanism that causes the accumulation of ethanol in the blood. In the report by Peng et al,¹⁷ they compared the time-concentration profile of 3 subject groups that differed in ALDH2 genotypes (ALDH2*1/*1, ALDH2*1/*2, and ALDH2*2/*2) but were matched in ethnicity, sex, age, body mass index, nutritional status, and homozygosity at ADH genotypes. The mean BAC at each time point was shown to be higher in subjects who were heterozygous (ALDH2*1/*2) compared with those representing the wild type (ALDH2*1/*1). It was also shown to be higher in subjects who were homozygous for the (ALDH2*2/*2) variant compared with those who were heterozygous (ALDH2*1/*2).¹⁷

In the final model that we developed, $V_d/F$ in subjects with ALDH2*1/*2 was estimated to be 20.4 L smaller than that in subjects with ALDH2*1/*1. There is no physiological basis for which ALDH2 genotype is thought to be associated with $V_{di}$, but rather it makes sense that the genotypes of ALDH2 influence the rate of elimination. However, when we tried to add the ALDH2 genotype of ALDH2 to the final model as a covariate of $V_{max}$, the difference between the subjects with ALDH2*1/*2 and the subjects with ALDH2*1/*1 was estimated to be –246 mg/h (95% CI, –1702–1417) and a significant effect was not shown. As described above, the analyzed data consist of BACs of the absorption phase and around the peak, and are not information-rich about the interindividual variability in the rate of elimination. This might be a reason why a significant relationship between the ALDH2 genotype and the individual $V_{max}$ was not interpreted. We considered that, on the other hand, the interindividual difference in the peak BAC had been interpreted as the interindividual difference in $V_d/F$.

If we had subjects with ALDH2*2/*2 from whom BAC data were obtained, we could have verified the additive effect of ALDH2*2 on $V_d/F$. However, no subject with ALDH2*2/*2 was involved, which is a weakness of our research, and there are 2 possible reasons for this. First, the proportion of subjects with ALDH2*2/*2 is small in the Japanese population and the probability of it being present in the subjects in this study was relatively low: the frequency of genotypes of ALDH2 in 524 healthy Japanese subjects were reported as 56.8% (*1/*1), 36.6% (*1/*2), and 6.5% (*2/*2).¹⁹ Second, homozygous ALDH2*2 individuals may have avoided participation in a study that requires alcohol consumption because they are strikingly responsive to small amounts of alcohol. It has been reported that 1 individual who was homozygous for ALDH2*2 experienced an intoxicated state requiring hospitalization after a moderate dose of alcohol (0.59 g/kg).²⁰ For modeling the difference in PK parameters between subjects with ALDH2*1/*2 and ALDH2*2/*2, a carefully planned clinical trial will be needed.

In contrast to the Phase I study data (ie, dense sampling over time-concentration profiles), our data are not informative about all of the PPK parameters. It has been suggested that incorporation of external data helps to stabilize the modeling process even if the current dataset is not informative to estimate all PPK parameters, due to small sample size and/or few numbers of time points for an individual.²¹ Dansirikul et al¹² pointed out that a Bayesian approach to develop a PPK fully conditional Bayesian method have not been previously reported. Alcohol is a model with informative priors allowed interpretation of a significant covariate relationship, even using poorly informative data. Our results support this hypothesis. Results of a model development for PPK of alcohol using the world’s oldest recreational drug has been studied by many researchers. By applying the Bayesian method, as shown in this research, it is expected that the research on alcohol metabolism will develop through integrating individual research results and discovering new findings utilizing past findings.

Conflicts of Interest

The authors have indicated that they have no conflicts of interest regarding the content of this article.

Appendix 1.

For the base model, the structural model of the population pharmacokinetic (PK) parameters and the covariates is expressed as,

$$k_{a_i}=(k_a+{\theta }_{SEX\left(ka\right)}\times FEMALE)\times exp\left({\eta }_{k_a}\right),$$ (A1)

$$V_d/F_i=(V_d/F+{\theta }_{SEX\left(V_d/F\right)}\times FEMALE)\times {\left(WT/Media{n}_{WT}\right)}^{{\theta }_{WT\left(V_d/F\right)}}\times exp\left({\eta }_{V_d/F}\right),$$ (A2)

and

$$K_{m_i}=K_m\times exp\left({\eta }_{K_m}\right),$$ (A3)

where WT is body weight, FEMALE is an indicator variable for sex of 0 or 1 (ie, male or female, respectively), and ${\theta }_{cov\left(PKparameter\right)}$ is a covariate scale factor for $cov$ when $cov$ is a continuous variable and is the change in the PK parameter value if $cov$ is an indicator variable. $V_{ma{x}_i}$ was modeled in the expression described below, if the genotype of ADH1B was ADH1B *2/*2,

$$V_{ma{x}_i}=V_{ma{x}_{ADH1B⁎2/⁎2}}\times {\left(WT/Media{n}_{WT}\right)}^{{\theta }_{WT(V_{max})}}\times exp\left({\eta }_{V_{max}}\right),$$ (A4)

or in the expression described below, if the genotype of ADH1B was ADH1B*2/*1,

$$V_{ma{x}_i}=V_{ma{x}_{ADH1B⁎2/⁎1}}\times {\left(WT/Media{n}_{WT}\right)}^{{\theta }_{WT(V_{max})}}\times exp\left({\eta }_{V_{max}}\right).$$ (A5)

In the final model (Table II, and model 5 in Table III), the structural model of the population PK parameters and the covariates is different from the base model for $k_{a_i}$ and $V_d/F_i$:

$$k_{a_i}=(k_a+{\theta }_{SEX\left(k_a\right)}\times FEMALE)\times {\left(age/Media{n}_{age}\right)}^{{\theta }_{age(k_a)}}\times exp\left({\eta }_{k_a}\right),$$ (A6)

$$V_d/F_i=(V_d/F+{\theta }_{SEX\left(V_d/F\right)}\times FEMALE+{\theta }_{ALDH2\left(V_d/F\right)}\times ALDH2)\times {\left(WT/Media{n}_{WT}\right)}^{{\theta }_{WT\left(V_d/F\right)}}\times {\left(age/Media{n}_{age}\right)}^{{\theta }_{age\left(V_d/F\right)}}\times exp\left({\eta }_{V_d/F}\right),$$ (A7)

where ALDH2 = 1 if ALDH2 genotype is *1/*2; ALDH2 = 0 if ALDH2 genotype is *1/*1.