ACCURATE CHARACTERIZATION OF DELAY DISCOUNTING: A MULTIPLE MODEL APPROACH USING APPROXIMATE BAYESIAN MODEL SELECTION AND A UNIFIED DISCOUNTING MEASURE

Abstract

The study of delay discounting, or valuation of future rewards as a function of delay, has contributed to understanding the behavioral economics of addiction. Accurate characterization of discounting can be furthered by statistical model selection given that many functions have been proposed to measure future valuation of rewards. The present study provides a convenient Bayesian model selection algorithm that selects the most probable discounting model among a set of candidate models chosen by the researcher. The approach assigns the most probable model for each individual subject. Importantly, effective delay 50 (ED50) functions as a suitable unifying measure that is computable for and comparable between a number of popular functions, including both one- and two-parameter models. The combined model selection/ED50 approach is illustrated using empirical discounting data collected from a sample of 111 undergraduate students with models proposed by Laibson (1997); Mazur (1987); Myerson & Green (1995); Rachlin (2006); and Samuelson (1937). Computer simulation suggests that the proposed Bayesian model selection approach outperforms the single model approach when data truly arise from multiple models. When a single model underlies all participant data, the simulation suggests that the proposed approach fares no worse than the single model approach.

Excessive devaluation of future outcomes has been linked with a variety of pathological behaviors, including substance abuse (Bickel & Marsch, 2001; Reynolds, 2006; MacKillop et al., 2011); problem gambling (Petry & Casarella, 1999); and overeating (Weller et al., 2008). The literature on the theoretical underpinnings of and quantification between devaluation and delay has a long history that spans many fields including economics, psychology, and sociology (Ainslie, 1975). In the study of temporal discounting, many functions have been proposed that quantify the rate an individual devalues future rewards (e.g., Mazur, 1987; Myerson & Green, 1995; Laibson, 1997; Samuelson, 1937; Rachlin, 2006; Yi et al., 2009). Moreover, efforts to change temporal discounting (e.g., Koffarnus et al., 2013), in addition to changing the rate of discounting, may alter the function.

Adoption of a single discounting function on a study-wide basis implies that one process or model underlies future devaluation in humans, that deviations from this pattern are attributable to random chance, and that this process is known ahead of time. This strategy ignores the potential for heterogeneity in discounting patterns among subjects. If a single model does not describe discounting in all humans, then different models should be used for different people.

Intuitively, when many models are under consideration, using the model that is most probably correct seems like a worthwhile approach. In this paper, we propose Bayesian model selection for this purpose. Bayesian model selection operates by assessing the probability of each model under consideration and favoring the model that is most probably true among the candidates. We assess model probability using a simple approximation based on the readily-available Bayesian information criterion (BIC) (Schwarz, 1978).

Effective delay 50 (ED50) (Yoon & Higgins, 2008) is the delay at which a reward loses 50% of its value. Although ED50 has not been used widely in the delay discounting literature, it has unique value because it can unify the interpretation of competing models. ED50 is an intuitive measure that can be obtained from virtually any discounting function, and its interpretation is consistent even when the models under consideration differ in the number and role of their respective parameters. ED50 is analogous to effective dose 50 in the field of pharmacology, which is the dose of a drug for which half of the maximum drug effect is observed (Ross & Kenakin, 2001). While we use ED50 for this study, another ED value (such as ED20 or ED70) could be used in principle. Table 1 includes ED50 formulas for the models under consideration in this study. Since the interpretation of ED50 is the same regardless of model, ED50 values among different models are comparable. Using ED50 as a unified discounting measure sidesteps the difficulty of interpreting and equating model parameters from different models and seamlessly allows both one- and two-parameter models to be incorporated into the same study.

Table 1.

Discounting equations, parameters, and ED50 values for the functions under consideration.

Model Name	Equation	parameters	ED50	Citation
Mazur	E(Y) = 1/(1 + kD)	k	$\frac{1}{k}$	(Mazur, 1987)
Samuelson	E(Y) = e−kD	k	$\frac{\text{ln}\left(2\right)}{k}$	(Samuelson, 1937)
Myerson & Green	E (Y) = 1/(1+kD)s	k, s	$\frac{\left(2^{1/s}-1\right)}{k}$	(Myerson & Green, 1995)
Rachlin	E (Y) = 1/(1+kDs)	k, s	${\left(\frac{1}{k}\right)}^{1/s}$	(Rachlin, 2006)
Laibson*	E (Y) = βδD	β,δ	$lo{g}_{\delta }\left(\frac{1}{2\beta }\right)$	(Laibson, 1997)
Random Noise	E(Y) = c	c	–	–

Note. E(Y) represents the expected indifference point at delay D. Model residuals are assumed Gaussian with constant variance.

^*The Equation for the Laibson model is assumed to hold for D > 0, and E(Y) = 1 when D = 1.

Past work has statistically compared competing discounting models for all subjects within a study (e.g. Yi et al., 2009; Zarr et al., 2014), but less attention has been devoted to selecting models at the individual subject level within a single study. The multimodel approach is a departure from much of what has been considered in the literature. Generally, a single process is assumed to underlie discounting in humans, and that different participants perform differently within the context of the single model. The proposed work instead allows multiple processes to underlie discounting in different subjects, which is a departure from what is assumed in much of the existing literature.

In order to explore the utility of this multi-model strategy, we (1) establish a set of candidate models, (2) propose Bayesian model probability as a metric to decide among competing models for each participant, (3) use ED50 (Yoon & Higgins, 2008) as a unifying measure to render results comparable across models, and (4) devise screening criteria based on the model selection approach and other statistical principles. The performance of this method is demonstrated in two ways. First, the method is employed on empirical discounting data, and resulting model selections, parameter estimates, and screening outcomes are reported (Study 1). Second, a Monte Carlo computer simulation study assesses the performance of the approach (Study 2). In both studies, the model selection approach is compared with single model approaches. Due to its prevalence in the literature (MacKillop et al., 2011), the single model approach using the one-parameter hyperbolic model (Mazur 1987) is an appropriate baseline method with which to compare the performance of our model selection procedure in both studies. Study 2 also compares the model selection approach to the Rachlin (2006) model alone in order to assess the comparative predictive accuracy using both one- and two-parameter models.

Study 1: Empirical Discounting Data

In Study 1, empirical discounting data collected for another purpose (Koffarnus & Bickel, 2014) were reanalyzed to test the performance of this Bayesian model selection approach.

Method

Participants

This study included 111 under-graduate students from Virginia Tech who participated in a computerized discounting task. The sample was 64% female with ages ranging from 18 to 31 years old (IQR 19–21 years). Students completed the task and other measures (see Koffarnus et al., 2014) outside of class time and were offered course credit for completion of the approximately 15-min session. This study was approved by the Virginia Tech Institutional Review Board.

Procedure

Participants were asked to make a series of choices between smaller immediate amounts of hypothetical money, or larger delayed rewards for a variety of delays. A computerized titration task (see Du, Green, & Myerson, 2002) was used to obtain indifference points for each participant. An indifference point represents the subjective value where an immediate reward is equivalent to a larger delayed reward. Hypothetical amounts of money constituted both smaller immediate rewards and larger delayed rewards. Delays were 1 day, 1 week, 1 month, 6 months, 1 year, 5 years, and 25 years, and the larger delayed amount was $1000.

Models

We selected five discounting models including those proposed by Laibson (1997) Mazur (1987) Myerson and Green (1995; see also Green, Fry & Myerson 1994 and Rachlin 1989), Rachlin (2006) and Samuelson (1937). McKerchar et al. (2009) reviewed many of these models. These models were chosen because they include common one- and two-parameter models. Models were included from the behavior analytic tradition, for example, Mazur (1987) Myerson and Green (1995) and Rachlin (2006) and also the economic tradition, for example, the quasihyperbolic or beta delta model of Laibson (1997). Rachlin (2006) popularized the use of a two-parameter function with an exponent on the delay term for delay discounting, although this function had been previously proposed in other contexts (see Mazur, 1987). The double exponential model proposed by Van Den Bos and McClure (2013) from the neuroscience tradition is another model of interest in this context. This three-parameter model was excluded from this study because there is no analytical solution for ED50 for this model. Numerical methods can be employed to determine ED50 when there is no analytical solution. Additionally, parallel, hyperbolically discounted temporal difference, mixed, and serial models are of general interest (see, e.g., Zarr et al., 2014) in the study of discounting but are not included in this investigation. The purpose of the present work is to illustrate the variable selection procedure in combination with ED50 as a flexible method for a set of popular discounting models, rather than to perform a comprehensive review of all existing discounting models. In principle, any existing (or future) discounting model with a likelihood function can be accommodated with this approach. Hence-forth, models will be referred to as labeled in Table 1, and year of publication will be suppressed to simplify the prose.

The Mazur and Samuelson models include a single discount rate (k) parameter. As k increases, valuation of the reward declines more steeply as a function of delay according to the functions presented in Table 1. The two-parameter Myerson and Green and Rachlin models extend the Mazur model by allowing a second s parameter, which allows the models more flexibility. The Laibson model’s δ parameter controls how steep the decay is as a function of delay, while the β parameter allows the model to scale vertically.

The Myerson and Green and Rachlin models are actually generalizations of the Mazur model in the sense that if s = 1 then these models reduce to the Mazur model. When a statistical model selection routine favors either of these two-parameter models, this indicates that the additional complexity for adding a second parameter to vary freely is justified due to substantial improvement in model performance. When the Mazur model is most probable, this indicates that the data are sufficiently described under the restriction that s = 1 and k alone varies freely. In fact, when the Myerson and Green or Rachlin models are fit in practice, the probability that the observed s would be 1 (hence inducing the Mazur model) is actually zero, because the probability of a continuous variable (the s statistic in this case) taking a single individual value is zero.

In addition to the above models, a “random noise” model was included to identify non-orderly data. The random noise model was represented as a delay-invariant constant, and departures from this constant are attributed to random chance. This is identical to an ‘intercept only’ regression model and is used to identify cases where a subject does not systematically discount rewards as a function of delay. Participant data may be nonorderly in this fashion when a participant fails to understand the questionnaire, answers dishonestly, or genuinely does not discount future rewards over the course of delays presented.

Throughout the study, we assume that indifference points are measured with error, but the delays are fixed and known constants. While subjects may exhibit some variability between their perception of a certain delay and that exact delay (i.e., a measurement error in delay) we assume that the delays are measured without error, mostly out of convenience. This is a common assumption in many regression applications.

Analytic Plan

The models in Table 1 were each fitted to all indifference point data. The nls package in R (R Foundation for Statistical Computing, Vienna, Austria) was used to estimate parameters by minimizing residual sums of squares via Gauss-Newton optimization (Bates & Watts, 1988). Models that failed to optimize for a given participant were removed from the candidate model list for that data set, and variable selection for the given participant was conducted among the models that converged. The Laibson model parameter values β and δ are bounded between zero and one, and this constraint was enforced in the optimization. In a section below we discuss nonlinear optimization and associated challenges in this study. The Bayesian information criterion (BIC) was computed for each model in Table 1, and model probabilities were approximated as described in the next section. ED50 was computed on the basis of the most probable model for each participant. The frequency and proportion of selections favoring each model were computed, and the estimated parameters among all of the selections were summarized. The natural log (ln) of ED50 was computed for both the most probable model and also the Mazur model and these ln(ED50) distributions were compared. Mazur’s one-parameter hyperbolic function (Mazur, 1987) is used in this study to exemplify the single model strategy, which is a frequently used model in practice (See e.g. MacKillop et al., 2011).

The probability that a subject does not discount the value of a reinforcer as a function of delay is assessed formally by including a “random noise” model among the candidate functions. Additional screening rules flag instances where ED50 is not reached within the range of delays presented (i.e., extrapolation), or subjects who exhibit discounting trends that increase as a function of delay. Different approaches to screening are compared in the Results section.

Model selection

Statistical model selection requires adoption of a set of candidate models and choice of a metric that characterizes model performance (e.g., information criteria, model probability, goodness of fit measures). The model that demonstrates the best performance in terms of the chosen metric is selected and inference is subsequently performed in the context of the chosen model.

Bayesian model selection was accomplished by using Bayes’ rule to obtain model probabilities. Exact analytical solutions for model probabilities are not available for models such as these, so computational sampling methods or asymptotic approximations are needed in order to estimate model probabilities. Kass and Raftery (1995) provide a convenient approximation to model probability using BIC (Schwarz, 1978). BIC may be obtained for any model that has a computable log-likelihood, and the formula for BIC is

$$\mathit{BIC}=-2\ast \mathit{log}L+\mathit{log}\left(n\right)\ast p$$ (1)

where log L represents the log of a model’s maximized likelihood function, n is the sample size, and p is the number of parameters in the model. Lower values of BIC correspond to models that have a favorable balance of predictive ability and model complexity. Because BIC measures the likelihood of a given model subject to a penalty for complexity, two-parameter models such as those proposed by Myerson and Green, Laibson, and Rachlin are appropriately penalized for complexity compared to competing one-parameter models in this approach.

For a set of competing models, the BIC values are rescaled to model probabilities as described in the Appendix. The model with the lowest BIC is the most probable model according to this approximation, which simplifies Bayesian model selection by obviating the need for numerical integration routines. For a more complete overview of Bayesian model selection, see Kass and Raftery (1995). For a detailed description of statistical inference using the Bayesian paradigm, see Gelman, Carlin, Stern, and Rubin (2004). In practice the proposed approach is flexible and allows for any set of parametric candidate models.

Effective Delay 50

ED50 was computed based on the most probable model for each participant according to the formulas in Table 1. ED50 is computed by setting the discounted value of the larger–later reward as 0.5 (half the value of the objective amount of that reward, normalized to 1) and solving for delay D (Yoon & Higgins, 2008). In the context of the Mazur model, the natural log of k typically satisfies parametric modeling assumptions better than the untransformed k; that is, for the Mazur model, $\text{ED}50=\frac{1}{k}$ (Yoon & Higgins, 2008), and ln(ED50) = −ln(k) (Washio et al., 2011). Because statistical inference is generally invariant to linear transformation, inference based on ln(k) is identical to statistical inference based on ln(ED50) if the Mazur model is adopted. This equivalency increases the appeal of ED50 as a natural measure of discounting across models.

Screening criteria

In any statistical analysis, the researcher should be wary not to allow a few individual data points to disproportionately affect inferences drawn about larger populations. Discounting patterns can vary widely among participants, and screening criteria (e.g., Johnson & Bickel, 2008) can be used to identify participants who discount according to unexpected or atypical patterns. Subjects identified in this fashion should potentially be analyzed separately to prevent undue influence on the broader analysis. Generally, screening criteria should be regarded as “rules of thumb,” and researchers should use their own expert opinion to screen, subset, analyze, and transparently describe and justify their methods. Several criteria have been proposed to assess the orderliness of individual participant indifference point data. The model R² is not ideal because it is confounded with discount rate (Johnson & Bickel, 2008). Other criteria have been proposed to evaluate the logical consistency of discounting data (Johnson & Bickel, 2008). These criteria flag participants for whom either (1) the earliest indifference point is not greater than the latest indifference point by at least 10% of the delayed reward, or (2) any indifference point (starting with the second delay) exceeds the preceding indifference point by a magnitude greater than 20% of the delayed reward amount. These criteria are suggested as a generally flexible approach to consider possibly problematic participant data. For the purpose of subsequent analysis, datasets that violate either of these criteria might be subject to further screening for orderliness (usually via a graphical plot of the indifference points), analyzed separately from nonviolators, or excluded from further analysis. Figure 1 depicts individual participant data that violate the second of these criteria.

Fig. 1.

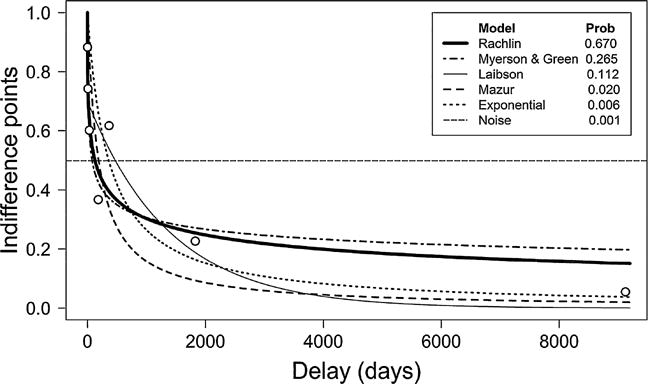
Delays, indifference points, model fits, and probabilities for subject 17. The Rachlin model is most probable for this subject (probability = 0.67). Most probable ED50 = 126.15 (Rachlin). Mazur ED50 = 188.14. This participant violates one Johnson-Bickel criterion but is retained under proposed model selection routine.

The proposed approach screens data that most probably arise from the random noise model, fails to achieve ED50 within the delays presented, or exhibits an increasing trend (i.e., both s < 0 and Rachlin or Myerson and Green is chosen). The rationale for screening based on each of these criteria follows. First, if data truly arise from the random noise model, this indicates that reward valuation does not decrease systematically as a function of delay. Second, if ED50 is not achieved over the range of the delays presented, the participant is also screened in order to avoid excessive extrapolation beyond the assessed delays. Avoiding the extrapolation of results from statistical models far from the range of data that was collected is generally wise (Utts & Heckard, 2007). ED50 may perform particularly poorly in cases where the delay associated with 50% devaluation in the delayed reward is far from the range of delays in the task. In practice a researcher could relax this condition by specifying a delay threshold slightly outside of the range of delays. Finally, data that exhibits an increasing trend as delay increases (possible with Rachlin and Myerson & Green models when s is negative) is generally not reflective of the behavior expected for the discounting task (see Johnson & Bickel, 2008) and, therefore, these participants’ data are screened out.

Results

Results of model selection

The Bayesian model selection routine selected the Rachlin model as most probable in 34.3% of the cases. The Myerson and Green, Mazur, Laibson, Samuelson, and Noise models were chosen 27.0%, 18.0%, 10.8%, 8.1%, and 1.8% of the time, respectively. The model selection routine identified 11 participants who violated the above screening criteria. Eight of these cases exhibited ED50 exceeding the delay range, one case had s < 0 with the Rachlin model chosen as most probable (i.e., increasing trend), and two cases were most probably attributable to random noise. There were 20 participants who violated at least one of the Johnson-Bickel criteria, but for 14 of those participants there was only one instance where a single indifference point (starting with the second delay) exceeded the preceding indifference point by a magnitude greater than 20% of the delayed reward amount. Two individuals provided indifference points which were unvarying across all delays. Among the participants who provided varying indifference points, the Laibson model failed to optimize three times, and the Myerson and Green model was not considered in 29 cases for the same reason (see below for a discussion of parameter estimation and modeling difficulties for these models). Figure 1 illustrates the computed model probabilities for a single subject whose data violated one of the criteria proposed by Johnson and Bickel (2008); but where the Bayesian model selection criteria identified the Rachlin model as the most probable fit.

ED50 summary

Among data retained by the model selection approach, ED50 distributions were positively skewed from both the most probable model (skew = 1.88) and for the Mazur model (skew = 2.33). Logarithmic transformation reduced the skew in both cases (−0.85 and −0.73 for most probable and Mazur approaches, respectively), suggesting that the log transformation strategy for Mazur’s k performs similarly on the ED50 computed from the most probable model. These distributions are displayed graphically in Figure A1 of the Appendix.

For these data the median ED50 was 871.6 days for the most probable model, and 720.3 days when the Mazur model was fitted to all participant data. A shift of about 150 days is arguably of some practical significance in this instance, although Figure A1 suggests no substantial shift in distribution between ED50 or ln(ED50) between Mazur and most probable settings. The ln(ED50) distributions differ by only 0.012 standard deviations, further suggesting no practically significant shift between these distributions. A paired t-test comparing the ln(ED50) distributions between Mazur and most probable approaches was not statistically significant at the α = 0.05 level (t₉₈ = 0.13; p = .899). The ED50 and ln(ED50) values from the single model approach and model selection approach were highly correlated (Spearman correlation is 0.99 in both cases, see Fig. 2.) Despite these high correlations, Figure 2 suggests that the single model and model selection approaches can differ substantially in individual cases. For instance, among the 12 cases where the Laibson model was found to be the most probable model, the ED50 value arising from this model was larger than the ED50 from the Mazur model in 9 out of 12 cases (see Fig. 2). When the Rachlin model is called the most probable ED50 is smaller than the Mazur ED50 in 24 out of 38 cases.

Fig. 2.

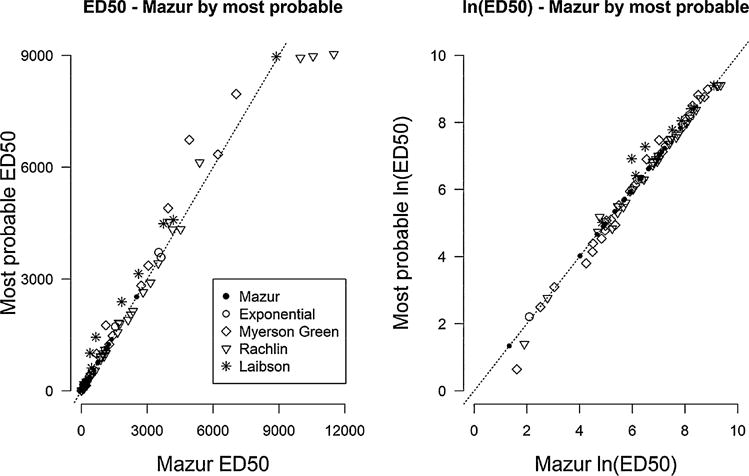
Concordance between Mazur and most probable ED50 estimates by selected model. Left panel shows ED50 values and right panel shows ln(ED50) values. Spearman correlation between these values was 0.99 in both cases. The dashed line is the 45 degree X=Y line. Despite high correlation, ED50 estimates vary between Mazur and most probable approach for several individual participants.

Parameter estimation

Table 2 reports the mean, standard deviation, and interquartile range of the parameter estimates among the selected models. The correlation between parameter estimates is reported for the two-parameter models. These values were used as inputs for the heterogeneous setting in the computer simulation in Study 2. Table 3 summarizes correlations among parameters and also area under the curve (Myerson et al., 2001). Table 4 summarizes distributional features for model mean squared error (MSE) and ED50 in the Mazur and most probable settings.

Table 2.

Summary of model parameter estimates among chosen models in experiment 1.

Model	ln (k)				s				r
	mean	sd	median	IQR	mean	sd	median	IQR
Mazur	−5.81	1.43	−5.92	−6.74, −5.25	–	–	−	–	–
Samuelson	−6.92	1.91	−7.27	−8.00, −6.67	–	–	−	–	–
Myerson & Green	−3.72	2.88	−3.91	−5.79, −2.10	0.46	0.44	0.36	0.27, 0.49	−0.52
Rachlin	−12.62	9.17	−10.95	−18.45, −5.39	1.82	1.2	1.66	0.75, 2.69	−0.92
	β				δ				0.39
Laibson	0.84	.0.11	0.81	0.74, 0.93	0.9995	0.0009	0.9997	0.9996, 0.9999

Note. Mean, standard deviation (sd), and interquartile range (IQR) reported for ln (k), s, β, and δ. r denotes the correlation between parameter estimates in the two-parameter models.

Table 3.

Correlations among model parameter estimates in study 1.

	Mazur ln (K)	Samuelson ln (k)	Myerson & Green ln (k)	Myerson & Green s	Rachlin ln (k)	Rachlin s	Liabson β	Liabson δ
Samuelson ln (k)	0.995
Myerson & Green ln (k)	0.701	0.685
Myerson & Green s	−0.165	−0.154	−0.597
Rachlin ln (k)	0.452	0.433	0.746	−0.559
Rachlin s	−0.166	−0.128	−0.378	0.446	−0.899
Liabson β	−0.508	−0.461	−0.707	0.307	−0.498	0.504
Liabson δ	−0.441	−0.479	−0.312	0.010	−0.163	−0.145	0.090
AUC	−0.741	−0.769	−0.404	−0.010	−0.292	−0.025	0.119	0.266

Note. Sample sizes ranged between 78 and 80 for correlations involving the Myerson & Green model, and sample sizes ranged between 106 and 111 for all other correlations.

Table 4.

Summary of individual model MSE and ED50 according to the most probable model and the Mazur model, respectively.

Value	Mean	sd	skew	median	IQR
Mazur ED50	1644.682	2326.152	2.332	210.8	210, 2164
Most probable ED50	1684.432	2244.652	1.884	871.606	196, 2067
Mazur model MSE	0.018	0.018	1.632	0.013	0.005, 0.020
Most probable model MSE	0.011	0.015	2.941	0.005	0.002, 0.013

Note. Entries computed based on 100 participants not flagged by the model selection criteria.

Nonlinear optimization and associated challenges

The nls package in R was used to fit the nonlinear models in the present analyses. This package implements a Gauss-Newton optimization algorithm to find the values of k and s that minimize the sum of squared residuals between the model fit and observed data. This algorithm iteratively refines parameter estimates from a user-provided starting value until the change in the error sum of squares between iteration becomes arbitrarily small. If the algorithm exceeds a preset number of iterations, or if the change in the estimates between steps becomes very small before the change in error sum of squares becomes sufficiently small, then the algorithm fails to converge, and the validity of parameter estimates is questionable.

In this study the maximum iteration was set to 50, change in error sum of squares to elicit convergence was set to 0.00001, and the minimum step size was set to 1/1024, which are all default for the nls package in R. In order to minimize convergence problems associated with poor starting values, the starting values were chosen from a grid as those that minimized the sum of squared residuals between observed and predicted data. The grid for k spanned 25 entries from 6.1*10⁻⁶ to 6.0*10⁴ (or equivalently, each integer ln(k) from −12 to 12 inclusive). The grid for s spanned 1,000 equally spaced entries between 0.01 and 10. Under these conditions, the Mazur and Samuelson models had 25 eligible starting points, and no convergence issues emerged. The Myerson-Green and Rachlin models had 25,000 eligible starting points. The Myerson-Green model failed to converge in 29 of 111 cases, and the Rachlin model did not fail to converge in any cases. Attempts to adjust the maximum iterations, minimum step size, and convergence criteria did not recover any of these non-optimizing datasets.

The 29 non-optimizing Myerson-Green datasets were also analyzed using the solver package in Microsoft Excel, and an interesting pattern emerged. Figure 3 includes a plot of indifference point data from subject 7 and two Myerson-Green model overlays. The solid line plots the fit from the estimated k and s estimates from the final iteration of a failed nls optimization, and the series of ‘+’ symbols corresponds to a fit that was achieved using Microsoft’s Solver in Excel. Despite the fact that nls convergence failed, and the fact that the parameter estimates differed substantially, the model fit in both cases appears visually identical and also appropriate for the data. The fact that substantially different parameter values can produce nearly identical model fits in the Myerson-Green model may be one reason that difficulty in parameter estimation was observed for this model in this study.

Fig. 3.

Discounting data for subject 7. The left panel plots indifference points by delay and the right panel plots indifference points by log delay. The two separate overlays consist of a solid line and a series of ‘+’ symbols, which fall very close to each other on the plots. These correspond to two different sets of parameter estimates for the Myerson-Green model as indicated in the legend.

Study 2: Simulation Study

Scientific data analyses typically proceed by using well-established analytical approaches to glean insight about thematic or underlying features in data that are unknown at the outset of the study. This approach is ideal when established methods are available and the researcher aims to characterize the structure behind previously uncharacterized data. Monte Carlo simulation is a powerful approach that inverts this paradigm. In order to determine the comparative performance of competing methods, Monte Carlo simulation allows us to generate large amounts of virtual data with specified underlying characteristics. Since the researcher programs the data generation procedure (informed by Study 1 data), the “true” structure of the data is known, and methods are compared according to their ability to correctly identify the true state of the underlying data. In Study 2 a Monte Carlo computer simulation was performed to assess the accuracy of ED50 estimates and model selections for a variety of modeling approaches under a set of corresponding hypotheses.x

Methods

Experimental layout

The study design considers three data generating scenarios. The Mazur and Rachlin models were chosen as single model comparators to the multiple model hypothesis. The Mazur model was chosen due to its prevalence in the literature. For example, a recent meta-analysis comparing discounting in control groups and addictive behavior groups revealed that approximately 70% of studies used the Mazur model (MacKillop et al., 2011). The Rachlin model was chosen as a suitable two-parameter model since it was selected most frequently in Study 1 and also converged for the great majority of data sets.

In order to reflect empirical data as closely as possible, the inputs to the simulation were based on the data in Study 1. In the “Mazur only” scenario, all participant data were generated under the Mazur model (mean ln(k) −6.34, sd ln(k) = 1.72). This means that for each participant, a single value of ln(k) was drawn from a normal distribution with mean and standard deviation matching the data from Study 1, and then indifference data were generated according to that value of ln(k). In the “Rachlin only” scenario, data were similarly generated according to the behavior of Rachlin fits to the data from Study 1 (mean ln(k) = −8.34, sd ln(k) = 7.34, mean s< sd = 1.28, s< 0.97, correlation between ln(k) and s −0.90). Finally, a “heterogeneous” scenario was explored, where participant data arise from models chosen at random in the proportions observed in the Study 1 data, omitting random noise selections: Rachlin 34.9%, Myerson & Green 27.5%, Mazur 18.3%, Laibson 11.0%, and Samuelson 8.3%. When the true underlying model was the Mazur, Samuelson, Myerson and Green, or Rachlin model, the parameter values were generated as Gaussian variates according to the means, standard deviations, and correlations shown in Table 2. When the true underlying model was the Laibson model, the β and δ parameters were generated according to a uniform distribution on the range observed among the Laibson selections in the Study 1 data: 0.7147 < β < 0.9802, 0.9972 < δ < 0.9999.

Modeling approaches

The data generated from each of the three above scenarios were analyzed using three modeling strategies. The first two strategies apply the Mazur and then the Rachlin model to all simulated data. For the first two strategies, the appropriate ED50 formula was used (see Table 1) to estimate the ED50 value from each simulation run. The model selection approach described in Study 1 was then applied as a third strategy. For the model selection approach, ED50 was computed as described in Study 1. Each of these estimated ED50 values was compared to the true ED50 value, which is known in this context because this is a Monte Carlo simulation. We hypothesize that single model approaches will outperform the model selection approach in the cases where the corresponding model truly underlies the data, while the model selection approach will perform best when multiple models underlie data. Each modeling strategy is applied to each of the three data generating scenarios, which allows for the comparative assessment of different data analysis approaches under different plausible hypotheses about the underlying structure of the data.

Indifference points were then generated according to the sampled parameters with Gaussian errors. The model MSE was set to the median from the Study 1 data (σ² = 0.005) for all participants. Indifference points that fell outside of the [0,1] range were reassigned to 0 and 1 as appropriate. This ensures that simulated data cannot take values that are impossible for participants to generate in the titration questionnaire used in the empirical study. The same inclusion criteria were used in the simulation as in the empirical data (i.e., random noise model not most probable, no increasing trends, no ED50 outside the delay range observed) to further ensure that the simulation is as similar as possible to the analysis plan of Study 1.

Monte Carlo simulation proceeds by replicating an experiment many times in order to assess the long-run performance of the methods under study. We designed the computer simulation to replicate 1000 runs of the data described above for each of the 111 Study 1 participants. This sampling process was repeated for all three data-generating scenarios for a total of 333000 simulation runs.

Assessment of model performance

The performances of the Mazur only, Rachlin only, and model selection strategies were compared. The discrepancy between estimated and true ED50 values was summarized on a study-by-study basis using the mean square error (MSE_T) which compares the estimated ED50 value to the true ED50 value for each participant:

$$MS{E}_T=\frac{1}{1000}{{\displaystyle {\sum }_{i=1}^{1000}\left({\widehat{ED50}}_i-ED{50}_i\right)}}^2,$$ (2)

where ${\widehat{ED50}}_i$ represents the estimated effective delay 50 for participant i and ED50_i represents the true ED50 computed from the known model and parameters. The subscript T in Equation 2 indicates that the proposed metric is a comparison between estimated and true ED50 values in the simulation. This metric summarizes how well a given modeling approach performs relative to the true ED50 value in simulation. Importantly, this MSE_T value should not be confused with the mean square error, which summarizes the departure of indifference points from model fits for individual participant data. This computation is only possible in the computer simulation because the true ED50 values are known in the simulation but unknown in practice.

High values of MSE_T correspond to studies where the predicted ED50 values were far from the true values. MSE_T was computed in this fashion for 1000 simulated studies in all three conditions. The accuracy and screening rates of model selections across all participants were reported.

Results

Figure 4 depicts the distribution of MSE_T across 1000 simulated experiments in every combination of condition and modeling strategy. The three panels correspond to different underlying data-generating scenarios: Mazur (A), Rachlin (B), and heterogeneous (C). The three boxplots in each panel indicate the performance of each modeling strategy. Low values in this plot correspond to settings in which the chosen modeling approach performs well.

Fig. 4.

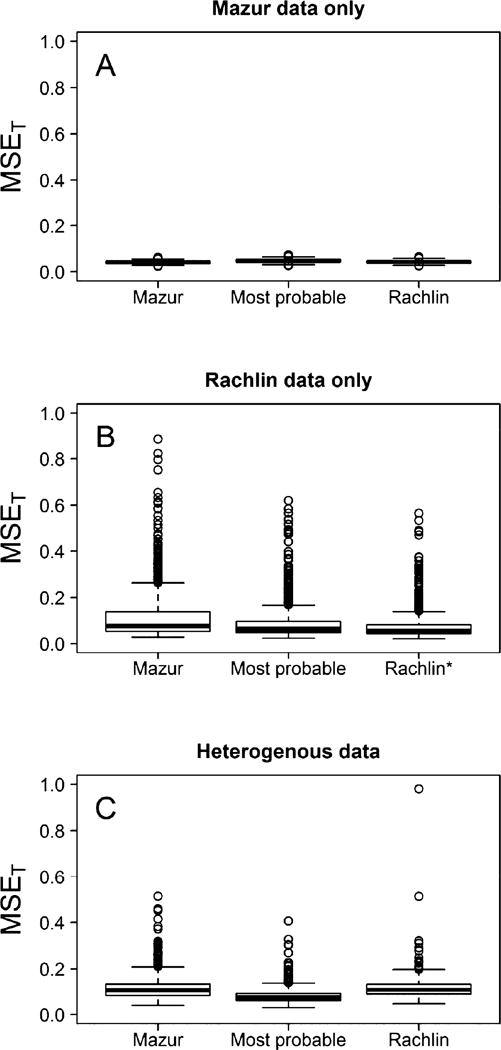
MSE_T values comparing the estimated ln(ED50) to the true value of ln(ED50) used in the simulation. Panels A, B, and C correspond to data that arise from the Mazur only, Rachlin only, and heterogeneous settings. In the heterogeneous setting, MSE_T is lowest when model selection is used, indicating that if the multiple model hypothesis is correct, then the model selection approach more accurately estimates ED50. * indicates that two points are above the plotted vertical range.

Wilcoxon signed rank tests indicated that the optimal modeling strategy in each case matched the model that was used to generate the data (i.e., MSE_T was lower with the Mazur model for Mazur data, Rachlin model for Rachlin data, and model selection approach for heterogeneous data; p < 0.00001 for all comparisons). The plot indicates, however, that the magnitude by which the optimal strategy outperforms the competing methods varies from trivially small (e.g., the Mazur case, panel A, Fig. 4), but is more pronounced in other cases (e.g., heterogeneous approach, Rachlin model, panels B and C, Fig. 4). Of special note: The model selection approach outperforms both single model approaches in the heterogeneous scenario (panel C, Fig. 4). In both of the single model scenarios, the model selection approach appears to suffer very little and is likely noninferior in a practical sense (panels A and B, Fig. 4). Taken together, these results suggest that if multiple models or processes truly underlie discounting in different subjects, then the model selection approach can have a distinct advantage over a single model approach. In the event that all subjects truly discount according to a single model, then the model selection approach performs similarly to the correctly specified model (e.g., panels A and B, Fig. 4). Interestingly, the model selection approach outperforms the Mazur-only approach in the Rachlin scenario (panel B, Fig. 4). Hence, adopting the model selection approach would seem to be a pragmatic, low-risk, and potentially high-reward strategy when estimating ED50 regardless of which underlying data structure is actually true.

Among all 333000 simulation runs (111 “participants” × 3 scenarios × 1000 runs), the number of noise selections was 14108 (4.2%). The number of increasing trends (i.e., negative estimates for s when Rachlin or Myerson & Green was called) was 2148 (0.6%). The number of instances where the estimated ED50 was off the range of the delays presented was 38298 (11.5%). The number of participants who exhibited at least one of these violations was 52406 (15.7%). Hence, 280594 sessions survived the screening criteria described above. The greatest number of screenings arose from the extrapolation rule, and among the 38298 participants who violated this rule, 31330 (82%) corresponded to participants where the true underlying model was either Rachlin or Myerson and Green. Hence, a better understanding of the bivariate relationship between s and k for these models might enable a simulation study that had a reduced number of screenings for these models. While the screening rate for the simulation was higher than the Study 1 data, we nonetheless have generated and analyzed a large amount of participant data which is highly similar to observed data from Study 1, allowing valuable insight for the potential upside of the model selection approach.

The discussion above indicates that the model selection approach appears at worst to be noninferior to the single model approach under the single model hypotheses, and superior under the multiple model hypothesis. To further explore the model selection method, accuracy of the model selections was assessed. In the Mazur-only scenario, the model selection approach correctly called the Mazur model 49.6% of the time in the seven-delay schedule. In the Rachlin-only scenario, the model selection approach correctly called the Rachlin model 55.8% of the time. In the heterogeneous scenario, the model selection approach identified the correct model 43.4% of the time. Hence the model selection routine is more accurate than calling models by chance alone (which would work about 16.7% of the time). This indicates that the model selection approach estimates ED50 with high accuracy relative to single model approaches (Fig. 4) despite the fact that the true model is not always identified. All percentages are computed among the participants that did not violate the screening criteria described in Section 2.1.7.

General Discussion

This paper is the result of a novel combination of perspectives, including statistics, behavioral economics, and pharmacology. In this study, we found that the proposed model selection approach had lower average MSE than the Mazur model approach using the Study 1 data. The log transformation of ED50 elicited a roughly symmetric distribution, allowing for parametric analyses. The most probable discounting model in the Study 1 data differed among participants, suggesting the possibility that a single model or process may not underlie discounting in all people and that these differences may be systematic. The screening criteria based on this method flagged a lower number of participants when compared with the Johnson and Bickel screening method. The simulation study suggests that if multiple models truly underlie discounting data in humans, then ED50 estimates based on model selection fall closer to true ED50 values compared to the single model approaches, as measured by MSE_T. If, for example, the Mazur model underlies all discounting data, then the model selection approach was outperformed by the single model approach by a trivially small margin (Fig. 4). Under the Rachlin-only scenario, the model selection approach fared worse than the Rachlin-only modeling approach, but better than the Mazur-only modeling approach.

Figure 1 displays discounting data for a single subject. These data violate the Johnson and Bickel criteria, yet the probability that these data are best modeled by random noise (i.e., change in valuation is independent of delay) is 0.2% according to the model selection approach. Since the task in this experiment adjusted questions based on the participant’s responses, data such as these could arise if a subject miscodes a single early question in the titration sequence. The Johnson and Bickel criteria are intended as a flexible set of guidelines and could be relaxed to allow one such violation without excluding data from subsequent analysis. The model selection method will typically retain participant data that has a single unusual point such as this.

The proposed method in combination with a seven-delay schedule task cannot directly address the one-versus-several model hypotheses, because as the simulation indicates, multiple models are chosen whether or not the true underlying process involves multiple models or just one. Despite the low accuracy of model selections, the model selection procedure estimates ED50 nearly as accurately as the single model approaches when a single model governs discounting for all subjects, and the proposed method is superior when multiple models underlie participant response. These ED50 values leverage a multitude of available models to provide appropriate one-number summaries of discounting, which is generally of primary interest. The simulation study suggests that in the heterogeneous scenario, the proposed method tends to outperform single model approaches based on the Mazur and Rachlin models. Applying the model selection approach is therefore a low-risk and potentially high-reward approach since it performs nearly as well as the single model approach when all subjects obey a single model, and it performs substantially better when subjects truly discount according to multiple models based on this simulation study. Additionally, the utility of ED50 as a unifying measure could potentially have important applications in meta-analysis since ED50 can be computed and is comparable between studies that use different discounting functions.

The proposed method has some weaknesses. First, the method can only accommodate likelihood-based models that have a computable BIC. Area under the curve has been proposed as a discounting measure that does not rely on parameter estimation using a theoretical discounting function (Myerson et al., 2001). Second, the accuracy of model selections is imperfect. However, the improvements in MSE_T shown in Figure 4 indicate the accuracy of the model selection approach. If the Rachlin model is estimated as most probable when in fact the Myerson and Green pattern is the true underlying model, then this is generally of secondary importance given that the approach ultimately tends to improve the accuracy of ED50 estimates. The most probable model tends to more adequately estimate ED50 even when the chosen models are different from the true models overall. This is likely due to the fact that the asymptotic approximation for the model probabilities is based on a relatively small number of indifference points.

This report describes a new approach for characterizing discounting data by employing approximate Bayesian model selection and allowing for multiple models to be chosen within a single study. Further, ED50 is shown to be a suitable unifying measure which allows for sensible between-model comparisons of discounting.

Appendix

Distribution of ED50 Measures

Figure A1 shows the distribution of ED50 measures for the Mazur model and the model selection approach from Study 1. In both cases, the natural log transformation reduces skew and yields discounting measures more appropriate for parametric analysis.

Bayesian Model Selection

The probability of data being observed given model candidate d is

$$P\left(\mathit{X}|M_d\right)={\displaystyle \int P\left(X|{\theta }_d,M_d\right)P\left({\theta }_d|M_d\right)d{\theta }_d},$$ (A1)

where X represents observed data, M_d represents the dth candidate model, d = 1,…, D, and θ_d is the vector of parameters for model d. The likelihood is P(X|θ _d, M_d), which is the probability density function of the data given the parameters and model, and P(θ_d|M_d) is the prior distribution of the parameters given the model.

By Bayes’ rule

$$P\left(M_d|X\right)=\frac{P\left(X|M_{\mathrm{d}}\right)P\left(M_d\right)}{{\displaystyle {\sum }_{j=1}^{D}P\left(X|M_j\right)P\left(M_{\mathrm{j}}\right)}}.$$ (A2)

This implies that for models m and l

$$\frac{P\left(M_m|X\right)}{P\left(M_l|X\right)}=\frac{P\left(X|M_m\right)}{P\left(X|M_l\right)}\frac{P\left(M_m\right)}{P\left(M_l\right)},$$ (A3)

where the quantity $B{F}_{ml}=\frac{P\left(X|M_m\right)}{P\left(X|M_l\right)}$ is known as the Bayes’ factor comparing models m and l.

Generally, (A1) is not analytically tractable and must be assessed via numerical integration or approximated asymptotically. Kass and Raftery (1995) show that for models m and l, BIC_m−BIC_l asymptotically approximates −2ln (BF _ml) as n →∞. This implies that $B{F}_{ml}\approx e^{-\frac{1}{2}\left(BI{C}_m-BI{C}_l\right)}$.

Model probabilities are approximated with the following formula:

$$P\left(M_d|X\right)\approx \frac{\widehat{B{F}_{d1}}}{\widehat{Q}}\text{for all}d=1,\dots ,D,$$ (A4)

where

$${\widehat{\mathrm{BF}}}_{11}=e^{-\frac{1}{2}\left(BI{C}_1-BI{C}_1\right)}=1$$

$$\begin{array}{c}{\widehat{\mathrm{BF}}}_{21}=e^{-\frac{1}{2}\left(BI{C}_2-BI{C}_1\right)}\\ ⋮\\ {\widehat{\mathrm{BF}}}_{\mathrm{D}1}=e^{-\frac{1}{2}\left(BI{C}_D-BI{C}_1\right)}\end{array}$$

and

$$\widehat{Q}={\displaystyle {\sum }_{d=1}^D{\widehat{BF}}_{d1}}\approx \frac{{\displaystyle {\sum }_{d=1}^{D}P\left(M_{\mathrm{d}}|X\right)}}{P\left(M_1|X\right)}=\frac{1}{P\left(M_1|X\right)}$$ (A5)

The largest value of $\frac{{\widehat{BF}}_{d1}}{\widehat{Q}}$ corresponds to the model with the highest estimated probability.

Fig. A1.

Distribution of ED50 and ln(ED50) values for Mazur model and model selection approaches on the data from Experiment 1.