Leveraging output term co-occurrence frequencies and latent associations in predicting medical subject headings

Abstract

Trained indexers at the National Library of Medicine (NLM) manually tag each biomedical abstract with the most suitable terms from the Medical Subject Headings (MeSH) terminology to be indexed by their PubMed information system. MeSH has over 26,000 terms and indexers look at each article’s full text while assigning the terms. Recent automated attempts focused on using the article title and abstract text to identify MeSH terms for the corresponding article. Most of these approaches used supervised machine learning techniques that use already indexed articles and the corresponding MeSH terms. In this paper, we present a new indexing approach that leverages term co-occurrence frequencies and latent term associations computed using MeSH term sets corresponding to a set of nearly 18 million articles already indexed with MeSH terms by indexers at NLM. The main goal of our study is to gauge the potential of output label co-occurrences, latent associations, and relationships extracted from free text in both unsupervised and supervised indexing approaches. In this paper, using a novel and purely unsupervised approach, we achieve a micro-F-score that is comparable to those obtained using supervised machine learning techniques. By incorporating term co-occurrence and latent association features into a supervised learning framework, we also improve over the best results published on two public datasets.

1. Introduction

Indexing biomedical articles is an important task that has a significant impact on how researchers search and retrieve relevant information. This is especially essential given the exponential growth of biomedical articles indexed by PubMed®, the main search system developed and maintained by the National Center for Biotechnology Information (NCBI). PubMed lets users search over 22 million biomedical citations available in the MEDLINE bibliographic database curated by the National Library of Medicine (NLM) from over 5000 leading biomedical journals in the world. To keep up with the explosion of information on various topics, users depend on search tasks involving Medical Subject Headings (MeSH®) that are assigned to each biomedical article. MeSH is a controlled hierarchical vocabulary of medical subjects created by the NLM. Once articles are indexed with MeSH terms, users can quickly search for articles that pertain to a specific subject of interest instead of relying solely on key word based searches.

Since MeSH terms are assigned by librarians who look at the full text of an article, they capture the semantic content of an article that cannot easily be captured by keyword or phrase searches. Thus assigning MeSH terms to articles is a routine task for the indexing staff at NLM. The manual indexing task is observed to consume a significant amount of time leading to delays in the availability of indexed articles. It is observed that it takes about 90 days to complete 75% of the citation assignment for new articles [1]. Moreover, manual indexing is also a fiscally expensive initiative [2]. Due to these reasons, there have been many recent efforts to come up with automatic ways of assigning MeSH terms for indexing biomedical articles. However, automated efforts (including our current work) mostly focused on predicting MeSH terms for indexing based solely on the abstract and title text (henceforth referred to as ‘citation’) of an article. This is because most full text articles are only available based on paid licenses not subscribed by many researchers. Furthermore, it was found that using full text adds additional complexity requiring a careful selection of particular sections and was found to have limited utility [3].

Many efforts in MeSH term prediction generally rely on two different methods. The first method is the k-nearest neighbor (k-NN) approach. In this approach, first, k citations whose corresponding articles are already tagged with MeSH terms and whose content is found to be “closest” to the citation of the new article to be indexed, are obtained. The MeSH terms from these k citations form a set of candidate terms for the new citation. The candidate terms are ranked by according to certain criteria and the top ranked terms constitute the predicted set for the new citation. A second method is based on applying machine learning algorithms to learn binary classifiers for each MeSH term. A new citation would then be put through all the classifiers and the corresponding MeSH terms of classifiers that return a positive response are chosen as the indexed terms for the abstract. An additional ranking mechanism may be imposed if too many classifiers return a ‘yes’ answer. We note that both k-NN and machine learning approaches need large sets of citations and the corresponding MeSH terms to make predictions for new abstracts. On the other hand unsupervised approaches do not need any training data but in general do not achieve performance comparable with supervised approaches. In this paper,

1. We first propose a new unsupervised ensemble method¹ that uses named entity recognition (NER), relationship extraction, knowledge-based graph mining, and output label co-occurrence statistics to extract MeSH terms. Prior attempts have used NER, relationship extraction, and graph mining approaches as part of their supervised approaches and we believe this is the first time output term co-occurrences are applied for MeSH term extraction. We achieve a micro-F-score that is comparable to those that employ a k-NN based strategy on two public datasets.

2. We adapt our methods from the unsupervised framework to a supervised k-NN and learning-to-rank [5] based framework by additionally introducing latent term associations computed using reflective random indexing [6] to term sets. We show that this results in better precision, recall, F-score, and mean average precision (MAP) over the best published results at the time of this writing on two public datasets.

Before we continue, we would like to emphasize that automatic indexing attempts, including our current attempt, are generally not intended to replace trained indexers but are mainly motivated to expedite the indexing process and increase the productivity of the indexing initiative at the NLM. Hence in these cases, recall might be more important than precision although an acceptable trade-off is necessary. In the rest of the paper, we first discuss MeSH background, related work in MeSH term prediction, and also the context of our paper in Section 2. We briefly discuss the two public datasets used and present the measures used for evaluation in Section 3. In Section 4, we start out by introducing the unified medical language system (UMLS), biomedical NER, semantic predications (relations) and finally build on these to present our novel unsupervised MeSH term extraction method with the corresponding evaluation. Section 5 outlines the k-NN and learning-to-rank approaches employed for supervised prediction. In this section, we also give an overview of a specific variant of reflective random indexing used to compute latent inter-term associations. Finally, we formally specify all the features used in learning a function that ranks the candidate terms and evaluate the resultant predictions.

2. Background and related work

MeSH is a hierarchical terminology whose main application is indexing biomedical articles. Hence strict notions of meronymy were not used in its design; the hierarchical relationships are actually guided by “aboutness” of a child to its parent. Hence a term could be a descent of multiple other terms whose least common consumer is not one of them. That is, a term could have multiple paths from the root.

NLM initiated efforts in MeSH term extraction with their Medical Text Indexer (MTI) program that uses a combination of k-NN based approach and NER based approaches with other unsupervised clustering and ranking heuristics in a pipeline [7]. MTI recommends MeSH terms for NLM indexers to assist in their efforts to expedite the indexing process². Another recent approach by Huang et al. [1] uses k-NN approach to obtain candidate MeSH terms from a set of k already indexed articles and use the learning-to-rank approach to learn a ranking functions that ranks these candidate terms. They use two different datasets one with 200 citations and the other with 1000 citations, which are also used for our experiments in this paper.

Several other efforts employed machine learning approaches with novel feature selection [8] and training data sample selection [9] techniques. Vasuki and Cohen [10] use an interesting approach that employs reflective random indexing to find the nearest neighbors in the training dataset and use the indexing based similarity scores to rank the terms from the neighboring citations. A recent effort by Jimeno-Yepes et al. [11] uses a large dataset and uses meta-learning to train custom binary classifiers for each MeSH term and index the best performing model for each terml for usage on new testing citations; we request the reader to refer to their work for a recent review of machine learning approaches used for MeSH term assignment.

As mentioned in Section 1, most current approaches rely on large amounts of training data. We first take a purely unsupervised approach under the assumption that we have access to output term sets where training citations may not be available. We then adapt our methods and also add an additional random indexing component to a learning-to-rank framework to achieve better results on two public datasets.

3. Datasets and evaluation metrics

Before we go into the details of our methods, we briefly present the datasets used in experiments and establish notation used for evaluation measures. Essentially, each testing dataset citation will have an associated set of correct MeSH terms it is assigned and our goal is to automatically predict a set of MeSH terms from title and abstract that best matches the correct set of terms. We experiment with two public datasets used by Huang et al. [1]. The NLM2007 dataset has 200 test citations and is used by other recent studies on this subject [10]. The L1000 dataset is curated by Huang et al. by random selection for the purposes of their work to test their methods on a larger dataset that spanned a large number of years. Both datasets can be obtained from the NLM website: http://www.ncbi.nlm.nih.gov/CBBresearch/Lu/indexing/paperdat.zip.

Next we discuss the standard evaluation measures used when discussing multi-label classification results. We chose to present them here because of the layout of the paper, where results of unsupervised and supervised methods are discussed separately for the purposes of clarity. Let L be the set of all biomedical citations to be assigned MeSH terms; Let E_i and G_i, i = 1, …, |L|, be the set of predicted MeSH terms using our methods from the PubMed citations (here, abstract and title fields) and the corresponding correct gold standard terms, respectively, for the i-th citation. Since the task of assigning multiple terms to a citation is the multi-label classification problem, there are multiple complementary methods for evaluating automatic approaches for this task. Since these are relatively smaller datasets with very few citations per label, we use micro-precision, micro-recall, and micro-F-score used by Huang et al. [1]. The average micro precision P_μ and micro recall R_μ are

$$P_{\mu }=\frac{{\sum }_{{\mathbf{L}}_i\in \mathbf{L}}c(N,{\mathbf{L}}_i,E_i)}{\mid \mathbf{L}\mid ·N}\text{and}{R}_{\mu }=\frac{{\sum }_{{\mathbf{L}}_i\in \mathbf{L}}c(N,{\mathbf{L}}_i,E_i)}{{\sum }_{i=1}^{\mid \mathbf{L}\mid }\mid G_i\mid },$$

where c(N, L_i, E_i) is the number of true positives (correct gold standard terms) in the top N ranked list of candidate terms in E_i for citation L_i. Given this, the micro-F-score is F_μ = 2P_μR_μ/(P_μ + R_μ). We also define average precision of a citation AP (L_i) computed considering top N terms as

$$\text{AP}({\mathbf{L}}_i,N)=\frac{1}{\mid G_i\mid }\sum _{r=1}^{N}I(E_i^r)·\frac{c(r,{\mathbf{L}}_i,E_i)}{r},$$

where $E_i^r$ is the r-th ranked term in the set of predicted terms E_i for citation L_i and the function $I(E_i^r)$ is a Boolean function with a value of 1 if $E_i^r\in G_i$ and 0 otherwise. Finally, the mean average precision (MAP) of the collection of citations L when considering top N predicted terms is given by

$$\text{MAP}(\mathbf{L},N)=\frac{1}{\mid \mathbf{L}\mid }\sum _{{\mathbf{L}}_i\in \mathbf{L}}\text{AP}({\mathbf{L}}_i,N).$$

For more details of various other relevant measures and their optimization strategies we encourage the readers to refer to well known surveys [12,13].

4. Unsupervised MeSH term extraction

This section details our unsupervised approach to MeSH term prediction using semantic features and output term co-occurrences. We first use a combination of NER, knowledge-based graph mining, and output label co-occurrence frequencies to predict a set of candidate MeSH terms. We then use semantic predications to rank the candidates and also use the traditional Borda rank aggregation to merge various ranked lists of the candidate set into a final ranking. Next, we elaborate on the specifics of each of the components of our approach before discussing the candidate generation. We first discuss the UMLS, a biomedical knowledge base used in NER, a graph mining method to enhance NER output, and extraction of semantic predications from free text.

4.1. Unified medical language system (UMLS)

The UMLS³ is a large domain expert driven aggregation of over 160 biomedical terminologies and standards. It functions as a comprehensive knowledge base and facilitates interoperability between information systems that deal with biomedical terms. It has three main components: Metathesaurus, semantic network, and SPECIALIST lexicon. The Metathesaurus has terms and codes, henceforth called concepts, from different terminologies. Biomedical terms from different vocabularies that are deemed synonymous by domain experts are mapped to the same Concept Unique Identifier (CUI) in the Metathesaurus. The semantic network acts as a typing system that is organized as a hierarchy with 133 semantic types such as disease or syndrome, pharmacologic substance, or diagnostic procedure. It also captures 54 important relations (called semantic relations) between biomedical entities in the form of a relation hierarchy with relations such as treats, causes, and indicates. The Metathesaurus currently has about 2.9 million concepts with more than 12 million relationships connecting these concepts. The relationships take the form C1 → rel - type → C2 where C1 and C2 are concepts in the UMLS and rel-type is a semantic relation such as treats, causes, or interacts. The semantic interpretation of these relationships (also called triples) is that the C1 is related to C2 via the relation rel-type. The SPECIALIST lexicon is useful for lexical processing and variant generation of different biomedical terms.

4.2. Named entity recognition: MetaMap

NER is a well known application of natural language processing (NLP) techniques where different entities of interest such as people, locations, and institutions are automatically recognized from mentions in free text (see [14] for a survey). NER in biomedical text is difficult because linguistic features that are normally useful (e.g., upper case first letter, prepositions before an entity) in identifying generic named entities are not useful when identifying biomedical named entities, several of which are not proper nouns. Hence, NER systems in biomedicine rely on expert curated lexicons and thesauri. In this work, we use MetaMap [15], a biomedical NER system developed by researchers at the NLM. So as the first step in identifying MeSH terms for a given abstract, we extract non-negated biomedical named entities by running MetaMap on the abstract text using MetaMap’s ability to identify negated terms. Once we obtain non-negated UMLS concepts using MetaMap from the abstract and title text, we convert these concepts to MeSH terms, when possible. Specifically, we first note that MeSH is one of the source vocabularies integrated into the UMLS Metathesaurus. As such, concepts in MeSH also have a unique identifier (or CUI) in the Metathesaurus. As part of its output, for each concept, MetaMap also gives the source vocabulary. So, the concepts from MetaMap with source vocabulary MeSH finally become the set of extracted ‘candidate’ terms for each citation. However, these MeSH term sets may not be complete because of missing relationships between UMLS concepts. That is, in our experience, although MetaMap identifies a medical subject heading, it might not always map it to a CUI associated with a MeSH term; it might map it to some other terminology different from MeSH, in which case we miss a potential MeSH term because the UMLS mapping is incomplete. We deal with this problem and explore a graph based approach in the next section. We also note that just because a MeSH term appears in a citation, it may not be the case that the citation should be assigned that term (more on this later).

4.3. UMLS knowledge-based graph mining

As discussed in Section 4.2, the NER approach might result in poor recall because of lack of completeness in capturing synonymy in the UMLS. However, using the UMLS graph with CUIs as nodes and the inter-concept relationships connected by relationship types parent and rel _ broad as edges (high level relationship types in UMLS), we can map a original CUI without an associated MeSH term to a CUI with an associated MeSH term. The parent relationship means that concept C1 has C2 as a parent. The rel _ broad type means that C1 represents a broader concept than C2. We use a simplified version of the algorithm originally proposed by Bodenreider et al. [16] for this purpose. Here, we map a CUI c output by MetaMap that is not associated with a MeSH term to the set of all MeSH terms whose corresponding CUIs in the UMLS are ancestors of c using the parent or rel _ broad edges. Intuitively, by capturing all one-hop MeSH terms that are semantically broader compared with the CUIs extracted by MetaMap, we are accounting for MeSH terms that have more specific concepts (in the UMLS), which are more likely to be identified by MetaMap. Although the original algorithm [16] captures terms at longer distances, we did not find it particularly useful for our current purpose [4].

4.4. Candidate set expansion using output label co-occurrences

Using NER and graph-based mining discussed in Sections 4.2 and 4.3, we obtain a pool of candidate MeSH terms. However, note that the trained coders will look at the full text when assigning MeSH terms. Thus, merely looking for terms mentioned in the title and abstract may not be sufficient. To further expand the pool of candidate terms, we propose to exploit the frequencies of term co-occurrences as noticed in already indexed articles. To elaborate, note we already have nearly 22 million articles that are manually assigned MeSH terms. Hence we can determine the number of times different term pairs co-occur and represent those frequencies in a matrix where both rows and columns are all possible MeSH terms (nearly 26,000). Before we go into specific details, we give a high level overview of our unsupervised approach that exploits output term co-occurrences. Intuitively, given a MeSH term that we already know with high confidence should be assigned to a particular citation, other terms that frequently co-occur with this high confidence term might also make good candidates for the input citation. However,

1. there might be many highly co-occurrent terms; high co-occurrence does not necessarily mean that the new term is relevant in the context of the current citation that is being assigned MeSH terms. To address this, we propose to model the context using MeSH terms extracted from title and abstract using NER and graph-mining (Sections 4.2 and 4.3). We still need a way of applying this context to separate highly co-occurrent terms that are also relevant for the current citation.

2. Furthermore, we also need an initial seed set of high confidence candidate terms to exploit the term co-occurrences. We propose to use, again, the MeSH terms extracted from title and abstract using NER and graph-mining. The title MeSH terms are directly included in the seed set of candidate terms. However, the terms extracted using NER from the abstract are subject to the context (as indicated in the first step) and are only included in the seed set if they are still deemed relevant after applying the context.⁴

Given the outline explained thus far, next we present specifics of how the highly co-occurrent terms are obtained from the seed set and how the context terms (that is, MeSH terms from title and abstract) are used to select a few highly co-occurrent terms that are also contextually relevant for the current article to be indexed. Before we proceed, as a pre-processing step, we build a two dimensional matrix⁵ ℳ of row-normalized term co-occurrence frequencies where both rows and columns are all possible MeSH terms and the cells are defined as

$$\mathcal{M}[i][j]=\frac{\text{number}\text{of}\text{articles}\text{assigned}\text{both}i-\text{th}\text{and}j-\text{th}\text{MeSH}\text{terms}}{\text{number}\text{of}\text{articles}\text{assigned}\text{the}i-\text{th}\text{term}}.$$ (1)

ℳ [i][i] = 1 because the numerator would be equal to the denominator. We note with this definition of ℳ [i][j] is an estimate of the probability P(j - th term|i - th term). Let 𝒯 and 𝒜 be the set of title and abstract MeSH terms extracted using NER, respectively, and 𝒞 = 𝒯 ∪ 𝒜 be the set of context terms which includes the MeSH terms extracted from both title and abstract. Let α and β be the thresholds used to identify highly co-occurrent terms and to select a few of these terms that are also contextually relevant, respectively; details of these thresholds will be made clear later in this section. Next we present the pseudocode of candidate term expansion algorithm.

Algorithm.

Expand-Candidate-Terms (𝒯, 𝒜, α, β, ℳ[ ][ ]).

1:	Initialize seed list S = 𝒯
2:	Set context terms 𝒞 = 𝒯 ∪ 𝒜
3:	S.append( Apply-Context(𝒜, β, 𝒞, ℳ[][]))
	{Next, we iterate over terms in list S}
4:	for all terms t in S do
5:	Let H = [] be an empty list
6:	for each i such that ℳ[t][i] > α do
7:	H.append(i-th MeSH term)
8:	relevantTerms = Apply-Context (H, β, 𝒞, ℳ[][])
9:	relavantTerms = relevantTerms - S {avoid adding existing terms}
10:	S.append(relevantTerms)
11:	return S

Procedure.

Apply-Context (H, β, 𝒞, ℳ [ ][ ]).

1:	for all candidate terms t in H do
2:	Set co-occurrence score F = 0
3:	for each context term c in 𝒞 do
4:	F = F + ℳ[c][t]
5:	if F/|C| < β then
6:	H.delete(t) {F/|𝒞| is the average co-occurrence}
7:	return H

First, we discuss the Expand-Candidate-Terms algorithm. It takes the title and abstract MeSH terms as input and also the thresholds α (to extract terms that highly co-occur with the seed terms) and β (to apply context and prune the expanded set of terms). We initialize the seed set to be just the title terms (line 1). In line 3, we add to the seed set, abstract terms that have an average co-occurrence score ≥β with the context terms. In lines 4–10, we expand the seed set to add new candidate terms. For each seed term t considered in the for loop on line 4, we curate a list of highly co-occurrent terms according to the term pair co-occurrence matrix (lines 6–7). We then prune this list of terms based on their average co-occurrence with context terms by calling Apply-Context in line 8. To ensure termination and avoid looking at terms that we have already expanded, we only append terms that are not already in S (lines 9–10).

In the Apply-Context procedure, we add the co-occurrence scores of each term in the list H with all terms in the context term set 𝒞 (lines 3–4). We delete all terms from H that have an average co-occurrence less than β. In our experiments, 0.03 ≤ β ≤ 0.05 and 0.06 ≤ α ≤ 0.1 proved to be best ranges for the thresholds. Using very low thresholds will increase the size of the expanded candidate set output by Expand-Candidate-Terms (line 11). Given this expanded candidate set, we rank its terms to retain only the top few; in our experiments, the candidate sets were found to have anywhere between 25 and 200 terms while the label cardinality of our datasets is less than 15.

4.5. Ranking approaches and semantic predications

In this section, we explore different unsupervised ranking approaches to rank the resulting candidate MeSH terms obtained using the methods from Section 4.4. A straightforward method we use is to rank them based on the average co-occurrence score computed in line 5 (F/|𝒞|) of the procedure Apply-Context from Section 4.4; a second approach we follow is to rank by the number of context terms in 𝒞 with which the candidate term has a co-occurrence value ≥ the average co-occurrence on line 5. That is the number of terms c such that ℳ[c][t]≥F/|𝒞| in Apply-Context. Both these approaches are based on our co-occurrence frequency based methods.

We also experiment with a novel binning approach using binary relationships (popularly called semantic predications) extracted from the abstract text using the SemRep, a relationship extraction program developed by Thomas Rindflesch [17] and team at the NLM. Semantic predications are of the form C1 → rel - type → C2 (e.g., Tomoxifen → treats → Breast Cancer) introduced in Section 4.1 where C1and C2 are referred to as the ‘subject’ and ‘object’ of the predication, respectively. However, predications come from the sentences in the abstract text instead of the UMLS source vocabularies. The intuition is that entities C1 and C2 that participate as components of binary relationships should be ranked higher than those that do not participate in any such relationship. By virtue of participating in such a relationship asserted in one of the sentences of the abstract text, we believe they garner more importance as opposed to just being mentioned in a list of things in the introductory sentences of an abstract. Thus we divide the set of candidate terms from Section 4.4 into two bins. The first bin contains those MeSH terms that participate as a subject or an object of a semantic predication extracted from the text. The second bin consists of those candidate terms that did not occur as either a subject or an object of some predication. Terms in the first bin are always ranked higher than terms in the second bin. Within each bin, terms are ranked according to their average co-occurrence score or according to the number of context terms with which the candidate term has co-occurrence greater than or equal to the average. We also subdivided each main bin into two sub-bins where the first sub-bin consists of those terms that are extracted from the abstract (using NER) and the second that consists of only those terms that were extracted using the co-occurrence statistics. Again, ranking within sub-bins is based on scores resulting from the co-occurrence based expansion algorithms. Finally we use Borda’s [18] positional rank aggregation method to aggregate different full rankings produced by purely co-occurrence based scoring methods and bin-based scoring methods. In all these approaches, ties are broken using the average co-occurrence score and the rare ties where these scores are equal are broken by maintaining the original order in which terms are added in the expansion algorithm.

Remark 4.1

We also curated a small set of generic MeSH terms that had very low precision when our methods were applied on the NLM200 dataset. These terms were mostly non-specific in nature such as Diagnosis, Patients, and Genes, and included some check-tags.⁶ We applied a discount to the average contextual scores of such terms if they were found in the candidate terms for the L1000 dataset.

Remark 4.2

Suitable parameters α and β were obtained using an exhaustive combinatorial search on parameter settings to maximize the MAP for the NLM200 dataset with increments of 0.01 (for both α and β) in combination with different ranking schemes and values of N, the cut-off threshold for number of terms. We recall that lower values of α and β bias the results toward high recall and low precision outcomes.

4.6. Results and discussion

In this section, we discuss the results of the unsupervised ensemble approach outlined in Sections 4.4 and 4.5 using measures introduced in Section 3. Before we proceed with our results, we would like to point out that although we term our approach unsupervised, we note that it heavily relies on the output term sets. We call our approach unsupervised in the sense that we do not need any mappings from a biomedical citation to the corresponding MeSH terms. However, such mappings are essential in conventional binary relevance approaches to multi-label classification or in instance based learning approaches such as the k-NN approach where given an instance the mapping between its neighbors and their corresponding MeSH term sets is needed.

We first present our best micro-average precision, micro-recall, micro-F-score, and MAP in Table 1 in comparison with the results obtained by supervised ranking method by Huang et al. [1] and the results obtained when using NLM’s MTI program (as reported by Huang et al. in their paper). From the table we see that the performance of our unsupervised methods is comparable (except in the case of the MAP measure) to that of the MTI method, which uses a k-NN approach. However, as can be seen, a supervised ranking approach that relies on training data and uses the k-NN approach performs much better than our approaches. We emphasize that our primary goal in this section has been to demonstrate the potential of unsupervised approaches that can complement supervised approaches when training data is available but can work with reasonable performance even when training data is scarce or unavailable, which is often the case in many biomedical applications.

Table 1.

Comparison of micro measures with N = 25.

Method	NLM2007 dataset				L1000 dataset
	Rμ	Pμ	Fμ	MAP	Rμ	Pμ	Fμ	MAP
Our method	0.54	0.32	0.40	0.36	0.56	0.29	0.38	0.38
MTI	0.57	0.31	0.40	0.45	0.58	0.30	0.39	0.46
Huang et al.	0.71	0.39	0.50	0.62	0.71	0.34	0.46	0.61

Next we contrast the performance of our unsupervised methods involving co-occurrence statistics and semantic predication based ranking approaches with some baseline methods that only use NER and graph-mining based approaches in Table 2; we do not show MAP values because the baseline approaches do not involve a ranking scheme. We see that graph-mining approach did not increase recall by more than 2%.⁷ However, our co-occurrence based candidate term expansion (Section 4.4) improved the recall by 18% in both the NLM2007 and L1000 datasets with an increase in precision of at least 10% and an increase in F-score of at least 14%. This shows that using simplistic approaches that rely only on NER may not provide reasonable performance.

Table 2.

Comparison with baseline measures.

Method	NLM2007 dataset			L1000 dataset
	Rμ	Pμ	Fμ	Rμ	Pμ	Fμ
Our method	0.54	0.32	0.40	0.56	0.29	0.38
NER only	0.35	0.20	0.25	0.36	0.19	0.25
NER + graph-mining	0.36	0.19	0.25	0.38	0.18	0.24

Whether using unsupervised or supervised approaches, fine tuning the parameters is always an important task. Next, we discuss how different thresholds (α and β in Section 4.4) and different values of N affect the performance measures. We believe that this is important because low values for thresholds and high cut-off values for N have the potential to increase recall by trading off some precision. We experimented with different threshold ranges for α and β and also different values of N. We show some interesting combinations we observed for the L1000 dataset in Table 3. We gained a recall of 1% by changing N from 25 to 35 with the same thresholds. Lowering the thresholds with N = 35 leads to a 5% gain in recall with an equivalent decrease in precision, which decreases the F-score by 5% while increasing the MAP score by 1%. Recall that we fine tune the parameter values and select the best rank aggregation scheme based on parameter search conducted on the NLM200 dataset (Remark 4.2). By using the best configuration that maximized the MAP score on that smaller dataset, from Table 1 we show that similar performance is also obtained on the larger L1000 dataset.

Table 3.

Different combinations of N, α, and β.

Parameters	L1000 dataset
	Rμ	Pμ	Fμ	MAP
N = 25, α = 0.10, β = 0.05	0.51	0.33	0.40	0.36
N = 25, α = 0.08, β = 0.04	0.56	0.29	0.38	0.38
N = 35, α = 0.08, β = 0.04	0.57	0.28	0.38	0.38
N = 35, α = 0.06, β = 0.03	0.62	0.23	0.33	0.39

Finally, among the ranking approaches we tried, the best ranking method is Borda’s aggregation of the two ranked lists, the first of which is based on average co-occurrence scores and the second is the semantic predication based binning approach with average co-occurrence as the tie-breaker within each bin. This aggregated ranking is used to obtain the best scores we reported in all the tables discussed in this section. The semantic predication based binning provided a 3% improvement in the MAP score for both datasets.

5. Supervised prediction with co-occurrences and latent associations

In Section 4, we introduced an unsupervised ensemble approach that uses named entities, semantic predications, and output label co-occurrence frequencies to predict MeSH terms for a given biomedical citation. Although unsupervised approaches are useful when training data is unavailable, clearly, when we have access to training data, we would want to develop methods that give the best performance. Interestingly, as we show in this section, output label co-occurrences also help improve performance of k-NN based approaches that use training data. Specifically, we use a learning-to-rank framework similar to that employed by Huang et al. [1] and incorporate co-occurrence frequencies (from Section 4.4) and latent label associations computed using reflective random indexing [6] as new features in addition to the neighborhood based features to obtain the best results known at the time of this writing on the two datasets introduced in Section 3. First, we introduce the k-NN approach and the learning-to-rank framework used in the rest of the paper.

5.1. Nearest neighbors for biomedical citations

The k-NN approach for multi-label classification starts out by identifying k instances T_i, i = 1, …, k, in the training dataset that are ‘closest’ to the testing instance I under consideration. Intuitively, because nearest neighbor instances significantly resemble the current instance we assume they share the same characteristics and believe most correct labels for I are going to be in the neighborhood

$${\mathcal{N}}_k(I)=\underset{i=1}{\overset{k}{\cup }}G(T_i),\text{where}{T}_1,\dots ,T_k\text{are}\text{the}k\text{nearest}\text{neighbors}$$ (2)

and G(T_i) is the set of correct labels for the training instance T_i. However, 𝒩_k(I) may be very large compared with the average number of labels assigned per instance (which is in the range 13–15 MeSH terms for our current problem). Hence, a ranking on labels in 𝒩_k(I) is imposed and a small subset of top ranked labels is chosen to be the final predicted set of labels for I. In the case of predicting MeSH terms for biomedical citations it was shown [1] that k = 40 leads to a coverage of up to 90% of all the correct terms for new unseen instances. The nearest neighbors of the citations are computed based on a ranking of neighboring training documents determined using a similarity score between them and the testing instance. The similarity score is based on the weighted score of the words that are contained in both a neighbor training instance and the testing instance, where the weight of a word is determined based on its frequency in the entire training corpus, its local frequency in the current instances being compared, and also on the document lengths (in terms of number of words) of the instances [19]. Huang et al. [1] use this approach to compute the top 50 neighbors for both testing datasets we use in this paper and for our experiments we use the same top 50 neighbors made available by them.

5.2. Learning-to-rank using a linear feature based model

In information retrieval, for an input query, an effective search system is expected to return a ranked list of documents where the relevance decreases as the rank increases. Traditionally, this ranking was done based on cosine similarity of query terms’ vector with document vectors in a vector space model [20] of a corpus or based on specific retrieval scoring methods such as BM25 [21]. Similar to how we aggregated the rankings in Section 4.5, different rankings according to different scores are aggregated in an unsupervised fashion. However, such schemes assume that all constituent scoring mechanisms are equally important. However, this might not be the case and learning-to-rank [5] has emerged from the machine learning community as an automated way of learning functions that can rank a list of documents in response to an input query based on different query-specific features extracted from the documents. A learning-to-rank algorithm follows a supervised approach and in its training phase, takes as input a training dataset of queries and the corresponding ranked lists of documents:

$$\{(Q_i,\mathcal{R}(D_i)):i=1,\dots ,n\},$$ (3)

where Q_i is a query, D_i is the set of documents associated with Q_i, ℛ(D_i) is the ground truth ranking on the documents for Q _i, and n is the size of the training dataset. The algorithm then learns a ranking model that minimizes an appropriate loss function that pertains to the ranking. We note that the training process actually extracts features $f_j(D_i^r)$, where r = 1, …, t(i), for each document $D_i^r\in D_i$ where t(i) is the number of documents provided to the i-th query instance for training and j is an index for the particular features used. Note that features extracted from the documents are heavily based on the specific query to tightly constrain the ranking based on information available in the query. Finally, given a new query and a specific set of documents as input, the learned model imposes a ranking on the document set based on query specific document features. This is a general description of the problem; for a more detail discussion of the pointwise, pairwise, and listwise variants, please see Section 1.3.3 in [5].

Next we map our problem of predicting MeSH terms to a listwise variant, specifically the linear feature based coordinate ascent method by Metzler and Croft [22] which is part of the RankLib library.⁸ In Eq. (3), our queries Q_i are the biomedical citations and the documents D_i are candidate MeSH terms from the nearest 50 neighbors as shown in Eq. (2). The listwise variant in [1] minimizes cross entropy of probability distributions obtained by using a sotfmax activation function of the ground truth and predicted relevance judgment vectors for training instances. We chose the coordinate ascent method in [22] instead, as it maximizes the mean average precision (MAP), which directly corresponds to our goal of getting as many relevant MeSH terms as high as possible in the ranked list. While coordinate ascent is the parameter estimation method used, the actual approach in [22] uses a linear feature based model; we refer the readers to the original paper [22] for further details.

For the learning-to-rank training dataset, we used the 200 (citation, MeSH-term-set) pairs used by Huang et al. [1] in their paper to retain the same level of available training data. Next we discuss the features extracted for each candidate MeSH term in Eq. (2) for a given citation I.

5.3. Features for candidate MeSH terms

Based on the input testing citation (title and abstract text), we extract features for each candidate term obtained from the 50 nearest neighbors of the citation (≈200 such terms occur in each neighborhood) in the training dataset. In this section we describe all the features considered for candidate terms in our experiment. We start out with features that are based on the degree of similarity of the nearest neighbors and continue with a few other features introduced for unsupervised extraction in Section 4.

5.3.1. Neighborhood features

For each citation C in the k-nearest neighborhood of a given testing instance I, we have the similarity score 𝒮(C, I), which is essential to find the nearest neighbors in the first place. Using these similarities, for a given candidate term t from the neighborhood 𝒩_k(I), we compute the neighborhood feature as the sum

$$f_k^N(t,I)=\sum _{t\in G(T_j),j=1,\dots ,k}\mathcal{S}\left(T_j,I\right),$$ (4)

where T₁, …, T_k are the nearest neighbors and G(T_j) are the correct MeSH terms for training citation T_jas in Eq. (2). We experimented with neighborhood score sum features for different k values from k = 10 to 50 with increments of 10. Intuitively, using a combination of neighborhood features for several k helps the algorithm learn the optimal importance (feature weights) it should assign to neighbors at different distances from the testing instance; choosing a fixed k handicaps the learning process in this sense. Hence we also experimented with combinations of $f_k^N$ for different values of k (more on this in Section 5.4).

5.3.2. Context term and semantic predication features

From Section 4.4, we recall that context terms 𝒞(I) are MeSH terms extracted from the title and abstract of a citation I through named entity recognition. Although context terms may not necessarily be tagged for a biomedical citation, they can nevertheless be included as a Boolean feature

$$f^A(t,I)=\{\begin{array}{ll}1\hfill & \text{if}t\in \mathcal{C}(I);\hfill \\ 0\hfill & \text{otherwise.}\hfill \end{array}$$ (5)

Another Boolean feature is if the candidate term participated either as the subject or object of a semantic predication extracted from the title and abstract text. Recall from Section 4.5, predications are binary relationships between named entities (mapped eventually to MeSH terms through graph-mining) extracted from title and abstract text. In the unsupervised approach, this feature was used for binning candidate terms, here it is used as the binary feature

$$f^p(t,I)=\{\begin{array}{ll}1\hfill & \text{if}t\text{is}\text{subject}/\text{object}\text{of}\mathrm{a}\text{predication}\text{extracted}\text{from}I;\hfill \\ 0\hfill & \text{otherwise.}\hfill \end{array}$$ (6)

5.3.3. Co-occurrence score based feature

The average co-occurrence score of a candidate term with all context terms 𝒞(I) is used as one of the methods used to rank candidate terms in the unsupervised ensemble approach in Section 4.5; the co-occurrence sum is actually computed in lines 3–4 of the Apply-Context procedure in Section 4.4. Here we introduce the co-occurrence frequency based feature for a candidate term t as

$$f^F(t,I)=\sum _{c\in \mathcal{C}(I)}\mathcal{M}[c][t],$$ (7)

where ℳ is the normalized co-occurrence matrix from Eq. (1) for all MeSH terms computed purely using MeSH term sets of all available biomedical citations.

5.3.4. Reflective random indexing based feature

Before going into the details of this feature, we first discuss the general rationale and the intuition behind random indexing. Although the co-occurrence based feature in Eq. (7) captures direct association between the candidate terms with context terms of a testing citation, it does not capture latent or implicit associations between terms that might not have co-occurred frequently in historical data but are nevertheless strongly associated from a distributional semantics perspective. In traditional information retrieval research that employs the conventional vector space models (VSM), these implicit associations are captured using latent semantic analysis (LSA) through singular value decompositions (SVD) of the term-document matrices. Owing to the significant computational burden imposed by SVDs, newer distributional approaches that obviate these expensive operations have been developed. Random indexing (RI) is one such alternative that has been shown to have several applications in indirect inference, literature based knowledge discovery [6], and clinical concept extraction from textual narratives [23].

In the traditional sense of deriving word associations from a document corpus using distributional semantics, RI starts out by assigning elemental vectors to each word in the vocabulary. These initial word vectors have an empirically chosen dimension anywhere from 100 to a few thousand. Initially, most values in each vector are zeros except for a small number (around 10) of randomly chosen positions flipped to +1 and −1, both equal in number. Since the documents are composed of words, document vectors are then built using a weighted sum (based on frequency among other aspects) of vectors of the constituent words. This approach is repeated one more time, where the document vectors formed earlier are again used to update the word vectors where a word vector is set to the sum of the vectors corresponding to the documents that contain it. This three step process of starting with randomly initialized term vectors, composing them to form document vectors, and using the resultant document vectors to further update the term vectors is called the term based reflective random indexing (TRRI). Once this process is complete, given a query word, we can rank all words in the vocabulary based on their similarity to the input word using cosine similarity of the word vectors learned through the TRRI method. For a detailed analysis of other RI variants and a thorough introduction, please see [6]. We note that Vasuki and Cohen [10] use TRRI to obtain the nearest neighbors of a testing citation and rank the neighbors’ terms using the citation similarity score sums as discussed in Section 5.3.1. Using this approach they obtain results better than the MTI method. However, since best results are reported in [1], we directly compare with those results.

Coming back to our RI feature to capture MeSH term associations, we map the terms to words in the TRRI framework outlined earlier, and map collections of terms (that are assigned to all citations available through PubMed as of 2011) as documents. So for our purposes, a document is a biomedical citation and is essentially composed of MeSH terms that are assigned to it by human indexers at the NLM. That is, instead of treating the citation title/abstract text as the content, we treat the bag of MeSH terms assigned to it as its content.⁹ Based on experimentation (see Section 5.4), we chose the TRRI variant of RI and the dimension of 500 for the vectors to extract our feature. Finally, the TRRI feature for a candidate term t is defined as

$$f^R(t,I)=\sum _{c\in \mathcal{C}(I)}\mathcal{R}(c,t),$$ (8)

where ℛ (c, t) is the TRRI based similarity score of t with c. We note that this feature is very similar to the co-occurrence feature in Eq. (7) in that we still measure the similarity of the candidate term with all context terms of I. We used the semantic vectors package [24] to construct the MeSH term vectors using TRRI.

5.4. Results and discussion

We use all the features described in Sections 5.3.1–5.3.4 and learn a linear feature based ranking function using a small set of 200 training citations. We extract these features for the NLM2007 and L1000 datasets and predict MeSH terms by considering the top N = 25 terms in the ranked neighborhood terms.

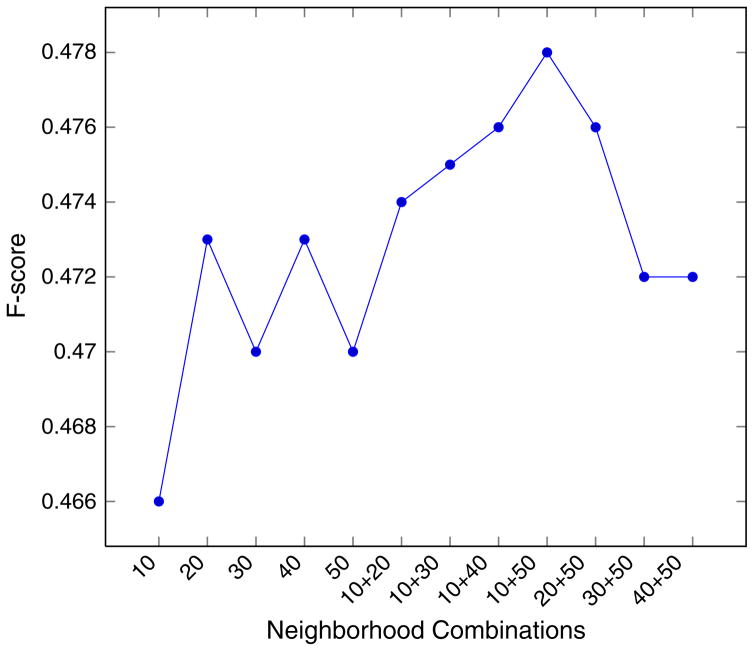
The comparison of the best current results by Huang et al. with results obtained using our method is shown in Table 4. As we can see, our method improves over all four measures (Section 3) used for both datasets. We see a MAP score improvement of 1.8% for the NLM dataset and 1.5% for the L1000 dataset. In the third row, we show performance measures if we only used the neighborhood features (Eq. (4)) considering top 10 and top 50 neighbors both as separate features. The difference in performance measures when using all features (row 2) and neighborhood features is nearly twice that of the corresponding difference between Huang et al.’s and our method with all features. It is straightforward to see that most of the predictive power comes from neighborhood features, a typical characteristic of k-NN approaches, because of the strong link between similarity of neighborhood citations and the MeSH terms of a testing instance. We also note that instead of using the neighborhood score for only top 50 neighbors, experiments show that using top k neighbors for different values of k also helps; in our case k = 10 and 50 when used simultaneously maximized both F-score and MAP for both datasets. In Fig. 1 we show the variation of F-score for various neighborhood feature combinations for the L1000 dataset. We believe neighborhood score features with k = 10 and k = 50 neighbors provide complementary information with score in the top 10 neighbors indicating the high relevance of a candidate term and the score from top 50 neighbors providing the plausibility of candidates that may be included in the final terms if they are favored by other feature types.

Table 4.

Comparison of micro measures with N = 25.

Method	NLM2007 dataset				L1000 dataset
	Rμ	Pμ	Fμ	MAP	Rμ	Pμ	Fμ	MAP
Huang et al. [1]	0.712	0.390	0.504	0.626	0.714	0.347	0.467	0.615
Our method	0.727	0.398	0.514	0.644	0.730	0.355	0.478	0.630
$f_{10}^N,f_{50}^N$ only	0.696	0.382	0.493	0.620	0.698	0.339	0.456	0.603

Fig. 1.

F-scores with various neighborhood feature combinations in L1000 dataset.

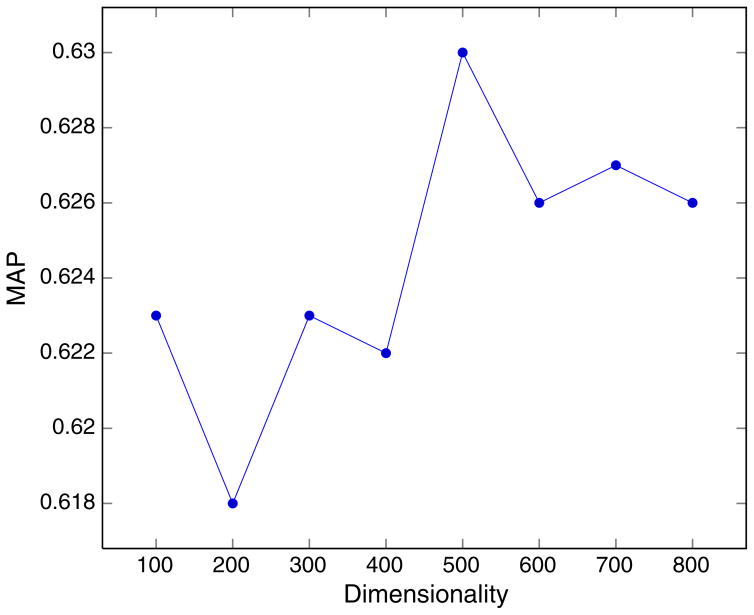
We also conducted experiments on the best dimension value for random indexing of MeSH term sets. We observed that we got the best F-score and MAP values for both datasets when the dimension is 500. In Fig. 2, we plot MAP values for the L1000 dataset. We do not see major variations at higher dimensions although the MAP value decreases slightly for dimensions greater than 500. This is expected because at higher dimensions larger amounts of training data is needed to ensure convergence of the term vectors to an extent that can actually capture the distributional semantics.

Fig. 2.

MAP variation with RI dimensionality for the L1000 dataset.

Next, we measure the contribution of each feature to the overall performance by doing a feature ablation analysis where we compare our best results with constrained configurations where we drop some feature(s). The results of this analysis are shown in Table 5 where a feature with a ~ symbol next to it implies that it has been dropped from the learning-to-rank framework. The first row of the table gives the best performance obtained when using all features. The second row in Table 5 demonstrates that most loss occurs when we remove the neighborhood features as expected; interestingly the performance here is close to that of our unsupervised method as can be observed from Table 1. However, as was discussed earlier, from Table 4, neighborhood features alone cannot achieve the best results without the other features among which the co-occurrence based feature (f^F) and the random indexing based feature (f^R) add most value. Interestingly, the performance drop after removing only one of these features (rows 3 and 4 of the table) is much smaller compared to the drop when both of them are removed (row 5). This demonstrates the complementary nature of the contributions of explicit associations measured with co-occurrence frequencies and latent associations captured using random indexing. Dropping both the co-occurrence and RI features leads to a loss of over 3% in recall, 2% in F-score, and nearly 3% in MAP for the bigger L1000 dataset.

Table 5.

Feature ablation analysis of micro measures with N = 25.

Method	NLM2007 dataset				L1000 dataset
	Rμ	Pμ	Fμ	MAP	Rμ	Pμ	Fμ	MAP
All features	0.727	0.398	0.514	0.644	0.730	0.355	0.478	0.630
$~f_{10}^N,~f_{50}^N$	0.574	0.314	0.406	0.382	0.578	0.281	0.378	0.376
~fF	0.719	0.393	0.508	0.637	0.719	0.349	0.470	0.621
~fR	0.720	0.394	0.509	0.642	0.726	0.353	0.475	0.625
~fF, ~ fR	0.697	0.382	0.493	0.621	0.697	0.339	0.456	0.603
~fA	0.720	0.394	0.509	0.644	0.727	0.353	0.476	0.625
~fP	0.720	0.394	0.509	0.644	0.730	0.354	0.477	0.627

At this point we would like to note that the only common feature between our approach and Huang et al. [1] method is the k-nearest neighborhood based feature $f_k^N(t,I)$ from Section 5.3.1. They also use more sophisticated features that use an additional training dataset of nearly 14,000 citations and the corresponding MeSH term sets to obtain probability estimates P(t|I) of the probability of a MeSH term t given the title and abstract text of the instance I. These estimates rely on the distributions of individual tokens of the preferred name of the MeSH term and those present in abstract and title text of the citation. In contrast, we use inter-term associations that lead to higher performance gains without relying on the associations between the words in the citation and candidate terms.

Because the average number of MeSH terms per citation is around 13, we have an approximate upper limit of 52% on precision given that we choose the top 25 terms as our final extracted term set. However, since the eventual purpose is to recommend terms to human coders who generally tend to tolerate some false positives when several other correct terms are recommended, the low precision is not perceived as much a bottleneck as low recall [3]. As we mention in Section 5.1, over 90% of the correct terms are expected to be in the neighborhood, which imposes a recall limit too. However, from Table 4, our best results only achieve a recall of 73% even when choosing the top 25 terms. With this mind, we also conducted a manual qualitative errors analysis of false negatives (FNs) after applying our methods. Since this is a manual process, we chose to do it only for the smaller NLM2007 dataset with 200 citations. We got perfect recall for 32 of these citations which is close to 15% of the dataset. For several false negatives, a more specific term or a more generic term of the correct term is included in the top 25 terms. For example, when ‘Social Behavior’ was the correct term for a citation, we had the generic term ‘Behavior’ as one of the predicted terms. When ‘Doppler Ultrasonography’ was the correct term, our method extracted a more specific term ‘Duplex Doppler Ultrasonography’. Since MeSH is inherently hierarchical in nature, using such information [25] in our framework might help improve the accuracy. Also, terms that are not specific but are used to characterize the study discussed in the paper are often missed by our methods. Examples of such terms are ‘sex factors’, ‘time factors’, and ‘follow-up studies’. A manual examination of a citation where we missed ‘sex factors’ shows no indication of stratification or analysis based on the sex of the patient. This is probably discussed in the full text but ‘sex factors’ was ranked 98th for this particular citation using our method and is a FN as we ignore those after the 25th term. A more thorough analysis is needed to identify various types of FNs and to tailor specific techniques to handle such important classes of FNs.

6. Conclusion

Expediting indexing tasks at the NLM has been a priority and many efforts (including several from the NLM) have been pursued thus far using mostly supervised approaches to automatically predict MeSH terms for biomedical citations. In this paper we improved over the current state-of-the-art on two public datasets by introducing new features based on the semantic content of the abstract and title text and using explicit and latent associations between MeSH terms based on output term sets. Using these features, we first proposed a purely unsupervised approach that leverages term pair co-occurrence frequencies to perform a constrained expansion of a seed set of terms obtained from the title of a citation. We used semantic predications to bin candidate terms and then applied average co-occurrence scores (computed using normalized co-occurrence frequencies with certain context terms) to rank terms within the bins. We then used Borda’s rank aggregation method to combine different ranked lists. Micro-measures obtained using our methods are comparable to those obtained using k-NN based approaches such as the MTI program from NLM.

We used the features developed for unsupervised prediction to learn a linear ranking function and applied it to the candidate term set obtained from the k-nearest neighbors of testing instances. Our results with this approach improve upon the best published results on the datasets used in the experiments. Our analysis also shows the complementary nature of the contributions of explicit co-occurrence based and latent random indexing based term associations computed using output MeSH term sets. Although we only used pairwise associations of terms using both co-occurrence frequencies and random indexing based methods, a natural extension is to use high confidence association rules that involve frequent term sets to further improve the ranking of candidate set terms. Given the hierarchical nature of MeSH, we expect rules that incorporate the taxonomical information [26] to yield better results.

Based on our current results, we believe that output label associations have strong potential in developing more accurate systems in solving the general problem of multi-label classification especially in situations with hundreds or thousands of labels but where large training datasets are not available. This situation is not uncommon in biomedical domains where the sensitive nature of the information present in textual narratives typically prevents access to large amounts of training data. However, since the labels themselves are not sensitive, large numbers of output label sets corresponding to real world instances are not hard to obtain. Assigning diagnosis codes to electronic medical records that contain private health information of patients is a classical example of this situation and one of our immediate goals is to extend our research to this particular domain.

Biographies

Ramakanth Kavuluru received a B.Tech degree in computer science and engineering from the Jawaharlal Nehru Technological University, India, in 2002. He received an M.S degree in computer science from the Western Kentucky University, USA, in 2004, and a Ph.D degree in computer science from the University of Kentucky, USA, in 2009. He currently works as an Assistant Professor in the Division of Biomedical Informatics in the Department of Biostatistics at the University of Kentucky; he also holds a joint appointment in the Department of Computer Science. Earlier, he worked as a Postdoctoral Research Scientist in the Kno.e.sis Center at the Wright State University. His current research interests include biomedical and health informatics, text/data mining, knowledge-based approaches to machine learning and data mining, Semantic Web techniques, and information security and privacy. Earlier, for his doctoral thesis, he pursued research in analysis of security measures for pseudorandom sequences in the context of stream ciphers. Dr. Kavuluru is a member of the American Medical Informatics Association and the Association for Computing Machinery.

Yuan Lu received a B.S. degree in chemical physics from the University of Science and Technology of China in 2010. She is currently pursing an M.S degree in computer science at the University of Kentucky. She also works as a developer at the weather center at the University of Kentucky. Her research interests include bioinformatics, data and text mining, information retrieval and machine learning.