A Primer on Bayesian Analysis for Experimental Psychopathologists

Abstract

The principal goals of experimental psychopathology (EPP) research are to offer insights into the pathogenic mechanisms of mental disorders and to provide a stable ground for the development of clinical interventions. The main message of the present article is that those goals are better served by the adoption of Bayesian statistics than by the continued use of null-hypothesis significance testing (NHST). In the first part of the article we list the main disadvantages of NHST and explain why those disadvantages limit the conclusions that can be drawn from EPP research. Next, we highlight the advantages of Bayesian statistics. To illustrate, we then pit NHST and Bayesian analysis against each other using an experimental data set from our lab. Finally, we discuss some challenges when adopting Bayesian statistics. We hope that the present article will encourage experimental psychopathologists to embrace Bayesian statistics, which could strengthen the conclusions drawn from EPP research.

What’s wrong with NHST?

Well, among many other things, it does not tell us what we want to know…

Cohen (1994), p. 997

Introduction

Experimental psychopathology (EPP) research stands on the cusp between basic and applied research, spanning those fields in both theory and practice (Zvolensky, Lejuez, Stuart, & Curtin, 2001). Throughout the years, EPP research has provided rich insights into the cognitive mechanisms of, among others, anxiety related disorders, depression, and psychosis (see Forsyth & Zvolensky, 2001, and Zvolensky et al., 2001, for discussions of the role of EPP research in psychological science). Crucially, those insights have allowed the development and refinement of intervention programs for mental disorders (e.g., exposure therapy; Foa & McNally, 1996).

As in most branches of psychology, p-value null hypothesis significance testing (NHST) is typically used to statistically support experimental hypotheses in EPP research. To illustrate, we could find only two empirical papers published in 2015 in the Journal of Abnormal Psychology, one of the most prominent journals in the field of psychopathology research, that did not report NHST p-values in their results sections.¹

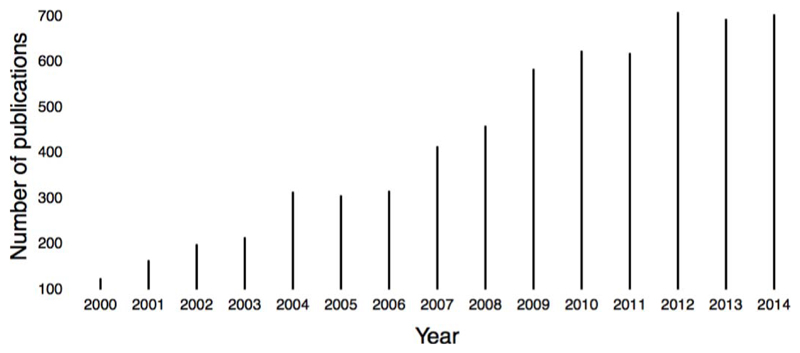
Here, we show that despite its popularity, the widespread use of NHST in EPP research conveys important disadvantages. As we argue below, NHST is unsuitable for answering common statistical questions, such as what is the probability of the observed data originating from the null hypothesis (H₀) or the alternative hypothesis (H_A). As an alternative to NHST, we suggest the use of Bayesian analysis, a statistical approach that is quickly gaining popularity in social sciences in recent years (see Figure 1).

Figure 1.

Number of publications indexed in Thomson Reuters’ Web of Science, research area social sciences, that have the word “Bayes” in their topic fields (i.e., title, abstract, or keywords), by year, 2000-2014 (as of November 04, 2015). See Wetzels, van Ravenzwaaij, and Wagenmakers (in press) for a similar analysis.

The present paper is organized as follows: We first present the advantages and limitations of NHST. Then, we demonstrate how the limitations of NHST can be overcome by the use of Bayesian analysis. In the third section we compare the conclusions afforded by NHST and Bayesian analysis for an experimental data set we recently collected in our lab. We conclude with a discussion of challenges and solutions when applying Bayesian analysis.

Why NHST is ill-suited for EPP research

There are a number of reasons as to why NHST dominates our research field. First, bachelor curricula in psychology cover this type of inference almost exclusively. Second, user-friendly software programs (e.g., IBM SPSS; SPSS, 2011) have, until recently, been able to return statistics of use for NHST only. Lastly, the likelihood of acceptance of a research paper for publication correlates with the p-values of the main results falling below common standards of statistical significance (see the file-drawer problem, Rosenthal, 1979). Given those reasons, it is understandable why NHST is so prevalent in our field. However, as noted in a recent statement by the American Statistical Association (ASA), “While the p-value can be a useful statistical measure, it is commonly misused and misinterpreted” (Wasserstein & Lazar , 2016, p. 131).²

For illustration, consider the fictitious researcher Prof. Vonnegut who wants to test whether there is a difference in the acquisition of conditioned fear responses via direct experience or via instructions (see Rachman, 1977, for the relevant theoretical background). For her study, she recruits participants that are randomly divided into two equally sized groups, an experimental group and an instructed group. The participants of the first group are presented with two initially neutral stimuli (e.g., pictures of a cube and a cylinder), one of them (i.e., Conditioned Stimulus, CS⁺) sometimes followed by a shock (i.e., Unconditioned Stimulus or US) and the other stimulus never followed by a shock (CS⁻). The participants in the second group are merely informed about the CS-US contingencies, without actually experiencing them (see Olsson & Phelps, 2004, and Raes, De Houwer, De Schryver, Brass, & Kalisch, 2014, for examples of similar experimental designs). Participants in both groups then receive a number of presentations of both stimuli, without shock, and participants provide fear ratings upon every CS presentation (say, 4 presentations per CS). At the end of the experiment, she performs a 2 (stimulus: CS⁺ versus CS⁻) × 2 (group: experimental group versus instructed group) repeated measures Analysis of Variance (ANOVA), with fear ratings for the different CSs as the dependent variable, stimulus as the within-subject factor and group as the between-subject factor. Her results show that both groups report higher fear for the CS⁺ than for the CS⁻ (main effect of stimulus; p = .001), with that effect not being statistically different between the two groups (stimulus × group interaction; p = .8). Based on those results, Prof. Vonnegut critically concludes that both groups acquired fear responses and that there is no fundamental difference between the learning of fear by experience or by instruction. However, NHST does not actually allow such a conclusion.

Specifically, given the research question of Prof. Vonnegut, it follows that the statistical test to be used should directly compare two different hypotheses: a) the two groups report different levels of fear towards the CSs, with that difference falling within a specific range of values (i.e., H_A), versus b) the two groups report same levels of fear towards the CSs, in other words the difference is 0 (i.e., H₀). Such balanced inference would be more informative, as it considers both hypotheses (i.e., H_A and H₀), than having an alternative hypothesis that is unspecified (i.e., the H_A) while trying to gather evidence against the null hypothesis (H₀). The latter type of inference, however, is the only type of inference NHST is able to make.

The reasoning of NHST (e.g., Fisher, 1935) develops as follows: a) if H₀ is true, then some data would be highly unlikely to occur, b) one observes such data, c) therefore H₀ is probably not true (Cohen, 1994; Pollard & Richardson, 1987). P-values are used to indicate how extreme the data are if the null hypothesis were true, with small p-values (typically below the 0.05 level) indicating that the data are sufficiently extreme to assume that H₀ must be false. But what happens when a p-value is above .05? In that case it would be mistaken to take the absence of a significant result as supporting evidence for H₀, as p-values are unable to provide such evidence. Specifically, p-values consider only one hypothesis (H₀) and evidence is accumulated against that hypothesis (with p-values often overstating evidence against H₀; see Wetzels et al., 2011). Also, the distribution of p-values under H₀ is uniform from 0 to 1. Consequently even when the sample size increases, no evidence can be gained for H₀, as the distribution of p-values remains the same irrespective of the sample size (e.g., Rouder, Speckman, Sun, Morey, & Iverson, 2009). Therefore, whenever one predicts a non-difference, NHST is inherently unsuitable (Dienes, 2014). Of importance, this is a situation that is very common in EPP research, where researchers often need to evaluate the support for H₀, such as in the fictitious example of Prof. Vonnegut above, where the absence of an effect (i.e., no difference in fear acquisition between the different learning pathways) is plausible (see Rachman, 1977). Other examples include situations where one wants to establish that experimental and control groups are similar on important variables like age, sex, or potential confounds, or randomized clinical trials where one may want to ascertain that competing interventions have comparable effects. In all those cases, NHST is unable to provide evidence for H₀.

Another problem with NHST is that p-values depend on the sampling plan of the investigator; this means that researchers should decide when to stop data collection (i.e., how many participants to include) prior to the start of data accumulation. One therefore cannot simply continue to test participants until clear evidence against H₀ is obtained. As a result, data collection may be stopped prematurely (but see Lakens, 2014; Pocock, 1977). Returning to our fictitious example, Prof. Vonnegut may have decided on the sample size for her experiment on the basis of a power analysis (Cohen, 1992), as is often done in experimental practice. Defining a priori when one will stop collecting data (i.e., a stopping rule) is a prerequisite for the correct interpretation of p-values for two reasons mainly. First, p-values are defined as long term frequencies of an event happening, meaning that any change in the sampling procedure after the beginning of data collection (e.g., increasing the sample size) will lead to invalid results (Dienes, 2011; Kruschke, 2014). Second, p-values can always turn below the 0.05 level given sufficient data, even when H₀ is true (Armitage, McPherson, & Rowe, 1969; Dienes, 2011). Yet, a stopping rule that specifies the exact sample size in advance can often be problematic. Especially in EPP research that involves sensitive populations (e.g., individuals diagnosed with depression) or highly aversive stimuli (e.g., traumatic film clips; Holmes & Bourne, 2008), experimenters may want to be able to stop collecting data as soon as sufficient evidence has been collected to support either of the competing hypotheses. Such a data-driven stopping plan is more efficient for researchers and more ethical towards the participants.

Related to the previous problems, NHST has a dichotomous reject-no reject logic of H₀ (Cumming, 2014), with values falling above a predefined level (i.e., 0.05) providing no evidence for any hypothesis whatsoever. This is particularly problematic when EPP research is supposed to serve as a basis for the evaluation of novel interventions. To illustrate, if the application of a novel intervention protocol yields an outcome that is significantly better than the outcome achieved by a control protocol, with a p-value just below alpha levels (e.g., 0.04), it would imply that the intervention protocol should be further developed. However, in case the p-value is just above significance level (e.g., 0.06), then, according to NHST logic, no evidence that the intervention is better that the control protocol has been accumulated. As such, further development of the said intervention would be discouraged. Instead of such dichotomous logic, what would be more helpful is having a way to quantify the amount of evidence accumulated, so as to let the researcher, and the reader of a study, decide what constitutes sufficient evidence for or against a given hypothesis.

Lastly, p-values are particularly unsuitable for EPP research as, compared to many other fields of psychology, EPP research is often constrained to the use of small samples sizes, due in part to the involvement of sensitive and/or inaccessible populations. The reliance on small samples is a cause for concern for at least two reasons. First, a small sample size may fail to detect an effect, even when the tested effect is real (Cohen, 1992). On the other hand, if a significant effect is obtained in a small sample, it may turn out to be difficult to replicate (Button et al., 2013). An analytic strategy that allows meaningful inferences from small samples is therefore of great relevance for EPP research.

To summarize, NHST is often not appropriate for EPP research because NHST a) does not allow the comparison of competing hypotheses, b) is unable to gauge evidence in favor of H₀, c) necessitates a predefined sampling plan, d) involves a dichotomous rejection logic and e) often does not allow meaningful inference from small sample sizes. These shortcomings should make experimental psychopathologists wary about the use of NHST for their data analyses. On the other hand, given the strong tradition of using NHST for statistical inference, it is tempting to disregard those disadvantages, stick with NHST and be a bit more careful when drawing conclusions. We acknowledge that this is a solution, although not quite an optimal one. A better solution for overcoming the drawbacks of NHST is to use Bayesian analysis. Bayesian analysis allows the quantification and comparison of evidence for H_A and H₀ simultaneously. Further, Bayesian analysis yields conclusions that better reflect the size of the effect under study, and allows researchers to accumulate evidence until sufficient support for either hypothesis has been obtained. We present this statistical approach below.

Bayesian analysis as an alternative to NHST or How I learned to stop worrying and love the data

In this part of the paper we provide a primer on Bayesian analysis. In order to explain the approach and illustrate the basic concepts of Bayesian analysis (e.g., the role of prior distribution; see below), we start by presenting how a single model parameter can be estimated through Bayesian parameter estimation. We then turn to Bayesian hypothesis testing, which is perhaps most relevant for the type of research conducted in the EPP field.

Bayesian parameter estimation

The main principle of Bayesian analysis is that current knowledge is updated in light of incoming information. To explain, let us return to Prof. Vonnegut. In a new study, she wants to investigate the prevalence of anxiety disorders among first year psychology students. In order to collect the relevant data, she screens 100 first-year students using the Anxiety Interview Schedule for DSM-IV (Brown, Barlow, & Di Nardo, 1994). Based on the results of this interview schedule, students who are and are not diagnosed with an anxiety disorder are scored with 1 and 0 respectively. So, the to-be-estimated parameter is the rate parameter of a binomial likelihood.³

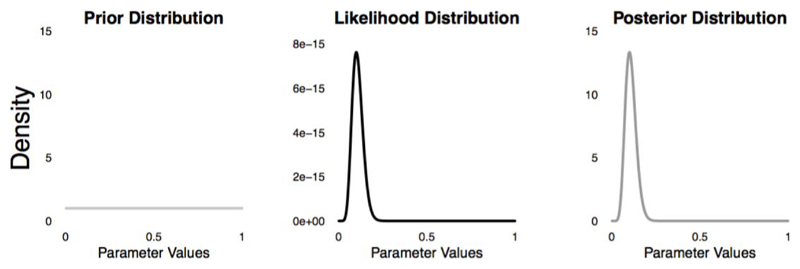
In Bayesian analysis, the uncertainty of the rate parameter before considering any new information (e.g., incoming data) is quantified in the form of a probability distribution (Lee & Wagenmakers, 2013). In our example, that would mean that Prof. Vonnegut should first make a specific assumption regarding the prevalence of anxiety disorders among students. Since she does not have a specific basis for prediction, and since the rate parameter can take values between 0 and 1 only, she may for instance simply assume a uniform prior probability distribution that assigns equal probability to each possible parameter value. If we visualize this prior assumption, we get a picture such as the one presented in the left panel of Figure 2. The distribution that we assume before seeing the data is called the prior distribution. It represents the relative likelihood of possible values (here any value between 0 and 1) of the parameter of interest (here the rate parameter) before any new information is taken into account. Prof. Vonnegut, as we have mentioned before, opted for a prior distribution that expresses only general knowledge about the tested parameter (e.g., that the values are bounded between 0 and 1). However, one might also opt for a prior distribution in which substantive knowledge about the tested parameter is included. For instance, based on previous literature, one might assume that the prevalence of anxiety disorders in first year psychology student is low, in line with the general population. In that case, a prior distribution that places more probability mass on low values and less mass on high values of the rate parameter could be used (we elaborate more on prior distributions in the Discussion section).

Figure 2.

Plots of the prior distribution (left panel), likelihood distribution (middle panel), and posterior distribution (right panel).

After defining a prior distribution, Prof. Vonnegut observes the data and she finds that 10% of the students are identified as having an anxiety disorder. In Bayesian analysis, past knowledge (in this case contained in the prior distribution) is updated in light of incoming observations (in this case the data) using Bayes’ rule. This is done by first multiplying the prior with the likelihood. In broad terms, the likelihood is defined as the probability of observing the data at hand given a specific hypothesis (Dienes, 2011). In our example, this would mean that one has to compute the probability of the observed data (here the observation that 10% of the sampled participants are found to have an anxiety disorder) given the different parameter values (all values from 0 to 1; see middle panel of Figure 2) using the probability mass function of the binomial distribution. The proportional result of this product (i.e., prior × likelihood) is the posterior distribution that represents our updated knowledge and quantifies the relative probability that each value of the parameter is the true population value (see right panel of Figure 2). In the present example, it is obvious that although Prof. Vonnegut assumed an equal probability for each parameter value initially, the posterior distribution suggests that a range of the parameter space near .1 (i.e., the mode of the distribution) is more probable compared to other ranges of comparable length elsewhere. Of importance, apart from the modal value of .1, the posterior distribution also shows one’s uncertainty in the parameter estimate given the observed data. As we see in the right panel of Figure 2, other parameter values than .1 are also probable (e.g., .12). In Bayesian analysis, this uncertainty can be expressed by reporting credible intervals. For instance, in our example, the 95% credible interval encompasses parameter values between .05 and .17, indicating that one can be 95% confident that the true value of the parameter lies between .05 and .17 (see Edwards, Lindman, & Savage, 1963, for more details).

Bayesian hypothesis testing

In the previous example we were concerned with the value of a single parameter. Although sometimes useful, in most EPP studies researchers rather want to assess which of two competing hypotheses is better supported by the observed data. Bayesian analysis, and specifically Bayesian hypothesis testing, allows researchers to do just that.

In Bayesian hypothesis testing, someone is typically interested in evaluating the relative likelihood of the data under two competing hypotheses. Returning to the example of fear learning through experience or instructions, we could say that Prof. Vonnegut would be interested in comparing H_A (i.e., that there are between-group differences and that this difference follows a specific distribution a priori) with H₀ (i.e., that there are no between-group differences). Bayes factors enable such comparison. Specifically, Bayes Factors (BFs) quantify the relative marginal likelihood of the data under H_A and H₀. To calculate a Bayes Factor, one should first specify the distribution of the effect size under the H_A, something that is quite challenging and, arguably, subjective. Recently, however, efforts have been made to define default prior distributions; that means prior distributions that can be used in a range of statistical models. By using a Cauchy prior distribution to estimate Bayes Factors, the resulting Bayes Factors meet three desirable theoretical characteristics (Rouder & Morey, 2012). First, the Bayes Factors that are obtained are not sensitive to the measurement scale of the dependent variable (location and scale invariance criterion). For example, the Bayes Factor for a time variable would not be different if the dependent variable is measured in milliseconds or in seconds. Second, the Bayes Factors that are obtained with Cauchy priors are consistent; the more data, the more the Bayes factor will tend to yield support for the hypothesis in favor of the true effect (consistency criterion). Lastly, the Bayes factor, for any sample size above 2, will reach infinity as the data undoubtedly support one of the two hypotheses (consistent in information criterion).

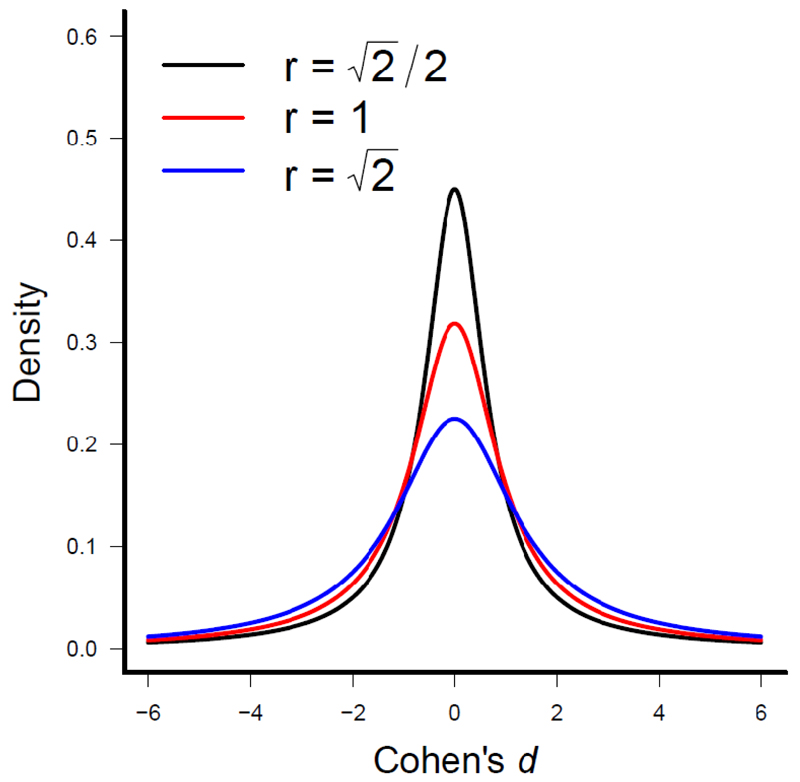
When using a Cauchy distribution, one has to specify a scale parameter, which determines the width of each effect size under the H_A. For illustration, we plotted three Cauchy distributions with three different scale factors (see Figure 3). In this plot we see that when larger effects are predicted, a wider Cauchy that assigns higher probability to large effects would be more appropriate. Although scale factors of 1 or $\sqrt{2}/2$ are commonly used for the calculation of Bayes Factors, other scale factors have also been suggested (e.g., $\sqrt{2}$). Still, one could opt for another scale factor, or another prior distribution altogether. Because the choice of a particular prior distribution is always debatable, it is desirable to test the robustness of one’s conclusions across a range of priors, as different priors will by definition result in different outcomes (Wagenmakers et al., in press).

Figure 3.

Three Cauchy distributions for three different scale parameters (see legend). Each distribution depicts the prior distribution of Cohen’s d effect size under the HA. This plot is based on a similar plot by Schönbrodt, Wagenmakers, Zehetleitner, & Perugini, (in press).

In Bayesian hypothesis testing, the value of the Bayes factor grades the relative likelihood of the data given the competing hypotheses. For example, a BF_A0 of 8 implies that the data are 8 times more probable under H_A than under H₀. In a similar vein, a BF_A0 of 1/8 implies that the data are 8 times more probable under H₀ than under H_A. A BF_0A has the opposite implication as a BF_A0. Note that although Bayes factors are taken as the Bayesian approach to hypothesis testing (Kass & Raftery,1995; Lewis & Raftery, 1997), a Bayes factor does not provide any information as to whether each hypothesis is correct or not. In other words, BFs look at the relative plausibility of competing hypotheses, and even in case of a large BF, it may well be the case that the data are not well described by either H₀ or H_A.

Advantages of Bayesian analysis over NHST

Bayesian data analysis has important advantages that make it much more informative than NHST. First, both Bayes factors and Bayesian parameter estimation allow researchers to accumulate evidence for H₀, which is impossible within the NHST framework. This is an important asset for data analysis in EPP research, as quite often researchers are interested in supporting H₀ (see above).

Second, the results of Bayesian hypothesis testing, or of Bayesian parameter estimation, are not affected by the sampling plan. Specifically, as more data are accumulated, the p-value will sooner or later take on a value below 0.05 on occasion, even if H₀ is true. In contrast, in Bayesian analysis, it is perfectly valid to monitor the data after each individual participant until sufficient evidence is collected to be able to decide between the tested hypotheses with a desired level of certainty (Edwards et al., 1963; Schönbrodt, Wagenmakers, Zehetleitner, & Perugini, in press). This feature may be of particular importance for EPP research, as it frequently involves clinical populations or demanding procedures.

Third, by evaluating the relative probability of the data under both hypotheses, Bayesian hypothesis testing provides a more balanced solution than NHST, where one simply accumulates evidence against H₀ (Rouder, Morey, Verhagen, Province, & Wagenmakers, in press).

Fourth, Bayes factors have a continuous scale, in contrast to the dichotomous logic of NHST. As such, it is up to the experimenter to decide when there is conclusive evidence for either of the hypotheses being compared. For example, one experimenter might regard a BF of 100 as conclusive evidence for the presence of an effect, whereas another researcher might regard only Bayes Factors of a 1000 or more as sufficient (Evett, 1991). Although categories for interpreting Bayes factors have been suggested (e.g., Jeffrey, 1961; Wetzels, et al., 2011), no consensus has been reached as to if they should be used since Bayes factors are expressed on a continuous scale (Kass, & Raftery, 1995). Regardless of whether a researcher chooses to use Bayes factor categories or not, the ability to quantify evidence, rather than the dichotomous way of thinking that prevails in NHST, should be beneficial for nuanced statistical inference.

Fifth, an advantage of Bayesian parameter estimation is that one can compute credible intervals over estimated parameter values. Credible intervals are fundamentally different from more commonly used confidence intervals. Specifically, a 95% credible interval indicates with 95% probability that the true parameter value falls within the specified limits. Confidence intervals merely indicate that if an experiment were repeated multiple times, then 95% of the times the confidence intervals obtained from the experiment would include the true parameter value (McElreath, 2016; see Morey, Hoekstra, Rouder, Lee, & Wagenmakers, 2015, for an excellent discussion of interval estimates). Arguably, the former type of interval is more informative of the true parameter value than the latter one.

Lastly, Bayesian analysis helps to overcome the problem of small sample size. Specifically, research suggests that by selecting prior distributions based on past literature (see Discussion section for more details on prior distributions), Bayesian analysis allows to reach meaningful conclusions even with small sample sizes, which is often impossible when using frequentist analysis techniques (van de Schoot, et al., 2015).

Of importance, and despite the principled differences between Bayesian analysis and NHST, it would be a mistake to assume that the two approaches will forcibly result in different experimental conclusions. On the contrary, Bayesian estimation will converge with classical estimation procedures (e.g., maximum likelihood) if particular priors are selected. To illustrate, in our binomial example above, the mode of the posterior distribution will equal the maximum likelihood estimator (i.e., number of successes/number of trails) if the selected prior distribution is a uniform distribution ranging from 0 to 1.

To further illustrate the differences between NHST and Bayesian hypothesis testing, we next present the data of a recent experiment conducted in our lab.

Pitting inferences from NHST and Bayesian hypothesis testing against each other: An example from the field of EPP

In our experiment (Blanken, Krypotos, & Beckers, 2014) we tested whether conditioned fear responses acquired through mere instruction are equivalent to conditioned fear responses established through a combination of instruction and experience (Olsson & Phelps, 2004; Rachman, 1977, 1991; Raes et al., 2014). To sample conditioned fear across relevant response systems (Beckers, Krypotos, Boddez, Effting, & Kindt, 2013; Mauss & Robinson, 2009), we measured subjective (fear and US-expectancies ratings), physiological (fear-potentiated startle responses, FPS, and skin conductance responses, SCR), and behavioural (performance in an approach–avoidance reaction time task) indices of fear. We here restrict ourselves to a subset of those data, in particular the US-expectancy ratings and the FPS data. For the full set of results, see the online materials (doi: osf.io/7x5sd). There we also provide detailed information about how to perform the Bayesian analyses we report below, using the BayesFactor package (Morey & Rouder, 2015) in R (R Core Team, 2015) as well as the JASP statistical software package (Love et al., 2015) that allows to perform Bayesian hypothesis testing through a user-friendly, menu-based graphical user interface.

Methods

Participants

Forty healthy adults (26 females) participated in our study (age: M = 22.1, SD = 2.8) for partial course credit or a monetary reward (€10). Participants were equally and randomly assigned to either an Instructed Acquisition group or a Combined Acquisition group. The study was approved by the University of Amsterdam Human Ethics Committee (EC number: 2014-CP-3566).

Procedure

Upon entering the lab, participants read an information brochure and provided informed consent. They then completed the state portion of the Spielberger State and Trait Anxiety Inventory (STAI; Spielberger, Gorsuch, & Lushene, 1970), after which the SCR, FPS, and shock electrodes were fitted. US intensity was then individually set to a level that was uncomfortable but not painful (see Sevenster, Beckers, & Kindt, 2012). The actual experiment then started and consisted of three phases, habituation, acquisition, and test (see Table 2).

On each conditioning trial, one of the CSs (three 2D pictures of geometrical objects) was presented for 8 s. A startle probe was delivered once on every trial, 7 s after stimulus onset. In case of a reinforced trial, the US was presented 7.5 s after CS onset. Inter-trial intervals (ITIs) were 15, 20, or 25 s, with an average of 20 s. To assess baseline startle responding, startle probes were also presented during the ITIs (noise alone, NA). Order of the CS and noise alone (NA) trials was semi-random (no more than two consecutive trials of the same CS or NA).

Habituation phase

Each CS (CS1, CS2, CS3) and NA trial was presented twice, to measure baseline responding to the CSs. No USs were presented.

Acquisition phase

Before the start of the acquisition block, the stimuli were presented on-screen and the experimenter indicated which object (i.e., CS1) would be followed by a shock most of the times and which objects (i.e., CS2, CS3) would never be followed by a shock. Participants were also asked to try and learn the contingencies between the different CSs and the US.

The three CSs were then presented six times each, in random order, intermixed with 6 NA presentations. One of the pictures (CS1) was paired with a shock on five out of six trials, whereas the CS2 and CS3 were never paired with shock.

Test phase

After the acquisition phase, the CS were presented on the screen and participants in both groups were instructed that in the next phase, both the previously reinforced CS1 and one of the previously unreinforced stimuli (CS2) would sometimes be followed by a shock, whereas the other previously unreinforced stimulus (CS3) would as before not be followed by a shock.

Crucially, participants in the instructed acquisition group were then presented with the previously unreinforced pictures (CS2 and CS3), while participants in the combined acquisition group were presented with the originally reinforced picture (CS1) and one of the originally unreinforced pictures (CS3). The CSs were each presented twice, intermixed with two NA trials, in random order. No shocks were actually administered during the test phase.

Exit Interview and Questionnaires

Upon completion, participants rated the CSs and the US on a number of dimensions and filled out the trait portion of the STAI (i.e., STAI-T) and the Anxiety Sensitivity Index (ASI; Peterson & Reiss, 1993).

Data Analyses

For the frequentist analyses, we set the alpha-level to .05. The STAI-T, STAI-S, ASI, and the US ratings were analyzed with separate independent samples t-tests with group (instructed versus combined group) as between-subject factor.

To reduce heteroscedasticity, we standardized the FPS values by computing the square root of each value. In case of a negative value, the square root of the absolute value was computed after which the negative sign was reapplied (Milad et al., 2006).

To test for baseline differences between stimuli during the habituation phase, we performed separate 3 (stimulus: CS1, CS2, CS3) × 2 (group: instructed versus combined) ANOVAs on mean US-expectancies and FPSs during habituation, with stimulus as within-subject factor and group as between-subject factor.

To ascertain the successful establishment of differential fear responses during acquisition, we analyzed mean US-expectancy ratings, FPSs, and SCRs during acquisition with separate ANOVAs, with stimulus as within-subject factor and group as between-subject factor.

Finally, to test whether mere instructions led to similar levels of differential responding as a combination of instructions and experience in the test phase, we performed separate 2 (stimulus: Final CS versus CS3) × 2 (group: instructed versus combined) ANOVAs on mean US-expectancy ratings, FPSs, and SCRs during the test phase, with stimulus as within-subject factor and group as between-subject factor. Greenhouse-Geisser corrections were applied for all ANOVAs in case the assumption of sphericity was violated.

For the Bayesian independent samples t-tests, we computed separate Bayes factors for each of the relevant variables (see above). For the Bayesian repeated measures ANOVAs, we computed separate Bayes factors for each main effect and interaction effects model (Rouder & Morey, 2012; Wetzels, Grasman, & Wagenmakers, 2012). Specifically, for the US-expectancy ratings, FPS responses, and SCRs, we tested for the main effects of stimulus and group by comparing the non-interaction model with both main effects (model with the effect) to a non-interaction model with only one main effect (model without the effect). So, for testing the main effect of stimulus, we compared the non-interaction model with both main effects (M_S+G, with M standing for model, S for stimulus and G for group) to a non-interaction model with the main effect of group (M_G). Similarly, we tested the main effect of group by comparing M_S+G to M_S. To test for the effect of the interaction term we compared the full model containing both main effects and the interaction effect (M_F, with F standing for full) to the same model without the interaction term (M_S+G). For all our Bayesian analyses, we used the default Cauchy prior distribution with scale $\sqrt{2}/2$, as implemented in the BayesFactor R package and in JASP (see Ly, Verhagen, & Wagenmakers, 2016, and the discussion below for more details). The direction of results remains similar when a scale factor of 1 is used instead. Please note that because the resulting Bayes factors in the BayesFactor package and JASP are not exactly the same after each rerun, we report the size of Bayes factors using the “≈” symbol rather than the equal sign.

Results

Questionnaires and Evaluations

No significant between-group differences arose for scores on STAI-T, STAIT-S, or for US evaluations. Between-group differences did arise for the ASI, t(38) = -2.15, p = 0.038, with participants in the combined acquisition group (M = 15.2, SD = 6.90) scoring higher than participants in the instructed acquisition group (M = 11, SD = 5.34). The direction of the ASI difference would work, if anything, against our hypothesis of equivalent acquisition through mere instruction.

The BF_0A for US pleasantness, BF_0A ≈ 2.43, and for US intensity, BF_0A ≈ 2.30, suggested that the data were more probable under H₀ (i.e., no between-group differences) than H_A (i.e., between group differences). Given the size of the Bayes factors, this is not strong support for H₀, but it still indicates that this hypothesis is more plausible than the H_A. Also, the BFs for STAI-T, BF_0A ≈ 3.09, and STAI-S, BF_0A ≈ 3.10, indicated that the data, across measures, were more probable under H₀ than H_A. However, the Bayes factor for the ASI, hardly provided any support for the data coming from H₀ or H_A, BF_0A ≈ 0.534.

US-expectancy Ratings

One participant indicated during the exit interview that he interpreted the US-expectancy scale the other way around. Therefore his responses were reversed.⁴

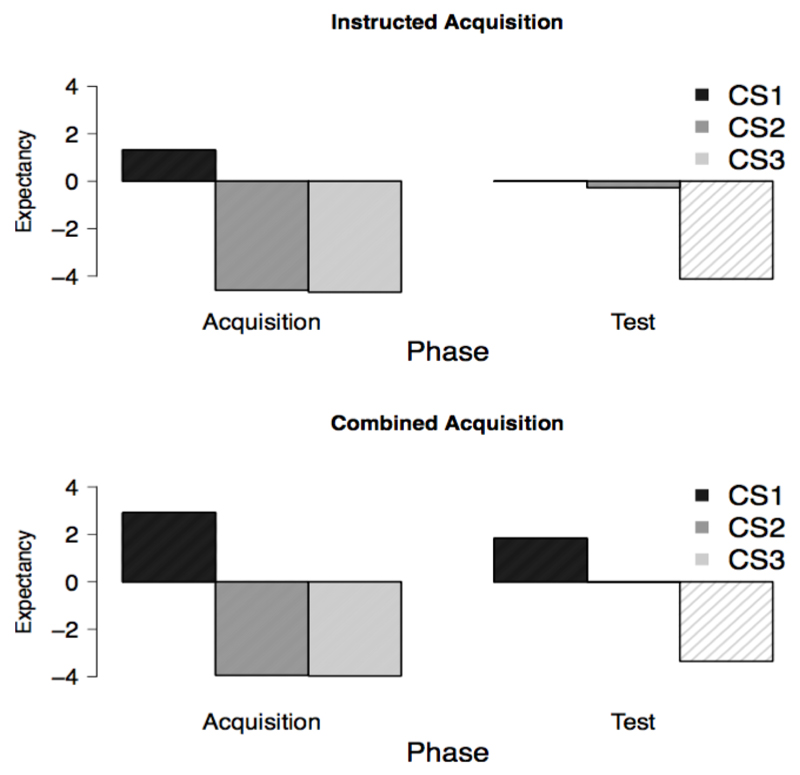
The plots for US-expectancy ratings, across all conditioning phases, are in Figure 4.

Figure 4.

Mean US-expectancy ratings during acquisition and test, by CS, for the instructed acquisition group (top) and the combined acquisition group (bottom).

The results for the acquisition phase indicate that both groups learned to expect the US after the CS1 but not after CS2 and CS3, stimulus main effect, F(1.02, 38.66) = 30.61, p < .001, η²_p = 0.45. The stimulus × group interaction failed to reach significance, F < 1. Bayesian analyses showed that it was 29.99 × 10⁸ more probable that the data came from the CS differences hypothesis than the null hypothesis, BF_MS+G/MG ≈ 29.99 × 10⁸. Also, the data were much more in line with the hypothesis that there was no stimulus × group interaction than with the hypothesis that there was an interaction, BF_MS+G/MF ≈ 6.25.

In the test phase, US-expectancy was higher for CS1/2 than CS3, F(1, 38) = 21.31, p < 0.001, η²_p = 0.36. Again no significant stimulus × group interaction was obtained, F < 1. The Bayesian analysis suggests that it was decisively more probable, BF_MS+G/MG ≈ 3299, that the data came from the CS differences hypothesis, than the reversed. Also, it was only 2.6 (BF_{MS+G/ MF} ≈ 2.6) more likely that the data came from the hypothesis that postulates no stimulus × group interaction than the reversed. This level of support is not strong. Collectively, the results suggest that there is no added effect of direct experience on fear acquisition beyond the effect of instruction.

FPS results

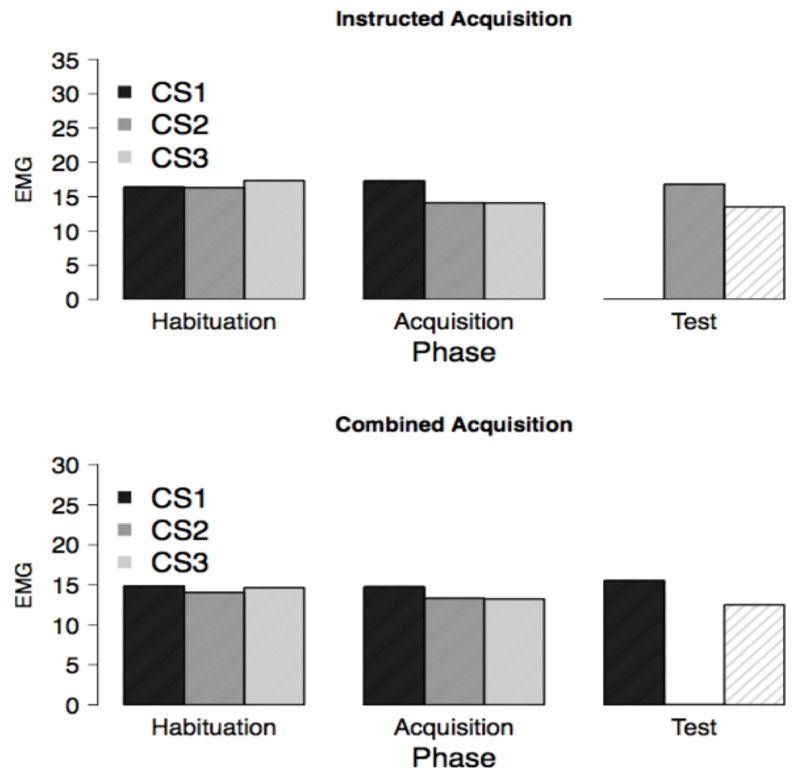
We provide the plots for the FPS results, for all conditioning phases, in Figure 5.

Figure 5.

Mean FPS responses during acquisition and test, by CS, for the instructed acquisition group (top) and the combined acquisition group (bottom).

Due to a technical error the habituation data of two participants were not saved. The missing values were replaced with the mean EMG response per stimulus in the habituation phase.

For the habituation phase, no significant main effect of stimulus, F(2, 76) = 1.56, p = 0.218, η²_p = 0.04, nor a stimulus × group interaction, F < 1, were obtained. The Bayesian analyses provided more evidence for the data coming from the no CS differences hypothesis than for the data coming from the alternative hypothesis, BF_MG/MS+G≈ 3.45, and more evidence for the absence of a stimulus × group interaction than for its presence, BF_MS+G/MF ≈ 2.70.

In the acquisition phase, there was a significant difference in responding to the CSs, F(1.45, 55.16) = 22.69, p < .001, η²_p = .40. The stimulus × group interaction just exceeded significance, F(1.45, 55.16) = 3.45, p = 0.053, η²_p = 0.08. The Bayesian analyses suggest that it was decisively more probable that the data came from the hypothesis that the CSs differ from each other than from the alternative hypothesis, BF_MS+G/MG≈ 15.49 ×10⁵. It was only 1.55 times, BF_MF/MS+G ≈ 1.55, more probable that there was a stimulus × group interaction, than that there was none.

The results of the test phase showed that there was a significant stimulus effect, F (1, 38) = 22.46, p < .001, η²_p = 0.37, whereas no significant results were found for the stimulus × group interaction, F < 1. The Bayesian hypothesis testing results of the test phase showed that it was decisively more probable that the CSs differed from each other than that they did not, BF_MS+G/MG≈ 872.43. Lastly, it was 3.33 times more probable, BF_MS+G/MF ≈ 3.33, that there were no between group differences than that there were.

Experimental Conclusions

From the NHST analysis, we can only conclude that participants in both groups acquired differential subjective (i.e., US-expectancies) and physiological (i.e., FPS) fear responses towards the different CSs. Since the test phase produced non-significant stimulus × group interactions, we are unable to conclude anything concerning the presence or absence of between-group differences. Such conclusions can be drawn from the Bayesian analyses results, however. Of importance, for US-expectancy, the resulting BF (i.e., BF_MS+G/MF ≈ 2.6) suggested that there was only slightly more evidence for similarity between the groups than for a difference. As such, it could be argued that more data should have been collected, in order to allow for more robust conclusions.

Discussion

NHST dominates, among many others, the field of EPP. In the present article we have argued that despite its popularity, the use of NHST in EPP research has important disadvantages because it cannot provide evidence for the absence of an effect, does not consider the plausibility of the data under H_A, requires a specific sampling plan before the beginning of data accumulation, has a dichotomous nature, and often does not allow meaningful conclusions from small sample sizes. We have proposed Bayesian analysis as an alternative to NHST. We have illustrated the advantages of Bayesian analysis by means of a data set from our lab. As we argue in the conclusion section above, Bayesian analysis provided for clearer interpretation of the data, particularly there where NHST could merely indicate failure to reject H₀.

Given that the goal of our article was to provide a practical primer to Bayesian analysis for EPP research, we intentionally left out any philosophical discussions about the role of Bayesian statistical inference in science (see Gelman & Shalizi, 2013, and Borsboom & Haig, 2013, for relevant discussions). We end our article by highlighting and discussing a few important challenges when applying Bayesian analysis.

One of the most common arguments against the use of Bayesian analysis is that because it is up to the researcher’s judgment to decide what prior distributions will be entertained, the analyses can be influenced by experimenter biases. We acknowledge that the incorporation of prior beliefs, in the form of specific prior distributions, should be done with care. Although parameter estimation may be less sensitive to the prior distributions, given sufficiently informative data, Bayesian hypothesis testing is always sensitive to the priors (Liu & Aitkin, 2008). For the experiment we described above, we performed all Bayesian analyses using default prior distributions (Rouder & Morey, 2012; Rouder et al., 2009). Even then, however, there can be arguments as to what the scale factor for the Cauchy prior should be and researchers should not choose their priors blindly. This is because even with default priors, the results can change quite dramatically depending on the choice of the scale factor of the Cauchy. However, we believe that at least for routine analyses (e.g., repeated measures ANOVAs or t-tests; see Rouder & Morey, 2012; Rouder et al., 2009; Wetzels, Raaijmakers, Jakab, & Wagenmakers, 2009; Wetzels et al., 2012; Wetzels & Wagenmakers, 2012), such default prior distributions are indispensable tools for Bayesian analysis in EPP research. Of course one can argue for other priors, in which additional information is taken into account and incorporated in the priors (see Dienes, 2011; for example applications of this idea into computational modeling see Vanpaemel, 2010; Vanpaemel & Lee, 2012), or just select vague priors that only include general knowledge regarding the model parameters. No matter what the choice of prior may be, it should always be guided by a good rationale. Also, under any scenario, we would argue that researchers may want to follow up their initial analyses with robustness analyses, where the results are compared across a range of alternative priors (see Liu & Aitkin, 2008 for an example). Additionally, researchers should be encouraged to share their data and analysis scripts with the rest of the scientific community so that other researchers are in the possibility to reanalyze the data with different priors (for our data set, see doi: osf.io/7x5sd). Despite different priors resulting in different numerical values of the BF, what is important to gauge in robustness analyses is whether the substantive conclusions hold across different priors.

Another common argument against Bayesian analysis is the practical difficulties involved. Bayesian models are inherently more complex than NHST models, with every model parameter requiring a prior distribution and the particular choice of prior distribution being debatable (see above). As such, Bayesian hypothesis testing is more complex, and requires more thought, than the corresponding NHST. Still, when balancing the amount of effort against the quality of the conclusions that are drawn, we believe that the scale tilts towards the use of Bayesian analyses.

A final argument against embracing Bayesian statistics is that Bayesian analyses will not be understood by reviewers. Given that Bayesian analysis is not common in EPP research, it is indeed likely that reviewers lack the appropriate background. As such, it may be useful to report NHST results and Bayesian results side by side (see Dienes, 2014, for a similar suggestion).⁵ Of importance, even though the direction of the results will often be the same and p-values will often seem to provide stronger evidence against H₀, Bayesian analyses allow one to draw conclusions in support of H₀, which is impossible with NHST (Wetzels et al., 2011).

Despite the challenges listed above, we strongly believe that Bayesian analysis is superior to NHST for many if not all instances of EPP research. Given that current software (see BayesFactor and JASP) makes it increasingly easy to perform routine statistical analyses within a Bayesian framework, we believe that there remains little reason for experimental psychopathologists not to include Bayesian results in their papers. By relying on a statistical approach that is actually able to “tell us what we want” our conclusions can be founded on a much more stable basis than that of NHST.

Table 1.

Schematic representation of the experimental design (see text for details).

Group	Habituation	Acquisition	Test
Instructed	2 CS1	6 CS1	2 CS2
	2 CS2	6 CS2	2 CS3
	2 CS3	6 CS3	2 NA
	2 NA	6 NA
Combined	2 CS1	6 CS1	2 CS1
	2 CS2	6 CS2	2 CS3
	2 CS3	6 CS3	2 NA
	2 NA	6 NA