In vivo quantification of spatially-varying mechanical properties in developing tissues

Abstract

It is generally believed that the mechanical properties of the cellular microenvironment and their spatiotemporal variations play a central role in sculpting embryonic tissues, maintaining organ architecture and controlling cell behavior, including cell differentiation. However, no direct in vivo and in situ measurement of mechanical properties within developing 3D tissues and organs has been performed yet. Here we introduce a technique that employs biocompatible ferrofluid microdroplets as local mechanical actuators and allows quantitative spatiotemporal measurements of mechanical properties in vivo. Using this technique, we show that vertebrate body elongation entails spatially-varying tissue mechanics along the anteroposterior axis. Specifically, we find that the zebrafish tailbud is viscoelastic (elastic below a few seconds and fluid after just one minute) and displays decreasing stiffness and increasing fluidity towards its posterior elongating region. This method opens new avenues to study mechanobiology in vivo, both in embryogenesis and in disease processes, including cancer.

INTRODUCTION

As suggested by D’Arcy Thompson a century ago¹ and widely accepted today^2–7, the sculpting of tissues and organs necessarily involves spatial and temporal variations in tissue mechanics. While cell-generated mechanical forces power morphogenesis^2–4, the resulting tissue movements depend on the local tissue mechanical properties, such as its stiffness and fluidity, which govern the system’s response to the internally generated forces^4,5,8,9. As a consequence, spatiotemporal variations in both mechanical forces and mechanical properties can, independently or in combination, guide morphogenesis. Dissecting their distinct contributions and, more generally, connecting the molecular information that orchestrates development to the mechanical processes that sculpt tissues, requires direct measurements of tissue mechanics during embryogenesis. While several techniques exist to probe mechanical forces in living tissues^10,11, measuring the mechanical properties of developing 3D tissues and organs in vivo and in situ remains a considerable challenge.

In addition to guiding tissue movements, the mechanical properties of the cellular microenvironment have been shown to critically affect several cell behaviors that are central to morphogenesis. In vitro experiments using elastic 2D substrates and 3D scaffolds of controlled stiffness have shown that cell migration¹², cell differentiation^13,14, tumor progression¹⁵, and even the magnitude of cell-generated forces¹⁶, specifically depend on the stiffness of the cellular microenvironment. Despite strong evidence that the mechanical properties of the microenvironment affect cell behavior to a similar degree than biochemical cues, both the mechanical properties that cells perceive in vivo and the cellular response to such mechanical cues remain unknown, as no direct, local measurement of the mechanical properties of the cellular microenvironment has been achieved within developing embryos.

Measuring mechanical properties in living embryonic tissues at the length and time scales characteristic of developmental processes¹⁷ has been quite challenging, mainly due to the difficulties associated with performing measurements in samples undergoing complex 3D shape changes¹¹. Morphogenetic movements involve tissue reorganization at timescales ranging from about a minute to hours^2,5,17 and depend on the mechanical properties that arise from the local multicellular tissue architecture and structures^2,3,5, which include contributions from the extracellular matrix^5,18 and cell-cell junctions^2,3, rather than from a specific subcellular structure. While several techniques, such as optical and magnetic tweezers, allow measurements of mechanical properties of subcellular structures at micron length scales and second time scales^19–24, these mechanical properties are generally different from the supracellular (tissue-level) mechanical properties controlling tissue reorganization and morphogenesis^2,3,5,17. Supracellular (tissue-level) measurements of mechanical properties have only been performed in dissected tissues or multicellular aggregates, and limited to either (global) bulk^25–30 or surface^31,32 measurements.

Here we introduce a technique that allows the direct measurement of local mechanical properties within developing 3D tissues and organs, thereby enabling quantification of spatiotemporal variations in tissue mechanics during embryogenesis. We use biocompatible ferrofluid oil microdroplets, embedded between the cells in a tissue, to apply local and controlled mechanical stresses within the developing tissue while simultaneously monitoring its response (Fig. 1). The application of a controlled, uniform magnetic field deforms the ferrofluid microdroplet along the direction of the magnetic field (Fig. 1a), generating a force dipole of known magnitude and direction in the tissue (Fig. 1b). By imaging the droplet deformation dynamics upon actuation, and knowing the physical properties of the ferrofluid droplet as well as the applied magnetic field, we are able to obtain the mechanical properties of the tissue within a small region surrounding the droplet (Fig. 1b). Therefore, this technique employs ferrofluid oil microdroplets as active probes to apply controlled, ectopic mechanical stresses and uses the droplet deformation dynamics (rather than its static shape) to quantify the local mechanical properties of the surrounding material. This is in contrast, and complementary, to a recent technique³³ that uses the static deformations of oil microdroplets (passive probes) to measure a different mechanical quantity, the endogenous cell-generated forces. After successfully testing the ferrofluid microdroplet technique in materials with controlled mechanical properties, we use it to quantify the endogenous, subcellular and supracellular (tissue-level) mechanical properties within developing zebrafish embryos. We show that during tailbud elongation, a model system for vertebrate body axis extension, the tissue behaves as a viscoelastic material with increasing tissue stiffness and decreasing fluidity towards its most anterior region, where new somites are formed.

Figure 1. Ferrofluid microdroplets as mechanical actuators.

(a) A ferrofluid oil droplet, spherical in the absence of a magnetic field $(\overrightarrow{H}=0)$, deforms into an ellipsoid elongated along the axis defined by the direction (black arrow) of an externally applied, uniform magnetic field $(\overrightarrow{H}\ne 0)$. (b) When a ferrofluid oil droplet, inserted between the cells forming a tissue, is actuated by applying a uniform magnetic field, it deforms and generates a local force dipole (red arrows) in the tissue. Imaging the droplet deformation over time upon controlled actuation allows the quantification of the local tissue mechanical properties within a small neighborhood of the droplet (dashed circle).

RESULTS

Measuring mechanical properties using ferrofluid droplets

In order to measure local mechanical properties within developing embryos, it is necessary to preserve normal embryonic development and precisely control the mechanical stresses applied within the tissue. As the application of net forces can substantially disturb morphogenetic flows, we employed ferrofluid droplets to generate a mechanical stress dipole within the tissue, but no net force. To ensure biocompatibility of the ferrofluid and prevent mixing with cell membranes, we used fluorocarbon-based ferrofluids (Methods), which have been shown to be biocompatible^33,34 and are immiscible in hydrocarbon oils. In addition, fluorinated-PEG surfactants dissolved in the ferrofluid were used to minimize non-specific interactions at the droplet surface (Methods). The mechanical stress dipole is generated by deforming ferrofluid droplets using a uniform, unidirectional magnetic field, which we created using an array of eight permanent magnets with a specific arrangement of their individual magnetizations (Fig. 2a–c). Both the direction and magnitude of the magnetic field $\overrightarrow{H}$

Figure 2. Module for ferrofluid droplet actuation.

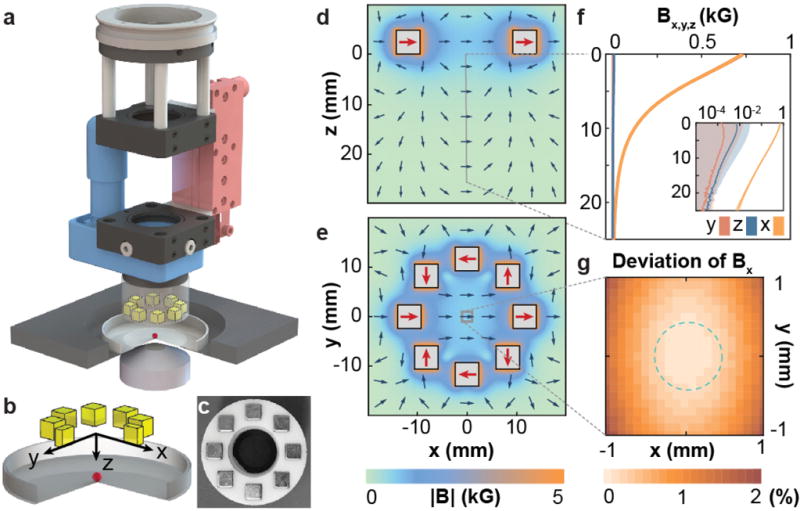
(a) 3D drawing of the module. The uniform magnetic field is generated using an array consisting of eight permanent magnets (yellow). The magnitude and direction of the magnetic field on the sample are specified by controlling the distance between the magnet array and the sample using a piezo stage (red) and the magnet array orientation using a rotatory motor (blue), respectively. (b) Magnified sketch of the system geometry, including the magnets, glass-bottom dish (gray) and sample (red). (c) Picture of the magnet array mounted on a 3D-printed holder. (d–e) Finite element simulation of the magnetic flux density $\overrightarrow{B}$ (direction, blue arrows; magnitude, color coded), or magnetic field $\overrightarrow{H}=\overrightarrow{B}/{\mu }_0$ equivalently, generated by the magnet array in the x-z (d) and x-y planes (e). Homogeneous magnetic fields of up to 1 kG = 0.1 T are achieved at the center of the array (e; red arrows). (f) Measured values of the three components of the magnetic flux density (B_x, B_y B_z) at the center of the array (x=y=0) along the z-axis (inset: log-linear scale; error bands indicate the s.d.; Methods). (g) Measured deviation of B_x in the x-y plane at z=0 from its value at the center (x=y=0). Dashed circle indicates the typical size of a zebrafish embryo (~0.6 mm).

, or equivalently the magnetic flux density $\overrightarrow{B}$ ( $\overrightarrow{B}={\mu }_0\overrightarrow{H}$, with μ₀ being the vacuum permeability), can be controlled using a motorized module compatible with any inverted microscope (Fig. 2a; Methods). This module generates a magnetic field $\overrightarrow{H}=H_x(z)\widehat{x}$, tunable magnitude by moving the magnet array vertically (z direction) and uniform in the x-y plane over a region spanning several millimeters, as shown by both simulations and measurements of the magnetic field at the sample location (Fig. 2d–g). Importantly, the application of a uniform magnetic field across the embryo (of size <1 mm) enables uninterrupted, quantitative measurements at any 3D location, even as the droplet moves inside the embryo following morphogenetic flows.

Quantifying local mechanical properties using ferrofluid droplets requires relating the mechanical stresses generated by the actuated droplet and the resulting deformation of the surrounding material, characterized by its strain response. Upon application of a uniform magnetic field, a ferrofluid droplet deforms axisymmetrically into an ellipsoid elongated along the direction of the magnetic field^35,36 (Figs. 1a and 3c). This deformation is driven by an induced magnetic stress σ_M with value σ_M = μ₀M²/2 at the poles^35,36, where M is the ferrofluid magnetization, which increases with increasing magnetic field H up to a saturation value following the ferrofluid magnetization curve M(H), as measured in our experiments (Methods and Supplementary Fig. 1). Increasing the magnetic field below the saturation regime results in larger magnetic stresses and greater drop deformations, which are resisted by capillary stresses σ_C of order σ_C ~ γ/R, with γ and R being the droplet’s interfacial tension and the radius of the undeformed droplet, respectively (Fig. 3a). In order to relate the temporal changes in droplet deformation to the mechanical properties of the surrounding material, we reduce the 3D problem of droplet actuation to a 1D formulation allowing the use of 1D rheological diagrams to describe arbitrarily complex mechanical properties of the surrounding material (Supplementary Note). In this effective 1D description (Fig. 3b), the droplet imposes a stress σ_M on the surrounding material and a spring element k_d accounts for the droplet’s capillary stress. This spring element acts in parallel to the material’s viscous (μ) and elastic (k) elements that describe the viscosity η (inverse of fluidity) and elastic modulus E (stiffness) of the surrounding material, respectively. The viscosity of the ferrofluid droplet can be neglected in our experiments (Methods). The relations between the material’s viscous or elastic elements in the 1D description, as well as the spring element accounting for capillary stresses, and the real mechanical parameters in the system read k_d = 6γ/R, μ = 36 η/5 and k = 12 E/5 (Supplementary Note).

Figure 3. Measuring mechanical properties using ferrofluid droplets.

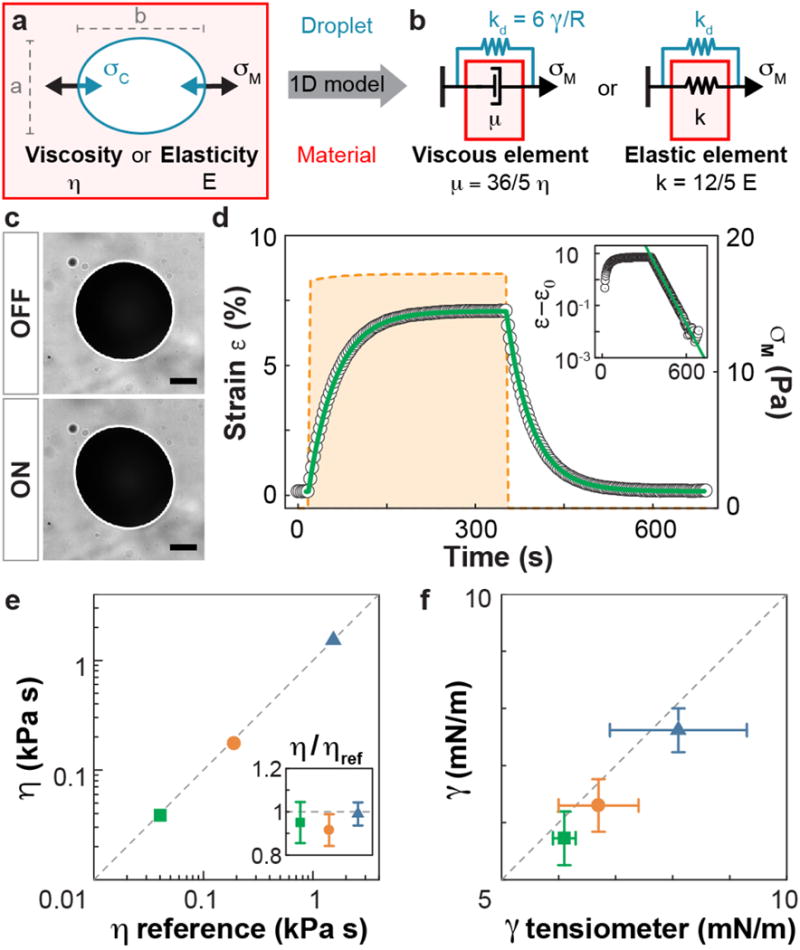
(a) Sketch of a ferrofluid droplet (blue) in a material (red) characterized by viscosity η or stiffness E. Magnetic stresses σ_M deform the ferrofluid droplet into an ellipsoid with major and minor axis b and a, respectively, and are resisted by capillary stress σ_C. (b) Effective 1D diagrams representing the combined system of the droplet within a Newtonian fluid or elastic material, characterized by viscous (μ) and elastic elements (k), respectively. (c) Fluorocarbon-based ferrofluid oil droplet in an immiscible, Newtonian hydrocarbon oil, with (ON) and without (OFF) magnetic field. The strain ε is obtained from the droplet’s aspect ratio, b/a, by detecting the droplet’s elliptical contour (white ellipse). Scale bar, 100 μm. (d) Strain evolution (black dots) upon actuation of the droplet in (c) with a controlled magnetic stress σ_M (orange dashed line), showing an exponential relaxation (inset: log-linear scale). The green line represents the fit to the solution of the 1D rheological model for a Newtonian fluid. (e) Viscosity values of three reference Newtonian hydrocarbon oils (N15000, green square; N62000, orange circle; N450000, blue triangle; Methods) measured using ferrofluid droplets and compared to their reference viscosity values (N=4 samples and 4 actuations per sample). The inset shows the ratio of measured to reference viscosities; error bars indicate the s.d. (f) Interfacial tension of the ferrofluid droplet in the same reference hydrocarbon oils measured using the ferrofluid drop deformation (N=7) and compared to independent bulk measurements using a pendant drop tensiometer (N=7). Error bars indicate the s.d. In all cases, N indicates the number of samples.

To confirm that ferrofluid droplets accurately probe the mechanical properties of materials, we tested them in materials with known mechanical properties. We first used hydrocarbon oils (Newtonian fluids) with reference viscosities. After injecting a ferrofluid droplet into the hydrocarbon oil (Methods), we actuated it with a magnetic field and imaged it over time (Fig. 3c; Supplementary Video 1 and Supplementary Fig. 2). The ellipsoidal droplet deformation, characterized by its aspect ratio b/a (Fig. 3a), provides a direct readout of the uniaxial material strain ε via ε = 2(b/a − 1)/3 (Supplementary Note). The time evolution of the material strain ε when imposing a magnetic stress σ_M shows an exponential approach to an equilibrium ellipsoidal shape followed by an exponential relaxation to the spherical shape after turning off the magnetic field (Fig. 3d). This response is in perfect agreement with the predictions from theoretical descriptions of the full 3D system^35,37 as well as the effective 1D description (Fig. 3b and Supplementary Note). By fitting the solutions of the effective 1D description (Supplementary Note) to the measured strain response, we obtained both the viscosity of various reference hydrocarbon oils (Fig. 3e) and the droplet’s interfacial tension in each reference fluid (Fig. 3f). Our measurements are in very good agreement with the reference viscosity values (Fig. 3e) and with independent measurements of the droplet interfacial tension (Fig. 3f) using a pendant drop tensiomenter (Methods). In addition to Newtonian fluids, we tested the technique in purely elastic materials using polyacrylamide gels and found very good agreement between the values of the elastic modulus obtained using ferrofluid droplets and a parallel plate rheometer (Methods; Supplementary Video 2 and Supplementary Figs. 3 and 4). These results show that ferrofluid droplets can be used as both micro-rheometers and micro-tensiometers to perform in situ measurements.

In vivo quantification of mechanical properties within developing zebrafish embryos

After calibrating and testing the technique, we used it to measure the intracellular mechanical properties of blastomeres and the yolk cell in early zebrafish embryos, as the subcellular mechanical properties of the cell cytoplasm have been previously investigated both in vitro²¹ and in vivo^11,20. To visualize the ferrofluid droplets using confocal microscopy, we fluorescently labeled them using a fluorinated dye³⁸ (Methods). After injecting a single ferrofluid droplet into individual blastomeres at early cleavage stages or into the yolk cell at blastula stages (Methods), we imposed a magnetic stress σ_M and monitored the material strain over time (Fig. 4a–b and Supplementary Videos 3 and 4). Both in the blastomere cytoplasm and in the yolk cell, the observed strain response is characteristic of viscoelastic materials, displaying elastic behavior at short timescales and fluid behavior at long timescales (Fig. 4d–e). The simplest constitutive law describing the observed response is that of a two-branch Maxwell fluid with two characteristic stress relaxation times τ₁ = η₁/E₁ and τ₂ = η₂/E₂ controlled by the elastic modulus E and viscosity η in each branch (Fig. 4c). For timescales below the shortest relaxation time, the system behaves elastically with an elastic modulus E = E₁ + E₂. In contrast, for timescales above the longest relaxation time, the system behaves as a fluid characterized by the larger of the two viscosities. The two stress relaxation time scales (Fig. 4f), as well as the measured values of the cytoplasm elastic moduli and viscosities (Fig. 4g), are similar to those reported in previous in vitro studies²¹. Compared to the cytoplasm of blastomeres, the yolk cell shows similar elasticity but a 10-fold larger viscosity when probed at length scales larger than individual yolk granules.

Figure 4. In vivo quantification of local, intracellular mechanical properties in early zebrafish embryos.

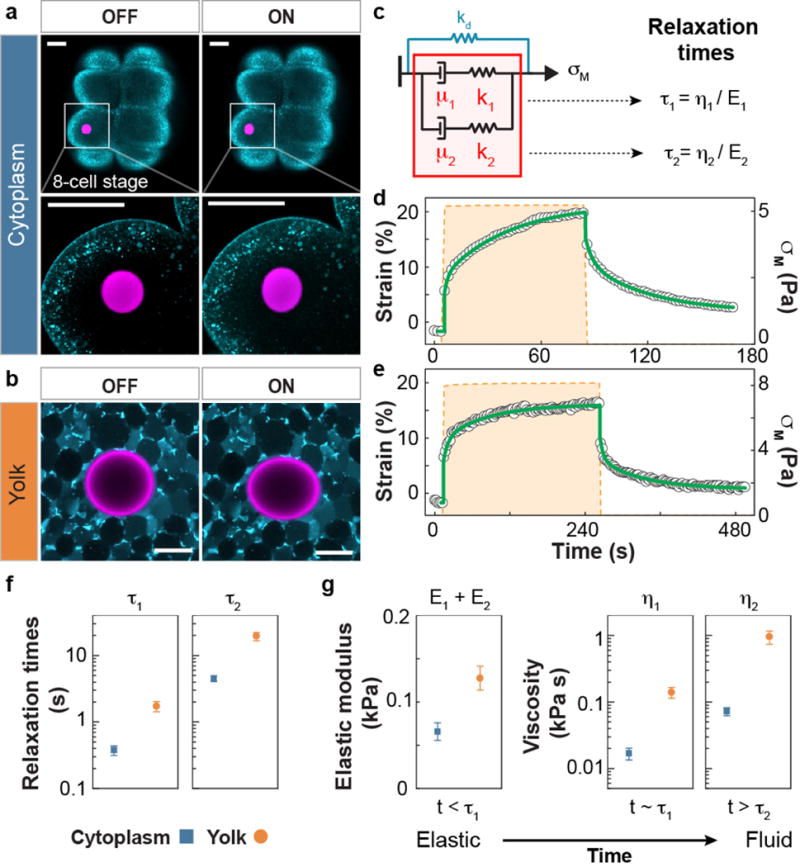
(a–b) Confocal sections showing a ferrofluid droplet (rhodamine label; magenta) within a single blastomere of an 8-cell stage wild type (WT) zebrafish embryo (a) and within the yolk cell of a WT embryo between one- and 8-cell stage (b), with (ON) and without (OFF) applied magnetic field (Tg(actb2:MA-Citrine), membrane label; cyan). (c) Simplest 1D rheological model capturing the two-time scale response observed in all in vivo measurements. The elastic (k_i) and fluid (μ_i) elements in the 1D description (i = 1,2) are related to the stiffnesses (E_i) and viscosities (η_i) of the 3D system via k_i = (12/5)E_i and μ_i = (36/5)η_i (see also Fig. 3b and main text). (d–e) Strain response (black dots) of the cytoplasm of the blastomere (d) and the yolk cell (e), upon actuation with a magnetic field generating a controlled magnetic stress σ_M (orange dashed line). Green lines represent fits to the rheological model in c. (f–g) Measured values of the relaxation time scales (f), as well as time-dependent material properties (g) of both the blastomere cytoplasm (blue squares; N=8) and yolk cell (orange circles; N=6). At short time scales (t < τ₁) both behave as elastic materials, but progressively relax the mechanical stresses (t ~ τ₁) and display pure fluid behavior for t > τ₂. Error bars indicate the s.e.m. Scale bars, 50 μm. In all cases, the measurements involved only a single droplet actuation per embryo, with N indicating the number of embryos (samples).

While ferrofluid droplets can be used intracellularly, they are uniquely suited to measure the local mechanical properties at the supracellular (tissue-level) scale. We used this technique to measure potential spatial variations in tissue mechanical properties during vertebrate body axis elongation, using the zebrafish tailbud as a model system. In order to quantitatively measure local, supracellular (tissue-level) mechanical properties, we injected a single ferrofluid droplet of radius ranging between 10 and 25 μm (Methods) between the cells of the progenitor zone (PZ) or presomitic mesoderm (PSM) of developing zebrafish embryos at 6-somite stage (12 hours post-fertilization). Approximately two hours after injection (10-somite stage), we imposed a magnetic stress σ_M on the ferrofluid droplet and monitored the strain response over time (Fig. 5a–b and Supplementary Video 5). Both PZ and PSM tissues behaved as viscoelastic materials, displaying elastic behavior at short timescales and fluid behavior at long timescales, with two relaxation times characterizing the transition from elastic to fluid behavior. The observed response can be minimally described by the constitutive law in Fig. 4c, as previously done for cellular aggregates in vitro²⁷. Both PZ and PSM tissues display short (~ 1 second) and long (~1 minute) characteristic relaxation times (Fig. 5d), indicating that both tissues relax internal stresses and flow after just one minute. Despite showing similar relaxation times, the elastic modulus and viscosity in the PSM are considerably larger than in the PZ (Fig. 5e), indicating a stiffening and thickening of the tissue towards the region where new somites are formed (Fig. 5c). The reported mechanical properties do not depend on droplet size for the range used in these experiments (Supplementary Fig. 5), and no developmental defects were observed in 2 days post-fertilization larvae after performing the experiments (Supplementary Fig. 6 and Supplementary Video 6), indicating that the measurements did not perturb normal developmental processes.

Figure 5. In vivo and in situ quantification of spatial variations in tissue stiffness and fluidity during zebrafish tailbud elongation.

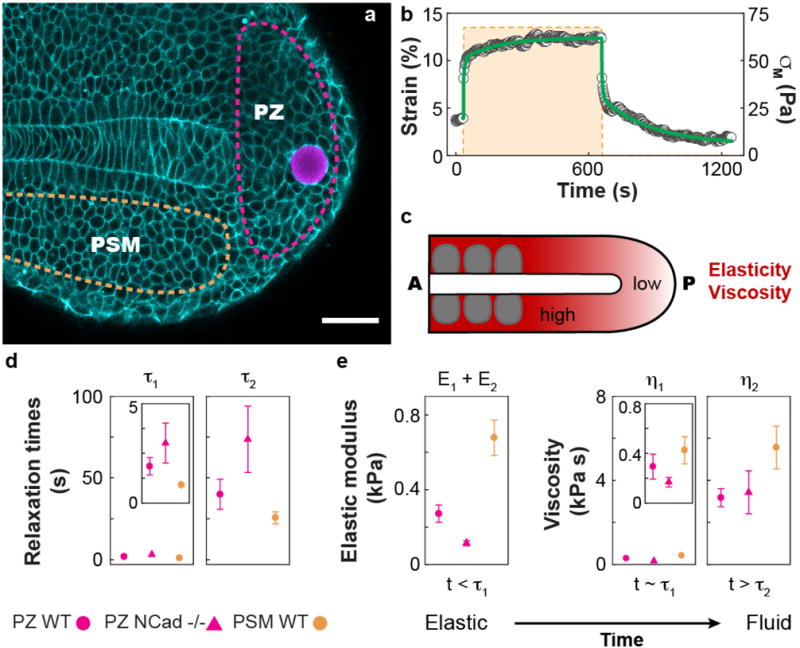
(a) Confocal section showing a ferrofluid droplet (rhodamine label; magenta) embedded between the cells of a developing zebrafish tailbud at 14-somite stage (Tg(actb2:MA-Citrine), membrane label; cyan). Dashed lines highlight the progenitor zone (PZ; pink) and the presomitic mesoderm (PSM; orange). Scale bar, 50 μm. (b) Strain response (black dots) of the PZ tissue, upon actuation with a magnetic field generating a controlled magnetic stress σ_M (orange dashed line). The green line represents the fit to the rheological model in Fig. 4c. (c) Schematic representation showing the spatially-varying mechanical properties along the anterior-posterior (A-P) axis during tailbud extension. The tissue at the posterior-most end of the growing tailbud shows lower viscosity and elasticity compared to mesodermal tissues located anteriorly, closer to the newly forming somites (gray). (d–e) Measured values of the relaxation time scales (d), as well as time-dependent mechanical properties (e) of the PZ tissue of WT (N=11) and pac mutant (N-cadherin^−/−; N=9) embryos, as well as of the PSM tissue of WT embryos (N=11). Measured tissues behave as elastic materials at short time scales (t < τ₁) and display pure fluid behavior for t > τ₂, with a transient crossover (t ~ τ₁). Error bars indicate the s.e.m. In all cases, the measurements involved only a single droplet actuation per embryo, with N indicating the number of embryos (samples).

To ensure proper development, the tissue mechanical properties need to be under tight molecular control. N-cadherin (Cadherin-2) mutations lead to a defective extension of the body axis^39,40 that is thought to be related to changes in tissue mechanics⁴¹. In order to show that changes in tissue mechanical properties arising from specific molecular perturbations can be detected with this technique, we performed proof-of-principle experiments and measured the mechanical properties of the PZ tissue in the developing tailbud of parachute (pac) mutants, which are characterized by impaired N-cadherin function³⁹. Our measurements indicate that the mechanical properties of the PZ tissue change as a consequence of impaired N-cadherin function, leading to substantially less stiff PZ tissue and longer stress relaxation times (Fig. 5c–d).

DISCUSSION

Our work shows that ferrofluid droplets can be used as mechanical actuators and micro-rheometers to apply controlled forces and quantify endogenous mechanical properties within developing embryos, both at subcellular and supracellular scales. In the absence of a magnetic field, ferrofluid droplets could also function as in vivo force sensors if coated with ligands for cell adhesion receptors, mirroring a recently developed technique³³. Therefore, ferrofluid droplets can potentially be used as a multifunctional single probe to measure local forces and mechanical properties, as well as to apply ectopic forces within developing 3D tissues and organs.

The direct in vivo measurements of tissue mechanics reported here show that developing zebrafish tailbud tissues behave as viscoelastic materials, elastic at timescales shorter than about one second and fluid at timescales longer than about a minute, with an intermediate response on the order of a few seconds (Fig. 5c). Previous experiments using dissected tissues or multicellular aggregates reported similar viscoelastic responses of the average bulk mechanics, but with relaxation timescales and mechanical parameters (elasticity and viscosity) dependent on the specific cell or tissue studied^28,29,42. In our in vivo experiments, the intermediate stress relaxation time scale at supracellular scales (tissue level) is comparable to the characteristic time scale of (subcellular) cytoplasmic fluidization in blastomeres (also of a few seconds; Fig. 4f), suggesting that the cytoplasm of cells may contribute to the initial dissipative response of the tissue. However, tissue-level stress relaxation at time scales of about one minute (Fig. 5c) is most likely controlled by different dissipative processes associated with local tissue reorganization, which may include cell cortex/adhesion remodeling², cell proliferation and/or cell rearrangements^29,43. Importantly, the observed time-dependent mechanical response of the tissue may have a physiological function in developmental processes, as suggested by recent in vitro experiments revealing that different cell behaviors, including cell proliferation and differentiation, depend on the stress relaxation time scale of the cellular microenvironment⁴⁴.

Our results reveal that tailbud elongation in zebrafish involves spatially-varying tissue stiffness and fluidity along the anteroposterior axis, and suggest that differential tissue mechanics may be important to guide morphogenesis and/or to define the functional tissue architecture. Along these lines, previous experiments with explants of different embryonic tissues reported substantial differences in stiffness and fluidity depending on the portion of dissected tissue^25,26,30, and experiments using atomic force microscopy on dissected brain slices reported spatial variations in tissue stiffness that follow tissue architecture³². Given that the stiffness of the cellular microenvironment is known to strongly affect cell behavior in vitro^12,13,45, it is possible that spatial variations in tissue mechanical properties differentially affect cell behavior in developing embryos. For instance, the previously observed differential cell movements during vertebrate body axis elongation^46,47 are consistent with the spatially-varying stiffness and fluidity reported here. Future studies will determine if other types of cell behavior, including cell differentiation, are controlled by differential mechanical cues in vivo.

The ability to perform measurements of mechanical properties within intact, developing embryos, enables experiments to directly connect the mechanical phenotype to the molecular information orchestrating development and the morphogenetic flows that sculpt organs during embryogenesis. As a proof-of-principle, we showed that impaired N-Cadherin function induces changes in the local, supracellular (tissue-level) mechanical properties. Future experiments will reveal how specific molecules affect particular mechanical parameters, thereby controlling independent aspects of tissue mechanics during morphogenesis.

Beyond embryonic development, this technique may help design synthetic scaffolds for tissue engineering applications that closely mimic the mechanical cues that cells perceive in vivo^44,48, and also facilitate studies to understand how mechanical cues affect tumor progression^15,49 within developing organisms, thereby empowering a wide range of mechanobiology studies in vivo.

The use of this new technique in different contexts may therefore provide new insights into morphogenesis, help decode how mechanical cues affect cell behavior in their native environment, and open new avenues to study the role of mechanics in disease processes.

ONLINE METHODS

Generation and control of the magnetic field

The magnetic field was generated using an array of 8 neodymium cube magnets of size 3/16” and grade N52 (K&J Magnetics Inc.). The magnets were mounted on a 3D printed holder (material: RGD525, Stratasys Ltd., printer: Objet 30 Pro, Stratasys Ltd.) in a ring geometry with a diameter of 23.4 mm as indicated in Fig. 2c. The magnitude of the magnetic field at the sample was adjusted by controlling the distance between the magnets array and the sample using a piezo stage (SLC-1760-D-M-E, Smaract GmbH). The direction of the magnetic field in the imaging plane (x-y plane; Fig. 2a,b) was controlled using a rotation motor (DT-34, Physik Instrumente GmbH & Co. KG). All parts were assembled into a module using standard optomechanics parts (Thorlabs Inc.), as specified in Fig. 2a. The module was then connected to the condenser mount of a laser scanning confocal microscope (LSM 710, Carl Zeiss Inc.) via a custom made aluminum adapter. Both the translation and rotation stages were controlled using a custom written software (LabVIEW, National Instruments) which also synchronized the movement of the magnets array with image acquisition using either a camera or the confocal microscope.

Magnetic field measurements

The magnetic field was measured using a Hall sensor (HGT-2010, Lake Shore Cryotronics Inc.) supplied with a constant current (Linear Technology Corporation). The output voltage from the Hall sensor was measured using a data acquisition card (USB-6211, National Instruments). The three components of the magnetic field (B_x, B_y, B_z) generated by the magnets array were measured with the module attached to the confocal microscope, using exactly the same set-up used to perform all the ferrofluid droplet actuation experiments (Fig. 2). To measure the three components of the magnetic field (B_x, B_y, B_z) the active area of the Hall sensor was mounted either vertically or horizontally on the microscope’s xy-translation stage. To find the position of the center axis of the magnet array (x=y=0; Fig. 2b), we simultaneously moved the xy-stage along one spatial direction while rotating the magnets to generate an oscillatory Hall voltage. The center axis was found by minimizing the amplitude of the oscillatory signal while translating the Hall sensor in the xy-plane. Once the probe was centered, we defined the x-axis of the system (Fig. 2b) as the direction of strongest magnetic field in the xy-plane. Measurements of B_x, B_y and B_z (Fig. 2f) along the vertical direction z at the array center (x=y=0) were performed by recording the average of 1024 samples of the Hall voltage at 100 micron increments in z using the module’s piezo stage. The uniformity of $\left|\overrightarrow{B}\right|$ (Fig. 2g) was measured at 100 μm increments along both the x and y directions, at a fixed vertical position of the magnets (z=0).

Simulations of the magnetic field

Simulations of the magnetic field generated by the magnet array (Fig. 2d–e) were performed using finite element software (COMSOL Multiphysics, COMSOL, Inc.). The configuration of the magnet array, magnet sizes and the orientations of each magnet magnetization used in all our experiments (Fig. 2a–c) were implemented in COMSOL. In order to compare these simulations to measurements of the magnetic field, the surface magnetization of the magnets was determined as previously described⁵⁰. The measured value B_r = 1.24 ± 0.02 T was used in the simulations, which were found to agree with our measurements at the center of the magnet array within a 2% relative error.

Imaging and image analysis

Ferrofluid droplets were imaged using either transmitted light illumination in combination with a camera (MQ042RG-CM, Ximea Corp.) or the transmitted light photomultiplier tube (TPMT) of a confocal microscope (LSM 710, Carl Zeiss Inc.) when fluorescence imaging was not required (Fig. 3c). Experiments with living embryos requiring fluorescence imaging were performed using laser scanning confocal imaging. For these experiments, the ferrofluid droplets were fluorescently labelled using a custom-synthesized fluorinated Rhodamine dye³⁸, which was dissolved in the fluorocarbon-based ferrofluid oil at a final concentration of 37 μM. Images were taken using the confocal TPMT (camera) at 2.5–5 s (0.3–0.5 s) temporal resolution. Ferrofluid droplets in reference materials (Fig. 3c and Supplementary Videos 1 and 2) were imaged using a 10x air objective (EC Epiplan-Neofluar 10x 0.25, Carl Zeiss Inc.), whereas experiments with living embryos were performed using a 40x water immersion objective (LD C-Apochromat 1.1W, Carl Zeiss Inc.).

Ferrofluid droplets actuated by a uniform magnetic field deform into axisymmetric ellipsoids^35,51. Therefore, their deformation can be fully quantified by imaging one of their elliptical xy-sections (Fig. 3c). The aspect ratio of the droplet ellipsoidal deformation was determined using an algorithm we developed using the software LabVIEW (National Instruments). First, we use a standard edge detection technique based on the convolution of the image with Gaussian and Laplacian kernels and apply a threshold to the resulting image. These steps result in the segmentation of the central cross-section of the droplet. We then obtain the moment of inertia tensor of the drop area (elliptical section) and diagonalize it to obtain the principal axes of deformation and their associated eigenvalues. The aspect ratio of the droplet is then obtained as the ratio of the largest to smallest eigenvalues. In many experiments, droplets show a slight preexisting deformation due to mechanical stresses present in the tissue in the absence of a magnetic field. To remove the effect of this preexisting deformation we take the following steps: first, we measure the droplet’s aspect ratio and the direction of the droplet’s major axis for every image as the droplet is actuated by a magnetic field. Then, the direction of the magnetic field is determined with respect to the image coordinates. As a final step, the droplet’s aspect ratio along the axis defined by the magnetic field is obtained for each image using a coordinate transformation.

Physical and chemical properties of ferrofluid droplets

In all experiments we used a fluorocarbon-based ferrofluid oil prepared as follows. Starting with a commercially available fluorocarbon-based ferrofluid (DFF1, Ferrotec), the interfacial tension and saturation magnetization of the ferrofluid were adjusted by diluting the DFF1 ferrofluid in a fluorinated oil (Novec HFE7300, 3M) at concentrations ranging from 1:1 (v/v) to 1:7 (v/v). The ferrofluid concentration defines the maximal magnetic stresses that can be applied by the droplet on the tissue. Measurements of mechanical properties in the tailbud tissues required larger stresses to deform the droplet than in the yolk or the intracellular medium in blastomeres. Therefore, higher ferrofluid concentrations were used in tailbud tissues (1:1.5) than in the yolk (1:3.8) or inside blastomeres (1:3).

To prevent non-specific adhesion between the cells and the ferrofluid droplet, a fluorinated Krytox-PEG(600) surfactant (008, RAN Biotechnologies⁵²) was diluted in the ferrofluid at a 2.5% (w/w) concentration.

The magnetization curve of the ferrofluid for a 1:1 (v/v) dilution was measured using a superconducting quantum interference device (SQUID) (MPMS 5 XL, Quantum Design Inc.) for magnetic fields ranging from −0.5 Tesla to 0.5 Tesla (Supplementary Fig. 1). Measuring a large dynamic range of mechanical properties requires adjusting the scale of applied magnetic stresses and thus controlling the scale of ferrofluid magnetization. Because the magnetization of the ferrofluid depends linearly on the volume fraction of magnetic nanoparticles⁵³, we were able to adjust the range of applied stresses by changing the volume fraction of magnetic nanoparticles in the ferrofluid. Experiments in zebrafish embryos required the application of a lower magnetic stress compared to experiments performed in Newtonian fluids (Fig. 3). Consequently, we diluted the ferrofluid with a fluorinated oil (Novec HFE7300, 3M) and calibrated the resulting magnetic stress using a Newtonian fluid reference viscosity (N62000, Canon Instrument Company).

In order to determine the viscosity of the ferrofluid used in the experiments, we measured its flow rate through a small capillary at a constant known pressure difference, which follows the Hagen-Poiseuille equation. We obtained η = 2.1 ± 0.5 mPa s, which is 4 orders of magnitude lower than the lowest viscosity reported in the main text, both for reference fluids and zebrafish embryos.

Viscosity measurements in reference fluids

Fluorocarbon-based ferrofluid oil was injected into polybutene oils (Cannon Instrument Company) with manufacturer-specified viscosities at T=25°C: η = 40.62 ± 0.09Pa s for N15000; η = 191.0 ± 0.6 Pa s for N62000; η = 1539 ± 0.6 Pa s for N450000. The value of the N62000 reference viscosity was crosschecked using a parallel-plate rheometer (AR-G2, TA Instruments) and a value of η = 196 ± 9 Pa s was obtained, which is consistent with the value of the viscosity provided by the manufacturer. Given that the viscosity of polybutene oils varies with temperature, we maintained the temperature constant at 25.0 ± 0.1 °C by controlling it using a heated stage as well as an incubation chamber on the confocal microscope. Experiments were started after the temperature within the incubation chamber was stabilized. The air temperature was monitored inside the incubator using a built-in Pt100 resistance thermometer within a 0.1 °C accuracy. For each of the hydrocarbon oils N=24 measurements were performed.

The range of measurable viscosities is approximately 10 – 10⁵ Pa s, limited on the lower end by the time necessary to modify the magnetic field and on the upper end by the long droplet deformation time scale, which becomes on the order of morphogenetic events.

Elasticity measurements in polyacrylamide gels

Polyacrylamide gels were prepared using standard methods⁵⁴. Acrylamide monomers diluted from a 40% solution (161-0140, Bio-Rad) were cross-linked in solution with N,N′-methylenebisacrylamide (161-0142, Bio-Rad). Ammonium persulfate (161-0700, Bio-Rad) was added as a source of free radicals to initiate the polymerization and N,N,N′,N′-tetramethylethylenediamine (161-0800, Bio-Rad) was used to stabilize the free radicals, affecting the polymerization rate. The polymerization was performed under vacuum and controlled temperature.

Using 10 μm outer diameter micro-needles (BioMedical Instruments) and also larger (up to 50 μm outer diameter) homemade microneedles, as well as a pressure-controlled microinjector (PLI-100A, Warner Instruments LLC), we injected several ferrofluid droplets into the polyacrylamide gel. The droplets were separated from each other by several droplet diameters to avoid mechanical interactions between them upon actuation. We then actuated the droplets with a step in magnetic field and monitored the resulting strain (Supplementary Video 2 and Supplementary Fig. 3). From the applied magnetic stress and the equilibrium aspect ratio of the droplet, we obtained the gel’s elastic modulus, as described above. Since the droplet’s capillary stress, in addition to the elastic gel surrounding the droplet, resists droplet deformations, it is necessary to decouple these contributions. Unlike the elastic modulus of the gel, the capillary stress depends on the droplet size (σ_C ~ γ/R). Therefore, injecting droplets with different radius R and measuring the apparent elastic modulus, which combines the gel elastic modulus and the effect of capillary stress, allows the decoupling of their contributions. To do so, we measured the apparent elasticity E_A of gels with three different elastic moduli (Supplementary Fig. 4a) using droplets with different radius R, thereby changing the scale of capillary stress γ/R. We then obtained the value of the elastic modulus of the gel surrounding the droplet by fitting the data using a linear relation and extrapolating this relation for vanishing capillary stress (1/R → 0) (Supplementary Fig. 4a). The elastic modulus of each gel was independently measured on a parallel-plate rheometer (AR-G2, TA Instruments) with a 40 mm parallel plate geometry. The dish with the gel and a few embedded droplets was taped to the bottom plate of the rheometer and 60-grit sandpaper was taped to the head. Measurements of the gel elastic modulus in the rheometer were performed at 1% strain, with the frequency of oscillation stepped logarithmically from 0.1 Hz to 10 Hz. In this regime, the elastic modulus was measured to be frequency independent, and a single average value (relative error <10%) was taken from each experiment. Supplementary Fig. 4b compares the values of the elastic modulus measured using ferrofluid droplets and those obtained using the rheometer, which are in good agreement.

The range of measurable stiffness is approximately 1 – 10⁴ Pa, limited on the lower end by capillary stresses, which become much larger than the surrounding material stiffness below 1 Pa, and on the upper end by the ability to detect droplet deformations arising from the applied stresses.

Measurement of interfacial tension between ferrofluids and reference fluids

The interfacial tension of a ferrofluid at a 1:1 (v/v) solution (DFF1:HFE7300) and polybutene oils (N15000, N62000, N450000, Canon Instrument Company) were performed using a pendant-drop tensiometer (Biolin Scientific). In each case, the oil was placed in a plastic cuvette (Sigma-Aldrich) and a 3 μL glass capillary (Microcaps, Drummond Scientific) was used to dispense the ferrofluid. We hung ferrofluid drops in the oil using the glass capillary. The equilibrium interfacial tension values were obtained by analyzing the droplet equilibrium shape (using the analysis software OneAttension, Biolin Scientific) using the measured density of the ferrofluid (1.82 ± 0.02g/ml) and the specified density of the polybutene oils (0.8900 g/ml for N15000; 0.8994 g/ml for N62000; 0.9071 g/ml for N450000). The measured interfacial tension of the ferrofluid in the different oils is shown in Fig. 3f. In all cases, the temperature was maintained at 23°C.

Zebrafish husbandry and fish lines

Zebrafish (Danio rerio) were maintained as previously described⁵⁵. Animals were raised and experiments were performed following all ethical regulations and according to protocols approved by the Institutional Animal Care and Use Committee (IACUC) at the University of California, Santa Barbara. For ubiquitous labeling of cell membranes we used Tg(actb2:MA-Citrine) embryos⁵⁶. Experiments to test the role of N-cadherin in the control of tailbud mechanics were done in pac^tm101/tm101 embryos³⁹.

Injection of ferrofluid droplets in zebrafish embryos

To measure the mechanical properties of the cytoplasm in blastomeres of early zebrafish embryos and also in the yolk cell, Tg(actb2:MA-Citrine) embryos were dechorionated at 1-cell stage and a single ferrofluid droplet was injected with a 5 μm outer diameter micro-needle (BioMedical Instruments) either in the cytoplasm of the blastodisc or in the yolk, close to the vegetal pole. For measurements in the cytoplasm and yolk, droplets had radii ranging between 20–40 μm and 26–34 μm, respectively. Ferrofluid droplets were formed by direct injection in the embryo and their sizes were set by controlling the pressure and injection time of the pressure-controlled microinjector (PLI-100A, Warner Instruments LLC) used. Embryos were mounted for imaging in 0.8% low melting point agarose on 35 mm glass-bottom dishes (MatTek Corporation) 15 minutes post-injection.

To probe the local mechanical properties at supracellular scales during tailbud extension, the droplet’s radius needs to be similar or larger than the average cell size (~10 μm in PZ and PSM tissues; Fig. 5a), as the droplet probes the tissue surrounding the droplet up to a distance similar to the droplet radius from the droplet surface (Fig. 1b). However, using considerably larger droplets compromises the ability to perform local measurements at the tissue level and may prove more difficult, as larger droplets have more tendency to leave the tissue of interest over time (Supplementary Figs. 5 and 6). For these reasons, we used ferrofluid droplets with radii ranging between 10–25 μm were injected as described above into the PZ and PSM of dechorionated 6-somite stage embryos (12 hours post-fertilization). Embryos were mounted for imaging as described above, 2 hours post-injection. Imaging was performed on a confocal microscope (LSM 710, Carl Zeiss Inc.) maintaining a constant temperature of 25°C using an incubation chamber.

Microdroplets can be injected at most desired locations in the developing embryo, with a spatial resolution set by the precision of the micromanipulators and the resolution of the microscope used for injection. We used a standard set-up combining micromanipulators (Narishige MN-153) and a stereoscope (Leica FluoCombi III), leading to a spatial resolution in droplet injection of about 50 μm.

Measurement of mechanical properties in developing embryos

Embryos with a previously injected ferrofluid droplet were mounted for imaging (Methods) and inspected on the confocal microscope. Once the droplet was located, we lowered the magnets array to the distance from the sample that generates the desired magnetic field (and magnetic stress) on the ferrofluid droplet (Fig. 2f). The magnets array was kept at this position for a pre-established period of time and then moved away from the sample, thereby lowering the magnetic field to negligible values (Figs. 4d,e and 5b). The initial downward and final upward movements of the magnets array in the actuation cycle were completed in approximately 1 second (Figs. 4d,e and 5b). The ferrofluid droplet is imaged throughout the actuation cycle, permitting the quantification of the droplet’s shape in each frame and the droplet deformation dynamics (Methods). In all experiments reported herein, the measured values of mechanical properties were obtained from the first droplet deformation upon application of the magnetic field (Figs. 4d,e and 5b) to minimize the potential of any mechanical feedback response of the cells affecting the measured values. The mechanical properties measured with ferrofluid droplets correspond to a local average of the mechanical properties in the material surrounding the droplet, along different spatial directions. While it is theoretically possible to detect anisotropy in the local mechanical properties with this technique, droplet incompressibility couples the mechanical response of the tissue along the direction of applied magnetic field and the perpendicular direction (Supplementary Note), complicating the detection of anisotropy at a practical level. In our measurements in PZ and PSM tissues, cells shapes are not elongated along specific spatial directions (Fig. 5a), suggesting that in our experiments, the mechanical properties are unlikely to be anisotropic at the supracellular scales probed.

Statistics

In experiments involving zebrafish embryos, the sample size was chosen so that new data points would not change significantly the standard deviation. No samples were excluded from the analysis and the analysis of all the data was done by an automated software (see Methods section ‘Imaging and image analysis’) to ensure full blinding and avoid biases in the analysis. No randomization of the data was used. Whenever the objective was to obtain the dispersion of the data, we reported the s.d. (Figs. 2 and 3). Whenever the objective was to see how the mean of the sample varies, we reported the s.e.m. (Figs. 4 and 5). In all cases were numerical data is shown, the value reported corresponds to the average.

Code availability

The custom-made LabVIEW (National Instruments) code to analyze the data (see Methods section ‘Imaging and image analysis’) and obtain the values of the mechanical properties is available as Supplementary Software, which includes basic instructions of use.