Abstract
We calculated electron inelastic mean free paths (IMFPs) for liquid water from its optical energy-loss function (ELF) for electron energies from 50 eV to 30 keV. These calculations were made with the relativistic full Penn algorithm (FPA) that has been used for previous IMFP and electron stopping-power calculations for many elemental solids. We also calculated IMFPs of water with three additional algorithms: the relativistic single-pole approximation (SPA), the relativistic simplified SPA, and the relativistic extended Mermin method. These calculations were made using the same optical ELF in order to assess any differences of the IMFPs arising from choice of the algorithm. We found good agreement among the IMFPs from the four algorithms for energies over 300 eV. For energies less than 100 eV, however, large differences became apparent. IMFPs from the relativistic TPP-2M equation for predicting IMFPs were in good agreement with IMFPs from the four algorithms for energies between 300 eV and 30 keV but there was poorer agreement for lower energies. We calculated values of the static structure factor as a function of momentum transfer from the FPA. The resulting values were in good agreement with results from first-principles calculations and with inelastic X-ray scattering spectroscopy experiments. We made comparisons of our IMFPs with earlier calculations from authors who had used different algorithms and different ELF data sets. IMFP differences could then be analyzed in terms of the algorithms and the data sets. Finally, we compared our IMFPs with measurements of IMFPs and of a related quantity, the effective attenuation length (EAL). There were large variations in the measured IMFPs and EALs (as well as their dependence on electron energy). Further measurements are therefore required to establish consistent data sets and for more detailed comparisons with calculated IMFPs.
Keywords: electron inelastic mean free path, IMFP, liquid water, relativistic full Penn algorithm, relativistic TPP-2M, static structure factor, effective attenuation length, EAL
Introduction
It is important to know details of the interactions of low-energy electrons with liquid water for many biological applications, especially for investigations of cellular and sub-cellular dosimetry [1] and for investigations of chemical processes at the surfaces of atmospheric aerosols [2]. There have been many calculations of electron inelastic mean free paths (IMFPs) in water [3,4,5,6,7,8,9,10,11,12,13], typically for energies from several tens of eV to 10 keV, but there are large variations in the reported IMFP values. These variations are mainly due to the use of different algorithms in the calculations and to different choices of data for the water energy-loss function (ELF). There have been some measurements of IMFPs for water and some measurements of a related quantity, the effective attenuation length (EAL). The EAL has been defined as the parameter which, when introduced in place of the IMFP into an expression derived on the assumption that elastic-scattering effects are negligible for a given quantitative application, will correct that expression for elastic-scattering effects [14,15]. The EAL may have different values for different quantitative applications. However, the most common application of the EAL is for describing the near-exponential attenuation of a substrate photoelectron or Auger-electron signal following deposition of an overlayer film [15]. IMFPs [16,17] and EALs [18,19,20] have been reported for water for energies ranging from several eV to 1 keV but there are also large numerical differences among these IMFPs and EALs as well as in their dependencies on electron energy.
We report new calculations of electron IMFPs for liquid water for electron energies from 50 eV to 30 keV with the relativistic full Penn algorithm (FPA) [21] that has previously been used for calculations of IMFPs and electron stopping powers for 41 elemental solids[22,23]. These calculations are based on an ELF for each solid derived from experimental optical data (an optical ELF). IMFPs and stopping powers from the FPA agreed satisfactorily with available experimental measurements of each quantity [22,23,24].
We previously used a non-relativistic version of the FPA to calculate IMFPs for groups of elemental solids, inorganic compounds, and organic compounds [24, 25, 26, 27, 28]. These IMFPs were analyzed to yield a predictive IMFP equation, designated TPP-2M [26], which has recently been expressed in a relativistic form [22]. We compare our IMFPs for water with values from the relativistic version of the TPP-2M equation.
Most previous IMFP calculations for water [3–9] were performed with a simpler and more approximate form of the FPA, the simple Penn algorithm or single-pole approximation (SPA), [21] or with the extended-Drude model [29]. Although the simple Penn algorithm utilizes a quartic dispersion equation to relate the excitation energy in an inelastic-scattering event to the momentum transfer, q, most authors utilized a more approximate quadratic dispersion relation for their IMFP calculation in the single-pole approximation and the extended-Drude model. The SPA with this latter approach will be referred to as the simplified single-pole approximation (SSPA). We also performed IMFP calculations for water using the SPA and the SSPA (and the same optical ELF as for our FPA calculations) to determine the effects of algorithm choice on the resulting IMFPs. We determined ELFs for q > 0 from the optical ELF (where q = 0) with the extended Mermin model proposed by Da et al. [30] to determine differences between the resulting IMFPs and those obtained with the FPA.
We compare the water IMFPs from the four algorithms and analyze them with Fano plots. We also make comparisons of the static structure factors as a function of momentum transfer that were derived from the four algorithms with corresponding first-principles calculations and results from inelastic X-ray scattering spectroscopy. Finally, we compare our water IMFPs from the four algorithms with IMFPs from previous calculations [3–13] and with measured IMFPs [16,17] and EALs [18,19,20] for water and ice.
Inelastic mean free path calculations
The relativistic differential cross section (DCS) for inelastic scattering is expressed as the sum of a longitudinal DCS and a transverse DCS.[31] Since the transverse DCS can be neglected for electron energies less than about 0.5 MeV,[32] the relativistic inelastic DCS can then be written as
| (1) |
where σ is the inelastic cross section, ω is the energy loss, q is the momentum transfer, N is the number of molecule per unit volume and v is the velocity of electron and Im [−1/ε (q,ω)] is the energy loss function (ELF). We use Hartree atomic units ( me = e = h̄ = 1) where me is the electron rest mass, e is the elementary charge, and h̄ is the reduced Planck constant.
The probability p(T,ω) for an energy loss ω per unit distance traveled by an electron with kinetic energy T above the Fermi level can be expressed from Eqn (1) as [22]:
| (2) |
where T′ = T + EF, EF is the Fermi energy and c is the speed of light. The integration limits in Eqn (2),
are the kinematically allowed limits of momentum transfer. The IMFP, λ(T), can then be calculated from p(T,ω):
| (3) |
where ωmax = T′ – EF. Several algorithms have been used to determine the ELF, Im [−1/ε(q,ω)], and these will be described in the following subsections.
Full Penn algorithm (FPA)
Penn [21] proposed an algorithm for the calculation of Im [−1/ε(q,ω)] in Eqn (1) based on the Lindhard model dielectric function [33] and the use of measured ELF data for q = 0 (i.e., optical data). With this method, referred to as the full Penn algorithm, the ELF for Eqn (1) is
| (4) |
where
| (5) |
and εL denotes the dielectric function from the Lindhard model of a free electron gas with plasmon energy and n is the electron density. The term g(ωp) in Eqn (4) is a coefficient to satisfy the condition Im [−1/ε (q = 0,ω)] = Im [−1/ε (ω)], where Im [−1/ε (ω)] is the optical ELF derived from experimental data.
The energy-loss function in Eqn (4) can be described as the sum of two contributions, one associated with the plasmon pole and the other with single-electron excitations:
| (6) |
Details of the calculation procedures for each term in Eqn (6) have been published [22].
Single-pole approximation or simple Penn algorithm (SPA)
A simple method to reduce the complexity in the calculation of the ELF, Im [−1/ε (q,ω)], with the FPA is to utilize the single-pole approximation or simple Penn algorithm. The Lindhard ELF in Eqn (4) is then approximated by a single delta function,
| (7) |
where
| (8) |
and
It is necessary to expand the delta function in Eqn (7) correctly in order to perform the ωp integration in Eqn (4). We define a function h(ωp) as
| (9) |
We then obtain
| (10) |
where ω0 is a solution of the equation h(ω0) = 0. ω0 can be determined from the following cubic equation:
| (11) |
This equation has a single real and non-zero solution when b(q,ω) < 0 because ω0 > 0, ω > 0, and q > 0. If there is no solution for ω0 with a given set of (q,ω) values, the delta function vanishes. We can easily obtain
| (12) |
The expression for the ELF from Eqn (4) is then
| (13) |
The integration over q in Eqn (2) with the ELF from Eqn (13) is difficult because the measured optical ELF, Im [−1/ε (ω0)], has discrete energy steps. Furthermore, most optical ELFs have relatively small energy steps at small energy losses (e.g., for energy losses less than 30 eV) and larger energy steps for higher energy losses (e.g., energy losses over 100 eV). We usually have detailed information of the optical ELF, Im [−1 ε (ω0)], for q values near q+. On the other hand, we often find only rough data for Im [−1 ε (ω0)] at q values near q−. We then have to interpolate Im [−1 ε (ω0)] properly in order to perform the q-integration with sufficient accuracy. We emphasize the form of Eqns (12) and (13) because inappropriate expressions for Im [−1 ε (q,ω)] from the SPA are given in some papers.
Simplified single-pole approximation (SSPA)
The SPA can be simplified further with what we call the simplified SPA (SSPA) where the plasmon dispersion in Eqn (8) is reduced to a quadratic equation:
| (14) |
We then have
| (15) |
Extended Mermin (EM) model
Da et al. proposed an extended Mermin model for the dielectric function [30]. In their algorithm, the ELF of a material in the optical limit (q = 0) is obtained by a fit to the experimental ELF with a summation of Mermin-type ELFs,
| (16) |
where εM (q = 0, ω; ωpi, γi) is the Mermin dielectric function [34]. The parameters ai, ωpi, and γi are the oscillator strength, peak energy, and peak width of the i-th oscillator, respectively, that are determined in the fit. In the EM method, an unlimited number of Drude oscillators (and some with negative oscillator strengths) are allowed in order to obtain satisfactory fits with Eqn (16) to ELFs with a variety of spectral shapes. This flexibility is needed in order to fit well-defined peaks (e.g., those arising from plasmon excitation), edge structures (e.g., those arising from the thresholds for inner-shell excitations), and continua (i.e., energy-loss features with slowly varying intensities). The ELF for finite q is then:
| (17) |
We used 210 Drude functions to fit the measured ELF (q = 0) of water for energies from 10−7 eV to 30 keV.
Material parameters and optical energy-loss function for water
The material parameters of water that were used in the IMFP calculations and in the analysis of ELFs and IMFPs are the molecular weight (M = 18.0152), density (ρ = 0.999973 g cm−3), number of valence electrons per molecule (Nv = 8), and band-gap energy (Eg = 7.9 eV, the median of literature values that range between 7 eV and 8.9 eV [35,36,37,38]). In the present study, we require the ELF for energy losses up to 30 keV.
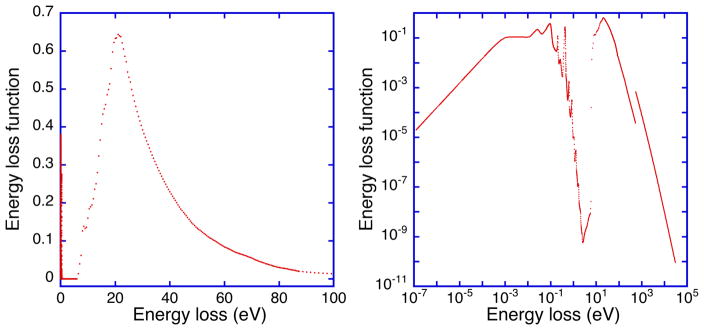
We determined the water ELF from the measured optical constants of Segelstein [39] (for energies between 1.24 × 10−7 eV and 5.9 eV) and of Hayashi et al. [40] (for energies between 6.0 eV and 87.0 eV). For energies between 87 eV and 30 keV, we calculated the ELF from the photoabsorption data of Henke et al. [41]. Figure 1 shows the ELF of water on both logarithmic and linear scales.
Fig. 1.
Plot of the optical electron energy-loss function of liquid water, Im[−1/ε (q = 0,ω)], as a function of energy loss h̄ω that was calculated from the optical constants of Segelstein [39] (for energies between 1.24 × 10−7 eV and 5.9 eV) and of Hayashi et al. [40] (for energies between 6.0 eV and 87.0 eV). For energies between 87 eV and 30 keV, optical constants of water were calculated from the photoabsorption data of Henke et al.[41].
We checked the internal consistency of our ELF data for water through use of the oscillator-strength sum rule (or f-sum rule) and the Kramers-Kronig (KK) sum rule [25,42,43]. The f-sum rule can be evaluated as the total effective number of electrons per molecule, Zeff, contributing to electronic excitations in the inelastic scattering (in Hartree atomic units):
| (18) |
where ΔE =ω, Ωp = (4π na )1/2, na = Naρ /M is the density of molecules, and Na is Avogadro’s number. The maximum energy loss in Eqn (18), ΔEmax, was 30 keV.
The KK sum rule is a limiting form of the Kramers-Kronig integral and can be expressed as:
| (19) |
where n(0) is the limiting value of the refractive index at low photon energies (below those where absorption maxima are observed). In the limit ΔEmax → ∞, Z eff → Z, the total number of electrons in the molecule (10), and Peff →1.
We determined Zeff = 10.51 from Eqn (18) and eff =1.037 P from Eqn (19) for our water ELF. These values were larger than the expected values by 5.1 % for the f-sum rule and by 3.7 % for the KK-sum rule. These deviations are similar to those found in our similar analyses of ELFs for a group of 41 elemental solids (a root-mean-square (RMS) deviation between Zeff and Z values of 4.2 % and a RMS deviation between Peff values and unity of 7.7 %) [22].
Results
Calculated IMFPs from the four algorithms
Table 1 shows our calculated IMFPs for water from the FPA as a function of electron energy with respect to the Fermi energy between 50 eV and 30 keV. The Fermi energy of water (= 15 eV) was estimated from the density of states and the difference between the energies of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) calculated by Cabral do Couto et al. with density functional theory[44]. We also assumed that the Fermi energy of water was located midway between the HOMO and LUMO energies.
Table 1.
IMFPs for water, λ, calculated with the relativistic full Penn algorithm as a function of electron kinetic energy, T, with respect to the Fermi level EF.
| T (eV) | λ (nm) | T (eV) | λ (nm) |
|---|---|---|---|
| 54.6 | 0.986 | 1339.4 | 4.80 |
| 60.3 | 0.967 | 1480.3 | 5.19 |
| 66.7 | 0.956 | 1636.0 | 5.62 |
| 73.7 | 0.954 | 1808.0 | 6.09 |
| 81.5 | 0.958 | 1998.2 | 6.60 |
| 90.0 | 0.969 | 2208.3 | 7.16 |
| 99.5 | 0.986 | 2440.6 | 7.77 |
| 109.9 | 1.01 | 2697.3 | 8.43 |
| 121.5 | 1.04 | 2981.0 | 9.15 |
| 134.3 | 1.07 | 3294.5 | 9.93 |
| 148.4 | 1.12 | 3640.9 | 10.78 |
| 164.0 | 1.17 | 4023.9 | 11.71 |
| 181.3 | 1.22 | 4447.1 | 12.72 |
| 200.3 | 1.28 | 4914.8 | 13.83 |
| 221.4 | 1.35 | 5431.7 | 15.03 |
| 244.7 | 1.43 | 6002.9 | 16.33 |
| 270.4 | 1.52 | 6634.2 | 17.75 |
| 298.9 | 1.61 | 7332.0 | 19.30 |
| 330.3 | 1.72 | 8103.1 | 20.99 |
| 365.0 | 1.84 | 8955.3 | 22.82 |
| 403.4 | 1.96 | 9897.1 | 24.81 |
| 445.9 | 2.10 | 10938.0 | 26.97 |
| 492.7 | 2.26 | 12088.4 | 29.32 |
| 544.6 | 2.42 | 13359.7 | 31.87 |
| 601.8 | 2.60 | 14764.8 | 34.64 |
| 665.1 | 2.80 | 16317.6 | 37.65 |
| 735.1 | 3.02 | 18033.7 | 40.90 |
| 812.4 | 3.26 | 19930.4 | 44.42 |
| 897.8 | 3.51 | 22026.5 | 48.23 |
| 992.3 | 3.79 | 24343.0 | 52.35 |
| 1096.6 | 4.10 | 26903.2 | 56.80 |
| 1212.0 | 4.43 | 29732.6 | 61.60 |
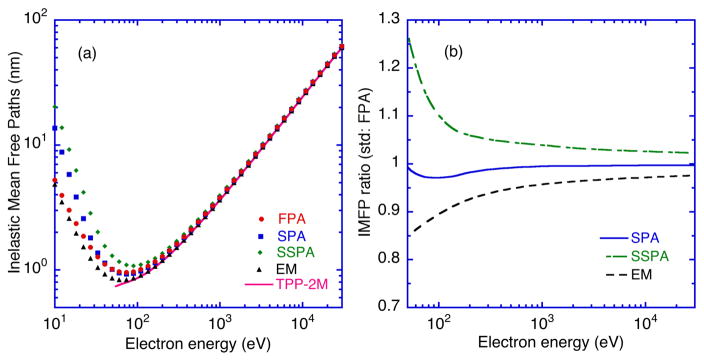
We also show plots of IMFPs from the FPA, SPA, SSPA, and EM methods as a function of electron energy in Fig. 2(a). IMFPs are included in these plots for energies less than 50 eV to illustrate trends but these values are not considered as reliable as those at higher energies [28,45].
Fig. 2.
Plots of (a) calculated electron inelastic mean free paths (IMFPs) and (b) ratios of IMFPs as a function of electron kinetic energy for liquid water. (a) The solid circles, squares, diamonds, and triangles indicate IMFPs calculated from the FPA, SPA, SSPA, and EM methods, respectively. The solid curve shows IMFPs calculated from the relativistic version of the TPP-2M equation [Eqns (20) – (25)]. (b) Plots of ratios of IMFPs for liquid water from the SPA (solid line), SSPA (dot-dashed line), and EM method (dashed line) to IMFPs from the FPA as a function of electron energy.
We see good agreement in Fig. 2(a) among the IMFPs from the four algorithms for energies over 300 eV. For energies less than 100 eV, however, large differences become apparent. IMFPs from the SSPA (SSPA IMFPs) are largest among IMFPs from the four algorithms for energies between 10 eV and 30 keV while IMFPs from the EM model (EM IMFPs) are smallest. IMFPs from the FPA (FPA IMFPs) agree well with IMFPs from the SPA (SPA IMFPs) for energies over 50 eV. For energies less than 30 eV, the SPA IMFPs become larger than the FPA IMFPs with decreasing electron energy. The smaller FPA IMFPs in this energy range must be due to the contributions of single-electron excitations to the ELF, as shown in Eqn (6), that were neglected in the SPA.
In order to see differences among IMFPs from the four algorithms more clearly, we plot ratios of IMFPs from the SPA, SSPA, and EM methods to those from the FPA as a function of electron energy in Fig. 2(b) for energies between 50 eV and 30 keV. The SSPA IMFP to FPA IMFP ratios are less than 1.05 for energies over 330 eV but increase to 1.24 for an energy of 54.6 eV. The SPA IMFP to FPA IMFP ratios are slightly less than unity (between 0.97 and 1.00) for the 54.6 eV to 29.7 keV energy range. Finally, the EM to FPA ratios are less than unity in Fig. 2(b), varying from 0.86 at 54.6 eV to about 0.95 at 492 eV and 0.98 at 29.7 keV. The latter differences must be mainly due to the different q-dependences of the ELFs from the FPA and EM methods for q > 0; we will discuss these differences later.
Figure 2(a) also shows IMFPs calculated from the relativistic predictive IMFP equation that was designated as the relativistic TPP-2M equation [22]. This equation is:
| (20) |
where
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
α(T) = [1 + (T / 2mec2 )] /[1 + (T /mec2)]2, and mec2 is the electron rest energy (510998.9 eV). The value of Ep for water is 19.202 eV.
IMFPs from the TPP-2M equation (TPP-2M IMFPs) are shown in Fig. 2(a) as a solid line. These IMFPs are generally in good agreement with the IMFPs calculated from the four algorithms for energies over 300 eV. In particular, the TPP-2M IMFPs agree with the EM IMFPs within 1 % for energies between 150 eV and 30 keV. RMS differences between TPP-2M IMFPs and IMFPs from the FPA, SPA, SSPA, and EM algorithms are 7.9 %, 6.9 %, 13.0 %, and 2.4 %, respectively, for energies between 50 eV and 30 keV. For energies between 200 eV and 30 keV, the RMS differences are reduced to 4.6 %, 4.0 %, 7.9 %, and 0.4 %, respectively. The TPP-2M equation thus provides satisfactory estimates of the water IMFPs from the FPA, SPA, and EM algorithms for energies between 50 eV and 30 keV.
Fano plots of calculated IMFPs
We analyzed our water IMFPs calculated from the four algorithms using Fano plots[45,46] in which α(T)T/λ is plotted versus ln(α(T)T). From equation (20), which is a modified form of the relativistic Bethe equation for inelastic electron scattering in matter, the equation for Fano plots is given by:
| (26) |
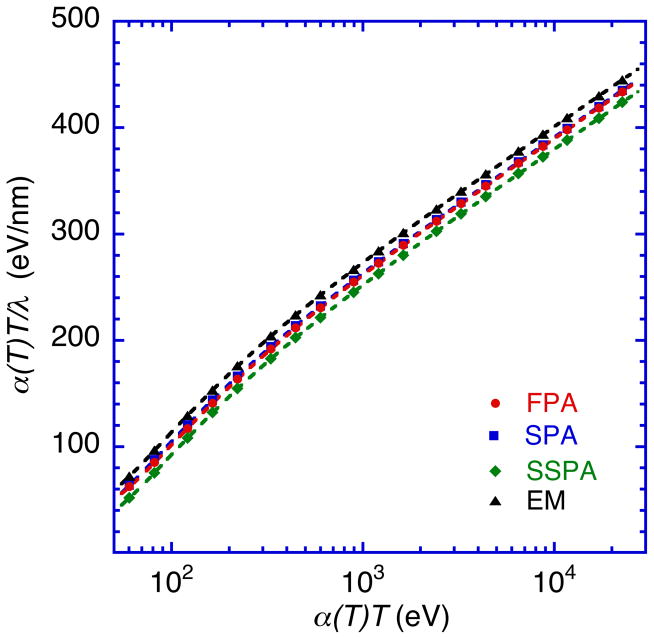
We utilized Eqn (26) to fit IMFPs for a group of 41 elemental solids that were calculated from the FPA for energies up to 200 keV [22]. These fits were performed with βr, γr, Cr, and Dr as parameters. Satisfactory fits were made with Eqn (26) to the calculated IMFPs of water (indicated by the lines in Fig. 3) with RMS differences of 0.13 %, 0.06 %, 0.09 %, and 0.08 % for IMFPs from the FPA, SPA, SSPA, and EM methods, respectively. Table 2 shows values of βr, γr, Cr, and Dr from these fits for IMFPs calculated by each of the four algorithms. These parameter values can be used with Eqn (20) to determine IMFPs for any energy between 50 eV and 30 keV.
Fig. 3.
Fano plots of IMFPs for liquid water based on Eqn (26) for energies between 50 eV and 30 keV. The solid circles, open squares, solid diamonds, and solid triangles show plots with IMFPs calculated with the FPA, SPA, SSPA and EM methods, respectively. The solid, long-dashed, and short-dashed lines show results of fits with Eqn (26) using IMFPs obtained from the FPA, SSPA and EM methods, respectively. The fit with IMFPs from the SPA is essentially identical to the fit with the FPA IMFPs.
Table 2.
Values of the parameters βr, γr, Cr and Dr found in the fits of Eqn (26) to the IMFPs for liquid water calculated with the full Penn algorithm (FPA), simple Penn algorithm (SPA), simplified single-pole approximation (SSPA), and extended Mermin (EM) model for energies between 50 eV and 30 keV. The final column shows the average root-mean-square deviation, RMS, in the fits.
| βr (eV−1nm−1) | γr (eV−1) | Cr (nm−1) | Dr (eVnm−1) | RMS (%) | |
|---|---|---|---|---|---|
| FPA | 0.1456 | 0.1439 | 15.07 | 378.2 | 0.13 |
| SPA | 0.1455 | 0.1476 | 13.94 | 311.0 | 0.06 |
| SSPA | 0.1449 | 0.1234 | 14.99 | 356.1 | 0.09 |
| EM | 0.1450 | 0.1828 | 14.73 | 334.1 | 0.08 |
The Fano plots are expected to be linear at sufficiently high energies (the asymptotic Bethe region), where Eqn (26) then becomes:
| (27) |
Figure 3 shows Fano plots of water with IMFPs calculated from the FPA, SPA, SSPA, and EM methods for energies between 50 eV and 30 keV. We see that these plots are close to linear, as expected, for energies above about 2 keV.
The slopes of the Fano plots at high energies provide values of the parameter βr. A useful check of our analysis is to determine the expected slope of the Fano plot in the asymptotic high-energy region directly from the experimental ELF for water. The corresponding value of β, designated βopt, can be obtained from the following relations [28]:
| (28) |
| (29) |
where is the square of the dipole matrix element for all possible inelastic-scattering processes (with Hartree atomic units). The resulting value of βopt is 0.144. This value is in excellent agreement with the βr values (0.1449 eV−1nm−1 to 0.1456 eV−1nm−1 ) obtained from the fits with Eqn (20) to the IMFPs calculated from the four algorithms as shown in Table 2.
The linear fits with Eqn (27) in the Fano plots also provide values of from which γr can be determined. The latter parameter is a complicated function of the q-dependence of the ELF [47] to be discussed in the next section. Pauly and Tougaard have reported that the simple quadratic dispersion equation for q used in the SSPA [Eqn (14)] was not consistent with results from their analyses of reflection electron energy-loss spectra [48,49,50]. They utilized the following dispersion equation in their analysis (in Hartree units):
| (30) |
where δ is a parameter that was found to be between 0.02 and 0.05 for insulators (with Eg greater than about 3 eV), 0.5 for semiconductors (with Eg less than about 2 eV), and 1.0 for metals [48–50].
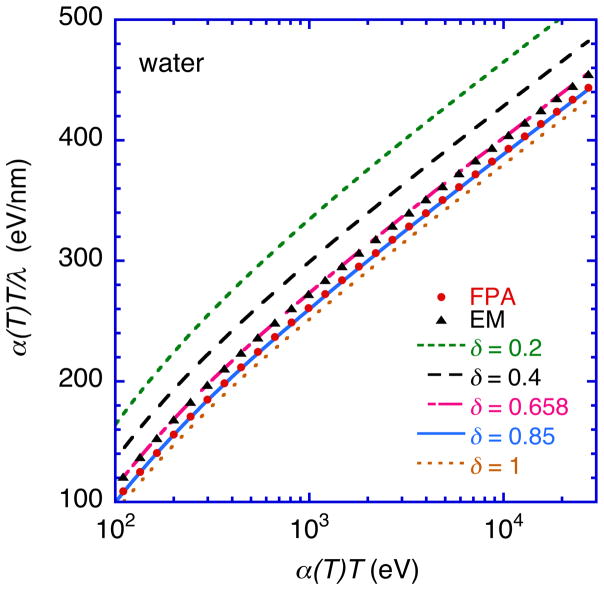
Figure 4 shows Fano plots with IMFPs that were calculated with the SSPA and with Eqn (30) as the dispersion equation instead of Eqn (14) for energies between 100 eV and 30 keV. We chose different values of δ in Eqn (30) for the Fano plots in Fig. 4 to determine the effect of this parameter on the resulting IMFP values. We see that the curves in Fig. 4 shift downward (i.e., the IMFP increases) as δ increases from 0.2 to 1.0. We also include Fano plots with the FPA IMFPs and EM IMFPs in Fig. 4 to examine whether we could match these IMFPs with IMFPs from the SSPA by changing δ in Eqn (30). We found that the FPA IMFPs were in excellent agreement with IMFPs from the SSPA with δ = 0.85, as shown in Fig. 4. In this comparison, the maximum difference between the IMFPs was less than 1 % over the 100 eV to 30 keV range, and the RMS difference was 0.42 %. The resulting δ value is in good agreement with the δ value (0.84) obtained from an equation [51,52] that was developed including electron correlation and avoiding the random-phase approximation:
| (31) |
Fig. 4.
Fano plots of IMFPs calculated from the SSPA using the dispersion equation of Eqn (30) instead of Eqn (14) for electron energies between 100 eV and 30 keV. The dotted lines indicate IMFPs calculated using δ = 0.2, 0.4, 0.658, 0.85, 1 in Eqn (30). The symbols show Fano plots with IMFPs from the FPA (solid circles) and the EM method (solid squares).
We also found that the EM IMFPs agreed well with IMFPs from the SSPA with δ = 0.658, as shown in Fig. 4. In this case, the maximum difference between the IMFPs was less than 1 % and the RMS difference was 0.25 %. We thus see that the SSPA can agree with IMFPs from the FPA and the ME method for energies over 100 eV if Eqn (30) is used as the dispersion relation and δ is chosen appropriately (0.85 for the FPA comparison and 0.658 for the ME method comparison). We note that Ashley has reported that δ should be approximately unity for organic solids [53]. Our values of δ, however, are appreciably larger than those found by Pauly and Tougaard for insulators with similar bandgap energies (e.g., δ = 0.05 for Al2O3 with Eg = 7.1 eV and δ = 0.02 for SiO2 with Eg = 9.3 eV). Their low values of δ probably arise from the flat energy bands in insulators associated with the band gap.[50] For water which has a wide energy gap (Eg = 7.9 eV), one might therefore expect lower values of δ. Our result indicates that “band-structure” effects (which are neglected in the dielectric models considered in the present paper) could play a role in the IMFPs of water. While band structures are well-defined only for crystalline solids, liquid metals can have similar electronic structures and ELFs as the corresponding solids unless there is a change of the local atomic structure [54,55,56]. Further investigations should be made of the effects of electronic structure on the IMFPs of water and other liquids (e.g., aqueous solutions [57]).
ELFs and the static structure factor of water for q > 0
Garcia-Molina et al. [58] reviewed energy-loss functions of water at non-zero momentum transfers that were obtained from various extended optical-data models. Unfortunately, their comparison did not include results from the FPA and simplified Penn algorithm (SPA). We therefore make comparisons here between ELFs for q > 0 obtained from the FPA, SPA, SSPA, and EM methods as well as those obtained experimentally by inelastic X-ray scattering spectroscopy (IXSS).
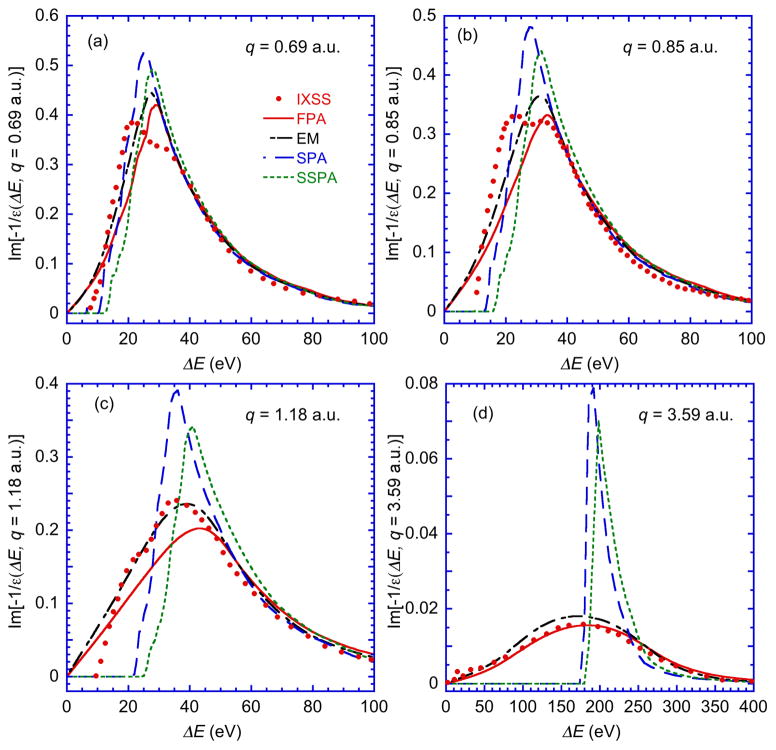
Figures 5 show plots of water ELFs as a function of energy loss that were calculated from the optical ELF for q = 0 with the four different algorithms together with those obtained by IXSS at q = 0.69 atomic units (a.u.), 0.85 a.u., 1.18 a.u., and 3.59 a.u. [59]. We see considerable broadening of the ELFs from the FPA and EM methods with increasing q, particularly in Figs. 5(c) and 5(d). These broadenings are mainly due to the plasmon damping as q increases. The FPA ELF at q = 3.59 a.u. in Fig. 5(d) is in better agreement with the measured ELF from IXSS compared to the other models. On the other hand, for q = 1.18 a.u. as shown in Fig 5(c), the EM ELF agrees better with the IXSS data. This result must be due to the improved ELF for small q values from the Mermin dielectric function, which is the basis of EM model, compared to the original Lindhard dielectric function [60]. However, the differences between the EM ELFs and the FPA ELFs are small for q = 0.69 a.u. (Fig. 5(a)) and for q = 0.85 a.u. (Fig. 5(b)). We also note that the IXSS data for q = 0.69 a.u. and for q = 0.85 a.u. show a double-peaked structure that is not observed in any of the theoretical model ELFs.
Fig. 5.
Comparison of the experimental ELFs of liquid water for q = 0.069 a.u., q = 0.85 a.u., q = 1.18 a.u., and q = 3.59 a.u. with ELFs calculated from the optical ELF (q = 0) using four different extension algorithms for q > 0. The solid circles represent ELFs measured with inelastic X-ray scattering spectroscopy (IXSS) by Watanabe et al. [59]. The solid line, short- and long-dashed line, long-dashed line, and dotted line show the ELFs for q > 0 obtained from the FPA, EM, SPA, and SSPA algorithms, respectively.
The SPA and SSPA are based on the single-pole approximation and thus do not include the broadening effects of plasmon decay caused by electron-hole pair excitations at large q. As a result, the SPA and SSPA ELFs in Figs. 5(c) and 5(d) do not show damping like that seen for the FPA and EM ELFs. Nevertheless, there is reasonable agreement between the SPA and SSPA ELFs with the IXSS ELFs for small q values, as shown in Figs. 5(a) and 5(b), as well as with the FPA and EM ELFs. This result means that the single-pole approximation is a useful method for small q (i.e., for q < 0.85 a.u.).
While the comparison of the model ELFs with the measured ELFs for q > 0 in Figs. 5(a) to 5(d) was a useful guide to the relative validity of the models, it is difficult to make a quantitative assessment of the different q-dependences on the IMFP calculations. We therefore calculate the static structure factor, S(q), which is known to be a very sensitive quantity for electron-correlation effects [61,62], from the following equation [59]:
| (32) |
where S(q,E) is the dynamic structure factor that can be calculated from the ELF [59,63] and, using Hartree atomic units, is given by
| (33) |
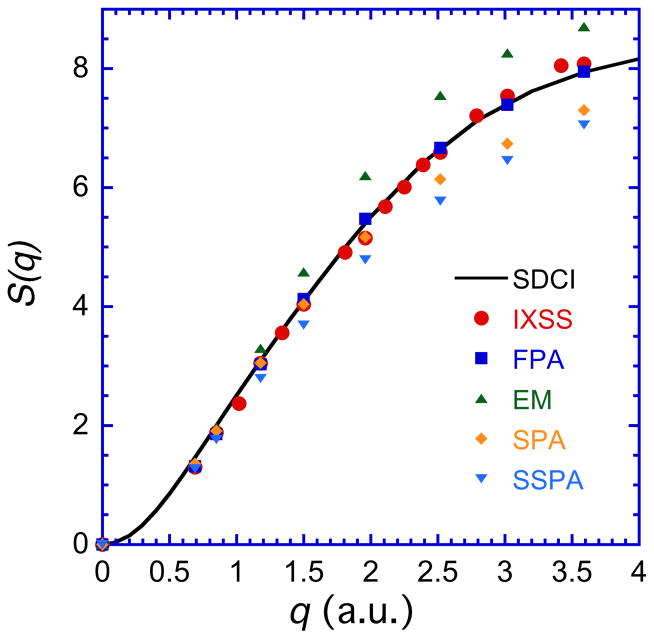
We calculated S(q) from the ELFs obtained with the FPA, SPA, SSPA, and EM algorithms for momentum transfers of q = 0.69 a.u., 0.85 a.u., 1.18 a.u., 1.5 a.u., 1.96 a.u., 2.52 a.u., 3.02 a.u., and 3.59 a.u. These values of S(q) are plotted in Fig. 6 together with results of first-principle calculations of S(q) (solid line) by Wang et al. [64] that were calculated with configuration-interaction (CI) wave functions and the inclusion of all single and double excitations (SDCI) [64]. We also plot S(q) [59] obtained from IXSS measurements as a function of q. These S(q) values were corrected for the O 1s contributions with the Thakkar and Smith formula [65] because the O 1s contributions were not taken into account in the measurements[59].
Fig. 6.
Plots of the static structure factor S(q) of water as a function of momentum transfer q. The solid line shows results of first-principle calculations with configuration iteration (CI) wave functions including all single and double excitations (SDCI) [64]. The solid squares, diamonds, downward triangles, and upward triangles show S(q) values calculated with Eqns (32) and (33) from ELFs (q > 0) obtained with the FPA, SPA, SSPA, and EM methods, respectively. The solid circles represent S(q) values obtained with Eqn (32) from measured dynamic structure factors as a function of q by IXSS [59] with the corrections described in the text.
Figure 6 shows excellent agreement between S(q) values obtained from the FPA (FPA S(q)) and the calculated S(q) values (SDCI S(q)) for 0.69 a.u. ≤ q ≤ 3.59 a.u.. The RMS difference between these S(q) values is 4.5 %. The FPA S(q) values are also in excellent agreement with those from the IXSS experiments (IXSS S(q)); the RMS difference between them is 2.7 %. The SPA S(q) values also agree reasonably well with the SDCI S(q) and IXSS S(q) plots for all q values, with RMS differences of 6.2 % and 5.9 %, respectively. However, the SPA S(q) values are smaller than the SDCI S(q) and IXSS S(q) values by between 7 % and 11 % for q ≥ 2.5 a.u. For q ≤ 1 a.u., we see that S(q) values from the SSPA and the EM method are also in excellent agreement with the S(q) values from IXSS and the SDCI calculations for q <1 a.u. For q > 1 a.u., however, the EM S(q) values are always larger than the IXSS and SDCI values by between 7 % and 20 %. On the other hand, the SSPA S(q) values are smaller than the IXSS and SDCI S(q) values for q > 1 a.u. by between 9 % and 14 %.
The relative magnitudes of the S(q) values from the four theoretical models in Fig. 6 for 0 ≤ q ≤ 2 a.u. show a good inverse correlation to the corresponding IMFPs in Fig. 2(a). This result is reasonable because the IMFP is approximately proportional to the inverse of the integral of the ELF over ω and q [Eqns (2) and (3)].
Discussion
We will now make comparisons of our calculated IMFPs for water with the results of other IMFP calculations and with measurements of IMFPs and EALs by various techniques.
Comparisons with calculated IMFPs
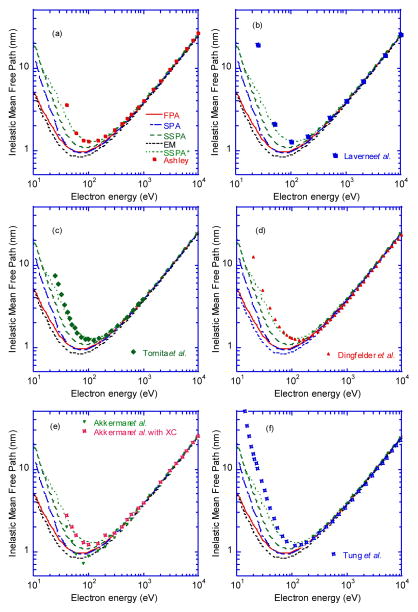
Figure 7 shows comparisons of our water IMFPs from the FPA, SPA, SSPA, and EM with IMFPs calculated by Ashley [3], LaVerne and Pimblott [4], Tomita et al. [5], Dingefelder et al. [6], Akkerman and Akkerman [7], and Tung et al. [8]. Some of these IMFPs were calculated with the SSPA and with ωmax = T′/2 in Eqn (3) rather than our choice of ωmax = T′ – EF that was used for the FPA, SPA, SSPA and EM method. The former choice of maximum energy loss is based on the indistinguishability of incident and emerging electrons while the latter choice allows all energetically permitted excitations to contribute to λ(T) with Eqn (3). The choice of maximum energy loss ωmax = T′/2 increases IMFP values from the FPA (e.g., by up to 50% at around 50 eV compared to IMFPs with ωmax = T′ – EF). This change is larger than the effect of the correction due to electron exchange (neglected so far) that we expect would increase IMFPs by between 10 % and 15 % for electron energies between 50 and 100 eV [66]. We therefore show plots of IMFPs calculated from the non-relativistic SSPA with ωmax= min[T′/2, T′-EF] in Eqn (3), designated SSPA*, in order to show the effects of this choice of ωmax on the IMFP results.
Fig. 7.
Comparison of IMFPs for water calculated from optical data by various authors with our IMFPs from the FPA (solid line) as shown in Table 1, the SPA (long- and short-dashed line), SSPA (long-dashed line), EM (short-dashed line) and the SSPA* (dotted line) models for energies between 10 eV and 10 keV. (a) The solid circles show the IMFPs calculated by Ashley et al. [3] for energies from 40 eV to 10 keV. (b) The solid squares show the IMFPs calculated by Laverne et al. [4] for energies from 25 eV to 10 keV. (c) The solid diamonds show the IMFPs of Tomita et al. [5] for energies from 25 eV to 10 keV. (d) The solid diamonds show the IMFPs of Dingfelder et al. [6] for energies from 10 eV to 10 keV. (e) The downward triangles and half-solid squares show the IMFPs of Akkerman and Akkerman [7] for energies from 40 eV to 10 keV with and without an exchange correction, respectively. (f) The half-solid squares show the IMFPs of Tung et al. [8] for energies from 10 eV to 10 keV.
Ashley [3] calculated IMFPs of water in 1988 for energies from 40 eV to 10 keV with the SSPA and the non-relativistic Moller cross section [67,68] as an exchange correction. He determined the water ELF from a fit to the limited data then available for ε2(ω) between 7.6 eV and 26 eV [69], an extension to higher energies, and with ε1(ω) determined by Kramers-Kronig analysis. He also chose ωmax = T′/2.
Figure 7(a) shows comparisons of Ashley’s IMFPs with our IMFPs from the FPA, SPA, SSPA, EM and SSPA*. In spite of the use of different optical ELFs for water in each IMFP calculations, we see excellent agreement between Ashley’s IMFPs and the SSPA* IMFPs for energies between 60 eV and 10 keV where the RMS difference between them is only 1.1 %. The exchange correction based on the Moller cross section must therefore be negligibly small. For energies between 500 eV and 10 keV, there is good agreement between Ashley’s IMFPs and those from the FPA; the RMS difference between these IMFPs is 5.5 %. At lower energies, however, there are increasing differences between the Ashley and FPA IMFPs, with a difference of 29 % at 100 eV. These differences are associated with use of the SSPA and the choice of ωmax = T′/2 in Eqn (3).
LaVerne et al. [4] reported water IMFPs for energies from 25 eV to 1 MeV with a dielectric model similar to our SSPA*. They utilized Ashley’s ELF [3] and ωmax = T′/2. Figure 7(b) shows very good agreement between the LaVerne IMFPs and our SSPA* IMFPs for energies between 100 eV and 20 keV where the RMS difference is 2.6 %. For energies between 500 eV and 20 keV, there is good agreement between the LaVerne IMFPs and our IMFPs from the FPA where the RMS difference is 5 %.
Tomita et al. [5] published a plot of calculated inverse IMFPs of water for energies from 9 eV to 10 keV. They used Ashley’s dielectric model for the ELF [70] together with a quadratic dispersion equation for q and an exchange correction. Tomita et al. fitted 10 Drude functions to the ε2 values of Heller et al. [69] and chose ωmax = T′/2. We compare the IMFPs of Tomita et al. for energies between 25 eV and 10 keV in Fig. 8(c) with our IMFPs from the FPA, SPA, SSPA, EM, and SSPA* algorithms. For energies between 47 eV and 990 eV, there is good agreement between the Tomita et al. IMFPs and our SSPA* IMFPs, with an RMS difference of 4.2 %. We point out, however, that we could not see any effect of the exchange correction on the Tomita IMFPs for this energy range. There is also good agreement between the Tomita IMFPs and our FPA IMFPs for energies between 200 eV and 990 eV, with an RMS difference of 4.3 %.
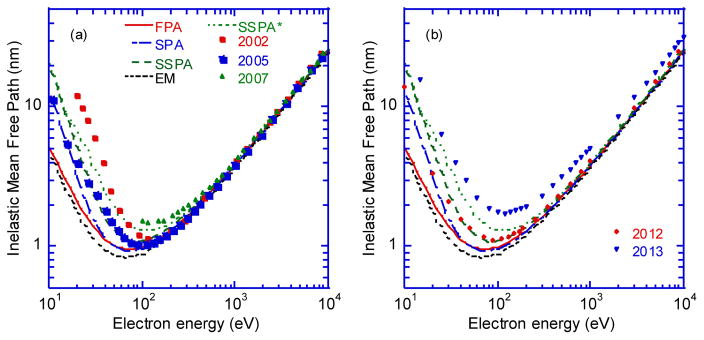
Fig. 8.
Comparison of IMFPs for water calculated from optical data by Emfietzoglou et al. with our IMFPs from the FPA (solid line, Table 1), the SPA (long- and short-dashed line), SSPA (long-dashed line), EM (short-dashed line) and the SSPA* (dotted line) models for energies between 10 eV and 10 keV. (a) The solid circles, squares, triangles show the IMFPs of Emfietzoglou et al. published in 2002 [9], 2005 [10], and 2007 [11], respectively. (b) The solid triangles and downwards triangles show the IMFPs of Emfietzoglou et al. published in 2012 [12] and 2013 [13], respectively.
Dingfelder et al. [6] reported calculations of total inelastic-scattering cross sections of water for energies from 10 eV to 10 keV. They constructed a dielectric-response function based on optical data and other experimental and theoretical information. Their calculations were performed with the inclusion of electron-exchange effects and semi-empirical corrections to account for the expected breakdown of the first Born approximation for energies less than about 100 eV. They fitted ε2 data [69] with modified Drude functions to represent discrete and continuum excitations, and determined ε1 from a Kramers-Kronig analysis. Their dispersion relation for discrete excitations was obtained from the q-dependence of the generalized oscillator strength given by Hamm et al. [71].
Figure 7(d) shows a comparison of the Dingfelder et al. IMFPs with our IMFPs from the FPA, SPA, SSPA, SSPA*, and EM methods. Our SSPA* IMFPs agree well with the Dingfelder et al. IMFPs for energies between 60 eV and 10 keV with an RMS difference of 10 %. For energies between 400 eV and 10 keV, good agreement was found between the Dingfelder et al. IMFPs and our FPA IMFPs (with an RMS difference of 6.2 %) and even better agreement with our IMFPs from the EM method (with an RMS difference of 2.5 %).
Akkerman and Akkerman [7] calculated water IMFPs for energies from 40 eV to 10 keV using a dielectric model with a quadratic dispersion equation. They fitted Drude functions to an optical ELF [69] for valence-electron excitations [72]. They also made a separate IMFP calculation for O K-shell excitations using an atomic model. Total IMFPs were reported with and without a correction for the effects of electron exchange that was based on Ashley’s expression [73].
Figure 7(e) shows the IMFPs of Akkerman and Akkerman, with and without their exchange correction, together with our IMFPs from the FPA, SPA, SSPA, and SSPA*. We see that there is good agreement of the Akkerman and Akkerman IMFPs that include the exchange correction with our SSPA* results for energies between 40 eV and 10 keV; the RMS difference between them is 5.3 %. For energies over 300 eV, there is also good agreement between the Akkerman and Akkerman IMFPs both with and without the exchange correction and our IMFPs from the FPA; the RMS deviations between each data set are 3.7 % and 4.2 %, respectively. For energies between 40 eV and 200 eV, the Akkerman and Akkerman IMFPs without the exchange correction show a different energy dependence compared to our IMFPs from the FPA and SSPA.
Tung et al. [8] reported IMFPs of water for energies between 10 eV and 10 keV. They calculated IMFPs with an extended-Drude model and a quadratic dispersion relation using an optical ELF (from data tabulated in Ref. 74) that was fitted with seven Drude functions to represent valence-electron excitations. They included an exchange correction for the IMFP based on the Moller formula [67, 68] and used an atomic model to represent O K-shell excitations. The minimum and maximum energy transfers were W0 and (T′ + W0 )/2, respectively, where W0 is the ionization energy of liquid water.
Figure 7(f) shows comparisons of the Tung et al. IMFPs (Tung IMFPs) with our IMFPs. For energies between 60 eV and 200 eV, the Tung IMFPs are similar to our SSPA* IMFPs (the differences between them are less 10%) but each data set shows a different energy dependence under 200 eV. This result must be due to differences between the ELFs used in each calculation or to the effects of the exchange correction used by Tung et al. For energies less than 100 eV, the Tung IMFPs are larger than our IMFPs from the FPA, SSPA, and EM methods. For energies between 200 eV and 10 keV, the Tung IMFPs are in good agreement with those from the FPA, SSPA, and EM methods, with RMS differences of 5.7 %, 8.7 %, and 4.1%, respectively. Nevertheless, the Tung IMFPs are generally smaller than our IMFPs.
We turn now to comparisons of our water IMFPs with those published by Emfietzoglou and various coworkers in a series of papers [9,10,11,12,13]. In their earlier papers [9,10,11], they made fits to available ε2 data for water with Drude functions. In later papers [12,13], they fitted optical ELF data for water with Drude functions. Fits to ε2 data rather than ELF data may give different IMFPs, even if one uses the same set of optical constants to derive ε2 and the ELF [75]. The IMFP differences are small (about 1 %) for energies above 100 eV but could become up to 15 % at 50 eV and larger at lower energies [75]. We will therefore make separate comparisons of our IMFPs with those in the earlier [9–11] and later [12,13] papers of Emfietzoglou et al.
In 2002, Emfietzoglou et al. [9] calculated IMFPs of water for energies from 20 eV to 10 keV using a dielectric model and a fit to the Oak Ridge ε2 data [69] with nine Drude transitions. In 2005, they investigated the use of two different optical-data sets (Oak Ridge, data [69] and the ε1, ε2, and ELF data of Hayashi et al. [40]), different dispersion algorithms, and different corrections for correlation and exchange effects on the calculated IMFPs [10]. In 2007, they reported water IMFPs using a new empirical dispersion relation deduced from an analysis of the Hayashi ε2 data at both zero and non-zero q [11].
Figure 8(a) shows water IMFPs calculated by Emfietzoglou et al. in 2002 [9], 2005 [10], and 2007 [11] for energies between 10 eV and 10 keV together with our IMFPs from the FPA, SPA, SSPA, SSPA*, and EM methods. The 2002 IMFPs of Emfietzoglou et al. are in good agreement with our FPA and SPA IMFPs for energies over 100 eV, with RMS differences of 6.4 % and 5.3 %, respectively. For energies under 100 eV, however, the Emfietzoglou et al. IMFPs are larger than our IMFPs from the FPA and SSPA. These differences are due to the use of different optical-data sets in the IMFP calculations as well as to fits of the ε2 data by Emfietzoglou et al. rather than to the direct use of the optical ELF in our work.
The 2005 IMFPs of Emfietzoglou et al. [10] in Fig. 8(a) are in good agreement with our IMFPs from the SSPA for energies between 50 eV and 10 keV (with an RMS deviation of 4.3 %) and are in better agreement with our IMFPs from the FPA for energies between 100 eV and 10 keV (with an RMS deviation of 2.7 %).
The 2007 IMFPs of Emfietzoglou et al. [11] for energies over 100 eV in Fig. 8(a) are larger than our IMFPs from the FPA, SPA, SSPA, SSPA*, and EM methods. At 200 eV, the Emfietzoglou et al. IMFP is larger than those from the FPA and SSPA* by 24 % and 10 %, respectively. For energies between 500 eV and 10 keV, the Emfietzoglou et al. IMFPs remain larger than those from the SSPA* algorithm but the RMS difference between them is only 2.7 %.
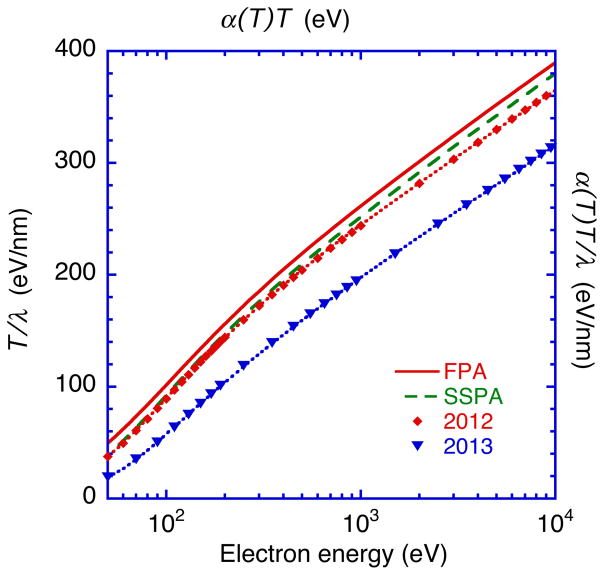
Figure 8(b) shows comparisons of the water IMFPs of Emfietzoglou et al. that were published in 2012 [12] and 2013 [13] with our IMFPs from the FPA, SPA, SSPA, SSPA*, and EM methods. In their 2012 paper, Emfietzoglou et al. reported total inelastic-scattering cross sections based on an empirical extension algorithm that was chosen to match the q-dependence of IXSS data [59] and Fig. 8(b) shows the corresponding IMFPs. We see that our IMFPs from the SSPA are in excellent agreement with those of Emfietzoglou et al. for energies between 40 eV and 10 keV, with an RMS difference of 3.6 %. Our IMFPs from the FPA in Fig. 8(b) are smaller than those of Emfietzoglou et al. although these authors reported that their IMFPs were smaller than those obtained from their use of the Penn algorithm, possibly as a result of choosing ωmax = T′/2 as in their earlier work [9,10,11]. We could obtain better agreement between the Emfietzoglou et al. IMFPs and IMFPs from the FPA by choosing ωmax = min [T′/ 2, (T′ – Ef)]; the RMS differences between these sets of IMFPs were 5.1 % for energies between 40 eV and 10 keV and 3.6 % for energies between 40 eV and 1 keV. The slightly larger RMS difference for the wider energy range is probably due to the fact that our IMFP calculations were made with a relativistic framework and those of Emfietzoglou et al. [11] were based on nonrelativistic energies.
In 2013, Emfietzoglou et al. [13] reported total inelastic-scattering cross sections in water from an optical-data model that included corrections due to exchange and correlation effects. The corresponding IMFPs are shown in Fig. 8(b) (indicated as 2013). We see that these IMFPs are appreciably larger than our IMFPs from the FPA, with differences by factors of 2.6, 1.8, and 1.3 for energies of 50 eV, 100 eV, and 10 keV, respectively. These large differences must be mainly due to the effects of the electron exchange and correlation. We also see that the Emfietzoglou et al. IMFPs are larger than those from the SSPA* by between 20 % and 40 % for energies over 50 eV. We analyzed the Emfietzoglou et al. IMFPs in Fig. 8(b) using non-relativistic Fano plots in which T/λ is plotted versus ln(T) from 50 eV to 10 keV. We show these Fano plots in Fig. 9 together with fits using Eqn (26) in which α(T) is unity for non-relativistic electrons. The non-relativistic Fano plot is given by
Fig. 9.
Fano plots, T/λ vs. T, with the IMFPs of Emfietzoglou et al. [12,13] shown in Fig. 8(b) (diamonds and downward triangles) for liquid water and energies between 50 eV and 10 keV together with relativistic Fano plots of IMFPs, α(T)T/λ vs. α(T)T, with our IMFPs from the FPA (solid line) and SSPA (long-dashed line). The dotted lines show curve-fit results with Eqn (34) to the IMFPs of Emfietzoglou et. al. [12,13].
| (34) |
We see satisfactory fits with Eqn (34) in Fig. 9 using the 2012 and 2013 IMFPs of Emfietzoglou et al. with RMS differences of 0.22 % and 0.37 %, respectively. The resulting parameter values are βr = 0.135 eV−1nm−1, γr = 0.152 eV−1, Cr = 16.5 nm−1, and Dr = 392 eVnm−1 for the 2012 IMFPs, and βr = 0.134 eV−1nm−1, γr = 0.059 eV−1, Cr = 11.7 nm−1, and Dr = 354 eVnm−1 for the 2013 IMFPs. These βr values are slightly smaller than our values that are listed in Table 2 (by less than 10 %). Each βr value corresponds to an integral of the ELF used for the particular IMFP calculation through , as shown by Eqns (28) and (29). The relatively close agreement between our value of βr and the values of βr from the 2012 and 2013 IMFPs of Emfietzoglou et al. is reasonable because the main part of the optical ELF in Fig. 1 (between 6 eV and 87 eV) comes from the IXSS data of Hayashi et al. [40] that were used for the three IMFP calculations.
On the other hand, we see a large difference (a factor of more than two) in the γr values from the Fano plots with the 2012 and 2013 IMFPs of Emfietzoglou et al. The γr value from the 2012 IMFPs (0.152 eV−1) is in good agreement (within 3 %) with the value from the SPA (0.1476 eV−1). Since the γr value is a complicated function of the q-dependence of the ELF [47], the q-dispersion equation used by Emfietzoglou et al. in 2012 must resemble that of the SPA. However, the γr value (0.059 eV−1) for the 2013 IMFPs is substantially smaller than the value from the 2012 IMFPs (γr = 0.152 eV−1) and those found from our results in Table 2 (between 0.1234 eV−1 and 0.1828 eV−1 for the four algorithms we employed). These large differences must be mainly due to the effects of electron exchange and correlation that were introduced using the concept of a many-body local-field correction [13].
In a recent review, Emfietzoglou et al. [76] described the several theoretical approached used in calculations of IMFPs for liquid water. They showed comparisons in which water IMFPs from the SSPA, SPA (identified as the Ritchie-Howie model [29]), FPA, and EM method were plotted as a function of energy from 10 eV to 10 keV. Their results are similar to our comparisons in Fig. 2. They also showed that inclusion of correlation and exchange effects [13] increased IMFPs by between about 15 % (at 10 keV) and about 45 % (at around 100 eV). These increases were much larger than those predicted by the Mott-like correction of Ashley [3] (a maximum of about 25 % at 100 eV) and the Ochkur correction of Fernandez-Varea et al. [77] (a maximum of about 14 % at 20 eV). The large exchange and correlation corrections found by Emfietzoglou et al. [13,76] are surprising since detailed comparisons of calculated IMFPs from the FPA for many elemental solids agree reasonably with IMFPs determined by elastic-peak electron spectroscopy [28,66]. The latter comparisons were made for energies between 100 eV and 5 keV, and the average RMS difference was 12 % for one data set with 11 elemental solids while the average RMS difference for another data set with 17 elemental solids was 15 % [28]. We also mention that Bourke and Chantler[78,79,80] have derived IMFPs of Cu and Mo for energies between 5 eV and 120 eV from detailed analyses of near-edge X-ray absorption spectra. Their IMFPs, however, were smaller than those expected from the FPA. We finally mention that the Cu IMFPs of Bourke and Chantler [78] are roughly consistent with the “lower bounds” of IMFPs that were calculated based on an exchange hole in a fermionic many-body system for energies between 5 eV and about 75 eV [81]. Nevertheless, the Cu IMFPs of Bourke and Chantler appear to be inconsistent with Cu IMFPs from the FPA that enabled good agreement between calculated and measured intensity-voltage profiles in low-energy electron diffraction [82].
Comparison of calculated IMFPs with measured IMFPs and EALs
We now make comparisons of our IMFPs for liquid water that were calculated from the FPA with available measurements of IMFPs [16,17] and EALs [18,19,20]. These measurements were made for condensed films of amorphous ice on a substrate [16,18] or for a liquid-water jet[17,19,20].
As mentioned in the Introduction, the EAL can be conveniently used as a replacement for the IMFP in an algorithm that describes the effects of elastic scattering in a particular quantitative measurement [15]. There are, however, different possible applications of EALs. One common application is the measurement of film thicknesses from the attenuation of a photoelectron signal from a substrate by an overlayer film. The EAL can be derived from the change in photoelectron intensities if the film thickness is known, and we will refer to this as an EAL from Method 1. We note here a complication in that different EALs can result from the use of different algorithms for the determination of film thicknesses and different instrumental configurations [83]. It is also possible to define a second type of EAL. Jablonski and Powell defined an EAL for quantitative analysis that is based on the expected changes in photoelectron intensities from a homogeneous sample due to elastic scattering [84,85], and we will refer to this as an EAL from Method 2.
Jablonski and Powell [86] developed an empirical equation to determine EALs from Method 1, L1:
| (35) |
where ωsa is the single-scattering albedo and λtr is the transport mean free path. Equation (35) was obtained from a fit to calculations of L1 for a group of 16 photoelectron lines and 9 Auger-electron lines of five elemental solids (Si, Cu, Ag, W, and Au) and four inorganic compounds (ZrO2, ZrSiO4, HfO2, and HfSiO4). These calculations were made for electron energies between 61 eV and 2016 eV.
Jablonski and Powell [84,85,87] derived an expression for the EAL from Method 2, L2, based on an analysis of calculated photoelectron intensities from a semi-infinite material using unpolarized X-rays:
| (36) |
where Qx and βeff are correction parameters, σ(β,ψ ) is the photoionization cross section, β is the photoionization asymmetry parameter, and ψ is the angle between the X-ray direction and the photoelectron emission direction. Analytical expressions are available for Qx and for Reff = βeff/β based on extensive Monte Carlo simulations for four elemental solids (Al, Cu, Ag, and Au) and for Mg Kα, Al Kα, Zr Lα, and Ti Kα X-rays [88]. Unfortunately, similar expressions are not yet available for polarized X-rays from synchrotron sources, and we therefore utilize EALs from Eqn (35) in our comments on water EALs from Method 2.
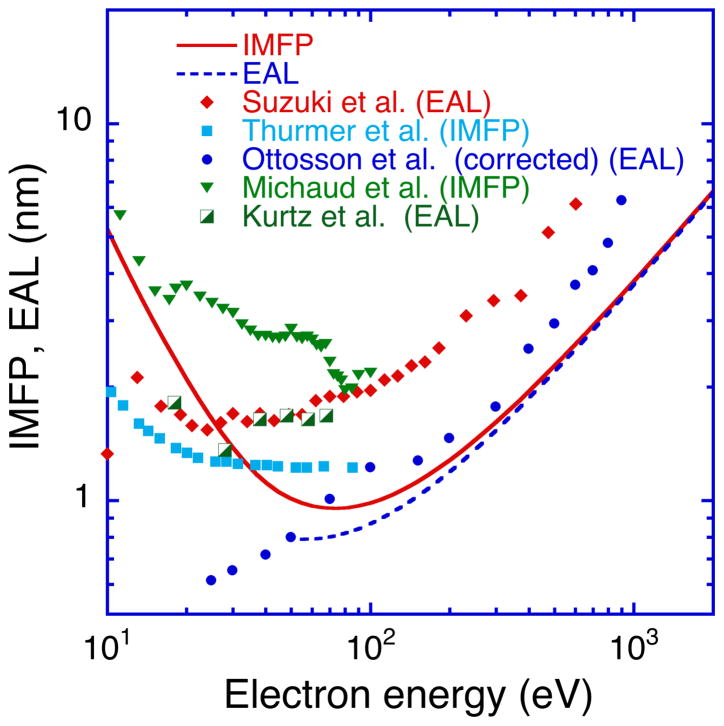
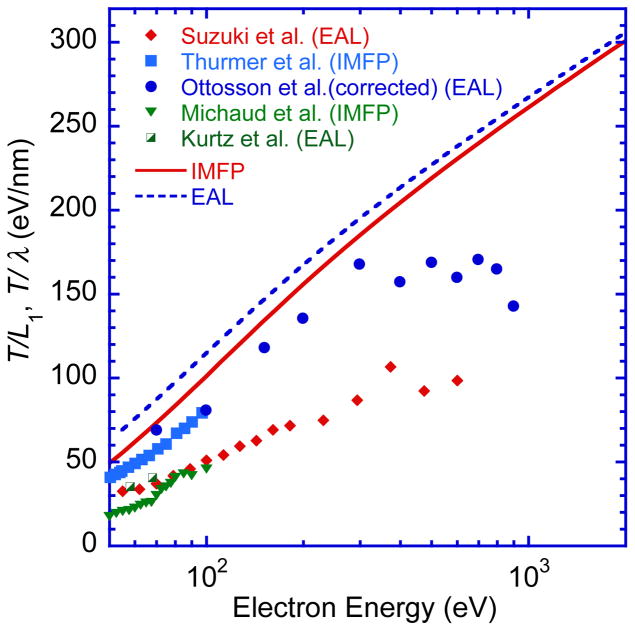
The dashed line in Figure 10 shows a plot of L1 for water versus electron energy from Eqn (35) for energies between 50 eV and 2 keV. We used our FPA IMFPs (indicated by the solid line in Fig. 10) and values of λtr were obtained from the empirical equation proposed by Jablonski and Powell [89]. Values of ωsa ranged from 0.270 at 54.6 eV to 0.0145 at 1998.2 eV. We thus see that L1 is 20 % less than our IMFP at 54.6 eV and 1.1% less than the IMFP at 1998.2 eV.
Fig. 10.
Plots of measured EALs and IMFPs for liquid water and ice together with our IMFPs from the FPA (solid line) and EALs calculated from these IMFPs using Eqn (35) (dashed line) as a function of electron energy between 10 eV and 2 keV. We show the measured EALs of Suzuki et al. [20] (solid diamonds), Ottoson et al. [19] (solid circles) as corrected by Thurmer et al. [17], and Kurtz et al. [18] (half-solid squares) and the IMFPs from the experiments of Thurmer et al. [17] (solid squares) and Michaud et al. [16] (downward triangles). The solid line shows our IMFPs from the FPA (Table 1) and the dashed line shows EALs calculated from Eqn (35) using these IMFPs.
Kurtz et al. [18] reported EALs for condensed films of water ice using Method 1. The films were deposited on a Cu(100) substrate cooled to approximately 90 K with a calibrated microcapillary-array H2O gas doser, and film thicknesses were determined using a literature value for the ice density (0.94 g cm−3). EALs were determined from the attenuation of Cu 3d photoelectrons (excited by X-rays from a synchrotron source) as a function of film thickness. These EALs (between 1.36 nm and 1.82 nm, as plotted in Fig. 10) did not vary appreciably for photoelectron energies between 18 eV and 68 eV. The EALs had estimated total uncertainties of about 35 % [20] but are about a factor of two larger than the EAL from Eqn (35) at 55 eV (0.8 nm) based on the FPA IMFP at this energy. This disagreement might be due to porosity in the ice films and to photon-induced dissociation of the water molecules [90] or possibly to thickness non-uniformities.
Michaud et al. [16] reported cross sections for elastic and inelastic scattering in amorphous ice condensed on a substrate at 14 K for electron energies between 1 eV and 100 eV using high-resolution electron energy-loss spectroscopy. These cross sections were determined using a multiple-scattering analysis of the electron energy distributions as a function of film thickness. They used the same ice density (0.94 g cm−3) as Kurtz et al. and reported a total systematic uncertainty of ± 25 % for their cross-section scale and an uncertainty of their molecular coverage of ± 15 %. Figure 10 shows their IMFPs for energies between 10 eV and 100 eV. These IMFPs are larger than our FPA IMFPs by a factor of over two for energies between 50 eV and 100 eV. We also see that the energy dependence of the Michaud et al. IMFPs is noticeably different from that of the plot of FPA IMFPs. We will comment later on these different energy dependences.
We now describe EALs determined from O 1s photoelectron intensities using Method 2. Ottosson et al. [19] reported EALs for liquid water for photoelectron energies between 25 eV and 900 eV using a liquid micro-jet in combination with soft X-ray synchrotron radiation. They determined relative yields of O 1s photoelectrons to give relative EALs as a function of photoelectron energy; these relative EALs were later converted to an absolute scale using measurements of Na and I photoelectron intensities from NaI solutions and results of molecular dynamics simulations. These EALs were later corrected in the paper of Thurmer et al. [17] for photoionization-anisotropy effects. Figure 10 shows the corrected EALs of Ottosson et al. These EALs are larger than those from Eqn (35) by factors between 1.1 and 1.8 for energies between 70 eV and 900 eV; the average factor is 1.3. For lower energies, however, the Ottosson et al. EALs are less than those from Eqn (35).
Thurmer et al. [17] also reported an analysis of measured O 1s photoelectron angular distributions of liquid water for photoelectron energies between 10 eV and 450 eV. They found that values of the photoionization asymmetry parameter, β, for liquid water were between 20 % and 70 % less than the corresponding values for gas-phase water (that were derived from concurrent measurements of O 1s photoelectron angular distributions from the H2O vapor around the micro-jet). These changes in β were analyzed with a simple model of elastic scattering to yield effective IMFPs (labeled IMFP* in their paper [17]) for energies between 10 eV and 100 eV. These IMFP values are plotted in Fig. 10 where we see that they are essentially constant for energies between 50 eV and 100 eV, and larger than our IMFPs from the FPA by up to 30 %.
Suzuki et al. [20] measured EALs of liquid water using soft X-ray O 1s photoemission spectroscopy of a water beam. They compared photoelectron intensities from liquid-phase and gas-phase water to obtain EALs for energies between 5 eV and 600 eV. These EALs are shown in Fig. 10 where we see that they are larger than our EALs from Eqn (35) by factors between 2.0 and 2.4 for energies between 50 eV and 600 eV. Their EALs are in good agreement with the EALs of Kurtz et al. [18] for energies between 18 eV and 60 eV.
We now show Fano plots in Fig. 11 of the measured EALs and IMFPs for water together with our IMFPs from the FPA and EALs from Eqn (35). Powell has previously shown that measured EALs for Al, Si, Ge, Au, Al2O3, SiO2, NaF, NaCl, and KI display linear Fano plots for energy ranges that were different for each solid; the overall energy range was between 50 eV and about 3.5 keV [91]. This result not only indicates that these measured EALs are consistent with the Bethe equation for inelastic scattering in matter but, like cross-section data for a variety of inelastic-scattering processes, shows that Fano plots provide a useful test of self-consistency for data from a particular source [47]. Figure 11 shows that the EALs of Ottosson et al. (corrected by Thurmer et al.) and the IMFP* values of Thurmer et al. are approximately linear for energies between about 70 eV and 300 eV but that there are significant deviations for higher energies. We note that the slope of the Fano plot for energies between 70 eV and 300 eV is very similar to the slopes of the Fano plots for our IMFPs from the FPA and for the EALs from Eqn (35). This result and the relatively close agreement of the calculated IMFPs and EALs with the EALs of Ottoson et al. and the IMFP* values of Thurmer et al. in Fig. 10 suggest that the correlation and exchange effects on the IMFPs calculated by Emfietzoglou et al. [13] (as shown in Fig. 8(b)) have been over-estimated. The Fano plots of the EALs of Suzuki et al. show satisfactory linearity in Fig. 11 for energies between 55 eV and 600 eV, but the slope of this Fano plot is much less than those of the Fano plots with the Ottosson et al. and Thurmer et al. results. The Suzuki et al. EALs therefore appear to be less reliable than the results of Ottosson et al. and Thurmer et al. for energies between 70 eV and 300 eV. Finally, the Fano plot of the Michaud et al. IMFP results does not show satisfactory linearity.
Fig. 11.
Fano plots of measured EALs and IMFPs for liquid water shown in Fig. 10 and Fano plots of our IMFPs from the FPA (solid line) and of EALs calculated from Eqn (35) with these IMFPs (dashed line). See caption of Fig. 10 for symbols.
Summary
We calculated IMFPs for liquid water from its optical ELF for electron energies from 50 eV to 30 keV with the relativistic FPA. Our optical ELF was obtained from optical constants of Segelstein [39] for energies between 1.24 × 10−7 eV and 5.9 eV, the IXSS measurements of Hayashi et al. [40] for energies between 6.0 eV and 87.0 eV, and the photoabsorption data of Henke et al. [41] for energies between 87 eV and 30 keV.
We also calculated water IMFPs with three other algorithms (the relativistic SPA, SSPA, and EM method) using the same optical ELF. We found good agreement among the IMFPs from the four algorithms for energies over 300 eV. For energies less than 100 eV, however, large differences became apparent. The SSPA IMFPs were largest among IMFPs from the four algorithms for energies between 10 eV and 30 keV while IMFPs from the EM model were smallest. The FPA IMFPs agreed well with the SPA IMFPs for energies over 50 eV. For energies less than 30 eV, the SPA IMFPs became larger than the FPA IMFPs with decreasing electron energy. The differences between the FPA and SPA IMFPs must be due to the contributions of single-electron excitations to the ELF used in the FPA calculations, as shown in Eqn (6), which were neglected in the SPA.
IMFPs from the relativistic TPP-2M equation [Eqns (20) – (25)] for predicting IMFPs were generally in good agreement with IMFPs calculated from the FPA, SPA, SSPA, and EM method for energies over 300 eV. In particular, the TPP-2M IMFPs agreed with the EM IMFPs within 1 % for energies between 150 eV and 30 keV. RMS differences between the TPP-2M IMFPs and IMFPs from the FPA, SPA, SSPA, and EM algorithms were 7.9 %, 6.9 %, 13.0 %, and 2.4 %, respectively, for energies between 50 eV and 30 keV.
We have previously used the FPA in calculations of IMFPs for a group of 41 elemental solids for electron energies between 50 eV and 200 keV [22]. These IMFPs agreed satisfactorily not only with measured IMFPs for energies of 100 keV and 200 keV [22] but also with measured IMFPs for energies between 100 eV and 5 keV [28]. In the latter comparisons, there are some sources of uncertainty in IMFP measurements by elastic-peak electron spectroscopy [28] and in IMFP calculations with the FPA [15] that indicate that the FPA IMFPs in Table 1 have uncertainties of about 10 % [15]. Numerical evaluations of IMFPs for other electron energies can be found using the fit parameters shown in Table 2 for Eqn (26) or the TPP-2M equation. Numerical values of IMFPs from the SPA, SSPA, and EM algorithms can be readily found by interpolation with Eqn (26) and the fit parameters in Table 2.
We calculated values of the static structure factors, S(q), from the optical ELF (for q = 0) using the FPA, SPA, SSPA, and EM algorithms for 0.69 a.u. ≤ q ≤ 3.59 a.u. and compared the resulting values with those from experiment and from theoretical calculations. We found excellent agreement between the FPA S(q) values and the theoretical S(q) values that were calculated from first-principle SDCI calculations for 0.69 a.u. ≤ q ≤ 3.59 a.u.. The RMS difference between these S(q) values was 4.5 %. The FPA S(q) values were also in excellent agreement with those from IXSS experiments, with an RMS difference of 2.7 %. For q ≤ 1 a.u., we found that S(q) values from the SPA, SSPA, and EM method were also in excellent agreement with S(q) values from IXSS experiments and from SDCI calculations. For q > 1 a.u., however, the EM S(q) values were always larger than those from the IXSS and SDCI values by between 7 % and 20 %. On the other hand, the SSPA S(q) values were smaller than those of the IXSS and SDCI values for q > 1 a.u. by between 9 % and 14 %.
We made comparisons of our calculated IMFPs for water from the four algorithms with IMFPs from the calculations of Ashley [3], LaVerne and Pimblott [4], Tomita et al. [5], Dingefelder et al. [6], Akkerman and Akkerman [7], and Tung et al. [8] who used different algorithms for their calculations as well as different optical ELFs. We found that our FPA IMFPs were in good agreement with the other IMFPs for energies over 300 eV. For lower energies, we found large variations of IMFP values that must be due to the different ELFs used and to the different algorithms chosen to represent the q-dependence of the ELF.
We also made comparisons of the IMFPs for water published by Emfietzoglou et al. in 2002 [9], 2005 [10], 2007 [11], 2012 [12] and 2013 [13] with our IMFPs for energies between 10 eV and 10 keV. Our FPA IMFPs were in good agreement with the IMFPs of Emfietzoglou et al. published in 2002, 2005, 2007, and 2012 for energies between 200 eV and 10 keV. For lower energies, the FPA IMFPs were smaller than those of Emfietzoglou et al. The 2007 IMFPs of Emfietzoglou et al. [11] for energies over 100 eV were larger than our IMFPs. For energies between 500 eV and 10 keV, the IMFPs of Emfietzoglou et al. published in 2007 are larger than our IMFPs, but the RMS difference between our SSPA* IMFPs and those of Emfietzoglou et al. was only 2.7 %. We also found that their IMFPs published in 2013 were appreciably larger than our FPA IMFPs, with differences by factors of 2.6, 1.8, and 1.3 for energies of 50 eV, 100 eV, and 10 keV, respectively. These large differences must be due mainly to the effects of the electron exchange and correlation in the algorithm used by Emfietzoglou et al. in their 2013 report [13].
We also made comparisons of our FPA IMFPs and of EALs calculated with the Jablonski-Powell equation, Eqn (35), with available measurements of IMFPs [16,17] and EALs[18,19,20]. These measurements were made for condensed films of amorphous ice on a substrate [16,18] or for a liquid-water jet [17,19,20]. We found a large variation among the measured EALs and IMFPs. In addition, our EALs and IMFPs were smaller than the experimental values for energies between 50 eV and 1000 eV. We also analyzed the measured IMFPs and EALs with Fano plots. We found that the EALs of Ottosson et al. (corrected by Thurmer et al.) and the IMFP* values of Thurmer et al. were approximately linear for energies between about 70 eV and 300 eV but that there were significant deviations for higher energies. We note that the slope of the Fano plot for energies between 70 eV and 300 eV is very similar to the slopes of the Fano plots for our IMFPs from the FPA and for the EALs from Eqn (35). The EALs of Suzuki et al. showed satisfactory linearity in Fig. 11 for energies between 55 eV and 600 eV, but the slope of this Fano plot was much less than that of the Fano plots with the Ottosson et al. and Thurmer et al. results. We found the Fano plot of the Michaud et al. IMFP results did not show satisfactory linearity. Further measurements of IMFPs and EALs are therefore required to establish consistent sets of experimental values and for more detailed comparisons with our IMFP calculations from the FPA.
Acknowledgments
We thank Professors H. Hayashi and D. Emfietzoglou for useful comments and for supplying numerical data and Dr. F. Salvat-Pujol for useful comments on the manuscript.
References
- 1.Tung CJ, Chao TC, Hsieh HW, Chan WT. Nucl Instr Methods Phys Res B. 2007;262:231. [Google Scholar]
- 2.Ghosal S, Hemminger JC, Bluhm H, Mun BS, Hebenstreit ELD, Ketteler G, Ogletree DF, Requejo FG, Salmeron M. Science. 2005;301:563. doi: 10.1126/science.1106525. [DOI] [PubMed] [Google Scholar]
- 3.Ashley JC. J Electron Spectrosc Rel Phenom. 1988;46:199. [Google Scholar]
- 4.LaVerne JA, Pimblott SM. Radiation Res. 1995;141:208. [PubMed] [Google Scholar]
- 5.Tomita H, Kai M, Kusama T, Ito A. Radiat Environ Biophysics. 1997;36:105. doi: 10.1007/s004110050061. [DOI] [PubMed] [Google Scholar]
- 6.Dingfelder M, Hantke D, Inokuti M, Paretzke HG. Rad Phys Chem. 1988;53:1. [Google Scholar]
- 7.Akkerman A, Akkerman E. J Appl Phys. 1999;86:5809. [Google Scholar]
- 8.Tung CJ, Chao TC, Hsieh HW, Chan WT. Nucl Instr Methods Phys Res B. 2007;262:231. [Google Scholar]
- 9.Emfietzoglou D, Moscovitch M. Nucl Instr Methods Phys Res B. 2002;193:71. [Google Scholar]
- 10.Emfietzoglou D, Nikjoo H. Rad Res. 2005;163:98. doi: 10.1667/rr3281. [DOI] [PubMed] [Google Scholar]
- 11.Emfietzoglou D, Nikjoo H. Rad Res. 2007;167:110. doi: 10.1667/RR0551.1. [DOI] [PubMed] [Google Scholar]
- 12.Emfietzoglou D, Kyriakou I, Abril I, Garcia-Milina R, Nikjoo H. Int J Rad Biology. 2012;88:22. doi: 10.3109/09553002.2011.588061. [DOI] [PubMed] [Google Scholar]
- 13.Emfietzoglou D, Kyriakou I, Garcia-Molina R, Abril I, Nikjoo H. Rad Res. 2013;180:499. doi: 10.1667/RR13362.1. [DOI] [PubMed] [Google Scholar]
- 14.ISO 18115-1, Surface chemical analysis — Vocabulary — Part 1: General terms and terms used in spectroscopy. Geneva: 2013. [Google Scholar]
- 15.Powell CJ, Jablonski A. Nucl Instr Methods Phys Res A. 2009;601:54. [Google Scholar]
- 16.Michaud M, Wen A, Sanche L. Rad Res. 2003;159:3. doi: 10.1667/0033-7587(2003)159[0003:csflee]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 17.Thurmer S, Seidel R, Faubel M, Eberhardt W, Hemminger JC, Bradforth SE, Winter B. Phys Rev Letters. 2013;111:173005. doi: 10.1103/PhysRevLett.111.173005. [DOI] [PubMed] [Google Scholar]
- 18.Kurtz RL, Usuki N, Stockbauer R, Madey TE. J Electron Spectrosc Relat Phenom. 1986;40:35. [Google Scholar]
- 19.Ottosson N, Faubel M, Bradforth SE, Jungwirth P, Winter B. J Electron Spectrosc Rel Phenom. 2010;177:60. [Google Scholar]
- 20.Suzuki Y, Nishizawa K, Kurahashi N, Suzuki T. Phys Rev E. 2014;90:010302(R). doi: 10.1103/PhysRevE.90.010302. [DOI] [PubMed] [Google Scholar]
- 21.Penn DR. Phys Rev B. 1987;35:482. doi: 10.1103/physrevb.35.482. [DOI] [PubMed] [Google Scholar]
- 22.Shinotsuka H, Tanuma S, Powell CJ, Penn DR. Surf Interface Anal. 2015;47:871. doi: 10.1002/sia.6123. [DOI] [PMC free article] [PubMed] [Google Scholar]; Shinotsuka H, Tanuma S, Powell CJ, Penn DR. Surf Interface Anal. 2015;47:1132. doi: 10.1002/sia.6123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Shinotsuka H, Tanuma S, Powell CJ, Penn DR. Nucl Instrum Methods Phys Res B. 2012;270:75. [Google Scholar]
- 24.Tanuma S, Powell CJ, Penn DR. Surf Interface Anal. 1991;17:911. doi: 10.1002/sia.6123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tanuma S, Powell CJ, Penn DR. Surf Interface Anal. 1991;17:929. doi: 10.1002/sia.6123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tanuma S, Powell CJ, Penn DR. Surf Interface Anal. 1994;21:165. doi: 10.1002/sia.6123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tanuma S, Powell CJ, Penn DR. Surf Interface Anal. 2005;37:1. doi: 10.1002/sia.6123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tanuma S, Powell CJ, Penn DR. Surf Interface Anal. 2011;43:689. doi: 10.1002/sia.6123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ritchie RH, Howie A. Philos Mag. 1977;36:463. [Google Scholar]
- 30.Da B, Shinotsuka H, Yoshikawa H, Ding ZJ, Tanuma S. Phys Rev Letters. 2014;113:063201. doi: 10.1103/PhysRevLett.113.063201. [DOI] [PubMed] [Google Scholar]
- 31.Fernandez-Varea JM, Salvat F, Dingfelder M, Liljequist D. Nucl Instrum Meth Phys Res B. 2005;229:187. [Google Scholar]
- 32.Fernandez-Varea JM, Liljequist D, Csillag S, Raty R, Salvat F. Nucl Instrum Methods Phys Res B . 1996;108:35. [Google Scholar]
- 33.Lindhard J. Dan Mat Fys Medd. 1954;28(8):1. [Google Scholar]
- 34.Mermin ND. Phys Rev B. 1970;1:2362. [Google Scholar]
- 35.Grand D, Bernas A, Amouyal E. Chem Phys. 1979;44:73. [Google Scholar]
- 36.Goulet T, Bernas A, Ferradini C, Jay-Gerin JP. Chem Phys Lett. 1990;170:492. [Google Scholar]
- 37.Bernas A, Ferradini C, Jay-Gerin JP. Chem Phys. 1997;222:151. [Google Scholar]
- 38.Coe JV, Earhart AD, Cohen MC, Hoffman GJ, Sarkas HW, Bowen KH. J Chem Phys. 1997;107:6023. [Google Scholar]
- 39.Segelstein DJ. MS Thesis. University of Missouri; Kansas City: 1981. The Complex Refractive Index of Water. [Google Scholar]
- 40.Hayashi H, Watanabe N, Udagawa Y, Kao C-C. Proc Nat Acad Sciences. 2000;97:6264. doi: 10.1073/pnas.110572097. private communication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Henke BL, Davis JC, Gullikson EM, Perera RCC. Lawrence Berkeley Laboratory Report. 1988:26259. [Google Scholar]; Henke BL, Gullikson EM, Davis JC. At Data Nucl Data Tables. 1993;54:181. [Google Scholar]
- 42.Tanuma S, Powell CJ, Penn DR. J Electron Spectrosc Relat Phenom. 1993;62:95. [Google Scholar]
- 43.Egerton RF. Electron Energy-Loss Spectroscopy in the Electron Microscope. 3. Springer; New York: 2011. p. 245. [Google Scholar]
- 44.Cabral do Cuoto P, Guedes RC, Costa Cabral BJ. Brazilian Journal of Physics. 2004;34:42. [Google Scholar]
- 45.Tanuma S, Powell CJ, Penn DR. Surf Interface Anal. 1993;20:77. doi: 10.1002/sia.6123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Fano U. Phys Rev. 1954;95:1198. [Google Scholar]
- 47.Inokuti M. Rev Mod Phys. 1971;43:297. [Google Scholar]
- 48.Pauly N, Tougaard S. Surf Sci. 2008;602:1974. [Google Scholar]
- 49.Pauly N, Tougaard S. Surf Interface Anal. 2009;41:735. [Google Scholar]
- 50.Pauly N, Tougaard S. Surf Sci. 2011;605:1556. [Google Scholar]
- 51.Nozieres P, Pines D. Phys Rev. 1959;113:1254. [Google Scholar]
- 52.Egerton RF. Electron Energy-Loss Spectroscopy in the Electron Microscope. 3. Springer; New York: 2011. p. 142. [Google Scholar]
- 53.Ashley JC. J Electron Spectrosc Relat Phenom. 1982;28:177. [Google Scholar]
- 54.Powell CJ. Phys Rev Letters. 1965;22:29. [Google Scholar]
- 55.Powell CJ. Advances in Physics. 1967;16:203. [Google Scholar]
- 56.Powell CJ. Phys Rev. 1968;175:972. [Google Scholar]
- 57.Olivieri G, Parry KM, Powell CJ, Tobias DJ, Brown MA. J Chem Phys. 2016;144:154704. doi: 10.1063/1.4947027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Garcia-Molina R, Abril I, Kyriakou I, Emfietzoglou D. In: Radiation Damage in Bimolecular Systems. Gomez-Tejedor GG, Fuss MC, editors. Springer; New York: 2012. p. 239. [Google Scholar]
- 59.Watanabe N, Hayashi H, Udagawa Y. Bull Chem Soc Jpn. 1997;70:719. [Google Scholar]
- 60.Hu GY, O’Connell RF. Phys Rev B. 1989;40:3600. doi: 10.1103/physrevb.40.3600. [DOI] [PubMed] [Google Scholar]
- 61.Meyer H, Muller T, Schweig A. Chem Phys. 1995;191:213. [Google Scholar]
- 62.Watanabe N. Mol Sci. 2013;7:A0059. [Google Scholar]
- 63.Kittel C. Quantum Theory of Solids. Wiley; New York: 1963. [Google Scholar]
- 64.Wang J, Tripathi N, Smith H., Jr J Chem Phys. 1994;101:4842. [Google Scholar]
- 65.Thakkar AJ, Smith VH. J Phys B. 1978;11:3803. [Google Scholar]
- 66.Powell CJ, Jablonski A. J Phys Chem Ref Data. 1999;19:28. [Google Scholar]
- 67.Bethe HA, Ashkin J. In: Experimental Nuclear Physics. Segre E, editor. Vol. 1. Wiley; New York: 1953. pp. 166–357. [Google Scholar]
- 68.Davydov AS. Quantum Mechanics. Addison-Wesley; Reading, Massachusetts: 1968. pp. 404–406. [Google Scholar]
- 69.Heller JM, Hamm RN, Birkhoff RD, Painter LR. J Chem Phys. 1974;60:3483. [Google Scholar]
- 70.Ashley JC. J Electron Spectrosc Relat Phenom. 1990;50:323. [Google Scholar]
- 71.Hamm RN, Wright HA, Ritchie RH, Turner JE, Turner TP. In: Booz J, Ebert HG, Smith BGR, editors. 5th Symp. On Neutron Microdosimetry, EUR-5452; Verbania, Pallanza. Sept., 1975; p. 1037. [Google Scholar]
- 72.Akkerman A. private communication.
- 73.Ashley JC. J Appl Phys. 1991;69:674. [Google Scholar]
- 74.Querry MR, Wieliczka DM, Segelstein DJ. In: Handbook of Optical Constants of Solids II. Palik ED, editor. Academic Press; New York: 1991. p. 1059. [Google Scholar]
- 75.Emfietzoglou D. private communication.
- 76.Emfietzoglou D, Kyriakou I, Garcia-Molina R, Abril I. Surf Interface Anal. doi: 10.1002/sia.5878. in press. [DOI] [Google Scholar]
- 77.Fernandez-Varea JM, Mayol R, Liljequist D, Salvat F. J Phys: Condens Matter. 1993;5:3593. [Google Scholar]
- 78.Bourke JD, Chantler CT. Phys Rev Letters. 2010;104:206601. doi: 10.1103/PhysRevLett.104.206601. [DOI] [PubMed] [Google Scholar]
- 79.Bourke JD, Chantler CT. J Phys Chem A. 2012;116:3202. doi: 10.1021/jp210097v. [DOI] [PubMed] [Google Scholar]
- 80.Bourke JD, Chantler CT. J Phys Chem Letters. 2015;6:314. doi: 10.1021/jz5023812. [DOI] [PubMed] [Google Scholar]
- 81.Nagi I, Echenique PM. Phys Rev B. 2012;85:115131. [Google Scholar]
- 82.Rundgren J. Phys Rev B. 1999;59:5106. [Google Scholar]
- 83.Powell CJ, Werner WSM, Smekal W, Tasneem G. Surf Interface Anal. 2013;45:628. [Google Scholar]
- 84.Jablonski A, Powell CJ. Surf Science Reports. 2002;47:33. [Google Scholar]
- 85.Powell CJ, Jablonski A. Surf Interface Anal. 2002;33:211. [Google Scholar]
- 86.Jablonski A, Powell CJ. J Vac Sci Technol A. 2009;27:253. [Google Scholar]
- 87.Jablonski A, Powell CJ. Surf Science. 2012;606:644. [Google Scholar]
- 88.Jablonski A. J Electron Spectrosc Relat Phenom. 2013;189:81. [Google Scholar]
- 89.Jablonski A, Powell CJ. Phys Rev B. 2007;76:085123. [Google Scholar]
- 90.Tzvetkov G, Zubavichus Y, Koller G, Schmidt Th, Heske C, Umbach E, Grunze M, Ramsey MG, Netzer FP. Surf Science. 2003;543:131. [Google Scholar]
- 91.Powell CJ. Surf Interface Anal. 1985;7:256. [Google Scholar]