The importance of offshore origination revealed through ophiuroid phylogenomics

Abstract

Our knowledge of macro-evolutionary processes in the deep sea is poor, leading to much speculation about whether the deep sea is a source or sink of evolutionary adaptation. Here, we use a phylogenetic approach, on large molecular (688 species, 275 kbp) and distributional datasets (104 513 records) across an entire class of marine invertebrates (Ophiuroidea), to infer rates of bathymetric range shift over time between shallow and deep water biomes. Biome conservation is evident through the phylogeny, with the majority of species in most clades distributed within the same bathome. Despite this, bathymetric shifts have occurred. We inferred from ancestral reconstructions that eurybathic or intermediate distributions across both biomes were a transitional state and direct changes between shallow and deep sea did not occur. The macro-evolutionary pattern of bathome shift appeared to reflect micro-evolutionary processes of bathymetric speciation. Results suggest that most of the oldest clades have a deep-sea origin, but multiple colonization events indicate that the evolution of this group conforms neither to a simple onshore–offshore hypothesis, nor the opposite pattern. Both shallow and deep bathomes have played an important role in generating the current diversity of this major benthic class.

1. Introduction

Depth is known to play a crucial role in determining marine species distribution ranges [1], as it correlates with many environmental factors that impose physiological constraints [2]. The most important of these are hydrostatic pressure, temperature, light and food availability, although predation, competition, oxygen levels, salinity and bottom type could also affect species' bathymetric distributions [1]. Distinct depth-related faunal assemblages can be also recognized [1]. A primary distinction is often made between shallow (or continental shelf, 0–200 m) and deep sea (greater than 200 m); although the latter category is often split into bathyal (or continental slope, 200–3500 m), abyssal (3500–6500 m) and hadal (trenches, greater than 6500 m) bathomes [1,3,4]. Identifying the environmental and historical drivers of these patterns remains a central priority for marine biogeographic research (e.g. [4]).

There have been two contrasting explanations about the origin of deep-sea organisms, with some authors considering them to be ancient [5] and others of recent origin [6]. An ancient origin has been suggested by the discovery of relict species from bathyal and abyssal depths [3], the assumption being that the deep-sea environmental conditions have remained stable over evolutionary time [7], and the inferred age of some deep-sea clades (e.g. deep-sea isopods from 232 to 314 Ma [8]). However, ‘archaic’ forms have been also found at shelf depths [9]. Moreover, geological records provide evidence of extreme changes in temperature, oxygen and circulation that have potentially caused mass extinction of the deep-sea fauna [4,6] followed by reinvasions from shallow-water refuges [5]. These explanations are not mutually exclusive but together suggest a more complex history.

Evidence now suggests that different faunal groups may have originated in shallow water (e.g. [10]), deep sea (e.g. [11]) or from multiple colonization events from both shelf and slope [4,12]. Despite this, it is still mostly assumed that evolutionary innovations are generated in shallow water [13] and the role of the deep sea in biogeographic processes [14] has been discounted or ignored [15]. Therefore, a key focus for new research should be quantifying the role of deep sea in macro-evolutionary processes and the transition dynamics between shelf and slope habitats.

Brittle stars and basket stars represent a good model for addressing deep-sea macro-evolutionary questions for several reasons. They belong to the most species-rich class (class Ophiuroidea) of the important marine phylum Echinodermata and are found in almost every marine habitat, from tide pools to the greatest ocean depths [16]. A large global database of brittle star distribution records has been assembled [17], which shows that the species composition of this group is distinct between shelf and slope depth strata [18]. Furthermore, there is a robust and extensive phylogeny of the class based on a transcriptome and exon-capture derived phylogenomic dataset [19] that can facilitate testing macro-evolutionary hypotheses.

We used a fossil-calibrated super-matrix phylogeny of 688 species to assess bathome shifts within the class Ophiuroidea. We focused on the shelf/slope transition (200 m) as this depth range was well sampled in our dataset. We asked (i) what was the bathymetric range of the ancestors of the major extant lineages of brittle stars, (ii) which was the most common direction of bathome shifts, and (iii) did shifts of bathome (shallow–deep (S-D)) occur at different rates for different lineages or is this conserved throughout the entire class?

2. Material and methods

(a). Sequence dataset and phylogenetic analyses

The super-matrix phylogeny used here is an extension of a 576 taxa tree [20] spanning all known families, built from 275 kb of exon-capture and transcriptome data comprising 1484 exons in 416 genes with less than 11% missing data. In addition, we obtained approximately 1.4 kb of the mitochondrial gene COI from the majority of samples. This enabled us to incorporate a further 112 species with only public database COI, for a final combined total of 688 taxa. Details on taxon sampling per family are included in the electronic supplementary material, and family and higher level clades are defined according to the most recent classification [20].

Owing to the very large size of the data matrix, we generated a tree via the mega-phylogeny approach [21] widely used in large-scale macro-evolutionary studies (e.g. [22]). Phylogenetic tree generation started with a consensus topology derived from 200 RAxML (v. 7.2.8) [23] fast bootstrap replicates using a four partition (first, second, third exon codon position + COI) GTR-G model, with maximum likelihood branch lengths then optimized onto the consensus topology (see [24] for details). This tree was subsequently converted into an ultrametric chronogram via penalized likelihood rate smoothing (PLRS; r8 s v. 7.3) [25] using 12 fossil-based calibration points as described in [20]. Analyses of 185 taxa datasets [20] showed that this method produced trees with dating and support congruent with Bayesian methods, and hence are appropriate for very large datasets where Bayesian analysis is computationally unfeasible.

Distribution data were gathered from museum collections by TOH (see [17] for description). The dataset used for this study included 104 513 records, with both accurate depth and locality information, for 2120 described species of brittle stars. Because we were interested in the dynamics between continental shelf and slope, continuous bathymetric data were classified into two depth bathomes: shallow (less than 200 m; continental shelf) and deep (greater than 200 m; including upper, lower slope and deep sea), according to a widely accepted definition [26]. The criteria for assigning each species into shallow (S) or deep-sea (D) categories was that at least 10% of its total occurrence records were collected from this depth bathome. We created a third category for species assigned to both (B) bathomes, for intermediate and eurybathic distributions. As the depth of the shelf-break is known to vary [1], we also tested different cut-off values (100, 150, 250 and 300 m) in our analyses by categorizing species in the same manner. We did not pursue analysing occurrence depth as a continuous character. Firstly, because coding depth as a discrete state allowed us to focus on S-D water dynamics. But more importantly, because a bathymetric range is not a single point but instead can be considered a distribution around a mean.

(b). Modelling bathome evolution

All analyses were performed on the 688-taxon ultrametric tree with fixed topology and branch lengths. Owing to some uncertainty in absolute dating [20] we refer only to broad era ages. We tested for asymmetry in the transition rates using a likelihood (ML) approach for evolution of discrete traits, fitDiscrete, implemented in the R [27] package ‘Geiger’ [28], which allows the user to specify different models of transition matrices for hypothesis testing. We considered seven different models, including ‘equal rates’ (ER) and ‘all rates different’ (ARD6), and other ordered (direct transitions between S-D forbidden) models that constrained transitions in several ways (table 1). We preformed 1000 iterations for each model. Model selection was based on AIC score values [29], and four more datasets using different values for shelf-break (100, 150, 250 and 300 m) were also analysed under the best-fitting model (see the electronic supplementary material). Lastly, we briefly assessed the effect of incomplete sampling by comparing estimated parameters from a simulated phylogeny with simulated character states, against estimated parameters from smaller phylogenies (see the electronic supplementary material).

Table 1.

Summary of the seven different dispersal models tested using ML and their equivalent under BI. Values of fit of each model (AIC values for ML and SS and PS for BI) and model comparison (ΔAIC for ML and 2lnBF for BI) are shown for the dataset with a shelf-break value of 200 m. Asterisk (*) indicates ordered models with direct (S-D) transition rate = 0.

type	no. rates	transition matrix	character	description	ML			BI
					lnL	AIC	ΔAIC	clock	SS	2lnBF	PS	2lnBF
ER	1		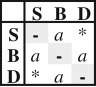ordered	all dispersal events occurred at the same rate	−512.41	1026.82	25.95	strict	−564.57	119.04	−564.57	119.04
								RLC	−562.69	115.28	−562.68	115.26
SYM	2		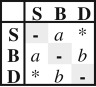ordered	transitions between the same areas occurred at the same rate	−506.47	1016.94	16.07	strict	−511.19	12.28	−511.19	12.28
								RLC	−510.99	11.88	−510.99	11.88
EC	2		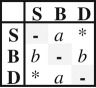ordered	events of range expansion occur at a different rate than range contraction events	−504.53	1013.06	12.19	—
E2C	3		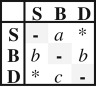ordered	two rates for range expansion and one for range contraction events	−500.78	1007.56	6.69	—
EC2	3		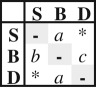ordered	two rates for range contraction events and one for rate expansion	−501.97	1009.93	9.06	—
ARD4	4		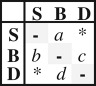ordered	all events occurred at different rates	−496.44	1000.87	n.a.	strict	−505.05	n.a.	−505.05	n.a.
								RLC	−505.11	0.12	−505.22	0.12
ARD6	6		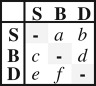unordered	all events occurred at different rates; transitions between shelf and slope were allowed	−496.44	1004.87	4.0	strict	−512.61	15.21	−512.62	15.21
								RLC	−512.57	15.04	−512.57	15.14

Heterotachy, the heterogeneity in rates of evolution of bathymetric ranges across different lineages, was investigated by implementing Bayesian inference (BI) models in BEAST v. 1.8.3 [30] using a ‘random local clock’ (RLC) [31]. Asymmetry and constraints in transitions were considered in four of the six models previously used (table 1); each including both RLC and ‘strict clock’ (assuming a single rate) versions. Depth stratum was coded as a discrete, ordered or unordered trait with three character states (shelf (0), both (1) and slope (2)). The analyses were performed using a standard continuous-time Markov chain (CTMC) with priors as in Ukuwela et al. [32] and Lemey et al. [24] (see the electronic supplementary material for details). Estimation of ancestral bathomes was carried out simultaneously using a stochastic mapping based on an MCMC approach (MarkovJumpsTreeLikelihoood [33]), which maps the bathome shifts on each sampled tree and records the number of shifts in each direction. Model selection was based on the log marginal likelihood for each model estimated by path sampling (PS) and stepping stone (SS) methods [34] (see the electronic supplementary material). State probabilities at nodes were visualized using FigTree v. 1.4.2 [35] and values greater than or equal to 90% of state probability for any of shelf (S or S + B) or slope (D or D + B) habitats were considered as strong support (i.e. decisive).

3. Results

Our relative taxon sampling across biomes was broadly congruent with the full occurrence dataset, but deep-sea species are slightly underrepresented. Using 200 m as the shelf-break value, the phylogeny (688 species) had 257 (37.5%) shallow-water species, 272 (39.5%) deep-sea species and 159 (23%) species distributed in both strata, whereas the complete distributional dataset (2120 species) included 695 (33%), 1012 (48%) and 413 (19%), respectively. The number of records per species varied from 1 to 3338 with median 33 for taxa in the phylogeny (with a similar range and median 9 for the complete dataset).

The best-fitting model under ML was ARD4 (table 1), which set direct transitions from S to D and D to S to zero. Although this model was only slightly preferred over the unordered model (ARD6, ΔAIC = 4.1) due to fewer parameters, the direct transition rates between shelf and slope estimated under the ARD6 model were close to zero (S → D = 1.19 × 10⁻¹¹⁵, D → S = 2.65 × 10⁻⁹¹, see the electronic supplementary material). Also, simulations on different size phylogenies, even when the proportion of character states differ between them, showed that there is little uncertainty in parameter estimates until sub-sampling is about 20% (see the electronic supplementary material).

The ML and BI estimates for rate transitions (figure 1) were higher to/from deep-water environments than to/from shallow water. The highest rate was for range contractions to deep sea, estimated to be almost twice that of any other rate. This is not just an artefact of the choice of 200 m for our boundary between bathomes, as the relative difference between rates was similar for other boundaries (200–300 m, see electronic supplementary material). The exception is for the shallowest depths (100 and 150 m), where the observed pattern was the reverse (100 m) or both rates are estimated to be equal (150 m), which can be explained by the relatively high number of deep species.

Figure 1.

Estimated rates of bathome shifts (shelf-break = 200 m) for the best-fitting model under (a) ML and (b) BI (ARD4); 95% CI are shown in brackets. Arrows indicate direction of bathome shift and width is proportional to the rates; direct transitions between S and D were not allowed. For BI, the mean values for the estimated number of bathome shifts in each direction are shown in parenthesis (S = shallow, B = both, D = deep).

We found little evidence for heterotachy. In the best-fitting BEAST model, ARD4 with a random clock (table 1) had only slightly higher marginal lnL values (2lnBF = 0.06) than the same model under a strict clock. Moreover, the number of rate changes inferred in most of the trees was zero (varying from 0 to 6), implying that just one rate can explain the evolution of bathomes in this phylogeny (mean = 0.753, median = 1, mode = 0, 95%HDP = [0, 2]). The coefficient of variation supported the simpler model with one rate, as it was most frequently estimated to be close to zero (mean = 0.045, median = 0.006, 95%HDP = [0, 0.1989]). The overall BEAST ARD4 (strict clock, table 1) transition rate was estimated to be 0.015 per lineage per Mya (95%HDP = [0.011, 0.019]).

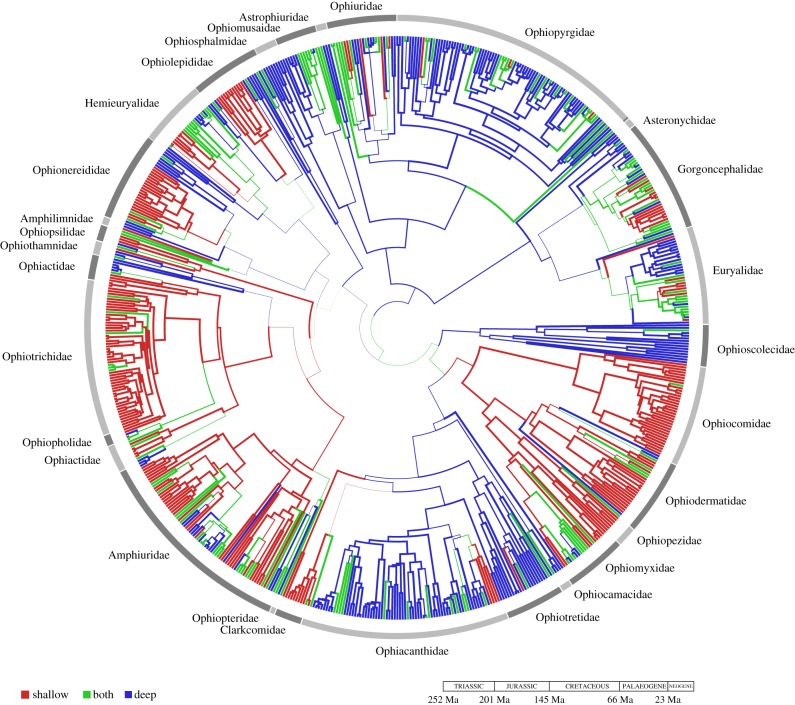
The total number of transitions across the phylogeny, occurring along the branches, was estimated at 390 (mean value; median = 384, 95%HDP = [295,494]; table 1; ARD6 inferred very few direct transitions between S and D, mean of 2.0 from D to S and 1.7 from S to D, see the electronic supplementary material). More than 60% of internal nodes showed decisive ancestral reconstructions. The first decisive node (greater than or equal to 0.9) appears during the Mid-Jurassic (ca 175 Ma). Twelve out of 34 putative family-level nodes (Mid-Cretaceous ca 110 Ma [20]) were decisive. There appears to have been numerous colonization events in both directions from shallow to deep water and vice versa (figure 2), but the oldest nodes showed stronger support for the deep bathome. Clades such as the order Ophiacanthina, Euryalida and Ophiurida, were inferred to have originated in the deep sea but include smaller clades (Clarkcomidae and Ophiopteridae; sub-clade in Euryalidae and Gorgoncephalidae: Ophiopyrgida, Astrophiuridae and Asteronychidae, respectively) mostly restricted to shallow waters (see the electronic supplementary material, figure S5). Also, the super-families Ophiodermatidea and Amphiuridea, for which a shallow origin was inferred, include some deep-sea sub-clades. The phylogeny exhibits conserved bathome structure (electronic supplementary material); families are composed predominantly of species inhabiting the same bathome (electronic supplementary material).

Figure 2.

Phylogeny with bathome ancestral state estimates recovered from BEAST using the ARD4 model. Branch thickness is proportional to the state probability of the ancestral reconstruction at each node. Families are indicated with bands and names of the largest ones are annotated.

4. Discussion

In this study, we used one of the most comprehensive benthic metazoan phylogenies to date in order to test hypotheses on transitions between bathomes and infer ancestral bathome distributions for brittle stars. We found, for the first time across an entire class of marine invertebrates, that (i) there is a trend for biome conservatism of depth strata, (ii) eurybathy is transitory at macro-evolutionary scales, (iii) deep-sea lineages extend their ranges into shallow water more often than shallow lineages into deep sea, and (iv) the evolution of this group conforms neither to a simple onshore–offshore (shallow-deep) hypothesis, nor the opposite pattern, as there have been multiple transitions back and forth between deep-sea and shallow-water lineages.

(a). Phylogenetic patterns

Brittle stars exhibited bathome conservatism because the trait was clearly structured phylogenetically, evolutionary rates of bathome transition were low (figure 1), and families tended to be dominated by species restricted to a specific depth zone (figure 2; see the electronic supplementary material). The most likely cause of bathome conservation is that shifts require evolutionary adaptation. Temperature and hydrostatic pressure have been found to be important limiting factors for expansion into new bathymetric ranges, as they affect the function of important biomolecules [2] resulting in biomolecular differences evolving between species adapted to shallow and bathyal depths [36]. Other studies have suggested that habitat suitability [37] and food availability [38] can also limit expansion into deep water. There is growing evidence that species with apparently wide depth distributions have bathymetrically stratified genetic structure and may consist of complexes of cryptic species [39].

(b). Shelf/slope transitions and bathyal speciation

Although transitions between bathomes are relatively rare, across such a large group they have occurred numerous times including at quite shallow phylogenetic levels (within genera). Experiments have shown than some echinoderm larvae have the capacity to survive hydrostatic pressure gradients if the temperature remains stable [37,40], thus allowing them to potentially shift between bathomes. This situation occurs today in regions with near-isothermal water columns such as the Mediterranean [37] or in polar regions during winter [40]. Such homogeneous water columns could have allowed the colonization of shallow waters from bathyal species (emergence [12]), as well as bathyal colonization from shallow-water species (submergence [10]).

Bathyal speciation can occur in species with wide bathymetric ranges when gene flow from more central populations decreases or ceases and populations at the extremes of the distribution range become locally adapted and split into new lineages [41]. Gene flow between populations of marine organisms broadly distributed across the water column could maintain eurybathy [41]. Conversely, speciation could occur if natural selection overwhelms gene flow [42]. Although 23% of species in the phylogeny are distributed in both depth bathomes (B), including both narrow and widespread bathymetric ranges, our analyses suggest that this is mostly a transitional state.

Critically, despite 80% of the taxa being the S or D state, transitions between them are modelled exclusively as being via the state B even when direct transitions are allowed to occur directly between S and D (ARD6, table 1). There are two major reasons for this: many of the B state taxa occur at intermediate depths around the shelf/slope transition, and that the B state, unlike the S and D states, is not phylogenetically structured but scattered across the tree (figure 2). Thus, the B state is an evolutionary intermediate, and the resulting transition rate model mirrors hypothesized micro-evolutionary population processes of bathymetric speciation (e.g. the few genera that show recent bathome transitions include B species as well). A corollary of this is that many of the apparently eurybathic taxa with very wide depth distributions may not be ‘Darwinian demons’ [43] defying divergent selection regimes but actually comprise multiple species that have yet to be recognized [44]. The phylogeny highlights several possible examples of recent depth-driven diversification, where pairs of closely related species occur in the same geographical region but, in most cases, one of them has a wide or intermediate distribution (B) and the other is restricted to either shelf (S) or slope (D) environments.

Our estimated transition rates showed that there is a general trend of deep-sea species extending their range more frequently into shallow environments, than shallow-water species into the deep sea. The general trend in transition rates could reflect: (i) the existence of a strong lower boundary in shallow-adapted species or (ii) support for the hypothesis that deep-sea habitats are an important site for origination [2,14]. As organisms tend to be physiologically adapted to specific pressures and temperatures [45], shallow-water species are more restricted to narrower bathymetric ranges due to these parameters changing more dramatically with increasing depth, compared with the deep sea [1]. On the contrary, deep-sea species appear to be physiologically capable (albeit rarely) of dispersing to shelf environments [45], which is supported by the fossil record of the deep-sea ophiacanthid ophiuroids, where several lineages originated in the deep sea and have ephemerally invaded shelf environments [14].

We provide evidence that the deep sea was the site of origin of some taxonomic groups and has functioned as a centre of diversification [14,17]. Our reconstruction of ancestral bathomes recovered eight out of 32 nodes with high support (six S and two D) at the taxonomic rank of family clades [20] (mostly of Mid-Cretaceous age). Although, the oldest node with high state support was the shallow-water super-family Ophiodermatidea (Mid-Jurassic ca 170 Ma), most of the older nodes were estimated to have predominantly inhabited deep water (e.g. Euryophiurida), although in some cases we cannot rule out ancestral eurybathic or intermediate distributions. Importantly, we infer a deep-sea origin for the order Ophiacanthina, which is concordant with the fossil record [14].

(c). Biodiversity patterns

Our data do not support a consistent offshore–onshore or onshore–offshore pattern across the ophiuroid phylogeny, but rather multiple colonization events from both bathomes. Direct comparison with other studies is difficult, as the definition of offshore environments or deep sea is often imprecise [8,46] or not uniform (e.g. greater than 50 m for stylasterid corals [8], greater than 200 m for ophiacanthid brittle stars [14], maximum depth range greater than 2000 m or minimum depth range greater than 500 m for sea urchins [13]). Nevertheless, since the development of the onshore–offshore origination hypothesis [46], studies on different taxa have inferred biogeographic histories showing this pattern in higher taxa (summarized in [2], mostly of marine benthic invertebrates), while a few have shown no support [47], the opposite pattern [11] or a mixed origin. For example, different clades of octopuses have been inferred to have originated by polar ‘emergence’ [12] and polar ‘submergence’ [10]. Another example is the isopods, where important radiations occurred in the deep sea after invasions from onshore taxa, followed by recolonizations of shelf environments [8], supporting a mixed origin [4]. Evolution rarely proceeds in a single direction, and, as often stated for ecology [48], much of the foundations of biogeography must rely on broad statistical generalizations rather than empirical ‘laws of nature’.

5. Conclusion

This study provides a novel insight towards understanding the role of the deep sea in macro-evolutionary processes by combining modern, extensive and powerful distribution and phylogenetic databases. Our results do not support a uniform onshore or offshore origin, but a long history of multiple transitions between deep and shallow water lineages in a class of marine invertebrates that, overall, exhibit biome conservatism at intermediate taxonomic levels. We suggest that our conclusions on the role of the deep-sea lineages and the process of bathome evolution in shaping ophiuroid diversity are robust to our data sampling, because in our current dataset deep-sea species are slightly underrepresented and therefore adding more slope lineages will likely provide additional support for the role of the deep sea in the diversification of the group. Further studies with more species sampling and including fossil information will allow quantitative investigation of diversification patterns among bathomes.

Authors' contributions

G.B.C. designed the study, carried out data analyses and drafted the manuscript; H.V. designed the study and helped draft the manuscript; A.H. built the phylogeny, participated in the design of the study and critically revised the manuscript; T.O.H. gathered the data, conceived of the study, designed the study and helped draft the manuscript. All authors gave final approval for publication.

Funding

T.O.H., A.F.H. and G.B.C. (partially) were supported by the Marine Biodiversity Hub, funded through the National Environmental Research Program (NERP), and administered through the Australian Government's Department of the Environment. G.B.C. received support from the University of Melbourne. H.V. was supported by the Australian Research Council (FT110100585).

Competing interests

We declare we have no competing interests.