A new inverse method for estimation of in vivo mechanical properties of the aortic wall

Abstract

The aortic wall is always loaded in vivo, which makes it challenging to estimate the material parameters of its nonlinear, anisotropic constitutive equation from in vivo image data. Previous approaches largely relied on either computationally expensive finite element models or simplifications of the geometry or material models. In this study, we investigated a new inverse method based on aortic wall stress computation. This approach consists of the following two steps: (1) computing an “almost true” stress field from the in vivo geometries and loading conditions, (2) building an objective function based on the “almost true” stress fields, constitutive equations and deformation relations, and estimating the material parameters by minimizing the objective function. The method was validated through numerical experiments by using the in vivo data from four ascending aortic aneurysm (AsAA) patients. The results demonstrated that the method is computationally efficient. This novel approach may facilitate the personalized biomechanical analysis of aortic tissues in clinical applications, such as in the rupture risk analysis of ascending aortic aneurysms.

1. Introduction

Advances in imaging techniques and numerical methods have made it possible to investigate the in vivo biomechanics of the cardiovascular system on a patient-specific level. For the three key components in a mechanical analysis (geometries, loading and boundary conditions, and material properties), patient-specific geometries (e.g., anatomic structures of the aorta) and physiological loading conditions (i.e., diastolic and systolic pressures) can be obtained at a high level of spatial and temporal resolutions from clinical diagnostic imaging tools, such as CT scans, and hemodynamic measurements, respectively [1]. However, even though tremendous efforts have been devoted to the development of techniques for the accurate estimation of in vivo tissue material properties, the results are far from satisfactory.

Numerical estimation of the material properties of a particular material often employs inverse techniques. In such methods [2, 3], the estimation of constitutive parameters of the material is often obtained based on boundary conditions and displacement/strain fields, measured experimentally. An inverse approach, known as the virtual field method [4], has been developed for extracting homogenous [5] and heterogeneous constitutive parameters from in vitro full-field measurement data [6] of blood vessels whose reference configurations are unloaded. However, the configuration of in vivo imaging data is always loaded, which makes estimating the constitutive parameters from in vivo loaded geometries challenging.

In vivo material properties are typically characterized by: (1) recovering or estimating the unpressurized geometry, (2) deforming the geometry in finite element (FE) simulations with in vivo loading and boundary conditions with the estimated constitutive parameters, and (3) by using certain optimization methods, the estimated constitutive parameters will be adjusted, and optimal parameters will be identified such that some physical measurements (e.g. strain/displacement) are matched between the simulated, deformed configuration and the in vivo loaded configuration. Using such strategies, Wittek et al. [7, 8] developed two methods to determine patient-specific material parameters of the human aorta from in vivo strain measurements. The Holzapfel–Gasser–Ogden (HGO) model [9] was used in Wittek’s study. Zeinali-Davarani et al. [10] evaluated local wall thickness and material anisotropy of the human aorta, while other constitutive parameters were determined through biaxial tests. Using similar strategies, Liu et al. [11], Zhang et al. [12] and Franquet et al. [13] identified linear elastic material parameters from in vivo images.

Despite the differences in constitutive models and optimization objective functions, all of the abovementioned studies used nonlinear optimization algorithms to find the optimal material parameters in an iterative manner, and FE simulations were performed in each iteration. Since a large number of iterations are needed to reach the optimal solution, these methods are very time consuming. For example, in the study reported in [7, 8], it took about 2 weeks to find the optimal material parameters. Such high computing cost prevents the practical use of these methods, particularly in a clinical setting requiring fast feedback to clinicians. To avoid costly FE simulations, some forms of simplifications and assumptions were made in several studies. By assuming an perfectly cylindrical shape of the aorta, Astrand et al. [14] and Smoljki´c et al. [15] estimated the HGO model parameters. Trabelsi et al. [16] proposed a multiple linear regression-based method to estimate the constitutive parameters by assuming a linear relation between the volume of the aorta and the constitutive parameters of the Demiray model.

In this study, we proposed a new inverse approach based on stress computation for the in vivo nonlinear material parameter estimation of the aortic wall. This method is less computationally expensive. Firstly, we leveraged the fact that the in vivo aortic wall stress is approximately statically determinate, which means, for given geometries and loading and boundary conditions under a known blood pressure, different material parameters and constitutive models will give nearly the same stress field. Therefore, the “almost-true” in vivo stress field at any cardiac phase can be obtained by using an infinitesimal linear elastic model with sufficiently stiff material parameters. Secondly, given a constitutive model with an initial guess of the material parameters, by using the constitutive equations and deformation relation between the two loading states (e.g., diastolic and systolic pressures), we applied optimization algorithms to find the “true” material parameters such that the difference between the estimated and the “almost-true” stress fields is minimized. Since FE simulation is not used iteratively in this optimization process, our approach is much faster than the other methods [7, 8] that require numerous iterations of FE simulations. The proposed approach may facilitate the subject-specific biomechanics analysis of aortic wall stresses in clinical applications, such as in the rupture risk analysis of ascending aortic aneurysm [17].

2. Methods

2.1 Prerequisites and Assumptions

Our method was formulated based on the following assumptions: (1) In vivo loaded geometries of the aorta and blood pressure levels are known at 2 phases, e.g., at diastole and systole; (2) Finite element meshes of the geometries at the two phases can be constructed with mesh correspondence, i.e., the displacement field from systole to diastole is obtainable, similar to the full field measurement [6]; (3) the thickness of the aortic wall can be either directly inferred from the clinical images or can be reasonably assumed; and (4) by assuming the aorta is statically determinate, the circumferential and longitudinal residual stresses are ignored. The mesh correspondence condition may be satisfied by using 4D (3D+t) ultrasound image data processed with speckle tracking algorithms [18], or 4D CT image data processed with surface tracking algorithms [19]; the heterogeneous thickness of the aortic wall may be extracted by using CT [20–22], MR[23] and ultrasound [24, 25] imaging techniques.

In this paper, we only considered the homogeneous (average) constitutive behavior of the aortic segment and across the wall thickness. However, our approach can be extended to heterogeneous tissues since it is not based on the assumption of homogeneity.

2.2 Constitutive Model

The fiber reinforced HGO hyperelastic material model from Gasser et al. [9] was used to model the constitutive response of aortic wall tissue. In this model, tissues are assumed to be composed of a matrix material with two families of embedded fibers, each of which has a preferred direction. The fiber directions can be mathematically described using two unit vectors. The strain energy function can be expressed by

$$\mathrm{\Psi }=C_{10}({\overline{\mathit{I}}}_1-3)+\frac{k_1}{2k_2}{\sum }_{i=1}^2[\mathit{\text{exp}}\{k_2{[\kappa {\overline{\mathit{I}}}_1+(1-3\kappa ){\overline{\mathit{I}}}_{4i}-1]}^2\}-1]+\frac{1}{D}[\frac{J^2-1}{2}-\text{ln }J]$$ (1)

$$i=1,2$$

where C₁₀ is material parameter to describe the matrix material. k₁ is a positive material parameter that has the same dimension of stress, while k₂ is a dimensionless parameter. The deviatoric strain invariant Ī₁ is used to characterize the matrix material; and the deviatoric strain invariant Ī_4i is used to characterize the fiber families. Ī_4i is equal to squares of the stretches in the fiber directions. k is used as a dispersion parameter describing the distribution of fiber orientation. When k = 0, the fibers are perfectly aligned. When k = 0.33, the fibers are randomly distributed, and the material becomes isotropic. D is a parameter that controls material incompressibility and is fixed to 10⁻⁴. during all computations. A parameter θ defines the angle between mean local fiber direction and the circumferential axis of the local coordinate system. Thus, five material parameters are included in this model as denoted by C₁₀, k₁, k₂, k, θ.

2.3 The Method for Constitutive Parameter Estimation

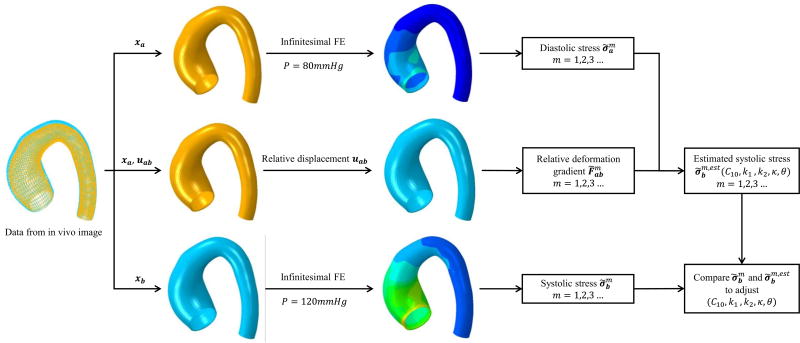
The work flow of our material parameter estimation process is shown in Figure 1. This approach leverages the fact that the “almost-true” stress field of the aortic wall can be approximately determined by the geometry and blood pressure load, and only weakly depends on material properties. This fact has been theoretically justified by Miller and Lu [26] and numerically verified by Lu et al. [27] and Joldes et al.[28]. Therefore, given the deformed configurations at the two cardiac phases, x_a at the diastole phase and x_b at the systole phase, the “almost-true” stress of each element m of the aortic wall at the two phases, ${\stackrel{\sim }{\mathit{\sigma }}}_{\mathit{a}}^m$ and ${\stackrel{\sim }{\mathit{\sigma }}}_{\mathit{b}}^m$, respectively, can be calculated by using an infinitesimal finite element method (see Section 2.4). In this paper, we use subscript a and b to denote the diastole and systole respectively, but generally they can represent any two loaded phases as long as the pressure levels and geometries are known. The relative deformation gradient ${\stackrel{\sim }{\mathit{F}}}_{\mathit{a}\mathit{b}}^m$ from the diastolic configuration to the systolic configuration can be calculated using the relative displacement field u_ab between the two configurations. As a result, the systolic stress of each element can be estimated by using the constitutive model with the candidate parameters and relative deformation gradient. The estimated systolic stress, ${\stackrel{\sim }{\mathit{\sigma }}}_{\mathit{b}}^{m,\mathit{\text{est}}}$, which depends on the constitutive parameters (C₁₀, k₁, k₂, k, θ), can be compared with the “almost-true” systolic stress ${\stackrel{\sim }{\mathit{\sigma }}}_{\mathit{b}}^m$, and any discrepancy will indicate that the set of candidate parameters are different from the optimal “true” parameters and hence need to be adjusted by a nonlinear optimization algorithm.

Figure 1.

The flowchart of the material parameter estimation process.

This optimization process can be formulated as follows: the objective is to find a set of constitutive parameters (C₁₀, k₁, k₂, k, θ) that minimize the difference between the “almost-true” systolic tress ${\stackrel{\sim }{\sigma }}_{b,i}^m$ and the estimated systolic tress ${\stackrel{\sim }{\sigma }}_{b,i}^{m,\mathit{\text{est}}}$ for every integration point of each element m, which is defined as

$$g_{\mathit{\text{err}}}={\sum }_{m=1}^N{\sum }_{i=1}^6{[{\stackrel{\sim }{\sigma }}_{b,i}^m-{\stackrel{\sim }{\sigma }}_{b,i}^{m,\mathit{\text{est}}}(C_{10},k_1,k_2,\kappa ,\theta )]}^2$$ (2)

where N is the number of elements used in the optimization, i is the component index of the stress tensor in Voigt notation. At element m, ${\stackrel{\sim }{\sigma }}_{b,i}^{m,\mathit{\text{est}}}$ is the component of the estimated systolic stress given a set of candidate constitutive parameters (C₁₀, k₁, k₂, k, θ). For a type of element that has more than one integration point such as C3D8 in the ABAQUS (Simulia, RI), we calculated the squared stress-errors at all integration points and sum them together as the value of the objective function of Eq. (2).

The details of each step in the approach are presented in the following sections. The infinitesimal finite element method that was used for calculating ${\stackrel{\sim }{\mathit{\sigma }}}_{\mathit{a}}^m$ and ${\stackrel{\sim }{\mathit{\sigma }}}_{\mathit{b}}^m$ is described in Section 2.4. The method for estimating ${\stackrel{\sim }{\mathit{\sigma }}}_{\mathit{b}}^{m,\mathit{\text{est}}}$ is described in Section 2.5. The optimization process and the entire work flow are described in Section 2.6. To verify the approach, numerical experiments were carried out on the data from four ascending aortic aneurysm patients in Section 3.3.

2.4 Computation of the “Almost-true” Stress using Infinitesimal FE

Generally, the stress of a deformable body depends not only on its geometry, load and boundary conditions, but also on the mechanical properties of the material. However, in statically determinate problems [26], the stress in a deformed configuration is insensitive to the material properties. For example, the stress of a thin cylindrical wall can be directly obtained using Laplace’s law, which has been used extensively in studies of aneurysms [29]. The pressurized aneurysms have been shown to be approximately “statically determinate” [28].

Therefore, if we specify a very stiff material on the aortic wall, the deformation should be infinitesimal and the stress can be computed by directly applying physiological pressure to the loaded geometry in a linear elastic finite element solver [28]. The computed stress is considered to be “almost-true”, i.e., very close to the true stress in the aortic wall. In this study, we selected a very stiff material (E = 2 × 10⁴ GPa and ν = 0.49) for the aortic wall to obtain the wall Cauchy stress (Figure 1). This stress estimation method was numerically validated in Section 3.1.

2.5 Continuum Mechanics Framework for Systolic Stress Estimation

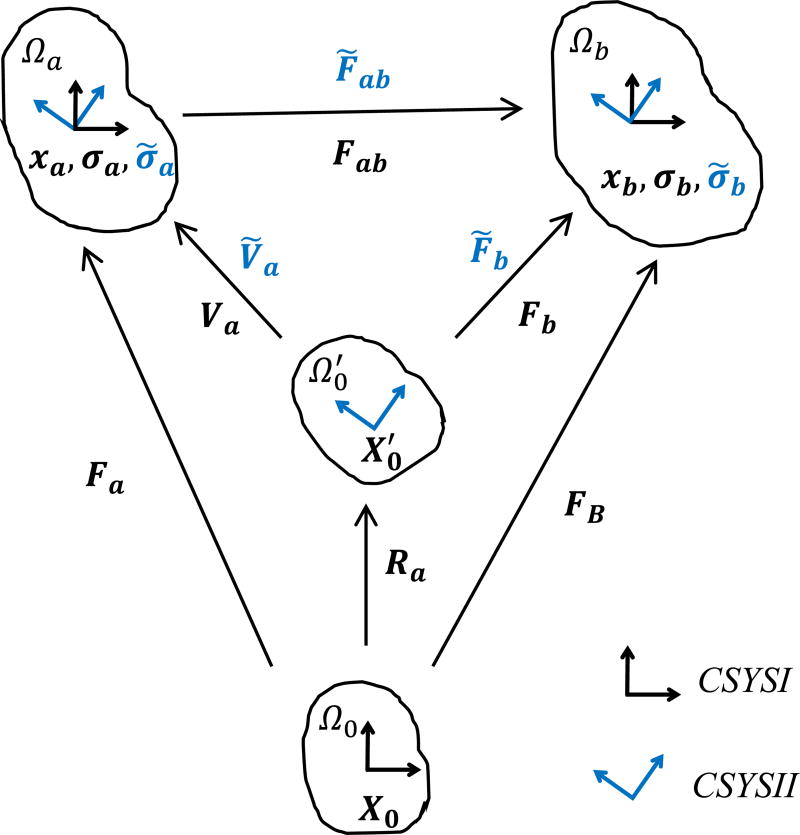
In this section, we presented a method using the corotational coordinate frame to estimate the systolic stress ( ${\stackrel{\sim }{\mathit{\sigma }}}_{\mathit{b}}^{m,\mathit{\text{est}}}$) given the candidate material parameters (C₁₀, k₁, k₂, k, θ) of Eqn (1). Figure 2 illustrates the related variables in the unloaded configurations and the two deformed configurations. The diastolic deformation gradient F_a contains complete information about rotation and stretch that can be uniquely defined via polar decomposition

$${\mathit{F}}_{\mathit{a}}={\mathit{V}}_{\mathit{a}}{\mathit{R}}_{\mathit{a}}={\mathit{R}}_{\mathit{a}}{\mathit{U}}_{\mathit{a}}$$ (3)

where V_a is the left stretch tensor, U_a is the right stretch tensor, R_a is the rotation tensor. We defined two coordinate systems CSYSI and CSYSII, where CSYSI refers to a fixed Cartesian coordinate system, and CSYSII is the coordinate system corotated with the diastolic rotation R_a. Let Ω₀ be the unloaded configuration and ${\Omega }_0^{\prime }$ be the corotated unloaded configuration obtained by applying the diastolic rotation R_a on Ω₀. Ω_a and Ω_b are the diastolic and systolic configurations respectively.

Figure 2.

Deformation measures that map the unloaded configuration Ω₀, the corotated unloaded configuration ${\Omega }_0^{\prime }$, the diastolic configuration Ω_a and the systolic configuration Ω_b.

2.5.1 Calculation of Deformation Gradient Tensors

As shown in Figure 2, the diastolic deformation gradient F_a, the systolic deformation gradient F_B and the relative deformation gradient F_ab in CSYSI are defined through:

$${\mathit{F}}_{\mathit{a}}=\frac{\partial {\mathit{x}}_{\mathit{a}}}{\partial {\mathbf{X}}_{\mathbf{0}}},{\mathit{F}}_{\mathit{B}}=\frac{\partial {\mathit{x}}_{\mathit{b}}}{\partial {\mathit{X}}_{\mathbf{0}}},{\mathit{F}}_{\mathit{a}\mathit{b}}=\frac{\partial {\mathit{x}}_{\mathit{b}}}{\partial {\mathit{x}}_{\mathit{a}}}$$ (4)

where X₀, x_a and x_b are coordinate vectors of the unloaded, diastolic and systolic configurations respectively, which are defined in CSYSI. Similarly, the deformation tensors Ṽ_a, F̃_ab, F̃_b, are measured in CSYSII.

2.5.2 Obtaining the Diastolic Deformation Gradient using the Corotational Frame

Given the diastolic Cauchy stress, we need to first inversely compute the diastolic deformation gradient F_a in order to obtain the systolic deformation gradient. The main challenge came from the fact that the symmetric Cauchy stress tensor has only 6 independent components, which makes it impossible to get a unique solution of the diastolic deformation gradient F_a that has 9 independent components. To solve this issue, taking advantage of the material objectivity [30, 31], we have the following restriction on the constitutive function h using the corotational frame

$${\mathbf{\sigma }}_{\mathit{a}}={\mathit{R}}_{\mathit{a}}{\stackrel{\sim }{\mathit{\sigma }}}_{\mathit{a}}{\mathit{R}}_{\mathit{a}}^T=\mathrm{h}({\mathit{F}}_{\mathit{a}})={\mathit{R}}_{\mathit{a}}h({\stackrel{\sim }{\mathit{V}}}_{\mathit{a}}){\mathit{R}}_{\mathit{a}}^T$$ (5)

where σ̃_a is the diastolic Cauchy stress observed in CSYSII. Instead of fully computing the deformation gradient F_a, knowing the σ̃_a, the only quantity we need to explicitly derive is the left stretch tensor Ṽ_a in CSYSII (the value of Ṽ_a is equal to U_a in CSYSI, ${\mathit{Ṽ}}_{\mathit{a}}={\mathit{R}}_{\mathit{a}}^{-1}{\mathit{V}}_{\mathit{a}}{\mathit{R}}_{\mathit{a}}={\mathit{R}}_{\mathit{a}}^{-1}{\mathit{F}}_{\mathit{a}}={\mathit{U}}_{\mathit{a}}$). According to the chain rule, we can arrive at the relation among the deformation gradients:

$${\stackrel{\sim }{\mathit{F}}}_{\mathit{b}}={\stackrel{\sim }{\mathit{F}}}_{\mathit{a}\mathit{b}}{\stackrel{\sim }{\mathit{V}}}_{\mathit{a}}$$ (6)

where F̃_ab is known. As a result, the systolic Cauchy stress σ̃_b can be correctly recovered in CSYSII.

2.5.3 Inverse Computation of Diastolic Left Stretch Tensor

On account of the nature of strain energy function Ψ(F), i.e. σ is always expressed in terms of deformation in a forward computation, given a deformation gradient, the Cauchy stress of a hyperelastic material can be calculated using [32]

$$\mathit{\sigma }={\mathit{\sigma }}_{\mathit{\text{vol}}}+{\mathit{\sigma }}_{\mathit{\text{iso}}}=p\mathit{I}+J^{-1}\overline{\mathit{F}}\mathit{\text{Dev}}(\overline{\mathit{S}}){\overline{\mathit{F}}}^T$$ (7)

where σ_vol and σ_iso denotes the volumetric and isochoric contribution respectively, p is the hydrostatic pressure p = dΨ_vol(J)/dJ, I is identity. F̄ is the modified deformation gradient calculated by F̄ = J^−1/3F. S̄ can be expressed by S̄ = 2∂Ψ_iso (C̄)/∂C̄ and Dev(■) = (■) − (1/3)[(■):C]C⁻¹, where the modified right Cauchy-Green deformation tensor C̄ = J^−2/3 C. For fixed constitutive parameters, the stress σ is essentially a function of F. If a deformation does not have rotation, we can also compute σ using the above formulations by substituting F with left stretch tensor V.

An inverse computation scheme was introduced to compute the diastolic left stretch tensor Ṽ_a in the CSYSII. Nonlinear least square optimization was used for the computation of Ṽ_a, with 6 unknowns and as many as the number of equations. The objective function was defined by

$$f_{\mathit{\text{err}}}={\sum }_{i=1}^6{[{\stackrel{\sim }{\sigma }}_{a,i}-{\stackrel{\sim }{\sigma }}_{a,i}^{\mathit{\text{est}}}({\overline{\mathit{V}}}_{\mathit{a}})]}^2$$ (8)

where the stress tensor is represented in Voigt notation. ${\stackrel{\sim }{\sigma }}_{a,i}^{\mathit{\text{est}}}$ represents the components of estimated diastolic stress computed using a guess of Ṽ_a. The trust region algorithm is used and gradients are estimated using finite differences. The optimization was implemented in MATLAB (Mathworks, MA), and a numerical validation was performed in Section 3.2.

2.6 Implementation of the Parameter Estimation

The finite element simulations were performed in ABAQUS/Standard 6.14 using the 3D brick element C3D8. Since the stress of each integration point in an element outputted from ABAQUS is in the local coordinate system associated with the element, the local coordinate system of the output diastolic stress σ̃_a of the element is defined as CSYSII. The systolic stress of the same element output from ABAQUS was converted to σ̃_b in CSYSII. Here, the infinitesimal finite element method was used to obtain σ̃_a and σ̃_b at the two phases. For convenience, displacement u_ab was applied as a boundary condition at every node in ABAQUS to obtain the relative deformation gradient, which is output and converted to F̃_ab in CSYSII.

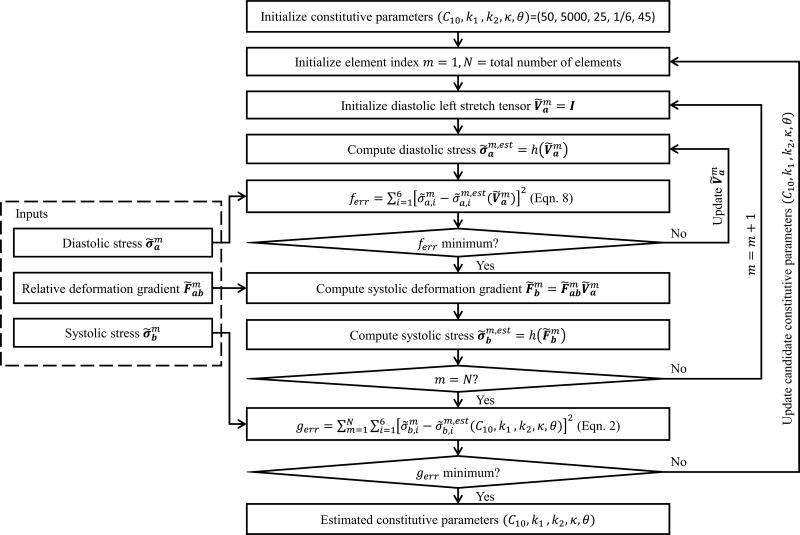
The work flow of the parameter estimation process is depicted in Figure 3. The inner loop is responsible for the inverse calculation of the left stretch tensor Ṽ_a at each element, the second loop is repeated for all of the elements, and the outer loop updates candidate material parameters in each iteration. The method was implemented in MATLAB. We used the finite difference and trust-region-reflective algorithm for the optimization, which is “lsqnonlin” in MATLAB.

Figure 3.

Implementation of the constitutive parameter estimation.

3. Numerical Validations

The approach was validated by numerical experiments. Clinical cardiac CT image data at the systolic phase (assuming 120mmHg systolic pressure) from four de-identified patients with ascending aortic aneurysms (AsAA) were chosen for the verification, whose “true” constitutive parameters were extracted from 7-protocol biaxial tensile tests in a previous study [33] by nonlinear regression. The “true” material parameters are within the upper and lower bounds, which are also comparable to other testing results [34–36]. The initial value, upper and lower bounds of the constitutive parameters are shown in Table 1.

Table 1.

Initial value, upper and lower bounds of constitutive parameters.

	C10 (kPa)	k1(kPa)	k2	κ	θ(°)
Initial	50	5000	25	1/6	45
Lower bound	0	0	0	0	0
Upper bound	100	10000	50	1/3	90

The geometries of the aorta were reconstructed by using the semi-automatic method developed in our previous study [37]. For simplicity, the branches at the aortic arch were trimmed. We used the following methods to numerically obtain the “true” geometries and stress fields at the diastolic and systolic phases. We assigned experimentally derived material parameters [33] to the corresponding geometries. From CT image data, the unloaded geometries were recovered by the backward displacement method [38], and they were assumed to have a constant wall thickness of 2 mm [17]. The “true” diastolic and systolic geometries were obtained from FE simulations by applying diastolic (P=80mmHg) and systolic (P=120mmHg) pressures on the unloaded geometries. Thus, this only represents an idealized situation where the influence of residual stress is not present in the numerically generated data. Each finite element mesh consists of 10,000 nodes and 4950 elements. Mesh convergence analysis was performed in our previous work [17], and the number of elements is adequate for accurate stress predictions. Mesh correspondence at the two phases was automatically established because the two meshes at the two phases were deformed from the same mesh at the unloaded state.

In all FE simulations, constant pressures were applied uniformly to the inner surface of the FE models, and the boundary nodes of the models, i.e. the proximal and distal ends of the models, were constrained to only allow displacement in the radial direction in the local cylindrical coordinate system. The centerline of the aorta was estimated to define the longitudinal direction of the local coordinate system, and the radial direction was computed using the outward normal direction of the outer surface of the aorta. The local coordinate system followed the average rotation of the element [30], the stress of an element was outputted in the rotated coordinate system. In the parameter estimation procedure, five layers of elements adjacent to the mesh boundaries were excluded in order to avoid the boundary layer phenomenon [26]: the influence of material properties is pronounced only in a thin layer near the fixed edge; and the stress approaches asymptotically a static solution outside the boundary layer.

3.1 “Almost-true” Stress Computation

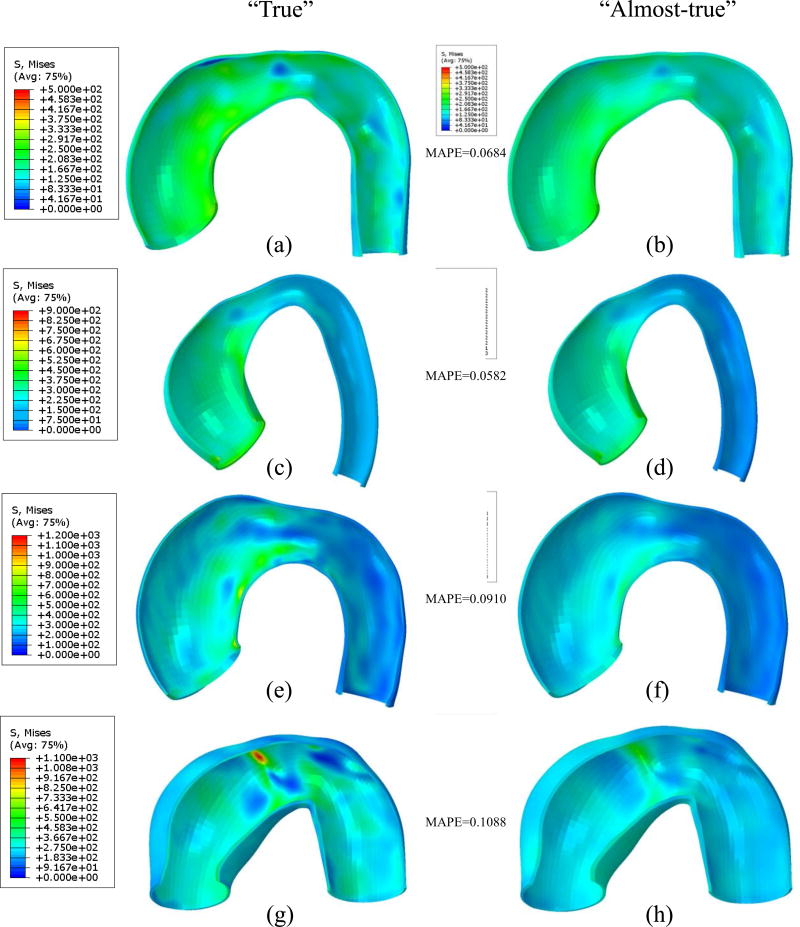
We compared the “true” stress field computed from nonlinear finite deformation FE with “true” material parameters, to the “almost-true” stress field computed from infinitesimal linear elastic FE with a stiff material (E = 2 × 10⁴ GPa and ν = 0.49) under the same loading conditions. As shown in Figure 4, for each FE method, the scalar-valued Von Mises stress field was visualized at the pressure level of 120mmHg. Mean absolute percentage error (MAPE) was calculated for each patient (named as AsAA1, AsAA2, AsAA3, and AssAA4), which is in the range of 6% ~ 10%. The results demonstrate that the simple linear elastic FE can produce the “almost-true” stress field within 10% of the “true” values.

Figure 4.

Comparison of Von Mises stress computed using nonlinear finite deformation FE (a), (c), (e) and (g) and that computed from infinitesimal linear elastic FE (b), (d), (f) and (h). Pressure = 120mmHg. Mean absolute percentage error (MAPE) for patient geometry AsAA1 ((a)&(b)), AsAA2 ((c)&(d)), AsAA3 ((e)&(f)) and AsAA4 ((g)&(h)) is obtained by taking the nonlinear FE computed stress as “true” value.

3.2 Inverse Computation of Diastolic Left Stretch Tensor

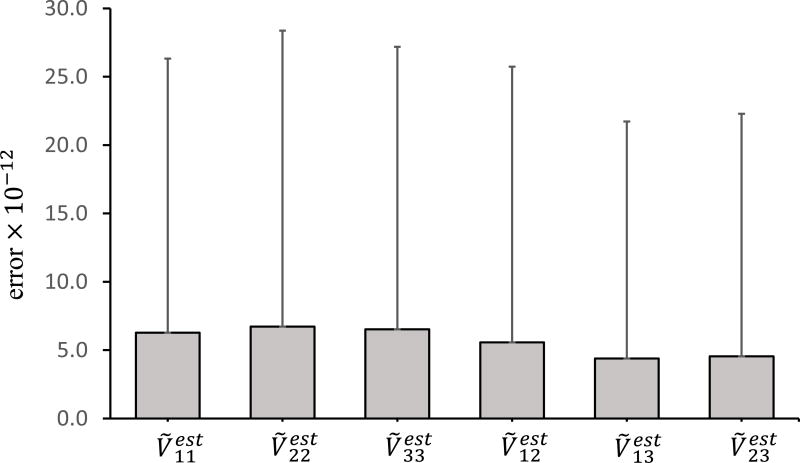
The validation for the inverse computation of Ṽ_a was performed by using randomly generated F_a and the “true” material parameters of patient AsAA2 (see the Appendix for the method to randomly generate F_a). For the given set of constitutive parameters, the Cauchy stress σ_a = h(F_a) was computed and rotated to σ̃_a in CSYSII (Figure 2). The “true” ${\mathit{Ṽ}}_{\mathit{a}}={\mathit{R}}_{\mathit{a}}^T{\mathit{V}}_{\mathit{a}}{\mathit{R}}_{\mathit{a}}$ was computed by using polar decomposition and coordinate transformation of F_a. Using the inverse computation scheme from Section 2.5.3, we estimated the Cauchy stress and left stretch tensor in CSYSII ${\stackrel{\sim }{\mathit{\sigma }}}_{\mathit{a}}^{\mathit{\text{est}}}=\mathrm{h}({\mathit{Ṽ}}_{\mathit{a}}^{\mathit{\text{est}}})$. The mean errors between the components of the estimated ${\mathit{Ṽ}}_{\mathit{a}}^{\mathit{\text{est}}}$ and “true” Ṽ_a were calculated. The procedure was implemented in MATLAB, and it was repeated for numerous randomly generated F_a. As shown in Figure 5, the result demonstrated that the error of the estimated left stretch tensor was negligible, and the optimization algorithm worked well for the inverse computation.

Figure 5.

Validation of the inverse computation of left stretch tensor Ṽ_a using the constitutive parameters of patient AsAA2 (C₁₀, k₁, k₂, k, θ) = (29.91, 512.56, 0.00, 0.3190, 90.00). The error is calculated by comparing the estimated ${\mathit{Ṽ}}_{\mathit{a}}^{\mathit{\text{est}}}$ with “true” Ṽ_a, the error bars represent the standard deviations.

3.3 Constitutive Parameters Estimation of Ascending Aortic Aneurysms

We applied the method to estimate the material parameters of the four patients (AsAA1, AsAA2, AsAA3, and AsAA4). To evaluate the estimation results, in MATLAB, we simulated biaxial tensile stretches of 3 protocols using the estimated parameters and the “true” parameters, and the stresses and stretches in the circumferential and longitudinal directions were compared. σ₁ and λ₁ denote the circumferential stress and stretch. σ₂ and λ₂ denote the longitudinal stress and stretch. For each patient, we obtained σ₁ and σ₂ using the following 3 protocols: (1) in the circumferential strip biaxial tension, we fixed λ₂ = 0 while increasing λ₁; (2) in the equi-biaxial tension, we kept the ratio λ₁/λ₂ = 1 ; (3) in the longitudinal strip biaxial tension, we fixed λ₁ = 0 while increasing λ₂.

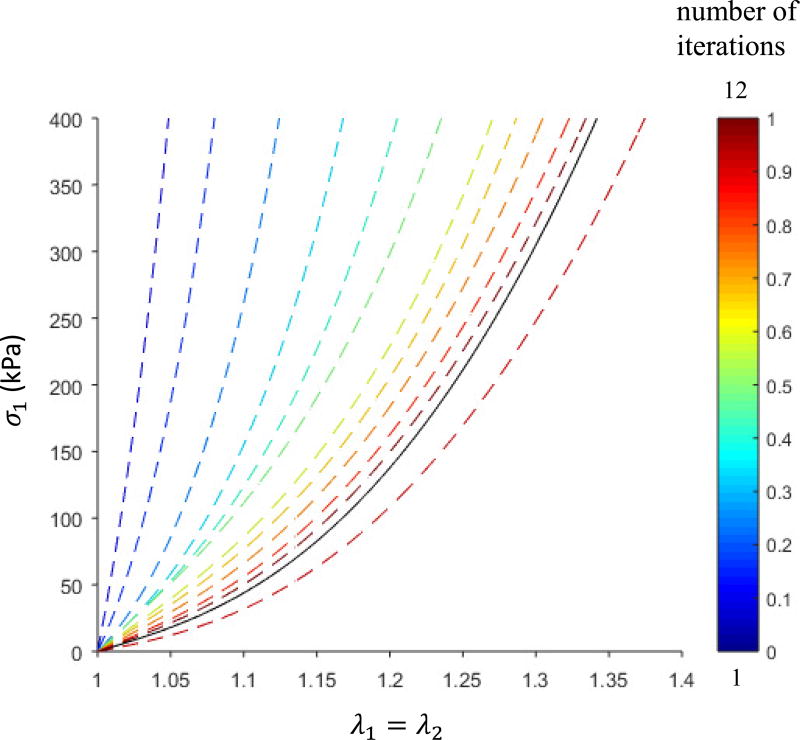
During the optimization process, the parameters were converged in iterations from the initial values toward the optimal values. An example from patient AsAA2 is shown in Figure 6. The optimization started from a set of initial parameters representing a very stiff material, and gradually the stretch-stress curves converged and approached to the “true” curve.

Figure 6.

Equi-biaxial stretch-stress curves show the convergence of the optimization for AsAA2. The solid black line is the “true” curve, and the dashed curves correspond to the estimated parameters in each iteration. Stress in the circumferential direction is plotted.

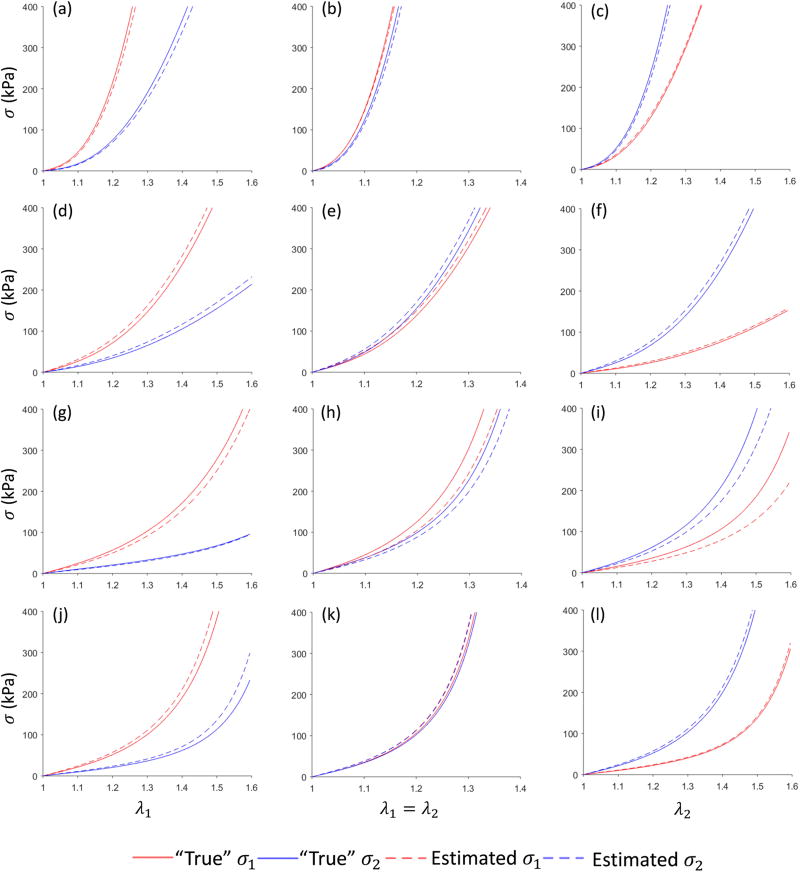
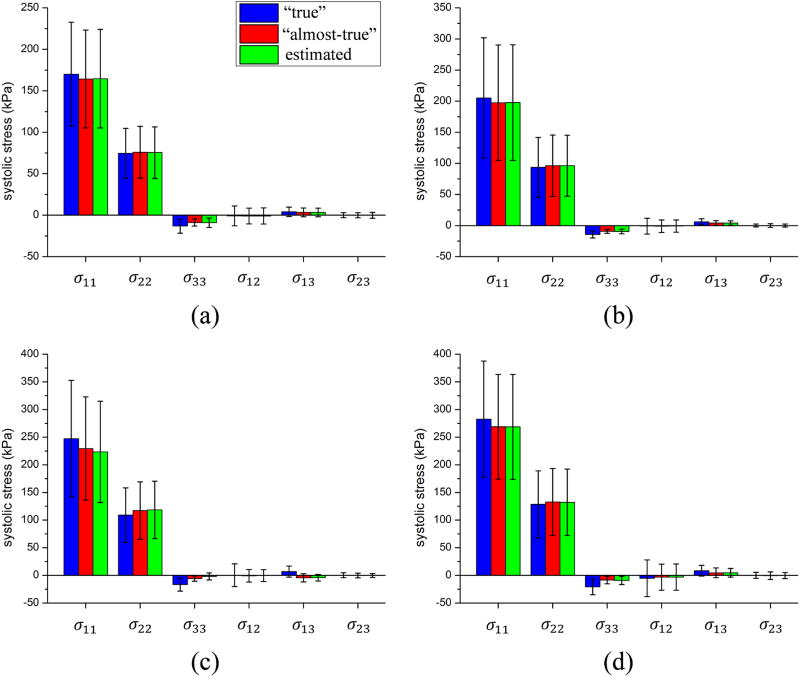
After running the parameter estimation procedure for each patient, the estimated material parameters were compared with the “true” parameters, and the result is shown in Table 2, which demonstrated that the estimated parameters have good agreement with the “true” values, except θ. To evaluate how the difference between the estimated and the “true” parameters affects stress and stretch, we plotted the stretch-stress curves from numerical experiments in Figure 7. The coefficient of determination was calculated to measure the discrepancy between the estimated and “true” curves for each patient, as shown in Table 3. The mean and standard deviation of the systolic stresses are shown in Figure 8. Close agreements can be clearly seen. In addition, it was observed that the stress in the circumferential direction was largest in all cases and approximately twice the longitudinal stress; the stress across the thickness and the shear stress were relatively small.

Table 2.

“True” and estimated constitutive parameters of the four patients.

Patient		C10 (kPa)	k1(kPa)	k2	κ	θ(°)
AsAA1	“True”	22.91	3622.72	0.00	0.3216	0.00
	Estimated	10.57	3001.25	1.12	0.3079	35.60
AsAA2	“True”	29.91	512.56	0.00	0.3190	90.00
	Estimated	33.52	512.32	0.01	0.3160	86.82
AsAA3	“True”	28.82	222.76	4.37	0.2935	0.00
	Estimated	24.23	196.47	3.67	0.2933	22.79
AsAA4	“True”	25.41	285.19	11.19	0.3284	0.00
	Estimated	28.42	287.96	12.15	0.3260	40.37

Figure 7.

Stretch-stress curves in 3-protocol numerical stretch-controlled tensile experiments for (1) strip biaxial tension in the circumferential direction (a), (d), (g) and (j); (2) equi-biaxial tension (b), (e), (h) and (k); (3) strip biaxial tension in the longitudinal direction (c) (f) (i) and (l). The comparison of “true” and estimated curves for one patient is in the same row, i.e., (a)(b)(c) for AsAA1, (d)(e)(f) for AsAA2, (g)(h)(i) for AsAA3, (j), (k)(l) for AsAA4.

Table 3.

Coefficient of determination in the stretch-stress curves for the four patients.

Patient	R2 in protocol 1		R2 in protocol 2		R2 in protocol 3
	σ1	σ2	σ1	σ2	σ1	σ2
AsAA1	0.987	0.987	0.998	0.988	0.998	0.990
AsAA2	0.981	0.973	0.989	0.981	0.992	0.985
AsAA3	0.974	0.995	0.908	0.959	0.781	0.920
AsAA4	0.968	0.891	0.983	0.967	0.997	0.989

Figure 8.

Comparison of “true”, “almost-true” (i.e. computed from infinitesimal FE), and estimated systolic stress from optimization for patient (a) AsAA1, (b) AsAA2, (c) AsAA3 and (d) AsAA4. The error bars represent the standard deviation.

The parameter estimation program was run on a desktop computer with quad-core CPU and 32 GB RAM. Table 4 shows the computing time cost for each patient. All of the computations were done within 2 hours, much faster than other methods reported in the literature [7, 8].

Table 4.

Time spent for the parameter estimation for each patient.

	AsAA1	AsAA2	AsAA3	AsAA4
Time cost(min)	56	104	117	84

4. Discussion

In this study, we presented a novel inverse method that can estimate the in vivo material properties of the aortic wall in a fast manner. The method utilized the fact that infinitesimal FE simulations can be used to estimate the in vivo stress distributions of the loaded aortic wall, provided the in vivo geometry and loading conditions of the aortic wall are known. We built an objective function (Eq.2) directly from the constitutive equations to iteratively search for the optimal material parameters. The accuracy of the method was validated by using four AsAA patient data. The constitutive parameters and the aortic wall material responses have been successfully recovered. The largest error can be observed in the constitutive parameter θ, describing the local fiber mean direction, which is possibly caused by the fact that the parameter κ derived from biaxial experiment is close to 1/3 (isotropic), and therefore θ does not affect the stress computation.

This approach is much less computationally expensive (1–2 hours) than the iterative FE simulation based approach [7, 8] (1–2 weeks), because It avoids solving finite element problems iteratively. We defined the objective f_err and g_err in terms of stress, and the analytical expression of the Jacobian (i.e. derivative of the objective function with respect to constitutive parameters) exists, which means the Jacobian can be well approximated by finite difference. This probably helps the optimization to converge in a relatively small number of iterations, e.g., 12 iterations for patient AsAA2.

In general, the constitutive parameter optimization problem is nonlinear, multivariate and non-convex; and such a problem may exhibit several local optima. Jacobian-based optimization methods (e.g. the method used in this approach) may not guarantee a global optimum as shown by the difference in parameters in Table 2. However, using the sub-optimal parameters, we obtained very good material responses and wall stress distributions compared to the “true” values, and therefore the suboptimal parameters are indeed acceptable. Optimization using many initial guesses may improve the results, but it will lead to a much longer computing time.

The difference between the “true” stress field computed from nonlinear finite deformation FE and the “almost-true” stress field computed from infinitesimal linear elastic FE is clearly visible in Figures 4 and Figure 8. This discrepancy probably came from the boundary effects [26]. The restricted boundary nodes limited the longitudinal deformation of the aorta model. Although the “almost-true” stress alone can be used in many applications, such as using the stress-based rupture potential index as an aneurysm rupture risk predictor [39], different tissue damage and failure models exist such as accumulated energy [40, 41], stretch based criterion [42] and distensibility [43] which rely on the deformation and thus depend on patient-specific material properties. Previous works in our group [17] showed that the failure pressure of ascending aortic aneurysm was much higher than the measured systolic pressure, and the failure behavior of the aorta were highly correlated with material properties. Thus, patient-specific material properties enable the analysis of the wall stress at various loading and deformation conditions that cannot be recorded by in vivo imaging.

Motion tracking using ultrasound images (known as speckle tracking) has been applied for left-ventricle (LV) motion analysis and strain measurement. The 2D+t (2-dimension plus time) speckle tracking was validated using a rabbit heart model and a simulated heart which shows an average strain error of 0.08% [44]. Automatic algorithms [45–50] for 3D+t LV segmentation and tracking using ultrasound images have been developed over the last eight years. As for ultrasound speckle tracking of vessel wall, Larsson, et al. [51] performed validation experiments, in which crystal markers were implanted on the artery wall in order to obtain the “ground truth” strain measurement. 3D+t ultrasound speckle tracking has been applied to study aortic wall strain of healthy and abdominal aortic aneurysms patients in vivo by Karatolios, et al. [52]. By using this method to obtain in vivo strain measurement, Wittek et al. [7, 8] developed the FE updating approach for in vivo material parameter estimation. For clinical applications, fully automatic segmentation and speckle tracking algorithms for the aortic wall are needed, which can be developed based on the algorithms for LV segmentation and tracking.

The unloaded configuration was assumed to be stress-free in this approach, and thus residual strain and stress was ignored, which is a limitation of this study. Several methods have been developed to incorporate residual stress into patient-specific modeling [53–55]. The circumferential residual stress mainly affects the hoop stress distribution, which homogenizes the hoop stress field (i.e., decreasing stress in the inner layer, and increasing stress in the outer layer). Our approach aims for the averaged (homogeneous) constitutive behavior across the thickness direction. To account for the residual stress, typically a three-layer residual stress model [53] (intima, media, adventitia) should be used with layer-specific material properties and geometrical parameters, which was not the setup for our study. Without taking into account of the circumferential residual stress, we may overestimate the inner layer stress and underestimate the outer layer stress. However, the assumption of static determinacy requires a thin wall structure, in which the stress is assumed to be nearly constant over the wall thickness. In addition, as suggested by Labrosse et al. [56], whether account for the residual stress or not did not appreciably affect the material constant estimation. For the FE studies of abdominal aorta, the longitudinal pre-stretch is often prescribed as a boundary condition (BC) by an age- or gender- match as suggested by Horny et al [57]. For the abdominal aorta, the BC can be relatively easily applied to the “tubular” geometry. However, for the ascending aorta, there are limited data on the longitudinal pre-stretch of humans in the literature. For a mouse model study [58], the longitudinal pre-stretch is about 1.1~1.2 for the ascending and proximal thoracic aorta, compared to a high value of 1.6 in the abdominal aorta. Furthermore, as the geometry of the ascending aorta is actually a “curved tube”, the direction in which the force or displacement BC should be applied is unknown, and we have tried to apply such BCs (with random directions) but got severe FE convergence problems. Also, the pre-stretch would introduce another unknown, which will make the static determinacy of the aorta questionable. Due to these considerations and difficulties, we did not incorporate residual stress in the current approach.

In clinical applications, the thickness of aortic wall is measurable. It has been reported that the wall thickness of the abdominal aorta could be measured by using CT [20–22], MR[23] and ultrasound [24, 25] imaging techniques. It is challenging to measure the thickness of the ascending aorta because of the surrounding tissue and partial volume effect. By combining CT and MR as did in [28], it is feasible to approximately measure the wall thickness of the ascending aorta. Our future work will test the approach in a real case which will incorporate the wall thickness measurement. Typically, in a forward analysis, a constant wall thickness of the unloaded state is assumed, whereas in our inverse approach, the wall thicknesses of the in vivo loaded states is needed. In our verification, a constant wall thickness of the unloaded configuration was assumed, and thus the numerically generated data contained the heterogeneous wall thickness. By assuming the aortic wall is statically determinant, even if the thickness is unknown, the wall tension can be reliably computed [28]. Thus, by assuming a constant wall thickness, the tension field is essentially the stress filed multiplied by a factor. Therefore, we hypothesize that it might be possible to build the optimization approach upon the tension field instead of the stress field in the objective function, which then does not need the wall thickness. Heterogeneous wall thickness may have a significant impact on the wall stress distribution, making it different from the wall tension field. Hence, verifications are needed to ensure the validity of constant wall thickness assumption, which will be our future work.

For the convenience of numerical validation, only the homogenous constitutive behavior was studied in this paper. The approach can be extended to heterogeneous thickness and constitutive parameters by slightly altering the work flow, i.e., evaluating one objective function g_err for one element or one group of elements at a time. In the numerical validations, the backward displacement method [38] was used to recover the unpressurised geometries for generating “true” diastolic and systolic geometries. The unpressurised geometries can also be obtained by using other approaches [59–62].

5. Conclusion

We proposed a fast and effective method for constitutive parameter estimation of the aortic wall by using the in vivo loaded geometries at 2 cardiac phases with known blood pressures. For each patient, the method only needs to run infinitesimal linear elastic FE simulations twice to obtain the stress fields at the 2 cardiac phases, and the rest of the computation can be run in MATLAB. The inverse computation is mainly dependent on solving nonlinear constitutive equations and optimization algorithms. Good agreement has been achieved between the estimated and “true” material parameters in the numerical verification. The method can be applied to estimate in vivo material properties of the aortic wall in applications, such as the AsAA rupture risk analysis.

Appendix

The Method to Randomly Generate Deformation Gradient F_a

The following steps were used to generate a random F_a: 1) the in-plane principle stretches λ₁ and λ₂ were randomly sampled in the range [1, 1.6], 2) the out-of-plane principle stretch λ₃ was randomly sampled in the range determined by the constraint that λ₁λ₂λ₃ is in the range of [0.9, 1.1], 3) orthogonal basis N_k (k = 1,2,3) was also randomly generated, 4) U_a was assembled as ${\mathit{U}}_{\mathit{a}}={\sum }_{k=1}^3{\lambda }_k{\mathit{N}}_{\mathit{k}}$, 5) An orthogonal rotation tenor R_a was randomly generated, and finally 6) we obtained a random F_a by using F_a = R_aU_a.