The demography of words: the global decline of non-numeric fertility preferences, 1996–2011

Abstract

This paper examines the decline in non-numeric responses to questions about fertility preferences among women in the developing world. These types of responses—such as “don’t know” or “it’s up to God”—have often been interpreted through the lens of fertility transition theory as an indication that reproduction has not yet entered women’s “calculus of conscious choice” (Coale 1973, p. 65), but have yet to be investigated cross-nationally and over time. Using 19 years of data from 32 countries, we find that non-numeric fertility preferences appear to decline most substantially in the early stages of a country’s fertility transition. Using country-specific and multilevel models, we explore the individual- and contextual-level characteristics that are associated with women’s likelihood of providing non-numeric responses to questions about their fertility preferences. Non-numeric fertility preferences are influenced by a host of social factors, with educational attainment and knowledge of contraception being the most robust and consistent predictors.

Introduction

When women are asked how many children they would want to have under ideal conditions, they sometimes provide answers using words rather than numbers, such as “it’s up to God,” “as many as possible,” or simply, “I don’t know.” Such non-numeric answers to questions about ideal family size (IFS) have long captivated researchers studying the cultural and developmental processes underlying fertility change (e.g., Caldwell 1976; Morgan 1982; Olaleye 1993; Hayford and Agadjanian 2011; Castle 2001) and have played a central role in classical theories of the fertility transition (Coale 1973; van de Walle 1992). Yet despite general consensus that non-numeric responses are meaningful, demographers’ understanding of how they cohere with broader fertility paradigms remains limited. Using over 90 surveys that span 19 years and 3 world regions, this article provides the first comprehensive analysis of non-numeric responses to the ideal family size question. Combining a detailed examination of aggregate-level trends in fertility rates and non-numeric IFS with a multi-pronged investigation into the correlates of these types of responses among individual women, our results provide insights into the demographic and social processes underlying non-numeric fertility preferences across much of the developing world.

Our analysis centered on three research questions. First, we asked: What countries and regions have the highest levels of non-numeric response, and how has the prevalence of non-numeric IFS changed over time? We harnessed the full analytic potential of the Demographic and Health Surveys to describe geographic and temporal trends in non-numeric fertility preferences.

Second, we built on fertility transition theory to ask: To what extent do aggregate-level patterns of non-numeric responses cohere with patterns of national fertility rates? Non-numeric IFS responses are typically conceptualized in relation to Coale’s pre-conditions of fertility decline, specifically that fertility reductions happen when childbearing decisions enter the “calculus of conscious choice” (Coale 1973, p. 65). When survey questions about IFS yield high levels of non-numeric responses, demographers often assume that a country has not yet entered the fertility transition (Caldwell 1976; Castle 2001). A decline in non-numeric IFS has been said to foreshadow widespread fertility decline within countries – that is, fertility is expected to fall shortly after women develop a numeric understanding of their fertility (van de Walle 1992). Yet the relationship between these types of responses and cross-national fertility trends has not yet been examined empirically. We compared aggregate patterns and trends in the total fertility rate (TFR) and non-numeric IFS and investigated whether the timing of fertility transitions is related to country-level changes in non-numeric IFS.

Third, moving from aggregate trends to individual-level responses, we asked: What individual- and contextual-level characteristics are associated with women providing a non-numeric response to the IFS question? According to demographic transition theory, women who provide non-numeric IFS responses approach their fertility from a “pre-transition mindset” rather than envisioning and pursuing a particular family form (van de Walle 1992), and this mindset is thought to be related to a lack of awareness that fertility can be intentionally controlled (Coale 1973; Johnson-Hanks 2007). A small body of research has found that non-numeric IFS responses are associated with low educational attainment (McCarthy and Oni 1987; Riley et al. 1993) and uncertainty stemming from high mortality (LeGrand, Koppenhaver, Mondain, and Randall 2003; Sandberg 2005; Hayford and Agadjanian 2011). However, this literature is limited to cross-sectional analyses with narrow geographic coverage, and thus we know little about what experiences and characteristics are most salient in predicting non-numeric responses to this question. Using both country-specific and multilevel regression models, we examined several individual and contextual factors that previous research suggests might be associated with non-numeric IFS responses. We organized this part of our analysis around three theoretical perspectives that other scholars have used to understand nonnumeric IFS: perceived ability to limit family size, exposure to formal schooling, and mortality-related uncertainty.

Previous Research on Non-Numeric Ideal Family Size

Before describing our data and methodological approach, we introduce the central theoretical paradigms and empirical findings from previous research related to non-numeric fertility preferences. We outline the roles that non-numeric IFS responses have played in fertility transition theories. This research motivates how we approached our second research question. Next, we outline previous research that has examined the attributes and experiences that predict whether individual women provide a non-numeric IFS response. This research motivates a set of alternative theoretical perspectives that we examine in the third stage of our analysis.

Non-numeric IFS and the Fertility Transition

The fertility transition refers to a shift from a fertility regime characterized by an absence of parity-specific control to a system of deliberate family size limitation (Henry 1961; Knodel 1977, 1979). The onset of this shift is typically defined as a net ten percent reduction in a country’s TFR; once this threshold has been crossed, no country has ever recovered to pre-transition fertility levels (Bongaarts and Casterline 2013; Dyson and Murphy 1985; Kirk 1996; Knodel 1977).

Scholarly interest in the fertility transition has often centered on cognitive orientations and culturally-mediated systems of ideals and aspirations around childbearing (Cleland and Wilson 1987; Hammel 1990; Mason 1992; Bongaarts and Watkins 1996; Bachrach 2013). This research focuses on variation across time and space in whether these systems of meaning construe fertility as requiring careful planning and management or, alternatively, as something that unfolds inevitably (Cleland and Wilson 1987; Hammel 1990; Mason 1992; Bongaarts and Watkins 1996; Bachrach 2013). To these scholars, non-numeric IFS responses are particularly pertinent as these responses may suggest an alternate perspective according to which childbearing cannot (or should not) be conceptualized in quantitative terms (Coale 1973; Caldwell 1976; Castle 2001; Hayford and Agadjanian 2011). Indeed, Caldwell (1976) explicitly acknowledges that in high-fertility countries, “up to God” and “don’t know” responses to IFS questions are likely more truthful than numeric responses, as pronatalist cultural norms engender preferences for “many” children rather than encouraging women to select a specific number as their ideal (Jensen 1985; Olaleye 1993).

Some scholars view the onset of the fertility transition as an indication that women have begun to construct specific plans for childbearing; from this perspective, non-numeric responses are an indication of women’s perceived lack of control over their fertility and a sign that the transition has not yet begun (Caldwell 1976; Morgan 1982; van de Walle 1992; Hayford and Agadjanian 2011). Van de Walle (1992, p. 501) finds that a numeric understanding of fertility was absent from pre-transition European populations and predicts that a decline in non-numeric IFS will immediately precede the onset of a country’s fertility transition, writing, “I hypothesize that numeracy about children and the norm of an ideal family size appear not long before the fertility transition. Fertility decline is not far away when people start conceptualizing their family size, and it cannot take place without such conceptualizing.” Critics of this perspective claim that women in high-fertility settings do think numerically and deliberately about childbearing, and interpret non-numeric IFS as revealing a disinclination to verbalize these conceptions, either due to discomfort with the interview setting (Olaleye 1993) or to concern about the supernatural risks such statements might incite (Castle 2001). According to these alternative perspectives, a decline in non-numeric IFS would not be expected to regularly occur shortly before the onset of the fertility transition.

The Correlates of Non-Numeric IFS Response Among Individual Women

We focused our analysis of the individual- and contextual-level predictors of non-numeric fertility preferences around three theoretical perspectives: perceived ability to limit family size, a woman’s exposure to formal schooling, and mortality-related uncertainty. These perspectives are complementary rather than competing, and offer a set of theoretically motivated alternative explanations that guided our investigation into the factors associated with women offering words rather than numbers when describing their IFS.

Perceived Ability to Limit Family Size

Coale’s (1973) seminal treatise posits that fertility will fall only when people are aware that family size can be the subject of intentionality and choice, are knowledgeable about methods of fertility limitation, and are convinced of the advantages of smaller families. This triumvirate sparked a wellspring of “ideational” theories of fertility change, which, unlike those emphasizing “structural” factors, centered around changing knowledge and attitudes about future fertility (Cleland and Wilson 1987; Mason 1992). Some scholars have suggested that Coale’s preconditions are interrelated: awareness of new contraceptive technologies can awaken a “latent demand” for small families through the realization that fertility can be consciously controlled (Easterlin and Crimmins 1985; van de Walle 1992; Freedman 1997). Ideational theorists have also championed the idea that women may not want to limit their fertility until they see others doing so, articulating fertility decline as a process of social diffusion (Montgomery and Casterline 1993; Rosero-Bixby and Casterline 1993; Bongaarts and Watkins 1996; Casterline et al. 2001; Cleland 2001b;).

Considerable empirical support exists for ideational theories. Evidence from rural Pakistan, where a majority of women express non-numeric IFS, suggests that women who are familiar with a modern method of contraception are more likely to express a desire to limit their fertility (Mahmood and Ringheim 1997). In Kenya, messages promoted by the international family planning movement, interpreted through local discussions and debates, led to the increasingly widespread belief that fertility control is “a legitimate choice” (Watkins 2000). In Ghana, women were more likely to express a desire to limit childbearing if their communities received an experimental intervention that introduced women to modern methods of contraception (Debpuur et al. 2003). Likewise, participation in family planning through the use of contraception signals that women are managing their reproductive futures. Unsurprisingly, use of contraception has been linked to the desire to stop childbearing in a variety of pre- and post-transition societies (Westoff 1990). Together, this research suggests that as women become aware of methods enabling them to control their fertility, and as they see other women limiting their childbearing, women will begin to think of their own family size as something to approach with a numeric mindset (Coale 1973; Rosero-Bixby and Casterline 1993; Hayford and Agadjanian 2011). Given these findings, we expected that knowledge of modern contraception, ever use of contraception, and contextual-level TFR would be negatively associated with non-numeric IFS responses.

Formal Education

Across contexts, educated women report smaller IFS, though the magnitude of this association varies widely across world regions (Martin 1995; Cleland 2002; Bongaarts 2003). Recent research from Malawi documents this relationship using longitudinal data and shows that when women attend an additional year of school, they reduce their IFS (Yeatman, Sennott, and Culpepper 2013). Additionally, evidence from Costa Rica and Mozambique show that educated women are more likely to respond numerically to IFS questions (Riley et al. 1993; Hayford and Agadjanian 2011).

The mechanisms through which education influences fertility preferences are contested (Basu 2002; Martin 1995). Some scholars suggest that education provides women with mathematical and conceptual knowledge necessary to numerically state their fertility preferences (Levine et al. 1994; Diamond, Newby, and Varle 1999). An alternative perspective posits that the effect of schooling is cultural rather than academic: schools transmit Western values emphasizing nuclear families and intensive investment in children, leading to preferences for smaller families and more conscious deliberation about the issue of ideal family size (Caldwell et al. 1985; Caldwell and Caldwell 1987; Thornton 2001, 2013). Others suggest that population-level increases in educational attainment result in quality-quantity economic tradeoffs that favor smaller families, leading women to shift their fertility goals from maximization to limitation (Becker and Lewis 1973; Becker 1991). While it was beyond the scope of this article to identify which mechanism links education with numeric IFS responses, this research collectively suggests that exposure to formal schooling would be negatively associated with non-numeric IFS responses.

Mortality-Related Uncertainty

A growing body of literature, particularly focused on sub-Saharan Africa, documents how situational uncertainty shapes actions and decisions (Johnson-Hanks 2004, 2006; Trinitapoli and Yeatman 2011). Everyday life in developing countries presents multiple sources of uncertainty, including spiritual insecurity (e.g. witchcraft), social vulnerability due to poverty, and existential uncertainty due to child and young-adult mortality.

Mortality-related uncertainty is particularly salient to the phenomenon of non-numeric fertility preferences. Witnessing repeated incidents of infant and child mortality leads women to question whether their children will survive to adulthood, making the task of choosing an “ideal” number of children considerably more complex (Cleland 2001a; Lee 2003; Doepke 2005). Indeed, localized, cross-sectional studies have demonstrated that child mortality is positively associated with non-numeric IFS responses (LeGrand et al. 2003; Sandberg 2005; Hayford and Agadjanian 2011). Adult mortality is another important dimension of uncertainty in these settings. In particular, the AIDS epidemic in sub-Saharan Africa strongly influences both men’s and women’s fertility preferences, especially when perceived risk of infection is high (Yeatman 2009a, 2009b ; Hayford, et al. 2012). Drawing from this research, we expected that both child mortality and HIV prevalence would be positively associated with non-numeric IFS.

Data and Methods

Data

This study used Demographic and Health Survey (DHS) data from 32 countries representing 3 world regions: South and Southeast Asia, Latin America, and sub-Saharan Africa. The DHS are nationally representative household-based surveys designed to collect data on sexual and reproductive health, child health, and fertility that are comparable across countries and over time (bICF International 2012b). To incorporate national-level information not measured consistently in the DHS, we also included data from the World Development Indicator Database corresponding to each survey in our sample (World Bank 2012).

The DHS questionnaires are revised roughly every 5 years, corresponding with “phases” of the survey. Our sample was restricted to countries with at least two surveys administered between Phases III and VI of the DHS program, resulting in a sample of 91 surveys administered between 1993 and 2011. Appendix Table A.1 lists the primary years of data collection, analytic sample size, total number of years spanned for each country, and information on which surveys we exclude and why. There were very low levels of missing data for our variables of interest: only 0.65 percent of all respondents had missing data and the survey with the largest proportion with missing values is Uganda in 2006 at only 4.5 percent. For this reason, we limited our analytic sample to surveys and respondents with valid data on all variables used in our analysis. Our analytic sample contains 1,045,897 women.

Dependent Variable

The outcome of interest was whether a woman provided a non-numeric response to the question: “If you could chose exactly the number of children to have in your whole life, how many would that be?” For women who already have children, the question is prefaced with, “If you could go back to the time when you did not have any children…”

The wording and placement of this question remained consistent for all surveys included in our analytic sample. Starting with Phase III of the DHS surveys, interviewers were instructed to probe for numeric responses in a non-suggestive manner before recording a non-numeric response. If interviewers were unable to solicit a numeric response after probing, they were instructed to record the woman’s exact response in the “other” category. While we are unable to assess the effect of this change in protocol because we lack information on which individuals were probed, aggregate-level analyses (see Appendix C) suggest that the probing instructions led to lower rates of non-numeric IFS response. Thus, we limited our sample to Phase III and later.

The majority of surveys included only one “non-numeric response” category for the question about IFS. We therefore treated this outcome as binary, while recognizing that nonnumeric responses stem from heterogeneous motivations and perspectives. An analysis of specific non-numeric response categories reported in a minority of surveys is found in Appendix C.

Individual-level Independent Variables

A descriptive summary of all variables is provided in Table A2 and further information can be found in Appendix C. To assess the extent to which fertility control has permeated women’s “calculus of conscious choice” and whether such choice is associated with women’s likelihood of expressing numeric IFS, we used two binary measures: knowledge of a modern method of contraception and ever use of any method of contraception (for this measure, we used a subsample of sexually active women). To evaluate the role of formal schooling in predicting non-numeric IFS, we used a categorical variable specifying the highest educational level she completed—no school, incomplete primary school, or complete primary school and above. To explore whether mortality-related uncertainty is associated with non-numeric IFS, we included a variable indicating whether a woman has experienced a child death.

In addition to these measures corresponding directly to the three theoretical perspectives described above, our analyses accounted for other variables that are known to be associated with fertility preferences: age, marital status, parity, whether the respondent is Muslim, and whether she resides in an urban (versus rural) area. To control for household socioeconomic status (SES), we used the DHS wealth index quintiles, which were constructed separately for each country and therefore should be interpreted as a measure of relative wealth within countries. To account for how translation of the IFS question may impact the results, we also accounted for the language in which the interview was conducted. Finally, in ancillary analyses summarized in Appendix C, we examined interviewer effects.

Survey-level Independent Variables

We measured time using the year that each survey was administered. To examine whether contextual-level characteristics play a role in predicting non-numeric IFS, we used national-level estimates of several macro-demographic and socioeconomic indicators in our multilevel models, corresponding with the relevant year and country for each survey in our sample. Unless otherwise noted, all contextual level variables were constructed using the World Development Indicator Databank (World Bank 2012). To examine contextual-level effects of changes in the perceived ability to limit family size, we used the TFR. To examine contextual-level effects of mortality-related uncertainty, we used the under-five child mortality rate and adult HIV prevalence. To explore contextual level effects of increasing educational attainment, we used a measure representing the proportion of women that have ever attended school (any level), aggregated from the DHS survey data. Finally, we also used contextual-level measures of the percent of the population living in an urban area and gross domestic product (GDP) per capita.

Analytic Approach

Our analysis proceeded in three sections, corresponding to our research questions. We began with a descriptive analysis of trends over time in non-numeric IFS across countries and regions. Second, we compared proportions of non-numeric IFS responses to total fertility rates using three different time horizons: (1) the cross-sectional relationship between non-numeric responses and TFRs across the 91 surveys in our sample; (2) national-level trajectories in TFRs and proportions of non-numeric responses for each country; and (3) longer-term fertility trends within countries, specifically the extent to which changes in non-numeric IFS responses differ according to the timing of onset of the fertility transition.

Third, after providing this overview of aggregate-level changes in non-numeric responses, we used a combination of modeling strategies to examine the most salient predictors of non-numeric IFS responses among individuals. We first estimated separate logistic regression models predicting non-numeric IFS for each of the 91 surveys included in our analytic sample. These models included all individual-level variables described above. We then estimated multilevel logistic regression models predicting non-numeric IFS for the full sample and the sexually active subsample (to examine the contraceptive use measure). These models employed a three-level modeling strategy that nests women within surveys, which are nested within countries. Logistic regressions with random coefficients for each survey and country were estimated using HLM 6. For further technical details about our multilevel models, see Appendix B.

These different modeling strategies offered distinct and complimentary advantages. The survey-specific models allowed us to estimate individual-level effects within specific national contexts at particular points in time, and to assess variation in these associations across surveys. In contrast, the multilevel models allowed us to estimate the effects of the covariates across the entire sample. Additionally, in the multilevel modeling framework, we included the survey-level variables, which reflect differences in national context at the time when each survey was conducted. Finally, by comparing differences in the contextual-level terms in the multilevel models, we were able to assess which countries and years had unexpectedly high or low levels of non-numeric IFS response, net of the effects of individual-level covariates.

Results 1: Descriptive Overview of Prevalence and Trends in Non-Numeric IFS Response

We begin by examining trends over time in non-numeric IFS for countries in our sample. Table 1 gives the weighted proportion of nun-numeric IFS responses for each of the 91 surveys included in our analysis, and indicates whether each country experienced a significant decline, significant increase or no significant change between the first and last surveys (two-tailed t-tests, p<0.05). The proportion providing non-numeric responses to the IFS question declines significantly over time within the majority (70 percent) of countries included in this analysis.

Table 1.

Proportion who provided a non-numeric IFS response for each survey, net change in non-numeric IFS between first and last survey in each country, and year of onset of fertility transition.

Country	1993–1995	1996–1998	1999–2001	2002–2004	2005–2007	2008–2011	Net Change	Onset of Fert. Trans.
SUB-SAHARAN AFRICA
Benin		0.056	0.109		0.076		+ ***	2004
Burkina Faso			0.210	0.050	0.035		− ***	Not Yet
Cameroon		0.149		0.145		0.070	− ***	2010
Cote D’Ivoire	0.024	0.014					−	1989
Ethiopia			0.180		0.103	0.106	− ***	2003
Ghana	0.073	0.072		0.020		0.016	− ***	1986
Guinea		0.042			0.105		+ ***	2007
Kenya	0.057			0.052		0.036	− *	1984
Madagascar		0.100		0.091		0.059	− ***	1980
Malawi			0.034	0.034		0.021	− ***	2001
Mali		0.107	0.246		0.172		+ ***	Not Yet
Mozambique		0.168		0.017			− ***	1996
Namibia			0.041		0.010		− ***	1988
Niger		0.238			0.153		− ***	Not Yet
Nigeria				0.108		0.135	+ **	Not Yet
Rwanda					0.037	0.011	− ***	1990
Tanzania		0.078	0.028	0.018			− ***	1992
Uganda	0.068		0.053		0.036	0.026	− ***	2009
Zambia		0.052		0.061	0.064		+ *	1993
Zimbabwe	0.007				0.012	0.009	+	1984
ASIA
Bangladesh	0.110	0.058	0.030		0.017		− ***	1983
Cambodia			0.071		0.034	0.017	− ***	1972
Indonesia		0.205		0.144			− ***	1975
Nepal	0.025		0.017		0.002	0.003	− ***	1987
Philippines	0.015	0.018		0.011		0.010	− ***	1969
Vietnam		0.004		0.003			−	1977
LATIN AMERICA
Bolivia	0.085	0.033		0.020		0.016	− ***	1977
Dom. Republic		0.016	0.020	0.015	0.009		− ***	1967
Guatemala	0.136		0.181				+ ***	1986
Haiti	0.015		0.026		0.001		− ***	1972
Nicaragua		0.030	0.035				+	1975
Peru		0.042	0.017				− ***	1972

^*p<0.05;

^**p<0.01;

^***p<0.001

Source: As for Figure 1. Notes: Estimates of proportion of NNR respondents are weighted to adjust for regional variation in sampling within countries. T-statistics were used to measure net change, comparing the proportion providing a non-numeric response for the first survey and last survey included for each country. See Appendix A for more information about onset of fertility transition variable.

Burkina Faso experiences the most substantial decline in non-numeric responses between the two surveys, with 21 percent of women providing non-numeric responses in 1999 and 4 percent doing so in 2010. Other countries that experienced notable declines include Mozambique (from 17 percent in 1997 to 2 percent in 2003), Bangladesh (from 11 percent in 1994 to less than 1 percent in 2011), Niger (from 24 percent in 1998 to 15 percent in 2006) and Bolivia (from 9 percent in 1994 to 2 percent in 2008).

Figure 1 plots the proportion of women who provided a non-numeric IFS response for each survey as well as the average linear trend over time across each region. In all three regions, the trend lines plotted in Figure 1 show declining proportions of non-numeric IFS over time; this decline is steeper in Latin America relative to Asia and Africa. This difference in slope may be an artifact of the more uneven coverage of surveys across years for Latin America and Asia. Nonetheless, it is worth noting that Coale’s (1973) and van de Walle’s (1992) postulate that non-numeric IFS responses should decline prior to the onset of a country’s fertility transition would predict a greater decline in non-numeric IFS over time for Africa, where more countries are at earlier stages of their fertility transitions, compared to Latin America and Asia, where most countries entered the fertility transition decades before the period of observation.

Figure 1.

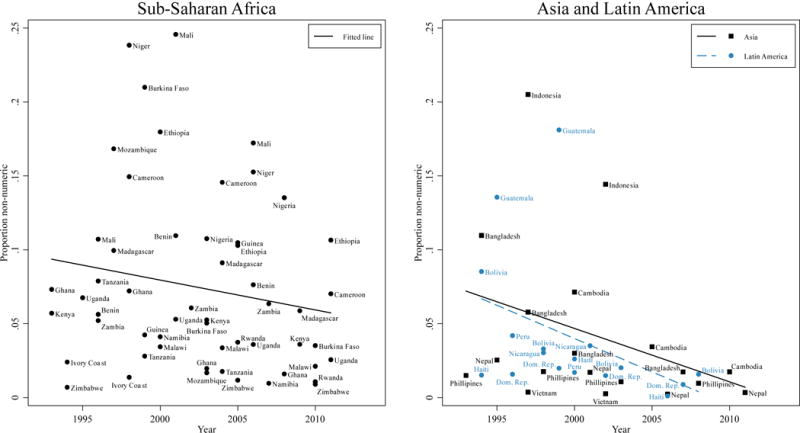
Scatterplot of proportion of women providing a non-numeric response to the ideal family size question against year of survey.

Source: DHS implementing partners and ICF International. Demographic and Health Surveys 1993–2011.

Notes: Each dot represents one of the 91 DHS surveys included in our sample. Proportions are weighted to adjust for regional variation in sampling within countries. Surveys conducted in sub-Saharan Africa appear in the left-hand panel, and surveys conducted in Asia (black) and Latin America (blue) appear in the right-hand panel. Linear regression lines were calculated separately for each world region.

Results 2: Non-Numeric IFS Responses and Aggregate-Level Fertility Change

In this section, we further explore whether fertility transition theorists’ predictions have borne out by examining the association between changes in aggregate fertility rates and trends in non-numeric IFS responses. We begin by doing so cross-sectionally; Figure 2 plots the proportion of women who provide a non-numeric response for the survey against the TFR for the corresponding year. This graph shows that as fertility rates decrease across surveys, the proportion of women who provide a non-numeric IFS response also decreases. These results offer preliminary support for interpreting non-numeric IFS responses through the lens of the fertility transition theory. However, the observations become more spread out around the regression line with increasing TFR. This pattern suggests that there are likely additional factors influencing the relationship between fertility rates and rates of non-numeric IFS response.

Figure 2.

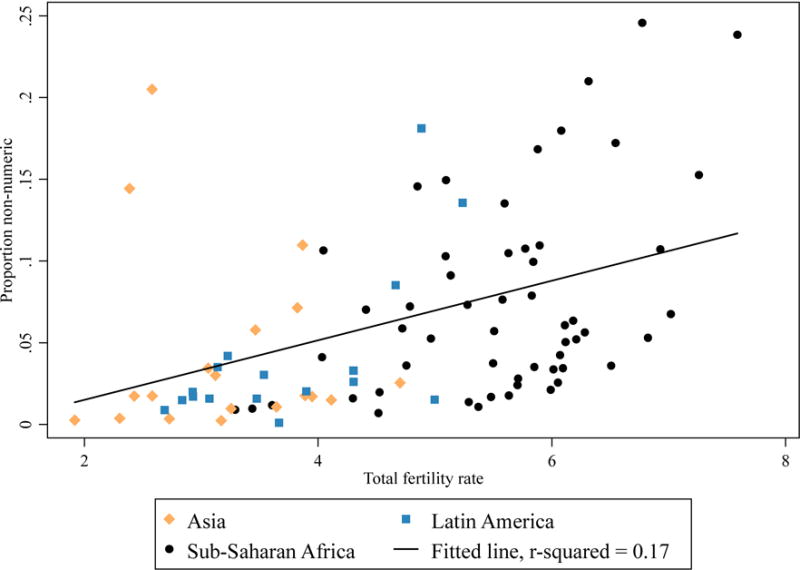
Scatterplot of proportion of women providing a non-numeric response to the ideal family size question against total fertility rate for the year during which the majority of respondents were surveyed.

Source: As for Figure 1.

Notes: The two outlying points in the upper left corner are from Indonesia, which has unusually high levels of non-numeric response considering its fertility profile (see also Figure 3).

While Figure 2 shows that in a given year, countries with higher TFRs also tend to have higher proportions of women providing non-numeric responses, it does not tell us about how these two phenomena are related within countries, or whether national-level trends in non-numeric responses correspond to different patterns of decline in the TFR. Figure 3 shows the association between non-numeric IFS responses and the TFR across the window of observation for each country. All countries in our sample experience a decline in TFR between the first and last survey, so the lines move from left (higher fertility) to right (lower fertility) over time. To more clearly visualize the relationship between aggregate fertility rates and proportions of non-numeric IFS responses, this figure is divided into three panels according to different trajectories of TFR across the observation period. The top panel shows the 14 countries with consistently high TFRs throughout the observation period (starting with a TFR above 4.5 and experiencing a total decline in TFR of less than 0.7); these countries experience the most substantial decline in non-numeric IFS response. The middle panel shows the 10 countries that started off with high TFR (above 4.5) and experience substantial declines in TFR (at least 0.7); these countries tend to start off with lower levels of non-numeric response (with the exception of Ethiopia and Cameroon) and to experience a smaller net change in non-numeric responses. Finally, the bottom panel shows the 9 countries that enter the observation period with a lower TFR (below 4.5), and reveals that countries that begin the observation period with lower total fertility rates tend to have lower levels of non-numeric response, with the obvious exception of Indonesia.

Figure 3.

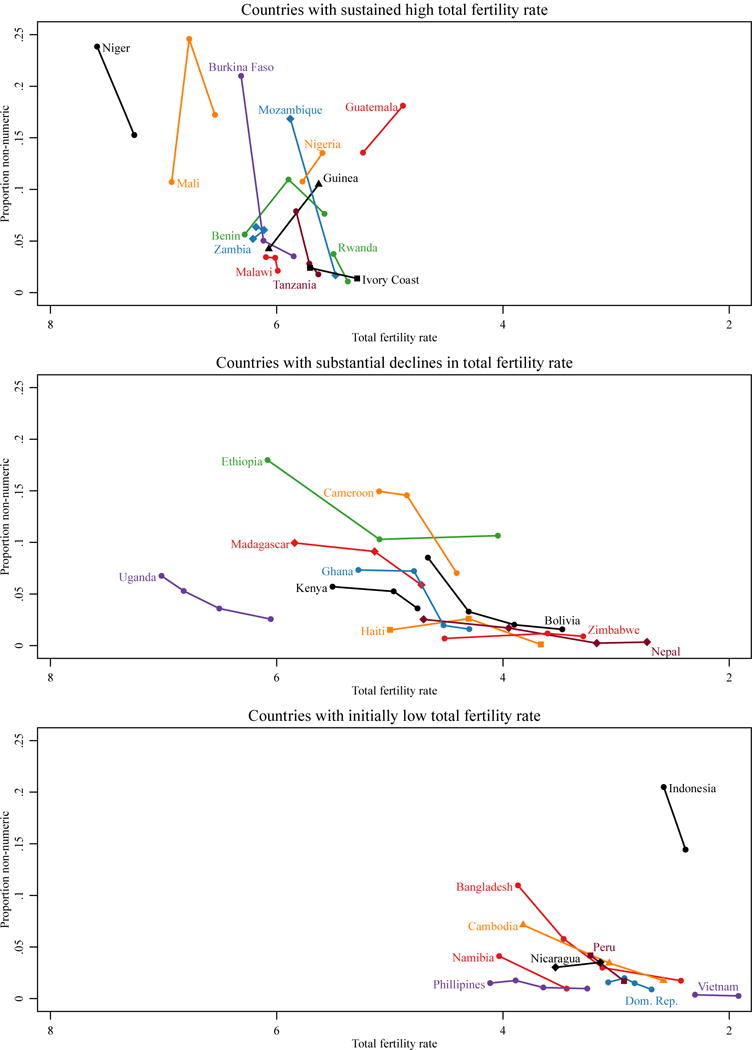
Connected lines showing the proportion of women providing a non-numeric response to ideal family size against total fertility rate for each country, differentiated according to patterns in total fertility rate during the window of observation.

Source: As for Figure 1.

Note: Total fertility rates declined throughout the period of observation for all countries in our sample, so all lines can be read from left (higher TFR) to right (lower TFR) over time.

After having examined how TFR and aggregate levels of non-numeric IFS are related during the period of observation for each country, we next explored the extent to which non-numeric IFS responses may reflect the types of longer-term fertility trends that are the focus of fertility transition theory. While Figure 3 plots the association between non-numeric IFS and contemporaneous estimates of TFR for each survey; Figure 4 displays the association between non-numeric IFS and year of survey, differentiated according to the period in which each country entered the fertility transition—a demographic milestone that occurred prior to our observation window for most countries in our sample (see Table 1 for the year of onset for each country and Appendix A for more information about how the timing of onset was determined).

Figure 4.

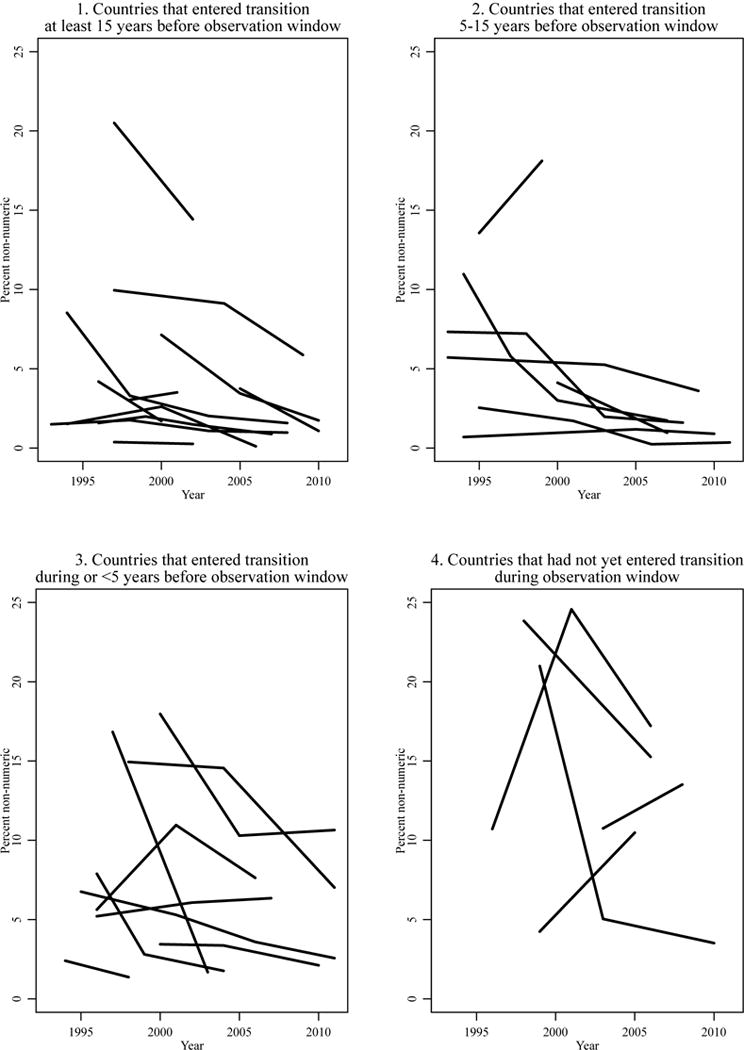
Percent of women who provide non-numeric IFS against year of observation, differentiated according to the onset of the country’s fertility transition.

Source: As for Figure 1.

Notes: Onset of the fertility transition is defined as the year in which a country experienced a net decline in TFR of more than 10 percent compared to its 1960 value. Information about TFR is sourced from the World Indicators Database. For more information about each country’s year of onset of the fertility transition, see Table 1. Average slopes of lines: −0.23 for Panel 1, −0.10 for Panel 2, −0.54 for Panel 3, and −0.05 for Panel 4.

There are four possible ways that trends in non-numeric IFS during the period of observation might be related to the timing of the onset of the fertility transition. If a shift in non-numeric IFS were an antecedent to fertility change, something that takes place well before any changes in actual childbearing behavior, one would expect to see a more marked decline in countries that have not yet entered the fertility transition. If, as suggested by van de Walle (1992) and Coale (1973), a shift from non-numeric to numeric IFS were a necessary pre-condition for the fertility transition, one would expect that countries which entered the fertility transition either shortly before or during the period of observation would exhibit steeper declines in non-numeric IFS. If declines in non-numeric IFS were a consequence of the onset of a country’s fertility transition—if numeric IFS responses were more closely connected to other indicators of development that occur at later stages in a country’s fertility transition, such as universal primary education—then one would expect countries that began their fertility transition well before the window of observation to exhibit more marked patterns of decline in non-numeric IFS. Finally, if non-numeric IFS is unrelated to how women conceptualize fertility at all, but is triggered by other factors such as experiences during the survey interview (Olaleye 1993) or beliefs about the risks related to verbalizing one’s desires (Castle 2001), then one might not see any relationship between this measure and the timing of the fertility transition.

Figure 4 shows modest support for interpreting non-numeric responses through the lens of the demographic transition theory as a precondition or early indication of aggregate fertility decline (Coale 1973; van de Walle 1992). The proportion of respondents who provide a non-numeric response is higher, on average, in the bottom two panels, which display countries that entered the fertility transition most recently (panel 3) or which have yet to enter the fertility transition (panel 4), compared to the top two panels, which display countries that experienced the onset of the transition earlier. Further, the average slope of the lines is steepest (most negative) in Panel 3, which displays countries that entered the fertility transition during or less than five years before the observation window, compared to any of the other three panels (the average slope in panel 3 is −0.54 compared to an average of −0.21 for the other three panels). Lastly, for the five countries that have not yet entered the fertility transition at the time of the last survey administered in that country (panel 4), we see no clear pattern in terms of trends in non-numeric response: a slight majority of these countries (three out of five) actually experience a net increase in rates of non-numeric fertility over time. Together, these results support van de Walle’s (1992) postulate that declining non-numeric IFS will occur around the time of onset of a country’s fertility transition.

When examined according to aggregate-level trends as well as national-level trajectories, our results broadly support the idea that as fertility rates decline in countries, women are more likely to assign numeric values to their fertility preferences. However, the heterogeneity in the magnitude of these associations indicates that TFR is likely not the only factor associated with the decline in non-numeric IFS responses, and suggests that researchers should use caution when interpreting non-numeric responses through the lens of fertility transition theory.

Results 3: Identifying Predictors of Individual-Level Non-Numeric IFS Response

Survey-specific Models

We next examined which characteristics are associated with variation in non-numeric responses at the individual level. We began by estimating a separate logistic regression model for each of the 91 surveys, with all individual-level independent variables listed above included in each model. This method allowed us to examine whether associations between these measures and non-numeric IFS vary considerably across the different contexts and time periods in our data. For the variables that are related to the three theoretical perspectives described above, Table 2 summarizes the results of these models in terms of (1) the average magnitude of the associations and (2) the proportion of surveys in which each measure was significant. These summaries are provided for the sample as a whole as well as for each region and time period.

Table 2.

Summary of results from logistic regression models predicting non-numeric responses to the ideal family size question, estimated separately for each survey.

	All Surveys	Regional Comparison				Temporal Comparison
		Africa	Asia	Latin America	Wald Chi Square	1993–1998	1999–2004	2005–2011	Wald Chi Square
	Mean Discrete Change in Predicted Probability
Experienced Child Death	0.005	0.005	0.01	0.004	1.91	0.005	0.006	0.006	0.46
Literate	−0.011	−0.012	−0.006	−0.008	4.11	−0.012	−0.01	−0.009	0.67
In Primary (Ref: No school)	−0.010	−0.016	−0.002	−0.004	17.54***	−0.011	−0.013	−0.011	0.21
Completed Primary (Ref: No school)	−0.025	−0.031	−0.01	−0.015	15.91***	−0.026	−0.029	−0.019	2.53
Knows Modern Method of Family Planning	−0.031	−0.025	−0.042	−0.039	4.98+	−0.034	−0.031	−0.026	1.29
Ever Used Any Method of Family Planning1	−0.018	−0.017	−0.026	−0.018	0.62	−0.020	−0.019	−0.015	1.39
	Proportion of Surveys in which Coefficient Was Significant
Experienced Child Death	0.349	0.382	0.105	0.353	8.53*	0.310	0.312	0.333	0.04
Literate	0.446	0.491	0.263	0.294	4.38	0.414	0.344	0.467	0.97
In Primary (Ref: No school)	0.410	0.473	0.105	0.353	13.88**	0.345	0.406	0.367	0.25
Completed Primary (Ref: No school)	0.614	0.691	0.211	0.529	17.51***	0.552	0.656	0.467	2.29
Knows Modern Method of Family Planning	0.880	0.818	0.684	0.882	2.13	0.828	0.844	0.733	1.2
Ever Used Any Method of Family Planning1	0.859	0.895	0.900	0.800	0.560	0.852	0.862	0.923	0.37

^*p<0.05;

^**p<0.01;

^***p<0.001

Source: As for Figure 1.

Notes: Models were estimated separately for each of the 91 surveys in the analytic sample, and control for age, number of living children, whether the respondent is currently pregnant, Muslim religion, marital status, educational attainment, literacy, and experience of child death, and knowledge of modern contraception. Wald Chi-square tests are used to compare across regions and time periods.

¹Because of the additional sample size reductions for ever use of contraception (excluding respondents who never had sex and surveys that do not provide information on use of contraception or prior sexual intercourse), a separate set of models were estimated for this variable, and all other results in Table 5 exclude this measure. These models predicting ever use of contraception do not include knowledge of modern contraception, due to issues of multicollinearity.

Knowledge of and experience using contraception are the most consistently significant predictors of non-numeric family size out of the five variables of interest. Women who report knowledge of modern contraception are less likely to provide non-numeric IFS responses in 80 percent of the surveys, although the small proportion of women who report that they do not know a modern method of contraception in some surveys (notably Bangladesh, the Dominican Republic, and Nepal; see Appendix C for more information) should be kept in mind when interpreting results for this variable in the country-specific models. Among the subsample of sexually-active women, those who report having ever used contraception are significantly less likely to provide a non-numeric response to this question in 87 percent of the survey specific models.

When we examined the measures representing exposure to formal education, women who have attended primary school are significantly less likely to report non-numeric IFS 39 percent of the time, and having completed primary school is significant in the expected direction 57 percent of the time (omitted category: no schooling). Of our three theoretical perspectives, mortality-related uncertainty is the least consistently supported in these models: women who have experienced a child’s death are significantly more likely to offer a non-numeric response in only 33 percent of the survey-specific models.

The magnitude of the associations was assessed using the discrete changes in predicted probability for these six dichotomous variables. Unlike coefficients or odds ratios, discrete changes in predicted probabilities have the advantage of being able to be averaged across multiple logistic regressions and still be substantively meaningful (Long and Freese 2006; Mood 2010). The measures presented in the bottom panel of Table 2 represent the average change in predicted probability associated with moving from the reference category to the value described in each row of the table (e.g., from no schooling to some primary school). This measure shows that change in predicted probability of providing a non-numeric response is largest, on average, for the variable representing having completed primary school: relative to having no schooling, women who completed primary school are about 4 percent more likely to offer non-numeric responses, on average. The smallest changes in predicted probability of offering a non-numeric IFS response correspond to having experienced a child death and having completed some primary school.

Moving to regional and temporal comparisons, we found substantial variation across world regions, but not over time (significant differences were identified using one-way ANOVA tests). The educational attainment variables are both more likely to be significant (bottom panel) and produce larger differences in predicted probability (top panel) in Africa relative to Asia and Latin America. Knowledge of modern contraception predicts significantly larger changes in non-numeric IFS responses in Asia relative to Africa and Latin America. Experiencing a child death is associated with larger changes in predicted probability of non-numeric fertility in Asia, compared with the other two regions.

Multilevel Models

To assess these associations across our entire sample of women while accounting for the non-independence of observations and to examine whether differences in national context influence women’s likelihood of thinking numerically about her fertility, we estimated a pair of three-level logistic regression models, with women nested within surveys and surveys within countries. Table 3 presents these results. For the individual-level variables corresponding to the three theoretical perspectives, the results from these models largely confirm the findings from the survey-level models. Consistent with our findings in Table 2, at the individual level we found the strongest support for the effect of knowledge and use of contraception and for the effect of formal education. Experiencing a child’s death, on the other hand, has a smaller association with non-numeric IFS responses, though this association is still highly significant (given the large sample size, the majority of individual-level variables are expected to be highly significant in the pooled models).

Table 3.

Odds ratios from 3-level logistic regression models predicting non-numeric ideal family size.

	Model 1	Discrete Change in Predicted Probability‡	Model 2	Discrete Change in Predicted Probability‡
Intercept	0.052*** (0.204)		0.042       (0.145)
Level-1 Variables
Age	1.013*** (0.001)	0.004	1.017*** (0.001)	0.014
Currently Pregnant	1.088*** (0.015)	0.002	1.095*** (0.015)	0.024
Parity	1.069*** (0.002)	0.001	1.080*** (0.002)	0.003
Muslim	1.367*** (0.014)	0.008	1.297*** (0.016)	0.029
Married	0.744*** (0.011)	−0.008	0.984       (0.013)	0.020
Socio-economic Status (ref. = middle quintile)
Lowest quintile	1.116*** (0.013)	0.003	1.106*** (0.014)	0.024
Second quintile	1.016       (0.014)	0.000	1.017       (0.015)	0.020
Fourth quintile	0.968*      (0.015)	−0.001	0.976       (0.016)	0.019
Highest quitile	0.959*      (0.017)	−0.001	0.980       (0.018)	0.019
Urban residence	0.873*** (0.013)	−0.003	0.919*** (0.013)	0.018
Knows Modern Contraception	0.554*** (0.012)	−0.018	—        —	—
Ever Used Modern Contraception	—       —	—	0.554*** (0.012)	0.018
Education Level (ref. = no education)
Incomplete Primary	0.779*** (0.012)	−0.006	0.794*** (0.013)	0.013
Complete primary	0.447*** (0.015)	−0.019	0.482*** (0.016)	0.010
Experienced a child’s death	1.228*** (0.010)	0.005	1.209*** (0.010)	0.026
Level-2 Variables
Year	0.940**   (0.016)	−0.004	0.952**   (0.016)	−0.008
% Urban	1.012       (0.014)	0.009	1.016       (0.015)	0.031
GDP per capita (in 100 USD)	0.976       (0.020)	−0.004	0.975       (0.021)	−0.010
TFR	1.021       (0.191)	0.001	0.993       (0.200)	−0.001
% Ever attended school	1.660       (0.970)	0.004	2.112       (0.953)	0.018
Child Mortality Rate	1.000       (0.005)	0.000	1.001       (0.005)	0.002
HIV Prevalence	0.921*     (0.036)	−0.006	0.938+      (0.038)	−0.012
Variance Components
Level-2 Variance	0.210***		0.225***
Level-3 Variance	0.546***		0.508***

^*p<0.05;

^**p<0.01;

^***p<0.001

Source: As for Figure 1.

Notes: Standard Errors in parentheses. All models also control for the language of the interview.

Model 1: N1=1,045,897; N2=91; N3=32

Model 2: N1 = 810,781; N2=84; N3=30 (sexually-active subsample)

¹Discrete change in predicted probability assumes other variables are held at their mean level. For continuous variables, the change indicates the difference between the mean and one standard deviation above the mean.

Regarding the contextual-level variables, the results in Table 3 show that even after accounting for all individual- and survey-level covariates, survey year remained a statistically significant (p<0.01) and negative predictor of non-numeric IFS. This shows that even after accounting for all individual- and contextual-level variables, as well as random variation across surveys and countries, the decline in non-numeric IFS responses during this period remains significant. For each additional year, women’s odds of providing a non-numeric response decrease by five percent on average.

Model 1 in Table 3, which is estimated among the full sample of women, indicates that the relationship between HIV prevalence and non-numeric IFS is also significant. However, the direction of this relationship runs contrary to prior literature on mortality-related uncertainty: women living in higher-prevalence countries are less likely to provide non-numeric IFS responses. We interpret this relationship as perhaps being an indicator of greater exposure to HIV prevention programming, much of which overlaps with family planning rhetoric. More broadly, higher national-level HIV prevalence might suggest a context in which sex is more frequently discussed as something requiring caution and planning (Cleland and Watkins 2006; Robinson 2011). The significance of this association diminishes among the sample that is limited to sexually active women (Model 2), but this is likely due to the smaller number of countries in this sample (84). We found no evidence to indicate that any of the other survey-level variables were significantly associated with nonnumeric IFS. These null findings for contextual-level variables, however, should be interpreted with caution, as significant effects are difficult to detect in a sample of 91 surveys.

Figure 5 shows variation in magnitude of the country- and survey-level coefficients in the multilevel models, holding individual-level variables constant. This approach identifies countries and surveys that are outliers in terms of the prevalence of non-numeric IFS, given their values for the individual-level variables. To examine country-level effects, we present posterior mean estimates for the country-level random intercepts. These values provide a measure of the total amount of variation between countries that is not explained by individual- or survey-level covariates. For example, a positive value for this measure indicates that individuals within a country have higher levels of non-numeric response than would be expected, given their observed values for individual and survey-level covariates. In Figure 5, these country-level values are represented with a dot for each country. The figure shows that 10 out of 32 countries have country-level estimates that are significantly different than what would be predicted given the individual- and survey-level variables included in the model, suggesting that the random coefficients at the country level are capturing substantial variation in non-numeric IFS between countries.

Figure 5.

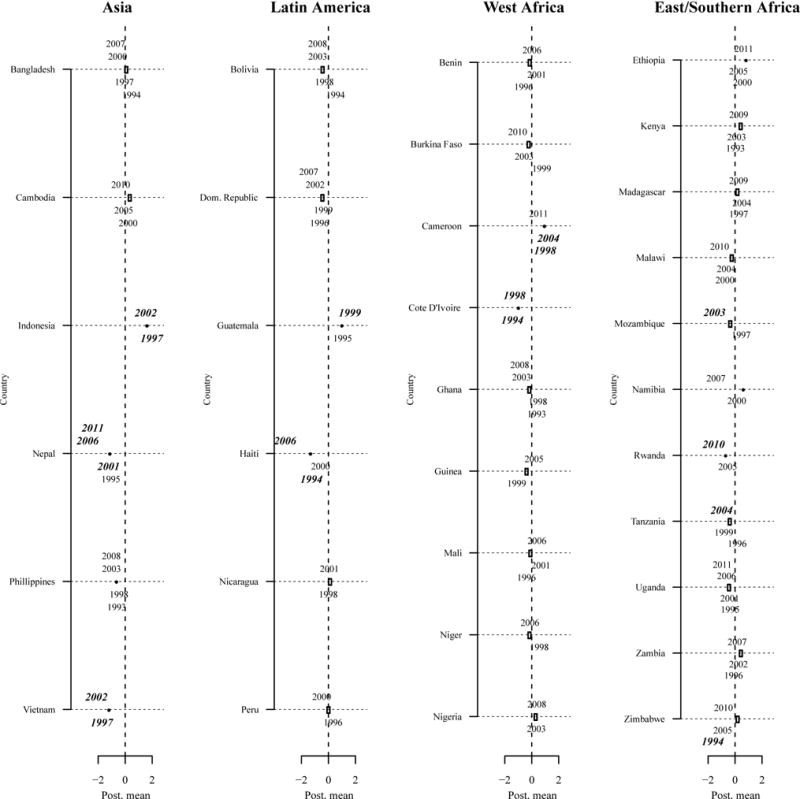
Country-level effects and total contextual effects (combining country- and survey-levels) from a multilevel logistic regression model predicting non-numeric response.

Source: As for Figure 1.

Notes: The dots represent the country-level effects, estimated using posterior means of the random intercepts for each country. Positive values (e.g., Cameroon, Indonesia) indicate that a country has higher levels of non-numeric IFS than would be predicted given observed values for all individual- and survey-level variables. Values that are significantly different from 0 at a 95% level of confidence are displayed with filled circles, while values that are not statistically significant are displayed with open circles.

The printed years represent the combined country- and survey-level effects, or the posterior intercepts for levels 2 and 3. They represent the total group-level variation included in the model. When compared to country-level effects, these values show the additional variation captured at the survey level. The labels are centered around the data points, so the precise estimate is between the 2^nd and 3^rd digits of each year. Values that are significantly different from 0 at a 95% level of confidence are printed in bold italic.

To assess variation at the survey level, we present the model estimates of the total group-level effects for each survey, often referred to as the posterior intercepts (Snijders and Boskers 1999, p. 60). These provide an estimate of the total main effect of country i and survey j, controlling for individual-level variables, while including the observed values of all group-level variables and random effects. When compared to the country-level random intercepts, these values show the additional variation captured through survey-level variables and random coefficients. Surveys with positive posterior intercepts have a higher level of non-numeric IFS than would be expected based on their individual-level variables, while surveys with negative values for this measure have lower than expected levels of non-numeric IFS responses than would be expected given their individual-level variables. In Figure 5, these values are represented with labels identifying the year that each survey was administered, with significant values printed in black. 18 of 91 surveys have posterior intercepts that are significantly different from 0.

Taking the country-level and survey-level estimates together, these results show that Indonesia, Guatemala, and Cameroon have higher levels of non-numeric fertility than expected given their individual-level variables, though when the survey-level estimates for Guatemala 1995 and Cameroon 2011 are taken into consideration, this difference is no longer significant. The differences between country- and survey- level estimates are due to changes over time in non-numeric IFS. In Guatemala, non-numeric IFS increases over time, thus once the negative coefficient for time of survey is accounted for, the value for 1999 reveals itself to be an outlier. In Cameroon, non-numeric IFS is twice as high in the two earlier surveys than in the 2011 survey; thus the contextual-level effect is not significant for the later survey. On the other hand, Vietnam, Ivory Coast, and Nepal have lower levels of non-numeric fertility than predicted given their values for the individual-level variables, though the total contextual effect for Nepal 1995 is not significantly different from zero. Again, this difference is due to the fact that the proportion of non-numeric IFS changes substantially between surveys: it is more than twice as high in 1995 than in any other survey in Nepal. Ethiopia and Namibia have country-level effects that are significantly higher than would be expected, but once the survey-level variables are taken into consideration, the group-level effects are no longer significant for any surveys. These results are driven by the survey-level variables in each country—the low percent of women have ever been to school and low GDP per capita in Ethiopia and the high HIV prevalence and low percent urban in Namibia—which move the total group-level estimates closer to what the model would predict. Finally, this figure also highlights cases in which one survey within a country is a significant outlier; for example Zimbabwe 1994, which has unexpectedly low levels of non-numeric IFS.

Discussion and Conclusions

This article focused on a topic that demographers have long theorized—when women offer words instead of numbers when asked about their IFS. The proportion of women offering non-numeric responses to the IFS question declined significantly in the majority of the 32 countries in our sample over the past two decades, and this decrease over time remains significant in all of our multilevel models. This suggests that “numeracy about children,” as van de Walle (1992:490) termed this concept 25 years ago, has indeed increased across the developing world over the past 3 decades.

Our results also provide evidence for fertility theorists’ postulate that changes in the prevalence of non-numeric IFS responses are associated with changes in fertility behavior. National-level comparisons between rates of non-numeric response and TFRs offer support for the common assumption that such responses are indicative of high fertility, pre-transition contexts. When we look cross-sectionally across surveys, we find that surveys conducted in countries with a higher TFR also tend to include more women offering non-numeric IFS responses. When we look within countries over time, changes in these two phenomena are correlated for the majority of our sample; as fertility rates decline, so do levels of non-numeric IFS. We also find that countries that entered the fertility transition shortly before or during the observation window experience the steepest declines in non-numeric IFS. Conversely, countries that have not yet entered the transition show no consistent pattern of decline in non-numeric IFS. These results together provide empirical support for van de Walle’s (1992) hypothesis that the steepest declines in non-numeric IFS will occur around the time of onset of a country’s fertility transition.

Results from our multivariate analysis suggest that at an individual level, non-numeric IFS is tied less to mortality-related uncertainty and more to knowledge (both general and fertility-specific). Women who report knowledge of or experience using contraception are substantially less likely to provide non-numeric IFS responses. Exposure to formal education also decreases the odds of women providing non-numeric IFS responses, consistent with previous small-scale studies (Riley et al. 1993; Hayford and Agadjanian 2011). Our findings also corroborate findings from Nepal and Mozambique that experiencing a child death is positively associated with non-numeric IFS (Sandberg 2005; Hayford and Agadjanian 2011). On the other hand, our results deviate from previous studies concerning the contextual effect of HIV prevalence: our results indicate that as HIV prevalence increases, women are less likely to provide non-numeric responses, suggesting that this measure may capture other factors such as family planning and safe-sex discourses.

Our study provides new insights into how non-numeric IFS relates to broader patterns of fertility and social change across the developing world. Yet we acknowledge three key limitations. First, the countries in our analysis contribute different numbers of surveys from varying time points. We structured our analysis to accommodate this heterogeneity, both in our descriptive analyses and the multivariate models. Nonetheless, this heterogeneity limits the conclusions we can draw from our data. Relatedly, because only six countries in Latin America and Asia fit our sampling criteria, we were unable to examine regional trends in our multilevel analysis. And because our data span only 20 years, we are unable to disentangle period-specific effects from processes that might occur during other episodes of widespread fertility decline.

Second, like all survey researchers, we can only analyze questions as they were asked. The quasi-counterfactual nature of the IFS question has been criticized by scholars who worry that family size preferences are subject to poor reliability and construct validity (Bankole and Westoff 1998). The concept of “ideal family size” may also fail to capture the complex nature of family planning by relying too heavily on rational-choice models of fertility (Cleland 1973; Johnson-Hanks 2007). Although we control for language, cultural and ideational differences within our sample may influence how this question is interpreted. Additionally, we have no information about the extent to which women’s IFS responses are driven by extra-individual factors, including influence from husbands or extended families (Isiugo-Abanihe 1994; Dodoo 1998).

Third, our contextual variables are measured at the country level. This aggregation likely does not accurately capture the contexts of many women in our sample, which are much more heterogeneous and localized. While defining contexts using smaller geographical areas would have been preferable, certain measures—such as HIV prevalence and GDP per capita—are unattainable for sub-country units.

Our results point to additional lines of inquiry that extend beyond the scope of our study, which we hope will inspire future research. While ancillary analyses explored differences across types of non-numeric IFS responses using the surveys that include multiple non-numeric categories (Appendix C), we did not fully investigate these nuances. Yet non-numeric responses could indicate various perspectives, only some of which cleave to fertility transition theory. One woman might provide a non-numeric response because she is in school and does not yet know what her career might look like, another might not provide a number because she believes that family size is determined by God, while another might want as many children as possible. Data that enable researchers to investigate the answers people give, rather than simply whether they are words or numbers, would further enhance our understanding of how non-numeric fertility preferences are socially patterned. Additionally, many of the individual- and survey-level factors explored here are inter-related, such as women’s knowledge of family planning and educational attainment.

Despite these limitations, by extending our knowledge of non-numeric fertility preferences across space and time, the research presented here shows what such responses reveal about aggregate-level fertility trends and individual-level perspectives. In the aggregate, non-numeric IFS declines most substantially in the early stages of countries’ fertility transitions. Among individuals, women’s propensity to provide non-numeric IFS responses is influenced by a host of factors, most notably knowledge of modern contraception and exposure to formal education. Like demographers before us have presupposed, understanding the dynamic nature of declining non-numeric IFS illuminates the subjective underpinnings of demographic data.

Appendix A: OVERVIEW OF Analytic Samples AND DESCRIPTIVE STATISTICS FOR VARIABLES INCLUDED IN THE ANALYSIS

Table A.1.

List of countries included in the analytic sample, and for each country: year in which each survey was conducted, number of years between first and last survey, and total number of women.

Country	First Survey	Second Survey	Third Survey	Fourth Survey	Years Spanned	Analytic N
Sub-Saharan Africa
Benin	1996	2001	2006		10	28,830
Burkina Faso	1999	2003	2010		11	35,804
Cameroon	1998	2004	2011		13	31,236
Cote D’Ivoire	1994	1998			4	11,137
Ethiopia	2000	2005	2011		11	45,113
Ghana	1993	1998	2003	2008	15	19,989
Guinea	1999	2005			6	14,642
Kenya	1993	2003	2009		16	24,059
Madagascar	1997	2004	2009		12	32,298
Malawi	2000	2004	2010		10	47,800
Mali	1996	2001	2006		10	36,967
Mozambique	1997	2003			6	21,093
Namibia	2000	2007			7	16,260
Niger	1998	2006			8	16,726
Nigeria	2003	2008			5	40,652
Rwanda	2005	2010			5	24,900
Tanzania	1996	1999	2004		8	22,430
Uganda	1995	2001	2006	2011	16	30,802
Zambia	1996	2002	2007		11	22,582
Zimbabwe	1994	2005	2010		16	24,110
Asia
Bangladesh	1994†	1997†	2000†	2007†	13	40,249
Cambodia	2000	2005	2010*		10	50,772
Indonesia	1994	2002			8	58,092
Nepal	1995	2001	2006	2011	16	40,592
Philippines	1993	1998	2003	2008	15	55,958
Vietnam	1997†	2002†			5	11,326
Latin America
Bolivia	1994	1998	2003	2008	14	54,160
Dom. Republic	1996	1999	2002	2007	11	59,560
Guatemala	1995	1999			4	18,360
Haiti	1994	2000	2006		12	26,217
Nicaragua	1998	2001			3	26,542
Peru	1996	2000			4	56,640

^†Excluded from models predicting ever use of contraception due to missing measure of previous sexual intercourse.

^*Excluded from models predicting ever use of contraception due to missing measure of ever use of contraception.

Surveys Excluded from Study

We excluded all Phase II and Phase III surveys due to the change in probing protocol after respondents provide a non-numeric answer to the IFS question. The following surveys were excluded due to missing values on variables included in our models: Zimbabwe 2005 and Bangladesh 2004 (due to missing education measures), Rwanda 2000, Tanzania 2010, and all Senegal surveys (due to missing religious affiliation), Bangladesh 2011 (due to missing information on contraceptive knowledge), Chad 2004, Indonesia 2007, Kenya 1993, and Mozambique 2011 (due to no information on language). Additionally, we excluded Haiti 2012 because it was administered shortly after the country’s earthquake.

A.2.

Descriptive Statistics for All Variables Used in the Analysis for First and Last Survey in Each Country

	First Survey		Last Survey		T-Statistic
	Mean/Percent	SD	Mean/Percent	SD
Non-Numeric Response to Ideal Family Size	11.0%	0.3	6.8%	0.3	29.6***
Control Variables
Age	29.9	9.4	30.4	9.5	−10.6***
Number of Living Children	2.5	2.2	2.4	2.1	14.8***
Currently Pregnant	8.2%	0.3	7.2%	0.3	8.7***
Muslim	44.2%	0.5	43.2%	0.5	5.4***
Married	77.6%	0.4	74.4%	0.4	18.0***
Urban Residence	28.8%	0.5	35.3%	0.5	−30.8***
Individual-level Independent Variables
Experienced Child Death	26.1%	0.4	20.2%	0.4	33.5***
Educational Attainment
No Schooling	31.5%	0.5	23.1%	0.4	42.7***
Attended Some Primary School	21.6%	0.4	20.5%	0.4	5.9***
Completed Primary School	46.8%	0.5	56.4%	0.5	−41.4***
Knows Modern Method of Contraception	90.1%	0.3	94.0%	0.2	−34.5***
Country-Level Independent Variables
Child Mortality Rate	126.0	53.6	91.8	48.1	2.7**
% in School	64.2%	0.3	71.7%	0.2	−1.2
Total Fertility Rate	5.1	1.3	4.4	1.4	2.0*
HIV Prevalence	4.4	5.7	3.7	4.6	0.5
GDP Per Capita	601.8	598.8	990.5	978.6	−1.9*
% of Population Living in Urban Area	32.2%	0.2	36.7%	0.2	−1.13

^*p<0.05;

^**p<0.01;

^***p<0.001

Notes: Estimates in this table are weighted to adjust for regional variation in sampling within countries (individual-level variables only) and for differences in population size across countries (all variables). Population estimates for adults aged 15–45 were obtained from the United Nations Population Division (UNPD 2012) For binary variables, the percent of women who report characteristic of interest is provided. T-statistic compares average values for first survey and last survey. Estimates are weighted to adjust for regional variation in sampling within countries (individual-level variables only) and for differences in population size across countries (all variables).

Appendix B: Multilevel equations

All multilevel models were estimated using three-level logistic regression models, with random intercepts for surveys (level 2) and countries (level 3). The three-level modelling strategy nested women within surveys, which were nested within countries. This strategy is uniquely suited for repeated cross-sectional data with different periods of observation for each country and has been used and advocated by a number of scholars (Duncan et al. 1996; Ruiter and de Graaf 2006). To adjust for the fact that countries in our sample contributed different numbers of surveys at various time intervals, previous versions of our models estimated year as a random slope. However, results from likelihood ratio tests suggested that the random-coefficient approach was a better fit for our data.

For individuals i in survey j and country k, the level-1 equation is:

$$\ln \left[\frac{p_{\mathit{ijk}}}{1-p_{\mathit{ijk}}}\right]={\alpha }_{0jk}+{\displaystyle \sum }_{n=1}^N{\beta }_n{x}_{\mathit{ijk}}+e_{\mathit{ijk}}$$

where

• $p_{\mathit{ijk}}$ is the probability of responding non-numerically;

• ${\alpha }_{0jk}$ is an intercept for survey j in country k;

• ${\beta }_n$ are a series of level-1 coefficients for the matrix (X) of individual-level variables;

• and $e_{\mathit{ijk}}$ is the level-1 error component.

The level-2 equation defines the level-1 intercept ${\alpha }_{0jk}$ as an outcome variable:

$${\alpha }_{0jk}={\theta }_{00k}+{\displaystyle \sum }_{m=1}^M{\beta }_m{z}_{0jk}+{\gamma }_{0jk}$$

where

• ${\theta }_{00k}$ is an intercept for country k;

• ${\beta }_m$ are a series of level-2 coefficients for the matrix (Z) of survey-level variables;

• and ${\gamma }_{0jk}$ is a random component that allows the intercept to vary for each survey.

The level-3 equation defines the level-2 intercept ${\theta }_{00k}$ as an outcome variable:

$${\theta }_{00k}={\delta }_{000}+{\mu }_{00k}$$

where

• ${\delta }_{000}$is a non-varying intercept;

• and ${\mu }_{00k}$ is a random component that allows the intercept to vary for each country k.

All variables were mean-centred for the multilevel models. Models were estimated with the HLM 6 software package, using the PQL parameter estimation strategy (Raudenbush et al. 2004). We also estimated the models using the alternative estimator available in HLM 6 for non-linear models, Laplace 6, which produced nearly identical results.