Abstract
This paper demonstrates through Monte Carlo simulations that a practical positron emission tomograph with (1) deep scintillators for efficient detection, (2) double-ended readout for depth-of-interaction information, (3) fixed-level analog triggering, and (4) accurate calibration and timing data corrections can achieve a coincidence resolving time (CRT) that is not far above the statistical lower bound.
One Monte Carlo algorithm simulates a calibration procedure that uses data from a positron point source. Annihilation events with an interaction near the entrance surface of one scintillator are selected, and data from the two photodetectors on the other scintillator provide depth-dependent timing corrections. Another Monte Carlo algorithm simulates normal operation using these corrections and determines the CRT. A third Monte Carlo algorithm determines the CRT statistical lower bound by generating a series of random interaction depths, and for each interaction a set of random photoelectron times for each of the two photodetectors. The most likely interaction times are determined by shifting the depth-dependent probability density function to maximize the joint likelihood for all the photoelectron times in each set.
Example calculations are tabulated for different numbers of photoelectrons and photodetector time jitters for three 3 × 3 × 30 mm3 scintillators: Lu2SiO5:Ce,Ca (LSO), LaBr3:Ce, and a hypothetical ultra-fast scintillator. To isolate the factors that depend on the scintillator length and the ability to estimate the DOI, CRT values are tabulated for perfect scintillator-photodetectors. For LSO with 4000 photoelectrons and single photoelectron time jitter of the photodetector J = 0.2 ns (FWHM), the CRT value using the statistically weighted average of corrected trigger times is 0.098 ns FWHM and the statistical lower bound is 0.091 ns FWHM. For LaBr3:Ce with 8000 photoelectrons and J = 0.2 ns FWHM, the CRT values are 0.070 and 0.063 ns FWHM, respectively. For the ultra-fast scintillator with 1 ns decay time, 4000 photoelectrons, and J = 0.2 ns FWHM, the CRT values are 0.021 and 0.017 ns FWHM, respectively. The examples also show that calibration and correction for depth-dependent variations in pulse height and in annihilation and optical photon transit times are necessary to achieve these CRT values.
Keywords: positron emission tomography, calibration, time of flight, scintillator, coincidence resolving time, Monte Carlo, statistical lower bound
1. Introduction
Positron emission tomography (PET) has a unique role in diagnostic medical imaging because it can noninvasively image metabolic diseases such as amyloid deposits in the brain and metastatic tumors anywhere in the body. In conventional PET annihilation events are recorded as coincident detections in pairs of scintillators, but only the line between them is used in the image reconstruction process. If two detectors can measure the time difference between the arrival of the annihilation photons to a coincidence resolving time (CRT) of Δt FWHM (full-width at half-maximum), then the position of the annihilation can be localized along the line between them to a spatial accuracy Δx = cΔt/2 (c/2 ≈ 15 cm ns−1). By using this time of flight (TOF) information the statistical noise in the reconstructed image will be reduced and the effective sensitivity will be increased by an approximate factor of D/Δx, where D is the size of the emitting region (Budinger et al 1977, Snyder et al 1981, Vunckx et al 2010). A CRT Δt = 0.08 ns FWHM corresponds to a spatial uncertainty Δx = 1.2 cm FWHM. If D = 24 cm the sensitivity will be 20 times that of a non-TOF tomograph. This will allow the detection of disease at an earlier stage (by improving image quality) or more frequent assessments of the response to therapy (by reducing the radiation dose per image) (Karp et al 2008, El Fakhri et al 2011).
In a PET system designed to achieve the best possible TOF resolution, three classes of timing error must be considered: (1) the random time distribution of the scintillation photons produced at the interaction point and the time jitter between the creation of a photoelectron and the resulting amplified output pulse, (2) the random distribution of interaction depths in the scintillator that results in variations in pulse height and in the transit times of the annihilation and optical photons, and (3) differences in timing among the individual photodetector and trigger circuits. In a previous work (Derenzo et al 2014) Monte Carlo calculations were used to characterize the effects of class (1) errors on the timing precision of a scintillation detector and to develop a closed-form analytical expression for a range of scintillator rise and decay times, optical photon time dispersions, photodetector timing jitters, and photoelectron numbers. This paper presents Monte Carlo calculations that simulate class (1) and (2) errors for a pair of scintillators and procedures for calibrating each scintillator-photodetector for class (2) and (3) errors.
This paper is organized as follows: Background section 2.1 summarizes the use of double-ended readout to estimate the depth of interaction (DOI). Background section 2.2 summarizes the optical photon time dispersion and its dependence on the DOI. Background section 2.3 summarizes the differences between fixed-fraction and fixed-level triggering. Section 3.1 describes a Monte Carlo algorithm that simulates all the important factors that contribute to the CRT. Section 3.2 describes a Monte Carlo calibration algorithm that acquires data from a positron point source and determines the factors that are shown in section 6 to successfully correct timing data taken in normal operation. Section 4 describes a Monte Carlo algorithm that determines the CRT statistical lower bound by generating a set of photoelectron times for each interaction and then shifting a DOI-dependent probability density function in time to maximize the joint likelihood for all the photoelectron times. Section 5 compares a Monte Carlo calculation with the best experimental CRT value. Section 6 tabulates values of the CRT for LSO, for LaBr3:Ce, for a hypothetical scintillator with 1 ns decay time, and for a perfect scintillator-photodetector combination. Section 7 lists the conclusions. Appendix lists the variables and abbreviations used.
2. Background
2.1. Use of double-ended readout to estimate the DOI
This section summarizes the use of double-ended readout, which has three significant advantages for PET: (1) it provides DOI information that effectively eliminates parallax error and provides good spatial resolution throughout the reconstructed images, (2) the trigger times can be corrected for depth-dependent factors so lengthening the scintillator for good detection efficiency has little effect on the CRT, and (3) it minimizes optical photon path lengths and time dispersion because the photons are absorbed by the photodetectors as soon as they reach either end. It can also provide the 3D position and energy deposition of Compton and photoelectric interactions in a block of long, narrow crystals, but a simulation of this capability is beyond the scope of this paper.
Double-ended readout can provide DOI sensitivity if the sides of the crystal absorb some of the photons so that the photodetector signal decreases with increasing distance to the interaction point. Experimental measurements show that this dependence is nearly linear, that the difference of the two photodetector outputs can be used to measure the DOI, and that the sum can be used to measure the energy deposited (Yang et al 2006, Ren et al 2014, Kang et al 2015, Seifert and Schaart 2015).
Under these conditions the average number of photons MA reaching the front (Z = 0) photodetector A can be expressed as MA = Mtot(0.5 – aZ/Zmax) where Mtot is the total number of optical photons, Z is the interaction depth, and a is the fraction absorbed. Similarly, the average number of photons MB reaching the rear (Z = Zmax) photodetector B is MB = Mtot(0.5 – a(Zmax –Z)/Zmax). The sum of the photons reaching both photodetectors is MA + MB = Mtot(1 – a). Thus the average fraction of photons absorbed is equal to a for an interaction at any Z. The value a = 0.3 is used in the example calculations (section 6). Based on experimental measurements it is a good compromise between smaller values that result in poorer DOI estimates and larger values that reduce the pulse height (Ren et al 2014).
The average numbers of optical photons that produce photoelectrons that contribute to the photodetector A and B outputs are given by:
| (1a) |
| (1b) |
where PDE is the photon detection efficiency (the product of the photodetector fill factor, the quantum efficiency and the avalanche probability) (Renker 2006, Kolb et al 2010). For SiPMs the avalanche probability is a strong function of the applied voltage.
The depth Z can be computed from the contributing photoelectron numbers using the equation:
| (2) |
Equation (2) is used in the Monte Carlo example calculations (section 6). In practice the actual dependence between pulse height and contributing photon number would be measured in a DOI calibration procedure that captures the effect of photodetector nonlinearity (Yang et al 2009). Note that for SiPM photodetectors the pulse height nonlinearity has little effect on the CRT values because it arises from late photons that arrive at microcells that have already been triggered by earlier photons. For simplicity this paper treats the PDE as a constant for all photons.
2.2. Optical photon time delay and dispersion as a function of the DOI
Published Monte Carlo calculations of the optical photon time dispersion in long scintillators show that the time distribution at the photodetector has a sharp rise (< 10 ps) at the time of arrival of a direct path (earliest possible) photon followed by an exponential decay for both rough and polished surfaces (Yeom et al 2013, Moses et al 2014, Gundacker et al 2014, Vinke et al 2014). This is consistent with experimental measurements of LSO crystals (de Haas et al 2014).
For an annihilation photon entering surface A at T = 0 and interacting at DOI Z in a scintillator with depth Zmax and refractive index n, direct path optical photons will reach photodetectors A and B at the following times.
| (3a) |
| (3b) |
(Derenzo et al 2015) presented Monte Carlo calculations of the optical photon time dispersion as a function of Z in a polished 3 mm × 3 mm × 30 mm LSO crystal with an external Teflon reflector. For the photodetectors on the surfaces X = A and B, the optical photon intensity IX(T) for T > λX(Z) was described by IX(T) = IXλX(Z)exp[−(T – λX(Z))/DX(Z)], and the time dispersion parameters DX(Z) were fitted as functions of Z by
| (4a) |
| (4b) |
with the best-fit values d1 = 0.008 73 ns and d2 = 0.0186 ns cm−1.
These relations were used in the Monte Carlo example calculations (section 6). For different scintillator geometries and models of surface reflections a simulation program such as Geant4 (Agostinelli et al 2003) can be used to calculate the appropriate D(Z) relation as described in Moses et al (2014). For a full tomograph the calibration procedure of section 3.2 includes the effect of time slewing due to the depth-dependent optical photon time dispersion without the need to know it separately.
2.3. Fixed-fraction versus fixed-level triggering
In Derenzo et al (2014) it was shown that fixed-fraction triggering resulted in optimal timing precision over large variations in pulse height. This is understandable because the timing information is greatest where the trigger level is at the point of highest pulse slope, and that point scales with pulse height. However, fixed-fraction triggering is more difficult to implement than fixed-level triggering because the trigger time depends on the pulse height, and this is only known after the pulse has peaked.
In Derenzo et al (2015) fixed-fraction triggering was used for estimating the CRT in PET, and a calibration procedure was necessary to correct for time slewing due to depth-dependent variations in optical photon dispersion. This paper shows that in PET the variations in pulse height over the DOI range are sufficiently small that a similar calibration procedure can also correct for fixed-level time slewing, and the resulting CRT values are essentially the same.
3. Monte Carlo algorithms for analog pulse processing
Section 3.1 lists the Monte Carlo algorithm steps that simulate the data generation and correction processes for two coincident scintillators with double-ended readout. Section 3.2 describes a Monte Carlo algorithm that simulates a calibration procedure for determining depth-dependent corrections and variances.
3.1. Monte Carlo simulation of the detection and timing of annihilation photon pairs
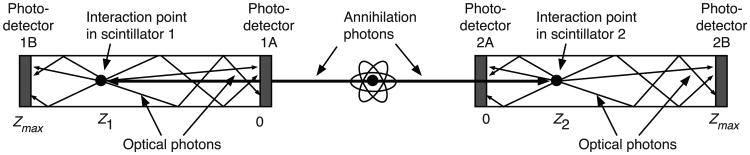
Entrance surfaces A and rear surfaces B of scintillators 1 and 2 are coupled to photodetectors 1A, 1B, 2A, and 2B (figure 1). For each annihilation photon pair the algorithm (1) selects exponentially distributed random DOIs in the two scintillators, (2) determines the randomized numbers of photons produced in the two scintillators, (3) determines the randomized number of photons that contribute to the four photodetector outputs, (4) estimates the DOIs in the scintillators from the four photodetector outputs, (5) computes four lists of randomized times when the photons contribute to the outputs, (6) generates four analog output pulses by convolving the times with the single electron response (SER), and (7) uses interpolation to determine the four trigger times for a sequence of trigger levels. This simulates the generation of pulse height and trigger timing data from the four photodetectors, as would happen for two opposing scintillators in a PET system.
Figure 1.
Annihilation photons enter scintillators 1 and 2 at surfaces 1A and 2A and interact at depths Z1 and Z2 at times Z1/c and Z2/c. Direct path optical photons will reach photodetectors 1A at time Z1/c + nZ1/c and 2A at time Z2/c + nZ2/c. Direct path optical photons will reach photodetectors 1B at time Z1/c + n(Zmax – Z1)/c and 2B at time Z2/c + n(Zmax – Z2)/c.
The algorithm then assumes the role of the experimenter and uses the randomized trigger times and pulse heights to estimate the times that the annihilation photons entered the scintillators at surfaces 1A and 2A. Specifically it corrects the trigger times for four depth-dependent factors: (1) the transit time of the annihilation photon to the point of interaction, (2) the transit time of an optical photon along a direct path to the photodetector (i.e. the earliest possible photon), (3) time dispersion of the optical photons, and (4) variations in pulse height. Factors (1) and (2) can be readily calculated and are shown in the caption of figure 1. Factors (3) and (4) depend in a complicated way on the shape and surface treatment of the scintillator, and on the shape of the photodetector output pulse; their combined effect is determined in the calibration procedure described in section 3.2.
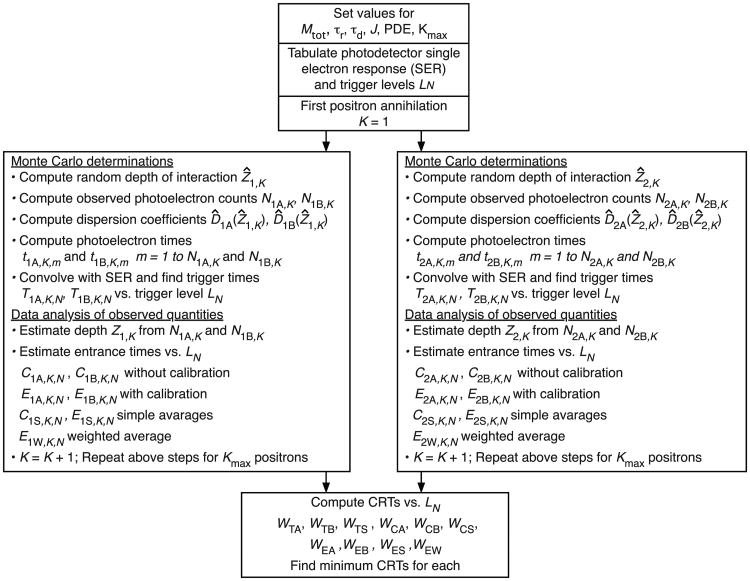
These steps are shown in a simplified block diagram in figure 2 and are described in detail in the following sections. Symbols with an over-caret (e.g. Ẑ) indicate Monte Carlo variables that are internal to the calculation and cannot be measured. Symbols without an over-caret (e.g. Z) indicate variables that can be measured or can be estimated using only measurable values. Symbols with an over-tilde (e.g. Ẽ) indicate the variance. Upper case symbols indicate variables associated with annihilation photons. Lower case symbols indicate variables associated with the photoelectrons generated by specific annihilation photons. Appendix lists the variables used in the calculations and the abbreviations used in the text.
Figure 2.
Simplified diagram of the Monte Carlo calculation of CRT values. See section 3.1 for details.
Intel 2.2 GHz Core i7 processors were used for the calculations. Four hours were required for a typical case where 4000 photoelectrons were produced by each of 200 000 annihilation photons. The REALbasic programming language (Xojo, Inc., Austin, TX) was used for the calculations but any programming language designed for scientific computing would work as well.
-
3.1.1. Tabulate the SER S(t) as a bi-exponential function with rise time Sr and decay time Sd, on a fine time grid (0.0001 ns was used in this work).
(5) where t = tpeak at the maximum value where dS/dt = 0.
This formulation was used in the Monte Carlo example calculations (section 6). In practice the shape of the SER would be included in the depth-dependent trigger delay corrections that are measured for each scintillator-photodetector in the calibration procedure (section 3.2).
3.1.2. Determine the maximum photodetector output pulse height from the calibration procedure (section 3.2) and tabulate a logarithmically spaced sequence of trigger levels LN in multiples of S(tpeak) from 0.001 to the maximum pulse height.
3.1.3. For each annihilation photon pair K, draw two random numbers R̂2K and R̂2K+1 from a set uniformly distributed between exp(−Zmax/μ) and 1. Compute the interaction depths Ẑ1,K = −μln(R̂2K) and Ẑ2K = −μln(R̂2K+1) in scintillators 1 and 2, where μ is the exponential interaction length of the annihilation photons. Ẑ = 0 at the entrance surface A, and Ẑ = Zmax at the rear surface B.
-
3.1.4. The average number of optical photons Mtot produced by an annihilation photon interaction is listed in table 1 and is the product of the scintillator luminosity and the energy (0.511 MeV).
Compute the randomized numbers of optical photons M̂X,K produced in scintillators X = 1 and 2 by annihilation photon pair K. The Fano factor is a characteristic of the scintillator (see table 1).
-
3.1.5. For scintillators X = 1 and 2 compute the most probable numbers N̂XY,K of optical photons from annihilation photon pair K that produce photoelectrons in photodetectors Y = A and B that contribute to their output. PDE is the photon detection efficiency and a is the depth-dependent absorption coefficient. (See section 2.1 for details.)
(6a) (6b) Note: The average number of photons that contribute to the photodetector outputs is the average of N̂XA,K + N̂XB,K = PDE × Mtot (1 – a) = Nave. In the example tables of section 6, Nave was constrained to different values by setting PDE equal to Nave/ ((1 – a)Mtot).
-
3.1.6. For scintillators X = 1 and 2 draw M̂X,K random numbers from a set uniformly spaced between 0 and M̂X,K.
Find NXA,K as the number of drawn numbers less than N̂XA,K. NXA,K is the randomized number of photons that produce photoelectrons in photodetector XA that contribute to the output.
Find NXB,K as the number of drawn numbers between N̂XA,K and N̂XA,K + N̂XB,K. NXB,K is the randomized number of photons that produce photoelectrons in photodetector XB that contribute to the output.
This random process generates the trinomial distribution of the optical photons that contribute to the photodetector A and B outputs, and those that do not.
-
3.1.7. Compute the optical photon time dispersion parameters for the photons that reach the 1A and 2A photodetectors (direct path length ẐX,K) and those that reach the 1B and 2B photodetectors (direct path length Zmax – ẐX,K). See section 2.2 for a discussion of these equations and the determination of the parameters d1 and d2.
(7a) (7b) These relationships were used in the Monte Carlo example calculations (section 6). In practice the actual dependence would be included in the depth-dependent trigger delay that is measured for each scintillator in the calibration procedure (section 3.2).
-
3.1.8. Generate the random times when the NXY,K photons from annihilation photon pair K start contributing to the photodetector XY = 1A, 1B, 2A, and 2B outputs. The random contributions from the scintillator rise time, the scintillator decay time, and the optical photon time dispersion are exponentially distributed. Every occurrence of R̂ is a new random number drawn from a set uniformly distributed between 0 and 1. The random contributions from the photodetector single photoelectron time jitter J are Gaussian distributed. The transit times of the annihilation photons and direct path optical photons will be included in a subsequent step.
For m = 1 to NXA,K compute
For m = 1 to NXB,K compute
3.1.9. For each photodetector XY sort the output start times t̂XY,K,m of the contributions of the NXY,K photons.
-
3.1.10. For scintillators X = 1 and 2 and at each trigger level LN (tabulated in section 3.1.2), use linear interpolation of the SER S(t) (tabulated in section 3.1.1) to find the relative trigger times
T̂XA,K,N and T̂XB,K,N when the sum of all earlier SER amplitudes is equal to LN.
-
3.1.11. For scintillators X = 1 and 2 and each trigger level LN, compute the observed trigger times TXA,K,N, TXB,K,N and their simple average TXS,K,N by adding the annihilation photon transit times and the direct path optical photon transit times (equations (3a) and (3b)) to the relative trigger times.
-
3.1.12. Estimate the DOIs in scintillators X = 1 and 2 (section 2.1, equation (2))
This algorithm was used for the example calculations (section 6). In practice the relationship between pulse height and number of contributing optical photons would be determined in a calibration procedure (Yang et al 2009).
-
3.1.13. For scintillators X = 1 and 2, and each trigger level LN, correct the observed trigger times from photodetectors Y = A and B by subtracting the annihilation and optical photon delays λ. This is an approximate estimate of the annihilation photon entrance times that does not include the depth-dependent trigger delays Δ and δ.
-
3.1.14. For scintillators X = 1 and 2 compute the simple average of the trigger times that have been corrected for the photon delays.
-
3.1.15. For scintillators X = 1 and 2, photodetectors Y = A and B, and each trigger level LN estimate the entrance times of the annihilation photons at surfaces 1A and 2A by subtracting the photon and trigger delays from the observed photodetector 1A, 2A, 1B and 2B trigger times.
The calibration procedure described in section 3.2 computes the relative trigger delays in intervals of Z. The center of the Ith interval is ZI = IZmax/Imax. The values of δXY,N(Z) are determined from a linear interpolation using the values at ZI and ZI+1 where ZI < Z < ZI+1. For a full PET system the base trigger delays Δ can be different for different scintillator-photodetector combinations, and these are measured in the calibration procedure (section 3.2). For the Monte Carlo example calculations (section 6) the base trigger delays do not vary from annihilation event to annihilation event and do not contribute to the CRT values.
-
3.1.16. The corrected trigger times from photodetectors 1A, 2A, 1B and 2B are independent estimates of the annihilation photon entrance times at surfaces 1A and 2A. For scintillators X = 1 and 2 compute the simple averages at each trigger level LN.
-
3.1.17. For scintillators X = 1 and 2 compute the statistically weighted averages at each trigger level LN. Since the variances of the corrected trigger times from photodetectors A and B are not equal, the average weighted by the inverse of their variances is statistically the best way to combine them. The calibration procedure that measures the variances is described in section 3.2.
ẼXA,N(Z) and ẼXB,N(Z) for scintillators X = 1 and 2 are determined from a linear interpolation using the values at ZI and ZI+1 where ZI < Z < ZI+1.
3.1.18. Repeat sections 3.1.3–3.1.17 for K = 1 to Kmax annihilation events.
-
3.1.19. Use the data from the Kmax annihilation events to compute the rms of the various raw and corrected time differences between the two scintillators. Convert these to CRT FWHM values and find the optimum trigger levels. In a full tomograph the optimum trigger level would be determined in the calibration procedure (section 3.2).
WTA = 2.355 × (T1A,K,N – T2A,K,N)rms at the optimal trigger level.
WTB = 2.355 × (T1B,K,N – T2B,K,N)rms at the optimal trigger level.
WTS = 2.355 × (T1S,K,N – T2S,K,N)rms at the optimal trigger level.
WCA = 2.355 × (C1A,K,N – C2A,K,N)rms at the optimal trigger level.
WCB = 2.355 × (C1B,K,N – C2B,K,N)rms at the optimal trigger level.
WCS = 2.355 × (C1S,K,N – C2S,K,N)rms at the optimal trigger level.
WEA = 2.355 × (E1A,K,N – E2A,K,N)rms at the optimal trigger level.
WEB = 2.355 × (E1B,K,N – E2B,K,N)rms at the optimal trigger level.
WES = 2.355 × (E1S,K,N – E2S,K,N)rms at the optimal trigger level.
WEW = 2.355 × (E1W,K,N – E2W,K,N)rms at the optimal trigger level.
Table 1.
Parameters used in the Monte Carlo calculations for two known and two hypothetical scintillators.
| Lu2SiO5:Ce,Ca (LSO) | LaBr3:Ce | Ultra-fast | Perfect | |
|---|---|---|---|---|
| Size (mm) | 3 × 3 × 30 | 3 × 3 × 30 | 3 × 3 × 30 | 3 × 3 × 30 |
| Interaction length μ for 511 keV photons (cm) | 1.2 | 2.3 | 1.2a | 1.2a |
| Refractive index n | 1.82 | 2.1 | 2a | 1.5 and 2.0a |
| Scintillator Fano factor | 6.5 | 1 | 1a | 1a |
| Photons per 511 keV Mtot | 20 000 | 38 000 | 20 000a | >10 000a |
| Rise time τr (ns) | 0.021 (Nemallapudi et al 2015) | 0.2 (Glodo et al 2005) | 0.0a | 0.0a |
| Decay time τd (ns) | 28 (Nemallapudi et al 2015) | 18 (Glodo et al 2005) | 1a | 0.0a |
Hypothetical values.
3.2. Monte Carlo simulation of the calibration for measuring timing corrections and variances
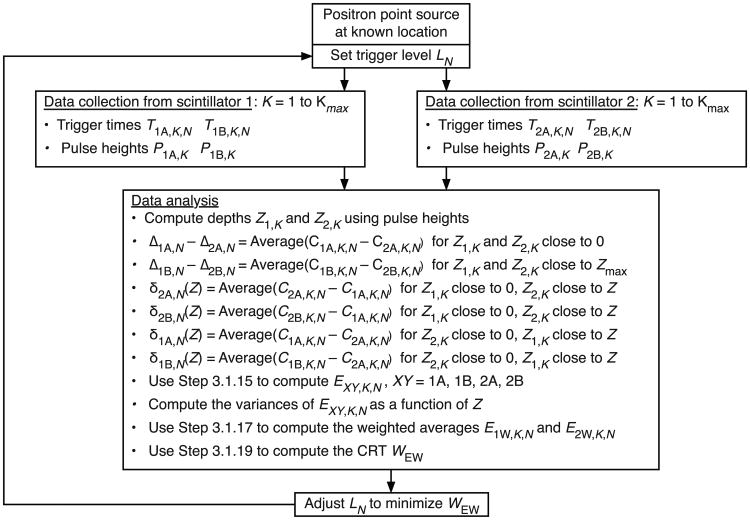
This section describes a Monte Carlo algorithm that simulates the acquisition of calibration data from a positron point source and determines depth-dependent trigger time correction factors and variances (figure 3). Annihilation photons that interact near the entrance surface of one scintillator are selected, and the relative trigger delays from the photodetectors on the other scintillator are calculated and averaged over intervals of depth to provide depth-dependent trigger-time corrections for section 3.1. This simulates the calibration procedure for a full positron tomograph.
Figure 3.
Simplified diagram of the Monte Carlo simulation of data acquisition and the calculation of trigger corrections and variances. See section 3.2 for details.
For interactions close to the entrance surface in one scintillator the pulse height in photodetector A is maximal and the optical photon time dispersion is minimal. This is used as a reference time that allows the relative trigger delays δA,N(Z) and δB,N(Z) of photodetectors A and B of the other scintillator to be measured as a function of interaction depth Z and trigger level LN. The relative trigger delays increase with increasing distance from the interaction point to the photodetector, because the pulse height decreases and the optical photon time dispersion increases. These relationships are difficult to predict and depend on the surface treatment of the scintillator and the photodetector SER. The calibration procedure described in this section is designed to empirically measure the combined effect of these factors without the need to know them individually.
3.2.1. Place a positron point source between the scintillation detectors being calibrated and acquire data on pulse height and trigger times from the four photodetectors 1A, 1B, 2A, and 2B. The corresponding Monte Carlo calculation is in steps 3.1.1–3.1.11.
3.2.2. Perform section 3.1.12 to estimate the depths of interaction Z1,K and Z2,K in scintillators 1 and 2 for each annihilation photon pair K.
-
3.2.3. For scintillators X = 1 and 2, and each trigger level LN, correct the observed trigger times from photodetectors Y = A and B by subtracting the annihilation and optical photon delays λ (equations (3a) and (3b)).
-
3.2.4. Select events where the two annihilation photons interact in the two scintillators close to photodetectors 1A and 2A. These interactions produce the highest pulse heights, the least optical photon dispersion, and the earliest trigger times in those photodetectors. For these interactions both the photon transit times λ1A and λ2A and the relative trigger delays δ1A,N and δ2A,N are minimal, and the difference in the trigger times corrected for photon delays is equal to the difference in base trigger delays.
-
3.2.5. Similarly, select events where the two annihilation photons interact in the two scintillators close to photodetectors 1B and 2B.
For simplicity in the sections below and in the section 6 example calculations the base trigger delays are set to zero since they do not change from interaction to interaction and do not contribute to the CRT. In practice the base trigger delay for each photodetector circuit in a PET system would be estimated using calibration data (Werner and Karp 2013).
-
3.2.6. Select events close to surface A in scintillator 1 (i.e. Z1 is between 0 and cutoff Zcut)and distributed in depth in scintillator 2. Tabulate the relative trigger delays δ2A,K,N and δ2B,K,N as the difference between the 2A and 2B trigger times and the 1A reference trigger times that have been corrected for photon delays.
-
3.2.7. For photodetectors Y = A and B compute the relative trigger delays and variances averaged over the interactions in each depth interval centered at depth Zi in scintillator 2. The average trigger delays include (1) time slewing due to variations in pulse height with depth and (2) time slewing due to variations in optical photon time dispersion with depth. For the examples in section 6, the calculations used Imax = 10. The variances are the weighting factors for the statistically weighted average of the corrected trigger times that are used in section 3.1.16.
-
3.2.8. Select events close to surface A in scintillator 2 (i.e. Z2 is between 0 and cutoff Zcut) and tabulate the trigger delays δ1A,K,N and δ1B,K,N as the difference between the 1A and 1B trigger times and the 2A reference trigger times that have been corrected for photon delays.
-
3.2.9. For photodetectors Y = A and B compute the relative trigger delays and variances averaged over the interactions in each depth interval centered at depth ZI in scintillator 1.
In practice calibration data would be collected for different trigger levels, and sections 3.1.17 and 3.1.19 would be used to find the trigger level that minimized the CRT WEW.
4. Computation of the statistical lower bound
In this section we present a realistic Monte Carlo simulation where the DOIs are exponentially distributed throughout the length of the scintillator and the scintillation photons are shared between the two photodetectors according to depth (equations (1a) and (1b)). For each interaction a set of photoelectron times is generated for the A and B photodetectors and a DOI-dependent probability density function (PDF) is shifted in time to maximize the joint likelihood. Since the variances of the best-fit A and B times are not equal a statistically weighted average is used to combine them. The lower bound CRT values are the same as in previous calculations where all interactions were placed at the center of the scintillator (Derenzo et al 2015). This shows that the CRT lower bound is determined by the scintillator and photodetector properties and the total number of photoelectrons, not by how the photo-electrons are distributed between the two photodetectors.
Section 4.1 describes the computation of lookup tables of the natural logarithm of the PDF as a function of time and DOI. Section 4.2 describes the Monte Carlo algorithm that computes the CRT statistical lower bound for the example calculations (section 6). Section 4.3 describes the calculation of the variances needed for the statistically weighted average.
4.1. Analytical computation of the probability density function (PDF) versus DOI
The PDF depends on the scintillator rise and decay times (τr and τd), the optical photon time dispersion parameter (d), and the FWHM timing jitter of the photodetector (J). J = 2.355σ. The analytical formula for the PDF was taken from Derenzo et al (2014) with modifications for the special cases where the photodetector timing jitter J or the scintillator rise time τr was zero. Erfc is the complementary error function.
| (8) |
For the particular values of τr, τd, and J in each run, the natural logarithm of the PDFX,I(t) was tabulated for t = −100 ns to +1900 ns on a 0.001 ns grid, for photodetectors X = A and B, and for ZI = IZmax/10, I = 0–10. Equations (4a) and (4b) were used to relate the optical photon dispersion coefficient DX,I to the depth ZI.
4.2. Monte Carlo computation of the CRT statistical lower bound
This section describes a Monte Carlo algorithm that computes the statistical lower bound of the CRT for particular values of the scintillator length Zmax, refractive index n, rise time τr, decay time τd, photodetector FWHM timing jitter J, and average number of photoelectrons Nave. For each annihilation photon the algorithm (1) generates a random DOI, (2) generates a set of random times for the photoelectrons produced in the A and B photodetectors, and (3) shifts PDFA,I(t) and PDFB,I(t) in time to maximize the joint likelihood for all the photoelectron times in the A and B sets, respectively. For each photoelectron ln(PDFX,I(t)) is determined by quadratic interpolation in t of the tables generated in section 4.1. The best fit times for the A and B photodetectors are combined using their statistically weighted averages, where the weights are the inverse of the variances. The CRT lower bound is calculated as √2 times the FWHM of the distribution of the statistically weighted averages for the single scintillator.
4.2.1. For photodetectors X = A and B tabulate the natural logarithm of PDFX,I(t) as described in section 4.1.
4.2.2. As in section 3.1.3, for each interacting annihilation photon K select a random number R̂K from a set uniformly distributed between exp(−Zmax/μ) and 1. Compute the interaction depth ẐK = −μln(R̂K) and determine the index I for the ZI interval that contains it.
4.2.3. As in sections 3.1.4–3.1.6, compute the randomized number of photons NA,K and NB,K that produce photoelectrons in photodetectors A and B.
-
4.2.4. As in section 3.1.7, compute the optical photon time dispersion parameters for the photons that reach detectors A and B.
-
4.2.5. As in section 3.1.8, generate random photoelectron pulse times in the photodetectors Y = A and B for annihilation photon K.
For the statistical lower bound it is assumed that the DOI is known perfectly (i.e. sections 3.1.11 and 3.1.13 cancel), so time zero is the time that the annihilation photon entered the front surface A.
-
4.2.6. Perform a maximum likelihood fit of PDFX,I(t) to the photoelectron times t̂Y,K,m generated in section 4.2.5 to determine the most likely entrance time ΨY,K. Specifically, for photodetectors Y = A and B find the time shift ΨY,K that maximizes the joint likelihood. This uses the time information from all the photoelectrons.
Vary ΨY,K to maximize where ẐK is in the Ith depth interval.
Quadratic interpolation on the 0.001 ns time grid (section 4.2.1) was necessary for the joint likelihood to be smooth at the maximum value.
-
4.2.7. Photodetectors A and B receive different numbers of photons (depending on depth ẐK), and the variances of the best fit entrance times will not be equal. The best way to combine them statically is with the inverse variance weighted average.
4.2.8. Repeat sections 4.2.2–4.2.7 for K = 1 to Kmax annihilation photons.
4.2.9. Compute the CRT statistical lower bound WWLB as √2 times the FWHM of the distribution over K of the statistically weighted average ΨWAB,K.
4.3. Monte Carlo calculation of the variances of the maximum likelihood fits
This section computes the variances of the entrance times of photodetectors A and B as a function of the depth (Z) used in section 4.2.7.
4.3.1. Perform sections 4.2.2–4.2.7 to fnd the randomized photoelectron numbers NA,K and NB,K, and the best ft maximum likelihood times ΨA,K and ΨB,K for annihilation photon K detected in photodetectors A and B.
4.3.2. Repeat for K = 1 to Kmax annihilation events.
-
4.3.3. Loop over K and compute the variances of the maximum likelihood fits:
5. Comparison with an experimental value of CRT for LSO
An excellent CRT value of 0.085 ± 0.004 ns FWHM was reported for 2 mm × 2 mm × 3 mm deep LSO crystals codoped with Ca and read out by single SiPM photodetectors (Nemallapudi et al 2015). The scintillation properties were described as follows: rise time 0.021 ± 0.020 ns, decay times 8 ns (6%) and 33 ns (94%), and light output 26 200 photons MeV−1. The photodetectors used had single photoelectron timing jitters J = 0.177 ns FWHM and photon detection efficiencies of 35.6 ± 2.5%. Using these figures, the number of photoelectrons can be estimated as (26 200 photons MeV−1) × (0.511 MeV) × (35.6%) = 4766. This is close to the value of 4700 photoelectrons reported in Seifert et al (2012). The sum of the initial intensities of the two components is 6%/8 ns (0.8% ns−1) plus 94%/33 ns (2.8% ns−1) for a total of 3.6% ns−1. The same initial intensity is produced by a single component with a decay time of 28 ns (3.6% ns−1).
The Monte Carlo algorithm (section 3.1) was validated against the experimental value of the CRT. The calculation used τr = 0.021 ns, τd = 28 ns, J = 0.177 ns FWHM, Zmax = 0.3 cm, Nave = 9532 and fmax = 0.5. As in the experiment, an average of 4766 photoelectrons is produced in each of two separate photodetectors. The calculated CRT value between the two photodetectors is 0.085 ns FWHM, in excellent agreement with the measured value of 0.085 ns FWHM. Because the scintillator is short, these CRT values are dominated by statistical fluctuations in the scintillation and photodetection processes rather than by the variations in the DOI. Using the methods of section 4, the statistical CRT lower bound for the 0.3 cm deep LSO crystal is 0.078 ps FWHM, only 9% lower than both the measured value and the Monte Carlo calculation.
6. Example calculations of CRT values for two known and two hypothetical scintillators
6.1. Scintillator and photodetector parameters used in the calculations
Table 1 lists the properties of the four scintillators used in the example calculations. The first two are in common use. The third is a hypothetical ultra-fast scintillator that could be based on allowed donor-acceptor radiative transitions in a heavy-atom semiconductor (Lehmann 1966, Bourret-Courchesne et al 2009, Derenzo et al 2013, 2016). The fourth is a perfect scintillator-photodetector combination used to isolate the factors that depend on the scintillator length and the ability to estimate the DOI using double-ended readout.
The Fano factor for LaBr3:Ce was taken to be 1 because of its known proportionality and excellent energy resolution. The energy resolution of LSO is much poorer and its Fano factor is significantly larger, with published values of 6.5 (Lecomte et al 1998) and 4.2 (Lecomte et al 1999). The example calculations of section 6.2 use a Fano factor of 5 as an approximate average of the two values.
The optical photon time dispersion parameters were calculated from equations (4a) and (4b) using d1 = 0.008 73 ns and d2 = 0.0186 ns cm−1. The photoelectrons were distributed between the two photodetectors according to equations (1a) and (1b) with a = 0.3 and the resulting DOI uncertainty was 8.2 (Nave)−1/2 cm FWHM. The photodetector SER was a bi-exponential with a 0.2 ns rise time and a 2 ns decay time. As shown in Derenzo et al (2015) the CRT at the optimum trigger level does not depend strongly on the shape of the photodetector SER.
6.2. Example calculations: LSO
Table 2 lists the calculated CRT values for LSO. For the typical values Nave = 4000 and J = 0.2 ns FWHM the CRT using the statistically weighted average of the fully corrected trigger times (WEW) is 0.098 ns FWHM, 24% lower than the simple average of the trigger times and 8% higher than the statistical lower bound. A total of 100 000 annihilation photon pairs were used in each case and the rms uncertainties are 0.22% of the CRT values.
Table 2.
CRT values for Lu2SiO5:Ce,Ca. See table 1 for scintillator properties and appendix for variable definitions. Columns 3–12 are CRT values in ns FWHM for optimal trigger levels.
| Nave | J (ns FWHM) | WTA | WTB | WTS | WCA | WCB | WCS | WEA | WEB | WES | WEW | WLB |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1000 | 0.0 | 0.383 | 0.342 | 0.193 | 0.225 | 0.312 | 0.178 | 0.206 | 0.290 | 0.177 | 0.149 | 0.141 |
| 2000 | 0.0 | 0.321 | 0.224 | 0.131 | 0.138 | 0.189 | 0.105 | 0.122 | 0.172 | 0.105 | 0.088 | 0.079 |
| 4000 | 0.0 | 0.290 | 0.164 | 0.104 | 0.090 | 0.123 | 0.067 | 0.077 | 0.109 | 0.066 | 0.055 | 0.048 |
| 8000 | 0.0 | 0.272 | 0.130 | 0.092 | 0.063 | 0.084 | 0.044 | 0.051 | 0.073 | 0.044 | 0.037 | 0.030 |
| 16 000 | 0.0 | 0.260 | 0.109 | 0.086 | 0.044 | 0.059 | 0.030 | 0.035 | 0.049 | 0.030 | 0.025 | 0.020 |
|
| ||||||||||||
| 1000 | 0.1 | 0.408 | 0.364 | 0.206 | 0.254 | 0.333 | 0.193 | 0.231 | 0.309 | 0.192 | 0.170 | 0.162 |
| 2000 | 0.1 | 0.347 | 0.255 | 0.145 | 0.172 | 0.219 | 0.124 | 0.150 | 0.196 | 0.123 | 0.111 | 0.103 |
| 4000 | 0.1 | 0.318 | 0.199 | 0.114 | 0.127 | 0.156 | 0.084 | 0.102 | 0.133 | 0.083 | 0.075 | 0.069 |
| 8000 | 0.1 | 0.302 | 0.165 | 0.097 | 0.099 | 0.118 | 0.058 | 0.071 | 0.091 | 0.057 | 0.052 | 0.048 |
| 16 000 | 0.1 | 0.291 | 0.145 | 0.087 | 0.080 | 0.093 | 0.041 | 0.050 | 0.064 | 0.040 | 0.037 | 0.033 |
|
| ||||||||||||
| 1000 | 0.2 | 0.454 | 0.414 | 0.234 | 0.305 | 0.383 | 0.224 | 0.277 | 0.352 | 0.223 | 0.206 | 0.196 |
| 2000 | 0.2 | 0.392 | 0.307 | 0.169 | 0.222 | 0.270 | 0.153 | 0.188 | 0.239 | 0.151 | 0.140 | 0.131 |
| 4000 | 0.2 | 0.358 | 0.246 | 0.129 | 0.170 | 0.203 | 0.106 | 0.131 | 0.163 | 0.105 | 0.098 | 0.091 |
| 8000 | 0.2 | 0.337 | 0.207 | 0.105 | 0.137 | 0.158 | 0.074 | 0.091 | 0.113 | 0.073 | 0.068 | 0.063 |
| 16 000 | 0.2 | 0.322 | 0.182 | 0.091 | 0.114 | 0.129 | 0.053 | 0.064 | 0.080 | 0.051 | 0.048 | 0.045 |
|
| ||||||||||||
| 1000 | 0.3 | 0.502 | 0.470 | 0.269 | 0.359 | 0.439 | 0.261 | 0.328 | 0.401 | 0.259 | 0.244 | 0.230 |
| 2000 | 0.3 | 0.435 | 0.357 | 0.192 | 0.268 | 0.321 | 0.180 | 0.224 | 0.276 | 0.178 | 0.167 | 0.156 |
| 4000 | 0.3 | 0.394 | 0.288 | 0.143 | 0.209 | 0.244 | 0.125 | 0.156 | 0.191 | 0.123 | 0.116 | 0.109 |
| 8000 | 0.3 | 0.368 | 0.244 | 0.114 | 0.170 | 0.195 | 0.090 | 0.109 | 0.134 | 0.087 | 0.082 | 0.076 |
| 16 000 | 0.3 | 0.348 | 0.214 | 0.095 | 0.142 | 0.161 | 0.064 | 0.077 | 0.094 | 0.061 | 0.058 | 0.053 |
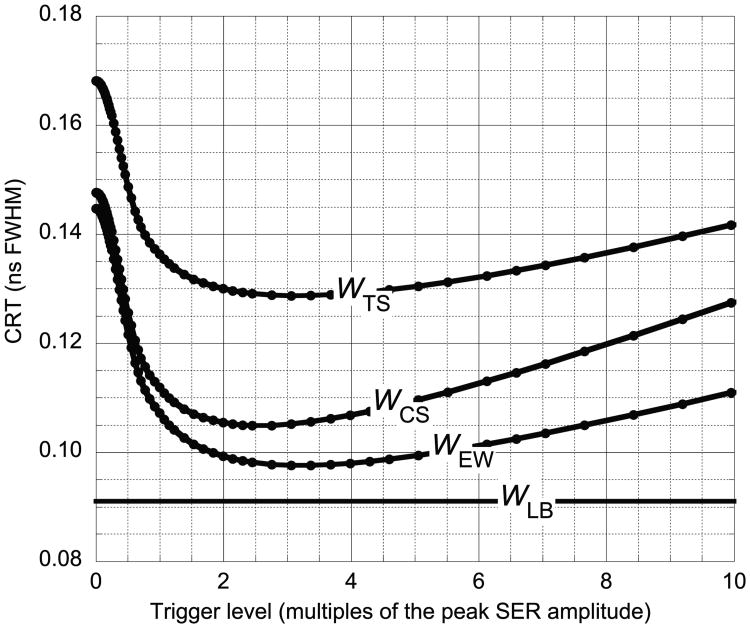
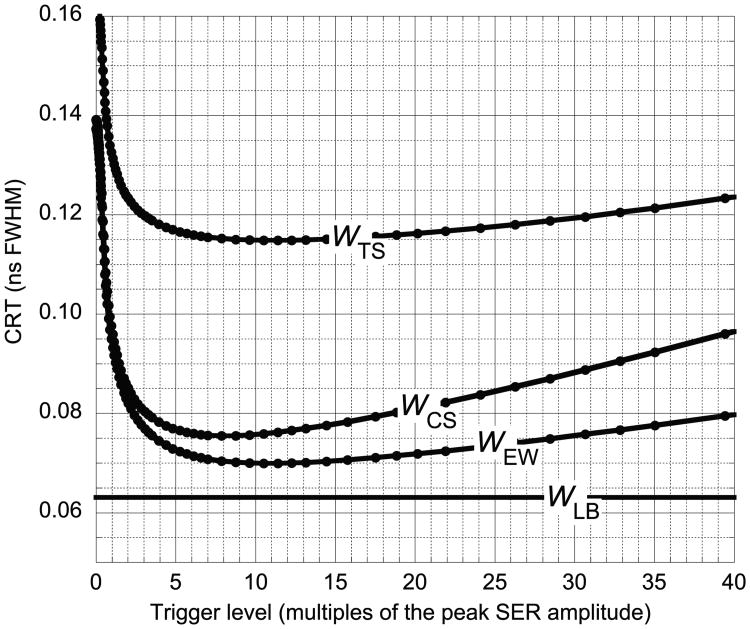
Figure 4 shows four CRT curves for LSO plotted as a function of trigger level in units of the peak SER. WTS is the CRT using the simple average of the uncorrected A and B trigger times. WCS is the CRT using the simple average of the A and B trigger times that have been corrected only for photon delays. WEW is the CRT using the statistically weighted average of the A and B trigger times that have been corrected for depth-dependent variations in the annihilation and optical photon transit times, and time slewing due to depth-dependent variations in optical photon time dispersion and pulse height. Wlb is the statistical lower bound. The WCS and WEW curves are considerably lower than the WTS curve and much closer to WLB.
Figure 4.
CRT curves for LSO with J = 0.2 ns FWHM and Nave = 4000 plotted as a function of trigger level. The average pulse heights from photodetectors A and B are 178 and 132 times the peak SER amplitude, respectively. See table 1 for scintillator properties and appendix for variable definitions.
Table 3 lists the calculated CRT values as a function of the scintillator length Zmax. Both WTS and WCS increase with Zmax. Wew increases very slowly with Zmax, showing that the calibration and correction procedures presented in this paper allow the use of deep scintillators with very little degradation in the CRT.
Table 3.
CRT values for Lu2SiO5:Ce,Ca four values of Zmax, with Nave = 4000, τr = 0.021 ns, τd = 28 ns, and J = 0.177 ns FWHM. See appendix for parameter definitions. Columns 2–11 are CRT values in ns FWHM for optimal trigger levels. The CRT lower bound is 0.091 ns FWHM.
| Zmax (cm) | WTA | WTB | WTS | WCA | WCB | WCS | WEA | WEB | WES | WEW |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.3 | 0.165 | 0.158 | 0.097 | 0.152 | 0.155 | 0.097 | 0.134 | 0.137 | 0.096 | 0.093 |
| 1.0 | 0.213 | 0.180 | 0.102 | 0.157 | 0.166 | 0.098 | 0.133 | 0.141 | 0.097 | 0.094 |
| 2.0 | 0.290 | 0.213 | 0.114 | 0.164 | 0.183 | 0.101 | 0.132 | 0.150 | 0.100 | 0.095 |
| 3.0 | 0.355 | 0.240 | 0.128 | 0.168 | 0.197 | 0.105 | 0.131 | 0.161 | 0.104 | 0.097 |
Table 4 lists the calculated CRT values for LSO with two assumed Fano factors (section 3.1.4). A Fano factor >1 increases the variation in the number of photons but has only a small effect on the CRT values. This is understandable because it does not affect the average number or time distribution of the photoelectrons.
Table 4.
CRT values for Lu2SiO5:Ce,Ca with Fano factors of 1 and 5. See appendix for parameter definitions. Columns 4–8 are CRT values in ns FWHM for optimal trigger levels.
| Fano | Nave | J | WTS | WEA | WEB | WES | WEW |
|---|---|---|---|---|---|---|---|
| 1 | 1000 | 0.0 | 0.193 | 0.206 | 0.290 | 0.177 | 0.149 |
| 5 | 1000 | 0.0 | 0.193 | 0.205 | 0.291 | 0.177 | 0.149 |
|
| |||||||
| 1 | 16 000 | 0.0 | 0.086 | 0.035 | 0.049 | 0.030 | 0.025 |
| 5 | 16 000 | 0.0 | 0.086 | 0.035 | 0.050 | 0.030 | 0.025 |
|
| |||||||
| 1 | 1000 | 0.3 | 0.269 | 0.328 | 0.401 | 0.259 | 0.244 |
| 5 | 1000 | 0.3 | 0.269 | 0.329 | 0.401 | 0.259 | 0.244 |
|
| |||||||
| 1 | 16 000 | 0.3 | 0.095 | 0.077 | 0.093 | 0.061 | 0.057 |
| 5 | 16 000 | 0.3 | 0.095 | 0.077 | 0.094 | 0.061 | 0.058 |
Table 5 lists the average number of photons (M̂A and M̂B) and trigger times (TA and TB) for photodetectors A and B, respectively, as a function of the DOI for LSO using the parameters listed in table 1. The trigger time TA increases with Z because the annihilation and optical photon transit times increase and the pulse height decreases. The trigger time TB decreases with Z for the same reasons. The simple average of the trigger times TS has a reduced dependence on Z due to the partial cancellation of these factors.
Table 5.
Average number of contributing photons and observed trigger times as a function of DOI for 3 × 3 × 30 mm LSO scintillator detectors. See text for interpretation.
| Z (cm) | N̂A | N̂B | TA(Z) | TB(Z) | TS(Z) |
|---|---|---|---|---|---|
| 0.15 | 2720 | 1280 | 0.134 | 0.437 | 0.286 |
| 0.45 | 2560 | 1440 | 0.172 | 0.407 | 0.289 |
| 0.75 | 2400 | 1600 | 0.212 | 0.380 | 0.296 |
| 1.05 | 2240 | 1760 | 0.253 | 0.355 | 0.304 |
| 1.35 | 2080 | 1920 | 0.296 | 0.331 | 0.313 |
| 1.65 | 1920 | 2080 | 0.339 | 0.308 | 0.323 |
| 1.95 | 1760 | 2240 | 0.383 | 0.285 | 0.334 |
| 2.25 | 1600 | 2400 | 0.428 | 0.264 | 0.346 |
| 2.55 | 1440 | 2560 | 0.475 | 0.243 | 0.359 |
| 2.85 | 1280 | 2720 | 0.525 | 0.225 | 0.375 |
Table 6 lists the average photon delays λA, λB, and their simple average λS; and the trigger times CA, CB corrected for photon delays, and their simple average CS as a function of the DOI for LSO with the parameters listed in table 1. The variation of CA and CB with Z is less than that of TA and TB but has not been eliminated due to the remaining dependence on the relative trigger delay. These errors partly cancel in the simple average CS, which has a significantly reduced dependence on Z.
Table 6.
Trigger times corrected only for photon delays.
| Z (cm) | λA(Z) | λB(Z) | λS(Z) | CA(Z) | CB(Z) | CS(Z) |
|---|---|---|---|---|---|---|
| 0.15 | 0.014 | 0.178 | 0.096 | 0.120 | 0.259 | 0.189 |
| 0.45 | 0.042 | 0.170 | 0.106 | 0.129 | 0.237 | 0.183 |
| 0.75 | 0.071 | 0.162 | 0.116 | 0.141 | 0.218 | 0.180 |
| 1.05 | 0.099 | 0.153 | 0.126 | 0.155 | 0.201 | 0.178 |
| 1.35 | 0.127 | 0.145 | 0.136 | 0.169 | 0.185 | 0.177 |
| 1.65 | 0.155 | 0.137 | 0.146 | 0.183 | 0.171 | 0.177 |
| 1.95 | 0.183 | 0.129 | 0.156 | 0.199 | 0.156 | 0.178 |
| 2.25 | 0.212 | 0.121 | 0.166 | 0.217 | 0.143 | 0.180 |
| 2.55 | 0.240 | 0.112 | 0.176 | 0.235 | 0.131 | 0.183 |
| 2.85 | 0.268 | 0.104 | 0.186 | 0.257 | 0.121 | 0.189 |
Table 7 lists the average relative trigger delays δA, δB, and their simple average δS; and the fully corrected trigger times EA, and EB and their average ES as a function of the DOI for LSO with the parameters listed in table 1. The relative trigger delay δA in the photodetector A circuit increases with Z for two reasons: (1) the pulse height decreases and (2) the increase in the optical photon time dispersion decreases the rate of rise of the output pulse. Both of these delay the time to reach a fixed-level trigger. The trigger time δB in the photodetector B circuit decreases with Z for the same reasons.
Table 7.
Annihilation photon entrance times estimated by fully correcting the observed trigger times for the photon delays and the trigger delays computed from the calibration data. ΔA = ΔB = 0.121 ns.
| Z (cm) | δA | δB | δS | EA(Z) | EB(Z) | ES(Z) |
|---|---|---|---|---|---|---|
| 0.15 | 0.000 | 0.138 | 0.069 | −0.001 | 0.000 | 0.000 |
| 0.45 | 0.009 | 0.116 | 0.062 | −0.001 | 0.000 | 0.000 |
| 0.75 | 0.021 | 0.098 | 0.059 | −0.001 | 0.000 | 0.000 |
| 1.05 | 0.034 | 0.080 | 0.057 | 0.000 | 0.000 | 0.000 |
| 1.35 | 0.048 | 0.064 | 0.056 | −0.001 | 0.001 | 0.000 |
| 1.65 | 0.063 | 0.049 | 0.056 | −0.001 | 0.000 | 0.000 |
| 1.95 | 0.079 | 0.035 | 0.057 | 0.000 | 0.000 | 0.000 |
| 2.25 | 0.096 | 0.022 | 0.059 | 0.000 | 0.000 | 0.000 |
| 2.55 | 0.115 | 0.010 | 0.062 | 0.000 | 0.000 | 0.000 |
| 2.85 | 0.137 | −0.001 | 0.068 | −0.001 | 0.001 | 0.000 |
When one calibration data set is used to determine the depth-dependent trigger delays, and the trigger times from a separate data set are corrected for both photon and trigger delays the results (EA, EB, ES) are close to zero for all DOIs. This shows that the depth-dependent corrections measured in a separate calibration procedure are able to fully compensate for depth-dependent timing variations. The 0.121 ns base trigger delays ΔA and ΔB depend on the shape of the photodetector output pulse and were determined in the calibration procedure (section 3.2).
6.3. Example calculations: LaBr3:Ce
Table 8 lists the calculated CRT values for LaBr3:Ce. For the typical values Nave = 8000 and J = 0.2 ns FWHM the CRT using the statistically weighted average of the fully corrected trigger times WEW is 0.070 ns FWHM, 39% lower than the simple average of the trigger times and 11% higher than the statistical lower bound. LaBr3:Ce has about twice the luminosity and 2/3 the decay time of LSO, but its longer rise time significantly reduces its CRT advantage.
Table 8.
CRT values for LaBr3:Ce. See table 1 for scintillator properties and appendix for variable definitions. Columns 3–12 are CRT values in ns FWHM for optimal trigger levels.
| Nave | J (ns FWHM) | WTA | WTB | WTS | WCA | WCB | WCS | WEA | WEB | WES | WEW | WLB |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2000 | 0.0 | 0.411 | 0.278 | 0.154 | 0.192 | 0.216 | 0.125 | 0.167 | 0.189 | 0.125 | 0.116 | 0.101 |
| 4000 | 0.0 | 0.374 | 0.224 | 0.125 | 0.139 | 0.157 | 0.087 | 0.116 | 0.132 | 0.087 | 0.080 | 0.067 |
| 8000 | 0.0 | 0.350 | 0.189 | 0.108 | 0.104 | 0.117 | 0.061 | 0.081 | 0.092 | 0.061 | 0.056 | 0.045 |
| 16 000 | 0.0 | 0.334 | 0.165 | 0.099 | 0.079 | 0.088 | 0.043 | 0.057 | 0.064 | 0.043 | 0.039 | 0.031 |
| 32 000 | 0.0 | 0.322 | 0.148 | 0.094 | 0.060 | 0.067 | 0.031 | 0.040 | 0.046 | 0.030 | 0.028 | 0.021 |
|
| ||||||||||||
| 2000 | 0.1 | 0.429 | 0.298 | 0.161 | 0.213 | 0.236 | 0.136 | 0.181 | 0.202 | 0.135 | 0.127 | 0.112 |
| 4000 | 0.1 | 0.394 | 0.247 | 0.129 | 0.162 | 0.178 | 0.094 | 0.126 | 0.142 | 0.094 | 0.088 | 0.078 |
| 8000 | 0.1 | 0.373 | 0.214 | 0.110 | 0.129 | 0.139 | 0.067 | 0.088 | 0.098 | 0.066 | 0.062 | 0.053 |
| 16 000 | 0.1 | 0.358 | 0.192 | 0.100 | 0.104 | 0.112 | 0.047 | 0.062 | 0.069 | 0.046 | 0.044 | 0.038 |
| 32 000 | 0.1 | 0.350 | 0.178 | 0.095 | 0.087 | 0.093 | 0.034 | 0.044 | 0.049 | 0.033 | 0.031 | 0.026 |
|
| ||||||||||||
| 2000 | 0.2 | 0.465 | 0.335 | 0.173 | 0.249 | 0.272 | 0.151 | 0.201 | 0.224 | 0.150 | 0.142 | 0.129 |
| 4000 | 0.2 | 0.430 | 0.284 | 0.137 | 0.196 | 0.212 | 0.107 | 0.141 | 0.157 | 0.105 | 0.100 | 0.090 |
| 8000 | 0.2 | 0.405 | 0.248 | 0.115 | 0.160 | 0.171 | 0.075 | 0.099 | 0.110 | 0.074 | 0.070 | 0.063 |
| 16 000 | 0.2 | 0.391 | 0.225 | 0.103 | 0.135 | 0.142 | 0.054 | 0.070 | 0.077 | 0.052 | 0.049 | 0.045 |
| 32 000 | 0.2 | 0.378 | 0.208 | 0.095 | 0.116 | 0.122 | 0.039 | 0.049 | 0.055 | 0.037 | 0.035 | 0.032 |
|
| ||||||||||||
| 2000 | 0.3 | 0.500 | 0.373 | 0.187 | 0.286 | 0.309 | 0.168 | 0.224 | 0.247 | 0.166 | 0.159 | 0.144 |
| 4000 | 0.3 | 0.461 | 0.317 | 0.146 | 0.227 | 0.244 | 0.119 | 0.156 | 0.173 | 0.116 | 0.111 | 0.101 |
| 8000 | 0.3 | 0.434 | 0.280 | 0.120 | 0.188 | 0.200 | 0.085 | 0.110 | 0.121 | 0.082 | 0.078 | 0.071 |
| 16 000 | 0.3 | 0.415 | 0.253 | 0.105 | 0.161 | 0.170 | 0.062 | 0.078 | 0.086 | 0.058 | 0.056 | 0.050 |
| 32 000 | 0.3 | 0.403 | 0.236 | 0.097 | 0.141 | 0.148 | 0.045 | 0.055 | 0.061 | 0.041 | 0.039 | 0.035 |
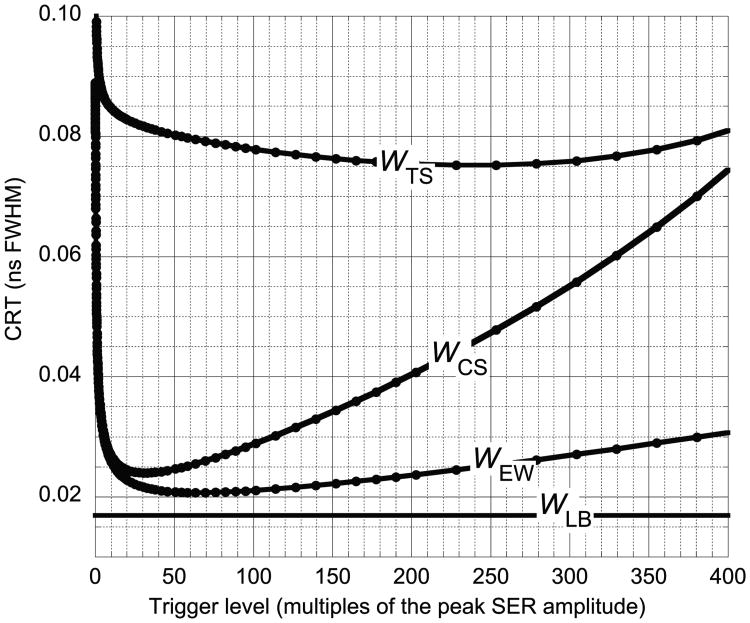
Figure 5 shows four CRT curves for LaBr3:Ce plotted as a function of trigger level in units of the peak SER. As for LSO, the WCS and WEW curves are considerably lower than the WTS curve and only slightly higher than WLB.
Figure 5.
CRT curves for LaBr3:Ce with J = 0.2 ns FWHM and Nave = 8000 plotted as a function of trigger level. The average pulse heights from photodetectors A and B are 477 and 402 times the peak SER amplitude, respectively. See table 1 for scintillator and photodetector parameters and appendix for variable definitions.
6.4. Example calculations: hypothetical ultra-fast scintillator
Table 9 lists the calculated CRT values for a hypothetical ultra-fast scintillator (table 1). For the values N ave = 4000 and J = 0.2 ns FWHM the CRT using the statistically weighted average of the fully corrected trigger times WEW is 0.021 ns FWHM, 3.6 times lower than the simple average of the trigger times and 24% higher than the statistical lower bound.
Table 9.
CRT values for a hypothetical ultra-fast scintillator. See table 1 for scintillator properties and appendix for variable definitions. Columns 3–12 are CRT values in ns FWHM for optimal trigger levels.
| Nave | J (ns FWHM) | WTA | WTB | WTS | WCA | WCB | WCS | WEA | WEB | WES | WEW | WLB |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1000 | 0.0 | 0.264 | 0.105 | 0.082 | 0.045 | 0.040 | 0.023 | 0.044 | 0.036 | 0.023 | 0.021 | 0.0105 |
| 2000 | 0.0 | 0.260 | 0.097 | 0.078 | 0.032 | 0.027 | 0.016 | 0.031 | 0.024 | 0.016 | 0.015 | 0.0068 |
| 4000 | 0.0 | 0.258 | 0.093 | 0.075 | 0.023 | 0.019 | 0.011 | 0.022 | 0.017 | 0.011 | 0.010 | 0.0045 |
| 8000 | 0.0 | 0.255 | 0.090 | 0.073 | 0.016 | 0.013 | 0.008 | 0.015 | 0.011 | 0.008 | 0.007 | 0.0030 |
| 16 000 | 0.0 | 0.252 | 0.087 | 0.071 | 0.011 | 0.009 | 0.005 | 0.011 | 0.008 | 0.005 | 0.005 | 0.0022 |
|
| ||||||||||||
| 1000 | 0.1 | 0.300 | 0.146 | 0.084 | 0.078 | 0.079 | 0.034 | 0.057 | 0.052 | 0.033 | 0.032 | 0.0246 |
| 2000 | 0.1 | 0.293 | 0.136 | 0.078 | 0.064 | 0.065 | 0.025 | 0.040 | 0.037 | 0.024 | 0.023 | 0.0173 |
| 4000 | 0.1 | 0.289 | 0.130 | 0.075 | 0.055 | 0.056 | 0.018 | 0.029 | 0.026 | 0.017 | 0.016 | 0.0122 |
| 8000 | 0.1 | 0.286 | 0.124 | 0.073 | 0.048 | 0.049 | 0.013 | 0.020 | 0.018 | 0.012 | 0.011 | 0.0086 |
| 16 000 | 0.1 | 0.282 | 0.120 | 0.071 | 0.043 | 0.043 | 0.010 | 0.014 | 0.013 | 0.008 | 0.008 | 0.0061 |
|
| ||||||||||||
| 1000 | 0.2 | 0.329 | 0.181 | 0.086 | 0.107 | 0.114 | 0.045 | 0.067 | 0.066 | 0.042 | 0.041 | 0.0339 |
| 2000 | 0.2 | 0.320 | 0.168 | 0.079 | 0.092 | 0.097 | 0.033 | 0.047 | 0.046 | 0.030 | 0.029 | 0.0238 |
| 4000 | 0.2 | 0.314 | 0.158 | 0.075 | 0.081 | 0.085 | 0.024 | 0.034 | 0.033 | 0.021 | 0.021 | 0.0169 |
| 8000 | 0.2 | 0.310 | 0.152 | 0.073 | 0.073 | 0.076 | 0.018 | 0.024 | 0.023 | 0.015 | 0.015 | 0.0120 |
| 16 000 | 0.2 | 0.304 | 0.145 | 0.072 | 0.066 | 0.069 | 0.014 | 0.017 | 0.016 | 0.011 | 0.011 | 0.0085 |
|
| ||||||||||||
| 1000 | 0.3 | 0.355 | 0.212 | 0.089 | 0.134 | 0.144 | 0.055 | 0.076 | 0.078 | 0.051 | 0.050 | 0.0413 |
| 2000 | 0.3 | 0.342 | 0.195 | 0.081 | 0.116 | 0.124 | 0.040 | 0.054 | 0.055 | 0.036 | 0.035 | 0.0292 |
| 4000 | 0.3 | 0.336 | 0.184 | 0.076 | 0.103 | 0.110 | 0.030 | 0.038 | 0.039 | 0.025 | 0.025 | 0.0207 |
| 8000 | 0.3 | 0.330 | 0.175 | 0.074 | 0.094 | 0.099 | 0.023 | 0.027 | 0.027 | 0.018 | 0.018 | 0.0145 |
| 16 000 | 0.3 | 0.324 | 0.167 | 0.072 | 0.086 | 0.091 | 0.018 | 0.019 | 0.019 | 0.013 | 0.013 | 0.0103 |
Figure 6 shows four CRT curves for the ultra-fast scintillator plotted as a function of trigger level in units of the peak SER. As will be explained in the next section the simple sum of the two trigger times does not compensate for the variations in annihilation photon transit time and this limits the optimal value of WTS. For the ultra-fast scintillator in this example the contributions from the random production of scintillation photons and the SER time jitter are relatively small and as a result WTS does not depend strongly on the trigger level. WCS is based on trigger times that have been corrected for photon delays and is much lower. WEW is based on fully corrected trigger times and is not far above the statistical lower limit WLB.
Figure 6.
CRT curves for a hypothetical scintillator with 1 ns decay time, J = 0.2 ns FWHM and Nave = 4000 as a function of trigger level. The average pulse heights from photodetectors A and B are 1457 and 1074 times the peak SER amplitude, respectively. See table 1 for scintillator and photodetector parameters and appendix for variable definitions.
6.5. Example calculations: perfect scintillator and photodetector
In this section we explore the CRT for perfect scintillators and photodetectors, where all the optical photons are produced in an instantaneous burst, and the photodetector has no timing jitter (i.e. τd = τr = J = 0). This isolates the factors that depend on the scintillator length and the ability to estimate the DOI, and excludes the random factors associated with optical photon production and detection. Specifically, the CRT value is due to the random depth-dependent variations in (1) the annihilation photon transit times, (2) the time distribution of the optical photons at the photodetector, and (3) the pulse heights. Table 10 lists the CRT values for scintillator depths Zmax = 0.3 and 3 cm, for Nave = 1000, 4000, and 10000 photoelectrons, and for refractive indexes n = 1.5 and 2.0.
Table 10.
CRT values for an instantaneous scintillation pulse (i.e. τd = τr = 0) and photodetectors with zero time jitter (i.e. J = 0). The interaction points are exponentially distributed in a scintillator of thickness Zmax, interaction length 1.2 cm, and refractive index n. See table 1 for scintillator properties and appendix for variable definitions. Columns 4–13 are CRT values in ns FWHM for optimal trigger levels.
| Nave | n | Zmax | WTA | WTB | WTS | WCA | WCB | WCS | WEA | WEB | WES | WEW | WLB |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1000 | 1.5 | 0.3 | 0.0240 | 0.0048 | 0.0096 | 0.0032 | 0.0006 | 0.0013 | 0.0031 | 0.0006 | 0.0013 | 0.0005 | 0.0002 |
| 4000 | 1.5 | 0.3 | 0.0238 | 0.0048 | 0.0095 | 0.0016 | 0.0003 | 0.0006 | 0.0016 | 0.0003 | 0.0006 | 0.0002 | 0.0001 |
| 10 000 | 1.5 | 0.3 | 0.0241 | 0.0048 | 0.0096 | 0.0010 | 0.0002 | 0.0004 | 0.0010 | 0.0002 | 0.0004 | 0.0002 | 0.0001 |
|
| |||||||||||||
| 1000 | 2.0 | 0.3 | 0.0288 | 0.0096 | 0.0096 | 0.0038 | 0.0013 | 0.0013 | 0.0037 | 0.0013 | 0.0012 | 0.0008 | 0.0002 |
| 4000 | 2.0 | 0.3 | 0.0288 | 0.0096 | 0.0096 | 0.0019 | 0.0006 | 0.0006 | 0.0019 | 0.0006 | 0.0006 | 0.0004 | 0.0001 |
| 10 000 | 2.0 | 0.3 | 0.0290 | 0.0097 | 0.0096 | 0.0012 | 0.0004 | 0.0004 | 0.0012 | 0.0004 | 0.0004 | 0.0002 | 0.0001 |
|
| |||||||||||||
| 1000 | 1.5 | 3 | 0.2084 | 0.0419 | 0.0733 | 0.0312 | 0.0063 | 0.0125 | 0.0307 | 0.0062 | 0.0123 | 0.0048 | 0.0004 |
| 4000 | 1.5 | 3 | 0.2086 | 0.0418 | 0.0713 | 0.0157 | 0.0031 | 0.0063 | 0.0157 | 0.0031 | 0.0063 | 0.0024 | 0.0002 |
| 10 000 | 1.5 | 3 | 0.2069 | 0.0414 | 0.0706 | 0.0100 | 0.0020 | 0.0040 | 0.0100 | 0.0020 | 0.0040 | 0.0015 | 0.0001 |
|
| |||||||||||||
| 1000 | 2.0 | 3 | 0.2502 | 0.0837 | 0.0733 | 0.0373 | 0.0124 | 0.0124 | 0.0367 | 0.0123 | 0.0122 | 0.0074 | 0.0004 |
| 4000 | 2.0 | 3 | 0.2506 | 0.0834 | 0.0717 | 0.0190 | 0.0063 | 0.0063 | 0.0189 | 0.0063 | 0.0063 | 0.0038 | 0.0002 |
| 10 000 | 2.0 | 3 | 0.2495 | 0.0832 | 0.0706 | 0.0120 | 0.0040 | 0.0040 | 0.0120 | 0.0040 | 0.0040 | 0.0022 | 0.0001 |
For both scintillator thicknesses (Zmax = 0.3 and 3 cm) WTA changes very little with the number of photoelectrons Nave, because it is dominated by the variations in the annihilation and direct path optical photon transit times that range from 0 to (1 + n)Zmax/c. For n = 2 and Zmax = 3 cm this time range is 0–0.3 ns.
Similar reasoning applies to WTB, which is dominated by the variations in the annihilation and direct path optical photon transit times that range from Zmax/c to nZmax/c. For n = 2 and Zmax = 3 cm this time range is 0.1–0.2 ns.
WTS is based on the average of the annihilation and direct path optical photon transit times from an interaction at depth Z to photodetector A (Z/c + nZ/c) and to photodetector B (Z/c + n(Zmax – Z)/c). Since this average is Z/c + nZmax/2c, the direct path optical photon transit times cancel and WTS is dominated by the annihilation transit time Z/c. For the 0.3 and 3 cm deep scintillators Z/c varies from 0 to 0.01 and 0 to 0.10 ns, respectively, and is not a function of n. An important consequence is that for 3 cm deep scintillators with double-ended readout, the simple average of the two trigger times can never produce CRT values below 0.07 ns FWHM, even with perfect scintillators and photodetectors (i.e. τd = τr = J = 0, any n) and with an infinite number of photoelectrons.
These limits are reduced for WCA, WCB, and WCS, which are based on trigger times that have been corrected for annihilation and optical photon transit times. These CRT values are dominated by time slewing due to the depth-dependent variations in optical photon dispersion and pulse height, and decrease as the inverse square root of Nave.
The lowest CRT values WEA, WEB, WES, and WEW are realized when the calibration procedure is performed to measure and correct for the depth-dependent variations in annihilation and optical photon transit times, and for time slewing due to depth-dependent variations in optical photon dispersion and pulse height. The CRT values result from the statistical uncertainty in estimating the DOI and decrease with the inverse square root of Nave.
The statistical lower bound CRT (WLB) is computed by fitting the depth-dependent PDF to the creation times of all the photoelectrons produced in each interaction (section 4). In this case WLB is solely due to the time dispersion of the optical photons. The CRT values are well below 1 ps FWHM and decrease with increasing Nave.
7. Conclusions
For double-ended readout the simple average of the two photodetector trigger times (CRT WTS) does not correct for depth-dependent variations in the annihilation photon transit time or time slewing due to depth-dependent variations in optical photon time dispersion or pulse height.
For 3 cm deep scintillators with double-ended readout, the simple average of the two trigger times can never produce CRT values below 0.07 ns FWHM, even with perfect scintillators and photodetectors (i.e. τd = τr = J = 0, any n) and with an infinite number of photoelectrons (Column WTS in tables 9 and 10).
Analysis of data from a positron point source can determine all the important depth-dependent correction factors, even for thick scintillators. With these corrections simple fixed-level triggering performs as well as fixed-fraction triggering and results in CRT values not far from the statistical lower bound.
A CRT value Δt = 0.02 ns FWHM (Δx = 0.3 cm FWHM) will provide an 80-fold sensitivity advantage over non-TOF PET and eliminate the need for tomographic image reconstructions. This will require a scintillator with a much higher number of photons per ns than LSO and a careful calibration to correct for the depth-dependent factors.
The CRT statistical lower bound is the same whether the DOIs are randomly distributed or placed at the center of the scintillator. It is determined by the scintillator and photodetector properties and the total number of photoelectrons, not by how the photoelectrons are distributed between the two photodetectors.
Since the trigger times occur early in the photodetector output pulse, saturation effects should have little effect on the CRT values.
The large Fano factor of LSO has a negligible effect on the CRT values.
Acknowledgments
I thank T Budinger, W-S Choong, P Lecoq, W Moses, Q Peng, and S Seifert for helpful discussions. This work was supported by Public Health Service grant R01EB012524, and was carried out at the Lawrence Berkeley National Laboratory under UC-DOE Contract No. DE-AC02-05CH11231.
Appendix. Variables and abbreviations
Table A1 lists the variables used in the calculations, and table A2 lists the abbreviations used in the text.
Table A1.
Glossary of variables used in the calculations. All times in ns. All distances in cm.
| a | Fraction of optical photons absorbed (section 2.2). |
| c | Speed of light in a vacuum (29.979 cm ns−1). |
| CXY,K,N | Trigger time of photodetector XY = 1A, 1B, 2A or 2B at trigger level LN corrected for photon delays (λ) but not the relative trigger delay (δ) (section 3.1.13). This calculation does not require the calibration procedure of section 4. |
| CXS,K,N | Simple average of CXA,K,N and CXB,K,N from scintillator X = 1 or 2, annihilation photon pair K and trigger level LN (section 3.1.14). |
| D̂XY(Z) | Optical photon time dispersion parameter for photons emitted from an interaction at depth Z that reach front surface XY = 1A or 2A, or reach rear surface XY = 1B or 2B (section 3.1.7). Equations (4a), (4b), (7a) and (7b) are used in the example Monte Carlo calculations. In practice the actual dependence would be included in the trigger delay that is measured for each scintillator in the calibration procedure. |
| d1 | Constant coefficient for the optical photon time dispersion (equations (4a) and (4b)) whose probability density function occurs after the arrival of a direct path optical photon at the photodetector. |
| d2 | Quadratic coefficient for the optical photon time dispersion (equations (4a) and (4b)). |
| EXY,K,N | Trigger time of photodetector XY = 1A, 1B, 2A or 2B corrected for photon delays λ and trigger delays δ (determined in the section 3.2 calibration procedure). This is also the estimated time of arrival of the annihilation photon at surface 1A or 2A (section 3.1.15). |
| EXS,K,N | Simple average of EXA,K,N and EXB,K,N from scintillator X = 1 or 2, annihilation photon pair K and trigger level LN (section 3.1.16). |
| EXW,K,N | Statistically weighted average of EXA,K,N and EXB,K,N from scintillator X, annihilation photon pair K and trigger level LN. The weighting factors are the inverses of their variances (section 3.1.17). |
| ẼXY,N(Z) | Variance of the corrected trigger times EX,K,N as a function of depth Z and trigger level LN for photodetectors XY = 1A, 1B, 2A, or 2B (sections 3.2.7 and 3.2.9). |
| Kmax | Number of annihilation photon pairs used in the Monte Carlo calculation. |
| LN | Trigger level (in units of the SER peak amplitude, sections 3.1.1 and 3.1.10). |
| J | Single photoelectron time jitter of the photodetector (Gaussian FWHM). |
| n | Refractive index of the scintillator at the wavelength of the scintillation light. |
| Mtot | Average number of optical photons produced by an annihilation photon interaction. |
| M̂X,K | Randomized numbers of optical photons produced in scintillators X = 1 and 2 by annihilation photon pair K (section 3.1.4). |
| Nave | Average number of photons that contribute to the combined A and B photodetector outputs. In the example tables of section 6, Nave is constrained by setting PDE equal to Nave/((1 − a)Mtot). |
| N̂XY,K | Most probable number of optical photons produced by annihilation photon pair K that produce photoelectrons in photodetectors XY = 1A, 1B, 2A and 2B that contribute to their output (sections 2.1 and 3.1.5, equations (6a) and (6b)). |
| NXY,K | Randomized number of optical photons produced by annihilation photon pair K that produce photoelectrons in photodetectors XY = 1A, 1B, 2A and 2B that contribute to their output (section 3.1.6). |
| PDE | Photon detection efficiency (for SiPMs the product of photodetector quantum efficiency, fill factor, and avalanche probability). |
| PDFY,I(t) | Probability density function for interactions at depth ZI for photodetector Y = A or B. Depends on the scintillator rise and fall times, the photodetector timing jitter, and the depth-dependent optical photon time dispersion (section 4.1). |
| R̂ | Each occurrence is a new random number drawn from a set uniformly distributed between 0 and 1 (sections 3.1.8 and 4.2.5). |
| S(t) | Photodetector SER (equation (5)). S(tpeak) is the peak amplitude. |
| Sr | Rise time of SER bi-exponential (equation (5)). |
| Sd | Decay time of SER bi-exponential (equation (5)). |
| τd | Decay time of the scintillator (ns). |
| τr | Rise time of the scintillator (ns). |
| TXY,K,N | Observed trigger times: time from the arrival of an annihilation photon K at entrance surface 1A or 2A to the time when the output pulse reaches trigger level LN in photodetector XY = 1A, 1B, 2A, or 2B (section 3.1.11). |
| TXS,K,N | Simple average of the observed trigger times TXA,K,N and TXB,K,N for scintillators X = 1 and 2 at trigger level LN. |
| T̂XY,K,N | Relative trigger times: time from the arrival of a direct path (first possible) optical photon at photodetector XY = 1A, 1B, 2A, or 2B to the time when the output pulse from annihilation photon K reaches trigger level LN (section 3.1.9). |
| t̂XY,K,m | The randomized time when photon m from annihilation photon pair K starts contributing to the output of photodetector XY = 1A, 1B, 2A, and 2B (section 3.1.8). |
| WTA | CRT (ns FWHM) = 2.355 × (T1A,K,N − T2A,K,N)rms at the optimal trigger level LN. |
| WTB | CRT (ns FWHM) = 2.355 × (T1B,K,N − T2B, K,N)rms at the optimal trigger level LN. |
| WTS | CRT (ns FWHM) = 2.355 × (T1S,K,N − T2S,K,N)rms at the optimal trigger level LN. This is the CRT value using only the simple average of the trigger times |
| WCA | CRT (ns FWHM) = 2.355 × (C1A,K,N − C2A,K,N)rms at the optimal trigger level LN. |
| WCB | CRT (ns FWHM) = 2.355 × (C1B,K,N − C2B,K,N)rms at the optimal trigger level LN. |
| WCS | CRT (ns FWHM) = 2.355 × (C1S,K,N − C2S,K,N)rms at the optimal trigger level LN. This is the CRT value using trigger times that have been corrected for annihilation and optical photon transit times but not for depth-dependent optical photon time dispersion or pulse height. |
| WEA | CRT (ns FWHM) = 2.355 × (E1A,K,N − E2A, K,N)rms at the optimal trigger level LN. |
| WEB | CRT (ns FWHM) = 2.355 × (E1B,K,N − E2B,K,N)rms at the optimal trigger level LN. |
| WES | CRT (ns FWHM) = 2.355 × (E1S,K,N − E2S,K,N)rms at the optimal trigger level LN. This is the CRT value using trigger times that have been corrected for annihilation and optical photon transit times, and depth-dependent optical photon time dispersion and pulse height. |
| WEW | CRT (ns FWHM) = 2.355 × (E1W,K,N − E2W,K,N)rms at the optimal trigger level LN. This is the CRT value similar to WES but uses the inverse variance weighted average. |
| WLB | CRT (ns FWHM) statistical lower bound (section 4). |
| XY | Designates photodetector Y = A or B on scintillator X = 1 or 2. |
| ẐX,K | Randomized DOIs for annihilation photon pair K in scintillators X = 1 and 2 (section 3.1.3). |
| ZX,K | Estimated DOIs for annihilation photon pair K in scintillators X = 1 and 2 using the contributing photon numbers measured by photodetectors A and B (equation (2) and section 3.1.12). |
| ZI | Center value of interaction depth interval I(ZI = IZmax/Imax). |
| Zcut | The upper DOI limit for selecting interactions for use in calibration (sections 3.2.6 and 3.2.8). |
| Zmax | Length of scintillator (distance between surfaces A and B). |
| ΔA,N | Base trigger delay: time difference between an interaction at surface A (Z = 0) and the time that the photodetector A output pulse reaches trigger level LN. |
| ΔB,N | Base trigger delay: time difference between an interaction at surface B (Z = Zmax) and the time that the photodetector B output pulse reaches trigger level LN. |
| Δx | Annihilation point uncertainty along the line between the coincident detectors (cm). Δx = cΔt/2. |
| Δt | Time of flight uncertainty, computed as the CRT between the coincident detectors (ns FWHM). |
| δXA,N(Z) | Relative trigger delay: difference in the trigger times of photodetector A between an interaction at Z = 0 and an interaction at Z > 0 at trigger level LN. This corrects for the time slewing due to depth-dependent variations in pulse height and optical photon time dispersion (sections 3.2.9). |
| δXB,N(Z) | Relative trigger delay: difference in the trigger times of photodetector B between an interaction at Z = Zmax and an interaction at Z < Zmax at trigger level LN. This corrects for the time slewing due to depth-dependent variations in pulse height and optical photon time dispersion (sections 3.2.7). |
| λA(Z) | Photon delays: transit time of an annihilation photon from entrance surface A to the interaction point at depth Z plus the transit time of a direct path (first possible) optical photon to the photodetector at surface A. (λA(Z) = Z/c + nZ/c). |
| λB(Z) | Photon delays: transit time of an annihilation photon from entrance surface A to the interaction point at depth Z plus the transit time of a direct path (first possible) optical photon to the photodetector at surface B. (λB(Z) = Z/c + n(Zmax − Z)/c). |
| μ | Interaction length for 0.511 MeV annihilation photons in the scintillator (including both Compton and photoelectric interactions). |
| ΨX,K | Time shift of the PDF that maximizes the joint likelihood of the photoelectron times from interaction K in photodetector X = A or B (section 4.2.7). |
| ΨWAB,K | Statistically weighted average of the maximum likelihood time shifts that maximize the joint likelihood for the photoelectron times from interaction K in photodetectors A and B (section 4.2.8). |
| Ψ̃X(ZI) | Variance of the maximum likelihood time shifts ΨX,K in photodetectors X = A or B for ẐK in the ZI interval (section 4.3.3). |
Table A2.
Glossary of abbreviations used.
| CRT | Coincidence resolving time (FWHM ns) |
| DOI | Depth of interaction (cm) |
| FWHMa | Full-width at half-maximum |
| LSO | Lu2SiO5:Ce,Ca scintillator |
| Probability density function | |
| PET | Positron emission tomography |
| Rms | Standard deviation from the mean (root mean square) |
| SER | Single electron time response of the photodetector |
| SiPM | Silicon photomultiplier |
| TOF | Time of flight difference between two annihilation photons |
Gaussian distribution has
Footnotes
Disclaimer: This document was prepared as an account of work sponsored by the United States Government. While this document is believed to contain correct information, neither the United States Government nor any agency thereof, nor the Regents of the University of California, nor any of their employees, makes any warranty, express or implied, or assumes any legal responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by its trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof, or the Regents of the University of California. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof or the Regents of the University of California.
References
- Agostinelli S, et al. Geant4—a simulation toolkit. Nucl Instrum Methods A. 2003;506:250–303. [Google Scholar]
- Bourret-Courchesne ED, Derenzo SE, Weber MJ. Development of ZnO:Ga as an ultra-fast scintillator. Nucl Instrum Methods A. 2009;601:358–63. [Google Scholar]
- Budinger TF, Derenzo SE, Gullberg GT, Greenberg WL, Huesman RH. Emission computer-assisted tomography with single-photon and positron-annihilation photon emitters. J Comput Assist Tomogr. 1977;1:131–45. doi: 10.1097/00004728-197701000-00015. [DOI] [PubMed] [Google Scholar]
- de Haas JTM, van der Kolk E, Dorenbos P. Measuring photon time spread distribution of scintillators on the picosecond time scale. IEEE Trans Nucl Sci. 2014;61:424–7. [Google Scholar]
- Derenzo SE, Bourret-Courshesne E, Bizarri G, Canning A. Bright and ultra-fast scintillation from a semiconductor? Nucl Instrum Methods A. 2016;805:36–40. doi: 10.1016/j.nima.2015.07.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derenzo SE, Bourret-Courchesne E, Yan Z, Bizarri G, Canning A, Zhang G. Experimental and theoretical studies of donor-acceptor scintillation from PbI2. J Lum. 2013;134:28–34. [Google Scholar]
- Derenzo SE, Choong WS, Moses WW. Fundamental limits of scintillation detector timing precision. Phys Med Biol. 2014;59:3261–86. doi: 10.1088/0031-9155/59/13/3261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derenzo SE, Choong WS, Moses WW. Monte Carlo calculations of PET coincidence timing: single and double-ended readout. Phys Med Biol. 2015;60:7309–38. doi: 10.1088/0031-9155/60/18/7309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El Fakhri G, Surti S, Trott CM, Scheuermann J, Karp JS. Improvement in lesion detection with whole-body oncologic time-of-flight PET. J Nucl Med. 2011;52:347–53. doi: 10.2967/jnumed.110.080382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glodo J, Moses WW, Higgins WM, van Loef EVD, Wong P, Derenzo SE, Weber MJ, Shah KS. Effects of Ce concentration on scintillation properties of LaBr3:Ce. IEEE Trans Nucl Sci. 2005;52:1805–8. [Google Scholar]
- Gundacker S, Knapitsch A, Auffray E, Jarron P, Meyer T, Lecoq P. Time resolution deterioration with increasing crystal length in a TOF-PET system. Nucl Instrum Methods A. 2014;737:92–100. [Google Scholar]
- Kang HG, Ko GB, Rhee JT, Kim KM, Lee JS, Hong SJ. A dual-ended readout detector using a meantime method for SiPM TOF-DOI PET. IEEE Trans Nucl Sci. 2015;62:1935–43. [Google Scholar]
- Karp JS, Surti S, Daube-Witherspoon ME, Muehllehner G. Benefit of time-of-flight in PET: experimental and clinical results. J Nucl Med. 2008;49:462–70. doi: 10.2967/jnumed.107.044834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolb A, Lorenz E, Judenhofer MS, Renker D, Lankes K, Pichler BJ. Evaluation of Geiger-mode APDs for PET block detector designs. Phys Med Biol. 2010;55:1815–32. doi: 10.1088/0031-9155/55/7/003. [DOI] [PubMed] [Google Scholar]
- Lecomte R, Pepin C, Rouleau D, McIntyre RJ, McSween D, Webb P. Radiation detection measurements with a new ‘Buried Junction’ silicon avalanche photodiode. Nucl Instrum Methods A. 1999;423:92–102. [Google Scholar]
- Lecomte R, Pepin C, Rouleau D, Saoudi A, Andreaco MS, Casey M, Nutt P, Dautet H, Webb PP. Investigation of GSO, LSO and YSO scintillators using reverse avalanche photodiodes. IEEE Trans Nucl Sci. 1998;45:478–82. [Google Scholar]
- Lehmann W. Edge emission of n-type conducting ZnO and CdS. Solid State Electron. 1966;9:1107–10. [Google Scholar]
- Moses WW, Choong WS, Derenzo SE. Modeling time dispersion due to optical path length differences in scintillation detectors. Acta Phys Pol B. 2014;7:725–34. doi: 10.5506/APhysPolBSupp.7.725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nemallapudi MV, Gundacker S, Lecoq P, Auffray E, Ferri A, Gola A, Piemonte C. Sub-100 ps coincidence time resolution for positron emission tomography with LSO:Ce codoped with Ca. Phys Med Biol. 2015;60:4635–49. doi: 10.1088/0031-9155/60/12/4635. [DOI] [PubMed] [Google Scholar]
- Ren SL, Yang YF, Cherry SR. Effects of reflector and crystal surface on the performance of a depth-encoding PET detector with dual-ended readout. Med Phys. 2014;41:072503. doi: 10.1118/1.4881097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renker D. Geiger-mode avalanche photodiodes, history, properties and problems. Nucl Instrum Methods A. 2006;567:48–56. [Google Scholar]
- Seifert S, Schaart DR. Improving the time resolution of TOF-PET detectors by double-sided readout. IEEE Trans Nucl Sci. 2015;62:3–11. [Google Scholar]
- Seifert S, van Dam HT, Vinke R, Dendooven P, Lohner H, Beekman FJ, Schaart DR. A comprehensive model to predict the timing resolution of SiPM-based scintillation detectors: theory and experimental validation. IEEE Trans Nucl Sci. 2012;59:190–204. [Google Scholar]
- Snyder DL, Thomas LJ, Terpogossian MM. A mathematical-model for positron-emission tomography systems having time-of-flight measurements. IEEE Trans Nucl Sci. 1981;28:3575–83. [Google Scholar]
- Vinke R, Olcott PD, Cates JW, Levin CS. The lower timing resolution bound for scintillators with non-negligible optical photon transport time in time-of-flight PET. Phys Med Biol. 2014;59:6215–29. doi: 10.1088/0031-9155/59/20/6215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vunckx K, Zhou L, Matej S, Defrise M, Nuyts J. Fisher information-based evaluation of image quality for time-of-flight PET. IEEE Trans Med Imaging. 2010;29:311–21. doi: 10.1109/TMI.2009.2029098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werner ME, Karp JS. TOF PET offset calibration from clinical data. Phys Med Biol. 2013;58:4031–46. doi: 10.1088/0031-9155/58/12/4031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang YF, Dokhale PA, Silverman RW, Shah KS, McClish MA, Farrell R, Entine G, Cherry SR. Depth of interaction resolution measurements for a high resolution PET detector using position sensitive avalanche photodiodes. Phys Med Biol. 2006;51:2131–42. doi: 10.1088/0031-9155/51/9/001. [DOI] [PubMed] [Google Scholar]
- Yang YF, Qi JY, Wu YB, St James S, Farrell R, Dokhale PA, Shah KS, Cherry SR. Depth of interaction calibration for PET detectors with dual-ended readout by PSAPDs. Phys Med Biol. 2009;54:433–45. doi: 10.1088/0031-9155/54/2/017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeom JY, Vinke R, Levin CS. Optimizing timing performance of silicon photomultiplier-based scintillation detectors. Phys Med Biol. 2013;58:1207–20. doi: 10.1088/0031-9155/58/4/1207. [DOI] [PMC free article] [PubMed] [Google Scholar]