Spatial distributions of pericellular stiffness in natural extracellular matrices are dependent on cell-mediated proteolysis and contractility

Abstract

Bulk tissue stiffness has been correlated with regulation of cellular processes and conversely cells have been shown to remodel their pericellular tissue according to a complex feedback mechanism critical to development, homeostasis, and disease. However, bulk rheological methods mask the dynamics within a heterogeneous fibrous extracellular matrix (ECM) in the region proximal to a cell (pericellular region). Here, we use optical tweezers active microrheology (AMR) to probe the distribution of the complex material response function (α = α′ + α″, in units of μm/nN) within a type I collagen ECM, a biomaterial commonly used in tissue engineering. We discovered cells both elastically and plastically deformed the pericellular material. α′ is wildly heterogeneous, with 1/α′ values spanning three orders of magnitude around a single cell. This was observed in gels having a cell-free 1/α′ of approximately 0.5 nN/μm. We also found that inhibition of cell contractility instantaneously softens the pericellular space and reduces stiffness heterogeneity, suggesting the system was strain hardened and not only plastically remodeled. The remaining regions of high stiffness strongly suggest cellular remodeling of their surrounding matrix. To test this hypothesis, cells were incubated within the type I collagen gel for 24 hours in a media containing a broad-spectrum matrix metalloproteinase (MMP) inhibitor. While the pericellular material maintained stiffness asymmetry, stiffness magnitudes were reduced. Dual inhibition demonstrates that the combination of MMP activity and contractility is necessary to establish the pericellular stiffness landscape. This heterogeneity in stiffness suggests the distribution of pericellular stiffness, and not bulk stiffness alone, must be considered in the study of cell-ECM interactions and design of complex biomaterial scaffolds.

Graphical abstract

1 Introduction

Interactions between cells and their extracellular matrix (ECM) are bi-directional. On one hand, the mechanical properties of the ECM have been shown to regulate key processes in cells; for example, increasing bulk ECM stiffness has been correlated to invasion of mammary epithelial cells[1], differentiation of mesenchymal stem cells[2,3], and maturation of cardiomyocytes[4]. On the other hand, cells actively alter their ECM through context-dependent degradation, remodeling, and deposition of new ECM[5]. Thus, quantifying the mechanical interactions between the cell and its ECM both spatially and temporally, at a scale relevant to the interaction, is imperative to study how cells are regulated in physiological and pathological processes.

One interesting aspect of cell-ECM physical interactions is the distribution of traction forces that cells exert onto their local ECM. 3D traction force microscopy (TFM) has been developed for cells fully embedded within a linear, homogenous, nano-porous, synthetic PEG hydrogel containing tracer microbeads[6,7], which can be modified to contain sites for cell adhesion and cell mediated degradation[8]. The strain field can be calculated by tracking bead displacement. Then, an estimation of traction forces can be computed under the assumption of hydrogel linear elasticity, homogeneity, and without consideration of cell-mediated degradation and deposition of new ECM. While these methods are elegant and provide important insight, results may not be generalizable to physiologically relevant tissues because these gels do not share the native architecture, pore size, or nonlinear properties of natural matrices[9]. Such differences have the potential to cause cells to remodel these ECMs differently, if at all, than they would in natural materials. Heterogeneities in local ECM architecture and stiffness have hindered efforts to extend TFM to natural matrices particularly in the pericellular space. For example, it has been reported that stresses within the ECM cannot be determined from bead displacements alone under the assumption of homogenous mechanical properties[7] and without accounting for local degradation[10]. Furthermore, stiffness of natural, type I collagen fibrous matrices increases non-linearly with deformation, and cannot be determined from collagen concentration alone[7,11]. Instantaneous stiffness should be determinable from strain if the nonlinear relationship between strain and stiffness is known a priori. However, such a calculation requires knowledge of the current stress free state of the material, which may not be available once cells plastically remodel the local matrix. Thus, the study of how pericellular stiffness changes over time requires the use of a technique that can directly measure stiffness locally.

Here we use optical tweezers active microrheology (AMR) to directly measure the complex material response function at multiple sites around cells grown in 3D type 1 collagen gels and observe the dependence of material property heterogeneity on both cell contractility and matrix metalloproteinase (MMP) activity. One potential way a cell can modulate its pericellular mechanical topography is through cytoskeletal contractile forces that locally deform the ECM and stiffen it through strain-hardening[12], a process that’s also essential for cell mechanoresponsiveness[13]. Another way in which a cell may modulate its local mechanical topography is through degradation of its local ECM, mediated by cell synthesized MMPs[14]. MMP mediated matrix degradation has been shown to be critical in processes including angiogenesis[15,16], cancer metastasis [17], or skeletal formation[18]. Thus, both cytoskeletal contractility and MMP activity are logical targets to explore the role of a cell in establishing or maintaining its pericellular stiffness, which we have shown can be significantly stiffer than values reported by bulk rheology [19–21] and are consistent in order-of-magnitude to stiffness reported by other groups using AMR in type I collagen[22], Matrigel, hyaluronic acid, and zebrafish in vivo[23]. In earlier studies, we used AMR to discover that during capillary morphogenesis, the pericellular space surrounding the tip of a sprouting capillary had increased stiffness as compared to distal regions[24]. We also showed that mouse skeletal stem cells required MMP14 (MT1-MMP) activity to stiffen the pericellular space within 3D collagen gels, a result that was associated with osteogenic fate commitment in vivo[25]. Here we use AMR to measure the distribution of pericellular stiffness surrounding isolated dermal fibroblasts as well as smooth muscle cells embedded within collagen gels and observe important new insights into how cells modulate their mechanical microenvironment in a contractility and MMP-dependent manner.

2 Methods

2.1 Cell Culture

Dermal fibroblasts (DFs) were acquired from Lonza (CC-2511) and were cultured in DMEM (Fisher) with 10% FBS (Gibco) and 1% penicillin streptomycin (Gibco). Human Aortic smooth muscle cells (HAoSMCs) were acquired from ATCC (PCS-100-012) and the media plus bullet kit (CC-3182) from Lonza. All cells in this study were used prior to passage 7.

2.2 Collagen Hydrogel Formation

Type 1 collagen was chosen for these studies given both its abundance as the one of the main structural protein of ECM within the body[26] and it’s relative prevalence within the natural context of each type cell used [27,28]. Collagen hydrogels were made at a final concentration of 1.0 mg/mL or 2.0 mg/mL using acid extracted rat tail type 1 collagen from vendors Advanced Biomatrix or Corning, respectively. Collagen of this type has been previously reported to vary significantly from lot to lot as has been previously noted by others[29]. Importantly, collagen lots and concentrations were kept consistent for each set of cells: 1mg/mL for DF experiments and 2 mg/mL for HAoSMC experiments. Structure (as assessed by reflection confocal) and mechanical properties (as probed by AMR) were roughly matched between the two cell-free conditions. For DF experiments, 3 cells in 3 separate gels were measured per condition. For HAoSMC experiments, 3 cells were measured within a single gel per condition.

Collagen gels were prepared with 10× PBS (Life Technologies), 1N NaOH (Fisher), sterile-filtered DI H₂O, 2 μm carboxylated silica microbeads (0.8 mg/ml, Bangs Laboratories), and cells (100 k/ml) in 35 mm glass bottom dishes (MatTek). The samples were placed in a standard tissue culture incubator at 37 °C for 40 minutes during the polymerization process, after which media was added to each dish.

Cells in control conditions were fed with normal media at the time of gelation. In the BB94 conditions, cells were fed with normal media supplemented with 10 μM BB94 (Sigma) after gelation. All dishes were incubated for 24 hours in a standard tissue culture incubator. Prior to AMR measurements, the culture media was supplemented with HEPES (20 mM) and the dish placed within stage. A custom-built incubation system plus an objective heater maintained temperature in the dish at 34° C. Gels were allowed to equilibrate to temperature for at least 1 hour to prevent focus drift[30]. Y27632 conditions were supplemented with 20 μM Y27632 (Sigma) during this 1 hour, on stage incubation period.

2.3 AMR system

The AMR system is illustrated in Figure S1a. Optical tweezers are generated by a continuous-wave fiber laser with emission at 1064 nm (IPG Photonics), hereafter referred to as the trapping beam. A pair of galvanometer mirrors (ThorLabs) placed conjugate to the back focal plane of the objective lens steers the trapping beam focus in the transverse plane of the microscope objective. The cover glass reflects a small fraction of the beam power and directs it onto a quadrant photo diode (QPD, Newport) labeled as trapQPD in Figure S1a. The trapQPD outputs analog signals proportional to the deflection of the trapping beam. A low power laser diode with emission at 785 nm (World Star Technologies), hereafter referred to as the detection beam, detects the probe bead response motion. A long pass dichroic beam splitting mirror (D1, Semrock) combines the two laser beams and introduces them into the white light path of an IX81 inverted microscope (Olympus).

The microscope is equipped with the Zero Drift Compensation package (Olympus) comprising an external laser/detector unit and a filter cube placed just below the microscope objective lens (D2 in Fig. S1a). We removed the laser/detector unit and replaced the stock dichroic beam splitting mirror with a short pass dichroic beam splitting mirror (Chroma) designed to reflect our laser beams into the microscope objective lens while passing visible light for confocal and brightfield microscopy. A high numerical aperture microscope objective lens (60×-oil PlanApo TIRFM 1.45 NA, Olympus) focuses both beams into the sample. The microscope condenser lens (0.55 NA, Olympus) collects the forward scattered laser light which is then reflected by a 50/50 beam splitter (Thorlabs), labeled D3 in Figure S1a, towards the detection beam quadrant photo diode (detQPD, Newport).

A short pass dichroic beam splitting mirror D4 (Chroma Technologies) is placed before the detQPD to reflect the trapping beam away from the detQPD. A band pass filter centered at 785 nm is placed directly in front of the detQPD to remove noise from non-detection laser sources. A laser trapped microbead oscillating in the hydrogel will deflect the detection beam across the surface of the detQPD, which outputs analog signals proportional to the position of that microbead.

The microscope is also equipped with a FluoView 1200 laser confocal scan head (Olympus) used here for reflection confocal microscopy (488 nm laser line). Samples are placed onto a piezoelectric XY stage (P-733.2CL, Physik Instrumente) which is housed within a motorized XY stepper motor stage (MS-2000, Applied Scientific Instruments), allowing for sub-nanometer resolution movements over an area of (100 × 100) μm².

Our microscope and optical tweezer components comprise a robotic system controlled by custom software developed in our laboratory (Supplementary Note 2). Net time to probe each bead is approximately 8 seconds. Each bead is probed at 50Hz. In support of probing at 50 Hz alone, previous microrheological studies have reported that probed stiffness is frequency independent in type I collagen gels at frequencies <100 Hz[31] and we further determined no difference in 1/α′ measured by frequency sweep or at 50 Hz alone (Fig. S2a). Accurate measurement of 1/α′ requires precise centering of each bead in the laser trap. We found errors in measured 1/α′ due to automated stage motion were 5.5% (Supplementary Note 2).

2.4 System Validation

To validate our automated system, we first conduct AMR in water at room temperature with a frequency sweep at [10 20 50 75 100] Hz. Viscosity, η, in water is empirically known to be 0.001 Pa s and can be determined by AMR using the relationship η = G″/2πf, where f is the frequency of oscillation[32]. Before each experiment, we validated the AMR system by measuring η of water and comparing it to the theoretical value. A typical measured value is 0.001 ± 5.76 × 10⁻⁵ Pa s, which agrees with the empirical value (n_beads = 5; p = 0.975).

We next probed beads in a hydrogel (type I collagen) to investigate potential sources of error originating from hardware automation. We randomly selected beads (n = 5) separated from each other by at least 75 μm. At this distance, the robotic system must move both the long-range stepper motor stage as well as the piezoelectric stage to center a bead within the optical trap with 0.10 μm repeatability. The AMR system (Supplementary Note 2) cycled between all beads five times (Fig. S2b), each time measuring 1/α′. On average, the percent error (standard deviation/mean × 100%) of 1/α′ for the same bead across all five measurements was 5.5%, demonstrating the small error introduced by automation. To assess the effect of rigid objects contained within a type I collagen gel on stiffness as probed by AMR, carboxylated 20 μm polystyrene beads (Polysciences) were embedded into a 1mg/mL type 1 collagen gel and AMR measurements were conducted proximal to the bead (Fig. S4). No significant difference was found between measurements proximal to the bead (N=3) and comparable measurements within a similar set of cell free gels (N=3, p=0.26).

2.5 Statistical Analyses

All statistical analyses were conducted in OriginPro using the Mann-Whitney test, unless otherwise stated, because typically data was not normally distributed (Shapiro-Wilk test, p < 0.05). The (statistical) alpha value used to determine statistical significance was adjusted in the cases of multiple comparisons according to the Bonferroni correction. For the case of viscosity measurement in water, comparison was made by the Student’s T-test. Data in the manuscript is presented as mean ± standard deviation.

3 Results

3.1 Active microrheology to measure pericellular stiffness

We use AMR to measure the complex valued material properties within natural ECMs[19,22]. In our method, cells are embedded within an ECM that also contains a dispersion of 2 μm diameter silica microbeads. The cells and ECM can be imaged by transillumination (brightfield) microscopy (Fig. 1a) and reflection confocal microscopy, which provides label-free images of cell and ECM architecture (Fig. 1b–c). Examination of co-aligned transmission and reflection confocal microscope images confirms that most beads are confined within a pore (Fig. S5). Qualitatively, we do not observe free diffusion of beads throughout the gel, even proximal to cells (Supp. Videos 1–4). In AMR, optical tweezers forces oscillate a microbead confined within the gel and a detection laser detects the change in bead position (Fig. 1d).

Figure 1.

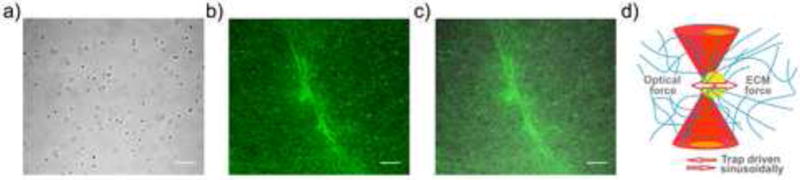
Probing pericellular stiffness with AMR. (a) Brightfield image of an isolated DF cultured in a type I collagen gel embedded with 2 μm diameter silica microbeads. (b) Reflection confocal microscopy image of the region in (a) showing both the cell and the fibrous collagen matrix. (c) Merged brightfield and confocal images. Scale bars are 20 μm. (d) Diagram of optical tweezers active microrheology (AMR). The optical tweezers microbeam (dark red) is spatially oscillated to exert oscillatory forces on a microbead (yellow) and forces are resisted by the complex material response of the local extracellular matrix (blue). Detection beam deflections (light red) are analyzed to compute the complex valued material response α.

The real (α′) and imaginary (α″) components of the complex valued material response function α are computed from experimental data (see Supplementary Note 1) with no simplifying assumptions regarding thermodynamic equilibrium and, X (ω) = α(ω)F(ω),where X(ω) and F(ω) are the amplitudes of the bead’s displacement and the applied optical force respectively at ω, the frequency of the sinusoidal force applied by the optical tweezers. Here α′ measures to the local material’s elastic response, whereas α″ reports on the dissipative forces acting on the microbead. An alternative method to AMR is particle tracking microrheology, a passive method in which the thermally driven motion of beads is recorded at video rate, or less commonly at kilohertz by a detection beam [33], and used to compute ECM material properties.

If the system were in thermal equilibrium one could rely on the fluctuation-dissipation theorem[34] to relate the observed fluctuation spectrum to the frequency-dependent imaginary part of the response function α(ω). From these data, one can also recover the real part of the response function using Kramer-Kronig relations and generally applicable assumptions regarding the unobserved, high frequency part of the dissipative response function. This method, however, is inapplicable to nonequilibrium systems since the fluctuation-dissipation theorem fails. In some cases this failure is dramatic[35]. Therefore, passive microrheology for characterizing the pericellular space has been limited to either detection of the formation of a hydrogel, dissolution of a hydrogel[36], or ECMs that are orders of magnitude softer than in vivo ECMs[37,38].

Typically in nonequilibrium systems, one must resort to active microrheology, although in some cases the combination of active and passive techniques has been used to quantify the nonequilibrium nature of various biological systems[39]. We note also that non-driven displacement fluctuations in the system are significantly smaller than the observed response to the driven displacement of our reference particles, on which we base our active microrheological studies. In this work, we report solely on active microrheological measurements, which are sufficient to extract mechanical or rheological data on an ECM network containing live cells that is clearly out of equilibrium.

3.2 AMR Around Living Cells Reveals Stiffness Heterogeneity

Human Aortic Smooth Muscle Cells (HAoSMCs) were cultured in type I collagen gels (2 mg/ml) containing 2 μm diameter microbeads at a concentration of 0.8 mg/ml. On average, each bead was located approximately 13 μm from its neighbors. Probe microbeads were found approximately 30 μm above the glass coverslip in a 350 × 280 μm² region, and were probed before and after contractility inhibition via 20 μM ROCK inhibitor Y27632. This has previously shown to result in a significant loss in contractility (within 15–30 minutes) for human uterine smooth muscle cells[40]. Figure 2a shows a significant decrease in the mean value of 1/α′ from 3.1 ± 3.0 nN/μm to 1.2 ± 1.0 nN/μm before and after treatment respectively (p < 0.001). Mapping stiffness spatially before treatment shows the material surrounding two cells was significantly stiffened (red box; n_beads = 42) as compared to cell-free regions (blue box; n_beads = 30) within the image montage (p < 0.001). Inhibiting contractility (Fig. 2b) results in a notable loss in spatial heterogeneity in 1/α′ (Fig. 2c). Note the handful of beads between cells 2 and 3 that reported stiff ECM before treatment (Fig. 2d), but did not soften as much compared to their neighbors after Y27632 treatment (Fig. 2e). We used reflection confocal microscopy to image this region and observed fiber alignment and increased ECM density pre-treatment (Fig. 2f). Confocal imaging after treatment (Fig. 2g) shows that the decrease in average ECM stiffness correlated with relaxation, but not abatement, of fiber alignment (Fig. 2g). In fact, the ECM density between the two cells remained high after treatment. This suggests roles for cell-mediated local remodeling and provides evidence that collagen concentration alone may not determine stiffness.

Figure 2.

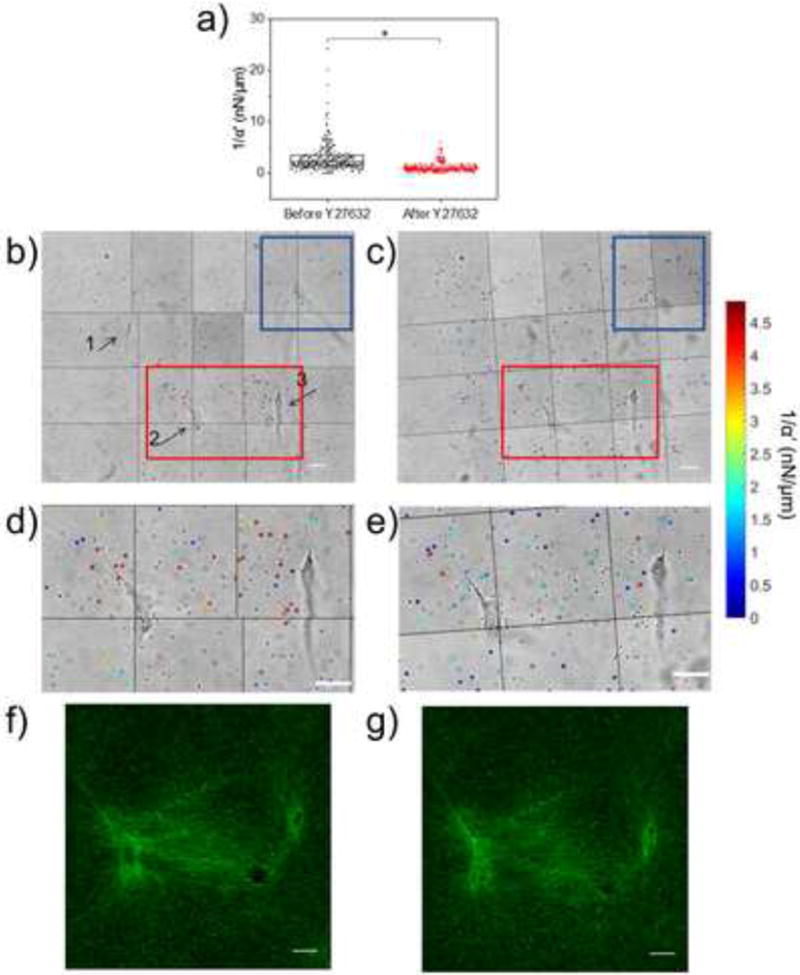
Mapping pericellular stiffness with AMR. (a) Scatterplot of AMR measurements of 1/α′ in 2 mg/ml type I collagen gel around multiple HAoSMCs in a ~ 350 × 280 μm² region taken before (n_beads = 288) and after (n_beads = 279) 1 hour incubation with 20 μM Y27632. 1/α′ values significantly decreased after treatment (p ≪ 0.001). Montage containing HAoSMCs (labeled 1, 2, and 3) and microbeads (represented in (a)) probed before (b) and after (c) treatment. Probed microbeads are overlaid with a colored circle corresponding to the measured 1/α′ (note color bar saturates at 5 nN/μm, but full range is shown in (a). (d, e) Zoomed in view of regions in (b) and (c) bound by red rectangle. (f, g) Reflection confocal images of region between cells 2 and 3 before and after treatment with Y27632. Scale bars are 20 μm.

3.3 Average pericellular stiffness depends on cytoskeletal contractility and MMP activity

We next studied the effects of both cytoskeletal contractility and local remodeling on pericellular material stiffness around isolated HAoSMCs as well as human dermal fibroblasts (DFs). AMR was conducted around isolated cells in control conditions as well as those treated with Y27632 and BB94 (Batimastat), a wide-spectrum inhibitor of matrix metalloproteinases (MMPs). The pericellular stiffness surrounding isolated cells was measured in four conditions: (1) control, (2) Y27632, (3) BB94 or (4) both BB94 and Y27632. For conditions 3 and 4, 10 μM BB94 was added just after gelation and followed by 24h incubation. For conditions 2 and 4, 20μM Y27632 was added after overnight incubation at one hour prior to measurements. As compared to control, average 1/α′ in the probed region decreased in all three experimental conditions for both cell types (DF: p < 0.001, Fig. 3a; HAoSMC: p < 0.001, Fig. S6). Additionally, average 1/α′ for condition 4 was lower than that for conditions 2 and 3 (DF: p < 0.001, HAoSMC: p < 0.001), showing that dual-inhibition was most effective at softening the pericellular ECM relative to control. To determine any effects of the drugs on the hydrogel, AMR was conducted in cell-free gels (1mg/mL type 1 collagen). No significant changes in 1/α′ were detected between gels treated with 20 μM Y27632 for one hour, gels treated with 10 μM BB94 for 24-hours, gels treated with Y27632 after a 24-hour treatment with BB94, and control gels (Fig. 3b, Kruskal–Wallis test, p=0.16).

Figure 3.

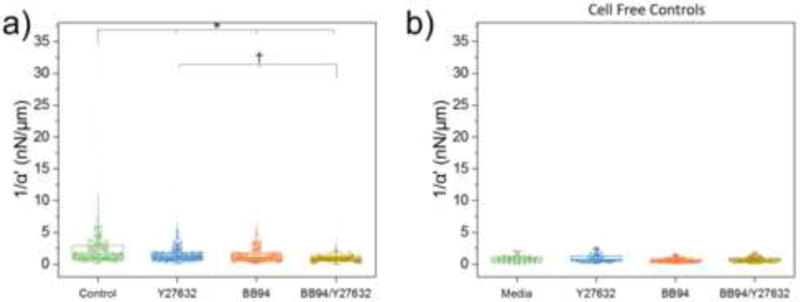
Pericellular stiffness distribution modulated by inhibition of contractility and MMP activity. (a) AMR measurements of 1/α′ in cell-free 1 mg/ml type I collagen gels under control conditions (n_beads = 59), as well as treatment conditions: 20 μM Y27632 (n_beads = 58), 10 μM BB94 (n_beads =58), and BB94+Y27632 (n_beads = 71). No significant differences were detected (Kruskal–Wallis test, p=0.16). (b) AMR measurements of 1/α′ in a ~280 × 280 × 30 μm³ volume surrounding isolated DFs in control conditions (n_cells = 3; n_beads = 1060) as well as treatment with Y27632 (n_cells = 3; n_beads = 994), BB94 (n_cells = 3; n_beads = 873) and BB94+Y27632 (n_cells = 3; n_beads = 804). Each experimental condition was significantly different as compared to control (*, p ≪ 0.001). Additionally, BB94+Y27632 was different as compared to Y27632 and BB94 (†, p ≪ 0.001).

3.4 Spatial distribution of pericellular stiffness depends on MMP activity and cytoskeletal contractility

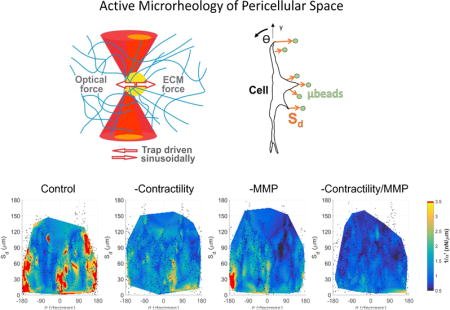
In order to aggregate pericellular stiffness distributions across multiple cells we first transformed the Cartesian coordinates of each bead into a polar coordinate system (r, θ), with origin at the cell centroid. As shown in Fig. 4a–d, all points were rotated such that the major axis of each cell (determined by a bounding ellipse) aligns with θ = 0 allowing superposition of all points across all cells, per condition. The decrease in stiffness and loss in spatial heterogeneity following drug treatment as compared to control (Fig. 4a–d) is better visualized by interpolated surface maps (Fig. 4e–h). Here interpolation is for visualization purposes only and likely not reliable between measured coordinates. We next computed S_d, the shortest distance between each probed microbead and the boundary of its corresponding cell. Figures 4i–l show 1/α′ plotted on a (S_d,θ) coordinate system to visualize relationships between ECM stiffening, cell orientation, and distances from cells across experimental conditions.

Figure 4.

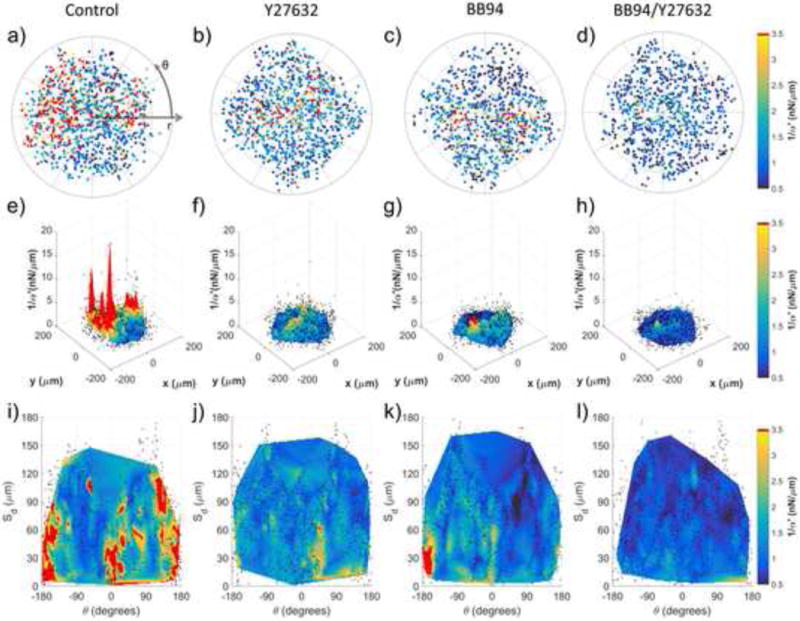
Characterization of pericellular stiffness for multiple isolated DFs. Polar plots of 1/α′ surrounding isolated cells for (a) control (n_cells = 3), (b) 20 μM Y27632 (n_cells = 3), (c) 10 μM BB94 (n_cells = 3) and (d) BB94+Y27632 (n_cells = 3) conditions. Concentric lines are drawn in 50 μm increments of r. (e–h) 3D surface plots of the aggregate data in (ad), respectively. (i–l) Data in (a–d) mapped to a Cartesian plot of θ vs. distance from cell boundary, S_d. For (e–l), probed beads are denoted by black dots. Data interpolation is restricted to regions containing data from all cells, per condition. Color maps in (a–d and i–l) range approximately from the average 1/α′ value of BB94+Y27632 to the average 1/α′ value plus one standard deviation of the control condition. Note that the color map saturates at 3.5 nN/μm.

In the case of DFs, which have an elongated morphology (Fig. S7), punctate regions of stiffening are observed near to the leading (−45° < θ < +45°) and trailing (135° < θ < 180° and −180° < θ < −135°) edges for S_d < 50 μm (Fig. 4i). Discrete punctate regions of elevated 1/α′ values were also found for S_d > 50 μm, supporting previous assertions that long range stiffening may not be a spatially continuous process, but dependent on the fibrous network[41] and/or the asymmetry[42] by which cells contract against their matrix. In support of this hypothesis, inhibition of cell contractility by Y27632 (Fig. 4b,f,j) resulted in a significant decrease in pericellular stiffness and stiffness asymmetry as compared to control (Fig. 4a,e,i). This observation implicates the important role of cytoskeletal contractility-mediated strain hardening in determining the mechanical landscape in the pericellular space.

We also found that inhibition of MMP activity by BB94 (Fig. 4c,g,k) lowers 1/α′ values relative to control but preserves asymmetry (Fig. 4k), as observed in control conditions, but without long range stiffening. Further incubation with Y27632 (Fig. 4d,h,l) nearly completely abrogates stiffening in the pericellular space. Similar results were observed for HAoSMCs in 2 mg/mL type 1 collagen gels, which show a less elongated morphology (Fig. S8 and S9). For both cell types, either cellular contractility (Fig. 4b,f,j; Fig. S9b,f,j) or MMP activity (Fig. 4c,g,k; Fig. S9c,g,k) alone were insufficient to create or maintain the asymmetry, stiffness, and long range stiffening observed in controls (Fig. 4a,e,i; Fig. S9a,e,i). Rather, it may be the cooperation between both MMP activity and cellular contractility that are required for creating a normal pericellular mechanical topography in the complex material of our type 1 collagen system.

4 Discussion

As we have previously demonstrated in cell-free systems, the distribution of local ECM stiffness values within a single gel are not observable via bulk rheological methods [19]. Consequently, studies relying on bulk measurements alone may miss important ways in which ECM heterogeneity can guide cell behavior with respect to stiffness. As a metric for heterogeneity, we examined the differences in 1/α′ as probed by neighboring beads (e.g. Fig. 4). This provides us with an estimate of errors when interpolating stiffness in regions not directly probed by a bead. For each bead, we determined d, the center-to-center distance to its closest neighbor (eliminating redundant pairs), and Δ(1/α′), the difference in 1/α′ reported by those beads (Fig. 5a). The lower limit of d is 2 μm, which occurs only if two beads are in contact. Histograms of Δ(1/α′) (Fig. 5b–f) show the effects of cell contractility and MMP-mediated ECM degradation on Δ(1/α′) in the pericellular space. For control cells (Fig. 5c), Δ(1/α′) values ranged up to 30 nN/μm and 75% of values were less than 2 nN/μm. In contrast, 75% of Δ(1/α′) values in a cell-free gel (Fig. 5b) were less than 0.5 nN/μm. Additionally, 75% of Δ(1/α′) values were less than 1, 1 and 0.5 nN/μm, following inhibition of contractility (Fig. 5d), MMPs (Fig. 5e) or both (Fig. 5f) respectively. This finding demonstrates that in control conditions, Δ(1/α′) can vary wildly between adjacent probe beads around a single cell. We next parsed beads into two groups, those found within and those beyond 50 μm of the cell boundary. Two important findings were observed relating to the limits of interpolation. First, for control cells, there is no clear trend between Δ(1/α′) and the distance between beads in both groups (Fig. 5g). This observation suggests that minimizing bead-to-bead distance does not improve accuracy of interpolation. Second, regions of long-range stiffening for control cells (Fig. 4i) also exhibit large Δ(1/α′) (Fig. 5g, black markers) particularly as compared to inhibited cells (Fig. 5h–j). Similar analysis was performed on HAoSMC, shown in Figure S10.

Figure 5.

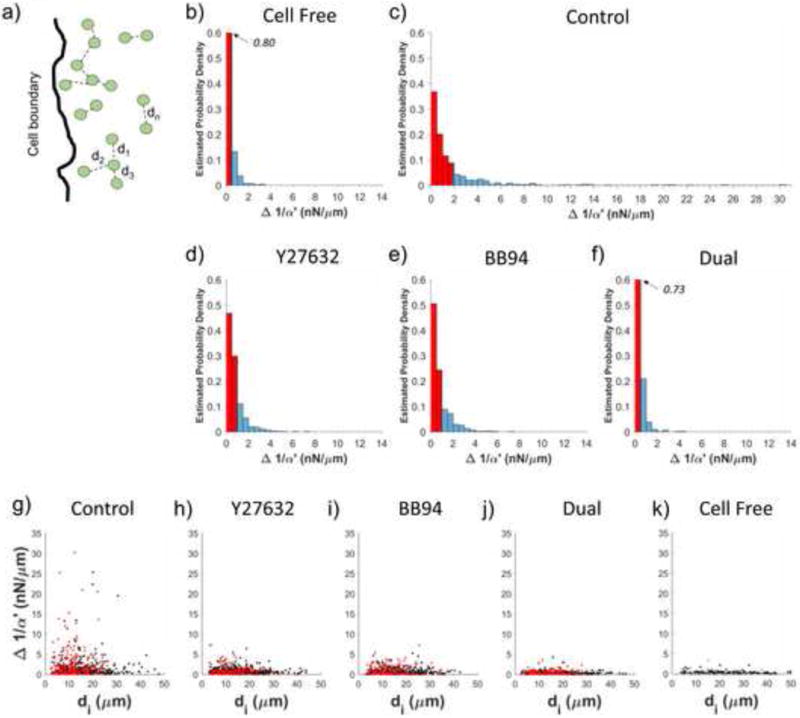
Variability in stiffness between adjacent beads. (a) For each bead, d_i is defined as the distance to its closest neighbor. Estimated probability density of Δ1/α′ in (b) cell free collagen as well as collagen gels containing DFs under (c) control conditions or treatment with (d) Y27632, (e) BB94 or (f) both. Red shaded region represents 75% of the data. (g–h) Scatter plots of d_i and Δ1/α′ for DFs under (g) control conditions or treatment with (h) Y27632, (i) BB94 or (j) both. Red dots indicate beads within S_d < 50 μm and black dots indicate beads within S_d > 50 μm. (k) Scatter plots of d_i and Δ1/α′ for a cell-free collagen gel.

Taken together, these observations suggest that estimation of a continuous stiffness function derived from interpolation between beads in natural matrices like collagen can produce errors in local stiffness estimates as large as tens of nN/μm, or under the assumption of a continuum, hundreds of pascals.

It is difficult to assess the consequences of such a wildly varying stiffness field on computing forces. In order to ascertain an order of magnitude understanding of errors in estimating force, we conducted a quantitative but rough estimate of such forces under assumptions of no strain hardening, viscoelastic creep, and stress relaxation. Specifically, we computed the force magnitude, F, required to displace a bead by distance x, where F = |x/α′|. We estimated values of F under a simplifying assumption that α does not change for the 1 and 5 μm displacements used in this analysis. Although we have data to contradict this assumption (not shown), our analysis will still provide insight into the significance of observed Δ(1/α′) values in an order of magnitude sense. As shown in Table 1, we estimated force magnitudes acting on a bead for values of 1/α′ ∈ [0.1, 0.5, 1, 5, 10, 30] nN/μm, a range observed surrounding control cells (Fig. 3a). F was estimated for x = 1 μm and 5 μm, which are values consistent with previously reported bead displacements surrounding single HT-1080 fibrosarcoma cells in a type I collagen gel[10]. By our estimate, F could range from 0.5 to 150 nN for a 5 μm displacement around an untreated cell (Table 1). Thus, if α is not directly measured, but estimated from other methods including parallel plate rheology, the error in F could be as large as two orders of magnitude. This estimated range of F spans the traction forces measured for a single cell using two-dimensional (2D) micropillar traction force microscopy[43,44]. Jin et al. computed cell contractile forces in 3D ECMs by monitoring the contraction of a type I collagen gel seeded with human aortic adventitial fibroblasts. They estimated the average cell contractile force was approximately 1.5 nN, which is well within our range of estimated forces[45]. Bloom et al. tracked displacements of 3.6 μm diameter beads around HT-1080 cells in a type I collagen gel. They estimated that a 4 nN force is required to displace a bead by 5 μm[10]. Both of these studies assumed homogenous material properties measured by bulk methods. But, as seen in our experiments, because 1/α′ can range across three orders of magnitude around each bead, force calculations are very sensitive to this uncertainly in 1/α′. Given this new insight, we caution the use of bead-based TFM in fibrous gels unless stiffness is determined continuously throughout the pericellular space.

Table 1.

Estimates of force magnitude required to displace a bead by 1 or 5 μm in a gel with given 1/α′.

$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\alpha }^{\prime }$}\right.$ [nN/μm]	F [nN]
	Δx = 1 μm	Δx = 1 μm
0.1	0.1	0.5
0.5	0.5	2.5
1	1	5
5	5	25
10	10	50
30	30	150

Quantification of the effects of cell contractility, remodeling, and fiber mesh architecture on the pericellular stiffness within a natural 3D ECM at physiological concentration has only been modeled[46] within the volume of a fibrous hydrogel, but not directly measured within the volume as is possible with AMR. Even within synthetic ECM constructs, specifically those with sites susceptible to cell-mediated degradation, pericellular mechanical properties are unknown unless measured directly, as has been recently noted[47]. Our method is generalizable to many tissue engineering systems because it is independent of ECM composition and cell type[19–21,24,48–50]. AMR is ultimately limited by the minimum detectable bead displacement as well as maximum bead density, which is not only restricted by pore structure and bead size, but can also influence ECM properties with excessive loading. There is a growing body of correlations between bulk ECM stiffness and cell phenotype in tissue models including progenitor cell differentiation[51], regulation of cell colony size[52], and signaling pathways that regulate tumor growth[53]. Cells in these experiments are seeded within a set of ECMs, each with unique but homogenous bulk stiffness, with shear moduli spanning 30 to ~1000 Pa. If we estimate shear moduli values from our observed α (under assumption of a material continuum and using the Generalized Stokes-Einstein Relation [32]), which inherently introduces error), then remarkably this same range was observed by AMR around single cells in our study. This begs the question: which stiffness value is important? We speculate that no single value of stiffness guides cells, rather it is the evolution and distribution of stiffness that is important.

Collagen is a fibrous extracellular matrix (ECM) protein that has been widely used to study cell-ECM interactions. Stiffness of ECM has been shown to instruct cells, which can in turn modify their ECM, as has been shown for cancer and regenerative medicine. Here we measure the stiffness of the collagen microenvironment surrounding cells and quantitatively observe the dependence of pericellular stiffness on MMP activity and cytoskeletal contractility. Competent cell-mediated stiffening results in a wildly heterogeneous micromechanical topography, with values spanning orders of magnitude around a single cell. We speculate studies must consider this notable heterogeneity that can be generated by cells when testing theories regarding the role of ECM mechanics in health and disease.