Improving Factor Score Estimation Through the Use of Observed Background Characteristics

Abstract

A challenge facing nearly all studies in the psychological sciences is how to best combine multiple items into a valid and reliable score to be used in subsequent modelling. The most ubiquitous method is to compute a mean of items, but more contemporary approaches use various forms of latent score estimation. Regardless of approach, outside of large-scale testing applications, scoring models rarely include background characteristics to improve score quality. The current paper used a Monte Carlo simulation design to study score quality for different psychometric models that did and did not include covariates across levels of sample size, number of items, and degree of measurement invariance. The inclusion of covariates improved score quality for nearly all design factors, and in no case did the covariates degrade score quality relative to not considering the influences at all. Results suggest that the inclusion of observed covariates can improve factor score estimation.

Measurement is arguably the single most important component of any empirical research endeavor and is a critical component in establishing construct validity (e.g., Shadish, Cook & Campbell, 2002). Thorndike (1918) famously wrote “Whatever exists at all, exists in some amount. To know it thoroughly involves knowing its quantity as well as its quality” (page 16). Later, Stevens (1946) proposed what might remain the most concise definition of measurement to date: "the assignment of numerals to objects or events according to rules" (page 677). What is most vexing about measurement in psychology and many allied fields, however, is that many of the constructs of critical interest are not directly observable. The difficulty is that we must infer the existence of what we did not directly observe as a principled function of what we did (Spearman, 1904). The field of psychometrics has embraced this challenge for more than a century, and we continue to make advances likely not even imagined by Thorndike and Stevens so long ago.

Contemporary psychometrics is dominated by two broad modeling approaches, item response theory (IRT; e.g., Thissen & Wainer, 2001) and factor analysis (FA, which may be further subdivided into exploratory and confirmatory; e.g., Cudeck & MacCallum, 2007). As is widely known, there are many points of similarity between these two approaches (see, e.g., Reise, Widaman, & Pugh, 1993; Takane & de Leeuw, 1987; Wirth & Edwards, 2007), making it increasingly difficult to differentiate what “is” or “is not” an IRT or an FA model. Both are rooted in the notion that the existence of one or more unobserved latent factors can be inferred through the associations that exist among a set of observed items. For instance, item responses to questions about sadness, hopelessness, guilt, and social withdrawal are inter-related to the extent that they all reflect latent depression.

There are three closely related uses of IRT and FA models in applied social and behavioral science research. First, IRT and FA models are used to better understand the psychometric structure underlying a set of items. For example, we might want to identify the optimal number of latent factors needed to best reproduce the characteristics of an observed sample of respondents to a given set of items. Second, IRT or FA procedures are used to construct tests that meet some targeted criterion in terms of reliability, validity, or test length (e.g., Thissen & Wainer, 2001). In a typical application, IRT or FA models are fitted to a large pool of test items, and a subset of items are eliminated or retained following some a priori criteria (e.g., based on simple structure, item discrimination, item communality, etc.). The third and often most ubiquitous goal relies directly on the first two and involves using the final IRT or FA model structure to obtain maximally valid and reliable scale scores to be used in subsequent statistical or graphical analysis. Such scores are sometimes referred to as factor score estimates, or more simply factor scores (e.g., Estabrook & Neale, 2013; Grice, 2001-a; Thissen & Wainer, 2001). Here we focus specifically on the third goal of scoring. In particular, because estimated scores are by definition imperfect, we wish to obtain the most accurate scores for a sample of individuals who differ on important between-person background characteristics such as gender, diagnosis, or age.

Given the imperfection of factor scores, some methodologists have argued that they should be avoided entirely, for instance by utilizing a structural equation model to directly model the relations between latent factors (Bollen, 1989, pp.305-306). Although we are highly sympathetic to this perspective (and even teach it in our classes), there remain a number of important applications in which factor score estimation is either beneficial or even necessary. For example, given a large number of repeated measures (e.g., annual assessments spanning three decades) it may be intractable to specify latent factors at each time point in a single large model, making factor scores an attractive alternative (e.g., Curran, McGinley, Bauer, Hussong, Burns, Chassin, Sher, & Zucker, 2014). Further, the simultaneous estimation of a structural and measurement model allows for the possibility of measurement being affected by misspecification of the structural model (Kumar & Dillon, 1987) and it might be useful for researchers to "quarantine" misspecification by estimating a factor score independent of structural relationships (Hoshino & Bentler, 2013). Factor scores may also be used not as independent or dependent variables in a standard structural model, but as ancillary variables to control for bias in subsequent analyses such as in propensity score analysis (Raykov, 2012; Rodriguez de Gil et al., 2015). Finally, factor scores are also extremely useful for integrative data analysis (IDA; Curran & Hussong, 2009) in which data are pooled across multiple independent studies that each measure the same underlying constructs in different ways (e.g., Curran et al. 2014; Rose, Dierker, Hedeker & Mermelstein, 2013; Witkiewitz, Hallgren, O’Sickey, Roos & Maisto, 2016). Taken together, there remain many widely used applications in which factor score estimation is highly relevant and in need of ongoing study and refinement.

An area of research in particular need of expansion is the importance of incorporating information about exogenous background variables, such as gender or age, when generating factor score estimates. The rather large literature on score estimation has primarily focused on the relative strengths and weaknesses of scoring approaches motivated by different traditions or goals. For example, the classical test theory model gives rise to sum, mean, or proportion score composites (e.g., Lord & Novick, 1968; Novick, 1966); see DeVellis (2006) for a review. The factor analytic tradition gives rise to a variety of estimation methods that vary primarily as a function of the target minimization or maximization criterion (e.g., Alwin, 1973; Bartlett, 1937; Harman, 1976; McDonald, 1981; Thurstone, 1935, 1947; Tucker, 1971); see Grice (2001-a) for a review. Finally, different scoring procedures have been developed within the IRT approach, including expected a posteriori (EAP) and modal a posteriori (MAP) scores (Bock & Aitken, 1981; Bock & Mislevy, 1982); see Thissen and Wainer (2001) for a review. Despite the different theoretical perspectives and practical goals underlying these different scoring methods, the scores they produce tend to be quite highly correlated (e.g., Cappelleri, Lundy & Hays, 2014; Flora, Curran, Hussong & Edwards, 2008; Fava & Velicer, 1992; Grice, 2001-b; Velicer, 1977). The vast majority of existing work on factor score estimation, however, has not considered the potential importance of including information on background characteristics.¹ Instead, it is assumed that the same scoring algorithm applies for all individuals, boys and girls, alcoholic and non-alcoholic, young and old, or any other individual difference characteristic.

Momentarily setting scoring aside, an equally large literature exists on evaluating whether background characteristics affect the measurement model itself (e.g., Kim & Yoon, 2011; Raju, Laffitte, & Byrne, 2002; Reise et al., 1993). We can distinguish between two kinds of effects. First, background characteristics may influence the distribution of a latent factor, for instance, impacting its mean and/or variance. Second, background characteristics may alter the process by which differences on the latent factor produce differences in item responses, as represented by the item parameters (e.g., intercepts or factor loadings in an FA, or difficulty and discrimination parameters in an IRT model). Within the IRT tradition, these two kinds of effects are commonly referred to, respectively, as impact and differential item functioning (DIF; e.g., Holland & Wainer, 1993; Mellenbergh, 1989; Thissen, Steinberg, & Wainer, 1988; 1993), whereas within the FA tradition, the equivalence of item parameters is referred to as measurement invariance (MI; e.g., Cheung & Rensvold, 1999; Meredith, 1964; 1993; Millsap & Everson, 2993; Millsap & Meredith, 2007; Millsap & Yun-Tein, 2004). Much research has been conducted to identify the best models, tests, and procedures for evaluating DIF and MI (e.g., Chalmers, Counsell & Flora, 2016; Holland & Wainer, 2012; Thissen et al., 1988), yet comparatively little work has directly addressed the question of how best to incorporate impact and DIF when generating factor scores in typical research applications within the social and behavioral sciences.

We are thus in a curious situation in which a great deal of careful research has been conducted on the topics of scoring and of measurement invariance, but with little consideration of their intersection. To better understand these issues, our goal here is to present a systematic empirical examination of the psychometric properties of factor score estimates obtained with and without the inclusion of information on background characteristics. We make use of the moderated nonlinear factor analysis (MNLFA) model, which generalizes other commonly used psychometric models to allow for impact and DIF as a function of multiple nominal and continuous background characteristics (Bauer, in press; Bauer & Hussong, 2009; Curran et al., 2014). Using the MNLFA model, we conduct a comprehensive computer simulation study in which we specify varying levels of impact and DIF that we believe to be reflective of applied psychological research. We systematically vary sample size, number of items, magnitude of measurement invariance, and whether/how background characteristics are included in the scoring model, and we then compare the estimated factor scores to the underlying true scores.

Our design is based upon the following hypotheses. First, drawing on both quantitative theory and prior empirical findings, we expect that score recovery will improve with greater available information, particularly in terms of larger item sets and larger sample sizes. Second, we expect that score recovery will improve when impact and DIF which exists in the population is also included in the scoring model. Third, we expect that score recovery will improve when background characteristics have stronger effects on the conditional mean of the latent factor (i.e., impact) thus leading to greater factor determinacy. Finally, we expect interactive effects such that optimal score recovery will be obtained with large item sets, large sample size, and small impact and DIF, and the weakest score recovery will occur when impact and DIF exist but are omitted from the scoring model. The motivating goal of our study is to systematically test these hypothesis to better understand the psychometric properties of factor scores in a variety of conditions commonly encountered in behavioral science research.

Methods

Model Definition

We generated data to be consistent with a one factor, multiple indicator, moderated nonlinear factor analysis (MNLFA; Bauer, in press; Bauer & Hussong, 2009; Curran et al., 2014). The MNLFA is a general framework for estimating a broad class of linear and nonlinear factor models that allows for the moderation of multiple model parameters as a function of multiple exogenous background variables. This approach is similar to the location-scale model for mixed-effects modeling (e.g., Hedeker, Mermelstein, & Demirtas, 2012), but the MNLFA is generalized to the full structural equation model. Importantly, the moderating effects allow for complex patterns of impact and DIF in ways that are not possible using traditional two-group models or multiple-indicator multiple-cause (MIMIC) models (Bauer, in press). The MNLFA can also be extended to multiple factors (Bauer et al., 2013) as well as to a mixture of linear or nonlinear link functions (Bauer & Hussong 2009). Here we studied a specific form of the MNLFA defined as a single latent factor underlying a set of binary items and three exogenous background variables with varying levels of impact and DIF. We focus our model definition on the specific conditions under study and refer the reader to Bauer (in press), Bauer and Hussong (2009) and Curran et al. (2014) for additional details about the general form of the MNLFA and its relations to other commonly used psychometric models.

Measurement model

We defined a single latent factor η_j for j = 1,2,…,J individuals assessed on i = 1,2,…,I binary items denoted y_ij. Each binary item y_ij follows a Bernoulli distribution with probability μ_ij defined by the underlying factor model as

$$\ln \left(\frac{{\mu }_{\mathit{ij}}}{1-{\mu }_{\mathit{ij}}}\right)={\nu }_{\mathit{ij}}+{\lambda }_{\mathit{ij}}{\eta }_j$$ (1)

where ν_ij and λ_ij represent the intercept and factor loading for item i and person j and η_j~(α_j,ψ_j).

Background characteristics

The MNLFA framework allows for a subset of model parameters to vary as a function of individual characteristics. To empirically evaluate the improvement in score accuracy when incorporating background characteristics, we drew upon recent IDA applications to inform data generation for three exogenous variables, as IDA is one of the few research contexts within which multiple background variables have been considered simultaneously (although all of our results generalize to non-IDA applications as well). The first covariate was a binary variable denoted study meant to represent an identifier for data that were obtained from one of two independent studies; this was effect coded as −1 and +1 with equal proportions of subjects within each group. Gender was drawn from a Bernoulli distribution with a mean of .35 for study one and .65 for study two. Age was drawn from a binomial distribution with seven trials and a probability of .70 for study one and from a binomial distribution with six trials and a probability of .50 in study two, with constants added to result in integer values for years of age from 10 to 17 in study one and from 9 to 15 in study two. To facilitate model specification and interpretation, we then effect coded gender as −1 and +1 and rescaled age to range between −4 and +4 with a mid-point of zero. The exogenous predictors thus had non-zero covariances with one another in the pooled aggregate sample: the correlation between gender and study was .30, between age and study was −.51, and between gender and age was −.15.

Parameter moderation

To produce impact, we defined specific moderating relations between the three covariates and the mean and variance of the latent factor. Drawing on the notation of Bauer (in press), this is given as:

$${\alpha }_j={\alpha }_0+{\gamma }_1{\mathrm{age}}_j+{\gamma }_2{\mathrm{study}}_j+{\gamma }_3{\mathrm{age}}_j\times {\mathrm{study}}_i$$ (2)

and

$${\psi }_j={\psi }_0\text{exp}\left({\beta }_1{\mathrm{age}}_j+{\beta }_2{\mathrm{gender}}_j+{\beta }_3{\mathrm{study}}_j\right)$$ (3)

respectively. We selected these terms as reflective of potential real-world applications and to introduce deterministic shifts in the factor mean and variance as a function of the observed covariates. The intercept terms (i.e., α₀ and ψ₀) reflect the factor mean and variance when all predictors equal zero, and the coefficients reflect the degree to which the mean and variance are shifted by changes in the values of the covariates. In the presence of covariates, the model-implied latent mean and variance thus vary as a function of the values of the covariates unique to each individual j (e.g., α_j and ψ_j). In the absence of covariates (as would occur in single-group CFA or IRT models) α_j = α₀ and ψ_j = ψ₀, reflecting that the latent mean and variance are constant across all individuals.

Covariates can also moderate item-level parameters to produce DIF. For the current study, the item intercept and item loading were defined as

$${\nu }_{\mathit{ij}}={\nu }_{0\mathit{ij}}+{\kappa }_{1i}{\mathrm{age}}_j+{\kappa }_{2i}{\mathit{gender}}_j+{\kappa }_{3j}{\mathrm{study}}_j$$ (4)

and

$${\lambda }_{\mathit{ij}}={\lambda }_{0\mathit{ij}}+{\omega }_{1i}{\mathrm{age}}_j+{\omega }_{2i}{\mathit{gender}}_j+{\omega }_{3j}{\mathrm{study}}_j$$ (5)

respectively. As with the factor mean and variance, we selected these terms as reflective of potential real-world IDA applications (that again directly generalize to non-IDA applications). As before, these equations introduce systematic shifts in the values of the item-specific intercepts and factor loadings (or slopes) as a function of the unique combination of the three covariates for a given individual.

Experimental Design Factors

Our simulation was structured around five design factors that were systematically manipulated during data generation and model fitting. These were sample size (3 levels); number of items (3 levels); magnitude of impact (3 levels); magnitude of DIF (2 levels); and proportion of items with DIF (2 levels). The full factorial design included 108 unique cells, within each of which we generated 500 independent replications.

Sample Size

We studied three total sample sizes of 500, 1000, and 2000, each of which was split evenly between the two “studies”. We chose these values to be consistent with a typical IDA application (e.g., Hussong et al., 2008; Rose et al., 2013; Witkiewitz et al., 2016).

Number of items

We studied three item set sizes: 6, 12, and 24. These values were selected to reflect a range of potential applications spanning small to large.

Magnitude of impact

We studied three levels of impact. Because impact reflects the joint contribution of the set of covariates on both the latent mean and variance, we defined impact in terms of the ratio of mean to variance moderation: small mean/large variance impact (SMLV), medium mean/medium variance impact (MMMV), and large mean/small variance impact (LMSV). The covariate effects on the mean of eta were selected to result in multiple r-squared values for eta equal to .05, .15, and .35, respectively. Due to the nonlinearity of the relation between the covariates and the conditional variance of eta (e.g., Equation 3), selection of covariate effects on the variance of eta was more complex. We chose values of covariate coefficients based on the interquartile range (IQR) of the conditional latent standard deviations such that the resulting IQR values were .20, .50, and .80, respectively. The final set of covariate coefficients are reflective of those that might realistically be encountered in practice and are presented in Table 1.

Table 1.

Population values of covariate moderation three impact conditions.

	Small Mean / Large Variance	Medium Mean / Medium Variance	Large Mean / Small Variance
Mean Model
Intercept	−0.01	−0.01	−0.02
Age	0.13	0.22	0.34
Gender	0	0	0
Study	0.21	0.37	0.56
Age × Study	−0.05	−0.09	−0.14
Variance Model
Intercept	0.58	0.71	0.65
Age	0.5	0.35	0.25
Gender	−1	−0.6	−0.05
Study	0.5	0.3	0.05

Magnitude of DIF

We studied two levels of DIF: small and large. Like impact, we defined DIF as the joint covariate moderation of both item loading and item intercept. For the subset of items that were not characterized by DIF (i.e., the invariant items), we selected population values for the item parameters (intercepts and loadings) that reflected those we obtained in our prior IDA applications (e.g., Curran et al., 2007; Curran et al., 2014; Hussong et al., 2008). These values resulted in endorsement rates ranging between approximately .20 to .40 and item communalities ranging between approximately .25 and .65.² For the remaining subset of items characterized by DIF (i.e., the non-invariant items), we selected values based on a generalization of the weighted area between curves index (wABC: Hansen, Cai, Stucky, Tucker, Shadel & Edelen, 2014; Edelen, Stucky, & Chandra, 2013). We selected specific values of the covariate coefficients to result in wABC values approximately equal to .15 for our small DIF condition and .30 for our large DIF condition (holding other covariates constant). We introduced both positive and negative covariate effects on the item parameters to produce DIF effects that were either consistent or inconsistent in their direction and to control endorsement rates. Specifically, age and gender exerted both positive and negative effects on item parameters whereas study only affected item parameters positively. All population item and DIF parameters are presented in Table 2.

Table 2.

Population values of item parameters under small and large DIF conditions.

Loading		Small DIF			Large DIF
	Baseline	Age	Gender	Study	Age	Gender	Study
Items 1, 7, 13, 19	1
Items 2, 8, 14, 20	1.3	0.05	−0.2	0.2	0.075	−0.3	0.3
Items 3, 9, 15, 21	1.6	−0.05	0.2	0.2	−0.075	0.3	0.3
Items 4, 10, 16, 22	1.9	0.05			0.075
Items 5, 11, 17, 23	2.2		−0.2	0.2		−0.3	0.3
Items 6, 12, 18, 24	2.5
Intercept		Small DIF			Large DIF
	Baseline	Age	Gender	Study	Age	Gender	Study
Items 1, 7, 13, 19	−0.5
Items 2, 8, 14, 20	−0.9	0.125	−0.5	0.5	0.25	−1	1
Items 3, 9, 15, 21	−1.3	−0.125	0.5	0.5	−0.25	1	1
Items 4, 10, 16, 22	−1.7	0.125			0.25
Items 5, 11, 17, 23	−2.1		−0.5	0.5		−1	1
Items 6, 12, 18, 24	−2.5

Proportion DIF

We studied two proportions of items with DIF: either one-third or two-thirds of each item set (6, 12, or 24 items) were characterized by DIF. This was again informed by our prior empirical findings using IDA in which it is common to identify a majority of items having some form of DIF (Curran et al., 2007; Curran et al., 2014; Hussong et al., 2008).

Data Generation

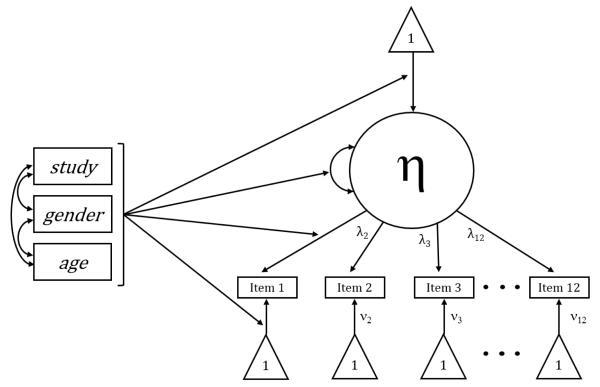
Data were generated using the SAS data system (SAS Institute, 2013) following four sequential steps. First, the covariates age and gender were randomly sampled within one of two equally-sized groups (representing study) as described above. Second, for each individual observation a true factor score was randomly sampled from a univariate normal distribution with conditional mean and variance defined by the unique set of covariates that were drawn for that observation (i.e., Equations 3 and 4 above). Third, a logit was computed as a function of the true factor score and the item-specific factor loading and intercept (i.e., Equation 1). Finally, binary responses were obtained via random draws from a Bernoulli distribution with the implied probability of endorsement (i.e., Equation 2). A conceptual path diagram for the population-generating model for 12 items is presented in Figure 1. This sequence resulted in 500 separate data files for each of 108 unique cells of the design, and it was to these data files that we fitted four distinct scoring models.

Figure 1.

Conceptual path diagram of MNLFA model with 12 items and impact and DIF effects from three background characteristics.

Scoring Models

Factor scores were estimated using four different model structures fitted to each individual replication across all cells of the design; that is, each of four models were fitted to the same sample data. The first scoring model was a simple mean of the set of items (i.e., proportion scores, indicating the proportion of items that were endorsed), and the remaining three models involved alternative specifications of the MNLFA that varied in how they incorporated information on the background covariates.

Model 1: Proportion Score

The first scoring model is not a psychometric model in the strict sense of the term, but is the simple unweighted mean of the set of items for each replication. Given the items were coded 0 and 1, this score represents the proportion of items endorsed as 1. This score was used to reflect how multiple-item scales are often scored in applied research settings.

Model 2: Unconditional MNLFA

The second scoring model was an unconditional one-factor nonlinear confirmatory factor analysis; this parameterization is analytically equivalent to a standard two parameter logistic (2PL) item response theory model (e.g., Takane & de Leeuw, 1987). More specifically, the set of binary items (6, 12, or 24) was used to define a single latent factor and no background characteristics were considered. Because both impact and DIF effects existed in the population generating model but are omitted in the scoring model, this unconditional model is misspecified in terms of both impact and DIF.

Model 3: Impact-only MNLFA

The third scoring model expands Model 2 with the inclusion of the properly specified influence of the three background characteristics on the latent mean and variance, but continues to omit DIF effects on the item-level parameters. This model is thus properly specified in terms of impact but is misspecified in terms of DIF.

Model 4: Impact+DIF MNLFA

The fourth and final scoring model expands Model 3 with the inclusion of the properly specified influence of the three background characteristics on the latent mean and variance, and on the item-level parameters. This model is thus properly specified in terms of both impact and DIF.

Model Estimation

The proportion scores were computed arithmetically and the three MNLFA models were estimated using maximum likelihood with numerical integration (adaptive Gaussian quadrature with 15 quadrature points) as programmed in Mplus (Version 7.2; Muthén & Muthén, 1998-2012). The latent factor was scaled to have a marginal mean of zero and marginal variance of one³, and each model used default start values and convergence criteria. Models that either failed to converge or converged and resulted in improper solutions were omitted (although these accounted for less than 1% of all estimated models; see results for further detail). For scoring models 2, 3, and 4, factor scores were estimated as expected a posteriori scores (EAPs), as originally described in Bock and Aitkin (1981).

Criterion Variables

Given our focus on score fidelity, we examined two criterion variables: score correlations and root mean squared error.⁴

Score correlations

We computed standard bivariate linear correlations between each of the four sets of score estimates and the underlying true factor scores for each replication; this can be thought of as a direct estimate of the reliability index (Estabrook & Neale, 2013). We also computed Fisher’s z-transformations of these correlations to be used as criterion measures in subsequent meta-models. Larger correlations reflect greater accuracy in estimated score recovery relative to the underlying true scores.

Root mean squared error (RMSE)

In addition to the correlations, for the three MNLFA-based score estimates we computed the associated RMSE. This was not computed for the proportion score as this is defined by a different scale than the underlying true score and the two cannot be directly compared. The RMSE was computed in the usual way as the root of the mean of the squared deviations between the estimated and true scores. Larger values of RMSE reflect greater variability in score estimates relative to the underlying true score.

Meta-Models

We estimated four separate general linear models (GLMs) using PROC GLM in SAS Version 9.4 (2013) to examine mean differences in the (z-transformed) correlations and the RMSE as a function of varying levels of our five design factors, one GLM for each obtained score. We estimated each model with all main effects (sample size, number of items, magnitude of impact, magnitude of DIF, and proportion of DIF) and all two-, three-, four-, and five-way interactions. Given the excessive power associated with the high number of replications (exceeding 50,000 replications for each outcome), we identified any design effect as potentially meaningful if the semi-partial eta-squared (denoted ${\eta }_{\mathit{sp}}^2$) term conservatively exceeded 1%. Finally, we used graphical representations to explicate meaningful effects identified in the GLMs, and we provide fully tabled results in the online appendix.

Results

Model Convergence

We fit a total of 162,000 MNLFA models across all replications and all conditions (three scoring models fit to 500 replications within each of 108 cells). We retained properly converged solutions for subsequent analyses, although the omitted models represented only a small fraction of the total estimated. More specifically, a total of 107 of the 162,000 models failed to converge; the rate of successful model convergence thus exceeded 99.99%. The models that failed to converge were most evident at the extreme conditions (e.g., small sample size, small numbers of items, large DIF, large proportion of items with DIF). The cell-specific non-convergence rates ranged from less than 1% to 3.8% with the highest rate representing 19 of 500 models failing to converge. Given these very low rates, we omitted non-converged solutions without replacement.

Meta-Models Fitted to Z-transformed Correlations

As expected, the four GLMs resulted in highly significant omnibus test statistics with associated eta-squared values ranging from .95 to .97 (see online Appendix A.1 for complete results). We next identified potentially meaningful specific effects as those that accounted for at least 1% of the variance in the criterion as measured by ${\eta }_{\mathit{sp}}^2$ as described above. To begin, none of the main effects of sample size (500 vs. 1000 vs. 2000) nor any interaction term involving sample size even approached the 1% effect size criterion across all models and all outcomes, indicating that the mean correlations did not vary as a function of sample size. We will thus focus the remainder of our discussion on results from the smallest sample size of 500. This greatly reduces the number of cells to consider and there is no loss of generality given that the findings are identical across the three sample sizes.⁵

Correlation between the proportion score and the true score

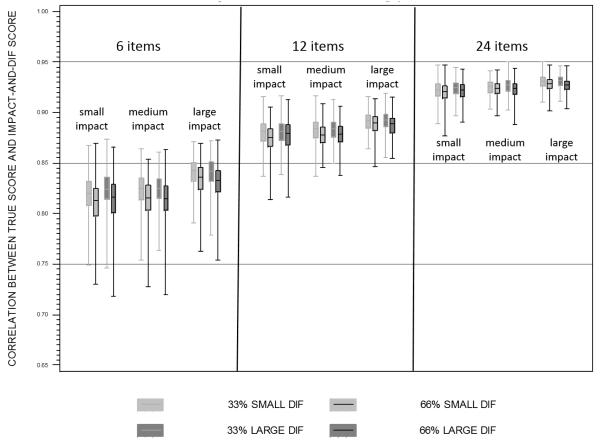
We began by examining the correlations between the true scores and the scores obtained by computing a simple proportion of the set of endorsed binary items. Average correlations between the proportion scores and the underlying true score ranged from a minimum of .75 to a maximum of .90 with a median of .84 across all 36 cells (recall we are focusing only on N=500, although these values are virtually identical for N=1000 and N=2000; see online Appendix A.2 for complete results). Two design factors exceeded the 1% effect size criterion in the GLM: the number of items (${\eta }_{\mathit{sp}}^2=.83$) and the magnitude of impact (${\eta }_{\mathit{sp}}^2=.10$). Table 3 presents the cell-specific mean correlations across each condition, and this reflects that the magnitude of the correlations increased with increasing number of items and increased with increasing impact (where “increasing impact” reflects higher mean-to-variance covariate moderating effects). We present these effects in boxplots in Figure 2.

Table 3.

Correlations between true and estimated scores across all scoring models and design factors at N=500.

6 Items	Proportion Score		Unconditional Score		Impact-Only Score		Impact-and-DIF Score
Small Mean/Large Variance	Mean	SD	Mean	SD	Mean	SD	Mean	SD
33% Small DIF	0.758	0.020	0.759	0.019	0.821	0.018	0.820	0.018
66% Small DIF	0.756	0.019	0.756	0.019	0.808	0.021	0.810	0.023
33% Large DIF	0.759	0.019	0.760	0.019	0.820	0.019	0.825	0.018
66% Large DIF	0.751	0.019	0.746	0.020	0.770	0.027	0.814	0.022
Medium Mean/Medium Variance	Mean	SD	Mean	SD	Mean	SD	Mean	SD
33% Small DIF	0.785	0.017	0.791	0.016	0.824	0.016	0.823	0.017
66% Small DIF	0.786	0.016	0.792	0.016	0.811	0.017	0.814	0.019
33% Large DIF	0.784	0.016	0.790	0.016	0.819	0.017	0.824	0.016
66% Large DIF	0.782	0.016	0.783	0.017	0.769	0.024	0.814	0.020
Large Mean/Small Variance	Mean	SD	Mean	SD	Mean	SD	Mean	SD
33% Small DIF	0.789	0.015	0.799	0.015	0.841	0.013	0.841	0.014
66% Small DIF	0.793	0.015	0.802	0.015	0.831	0.015	0.835	0.016
33% Large DIF	0.790	0.016	0.800	0.016	0.835	0.015	0.841	0.014
66% Large DIF	0.791	0.015	0.797	0.016	0.790	0.022	0.831	0.016
12 Items	Proportion Score		Unconditional Score		Impact-Only Score		Impact-and-DIF Score
Small Mean/Large Variance	Mean	SD	Mean	SD	Mean	SD	Mean	SD
33% Small DIF	0.826	0.016	0.835	0.015	0.879	0.012	0.880	0.013
66% Small DIF	0.820	0.017	0.829	0.015	0.868	0.014	0.875	0.014
33% Large DIF	0.824	0.017	0.830	0.016	0.871	0.014	0.881	0.013
66% Large DIF	0.812	0.017	0.815	0.017	0.837	0.018	0.877	0.015
Medium Mean/Medium Variance	Mean	SD	Mean	SD	Mean	SD	Mean	SD
33% Small DIF	0.852	0.013	0.864	0.012	0.882	0.011	0.883	0.012
66% Small DIF	0.847	0.012	0.859	0.011	0.871	0.011	0.878	0.011
33% Large DIF	0.852	0.012	0.863	0.011	0.874	0.012	0.883	0.011
66% Large DIF	0.840	0.012	0.849	0.012	0.839	0.016	0.878	0.011
Large Mean/Small Variance	Mean	SD	Mean	SD	Mean	SD	Mean	SD
33% Small DIF	0.855	0.011	0.872	0.010	0.890	0.010	0.891	0.010
66% Small DIF	0.854	0.010	0.871	0.010	0.882	0.010	0.889	0.010
33% Large DIF	0.858	0.010	0.874	0.010	0.883	0.010	0.892	0.010
66% Large DIF	0.850	0.010	0.863	0.010	0.853	0.013	0.888	0.010
24 Items	Proportion Score		Unconditional Score		Impact-Only Score		Impact-and-DIF Score
Small Mean/Large Variance	Mean	SD	Mean	SD	Mean	SD	Mean	SD
33% Small DIF	0.866	0.014	0.891	0.012	0.920	0.009	0.922	0.009
66% Small DIF	0.861	0.015	0.885	0.012	0.912	0.009	0.920	0.009
33% Large DIF	0.866	0.014	0.887	0.012	0.914	0.009	0.924	0.008
66% Large DIF	0.849	0.013	0.866	0.012	0.882	0.013	0.922	0.009
Medium Mean/Medium Variance	Mean	SD	Mean	SD	Mean	SD	Mean	SD
33% Small DIF	0.889	0.010	0.913	0.008	0.923	0.007	0.925	0.007
66% Small DIF	0.886	0.009	0.909	0.008	0.915	0.007	0.924	0.007
33% Large DIF	0.890	0.010	0.912	0.008	0.917	0.008	0.927	0.007
66% Large DIF	0.875	0.010	0.892	0.009	0.886	0.011	0.924	0.008
Large Mean/Small Variance	Mean	SD	Mean	SD	Mean	SD	Mean	SD
33% Small DIF	0.894	0.008	0.922	0.007	0.929	0.006	0.931	0.006
66% Small DIF	0.890	0.008	0.917	0.007	0.920	0.007	0.928	0.007
33% Large DIF	0.896	0.008	0.921	0.007	0.922	0.007	0.931	0.006
66% Large DIF	0.883	0.008	0.904	0.008	0.893	0.009	0.927	0.007

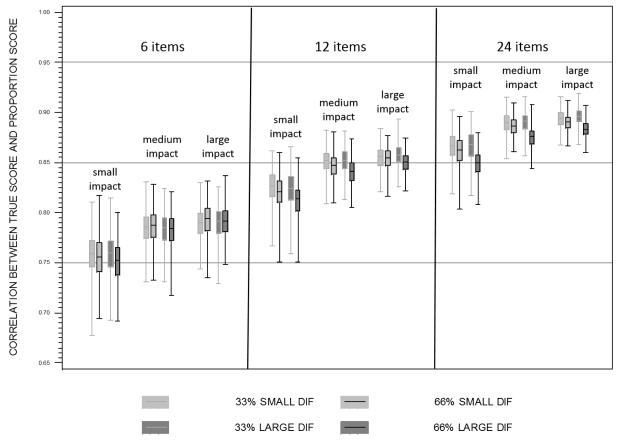
Figure 2.

Distributions of correlations between true scores and proportion scores across all design factors at N=500.

Pooling over all other design factors, the mean correlation between the proportion score and true score was .78 (sd=.023) for six items, .84 (sd =.020) for 12 items, and .88 (sd=.018) for 24 items. To better explicate the effect of impact, we pooled over the proportion of items with DIF and the magnitude of DIF within just the 12-item condition: the mean correlation for small mean/large variance condition was .82 (SD = .018), for medium mean/medium variance condition was .85 (SD = .013), and for large mean/small variance condition was .85 (SD = .011). Nearly identical patterns of findings held for 6 and 24 items (as is further reflected in the lack of any higher-order interactions in the GLMs). Consistent with the small effect size, although the magnitude of the correlations increased with increasing mean-to-variance impact effects, these differences were small in magnitude.

In sum, the mean correlation between the proportion scores and the true scores ranged from .75 to .90, and the magnitude of the correlations substantially increased with increasing number of items and modestly increased with larger mean-to-variance impact.

Correlation between the unconditional MNLFA score and the true score

We next examined the correlations between the true scores and the factor score estimates obtained from an unconditional MNLFA model that improperly excluded all effects associated with the three background characteristics (i.e., a standard 2PL IRT model). At a sample size of 500, the average correlations ranged from .75 to .92 with a median of .86. The pattern of GLM results were quite similar to those found for the proportion scores. Namely, two design factors exceeded the 1% effect size criterion: the number of items (${\eta }_{\mathit{sp}}^2=.84$) and the magnitude of impact (${\eta }_{\mathit{sp}}^2=.10$). Examination of cell-specific means (see Table 3) reflects that the magnitude of the correlations increased with increasing number of items and increased with increasing magnitude of mean-to-variance impact; the boxplots are presented in Figure 3.

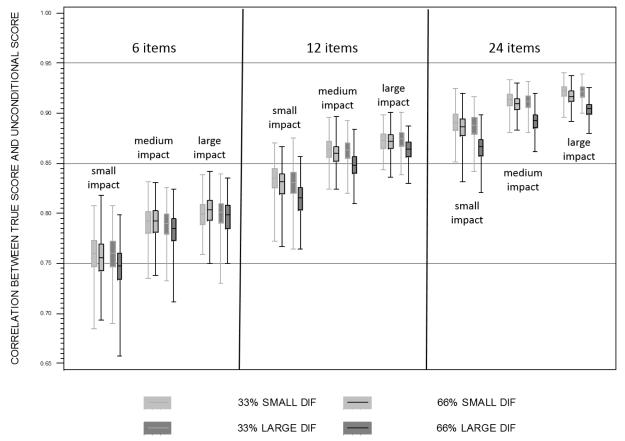
Figure 3.

Distributions of correlations between true scores and unconditional scores across all design factors at N=500.

Pooling over all of the design factors within N=500, the average correlation between the unconditional factor score and the true scores was .78 (sd=.026) for six items, .85 (sd=.023) for 12 items, and .90 (sd=.019) for 24 items. As before, the magnitude of the correlations increased as a function of increasing magnitude of mean-to-variance impact. For example, pooling over magnitude of DIF and proportion of items with DIF within the 12-item condition, the average correlation was .83 (sd=.018) for low impact, .86 (sd=.013) for medium impact, and .87 (sd=.011) for high impact. These effects closely reflect those found with the proportion score, but the modest effect of impact is somewhat more pronounced for the unconditional factor score estimates.

In sum, the correlations between the (impact and DIF misspecified) unconditional factor scores and the true scores ranged from .75 and .92, and the magnitude of the correlations substantially increased with increasing number of items and modestly increased with increasing magnitude of mean-to-variance impact.

Correlation between the impact-only factor score and the true score

We next examined the correlations between the true scores and the estimated scores from an MNLFA model that included the three background characteristics but limited these effects to the mean and variance of the latent factor. These scoring models are thus partially misspecified in that within the scoring model impact effects are properly specified but DIF effects are not (indeed, DIF effects are wholly omitted). The average correlations ranged from .77 to .93 with a median of .87. As expected, more complex results were identified in the GLMs relative to the prior two scoring models; cell means are presented in Table 3 and corresponding boxplots in Figure 4. Similar to the prior models, there was an effect of the number of items (${\eta }_{\mathit{sp}}^2=.80$) and magnitude of impact (${\eta }_{\mathit{sp}}^2=.02$), but unlike the prior models there were additional effects associated with the magnitude of DIF (${\eta }_{\mathit{sp}}^2=.05$), the proportion of items with DIF (${\eta }_{\mathit{sp}}^2=.07$), and their interaction (${\eta }_{\mathit{sp}}^2=.02$).

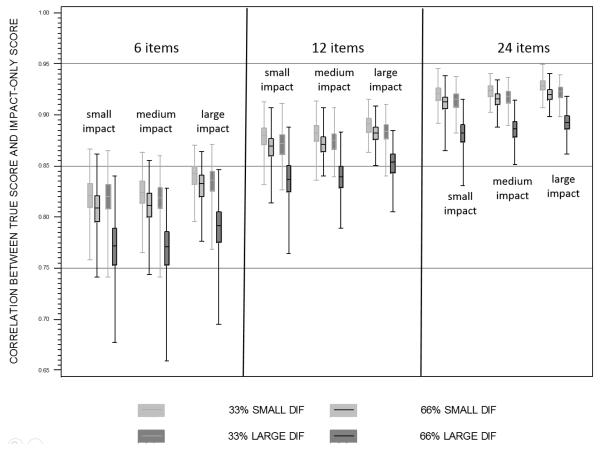
Figure 4.

Distributions of correlations between true scores and impact-only scores across all design factors at N=500.

As before, the magnitude of the correlations between the estimated and true scores increased with increasing numbers of items: pooling over all other design factors, the average correlation was .81 (sd=.030) for six items, .87 (sd=.021) for 12 items, and .91 (sd=.018) for 24 items. However, these correlations were differentially affected by other design factors. Also as before, increasing mean-to-variance impact was associated with increasing correlation magnitude. However, as was not found previously, increasing levels of DIF (small vs. large) were associated with decreasing mean correlations, and this effect was particularly salient for larger proportions of items with DIF (one-third versus two-thirds). For example, for six items at the smallest level of mean-to-variance impact, the average correlation was .82 (sd=.018) for small DIF/low proportion of items, .81 (sd=.021) for small DIF/ high proportion of items, .82 (sd=.019) for large DIF/low proportion of items, and .77 (sd=.027) for large DIF/high proportion of items. Similar patterns were found across all other design factors. As we describe in detail later, this conditional pattern of effects is due to the improper omission of DIF when DIF truly exists; thus the omission is logically more pronounced at higher levels of magnitude of DIF and when a larger number of items are characterized by DIF.

In sum, the mean correlation between the (DIF misspecified) impact-only MNLFA model scores and the underlying true scores ranged from .77 to .93. The magnitude of the correlations increased with increasing numbers of items, increased with increasing magnitude of mean-to-variance impact, and decreased with increasing magnitude of DIF, the latter effect being particularly salient when a higher proportion of items was characterized by DIF.

Correlation between the impact+DIF MNLFA score and the true score

Finally, we examined the correlations between the true scores and the estimated factor scores from an MNLFA that included both impact and DIF effects. These scores were thus obtained from a properly specified model in that all impact and DIF effects that existed in the population were estimated within the scoring model. The average correlations ranged from .81 to .93 with a median of .88. Two design factors exceeded the 1% effect size criterion in the GLM: the number of items (${\eta }_{\mathit{sp}}^2=.94$) and the magnitude of impact (${\eta }_{\mathit{sp}}^2=.01$); cell means are presented in Table 3 and the corresponding boxplots in Figure 5.

Figure 5.

Distributions of correlations between true scores and impact-and-DIF scores across all design factors at N=500.

Similar to the proportion score and unconditional MNLFA scoring model, the magnitude of the correlations markedly increased with increasing number of items and modestly increased with increasing mean-to-variance influence. For example, pooling across all other design factors, the average correlation was .82 (sd=.021) for six items, .88 (sd=.013) for 12 items, and .93 (sd= .008) for 24 items. As before, within item set, larger values of impact were associated with larger correlations, but this effect was small in magnitude. For example, for the 12-item condition the correlations between estimated and true scores varied by approximately .01 across all three levels of mean-to-variance impact.

In sum, the correlation between the (fully properly specified) impact+DIF MNLFA model and the true scores ranged from .81 and .93, and the magnitude of the correlations substantially increased with increasing number of items and only slightly increased with increasing magnitude of impact.

Comparing Estimated Scores Across Scoring Model

Our discussion up to this point has focused entirely on the effects of the design factors on score recovery within individual scoring models. However, we can also compare score recovery across scoring models. Such a comparison provides a direct examination of relative score recovery when holding all other design factors constant. We again focus our discussion on the smallest sample size condition of N=500 given the nearly identical pattern of results obtained at the two larger sample sizes.

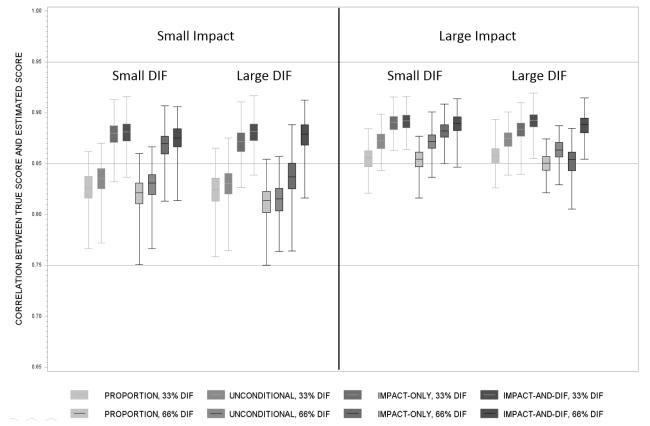
When considering just the smallest sample size of 500, our experimental design consists of 36 unique cells (three levels of number of items, three levels of impact, two levels of DIF, and two levels of proportion of items with DIF). Given that we fit four separate scoring models to the simulated data within each cell, we have a total of 144 mean bivariate correlations computed on the 500 cell-specific replications. Of these 144 correlations, the lowest mean correlation between the true and estimated scores was .75 for the proportion score in the condition defined by the smallest mean-to-variance impact, 6 items, and 66% of items defined by large DIF. The highest correlation between the true and estimated scores was .93 for the impact+DIF MNLFA score in the condition defined by the largest mean-to-variance impact, 24 items, and 33% of items defined by small DIF. These values imply overlapping variability between true and estimated scores ranging from 56% to 86% across the scoring models and experimental conditions. There are thus substantial differences in the ability of the four scoring models to recover the underlying true score as a function of variations in design characteristics. To better understand these differences, we conclude by focusing on all four scoring models within just 24 design cells: we consider four scoring methods, three levels of impact, and two levels of DIF holding sample size and number of items constant (500 and 12, respectively).

Comparing correlations obtained across various design features, several clear patterns can be seen (see Figure 6). First, although the proportion scores often correlate with the true scores in the mid-.70 to high-.80 range, these correlations are almost universally lower than any comparable score obtained using any form of the MNLFA model, even if the MNLFA model is substantially misspecified. Second, although the unconditional MNLFA almost always outperforms the proportion score model in terms of score recovery, this same model is itself almost always outperformed by the two MNLFA models that include exogenous covariate effects. However, this advantage of including covariates is partially mitigated under the condition in which the covariates are introduced into the MNLFA but their effects are restricted to just impact on the latent factor, particularly when the omitted DIF effects are large. In other words, if the covariates moderate DIF effects, and these moderating effects are improperly omitted, score quality is degraded. Finally, the fully specified impact+DIF MNLFA produced correlations in the mid-.80 and up to low-.90 range across nearly all experimental conditions, well in excess of other scoring model estimates based on the very same data.

Figure 6.

Distributions of correlations between true scores and scores generated by all four models under small and large mean impact in the 12-item condition.

In sum, although there are minor cell-to-cell variations in mean correlations, the overall pattern of findings suggests that optimal score recovery is obtained using the impact+DIF MNLFA model followed by the impact-only MNLFA, the unconditional MNLFA, and finally the unweighted proportion score.

Root mean-squared error (RMSE)

All of our discussion thus far has focused on score recovery as manifested in estimated-by-true score correlations. To examine absolute recovery of the true scores, we calculated the RMSE for the three variations of the MNLFA model. We did not compute this for the proportion score estimates because they do not retain the same scale as the underlying true scores. We fit meta-models to the RMSE for score estimates obtained from the unconditional model, the impact-only model, and the impact+DIF model just as we did for the (Fisher-z transformed) score correlations. These GLMs revealed precisely the same design effect influences for the RMSE values as were found for the score correlations. Further, examination of the RMSEs as a function of the design factors revealed the same trends as were identified with the correlations (although these were in the expected opposite direction; e.g., lower RMSE values reflect better score recovery). That is, whereas a higher number of items was associated with higher correlations, a higher number of items was associated with lower RMSEs, and so on. Given the complete overlap of effects for the RMSE as were found for the correlations, we do not present these results in detail; please see online appendix A.3 for a complete reporting of RMSE effects.

Discussion

Our motivating research question was whether the inclusion of background characteristics can improve the quality of factor score estimates. Our results indicate that the answer to this question is yes. We used computer simulation methodology to empirically compare four methods of factor score estimation and we compared each estimated score with the underlying true score. The four methods of score estimation were the traditional unweighted proportion score, and factor scores generated from an unconditional model excluding covariates, an MNLFA allowing only for impact, and an MNLFA allowing for both impact and DIF. We examined score quality in two ways. First, we calculated the correlation between each score estimate and the underlying true score; correlations of 1.0 indicate perfect recovery, and decreasing values reflected decrements in score quality. Second, we calculated the root mean squared error between each score estimate and the underlying true score; higher values of RMSE reflect lower accuracy. Because the pattern of results was identical for the correlations and the RMSE, we focus our discussion on the former.

Sample Size

We studied three levels of sample size: 500, 1000 and 2000. We found no evidence of any influence of sample size on the means of the correlations across any condition for any of the scoring models. Of course there was the expected reduction of variability of the score correlations at larger sample sizes, but the cell-specific means were unaffected by variations sample size. Because of this, we focused all of our attention on findings from the smallest sample size of 500.

Number of Items

We studied a single latent factor defined by three item set sizes: 6, 12, and 24. As expected, the strongest effects of all design factors were related to increasing number of items. We found marked improvements in score quality associated with increasing numbers of items regardless of scoring model. For example, we can consider the mean correlations obtained for different numbers of items while holding impact at medium mean/medium variance, DIF at small, proportion DIF at one-third, and sample size at 500. For the proportion score, the mean correlations for 6, 12, and 24 items were .79, .85, and .89, respectively. Similarly, for the fully specified DIF and impact MNLFA, the mean correlations for 6, 12 and 24 items were .82, .88, and .93, respectively. Similar patterns held for the other two scoring models as well.

The reason for improved score recovery with larger numbers of items primarily centers around factor indeterminacy (Guttman 1955; Schonemann, 1996; Wilson, 1928). Briefly, factor indeterminacy is an inherent component of nearly all latent factor models because the number of common and unique latent variables exceeds the number of observed indicator variables. As such, factor scores are not uniquely determined. However, it has been shown that the magnitude of indeterminacy varies as a function of the amount of available information, especially the number of observed items and the strength of the relations between the items and the factor. This is well known in EFA (e.g., Piaggio, 1933; McDonald & Mulaik, 1979) and Bollen (2002) explores this within the broader SEM (e.g., Equation 16). The larger the number of items, the lower the indeterminacy; the lower the indeterminacy, the higher recovery of the factor scores. This is precisely what we found here.

Magnitude of Impact

We studied three levels of impact defined as the joint contribution of the background characteristics on both the latent mean and variance: small, medium, and large ratio of mean-to-variance impact effects. There was consistent evidence that score quality increased with increasing levels of mean-to-variance impact, but the magnitude of this effect was more modest than the effect of increasing number of items. Specifically, the unique variability associated with magnitude of impact in the prediction of the (Fisher-z transformed) correlations ranged from a low of 1% (for the properly specified MNLFA) to a high of 11% (for the unconditional MNLFA). This compares to the unique variability associated with number of items that ranged from 80% to 94%. The modest effect size estimates from the GLM were further reflected in only slight improvements in the correlations between estimated and true scores. For example, holding constant the number of items at 12 and DIF, proportion of DIF and sample size at the same levels as were used just above, the mean correlation at small, medium and large impact for the unconditional MNLFA was .84, .86, and .87, respectively. Similar patterns of only modest increases in score recovery were evident across other design factors and other scoring models.

The reason for improved recovery associated with stronger covariate effects on the latent mean is due to greater determination of the latent factor as a function of the background characteristics. As we noted above, factor score recovery is improved under conditions of higher factor determinacy. Just as larger numbers of items improve determinacy, so does the lower residual variability of the latent factor in the presence of the explanatory predictors. This is analogous to the long-known finding that the inclusion of covariates in the general linear model reduces mean square error and increases statistical power and precision (e.g., Neter, Kutner, Nachtsheim & Wasserman, 1996, Section 25.1). Thus the inclusion of the background characteristics increases factor determinacy that in turn increases score recovery.

Magnitude of DIF and Proportion of Items with DIF

We studied two levels of magnitude of DIF defined as the joint contribution of the background characteristics on both the item loading and intercept (small and large) and two proportion of items with DIF (one-third and two-thirds). We discuss these two design factors jointly because these were found to exert interactive effects on score quality, but only for one method of scoring. For the proportion score, unconditional MNLFA, and fully specified MNLFA, neither magnitude of DIF, proportion of items with DIF, nor their interaction was meaningfully related to score quality. That is, the mean correlations between estimated scores and true scores were nearly equal for these three scoring models across all combinations of magnitude of DIF and proportion of items with DIF. But this did not hold for the impact-only MNLFA.

More specifically, for the impact-only model, there was a multiplicative interaction between magnitude of DIF and proportion of items with DIF in the prediction of the estimated and true factor correlations such that the larger magnitude of DIF was associated with lower score quality, and this was particularly pronounced with a larger proportion of total items that were characterized by DIF. The interesting aspect of this finding is that it was only evident in one scoring model: the impact-only MNLFA. The reason for this is clear. More specifically, the background characteristics were included in this scoring model but the DIF effects that truly existed in the population were not estimated in the scoring model. Thus the scoring model was properly specified in terms of impact but was substantially misspecified in terms of DIF. As is well known, when using full information estimators (as we did here), the inappropriate omission of parameters can commonly propagate bias throughout the entire system of equations (e.g., Bollen, 1996; Kumar & Dillon, 1987). Because the estimated effects of the covariates on the latent factor mean and variance will be biased due to the omitted effects of the same covariates on the item loadings and intercepts, these biased coefficients will in turn degrade score quality. This is precisely what occurred here.

However, there is a more interesting issue at hand compared to that of the predictable bias resulting from the omission of structural covariate effects. Although the interactive influences of magnitude of DIF and proportion of items with DIF were not evident in either of the scoring models that excluded the covariates entirely (i.e., the proportion score model and the unconditional MNLFA), the degraded scores obtained from the misspecified impact-only MNLFA still performed as well or better than the scores obtained from the models that omitted the influences of the covariates entirely. For example, holding sample size at 500, number of items at 24, magnitude of impact at small, the magnitude of DIF at large, and the proportion of items with DIF at large, the estimated true-score correlation for the proportion model was .85, for the unconditional MNLFA was .87, for the (misspecified) impact-only MNLFA was .88, and for the fully specified MNLFA was .92. These results reflect that scores are at least as good, and sometimes observably better, even when an incorrect scoring model is used that includes the covariates compared to a scoring model that does not include the covariates at all.

Relative Score Performance

It is also insightful to directly compare score recovery within design characteristics across each of the four scoring models. Several interesting patterns are clearly evident. First, with few exceptions, the unweighted proportion of endorsed items performed the worst of all other scoring models. With six items and small impact effects, the proportion scores and unconditional MNLFA performed equally (i.e., all correlations were within approximately .01). However, across all other conditions and scoring models the proportion score was inferior. This was fully expected given the nature of the population generating model that was defined by complex covariate effects and differential relations between items and the latent factor. However, this is further evidence that, when possible, the proportion (or sum or mean) score should be avoided in practice.

Second, although the unconditional MNLFA scores outperformed the proportion score across nearly all conditions, these same scores were inferior compared to both the misspecified impact-only MNLFA and the properly specified impact plus DIF MNLFA. Recall that the unconditional MNLFA is analytically equivalent to the standard 2PL item response theory model, an approach to scoring that continues to be widely used in practice. Across nearly every single cell of the design, the correlations were modestly or markedly lower in the unconditional MNLFA compared to the two other MNLFA parameterizations. This is clear evidence that the inclusion of background characteristics does result in improved score recovery, at least under the conditions that we studied here.

Finally, both versions of the MNLFA that included covariate effects produced superior score estimates relative to the two models that did not include the covariates at all. As expected, the partially misspecified impact-only MNLFA produced inferior scores to those of the properly specified impact and DIF MNLFA across all cells of the design. However, the improvements in score quality moving from the impact-only to the impact plus DIF covariate effects were surprisingly modest. In conditions in which there was more limited information (e.g., six items at the smallest magnitude of impact), the score correlations were virtually equal between the two conditional MNLFA models. However, even at the most highly determined conditions (e.g., 24 items at the largest magnitude of impact), the difference in score correlations was modest at best. Differences in correlations were often .01 or less and at no point exceeded a difference of .04. This is actually somewhat heartening news in that the largest improvement in score quality results from the inclusion of meaningful covariates in the scoring model, and the proper specification of these covariate effects is then of secondary importance.

Are the Improvements in Score Quality Due to the Inclusion of Covariates Meaningful?

It is clear from our results that the inclusion of background characteristics unambiguously improves the quality of the resulting factor score estimates. The improvement in score quality relative to scoring models that omit covariates is consistent across all of the design factors in varying degrees of magnitude. However, the inclusion of covariates led to increases in some correlations with the true scores by .01 or .02, many by .03 or .04, and a few by up to .06. A logical question is whether these improvements are meaningful, the answer to which is partly informed by thinking more closely about the true score correlations. We have focused nearly all of our discussion on the bivariate linear correlations between each estimated score and the underlying true score. As is widely known, these correlations primarily reflect the degree of monotonic rank ordering in a paired set of observations. Thus comparing a correlation of .82 between an estimated proportion score and the true score with a correlation of .84 between an estimated MNLFA score and the same true score primarily reflects similar ordering of observations in the score estimates. This is a fundamental characteristic of score recovery, but it also represents only one aspect of the scores.

Another important aspect is reflected in the accuracy of the score value for a given individual, and this is best represented by the RMSE. We did not present detailed results of the RMSE because the patterns of findings from the GLMs in terms of cell mean differences across the study design factors were identical to those found with the correlations. However, the cell means themselves reflect further information about score quality (see online Appendix A.3 for complete results). Just as one example, for N=500, 12 items, medium impact, large DIF, and one-third items with DIF, the unconditional, impact only, and impact plus DIF MNLFA score correlations were .85, .84, and .88, respectively. These differences are modest at best. However, the associated RMSE values are .53, .59, and .48, respectively. Because RMSE is a measure of distance (i.e., the root of the averaged squared distance between each estimated and true score), larger RMSE values reflect less accuracy. Here we see that although there is only a .04 difference in the true score correlations between the impact-only and the impact-plus-DIF MNLFA models, the associated RMSE is 23% larger for the former compared to the latter. As such, scores obtained from the fully parameterized MNLFA model are substantially more accurate with respect to distance than are those from the impact-only model. This additional metric of score recovery further highlights the clear improvement in score quality attributable to the inclusion of background characteristics.

Limitations and Future Directions

As with any computer simulation, there are a multitude of conditions that could have been included but were not. For example, we could have considered more sample sizes, more items sets, different parameter values, different endorsement rates, used ordinal items, used alternative MNLFA structures, used alternative methods of estimation, or induced missing data, among countless other factors. However, it is far less important to list the multitude of ways in which the simulation could have been different and more important to identify those specific factors that might serve to threaten the internal or external validity of the study.

With that in mind, the key limitation of this study is that we did not address the issue of model building. That is, we had oftentimes complex patterns of impact and DIF associated with the set of covariates and, when impact and DIF effects were included, these were always specified in accordance with the effects that existed in the population. The use of properly specified models of course did not hold across scoring models. The proportion score and unconditional MNLFA did not include covariates at all, and the impact-only MNLFA omitted all of the truly existing DIF effects. However, the mean and variance model were properly defined in the impact-only MNLFA and the impact plus DIF model was entirely properly specified. We of course did this with full intent. We wanted to first evaluate our ability to recover true factor scores when the scoring model corresponded to varying degrees to that of the population generating model. A very interesting yet separate question is the extent to which we could begin with a set of covariates and through some principled model building strategy approximate the population model. Importantly, this issue does not threaten the validity of our findings and inferences that we offer here.

Second, a logical next step is to consider how estimated scores perform when used in subsequent analyses. Rarely are factor scores estimated that are not intended to be used in some other form of model. They might be incorporated as predictors, criterions, mediators, moderators, for selection purposes, or fill a myriad of other roles. Statistical theory suggests that the performance of factor score estimates can be different depending on how the estimates were obtained and whether they take the role of predictor or criterion (e.g., Skrondal & Laake, 2001; Tucker, 1971). These differences could be even further exacerbated by the inclusion of covariates in the scoring model that might or might not be included in the subsequent predictive model. That is, omitting covariates from the scoring model risks generating bias when covariates and factors are used as joint predictors of some outcome (Mislevy, 1983; Skrondal & Laake, 2001). It will be important to carefully consider how factor score estimates from models including covariates perform when used in subsequent statistical models that might include the same covariates.

Conclusion

In conclusion, our motivating question was whether the inclusion of a set of correlated background characteristics using the moderated nonlinear factor analysis model could improve the quality of factor score estimates. Consistent with expectations, the inclusion of covariates improved score quality across nearly all factors under experimental study. In some cases the improvements were modest but in many others were substantial. In no case did the inclusion of covariates degrade score quality relative to not considering the influences at all. We conclude that if background characteristics are available and are believed to exert impact or DIF effects on the latent construct, these should be included in the subsequent scoring model. Further research is needed to better understand the complex process of model building and how the resulting score estimates perform when used in subsequent modeling applications. We are currently extending the results presented here to address this very question.